Building block properties govern granular hydrogel mechanics through contact deformations

Abstract

Granular hydrogels have been increasingly exploited in biomedical applications, including wound healing and cardiac repair. Despite their utility, design guidelines for engineering their macroscale properties remain limited, as we do not understand how the properties of granular hydrogels emerge from collective interactions of their microgel building blocks. In this work, we related building block features (stiffness and size) to the macroscale properties of granular hydrogels using contact mechanics. We investigated the mechanics of the microgel packings through dynamic oscillatory rheology. In addition, we modeled the system as a collection of two-body interactions and applied the Zwanzig and Mountain formula to calculate the plateau modulus and viscosity of the granular hydrogels. The calculations agreed with the dynamic mechanical measurements and described how microgel properties and contact deformations define the rheology of granular hydrogels. These results support a rational design framework for improved engineering of this fascinating class of materials.

Granular hydrogel mechanics arise from the properties of the constituent microscale building blocks.

INTRODUCTION

Granular hydrogels, a subclass of granular materials, are composed of jammed micron-scale hydrogel building blocks (here referred to as microgels) (1, 2). Because of their packed structure, granular hydrogels are viscoelastic on the macroscale while retaining micron-sized interstitial voids (3). Granular-scale microgels are distinct from colloidal-scale hydrogel particles, as the micron-sized constituents interact through discrete surface contact, creating voids on relevant length scales for cell migration and proliferation (4). External forces, such as shear, can disrupt the jammed state in granular hydrogels, allowing them to be used as embedding media and bioinks for three-dimensional (3D) printing or as injectable biomaterials (5–7). An emerging clinical application of granular hydrogels is direct extrusion into tissues to support endogenous tissue repair or regeneration, as cell infiltration and biomolecule delivery are facilitated in these macroporous environments (8–11). For these applications, function depends on the mechanical properties of the packing, such as stiffness and porosity, motivating the need to rationally engineer granular hydrogel scaffolds (4, 12–14).

The increasing use of granular hydrogels in biomedical research motivates an improved understanding of the origin of their mechanical properties. Specifically, there is a recognized need for a more complete understanding of how the emergent properties of jammed granular hydrogels arise from the properties of the microgel building blocks and how this knowledge can be translated into practical design rules. To date, the engineering of granular hydrogels has focused on the chemical nature, modularity, and assembly of the microgel building blocks (15–17). Interparticle cross-linking has been used to increase the shear moduli of granular hydrogels and make them more resistant to flow (14, 18, 19). The size and dispersity of charged dextran microgels controlled scaffold stiffness; this effect was related to surface charge, which varied with microgel size (20). The method of fabrication influenced the shape and cross-linking density of hyaluronic acid–based microgels, which resulted in variations in the mechanical response of the packings (21). While these studies acknowledge jamming as the underlying foundation of viscoelastic behavior, designing the macroscale rheology based on the stiffness and size of the microgels remains a challenge, restricting our ability to rationally engineer granular hydrogels for biomedical applications. To address this question, we proposed that a collective view of the physical contacts between the building blocks can describe the rheology of the jammed material, providing a framework to design granular hydrogels.

It has been generally accepted that interparticle interactions impart concentrated packings (such as granular materials, colloidal glasses, and emulsions) with macroscopic elasticity (22, 23). Within the physics community, there is a rich body of literature that discusses the emergence of an elastic response in packed systems across different scales (24, 25). At the colloidal scale, elasticity is often described as a function of an effective volume fraction of particles, which can change upon stimuli such as osmotic compression, temperature, and pH (26, 27). Bonnecaze and co-workers (28, 29) introduced predictive models of soft colloidal glasses, demonstrating that the macroscopic modulus can be calculated using the radial distribution function across a broad range of volume fractions. In contrast, thermal energy is insignificant in granular-scale packings, and stress is transmitted through particle contacts and force chains in the packing (30, 31). Behringer and colleagues (32) showed that the microscale forces in a granular packing of soft spheres can be connected to the macroscopic response using a mean-field approach. These foundational insights from the physics community provide a conceptual framework to understand the mechanics of jammed granular hydrogels. Nevertheless, it remains challenging to translate these findings into practical knowledge for the engineering and biomaterials communities. Specifically, designing the macroscopic behavior and function of granular hydrogels based on the properties of microgel building blocks has yet to be demonstrated.

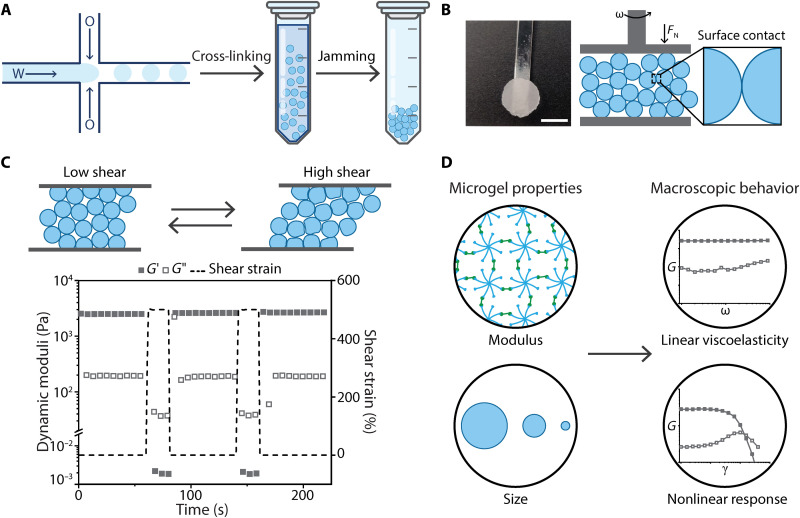
To advance our understanding of noncolloidal, granular hydrogels and extend their translational potential, we aimed to bridge concepts from the soft matter physics and the biomaterials fields. We present a systematic study on the effects of building block properties (size and elasticity) on the macroscale rheology of jammed granular hydrogels. We used thiol-ene chemistry and microfluidic templating to form covalently cross-linked and chemically inert microgels of defined elasticity and average microgel size (Fig. 1A). The designed microgels were assembled into granular hydrogels through centrifugal jamming (Fig. 1B). Granular hydrogels supported stress under small applied strain and demonstrated reversible shear thinning at high strain (Fig. 1C). A systematic investigation of the mechanical response of the packings measured via shear rheometry provided a detailed map of accessible properties of jammed granular hydrogels. We built upon the existing physical understanding of soft granular materials to introduce a simple design strategy based on microgel properties and contact mechanics to describe the linear and nonlinear rheology of granular hydrogels.

Fig. 1. Concentrated suspensions of microgel building blocks give rise to rigidity on the macroscale with shear-thinning and self-healing properties.

(A) Microgel building blocks formed via a microfluidic templating method, in which droplets of polymer solution [water-(W)-in-oil (O)] were collected, cross-linked, and subsequently jammed into granular hydrogels. (B) Macroscale hydrogels were produced owing to the microgel contacts in the jammed state. (C) The granular hydrogels [10 wt %, Ø = 55 μm microgels] exhibited rapid and reversible self-healing as shown via step-strain measurements with alternating intervals at low (γ = 0.5%) and high (γ = 500%) applied strain at constant angular frequency (ω = 10 rad s⁻¹). Closed and open symbols represent the storage moduli G′ and loss moduli G″, respectively. (D) The properties of the microgel building blocks controlled the linear and nonlinear mechanical response of the formed granular hydrogels.

We hypothesized that at volume fractions close to the jamming limit, where an interconnected 3D porous structure was present, deformation of the particle surfaces defined the macroscale response. Adapting concepts from molecular and colloidal physics, we developed a predictive framework that related building block size and elasticity to the linear and nonlinear rheology of the respective granular hydrogels (Fig. 1D). We applied contact mechanics principles and the Zwanzig and Mountain (ZM) formula, treating the granular packings as the summation of pairwise interactions. We found that the extent of deformation at the microgel contact was influenced by the elasticity of the internal polymer network of the microgels, and these changes in deformability and surface contacts dictated the linear viscoelastic (LVE) properties and viscosity of the granular hydrogels in a predictable manner. This work addresses the need for rational granular hydrogel design guidelines and will facilitate the engineering of complex biomaterials, including as inks for 3D printing, through controlled fabrication and interactions of constituent microgels.

RESULTS

Microfluidic templating produces microgels with uniform size and tunable stiffness

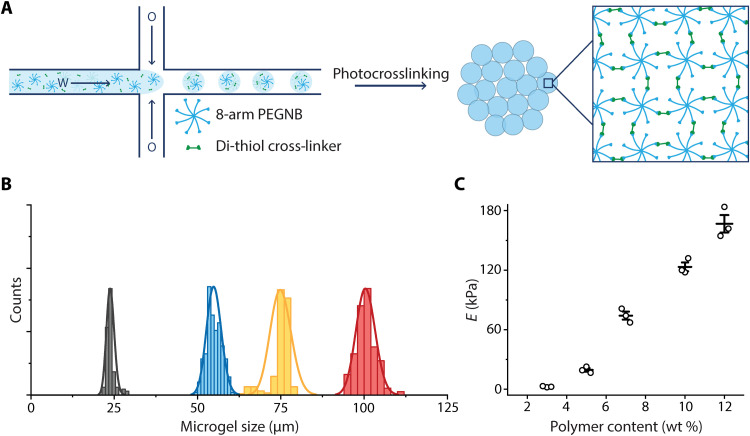
To investigate how macroscale rheology emerges from and is controlled by the features of the constituent microgels, we used droplet-based microfluidic templating to produce hydrogel microparticles (microgels) of defined size and modulus (33, 34). Droplet, and thus microgel size, was controlled through the variation of the volumetric flow rates of incoming water and oil streams (Fig. 2A). The microfluidic approach provides for improved control over droplet size and stiffness as compared with batch emulsification techniques. Microgels were formed from a poly(ethylene glycol) (PEG)–based hydrogel network via a photoinitiated thiol-ene reaction. After collection, droplets (separated by a thin layer of surfactant-laden oil) were cross-linked via exposure to ultraviolet (UV) light (λ = 365 nm; I = 15 mW cm⁻²; t = 60 s), resulting in near-uniform microgel populations (Fig. 2B). We used thiol-ene polymerization because of its reduced sensitivity to oxygen, which provided consistent size and mechanical properties within microgel batches (35). The resulting microgel PEG networks were chemically inert due to covalent cross-linking, limiting confounding effects of potential chemical interactions between microgels on the granular hydrogel properties. The elastic modulus (E) of the bulk hydrogel formulations increased with polymer fraction [3 to 12 weight % (wt %); Fig. 2C]. We used additional mechanical testing methods (compression and nanoindentation with the FluidFM) to validate the oscillatory rheology measurements of the bulk hydrogel properties as a measure of individual microgel building block properties (fig. S4) (36, 37). Furthermore, nanoindentation measurements highlighted that the stiffness and size of the microgels could be tuned independently (figs. S5 to S7). Accordingly, microfluidic templating provided a library of defined microgels across a range of sizes (Ø = 25 to 100 μm with low dispersity) and moduli (E = 2.5 to 165 kPa) that were used to study how microgel properties influence the macroscale rheology of jammed granular hydrogels.

Fig. 2. Microfluidic production of thiol-ene microgels.

(A) Schematic of the microfluidic synthesis procedure. Eight-arm PEG macromers (M_n = 10,000 g mol⁻¹) were end-functionalized with norbornene (PEGNB). Hydrogel precursor solutions containing PEGNB, DTT, photoinitiator (LAP), and droplet generation oil were injected into the microfluidic device, and aqueous droplets were produced at the flow-focusing junction. Microgels were formed by thiol-ene photopolymerization of PEGNB and DTT. (B) By controlling the microfluidic channel geometry and the relative flow rates of the aqueous and oil phases, distinct microgel sizes were achieved with low dispersity (calculated from at least 100 microgels), from left to right: Ø = 25 μm, gray; Ø = 55 μm, blue; Ø = 75 μm, yellow; Ø = 100 μm, red. (C) Stiffnesses (represented as means ± SEM, n = 3) of the hydrogels were controlled by the polymer content of the precursor solution. The measurements represent bulk network properties measured via shear rheology, which were converted to Young’s moduli (assuming ν = 0.5), and were supported by compression and nanoindentation measurements (figs. S4 to S7).

Microgel size and stiffness control granular hydrogel viscoelasticity

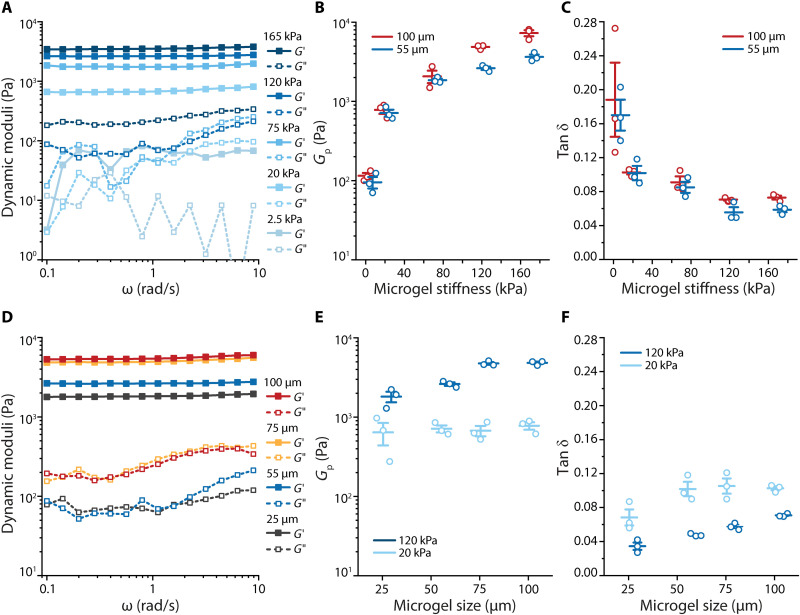
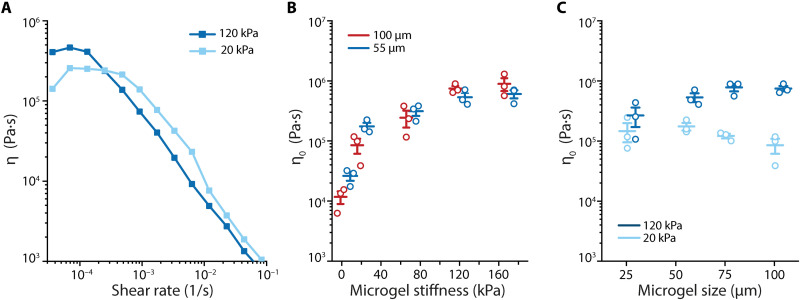
Jammed hydrogels are often formed via vacuum filtration or centrifugation of a dilute suspension of building blocks (38, 39). Centrifugal packing allowed us to generate jammed systems with volume fractions relevant to biomedical applications, which were distinct from the compressed soft colloidal systems that have been characterized previously (26, 28). Jammed granular hydrogels assembled from the fabricated microgels exhibited macroscopic elasticity (shear storage modulus, G′, greater than shear loss modulus, G″), with a broad plateau modulus (ω = 0.1 to 10 rad s⁻¹; Fig. 3, A and D). This indicated minimal structural rearrangements on these time scales, indicative of enduring microgel contacts at low applied strain (γ = 0.1%). The plateau moduli, G_p, of the granular hydrogels scaled with the elasticity of the building blocks between 0.08 kPa (E = 2.5 kPa, Ø = 55 μm) and 3.65 kPa (E = 165 kPa, Ø = 55 μm; Fig. 3B). This trend corroborated observations of granular-scale packings composed of agar microgels (40). For stiff microgels (E = 120 kPa), G_p increased with particle size from 1.8 kPa (Ø = 25 μm) to 5.5 kPa (Ø = 100 μm; Fig. 3E), whereas G_p was independent of microgel size for the soft microgels (E = 20 kPa). These data support an intuitive relationship between the macroscale shear modulus and microgel stiffness. Previously, it was found that G_p scaled linearly with increasing microgel stiffness in osmotically compressed colloidal systems, following a continuum hydrogel behavior (41). In the case of our jammed granular hydrogels, the scaling was nonlinear as a function of microgel stiffness, suggesting that the systems could not be described simply as hard spheres (42). We hypothesized that the nonlinear scaling was related to changes in deformation behavior, and therefore the extent of surface contacts of constituent microgels, that occur with varying microgel stiffness.

Fig. 3. Properties of the building blocks determine the LVE response in granular hydrogels.

(A) Frequency sweep (ω = 0.1 to 10 rad s⁻¹, γ = 0.1%, 25°C) of granular hydrogels (Ø = 55 μm building blocks) at various polymer weight percentages showed greater storage moduli G′ (closed symbols) than loss moduli G″ (open symbols) over the whole frequency range. (B) The plateau moduli, G_p, of granular hydrogels scaled nonlinearly with polymer weight percentage for Ø = 55 mm (blue) and Ø = 100 mm (red) building blocks (P < 0.001). (C) Loss factor, tan δ, of the packings decreased with the polymer content of the building blocks (P < 0.001). (D) Frequency sweeps (ω = 0.1 to 10 rad s⁻¹, γ = 0.1%, 25°C) of granular hydrogels with different size building blocks (E = 120 kPa microgels), G′ from top to bottom: Ø = 100 μm, red; Ø = 75 μm, yellow; Ø = 55 μm, blue; Ø = 25 μm, gray. (E) G_p of granular hydrogels depended on the building block size for E = 120 kPa (dark blue; P < 0.05) and was independent for E = 20 kPa [light blue; not significant (ns)] microgels. (F) Similarly, the tan δ value of the packings depended on the building block size for E = 120 kPa (dark blue; P < 0.05) but varied minimally as the size of the building blocks increased for E = 20 kPa (light blue; ns) microgels. (B, C, E, and F) Plots are represented as means ± SEM, n = 3. Statistical analysis was performed using one-way ANOVA, with Tukey’s test for post hoc analysis.

This hypothesis was supported by considering the loss (damping) factor, tan δ, which defines the ratio between the dissipative and elastic response in the LVE region. In granular systems, interactions between individual particles are dissipative because of the presence of static friction and inelastic collisions (30). Compared with bulk hydrogels having the same polymer content, granular hydrogels exhibited higher tan δ, due to a relative decrease in G′ and increase in G″ (fig. S9). In addition, Liu and co-workers (43) suggested that this change in dynamic moduli is a result of perturbations, such as local slipping of the particles under applied strain. Because thiol-ene microgels are non-Brownian particles, we considered that the observed tan δ values were a result of damping that originated from surface deformations of the microgels upon shear. For packings of both small (Ø = 55 μm) and large (Ø = 100 μm) microgels, tan δ increased as the microgel modulus decreased, implying greater viscous dissipation due to higher deformability of softer microgels (Fig. 3C). The variation in tan δ with building block size was less pronounced (Fig. 3F). When we jammed the microgels in the presence of high–molecular weight dextran (excluded from the microgel network), tan δ values were higher for all microgel sizes despite the unchanged polymer network density (fig. S18). This further pointed to contact phenomena as an important contributor to viscous dissipation or damping in the LVE regime of the granular hydrogels, as opposed to the internal elasticity of the microgels alone.

Microgel deformations control the nonlinear rheology of granular hydrogels

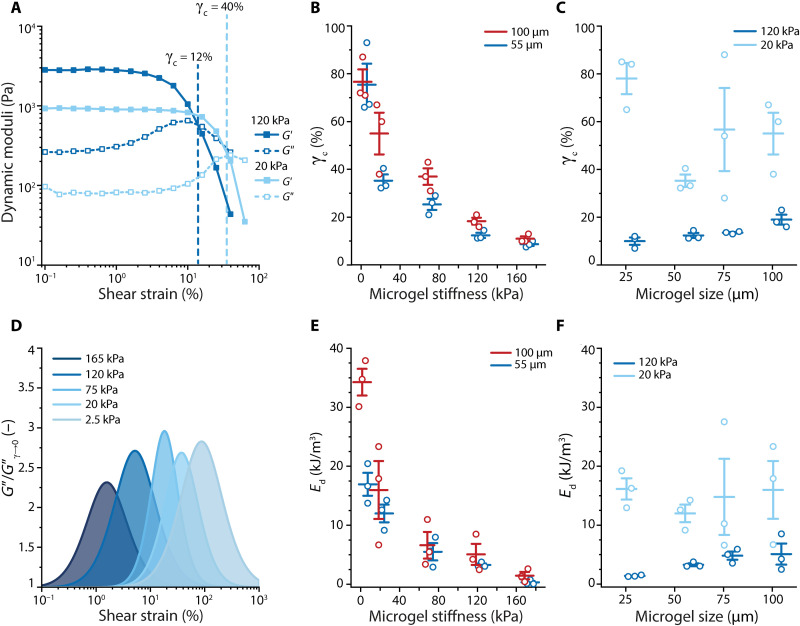
Beyond a critical strain, stable contacts in granular hydrogels break and cause individual and/or subpopulations of microgels to move past each other, resulting in material flow. The macroscale mechanics recover completely and rapidly when the applied shear is removed. This inherent design feature makes jammed granular hydrogels useful as cell carriers, injectable drug delivery vehicles, and inks for 3D printing (44, 45). The nonlinear response is described as the yielding transition in strain sweeps, where G′ decreases below its LVE value with increasing strain, eventually falling below G″ at the crossover point denoted as the critical strain γ_c (Fig. 4A). Engineering the nonlinear behavior of granular hydrogels is critical to exploit their shear-thinning and self-healing properties. We observed that γ_c increased as the polymer content of the building blocks decreased (Fig. 4B), whereas, at a fixed microgel elasticity, it was independent of building block size (Fig. 4C). Analogous to tan δ in the LVE region, we hypothesized that the yielding behavior was also a signature of the microgel contacts within the packings, such that, under a given strain amplitude, softer microgels deformed to a larger extent, increasing γ_c.

Fig. 4. Nonlinear rheology of granular hydrogels is modulated by the properties of the constituent microgels.

(A) Yielding transition of granular hydrogels (Ø = 55 μm building blocks) depicted in strain amplitude sweep measurements (γ = 0.1 to 100%, ω = 10 rad s⁻¹, 25°C) at different polymer contents. (B) Critical strain, γ_c, was measured as the strain at the crossover of G′ and G″ and showed a gradual decrease as a function of polymer content for Ø = 55 μm (blue) and Ø = 100 μm (red) building blocks (P < 0.001). (C) γ_c depended on the size of the building blocks for E = 120 kPa (dark blue; P < 0.05) and remained constant for E = 20 kPa (light blue; ns). (D) Loss moduli of granular hydrogels were normalized by their linear response value at low shear strain to calculate the energy dissipation during yielding. The overshoot in loss moduli, G″/G″_γ→0, was fitted to a log-normal distribution. The energy dissipated per unit volume was calculated by integrating the area under the curves of the loss moduli overshoot. Overlaid curves of the fitted G″/G″_γ→0, which shifted to higher shear strain values as microgel polymer content decreased. (E) Dissipated energies, E_d, increased as the stiffness of the microgel building blocks decreased, as shown for Ø = 55 μm (blue) and Ø = 100 μm (red) microgels (P < 0.001). (C) Fitted G″/G″_γ→0 curves of granular hydrogels of varying building block sizes. (F) E_d values both for soft (E = 20 kPa, light blue) and stiff (E = 120 kPa, dark blue) did not vary appreciably as a function of microgel size (ns). (B, C, E, and F) Plots are represented as means ± SEM, n = 3. Statistical analysis was performed using one-way ANOVA with Tukey’s test for post hoc analysis.

Granular hydrogels and other soft glassy materials—including physically associating gels, emulsions, and foams—often feature an overshoot in G″ during the yielding transition, referred to as the type III behavior that describes energy dissipation in the material (46, 47). It has been proposed that colloidal-scale packings are under cage effects due to restricted Brownian motion and that, upon increased shear, these cages can break, allowing the particles to diffuse to longer distances and giving rise to the type III behavior (41). The absence of Brownian motion in granular hydrogels suggests that the overshoot in G″ in granular hydrogels may be indicative of other microstructural events. On the basis of the observations for γ_c, we suggested that the overshoot in loss moduli was regulated by the contact breaking on microgel surfaces. For a constant microgel size, peaks shifted to higher shear strains by an order of magnitude with decreasing building block stiffness (Fig. 4D). Changes in microgel size did not induce a considerable difference in the overshoot (fig. S20). The energy dissipation per unit volume of material, E_d, was approximated by the integration of the area below the peak (48, 49). Calculated values indicated that softer microgel packings dissipated more energy per volume, corroborating the hypothesis that the yielding transition was prolonged likely due to larger deformations in softer microgel packings (Fig. 4E). An increase in microgel size did not substantially contribute to the energies calculated for microgel packings (Fig. 4F). Donley and co-workers (50) recently showed through time-resolved experiments that the solid-like to liquid-like transition in soft materials is a continuum behavior. We also characterized the yielding transitions and energy dissipation using large-amplitude oscillatory shear (LAOS) experiments (51). Lissajous-Bowditch projections corroborated the measured γ_c and trends in energy dissipation from the strain sweep tests (fig. S21).

Microgel properties govern granular hydrogel viscosity and the onset of shear thinning

We then measured the shear rate–dependent viscosity of the granular hydrogels, and all samples demonstrated a decrease in viscosity in response to increasing shear rate, as previously reported for various types of granular hydrogels (6). Samples showed a Newtonian plateau in the low–shear rate regions (Fig. 5A), designated as the zero-shear viscosity, η₀. We associated this response to the conservation of the packing constraints and hence the structural integrity of the hydrogel, as the rate of deformation was slower than any stress relaxation in the system. Conversely, increased shear rates led to contact breakage and flow. The rapid decrease in viscosity may be indicative of slip and/or shear banding; however, these phenomena were not observed in the low–shear rate region, allowing for robust measurements of η₀ (fig. S22). We observed that η₀ scaled with microgel polymer content similar to the scaling observed for G_p, indicating similar governing phenomena for both responses (Fig. 5B). The differences in η₀ with respect to microgel size were again subtle, with the scattered data for softer packings blurring an observable trend (Fig. 5C).

Fig. 5. Shear rate–dependent behavior and viscosity of jammed granular hydrogels are affected by microgel properties.

(A) Rotational shear rate measurements were performed (δγ/δt = 10⁻⁵ to 10⁻¹ s⁻¹, 25°C). All materials demonstrated a Newtonian plateau at low shear rates and a decrease in viscosity, η, with increasing shear rate. Granular hydrogels with stiff microgels (E = 120 kPa, Ø = 55 μm, dark blue) showed a rapid decrease in η, while soft building blocks (E = 20 kPa, Ø = 55 μm, light blue) resulted in a Newtonian plateau for an extended range of shear rates. (B) Zero-shear viscosity, η₀, of granular hydrogels scaled over two orders of magnitude with an increase in polymer weight percentage of building blocks, as shown for Ø = 55 μm (blue) and Ø = 100 μm (red) microgels (P < 0.001). (C) η₀ varied at E = 120 kPa (dark blue; P < 0.05) and remained constant for E = 20 kPa (light blue; ns) with changes in microgel size. (B and C) Plots are represented as means ± SEM, n = 3. Statistical analysis was performed using one-way ANOVA with Tukey’s test for post hoc analysis.

Microgel building blocks interact in the jammed state through elastic deformations that can be explained by contact mechanics

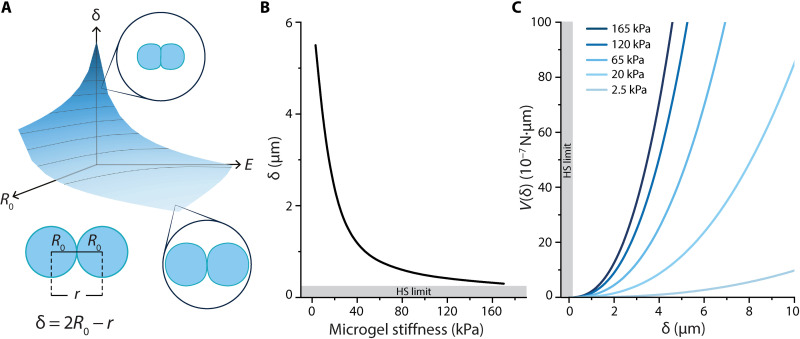
Our systematic investigation on the rheological measurements provided valuable insights into the influence of building block properties on the macroscopic response of granular hydrogels. To shed light on the origin of these observed effects, we set out to establish a framework that relates microgel features to macroscale properties of granular hydrogels. In granular matter physics, it has been shown that the packing fraction and particle modulus determine the macroscopic moduli of the packing (52, 53). For example, Baxter’s sticky hard sphere approach predicts the modulus of granular packings to scale linearly with the modulus of the constituent particles (42). This relationship was preserved for our stiff (E = 65, 120, and 165 kPa) microgel packings, which behave similarly to hard spheres. However, the macroscopic moduli of the soft (E = 2.5 and 20 kPa) packings were well below the hard sphere prediction (fig. S23). Including the associated changes in particle fraction for the more deformable soft microgels would predict moduli above the hard sphere estimate. Given that the hard sphere approach [i.e., δ = 0 and V(r) → ∞ at r = 2R₀; Fig. 6, B and C] does not capture the data for the whole range of microgel stiffnesses explored here, we developed a model that accounts for the deformable nature of the microgels and how the deformation behavior varies with microgel stiffness.

Fig. 6. Hertzian contact mechanics describe the pairwise interactions between microgels in the jammed state.

(A) Microgel building blocks come into contact in the jammed state where nonzero contact areas are generated. The depth of indentation, δ, on surfaces can be estimated via Hertzian contact based on the properties of the building blocks. In calculations, the normal force upon contact, F_N, was fixed to 0.1 μN for each pair of microgels. (B) δ as a function of microgel stiffness rises sharply as a result of the highly deformable surfaces of soft microgels. Elasticity of microgels will resist further deformation, developing repulsive potentials, V(r), that are stored as elastic energy in the system. (C) V(r) of microgels at a fixed δ increases as a function of polymer content cross-linking density and size due to higher elasticity that resists microgel deformation. For comparison, we have included the hard sphere (HS) limit (gray) showing that δ = 0 for all microgel stiffnesses and V(r) → ∞ for all nonzero δ.

Above, we hypothesized that contact phenomena play a crucial role in the emergence of the macroscopic properties. For a packing of soft athermal particles, microgel contacts will give rise to elastic deformations on the particle surfaces, thereby creating a nonzero contact surface that accommodates stresses. To build a representative model for the contact landscape in the jammed state, we considered pairwise contacts between the microgels as the governing feature. As a first approximation, we postulated that, in the LVE region, macroscopic stress in the material originated primarily from the normal component of the contact forces and described the deformation of microgels using the classical Hertz theory of contact for ideal elastic deformation (29, 54, 55). Centrifugal jamming in the absence of external compression gives rise to packings with small deformations of the microgels and allowed us to use the Hertzian contact model (see Supplementary section S2.5 for a full description and an extended discussion on the model calculations). On the basis of Eq. 1, the normal force, F_N, dictates the indentation depth, δ, of the contacting microgels of radius R₀ and depends on the Young’s modulus, E, of the microgel polymer network.

$$\delta ={\left[\frac{9F_{\mathrm{N}}}{4E{(2R_0)}^{1/2}}\right]}^{2/3}$$ (1)

Exact computation of the contact forces that give rise to deformations is complex, as the force distribution can be inhomogeneous in a packing (56, 57). For example, experimental and computational studies have shown that weak and strong force chains during force transmission in granular matter can lead to nonuniform contact forces throughout the material (58). However, Behringer and co-workers (32) demonstrated the validity of the Hertz contact theory for granular-scale hydrogel packings and suggested that a mean-field approximation of the contact forces could be used to relate microscale properties to the macroscopic stress response. On the basis of a mean-field approach and macroscopic contact forces measured from rheology, we estimated F_N to be ~0.1 μN per microgel contact (see Supplementary section S2.6). The average F_N was fixed in all packings comprising identical microgel size, because the packing fraction under centrifugal jamming conditions was not affected by microgel stiffness. At a fixed F_N, δ scales inversely with the microgel stiffness, E, and therefore polymer content, of the building blocks at a given microgel radius, R₀ (Fig. 6A). On the basis of the Hertzian contact, we predicted that the extent of indentation in microgel pairs decreased as building blocks became stiffer (Fig. 6B). The estimated indentations agreed with those calculated from images of the microgel packings, corroborating the applicability of the Hertzian contact model (fig. S27). Furthermore, for a given polymer content, δ increased with increasing building block size as the contact force is distributed over a smaller number of load-bearing columns in packings of larger building blocks (fig. S24).

Upon contact, microgels resist further deformation because of the elasticity of the cross-linked network. In the absence of any chemical interactions between microgels, this resistance can be represented as a soft repulsive potential, V(r), approximated by the Hertz contact model (Eq. 2) (59). This interaction potential is sensitive to the mean separation between particle centers, denoted as r, indicating the tendency for the particles to resist deformation via elastic restoring forces. Through control of the microgel size and polymer content, the magnitude and steepness of V(r) can be tuned. For a given size and δ = (2R₀ − r), V(r) markedly increases as the cross-linking density of the microgels increases, indicating that softer particles will result in a softer interaction, diverging further from hard sphere contact behavior (Fig. 6C). In addition, at a fixed polymer content, the increase in V(r) with respect to changes in microgel size becomes less pronounced (fig. S25). We note that for hard spheres, i.e., δ = 0 and V(r) → ∞ at r = 2R₀.

$$V(r)=\frac{16}{45}{\left(\frac{R_0}{2}\right)}^{1/2}{\delta }^{5/2}E$$ (2)

Packing structure that arises from contact deformations in granular hydrogels can be simulated in 3D

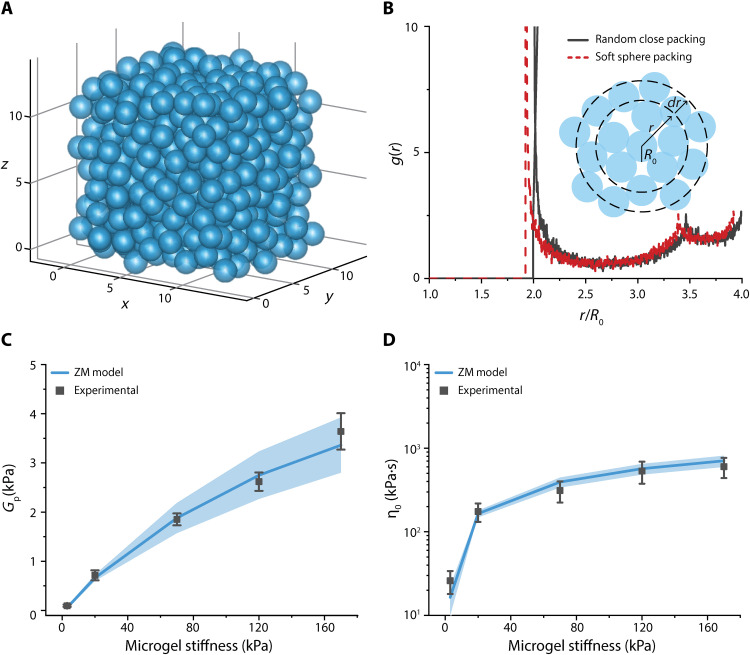
Constructing the macroscopic response requires a representation of contact phenomena in the 3D volume of the packing of microgels. Accordingly, we combined the above established pairwise interaction principle with the microstructure of granular hydrogels. For model packings of monodisperse frictionless hard spheres, experiments and computational studies showed the highest volume fraction, ϕ, as the random close packing limit ϕ_RCP = 0.64 (60–62). Consequently, we generated model hard sphere packings, based on the Lubachevsky-Stillinger algorithm and applied by Baranau et al. (63), to simulate the spatial organization of granular hydrogels and represent the extent of deformations (Fig. 7A). To represent the geometric coordinates of the building blocks, we extracted the radial distribution function, g(r), which describes the probability density of finding a particle at a distance r from the reference particle (Fig. 7B). For hard sphere packings, particles are in point contact, where the pair probability strongly peaks at the radial separation r that is twice the particle radius (2R₀ = r). However, this configuration does not account for the deformability of particles. From our microscopy analysis of jammed granular hydrogels, we observed that decreasing building block stiffness gave rise to an increase in ϕ, which resulted from the deformability of the building blocks (fig. S17). To account for the deformability and increased packing fraction, we modified r by shifting by δ as obtained from the Hertzian contact. Bonnecaze and co-worker (64) demonstrated that for small deformations (<15%) in soft particle packings, the spread and height of g(r) peak do not change substantially. This approach allowed us to capture the changes in packing fraction and contact landscape that occur with changes in microgel stiffness without the need for another adjustable parameter.

Fig. 7. Contact mechanics combined with the ZM formula predicts the plateau moduli and viscosity of granular hydrogels.

Random close packings for hard spheres were generated to simulate the microstructure and microgel contacts in granular hydrogels. (A) 3D rendering of a randomly close packed collection of particles (N = 492), generated computationally according to the Lubachevsky-Stillinger algorithm, at volume fraction ϕ_RCP = 0.64. The axes represent spatial coordinates x, y, and z. (B) Radial distribution function, g(r), of hard sphere particles with random close packing (black) and soft sphere particles with deformations accounted for (red) as a function of radial distance, r, normalized by the particle radius, R₀. The ZM formula was used to predict the LVE properties of granular hydrogels. (C) Experimentally measured (dark gray) and estimated G_p of granular hydrogels (Ø = 55 μm) as a function of polymer content of the microgel building blocks. (D) Zero-shear viscosity, η₀, measured (dark gray) at the low shear rate limit and estimated as a function of polymer content. Calculations were based on the shear moduli of bulk hydrogel, E_bulk (blue), that was measured via dynamic mechanical testing. Bands indicate the variation of the predicted G_p as the normal force during contact, F_N, values vary over the range of 0.26 ± 0.15 μN. Experimental values are represented as means ± SD (n = 3). Lines represent the mean estimated values (n = 5) of G_p and η₀.

Contact mechanics predict the plateau moduli and viscosity of granular hydrogels through the ZM approach

Above, we established a framework to model the contact landscape in terms of both pairwise contacts and 3D packing of microgels. To quantify how this contact landscape gives rise to the elastic response of granular hydrogels, we leveraged the liquid state theories developed by Zwanzig and Mountain that state that the total elastic energy stored by a fluid is equivalent to the summation of all the pairwise contact energies of the constituent atoms (Eq. 3) (65). This strategy has been reported previously to describe the rheology of colloidal and noncolloidal soft particle systems under compression (28, 40, 66).

We hypothesized that in a similar fashion, pairwise interactions in a suspension of granular particles can be treated as additive, resulting in macroscopic elasticity. As V(r) is zero for microgels that are not in contact and g(r) vanishes with increasing radial distance, microgel pairs that are in short-range contact contribute to the stored energy that can be integrated over the entire volume of the packing to predict the macroscopic response

$$G_{\mathrm{p}}=\frac{2\pi }{15}{N}^2{\int }_0^{2R_0}g(r)\frac{d}{dr}\left\{r^4\left[\frac{dV(r)}{dr}\right]\right\}dr$$ (3)

By calculating δ from the projected F_N, we performed numerical integrations using the ZM model. We numerically computed G_p values based on the bulk shear moduli measured via oscillatory rheology, E_bulk, which captured the scaling relationship between microgel stiffness and G_p and which agreed with the experimental results (Fig. 7C). In addition, when F_N was used as a free fitting parameter to collapse the numerical data onto the rheological measurements, we found that F_N = 0.26 ± 0.15 μN, which was within the expected range. This, considered together with a comparison between estimations of shear moduli of bulk networks and that of the granular hydrogels, displayed the predictive ability of the ZM model. We noted that an increase in microgel size at fixed polymer content resulted in no change in the predicted G_p. We explained this by the counterbalancing of the steep increase in V(r) (due to increased average F_N per contact) with a decrease in the number density of microgels, N, as a lower number of larger microgels can be packed into the same volume. Such an outcome, in agreement with experimental findings, explained why a difference in G_p is not seen upon change in microgel size and further strengthened the application of contact mechanics and the ZM model to the design of jammed granular hydrogels.

$${\eta }_0=\frac{2\pi }{15}{\tau }_{\mathrm{D}}{N}^2{\int }_0^{2R_0}g(r)r^2[\frac{d^{2}V(r)}{d{r}^2}+\frac{4}{r}\frac{dV(r)}{dr}]dr$$ (4)

Having demonstrated the ability of the ZM model to predict the plateau modulus of granular hydrogels, we extended the pairwise contact approach to estimate the low shear viscosity, η₀, of distinct packings according to Eq. 4. A similar method has been implemented for suspensions of block copolymer micelles (67). A critical challenge in estimating η₀ from this equation is establishing the diffusional relaxation time, τ_D, for microgels, due to the absence of thermal effects (Brownian motion) on the granular scale and possibly a complex local strain field with inhomogeneous shearing landscape. Furthermore, a structural breakdown can take place via subpopulations of microgels (clusters) flowing collectively. These considerations render setting an exact diffusion time difficult. Accordingly, we rationalized τ_D by using it as a parameter reflecting an order of magnitude for the critical time scale for relaxation in the packings (τ_D = 6 × 10⁵ s). We observed a sharp increase in η₀ at lower microgel stiffnesses (E = 2.5 kPa and E = 20 kPa) that converged to a plateau as the microgel stiffness increased (Fig. 7D). The variation in η₀ with respect to microgel stiffness was described well by the ZM model. Overall, the ZM model predicted experimental values for both G_p and η₀, supporting the view that understanding microgel contacts is sufficient to describe the macroscopic properties of granular hydrogels.

Design of jammed granular hydrogels informs printing of 3D structures

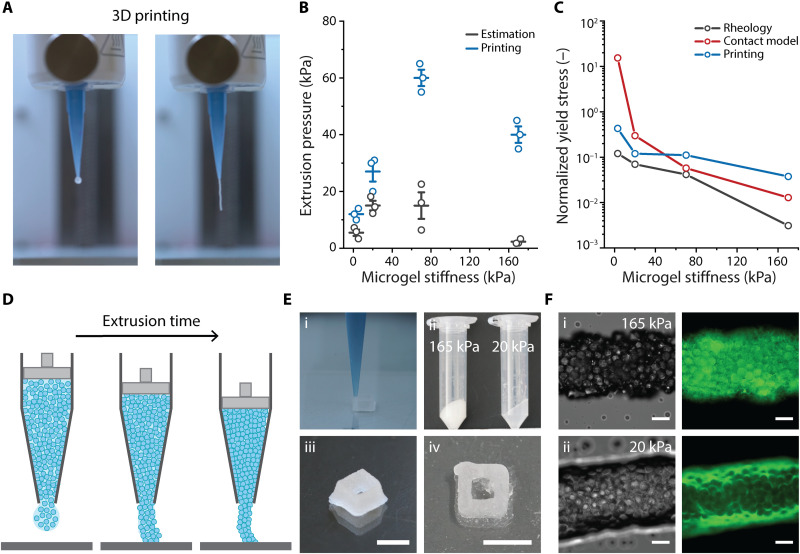
Granular hydrogel bioinks and injectable tissue repair scaffolds have demonstrated strong potential in recent years, owing to the reversible yielding behavior observed in this class of materials (11, 38). Alge and colleagues (68) showed that the flow initiation process was related to the geometry of the printing nozzle that consequently affects the printing quality and cytocompatibility. To enable engineering of granular hydrogels that satisfy the complex requirements of 3D printing, we investigated whether the knowledge gained from contact modeling can improve the printing process. During printing, the applied shear stress overcomes the energy necessary for the microgel packing to yield (Fig. 8A). In our experiments, we observed a nonmonotonic relationship between printing pressure and microgel stiffness (Fig. 8B). The deformable nature of the microgels (and how deformation changes with microgel stiffness) as explained by the contact model provides a better understanding of this complex process and trend. This is consistent with recent work discussing the role of microgel deformation in the 3D printing of granular hydrogels (68). We hypothesized that analyzing the yield stress of granular hydrogels would shed light on the role of contact deformation on the initiation of flow during printing. In our strain sweep experiments, the critical strain for the granular packings increased with decreasing microgel stiffness (Fig. 4B), yet the yield stress (calculated from strain sweep tests; fig. S15) was a nonmonotonic function of microgel stiffness. This unexpected behavior can be explained by the fact that the yielding behavior in granular hydrogels is an interplay between microgel deformability and granular hydrogel mechanics (defined by the microgel stiffness as described in the contact model). For example, Bhattacharjee and colleagues (39) have shown that the elastic stress originating from particle deformations can predict the yield stress of a packing. As opposed to rupture of the constituent polymer network, yielding involves the separation of established contact surfaces of neighboring microgels. To capture the elastic energy cost of contact deformations, we normalized the calculated yield stress to the respective macroscale modulus of the granular hydrogel (G_p), where we observed a decrease in the normalized yield stress as the building block stiffness increased (Fig. 8B).

Fig. 8. High-fidelity printing of stable structures was enabled by informed design of granular hydrogels.

(A) Granular hydrogels were extruded into square-shaped structures using direct ink writing. (B) Experimental (P < 0.001) and predicted extrusion pressures of granular hydrogels of varying building block stiffnesses represented as means ± SEM (n = 3). (C) Normalized yield stress values of granular hydrogels based on oscillatory rheology (gray), contact model (red), and experimental printing pressures (blue). (D) Schematic of jammed granular hydrogel extrusion process, showing the dependency of printing behavior on the decreased pore space due to contact deformations. (E) Extrusion process using a conical nozzle. (i) Representative printing of microgel packings (Ø = 55 μm) into multilayer structures via a conical nozzle (0.41 mm inner diameter). (ii) Representative image of jammed microgels before loading into extrusion cartridges. (iii) Printed square structures of granular hydrogels composed of stiff (E = 165 kPa, Ø = 55 μm) and (iv) soft (E = 20 kPa, Ø = 55 μm) microgels. Scale bars, 4 mm. (F) Bright-field and fluorescence microscopy images of extruded filaments of (i) stiff (E = 165 kPa, Ø = 55 μm) and (ii) soft (E = 20 kPa, Ø = 55 μm) jammed microgels suspended in fluorescein isothiocyanate–dextran–loaded PBS. Scale bars, 100 μm.

To relate information from the model to practical printing parameters, we calculated the expected normalized yield stress from the surface contacts. The yield stress of a concentrated nonattractive suspension can be linked to the interparticle potential via

$${\sigma }_y=K\frac{V(r)}{{(2R_0-\delta )}^3}$$ (5)

where K is a constant (69). The calculated normalized yield stress values were similar to those measured via rheology, supporting the role of the contacts in defining the yield behavior (Fig. 8C). This information can be useful to guide the printing parameters for granular hydrogels as the yield stress is proportional to the extrusion pressure, P, and dependent on the geometric details of the printing nozzle (70). In the case of a straight nozzle

$${\sigma }_y=P\frac{r_{\mathrm{n}}}{2L}$$ (6)

where L is the nozzle length and r_n is the nozzle diameter. This approach predicted the nonmonotonic extrusion pressure observed in the printing experiment and reinforced the need to understand the contact landscape for practical applications of granular hydrogels.

With the insight gained from the contact model, we performed fiber extrusion and layer-by-layer printing tests where microgel packings were extruded onto a glass surface as fibers or as square-shaped scaffolds. Both soft and stiff microgel packings were printed with high fidelity by tuning of the extrusion pressures (Fig. 8, E and F). In addition, we observed that several of the jammed granular hydrogels (E = 20, 65, and 165 kPa) extruded interstitial water before the initiation of material flow, as also described before (68). Furthermore, the pressure required to extrude these materials increased with the duration of extrusion. In comparison, the softest microgel packing (E = 2.5 kPa) showed no water extrusion and printed at relatively low extrusion pressures (P = 12 kPa). This behavior can also be understood by considering the deformable nature of the microgels in the context of the contact model. Water extrusion and increased printing pressures were likely correlated with a decrease in the pore space volume as a result of compression during printing, as has been described for porous media (71). This implies the formation of larger contact deformations. From the view of the contact model, increasing δ results in increased repulsive interactions, i.e., V(r) increases with δ, and therefore increased yield stresses and printing pressures. These effects were less pronounced in more deformable microgels [more subtle changes in V(r) with δ], explaining the absence of these effects in the softest microgel packing (E = 2.5 kPa).

DISCUSSION

In this work, we investigated the dynamic rheology of granular hydrogels composed of defined microgel building blocks to describe how the building blocks control macroscale properties in this class of materials. Specifically, we quantified how the stiffness and size of the building blocks give rise to distinct linear and nonlinear rheological properties. The experimental results confirmed that stiffer building blocks give rise to a higher plateau modulus, G_p, in the LVE compared with softer microgels. We did not observe a clear correlation between granular hydrogel modulus and microgel size. However, we noted that in the packings of stiff microgels, G_p and tan δ increased slightly with building block size. In our view, this suggests that other rich physics may be at play. For example, when the elastic network of hydrogels is deformed, solvent can flow through the network to avoid compression, termed the poroelastic effect (72). Because many hydrogels have a poroelastic diffusivity of approximately 10⁻¹⁰ m² s⁻¹, at low frequencies (ω = 10 rad s⁻¹), a poroelastic diffusion length of about 10 μm is obtained. Considering that this is on the order of the size of the building blocks, it is possible that poroelastic diffusion plays a role in the slight changes in tan δ observed with respect to microgel size. Furthermore, we found that softer microgel packings responded to shear at higher strain amplitudes, which was attributed to the larger contact deformations they experienced. This was supported by the estimation of energy dissipation during yielding, as granular hydrogels with softer microgels showed a marked increase in dissipated energies. In a similar manner to the LVE region, dissipated energies did not change substantially with microgel size. We attributed the limited effect of microgel size on granular hydrogel rheology to the number density of microgels in the different packings. As the microgel size increases, although each contact is expected to result in greater deformation, fewer can be packed into the same volume, which, in turn, generates fewer contact surfaces that contribute to the elastic energy storage.

We built a descriptive model to predict the plateau modulus and viscosity of our materials by combining classic contact mechanics with concepts from molecular physics. The modeling approach corroborated our hypothesis that microgel contacts control the rheological behavior of granular hydrogels. Previous literature on the rheology of soft particle suspensions emphasized the importance of polymer volume fraction under osmotic compression and did not include explicit estimations of contact deformation to understand the macroscopic properties (27, 66, 73). Distinctly, we predicted microgel deformations by viewing the packings through the lens of Hertzian contact. We generated random close packings for hard spheres and subsequently modified them to simulate the deformed microgel surfaces in the 3D packings. The ZM framework, developed originally for molecular physics, captured the relationship between the macroscopic response and microgel stiffness observed in the rheological measurements. In addition, the model captured the invariance of rheological properties as a function of building block size by rationalizing the balance of microgel deformation and number density in the packing. We found that larger microgels were subjected to increased deformations due to the changes in force distribution. However, this was counteracted by the reduced number density of microgels, which is a substantial contributor to the macroscopic response according to the ZM framework. The LVE properties of the granular hydrogels were calculated with the contact model using mechanical measurements of bulk hydrogels of the same formulation. These bulk values were supported by nanoindentation measurements of microgels; however, future work would benefit from more in-depth analysis of the microgel mechanics through further micro- and nanoscale measurements, including atomic force microscopy, FluidFM, and real-time deformability cytometry (36, 74, 75).

From a microstructural viewpoint, the deformations predicted for granular hydrogels suggest increased contact areas for softer microgels, which was consistent with the observed trend in yielding behavior. On the basis of these results, we hypothesized that the relationship between dissipated energy and the properties of the building blocks observed in the rheological tests was also related to the deformations explained by the Hertzian contact model. To confirm this, flow behavior and contact details can be distinctly visualized via methods such as refractive index matched scanning (76). In our rheological measurements, a detailed insight into the origin of energy dissipation was not accessible, but a possible explanation is the extent of friction in the contact areas, which can stabilize the packings by limiting particle movement such as rolling. Note that in the LVE region, forces acting on the microgels were assumed to be central, and frictional motion was ignored in the Hertzian contact and radial distribution function calculations. However, at increased amplitudes of strain, both δ and g(r) will be subject to spatial anisotropy and no longer radially symmetric (31). Therefore, consideration of the tangential component of the contact forces could paint a more elaborate picture of the yielding transition, allowing the extension of this predictive framework into the nonlinear rheology of granular hydrogels. A necessary extension of this work will be to investigate packings with increased complexity in the contact landscape, through stimuli responsiveness or the introduction of reversible and irreversible interparticle cross-linking. Attractive interactions between microgels will change the contact details and thus the rheology of the granular hydrogels, where the use of refined models, such as the Johnson-Kendall-Roberts model, which involves calculation of the attractive forces in the contact region, would be necessary. By considering the effective increase in contact area due to the presence of adhesive motifs on the surfaces of the microgels and the decreased elastic energy cost, the load bearing and flow behavior of granular hydrogels could be designed for specific applications. Our ongoing work on understanding granular hydrogel mechanics aims to investigate aspects of these features.

In this work, we developed a simple yet elegant schematization of jammed granular hydrogels combining microscopic contact details and microstructure to predict macroscale properties. The approach captured the mechanics of these materials without describing complex mesoscale phenomena, such as many-body interactions and force chains. The measured rheology and the model framework informed the processing and the practical utility of the materials. We showed that the elasticity of jammed granular hydrogels can be tuned over several orders of magnitude by varying the stiffness of the microgel building blocks. In addition, we demonstrated that increased pressures were needed to extrude softer microgel packings, which provided a lever to tailor the flow properties and printability of microgel-based bioinks and tissue repair scaffolds. We believe that this work lays the foundations for tunable granular hydrogel design and will contribute to bringing granular hydrogels to an advanced engineering platform for future engineering applications.

MATERIALS AND METHODS

Materials

Eight-arm PEG-NH₂HCl (M_n = 10,000 g mol⁻¹) was purchased from JenKem Technology USA. 5-Norbornene-2-carboxylic acid, 1-[bis(dimethylamino)methylene]-1H-1,2,3-triazolo[4,5-b]pyridinium 3-oxid hexafluorophosphate (HATU), N,N-diisopropylethylamine (DIPEA), N,N-dimethylformamide (DMF), diethyl ether (DEE), deuterated water (D₂O), dl-dithiothreitol (DTT), lithium phenyl-2,4,6-trimethylbenzoylphosphinate (LAP), dextran sulfate sodium salt (M_n = 500,000 g mol⁻¹), light mineral oil, and Amicon Ultra-0.5 centrifugal filter unit (3-kDa MWCO) were purchased from Merck. Regenerated cellulose dialysis tubing (1-kDa MWCO) was purchased from Spectrum Labs. Phosphate-buffered saline (PBS; pH 7.4) was manufactured by Gibco. Droplet generation oil for probes was purchased from Bio-Rad Laboratories Inc.

Methods

Synthesis of end-functionalized PEG-norbornene

The synthesis of eight-arm PEG-norbornene (PEGNB) was performed according to procedures published (77). Eight-arm PEG-NH₂HCl (M_n = 10,000 g mol⁻¹; 8 g, 0.8 mmol of PEG, and 6.4 mmol of NH₂) was dissolved in anhydrous DMF (5 ml) in a round-bottom flask with a stir bar and purged with argon. To the PEG solution, DIPEA (4.46 ml, 25.6 mmol, 4 eq.) and HATU (4.86 g, 12.8 mmol, 2 eq.) were added. 5-Norbornene-2-carboxylic acid (3.12 ml, 25.6 mmol, 4 eq.) was added to the mixture, and the solution was stirred overnight at room temperature. The reaction mixture was precipitated twice in DEE (4°C), and the precipitated product was dialyzed in a regenerated cellulose dialysis membrane against dH₂O for 3 days. The aqueous polymer solution was lyophilized to yield the white powder. Functionalization of the eight-arm PEGNB was determined from ¹H nuclear magnetic resonance (500 MHz, CDCl₃) via comparing the integrated peaks of norbornene vinyl protons (δ = 6.0 to 6.3, m, 1.62H) and PEG ether protons (δ = 3.5 to 3.9, m, 114H; fig. S1) to be ~80%.

Microfluidic device fabrication

The microfluidic devices were designed in AutoCAD (Autodesk). Master molds were fabricated by spin coating (WS-650-23B, Laurell) using SU-8 photoresist (GM1050) onto plasma-cleaned silicon wafers (Si-Wafer, Siegert Wafer). The coated layer was baked and patterned using the masks (high-resolution film mask, Microlitho) containing device designs by aligning onto the coated silicon wafers followed by postbaking and photoresist development. The resulting wafer was baked at 200°C for 10 min, which yielded smooth wafer surfaces. Patterned wafers were treated with chlorotrimethyl silane vapor before soft lithography to prevent adhesion of the polydimethylsiloxane (PDMS) to the wafer and SU-8 structures.

Microfluidic devices were then fabricated using standard soft-lithographic techniques. A mixture of PDMS monomer and curing agent (Sylgard 184, Dow Corning, Midland, MI, USA) in a 10:1 ratio was poured over a master mold and peeled off after polymerization at 70°C overnight. Inlet and outlets were punched using a hole puncher (20G Catheter Punch, Syneo), and the PDMS substrate was bonded to a glass slide (Menzel-Glaser, Germany) after oxygen plasma treatment (EMITECH K1000X, Quorum Technologies, UK) of both surfaces for 60 s. The bonded devices were left at a 120°C hot plate for 2 hours to allow complete bonding.

Microfluidic thiol-ene microgel production

Defined microgel building blocks were fabricated via microfluidic templating of water in oil emulsions according to literature procedures. While batch emulsification techniques allow rapid and large-scale production of microgels for the generation of such packings, the lack of control during the mixing of insoluble components leads to high dispersity, making it difficult to relate macroscale properties to building block size. Microgel generation in microfluidic flow–focusing devices provides improved control over droplet size and volume compared to batch emulsification techniques (35). Cetoni neMESYS syringe pump with Cetoni base 120 power adapter was used as displacement syringe pumps for the aqueous and oil phase. Nikon Eclipse Ts2 inverse microscope paired with uEye Cockpit by iDS7 was used for high-speed imaging of the microfluidic flow. Briefly, hydrogel precursor and oil solutions were loaded into gastight syringes and connected to the inlets of the microfluidic device via Tygon tubing (Cole Palmer GmbH). To form the droplets, an aqueous solution of the thiol-ene precursors was injected into the microfluidic device and pinched off by the fluorinated oil and surfactant phase (droplet generation oil for probes, Bio-Rad Laboratories Inc.) at varying relative volumetric flow rates. Oil and hydrogel precursor flow rates were varied to generate the desired droplet size according to table S1 (microgels; Ø = 25 to 100 μm). The generated droplets were collected in a collection vial with light mineral oil on top to prevent evaporation of the oil phase. After collection, droplets containing eight-arm star PEG macromers end-functionalized with norbornene groups (PEGNB) were cross-linked with a difunctional thiol (DTT) by exposing to UV light for 60 s (λ = 365 nm, I = 15 mW cm⁻²; M365L3-C1, Thorlabs).

Granular hydrogel formation

Cross-linked microgels were centrifuged at 12,700 rpm for 5 min to yield three phases in the collection vial, with microgels collected at the bottom of the vial. Mineral oil and droplet generation oil were discarded, and the microgels were suspended in PBS. Then, the suspension was centrifuged at 12,700 rpm for 5 min, and the supernatant was removed. This washing cycle was repeated three times to ensure removal of the oil phase. The washed microgels were jammed again at 12,700 rpm for 5 min to form granular hydrogels and stored at 4°C until rheological characterization.

Dynamic mechanical testing

Rheological characterizations were performed on a strain-controlled oscillatory shear rheometer (MCR 502; Anton Paar) equipped with a Peltier stage and plate temperature of 25°C. A water ring was applied around all samples to avoid drying of the samples. Bulk hydrogels were formed in situ via loading hydrogel precursor solutions between an 8-mm parallel plate geometry with sandblasted surface and a transparent-bottom plate at a 1-mm measuring gap. The pregel solution was cross-linked in between the two plates upon UV light exposure for 60 s (λ = 365 nm, I = 15 mW cm⁻²; M365L3-C1, Thorlabs). Gelation time and storage (G′) and loss moduli (G″) were probed via oscillatory strain tests over time at γ = 0.1% strain amplitude and an angular frequency of ω = 1 rad s⁻¹ that lie in the LVE region. The Young’s moduli (E) of bulk hydrogels were calculated according to E = 2G′(1 + ν) where ν (Poisson’s ratio of the hydrogels) was estimated to be 0.5.

Granular hydrogel testing was done by scooping jammed granular hydrogels onto the bottom plate of the rheometer and lowering the geometry to the desired measuring gap. In all measurements, a measuring gap of 1 mm was used to ensure that the ratio between the measuring gap and microgel size was at least 10 (based on the practical guideline provided by Anton Paar). Because the truncation gap of cone plate geometries is usually similar to or smaller than the size of our building blocks, we used an 8-mm parallel plate geometry with sandblasted surface and a gap size that was approximately one order of magnitude larger than the maximum microgel diameter. Microgel suspension rheology can be affected by wall slip under applied stress in the presence of smooth surfaces (41). Therefore, in all measurements, sandblasted geometries were used. Although granular-scale microgels lack Brownian motion, all measurements were performed after a preshear step to limit process dependency (fig. S11). In addition, we performed measurements showing a lack of variation in the rheological measurements for different geometries and gap sizes (figs. S12 and S16). Frequency sweep measurements were performed at γ = 0.1% for ω = 0.01 to 100 rad s⁻¹ to probe the LVE region, frequency dependence, and the loss factor of the materials. Strain amplitude sweeps were done at ω = 10 rad s⁻¹ for γ = 0.01 to 100% to determine the yield strain and the energy dissipation during yielding. Shear rate ramps were performed in rotational mode to characterize the flow behavior via measuring viscosity as a function of δγ/δt = 10⁻⁵ to 10² s⁻¹. Self-healing tests were performed by applying low (γ = 0.1%) and high (γ = 500%) amplitude of strain in a cyclic fashion at ω = 1 rad s⁻¹. In oscillatory shear measurements, normal force of at least 0.01 N and a torque of 50 nN·m were recorded. LAOS data were collected with an amplitude range of γ = 0.01 to 100% at ω = 1 rad s⁻¹. The data are collected in (biological) triplicates and presented as means ± SEM, unless otherwise indicated.

3D printing of granular hydrogels

We prepared microgel inks where microgels were jammed into densely packed scaffolds via cycles of centrifugal jamming with Amicon Ultra filter units (0.5 ml, 3-kDa MWCO). This step was performed to remove excess interstitial water and to allow seamless printing of the structures. Microgel packings were then loaded into 3-ml cartridges printed into filaments or layer-by-layer structures onto glass substrates. Filaments were extruded via 22G precision needle tips (0.41 mm inner diameter), and 3 mm by 3 mm square scaffolds (layer height of 0.2 mm, 10 layers) were 3D-printed with a BIO-X pneumatic-driven robotic dispenser (CELLINK) with 22G (0.41 mm inner diameter) conical nozzles at a constant speed of 2 to 5 mm s⁻¹. Extrusion pressures were determined via increasing the applied pressure in steps of 5 kPa. Once the extrusion conditions were found, the applied pressure was changed in steps of 1 kPa to find the minimum pressure needed to deposit structures. Printed filaments were imaged using a Leica THUNDER Live Cell microscope with HC PL APO 20×/0.95 dry objective.

Statistical analysis

Statistical analysis was performed using OriginPro 2021 (OriginLab Corporation). Unless otherwise noted, statistical significance for multiple comparisons was determined by one-way analysis of variance (ANOVA) with a Tukey post hoc test. Groups were considered significantly different if the P value was lower than 0.001 for microgel stiffness groups and 0.05 for microgel size groups.

Supplementary Materials

This PDF file includes:

Supplementary Text

Figs. S1 to S27

Tables S1 to S5

References