Optimizing deep neural networks to predict the effect of social distancing on COVID-19 spread

Abstract

Deep Neural Networks (DNN) form a powerful deep learning model that can process unprecedented volumes of data. The hyperparameters of DNN have a significant influence on its prediction performance. Evolutionary algorithms (EAs) form a heuristic-based approach that provides an opportunity to optimize deep learning models to obtain good performance. Therefore, we propose an evolutionary deep learning model called IPSO-DNN based on DNN for prediction and an improved Particle Swarm Optimization (IPSO) algorithm to optimize the kernel hyperparameters of DNN in a self-adaptive evolutionary way. In the IPSO algorithm, a micro population size setting is introduced to improve the search efficiency of the algorithm, and the generalized opposition-based learning strategy is used to guide the population evolution. In addition, the IPSO algorithm employs a self-adaptive update strategy to prevent premature convergence and then improves the exploitation and exploration parameter optimization performance of DNN. In this paper, we show that the IPSO algorithm provides an efficient approach for tuning the hyperparameters of DNN with saving valuable computational resources. We explore the proposed IPSO-DNN model to predict the effect of social distancing on the spread of COVID-19 based on the social distancing metrics. The preliminary experimental results reveal that the proposed IPSO-DNN model has the least computation cost and yields better prediction accuracy results when compared to the other models. The experiments of the IPSO-DNN model also illustrate that aggressive and extensive social distancing interventions are crucial to help flatten the COVID-19 epidemic curve in the United States.

1. Introduction

Deep learning is a sub-field of machine learning based on artificial neural networks, which includes processing neurons organized in input, hidden, and output layers. As one powerful deep learning model, Deep Neural Networks (DNN) are neural networks with multiple hidden layers of abstraction, outperforming other basic machine learning models in processing unprecedented volumes of data (Han et al., 2016). The hyperparameter setting of DNN has a significant influence on its prediction performance. The number of hidden layers, the number of neurons in each layer, and the activation function in each layer are three kernel hyperparameters of DNN, and their values need to be set appropriately to achieve high-quality results. However, most traditional methods tune these hyperparameters manually, which is quite time-consuming, and the solutions are usually not equally distributed in the objective space (Malitsky, Mehta, O’Sullivan, & Simonis, 2013).

Evolutionary Algorithms (EAs) provide an opportunity to find the optimal or near-optimal values of the hyperparameters of DNN models in an evolutionary way. EAs are the generic population-based metaheuristic optimization algorithms that simulate the natural evolution, and they have shown to be effective in solving multiple and complicated tasks in many fields. EAs exhibit a real potential for large-scale parallelization and distribution in the search space. It is essential for optimizing the hyperparameters of complex DNN architectures. Particle Swarm Optimization (PSO) algorithm is one of the most critical evolutionary algorithms first proposed by Kennedy and Eberhart in 1995 (Kennedy & Eberhart, 1995). PSO is easy to implement and shows rapid convergence towards an optimum (Shi, Liu, Cheng, Li, & Zhao, 2019). Nevertheless, many researchers have noticed that PSO tends to converge prematurely to local optima, especially when dealing with complex multimodal functions (Saeedi, Khorsand, Bidgoli, & Ramezanpour, 2020). This significant weakness has restricted the applications of the PSO to improve the performance of DNN comprehensively.

To address this challenge, we first develop an improved PSO (IPSO) algorithm, which is applied to optimize the hyperparameters of the DNN model. For the IPSO algorithm, we employ the generalized opposition-based learning strategy to guide the population evolution and introduce the micro population size setting to improve the search efficiency of the algorithm. In addition, IPSO explores a self-adaptive strategy to prevent premature convergence and thus enhances the algorithm's global exploitation and local exploration ability. Furthermore, deep learning models have achieved state-of-the-art performance for various application domains over the past few years, such as solving online batching problems (Cals, Zhang, Dijkman, & van Dorst, 2021), diagnosing and classification of faults in industrial rotation machinery (Souza, Nascimento, Miranda, Silva, & Lepikson, 2021), and forecasting supply chain demand (Punia, Singh, & Madaan, 2020).

Deep learning has also been widely used for COVID-19 pandemics, including infection detection. Controlling the spread of COVID-19 has been an important and emerging topic around the world today. Before COVID-19 vaccines were widely distributed, social distancing is the most powerful effort to control the pandemic, such as travel restrictions, quarantine, and issuing stay-at-home orders. The University of Maryland has developed a social distancing scoreboard, and a map of coronavirus confirmed cases to show how social distancing works within communities to slow the spread of COVID-19 in each state (Zhang et al., 2020). However, existing epidemiological contagion theories cannot explicitly measure the effect of these political decisions on reducing COVID-19 cases. Furthermore, few studies related to deep learning explore the significant influence of social distancing on the mitigation of COVID-19.

In this paper, we explore the evolutionary deep learning model, called IPSO-DNN, to predict the effect of social distancing on the spread of COVID-19 and provide new insights for controlling the COVID-19. Social distancing is explicitly considered in the IPSO-DNN model. The effect of social distancing interventions on COVID-19 can be measured by two indicators, daily growth rate and time to double cumulative cases (Tellis, Sood, & Sood, 2020). In order to better describe how COVID-19 spreads, we propose to define four levels of COVID-19 spread by using these two indicators: growth, moderation, control, and containment. Our first research objective is to improve the performance of DNN using the developed IPSO algorithm, which employs the self-adaptive strategy to adjust the evolutionary process to find the optimal values of hyperparameters for the DNN model. Second, we apply the hybrid IPSO-DNN model to show how social distancing interventions help mitigate the COVID-19 spread.

The significant contributions of this paper are summarized as follows:

• (1)An improved PSO algorithm is developed, which employs the self-adaptive strategy and generalized opposition-based learning ability in a micro-population setting to conquer the weaknesses of the basic PSO algorithm. As a result, the proposed IPSO algorithm has significantly improved the performance of basic PSO.
• (2)A parameter selection method is proposed for optimizing the DNN model using the IPSO algorithm. The proposed hybrid IPSO-DNN model optimizes the hyperparameters of DNN without degrading the DNN prediction precision. For instance, the number of hidden layers, the number of nodes in each layer, and the activation functions of each layer in the DNN model are properly tuned evolutionarily. It is found that the proposed IPSO-DNN model outperforms IPSO-SVM (Support Vector Machine), IPSO-LR (Logistic Regression), IPSO-DT (Decision Tree), PSO-DNN, GS (Grid Search)-DNN, and BO (Bayesian Optimization)-DNN models on prediction accuracy and computing time.
• (3)The IPSO-DNN based on the evolutionary deep learning model is introduced to predict the effect of social distancing on the spread of COVID-19. A challenge of this prediction is how to measure the influence of social distancing in response to COVID-19 properly. Therefore, we estimate the effect of social distancing in terms of mobility metrics and then explore our proposed evolutionary deep learning model IPSO-DNN to predict its influence on the spread of COVID-19. In experiments, the IPSO-DNN model performs very well to predict the daily new COVID-19 cases and the spread of the COVID-19 pandemic in the five selected states. The experimental results also explicitly show that aggressive and extensive social distancing is significant to help reduce COVID-19 infections in the United States.

The rest of this paper is organized as follows. In Section 2, we review the relevant literature. In Section 3, we introduce the methodology of our proposed model and develop the IPSO-DNN model to predict the COVID-19 pandemic based on social distancing influence. Section 4 describes the social distancing dataset, including social distancing metrics and levels of COVID-19 spread. Section 5 analyzes and discusses model performances, then explores the effect of social distancing on the spread of COVID-19 in the five selected states. Finally, we conclude our work and discuss future research directions in Section 6.

2. Literature review

2.1. Evolutionary algorithms for deep learning models

The kernel hyperparameter setting of deep learning models plays a significant role in prediction accuracy. But traditional methods of tuning hyperparameters, such as the manual trial and error method, cannot efficiently find the optimal values of hyperparameters. Some existing state-of-the-art hyperparameter optimization methods, such as simple grid and random search (Chaves, Gonçalves, & Lorena, 2018), model-based approaches (Abbasimehr, Shabani, & Yousefi, 2020), and Bayesian optimization based on Gaussian processes (Wang, Ma, Ouyang, & Tu, 2020), show that their performances are approximately like human experts and in some cases even surpass them. However, there are still many challenges in finding the optimal hyperparameters for the complex DNN architectures (Lorenzo, Nalepa, Kawulok, Ramos, & Pastor, 2017). For example, Grid Search is a common method to tune the hyperparameters for deep learning, but it is not efficient in searching a high-dimensional hyperparameter space (Xu et al., 2021).

EAs have been shown to be very efficient in solving a plethora of challenging optimization problems, which has the advantages of both searching the hyperparameter space in a random fashion and utilizing previous results to direct the search. Therefore, the combination of evolutionary algorithms and deep learning models has been a trendy topic over the past few years since hybrid models perform very well in many optimization fields. Most existing studies focus on optimizing the hyperparameters of deep learning models in an evolutionary way. For instance, Young, Rose, Karnowski, Lim, and Patton (2015) presented the multi-node evolutionary neural networks for automating network selection on computational clusters through hyperparameters optimization performed via genetic algorithm. It also showed that the PSO technique holds great potential to optimize parameter settings and thus saves valuable computational resources during the tuning process of deep learning models (Qolomany, Maabreh, Al-Fuqaha, Gupta, & Benhaddou, 2017). Ye (2017) introduced a new automatic hyperparameter selection approach for determining the optimal network configuration for DNN using PSO in combination with a steepest gradient descent algorithm. Darwish, Ezzat, and Hassanien (2020) developed the orthogonal learning particle swarm optimization algorithm to find optimal values for the hyperparameters of convolutional neural networks.

However, most evolutionary algorithms have high computational costs and come with premature convergence, significantly when solving highly complex problems in the real world. DNN suffers from a great variety of hyperparameters which all have specific architectures. These are considered a challenge when evolutionary algorithms are applied to identify the optimal or near-optimal hyperparameters for the DNN. Although many studies researched the hyperparameter optimization of deep learning using an evolutionary algorithm, there is little research exploring improved evolutionary algorithms to enhance the performance of deep learning models. In this paper, we propose an improved particle swarm optimization algorithm to avoid the disadvantages of the PSO algorithm with a self-adaptive strategy to optimize the hyperparameters of the DNN model.

2.2. Particle swarm optimization algorithm

Particle swarm optimization algorithm is a simple yet powerful evolutionary algorithm for global optimization used in many real-world research areas, such as logistics and supply chain management and engineering design optimization. It also has received increasing attention in optimizing the parameters for machine learning techniques because of its fast convergence and easy implementation. However, the PSO algorithm tends to fall into local optima, and its performance is affected by the control parameters and velocity updating strategy. Therefore, many works have been proposed to improve PSO to avoid the problem of premature convergence.

Accelerating convergence speed and avoiding the local optimal have become the two most essential and appealing goals in the PSO research. Hence, a few variant PSO algorithms have been developed to achieve these two goals (Gang, Wei, & Xiao, 2012). Major strategies include control of algorithm parameters and combination with auxiliary search. Moreover, some researchers used a self-adaptive method by encoding the parameters into the particles and optimizing them with the position during run time (Pornsing, Sodhi, & Lamond, 2016). For instance, an Adaptive Particle Swarm Optimization (APSO) algorithm with all automatically adjusted parameters of inertia weight, cognitive coefficient and social coefficient was developed to search for better solutions in scheduling problems (Hop, Van Hop, & Anh, 2021). Zhang, Li, and Wang (2017) proposed an immune particle swarm algorithm based on adaptive search, and the algorithm can dynamically adjust the subscale size and automatically adjust the search range using the maximum particle concentration value.

Nevertheless, it is seen to be difficult to simultaneously achieve both goals of accelerating convergence speed and avoiding the local optimal. For example, Liang, Qin, Suganthan, and Baskar (2006) introduced comprehensive-learning PSO (CLPSO) focuses on avoiding the local optimal but brings in a slower convergence and the higher computational cost of the algorithm. Therefore, to improve the algorithm performance and reduce the computational cost for DNN, an IPSO algorithm with a micro-population size setting is proposed in this paper. The self-adaptive strategy with generalized opposition-based learning ability is applied in the IPSO algorithm to adjust the population evaluation based on the particle updated rate of population in each iteration. This strategy can balance the algorithm's global exploitation and local exploration to prevent premature convergence. Moreover, the IPSO alogirthm employs nonparametric statistical tests to choose its best parameters for optimizing the DNN models. Finally, the proposed optimized evolutionary deep learning model IPSO-DNN is developed to find the optimal values for the hyperparameters of the DNN in a self-adaptive evolutionary way.

2.3. Deep learning application for COVID-19 research

Since COVID-19 first outbroke in mainland China, it has developed into a global pandemic, infecting millions of people worldwide. Over the past few months, deep learning has shown good performance in the application of COVID-19 research. For instance, the multi-objective differential evolution algorithm has been applied to tune the initial parameters of convolution neural networks in order to identify the COVID-19 patients from chest CT images (Singh, Kumar, & Kaur, 2020), and deep learning techniques have been introduced to link potential patients to suitable clinical trials (Dhayne, Kilany, Haque, & Taher, 2021). Nevertheless, although many studies have focused on exploring the deep learning techniques for the COVID-19 infection detection, there is little research to measure the effect of social distancing on the spread of COVID-19. Social distancing has been implemented around the world as a major community mitigation strategy. Therefore, many researchers have studied the relationship between social distancing measures and epidemics.

For instance, the social distancing index has been constructed to evaluate people’s mobility pattern changes along with the spread of COVID-19 (Pan et al., 2020). In addition, Te Vrugt, Bickmann, and Wittkowski (2020) developed an extended model for disease spread based on combining a SIR model with a dynamical density functional theory where social distancing is explicitly considered. A developed method was implemented to monetize the impact of moderate social distancing on deaths from COVID-19 (Greenstone & Nigam, 2020). Fong et al. (2020) presented the systematic reviews of the evidence base for the effectiveness of multiple mitigation measures, which shows that more drastic social distancing measures might be reserved for severe pandemics. Farboodi, Jarosch, and Shimer (2020) provided a quantitative framework for exploring how individuals trade off the utility benefit of social activity against the internal and external health risks that come with social interactions during a pandemic.

While many studies indicated that social distancing is one of the most critical measures in response to COVID-19, a big challenge is appropriately measuring the influence of social distancing and what factors will be the major ones that determine the impact. This paper estimates the effect of social distancing on mobility metrics and then explores the proposed evolutionary deep learning model IPSO-DNN to predict the influence on COVID-19 spread.

The literature review table of Section 2 is shown in Table 1 .

Table 1.

The literature review table.

Author	Previous Work	Research Gap	Our Contributions
Qolomany et al., 2017	Showed that the PSO technique holds great potential to optimize parameter settings and thus saves valuable computational resources during the tuning process of deep learning models.	Most existing studies focus on optimizing the hyperparameters of deep learning evolutionarily. However, there is little research exploring improved evolutionary algorithms to enhance the performance of deep learning models.	Propose an IPSO-DNN model to optimize the kernel hyperparameters of DNN in a self-adaptive evolutionary way without degrading the DNN prediction precision.
Young et al., 2015	Presented the multi-node evolutionary neural networks for automating network selection on computational clusters through hyperparameters optimization performed via genetic algorithm.
Darwish et al., 2020	Developed the orthogonal learning particle swarm optimization algorithm to find optimal values for the hyperparameters of convolutional neural networks.
Ye, 2017	Introduced a new automatic hyperparameter selection approach for determining the optimal network configuration for DNN using PSO in combination with a steepest gradient descent algorithm.
Pornsing et al., 2016	Used a self-adaptive method by encoding the parameters into the particles and optimizing them with the position during the run time.	Most pervious works have been proposed to avoid premature convergence to improve the performance of PSO. However, it is very challenge to simultaneously achieve both goals of accelerating convergence speed and avoiding the local optimal in evolutionary algorithms.	Develop an IPSO algorithm which employs the self-adaptive strategy and generalized opposition-based learning ability in a micro-population setting, to balance global exploitation and local exploration for improving the performance of the PSO algorithm.
Hop et al., 2021	Proposed an Adaptive Particle Swarm Optimization (APSO) algorithm with all automatically adjusted parameters of inertia weight, cognitive coefficient and social coefficient was developed to search for better solutions in scheduling problems.
Zhang et al., 2017	Presented an immune particle swarm algorithm based on adaptive search, and the algorithm can dynamically adjust the subscale size and automatically adjust the search range using the maximum particle concentration value.
Liang et al., 2006	Introduced comprehensive-learning PSO (CLPSO) focuses on avoiding the local optimal but brings in a slower convergence and the higher computational cost of the algorithm.
Singh et al., 2020	Apply the multi-objective differential evolution algorithm to tune the initial parameters of convolution neural networks in order to identify the COVID-19 patients from chest CT images.	Although many studies have focused on exploring the deep learning techniques for the COVID-19 infection detection, there is little research to measure the effect of social distancing on COVID-19 spread.	Estimate the effect of social distancing in terms of mobility metrics and then explore the proposed IPSO-DNN hybrid model to predict the effect of social distancing on the spread of COVID-19.
Dhayne et al., 2021	Introduced deep learning techniques to link potential patients to suitable clinical trials.
Te Vrugt et al., 2020	Developed an extended model for disease spread based on combining an SIR model with a dynamical density functional theory where social distancing is explicitly considered.
Greenstone & Nigam, 2020	A developed method was implemented to monetize the impact of moderate social distancing on deaths from COVID-19.
Fong et al., 2020	Presented the systematic reviews of the evidence base for the effectiveness of multiple mitigation measures, which shows that more drastic social distancing measures might be reserved for severe pandemics.

3. Proposed approach

3.1. Improved particle swarm optimization algorithm

3.1.1. Basic particle swarm optimization algorithm

PSO is an iterative algorithm that engages several simple entities iteratively over the search space of some functions. It uses a simple mechanism that mimics swarm behavior in birds flocking to guide the particles to search for globally optimal solutions. The population of PSO is called a swarm, and its individuals are called particles. The swarm is defined as a set of N particles $i\text{(}i=1,2,...,N)$. A swarm of particles is represented as a potential solution, and each particle i is associated with two vectors. One is the velocity vector defined as $v_i=(v_{i,1},v_{i,2},...,v_{i,D})$, and the other is the position vector defined as $x_i=(x_{i,1},x_{i,2},...,x_{i,D})$, where D denotes the dimensionality of the solution space. The velocity determines the next direction and distance to move. PSO remembers both the global best position located by all particles as well as the historical best position found by each particle during the search process. Random vectors initialize the velocity and the position of each particle within the corresponding ranges. During the evolutionary process, the velocity and position of particle i on dimension d are updated as

$$v_i^{t+1}=w\times v_i^t+c_1\times r_1\times \left(p_i^t-x_i^t\right)+c_2\times r_2\times \left(p_g^t-x_i^t\right)$$ (1)

$$x_i^{t+1}=x_i^t+v_i^{t+1}$$ (2)

where w is the inertia weight, c ₁ and c ₂ are the acceleration coefficients, and r ₁and r ₂ are uniformly distributed random numbers independently generated within [0,1] for the d ^th variable. In the Eq. (1), $p_i^t$ is the position with the best fitness found so far for the i ^th particle, and $p_g^t$ is the best position in the neighborhood. $v_i^{t+1}$ is the new updated velocity of particle I by the end of iteration t. $x_i^{t+1}$ is the new updated position of particle i by the end of iteration t and t = 1, 2,… indicates the iteration number.

As mentioned before, rapid convergence is one of the main advantages of PSO. However, this can also be problematic if an early solution is locally optimal. The swarm may stagnate around the local optimal without any pressure to continue exploration. Therefore, we develop an IPSO algorithm with generalized opposition-based learning and self-adaptive update strategy in the micro-population size setting to balance the global exploitation and local exploration in order to avoid premature convergence and enable the swarm to accurately search out local optimum with the lowest computational cost.

3.1.2. Generalized Opposition-Based Learning

Opposition-Based Learning (OBL) (Tizhoosh, 2005) is a new concept in computational intelligence and is normally applied to the current population during evolution. OBL is usually hybridized with different EAs, such as artificial bee colony algorithm (El-Abd, 2012) and differential evolution (Wang, Rahnamayan, & Wu, 2013). The main idea behind OBL is the simultaneous consideration of a candidate solution x and its corresponding opposite solution x*, which will provide another chance for finding a candidate solution closer to the global optimum. In the evolutionary process, let $X=(x_1,x_2,...,x_D)$ be an n-dimensional space, where x_i ∈ [a_i, b_i] and i = 1, 2, …, n. The opposite vector of X is denoted as $X^{\ast }=(x_1^{\ast },x_2^{\ast },...,x_n^{\ast })$. The opposite point of x is denoted as x * and defined as

$$x_i^{\ast }=a_i+b_i-x_i$$ (3)

The generalized opposition-based learning (GOBL) strategy is to transform candidates in the current search space to a new search space (Wang, Wu, & Rahnamayan, 2011). By simultaneously evaluating the candidates in the current search space and transformed search space, the solution could jump out from the current search domain and avoid any information gathered during the search. In the GOBL approach, let X _i = (x_i,1, x_i,2, … , x_i,D) be a solution for dimension D in the current search space S, x_ij ∈ [a_j, b_j]. The new solution $x_{\mathit{ij}}^{\mathit{GO}}$ in the transformed space S* is defined as

$$x_{\mathit{ij}}^{\mathit{GO}}=k(a_j+b_j)-x_{\mathit{ij}},x_{\mathit{ij}}\in [a_j,b_j],j=1,2,...D$$ (4)

where k is a random number coming from a uniform distribution in [0,1], which can help obtain a good solution performance in the search space. $x_{\mathit{ij}}^{\mathit{GO}}\in [k(a_j+b_j)-b_j,k(a_j+b_j)-a_j]$ is the generalized opposite candidate solution in the state space. The GOBL strategy has been shown that it can effectively help evolutionary algorithms to jump out of the local optimal and improve the algorithm performance (Chen, Yu, Du, Zhao, & Liu, 2016).

3.1.3. Self-adaptive strategy

The performance of the PSO algorithm highly depends on the control of parameters and velocity update strategy. In order to control the PSO objectively and optimally, a self-adaptive updated strategy is integrated into the GOBL approach for the real-time monitoring algorithm evolution process based on the actual evolution rate of particles in the swarm. During an IPSO process, a population updated rate z in each iteration is defined by the ratio of the actual updated number of particles in the swarm for each iteration, as in

$$z=\frac{s}{N}$$ (5)

where s is the number of updated particles in each iteration and N is the number of particles in the population.

If z is higher than a selected probability p, the global best position $p_g^t$ is used to update the velocity and position. Suppose the updated rate z is less than or equal to a selected probability p which means there is a larger probability that PSO would jump into the local optimal. In that case, the candidate particle $x_{\mathit{ij}}^{\mathit{GO}}$ instead of $p_g^t$ in the velocity updated strategy is employed to guide the population evolution. To be more specific,

$$v_i^{t+1}=w\times v_i^t+c_1\times r_1\times \left(p_i^t-x_i^t\right)+c_2\times r_2\times \left(p_{\mathit{GO}}^t-x_i^t\right)$$ (6)

where $p_{\mathit{GO}}^t$ is the generalized opposition-based point of $p_g^t$ in the search domain.

The basic steps of the proposed IPSO algorithm include:

Step 1: Initialization. Establish the initial values of micro-population size, two acceleration coefficients (c ₁ and c ₂), the maximum number of iterations, selected probability p, and updated rate z; calculate the fitness value for each particle; and set the personal best (p _i) and global best (p _g) for the population.

Step 2: Employ a self-adaptive strategy. Calculate the new update probability z based on Eq. (5); and generate the opposition-based learning particle (p _GO) as in Eq. (4).

Step 3: Update the position and velocity of particles. If z $\le$ p, then the new velocity is updated according to Eq. (5); otherwise, the new velocity is updated by Eq. (1). After we get the new velocity, the new position is updated based on Eq. (2).

Step 4: Update p _i and p _g. Calculate the fitness value for each particle. If the fitness value of the new location is better than the fitness value of p _i, the new location is updated to be the p _i. Then, if the currently best particle in the population is better than p _g, the best particle replaces the recorded global best.

Step 5: Stop and output. Repeat Steps 2–4 until the maximum number of iterations has been reached or the global best solution does not change anymore to save the computing time of algorithms. Then, we finally return the global best solution.

3.2. The proposed hybrid IPSO-DNN model

3.2.1. Deep neural networks

Deep learning (Goodfellow, Bengio, Courville, & Bengio, 2016) involves algorithms that endow machines with intelligence without explicit programming. DNN models have multiple hidden layers located in-between the input and output layers. The units in the hidden layer are fully connected to the input layer, and the output layer is fully connected to the hidden layer. Moreover, the activation function (Wang, Giannakis, & Chen, 2019) is between the input feeding the current neuron and its output going to the next layer. Activation functions are mathematical equations that determine the outcome of a neural network. The function is attached to each neuron in the network and determines whether it should be activated or not, based on whether each neuron’s input is relevant for predicting models. There are many types of activation functions in DNN models, such as Sigmoid, Tanh, and Softmax functions.

Let L be the number of hidden layers, N_i be the number of neurons in layer i and N = {N₁, N₂, …, N_L}, A_i is the activation function in layer i and A ={A₁, A₂, …, A_L}. Parameters L, N, and A are vital and have major influences on the performance of DNN models. Therefore, we propose the IPSO algorithm to optimize the hyperparameters of DNN models with self-adaptive strategy and then explore the evolutionary deep learning hybrid model, IPSO-DNN, to predict the effect of social distancing on the spread of the COVID-19. The DNN model is shown in Fig. 1 .

Fig. 1.

A DNN model with N hidden layers.

3.2.2. Hybrid IPSO with DNN

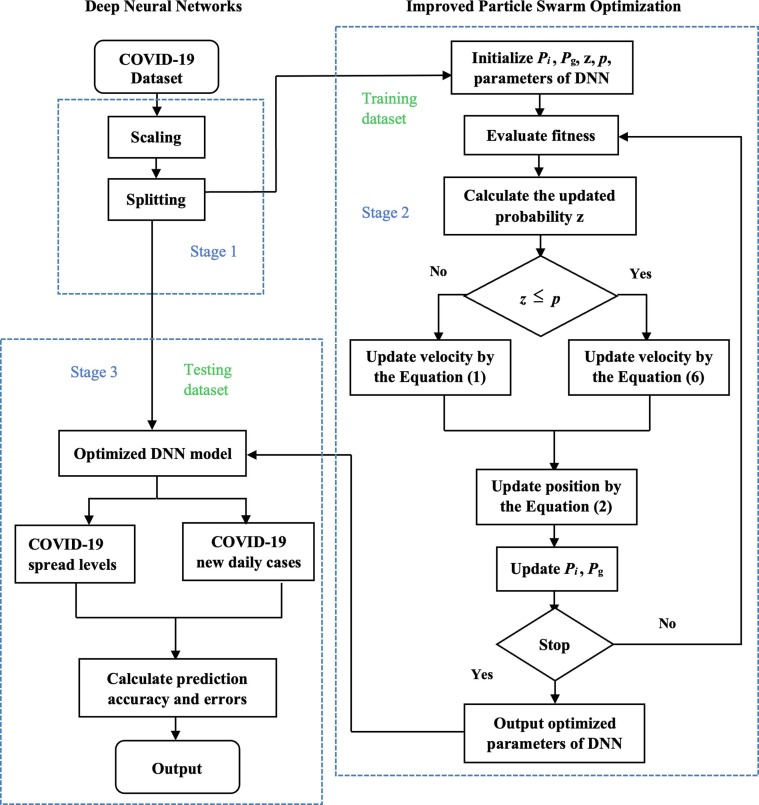
In order to better establish a parameter optimization system for the DNN model, the IPSO algorithm is explored to find the optimal hyperparameters for the DNN model. The flowchart of the hybrid model IPSO-DNN is illustrated in Fig. 2 . It consists of three major stages.

Fig. 2.

Flowchart of the proposed IPSO-DNN model.

Stage I. Prerequisites: data scaling and splitting. One advantage of scaling is avoiding features in large numeric ranges dominating those located in smaller numeric ranges. Another trait is to avoid numerical difficulties during the calculation. Using the standardization of scaling technique, we center the features at mean 0 with a standard deviation 1. The features take the form of a normal distribution, which makes the DNN model easier to learn a mapping from input variables to an output variable.

Moreover, the COVID-19 social distancing dataset (which will be discussed later in Section 4) is divided into two parts, which are training and testing datasets. The training dataset is employed to train the DNN model so that the optimized parameters will be obtained. The testing dataset is applied to the optimized model and outputs the resultant accuracies. In this paper, the ratios of the training and testing dataset are 0.7 and 0.3, respectively.

Stage II. IPSO for parameter optimization of DNN model. In this step, the input is the COVID-19 social distancing training dataset. The output is the optimal configuration in terms of the number of hidden layers, the number of neurons in each layer, and the activation function combinations of hidden layers of the DNN model.

The minimized fitness function of IPSO is defined as the mean squared error (MSE), which is computed as

$$\mathit{MSE}=\frac{1}{n}\sum _{i=1}^n{\left(\stackrel{\wedge }{y_i}-y_i\right)}^2$$ (7)

where n is the number of training datasets, $\stackrel{\wedge }{y_i}$ is the prediction value by the IPSO-DNN model and $y_i$ is the true target metric value of the observation in the social distancing training dataset. When the termination criteria are satisfied, the IPSO algorithm outputs the optimized parameters of the DNN model; otherwise, the next generation of the IPSO algorithm proceeds.

Stage III. Model prediction. The output of the IPSO algorithm is the optimized parameters of the DNN model, and it is used to predict the COVID-19 social distancing dataset. The optimized DNN model is explored to predict the effect of social distancing on the four spread levels and daily new cases of COVID-19. Finally, the prediction accuracy and error results are obtained from the optimized IPSO-DNN model.

4. Data

From the University of Maryland COVID-19 Impact Analysis Platform (Institute, 2020), we collected 603,456 county-level data with the related information of mobility and social distancing in all counties of the United States. The whole dataset contains eight social distancing metrics and the new daily COVID-19 cases in every county from January 1 to July 10, 2020.

4.1. Social distancing metrics

The major non-pharmaceutical interventions and social distancing policies are essential strategies of the public health response to the COVID-19 pandemic around the world. From the evidence of implemented social distancing measures in many countries, such as China and Italy, there is no doubt that social distancing is considered an effective way to mitigate the spread of COVID-19. Social distancing measures include avoiding mass gathering, closing schools and non-essential business, issuing mandatory stay-at-home orders, and having travel restrictions. This social distancing takes many forms, and the nature is to keep people apart from each other by confining them to their homes to reduce contact rates.

Therefore, in this study, from the COVID-19 Impact Analysis Platform, the values of mobility and social distancing metrics that represent people’s reactions to social distancing policies are considered the effect of social distancing on the spread of COVID-19. The platform aggregates mobile device location data from more than 100 million devices across the nation monthly to study human mobility behavior amid the COVID-19 pandemic. The basic metrics in our research are selected to cover the frequency, spatial range, and semantics of people’s daily travel. The eight basic mobility and social distancing metrics are described in Table 2 (Zhang et al., 2020).

Table 2.

Description of eight social distancing metrics.

Social Distancing Metrics	Description
Percentage of residents staying home	Percentage of residents that make no trips more than 1.61 km away from home.
Daily work trips per person	Average number of work trips made per person. A work trip is a trip going to or from one’s imputed work location.
Daily non-work trips per person	Average number of non-work trips made per person.
Distances traveled per person	Distances in kilometers traveled per person on all travel modes (car, train, bus, plane, bike, walk, etc.) per day.
Trips per person	Average number of all trips taken per person per day.
Percentage of out-of-county trips	Percentage of all trips that cross county borders.
Percentage of out-of-state trips	Percentage of all trips that cross state borders.
Transit mode share	Percentage of rail and bus transit mode share.

4.2. Spread level of COVID-19

Moreover, to better describe the spread of COVID-19 as to measure the effect of social distancing in the United States, this study explores four measurable levels (i.e., containment, control, moderation, and growth) based on two performance indicators, which are the daily growth rate and the time to double cumulative cases. The daily growth rate is the percentage increase in cumulative COVID-19 cases, and the time to double cumulative cases is the number of days for cumulative COVID-19 cases to double at the current growth rate. The four levels of COVID-19 spread include containment, control, moderation, and growth that are defined in Table 3 .

Table 3.

Definition of four levels of COVID-19 spread.

Indicators	Containment	Control	Moderation	Growth
Daily growth rate (%)	<=0.1% and	<=1% and	<=10% and	Daily growth rate stays above 10% or time to double cumulative cases stays below 7 days
Time to double cumulative cases (days)	>=700	>=70	>=7

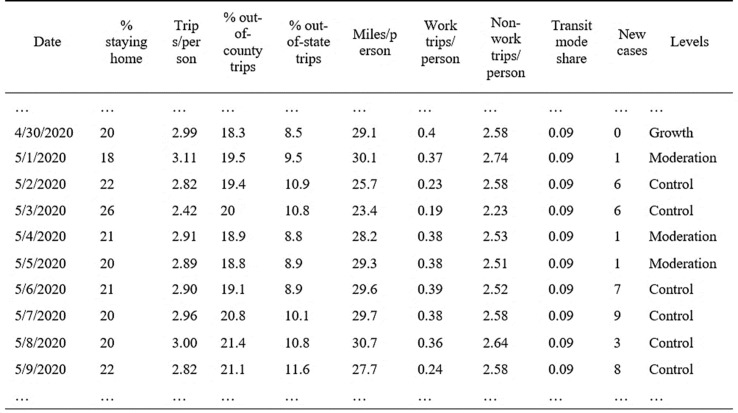
The full COVID-19 social distancing dataset then contains eight input social distancing metrics and two output variables: the new daily COVID-19 cases collected from the COVID-19 Impact Analysis Platform and four levels of COVID-19 spread. The example dataset of Baldwin County, Alabama, from April 30 to May 9, 2020, is shown in Fig. 3 .

Fig. 3.

The exemplary social distancing dataset of Baldwin County, Alabama.

5. Model performance

5.1. Parameters analysis for IPSO algorithm

To choose the appropriate parameters in the proposed IPSO algorithm, two nonparametric statistic tests, Friedman’s test (Friedman, 1937) and Iman-Davenport’s test (García, Molina, Lozano, & Herrera, 2009), are used to analyze the sensitivity of micro-population size and self-adaptive selected probability. The Friedman test (two-way analysis of variance by ranks) is a nonparametric analog of the parametric two-way analysis of variance, and the Iman-Davenport’s test is derived from Friedman’s test, less conservative than Friedman’s. These tests aim to answer whether there are global differences between the different sizes of parameters. The ranks of the Friedman test allow us to determine which sizes employed in the parameters of the IPSO algorithm are significantly better or worse than other sizes. The maximum number of fitness evaluation is 3,000, the learning coefficients of c ₁ and c ₂ are with the value of uniformly distributed between [0,1], and a total of 50 experimental runs for the fitness function are set in Python, except for two analyzed parameters (i.e., micro-population size and selected probability p). The significance level of these nonparametric statistical experiments is 5%.

5.1.1. Micro-population size analysis

In this research, the effect of micro-population size is investigated because the smaller population size is, the lower computational cost of the IPSO algorithm will be. We select the population size from the micro-population set {5,6,7,8,9,10} to verify the performance of IPSO.

Friedman’s test and Iman-Davenport’s test are employed to demonstrate whether the performance of IPSO is significantly affected by different micro-population size settings. In addition, Friedman’s test with multiple comparisons is used to determine the best population size for the proposed IPSO algorithm. The statistical analysis results are shown in Table 4 and Table 5 . From Table 4, we can see that the micro-population size has no significant effect on the overall performance of the proposed algorithm, indicating that the size of the micro-population is not extremely sensitive to the IPSO algorithm, and the algorithm is relatively robust. However, from Table 5, we conclude that when the population size is 8 and the overall performance of the IPSO algorithm is the best.

Table 4.

Results obtained by Friedman and Iman-Davenport tests under different micro-population size.

Friedman value	${\chi }^2$ value	p-value	Iman-Davenport value	value in FF	p-value
3	11.0705	0.70	0.5806	2.3683	0.7146

Table 5.

Ranking results obtained by Friedman’s test under different micro-population size.

Population size	5	6	7	8	9	10
Ranking	4.08	3.81	3.35	2.92	3.35	3.50

5.1.2. Self-adaptive selected probability analysis

In this experiment, the influence of selected probability p is investigated, because p can balance the exploration and exploitation capabilities of IPSO. A small selection probability will prompt IPSO to perform a local search. In contrast, a larger selection probability will encourage IPSO to conduct a global exploration, and the selection probability setting will affect the overall performance of the proposed algorithm. Since the population size in the proposed algorithm is eight, this paper selects parameters from the set {0.125, 0.25, 0.375, 0.5, 0.625, 0.75, 0.875, 1} for the simulation testing.

Friedman’s and Iman-Davenport’s tests are applied to examine whether the performance of the proposed IPSO algorithm is significantly sensitive to different self-adaptive selected probability settings. Moreover, Friedman’s test with multiple comparisons is used to identify the most suitable self-adaptive selected probability for the IPSO algorithm. The statistical results are shown in Table 6 and Table 7 . It can be seen from Table 6 that the choice of selection probability p has a non-significant effect on the optimization performance of the IPSO algorithm. However, from Table 7, when the selection probability is 0.75, the overall performance of the IPSO algorithm is the best, so the selection probability p of IPSO is set to be 0.75.

Table 6.

Results obtained by Friedman and Iman-davenport tests under different selected probability.

Friedman value	${\chi }^2$ value	p-value	Iman-Davenport value	value in FF	p-value
3.1538	14.0671	0.8704	0.4308	2.1206	0.8803

Table 7.

Ranking results obtained by Friedman’s test under different selected probability.

p	0.125	0.250	0.375	0.500	0.625	0.750	0.875	1.000
Ranking	4.65	4.29	4.84	5.04	4.27	3.65	4.31	4.31

5.2. Model comparisons

To evaluate the performance of the proposed IPSO-DNN model, we compare the IPSO-DNN model with other models. To be more specific, IPSO-SVM (Support Vector Machine), IPSO-LR (Logistic Regression), IPSO-DT (Decision Tree), PSO-DNN, GS (Grid Search)-DNN, and BO (Bayesian Optimization)-DNN, all these seven hybrid models prediction accuracy results obtained from the COVID-19 social distancing dataset are thoroughly evaluated. The whole social distancing dataset contains all eight social distancing metrics, the new daily COVID-19 cases, and the four spread levels of COVID in all 3,006 counties of the United States.

The hyperparameters of DNN that are optimized in this paper include 1) the number of hidden layers on the range [1, 100]; 2) the number of neurons in each layer on the range [1, 8]; 3) activation functions consist of Sigmoid, ReLU, Softmax, and Tanh; and 4) the learning rate of DNN model on the range [0.01, 0.99]. The experiments were conducted using Python language on a 4-core machine with a 3.60 GHz Intel® Core™ i7-7700 CPU and 16 GB RAM. In the case of IPSO and PSO, the algorithm terminates when the maximum number of iterations 100 is reached or when the global best solution does not change anymore. The hybrid models terminate when the maximum running time of 1,440 minutes is reached. The performance of the hybrid IPSO-DNN model on the validation, and test stages are examined using accuracy and the following three error measures, which are mean bias error (MBE), mean absolute error (MAE), and root mean squared error (RMSE).

The accuracy helpful to evaluating the performance of the deep learning model is based on the element from a matrix known as the confusion matrix. A confusion matrix is a table that is often used to describe the performance of a classification model on a set of test data for which the true values are known. The “accuracy” of performance of hybrid IPSO-DNN model is defined as following: $\mathit{Accuracy}=\frac{\mathit{TP}+TN}{\mathit{TP}+TN+FP+FN}$, where “TP” is for True Positive, “FP” is for False Positive, “TN” is for True Negative, and “FN” is for False Negative. It is the most common measure of the classification process, which can be calculated as the ratio of correctly classified examples to the total number of samples.

Moreover, MBE indicates whether the model is over-or under-predicted in general. $\mathit{MBE}=\frac{1}{n}{\sum }_{i=1}^n(\stackrel{\wedge }{y_i}-y_i)$. The lower MBE is the better the prediction model is. But you might have zero as some differences are positive and others are negative MAE and RMSE measure residual errors, giving a global idea of the difference between the observed and forecast values. They are defined as $\mathit{MAE}=\frac{1}{n}{\sum }_{i=1}^n\left|\stackrel{\wedge }{y_i}-y_i\right|$,$\mathit{RMSE}=\sqrt{\frac{1}{n}{\sum }_{i=1}^n{\left(\stackrel{\wedge }{y_i}-y_i\right)}^2}$ where n is the total number of observations, $\widehat{y_i}$ is the prediction value and the y_i is the actual value of a data point. The lower the absolute values of the MBE, MAE and RMSE indicate that the IPSO-DNN model is better.

• (1)Comparison with IPSO-SVM, IPSO-LR, and IPSO-DT models

In the first scenario, we compare the performance of the IPSO algorithm based on the optimizing parameters technique for the deep learning models and three different machine learning models to explore the effect of social distancing for COVID-19. SVM is an essential machine learning technique that trains the dataset with feature vectors and uses a large margin for classification. In this paper, the RBF kernel function is selected as the SVM for regression (Yu, 2017). The Logistic Regression (LR) technique is applied to describe data and analyze the relationship between one dependent binary variable and one or more nominal ordinal interval or ratio-level independent variables. Decision Tree (DT) uses the tree representation, and each leaf node corresponds to a class label, and attributes are represented on the internal node of the tree.

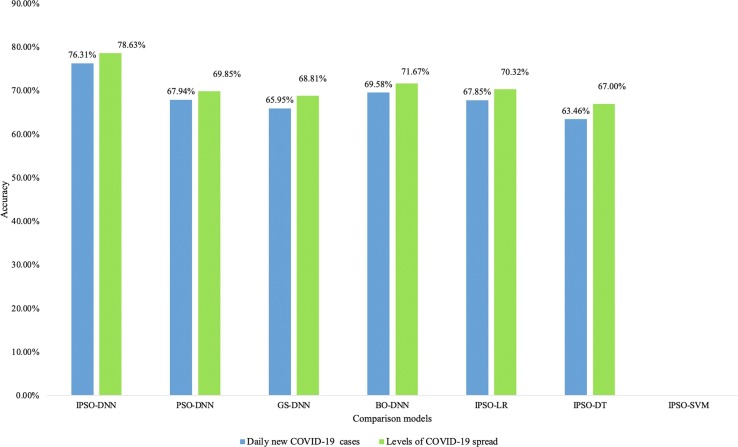
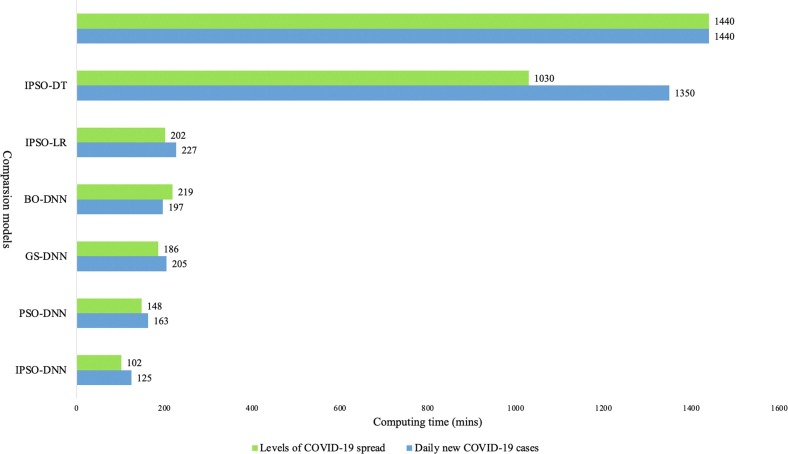
From Fig. 4 and Fig. 5 , we observe that the IPSO-SVM model could not find the optimal solution when it reached the terminated time of 1,440 minutes in the experiments. It fails to explore the effect of social distancing on the spread of COVID-19 according to the termination criteria of maximum running time. Therefore, the computing time of IPSO-SVM is defined as 1,440 minutes. The main reason is that IPSO-SVM needs more computing time to process the large-scale COVID-19 social distancing dataset to output the prediction results. In comparison, all other hybrid models could obtain the global best solution within the maximum running time of 1,440 minutes. The learning times required of IPSO-LR, IPSO-DT, and IPSO-DNN models are 148, 186, and 102 minutes to predict the four spread levels of COVID-19, respectively. For forecasting the new daily COVID-19 cases, the computing time of the above three models is 163, 205, and 125 minutes, respectively. It illustrates that a higher accuracy can be achieved when the proposed IPSO-DNN model has a minimum computing time compared to theIPSO-LR and modified PSO-DT models. This clearly exhibits the superiority of the DNN model over conventional machine learning models in terms of dealing with the large-scale social distancing dataset. Thus, the proposed modified PSO algorithm can serve as a promising candidate for the DNN model parameter tuning for the large-scale COVID-19 social distancing data analysis.

• (2)Comparison with PSO-DNN model

Fig. 4.

Accuracy results of different models.

Fig. 5.

Computing time results of different models.

In the second scenario, the basic PSO algorithm is used to find the best parameters for the DNN model to explore and predict the effect of social distancing for COVID-19. The population size of PSO is 30, and other parameters are defined as the same as the IPSO algorithm. The reason of different population sizes between PSO and IPSO is that the larger the population size, the more scattered the search performed in the PSO algorithm. With a larger population size, each generation takes more function calls, and a larger part of the search space may be visited (Piotrowski, Napiorkowski, & Piotrowska, 2020). Therefore, we set the population size of PSO to 30 instead of 8 to give a better outcome when compared with the modified PSO method.

From Fig. 4, we can see that the accuracy of the IPSO-DNN model is higher than the PSO-DNN model. The generalized opposition-based learning and self-adaptive strategy improve the performance of MODIFIED PSO algorithm to optimize the parameters of the DNN model. For the PSO-DNN, there is no self-adaptive exploitation strategy to help the basic PSO algorithm jump out of local optimal, and the search and optimization ability is also limited. From Fig. 5, the learning times required of the PSO-DNN model are 202 and 227 minutes on the four levels of COVID-19 spread and the new daily COVID-19 cases prediction, respectively. It shows that the computing time of modified PSO-DNN is much less than the PSO-DNN model, it indicates the micro-population setting in the IPSO algorithm decreases the compute cost of PSO algorithm. The results demonstrate that the proposed strategy of PSO in the IPSO-DNN model makes it outperforms the PSO-DNN model on the COVID-19 social distancing prediction.

• (3)Comparison with GS-DNN and BO-DNN models

In the third scenario, the selectable parameter range settings of GS-DNN and BO-DNN are the same as the IPSO-DNN model. The GS algorithm is a common approach for selecting parameter values of the DNN models. However, the GS approach is time consuming and does not perform well in DNN hyperparameter optimization. BO is a sequential model-based optimization algorithm that sets a prior over the optimization function and gathers the information from the previous sample to update the posterior of the optimization function. Therefore, by prioritizing more promising parameters from past results, the BO algorithm can find the best parameters in lesser tuning time than GS.

From Fig. 4, we know that the accuracy results obtained by GS-DNN and BO-DNN models are less than IPSO-DNN on the prediction of new daily COVID-19 cases and COVID-19 spread levels. Fig. 5 shows that the learning times required of the GS-DNN and BO-DNN models to forecast the new daily cases are 1,350 and 219 minutes, respectively. For identifying the four spread levels of COVID-19, GS-DNN and BO-DNN models need 1,030 and 197 minutes of computing time, respectively. Therefore, we learn that the proposed IPSO-DNN model outperforms the GS-DNN and BO-DNN models. The main reason is that the proposed modified PSO-DNN model performs parameters in an evolutionary way, which can balance the local exploitation and global exploration ability during parameter optimization. The results also manifest that the proposed IPSO algorithm is very efficient in determining the hyperparameters of the DNN model.

Table 8 summarizes the performance of seven models in terms of MBE, MAE, and RMSE. First, the proposed IPSO-DNN model performs very well in predicting new COVID-19 cases per day. The performances of PSO-DNN, GS-DNN, BO-DNN, and IPSO-LR are similar in predicting daily new cases and COVID-19 spread levels. The IPSO-SVM model fails to explore the effect of social distancing on new COVID-19 daily cases based on the limited computing time. Although the MAE and RMSE of IPSO-DNN and IPSO-DT models are close, the MBE of the IPSO-DT model is negative, which indicates IPSO-DT under-predict the daily new COVID-19 cases. The results demonstrate that the proposed self-adaptive strategy of IPSO-DNN can help find optimal parameters for the DNN model with fewer errors. In addition, for the four COVID-19 spread levels, the IPSO-SVM model cannot output the solution in a limited computing time. The proposed IPSO-DNN model outperforms other models in all MBE, MAE, and RMSE on predicting the effect of social distancing on COVID-19 spread. The summary results indicate that the IPSO-DNN model provides better prediction results than other models as the proposed methods have the advantage of employing optimal parameters. Therefore, the proposed IPSO algorithm with the self-adaptive strategy in deep evolutionary learning is significantly to predict and analyze the effect of social distancing on COVID-19 spread for the DNN model.

Table 8.

Results of seven models for predicting the effect of social distancing on COVID-19 spread.

Model	Daily new COVID-19 cases			Levels of COVID-19 spread
	MBE	MAE	RMSE	MBE	MAE	RMSE
IPSO-DNN	4.6767	4.8177	45.0471	0.4160	0.4755	1.0313
PSO-DNN	6.4295	6.8436	52.6956	0.6932	0.6636	1.2112
GS-DNN	7.4152	7.4152	65.8293	0.7569	0.7575	1.3121
BO-DNN	6.1002	6.1002	49.3345	0.4057	0.4032	1.1870
IPSO-SVM	–	–	–	–	–	–
IPSO-LR	6.3868	6.4229	55.5791	0.6291	0.6562	1.2086
IPSO-DT	−0.5064	5.7326	45.7731	−0.0336	0.6385	1.1933

5.3. Experimental results and discussion

Our experiments focus on predicting and analyzing the effect of social distancing on the spread of COVID-19 using the proposed IPSO-DNN model in the selected five states, Washington, California, New York, Florida, and Texas in the United States. In five selected states, collect and pre-process the COVID-19 social distancing county-level dataset from the first confirmed case date to July 10, 2020. This experiment explicitly considers the stay-at-home order, reopening state, and social distancing restrictions in each state. Set all experimental environments and parameters as the same as in Section 5.3. We predict the daily new COVID-19 confirmed cases and the spread of COVID-19 under the different social distancing measures adopted by each state and then analyze the distinct COVID-19 outcomes of taking social distancing interventions in the selected five states in the United States. Fig. 6 and Table 9 indicate the accuracy and error measures obtained from the proposed IPSO-DNN model. The detailed description of COVID-19 social distancing in the above selected five states is illustrated as follows.

• (1)Washington

Fig. 6.

Accuracy results of all selected five states obtained from IPSO-DNN.

Table 9.

Results of five states for COVID-19 social distancing prediction.

State	Daily new COVID-19 cases			Levels of COVID-19 spread
	MBE	MAE	RMSE	MBE	MAE	RMSE
Washington	6.2397	6.2397	23.9902	0.3738	0.5447	1.1004
California	26.2249	26.2249	30.1224	0.2756	0.5359	1.0723
New York	27.0441	27.5170	35.2950	0.1264	0.5069	0.9628
Florida	16.9829	18.0634	89.2466	0.2382	0.5958	1.0907
Texas	4.7137	5.2478	47.3079	0.3268	0.3877	0.9545

Since the Centers for Disease Control and Prevention (CDC) confirmed the first case of 2019 Novel Coronavirus in the United States occurred in Washington on January 21, 2020, the COVID-19 pandemic first began to outbreak in the state of Washington (Branswell, 2020). Because there was no vaccination available for the COVID-19 pandemic at that time, therefore Washington state issued a stay-at-home order on March 23 and reopened the state step by step on May 31 later.

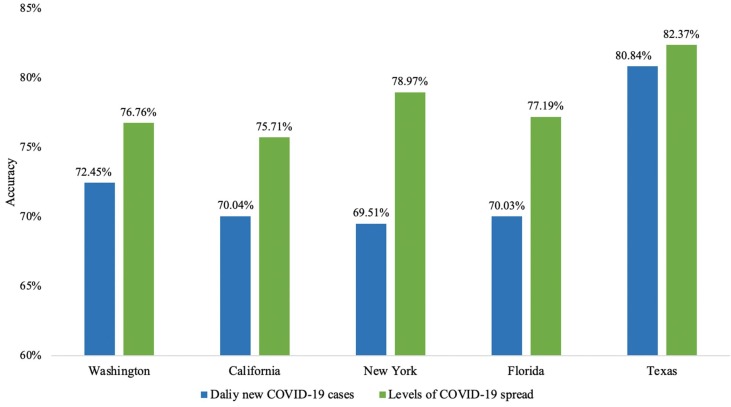
Using the IPSO-DNN model, we can obtain the prediction results of the effect of social distancing on the spread of COVID-19 in Washington state. Firstly, from Fig. 6, we can see that our proposed IPSO-DNN model acquires 72.45% and 76.46% accuracy in predicting new daily COVID-19 cases and COVID-19 spread levels, respectively. In Table 9, the results of error measure MBE, MAE, and RMSE are 6.2397, 6.2397, and 23.9902 on the prediction of new daily COVID-19 cases, respectively. And the results of these error measures are 0.3738, 0.5447, and 1.1004 on the forecasting of COVID-19 spread levels, respectively. The above prediction results manifest that the optimized IPSO-DNN model can self-adaptive tuning parameters of DNN for Washington state to achieve more than 70% prediction accuracy with minor errors.

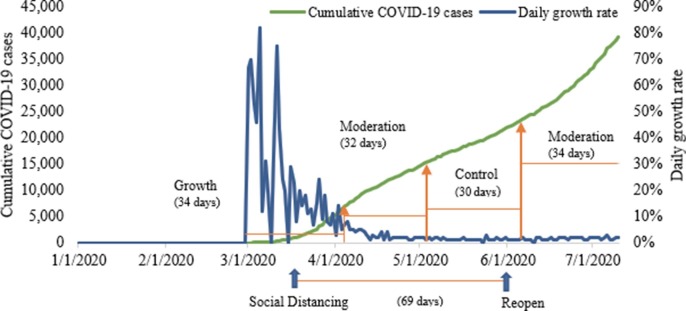
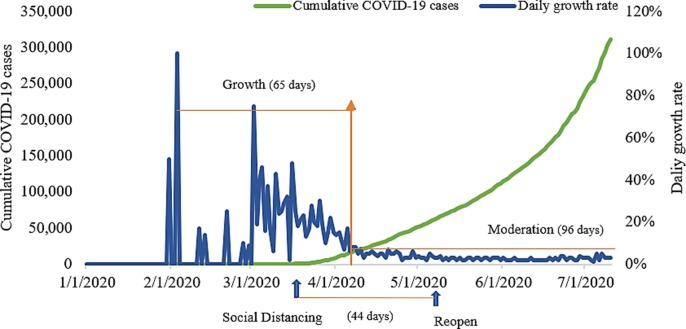
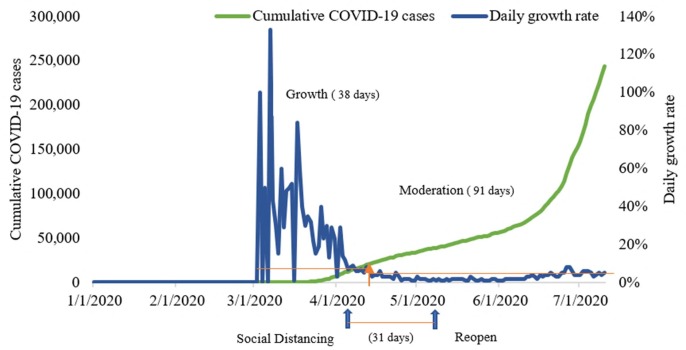
Secondly, Fig. 7 presents that the spread of COVID-19 has slowed down with the efforts of related social distancing measures. However, these aggressive interventions do not show immediate results, which are essential to control COVID-19 in the future. The duration of adopting restricted social distancing is 69 days in Washington. From levels of COVID-19 spread, we know that the number of new cases in Washington kept growing for 34 days from February 29 to April 2, 2020. And after being issued stay-at-home order on March 23, there was a distinct outcome in Washington. The spread of COVID-19 has been moderated for 32 days and controlled for 30 days. However, reopening the state on May 31 means that social distancing orders would not be taken as aggressively as before, so that the progress of control this coronavirus has been slowed down and the level of cumulative COVID-19 cases still increased in Washington till to the end, July 10, 2020. Therefore, following a spike in COVID cases in July, Washington announced a pause to the Safe Start reopening plan.

Fig. 7.

Cumulative COVID-19 cases & Daily growth rate in Washington.

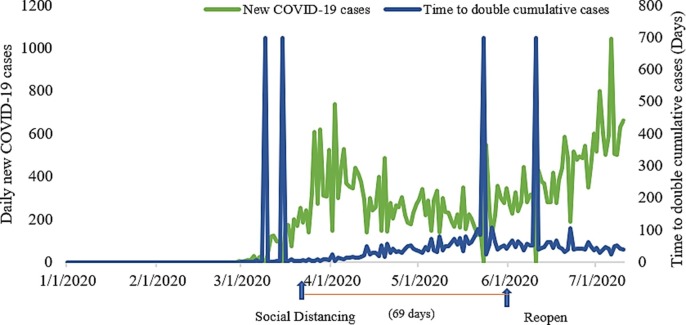
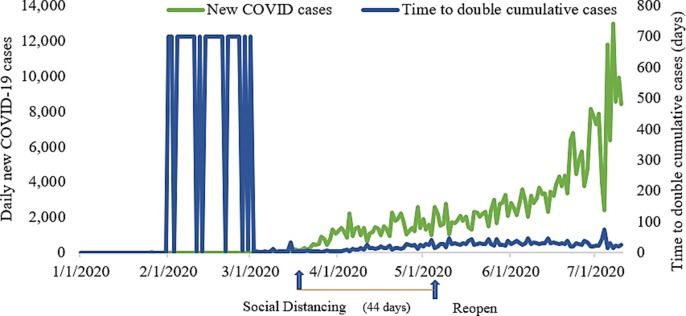
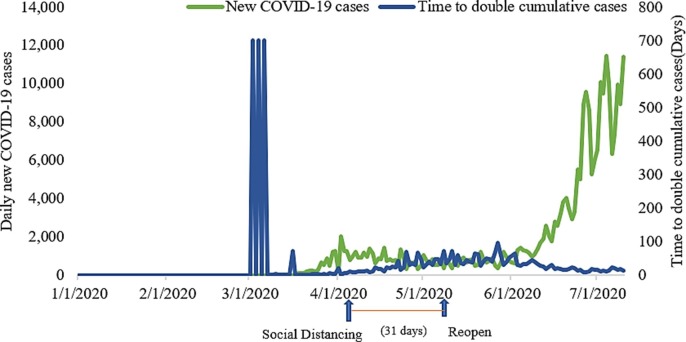
Finally, in Fig. 8 , we can see that the effective social distancing measures mitigate the spread of the COVID-19 pandemic with a significant decline in the new daily COVID-19 cases and extend the time to double the cumulative cases in Washington during the social distancing period. In addition, we can learn that reopening Washington state reduces the implementation efforts of social distancing policies and changes the state's mobility metrics values, which also increases the daily new COVID-19 cases and the time to double the cumulative cases decreasing from May 31 to July 10, 2020. After social distancing, the daily new COVID-19 cases are declining in Washington state. We can see that there is a relationship between social distancing and the spread of COVID-19. In general, if social distancing intervention has been implemented strictly and longer, COVID-19 infections would decrease quickly in an even shorter time. The above results also manifest that our proposed IPSO-DNN model can adjust the prediction direction continually to predict the effect of social distancing on the spread of the COVID-19 pandemic based on the changing value of mobility and social distancing metrics in Washington.

• (2)California

Fig. 8.

Daily new cases & Time to double cumulative cases in Washington.

California is the second state where the COVID-19 pandemic outbroke following Washington in the United States. Its first case of coronavirus was confirmed in Orange County on January 26, 2020. On March 19, California became the first state to issue a stay-at-home order, mandating all residents to stay at home except to go to an essential job or shop for essential needs in the United States (Linder, 2020). In California, social distancing interventions only last for 44 days.

From the experiment results, Fig. 6 indicates that the proposed IPSO-DNN model can obtain more than 70% accuracy on predicting new daily COVID-19 cases and COVID-19 spread levels in California. Table 9 shows that for predicting the new daily COVID-19 cases in California, the results of MBE, MAE, and RMSE are 26.2249, 26.2249, and 30.1224, respectively; for predicting the levels of COVID-19 spread, the results of these error measures are 0.1264, 0.5069, and 0.9628, respectively. The proposed IPSO-DNN model performs better on COVID-19 spread levels prediction than new daily COVID-19 cases because social distancing intervention has more distinct outcomes on controlling the spread of COVID-19 in California.

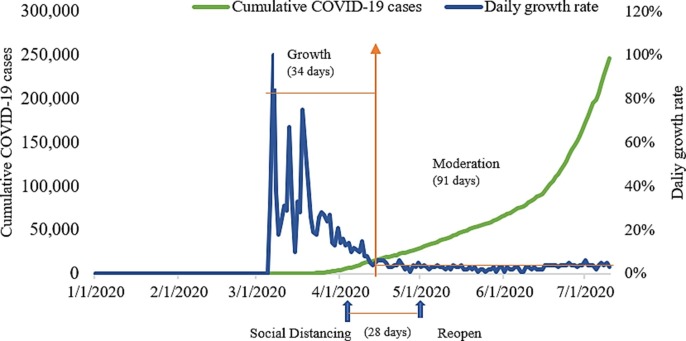
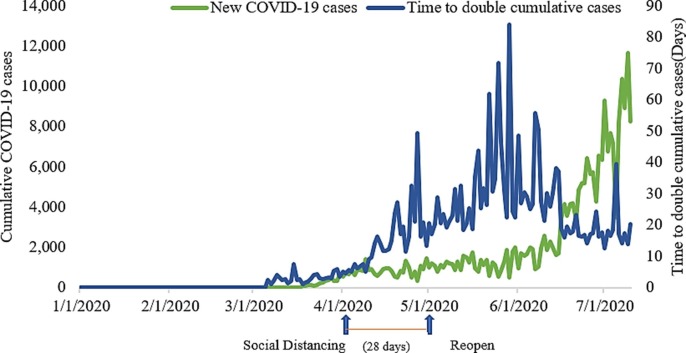
Fig. 9 demonstrates that social distancing mitigates the COVID-19 within two weeks. However, due to the limited time of implementing social distancing compared to Washington state, only moderation but not control of COVID-19 engendered in California during this period. For instance, after the stay-at-home order and related strict social distancing rules were issued on March 19, social distancing efforts took 16 days to slow down the spread of COVID-19 effectively and moderately not control COVID-19 spread for the following 96 days in California. Recently, California is mainly closing again amid a spike in COVID-19 cases across the state on October 10. Compared to Washington state, we can learn that aggressive social distancing and long-lasting social distancing interventions are required to control the spread of COVID-19. The new daily COVID-19 cases and time to double the cumulative cases are described in Fig. 10 . There is no doubt that social distancing plays a vital role in decreasing the daily new cases and increasing the time to double the cumulative cases in California. The results obtained from the proposed IPSO-DNN model demonstrate that the significant effect of social distancing on mitigating COVID-19 in California, and more importantly, the duration of social distancing interventions needs to be lasting longer to help flatten the COVID-19 pandemic curve.

• (3)New York

Fig. 9.

Cumulative COVID-19 cases & Daily growth rate in California.

Fig. 10.

Daily new cases & Time to double cumulative cases in California.

Although Washington and California COVID-19 outbroke before New York, New York was the first hotspot state of COVID-19 pandemic in the United States due to its soaring cases of COVID-19 in just a few days. As a result, New York became the U.S. epicenter of the novel coronavirus outbreak, which killed tens of thousands of state residents and left hundreds of thousands more infected with COVID-19. Although on July 10, New York still had the most COVID-19 cumulative cases, which is 401,193 cases, in the United States.

However, according to our analysis results, New York has already controlled the spread of the COVID-19 pandemic for the foreseeable future. The aggressive social distancing interventions are the only way New York obtained moderation and control events in the COVID-19. Under the New York state’s plan, all four phases of the reopening require New Yorkers to adhere to social distancing guidelines, including wearing masks or face coverings in crowded public spaces, on public or private transportation, or in for-hire vehicles (Gold & Stevens, 2020). In this paper, we consider when all counties in New York entered Phase 1, the start of the reopening process, as the reopen date of New York state, which was June 8, 2020.

In New York, strictly social distancing has been implemented 78 days which is the longest among the selected five states in the United States. New York is also the only state that mandates people to wear masks or face coverings in public whenever social distancing was not possible initially. Table 9 indicates that MBE, MAE, and RMSE results are 27.0441, 27.5170, 35.2950 on forecasting daily new cases, respectively; and 0.1264, 0.5069, and 0.9628 for the levels of COVID-19 spread prediction, respectively. Fig. 6 presents that the prediction accuracy is 69.51% for the daily new cases and 78.97% for the levels of COVID-19 spread. The accuracy result of COVID-19 spread levels is higher than the new daily COVID-19 cases. Presumably, the new cases soaring up abruptly in such a short time makes it hard to project.

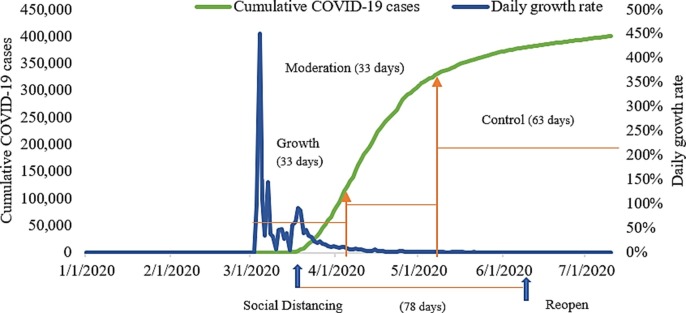
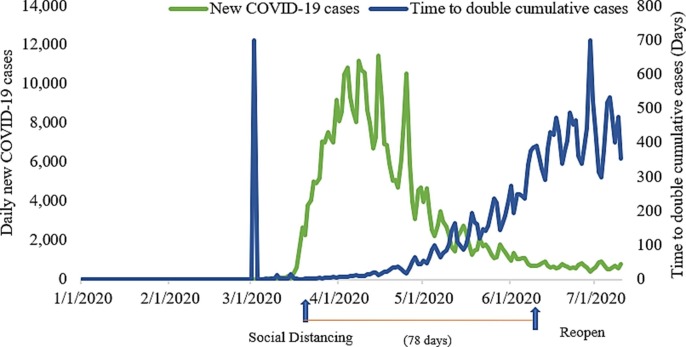
Fig. 11 and Fig. 12 illustrate New York has controlled the spread of COVID-19 and its new daily COVID-19 cases continue to decrease with implement aggressive social distancing interventions for 78 days. After social distancing, the days of moderation and control of COVID-19 are 33 days and 63 days, respectively. It is evident that social distancing helps to flatten the COVID-19 curve in New York. Moreover, it makes sense that the number of new daily COVID-19 cases has continued to decline and flatten. However, we can see from Fig. 12 that the time to double cumulative cases does not steadily increase. It means that even if New York state has controlled the COVID-19 pandemic, it may be vulnerable to contagion from other states who fail to control the COVID-19 or do not conduct aggressive social distancing interventions. The above results explicitly explain how social distancing flattens the COVID-19 pandemic curve in New York using our proposed IPSO-DNN model.

• (4)Florida and Texas

Fig. 11.

Cumulative COVID-19 cases & Daily growth rate in New York.

Fig. 12.

Daily new cases & Time to double cumulative cases in New York.

Florida and Texas have emerged as new hotspots in the COVID-19 pandemic in the United States due to the explosion of COVID-19 cases after reopening states in early May. These two states are also the states where the related social distancing politics are not adopted very strictly, and reopening the states is faster than other selected states. The date when issued the stay-at-home order on April 2 in Florida and Texas, and the date of reopening state was on May 4 in Florida and May 1 in Texas.

The sharp rise in COVID-19 cases in Florida and Texas illustrates the risk of letting people pack together in places such as bars and movie theaters and the need to take a cautious approach to reopen (Olson, 2020). Until October 6, Florida and Texas recorded a sharp increase in COVID-19 infections for many days (Provan, 2020). Especially, Texas has overtaken California as a US state with the second-highest death toll on September 21. The durations of practicing social distancing in Florida and Texas are just 31 days and 28 days, respectively. And there is no strict reopening social distancing guideline in these two states.

From Fig. 6, we know that prediction accuracy results obtained from the IPSO-DNN model are 70.03% on new daily COVID-19 cases and 77.19% on the levels of COVID-19 spread in Florida. Meanwhile, the accuracies of Texas on the prediction of new daily COVID-19 cases and COVID-19 spread levels are 80.84% and 82.37%, respectively. It is noticed that the IPSO-DNN model performs better in Texas than in Florida. Perhaps it is because Texas paused the state’s reopening plan after reporting a record increase in COVID-19 cases and hospitalizations in June (Jasmine, 2020). Therefore, Texas adopted more strict reopening guidelines, and the mobility values are more stable to predict the spread of COVID-19 than Florida. From Table 9, for predicting new daily COVID-19 cases, the results of MBE, MAE, and RMSE are 16.9829, 18.0634, and 89.2466 in Florida, 4.7137, 5.2478, and 47.3079 in Texas, respectively. For estimating the levels of COVID-19 spread, these results are 0.2382, 0.5958, and 1.0907 in Florida, 0.3268, 0.3877, and 0.9545 in Texas, respectively. In general, these evaluation results demonstrate that our proposed model performs very well on the spread of COVID-19 in the United States.

Fig. 13 and Fig. 15 show that the COVID-19 is still rapidly spreading in Florida and Texas. Although these two states still suffer from the COVID-19 pandemic, there is a significant development of social distancing in mitigating the spread of COVID-19. From Fig. 14 and Fig. 16 , the results illustrate that Florida and Texas perform very poorly in reducing the COVID-19 cases due to the lack of restricted social distancing guidelines. The new daily COVID-19 confirmed cases in Florida and Texas all speed up, and the time to double the cumulative cases has not reduced significantly after reopening the state. It indicates the consequence of COVID-19 outbreaks due to a lack of lasting and aggressive social distancing interventions. Therefore, we learn that social distancing plays a vital role in mitigating the spread of the COVID-19 pandemic in these states.

Fig. 13.

Cumulative COVID-19 cases & Daily growth rate in Florida.

Fig. 15.

Cumulative COVID-19 cases & Daily growth rate in Texas.

Fig. 14.

Daily new cases & Time to double cumulative cases in Florida.

Fig. 16.

Daily new cases & time to double cumulative cases in Texas.

Table 9 shows the summary results of the MBE, MAE, and RMSE evaluation measures acquired from our proposed IPSO-DNN model in the above selected five states. The performance of IPSO-DNN on predicting levels of COVID-19 spread in all five states is better than the daily new COVID-19 cases. It is possible that the value of daily new cases is more random than levels of COVID-19 spread. In general, the IPSO-DNN model performs very well on predicting COVID-19 based on social distancing influence in all the selected five states. Therefore, it reveals that the effect of social distancing can be represented as mobility metrics which has a significant impact on the COVID-19 spread. The duration of social distancing is also crucial to control this COVID-19 pandemic.

6. Conclusions

The kernel hyperparameters significantly influence the performance and must be set and tuned for the DNN model. It is quite time-consuming and computationally expensive for traditional methods to select the optimal hyperparameters for DNN. Therefore, we utilize the advantages of global and local exploration capabilities from Evolutionary Algorithms (EAs) to improve the hyperparameter configuration for deep learning models. Particle Swarm Optimization (PSO) is a powerful and efficient evolutionary method to help the DNN model find optimized hyperparameters. However, the PSO tends to converge prematurely on local optima, especially in complex multimodal functions. Therefore, we propose a hybrid IPSO-DNN model, which employs improved PSO to optimize the parameters of the DNN model by conducting a self-adaptive strategy and generalizing opposition-based learning in the micro population setting. We also analyze the parameters (i.e., micro-population size and the value of selected probability) on two nonparametric statistic tests: Friedman’s and Iman-Davenport’s tests to determine the best parameters of the IPSO algorithm to improve the performance of DNN.

In this paper, we explore the IPSO alogirthm based parameter value selection technique that optimizes the DNN model by selecting the number of hidden layers, the number of neurons in each layer, and the activation functions in each layer. Our results show that the proposed IPSO-DNN model is useful and efficient in exploring the effect of social distancing in deep learning on the spread of COVID-19. We demonstrate the performance of our proposed hybrid model outperforms other compared models, such as IPSO-SVM, IPSO-LR, IPSO-DT, PSO-DNN, BO-DNN, and GS-DNN, in terms of prediction accuracy and computing time. The obtained results indicate that the proposed self-adaptive strategy can help the IPSO algorithm find out optimization parameters for the DNN model. The developed IPSO-DNN model also explains how social distancing helps flatten the COVID-19 curve in Washington, California, New York, Florida, and Texas. It also shows social distancing is essential to control the spread of COVID-19, as well as the duration and degree of implementing social distancing interventions also matter. Therefore, our proposed IPSO-DNN model provides an effective method for tuning the hyperparameters of DNN in a self-adaptive evolutionary way and holds great potential to predict the effect of social distancing on the spread of COVID-19.

As for future work, we would consider improving the performance of the IPSO algorithm in a stricter environment and demonstrating its performances on public datasets for solving more generally challenging problems in the real world. We also intend to explore the modified PSO to optimize larger DNN or other deep learning models, such as Convolutional Neural Networks (CNN) and Recurrent Neural Networks (RNN), to solve multiple and challenging emergency management tasks. We will also consider many new powerful activation functions, such as Softplus, MPELU, PreLU, EreLU, to improve the performance of deep learning models. Moreover, some other improved versions of the PSO algorithm. For instance, the proposed exploiting barebones PSO (BBePSO) and a dynamic exploiting barebones PSO (DBBePSO) perform very well on optimizing hyperparameters. Therefore, we will focus on developing evolutionary algorithms and systematic adaptation schemes in hyperparameters configurations to balance the exploration and exploitation in the deep learning models.

CRediT authorship contribution statement

Dixizi Liu: Conceptualization, Methodology, Software, Writing – original draft. Weiping Ding: Investigation, Writing – review & editing. Zhijie Sasha Dong: Methodology, Writing – review & editing, Validation, Supervision. Witold Pedrycz: Writing – review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.