Seaport throughput forecasting and post COVID-19 recovery policy by using effective decision‐making strategy: A case study of Vietnam ports

Abstract

This study deals with the dynamic interactions between seaports and decision-making strategy for seaport operations by utilizing four-dimensional fractional Lotka-Volterra competition model under frequently disrupted by time-delay factor. Nonlinear analysis methods, including equilibrium analysis, stability evaluation, and time series investigation, are intensely explored to describe the cooperation and competition dynamics in maritime logistics. The dynamical analysis indicates that the port competition system shows a complex and highly nonlinear behaviour, notably illustrating unstable equilibria and even chaotic phenomena. Besides, nonlinear dynamical interactions in seaport management have been analysed by exploiting fractional calculus (FC) and system dynamics theory. Novel multi-criteria decision-making strategies realized by the neural network prediction controller (NNC) and adaptive fractional-order super-twisting sliding mode control (AFOSTSM) have been presented for dealing with throughput dynamics under parametric perturbations and external disturbances. Particularly, the active control algorithms are implemented to ensure the recovery strategy for throughput growth of Vietnam ports in the post-coronavirus (COVID-19) pandemic era. The case study has confirmed the efficacy of the proposed strategy by using system dynamics and control theory. The simulation results show that the average growth rates of container throughput can be ensured up to 7.46% by exploiting resilience management scheme. The presented method can be also utilized for providing managerial insights and solutions on efficient port operations. In addition, the control strategies with neural network forecasting can help managers obtain timely and cost-effective decision-making policy for port sustainability against unprecedented impacts on global supply chains related to COVID-19 pandemic.

1. Introduction

The port environment has substantially changed over the past decade with an increasing cooperative and competitive business settings. Seaport ecosystems can no longer be the isolated nodes in which they are dynamically interacted with each other at only a local scale in regional port governance; but within the globally integrated networks of complex supply chains (Marasco and Romano, 2018, Kavirathna et al., 2019). Port ecosystems are regarded as an essential maritime sector in facilitating trade, as well as taking on more responsibility in the global supply chain networks (Zhang & Lam, 2017). Thus, it is beneficial to understand underlying dynamics of complex seaport networks (Ishii, Lee, Tezuka, & Chang, 2013). Investigating dynamical behaviours of the seaport networks will play an important role for optimizing port ecosystems in the maritime transportation networks (Fleming & Baird, 1999). As such, dynamical analysis can be an effective tool to elucidate the internal behaviours of a large and complex seaport system and to describe dynamic interactions with other members in wide area network. Accordingly, this will enhance the efficiency and the viability of maritime port ecosystem (Lertpattarapong, 2002). Not surprisingly, several earlier studies have investigated how seaports are actually linked with each other going beyond a pure competition framework (Fleming and Baird, 1999, Ishii et al., 2013, Asgari et al., 2013, Marasco and Romano, 2018).

Regarding the evolution of species interactions, population studies have been extensively performed in biology and ecology by utilizing many models to investigate the dynamic relationships among various species (Bhargava and Jain, 1985, Zhang and Lam, 2017). There exists the analogy between biological species and maritime logistics systems in competition and coexistence environment; it will be interesting to explore multiple interactions among seaport ecosystems by exploiting solutions in population ecology (Marasco & Romano, 2018). The mathematical models used in ecology provide a unique approach for characterizing dynamic competition and coexistence among seaports (Zhang & Lam, 2013). As a mathematical model which was introduced for describing the predator–prey relationships among species, the Lotka-Volterra equation has been used to capture a wide range of competition and cooperation dynamics in many areas. This model was initially applied to analyze the dynamic interactions between competing groups and in-demand forecasting in the social science and industrial marketing (Bhargava and Jain, 1985, Modis, 2011, Chiang, 2012). The Lotka–Volterra model has been also applied to explore the evolution of competition for innovation resources between enterprises, third-party online payment systems, etc. (Wei et al., 2018, Mao et al., 2020). Several studies have been carried out for possible applications of the Lotka-Volterra model in the maritime supply chain networks (see Table 1 ). However, most current studies have examined the relationships between two or three ports located in the same area. In reality, seaport networks are often involved in the mix of competition and cooperation for many members located in different countries. Therefore, this paper explores dynamic interactions analytically as well as numerically in the seaport groups by extending Lotka-Volterra model up to a four-dimensional dynamical system.

Table 1.

Literature of competition in maritime logistics by utilizing Lotka-Volterra model.

Reference	Competitors	Model dimension	Methodology	Case study
Zhang and Lam (2013)	Maritime cluster	2	Forecasting evolution process by equilibrium point and its stability study	No case study
Twrdy and Batista (2016)	Container port	5	Time series analysis and forecasting	Northern Adriatic ports
Zhang and Lam (2017)	Maritime cluster	2	Investigating the evolution of maritime clusters empirically through equilibrium analysis	London and Hong Kong ports
Marasco and Romano (2018)	Inter-port	6	Exploring port competitive environment and quantitative analysis of port dynamics	Le Havre-Hamburg ports

In recent years, the theory of fractional calculus has been considered as a practical approach to deal with dynamical systems, in which mathematical models can describe many real-world phenomena more efficiently than classical integer-order methods. In fact, better memory and hereditary properties can be gained by exploiting fractional-order system. The fractional derivatives and integral provide more flexibility in real-world system design. The fractional-order Lotka-Volterra system has attracted a great deal of attention due to its theoretical and practical significance (Agrawal et al., 2012, Akinlar et al., 2014). Although fractional order calculus is a recent field of mathematical analysis with wide applications in many related fields (Aghababa, 2012, Yin et al., 2013, Akinlar et al., 2014, Wang et al., 2019, Ahmed et al., 2021), this technique has not yet been fully utilized in a real port management system. In this study, the fractional-order Lotka-Volterra model has been proposed to analytically explore the underlying mechanism and the interaction characteristics of the seaport operations.

Port enterprise is operating under constantly changing business environment with competition that makes it difficult to meet its strategic goals reliably. There exist severe disruptions due to unpredictable factors impacting the effectiveness and agility of the supply chain management (Justice et al., 2016, Zhang and Lam, 2017, Marasco and Romano, 2018). They can often lead to complex behaviours in system components and transportation service, eventually impacting port productivity. The existence of non-linear behaviour will also add to unpredictability. Dynamical analysis has been presented to describe underlying mechanisms of the cooperation and competition of port networks, and to improve system performance (Ishii et al., 2013, Sayareh and Ahouei, 2013, Zhang and Lam, 2017, Marasco and Romano, 2018). In fact, nonlinear system theory can provide a powerful tool to explore the dynamic properties of a real system (Slotine and Li, 1991, Morris and Pratt, 2003, Aghababa, 2012, Cuong et al., 2021). However, very few empirical studies have been attempted to describe the dynamical behaviours of the port competitions by utilizing nonlinear technique. This approach could provide a deeper understanding of the interaction mechanism between seaports, so that the decision makers can then come up with appropriate optimization and management strategies for their port operational business (Zhang & Lam, 2013). This paper aims to fill the research gaps between theory and practice in applying nonlinear analysis tools, such as equilibrium analysis, Lyapunov exponent (LE) evaluation, and time series investigation, to explore port dynamical behaviour. Then the managers and decision makers can gain greater insights into nonlinear phenomena, such as periodicity, stability with bifurcation, and chaotic behaviours of the port ecosystem.

In addition to traditional port operation management, several logistics enterprises are on their ways to improve the efficiency of maritime operations and to increase global competitiveness leading to productivity growth, against supply chain uncertainties such as the COVID-19 epidemic (Nikolopoulos, Punia, Schäfers, Tsinopoulos, & Vasilakis, 2020). The ongoing global pandemic has tested the ingenuity, resilience, and agility of global supply chains. New management strategies should dramatically improve visibility across supply chain networks, and support companies’ ability to reconcile such unexpected shocks. One novel way to characterize the port management business is to employ deep learning algorithms for forecasting and optimization strategies. Deep learning is a subset of machine learning where artificial neural networks can learn from large amounts of data. Recently, neural networks have become a useful tool in identifying mathematical models for complex dynamical systems (Lazar and Pastravanu, 2002, Åkesson et al., 2005, Vasičkaninová and Bakošová, 2015). The neural network algorithm can be utilized to obtain the optimal values such that it can effectively estimate non-linear system dynamics. The neural network predictive control schemes can be realized in many fields by minimization of a cost function, providing an approximated solution by the idea of using a neural network as function approximator (Lazar and Pastravanu, 2002, Åkesson et al., 2005, Ortega and Camacho, 1996, Khan et al., 2019). Moreover, the combination of NNC with other algorithms help the complete control system achieve goals and targets (Vasičkaninová and Bakošová, 2015, Yen et al., 2019). Novel adaptive fractional-order sliding mode control algorithm forces the dynamical system to slide along the sliding surface and achieve robustness against system uncertainties and external disturbances (Cuong et al., 2021). Moreover, it has already been shown that the dynamic effects of time-delays in goods and information are prevalent in the supply chain management. The stability and performance of the delayed system gradually deteriorates as the magnitude of the delay increases. This article will provide a new solution for seaport operations by utilizing neural network predictive techniques to optimize container throughput. An adaptive fractional-order super twisting sliding mode control scheme is incorporated to build a robust management algorithm against market volatility and external disruptions along with time-delay effects in maritime transport environment. Then, the port management system realized by neural network prediction controller (NNC) and adaptive fractional-order super-twisting sliding mode control (AFOSTSM) enables port authorities to make better use of labour and port equipment and to obtain real-time information for decision-making.

The rest of this paper is organized as follows. In Section 2, the port productivity integrations are described by four dimensions of fractional order Lotka-Volterra model, and then dynamical analysis is performed to illustrate system behaviour. In Section 3, the control schemes are implemented for chaos suppression and synchronization under disruptions. In Section 4, case studies and numerical simulations are carried out to demonstrate the effectiveness of the designed controller to describe the growth rate of container throughput. Finally, conclusions are made in Section 5.

2. Port interactions and dynamical analysis

2.1. Fractional order calculus (FC)

The concept of non-integer order calculus is increasingly used to describe the dynamic behaviour of real systems in various fields of science and engineering (Aghababa, 2012, Agrawal et al., 2012, Yin et al., 2013, Akinlar et al., 2014, Wang et al., 2019). This realm includes a branch of mathematical analysis dealing with arbitrary derivatives and integrals (including complex-order). Fractional-order differential equations are naturally related to most biological systems with memory (Agrawal et al., 2012). Furthermore, the fractional-order differential equation could be used for demonstrating the phenomena which cannot be described by the integers order method. In the realm of fractional order calculus, the popular definitions are Caputo and Riemann-Liouville derivatives. Caputo concept usually has more physical meaning and is simpler to obtain numerical solutions than Riemann–Liouville derivative (Sontakke & Shaikh, 2015). In addition, the initial value with Caputo derivative is the same as that of integer differential equation. The operator, denoted by D^αf(t), is a combined differentiation-integration of a function f(t) commonly used in fractional calculus with fractional order of α. The fractional order calculus can be defined in a unified way such that

$$D^{\alpha }f(t)=\frac{1}{\mathrm{\Gamma }(m-\alpha )}{\int }_0^t\frac{f^{(m)}(\chi )}{{(t-\chi )}^{\alpha +1-m}}d\chi$$ (1)

where $\mathrm{\Gamma }(.)$ is the gamma function defined as $\mathrm{\Gamma }(\alpha )={\int }_0^t{e}^{-t}{t}^{\alpha -1}dt$; $m-1⩽\alpha ⩽m$, in which $m$ is the smallest integer that is equal or greater than α. By using a non-integer order of α, the mathematical model can possibly capture more dynamics of the given systems. The Riemann–Liouville calculus is more commonly applied in pure mathematics. The Riemann-Liouville fractional differential operator is defined by

$$D^{\alpha }f(t)=\frac{1}{\mathrm{\Gamma }(m-\alpha )}\frac{d^n}{d{t}^n}{\int }_0^t\frac{f(\chi )}{{(t-\chi )}^{\alpha +1-m}}d\chi$$ (2)

For the Riemann-Liouville operator, fractional-order derivative problems require homogeneous initial conditions, whereas initial value problem holds for both homogeneous and non-homogeneous conditions for the Caputo fractional operator (Agrawal et al., 2012). As shown in Eqs. (1), (2), the Caputo fractional derivative is more restrictive than the Riemann-Liouville. In fact, it requires the existence of the m-th derivative of the function. Fortunately, most functions that appear in practical applications fulfil this requirement (Sun, Zhang, Baleanu, Chen, & Chen, 2018). In this paper, Caputo’s definition of fractional differentiation will be employed to explore dynamical behaviours of the Lotka-Volterra model.

2.2. Port competition and cooperation dynamics

Seaport operations play vital roles in maritime supply chain solutions. Managing seaports today requires understanding the diverse roles of multiple entities, their interactions, and the transaction models. For ecological system models among multiple competitors, the dynamics of species populations can be described in light of port management and operations. In reality, population dynamics depends on interactions or predator prey relationship between different competing species. The seaports will grab the limited customer resources and can profit by attempting to expand their market shares on a national level, as well as on more regional and local levels (Zhang & Lam, 2017). Considering that seaports are interacting with each other in the same area, the fractional Lotka-Volterra (or predator–prey) model can be used to characterize the system dynamics among multiple seaports in the framework of collaboration and competition (Zhang and Lam, 2013, Marasco and Romano, 2018) as follows:

$$\frac{d^{\alpha }{x}_i(t)}{d{t}^{\alpha }}=x_i(a_i+\sum _{j=1}^n{b}_{\mathit{ij}}{x}_i{x}_j)(i=1,2,...,n)$$ (3)

where n is the number of the port in the maritime logistics network; $x_i=x_i(t)$ is the transaction size of the container throughput of i-th port at time t; d^αx_i(t)/dt indicates the fractional-order growth rate of the throughput transaction at i-th port, for $\alpha \in \text{[}0,1]$; a_i denotes growth rate coefficient of port I; b_ij and b_ji are the interaction coefficients from port i to port j and vice versa. As explained in Table 2 , the dynamic model (3) shows that positive coefficients will increase the growth rate of a competitor, while negative coefficients decrease it.

Table 2.

Multi-mode competition and cooperation of the port management system.

i	j	Type of interaction	Explanation
Sign (bij)	Sign (bji)
+	+	cooperation	port i and port j mutually promote each other
+	–	competition	port j plays a facilitating role for port i and port i plays a role in blocking port j
–	+	competition	port j plays a role in blocking port i and port i play a role in promoting port j
–	–	pure competition	port i and port j mutually compete with each other
0	0	neutralism	There is no interaction

Recently, dynamical systems with delays have evolved as a major topic in nonlinear sciences. Time delays arise naturally in numerous systems such as traffic flow, supply chain management, and economic models. There exist many factors in supply chain disruptions which may affect the cost, timing, or risk. One of the main problems that can affect negative impact on operational performance will be the time-delay factors (Othman, Sanusi, Arof, & Ismail, 2019). The stability and performance of the system gradually deteriorates as the magnitude of the delay increases. In general, the delay factors can deter the successful completion or execution of port operations within the allocated time frame. Due to delay factors, the actual transport plans will be significantly affected, and the port enterprise spends more resources than usual on handling the port’s container volume (Othman et al., 2019). Delays factors also disrupt the container handling operation and affect the effectiveness of the cooperation between ports (Sayareh and Ahouei, 2013, Yousefi et al., 2012). In this paper, the time delay will be considered to characterize the interaction dynamics in port management and operations. Time delay is a shift in the effect of a state on an output dynamic response. The four-dimensional model contains fundamental system parameters with time delay terms that affect the growth rate of the port throughput. Based on Eq. (3), the fractional dynamic model can be obtained as follows:

$$\begin{array}{c}\frac{d^{{\alpha }_1}{x}_1(t)}{d{t}^{\alpha 1}}=x_1(t)\left[a_1+b_{11}{x}_1(t-{\tau }_1)+b_{12}{x}_2(t-{\tau }_2)+b_{13}{x}_3(t-{\tau }_3)+b_{14}{x}_4(t-{\tau }_4)\right]\\ \frac{d^{{\alpha }_2}{x}_2(t)}{d{t}^{\alpha 2}}=x_2(t)\left[a_2+b_{21}{x}_1(t-{\tau }_1)+b_{22}{x}_2(t-{\tau }_2)+b_{23}{x}_3(t-{\tau }_3)+b_{24}{x}_4(t-{\tau }_4)\right]\\ \frac{d^{{\alpha }_3}{x}_3(t)}{d{t}^{\alpha 3}}=x_3(t)\left[a_3+b_{31}{x}_1(t-{\tau }_1)+b_{32}{x}_2(t-{\tau }_2)+b_{33}{x}_3(t-{\tau }_3)+b_{34}{x}_4(t-{\tau }_4)\right]\\ \frac{d^{{\alpha }_4}{x}_4(t)}{d{t}^{\alpha 4}}=x_4(t)\left[a_4+b_{41}{x}_1(t-{\tau }_1)+b_{42}{x}_2(t-{\tau }_2)+b_{43}{x}_3(t-{\tau }_3)+b_{44}{x}_4(t-{\tau }_4)\right]\end{array}$$ (4)

where ${\tau }_i\in {\mathfrak{R}}^{+}$ is the plant dead time (or time-delay). The dynamical behaviour is explored to obtain greater insights into rich nonlinear phenomena, such as periodicity, limit cycle, and chaotic behaviours of the port operations. Port management system is a complex dynamical system composed of highly interconnected components in which the comprehensive underlying property cannot be described by dynamical behavior of the individual parts alone. The estimated coefficients and system parameters which used for numerical simulation are listed in Table 3 . The system parameters should be chosen appropriately to illustrate complex, dynamic, and highly competitive environment of port operations, notably illustrating unstable equilibria and chaotic phenomena. So, several parameters are referred from previous studies which exhibit the chaotic behavior of the Lotka-Volterra system (Agrawal et al., 2012, Vaidyanathan, 2016). Moreover, since the analogy exists between biological species and port ecosystems, the mathematical models used in ecology competition provide a unique approach for describing dynamic competition environment in the maritime sector and seaports (Zhang and Lam, 2017, Twrdy and Batista, 2016). Thus, the selected parameter in Table 3 was referred from previous works on biological systems (Bhargava and Jain, 1985, Vaidyanathan, 2016). In addition, these parametric values have been optimally adjusted through the simulation process by the built-in software to describe complete system dynamics of the port ecosystem.

Table 3.

Model parameters.

Parameters	Values	Parameters	Values	Parameters	Values
a1	1	b41	−0.15	b33	−0.57
a2	0.42	b12	−0.05	b43	−0.66
a3	0.57	b22	−0.42	b14	−0.40
a4	0.72	b32	−0.49	b24	−0.44
b11	−1	b42	−0.31	b34	− 0.08
b21	−0.12	b13	−1.75	b44	−0.72
b31	−0.64	b23	−0.02

2.3. Eigenvalue analysis

First, the eigenvalue analysis is presented to clearly describe the local stability around the equilibrium points. The equilibrium state means that there is no dynamic change over time for each port operation (Zhang & Lam, 2017). In reality, the port performance is affected by both the designed capacity and actual handling volume which are influenced by the competition and cooperation between ports in the port ecosystem (Wang, Monios, & Zhang, 2020). Thus, it is necessary to quantitatively assess the equilibrium analysis of the port network to find out the trajectory over time and local stability of the system at an equilibrium state.

Proposition 1

Consider the fractional-order Lotka-Volterra model(4),

$$D^{\alpha }x(t)=f(x(t-\tau ))\alpha \in \left(0,1\right]$$ (5)

where f(x) is a vector of nonlinear functions of the state variable vector x(t). The equilibrium points of the nonlinear system (5) are calculated by making all rates of the state variables simultaneously zeros, or f(x) = 0. These equilibrium points are locally unstable if all eigenvalues (${\lambda }_i$) of the Jacobian matrix $J\equiv \frac{\partial f}{\partial x}$ evaluated at the equilibrium points satisfy the following conditions:

$$\left|arg({\lambda }_i)\right|>\frac{\alpha \pi }{2},\alpha =max({\alpha }_1,...{\alpha }_n),i=1,...,n$$ (6)

Then the fractional system is asymptotically stable at the equilibrium point.

Proof

The equilibrium points of the system (3) are determined by letting $f_i(x_1,x_2,x_3,x_4)=0$, or solving the following equations:

$$\left\{\begin{array}{c}{a}_1{x}_1+b_{11}{x}_1^2+b_{12}{x}_1{x}_2+b_{13}{x}_1{x}_3+b_{14}{x}_1{x}_4=0\\ a_2{x}_2+b_{21}{x}_1{x}_2+b_{22}{x}_2^2+b_{23}{x}_2{x}_3+b_{24}{x}_2{x}_4=0\\ a_3{x}_3+b_{31}{x}_1{x}_3+b_{32}{x}_2{x}_3+b_{33}{x}_3^2+b_{34}{x}_3{x}_4=0\\ a_4{x}_4+b_{41}{x}_1{x}_4+b_{42}{x}_2{x}_4+b_{43}{x}_3{x}_4+b_{44}{x}_4^2=0\end{array}\right)$$ (7)

From the port operation perspective, all equilibria should be nonnegative for ensuring local stability. Hence by solving the Eq. (7) leads to equilibria, $E_1=({\overline{x}}_1^{*},{\overline{x}}_2^{*},{\overline{x}}_3^{*},{\overline{x}}_4^{*})=(0,0,0,0)$ and $E_2=({\overline{x}}_1^{**},{\overline{x}}_2^{**},{\overline{x}}_3^{**},{\overline{x}}_4^{**})$. By using the system parameters given in Table 3, the equilibrium E₂ is obtained by $E_2=(\text{2.9930},\text{0.4007,}\text{0.2764,}\text{0.4759})$. Then the Jacobian matrix (J_i) evaluated at the equilibrium point E_i (i = 1,2) is obtained by

$$J_i={\left[\begin{array}{cccc}{j}_{11}& b_{12}{\overline{x}}_{1i}& b_{13}{\overline{x}}_{1i}& b_{14}{\overline{x}}_{1i}\\ b_{21}{\overline{x}}_{2i}& j_{22}& b_{23}{\overline{x}}_{2i}& b_{24}{\overline{x}}_{2i}\\ b_{31}{\overline{x}}_{3i}& b_{32}{\overline{x}}_{3i}& j_{33}& b_{34}{\overline{x}}_{3i}\\ b_{41}{\overline{x}}_{4i}& b_{42}{\overline{x}}_{2i}& b_{43}{\overline{x}}_{3i}& j_{44}\end{array}\right]}_{E_i}$$ (8)

where

$$\begin{array}{c}{j}_{11}=a_1+2b_{11}{\overline{x}}_{1i}+b_{12}{\overline{x}}_{2i}+b_{13}{\overline{x}}_{3i}+b_{14}{\overline{x}}_{4i}\\ j_{22}=a_2+b_{21}{\overline{x}}_{1i}+2b_{22}{\overline{x}}_{2i}+b_{23}{\overline{x}}_{3i}+b_{24}{\overline{x}}_{4i}\\ j_{33}=a_3+b_{31}{\overline{x}}_{1i}+b_{32}{\overline{x}}_{2i}+2b_{33}{\overline{x}}_{3i}+b_{34}{\overline{x}}_{4i}\\ j_{44}=a_4+b_{41}{\overline{x}}_{1i}+b_{42}{\overline{x}}_{2i}+b_{43}{\overline{x}}_{3i}+2b_{44}{\overline{x}}_{4i}\end{array}$$ (9)

From the parameters given in Table 3, the eigenvalues of the characteristic equation with equilibrium point E ₁ are calculated as: λ ₁ = 0.420, λ ₂ = 0.5700, λ ₃ = 0.720 and λ ₄ = 1.000. Similarly, there are four eigenvalues in case of E ₂: λ ₁ = −5.932, λ ₂ = −1.653, λ ₃ = −0.773 and λ ₄ = −0.424. Based on Routh Hurwitz's stability criterion, the equilibrium E ₂ is a stable since all of the eigenvalues have negative; the equilibrium point E ₁ is saddle nodes since all eigenvalues have positive real roots, and the argument of eigenvalues is satisfying the condition, $\left|arg({\lambda }_i)\right|<\frac{\alpha *\pi }{2}$ (Matignon, 1996). These complete the proof.

For stable equilibrium E ₂, no matter what capacity size of each port has in the maritime network, the trajectory evolves over time and reaches equilibrium E ₂. In the opposite ways of growth near saddle node E ₁, the port dynamics will become unstable. As such, it can be concluded that mutual port competition and collaboration exist in unstable states, which makes the system behaviours complex and challenging to manage. In what follows, the chaotic phenomena are analysed to further clarify the underlying dynamical behaviours of the port ecosystem.

2.4. Lyapunov exponent analysis

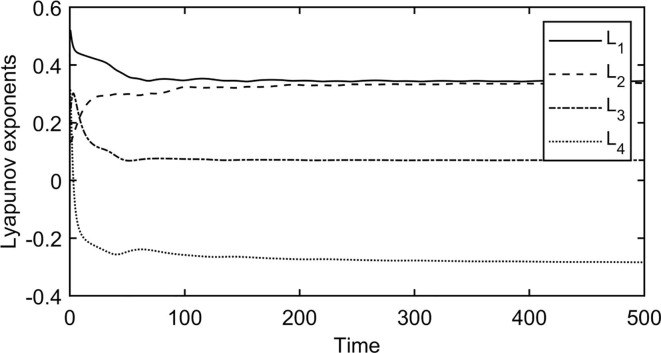
Deterministic chaos is a typical phenomenon for nonlinear dynamical system such as Lotka-Volterra model. The Lyapunov exponent (LE) is the principal criteria for characterizing chaotic behaviour of dynamical system (Lassoued et al., 2019, Açıkgöz et al., 2020, Othman et al., 2019). The LE detects the presence of chaos and quantifies the stability of the dynamical system. This criterion represents the growth or decline rate of small perturbation along each dimension of the phase space system. It is worthy to note that describing chaotic behaviour in port operations can help decision makers understand the dynamic fluctuations of the container throughput. By identifying chaos, they can obtain short-term container volume predictions with greater accuracy. For the port competition model (4), Lyapunov exponents are calculated using the method proposed by Wolf, Swift, Swinney, and Vastano (1985). Lyapunov exponent measures the mean exponential expansion or contraction of a system flow in phase space plane with the given initial conditions. Thus, the positive LE means chaos in the dynamical system with measuring sensitivity to changes in its initial conditions. The obtained Lyapunov spectrum is illustrated in Fig. 1 . The positive LEs (L₁, L_2, and L₃) which describe the expansion degree of the attractor in the phase space, are 0.3446, 0.3373, and 0.0701, respectively, while negative LE (or L₄ = −0.2838) will increases the contraction degree of the chaotic attractor.

Fig. 1.

Lyapunov exponent spectrum of the Lotka-Volterra model.

The Kaplan-Yorke dimension of the dynamical system (4), which describes the complexity of the strange attractor, is given by

$$D_L=j+\frac{1}{\left|L_{j+1}\right|}\sum _{i=1}^j(L_i)=2.6498$$ (10)

where j is equal to n − 1 with n numbers of Lyapunov exponents. As described in theory, the Kaplan-Yorke criterion is obtained in the range of 2–3. Thus, the dynamical system (2) generates chaotic behaviours characterized by fractional-order dimension (Kaplan & Yorke, 1979). The chaotic behaviour is identified in the seaport ecosystem. This phenomenon indicates that the system will be apparently chaotic under the dynamic interactions of port network. Consequently, the container throughput dynamics will be highly sensitive to initial conditions (Aghababa, 2012, Açıkgöz et al., 2020).

2.5. Time-series investigation

Under initial conditions (x ₁, x ₂, x ₃, x ₄) = (0.18, 0.30, 0.10, 0.45), the phase plane diagram of the strange attractor for the chaotic system are illustrated in Fig. 2 . Investigating system behaviours over time is a qualitative tool to describe the dynamics of container volume through the seaports.

Fig. 2.

2D-3D phase portraits of the port competition system with α₁ = α₂ = α₃ = α₄ = 0.98: x₁(t)-x₂(t), (b) x₁(t)-x₃(t), (c) x₁(t)-x₄(t), (d) x₁(t)-x₂(t)-x₃(t) , (d) x₁(t)-x₂(t)-x₄(t) , and (d) x₂(t)-x₃(t)-x₄(t).

Recently, the port operation integration with the global supply chain has received a great deal of attention. An efficient seaport management can be an important factor influencing competitive supply chain system. The operational delays can have a significant impact on efficiency and productivity of supply chains, such as the duration of a ship's stay in port, period of sedimentation of goods, and freight payment (Jafari, 2013). Thus, investigating the impact of time delay on port operations plays a major role in understanding port dynamics. In this analysis, the system behaviour is obtained by varying the time delay (or dead time) in the range [0, 2.7]. It is noted that τ = 0 represents a system that is not disrupted by any delay factor. As shown in Fig. 3 , the system behaviours are very sensitive to time-delay variations, which include changes in both amplitude and frequency of each operating cycle of port management.

Fig. 3.

Time evolution of the state variables by varying time delays: (a) x₁ plane, (b) x₂ plane, (c) x₃ plane and (d) (c) x₄ plane.

In addition, the vital advantage of the fractional systems in comparison with classical integer-order models is the ability to inherit the nature of the dynamic processes (Sun et al., 2018). Fig. 4 shows the time history of state variables of the Lotka-Volterra model by varying values of the fractional-order time-delay. It can be seen that system dynamics may significantly change even if fractional order variation is small. These dynamic properties have not been recognized in most previous studies which typically employed an integer-order calculus. Next, nonlinear control techniques will be introduced to deal with chaos behaviour as well as optimize port operations.

Fig. 4.

Time evolution of the state variables for different values of fractional order: (a) x₁ plane, (b) x₂ plane, (c) x₃ plane and (d) x₄ plane.

3. Improvement of port operation using control synthesis

3.1. The perturbed system model

Port operations might benefit from the active management strategy to maximize productivity and achieve a sustainable competitive advantage. In the port service system, the relationships among port operations are unknown or uncertain (Zhang & Lam, 2013). The uncertainties are generally represented by two kinds of risk terms including parametric perturbations and external disturbances caused by a range of factors such as socioeconomic aspects and supply chain disruptions in response to market changes. Recently, the influence of these factors on global economic activities and port logistics has been intensified by the COVID-19 pandemic (Nikolopoulos et al., 2020). COVID-19 has disrupted global supply chains severely. The port authority should take short-term actions to respond to business disruptions and supply chain challenges from global spread of COVID-19 crisis. The traditional operation model should be transformed into digital supply networks for ensuring visibility, sustainability, agility, and optimization. To deal with these uncertainties, the advanced management frameworks have been applied for optimizing decision-making strategy (Asgari et al., 2013, Ishii et al., 2013, Nguyen et al., 2020). It is known that an optimal management system for improving port efficiency and productivity can be realized by nonlinear control theory with machining learning algorithm. In this paper, the control schemes will be involved in implementing a synchronization strategy for all system states of Lotka–Volterra model to the reference system. Through the synchronization strategy by active control, the growth rate of the container throughput is enhanced by securing the growth rate of the benchmark reference port, eliminating the uncertainty and time delays against volatile market. For active control synthesis, the fractional dynamical model in Eq. (4) is rewritten by using a vector–matrix form with perturbed factors and control input as follows:

$$D^{\alpha }x=Ax(t-\tau )+f(x(t-\tau ))+\mathrm{\Delta }x(t-\tau )+\delta +u$$ (11)

where $x={[x_1,x_2,x_3,x_4]}^T\in {\mathfrak{R}}^4$ are state vector of the system, $\alpha ={\left[{\alpha }_1,{\alpha }_2,{\alpha }_3,{\alpha }_4\right]}^T\in {\mathfrak{R}}^4$ is the fractional-order vector and $u={[u_1,u_2,u_3,u_4]}^T\in {\mathfrak{R}}^4$ is the control input vector, and the external disturbances are described by $\delta ={[{\delta }_1,{\delta }_2,{\delta }_3,{\delta }_4]}^T\in {\mathfrak{R}}^4$. The perturbed term $\mathrm{\Delta }x(t-\tau )$ represents the parametric variations applied to the four state variables of the system with time delay, in which the time delays are given by $\tau ={\left[{\tau }_1,{\tau }_2,{\tau }_3,{\tau }_4\right]}^T\in {\mathfrak{R}}^4$. The system matrix A with a fixed nominal parameter is given by $A=diag(a_1,a_2,a_3,a_4)$. Besides, $f(v)$ is a vector of nonlinear terms in the system,

$$f(v)=\left[\begin{array}{c}{x}_1(t)\left[b_{11}{x}_1(t-{\tau }_1)+b_{12}{x}_2(t-{\tau }_2)+b_{13}{x}_3(t-{\tau }_3)+b_{14}{x}_4(t-{\tau }_4)\right]\\ x_2(t)\left[b_{21}{x}_1(t-{\tau }_1)+b_{22}{x}_2(t-{\tau }_2)+b_{23}{x}_3(t-{\tau }_3)+b_{24}{x}_4(t-{\tau }_4)\right]\\ x_3(t)\left[b_{31}{x}_1(t-{\tau }_1)+b_{32}{x}_2(t-{\tau }_2)+b_{33}{x}_3(t-{\tau }_3)+b_{34}{x}_4(t-{\tau }_4)\right]\\ x_4(t)\left[b_{41}{x}_1(t-{\tau }_1)+b_{42}{x}_2(t-{\tau }_2)+b_{43}{x}_3(t-{\tau }_3)+b_{44}{x}_4(t-{\tau }_4)\right]\end{array}\right]$$ (12)

The reference model by fixing the parameter values and neglecting external perturbation is described as the master system. For synchronization scheme, the fractional-order model in Eq. (11) under the time delay and perturbation is considered a slave system, in which the slave model should be synchronized to the master system (Agrawal et al., 2012).

The decision-making strategy is to determine control input vector u for manipulating the state variables of the closed-loop system (11) to track reference signals (or desired trajectories). Thus, the regulated error system is defined as follows:

$$D^{\alpha }e=A(e+x_m)+f(e+x_m)+\mathrm{\Delta }(e+x_m)-D^{\alpha }{x}_m+\delta +u$$ (13)

where $e={\left[e_1,e_2,e_3,e_4\right]}^T\in {\mathfrak{R}}^4$ be the error vector between the master ($x_m$) and the slave system, or $e=x(t-\tau )-x_m$. Based on the error dynamics Eq. (13), the control algorithms are designed to ensure that the error dynamics are asymptotically stable for all initial conditions, or $\underset{t\to \infty }{lim}∥e(t)∥=0$. More precisely, the active control action in Eq. (11) is realized in two stages with the hybrid design schemes: $u_{\mathit{NNC}}$ ($\in {\mathfrak{R}}^4$) is the vector of the neural network predictive controller (NNC) scheme, and $u_{\mathit{AFOSTSM}}$ ($\in {\mathfrak{R}}^4$) is the adaptive fractional-order super-twisting sliding mode control algorithm. The NNC control strategy has no feedback information to the input layer of the neural network and thus the output signal does not affect the closed-loop system. By adding AFOSTSM scheme which has an output feedback loop can provide more information on the neural network, thereby significantly improving control performance (Wang et al., 2019, Cuong et al., 2021). In fact, AFOSTSM algorithm will be activated when the state variables exceed some bounds causing overshoots or oscillations. The adaptive controller will eliminate these disruptions ensuring the closed-loop stability and performance. The schematic diagram of the container throughput management with the hybrid scheme is illustrated in Fig. 5 .

Fig. 5.

Block diagram of the proposed NNC and AFOSTSM control scheme.

3.2. Neural network predictive control

As illustrated in Fig. 6 , the neural network model utilizes the previous control input and the previous plant output to predict future values of plant output. Then the neural network predictive controller uses a neural network model to predict plant performance (Beale, Hagan, & Demuth, 2017). This strategy defines the control input $u_{\mathit{NNC}}$ that will optimize plant performance over a specified future time horizon $N_{u_{\mathit{NNC}}}$.

Fig. 6.

Neural network structure with multi-layers of artificial neurons.

The first step to obtain the predictive value is to identify the plant model by training a neural network for representing the future dynamics of the plant. The training signal is the error between the network output and actual plant output. Cost function quantifies the error signal and presents it in the form of a single real number. Next, the plant model is utilized by the neural network controller (NNC) for performance prediction (see Fig. 7 ). The predictive algorithm is used to define the control action that optimizes the following cost function in the specific horizon of time:

$$J=\sum _{j=N_1}^{N_2}{\left[x_d(t+j)-x_m(t+j)\right]}^2+\varsigma \sum _{j=1}^{N_u}{\left[u_{\mathit{NNC}}^{,}(t+j-1)-u_{\mathit{NNC}}^{,}(t+j-2)\right]}^2$$ (14)

with additional condition:

$$\mathrm{\Delta }{u}_{\mathit{NNC}}(t+j-1)=0,\text{and}1⩽N_{\mathit{uNNC}}⩽j⩽N_2$$ (15)

where N ₁ is the minimum prediction horizon, N ₂ is the prediction horizon, $N_{u_{\mathit{NNC}}}$ is control input horizon, x_m is reference trajectory, and $\varsigma$ is the weighting factor which is often chosen by $\varsigma =0$. The variable $u_{\mathit{NNC}}^{,}$ is the tentative control signal from the optimization block to the neural network model for training (see Fig. 7). The most important parameter in the predictive control algorithm is the control horizon $N_{u_{\mathit{NNC}}}$ since the control output should be kept at a constant value over infinite time. The optimization goal is to find the values of model parameters for which cost function returns as small as possible. The control action sequence can be achieved over the prediction horizon by reducing the cost function J with respect to the vector $u_{\mathit{NNC}}$,

$$\frac{\partial J}{\partial u_{\mathit{NNC}}}=0,\text{and}{u}_{\mathit{NNC}}={\left[u_{\mathit{NNC}}(t-d),u_{\mathit{NNC}}(t-d+1),...,u(t-d+N_{u_{\mathit{NNC}}})\right]}^T$$ (16)

Fig. 7.

Schematic diagram of neural network predictive controller.

Numerical analysis is utilized for minimization of the cost function. The cost function J is defined as fitting parameters that should be minimized. In fact, this function measures the performance of a neural network model for given data. Some parameter constraints such as upper or lower bounds are imposing for this optimization (Beale et al., 2017). The testing scenario and numerical simulation result will be provided in Section 4.

3.3. Adaptive fractional-order super twisting controller

Based on the sliding mode control theory (Wang et al., 2019, Ahmed et al., 2021, Lee et al., 2021), the sliding surface ($\sigma$) of each error variable e_i (i = 1, 2, 3, 4) and its time derivative are defined as follows:

$$\sigma (t)=h(D^{\alpha -1}e+D^{\alpha }e)\text{and}\dot{\sigma }(t)=h(D^{\alpha }e+D^{\alpha +1}e)$$ (17)

where $h\in {\mathfrak{R}}^4$ are the designed positive constants which determine the convergence rate for tracking error. The robust control synthesis is equivalent to solve the finite-time stabilization problem for the perturbed system against uncertainties as follows:

$$\dot{\sigma }=h(Ax+f(x)+\mathrm{\Delta }x-x_m+\delta +u+D^{\alpha +1}e)=h_1+h_2\delta +h_{3}u$$ (18)

where $h_1=h(Ax+f(x)+\mathrm{\Delta }x-x_m+u_{\mathit{NNC}}+D^{\alpha +1}e)$ and $h_2=h_3=h$. The control law u is realized by two-stage structure by combining the equivalent control and the sliding model control algorithm,

$$u(t)=u_{\mathit{eq}}+(1/h_3)u_{\mathit{AFOSTSM}}$$ (19)

In this scheme, the equivalent part u_eq = −h ₁ /h ₃ is a continuous control law for nominal dynamics of the supply chain system. To drive the state of the system on the sliding surface,$u_{\mathit{AFOSTSM}}$ is realized by a discontinuous control using AFOSTEM scheme. This switching control law can cope with external disturbance and parametric uncertainty, attenuating the chattering. This strategy can improve the control performance against disruptions which are a prevalent in managing supply chain networks. Thus, the sliding mode dynamics in Eq. (18) can be rewritten as $\dot{\sigma }=h_2\delta +u_{\mathit{AFOSTSM}}$. The AFOSTSM algorithm is realized as follows:

$$\left\{\begin{array}{c}{u}_{\mathit{AFOSTSM}}(t)=-\gamma {\left|\sigma \right|}^{1/2}\text{s}ign(\sigma )+\omega \\ \dot{\omega }(t)=-\lambda sign(\sigma )\end{array}\right)$$ (20)

where $\gamma =\gamma (\sigma ,\dot{\sigma },t)$ and $\lambda =\lambda (\sigma ,\dot{\sigma },t)$ are some gains to be designed; $\omega$ is the parameter to be updated by adaptive law.

Theorem 1

Consider the fractional order dynamical model in Eq.(11)and the sliding surface variable proposed by Eq.(17). If the control strategy(19)is realized to the port management system, then the tracking error in Eq.(13)will converge to zero asymptotically with the following adaptive gains:

$$\dot{\gamma }(\sigma ,\dot{\sigma },t)=\left\{\begin{array}{c}{\nu }_1\sqrt{\frac{{\epsilon }_1}{2}},if\sigma \ne 0\\ 0,if\sigma =0\end{array}\right)$$ (21)

$$\lambda (\sigma ,\dot{\sigma },t)=2\beta \gamma +\eta +4{\beta }^2$$ (22)

where the control gains (${\nu }_1,{\epsilon }_1,\beta$, and η) are arbitrary constants ($\in {\mathfrak{R}}^{+}$). The control scheme given by Eq. (20) is implemented in the following form:

$$\left\{\begin{array}{c}\dot{\sigma }=-\gamma {\left|\sigma \right|}^{1/2}\text{s}ign(\sigma )+\omega +k_{2}d\\ \dot{\omega }=-\lambda sign(\sigma )\end{array}\right)$$ (23)

Proof

First, the sliding mode dynamics (23) could be converted into a convenient form for the stability analysis. A new state vector is introduced for this purpose,

$$z=\left[\begin{array}{c}{z}_1\\ z_2\end{array}\right]=\left[\begin{array}{c}{\left|\sigma \right|}^{1/2}\text{s}ign(\sigma )\\ \omega \end{array}\right]$$ (24)

Then the system (24) can be deduced as derivatives of the state variables,

$$\left\{\begin{array}{c}{\dot{z}}_1=\frac{1}{\left|z_1\right|}\left(\frac{-\gamma }{2}{z}_1+\frac{1}{2}{z}_2+\frac{1}{2}{k}_{2}d\right)\\ {\dot{z}}_2=-\frac{\lambda }{\left|z_1\right|}{z}_1\end{array}\right)$$ (25)

Eq. (25) can be rewritten in a vector–matrix form,

$$\dot{z}=\phi (z_1)z+g(z_1)d$$ (26)

where $\phi (z_1)=\frac{1}{\left|z_1\right|}\left[\begin{array}{cc}-\frac{\gamma }{2}& \frac{1}{2}\\ -\lambda & 0\end{array}\right]$, and $g(z_1)=\frac{1}{\left|z_1\right|}\left[\begin{array}{c}\frac{1}{2}{k}_2\\ 0\end{array}\right]$

Next, the following Lyapunov function is introduced to verify the closed-loop stability of the system given by Eqs. (22), (23):

$$V(z,\gamma ,\lambda )=V_0+\frac{1}{2{\epsilon }_1}{(\gamma -{\gamma }^{*})}^2+\frac{1}{2{\epsilon }_2}{(\lambda -{\lambda }^{*})}^2$$ (27)

where $V_0(z)=(\eta +4{\beta }^2)z_1^2+z_2^2-4\beta z_1{z}_2=z^{T}Pz$, and $P=\left[\begin{array}{cc}\eta +4{\beta }^2& -2\beta \\ -2\beta & 1\end{array}\right]$.

It is worth noting that the matrix P is positive definite if $\eta >0$ and $\beta \in \mathfrak{R}$. Some constants (${\gamma }^{*}>0$ and ${\lambda }^{*}>0$) are bounded as follows: $\left|\gamma \right|⩽{\gamma }^{*}$ and $\left|\lambda \right|⩽{\lambda }^{*}$. Then the time derivative of the Lyapunov function (27) is calculated by

$$\dot{V}(z,\gamma ,\lambda )={\dot{z}}^{T}Pz+z^{T}P\dot{z}+\frac{1}{{\epsilon }_1}(\gamma -{\gamma }^{*})\dot{\gamma }+\frac{1}{{\epsilon }_2}(\lambda -{\lambda }^{*})\dot{\lambda }$$ (28)

The first two terms of Eq. (28) are computed by recalling Eq. (27),

$${\dot{V}}_0={\dot{z}}^{T}Pz+z^{T}P\dot{z}⩽-\frac{1}{2\left|z_1\right|}{z}^{T}Qz$$ (29)

The symmetric matrix $Q={\phi }^{T}P+P\phi$ can be calculated such that

$$Q=\left[\begin{array}{cc}{Q}_{11}& Q_{12}\\ Q_{21}& Q_{11}\end{array}\right]$$ (30)

where

$$\left\{\begin{array}{c}{Q}_{11}=2\eta \gamma +4\beta (2\beta \gamma -\lambda )-2\rho (\lambda +4{\beta }^2)\\ Q_{12}=Q_{21}=(\lambda -2\beta \gamma -\eta -4{\beta }^2)+2\beta \rho \\ Q_{22}=4\beta \end{array}\right)\text{and}\lambda =2\beta \gamma +\eta +4{\beta }^2$$

Then, Q will be the positive definite matrix with a minimal eigenvalue ensuring ${\lambda }_{min}(Q)⩾2\beta$ if $\gamma$ satisfies the following inequality:

$$\gamma >\frac{\beta {\rho }^2+(\eta +4{\beta }^2)(2\beta +\rho )+\beta }{\eta }$$ (31)

Therefore, it can be derived from Eq. (29) such that

$${\dot{V}}_0(z)⩽-\frac{1}{\left|z_1\right|}{z}^{T}Qz⩽-\frac{\beta }{\left|z_1\right|}{z}^{T}z=-\frac{\beta }{\left|z_1\right|}{∥z∥}^2$$ (32)

where ${\lambda }_{min}\left\{P\right\}{∥z∥}^2⩽z^{T}Pz⩽{\lambda }_{max}\left\{P\right\}{∥z∥}^2$. Now, Eq. (24) can be rewritten as

$${∥z∥}^2=z_1^2+z_2^2=\left|\sigma \right|+z_2^2\text{and}\left|z_1\right|={\left|\sigma \right|}^{1/2}⩽{∥z∥}^2⩽\frac{V_0^{1/2}(z)}{{\lambda }_{min}^{1/2}\left\{P\right\}}$$ (33)

Finally, it can be obtained as

$${\dot{V}}_0⩽-\varsigma V_0^{1/2}$$ (34)

where $\varsigma =\frac{2\beta {\lambda }_{min}^{1/2}(P)}{{\lambda }_{max}(P)}$. In view of Eq. (34), Eq. (28) can be rewritten as follows:

$$\dot{V}(z,\gamma ,\lambda )={\dot{z}}^{T}Pz+z^{T}P\dot{z}+\frac{1}{{\epsilon }_1}(\gamma -{\gamma }^{*})\dot{\gamma }+\frac{1}{{\epsilon }_2}(\lambda -{\lambda }^{*})\dot{\lambda }$$

$$⩽-\frac{1}{\left|z_1\right|}{z}^{T}Qz+\frac{1}{{\epsilon }_1}(\gamma -{\gamma }^{*})\dot{\gamma }+\frac{1}{{\epsilon }_2}(\lambda -{\lambda }^{*})\dot{\lambda }$$

$$⩽-\varsigma V_0^{1/2}+\frac{1}{{\epsilon }_1}(\gamma -{\gamma }^{*})\dot{\gamma }+\frac{1}{{\epsilon }_2}(\lambda -{\lambda }^{*})\dot{\lambda }$$

$$\begin{array}{c}=-\varsigma V_0^{1/2}-\frac{{\nu }_1}{\sqrt{2{\epsilon }_1}}\left|\gamma -{\gamma }^{*}\right|-\frac{{\nu }_2}{\sqrt{2{\epsilon }_2}}\left|\lambda -{\lambda }^{*}\right|+\frac{1}{{\epsilon }_1}(\gamma -{\gamma }^{*})\dot{\gamma }+\frac{1}{{\epsilon }_2}(\lambda -{\lambda }^{*})\dot{\lambda }\\ +\frac{{\nu }_1}{\sqrt{2{\epsilon }_1}}\left|\gamma -{\gamma }^{*}\right|+\frac{{\nu }_2}{\sqrt{2{\epsilon }_2}}\left|\lambda -{\lambda }^{*}\right|\end{array}$$ (35)

By recalling a well-known inequality,

$$x^2+y^2+z^2⩽\left|x\right|+\left|y\right|+\left|z\right|$$ (36)

and combining with Eqs. (25), (30), one can obtain the following inequality:

$$-\varsigma V_0^{1/2}-\frac{{\nu }_1}{\sqrt{2{\epsilon }_1}}\left|\gamma -{\gamma }^{*}\right|-\frac{{\nu }_2}{\sqrt{2{\epsilon }_2}}\left|\lambda -{\lambda }^{*}\right|⩽\mu \sqrt{V(z,\gamma ,\lambda )}$$ (37)

where $\mu =min(\varsigma ,{\nu }_1,{\nu }_2)$. By utilizing Eq. (37), Eq. (35) can be further rewritten as

$$\dot{V}(z,\gamma ,\lambda )=-\mu \sqrt{V(z,\gamma ,\lambda )}+\frac{1}{{\epsilon }_1}(\gamma -{\gamma }^{*})\dot{\gamma }+\frac{1}{{\epsilon }_2}(\lambda -{\lambda }^{*})\dot{\lambda }+\frac{{\nu }_1}{\sqrt{2{\epsilon }_1}}\left|\gamma -{\gamma }^{*}\right|+\frac{{\nu }_2}{\sqrt{2{\epsilon }_2}}\left|\lambda -{\lambda }^{*}\right|$$ (38)

Now the adaptive gains $\gamma (t)$ and $\lambda (t)$ are calculated by the updated law Eqs. (18), (19) which can be assumed as bounded. Then there exist positive constants (${\gamma }^{*}$ and ${\lambda }^{*}$) satisfying $\gamma (t)<{\gamma }^{*}$ and $\lambda (t)<{\lambda }^{*}$, $\forall t⩾0$. By using these assumptions, Eq. (38) can be bounded as follows:

$$\dot{V}(z,\gamma ,\lambda )⩽-\mu \sqrt{V(z,\gamma ,\lambda )}-\left|\gamma -{\gamma }^{*}\right|\left(\frac{1}{{\epsilon }_1}\dot{\gamma }-\frac{{\nu }_1}{\sqrt{2{\epsilon }_1}}\right)-\left|\lambda -{\lambda }^{*}\right|\left(\frac{1}{{\epsilon }_2}\dot{\lambda }-\frac{{\nu }_2}{\sqrt{2{\epsilon }_2}}\right)$$ (39)

In turn, this will be rewritten by

$$\dot{V}(z,\gamma ,\lambda )⩽-\mu \sqrt{V(z,\gamma ,\lambda )}+\xi$$ (40)

where $\xi =-\left|\gamma -{\gamma }^{*}\right|\left(\frac{1}{{\epsilon }_1}\dot{\gamma }-\frac{{\nu }_1}{\sqrt{2{\epsilon }_1}}\right)-\left|\lambda -{\lambda }^{*}\right|\left(\frac{1}{{\epsilon }_2}\dot{\lambda }-\frac{{\nu }_2}{\sqrt{2{\epsilon }_2}}\right)$,$\dot{\gamma }={\nu }_1\sqrt{\frac{{\epsilon }_1}{2}}$ and $\dot{\lambda }={\nu }_2\sqrt{\frac{{\epsilon }_2}{2}}$.

From Eq. (40), $\dot{V}$ is a negative definite function. By Lyapunov’s stability theory, the time convergence of tracking error is guaranteed for all initial conditions, or $\underset{t\to \infty }{lim}∥e(t)∥=0$ (Ahmed et al., 2021, Wang et al., 2019). Then the proof is completed. By realizing a synchronization scheme, port authorities can make effective decisions for port management and operations.

3.4. Chaos suppression and synchronization

Real markets are naturally volatile and unpredictable. The chaotic behaviour is characterized as aperiodic, random, unpredictable, and bounded pattern in system responses governed by deterministic manners with a strong sensitivity to initial conditions. The maritime supply chain networks are linked together through physical and information flows. Decision makers who rely on classical management technology will find it exceedingly tough to control today’s complex supply chains that will require them to respond quickly to the demands of contemporary users. Numerical simulations for chaos suppression and synchronization scenarios are tested to clearly demonstrate the validity of the proposed management strategy. The active control system can guarantee dynamic performance such as quick target tracking with vastly improved accuracy against disruptions. The closed-loop performance of port operations can be enhanced using hybrid algorithm advantages of AFOSTSM and NNC. First, to implement chaos suppression, the target value of all state variables is set at zero. The comparison between the adaptive fractional-order control and traditional control schemes has been illustrated in Fig. 8 . It is clearly observed that satisfactory dynamical response is obtained in case of AFOSTSM scheme. Under AFOSTSM strategy, the system response has quickly reached the desired values owing to the characteristics of adaptive and fractional-order algorithm. The transient responses are also superior in terms of rise time, maximum overshoot, and settling time compared with those of other control algorithms. By using sliding mode controller (SMC) and adaptive sliding mode controller (ASMC), the control system provides the poor transient response such as taking a longer time to settle its target value. The port management platform will have the support to make sure that strategic goals are achieved.

Fig. 8.

Time histories for chaos suppression when controllers are activated at t = 250 (time periods): (a) x₁(t), (b) x₂(t), (c) x₃(t), (d) x₄(t).

Next, synchronization scheme in a master–slave framework is one of key topics for applying nonlinear control theory to chaotic systems. Recently, chaos synchronization has received increasing attention due to its potential applications in many areas. As stated before, port management is typically a complex and nonlinear system in which chaotic behaviour is generally predominant. By realizing synchronization, decision makers can optimize their supply chains to achieve strategic goals with faster speed to market changes, thereby achieving the highest level of productivity and efficiency. The synchronization behaviours between the perturbed port system (or slave system) and the reference model (or master system) have been tested by using control algorithms. The setting of the synchronized behaviour for chaotic systems has become of great importance, especially considering the growing interest in decision making against volatile market. The control schemes have been activated at t = 250 (time periods) for all numerical simulations. The observed results for synchronizing chaos are illustrated in Fig. 9 . As expected, the state variables of the slave system can track the master system in a relatively short time period after control strategy is activated. In fact, a synchronized strategy enables supply chain partners to mitigate management risks and minimize potential losses when something unpredicted arises in real market. With supply chain synchronization in mind, port authorities can respond rapidly and confidently to shape and accomplish a short-term strategic plan that will mitigate the management risks.

Fig. 9.

Time histories for chaos synchronization when controllers are activated at t = 250 (time periods): (a) x₁(t), (b) x₂(t), (c) x₃(t), (d) x₄(t).

Port management represents a cognizant strategy by port authority to coordinate maritime supply chain partners in the most effective and efficient ways possible. From the analysis results, it can be concluded that the proposed strategy can provide the optimal responses by realizing control algorithms, guaranteeing higher tracking accuracy and faster convergence rates against disruptions. The novel control scheme can be utilized for efficient synchronization and suppression of chaotic dynamics of the port competition model. Port authorities and maritime enterprises can mitigate supply chain risks caused by market uncertainty, in which policy makers can make their businesses more resilient as well as sustainable possible on matching port throughput plan with optimizing terminal resources. Next, the proposed strategy is employed to improve the growth rate of container throughput, with ensuring a smooth, balanced and cost-effective flow of cargo.

4. Case study of Vietnam ports

4.1. Dynamic port groups in Vietnam

A port authority should constructively collaborate with its supply chain partners. Recently, the role of seaport has evolved from traditional functions to becoming a vital part of global supply chains. This paper deals with key development strategies for Vietnam major seaports. Vietnam’s coastal areas covers over 1 million km² and the country has an S-shaped coastline that stretches for more than 3260 km. Owing to favourable natural environment, the country has 44 seaports, including 272 terminals with a berth length of 92.2 km (Nguyen et al., 2020). In addition, Vietnam is located near one of the world’s busiest maritime trade routes (linking the Indian Ocean and the Pacific Ocean). Improving the management strategy on seaport operations may boost the nation’s economy. As a result, maritime transportation has been responsible for nearly 90% of the imported and exported cargos (Vietnam Seaports Association, 2019).

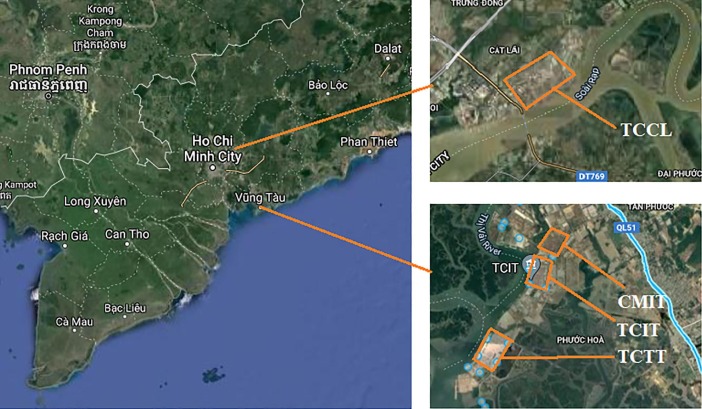
The southern sector of Vietnam plays an important role on the nation's economy and it is recognized as handling the most dynamic maritime transportation in the country. Especially, the Ho Chi Minh–Ba Ria Vung Tau (HCM-BRVT) port area, which is also known as the Southeast port group located in Southeast Vietnam, has handled more than 99.24% of the sea cargo volumes in the southern sector. It has also become the most modern and active container terminal operator in Vietnam (Nguyen et al., 2020). This group of seaports is mainly responsible for a large proportion of transport volumes in Vietnam for many years. In particular, it handles more than 70% of the country’s cargo throughput. It is the busiest port group in Vietnam due to its excellent port operations. Top four biggest terminals in the HCM-BRVT port group include TCCL, TCIT, CMIT, and TCTT (Fig. 10 ). It is noted that throughput is typically described in twenty-foot equivalent unit (TEU), which is a measure of volume in units of twenty-foot long containers. The group’s highest recorded cargo throughput is 77% for the regional areas and 56% for the country (Table 4 ). The total container handling volumes through this port group are approximately 8.12 million TEU in 2019. Thus, these container terminals extremely play an essential role on maritime transportation in the country.

Fig. 10.

Location of the HCM-BRVT port group (Nguyen et al., 2020).

Table 4.

Top four terminals of the HCM-BRVT port group in 2019.

No.	Container terminals	Full name	Established year
1	TCCL	Tan Cang Cat Lai	2007
2	TCIT	Tan Cang Cai Mep International Terminal	2011
3	CMIT	Cai Mep International Terminal	2011
4	TCTT	Tan Cang Cai Mep Thi Vai	2016
Total amount of cargo (%) handled by four major ports: 77 (southern) and 56 (country)

Source: Vietnam Seaports Association (2019).

Recently, the coronavirus has spread to every corner of the globe and the disease outbreaks seriously impact many aspects of human society (Corlett et al., 2020, Xu et al., 2021). The coronavirus pandemic has posed significant challenges for supply chains globally. In fact, the COVID-19 pandemic has afflicted not only human beings but also world economy. The outbreaks have led to the largest number of lockdowns/shutdowns worldwide in which typical negative impacts on port operations include closure of shipping line, transportation disruptions, and increased health risks of international trade (Campbell et al., 2021, Chowdhury et al., 2021). In general, maritime ports and terminals can be adversely affected by any downturn in global trade. Port authority can take actions to respond to business disruptions and supply chain challenges from the global spread of COVID-19. Vietnam is one of the most vulnerable countries to the pandemic on both nation’s economic and public health aspects (Tran et al., 2020). Although having a fewer incidence of confirmed cases and deaths related to COVID-19, the nationwide partial lockdown was implemented on the early stage, starting from April 2020. This lockdown policy has been effective in reducing the spread of COVID-19 crisis. However, the quarantines and severe lockdowns that are needed to fight the virus's spread are freezing the economy through trade. Especially, according to the Ministry of Transport, the volume of goods through Vietnam's seaports in 2020 still maintained the growth trend, but was lower than average annual volumes. Moreover, there are a lot of potential risks for maritime transportation due to impact of the ongoing complicated epidemic with new virus variants in the UK, India, Brazil, etc. This study aims to realize novel control theory for recovering the growth rate of throughput of the golden port group - HCM-BRVT against impacts of uncertainty and risks, eventually ensuring sustainability, viability, and resilience of nation’s maritime supply chains. As world economies restart, the maritime supply chains will be critical to supplying goods and services quickly, safely and securely.

4.2. Resilience strategy for HCM-BRVT group port

As stated before, maritime ports are among the key components of the global supply chain networks that are currently experiencing severe disruptions due to the pandemic. Port authority should develop a robust management scheme that includes crisis management and disaster recovery, providing risk management policy. To improve the efficiency of TCCL, TCIT, CMIT, and TCTT container terminals, the terminal growth volumes should be matched at least to the throughput growth rate of the previous period 2015–2019 when these terminals were recorded as the golden port group. The following assumptions are made to establish a recovery strategy for container throughput of golden container terminals and describe the critical variables for the prediction model:

A1. The growth rate relationship of container terminals in the HCM-BRTV group port, including TCCL, TCIT, CMIT, and TCTT terminals are represented by a class of four-dimensional competitive Lotka-Volterra system (4) (see Fig. 11 ).

Fig. 11.

Dynamic interactions of the HCM-BRTV group port via Lotka Volterra model.

A2. The container throughput data in total volume over the last 10 years of HCM-BRTV group port are presented in Table 5 for predicting container handling capacity.

Table 5.

Container throughput of the HCM-BRVT port group.

Container terminal	Throughput (million TEU)
	2011	2012	2013	2014	2015	2016	2017	2018	2019
TCCL	2.6	2.96	3.25	3.83	3.82	4.04	4.46	4.72	5.25
TCIT	0.28	0.54	0.64	0.92	0.98	1.11	1.32	1.63	1.96
CMIT	0.1	0.31	0.61	0.4	0.72	0.65	0.72	0.79	0.91
TCTT	–	–	–	–	0.1	0.22	0.39	0.47	0.65

Source:Vietnam Seaports Association (2019).

According to assumption A2, the average growth rate over the past 10 years (2015–2019) of the golden port group HCM-BRVT is considered as the target growth rate. Then combined control strategy of NNC and AFOSTSM algorithm is implemented to achieve the target growth rate of the HCM-BRVT group port. The observed data in Table 5 is used to train a neural network to predict the growth rate of each port. A digital port management platform will support decision maker’s goals in real-time with vastly improved accuracy and efficiency. Then the hybrid control strategy will eliminate the disruptions and perturbations affecting the system behaviours. The observed results for synchronization scheme are illustrated in Fig. 12 . As expected, the state variables of the perturbed throughput dynamics under digital management strategy can track to the target system with small tracking errors against disruptions. On the contrary, the future growth rates are failed to attain their target trends without control actions. In details, Table 6 shows the improvement of the annual growth rate of the HCM-BRVT group port. The future growth rates of all terminals under the proposed management strategies have been significantly improved. Based on the prediction algorithm using the adaptive strategies with neural network, the growth rates of TCCL TCIT, CMIT, and TCTT terminals have been approximately 97.20%, 97.46%, 97.65%, and 95.85% compared to target growth rates, respectively. Meanwhile, if the port management system is in operations without controllers, the obtained results are approximately 16.11%, 29.40%, 18.35%, and 35.56% compared to targets set, respectively. Table 7 shows some statistical metrics about the system performance under the proposed strategies. It can be seen that TCIT, CMIT, and TCTT terminals can achieve average growth rates over the next 10 years of 5.30%, 3.43%, and 4.31%, respectively while TCCL will achieve modest growth rate of 7.46%. In contrast, if port authority maintains current operation strategies without active decision schemes, the estimated growth rates of the terminals will be approximated 1.24%, 1.6%, 0.65%, and 1.6% for TCCL TCIT, CMIT, and TCTT terminals, respectively.

Fig. 12.

Time histories for growth rates using synchronization scheme: (a) CTTL, (b) TCIT, (c) CMIT and (d) TCTT.

Table 6.

Growth rate improvement (%) by using decision-making strategy.

Time (Year)	CTTL			TCIT			CMIT			TCTT
	Target	Under control	Without control	Target	Under control	Without control	Target	Under control	Without control	Target	Under control	Without control
1	5.45	5.30	1.64	2.15	2.07	2.61	1.03	0.91	1.34	0.77	0.74	2.61
2	5.76	5.61	1.12	2.47	2.39	2.10	1.22	1.16	0.94	0.98	0.89	2.10
3	6.50	6.30	0.98	3.34	3.24	1.69	1.81	1.75	0.67	1.66	1.54	1.69
4	6.83	6.63	1.01	3.78	3.67	1.60	2.12	2.06	0.62	2.07	1.93	1.60
5	7.32	7.11	1.07	4.50	4.38	1.50	2.64	2.58	0.57	2.80	2.64	1.50
6	7.82	7.60	1.15	5.30	5.17	1.43	3.27	3.20	0.53	3.74	3.56	1.43
7	8.35	8.12	1.23	6.26	6.10	1.36	4.04	3.96	0.49	5.00	4.78	1.36
8	8.92	8.67	1.31	7.38	7.20	1.30	5.00	4.91	0.46	6.68	6.42	1.30
9	9.66	9.39	1.40	8.99	8.79	1.22	6.44	6.34	0.43	9.46	9.14	1.22
10	10.16	9.87	1.45	10.21	9.99	1.18	7.58	7.47	0.41	11.82	11.46	1.18

Table 7.

Descriptive statistical analysis of growth rates.

Index	CTTL		TCIT		CMIT		TCTT
	Under control	Without control	Under control	Without control	Under control	Without control	Under control	Without control
Mean	7.46	1.24	5.30	1.60	3.43	0.65	4.31	1.60
Standard deviation	1.55	0.21	2.69	0.45	2.22	0.29	3.66	0.45
Maximum	9.87	1.64	9.99	2.61	7.47	1.34	11.46	2.61

4.3. Discussion

First, the dynamical analysis by nonlinear methods such as equilibrium points, Lyapunov exponent (LE), and time series investigation has been presented in Section 2 to describe the underlying mechanisms of the port ecosystem. Some highlights in the system dynamic properties include the instability of the interaction around equilibrium points, and chaotic behaviour through Lyapunov exponent. By introducing small variations of time delays in the range of [0 2.7], there are serious changes in the dynamical behaviours. A similar dynamical pattern is also found when the factional order is changing in the range of [0.94 1]. Thus, it is shown that the port ecosystem is highly sensitive to a different amount of time delay and different fractional-order values. In Section 3, the hybrid management strategy based neural network prediction and benchmark control algorithms has been implemented for suppression and synchronization of chaotic port dynamical systems. In fact, port authorities may not be fully aware of the underlying risks and vulnerability of their supply chains to global pandemics. Holistically, the test results show that the proposed method significantly outperforms other benchmarking methods on all states of the port competition models. For chaotic suppression, the proposed hybrid algorithm (AFOSTSM and NNC) is the top-performing one across all states of port interaction model. The hybrid algorithm of NNC and ASMC provides the second-best solution, and the combination of NNC with SMC has been recognized as the worst-performing method. The results are also well in agreement with the existing literature which implements the adaptation mechanism for dealing with parametric uncertainty and external disturbance (Yin et al., 2013, Ahmed et al., 2021).

In Section 4.2, the adaptive algorithm with the neural network forecasting provides novel solutions for enhancing operational performance and efficiency while guaranteeing excellent growth rate of the HCM-BRVT port group in the long term. In particular, by using the prediction algorithm using adaptive strategy with neural network, the growth rates of TCIT, CMIT, TCTT and TCCL terminals can be improved on average over the next 10 years of 5.30%, 3.43%, 4.31%, and 7.46%, respectively. On the contrary, if port authorities implement operational strategies without proactive scheme, the estimated growth rates of terminals will be only achieved by 1.24%, 1.6%, 0.65% and 1.6% for TCCL, TCIT, CMIT and TCTT, respectively. The port authorities might exploit the port resources suggested by the proposed management strategy to ensure sustainability of port operations in line with the growth rate target. The optimized management schemes by utilizing control techniques offer the managerial solutions to guarantee the profitability and sustainability of port operations for increasing potential market share. Moreover, the proposed strategy can also mitigate supply chain risks and minimize potential variability when something unexpected arises in real market. The study also has some potential limitations in ensuring optimal port operations. For example, the financial feasibility study should be taken into consideration for accommodating a recovery strategy. Leveraging advanced strategies based on deep machining learning algorithm should be considered for meeting future challenges. Finally, new management strategies can improve visibility across the end-to-end supply chain network, and support decision making strategy to mitigate the impact of unexpected shocks disrupted by COVID-19 pandemic.

5. Conclusions

The present study proposes decision-making strategies for characterizing dynamic interactions between seaports and regulating port productivity in the maritime logistics. The fractional-order Lotka-Volterra model has been employed for describing complex underlying mechanism of competition and cooperation dynamics among seaports. The container throughput models have been presented under parametric variations and external disturbances which certainly occur in real market (Justice et al., 2016). There have also been some novel attempts to develop managerial guidelines specifically for enhancing port productivity and sustainability. The first attempt is that an analytical framework based on nonlinear techniques, such as equilibrium analysis, Lyapunov exponents, time series investigation, and stability evaluation, has been presented to explore the dynamic properties of the port ecosystem with time delay. As a result, highly complex and chaotic behaviours are clearly demonstrated through multiple interaction models between the seaports. In particular, the port dynamics will become unstable near saddle node. Therefore, the mutual port competition and collaboration exist in unstable states, which makes system behaviours complex and challenging to manage. Moreover, by applying the Lyapunov Exponents, the Kaplan-Yorke criterion is obtained in the range of 2 to 3. Thus, the port ecosystem generates chaotic behaviours characterized by fractional-order dimension (Kaplan & Yorke, 1979). This phenomenon indicates that the port ecosystem will be apparently chaotic under certain dynamic interactions. This finding will be especially interesting for policy makers because no prior studies have fully examined dynamical behaviours through multiple interactions with time delay (Zhang and Lam, 2013, Twrdy and Batista, 2016, Zhang and Lam, 2017, Marasco and Romano, 2018). Furthermore, the simulation results show that the dynamic properties are significant changed even if fractional order variation is small and port operation is very sensitive to an amount of time delay. The proposed analysis method offers a better understanding of the dynamics of complexity and emergent behaviour of port interaction system.

Second, the decision-making strategy based on hybrid algorithms is implemented in order to improve the port performance and resilience against market volatility. Particularly, active control scheme has employed to make port operations more efficient and smarter, by exploiting neural network prediction and fractional order adaptive scheme. The proposed algorithm (NNC and AFOSTSM) is outperforming other benchmarking methods on all characteristics. The NNC and ASMC algorithm provide the second-best solution, and the combination of NNC with SMC has the worst performance. This can be attributed to the inability of pure SMC algorithm to cope with highly complex behaviour of the seaport interactions. The results are also in a good agreement with the existing literature which implements the fractional order and adaptation mechanism for dealing with parametric uncertainty and external disturbance. The stability of the complete control system has been verified through Lyapunov theory under the influence of uncertainties. Thus, the robust performance and stability of the proposed management strategy have been verified under effects of exogenous and endogenous shocks (Justice et al., 2016).

Third, the case studies are presented to deal with managing maritime supply chain risks for the HCM-BRVT port group in Vietnam, in which port productivity has been obviously impacted by COVID-19 pandemic. The simulation results indicate that the optimal management framework based on decision-making strategy will be able to sustain throughput growth rates while guaranteeing port resilience against disruptions. By utilizing the prediction algorithm, the growth rates of HCM-BRVT group can be improved on average by 5.12%, and it is far better than the case of without proactive strategy, which only achieves an average growth of 1.27% over the next 10 years. The efficient control scheme with prediction strategy can help policymakers achieve high growth rates and allow them to accomplish strategic goals against disruptions. Finally, the port authority can connect the maritime supply networks to ensure end-to-end visibility, collaboration, and agility.

There are some limitations in the current study, which should be addressed by future research. On the methodological side, more advanced neural network algorithms might be exploited for efficient forecasting. In addition, the number of data points used for training should be expanded to guarantee the accuracy and efficiency of the predictive control strategy.

CRediT authorship contribution statement

Truong Ngoc Cuong: Conceptualization, Methodology, Software, Writing – original draft. Hwan-Seong Kim: Methodology, Investigation, Resources. Sam-Sang You: Conceptualization, Validation, Writing – review & editing, Supervision. Duy Anh Nguyen: Data curation, Formal analysis, Software, Visualization.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.