Graphical abstract
Keywords: School bus routing problem, New normalcy, On-time reliability, Bus scheduling problem, COVID-19, Stop-skipping, Multiple bell times
Abstract
One of the critical actions that emerged during the onset of the New Normalcy after COVID-19 lockdowns, is the safe return to schools and workplaces. Therefore, dedicated transportation services need to adapt to meet new requirements such as arrival reliability for multiple bell times, the consequent staggering of arrivals and departures, and the decrease in bus capacity due to the physical distancing required by regulators. In this work, we address these issues plus additional labor conditions concerning drivers for a university context; with the goal of optimizing social interests such as covering demand and travel time under limited resources. We propose a bi-level approach, where firstly a bus routing generation sub-problem is solved before a bus scheduling sub-problem. This (strategic) solution is then considered as the baseline for subsequent dynamic (operational) routing. The latter is based on real-time demand provided by the students via a mobile app and considers stop-skipping to further minimize travel time. This integrated transport solution was tested in a university case, showing that with the same resources, it can meet these new requirements. In addition, numerical experimentation was also carried out with benchmark instances to identify, among available and literature-recommended solution algorithms and an effective tailored Tabu Search implementation, those that perform best for this type of problems.
1. Introduction
The school bus routing problem (SBRP) deals with the design and operation of the transportation service for students from and to schools in a cost-efficient manner (for operators), reliable (for schools), with good quality of service (for students), and safe (for everyone) (Corberán et al., 2002, Ellegood et al., 2020, Kim et al., 2012). Quality of service is seen as a social measure that directly impacts the students, where the number of stoppages, travel times, walking distances, and other equity measures are considered (Banerjee & Smilowitz, 2019).
University transport services face the common challenges addressed in SBRPs found in literature, as well as other variants that are discussed in this work. Among the new conditions that respond to the ongoing COVID-19 pandemic is the consequent reduction in bus capacity due to the physical distance requirements (World Health Organization, 2020). In addition, school tactics such as staggering school times and hybrid courses, are being implemented to avoid overcrowding but have already been present in university contexts. Moreover, university transport services also face uncertain demand in terms of the number of users and stop locations, since their use is optional unlike most school contexts.
These operational conditions in the New Normalcy era led to review the way SBRPs are addressed and solved. With the information technology advances that are now easily available, it is possible to have: i) real-time travel times that can be obtained through a free or commercial service (like Google Maps API), ii) GPS location of buses and passengers, iii) real-time demands which can be obtained from an online reservation system, and finally iv) overcrowding prevention, particularly useful during the New Normalcy, and easily obtainable through a reservation system. With this said, it is now possible to face SBRPs in a dynamic and real-time manner.
The contribution of this work is the proposal of an integrated transport solution for a university context that incorporates the modeling of: i) the multi-loading characteristic, this is, students with different shifts can ride at the same bus at the same time (Miranda et al., 2018); ii) a strategic bus routing generation sub-problem to minimize uncovered demand as well as maximum travel time. With a bi-level approach, this solution is considered the baseline for subsequent dynamic routing; iii) a combined operational and dynamic sub-problems of bus stop selection and bus routing, based on real-time demand that considers stop-skipping in the trips, and the on-time arrival reliability in both directions, which means the bus will be on time but not too early for class, and will not wait too long at school before going home. In addition, specific labor constraints are also incorporated; and finally, iv) on-time surveillance of the dynamic availability during the trips based on the real-time demand information registered by the users.
The rest of this paper can be described as follows: Section 2 presents related work that address the different components of our approach. The problem definition and explanation of the strategic and operational optimization models are detailed in Section 3. Section 4 describes the solution methods used to solve the models while Section 5 describes the UDEM case that motivated this work and the set of benchmark instances used to test the models, with the respective computational results; and finally, conclusions are highlighted in Section 6.
2. Literature review
The SBRP has been extensively studied for more than fifty years since it was first looked at (Newton & Thomas, 1974). Most reviews on SBRP focus on identifying the problem classification, its variants, multi-objective approaches, and the most common and successful solution methods used to solve these problems (Chen et al., 2015, Ellegood et al., 2020, Miranda et al., 2018, Park and Kim, 2010, Zajac and Huber, 2021).
The SBRP is divided into highly interrelated sub-problems that must be addressed at different planning horizons and often solved sequentially, in which the first solution is the entry to the next. The first strategic sub-problem is bus stop selection (BSS) which identifies bus stops and assigns students to them. With the bus stops defined, a tactical sub-problem known as bus route generation (BRG) builds bus trips for each school. Afterward, the operational problem consists of the bus route scheduling (BRS) which determines the sequence of trips that will be covered throughout a working day, considering school times and labor constraints. When multiple schools are served by the same fleet, the school bell time sub-problem (SBA) determines the start and end times for each school (Chen et al., 2015, Ellegood et al., 2020, Park and Kim, 2010, Zhang et al., 2018).
Many recent approaches solve the bus route generation along with another sub-problem, either BSS or BRS, and only a few address three or the four sub-problems together. For example, (Bögl et al., 2015) deal with the first three sub-problems allowing transfers in order to increase flexibility and reduce operating costs. (Kang et al., 2015) address the same sub-problems in two stages, considering the mixed loading effect; this allows a bus to take students to multiple schools (Ellegood et al., 2015). (Bertsimas et al., 2019) focus on finding start times (SBA) for single and multiple schools and solving the other three sub-problems with a bi-objective routing decomposition algorithm, which is successfully applied to real school districts.
General multi-objective transportation problems usually combine two of the following objectives: minimization of fleet size or costs, (max) travel time or length, and passenger time (Zajac & Huber, 2021)). However, many SBRP applications look to optimize single objective functions, such as the minimization of bus travel distance or time, the latter being the most common one (Ellegood et al., 2020). Multi-objective models generally optimize total time/distance along with total cost, student walking distance, fleet size, among other objectives. For example, (Ezquerro Eguizábal et al., 2018) recently presented a multi-objective optimization approach where economic costs and average route times are minimized for a multi-school by solving a sequence of BRG, fleet size planning, and BRS sub-problems while considering different starting times for schools.
Service reliability takes a greater relevance in SBRP when comparing with other VRPs. However, reliability issues are rarely considered in SBRP. In fact, only on-time arrival reliability is included in the classification scheme proposed in a recent SBRP review (Ellegood et al., 2020), through the chance of being late (COL) constraint, and it is considered under uncertainty contexts. A reliability service performance measure should consider the capability of the service to deliver the students on time for their classes, but not too early, and vice versa to pick them up at school after they are ready to go home, but not too late. Unlike in schools where there is only one or very few start/end times, in a university context student schedules vary along with each individual and sometimes follow daily or weekly patterns; so, the transport service must include pick-up and delivery of students simultaneously, and sometimes a change in route direction. This situation is called “multi-loading” and addressed in (Miranda et al., 2018), which is seen as a type of mixed load (Ellegood et al., 2020). In addition, the response to the COVID-19 pandemic has staggered start times (within the same school) and will soon be implemented. This phenomenon incites further research on the SBA in a multi-loading context.
On-time reliability is only recently addressed. (Caceres et al., 2017) considered three stochastic constraints regarding a limitation on the expectation of maximal travel times, the probability of overcrowding a bus, and the probability of being late at school (COL). They proposed to partition the multiple stage SBRP problems into multiple multi-depot and one-school sub-problems that are solved sequentially and applied their model on a real-world school district to minimize the total number of buses used. More recently, (Babaei & Rajabi-Bahaabadi, 2019) also incorporated the COL constraint. They examined the impact of considering stochastic time-dependent travel times in the solutions.
Later (Wang & Haghani, 2020) developed a stochastic SBRP that simultaneously optimizes the school bell time and bus routes to minimize the number of buses and the total vehicle time. They proposed a deterministic model that considers traffic congestion at different times of the day and stochastic travel time at a fixed departure time, and a second chance-constrained model that assumes that the travel time (ride time and deadhead) is normally distributed. In this model, they also incorporate the COL constraint, based on (Caceres et al., 2017). Both models are solved with an effective column generation-based algorithm on randomly generated instances. Returning to the uncertainty issue, (Babaei & Rajabi-Bahaabadi, 2019) showed that not considering random travel times in SBRP results in sub-optimal solutions, and one way to address this is through stochastic time-dependent start times. Similarly, (Sun et al., 2018) also dealt with stochastic time-dependent networks and applied robust optimization to a single-school configuration. To deal with on-time reliability they employed hard time windows constraints.
Besides, when dealing with uncertain demand, skipping stops is also considered as a valid strategy when looking for service equity (e.g. (Shang et al., 2018)) but is not generally addressed in school transportation applications for the nature of the service.
3. Problem definition and modeling
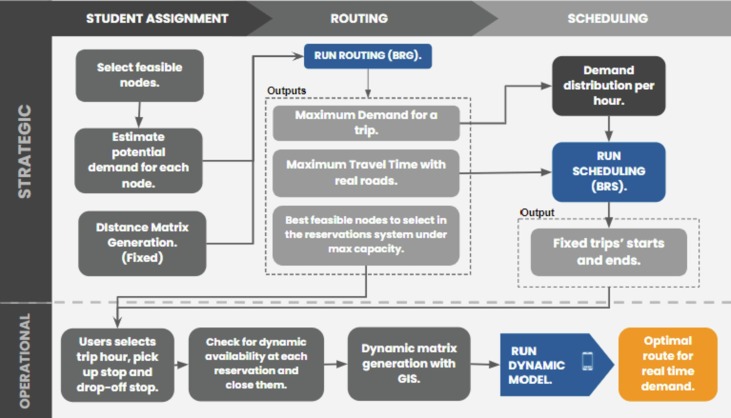
The integrated transport solution proposed in this work includes three optimization problems; the first one is a stop selection and routing problem to define the routes that are published to the students for a semester horizon; the second one schedules the routes to be covered by the buses, and the third one solves the routing problem for a specific vehicle each time it leaves the school. Fig. 1 describes the process in which these models are solved to offer a dynamic solution to the SBRP in a university context.
Fig. 1.
Conceptual Scheme for Solving Static and Dynamic SBRP.
3.1. The routing model for the strategic-static solution
The first optimization model that is solved in the proposed approach seeks to determine the sets of –potential– nodes to be visited in a trip. This gives a strategic and static solution, in the sense that all selected nodes in a trip are offered to the students as part of it so that later on, in the dynamic solution, students will be allowed to book a seat by selecting a pair of nodes (i.e. origin and destination) in either direction, such that one of them is the school and the other is one of the potential nodes identified by this model. In this section, the major constraint is the route time, with the maximum given as an input in the model. In this way, key performance indicators such as traveling time and maximum travel time for a passenger are controlled.
Following the classification scheme proposed in (Park & Kim, 2010), and complemented by (Ellegood et al., 2020), this is a model that addresses simultaneously BSS and BRG sub-problems, with a kind of ARL (allocation – routing – location) in which firstly, demand is grouped in clusters, then the routing determines the selected stops and the corresponding assigned demand. In addition, the problem deals with a single school, in an urban environment with multi loading and heterogeneous fleet. A covering objective function is not included in these schemes, since they always assume that all demand is covered. This is a unique VRP problem with time windows, known to be NP-hard.
Let the directed graph , where is the set of nodes (i.e., all the potential bus stops, with node , being the school), and the set of links (i.e., feasible street segments between nodes). Table 1 lists the sets, parameters, and variables used in the model. The set of nodes in are previously selected considering urban conditions, transport quality and safety policies (i.e. feasible walking distances from homes, maximum distance between stops, space in roads for bus stops, safe surroundings for students, etc.). Nodes are also grouped into districts , and is the list of such nodes for a district . Since demand is assumed to be known per district, , nodes in are assigned the demand of district . Therefore, in the model, the parameter used is directly and index is omitted for simplicity without losing generality. It is also true that the same district .
Table 1.
Indices, sets, parameters, and variables used in the routing model.
| Notation | Definition |
|---|---|
| Sets | |
| I | Set of nodes ; : school |
| Set of feasible links in the graph | |
| K | Set of buses, |
| D | Set of lists of districts then (shared demand) |
| Parameters | |
| Demand in node . | |
| Service time in node . | |
| Travel time from node to destination j, | |
| Time limit for total route time for bus k. | |
| RL,RU | Inferior and superior limits for school arrival time window. |
| Equals 1 if demand in node overlaps with the demand in node . | |
| Penalty for skipping stops | |
| M | A large number |
| Variables | |
| Time of the longest trip, to be minimized. | |
| Departure time for bus from node . | |
| Arrival time for bus to node . | |
| Binary variable that equals 1 if bus leaves node to destination . | |
| Binary variable that equals 1 if bus visits node . | |
| Binary variable that equals 1 if node (trip) is skipped. |
The routing model:
| (1) |
st
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
The objective function (1) seeks to minimize the maximum trip time for the route. Constraint (2) ensures flow conservation. Constraint (3) establishes whether bus visits node . Constraint (4) establishes if a node is skipped, while constraint (5) ensures that if arc is used in a route, the arrival time at node occurs after the departure time from node plus the travel time between nodes. Constraint (6) makes sure nodes with overlapping demand are not chosen. Constraint (7) limits the total trip time to be less than the established limit and constraint (8) sets the maximum trip time, to be minimized in (1). Constraint (9) restricts the departure of a node to be after its arrival plus the service time. Constraint (10) ensures that arrival to the school node happens after the departure from it. Constraint (11) specifies that the bus must arrive at school during the time window for the designated class schedule. Finally, constraints (11), (12) respectively, state the domain of the variables.
3.2. The scheduling model (a BSG)
Given the trips obtained in the first model, the second optimization model schedules the fleet of buses covering those trips in a way that is common and practical in a university transportation service: (a) multiple single-school bell times (i.e. several class start/end times in a day), (b) multiple trips (e.g. defined in the first model), (c) demand covering maximization, (d) On-time arrivals before class, this is, earlier but not too much, (e) labor constraints, such as breaks and shifts length, and (f) presence of pre-assigned vehicles to trips (for easiness of operation and student safety).
This model minimizes a hierarchical weighted sum of four objective functions (a) uncovered demand, (b) total arrival time before class, (c) fleet size, and (d) total trip changes. The first two objectives are socially oriented, looking for service coverage and quality, while the third is economically oriented, from the operator perspective. Finally, the last objective is a social one, since it considers driver welfare, minimizing the change of assigned trips.
Let the directed graph , where is the set of nodes and the set of links. Node , represents the school (at any time), and any other node represents the duple (trip, class’ start time). Let be a trip, so node is a combination of trip , and start class time . A link belongs to only if it is feasible for a vehicle to perform the trip arriving at school before after it performed trip that arrived at school before . For example, as shown in Fig. 2 , node 1 has the associated trip #1: Santa Catarina, and arrival time: 7:00 am, while node 2 has associated trip #2: San Pedro, and arrival time: 8:30 am. Trips to Santa Catarina and San Pedro last 60 and 63 min, respectively. So is feasible and belongs to since trip 2 must start at the latest at 7:27am (after 7:00am). Lastly, the depot, which is node 0, is used to represent the start and end of the bus shift at the school but the departure and arrival times are determined by and . A feasible route will be a sequence of nodes starting and ending at the depot with feasible links in . Table 2 describes the sets, parameters, and variables used in the scheduling model.
Fig. 2.
Scheduling Network Concept.
Table 2.
Indices, sets, parameters, and variables used in the scheduling model.
| Notation | Definition |
|---|---|
| Sets | |
| N | Set of nodes ; : school. Start and end of any route. |
| Set of feasible links in the graph | |
| K | Set of buses, |
| BT | Set of pair of nodes ( and a break between and is allowed. |
| Sets of nodes preassigned to bus | |
| Parameters | |
| Demand in node . | |
| Capacity of bus | |
| Start of shift for bus . | |
| End of shift for bus . | |
| Maximum arrival time to school for node (Start time of class) | |
| Time limit for earliest arrival to school to node . | |
| Maximum dead-time allowed between one period and another. | |
| Minimum break duration for each bus. | |
| nb | Amount of allowed breaks for each bus. |
| Weighted penalties | |
| M | A large number |
| Variables | |
| Departure time for bus from node (trip) . | |
| Arrival time for bus to node . | |
| Uncovered demand in node . | |
| Time that bus arrives at school before the start of period . | |
| Binary variable that equals 1 if bus covers node after node . | |
| Binary variable that equals 1 if bus covers node . | |
| Dead time between the end of node and the start of node for bus . | |
| Binary variable that equals 1 if bus has a break between nodes and . | |
| Binary variable that equals 1 if node (trip) is skipped. |
The time-before-class variable refers to how early bus k arrived at school, compared to the ideal arrival time before class. For example, for a class starting at 7:00 am, a bus should arrive 10 min before (6:50 am) but if it arrives 6:30am, the time before class is 20 min. If the deadhead (or length of a link in ) lasts at least , it is considered a break.
Following (Park & Kim, 2010), this model is a BRS sub-problem, for a single school, in an urban environment with a heterogeneous fleet. It is a capacitated VRP variant with time windows constraints (i.e. school bell ring constraints and shift length constraints).
The Scheduling Model:
| (14) |
st
| (15) |
| (16) |
| (17) |
| (18) |
| (19) |
| (20) |
| (21) |
| (22) |
| (23) |
| (24) |
| (25) |
| (26) |
| (27) |
| (28) |
| (29) |
| (30) |
| (31) |
| (32) |
| (33) |
Equation (14) states the multi-objective function of the school bus scheduling problem. Equations (13), (14) ensures flow balance and relationship between the binary variables meaning. Equation (17) counts the skipped nodes and the arrival time before class, and equation (18) allows multiple buses to cover the same schedule if the demand requires it. Equation (19) computes the time before class, equations (20), (21), (22), (23) ensures the correct relationships between arrival and departure times, equation (24) counts the uncovered demand, equations (25), (26), (27) track the breaks only between allowed nodes and limit the number of breaks. Equations (26), (27) set the shift time windows, equations (28), (29) set upper bounds on time before class and breaks duration, and finally, equations (30), (31) set the variable domains.
3.3. Dynamic routing model
This optimization model has the goal of minimizing the total travel time of a trip and it is intended to be solved in a dynamic context, under the following conditions: (a) there is a list of potential stops for each trip (i.e. defined for example, with the first model); (b) there are fixed bell times; (c) real demand is known in advance, this is, origin and destination (O-D) of each passenger (i.e. minutes before the start of a trip, for example, through a mobile reservation system); (d) all demand “accepted” has to be covered, and (e) it is applied for each duple (trip, class’ start time).
To accept a new reservation, the mobile application must keep track of the previous O-D reservations for the trip, and therefore, of the vehicle’s occupancy at each moment, so it can validate the availability to accept a new O-D request, with the rule in Eq. 34. Table 3 displays the meaning of the indices and parameters used in this rule:
| (34) |
Table 3.
Indices and parameters for the availability rule.
| Node index of the origin of the trip | |
| Demand (to be picked up) in node . | |
| Demand (to be get off) in node . | |
| Bus capacity | |
| Demand at the start of the trip (i.e. people on board at School) |
The third optimization model consists of the objective function (35), subject to equations (2), (5), (8), (9), (10), (11), (12), (13), (36), and (37) with the following simplifications: (a) the graph is previously simplified to include ordered nodes with positive demand; this is , where is the set of nodes . (b) There is no need for index , since it is solved for each vehicle, and (c) variables are not included, since all nodes in are visited. Note that equation (3) is replaced by equation (36). Equation (37) ensures that the order in which nodes are visited is consistent with (34).
| (35) |
| (36) |
| (37) |
4. Solution methods
To solve the models presented in the previous section, several solution methods were considered and compared, among the ones available in the OR-Tools library (Google, 2019). According to the recent review by Ellegood et al. (2020), the SBRP optimization solutions are obtained by the literature with exact methods and two types of approximation methods: heuristics and metaheuristics.
Regarding exact methods, the most frequently used is MIP, in its Branch & Bound and Branch & Cut variants, column generation, and cutting planes. They are often used to benchmark the proposed metaheuristics, in small problems or to mix them with a specific heuristic. We also tested the Saving and Christofides heuristics for its simplicity, and in the case of metaheuristics: Simulated Annealing (SA), Tabu Search (TS), and Iterated or Guided Local Search (GLS); they were the most frequently used according to (Ellegood et al., 2020).
As for metaheuristics, SA alone consists of an analogy between statistical mechanics and combinatorial optimization. It starts with an initial temperature, which has a decreasing rate throughout the main loop of the algorithm. The algorithm generates a probability that indicates if it should accept worse solutions or not on each step or loop. This algorithm, as well as all the so-called meta-heuristic algorithms, tries to help to escape local minima according to one of the authors of the algorithm (Kirkpatrick et al., 1983).
According to OR-Tools documentation (Omme et al., 2013), the library uses a simpler version of SA, generating random parameters for initial temperature, alpha, and neighbors, within proven ranges for generic problems. Although this algorithm is known to be one of the first metaheuristics in the market, it was used efficiently in Chen et al (2015) in a combination with local search operators. This work also mentions the common use of Tabu Search for this type of problem.
On the other hand, Guided Local Search, as well as previously mentioned meta-heuristics, takes advantage of search-related information to guide the search in the search space. In this algorithm, the cost function has a set of penalties for already visited solutions, which confine the local search and focus the attention on promising regions. According to (Voudouris & Tsang, 2006), the authors of GLS, this algorithm could be classified as a TS algorithm itself, the main difference is the generation of soft penalties to augment the cost function. They suggest that this algorithm can be used in a wide range of problems without any modification. A comparison was made between GLS, TS, and SA, suggesting a superiority from GLS, which it will be shown below, is consistent with the results of this study, by using OR-Tools.
It was found that the Savings heuristic algorithm was commonly applied for large instances and for the daily/operational aspect, for example in (Hashi, Hasan, & Zaman, 2016). This heuristic is sometimes used to find the initial solution in meta-heuristics and alone, as the main algorithm, to evaluate the relationship between the speed and the quality of solutions. Christofides Algorithm available in OR-Tools was also tested.
Tabu Search algorithm uses adaptive memory (tabu list), creating a flexible behavior throughout the search. This algorithm is also able to make worse moves along with prohibitions, hoping to find the global minima. It uses short and long-term memory structures, which help to prohibit recently visited solutions. TS also uses diversification to explore a new type of solutions with a defined frequency. As stated in (Glover et al., 2007). TS algorithm can be applied to a wide range of optimization problems, including those with non-linear or stochastic objective functions. Pacheco, J. (2006) uses TS with path relinking (an advanced version of TS) for a multi-objective SBRP, reporting good results.
4.1. A tailored Tabu Search
We propose a Tailored Tabu Search (TTS) to obtain better solutions than the metaheuristics available in the OR-Tools library, as it has been shown than some algorithm’s strategies and an adequate parameter tuning can lead to better solutions (Jia et al., 2013, Lagos et al., 2016). As we know, the Tabu Search algorithm has the following main elements (Montemanni et al., 2003):
-
•
Cost function: This function calculates the cost of each feasible solution and translates it into a value to optimize. The main purpose of implementing the algorithm is minimizing this value.
-
•
Solution representation: There must be a unique representation for each one of the feasible solutions of the search space.
-
•
Neighborhood: This consists of a function that creates sets of solutions, where feasible solutions are enlisted and the algorithm considers new solutions chosen from the neighborhood of current solutions.
-
•
Tabu list: List of last T moves realized which impedes the algorithm from repeating those same moves. This can also be interpreted as the short-term memory of the algorithm, which helps to explore different solutions.
-
•
Aspiration criteria: If a tabu move meets these criteria, then the solution obtained can be considered to be part of the neighborhood. Normally, the criteria is set in a way that the move results in obtaining the best solution so far.
-
•
Termination criteria: As the name implies, the algorithm is stopped once at least one of these criteria is met.
Once the general algorithm has been described, we present the TTS algorithm developed to solve our problem:
-
•
Cost function: The cost function includes the original MIP formulation elements (i.e. equation (14) for the scheduling model). Additionally, complex constraints such as driver lunch breaks and selection of node outside of working shifts are represented with penalizations in the cost function.
-
•
Solution representation: The solution is represented by a single list, where dummy nodes are created to represent the use of a new vehicle. Example: Dummy nodes are 0 and 1 in the next list: [0,2,3,1,4,5]. This means that vehicle 0 is going to visit node 2 and 3 and vehicle 1 is going to visit 4 and 5. This idea was obtained from (Jia et al., 2013).
-
•
Neighborhood: The neighborhood structure is generated by swapping two nodes in the list, without redundant swaps.
-
•
Tabu list: An experimentation determined that the best option in this parameter is to make the length dynamic, based on trends of previous solutions. The best initial length was 10 after preliminary tests using values from 5 to 50.
-
•
Aspiration criteria: If the solution is the best obtained so far, the move is accepted even if it is tabu.
-
•
Diversification: Every 100 iterations, three nodes are swapped only if the trend of previous solutions is positive.
-
•
Termination criteria: The termination criterion is the running time (30 min in this case) in order to compare with open-source libraries.
5. Numerical experimentation
This section presents the results of two experimental exercises. First, the case at UDEM is developed. It includes an analysis of scenarios for different demand levels and an experimental design and analysis of the performance of several different solution algorithms for randomly generated instances. Second, a set of benchmark routing problems, available at (Xavier et al., 2014) were used to test our routing model and also to assess the performance of the solution algorithms.
5.1. Case at UDEM
The motivation for this study arises from a specific case study that takes place at the University of Monterrey (UDEM), in Mexico. UDEM offers a free transportation service for its community, employees and students, through a transport operator and covers surrounding neighborhoods located in three different municipalities that are part of Monterrey’s Metropolitan Zone. The service is offered through a mobile application where students make a reservation for a seat in the route and schedule desired, based on a fixed timetable. Space for a trip will be available until the number of reservations reaches the bus capacity. Currently, its reservation system assumes that each passenger gets on or off the bus on Campus, and the capacity of the bus is filled with each reservation, regardless of the route segment they occupy. This system ignores the availability along the route that occurs when a passenger gets off the bus, causing an underutilization of the bus capacity.
After a demand study developed in 2020, it was found that: (a) there are two zones with high demand density that could also be covered by the transportation service, (b) the current capacity service exceeds the demand, (c) under New Normal conditions (i.e. post COVID-19), a decrease in transportation demand is expected, due to the hybrid (online plus face-to-face) scheme offered to students, and (d) there is an expected flattened demand, due to staggering of class schedules. Fig. 3 is a choropleth map, where the two current routes are shown, and the uncovered high-density zones (in darker red) are enclosed in ovals.
Fig. 3.
Choropletic Map of UDEM’s surrounding zone with the two uncovered high-density zones.
This situation motivated UDEM’s mobility department to seek; a new route for the uncovered demand with similar duration as the current ones, a feasible schedule for buses given a fixed fleet size that would be shared among the current and new routes, and a dynamic solution for the mobile application, given that the real demand for each trip is known in advance.
The bell begins at 7:00 am and ends at 10:00 pm. Classes usually last 1.5 h, so there are 10 periods a day, where students demand transportation. Demand for earlier trips is expected to be primarily toward school and vice versa for late-night trips. However, between approximately 11:00 am and 4:00 pm, the demand can be in either direction.
Distance matrix: To obtain the most accurate data of the distances to be traveled by the buses, a service called, Google Maps API was used. This tool considers the road network and current traffic, to ensure real and feasible distances and times. Said API was integrated directly into the code to generate the distance matrix quickly and accurately.
Students’ allocation: Potential and feasible nodes were placed in the selected postal codes and a polygon was formed to facilitate demand allocation for each node, all of this using the Street View Maps function. The nodes were spaced 500 m one from another, to avoid redundancy. When possible, nodes were placed on both sides of the street for flexibility in the algorithm solution process. With this done, the demand was spread proportionally through each node’s polygon. Each polygon contains a certain amount of street blocks, so an estimation of the number of people per block was made using postal codes, total population, and the total number of blocks. This makes each polygon contain a certain amount of demand inside its area. A reduction of 76% was made to each node’s demand, for representation of the number of hybrid classes imparted. Finally, a 47% demand reduction was also implemented, according to the user preference previously presented. This process established the final demand of each node. Reduction percentages were obtained from the demand study. Demand data and all input data can be consulted in https://github.com/carloslealgarza/SBRP_scripts.
Routing: A maximum total trip time of 65 min was set. The models were coded in Python 3.7 and run on an Intel ® Core (™) i5-8250u CPU @ 1.6 GHz computer with 8 GB RAM. Table 4 shows the results for the proposed routes in different demand scenarios plus the current routes, that are offered in both directions. The expected scenario corresponds to 24% of class sessions to be offered in a face-to-face (ftf) scheme. Fig. 4 shows examples of the resulting routes plotted in a map.
Table 4.
BRG solutions for different UDEM demand scenarios.
| Route (Trip) | Scenario | Number of stops | Length | Expected covered daily demand | Maximum trip time | Total time |
|---|---|---|---|---|---|---|
| Santa Catarina | Current | 36 km | 52 | 90 min | 90 min | |
| San Pedro | Current | 21 km | 23 | 65 min | 50 min | |
| San Jeronimo 1 | 24% ftf | 8 | 24 km | 43 | 65 min | 61 min |
| San Jeronimo 2 | 50% ftf | 8 | 24 km | 103 | 65 min | 61 min |
| San Jeronimo 3 | 80% ftf | 8 | 24 km | 167 | 65 min | 63 min |
| San Jeronimo 3 | 98% ftf | 8 | 24 km | 203 | 65 min | 61 min |
| Cumbres 1 | 24% ftf | 6 | 30 km | 24 | 65 min | 64 min |
| Cumbres 2 | 50% ftf | 6 | 30 km | 57 | 65 min | 64 min |
| Cumbres 3 | 80% ftf | 6 | 30 km | 92 | 65 min | 64 min |
| Cumbres 4 | 98% ftf | 6 | 30 km | 112 | 65 min | 64 min |
ftf: face-to-face scheme.
Fig. 4.
(a) Routing and (b) Scheduling results for the most probable UDEM scenario.
Dynamic solution: To test the effects of the smart mobility app that allows having real-time demand data for the dynamic routing problem, we used data from 2019 of pickups and getting offs for every day, route, and schedule. More than 24,000 experiments were performed. They were solved using the savings heuristic and MIP to estimate the total travel time reduction compared to the static solution. Fig. 5 shows the time frequency for the four current routes. The current average time is represented as a vertical red line.
Fig. 5.
Total travel time frequency of Dynamic model vs Static with 2019 demand.
As it can be seen, there is a notable difference between the travel times when the route was dynamically optimized. For the San Pedro route, the most frequent travel times are around 16–18 min less than the current time, and for Santa Catarina’s they are between 22 and 31 min less than what the current route takes.
Best Solution Algorithms: Five algorithms were tested to solve the models: the default OR-Tools MIP solver which is the third-party solver SCIP (referred as MIP), the savings heuristic, the guided local search heuristic, and the metaheuristics Tabu Search and Simulated annealing, available in OR Tools library. To evaluate their performance, a convergence analysis was made for three problem sizes: = 40, 80, and 160. This Fig. 6 was made by running first a MIP for one-hour limit to find the exact optimal solution and then, running all the algorithms with different time limits. At the end of each run, the relative gap between the solution and the optimal solution was plotted.
Fig. 6.
Absolute gap to optimality vs time limit in seconds.
This figure shows that MIP dominates the performance for the sizes tested. Beyond the 3 min mark, all the methods stayed with the same solution in two of the instances, without improving. It is worth noting that for the 160 nodes instance, MIP found the first feasible solution until around the 50-second mark.
This convergence analysis helped establish the time limit for a more extensive experiment, which is also conducted in this study to find the best algorithm in different scenarios. The design of this experiment consists of the following: (a) Eight instance sizes. Each following instance has twice the nodes of the previous one, starting with 10 and ending with 1280 nodes; (b) 15 replicas. In each replica, a random distance matrix and demand for each node is generated, based on the uniform distribution with bounds like the demand in COVID-19 context; and (c) On each replica 5 algorithms were used to solve each problem with a run time limit of 3 min. The results can be visualized in Fig. 6 that shows the frequency of the normalized coverage for each algorithm and instance, where 0 represents the average.
Fig. 7 clearly illustrates how the MIP model was able to outperform its counterparts when it was able to find a solution. When the instance exceeded 320 nodes, the MIP model couldn't find a solution with the given run-time limit, however, these amounts of nodes are not very common in an SBRP. Hypothesis tests on mean differences between the several methods were performed, getting large p_values (≥0.10) showing that there is no significant difference in the objective values. Data used in Fig. 7 and in the statistical analysis can also be found in https://github.com/carloslealgarza/SBRP_scripts.
Fig. 7.
Distribution of normalized percentage of coverage between different algorithms under several instances.
After conducting this analysis, it can be stated that for schools with less than 320 stops, exact methods turn out to be better in optimizing coverage while respecting the total trip time limit. For larger instances and networks with higher complexity, heuristics turn out to be the better option due to the relation between speed and quality of the solution.
5.2. Numerical experimentation with benchmark instances
A benchmark study was carried out to compare the performance of several solution algorithms and our routing model to other commonly used applications, such as capacitated vehicle routing problems. Benchmark instances were taken from a Capacitated Vehicle Routing Problem Library available at https://vrp.atd-lab.inf.puc-rio.br/index.php/en, (Xavier et al., 2014). Together with our TTS implementation, the approximation methods tested, available in the OR-Tools library, were Savings, Christofides, SA, TS, and GLS, as well as the exact MIP. Table 5 shows the results. It presents the optimal value reported in the benchmark site for 11 instances with sizes ranging from 22 to 200 nodes. For the two heuristic methods, objective value and run-time are reported for each instance. For the metaheuristics, only objective value and relative gaps are shown. The maximum run time was set to 30 min for these methods and for MIP.
Table 5.
Numerical results with benchmark instances.
| Problem | Opt | Sav. | Chr. | SA | GLS | TS | TTS | MIP | |
|---|---|---|---|---|---|---|---|---|---|
| E-n23-k3 | Z* | 569 - |
650.3 | 609 | 650.3 0.13 |
650.3 | 635.4 0.10 |
569 | 567.8 0.00 |
| GAP | 0.13 | 0.07 | 0.13 | 0.00 | |||||
| E-n22-k4 | Z* | 375 - |
375 | 432.8 | 375 0.00 |
375 | 375 0.00 |
375 | 375 0.00 |
| GAP | 0.00 | 0.00 | 0.00 | 0.00 | |||||
| E-n30-k3 | Z* | 534 - |
674.2 | 559 | 551 0.03 |
523.3 | 556 0.04 |
534 | 668.6 0.20 |
| GAP | 0.21 | 0.04 | 0.00 | 0.00 | |||||
| E-n51-k5 | Z* | 521 - |
653.6 | 615.8 | 627.5 0.17 |
536.7 | 556.6 0.06 |
536 | 1421.4 0.63 |
| GAP | 0.20 | 0.15 | 0.03 | 0.03 | |||||
| E-n76-k7 | Z* | 682 - |
835.3 | 757.8 | 795.3 0.14 |
719.6 | 757.3 0.10 |
707 | – |
| GAP | 0.18 | 0.10 | 0.05 | 0.04 | |||||
| E-n76-k8 | Z* | 735 - |
771.7 | 814.4 | 771.7 0.05 |
761.1 | 782.5 0.06 |
771 | – |
| GAP | 0.05 | 0.10 | 0.03 | 0.05 | |||||
| E-n76-k10 | Z* | 830 - |
919.8 | 941.3 | 919.8 0.10 |
848.1 | 900.8 0.08 |
893 | – |
| GAP | 0.10 | 0.12 | 0.02 | 0.07 | |||||
| E-n76-k14 | Z* | 1021 - |
1148.4 | 1111.1 | 1148.4 0.11 |
1068.8 | 1129.6 0.10 |
1095 | – |
| GAP | 0.11 | 0.08 | 0.04 | 0.07 | |||||
| E-n101-k8 | Z* | 817 - |
876.4 | 923.6 | 929.5 0.12 |
891.4 | 882.9 0.07 |
826 | – |
| GAP | 0.07 | 0.12 | 0.08 | 0.01 | |||||
| E-n101-k14 | Z* | 1071 - |
1155 | 1175.1 | 1155 0.07 |
1176.3 | 1142.5 0.06 |
1188 | – |
| GAP | 0.07 | 0.09 | 0.09 | 0.10 | |||||
| M-n200-k16 | Z* | 1274 - |
1497.3 | 1508.7 | 1497.3 0.15 |
1495.1 | 1494.1 0.15 |
1484 | – |
| GAP | 0.15 | 0.16 | 0.15 | 0.14 | |||||
| Shifted geometric Z* ratio to optimal | 1 | 1.136 | 1.119 | 1.111 | 1.061 | 1.083 | 1.050 |
Opt: optimal solution from (Xavier et al., 2014), Sav: Savings heuristics, Chr: Christofides algorithm, SA: Simulated Annealing, GLS: Global Local Search, TS: Tabu Search, TTS: Our Tailored TS, MIP: Exact solution. (“-”) means that no optimal solution was found in 30 min. The shifted geometric mean of with
As shown in Table 5, instances vary in the number of nodes and number of vehicles. As expected, MIP performed better in small instances (i.e. less than 30 nodes), and as observed in Fig. 8 , within the 30-minute running time, the gap increased exponentially. In fact, for instances with more than 51 nodes, MIP didńt even get any solution.
Fig. 8.
Relative gaps obtained with all solution methods tested for the benchmark instances.
As can be noted, the heuristic methods achieved similar objective function (OF) values to the metaheuristic counterparts, in much less time, lasting less than 5 s in all but the 200 nodes instance, while the metaheuristics run in 30 min. There was no statistical difference between the OF attained between them (i.e. with p_values or order of 0.78 and 0.81 when compared GLS with Savings and Christofides, respectively). Finally, to compare the performance of the approximation methods, the last row of Table 5 presents the shifted geometric mean of the ratio of the objective values achieved to the optimal solution with a shift factor of 10. The shifted geometric mean has the advantage of not being very sensitive to very large or very small outliers, and it is increasingly used for comparison of optimization algorithms or solvers (Achterberg, 2009, Mittelmann, 2021).
Another important takeaway is that our tailored Tabu Search produced better results over the other algorithms, for most instances, and in general, presents the best performance which is supported by the value of shifted geometric mean of 1.05, which is the closest to 1.0 among the options evaluated.
For the instances tested, Christofides was the heuristic that performed better in average, and as for metaheuristics, GLS was the best one. However, no statistical difference was proven between each pair of methods, with p_values greater than 0.8 in all cases. It is interesting to observe in Fig. 8, that there is no tendency in the performance of any of the approximation methods as instance size increases, which can be understood as that its performance is not sensitive to the size of the problem. In fact, gaps obtained by each method were tested for normality tests with p_values greater than 0.6, except for GLS in which a value of 0.07 was obtained.
Results from the studied case and from the numerical experimentation with benchmark instances are consistent and suggest the same: MIP is still suitable for real-life applications with a small number of nodes (e.g. up to 50 nodes), and there is no significant distinction among the approximation methods within 30-minute running times, though heuristics are much faster.
This sparks future research on optimizing resources and run time. Since metaheuristics will run for as long as they are limited, additional convergence analysis would be interesting to see where the difference among the methods starts to come up.
6. Final discussion and conclusions
The integrated transportation solution proposed in this work for a university context includes several features that are required in this new post-COVID-19 normalcy and that are not seen together in previous research; In particular, we solved a bi-objective problem which combines routing constraints with a covering problem and a scheduling problem that incorporates the notion of on-time arrival reliability by for multiple staggered bell-times and labor constraints for drivers, taking care of service quality with limited resources. Our proposal states that using a combination of known models, but adapted with these variants, fit better to solve university transportation needs in this new normalcy times, where school transportation services have become a more visible and safe mobility option for college students.
We show that our approach is feasible and practical for life-size instances as well as for benchmark instances. In addition, once the strategic transportation schedules (trips and routes) have been established, we show how, with on-time demand information provided by the students through a mobile booking application, further improvements can be made in terms of travel time by solving the routing problems dynamically. Maximum reductions in travel time of 25% to 50% were achieved for practical cases tested before and after COVID19.
On the other hand, we tested the most recommended solution algorithms in the literature, including exact, heuristic, and metaheuristic methods, to identify the ones that work best for the evaluated instances. For practical-sized cases, exact methods can deliver optimal solutions at suitable times for instances with less than 50 nodes. For larger sizes, we did not find any evidence of significant differences between the approximation methods in terms of the quality of the solutions, nor the sensitivity of any of the methods to the size of the instance. It was also shown that the tailored Tabu Search algorithm proposed in this work was effective in improving the quality of the solution compared to the set of algorithms tested.
As part of the different smart mobility strategies for cities, our approach could be extended not only for university applications or generally for schools, but also for any type of dedicated transport services, in which a company offers transport solutions to its employees, customers, and community of interest. Finally, we find interesting future research on the interaction and integration of the real-time demand obtained through mobile applications with the optimization of these transport problems to better adjust the solutions to the real-time needs of the users, as well as the interaction with other urban mobility alternatives.
CRediT authorship contribution statement
Jenny Díaz-Ramírez: Conceptualization, Methodology, Formal analysis, Writing – original draft, Writing – review & editing, Supervision, Project administration. Carlos Mario Leal-Garza: Methodology, Software, Validation, Formal analysis, Data curation, Writing – original draft, Visualization. Carlos Gómez-Acosta: Methodology, Validation, Formal analysis, Investigation, Writing – original draft, Visualization.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
Acknowledgments
To the Universidad de Monterrey, for data providing and its support to publish this article.
Funding
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
References
- Achterberg T. SCIP: Solving constraint integer programs. Mathematical Programming Computation. 2009;1(1) doi: 10.1007/s12532-008-0001-1. [DOI] [Google Scholar]
- Babaei M., Rajabi-Bahaabadi M. School bus routing and scheduling with stochastic time-dependent travel times considering on-time arrival reliability. Computers and Industrial Engineering. 2019 doi: 10.1016/j.cie.2019.106125. [DOI] [Google Scholar]
- Banerjee D., Smilowitz K. Incorporating equity into the school bus scheduling problem. Transportation Research Part E: Logistics and Transportation Review. 2019 doi: 10.1016/j.tre.2019.08.006. [DOI] [Google Scholar]
- Bertsimas D., Delarue A., Martin S. Proceedings of the National Academy of Sciences of the United States of America. 2019. Optimizing schools’ start time and bus routes. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bögl M., Doerner K.F., Parragh S.N. The school bus routing and scheduling problem with transfers. Networks. 2015 doi: 10.1002/net.21589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caceres H., Batta R., He Q. School bus routing with stochastic demand and duration constraints. Transportation Science. 2017 doi: 10.1287/trsc.2016.0721. [DOI] [Google Scholar]
- Chen X., Kong Y., Dang L., Hou Y., Ye X. Exact and metaheuristic approaches for a bi-objective school bus scheduling problem. PLoS ONE. 2015 doi: 10.1371/journal.pone.0132600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corberán A., Fernández E., Laguna M., Martí R. Heuristic solutions to the problem of routing school buses with multiple objectives. Journal of the Operational Research Society. 2002 doi: 10.1057/palgrave.jors.2601324. [DOI] [Google Scholar]
- Ellegood W.A., Campbell J.F., North J. Continuous approximation models for mixed load school bus routing. Transportation Research Part B: Methodological. 2015 doi: 10.1016/j.trb.2015.03.018. [DOI] [Google Scholar]
- Ellegood W.A., Solomon S., North J., Campbell J.F. Omega (United Kingdom) 2020. School bus routing problem: Contemporary trends and research directions. [DOI] [Google Scholar]
- Ezquerro Eguizábal S., Moura Berodia J.L., Ibeas Portilla Á., Benavente Ponce J. Optimization model for school transportation design based on economic and social efficiency. Transport Policy. 2018 doi: 10.1016/j.tranpol.2018.01.015. [DOI] [Google Scholar]
- Glover F., Laguna M., Martí R. Handbook of Approximation Algorithms and Metaheuristics. 2007. Principles of tabu search. [DOI] [Google Scholar]
- Google. (2019). Google’s OR-Tools. Https://Developers.Google.Com/Optimization. https://github.com/google/or-tools.
- Hashi E.K., Hasan M.R., Zaman M.S.U. GIS based heuristic solution of the vehiclerouting problem to optimize the school bus routing and scheduling. 19th International Conference on Computer and Information Technology, ICCIT 2016. 2016:56–60. doi: 10.1109/ICCITECHN.2016.7860167. [DOI] [Google Scholar]
- Jia H., Li Y., Dong B., Ya H. An Improved Tabu Search Approach to Vehicle Routing Problem. Procedia - Social and Behavioral Sciences. 2013;96 doi: 10.1016/j.sbspro.2013.08.138. [DOI] [Google Scholar]
- Kang M., Kim S.K., Felan J.T., Choi H.R., Cho M. Development of a genetic algorithm for the school bus routing problem. International Journal of Software Engineering and Its Applications. 2015 doi: 10.14257/ijseia.2015.9.5.11. [DOI] [Google Scholar]
- Kim B.I., Kim S., Park J. A school bus scheduling problem. European Journal of Operational Research. 2012 doi: 10.1016/j.ejor.2011.11.035. [DOI] [Google Scholar]
- Kirkpatrick S., Gelatt C.D., Vecchi M.P. Optimization by simulated annealing. Science. 1983 doi: 10.1126/science.220.4598.671. [DOI] [PubMed] [Google Scholar]
- Lagos C., Crawford B., Soto R., Cabrera E., Vega J., Johnson F., Paredes F. Improving Tabu Search Performance by Means of Automatic Parameter Tuning. Canadian Journal of Electrical and Computer Engineering. 2016;39(1) doi: 10.1109/CJECE.2015.2496338. [DOI] [Google Scholar]
- Miranda D.M., de Camargo R.S., Conceição S.V., Porto M.F., Nunes N.T.R. A multi-loading school bus routing problem. Expert Systems with Applications. 2018 doi: 10.1016/j.eswa.2018.02.014. [DOI] [Google Scholar]
- Mittelmann, H. D. (2021). Decision Tree for Optimization Software.
- Montemanni R., Moon J.N.J., Smith D.H. An improved tabu search algorithm for the fixed-spectrum frequency-assignment problem. IEEE Transactions on Vehicular Technology. 2003;52(4) doi: 10.1109/TVT.2003.810976. [DOI] [Google Scholar]
- Newton R.M., Thomas W.H. Bus routing in a multi-school system. Computers and Operations Research. 1974 doi: 10.1016/0305-0548(74)90047-1. [DOI] [Google Scholar]
- Omme, N. van, Perron, L., & Furnon, V. (2013). Google OR-Tools Open Source Library - User’s Manual. http://or-tools.googlecode.com/svn/trunk/documentation/%0Adocumentation_hub.html.
- Park J., Kim B.I. The school bus routing problem: A review. European Journal of Operational Research. 2010 doi: 10.1016/j.ejor.2009.05.017. [DOI] [Google Scholar]
- Shang P., Li R., Liu Z., Yang L., Wang Y. Equity-oriented skip-stopping schedule optimization in an oversaturated urban rail transit network. Transportation Research Part C: Emerging Technologies. 2018 doi: 10.1016/j.trc.2018.02.016. [DOI] [Google Scholar]
- Sun S., Duan Z., Xu Q. School bus routing problem in the stochastic and time-dependent transportation network. PLoS ONE. 2018 doi: 10.1371/journal.pone.0202618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Voudouris C., Tsang E.P.K. Handbook of Metaheuristics. 2006. Guided Local Search. [DOI] [Google Scholar]
- Wang Z., Haghani A. Column generation-based stochastic school bell time and bus scheduling optimization. European Journal of Operational Research. 2020 doi: 10.1016/j.ejor.2020.03.071. [DOI] [Google Scholar]
- World Health Organization. (2020). Considerations for school-related public health measures in the context of COVID-19. World Health Organisation.
- Xavier, I., Uchoa, E., Pecin, D., Pessoa, A., Poggi, M., Vidal, T., Subramanianc, A., Oliveira, D., & Queiroga, E. (2014). CVRPLIB - Capacitated Vehicle Routing Problem Library. http://vrp.atd-lab.inf.puc-rio.br/index.php/en/.
- Zajac S., Huber S. European Journal of Operational Research. 2021. Objectives and methods in multi-objective routing problems: A survey and classification scheme. [DOI] [Google Scholar]
- Zhang D., Wang X., Li S., Ni N., Zhang Z. Joint optimization of green vehicle scheduling and routing problem with time-varying speeds. PLoS ONE. 2018 doi: 10.1371/journal.pone.0192000. [DOI] [PMC free article] [PubMed] [Google Scholar]