The redistributive effects of pandemics: Evidence on the Spanish flu

Abstract

Which are the effects of pandemics on the returns to factors of production? Are these effects persistent over time? These questions have received renewed interest after the out-burst of deaths caused by Covid-19. The Spanish Flu is the closest pandemic to Covid-19. In this paper, we analyze the impact of the Spanish Flu on the returns to labor and capital in Spain. Spain is an ideal country to perform this exercise. First, the “excess death rate” was one of the largest in Western Europe and it varied substantially across regions. Second, Spain was transitioning towards industrialization, with regions in different stages of development. Third, Spain was developed enough to have reliable data. We identify the effect of the Spanish Flu by exploiting within-country variation in “excess death rate”. Our main result is that the effect of the Spanish Flu on daily real wages was large, negative, and broadly short-lived. The effects are heterogeneous across occupations and regions. The negative effects are exacerbated in (i) occupations producing non-essential goods like shoemakers and (ii) more urbanized provinces. Quantitatively, relative to pre-1918, the decline for the average region ranges from null to around 30 percent. In addition, we fail to find significant negative effects of the flu on returns to capital. Whereas the results for dividends are imprecisely estimated (we cannot reject a null effect), the effect on real estate prices (houses and land), driven by the post-1918 recovery, is positive. Experts on inequality have argued that pandemics have equalizing effects especially in a Malthusian setting, due to real wage increases. Our findings suggest that, at least, for a developing economy like Spain in the early 20th century, this result does not apply. Indeed, we document that the flu pandemic was conducive to a (short-run) reduction in real wages. In addition, we interpret our heterogeneous results as suggestive evidence that pandemics represent a demand shock.

1. Introduction

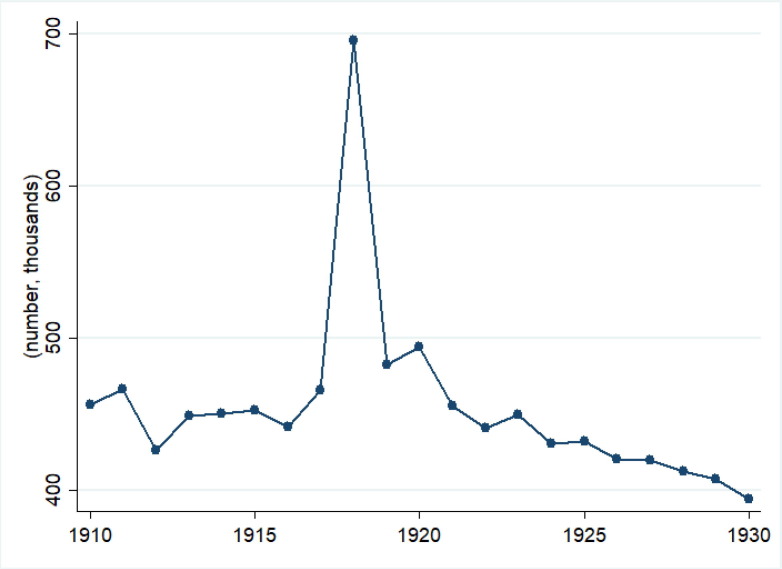
Which are the economic consequences of pandemics? How are the returns to capital and labor affected by pandemics? Are these effects persistent over time? Do they differ across regions? All these questions have become relevant after the outburst of confirmed cases and deaths of Covid-19 across the globe. In this paper, we attempt to answer these questions by analyzing the effects of the so-called “Spanish” flu in 1918 within Spain. Fig. 1 reports the evolution of the number of deaths in Spain between 1910 and 1930. The effect of the Spanish Flu on mortality is apparent from the figure. In 1918, there was a 54 percent increase in the number of deaths, relative to the pre-1918 average. To put this number into perspective, around 3.5 percent of the Spanish population died in 1918, with an estimated increase in deaths caused by influenza of 260,000. In the international context, the flu-related death rate was the highest among Western European countries and it was almost twice the rate in the United States (Johnson & Mueller, 2002).

Fig. 1.

Evolution of Number of Deaths in Spain, 1910–1930 Sources: Death data obtained from INE Base Hist́orica.

Spain is an ideal country to examine the economic effects of the Spanish Flu. First, in contrast to industrialized countries, Spain was neutral in World War I, which mitigates the bias induced for military spending and other side effects of the war. Second, early 20th century Spain was a very heterogeneous country (Rosés, Mart́ınez-Galarraga & Tirado, 2010). The levels of income and industrialization widely varied across provinces, which will help us to extrapolate from our results potentially heterogeneous effects of pandemics across countries at different levels of development. Third, the level of economic development in Spain was high enough to have good reliable data on real wages and proxies for the returns to capital across time and provinces to perform this exercise.

When evaluating policy reactions to the pandemic, given the economic and logistic costs of massive testing, the crucial trade off seems to be between enforcing strict social distancing to avoid excessive deaths and the damage done to the economy by the collapse of consumption and unemployment caused by drastic quarantine measures (Hollingsworth et al., 2011, Anderson et al., 2020, Acemoglu et al., 2020, Lin and Meissner, 2020). In many developing countries, social distancing is difficult to enforce due to cramped housing and the lack of safety nets (meaning the poor must work in the midst of the pandemic). In less democratic contexts, elites can shield themselves from the pandemic both physically and politically, meaning social distancing is more loosely enforced. The policy equilibrium in these contexts might consist of less drastic social distancing and higher mortality, but perhaps a milder downturn. This seems to be the case of Spain in 1918. Although, the flu in Spain was less deadly than in India or Indonesia, the mortality rate was more than double the rate of other Western European countries. In contrast, a drastic contraction of aggregate output is not apparent in the data.

There seems to be a consensus that pandemics tend to equalize societies (Scheidel, 2017). The evidence reported in Jorda (2020b), using a cross-section of countries dating back to the 14th century, is consistent with this view. Indeed, they document that pandemics tend to increase real wages and depress returns to capital (also in the long-run). A potential concern is that these results may be driven by ancient episodes and do not apply to modern pandemics like the Spanish Flu. This exercise has not been done for the Spanish Flu. The closest papers are Karlsson et al., 2014, Barro, 2020, which find negative effects of the Spanish Flu on capital income (within Sweden) and no significant effect on stock market returns (across countries), respectively. However, there is no evidence on the effect of the flu on both real wages and real returns to capital, which are required to properly assess the potential redistributive effects of pandemics.1 In this paper, we exploit within-country variation in the increase in the number of deaths in Spain to empirically assess the potential effects of the Spanish flu on real returns to factors of production in the short- and medium-run.2 To perform this exercise, we use data on real wages and returns to capital. We use disaggregated data on real wages, which are the ratio between daily nominal mean wages for nine occupations and cost-of-living indices for each Spanish province.3 Then, we approximate real returns to capital using dividends and real estate prices in each province deflated by provincial cost-of-living indicators.4

A related question is the mechanism through which pandemics affect economic activity in the short-run. A definitive answer to this question is outside the scope of this paper, due to data limitations. However, by analyzing the heterogeneous effects across occupations and regions, we can provide a tentative answer. Theoretically, pandemics can be thought of as a supply shock because the labor force is reduced by death, sickness or social distancing and production declines. However, they can also represent a demand shock because consumption declines as uncertainty about the future and unemployment increases.5 If the demand shock is driving the results, we would expect that the effects of the flu were exacerbated in occupations and regions hit by larger consumption declines. In our context, this should happen in occupations related to non-essential consumption and in more urbanized regions with greater awareness of the dangers of the flu and stricter social distancing.

The main contribution of the paper is to document the effects of the Spanish Flu on the returns to factors of production. We show that excess death rates during the flu reduced daily real wages, relative to pre-1918 levels, for most occupations (out of nine occupations, only metal workers and painters were not significantly affected). We find that these negative effects were broadly short-lived. These findings underestimate the full impact of the flu on workers’ incomes, as workers who kept their jobs may have worked fewer days during the peak months of the pandemic. In contrast, we fail to document that real returns to capital (dividends and real estate prices) were negatively affected by the flu. Indeed, whereas the effect of the flu on dividends is imprecisely estimated (we cannot reject it is null), the effect on real estate prices, driven by the post-1918 recovery, is positive. In addition, we document that the negative effects on real wages are stronger in more urbanized provinces (with higher population density), where the decline (or delay) of consumption in non-essential goods may be larger. We interpret this overall evidence as supporting the hypothesis that the Spanish Flu represented a negative demand shock.

To proxy for the intensity of the pandemic, we obtain data at the province level of the number of deaths by year from INE Historical Database (Spanish National Institute of Statistics). Our measure of the Spanish Flu is excess death rate in the province, defined as the difference between the actual number of deaths and the number of deaths predicted by a province-specific linear trend and normalized by the population size of the province. As it can be seen from Fig. 1, the number of deaths was relatively stable between 1910 and 1930, except in 1918, when it suddenly increase.

The core of the paper is to examine the effect of cross-sectional and temporal variations of mortality on (daily) real wages. As a first step, we regress the annual growth rate of real wages on the province-year deviation of mortality from its linear trend. This regression is meant to capture a correlation between excess death rate and contemporaneous changes in real wages. All regressions include province and year fixed effects. We have data for nine different occupations: agricultural workers, builders, stone-cutters, carpenters, blacksmiths, metal workers, painters, tailors and shoemakers. We document that the effect of excess death rates is generally negative but it is very heterogeneous across occupations. It ranges from a very large and significant effect for shoemakers to a non-statistically significant effect for metal workers. Quantitatively, a one percent increase in excess death rate results into a decline of real wages between 12 per cent (shoemakers) and null (metal workers).

In the previous regression analysis, we allowed all mortality deviations (positive and negative) to enter into the regression. To formally analyze the short- and medium-run effect of the flu, we perform a differences-in-differences estimation and focus on the excess mortality rate in 1918. We find that the short-run effect is negative for most occupations but it differs across them. It ranges from non-statistically significant for metal workers to very large and negative for shoemakers. Quantitatively, for the average province, the flu reduced real wages of shoemakers 30 percent, relative to pre-1918. We also document that these negative effects on real wages were, in general, short-lived. Even though most of the pandemic took place in 1918, there were also a large number of deaths reported in 1919. If we consider both years as the same pandemic episode, the qualitative results do not substantially change. The most re-markable change is that the negative short-run effects are only exacerbated for shoemakers and tailors. For example, the quantitative short-run effect for shoemakers, in the average province, increases from 30 to 40 percent.6 We interpret this exacerbation in occupations in non-essential consumption sectors as suggestive evidence in favor of a demand-driven interpretation.

We also document heterogeneity of the effects on real wages across provinces. The negative effect is exacerbated in more urbanized and densely populated provinces. Since these provinces had actually lower excess death rates, our interpretation is that, in these provinces, people were more aware of the dangers of the flu and kept stricter social distance measures. Moreover, we fail to find a mitigation effect of the flu in more industrialized provinces. The coefficient on the interaction term between industrialization and excess death rate is negative for all occupations and significant in four out of the nine. We view this result as evidence against the supply-driven hypothesis. We would expect that in more industrialized provinces an increase in excess mortality should have reduced job competition and attenuate the negative effect on real wages. Therefore, this overall evidence on the heterogeneity across provinces paints a picture consistent with the demand-driven interpretation.

We also investigate the effects of the flu on the returns to capital. We do not have an annual series of the returns to capital at the province level. However, we have two measures that proxy for capital returns. First, we have data on the evolution of dividends paid by public companies. The effect of the flu on dividends is imprecisely estimated but we cannot reject that it is null. Real estate prices is our second proxy for rents. As documented in Jorda et al. (2019), housing seems to be the most important asset throughout history, the Spanish case is no exception (Prados de la Escosura and Rosés (2010)). Thus, changes in housing prices could be a good proxy of returns to capital in early 20th century Spain. In addition, we consider land prices. We do not see land prices as proxies for the returns to land ownership. Rather, we view them as another asset class to approximate the returns to capital. The estimated coefficients imply that the flu had a positive effect on real estate prices, driven by the post-1918 recovery. Thus, we fail to document that the Spanish Flu had significant negative effects on returns to capital. Our interpretation of the results is that the Spanish Flu represented a large demand shock that was not generally persistent over time. The losses were mostly concentrated among workers, which experienced a substantial reduction in real wages. One potential mechanism is that, due to uncertainty and social distancing, consumption in non-essential goods declined. Firms reacted to this decline in demand constraining real wage growth. We leave for future research to empirically investigate this channel.

Will this time be different? It is too soon to assess whether the redistribution and persistence of the effects of Covid-19 will be the same as the effects of the Spanish Flu. The fact that the decline in real wages was exacerbated in more urbanized provinces, suggests that the decline in consumption, due to social distancing, is the driver of the effects. Moreover, the finding that workers seem to absorb most of the shock is likely to be repeated, according to initial anecdotal evidence and economic forecasts (e.g, Baldwin & di Mauro, 2020). Indeed, forecasts predict large economic effects and large losses for workers. In addition, most developed countries have experienced a huge increase in unemployment claims.

Related literature Our paper relates to different strands of the literature. First, it is related to the large literature that examines the long-run effects of economic crises. This list includes, among others, Reinhart and Rogoff, 2009, Jorda et al., 2013. The type of analysis is similar, even though they focus on financial crises and here we study the effect of an “exogenous” increase in the number of deaths. It is also related to the emerging literature on the economic effects of the flu in 1918. For example, Barro (2020) uses a cross-section of countries and finds that the Spanish Flu generated a decline on GDP and consumption of 6 and 8 percent, respectively, for the average country. Another related paper is Correia, Luck, and Verner (2020), which uses within-country variation in the United States and find that the flu had a negative effect on employment and output, while focusing on the heterogeneity on non-pharmaceutical interventions. We use the same empirical strategy as Barro (2020). The main departure from this literature is that we are interested in the effects of the pandemic on the returns to factors.

In addition, there exists a more recent empirical literature examining the economic persistence of large shocks. There is no consensus about what sort of shocks and what circumstances generate persistent effects. On the one hand, there is evidence that pandemics and other disasters have long run effects (Scheidel, 2017, Jorda et al., 2020b) or are more persistent than expected (Jorda et al., 2020a, Vonyó, 2012). On the other hand, there is also a large literature showing that very large shocks can be followed by quick reversions to the long run trend (Davis and Weinstein, 2002, Miguel and Roland, 2011). For the particular case of the Spanish Flu, most authors point at short-run effects with quick reversions to the trend. For the United States, although Almond (2006) uncovered large individual effects, Velde, 2020, Brainerd and Siegler, 2003 document quick reversions to the trend. Barro (2020) also documents short-run effects of pandemics using a cross-section of countries. Our findings also suggest that the effects of Spanish Flu in Spain were overall non-persistent.

There is a vast economic growth theory discussing the theoretical effects of population growth and its empirical validity throughout history (see, for example, Galor, 2011). In a Malthusian model, it is assumed that there are decreasing returns to scale and population growth is constrained by output growth. This is the well-known Malthusian trap or “iron law of wages”, which can explain pre-industrial stagnation (Clark, 2007). In the opposite side, we find the endogenous growth literature or economics of ideas (see, Romer, 1990), in which population growth is related to new ideas, productivity and economic growth. Along this line of research, the closest paper is the recent contribution by Jorda (2020b). They conduct a very large cross-country analysis on the effects of pandemics dating back to the 14th century. They focus, as we do, on the effect of the pandemics on real wages and return to capital. Given their time horizon, they can perform very long-run analysis, which we can not do. Our contribution to this debate is limited given that we perform a shorter-term analysis for a specific pandemic and country. However, it seems that we obtain different results. Jorda (2020b) isolate a Malthusian effect in which mortality crises increase real wages. Here, our results are more consistent with a increasing returns framework in which a pandemic reduces wages. Moreover, while Jorda (2020b) document negative effects for returns to capital, we fail to find them.

Our work is also related to the large literature on the economic consequences of health shocks. One important result is that negative health shocks are associated with significant consumption declines in the presence of imperfect capital markets and low household savings (Gertler and Gruber, 2002, Asfaw and von Braun, 2004, Wagstaff, 2007, Genoni, 2012, Islam and Maitra, 2012, Mohanan, 2013, Omar Mahmoud and Thiele, 2013, Sparrow et al., 2014, Khan et al., 2015). Our findings on the heterogeneous effects of the Spanish Flu on real wages in Spain seem consistent with these results. Furthermore, our results are similar to those of Wagstaff (2007), who shows that Vietnamese urban households are relatively more vulnerable to health shocks than rural households.

Lastly, we also contribute to the economic history literature that examines the evolution of the Spanish economy in the early 20th century. The pandemic has not had a prominent role in explaining economic trends in the first third of the 20th century. Indeed, the debate has mostly centered around the (not positive) impact of Word War I on a neutral economy and on the factors driving fast structural change, catch up and industrial growth in the 1920s (Prados de la Escosura & Rosés, 2009). The pandemic is generally not mentioned as a factor affecting economic performance. In addition, when analyzing the factors driving the spatial and temporal variation in living standards in the first third of the 20th century, real wages, inflation, collective action, and pro-worker legislation are stressed (Maluquer de Motes & Llonch, 2006), whereas the flu pandemic is not even considered as an explanatory factor. For spatial variation, World War I and de-globalization increased wage differentials in the late 1910s, while internal mobility drove convergence in real wages in the 1920s (Rosés & Sánchez-Alonso, 2004). Our contribution to this literature is to include the Spanish Flu as an important variable driving temporal and spatial variation in real wages. We will show that the flu slowed down real wage growth in 1918, perhaps anticipating the social discontent of 1919–1920.

The rest of the paper is structured as follows. Section 2 describes the historical setting of Spain in the time of the Spanish Flu. Section 3 explains the empirical setting and the data. Section 4 presents the main results of the paper. Lastly, Section 5 concludes

2. The Spanish flu in Spain

The first news of an increasing death toll due to respiratory diseases appeared in the Spanish press in May 1918, in the wake of the first wave of the pandemic starting in March 1918. The second, much deadlier, wave apparently starting in late August in France, spread to Spain via seasonal workers returning from France. This wave peaked in October 1918, with mortality rates increasing by 300 per cent with respect to the pre-influenza mortality rates (Trilla, 2008). A third, milder, connected wave was detected in the winter of 1919. According to some existing estimates, deaths caused by respiratory diseases increased by 2.4 per 10,000 in the first wave of May-July 1918 and by 92.6 per 10,000 during the Fall 1918-Winter 1919 wave. Excess deaths from all causes in the wave Fall 1918-Winter 1919 increased by 112.9 per 10,000 (Chowell, Erkoreka, Viboud, & Echeverri-Dávila, 2014). Mortality rates were higher in the 25–34 age group, while there were below trend among those above 65. As a result of the pandemic, Spain’s population growth was negative in 1918 (net loss of 83,121 persons). Table 1 shows how death rates in Spain were among the highest in Western Europe and North America.

Table 1.

Mortality rates per 1000, Spanish Flu.

Country	Death toll	Death rate (per 1000)
Austria	20,458	3.3
Denmark	12,374	4.1
Eire	18,367	4.3
England and Wales	approx. 200,000	5.8
Scotland	27,650–33,771	5.7–6.9
Finland	18,000	5.8
France	240,000	7.3
Germany	225,330	3.8
Hungary	approx. 100,000	12.7
Italy	390,000	10.7
Netherlands	48,042	7.1
Norway	14,676	5.7
Portugal	59,000	9.8
Spain	257,082	12.3
Sweden	34,374	5.9
Switzerland	23,277	6.1
US	675,000	6.5
Mexico	300,000	20.6

Sources: Johnson and Mueller (2002).

We do not have much information on the adoption of quarantines and related policies to reduce the rate of infection. News on the pandemic appeared regularly in the main newspapers. King Alfonso 13th was apparently infected in the first wave of the pandemic before the summer of 1918. As mortality levels increased, a newspaper in Barcelona (La Vanguardia) opened up with several pages of obituaries of people killed by the flu virus. Madrid newspapers like ABC or El Debate provided very detailed reports of the spread of infection in the provinces. Schools and universities were closed, but mass and other gatherings were still organized, facilitating the spread of the virus. Some public health measures were adopted. Streets were cleaned with water and sodium hypochlorite. Trains, tramways, baggages, bars, cafeterias, even the mail, were regularly disinfected with phenolic oil. Social distancing and disinfection measures were recommended by state authorities, but these measures were difficult to enforce. Therefore, even though mortality rate peaked in late 1918, the economic disruption, driven by increased uncertainty and fear, is likely to have started during the spring of 1918, when news and social distancing measures started to emerge.

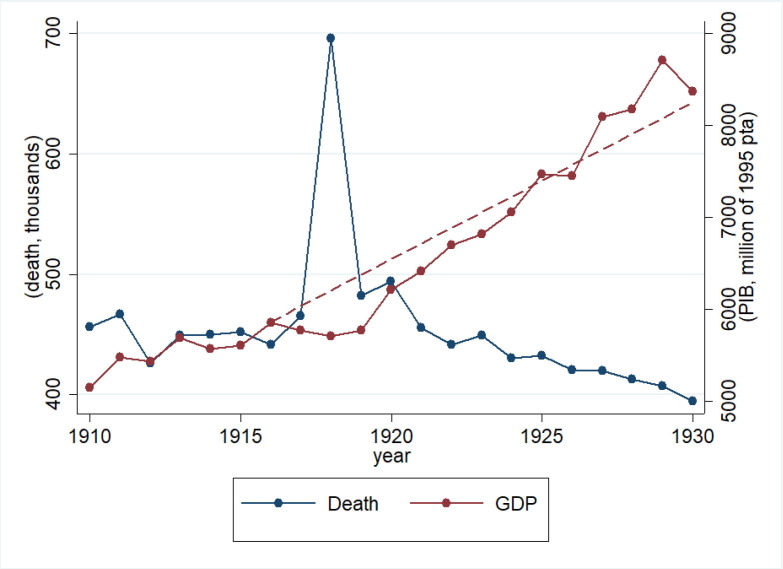
In the early 20th century, Spain was still a developing economy. Using data from the Maddison project latest release, Gross Domestic Product (GDP) per capita was 62 per cent of UK’s and 51 per cent of the US’ in 1918 (Bolt, Inklaar, de Jong, & van Zanden, 2018). Manufacturing represented 27 per cent of total output in 1920 and employed slightly less than 20 per cent of the working population (Carreras, 2006). Real GDP increased until 1916 but declined thereafter. 1918 culminated two years of straight falls in total output, with output increasing in 1919 and 1920 and accelerating in the 1920s (Prados de la Escosura, 2009). Fig. 2 illustrates this evolution of GDP along with the sudden increase in the number of deaths in 1918. GDP reaches a trough in 1918. Note that even though the decline in aggregate GDP in 1918 does not seem large (only 1 percent decline), it represents a substantial deviation from the 1910–1930 trend (6.5 percent).

Fig. 2.

Evolution of Gross Domestic Product and Deaths, 1910–1930 Sources: Death data obtained from INE Base Historica and Gross Domestic Product (GDP) in 1995 constant prices from Prados de la Escosura (2017).

Table 2 reports some aggregate statistics to put 1918 into perspective. The numbers in the table represent percentage deviations from the 1910–1930 linear trend. As we could see in Fig. 2, the deviation from the trend of GDP was quite large in 1918. However, we want to notice the difference across sectors. Most of the decline is found in the services and manufacturing. The decline in production of the agricultural sector was mild.

Table 2.

Output and consumption. Percentage deviations with respect to linear trend.

Output	GDP	GDPpc	Agricultural	Manufacturing	Services
1915–1917	−1.13	−0.70	3.07	−0.74	−3.65
1918	−6.45	−5.52	2.18	−7.46	−9.66
1919–1930	−0.97	−0.69	0.04	−2.56	−0.61
Fixed Capital Formation	Total	Dwellings	Other construction	Machinery	Transport
1915–1917	−19.02	−15.71	−16.9	−10.47	−30.71
1918	−34.15	−49.49	−52.48	−34.29	6.47
1919–1930	−6.09	−3.4	−12.09	−3.43	−5.59
Consumption	Total	Food	Textiles	Utilities	Services
1915–1917	−7.26	−3.88	8.94	−2.53	−8.16
1918	−6.11	4.11	−10.34	0.73	−20.48
1919–1930	−0.49	0.17	−2.31	−0.95	−1.92

Notes: Each cell is the average of the difference between variable in real terms and the predicted value given a linear trend. Original consumption variables are real values indexed at 100 in 1958. Original production variables are real values indexed at 100 in 1913.Prados de la Escosura (2017).

Investment was very volatile in the period. Aggregate investment sharply declined in 1918 and the fall was generalized across all investment types. Building construction represented 70 per cent of all domestic capital formation (Prados de la Escosura, 2017). Compared to pre-1918 average, investment in both new dwellings and other construction significantly fell in 1918 and recovered later on. A very similar pattern emerges for machinery, which represented between 10 and 20 percent of total investment. The only exception is investment in transport, which increased in 1918 and was above trend.

Consumption seem to be affected by accelerating prices, changes in relative prices and the pandemic. Real consumption slightly increased in 1918, with respect to pre-1918 average. However, this aggregate measure masks substantial heterogeneity across sectors. The consumption of textiles significantly decreased in 1918 and it was 10.3 per cent below trend. Consumption of services also fell and it was 20.5 per cent below trend in 1918. This is in stark contrast with food consumption, which increased in 1918 and it was 4 per cent above trend. This heterogeneity in consumption suggests that demand for non-essential goods significantly declined in 1918. We want to emphasize that consumption in this four items comprises around 90 percent of total consumption (Prados de la Escosura, 2017).

To conclude, the Spanish Flu reached Spain in a moment in which it was transitioning towards a developed economy. The aggregate data seems to indicate that the decline in production and consumption was heterogeneous across sectors. Given this heterogeneity, controlling for year and taking into account province-specific prices, it is possible that the economic effects of the flu were also heterogeneous across provinces and the distribution of the potential losses were different within provinces. We will empirically analyze these questions in the ensuing sections.

3. Identification, empirical strategy, and data

3.1. Measure of flu at province level

In the previous section, we have argued that, at the country level, the Spanish Flu did not seem to have a very large effect on the economy. However, this aggregate effect could be masking substantial heterogeneity across provinces. To assess this effect, we need first to obtain a measure of the intensity of the flu at the province level.

We use two measures of the flu. In our first measure, we just compute excess mortality in each province over time, allowing for the flu pandemic to increase mortality in various years and allowing other unnoticed excess mortality episodes to have effects on our variables of interest. Our second measure is excess mortality only in 1918, which is the year with the greatest mortality. This measure will allow us to assess the effect of the Spanish flu over time and its potential persistence.

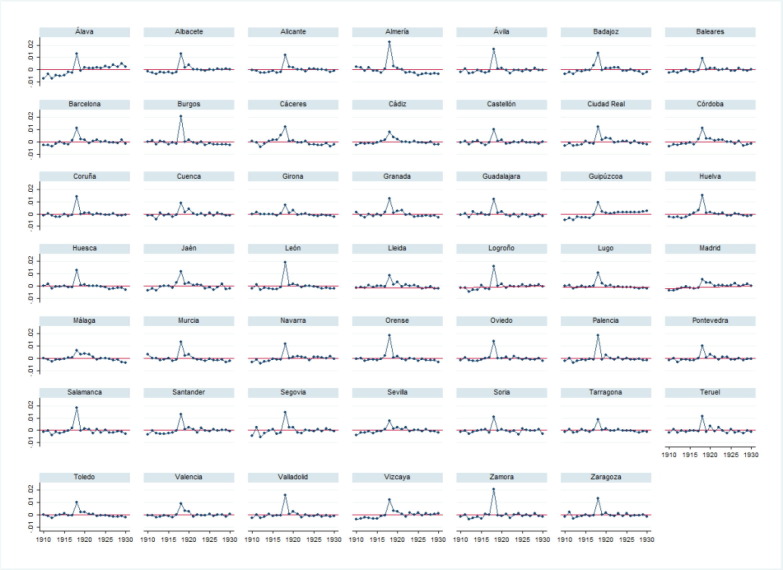
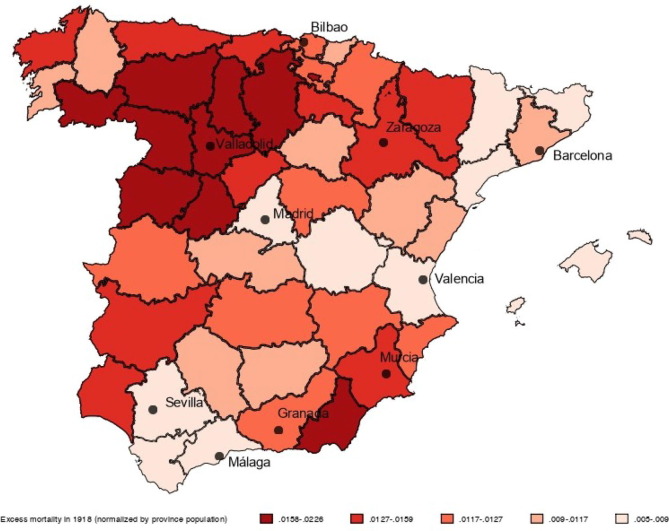
Fig. 3 reports the evolution of our excess death rate measure for the different provinces. As it can be seen from the figure, this variable is mostly zero for all years, except in 1918, when there is a peak. This peak in 1918, the “Flu”, is clearly noticeable across provinces. Fig. 4 plots the geographical distribution of excess death rate in 1918 across provinces. We want to emphasize that there is substantial heterogeneity across provinces. In particular, the average value of the “Flu” is 12.6 per thousand people and the standard deviation is 4 per thousand. We will exploit this within-country variation in our empirical exercise. In addition, it does not seem that excess death rates are positively correlated to population or urbanization. Indeed, large populated and urbanized provinces like Barcelona and Madrid belong to the group of less affected provinces. We will use this heterogeneity to discuss the relative relevance of the supply and demand-driven interpretation.

Fig. 3.

Excess Death Rate, 1910–1930 Notes: Excess death rate obtained as deviation from the predicted linear trend (normalized by population), by province. Death data obtained from INE Base Hist́orica and Census Data.

Fig. 4.

The Flu: Excess Death Rate in 1918 Notes: The map represents excess mortality rate in 1918. Excess death rate obtained as deviation from the predicted linear trend (normalized by population), by province. Includes the 10 largest capitals of provinces (1910). Death data obtained from INE Base Hist́orica and Census Data.

3.2. Empirical strategy

We start by analyzing the short-run effect of mortality fluctuations on our outcomes of interest. In this equation, most of the effect is absorbed by deviations from trend in 1918 and 1919, but we let any deviation of mortality from the province-specific trends to affect our outcomes of interest. This specification does not allow for persistence effects of large pandemics, mortality changes shift the market equilibrium in the short run, and markets bounce back to their original equilibrium once mortality goes back to its trend.

$$\mathrm{\Delta }{Y}_{\mathit{ct}}=\beta *\text{Excess}\text{Death}{\text{Rate}}_{\mathit{ct}}+\gamma *Y_{\mathit{ct}-1}+{\delta }_c+{\delta }_t+s_{\mathit{ct}},$$ (1)

where ΔY_ct is the annual growth rate of the outcome variable for province c and year t, following the main specifications in Barro (2020). Excess Death Rate_ct is the difference between actual number of deaths and predicted (normalized by population size) for province c at year t, and δ_c and δ_t are province and year fixed effects, respectively. We also include the lag of the outcome variable, Y_{ct− 1}, to control for potential mean reversion or convergence, as in, for example, Fields, Cichello, Freije, Menendez, and Newhouse (2003) or Barro and Sala-i-Martin (2003).7 Our data set covers the period from 1915 to 1930. The coefficient of interest is β. Indeed, β < 0 implies that one percent increase in the excess death rate, decreases the outcome variable by β percent. In this specification, the effect is symmetric on both sides of the trend: the size of the effect of a province having below or above mortality with respect to the province linear trend should be of the same size (and different sign).

Targeting specifically the impact of the pandemic and allowing for the persistence of the effects, we run differences-in-differences equations in which provinces vary by the intensity of the flu pandemic in 1918 only. In this equation, mortality deviations from trend in each year before and after 1918 do not matter and it is only the effect of the mortality deviations in 1918 that has effects in 1918 and later,

$$\mathrm{\Delta }{Y}_{\mathit{ct}}={\beta }_t*\sum _{t=t_1}^T{\text{Flu}}_c*D_t+\gamma *Y_{\mathit{ct}-1}+{\delta }_c+{\delta }_t+s_{\mathit{ct}},$$ (2)

where Flu_c is the excess mortality rate in 1918 in province c, D_t is a dummy equal to one for period t and zero otherwise. As in the above specification, we include the lag of the outcome variable, Y_{ct− 1}, and δ_c and δ_t are province and year fixed effects, respectively The sample is the same as above (1915–1930). In our baseline regressions, we consider two periods affected by the pandemic, 1918 and post-1918. The omitted variable is the pre-1918 period. That is, β_t should be interpreted as the change in the outcome variable relative to the pre-1918 mean of the outcome variable.8 We want to separate the effect at impact and afterwards to have a sense of the relative persistence of the shock. In addition, to gauge the speed of the potential recovery, we disentangle the post-1918 effect by adding more time dummy interactions. Then, as an additional robustness check on the potential persistence effect, we will interact Flu_c with post-1917.

Finally, as an extension, we also look at the heterogeneous effects of excess mortality as a function of the population density and industrialization level. In order to do that, we include the interaction of excess death rate with a dummy variable equal to one if the province is above the median of the population density (industrialization) distribution.

3.3. Data

We obtain our data from different official sources. Data on the number of deaths, disaggregated by provinces over time, are obtained from the Historical Database of the Spanish National Institute (INE Base Hist́orica). Table 3 reports the average and the standard deviation for the three sub-periods of interest. As it can be seen, the average number of deaths is quite similar both before and after 1918. However, as expected, the average number of deaths increased substantially in 1918. One interesting feature is that the standard deviation in 1918 is much higher than in any of the other two sub-periods. This higher standard deviation implies that the increase in the number of deaths was very heterogeneous across provinces.

Table 3.

Summary Statistics.

Variable	1915–1917 Average	St.Dev.	1918 Average	St.Dev.	Post-1918 Average	St. Dev.
Deaths	9296	4925	14,337	6976	8934	5120
Wages:
Agriculture	1.95	0.44	1.72	0.61	2.63	0.96
Builder	2.76	0.59	2.64	0.51	3.87	1.00
Stone-cutter	3.00	0.67	2.90	0.57	4.04	1.02
Carpenter	2.79	0.59	2.61	0.66	3.80	0.98
Blacksmith	2.85	0.72	2.58	0.61	3.76	0.94
Metal	2.85	1.22	2.68	1.10	3.76	1.66
Painter	2.69	0.64	2.54	0.57	3.62	1.03
Tailor	2.62	0.82	2.39	0.84	3.27	1.12
Shoemaker	2.40	0.63	2.24	0.64	3.16	0.95
Dividends:	403	1298	499	1605	464	1430
Real estate prices:
Urban housing	4797	7426	7150	12,152	9061	16,773
Land prices	1449	1397	1911	1968	2664	3011

Notes: Death is number of deaths for province and year from INE Historical Database. Wages are average real wages for province and data from Rosés and Sánchez-Alonso (2004). Real dividends are thousands of pesetas from the Estad́ıstica de Utilidades, deflacted by provincial cost-of-living index. Real Estate prices are the ratio of value of all transactions (in pesetas) over the number of transactions, deflacted by provincial cost-of-living index. Data obtained from Carmona and Rośes, 2012, Carmona et al., 2017, and Carmona, Rosés and Simpson (2019). All post-1918 are 1919–1930, except for dividends which the series stops in 1919.

The analysis on the effect of the flu on real wages will be the core of our paper. We have data on annual real wages for nine occupations at the province level between 1915 and 1930 (computed using prices and nominal wages for several occupations in the capitals of each province). We obtain these data from Spain’s annual statistical yearbook. The occupational groups are workers in agricultural sector, builders, stone-cutters, carpenters, blacksmiths, workers in metal sector, painters, tailors and shoemakers. These occupations comprised a large share of workers at the time and they also cover industries with different degrees of tradeability and skill-intensity. Actually, around 50 percent of the Spanish population was employed in the agricultural sector (Prados de la Escosura, 2017). Nonetheless, there was substantial heterogeneity on the levels of industrialization across provinces (see Table 10). As it can be see from Table 3, for most occupations, the real wage in 1918 was below the pre-1918 average. From this average values, it would seem that workers were negatively affected by the Spanish Flu. However, we need to formally test this effect. In addition, at first sight, we do not observe significant differences across occupations, but we will examine this potential heterogeneous effect in the next section. We are also interested in the effect of the flu on the returns to capital. This is a more difficult exercise because we do not have, at the province level, data on returns to capital. However, we have two proxies for these returns. On the one hand, we use data on dividends from the Estad́ıstica de Utilidades, which provide information on dividends paid by public companies Tafunell (2000).9 We obtain real values by deflacting these nominal values by provincial cost-of-living index. A noticeable fact from Table 3 is that the average value of dividends was substantially larger in 1918 than in the previous sub-period. Moreover, this larger average comes in hand with an also substantially larger standard deviation. Once again, it hints to a potential heterogeneous effect across provinces. We will exploit deviations from general year effects in the evolution of dividends to analyze the impact of the flu on the returns to capital.

Table 10.

Province Characteristics (1910).

Province	Population	Industrialization	Density
Álava	97,181	5.53	31.92
Albacete	264,698	3.92	17.81
Alicante	497,616	5.70	85.81
Almeŕıa	380,702	2.33	43.34
Ávila	208,863	1.83	25.95
Badajoz	593,206	4.38	27.15
Baleares	331,136	9.01	63.02
Barcelona	1,162,521	15.04	148.46
Burgos	346,934	1.75	24.14
Ćaceres	398,641	2.70	19.88
Cádiz	488,347	7.25	64.19
Castelĺon	322,391	5.17	48.36
Ciudad Real	379,674	4.11	19.24
Ćordoba	499,205	3.89	36.34
Coruña	680,225	4.20	85.63
Cuenca	269,634	2.54	15.88
Girona	322,523	10.49	54.51
Granada	522,695	3.51	41.71
Guadalajara	209,352	2.02	17.17
Guipúzcoa	226,684	13.32	120.28
Huelva	310,028	4.01	30.74
Huesca	248,299	3.07	16.39
Jáen	526,718	3.11	39.07
Léon	396,122	1.35	25.72
Lleida	284,971	3.25	23.45
Logroño	188,235	5.81	37.34
Lugo	479,965	1.02	48.58
Madrid	885,248	4.59	109.8
Ḿalaga	523,487	3.76	71.85
Murcia	615,146	2.59	54.35
Navarra	313,235	3.99	31.40
Orense	414,216	2.23	58.97
Oviedo	685,131	1.74	62.89
Palencia	196,053	3.07	23.85
Pontevedra	495,644	3.79	112.8
Salamanca	334,377	3.13	27.14
Santander	302,956	3.09	55.49
Segovia	167,747	3.03	24.16
Sevilla	597,031	5.12	42.16
Soria	156,354	1.92	15.16
Tarragona	340,019	5.33	52.15
Teruel	243,556	2.70	17.24
Toledo	413,217	3.19	26.95
Valencia	884,298	5.29	80.7
Valladolid	284,791	3.79	34.82
Vizcaya	349,923	6.65	161.59
Zamora	272,976	1.73	25.82
Zaragoza	452,100	3.91	26.77

Our second proxy for returns to capital are real estate prices. In particular, urban housing prices and rural land prices. Both prices have been deflated with a provincial cost-of-living indexes used in Rosés and Sánchez-Alonso, 2004, Carmona and Rośes, 2012, and Carmona, Lampe and Rosés (2014). We obtain data on real average house prices and real land prices at the province level from Carmona and Rośes, 2012, Carmona et al., 2017, and Carmona, Rosés and Simpson (2019). From Table 3, we want to emphasize two features. First, the value of average real estate prices (both urban and land) were higher in 1918 than in the previous period. Second, there is a substantial increase in the variation across provinces, especially in urban house prices. One shortcoming of using the average price of each year’s sales is that there may be a selection problem in the type of houses being sold. This problem may be more serious in 1918 as fewer housing units were sold. Thus, we must take these concerns under consideration in our analysis.

4. The effects of the flu on the returns of factors

This section presents the main results of the paper. We examine how the economic effects of the flu are shared within the country. The core of the paper is the analysis of the effect of the flu on real wages. Then, we also examine the effect on our two proxies for the real returns to capital (dividends and real estate prices). We will also investigate how these effects differ across provinces.

4.1. The effect of the flu on real wages

We start by looking at the impact of mortality changes on real wages. Equation (1) assumes factor markets flexibly adjust and recover from shocks. Theoretically, it is not clear which should be the effect of excess mortality on real wages. On the one hand, a decline in the labor supply should tend to increase real wages because, given demand, there is less competition for the job. On the other hand, a deterioration of general health conditions, social distancing and uncertainty, can be conducive to an overall decline in demand and, thus, a fall in real wages. It is outside the scope of this paper to disentangle both effects. We are only interested in empirically examining the overall effect of the flu on real wages.

Table 4 reports the effect of deviations from mortality rate trends on the annual growth rate of real wages for nine occupations. We have annual data for all provinces between 1915 and 1930. Panel A reports reports the coefficients of running Equation (1). Remember that we include province and year fixed effects. The first thing to notice is that, even though the sign of the coefficient is negative in all columns, there exists substantial heterogeneity across occupations. The negative coefficient ranges from 12 for shoemakers to non-statistically different from zero for metal workers. The coefficient is statistically significant for all occupations, except for stone-cutters, carpenters and metal workers. The coefficient for builders is significant at 10 percent. This overall negative coefficient means that increases in mortality (from trend) tend to reduce real wages and decreases in mortality tend to increase them.

Table 4.

Effect of Mortality and Flu on Real Wages, by Occupation.

	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)
	Agriculture	Builder	Stone-Cutter	Carpenter	Blacksmith	Metal	Painter	Tailor	Shoemaker
Panel A: Mortality
Excess Death Ratect	11.30***	−4.81*	−3.61	−6.01	−7.01**	−3.92	−7.91**	−11.07***	−12.09**
	(3.03)	(2.49)	(3.62)	(3.61)	(2.58)	(3.71)	(2.98)	(2.74)	(5.05)
Lag Real Wagect	-0.61***	−0.55***	−0.52***	-0.51***	−0.52***	−0.46***	−0.44***	−0.44***	−0.53***
	(0.08)	(0.07)	(0.06)	(0.07)	(0.08)	(0.06)	(0.07)	(0.06)	(0.09)
Panel B: Mortality(2)
Excess Death Ratect	-11.21***	−4.70*	−3.79	−6.25	−6.42**	−1.16	−8.16**	−11.01***	−12.57**
	(3.19)	(2.52)	(3.57)	(3.57)	(2.61)	(2.75)	(3.03)	(2.55)	(4.93)
Excess Death Rate Lagct	-1.27	−1.49	2.41	3.26	−7.75**	−2.95	3.22	−0.83	6.41*
	(5.03)	(3.49)	(2.23)	(1.90)	(3.25)	(2.94)	(2.88)	(4.75)	(3.14)
Lag Real Wagect	-0.61***	−0.55***	−0.52***	−0.51***	−0.52***	−0.43***	−0.44***	−0.44***	−0.52***
	(0.08)	(0.07)	(0.06)	(0.07)	(0.08)	(0.05)	(0.07)	(0.06)	(0.09)
Total Effect	-12.47**	−6.19	−1.38	−3.01	−14.17***	−4.11	−4.94	−11.84*	−6.17
	(5.03)	(4.14)	(4.08)	(4.62)	(3.38)	(3.07)	(2.96)	(6.40)	(7.53)
Panel C: Flu Effect
Flu1918c ∗ D1918	-19.23***	−10.10***	−8.13***	−7.07***	−6.02***	−1.54	−5.99	−15.84***	−23.45***
	(2.83)	(2.68)	(2.22)	(2.10)	(1.69)	(2.33)	(6.07)	(1.76)	(0.70)
Flu1918c ∗ DP ost−1918	-4.16	−6.51*	−9.25***	−6.32**	−3.38	−3.51	−0.95	−3.67	−2.44*
	(3.12)	(3.23)	(2.97)	(2.84)	(2.53)	(2.58)	(6.20)	(2.39)	(1.30)
Lag Real Wagect	-0.61***	−0.56***	−0.52***	-0.51***	−0.52***	−0.45***	−0.44***	−0.44***	−0.52***
	(0.08)	(0.07)	(0.06)	(0.07)	(0.08)	(0.06)	(0.07)	(0.06)	(.0.09)
Panel D: Flu Effect (2)
Flu1918c ∗ DP ost−1917	-5.34	−6.80**	−9.16***	−6.38**	−3.59	−3.36	−1.33	−4.59*	−4.04*
	(3.28)	(3.16)	(2.86)	(2.73)	(2.42)	(2.54)	(6.19)	(2.49)	(2.06)
Lag Real Wagect	-0.61***	−0.56***	−0.52***	-0.52***	−0.52***	−0.45***	−0.44***	−0.44***	−0.53***
	(0.08)	(0.07)	(0.06)	(0.07)	(0.08)	(0.06)	(0.07)	(0.06)	(0.09)
Observations	720	720	720	720	720	720	720	720	720

Notes: Dependent variable is annual growth rate of real wage for province and year. Excess Death Rate is difference number of deaths and predicted by linear regression (normalized by population). In Panel C and D, Flu1918 is the value of excess death in 1918. 1918 is a dummy equal to one for year 1918. Dt is a dummy equal to one for year t and zero otherwise. t = Pre-1918 is omitted from the regression and it is the control period. Total Effect is the sum of both coefficients. Province an year fixed effects included. The table reports fixed effects regressions weighted by population. Standard errors are clustered at the year level. * p < 0.10, ** p < 0.05, *** p < 0.01.

The size of coefficients means that there were large effects of mortality increases on real wages. For example, the average increase in mortality relative to trend in 1918 was 12.6 per thousand people, which according to our coefficients would translate in a reduction of real wages that ranged from 15 per cent in the case of shoemakers to null effect for metal workers. The highest mortality deviation in 1918 was 2.26 percent, meaning excess mortality reduced wages of shoemakers by around 27 per cent in 1918 in the most affected province. The lowest deviation from the province-specific mortality rate trend in 1918 is 0.5 percent, which would decrease wages by about 6 per cent for shoemakers. Since the largest deviations in mortality trends happened in 1918, it is likely that 1918 alone explains the negative coefficient. The year-fixed effect of 1918 is positive and significant in all categories, but excess mortality in 1918 dampened the general improvement in real wages.

To allow for a delayed recovery from deviations of the mortality trend, we include the one-year lag of the mortality deviation in our regression. If the shock were temporary, we would expect that the coefficient of the lag of the mortality deviation had the opposite sign of the contemporaneous one. This exercise is reported in Panel B of Table 4. There is large dispersion on the coefficient of the lag of mortality deviations (negative and positive), but none of the coefficients is significantly different from zero. The only exception is the negative coefficient for blacksmiths. The positive coefficient of shoemakers is significant at 10 percent. The fact that the coefficients on the lag are generally not statistically different from zero would seem to imply that the effects of mortality deviations were persistent. However, this interpretation would be wrong. Indeed, we need to test whether the sum of the two coefficients, labelled as “total effect”, is different from zero. When we do that, we see that the coefficients of “total effect” are negative but they are not statistically different from zero. The only exceptions are blacksmiths, agriculture workers and tailors (albeit only significant at 10 percent). For these occupations, the effects of mortality deviations linger for more than one year.

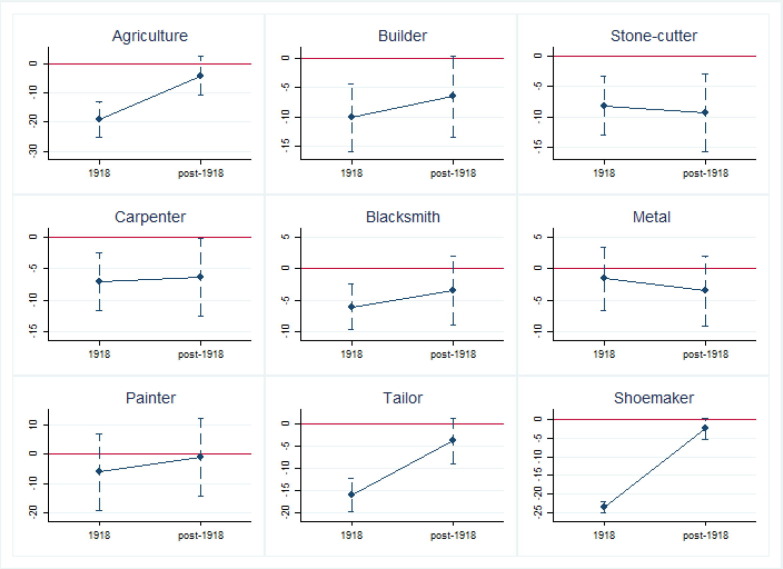
In order to formally analyze the short- and medium-run effect of the flu on real wages, we conduct a difference-in-differences estimation (Equation (2)). Panel C in Table 4 reports the coefficients on the interaction between excess death rate in 1918 (Flu 1918) and time dummies. Remember that in these specifications, the interaction with pre-1918 dummy is excluded from the regression and it is the control group. We include separate interactions for 1918 and post-1918 because, as shown above, mortality deviations do not seem to have persistent effects and if we only had a post-1917 dummy, it could mask the contemporaneous effect of the flu on wages (we do this exercise in Panel D). First, we focus on the interaction with the 1918 dummy. Note that the coefficient is negative and statistically different from zero for all occupations, except for metal workers and painters. This negative coefficient implies that real wages declined in 1918, relative to pre-1918. The coefficient ranges between being not statistically different (metal workers) to −23.45 (shoemakers). Quantitatively, these coefficients imply that, for the average province, the flu reduced real wages from zero (metal workers) to 29.5 percent (shoemakers). For agricultural workers, the largest occupational group (Prados de la Escosura, 2017), the coefficient implies an average decline of 24 percent. This evidence confirms the findings reported in the previous panel that the Spanish Flu had large contemporaneous effects on real wages.

To assess the persistence of the shock, we can look at the interaction between excess death rate in 1918 and the post-1918 dummy. Fig. 5 reports the coefficients of the interactions of “Flu 1918” and the 1918 and post-1918 dummies. If the flu had no persistent effects, we would expect that the coefficient for post-1918 period to be positive. If we look at the coefficients in the figures, it does seem that the coefficients tend to recover after the drop in 1918. The coefficients of the post-1918 are generally negative, but they are only statistically significant for four occupations (carpenters, stone-cutters and (mildly) blacksmiths and shoemakers). In order to test the persistence of the effect, we cannot just test whether the sum of these coefficients is different from zero because the post-1918 variable is an average of more than just one year (up to 1930). We formally test the persistence of the shock in Panel D. In this panel, we run the same type of differences-in-differences regression of Panel C (Equation (2)), however, we only include the interaction between “Flu 1918” and post-1917 dummy. If this coefficient were negative, it would imply that provinces with a higher excess death rate in 1918 had persistently lower wage growth after 1917. We note that this interaction is generally negative and it is statistically different from zero in five out of the nine occupations. This group includes shoemakers, tailors, stone-cutters, blacksmith and builders, even though the significance level is only at 10 percent for the first two. One possible interpretation is that real wages would have increased in absence of the flu, but the flu depressed real wages in 1918. It is important to note that in the inflationary context of the 1910s, there was no need for employers to cut nominal wages. In this case, just having upward stickier nominal wages would be enough, as inflation would erode the purchasing power of workers. In areas with greater flu intensity, employers perhaps resisted nominal wage increases. We plan to further investigate this channel in future research.

Fig. 5.

Effect of Spanish Flu on Real Wages (by Occupation) Notes: Each point is the coefficient of the interaction between excess death rate in 1918 and the time dummies. The dashed line is the 95 percent confidence interval. Pre-1918 was excluded from the regression and it is the reference group. The coefficients are reported in Table 4.

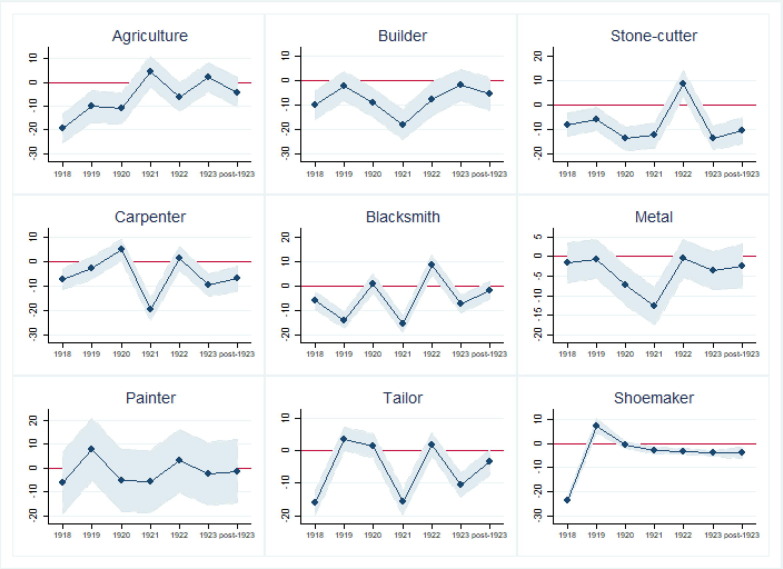
Finally, to assess the shape of the recovery, we disentangle the post-1918 coefficient in Panel C. This is a very demanding regression because we interact “Flu 1918” with several year dummies. Fig. 6 plots these coefficients for all nine occupations. Consistent with the previous evidence, the main negative effect of the flu on real wages is in 1918 and then they tend to recover over time, especially around 1921–22, when we observe some positive coefficients, meaning faster than average recovery in provinces particularly affected by the flu. However, as we argued before, there is a lot of heterogeneity across occupations. Agricultural workers, stone-cutters and blacksmiths are the first to experience some gains, whereas tailors and shoemakers, with the exception of the rebound in 1919, seem to remain below pre-1918 throughout the period.

Fig. 6.

Dynamic Effect of Spanish Flu on Real Wages Over TimeNotes: Each point in line is the coefficient of running the interaction between “excess death” in 1918 on different time dummies. The area represents the 95 percent confidence interval.

We conclude from this exercise that the Spanish Flu had large but, in general, short-lived effects on real wage growth. Moreover, the effects on real wages were heterogeneous across occupations. The fact that the negative effect on real wages was widespread and relatively larger in occupations like shoemakers and tailors lends support to a demand-driven interpretation.

Arguably, the uncertainty and social distance started to reduce consumption earlier than the peak in the number of deaths, specially among non-essential goods like shoes or dresses. The aggregate data documented in Table 2 also hints to this differential effect on consumption. A test of this channel is outside the scope of the paper. We provide additional suggestive evidence on this demand-driven hypothesis by comparing the effects of the flu across provinces. To formally test this hypothesis, we would need firm data, which is not currently available, and we leave it for future research.10

Total Flu EpisodeFig. 3 reported that the most important deviation of mortality from the trend was 1918. This is the reason why in our baseline results we use excess mortality in 1918 as our measure of the flu. However, we also observe some positive excess mortality in 1919. Arguably, some of this excess mortality is related to the final wave of the Spanish Flu. As an additional measure of the flu to better account for this last wave, we define “Total Flu” as the sum of excess mortality rate in 1918 and 1919. Table 5 reports the counterparts of Panel C and D of Table 4. Panel A reports the effects of the interaction between “Total Flu” and 1918 and post-1918 dummy. Note that in this specification we allow excess mortality in 1919 to have an effect in 1918. We think that this is a reasonable assumption given our demand-interpretation. That is, it may be the fear and uncertainty driving down demand more than the number of deaths per se. Note that the coefficients on 1918 are qualitatively and quantitatively similar to our baseline results (taking into account that the average value of the flu has changed from 1.26 to 1.36 percent when accounting for deaths in 1919). The most noticeable difference is the substantial increase in the coefficient for tailors and shoemakers. Quantitatively, the short-run effect increases from 29.5 to 40 for shoemakers and from 20 to 28 for tailors. Panel D investigates the persistence effect of the flu. That is, it reports the interaction between “Total Flu” and post-1917 dummy. We obtain similar quantitative and qualitative results to the counterpart in Table 4. The coefficient is now statistically for seven out of the nine occupations, even though the coefficient for tailors and builders is only mildly significant. We want to notice that the coefficient on shoemakers is larger and more statistically significantly. Indeed, the coefficient implies an average medium-run (up to 1930) decline in real wages of around 9 percent, compared to a mildly significant 5 percent decline in our baseline scenario. To conclude, we interpret the exacerbation of the short-run negative effects for occupations in non-essential sectors (tailors and shoemakers) as supporting evidence of our demand-driven interpretation.

Table 5.

Effect of Flu (1918–19) on Real Wages, by Occupation.

		(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)
		Agriculture	Builder	Stone-Cutter	Carpenter	Blacksmith	Metal	Painter	Tailor	Shoemaker
Panel A: Total Flu
Total Fluc ∗ D1918		−19.25***	−6.68*	−4.51	−4.19	−6.26**	−1.06	−3.81	−20.59***	−29.64***
		(2.19)	(3.41)	(3.51)	(2.43)	(2.13)	(4.88)	(7.26)	(3.36)	(1.35)
Total Fluc ∗		−8.22**	−7.30*	−11.21**	−8.23***	−6.79**	−4.06	−0.86	−6.69*	−5.03***
DPost − 1918		(2.85)	(3.92)	(4.16)	(3.43)	(2.98)	(4.92)	(7.37)	(3.80)	(1.04)
Lag Real Wagect		−0.61*** (0.08)	−0.56*** (0.07)	−0.53*** (0.06)	−0.52*** (0.07)	−0.52*** (0.08)	−0.46*** (0.06)	−0.44*** (0.07)	−0.43*** (0.06)	−0.52*** (0.09)
Panel D: Flu Effect (2)
Total Fluc ∗		−9.10***	−7.25*	−10.66**	−7.91**	−6.75**	−3.83	−1.08	−7.73*	−6.94**
DPost − 1917		(2.86)	(3.85)	(4.13)	(3.29)	(2.85)	(4.91)	(7.35)	(3.88)	(2.71)
Lag Real Wagect		−0.62***	−0.56***	−0.52***	−0.52***	−0.52***	−0.45***	−0.44***	−0.44***	−0.53***
		(0.08)	(0.07)	(0.06)	(0.07)	(0.08)	(0.06)	(0.07)	(0.06)	(0.09)
Province Fixed Effects		Y	Y	Y	Y	Y	Y	Y	Y	Y
Year Fixed Effects		Y	Y	Y	Y	Y	Y	Y	Y	Y
Observations		720	720	720	720	720	720	720	720	720

Notes: Dependent variable is annual growth rate of real wage for province and year. Total Flu is the value of excess death in 1918 and 1919. 1918 is a dummy equal to one for year 1918. Dt is a dummy equal to one for year t and zero otherwise. t = Pre-1918 is omitted from the regression and it is the control period. Total Effect is the sum of the two coefficients. The table reports fixed effects regressions weighted by population. Standard errors are clustered at the year level. * p < 0.10, ** p < 0.05, *** p < 0.01.

4.1.1. Heterogeneous effects across provinces

Spain in early twentieth century was a very heterogeneous country, Table 10 reports some province characteristics in 1910 (the latest Census before the pandemic). We focus on the share of the working population employed in manufacturing and the population density. Even though the two variables are correlated, they proxy different province characteristics. We use the share of the population employed in manufacturing as an index of industrialization.11 The population density is our proxy for urbanization.

Population Density Denser provinces concentrated more deaths in 1918 but they had lower mortality rates. Indeed, the pairwise correlation between population density in 1910 and excess mortality in 1918 (normalized by population in the province) is negative and statistically significant. For instance, the excess death rate in 1918 was 1.12 percent in Barcelona (one of the most densely populated provinces), while it was 1.93 in Léon (one of the least densely populated) (see Table 10). One possibility is that the diffusion of news on the Spanish Flu was more intense in more urbanized provinces. This is a plausible hypothesis given that population density in Spain was also associated with higher share of services, faster urbanization, and higher incomes (Rosés, Mart́ınez-Galarraga & Tirado, 2010), which tend to increase exposure to newspapers and other media. Following this argument, we would expect that the reduction in demand was exacerbated in provinces with higher population density. Thus, if the demand-driven interpretation is right, we should find that the negative effects of the flu on real wages are exacerbated in provinces with higher population density.

Panel A in Table 6 examines this potential exacerbation effect of the flu on real wages. In particular, we include in our baseline regression (Equation (1)) the interaction between excess death rate and a population density dummy. This dummy variable is equal to one if the population density is above the median of the distribution. Note that we still include province and year fixed effects. We find that the coefficient of the interaction term is negative and statistically significant in seven out of the nine occupations (albeit it is only mildly significant, 10 percent, for builders). The only positive coefficient is for stone-cutters but it is not statistically significant. The exacerbation effect is especially large for shoemakers and metal workers. Quantitatively, for shoemakers, one percent increase in excess death rate results in a negligible decline of real wages in a province below the median of the population density distribution. In contrast, in a province with a population density above the median, one percent increase in excess death rate reduces real wages 19 percent. This exacerbation effect is consistent with our demand-driven interpretation.

Table 6.

Heterogeneous Effect of Flu on Wages: Heterogeneous Effects.

	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)
	Agriculture	Builder	Stone-Cutter	Carpenter	Blacksmith	Metal	Painter	Tailor	Shoemaker
Panel A: Density
Excess Death Ratect	−8.03**	−3.79	−4.11	−5.83*	−3.61*	1.07	−6.46**	−7.98***	−8.56
	(2.96)	(2.23)	(3.73)	(3.31)	(1.81)	(2.74)	(2.46)	(2.37)	(5.11)
EDRct * Densityc	−9.46**	−2.87*	1.43	−0.50	−9.84***	−13.88***	−4.16**	−8.95**	−10.21**
	(3.72)	(1.50)	(2.08)	(1.40)	(1.99)	(2.51)	(1.45)	(3.43)	(3.49)
Lag Real Wagect	−0.62***	−0.56***	−0.51***	−0.51***	−0.51***	−0.48***	−0.45***	−0.44***	−0.53***
	(0.08)	(0.07)	(0.06)	(0.07)	(0.08)	(0.06)	(0.07)	(0.07)	(0.09)
Panel B: Industrialization
Excess Death Ratect	−11.27***	−4.11	−2.94	−5.34*	−6.47***	−2.98	−7.34***	−11.02***	−11.97**
	(2.87)	(2.61)	(3.00)	(2.77)	(1.73)	(2.44)	(2.36)	(2.87)	(5.12)
EDRct ∗ Industrializationc	−0.28	−5.65**	−5.42**	−5.26	−4.46**	−7.91***	−4.73	−0.42	−1.04
	(2.55)	(2.32)	(1.87)	(3.60)	(1.74)	(2.34)	(3.13)	(2.31)	(2.11)
Lag Real Wagect	−0.61*** (0.08)	−0.56*** (0.07)	−0.52*** (0.06)	−0.52*** (0.07)	−0.52*** (0.08)	−0.46*** (0.06)	−0.45*** (0.07)	−0.44*** (0.06)	−0.53*** (0.09)
Province Fixed Effects	Y	Y	Y	Y	Y	Y	Y	Y	Y
Year Fixed Effects	Y	Y	Y	Y	Y	Y	Y	Y	Y
Observations	720	720	720	720	720	720	720	720	720

Notes: Dependent variable is annual growth rate of real wage for province and year.Excess Death Rate is difference between actual number of death and predicted by linear regression (normalized by population). In Panel A, Density is a dummy equal to one if density (thousands of people by square-km in 1910) is above median. In Panel B, Ind. is dummy equal to one if share of population in manufacturing sector in 1910 is above the median. The table reports fixed effects regressions weighted by population. Standard errors are clustered at the year level. * p < 0.10, ** p < 0.05, *** p < 0.01.

These results are robust to alternative measures of urbanization. Table 7 reports the coefficients of the interaction with an urbanization measure based on the share of the population in the province living in municipalities of more than 25,000 inhabitants. Note that the sign and qualitative results are roughly the same (Panel A). The notable exceptions are that the coefficients for painters and agricultural workers are negative but they are not statistically significant. One possibility is that this measure of urbanization fails to fully capture the impact on aggregate demand of the province. In Panel B, we make use of our population density measure to reclassify five provinces that are potential outliers and, thus, they may distort our results. In particular, Badajoz, Zaragoza and Ćordoba are reclassified as non-urbanized, given their low population density and mostly rural population. Similarly, Pontevedra and Orense are reclassified as urbanized, given their large population density. If we compare both panels, we observe that most of the coefficients are roughly the same as the ones in Panel A in Table 6.

Table 7.

Heterogeneous Effect of Flu on Wages: Heterogeneous Effects (Robustness).

		(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)
		Agriculture	Builder	Stone-Cutter	Carpenter	Blacksmith	Metal	Painter	Tailor	Shoemaker
Panel A: Large cities
Excess Death		−10.18***	−4.34	−4.15	−6.47*	−4.83**	−1.35	−7.29**	−7.95***	−9.27*
Ratect		(2.45)	(2.25)	(3.62)	(3.41)	(1.93)	(2.43)	(2.51)	(2.59)	(4.99)
Excess Death		−3.04	−1.26	1.45	1.26	−5.91***	−6.70**	−1.69	−8.51**	−7.66**
Ratect * Urbc		(3.13)	(1.20)	(1.33)	(1.52)	(1.80)	(2.59)	(1.89)	(2.99)	(3.33)
Lag Real Wagect		−0.61*** (0.08)	−0.55*** (0.07)	−0.52*** (0.06)	−0.51*** (0.07)	−0.52*** (0.08)	−0.46*** (0.06)	−0.45*** (0.07)	−0.45*** (0.06)	−0.53*** (0.09)
Panel B: Large cities(2)
Excess Death		−8.49***	−3.87	−4.25	−6.84*	−3.62*	1.24	−6.41**	−8.30***	−8.74
Ratect		(2.73)	(2.36)	(3.77)	(3.46)	(1.89)	(2.93)	(2.52)	(2.26)	(5.01)
Excess Death		−7.19**	−2.37*	1.63	2.12	−8.68***	−12.65***	−3.84**	−7.08**	−8.56***
Ratect ∗UrbDensc		(2.94)	(1.24)	(1.57)	(1.42)	(1.69)	(2.55)	(1.65)	(2.86)	(2.58)
Lag Real Wagect		−0.61*** (0.08)	−0.55*** (0.07)	−0.52*** (0.06)	−0.51*** (0.07)	−0.51*** (0.08)	−0.47*** (0.06)	−0.45*** (0.07)	−0.44*** (0.06)	−0.53*** (0.09)
Pro. Fixed Effects		Y	Y	Y	Y	Y	Y	Y	Y	Y
Year Fixed Effects		Y	Y	Y	Y	Y	Y	Y	Y	Y
Observations		720	720	720	720	720	720	720	720	720

Notes: Dependent variable is annual growth rate of real wage for province and year. Excess Death Rate is difference between actual number of death and predicted by linear regression (normalized by population). Urb is share of the population living in municipalities with more than 25,000 inhabitants. Urb Dens is a modified version of Urb that takes into account population density to better capture the demand-driven interpretation. In particular, Zaragoza, Badajoz and Cordoba are reclassified as non-urbanized, given their low populated and mostly poor population. Similarly, Pontevedra and Orense are reclassified as urbanized, given their large population density. The table reports fixed effects regressions weighted by population. Standard errors are clustered at the year level. * p < 0.10, ** p < 0.05, *** p < 0.01.

Industrialization The levels of industrialization were very heterogeneous in Spain. Industrialization is correlated with the level of development. Industrial establishments also crowded people together facilitating the spread of the pandemic. In a supply-driven interpretation, the effects of the flu should be mitigated in more industrialized provinces. That is, given the same increase in excess death rate, the decline in job competition should be exacerbated in more industrialized provinces. In a demand-driven interpretation, the sign would tend to be negative because, arguably, the decline in demand should be larger in more industrialized and more developed provinces. As an imperfect measure of industrialization, we use the share of the population working in the manufacturing sector in 1910, when the latest Census before the Spanish Flu was made. As we can see from Table 10, there is a lot of heterogeneity across provinces. We also note that this measure of industrialization is correlated with our measure of urbanization, but they seem to proxy for different province characteristics. For example, it is true that Barcelona was a very urbanized and industrialized province. However, Madrid was a very urbanized province but with a relatively smaller industrial sector. On the other extreme, we have a province like Girona with a relatively large industrial sector but not very densely populated. That is, even though industrialization may also capture some elements of urbanization, it should allow us to indirectly test our demand-driven interpretation.

Panel B in Table 6 analyzes this potential exacerbation effect of the flu on real wages. Following the same strategy as in Panel A, we include the interaction between excess death rate and the industrialization dummy. All the coefficients of the interaction term are negative. They are statistically different from zero in four out of the nine occupations (builders, stone-cutters, blacksmiths and metal workers) Quantitatively, for builders, one percent increase in excess death rate has no effect on real wages in a province with industrialization levels below the median. In contrast, in a province above the median, the reduction would be 9 percent.

The overall evidence reported in Table 6 is consistent with a demand-driven explanation for the effect of the flu on wages. For a given increase in excess death rate, the effect on real wages is exacerbated in provinces with a larger population density, where the news on the dangers of the Spanish Flu and, thus, the increase in fear and uncertainty were, arguably, larger. In addition, the negative effects on real wages are not attenuated in more industrialized provinces, which also supports our demand-driven interpretation.

4.2. The effects of the flu on returns to capital

We next turn to the effect of the flu on the returns to capital. Since we do not have an annual series for the returns to capital at the province level, we use two proxies. First, we examine the evolution of the dividends of publicly listed firms, which proxy the returns of stocks. Since there were only a few stock markets (Madrid, Barcelona and Bilbao), average return on stocks cannot give us the return to owning stocks in each province. For this reason, we use dividends. Then, we look at the evolution of real estate prices (urban housing and land). If returns to all assets tend to converge, year-to-year changes in housing or land prices should also reflect average returns to capital.

4.2.1. The effects of the flu on dividends

Column 1 of Table 8 reports the effects of the flu on real dividends paid by public companies. Due to a change in the Spanish law, our last year with comparable data is 1919. Panel A reports the contemporaneous effect of deviations in mortality (from the trend) on dividends (Equation (1)). The coefficient of excess death rate is negative but not statistically different from zero. Therefore, it does not seem that an increase in excess death rate had any contemporaneous effect on dividends. In Panel B, we include the lag of the excess death rate. The rationale is that, even though dividends do not have a contemporaneous effect on dividends, it may affect future dividends. This could be the case if the effect of the flu on production is delayed and it accumulated as the death toll increased. We find that the coefficient of the lag of excess death rate is positive (around five times larger), which would be consistent with this hypothesis, but it is statistically insignificant. Panel C and D report the differences-in-differences estimation (Equation (2)) to analyze the effect of excess death rate in 1918. In Panel C, the coefficient on the interaction with the 1918 dummy turns out to be negative and the coefficient of the interaction with the post-1918 is positive (consistent with panel B), but none of them is statistically significant. Lastly, Panel D reports the coefficient on the interaction with the post-1917 dummy (the medium-run effect of the flu). Consistent with the previous panels, the coefficient is positive, but it is not statistically significant. Thus, we conclude that, for the average province, the Spanish Flu does not seem to have any significant negative effect on real dividends paid by public firms. We want to emphasize that given the large standard deviation of the coefficient, we cannot exclude the possibility that the effect was negative in some provinces. The fact that real dividends do not appear to be negatively affected by the Spanish Flu is consistent with the findings of Barro (2020). Indeed, they fail to obtain a significant effect of the flu on real stock returns. Finally, we do not find any robust pattern on the potential heterogeneity across provinces.12

Table 8.

Effects of the Flu on Rents.

	(1)	(2)	(3)	(4)
	Dividends	Urban House	Urban House	Land
		Price	Hedonic Price	Price
Panel A: Mortality
Excess Death Ratect	−6.27	−18.48*	−1.70**	−9.66
	(17.46)	(10.22)	(0.68)	(7.84)
Lag Real Rentct	−0.86*** (0.12)	−0.96*** (0.09)	−0.84*** (0.09)	−1.01*** (0.06)
Panel B: Mortality(2)
Excess Death Ratect	−2.21	−17.67*	−1.63**	−9.92
	(22.57)	(9.84)	(0.63)	(7.68)
Excess Death Rate Lagct	21.30	−11.41	−1.02	3.63
	(34.56)	(7.91)	(0.90)	(14.66)
Lag Real Rentct	−0.85*** (0.12)	−0.96*** (0.09)	−0.84*** (0.09)	−1.01*** (0.06)
Total Effect	19.09	−29.08*	−2.65*	−6.29
	(52.98)	(15.20)	(1.25)	(17.54)
Panel C: Flu Effects
Flu1918c ∗ D1918	−20.64 (18.81)	4.39 (5.50)	1.54** (0.71)	15.33*** (1.39)
Flu1918c ∗ DPost − 1918	36.74 (19.97)	24.22*** (6.68)	3.16*** (0.75)	22.66** (8.56)
Lag Real Rentct	−0.85*** (0.12)	−0.97*** (0.08)	−0.85*** (0.09)	−1.01*** (0.05)
Panel D: Flu Effects(2)
Flu1918c ∗ DPost − 1917	8.01 (32.55)	22.65*** (6.76)	3.02*** (0.77)	22.07** (7.96)
Lag Real Rentct	−0.85*** (0.12)	−0.96*** (0.09)	−0.85*** (0.09)	−1.01*** (0.05)
Province Fixed Effects	Y	Y	Y	Y
Year Fixed Effects	Y	Y	Y	Y
Observations	281	720	720	720

Notes: Dependent variable in column 1 is annual growth rate of dividends, in column 2 is annual growth rate of urban house, in column 3 is annual growth rate of urban house prices (hedonic adjustment) and column 4 is annual growth rate of land prices. Excess Death Rate is difference between actual number of death and predicted by linear regression (normalized by population). Flu1918 is the value of excess death in 1918. 1918 is a dummy equal to one for year 1918. Dt is a dummy equal to one for year t and zero otherwise. t = Pre-1918 is omitted from the regression and it is the control period. See text for more details. The table reports fixed effects regressions weighted by population. Standard errors are clustered at the year level. * p < 0.10, ** p < 0.05, *** p < 0.01.

A potential concern with these findings on dividends is that public firms represent a selected sample of firms. It could be that small and medium firms went bankrupt due to the decrease in demand. Unfortunately, we lack of firm level data to explore this possibility. This is a potential avenue for future research. In any event, this evidence seems consistent with the hypothesis that (public) firms were able to transfer the effect of the drop in demand to workers, while keeping returns to capital unaffected.

4.2.2. The effects of the flu on real estate prices

To examine the evolution of real estate prices is interesting by itself. There is a general consensus that house prices affect consumption, borrowing, investment and even aggregate productivity (see, for example, Basco, 2018). Moreover, as documented in Jorda et al. (2019), housing is throughout history the largest and most important asset class in the economy. Arguably, this was specially true in early 20th century Spain, in which capital markets were integrated but poorly developed, with really low levels of financial intermediation (Mart́ın Aceña, 1985, Nogués-Marco et al., 2019). As documented in Table 3 both urban housing and land prices were, on average, larger in 1918 than in previous years. Moreover, this higher growth went hand in hand with additional variability across provinces. This section analyzes how the Spanish flu affected the evolution of real estate prices. We follow the same strategy as in the previous outcome variables and focus on the variation of annual growth rates.

Theoretically, the effect of excess death rate on average real estate prices is ambiguous. First, the income effect should tend to reduce demand and, thus, decrease prices. Second, if the negative income effect is concentrated among low-income workers (as the previous evidence suggests), there may be selection on the type of real estate assets traded, which may result in a higher average price. Third, the supply of available assets may increase because people may be forced to sell, which should tend to decrease prices. To disentangle these effects is beyond the scope of this paper, we will just examine the total effect of excess mortality on real estate prices. One additional potential concern is that investors may purchase houses in provinces different from where they live, which could potentially distort our estimated effect of the flu on the return to housing.

Column 2 of Table 8 reports the effects of the flu on urban house prices. Panel A reports the contemporaneous effect of deviations in mortality on urban house prices (Equation (1)). The coefficient of excess death rate is negative and it is statistically different from zero at 10 percent. Thus, it seems that the excess mortality has a mild negative effect on house prices. In Panel B, we include the lag of excess death rate in our previous specification. We find that the coefficient of the contemporaneous effect remains negative at 10 percent but the coefficient on the lag is not significant. To formally analyze the effect of the Spanish Flu on house prices, we turn to the differences-in-differences specification. Panels C and D report the coefficients of the interaction between excess death rate in 1918 and time dummies (Equation (2)). In Panel C, we see that the coefficient of excess death rate in 1918 is positive for both 1918 and post-1918 dummies. In addition, the coefficient of the post-1918 dummy is positive and statistically significant, which suggests that the flu had a positive effect after the initial shock. To confirm this hypothesis,

Panel D reports that the coefficient for the interaction with post-1917 is positive and it is statistically significant.13 We also fail to find significant heterogeneous effects across provinces. Lastly, column 4 reports the coefficients of the effects of the flu on land prices. We repeat the same specifications as above. We can see in Panel A that the coefficient on excess death rate is negative but it is not statistically different from zero. Panel B includes the lag of excess death rate. In this case, the lag is positive but it is not statistically different from zero. Panel C and D report the coefficients of the interaction between excess death rate in 1918 and time dummies. In Panel C, we see that the interaction with 1918 dummy is positive and statistically significant. The coefficient is also positive and larger on the interaction with post-1918 dummy. Thus, it seems that the excess mortality in 1918 did have a positive effect on land prices. We confirm this view in Panel D, in which we report the interaction with post-1917 dummy. Note that the coefficient is positive and statistically significant. Therefore, it seems that the Spanish Flu had a positive effect on land prices.

To conclude, the overall evidence presented in Table 8 is consistent with the view that returns to capital did not significantly decline due to the Spanish Flu. Indeed, whereas the effect of the flu on dividends is imprecisely estimated (we cannot reject it is zero), it had a positive effect on real estate prices (house and land). This result is driven by the post-1918 evolution of real estate prices.

4.2.3. Additional evidence: effect of the flu on inflation

In this last section, we provide additional suggestive evidence on the mechanism through which the flu affected the economy. In the previous sections, we have emphasized that the Spanish Flu had an effect on real wages, possibly through a fall in demand. One potential mechanism is that consumption prices (mostly, food prices) increased, which reduced available resources for non-essential items and contributed to the exacerbation effect on occupations producing non-essential goods (like tailors and shoemakers). We have data on urban and rural consumption price indexes for each province (Rosés and Sánchez-Alonso, 2004, Carmona and Lampe, 2014, Carmona and Rośes, 2012). Since urban areas are net importers of food, we would expect that the effect of the flu on prices happened mostly on urban areas. Note that it is, arguably, also in urban areas where consumption in non-essential goods is more important.

Table 9 reports the effect of the flu on inflation. The dependent variable in column 1 is the log first difference of the urban consumption price index. Note that the contemporaneous effects of excess death rate is positive but it is not statistically significant (Panel A). When we include the lag of excess mortality, we observe that both effects are positive but they are no statistically significant (Panel B). This would seem to indicate that excess death rate has no effect on urban inflation. However, when we compute the total effect we observe that the coefficient is positive and statistically significant. Quantitatively, one percent increase in excess death rate has an overall effect on urban inflation of 1.22 percent. Column 2 reports the analogous results for rural consumption price index. In this case, we observe that all coefficients are positive by they are not statistically significant. Lastly, we do not report the counterpart of Panels C and D (the differences-in-differences estimation) because consumer prices indices violate the parallel growth pre-trend assumption.

Table 9.

Effects of the Flu on Inflation.

	(1) Urban CPI	(2) Rural CPI
Panel A: Mortality
Excess Death Ratect	0.78	3.39
	(0.45)	(2.58)
Lag CPIct	−0.05	−0.73***
	(0.05)	(0.07)
Panel B: Mortality(2)
Excess Death Ratect	0.75	3.33
	(0.44)	(2.57)
Excess Death Rate Lagct	0.47	1.06
	(0.36)	(1.98)
Lag CPIct	−0.05	−0.74***
	(0.05)	(0.07)
Total Effect	1.22**	4.39
	(0.52)	(2.93)
Province Fixed Effects	Y	Y
Year Fixed Effects	Y	Y
Observations	720	720

Notes: Dependent variable in columns 1 is urban inflation and in column 2 is rural inflation. Excess Death Rate is difference between actual number of death and predicted by linear regression (normalized by population). See text for more details. The table reports fixed effects regressions weighted by population. Standard errors are clustered at the year level. * p < 0.10, ** p < 0.05, *** p < 0.01.

To summarize, it does seem that excess mortality may be related to increase in consumption prices in urban areas. Even though the quantitative effect appears to be small, in a hand-to-mouth population, small price increases in an increasingly uncertain environment may have large effects on non-essential demand. We plan to formally investigate the mechanism through which the flu reduced real wages and may contribute to raise inequality and poverty.

5. Concluding remarks

The outburst of Covid-19 cases around the world has greatly increased the interest in the economics effects of pandemics. This paper contributed to this debate by examining the effects of the Spanish Flu (1918) within Spain. In particular, we exploited the variation in excess mortality across provinces to examine the effects of the pandemic on the real returns to factors of production.

The main result of the paper is to document large, negative and broadly short-lived effects of the Spanish Flu on real wages. These effects were heterogeneous across occupations. While shoemakers experienced the largest decline in real wages (around 30 percent, relative to pre-1918, for the average province), some occupations like metal workers were not significantly affected. In contrast, we fail to find significant negative effects on the returns to capital. We used two proxies for returns to capital: (i) dividends paid by public companies and (ii) real estate prices (urban housing and land). Whereas the effect of the Spanish Flu on dividends is imprecisely estimated (we cannot reject it is null), the effect on real estate prices, driven by the post-1918 recovery, was positive.

Even though it is outside the scope of the paper to disentangle the mechanisms through which the Spanish Flu affected the economy, our results suggest a demand-driven interpretation. First, the negative effects on real wages were exacerbated in more urbanized provinces, which had higher awareness of the mortality risks. Second, these negative effects were, if anything, stronger in more industrialized provinces, which arguably experienced larger reductions in demand and job competition. Third, when including deaths reported also in 1919, which better captures the fear and uncertainty during the pandemic, the negative short-run effects were only exacerbated for occupations in non-essential sectors (tailors and shoemakers).

Which will be the economic effects of Covid-19? According to our results, it seems that most of the effect of the Spanish Flu were related to a decline (delay) in non-essential consumption rather than to a fall in production. Needless to say, the world economy and the international organization of production are very different now compared to the early 20th century. However, the effect in Spain during the Spanish Flu could be an example of what could happen in a developing economy in which social distancing is difficult. Spain’s economy was more akin to today’s developing than developed economies. In particular, social protection and government economic support were scant, labour market was mainly unregulated, and household savings were scarce. For future research, we plan to empirically investigate the mechanism through which workers resulted more affected than entrepreneurs and why the effects were exacerbated in more urbanized regions. Our hypothesis is that firms reacted to the decline in demand, larger in these regions, by resisting nominal wages increases.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following are the Supplementary data to this article: