Abstract
Purpose
Our purpose was to assess the use of machine learning methods and Mobius 3D (M3D) dose calculation software to reduce the number of physical ion chamber (IC) dose measurements required for patient-specific quality assurance during corona virus disease 2019.
Methods and Materials
In this study, 1464 inversely planned treatments using Pinnacle or Raystation treatment planning software (TPS) were delivered using Elekta Versa HD and Varian Truebeam and Truebeam STx linear accelerators between June 2018 and November 2019. For each plan, an independent dose calculation was performed using M3D, and an absolute dose measurement was taken using a Pinpoint IC inside the Mobius phantom. The point dose differences between the TPS and M3D calculation and between TPS and IC measurements were calculated. Agreement between the TPS and IC was used to define the ground truth plan failure. To reduce the on-site personnel during the pandemic, 2 methods of receiver operating characteristic analysis (n = 1464) and machine learning (n = 603) were used to identify patient plans that would require physical dose measurements.
Results
In the receiver operating characteristic analysis, a predelivery M3D difference threshold of 3% identified plans that failed an IC measurement at a 4% threshold with 100% sensitivity and 76.3% specificity. This indicates that fewer than 25% of plans required a physical dose measurement. A threshold of 1% on a machine learning model was able to identify plans that failed an IC measurement at a 3% threshold with 100% sensitivity and 54.3% specificity, leading to fewer than 50% of plans that required a physical dose measurement.
Conclusions
It is possible to identify plans that are more likely to fail IC patient-specific quality assurance measurements before delivery. This possibly allows for a reduction of physical measurements taken, freeing up significant clinical resources and reducing the required amount of on-site personnel while maintaining patient safety.
Introduction
The presence of the corona virus disease 2019 (COVID-19) outbreak in the United States required an immediate assessment of clinical priorities and strategies for radiation oncology programs across the country. To mitigate the harm from the pandemic, on March 16, 2020, the City and County of San Francisco, along with a group of 5 other Bay Area counties and the City of Berkeley, issued parallel health orders imposing shelter in place limitations across the region.1 Additionally, the schools in the Bay Area closed and remained closed through the end of the school year (June 2, 2020), requiring educators and families to transition to a distance-learning format. The Bay Area experience parallels experiences across the country and around the world, posing childcare and other challenges for health care workers and their families, and introducing a new paradigm where on-site staffing is limited for many departments.
For our radiation oncology department, these staffing challenges are exacerbated by the wide array of special procedures, diverse equipment, and a uniquely divided campus composed of 3 separate and distinct clinical facilities. In addition to clinical risk assessments for patients, migrating the majority of the clinical physics team to a remote working environment was a priority and required an assessment of the essential needs for different equipment and procedures to ensure continued safe practices during this pandemic, particularly in the context of patient-specific intensity modulated radiation therapy (IMRT) quality assurance (QA). For patient-specific IMRT QA, it is common practice to measure point dose or 2-dimensional and 3-dimensional (3D) dose distributions before treating patients and then compare these measurements with treatment planning system (TPS) calculations.2 The identification of plans that require measurement has been previously discussed and justified clinically in the context of Virtual IMRT QA.2, 3, 4, 5, 6 To reduce the necessary on-site resources and to limit COVID exposure risk to the team performing IMRT QA while maintaining a high-level of confidence in the safety and accuracy of patient-specific IMRT treatments, use of Mobius 3D (Varian Medical Systems, Palo Alto, CA) was proposed to identify a subset of plans that would fail an ion chamber (IC) measurement. Measurements would then be performed only on the subset predicted to fail.
Mobius3D (M3D) is a commercially available independent dose verification software. M3D uses the full patient Digital Imaging and Communications in Medicine set—including the computed tomography (CT), plan, structures, and dose—to recalculate dose in 3 dimensions using a collapsed cone superposition algorithm and independent reference beam data.7 The software presents results as dose-volume histogram comparisons for regions-of-interest, target coverage, 3D gamma comparisons between the TPS and M3D’s secondary dose calculation, and M3D-calculated point doses at 7 points on a phantom.6 By including the patient anatomy and using independent beam data and dose calculation algorithms, M3D provides a robust second check of the treatment plan before the first fraction, as well as key information about overall plan quality and deliverability before IMRT QA measurement is performed. Furthermore, a recent Imaging and Radiation Oncology Core study implemented an independent dose recalculation system to evaluate contribution of dose calculation errors to failing phantom results and found that an independent calculation system is well suited for detecting plan errors and appropriate for conducting QA.8 , 9 This manuscript describes 2 novel methods for significantly reducing the necessary number of on-site personnel by reducing the number of required point dose measurements for IMRT QA: a threshold analysis of M3D data and the use of machine learning algorithms to build a predictive model to identify patient plans requiring a physical IC measurement.
Methods and Materials
Mobius QA process
The Mobius verification phantom is a water-equivalent phantom featuring 7 IC positions (labeled A-G) and a film plane. The M3D platform contains a digital Mobius phantom used for dose calculation while the TPS uses a CT data set of the Mobius phantom acquired and imported by the user for QA purposes. Each patient IMRT plan is transferred to the M3D server from the TPS for a plan check calculation. This plan check includes a phantom verification section, where M3D calculates the dose (mean ± standard deviation) at each IC position (“M3D dose”). One of the 7 positions is selected to obtain a physical point dose measurement for absolute dose verification. The selected point is ideally in a high dose, low gradient region, with a mean dose that is greater than 80% of the prescription dose and less than a 5% standard deviation. The patient plan is also copied to the phantom CT in the TPS and recomputed to determine the dose at each of the 7 chamber positions (“TPS dose”). The Mobius phantom is set up on the treatment couch with a small cylindrical IC (our clinic uses PTW PinPoint 3D ICs with a 0.016 cm3 sensitive volume) placed in the selected position, and a fraction is delivered to measure the dose (“IC dose”). The M3D dose, TPS dose, and IC dose for the chosen point are all recorded. The point dose percent difference between the TPS calculation and M3D calculation, and between the TPS calculation and IC measurement is calculated using the TPS calculation as ground truth. The QA process is illustrated in the flow chart in Figure E1.
Data sets
Threshold model data set
From June 2018 through February 2020, 1464 IMRT plans were evaluated using the Mobius QA process described previously. These plans were divided into 2 data sets: a training set (to build models and rules) and a testing set (which the models and rules do not see until it is time to make the final prediction). This is illustrated in Figure E2. The training data set was comprised of 1113 IMRT plans that were delivered on an Elekta Versa HD (n = 208), Varian Truebeam (n = 543), and Varian Truebeam STx (n = 362) between June 2018 and November 2019. The testing data set was comprised of 351 plans from the same machines: Versa (n = 41), Truebeam (n = 212), and Truebeam STx (n = 98), delivered between December 2019 and February 2020. This information is summarized in Table 1 . All plans were generated using Pinnacle version 16.0 (Philips Radiation Oncology Systems, Fitchburg, WI) or RayStation version 7 (RaySearch Laboratories, Stockholm, Sweden) treatment planning software.
Table 1.
Description and breakdown of training and testing data sets
| Model | Data set | Elekta Versa HD | Varian Truebeam | Varian Truebeam STx | Total |
|---|---|---|---|---|---|
| Mobius threshold | Training | 208 (18.7%) | 543 (48.8%) | 362 (32.5%) | 1113 |
| Testing | 41 (11.7%) | 212 (60.4%) | 98 (27.9%) | 351 | |
| Machine learning | Cross-validated | 0 (0%) | 462 (76.6%) | 141 (23.4%) | 603 |
A secure online electronic data collection system (REDCap)10 was used to collect IMRT plan parameters and QA results including machine, energy, M3D point dose, TPS point dose, and ion chamber measured point dose. In addition to this, M3D plan information, such as M3D calculated point dose, standard deviation on the M3D calculated point dose, gamma passing rate, beam monitor units, and number of segments, was also collected. The gamma index, introduced by Low11 is a common analysis metric used to quantify both the percent dose difference and distance-to-agreement (DTA) between 2 dose distributions. The gamma analysis in this study was performed within the M3D software using thresholds of 5% dose difference and 1 mm DTA. This threshold was chosen during commissioning of the software in 2017 using the 5% limit recommended by American Association of Physicists in Medicine (AAPM) Task Group (TG-40)12 for independent dose calculations and a 1 mm DTA to reflect the spatial accuracy required for stereotactic body radiation therapy (SBRT) treatments. The modulation factor, calculated by dividing the total number of monitor units by the number of segments, was included to provide an indication of plan complexity, as highly modulated plans tend to be more complex.13 Plans were excluded if a shift was necessary to move the phantom into a high dose low gradient region for QA, as the point dose data were not available on the server for extraction.
Machine learning models data set
In 603 of the 1464 plans in the data set described in the previous section, the M3D point dose was available for all 7 IC positions rather than that selected at the time of QA. This additional information was available due to the implementation of scripting in QA plan preparation in RayStation. This subset was comprised of only Truebeam (n = 462, 76.6%) and Truebeam STx (n = 141, 23.4%) plans, all of them computed in RayStation. The complete set of features described in Table E1 were included in a machine learning regression model, and its performance was assessed, which will be described in the following section. This data set will be referred to as the machine learning data set.
Classification system
Two models were generated based on the features described in Table E1: a threshold model and a linear model using statistical learning. These models were assessed by their ability to correctly identify plans that failed the IC measurement. The classification system described in Table 2 was used to calculate the sensitivity (proportion of failing plans that were correctly flagged as failing) and specificity (proportion of passing plans that were not flagged as failing) according to equations (1) and (2). To ensure the identification of any plans that might fail the IC measurement, a sensitivity of 100% was prioritized.
| (1) |
| (2) |
Table 2.
Classification system for plans using M3D and IC results
| Classification | Description | Indications |
|---|---|---|
| TP | Failing plans were correctly identified as failing (failed both M3D and IC) | IC measurement required |
| FP | Passing plans were incorrectly identified as failing (failed M3D but passed IC) | IC measurement required |
| TN | Passing plans were correctly identified as passing (passed both M3D and IC) | No IC measurement required |
| FN | Failing plans were incorrectly identified as passing (passed M3D but failed IC) | No IC measurement required |
Abbreviations: FN = false negative; FP = false positive; IC = ion chamber; M3D = Mobius3D; TN = true negative; TP = true positive.
Threshold model
The disagreement between the TPS dose and the IC dose was computed, and thresholds of 5%, 4%, and 3% were analyzed. Thresholds of disagreement between TPS and M3D point doses (M3D threshold) were evaluated for ability to predict IC results using confusion matrices and receiver operating characteristic curve analysis.14 , 15 In this model, a sensitivity of 100% was preferred while maximizing specificity. For further quantitative analysis, the plans were stratified by machine and disease site.
For the 4% and 3% thresholds, the gamma index and modulation factor were also analyzed to determine how inclusion of additional metrics could improve predictive power. A Mann-Whitney U test was used to test for statistical significance of using these factors in a predictive capacity. Analysis for this model was performed in Matlab version R2019a (The Mathworks Inc, Natick, MA).
Machine learning models
Various machine learning methods have been applied to patient-specific QA data in the last 5 years in an attempt to use their ability to model complex multivariable relationships to predict QA test results. For the machine learning data set, a linear least square regression model was first built, in which the sum of the square error is minimized to find the best fit.16 The features described in Table E1 were first normalized by subtracting the mean of each feature and dividing by its standard deviation, and then they were used as inputs to the linear regression model. To avoid overfitting the model, 10-fold cross-validation, which involves splitting the data into 10 parts and building a linear regression model 10 times, each time withholding a different part of the data on which to test the built model, was performed. The 10-fold cross-validated correlation between predicted and measured percent dose difference was reported.
These same features were also used as inputs to decision trees. Decision trees are a set of nodes where each node divides the data based on a single rule about a specific feature.17 To reduce the complexity of the trees the maximum number of splits can be defined. These decision trees were built with the maximum number of splits set between 20 and 30 inclusive. For each maximum number of splits, 10 trees were built with a random subsample of 500 out of the 603 patients. Each terminal node contained a set of patients who were grouped together based on the tree rules upstream of the node. Each of these terminal nodes was then considered a binary feature, meaning that for each patient a 1 or 0 was entered for each terminal node feature, which indicated whether the patient occupied the node. Using the terminal nodes as features together with the original features allowed for the modeling of nonlinearities.18 , 19 Both the terminal nodes and the original features (Table E1) were passed to a Lasso-regularized linear regression model, again following input normalization, to perform the final feature selection and for model building. Lasso-regularization adds a constraint to the size of the coefficients that serves as a feature selection tool. This algorithm, which used the decision tree output in a Lasso linear regression model, known as RuleFit, has been shown to be both highly interpretable while providing state of the art accuracy.20 The predicted output and correlation were reported from a 10-fold cross-validated model with hyperparameter tuning of the lambda parameter. The 10 most important variables according to the regularized linear model were identified, and the decisions that placed patients in that node (leaf rules) were fully described.
Linear regression was used over logistic regression to return a prediction of IC disagreement rather than a pass-or-fail parameter, which would be specific to a single institution’s passing threshold. A threshold of the predicted disagreement between TPS dose and IC measurement was found, which was able to identify plans failing the IC measurement by more than 3% while maintaining 100% sensitivity. Analysis for this model was performed in Matlab vR2019a (The Mathworks Inc) and R Studio v1.2 (RStudio Inc, Boston, MA).
Results
Threshold model
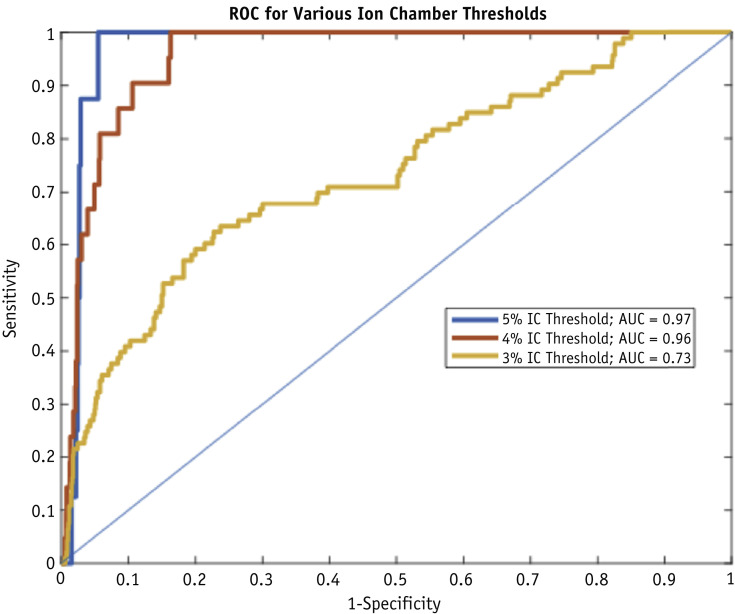
The percent difference between TPS and M3D dose and between TPS and IC dose in the training data set was not correlated, with an R-squared of 0.01, as shown in Figure E3. Figure 1 shows receiver operating characteristic curves to determine a threshold at which sensitivity can be kept at 100% while maximizing specificity for IC thresholds of 5%, 4%, and 3%.
Fig. 1.
Receiver operating characteristic (ROC) curve for Mobius3D (M3D)-treatment planning system (TPS) threshold analysis.
Confusion matrices for the different IC thresholds are shown in Table 3, Table 4, Table 5 for all plans, and are also broken down by machine. Table E2 shows the confusion matrices when an M3D threshold of 5% is applied to identify plans that fail at an IC threshold of 5%. There are no results for the testing data set because there are no plans above 5% difference for either M3D or IC. A total of 1032 plans (92.7%) passed both the M3D and IC threshold (Versa: 74.5%; Truebeam STx: 97.5%; Truebeam: 96.5%). The 8 plans that failed at the IC measurement threshold also failed at the M3D calculation threshold, and included 3 lung and 5 head and neck plans. In addition, 73 plans failed the M3D calculation but not the IC measurement. This indicates that a threshold of 5% for M3D has a sensitivity of 100% and a specificity of 93.4%, suggesting that only 7.3% of the 1113 plans required an IC measurement.
Table 3.
Breakdown of passing rates using M3D and IC for training data by selected disease sites
| 4% Ion chamber threshold | 3% Ion chamber threshold | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Brain | Brain | ||||||||
| n = 155 | Ion chamber | Plans to QA | n = 155 | Ion chamber | Plans to QA | ||||
| Fail | Pass | Fail | Pass | ||||||
| M3D | Fail | 0 | 18 | 11.6% | M3D | Fail | 2 | 124 | 81.3% |
| Pass | 0 | 137 | Pass | 0 | 29 | ||||
| Prostate | Prostate | ||||||||
| n = 146 | Ion chamber | n = 146 | Ion chamber | ||||||
| Fail | Pass | Fail | Pass | ||||||
| M3D | Fail | 0 | 16 | 11.0% | M3D | Fail | 14 | 22 | 24.7% |
| Pass | 0 | 130 | Pass | 0 | 110 | ||||
| Lung | Lung | ||||||||
| n = 106 | Ion chamber | n = 106 | Ion chamber | ||||||
| Fail | Pass | Fail | Pass | ||||||
| M3D | Fail | 9 | 51 | 56.6% | M3D | Fail | 19 | 82 | 95.3% |
| Pass | 0 | 46 | Pass | 0 | 5 | ||||
| Spine | Spine | ||||||||
| n = 142 | Ion chamber | n = 142 | Ion chamber | ||||||
| Fail | Pass | Fail | Pass | ||||||
| M3D | Fail | 2 | 36 | 26.8% | M3D | Fail | 7 | 118 | 88.0% |
| Pass | 0 | 104 | Pass | 0 | 17 | ||||
| Head & neck | Head & neck | ||||||||
| n = 87 | Ion chamber | n = 87 | Ion chamber | ||||||
| Fail | Pass | Fail | Pass | ||||||
| M3D | Fail | 6 | 35 | 47.1% | M3D | Fail | 15 | 63 | 89.7% |
| Pass | 0 | 46 | Pass | 0 | 9 | ||||
Abbreviations: IC = ion chamber; M3D = Mobius3D; QA = quality assurance.
Table 4.
Confusion matrices when a 1% machine learning model threshold is used to predict a 3% IC threshold
| All machines | ||||
|---|---|---|---|---|
| n = 603 | Ion chamber | Plans to QA | ||
| Fail | Pass | |||
| Machine Learning model | Fail | 41 | 257 | 49.4% |
| Pass | 0 | 305 | ||
| Truebeam STx | ||||
| n = 141 | Ion chamber | |||
| Fail | Pass | |||
| Machine Learning model | Fail | 6 | 31 | 26.2% |
| Pass | 0 | 104 | ||
| Truebeam | ||||
| n = 462 | Ion chamber | |||
| Fail | Pass | |||
| Machine Learning model | Fail | 35 | 226 | 56.5% |
| Pass | 0 | 201 | ||
Abbreviations: IC = ion chamber; QA = quality assurance.
Table 5.
Confusion matrices when a 3% M3D threshold is used to predict 4% IC threshold
| Training | Testing | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| All machines | All machines | ||||||||
| n = 1113 | Ion chamber | Plans to QA | n = 350 | Ion chamber | Plans to QA | ||||
| Fail | Pass | Fail | Pass | ||||||
| M3D | Fail | 21 | 259 | 25.2% | M3D | Fail | 1 | 103 | 29.7% |
| Pass | 0 | 833 | Pass | 0 | 246 | ||||
| Versa | Versa | ||||||||
| n = 208 | Ion chamber | n = 41 | Ion chamber | ||||||
| Fail | Pass | Fail | Pass | ||||||
| M3D | Fail | 18 | 96 | 54.8% | M3D | Fail | 0 | 28 | 68.3% |
| Pass | 0 | 94 | Pass | 0 | 13 | ||||
| Truebeam STx | Truebeam STx | ||||||||
| n = 362 | Ion chamber | n = 98 | Ion chamber | ||||||
| Fail | Pass | Fail | Pass | ||||||
| M3D | Fail | 2 | 61 | 17.4% | M3D | Fail | 0 | 21 | 21.4% |
| Pass | 0 | 299 | Pass | 0 | 77 | ||||
| Truebeam | Truebeam | ||||||||
| n = 543 | Ion chamber | n = 212 | Ion chamber | ||||||
| Fail | Pass | Fail | Pass | ||||||
| M3D | Fail | 1 | 102 | 19.0% | M3D | Fail | 1 | 57 | 27.4% |
| Pass | 0 | 440 | Pass | 0 | 154 | ||||
Abbreviations: IC = ion chamber; M3D = Mobius3D; QA = quality assurance.
Table 6 shows the confusion matrix results when an M3D threshold of 3% was applied to identify plans that fail at an IC threshold of 4%. In the training data set, a total of 833 plans (74.8%) passed both the M3D and IC thresholds (Versa: 45.2%; Truebeam STx: 82.6%; Truebeam: 81.0%). The 3 plans that failed the IC measurement that were not treated on the Versa were all spine SBRT plans. All plans that failed the IC measurement also failed the M3D calculation. In addition, 259 plans failed the M3D calculation but not the IC measurement. This indicates an M3D threshold of 3% yields a sensitivity of 100% and specificity of 76.3% when identifying plans that fail at an IC threshold of 4%. The testing data set had similar results with 70.3% of plans passing both the M3D and IC thresholds. Only 1 plan in the testing data set failed the IC measurement at the 4% threshold, and it also failed the M3D calculation at the 3% threshold. The testing data set shows 100% sensitivity and 70.3% specificity at these thresholds, indicating that only 29.7% of plans would require QA.
Table E3 shows the confusion matrix when an M3D threshold of 0.5% was applied to identify plans that fail at an IC threshold of 3%. In the training data set a total of 134 plans (12.0%) passed both the M3D and IC threshold (Versa: 6.7%; Truebeam STx: 14.6%; Truebeam: 12.3%). All plans that failed the IC measurement also failed the M3D calculation. In addition, 886 plans failed the M3D calculation but not the IC measurement. This indicates that an M3D threshold of 0.5% results in a sensitivity of 100% and a specificity of 13.1% when identifying plans that fail at an IC threshold of 3%. The testing data set had similar results, with 13.1% of plans passing both the M3D and IC thresholds. The testing data set shows 100% sensitivity and 13.8% specificity at this threshold.
Table 3 shows the breakdown of the 4% and 3% IC passing rates in the training data for selected disease sites. The median and the Mann-Whitney U test P values for the gamma passing rate and modulation factor at the 4% and 3% IC thresholds are shown in Table E4 for the training data set. Both the gamma passing rate and modulation factor differences were statistically significant between plans that passed an IC measurement at a 3% threshold and plans that failed. Only the modulation factor was statistically significantly different between plans that passed an IC measurement at a 4% threshold and plans that failed. A threshold model with 100% sensitivity was not able to be built using these metrics.
Machine learning models
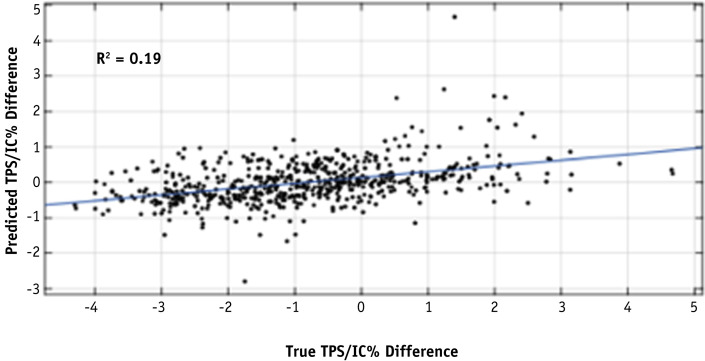
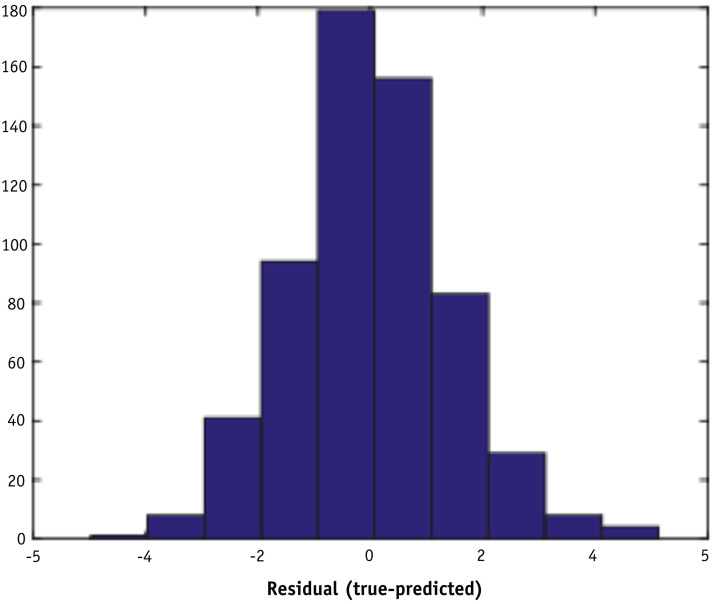
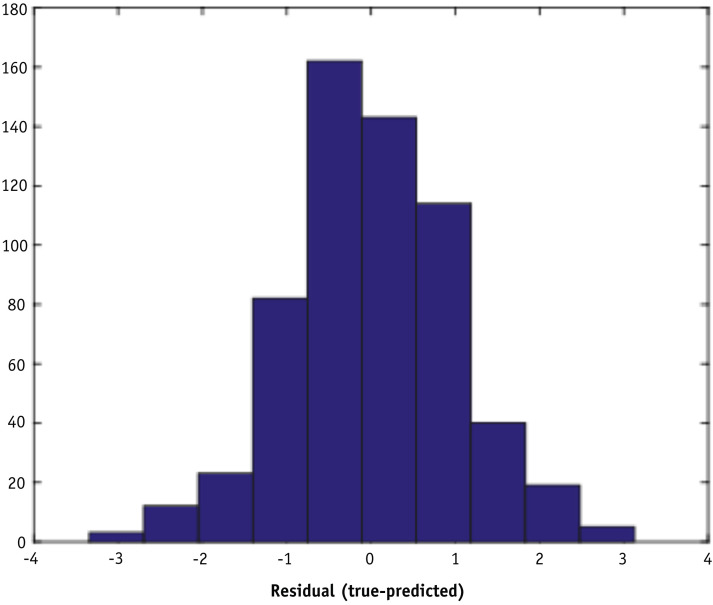
The linear least square regression model demonstrated a weak correlation (R-squared = 0.19) between the predicted percent difference and the measured percent difference in the machine learning data set, as shown in Figure 2 . The root mean square error of the fit is 0.53. Figure 3 shows a histogram of residuals between the predicted and measured percent differences. The mean and standard deviation of the distribution are 0.00 and 1.41, respectively.
Fig. 2.
Correlation between predicted and measured percent difference using a 10-fold cross-validated linear model with 36 features on the machine learning data set.
Fig. 3.
Histogram of residuals between measured and predicted percent differences using a 10-fold cross-validated linear model with 36 features on the machine learning data set.
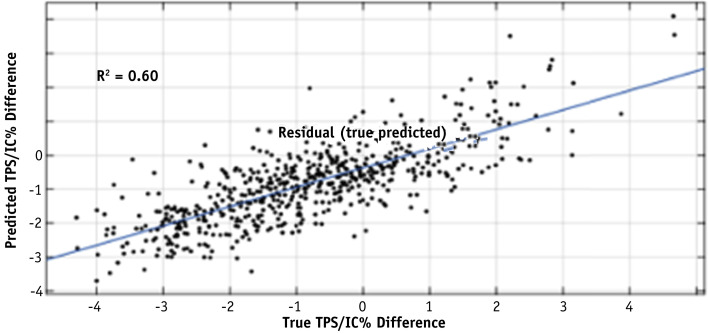
The 110 binary decision tree models created 2913 terminal nodes. These nodes were added to the 36 other features and used as input to the 10-fold cross-validated Lasso-regularized linear model. The 10 most important variables as selected by the regularized model were identified and their leaf rules described in Table E5. A leaf rule is a list of the decisions made in the decision tree that would place a plan in a terminal node. Using this model improved the correlation between the predicted percent difference and the measured percent difference in the machine learning data set to an R-squared of 0.60, as shown in Figure 4 , and the root mean square error to 0.71. Figure 5 shows a histogram of residuals between the predicted and measured percent differences. The mean and standard deviation of the distribution is 0.02 and 0.97, respectively.
Fig. 4.
Correlation between the predicted percent difference and the measured percent difference in the 10-fold cross-validated regularized linear model with the node features added to the 36 previous features on the machine learning data set.
Fig. 5.
Histogram of residuals between measured and predicted percent differences in the cross-validated Lasso-regularized linear model on the machine learning data set.
Table 4 contains the confusion matrices when a threshold on the machine learning model of 1% is applied to identify plans that fail at an IC threshold of 3%. Results are omitted for an IC threshold of 4% because there were only 4 plans above this threshold. No plans were above the 5% IC threshold. A total of 305 plans (50.6%) passed both the machine learning model (1%) and IC (3%) threshold (Truebeam STx: 73.8%; Truebeam: 43.5%). All 41 plans that failed the IC measurement also failed at the machine learning model threshold. In addition, 257 plans failed at the machine learning model threshold but not the IC measurement. This gives the 1% machine learning model threshold 100% sensitivity and 50.6% specificity when identifying plans at the 3% IC threshold, indicating that only 49.4% of these plans required an IC measurement.
Discussion
For this study, a large IMRT QA data set was used to determine whether M3D calculations could identify which IMRT plans require a physical IC measurement during the COVID-19 crisis and beyond. A threshold analysis using the difference between the TPS and M3D calculated dose was performed, along with the development of a machine learning regression model, and the resulting confusion matrices were compared. Additional plan complexity metrics such as gamma index and modulation factor were also considered to improve the power of the methods but ultimately were not shown to be advantageous at this time.
Our analysis demonstrated that meaningful thresholds could be found in which M3D had perfect (100%) sensitivity in identifying IMRT QA plans that failed IC measurements at the 5% and 4% thresholds. Applying a threshold of 5% on the M3D calculation to identify failing plans at the 5% IC threshold can safely reduce the quantity of plans requiring an IC measurement by 93%, leading to a significant reduction of required on-site measurement time. A more conservative M3D threshold of 3% identifies plans that fail the IC measurement at the 4% threshold while retaining perfect sensitivity and reducing the number of plans requiring physical measurements by 70%. Both of these scenarios would lead to a significant decrease in necessary on-site IMRT QA resources and personnel.
These thresholds can be easily adjusted to fit an institution’s comfort level and can be further adapted based on treatment site and machine. However, we found no correlation (R-squared = 0.01) between the Mobius model and the measurement. This suggests that the success of the threshold model was more likely to be related to suboptimal M3D modeling of the Versa HD machine, which in the training data set accounted for 100% of failing plans at the 5% IC threshold level and 85.7% at the 4% level. At the 3% IC threshold level, where Versa HD only accounted for 55.9% of the failures, the Mobius threshold model was only able to reduce the QA load by less than 15% (with a 0.5% threshold on the M3D calculation). It should also be noted that because the training and testing data sets were acquired at different time points, time-correlated biases may be present. Other groups have also found that Mobius3D modelled Varian accelerators better than Elekta accelerators,21 further supporting that Versa HD modeling issues may contribute to a systematic larger difference. A further confounder in the data is the fact that the Versa HD at our institution is used to treat more complex cases, such as lung and head and neck.
This led us to investigate a better model that would be correlated with the IC measurement. Although a linear model provided some weak correlation (R-squared = 0.19), this improved significantly when decision trees were incorporated into the model. The Lasso-regularized machine learning model incorporating these trees had a correlation R-squared of 0.60 and would reduce the QA workload by just over 50% when applying a model threshold of 1% to identify plans that fail at the 3% IC threshold, compared with a reduction of less than 20% that was observed at the 3% IC threshold in the Mobius threshold model. Once again, the model threshold can be adjusted to fit institutional tolerances and comfort level. It should be noted that the range of predicted disagreement is smaller than the range of measured disagreement because there are fewer measured data points at the extremes, which results in the prediction models being more likely to predict smaller values.
These machine learning models use the dose data at all 7 M3D phantom IC positions compared with the data from a single position as available for the threshold model. Removing the data related to the additional 6 IC positions from the machine learning data set shows a small reduction in correlation from the linear model from the R-squared of 0.19 to 0.17, but a more sizeable reduction in the correlation from the Lasso-regularized model of the tree output from the R-squared of 0.60 to 0.47.
For the purposes of a departmental COVID staffing action plan, we decided to implement the Mobius threshold approach using an M3D threshold of 3% in an attempt to ensure measurement of any IMRT plans that will fail an IC measurement with a 4% passing threshold. We also chose to continue with IC measurements for all SBRT and Elekta Versa plans. The choice of additional measurements for all Versa plans is due to the marginal agreement of the M3D and TPS for this machine. Furthermore, to detect any gross deliverability errors before a patient’s first fraction, and to allow for log file analysis in M3D, all plans would be run on the machine by a therapist or physicist before the first fraction without taking any measurements. Avoiding errors in deliverability is especially crucial in the context of COVID as these errors may result in extended time in the department. If deliverability or transfer errors are not detected before the first fraction, the length of time a potentially infected patient is in the clinic increases and puts other patients and staff at risk. Implementing the proposed strategy will reduce the number of required measurements while maintaining patient safety. Performing deliverability dry-runs without an IC measurement reduces the staff specialization level and therefore can be run by staff already on-site and in between patients. This also enables deliverability issues to be identified earlier in the day compared with traditional end-of-day QA. A second option also exists that can reduce QA further by replanning those plans that are higher than the model tolerance. Of course, consideration must also be given to the extra time and dosimetry staff burden of a replan. The difference between the predicted IC disagreement and the model threshold limit can be used to aid these decisions.
Although the machine learning model offered stronger correlation with IC measurement over the Mobius threshold model, there is still room for improvement. Limitations of this study include limited sensitivity to determine error causality and the use of the IC to obtain point dose measurements as ground truth, which can only probe a limited number of locations within a 3D irradiated volume. However, this study should be of interest to any sites that use IC for an IMRT QA passing metric. Furthermore, the method of data analysis presented here can be used to highlight systematic deviations for further examination. In the future, plan parameters that are commonly associated with IMRT QA failure modes, for example MLC positions, can be added to the machine learning models in an effort to further increase correlation and achieve a model that will be implemented post-COVID for general QA workload reduction.
In conclusion, an M3D threshold analysis strategy was developed to identify the IMRT plans that required physical IC measurements, reducing the necessary on-site personnel resources by 70% while maintaining institutional patient safety and accuracy standards during the COVID-19 pandemic. Plan characteristics associated with common IMRT QA failure modes will be investigated and added to new machine learning models to reduce the QA workload further with improved confidence to be implemented post-COVID.
Footnotes
Disclosures: A.W., G.V., and T.D.S. report an ownership stake in Foretell Med, LLC, which is developing machine learning models in medicine. J.S. reports personal fees from Varian Medical Systems, Inc, outside the submitted work. O.M. reports grants from Varian Medical Systems outside the submitted work. G.V. and T.D.S. have a patent, System and Method for Virtual Radiation Therapy Quality Assurance, pending to University of Pennsylvania.
Research data are stored in an institutional repository and can be shared upon request to the corresponding author.
Supplementary material for this article can be found at https://doi.org/10.1016/j.ijrobp.2020.10.035.
Supplementary Materials
References
- 1.Order of the Health Officer No. C19-07. San Francisco Department of Public Health. www.sfdph.org/dph/alerts/files/HealthOrderC19-07-%20Shelter-in-Place.pdf Available at:
- 2.Valdes G., Scheuermann R., Hung C.Y., Olszanski A., Bellerive M., Solberg T.D. A mathematical framework for virtual IMRT QA using machine learning. Med Phys. 2016;43:4323–4334. doi: 10.1118/1.4953835. [DOI] [PubMed] [Google Scholar]
- 3.Valdes G., Chan M.F., Lim S.B., Scheuermann R., Deasy J.O., Solberg T.D. IMRT QA using machine learning: A multi-institutional validation. J Appl Clin Med Phys. 2017;18:279–284. doi: 10.1002/acm2.12161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Interian Y., Rideout V., Kearney V.P., et al. Deep nets vs expert designed features in medical physics: An IMRT QA case study. Med Phys. 2018;45:2672–2680. doi: 10.1002/mp.12890. [DOI] [PubMed] [Google Scholar]
- 5.Lam D., Zhang X., Li H., et al. Predicting gamma passing rates for portal dosimetry-based IMRT QA using machine learning. Med Phys. 2019;46:4666–4675. doi: 10.1002/mp.13752. [DOI] [PubMed] [Google Scholar]
- 6.Potter N.J., Mund K., Andreozzi J.M., et al. Error detection and classification in patient-specific IMRT QA with dual neural networks. Med Phys. 2020;47:4711–4720. doi: 10.1002/mp.14416. [DOI] [PubMed] [Google Scholar]
- 7.Dunn L., Jolly D. Automated data mining of a plan-check database and example application. J Appl Clin Med Phys. 2018;19:739–748. doi: 10.1002/acm2.12396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kerns J.R., Stingo F., Followill D.S., Howell R.M., Melancon A., Kry S.F. Treatment planning system calculation errors are present in most imaging and radiation oncology core-Houston phantom failures. Int J Radiat Oncol Biol Phys. 2017;98:1197–1203. doi: 10.1016/j.ijrobp.2017.03.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kry S.F., Glenn M.C., Peterson C.B., et al. Independent recalculation outperforms traditional measurement-based IMRT QA methods in detecting unacceptable plans. Med Phys. 2019;46:3700–3708. doi: 10.1002/mp.13638. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Harris P.A., Taylor R., Thielke R., Payne J., Gonzalez N., Conde J.C. Research Electronic Data Capture (REDCap)—A metadata-driven methodology and workflow process for providing translational research informatics support. J Biomed Informat. 2009;42:377–381. doi: 10.1016/j.jbi.2008.08.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Low D.A., Harms W.B., Mutic S., Purdy J.A. A technique for the quantitative evaluation of dose distributions. Med Phys. 1998;25:656–661. doi: 10.1118/1.598248. [DOI] [PubMed] [Google Scholar]
- 12.Kutcher G.J., Coia L., Gillin M., et al. Comprehensive QA for radiation oncology. Med Phys. 1994;21:581–618. doi: 10.1118/1.597316. [DOI] [PubMed] [Google Scholar]
- 13.Hernandez V., Saiz J., Pasler M M., et al. Comparison of complexity metrics for multi-institutional evaluations of treatment plans in radiotherapy. Phys Imag Radiat Oncol. 2018;5:37–43. doi: 10.1016/j.phro.2018.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.DeLuca P.M. ICRU report 79: Receiver operating characteristic analysis in medical imaging. J ICRU. 2008;8 [Google Scholar]
- 15.Japkowicz N., Shah M. In: Machine Learning in Radiation Oncology. El Naqa I., Li R., Murphy M., editors. Springer; New York: 2015. Performance evaluation in machine learning. [Google Scholar]
- 16.Valdes G., Luna J., Eaton E., et al. MediBoost: a Patient Stratification Tool for Interpretable Decision Making in the Era of Precision Medicine. Sci Rep. 2016;6:37854. doi: 10.1038/srep37854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Schroeder L.D., Sjoquist D.L., Stephan P.E. Sage Publications; Beverly Hills: 1986. Understanding Regression Analysis: An Introductory Guide. 2nd ed. Bookshare. [Google Scholar]
- 18.Breiman L., Friedman J., Stone C.J., Olshen R.A. Routledge; Florida: 2017. Classification and Regression Trees. [Google Scholar]
- 19.Luna J.M., Gennatas E.D., Ungar L.H., et al. Building more accurate decision trees with the additive tree. Proc Natl Acad Sci. 2019;116:19887–19893. doi: 10.1073/pnas.1816748116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Friedman J., Popescu B. RuleFit with R. http://statweb.stanford.edu/∼jhf/R-RuleFit.html Available at: Accessed March 2020.
- 21.Nakaguchi Y., Nakamura Y., Yotsuji Y. Validation of secondary dose calculation system with manufacturer-provided reference beam data using heterogeneous phantoms. Radiol Phys Technol. 2019;12:126–135. doi: 10.1007/s12194-019-00499-6. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.