A flexible employee recruitment and compensation model: A bi-level optimization approach

Abstract

The growing practice of flexible work following the COVID-19 pandemic is likely to have a significant impact on management and human resource (HR) practices. In this paper, we propose a novel bi-level mathematical programming model that can serve as a decision support tool for firms in real-life settings to improve recruitment and compensation decisions associated with hybrid and flexible work plans. The proposed model is composed of two levels: the first level reflects the company’s goal of maximizing profitability by offering competitive salaries to candidates. The second level reflects the candidate’s goal of minimizing the gap between their desired salary and the perceived benefits of a preferred flexible plan. We show that the model provides an exact solution based on a mixed integer formulation and present a computational analysis based on changing candidate behaviors in response to the firm’s strategy, thus demonstrate how the problem’s parameters influence the decision policy. Our proposed model leads to efficient managerial practices, compared to conventional models that utilize a single non-flexible plan. Results indicate that introducing a flexible work plan leads to an improvement of up to 59 percent in the firm’s profitability. We apply the optimal solution of the bi-level model to a real-world case study of a company recruiting software engineers. Results demonstrate the applicability of the optimal solution to a real-world dataset. This paper advances knowledge by proposing a novel bi-level model for effective recruitment and compensation decisions in real-world flexible workforce settings.

1. Introduction

The future of work has drawn scholarly attention for several decades (Balliester and Elsheikhi, 2018, Chalutz Ben-Gal, 2020, Nolan and Wood, 2003, Valentine et al., 2017, Aronowitz and DiFazio, 1994). Yet there is limited research on how companies address the challenges associated with managing employees using flexible and hybrid work plans (Groen, van Triest, Coers, & Wtenweerde, 2018), an issue that has become particularly relevant in the post-pandemic era. In the pre-pandemic era, flexible and remote working were the exception in many organizations, and flexible work arrangements tended to be seen as a perk. A 2018 study found that only three percent of American employees worked from home more than half of the time (Hamermesh, Frazis, & Stewart, 2018). Yet, with recent advances in telecommunications technologies, flexible working should be an achievable prospect for many employees (Newport, 2020). One of the most challenging people-centered processes an organization can undertake is the efficient recruitment, compensation and retention of a suitable workforce. Recently, as a response to the COVID-19 pandemic, flexible work plans have become increasingly popular, especially in technology firms (Katie, 2020). For example, large silicon-valley based employers (e.g., Facebook, Google, and Twitter) announced large-scale remote work plans and flexible compensation packages, which are based on a cost-of-living index in a location preferred by the employee (Alberti et al., 2018, Katie, 2020). Moreover, some companies have allowed employees to request a permanent change in their jobs such that they can work remotely and flexibly (Harter, 2020). Additional adjustments have been known to occur within temporary organizations (Goetz, Wald, & Freisinger, 2020). These changes illustrate how swiftly the COVID-19 pandemic is reshaping the global workforce.

The additional variable of flexible working is likely to render the management of human capital in the post COVID-19 era even more complex. Additionally, it may lead to poor recruitment, compensation and retention decisions in the short term, as well as low-performing employees, increased turnover and downsizing (Cooper et al., 2012, Sainju et al., 2021, Tzafrir et al., 2012) in the longer term. This complexity may have a direct impact stemming from employee replacement costs (e.g., interviewing and rehiring costs, training costs, productivity loss, overtime of other employees and inflated compensation packages), as well as indirect effects, such as decreased employee retention, talent acquisition difficulties or a decline in employee morale (Boushey and Glynn, 2012, Newport, 2020). Thus, it can be extrapolated that adjusting the recruitment and compensation processes to the post COVID-19 era is likely to have a significant impact on organizational performance (Bernthal and Wellins, 2001, Lee, 2011, Pessach et al., 2020). It can be seen in the recent literature that COVID-19 has led to the development and adoption of many analytical methods and mathematical models to handle the new workforce challenges that it entails (Badr et al., 2020, Brynjolfsson et al., 2020, Singer and Marudi, 2020).

In this study, we draw on the optimization and management literature, as well as on the HR literature, to propose an optimization approach that can be used as a decision-support tool in real-world settings where companies seek to offer flexible work plans. The proposed optimization approach includes both company constraints and employee needs. Thus, with regards to the company, our model reflects the goal of maximizing profitability by setting a competitive salary, while offering an attractive, flexible work plan to achieve work-life balance (hereafter WLB) and hence encourage employee retention. From the perspective of the employee, the model reflects the employee’s goal of minimizing the gap between a requested salary and the perceived benefits of a preferred flexible plan.

A key property of our approach is the use of bi-level decision-making modelling (Lu, Han, Hu, & Zhang, 2016) to address the hierarchical nature of the decision-making process. The company (i.e., the leader) sets a competitive salary and offers flexible work by proposing WLB plans, while the candidate seeks optimization by choosing a tailored flexible plan that yields a salary level in line with competitive market practices.

We compared the results of our proposed bi-level decision-making model with the results of typical methods that utilize a single, non-flexible plan. The comparison revealed that the proposed bi-level optimization approach can perform well in terms of company profitability. We demonstrate how our optimization approach may be used to support the organizations’ managerial decision-making process. Our results indicate an increase the company’s profitability by up to 59 percent, while maintaining high levels of flexibility. Furthermore, we applied the optimal solution of the proposed bi-level model in a real-world case-study of a company, aiming to recruit software engineers. Our solution demonstrates the applicability of the optimal solution to a real-world data and setting. A particular strength of the model is that it is possible to optimize both the company’s and the candidates’ resources. Our proposed approach provides companies with an appropriate decision-support tool for flexible workforce management appropriate in the post COVID-19 era.

2. Background and literature review

We organize the relevant literature as follows. We first review studies that address the future of work and flexible working, including a number of studies that have specifically addressed the post COVID-19 era. We then review the related topics from the HR literature. Finally, we survey the literature on bi-level modeling.

2.1. Workforce flexibility and the future of work

There is a rich body of research on the topic of the future of work (e.g., Acemoglu and Restrepo, 2018, Balliester and Elsheikhi, 2018, Chalutz Ben-Gal, 2020, Nolan and Wood, 2003, Valentine et al., 2017, Aronowitz and DiFazio, 1994). In essence, the future of work refers to the ongoing process in which automation, machines and artificial intelligence replace the workforce in tasks that humans used to perform (Autor, 2014, Autor et al., 2003). These changes influence traditional work plans (Goetz et al., 2020, Neufeind et al., 2018, UpWork, 2019, Valentine et al., 2017). Advances in technology and machines should make flexible working easier. Because of the COVID-19 pandemic, many organizations have begun adapting their workforce-related practices (Alon et al., 2020, Katie, 2020, Newport, 2020, UpWork, 2019). These changes (e.g., an increase in flexible and remote working) are calling into question fundamental HR and organizational processes. For example, management research confirms that these types of changes can influence the organizational boundaries, employment relationships, and individuals’ identification with organizations, resulting in a new psychological contract (Chalutz Ben-Gal, 2020, Sousa and Wilks, 2018, Cajner et al., 2020).

In April 2020, a survey of chief financial officers conducted by the research firm Gartner found that three-quarters of companies planned to increase the number of employees who work remotely on a permanent basis (Gartner, 2020). From a managerial perspective, companies stand to make many potential gains from offering flexible work, including reduced office space costs and cheaper talent located outside of pricy cities. Likewise, many employees would welcome such an initiative. A recent study conducted by Gallup reported that almost sixty percent of respondents who have been working remotely and flexibly due to COVID-19 would welcome the opportunity to continue in this manner. Employees indicated that the main benefits of flexible work are the lack of commute and a greater work-life balance (Brenan, 2020, Harter, 2020). Yet previous managerial decision tools for devising work plans have paid little attention to the issue of flexible working (Jarrahi, 2018, Pinker and Larson, 2003).

2.2. HR literature

Employees are considered one of the most important assets of modern organizations; therefore, considerable effort is invested into optimizing their working conditions so as to maximize their chances of success in the workplace. This has led to the rise of fields such as human resources (HR) analytics (e.g. Pessach et al., 2020, Singer and Cohen, 2020). This refers to the analysis of traditional HR practices, such as job analysis, performance evaluation, and employee retention (Chalutz Ben-Gal, 2019, Crook et al., 2011, Trends and Capital, 2017). Recently, Chalutz Ben-Gal (2019) mapped the different tasks associated with HR analytics tools and investigated how these tasks can influence the organizational return on investment (ROI). The study demonstrates that workforce planning and employee recruitment have the highest impact on organizational ROI, while industry analysis, job analysis, and performance management have low expected ROI. Tasks such as compensation and retention have medium expected ROI. However, the cost effectiveness of implementing HR practices that promote employee success and organizational ROI in a flexible working environment is largely unknown. These findings—together with the growing post COVID-19 demand for workforce flexibility—provide the motivation for our optimization approach. Nevertheless, there is already evidence that flexible work practices can help optimize employee and organizational resources, even before the employment contract is finalized. Hence, it is highly beneficial to focus on the employee’s preferences, on the one hand, and company’s constraints, on the other hand, to maximize ROI (Chalutz Ben-Gal, 2019).

Little attention has been paid in the literature to the optimization of a flexible workforce. An exception is the study of Pinker and Larson (2003) who considered flexible working in the context of labor optimization techniques for business use. The researchers consider a flexible workforce to be comprised of regular workers—who have fixed schedules and may work overtime—and contingent workers, whose flexible hours are specified by a contract (such as temporary workers, on-call workers, and workers on comp-time arrangements). Therefore, the post COVID-19 era calls for more sophisticated tools to encompass flexibility—tools that also take into consideration the employee’s work-life balance (WLB).

To summarize, while the tools and actionable items yielded by HR analytics may assist with workforce analysis (Chalutz Ben-Gal, 2019, Pessach et al., 2020), most human resources studies are hypothesis-driven, descriptive or predictive. Furthermore, to the best of our knowledge no previous studies have devised optimization methodologies for the post COVID-19 era.

2.2.1. Work-life balance (WLB)

An important feature of flexible work is its effect on work-life balance, which refers to the balance between two central aspects of an individual’s life: work and leisure (including family) (Hill, 2005). When resources such as time and effort are simultaneously required for functioning in both domains, conflicts may arise. Studies have distinguished between different types of conflict, such as time-based and strain-based (Oriscoll, Brough, & Kalliath, 2006). Time-based conflict may be the result of shift work (Greenhaus & Beutell, 1985) or long working hours (Kinnunen & Mauno, 1998), whereas strain-based conflict is related to an unsupportive culture (Hill, 2005) or spouse (Greenhaus & Beutell, 1985). A third type of conflict is called behavior-based conflict (Fowler, Gudmundsson, & Whicker, 2006) and refers to a situation in which an individual is required to behave differently in work and leisure settings (e.g., task oriented at work and supportive and understanding at home). Other factors that can affect WLB include the ratio of leisure to work hours, salary level, age, number and ages of children, and amount of social support (Byron, 2005). It is becoming increasingly common for organizations to invest in WLB interventions, such as hybrid model, flex-time, part-time work, job-sharing, compressed work weeks, teleworking, paid family leave and on-site child care (Bond, Galinsky, Kim, & Brownfield, 2005).

A further strand of the literature has examined the relationship between WLB shortage and individual and organizational outcomes (e.g. Allen, Herst, Bruck, & Sutton, 2000). Examples of individual outcomes that have been examined include stress, depression, and marital dissatisfaction (Greenhaus and Beutell, 1985, Gutek et al., 1991, Voydanoff, 1988). Examples of organizational outcomes include burn-out, dissatisfaction at work, leave intentions, and turnover (Burke, 1988, Frone et al., 1992, Sainju et al., 2021). To avoid these negative consequences, our proposed bi-level optimization model includes salary and other WLB parameters in the objective of optimizing the employee’s flexible work setting.

The COVID-19 pandemic has forced organizations to adjust their practices towards remote and flexible working (Katie, 2020, Newport, 2020, Harter, 2020). It is important to note that while flexible work may have potential benefits, it can also present disadvantages (Bronstein, 1991). The advent of the COVID-19 pandemic has been shown to have an effect on WLB. For example, the demands and stresses on employees—some in the technology industry—have increased, resulting in high prevalence of burnout (Dewey, Hingle, Goelz, & Linzer, 2020). Some organizations are promoting interventions—organizational and individual—to address the burnout risk for employees and to promote wellness. These strategies include, for example, adjusted workload, mindfulness, improved work schedules, supporting digitization for flexible work, and personal coaching. As flexible work becomes more popular, the complexity of workforce management rises; thus, the need for effective managerial strategies and tools increases (Fessell & Cherniss, 2020). To date, there are no models of recruitment and compensation that allow for WLB parameters that apply to flexible working and include WLB parameters.

In this paper, we provide an optimization methodology that includes a bi-level solution approach and results in a decision-support tool for recruitment and compensation in a flexible work environment, which has the potential to benefit greatly both the company and employee (Boushey & Glynn, 2012). Our proposed tool allows management to incorporate valuable knowledge and experience into the model, and it yields actionable solutions (Pessach et al., 2020).

2.3. Bi-level modeling

Bi-level modeling is an optimization approach for solving hierarchical decision-making processes that are associated with two decision makers (i.e., a leader and a follower), each of whom has their own objectives and constraints. A bi-level decision-making model reflects an asymmetrical problem, such that the leader has complete knowledge of the follower. These players act in a sequential manner with the aim of optimizing their own objective functions, such that the leader (in our case, the company) assumes the priority acts first throughout the decision-making process. The follower (candidate) is free to take a decision that optimizes his/her individual needs in accordance with the decisions made by the leader (Küçükaydin, Aras, & Altınel, 2011).

Research on hierarchical leader–follower decision-making stems from two domains. The first is the game theory domain, developed by Stackelberg, the scholar who originally formulated a hierarchical game of two players known as the “Stackelberg Game” (Bard, 1998, Stackelberg, 1952). The second domain is that of mathematical programming. Within this domain, Bracken and McGill (1973) were the first scholars to consider the bi-level model as two distinct optimization problems, such that an inner optimization problem is the constraint of an outer optimization problem. The early bi-level modeling literature focused on military applications (Bracken & McGill, 1974) and on decision-making associated with production (Bracken & McGill, 1978).

According to Lu et al. (2016), the more recent real-world optimization problems modeled by the bi-level approach may be clustered into four domains: (a) supply chain management (Chalmardi and Camacho-Vallejo, 2019, Hsueh, 2015); (b) traffic and transportation (Bennajeh et al., 2019, Zhang et al., 2019); (c) energy management (Alipour et al., 2018, Guo et al., 2016), and (d) safety and accident management (Cerulli et al., 2019, Erkut and Gzara, 2008).

Only a limited number of studies have applied the bi-level modeling approach to the management and HR domains (Lei, Guang-nian, & Chen-xin, 2010), since, in most of the problems commonly studied in the operations research literature (e.g., employee recruitment), it is typically assumed that there is a single decision-maker and the problem is solved using a multi-objective mathematical model (Dorn et al., 2011, Pessach et al., 2020, Rahmanniyay and Yu, 2019, Zhang and Zhang, 2013).

As argued above, the contention of this study is that the goals and objectives of both the company and the candidate should be taken into consideration, especially in the post COVID-19 era. The firm’s goal is to maximize profits by setting a competitive salary while allowing employees to adopt a flexible work plan. The candidate’s goal is to find an optimal balance between a competitive salary and flexibility (i.e., WLB plans) offered by the firm. Thus, we claim that in the post-pandemic era, more than ever before, employee recruitment reflects a managerial decision-making process that is hierarchical in nature, thus leaving the bi-level modeling approach as the most appropriate solution.

The proposed model is composed of two levels: the first level reflects the firm, which sets a competitive salary and offers flexible work alternatives via work-life balance plans, while seeking to maximize profit. The second level reflects the candidate, who seeks to minimize the gap between the requested salary and the actual benefits by choosing among various work-plan alternatives proposed by the firm and the market, i.e., the firm’s competitor(s). The benefits of a given work-plan consists of proposed salary which depends on the candidate’s perceived quality of its WLB features.

3. Model description

In this section, we present our model by describing the problems faced by (i) the company (i.e., the leader), which wishes to maximize profitability by proposing a set of $n_1$ possible work plans $P_1=\left\{p_1^1,p_2^1,\cdots {,p}_{n_1}^1\right\}$, each of which is comprised of one or more WLB components from the set $W=\left\{w_1,w_2\cdots ,w_{\mathrm{m}}\right\}$, and (ii) the candidates, whose goal is to minimize the gap between a requested salary and the perceived benefits by choosing the optimal work plan. Let ${\mu }_{\mathit{wp}}$ be a binary parameter which takes the value 1 if WLB component $w\in W$ is included in work plan $p$ and zero otherwise; the same WLB component may appear in several work plans. Further, let $P_2$ be the set of $n_2$ work plans proposed by the competitor $P_2=\left\{p_1^2,p_2^2,\cdots {,p}_{n_2}^2\right\}$. The set of all potential work plans is defined by $P$ such that $P=P_1\cup P_2$. Each candidate $i$, among a set of potential candidates I, desires a job of time proportion $d_i$ (where a value of 1 denotes a full-time job), which can be satisfied by choosing one or more work plans. Thus, if the candidate chooses multiple work plans, the sum of the part-time jobs equals the candidate’s desired job proportion. We assume a candidate cannot choose more than one work plan from a single company. However, the candidate may choose simultaneously two work plans: one from the company and one from the competitor. For each candidate, the decision variable $h_p^i$ represents the percentage of employment associated with work plan $p\in P$. Fig. 1 illustrates the case where the company proposes three work plans each with a different set of WLB components.

Fig. 1.

Example of work plans and work-life balance (WLB) components.

To realize the decision-making process, a bi-level structure is proposed, where the upper layer contains the company (leader) and the lower layer consists of the candidates (followers). These two players together, with the competitor (the market), feed information into the decision-making process, represented between bold dashed lines in Fig. 2 . The company provides information regarding the number of full-time jobs available $\mathrm{D}$, the proposed flexible work plans ${p\in P}_1,$ and the WLB quality $q_p$of each work plan ${p\in P}_1$. The competitor provides information regarding his proposed work plans ${p\in P}_2$, and the WLB quality ${\overline{q}}_p$ and the monthly salary ${\overline{t}}_p$ of each work plan ${p\in P}_2$. Each candidate i contributes information regarding the desired proportion of work $d_i$, the importance given to quality of the work plans proposed by the company and by the competitor, ${\alpha }_i$, and the requested salary for each one of the work plans $T_p^i$. The bi-level model is designed so as to meet the company’s and the candidate’s goals throughout the decision-making process. The company gathers the information of the candidates and competitor together with the fixed cost for opening each work plan $C_p^F$, variable cost for operating each WLB $C_w^v$, expected monthly cost for each candidate $C_i$ and expected income from each candidate $V_i$. Then, based on this information, the company offers a monthly salary $t_p$ for each work plan $p\in P_1$. The candidate, on the other hand, chooses the optimal percentage of employment of each work plan $h_p^i,p\in P$, where $P=P_1\cup P_2$. The decision-making process of both the company and the candidates is presented in Fig. 2.

Fig. 2.

Schematic description of the bi-level decision-making process.

Table 1, Table 2 list the parameters and decision variables pertaining to the model.

Table 1.

Parameter notations in the bi-level model.

Decision Maker	Notation	Meaning
Company	$W$	Set of work-life balance (WLB) components,$W=\left\{w_1,w_2\cdots ,w_{\mathrm{m}}\right\}$
	$P_1$	Set of company work plans, $P_1=\left\{p_1^1,p_2^1,\cdots p_{n_1}^1\right\}$
	$C_i$	Fixed monthly cost per candidate $i$
	$V_i$	Expected income of the company per candidate $i$
	$D$	Number of full-time jobs the company is proposing
	$C_w^v$	Variable cost per WLB component $w,w\in W$
	$C_p^F$	Fixed cost per work plan $p$ if opened, $p\in P_1$
	${\mu }_{\mathit{wp}}$	$\left\{\begin{array}{cc}1& \mathrm{i}\mathrm{f}\mathrm{w}\mathrm{o}\mathrm{r}\mathrm{k}\mathrm{l}\mathrm{i}\mathrm{f}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}\mathrm{o}\mathrm{n}\mathrm{e}\mathrm{n}\mathrm{t}w\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{l}\mathrm{u}\mathrm{d}\mathrm{e}\mathrm{d}\mathrm{i}\mathrm{n}\mathrm{w}\mathrm{o}\mathrm{r}\mathrm{k}\mathrm{p}\mathrm{l}\mathrm{a}\mathrm{n}p,p\in P_1\\ 0& \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\end{array}\right)$
	$q_p$	WLB quality of work plan $p,p\in P_1$
Competitor	$P_2$	Set of competitor work plans, $P_2=\left\{p_1^2,p_2^2,\cdots {,p}_{n_2}^2\right\}$
	${\overline{t}}_p$	Monthly salary for work plan $p$ of the competitor for a full-time employee,$p\in P_2$
	${\overline{q}}_p$	WLB quality of work plan $p,p\in P_2$
Candidate	$I$	Set of potential candidates, $I=\left\{1,2,\cdots ,\left|I\right|\right\}$
	$d_i$	Part-time employment desired by candidate $i$
	$T_p^i$	Salary requested for work plan $p$ by candidate $i$, $p\in P$, where $P=P_1\cup P_2$
	${\alpha }_i$	Quality perception of candidate $i$

Table 2.

Decision-variable notations in the bi-level model.

Notation	Meaning
$h_p^i$	Percentage of employment in work plan $p$ performed by candidate $i$, $p\in P$, where $P=P_1\cup P_2$
$t_p$	Monthly salary for work plan $p$ of the company assuming a full-time job,$p\in P_1$
$f_w$	Number of candidates requesting WLB component $w$, $w\in W$
${\delta }_{\mathit{ip}}$	$\left\{\begin{array}{cc}1& \mathrm{i}\mathrm{f}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}\mathrm{a}\mathrm{n}\mathrm{y}\mathrm{h}\mathrm{i}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{c}\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{i}\mathrm{d}\mathrm{a}\mathrm{t}\mathrm{e}i\mathrm{o}\mathrm{n}\mathrm{w}\mathrm{o}\mathrm{r}\mathrm{k}\mathrm{p}\mathrm{l}\mathrm{a}\mathrm{n}p,p\in P_1\\ 0& \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\end{array}\right)$
$Z_p$	$\left\{\begin{array}{cc}1& \mathrm{i}\mathrm{f}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}\mathrm{a}\mathrm{n}\mathrm{y}\mathrm{o}\mathrm{p}\mathrm{e}\mathrm{n}\mathrm{s}\mathrm{w}\mathrm{o}\mathrm{r}\mathrm{k}\mathrm{p}\mathrm{l}\mathrm{a}\mathrm{n}p,p\in P_1\\ 0& \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\end{array}\right)$

We assume a deterministic model formulation in which the company proposes several options for work plans, each associated with its own WLB quality (from the company’s perspective). Candidates have their own perception of the quality. For example, a candidate may perceive a particular work plan to be of high quality, even if it has a relatively low salary level. Below we formulate the bi-level model in order to assign candidates to the proposed work plans, while maximizing the company’s profitability. The goal for the company is to offer competitive salaries and flexible work plans, while the candidates minimize the gap between the requested salary and the perceived benefits by choosing the optimum work plan. These two objectives can be expressed as follows:

$$\underset{t_p,Z_p,{\delta }_{\mathit{ip}},f_w}{\mathrm{Max}}\begin{array}{c}{\sum }_{p\in P_1}{\sum }_{i\in I}{V}_i{h}_p^i-\left({\sum }_{p\in P_1}{\sum }_{i\in I}{(h_p^i{t}_p+\delta }_{\mathit{ip}}{C}_i)+{\sum }_{w\in W}{f}_w\bullet C_w^v+{\sum }_{p\in P_1}{Z}_p\bullet C_p^F\right)\end{array}$$

$$\mathrm{s}.\mathrm{t}:h_p^i\le d_i{\delta }_{\mathit{ip}},\forall i\in I,\forall p\in P_1$$ (1)

$$\sum _{i\in I}{\delta }_{\mathit{ip}}\le \left|I\right|Z_p,\forall p\in P_1$$ (2)

$$\sum _{i\in I}\sum _{p\in P_1}{h}_p^i\ge D$$ (3)

$$\sum _{p\in P_1}{\delta }_{\mathit{ip}}\le 1,\forall i\in I$$ (4)

$$f_w=\sum _{p\in P_1}\sum _{i\in I}{\delta }_{\mathit{ip}}{\mu }_{\mathit{wp}},\forall w\in W$$ (5)

$$t_p\ge 0,\forall p\in P_1$$ (6)

$$f_w\ge 0\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{g}\mathrm{e}\mathrm{r},\forall w\in W$$ (7)

$${\delta }_{\mathit{ip}},Z_p\in \left\{0,1\right\},\forall i\in I,\forall p\in P_1$$ (8)

$$\underset{h_p^i}{\mathrm{M}\mathrm{i}\mathrm{n}}\sum _{P\in P_1}{h}_p^i\bullet \left(T_p^i-\left(t_p+{\alpha }_i{q}_p\right)\right)+\sum _{p\in P_2}{h}_p^i\bullet \left(T_p^i-\left({\overline{t}}_p+{\alpha }_i{\overline{q}}_p\right)\right),\forall i\in I$$

$$\mathrm{s}.\mathrm{t}:\sum _{p\in {(P}_1\cup P_2)}{h}_p^i=d_i,\forall i\in I$$ (9)

$$h_p^i\ge 0,\forall i\in I,\forall p\in P$$ (10)

In this model, the objective function of the company (leader) seeks to maximize the company’s profit, expressed by the difference between the potential income from the candidates after being hired and the sum of the costs. The latter include the monthly salaries paid to candidates, the fixed costs of hiring candidates, the variables costs of the work-life balance components, and the fixed costs of opening the work plans. Constraint (1) guarantees that the company hires the candidate for a given work plan in the case where he chooses this work plan with any percentage of employment. Constraint (2) guarantees that if a candidate chooses a work plan, then the latter is opened. Therefore, the maximum number of candidates (the upper bound) who may choose the same work plan is the number of candidates itself $\left|I\right|$. Constraint (3) is optional since it guarantees that the company hires at least as many candidates as the number of full-time jobs proposed; note that the company could hire more candidates if this would maximize the profit. Note also that constraint (3) implies that there are enough candidates such that the sum of their part-time job demands is greater than or equal to D. Constraint (4) limits the candidate to choose one company work plan. Note that we could remove this constraint if necessary, depending on the company preferences and that the candidate can choose simultaneously work plans from the competitor constraint (5) states the number of candidates using any WLB components. Constraints (6), (7), (8), (10) define constraints associated with the decision variables. Constraint (9) ensures that the percentage of employment desired by the candidate is satisfied by the company and/or by the competition.

The pricing definitions used in this study are inspired by those of Côté, Marcotte, and Savard (2003). These scholars presented a bi-level model for capacity allocation and pricing in the airline industry, where the objective function of the follower was expressed as the sensitivity of passengers to service quality. Following Côté et al.’s methodology, the expression $t_p+{\alpha }_i{q}_p$ in the candidate objective function, which represents the total benefit of a work plan $p$, consists of the monthly salary and the perceived quality of the work plan according to candidate $i$. The quality perception of candidate $i$, ${\alpha }_i$ is subjective and depends on the importance that candidate $i$ gives to any work compensations on top of the salary. For example, if flexibility and leisure at work are extremely important for candidate $i$, then its ${\alpha }_i$ will be higher than another candidate who ranks the monthly salary as most important. The notation $q_p$, represents the WLB quality of work plan $p$, which is derived from the number and quality of WLB components which are offered as part of the work plan. For example, a work plan $p$ which proposes flexible working hours, a three-day work from home will have higher value of $q_p$ compared to a work plan which proposes a meal card and a one-day work from home plan. Consequently, the expression ${\alpha }_i{q}_p$ represents the perceived increase in monthly salary by candidate $i$, when working at plan $p$. In other words, candidate $i$ who chooses a work plan based on its perceived high quality will perceive the monthly pay of that work plan higher compared to $t_p$, the monthly salary offered by the company for work plan $p$. In the same way, in our model, we define another, ${\overline{q}}_p$, for each work plan of the competitor (estimated by the company). Consequently, if the sum of the quality parameters of the company’s work plans exceeds that of the competitor’s work plans, then ${\sum }_{p\in P_1}{\alpha }_i{q}_p$ is greater than ${\sum }_{p\in P_2}{\alpha }_i{\overline{q}}_p$, and depending on the values of $t_p$ and ${\overline{t}}_p$, candidate $i$ will choose the maximum combination pay between the company and the competitor.

4. Solution method

In this section, we present a solution method proposed by Labbé et al., 1998, Côté et al., 2003 which is based on the substitution of the second level by its primal–dual optimality conditions. This approach enables an exact solution to be obtained by transforming the bi-level formulation into a single-level mixed integer mathematical program. In the proposed model, constraint (9) guarantees that the candidate’s job demand is fully satisfied by the company or by the competition or both. Thus, we assume enough jobs in the market to address the needs of all potential candidates. Moreover, we assume that if the candidate is presented with two equivalent solutions, they will choose the solution that optimizes the company’s profit. In other words, if the total value of the salary and perceived quality proposed by the company and by the market is the same, then we suppose that the candidate will choose the company’s flexible work plan.

The salaries of the company’s work plans are set using an optimization process, while also considering the salaries of the work plans of the competitor. After replacing the second level by its primal–dual optimality conditions, we obtain the dual mathematical problem of the second level as follows:

$$\underset{{\lambda }_i}{\mathrm{Max}}\begin{array}{c}{\lambda }_i{d}_i\end{array},\forall i\in I$$

$$\mathrm{s}.\mathrm{t}:{\lambda }_i\le T_p^i-\left(t_p+{\alpha }_i{q}_p\right),\forall i\in I,\forall p\in P_1$$

$${\lambda }_i\le T_p^i-\left({\overline{t}}_p+{\alpha }_i{\overline{q}}_p\right),\forall i\in I,\forall p\in P_2$$ (12)

$${\lambda }_i\in \mathbb{R},\forall i\in I$$ (13)

${\lambda }_i$ represents the dual variable vector associated with constraint (9). Moreover, we write the complementary constraints of the second level program as follows:

$$\left(\sum _{p\in {(P}_1\cup P_2)}{h}_p^i-d_i\right)\bullet {\lambda }_i=0,\forall i\in I$$ (14)

$$\left(T_p^i-\left(t_p+{\alpha }_i{q}_p\right)\right)\bullet h_p^i=0,\forall i\in I,\forall p\in P_1$$ (15)

$$\left(T_p^i-\left({\overline{t}}_p+{\alpha }_i{\overline{q}}_p\right)\right)\bullet h_p^i=0,\forall i\in I,\forall p\in P_2$$ (16)

Constraint (14) is always satisfied because of the demand constraint in (9). The bi-level model is then transformed into a single level program with the objective function of the company and constraints (1)–(13), (15), (16). Since the company’s objective is nonlinear, we apply the strong duality theorem that was applied to the candidate’s objective in order to replace the nonlinear expression $h_p^i{t}_p$ of the company’s objective as follows: according to the strong duality theorem, the primal optimal objective and the dual optimal objective are equal; thus we obtain:

$${\lambda }_i{d}_i=\sum _{P\in P_1}{h}_p^i\bullet \left(T_p^i-\left(t_p+{\alpha }_i{q}_p\right)\right)+\sum _{p\in P_2}{h}_p^i\bullet \left(T_p^i-\left({\overline{t}}_p+{\alpha }_i{\overline{q}}_p\right)\right),\forall i\in I$$

And thus:

$$-\sum _{P\in P_1}{h}_p^i{t}_p={\lambda }_i{d}_i-\sum _{P\in P_1}{h}_p^i{T}_p^i+\sum _{P\in P_1}{h}_p^i{\alpha }_i{q}_p-\sum _{P\in P_2}{h}_p^i{T}_p^i+\sum _{p\in P_2}{h}_p^i\bullet \left({\overline{t}}_p+{\alpha }_i{\overline{q}}_p\right),\forall i\in I(\ast )$$

Then, substituting the non-linear expression -$h_p^i{t}_p$ with the right hand side of equation $(\ast )$ as described above, we obtain a linear objective function of the first level as follows:

$$\underset{t_p,Z_p,{\delta }_{\mathit{ip}},f_w,{\lambda }_i,x_p^i}{\mathrm{Max}}\left[\begin{array}{c}{\sum }_{i\in I}{V}_i\bullet {\sum }_{p\in P_1}{h}_p^i+{\sum }_{i\in I}\left({\lambda }_i{d}_i-{\sum }_{P\in P_1}{h}_p^i{T}_p^i+{\sum }_{P\in P_1}{h}_p^i{\alpha }_i{q}_p-{\sum }_{P\in P_2}{h}_p^i{T}_p^i\right)\\ +{\sum }_{p\in P_2}{h}_p^i\bullet \left({\overline{t}}_p+{\alpha }_i{\overline{q}}_p\right)-{\sum }_{p\in P_1}\left({\sum }_{i\in I}{\delta }_{\mathit{ip}}\right)\bullet C_I-{\sum }_{w\in W}{f}_w\bullet C_w^v-{\sum }_{p\in P_1}{Z}_p\bullet C_p^F\end{array}\right]$$

Now, in order to linearize constraints (15), (16), we introduce one binary variable $x$ and the constant parameters $M$ and $M^{\text{'}}$, which represent the upper bounds of the constraint’s terms, so that at least one term of the constraint is equal to zero:

$$0\le h_p^i\le M{x}_p^i,\forall i\in I,\forall p\in P_1$$ (17)

$$0\le T_p^i-\left(t_p+{\alpha }_i{q}_p\right)-{\lambda }_i\le M\left(1-x_p^i\right),\forall i\in I,\forall p\in P_1$$ (18)

$$0\le h_p^i\le M^{\text{'}}{x}_p^i,\forall i\in I,\forall p\in P_2$$ (19)

$$0\le T_p^i-\left({\overline{t}}_p+{\alpha }_i{\overline{q}}_p\right)-{\lambda }_i\le M^{\text{'}}\left(1-x_p^i\right),\forall i\in I,\forall p\in P_2$$ (20)

$$x_p^i\in \left\{0,1\right\},\forall i\in I,\forall p\in {{(P}_1\cup P}_2)$$ (21)

In summary, the bi-level model linearized and transformed into a single-level model can be described as the final model with the linearized objective function presented above and constraints (1)–(13), (17)–(21).

5. Computational analysis

In this section we present a sensitivity analysis of the most relevant parameters of the bi-level model on the optimal solution.

5.1. Simulation setup and description

We design a simulation based on fixed parameters. We select those parameters for specific ranges in favor of performing the sensitive analysis such that interesting behaviors may be observed. We assume a monthly known fixed cost per candidate ($C_i=1000\mathrm{\$}$). The expected income per candidate is known and identical among candidates ($V_1=V_2=35,000\mathrm{\$}$). The company offers candidates three WLB components ($w=1,2,3$). The components could reflect, for example, $w_1$= “full remote work”, $w_2$= “partial remote work” and $w_3$= “gym membership included in compensation package”. The three WLB components are included in two flexible work plans offered by the company: $p_1$ and $p_2$. Work plan $p_1$ includes only the “full remote work” component, $w_1$. Work plan $p_2$ includes both partial remote work and gym membership; i.e., $p_2$ is composed of $w_2$ and $w_3$. We assume that the fixed costs associated with opening a flexible work plan are identical for both work plans, i.e., $C_{p_1}^F=C_{p_2}^F=200\mathrm{\$}$, and the variable costs per WLB component are $C_{w_1}^v=100\mathrm{\$},C_{w_2}^v=C_{w_3}^v=50\mathrm{\$}$. We assume a single work plan offered by the competitor, $p_3$. We further assume that one of the candidates requests a full-time job $d_2=1$ (the job proportion requested by the other candidate is variable) and that the salary requested by both candidates is identical for each of the work plans: $T_{p_1}^1=T_{p_2}^1=T_{p_3}^1=T_{p_1}^2=T_{p_2}^2=T_{p_3}^2=10000\mathrm{\$}$. In order to demonstrate the flexibility of the suggested model, we analyze several scenarios, by changing: the perceived quality parameters ${\alpha }_i$ of candidates i = 1, 2; the qualities of the work plans of the company,$q_{p_1}$ and $q_{p_2}$; the quality of the work plan of the competitor ${\overline{q}}_{p_3}$; the monthly salary proposed by the competitor ${\overline{t}}_{p_3}$; and the proportion of job time requested by the other candidate $d_1$. In each scenario, we investigate the effect of one of these parameters on the company profit by changing its value within a defined range (see Table 3 ). We formulate the bi-level model utilizing the IBM ILOG CPLEX Version 12.6.2.0 software. The computing time required to find the optimal solution of all the instances does not exceed 55 s for any scenario.

Table 3.

Scenarios and values of the parameters for the sensitivity analysis.

Parameter	Base case scenario	Scenario 1	Scenario 2	Scenario 3	Scenario 4
${\overline{t}}_{p_3}$	7000	7000	7000	7000	[5000,25000]
$d_1$	1	1	1	[0,1]	1
$q_{p_1}$	100	100	100	200	200
$q_{p_2}$	300	300	200	100	100
${\overline{q}}_{p_3}$	200	200	300	400	400
${\alpha }_1$	20	[0,20]	20	50	50
${\alpha }_2$	20	20	[0,150]	10	80

In the base case scenario, we assume that (i) the two candidates ($i=1,2)$ are both looking for a full-time position, (ii) the salary proposed by the competitor ${\overline{t}}_{p_3}=7,000\mathrm{\$}$, (iii) the quality of the competitor’s work plan is ${\overline{q}}_{p_3}=$ 200, while the company proposes two work plans, one with a lower quality value than that of the competitor and the other with superior quality: $q_{p_1}=$ 100, $q_{p_2}=$ 300, and (iv) both candidates have the same perception of all work plans offered by the company and by the competitor: ${\alpha }_1={\alpha }_2=20$. The candidates’ perceived quality values were chosen such that they could have an impact on the values of the decision variables, but at the same time would not affect the feasibility of the model results.

5.2. Experimental results and analysis

5.2.1. Scenario 1 – Effect of quality perception of candidate $i=1$ on optimal solution

In this scenario we test the impact of the perceived quality parameter of candidate $i=1$, ${\alpha }_1$, on the company profit. In Fig. 3, Fig. 4 , we present, respectively, the company profit and the salaries for each of the proposed work plans, as a function of ${\alpha }_1\in [0,20]$.

Fig. 3.

Company profit versus ${\alpha }_1$.

Fig. 4.

Salaries of flexible work plans $p_1$ and $p_2$ versus ${\alpha }_1$.

We define ${\alpha }_1=0$ to reflect cases where the qualities of the work plans proposed by the company and the competitor have no importance at all for candidate $i=1$; i.e., the salary is the only important parameter when choosing a work plan. In this case, the company offers a flexible work plan $p_1$ (i.e., the plan associated with the lowest quality $q_{p_1}$), which has the same salary as that proposed by the competitor for work plan $p_3$ (${\overline{t}}_{p_3}=7,000\mathrm{\$}$): since the quality is meaningless to candidate 1, the company is forced to align the offered salary with the competitor’s salary. However, candidate $i=2$, whose perceived quality parameter ${\alpha }_2=20$ is fixed and is not influenced by ${\alpha }_1$, prefers work plan $p_2$ because the latter offers a higher quality ($q_{p_2}=300$) than that of either $p_1$ or $p_3$; thus, he is willing to settle for a salary $t_{p_2}=5,000$$. When the perceived quality parameter of the candidate (${\alpha }_1$) increases, the company needs to offer a higher salary (than that offered by the competitor) for plan $p_1$, since $q_{p_1}$ is lower than ${\overline{q}}_{p_3}$. Thus initially, as ${\alpha }_1$ increases, the salary associated with $p_1$ increases, and the company’s profit decreases accordingly. However, this phenomenon is only observed up to a specific ${\alpha }_1$ value (${\alpha }_1=6$ in this case). Thereafter, it is only beneficial for the company to offer a single work plan (the one with higher quality WLB components), which enables a lower salary than the salary of $p_1$, yielding a higher company profit. Fig. 4 demonstrates that when ${\alpha }_1=6$, the candidate “moves” from $p_1$ to $p_2$, which causes the value of the $p_2$ salary to increase from 5000$ to more than 6000$, in order to match the perceived quality parameter of candidate $i=1$. Consequently, candidate $i=2$, who always prefers $p_2$, will receive a higher salary value.

Thus, a transition from one flexible work plan to another may occur when the value ${\alpha }_i$ of candidate $i$ increases to the point where the candidate gives sufficient weight to the quality such that they are no longer satisfied with the lower quality plan. In such a case, the company’s profit increases with further increases in the quality perception of the candidate, since the company offers a progressively lower salary for $p_2$. Note that the behavior observed for this scenario is partly due to the fact that the quality of work plan $p_2$ ($q_{p_2}$) is the highest of all three work plans offered by the company and the competition; otherwise we would have expected that at a specific ${\alpha }_1$ value, candidate $i=1$ would prefer the competitor’s work plan. We explain this below in scenario 2.

5.2.2. Scenario 2 - effect of quality perception of candidate $i=2$ on optimal solution

In this scenario, we permute the quality values of work plans $p_2$ and $p_3$ (such that $q_{p_2}$ = 200 and ${\overline{q}}_{p_3}$ = 300), and we test the impact of the perceived quality associated with candidate $i=2$ (${\alpha }_2$) on the company profit, with an ${\alpha }_2$ range [0, 150]. In this scenario, unlike in the previous scenario, we assume that the quality levels of both of the work plans offered by the company are lower than the quality of the competitor’s work plan. Fig. 5, Fig. 6 show, respectively, the profit of the company and the proposed salary of work plan $p_2$, $t_{p_2}$, as a function of ${\alpha }_2$.

Fig. 5.

Company profit versus ${\alpha }_2$.

Fig. 6.

Salaries of flexible work plans $p_1$ and $p_2$ versus ${\alpha }_2$.

Contrary to Scenario 1, in Scenario 2 only work plan $p_2$ is open for the full range of ${\alpha }_2$, due to the permutation in work plan between $p_2$ and $p_3$. Furthermore, when the perceived quality parameter of candidate $i=2$ is null (${\alpha }_2=0$), this candidate is indifferent to the quality associated with any work plan, thereby requiring the company to offer a salary which is at least equal to the salary offered by the competitor (${\overline{t}}_{p_3}$ = 7000$). Yet Fig. 6 shows that when ${\alpha }_2=0$, the company proposes a substantially higher salary for work plan $p_2$, $t_{p_2}=$ 9000$. This is because $p_2$ is open for candidate $i=1$ as well as $i=2$, where the perceived quality parameter of candidate 1 is ${\alpha }_1=20$. Therefore, the company needs to propose a higher salary to candidate $i=1$ (than the salary proposed by the competitor) in order to compensate for the lower quality of $p_2$ compared to $p_3$. Moreover, profit-wise it is beneficial for the company to open $p_2$ for candidate $i=1$ since its quality is higher than that of $p_1$. Consequently, the company can propose a lower salary level to candidate $i=1$ in work plan $p_2$ than in work plan $p_1$.

The model results are intriguing from the perspective of the actions of candidate $i=2$, who, at the value ${\alpha }_2=0$, is offered a salary of 9000$ for work plan $p_2$ compared to the competitor’s proposed salary of 7000$. At the value ${\alpha }_2=0$, candidate $i=2$ would rather earn a higher salary than receive WLB benefits of a higher quality. Hence, she would choose work plan $p_2$. When the quality perception of candidate $i=2$ exceeds the quality perception of candidate $i=1$ (i.e., when ${\alpha }_2>20$), the salary of work plan $p_2$ will be influenced by candidate $i=2$ instead of candidate $i=1$. Further, since the work-plan quality $q_{p_2}$ is lower than the work-plan quality $q_{p_3}$, for values of ${\alpha }_2>20$, the company needs to pay candidate $i=2$ more than it had previously been offering to candidate $i=1$; otherwise candidate $i=2$ may choose the competitor’s work plan. Consequently, the company’s profit decreases, and continues to do so with further increases in the quality perception of candidate $i=2$. This phenomenon occurs until the salary that the company offers to candidate $i=2$ rises to such a level that is not profitable for the company (when ${\alpha }_2=144.6)$. Beyond that, the company cannot propose any more advantageous salary to candidate 2, who chooses the competitor’s work plan, $p_3$, which allowing the company to adjust the proposed salary of work plan $p_2$ to the quality perception of candidate $i=1$, and yielding $t_{p_2}$ = 9,000$ (as is the case for ${\alpha }_2<20$). Hereafter, the company’s profit remains unchanged.

5.2.3. Scenario 3– Effect of job proportion required by candidate $i=1$ on optimal solution

In this scenario, we analyze the impact on the optimal solution parameters of the proportion of employment $d_1$ sought by candidate $i=1$, which is an important component of the candidate’s perception of flexibility. In this scenario, similar to scenario 2, we assume a much lower quality for both of the company’s work plans relative to the competitor’s work plan; however, the quality perception of candidate $i=1$ is much higher. When $d_1=1$ (corresponding to full-time employment), both candidates choose work plan $p_1$, since its quality $q_{p_1}$ is higher than that of work plan $p_2$ and since both candidates give a sufficient weight to the work plan quality $({\alpha }_i$). Moreover, the salary proposed by the company for work plan $p_1$ is much higher ($t_{p_1}=17,000\mathrm{\$}$) than that of the competitor (${\overline{t}}_{p_3}$ = 7000$), to compensate for the lower quality level. Fig. 7, Fig. 8 present, respectively, the company’s profit and the salary $t_{p_1}$ proposed by the company for work plan $p_1$, both as a function of the proportion of employment $d_1$.

Fig. 7.

Company profit versus $d_1$.

Fig. 8.

Salaries of flexible work plans $p_1$ and $p_2$ versus $d_1$.

As demonstrated in Fig. 7, for $d_1<0.5$, it is not profitable for the company to employ candidate $i=1$, since the costs of hiring a candidate ($t_p,C_i$ and $C_v^w$) are very high, which make recruitment of the candidate unprofitable. Note that the salary that the company needs to offer candidate $i=1$ depends on the candidate’s quality perception, which is very high in this case (${\alpha }_1=50$). Consequently, the salary of work plan $p_1$ (Fig. 8), $t_{p_2}=9,000\mathrm{\$}$, is adjusted to the preferences of candidate $i=2$, for whom ${\alpha }_2=10$. The value is higher than that of the competitor, ${\overline{t}}_{p_3}$= 7000$, in order to compensate for the lower quality (${\alpha }_2=10$). Thus, for $d_1<0.5$, the company doesn’t employ candidate 1 (see Fig. 7) and the profit value is constant as shown in Fig. 8. We underline that for lower values of ${\alpha }_1$ with the same range of $d_1$, the results would be different. Specifically, for ${\alpha }_1\le 10$, the salary for hiring candidate $i=1$ would be sufficiently low to maintain the company’s profitability.

When examining the impact on the company profit for $d_1\ge 0.5$, it is worth hiring candidate $i=1$ from a profit perspective, although the salary that the company has to propose to candidate $i=1$, $t_{p_1}=17000\mathrm{\$}$, is much higher that the salary proposed to candidate 2. As explained above $t_{p_2}$ was dictated only by the preferences of candidate 2. When $d_1\ge 0.5$, the salary of work plan $p_1$ is influenced by the preferences of candidate $i=1$, rendering the preferences of candidate $i=2$ irrelevant and yielding a value of $t_{p_1}=17,000\mathrm{\$}$. Hence, although only a proportion of this salary is paid (depending on the value of $d_1$), the profit increases from $d_1=0.5$ (50% employment) to $d_1=1$ (full-time employment), because the one-off fixed costs remain unchanged and the expected income of the candidate increases.

5.2.4. Scenario 4 – Effect of the proposed competitor salary ${\overline{t}}_{p_3}$ on the optimal solution

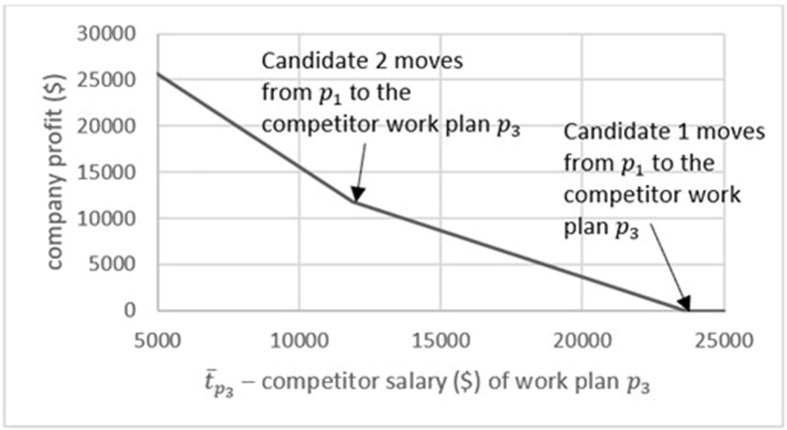
In this scenario we analyze the impact of a change in the competitor’s salary ${\overline{t}}_{p_3}$ on the company’s profit. The quality values of all three work plans are the same as in scenario 3. The quality perception of candidate $i=2$, ${\alpha }_2=80$, is much higher than the value used in scenario 3.

Fig. 9 presents the company profit versus the proposed competitor salary, ${\overline{t}}_{p_3}$. As can be seen, both candidates move to the competitor’s work plan at some different points, since it is not worthwhile for the company to increase their salary anymore. This phenomenon occurs when the quality perception varies between candidates. The fact that the two candidates switch to work plan p3 at a different salary can be explained by the differences in both the quality perception of the candidates (${\alpha }_1\ne {\alpha }_2$) and the quality levels of the work plans ($q_{p_1}\ne q_{p_2}\ne {\overline{q}}_{p_3})$. Since the quality perception of candidate $i=2$ is higher than that of candidate $i=1$, and ${\overline{q}}_{p_3}>q_{p_1}>q_{p_2}$, the perceived salary that the competitor offers to candidate 2 improves faster with an increase in $\stackrel{}{{\overline{t}}_{p_3}}$ than for candidate $i=1$ (see Fig. 10 ).

Fig. 9.

Company profit versus ${\overline{t}}_{p_3}$.

Fig. 10.

Salaries of flexible work plans $p_1$ and $p_2$ versus ${\overline{t}}_{p_3}$.

This section analyzed the effect of several parameters (the perceived quality values of both candidates, the desired job proportion of one of the candidates, and the competitor’s proposed salary) on the optimal decision of the work plans salaries and on the optimal solution of the company’s profit (which changes by up to ± 50% relative to the baseline scenario). We observed several interesting behaviors on the part of the candidates in response to the firm’s strategy, such as switching between the company’s work plans or accepting the competitor’s work plan. To conclude, we demonstrated the significant impact of some parameters on the optimal solution, thus showing that the decision-making process is partly non-intuitive in nature.

5.3. Analysis of the model performance compared to conventional model

In this section, we discuss the above results and we compare the performance of our model to that of conventional models that utilize a single, non-flexible plan. We demonstrate that the proposed model may be a useful decision-support tool for companies considering possible work plans that can accommodate some of the challenges associated with COVID-19. Furthermore, the results may assist companies throughout the recruitment, compensation and retention processes in an era where flexible work plans have become increasingly popular.

We evaluate the contribution of the work plan flexibility to the company profit by comparing and contrasting the results of the bi-level model (Section 3) with the company profit without flexible work plans. We conduct a case analysis of a company that manages and hires its workforce within guidelines pertaining to a single work plan, compared to cases in which the company implements a flexible work plan (Section 4). This enables us to calculate the estimated percentage of profit improvement, which depends on the perceived quality of the work plan based on its flexibility features, compared to traditional, non-flexible work plans.

In this section, we assume two candidates ($i=1,2$), a single work plan proposed by the company, $p_1$, and a single work plan proposed by the competitor, $p_3$. We present several scenarios with various quality values for the work plans $q_{p_1},{\overline{q}}_{p_3}=[100,150,200]$. We also consider various levels of quality perception of the candidates, ${\alpha }_1,{\alpha }_2=[10,15,20,25]$. For simplicity of the analysis and results, we assume ${\alpha }_1={\alpha }_2$. The company has to determine whether to propose a new work plan $p_2$, and if it decides to do so, to find the optimal quality $q_{p_2}$ of the work plan in the range [0,1000], i.e., the quality value that results in the highest improvement in the company profit relative to the case with no flexible work-plan.

The values of the coefficients for quality of work plans and quality perception are chosen such that rational values for the proposed salary [4000, 9000] would be accepted in the optimal solution as will be presented later in the results.

For this purpose, we assume a non-linear open cost function of the new work plan $p_2$, as shown in Fig. 11 .

Fig. 11.

Work plan costs versus required quality.

The cost functions in Fig. 11 are continuous at every point (quality value) in their domains. However, the cost functions have a derivative at almost every point in its domain. At each point where the function is not derivative, we assume a change in the rate of growth of costs as a function of the quality value. We group the quality values into three intervals: [0,39], [40,299], [300,1000] for cost function 1 and [0,39], [40,249], [250,1000] for cost function 2, which may be defined as low-, mid- and high-quality, respectively. This is based on the rational that a work plan associated with a higher quality entails higher costs and a different rate of change of costs than a work plan of lower quality. Examples of WLB features with high quality (and hence high cost) might include a large bonus or a trip abroad, while WLB features of mid-level quality might include a regular bonus, a discounted gym membership, or meal vouchers. We propose two possible cost functions, as shown in Fig. 11. Cost function 1 on the left-hand side reflects a faster rate of change of costs than cost function 2 on the right-hand side. These representations illustrate the nuances that are likely to be associated with various costs incurred by the company, which in turn affect its profitability.

Table 4, Table 5 demonstrate the cost functions 1 and 2, together with the maximum improvement in profit, for each chosen combination of the parameters ${\alpha }_i$, $q_{p_1}$ and ${\overline{q}}_{p_3}$. “Max” indicates the maximum percentage improvement in profit, and $q_{p_2}$ and $t_{p_2}$ are the quality and the salary values respectively of the added work plan $p_2$ for which the maximum improvement was achieved. “Max. average” indicates the mean of the maximum improvements.

Table 4.

Profit improvement and corresponding quality $q_{p2}$ and salary $t_{p2}$ values for work plan $p_2$ when applying quality cost function 1.

Work plan quality		Candidate quality perception												Max. average
		${\mathit{\alpha }}_{\mathit{i}}=10$			${\mathit{\alpha }}_{\mathit{i}}=15$			${\mathit{\alpha }}_{\mathit{i}}=20$			${\mathit{\alpha }}_{\mathit{i}}=25$
$q_{p_1}$	${\overline{q}}_{p_3}$	Max.	$q_{p_2}$	$t_{p_2}$	Max.	$q_{p_2}$	$t_{p_2}$	Max.	$q_{p_2}$	$t_{p_2}$	Max.	$q_{p_2}$	$t_{p_2}$
100	100	15.1	1	7990	13.6	300	4000	16.6	250	4000	18.7	220	4000	16
100	150	16	1	8490	14.8	300	4750	27	300	4000	32.9	270	4000	22.7
100	200	16.9	1	8990	16.2	300	5500	30.7	300	5000	47.2	300	4500	27.8
150	150	17.7	1	8490	13.3	300	4750	21.7	300	4000	23.6	270	4000	19.1
150	200	18.7	1	8990	14.5	300	5500	24.5	300	5000	35.2	300	4500	23.2
200	200	18	1	8990	10.4	300	5500	16.3	300	5000	22.3	300	4500	16.8
Average		17.1	1	8656.7	13.8	300	5000	22.8	291.7	4500	30.0	276.7	4250	20.9

Table 5.

Profit improvement and corresponding quality $q_{p2}$ and salary $t_{p2}$ values for work plan $p_2$ when applying quality cost function 2.

Work plan quality		Candidate quality perception												Max. average
		${\mathit{\alpha }}_{\mathit{i}}=10$			${\mathit{\alpha }}_{\mathit{i}}=15$			${\mathit{\alpha }}_{\mathit{i}}=20$			${\mathit{\alpha }}_{\mathit{i}}=25$
$q_{p_1}$	${\overline{q}}_{p_3}$	Max.	$q_{p_2}$	$t_{p_2}$	Max.	$q_{p_2}$	$t_{p_2}$	Max.	$q_{p_2}$	$t_{p_2}$	Max.	$q_{p_2}$	$t_{p_2}$
100	100	28.7	1	7990	22.9	1	8485	18.6	250	4000	20.9	220	4000	22.8
100	150	30.5	1	8490	25.1	1	9235	30.7	300	4000	37.5	270	4000	31
100	200	32.6	1	8990	27.8	1	9985	42.3	350	4000	59.6	320	4000	40.6
150	150	32.7	1	8490	23.2	1	9235	24.5	300	4000	26.6	270	4000	26.8
150	200	34.9	1	8990	25.7	1	9985	34.6	350	4000	44.6	320	4000	35
200	200	34	1	8990	20.5	1	9985	24.52	350	4000	28.9	320	4000	27
Average		32.2	1	8656.7	24.2	1	9485	29.2	316.7	4000	36.4	286.7	4000	30.5

As shown in Table 4, Table 5, our results indicate an average improvement of 20.9% and maximum improvement of 47.2% for cost function 1 and an average improvement of 30.5% and maximum improvement of 59.6% for cost function 2. As expected, the profit improvement is greater for cost function 2 than for cost function 1, since the average cost for a given quality level is higher for the latter cost function. Furthermore, as the difference between the qualities of the first work plan $q_{p1}$ of the company and the work plan of the competitor $\overline{q_{p3}}$ increases (which indicates a higher potential improvement by opening a new work plan), the improvement in profit also increases. Our results further indicate that as the quality perception increases, the average improvement increases, excluding the transition from ${\alpha }_i=10$ to ${\alpha }_i=15$ The fact that the transition from ${\alpha }_i=10$ to ${\alpha }_i=15$ doesn’t follow this trend is that on the one hand, the value ${\alpha }_i=15$ is not high enough for the candidates to be content with the minimal salary at the optimal improvement that is obtained s when $q_{p_2}=300$ (see Table 4), and on the other hand, when the optimal improvement is obtained at a low quality value, $q_{p_2}=1$, the salary needs to be high enough to keep candidates satisfied with the work plan (see Table 5).

As shown in Table 4, the maximum profit improvement for ${\alpha }_i=10$ occurs for $q_{p_2}=1$, i.e., the low-quality perception by the candidates makes the company pay a higher salary. However, the maximum improvement for ${\alpha }_i=15$ occurs at $q_{p_2}=300$, since the transition point in the cost rate of function 1 is high after a quality of 300. This means that the quality cost becomes too expensive, making it more advantageous to pay candidates more than the minimum salary than to spend the budget on quality improvement. For ${\alpha }_i=20$ and ${\alpha }_i=25$, the candidates’ quality perception is high enough for them to settle for a low salary (without exceeding the value 300 for quality).

It can be seen that the optimal improvement occurs at different quality values for cost function 2 (Table 5) than for cost function 1 (Table 4), since the gradient of the former is less steep. For example, for cost function 2, the maximal improvements are observed at $q_{p_2}=1$ for ${\alpha }_i=10$ and for ${\alpha }_i=15$. Furthermore, for ${\alpha }_i=20$ and ${\alpha }_i=25$, the salary offered is always the minimum salary ($t_{p_2}$ = 4,000$), yet some of the optimal improvements occur for quality values that exceed 300 but with lower salary than the minimum salary.

Fig. 12, Fig. 13 demonstrate the effect of the opening cost functions 1 and 2 on the company profit. Fig. 12a demonstrates the cases for ${\alpha }_i=20$ where cost function 1 is used (which happen to have a max profit at $q_{p2}=300$). However, in Table 4 we observed that not all scenarios demonstrated the optimal improvement at this value. For example, at the scenario $q_{{\mathit{p}}_{\mathit{1}}}\mathit{=}{\overline{\mathit{q}}}_{{\mathit{p}}_{\mathit{3}}}\mathit{=}\mathit{100},$ the fact that the optimal improvement doesn’t happen at the value $q_{{\mathit{p}}_{\mathit{2}}}\mathit{=}\mathit{300}$ but at the value $q_{{\mathit{p}}_{\mathit{2}}}\mathit{=}\mathit{250}$ occurs because of the minimal salary value that it achieved at $q_{{\mathit{p}}_{\mathit{2}}}\mathit{=}\mathit{250}$, before the optimal profit improvement. Additionally, we observe at least two peaks for each case the second peak occurs when the quality is so high that the workers are prepared to work free. Since this is not realistic, we do not refer to it as a feasible solution. We further observe that for low quality values the profit is characterized either by other small peaks or by a flat line, depending on the case. The small peaks represent the null cost value for $q_{p_2}=1$ and the transition cost at $q_{p_2}=40$, which corresponds to a change in gradient in the cost function 1.

Fig. 12.

Company profit vs. quality value when adding work plan $p_2$ for the case ${\alpha }_i=20$ for cost function 1 (a – left side) and cost function 2 (b – right side).

Fig. 13.

Company profit vs. quality value when adding work plan $p_2$ for the case $q_{p_1}=150$ and $q_{p_3}=200$ for cost function 1 (a – left side) and cost function 2 (b – right side).

Fig. 12b demonstrates the cases for ${\alpha }_i=20$ where cost function 2 is used (which happen to have a max profit at $q_{p_2}\ne 300$). First, in Table 5 we observed that all scenarios for ${\alpha }_i=20$ demonstrated the optimal improvement at the salary $t_{p_2}=4000$. This occurs because of the minimal salary (4000) value that cuts the optimum profit for all the cases before the peak with the maximal improvement is achieved. Second, we observe two peaks in some cases; as explained, the second peak occurs when the quality is sufficiently high such that candidates agree to work for free and we do not refer to it as a feasible solution. Third, as for Fig. 12a we demonstrate that for low quality values the profit is characterized by other small peaks or by a flat line, depending on the cases. Small peaks represent a null cost value for $q_{p_2}=1$ and the transition cost at $q_{p_2}=40$ which corresponds to a change in gradient in the cost function 2. Fig. 13a and b demonstrate how cost functions 1 and 2 influence respectively the firm’s profit for the cases that combine $q_{p_1}=150$ and ${\overline{q}}_{p_3}=200$. As expected, we achieve higher profit for cost function 2, since its associated costs are lower for the range which enables high quality. That is why the peaks appear mostly at $q_{p_2}=300$ for cost function 1, while they appear at different values for cost function 2.

This section presented the potential increases in profit when introducing a flexible work plan. We showed that the magnitude of improvement compared to conventional models with a single, non-flexible plan depends on the quality of the work plans, the candidates’ perception of the quality of the work plans, and the form of the costs function of the new work plan. The maximum average improvement in profit ranges from 10.4% to 59.6%.

5.4. Real-world case study

The following case study illustrates the implementation of the proposed model for the purpose of software engineer’s recruitment from ten potential candidates ($i=1,..,10$) with different quality perceptions. The company defines optimal salaries for both work plans $p_1$ and $p_2$. $p_1$ is an existing non-flexible work plan, with quality $q_{p_1}=100$ and $p_2$ is a new flexible plan with quality $q_{p_2}$ $\left(q_{p_2}=1,\cdots ,1000\right)$ such that the firm’s profit will be maximized.

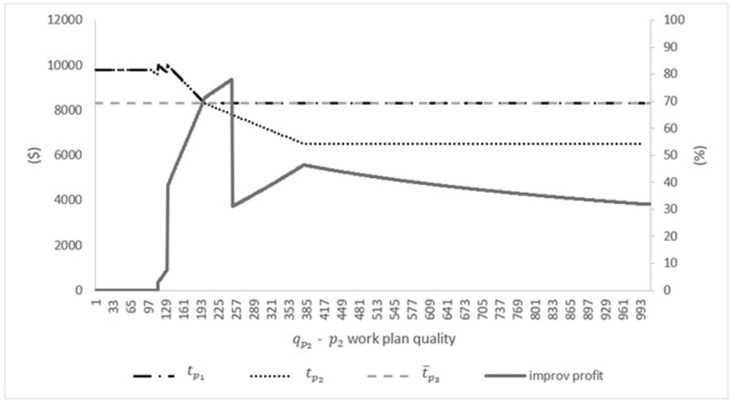
The case study is based on synthetic HR dataset of a company downloaded from the Kaggle website (https://www.kaggle.com/rhuebner/human-resources-data-set/). Data includes information regarding (i) employees’ salaries (ii) market’s benchmark salaries per position (iii) recruitment cost by position. For case study analysis purpose, we retrieved the data for software engineers in the following format. Based on the market’s salary per position table, a software engineer’s salary ranges from $6,619\frac{\mathrm{\$}}{\mathit{month}}$ to $10,037\frac{\mathrm{\$}}{\mathit{month}}$ ($\mathit{Median}=8,300\frac{\mathrm{\$}}{\mathit{month}}$). Note that the Glassdor website presents similar numbers. Additionally, we assume the competitor offers a single work plan with a quality of ${\overline{q}}_{p_3}=200$ and a median monthly salary of ${\overline{t}}_{p_3}=8,300\frac{\mathrm{\$}}{\mathit{month}}$. According to the salaries of ten software engineer’s employed in the dataset, we assume ten software engineers’ candidates with the same requested salaries, i.e., $T_{p\in P}^i\in \left[6,947\frac{\mathrm{\$}}{\mathit{motnh}},9,083\frac{\mathrm{\$}}{\mathit{month}}\right],\forall i=1,\cdots ,10$. Based on the recruitment cost per position table, we extracted the value of $C_i=430\frac{\mathrm{\$}}{\mathit{candidateXmonth}}$, $\forall i=1,\cdots ,10$. Based on profits reported by Fortune 500 tech companies and number of employees, we assume an income generated from an software engineer is equal to X2.5 of their actual monthly salary for work plan $p$, i.e., $V_i=2.5\bullet t_p,\forall i=1,\cdots ,10,p\in P_1.$ We assume that the candidates for the position of software engineer have diverse quality requirements in the range of 0 and 25, as following, ${\alpha }_i=0,i=1,2;{\alpha }_i=10,i=3,4;{\alpha }_i=15,i=5,6;{\alpha }_i=20,i=7,8;{\alpha }_i=25,i=9,10.$ Additionally, we assume a non-linear open cost function 2 of the new work plan $p_2$, as shown in Fig. 11. Fig. 14 presents the number of recruited engineers for each work plan as function of the quality value of the new proposed flexible work plan $p_2$. Fig. 15 presents the salaries and company’s profit improvement compared to a single non-flexible work plan $p_1$, as function of the quality value of the proposed work plan. As demonstrated, the optimal decision of adding a new flexible work plan yields a maximum profit improvement of 78%, while offering a salary of $t_{p_1}=8,300\frac{\mathrm{\$}}{\mathit{month}}$ for the existing non-flexible work plan and a salary of $t_{p_2}=7,810\frac{\mathrm{\$}}{\mathit{month}}$ and quality of $q_{p_2}=249$ for the new flexible work plan. Implementation of the optimal decision reflects recruitment of all ten candidates by the company, two of them for the non-flexible work plan and eight of them to the new suggested [flexible] work plan. In the compared model for which the company proposes only one non-flexible working plan, the company will recruit only 5 candidates and compensate them with an higher salary $t_{p_2}=9,800\frac{\mathrm{\$}}{\mathit{month}}$, which explains the high profit improvement (78%).

Fig. 14.

Number of recruited workers for the proposed work plans vs. quality value of a new work plan $p_2$.

Fig. 15.

Company profit and salaries for the proposed work plans vs. quality value of a new work plan $p_2$.

6. Conclusions

This paper proposes a novel and effective workforce management modeling strategy suitable for the post COVID-19 era, by solving a bi-level optimization problem. The two main contributions of the study are as follows. First, from a theoretical perspective, it proposes a novel approach based on bi-level modeling to offer flexible and hybrid work plans for candidates, which address labor-market challenges relevant for the modern (and in particular post COVID-19) era. Second, from a practical perspective, we provide an implementable managerial decision-support tool for companies that are transitioning towards flexible work plans. We address key challenges related to remote, hybrid and part-time candidates, which require new forms of compensation and WLB packages. Addressing these challenges can assist companies and candidates alike to achieve cutting-edge organizational performance in a competitive market.

We showed using bi-level modeling that an optimization solution of both the company’s and the candidates’ resources may be achieved, despite the fact that their objectives are generally found to be in conflict. Additionally, we illustrated, via a sensitivity analysis, the importance of specific decision parameters and demonstrated that changing their values over the full range that would be likely to be encountered in reality can alter the profit of the company by up to 50%. Furthermore, our results indicated that introducing a flexible work plan leads to an improvement of up to 59.6% in the company's profitability, compared to conventional models with a single, non-flexible plan.

We also demonstrate the applicability of an optimal solution to a real-world case study of a company aiming to recruit software engineers. Our analysis yields an improvement of 78 percent in the firm’s profitability implementing a flexible work plan and recruiting ten employees out of ten candidates. The results demonstrate the applicability of the optimal solution to a real-world dataset.

Although our model yields superior results compared to the conventional model with a single work plan, there are several limitations that should be considered. First, our model assumes that the costs in the profit function of the company, include only the monthly salaries paid to candidates, the fixed costs of hiring candidates, the cost of the work-life balance components, and fixed costs associated with opening the work plans. In real-world, however, technology and software companies may encounter wider human resources related costs. For example, turnover-related costs which may have a long-term impact on the organization, thus affecting the model performance (Chalutz Ben-Gal, 2019, Kim and Mauborgne, 1999). We acknowledge additional significant costs, such as software and hardware costs, office rental costs and other overhead costs which may affect the model. However, these costs are outside the scope of this study. Second, our model assumes a single competitor with a single work plan. Third, it assumes independent candidates who applied for the same position, while the proposed salary is associated with a wider work plan (and not with a specific candidate).

Future research avenues may include various cost types on top of recruitment costs, which may impact the model and expected outcomes. Another possible research direction may include multi-player modeling with several major competitors or could focus on modeling various candidates applying for various positions within the company, where all these variables may have a mutual influence. The goals would be to find a global optimum and a salary adjusted specifically for to each candidate. Furthermore, additional studies may apply the model to real-life company data, which truly represent the competitive and flexible nature of work plans offered by firms in the post COVID-19 era. The proposed model and associated case study described in this paper could serve human resource managers to decide on hiring candidates and design flexible and hybrid work plans, which may lead to an improvement of the firm’s profitability as shown in the company recruiting software engineers case study. Another avenue for future research may include adapting the model to allow workers to move from traditional to flexible working practices, by inviting them to choose between several work plans.

CRediT authorship contribution statement

Hila Chalutz Ben-Gal: Conceptualization, Writing – original draft, Writing – review & editing, Validation, Project administration, Writing – original draft, Supervision. Iris A. Forma: Conceptualization, Writing – original draft, Methodology, Validation, Data curation, Visualization, Writing – original draft. Gonen Singer: Conceptualization, Writing – original draft, Methodology, Writing – review & editing, Validation, Writing – original draft, Supervision.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.