A resilient hybrid payment supply chain inventory model for post Covid-19 recovery

Abstract

The present Covid-19 pandemic causes disruptions to markets and businesses in general, affecting the supply chain inventory system most significantly. This work investigates a hybrid payment inventory model considering inflation, cash discount, price-sensitive demand, and preservation technology investment for non-instantaneous deteriorating products. Due to the economic downturn, a hybrid payment scheme composed of multiple prepayments and a delay in payment is proposed to facilitate post Covid-19 recovery. The proposed model is one of the first models to consider a hybrid payment scheme in view of the Covid-19 pandemic, and to provide guidelines to retailers in planning the selling price, replenishment period, and preservation investment in view of the pandemic situation. The hybrid payment policy is suggested during the financial crisis to sustain orders from a retailer to the supplier and from the consumers to the retailer. During the supply disruptions, two cases for shortages and without shortages are studied. The nonlinear model is solved by Lingo 17 software. This study shows the effect of advance and delayed payments on the retailer’s total profit. It also shows that the total profit is extremely delicate to the inflation rate. The numerical examples illustrate the inventory model for different scenarios. Sensitivity analysis is carried out to provide managerial insights to management during post Covid-19 recovery.

1. Introduction

The Covid-19 pandemic is affecting the supply chain worldwide. It has affected health-related issues as well as our business model. From an economic and industry point of view, the pandemic brings uncertainties and disruptions to international businesses and supply chains (Sharma et al., 2020, Ivanov and Dolgui, 2020). Hence, the supply chain manager must carefully align their strategies. A supply chain may change the distribution network and route (Wang et al., 2020). Gupta and Chutani (2020) stated that during a pandemic situation, the retailer can support its supplier through advance-selling or prepayment. Harris (1913) pioneered the development of the basic economic order quantity (EOQ) model that assumes instant payment, constant demand, and without shortage or inflation effect. In this study, we relax these assumptions so that the proposed model is more suitable for the current situation. A hybrid payment policy is suggested to sustain the business during the financial crisis. This practice has been used in project management for many years (Elazouni and Gab-Allah, 2004, Gajpal and Elazouni, 2015).

There are three payment policies commonly used among buyers and sellers: there are instant payment, advance or prepayment, and trade credit or delay-in-payment. However, the hybrid policy is seldom discussed in previous studies. These payment policies provide mutual benefits to both the supplier and the buyer and thus are conducive to trade promotion. The first policy is an instant payment as in Harris (1913) well-known EOQ model. In the second policy, the buyer is enquired to pay for the products before delivering. The seller may request a full prepayment of the purchasing cost (Zhang, 1996; etc.) or prepay a portion of the cost known as partial prepayment (Zhang et al., 2014, Lashgari et al., 2016; etc.). In the third policy, the retailers allow delay-in-payments or trade credit. Researchers such as Teng (2002) adopted this phenomenon as a marketing strategy in their paper. The aim is to attract more buyers, increase their sales, and reduce inventory levels. There are two forms of delayed payment: a full and partial delayed payment. A full delay allows the payment of all purchasing costs after the allowed time, while a portion of the total purchase cost needs to be compensated in the process of partial delay in payment, at the delivery time, and the rest to be paid later. The optimum length of the delayed payment period is a challenge in this payment system.

According to Wee (1999), deterioration occurs in various goods such as fruits, vegetables, high-tech products and volatile liquids due to spoilage, obsolescence, and evaporation. Many researchers conducted their study by assuming instantaneous deterioration, i.e., the products start to deteriorate immediately after the stocks arrive. However, not all products conform to this pattern of instantaneous deterioration. Ouyang et al. (2006) identified this phenomenon as “non-instantaneous deterioration (NID)”. Some products, such as milk, have a specific expiration date. Before the expiration date, they are considered to be as good as new. Some preservation technology can extend the freshness lifetime of products (Iqbal & Sarkar, 2020). The investment of preservation technology affects inventory cost and pricing decisions. Inventory decisions also relate to the organization's efforts to satisfy consumer demand. For unsatisfied demand, either backorders, lost sales, or partial backorders are considered (Yang et al., 2006).

Considering the above challenges, our study incorporates advance and delay-in-payment, inflation, cash discount, and price dependent demand as an alternative solution; this is to stimulate post Covid-19 recovery. Moreover, we also consider non-instantaneous deterioration and the investment in preservation technology to extend the expired date. The major contributions of the study are as follows:

• (i)This model simultaneously studied two payment policies and their strategies under an inflationary environment in view of the pandemic situation.
• (ii)To stimulate post Covid-19 recovery, a hybrid payments policy and investment in preservation technology are considered.

2. Literature review

From the literature search, inventory deterioration is classified into instantaneous and non-instantaneous deterioration. To reduce deterioration, preservation technology (PT) is used. Hsu et al. (2010) were some of the first researchers to consider PT investment. Dye (2013) extended the previous model by considering non-instantaneous deteriorating items with PT. Later, Dye and Yang (2016) extended the model by incorporating pricing decisions. Mishra et al., 2017, Mishra et al., 2018) considered trade credit and price-dependent demand in maximizing the total profit of a retailer with a controllable deterioration rate. Recently, Li et al. (2019) projected a decision model for pricing, replenishment and PT investment considering price-dependent demand by allowing shortages before the non-deteriorating period. Feng (2019) also incorporated a pricing decision on deteriorating items, but for the effect of a quality investment. The demand was assumed to be price and quality dependent. Mishra et al., 2018 considered trade-credit and pricing strategies but ignored shortage situations, which play an important role in the retailing business. Li et al. (2019) solved this shortcoming. However, they worked in a normal environment rather than in an inflationary environment which is very important for retail businesses during an unleashed situation. Hence, we tried to bridge this gap in our proposed study.

Advance payment (or prepayment) has become a common business practice for many years. Therefore, researchers have incorporated the effect of this practice on inventory decisions. Zhang (1996) initiated the study on advance payment in inventory decisions. Then, Gupta et al. (2009) used a genetic algorithm to solve an inventory model under a simultaneous effect of the advance payment and price discount. Thangam (2011) introduced a simultaneous advance payment and delay payment (trade credit) to attract more customers. Taleizadeh et al. (2013) settled inventory models for multiple advance payments under three different shortages and backorder scenarios. Zhang et al. (2014) introduced inventory models with partial-advance-partial-delayed payment. Zia and Taleizadeh (2015) developed an EOQ model with multiple advance payments and delayed payment allowing backorders. Lashgari et al. (2016) worked with a simultaneous partial advance payment for the upstream chain and partial delay payment for the downstream chain. Further studies on advance payment for deteriorating items have been performed by Taleizadeh, 2014, Teng et al., 2016, and others. For example, considering both advance and delay in payments, Lashgari et al. (2018) examined the effect on non-instantaneous deterioration. Most advance payment studies did not consider the inflationary environment. Most importantly, they fail to incorporate any economical technique such as a discount to boost the sale. Some studies show the discount, but they do not incorporate discounts in multiple prepayments which is more realistic in the retailing business.

Trade credit or delay-in-payment is an extensively cast-off transaction practice in the business between seller and buyer, such as among suppliers, retailers, and customers. It is affected by the inter-organizational power among the supply chain parties (Liu et al., 2020). Trade-credit demonstrates a dominant source of short-term external finance for a buyer as well as an agreement for lesser unit purchasing cost. During the process of this period, the buyer does not pay any interest to the supplier. Therefore, trade credit also affects inventory holding costs. Goyal (1985) addressed the frequent use of trade-credit policy in an EOQ model considering a charged interest. Ouyang et al. (2005) developed an EOQ model assuming that suppliers offer both delays in payment and cash discount. A lot of research extended this study. Recently, Mohanty et al. (2018) extended trade credit studies by considering preservation technology investment. Mashud et al. (2020) considered trade credit and price-sensitive demand with fully backlogged shortages in an EOQ model. However, the study on hybrid payment which simultaneously considers multiple prepayments and trade-credit policy is still limited.

When the annual inflation rate of a region is high, it is no longer reasonable to use the assumption of fixed costs as in the basic EOQ model (Buzacott, 1975). Later, Ray and Chaudhuri, 1997, Moon and Lee, 2000 presented the joint consequence of inflation and the time value of money on the EOQ model. Yang (2006) also considered inflation and deterioration in an EOQ model. Recently, Tiwari et al. (2016) included inflation, discount, trade credit, and partial backlogging for non-instantaneous deterioration considering two storage facilities.

This paper allows a modification of previous studies by assimilating the effect of inflation and cash discount, advance and delay payment, partial backlogging, and preservation technology investment for the non-instantaneous deteriorating items, in a system with price-sensitive demand to respond to business disruption during a pandemic. Previous studies related to this problem are marked in Table 1 .

Table 1.

An assessment between the presented model with some other previously published work.

Authors	System of Payment	Type of Demand	Deterioration	Partially backlogged	Preservation technology	Inflation	Discount
Yang (2006)	No	Constant	Constant	Yes	No	Yes	No
Zhang et al. (2014)	Advance and Partial delay-partial advance	Constant	No	No	No	No	Yes
Taleizadeh (2014)	Advance	Constant	Constant	Yes	No	No	No
Zia and Taleizadeh (2015)	Multiple advances and delay	Constant	No	No	No	No	No
Lashgari et al. (2016)	Partial delay-partial advance	Constant	No	Yes	No	No	No
Lashgari et al. (2018)	Partial delay-partial advance	Constant	Non-instantaneous	Yes	No	No	No
Feng (2019)	No	Price and quality-dependent	Constant	No	No	No	No
Mashud et al. (2019)	Delay	Price dependent	Non-instantaneous	Yes	Yes	No	No
Mashud et al. (2020)	Delay	Price and advertisement	Non-instantaneous	Yes	Yes	No	No
Mishra et al. (2020)	Advance	Price and stock dependent	Non-instantaneous	No	Yes	No	No
This paper	Partial advance and delay-in-payments	Price- dependent	Non-instantaneous	Yes	Yes	Yes	Yes

3. Notations, research assumptions and Problem Description

3.1. Notations

This work uses the following notations:

Notations	Unit	Description
		Parameters
A	$/order	cost of an order
a	–	basic demand on the market
b	–	slope of the demand function
C	$/unit	purchase cost per unit item
C1	$/unit	cost of holding per unit item
C2	$/unit	cost of shortages per unit item
C3	$/unit	lost sale cost per unit item
D	units/year	demand per year
I(t)	units	different inventory level at any time t, where 0 ≤ t ≤ T
I1(t)	units	inventory level at any time t, where 0 ≤ t ≤ t1
I2(t)	units	inventory level at any time t, where t1 ≤ t ≤ t2
I3(t)	units	inventory level at any time t, where t2 ≤ t ≤ T
Ie	%/year	interest rate earned in a year
Icc	%/year	interest rate on loan per year
Ic	%/year	interest rate charges per year
i	–	index for cases dealing with shortages
k	–	index for cases dealing with the length of the permissible delay period
L	year	delivery lead time
M	year	permissible delay in the payment period
$n$	–	number of installments defined for prepayments during the lead time, 1 ≤ n ≤ 5
$r$	%/year	inflation rate
R	units	maximum shortage per cycle
S	units	maximum stock per cycle
t1	year	time at which the product remains fresh because of no deterioration
t2	year	time at which the stock reaches zero
$v$	–	backlogging parameter, $v>0$
θ	%	deterioration rate without preservation technology investment
α	%	discount rate for purchasing cost due to prepayments
σ	%	the portion of the purchase cost to be paid before delivery
p	$/unit	selling price per unit item (Decision variable)
T	year	replenishment cycle (Decision variable)
ξ	$	preservation investment (Decision variable)
BC	$	backorder cost
CCCP	$	cyclic capital costs of the prepayments
IHC	$	inventory holding cost
OLC	$	opportunity cost
PC	$	total purchase cost
PTC	$	preservation technology cost
IEik	$	interest earned, where i = 1, 2 and k = 1, 2, 3
ICik	$	interest charged, where i = 1, 2 and k = 1, 2, 3
m(ξ)	–	reduction in the deterioration rate
Q	units	order quantity
Δik(p,ξ,T)	$/year	total profit, where i = 1, 2 and k = 1, 2, 3

3.2. Assumptions

• (i)The rate of replenishment is considered infinite, while lead-time is constant.
• (ii)The demand rate D = (a - bp) is a price-sensitive linear type in which (a > 0, b > 0) and parallel to Tiwari et al. (2018).
• (iii)An infinite planning horizon for the whole system is considered.
• (iv)The non-deterioration period lies in the interval [0, t₁], then deterioration occurs during [t₁, t₂] at a constant rate θ if there is no preservation technology investment.
• (v)Unsatisfied demands are assumed to be partially backlogged. The fraction of backorder increases with a decreasing customer waiting time (T – t). The rate of partial backorder is e^-v(T-t), where v denotes the positive constraint of backlogging.
• (vi)The interrelationship between deterioration rate and preservation technology investment (PTI) continually fulfills the first-order derivative $\frac{\partial m\left(\xi \right)}{\partial \xi }<0,$ and second-order derivative $\frac{{\partial }^{2}m\left(\xi \right)}{\partial {\xi }^2}>0$, where m(ξ) = e^-ηξ designates the rate of deterioration with the investment of PT and η is the investment sensitive parameter to the rate of deterioration (Mishra et al., 2017, Mishra et al., 2018). The value m(ξ) represents a differentiable and decreasing function with respect to the preservation investment ξ.
• (vii)The supplier requests prepayment in n installments. Later, the retailer takes a loan from a financial institution with a certain interest rate. Then, a similar procedure is used throughout the paper to calculate the cyclic capital costs of the prepayments as that of Lashgari et al. (2018).
• (viii)A discount is presented by the supplier towards the retailer when the retailer agrees to prepay a portion of the purchased cost σCQ on n equal installments for L years before delivery (see Taleizadeh et al., 2013). The discount rate (α) increases when the number of installments decreases. The supplier will provide a maximum discount of J % if the retailer pays all the purchase cost in a single installment (see Khan et al., 2020).

3.3. Problem description

Based on the above assumption, a supplier allows a retailer to pay σ % of his total purchase cost after the order is made, while the remaining (1-σ) % will be paid upon order receipt. To promote sales during a pandemic situation, the supplier gives an additional discount to the retailer’s advance payment, that is, an extra J % discount based on the number of the installments. Similarly, the retailer may offer a delay-in-payment to the customers. Considering the influence of the pandemic on the market, the retailer will decide the cycle of replenishment, selling price, and preservation investment. The EOQ models are depicted in Fig. 1 (Case 1: with shortage) and Fig. 2 (Case 2: without shortage). This study considers the effect of non-instantaneous deterioration and partial backordering.

Fig. 1.

I(t) vs. time with shortages.

Fig. 2.

I(t) vs. time without shortage.

4. Mathematical formulation

This study proposed two different models on a hybrid payment system of prepayments and a trade-credit policy under the inflationary environment where Case 1 illustrates the situation by considering shortages and Case 2 without shortages.

4.1. Case 1: With shortages

In this case, the inventory level I(t) decreases following the demand rate during the period [0, t₁] and drops to zero at t = t₂ owe to both demand and the effect of deterioration. Then, the entire demand in the period [t₂, T] is partially backlogged. The left part of Fig. 1 shows that within the lead-time L several prepayments have been done in an equal length of L/n. The big shaded portion illustrates the payments which are paid in advance while the small one designates the remaining portion which needs to be paid by the retailer in time of receiving the products.

For the time interval 0 < t < t₁, the differential equation of the proposed inventory system is

$$\frac{d{I}_1\left(t\right)}{\mathit{dt}}=-\left(a-bp\right)$$ (1)

along with the situation I₁(t) = S at t = 0. Now using this boundary condition, the solution of Equation (1) in the interval 0 < t < t₁ is

$$I_1\left(t\right)=S-\left(a-bp\right)t$$ (2)

From the start of the deterioration until the end of the positive stock, one can write the differential equation in the following way:

$$\frac{d{I}_2\left(t\right)}{\mathit{dt}}+\theta m\left(\xi \right)I_2\left(t\right)=-\left(a-bp\right)t_1<t⩽t_2$$ (3)

while considering that the inventory level condition I₂(t) = 0 at t = t₂. Using these conditions, Equation (3) provides:

$$I_2\left(t\right)=\frac{\left(a-bp\right)}{\theta m\left(\xi \right)}\left(e^{\theta m\left(\xi \right)\left(t_2-t\right)}-1\right)t_1<t⩽t_2$$ (4)

Now, applying the continuity relation of I(t) at t = t₁ in which I₁(t₁) = I₂(t₁) one has

$$S=\left(a-bp\right)t_1+\frac{\left(a-bp\right)}{\theta m\left(\xi \right)}\left(e^{\theta m\left(\xi \right)(t_2-t_1)}-1\right)$$ (5)

After the period of t = t₂, the level of inventory slowly drops down below zero and shortages arise. In the shortage period [t₂, T], the demand is partially backlogged with a rate of (T - t). As a result, one can write the differential equation in the following way:

$$\frac{d{I}_3\left(t\right)}{\mathit{dt}}=-\left(a-bp\right)e^{-v(T-t)}{t}_2<t\le T$$ (6)

Through the boundary condition I₃(t) = 0 at t = t₂, the solution of the Equation (6) is

$$I_3\left(t\right)=\frac{D}{v}\left[e^{-v(T-t_2)}-e^{-v(T-t)}\right]t_2<t\le T$$ (7)

Therefore, the maximum shortage is given in the following form:

$$R=-I_3\left(T\right)=\frac{D}{v}\left[1-e^{-v(T-t_2)}\right]$$ (8)

The total initial stock and the total amount of shortages makes the total order quantity for the retailer and which has the mathematical form as:

$$\begin{array}{c}\\ Q=S+R=\left(a-bp\right)t_1+\frac{\left(a-bp\right)}{\theta m\left(\xi \right)}\left(e^{\theta m\left(\xi \right)(t_2-t_1)}-1\right)+\frac{D}{v}\left[1-e^{-v(T-t_2)}\right]\end{array}$$ (9)

Since the selling price of the item is p and the positive stock period is t₂ with demand D, the total sales revenue for the whole cycle length is:

$$\mathit{SR}=(pD{t}_2+pR)e^{\mathit{rt}}$$ (10)

The ordering cost of the system under the effect of inflation can be written mathematically as OC = Ae^rt.

A retailer spends some money to purchase goods from the supplier. Moreover, he has to maintain the inventory for a certain period. Therefore, the mathematical form for the holding cost is given as follows:

$$\mathit{IHC}=c_1{\int }_0^{t_1}{I}_1\left(t\right)e^{\mathit{rt}}dt+c_1{\int }_{t_1}^{t_2}{I}_2\left(t\right)e^{\mathit{rt}}dt$$

$$=C_1\left[\frac{\left(e^{r{t}_1}-1\right)}{r}\left[S+\frac{\left(a-bp\right)}{r}\right]-\frac{e^{r{t}_1}{t}_1(a-bp)}{r}+\frac{(a-bp)e^{\theta m\left(\xi \right)t_2}}{\theta m\left(\xi \right)\left[r-\theta m\left(\xi \right)\right]}\left[e^{\left[r-\theta m\left(\xi \right)\right]t_2}-e^{\left[r-\theta m\left(\xi \right)\right]t_1}\right]+\frac{(a-bp)}{\theta m\left(\xi \right)r}(e^{r{t}_2}-e^{r{t}_1})\right]$$ (11)

Equation (11) shows that the holding cost is applied for non-deteriorating inventories in the interval [0, t₁] and for the inventories that are affected by deterioration in the interval [t₁, t₂].

If C is the purchase cost per unit item and Q is the total purchased quantity under the inflation rate r, then the formula to represent the total purchase cost is $\mathit{PC}=CQ{e}^{\mathit{rt}}$. Putting the value of $Q$ from Equation (9), then the following Equation (12) represents the total purchase cost.

$$\mathit{PC}=C{e}^{\mathit{rt}}\left[\left(a-bp\right)t_1+\frac{\left(a-bp\right)}{\theta m\left(\xi \right)}\left(e^{\theta m\left(\xi \right)(t_2-t_1)}-1\right)+\frac{D}{v}\left[1-e^{-v(T-t_2)}\right]\right]$$ (12)

Due to shortages, several customers need to wait for the next lot to satisfy their demand. This means there is some unsatisfied demand in the interval t₂ < t ≤ T which has a value and is known as backorder cost. Therefore, the mathematical form of the backorder cost (BC) is given as follows:

$$BC=C_2{\int }_{t_2}^T-I_3{e}^{rt}dt=\frac{C_2\left(a-bp\right)}{v}\left[\frac{e^{-vT}}{v+r}\left[e^{\left(v+r\right)T}-e^{\left(v+r\right)t_2}\right]-\frac{e^{-v\left(T-t_2\right)}}{r}\left(e^{rT}-e^{r{t}_2}\right)\right]$$ (13)

This represents the number of backorder quantities due to shortage with the unit price C_2.

However, the characteristics of all customers are not the same. Some customers will go to an alternative store to fulfill their demand. So, there is value for this loss which is known as opportunity cost. The mathematical form of opportunity cost is given as

$$\mathit{OLC}=C_3{\int }_{t_2}^T(a-bp)\left[1-e^{-v(T-t)}\right]e^{\mathit{rt}}dt$$

$$=C_3\left(a-bp\right)\left[\frac{1}{r}\left(e^{\mathit{rT}}-e^{r{t}_2}\right)-\frac{e^{-vT}}{v+r}\left[e^{(v+r)T}-e^{\left(v+r\right)t_2}\right]\right]$$ (14)

Since some products quickly deteriorate, for which the retailer needs to use some preservative technology to preserve those products for a longer time, which will then cost some expenses. Thus, the preservation technology cost is given in the following mathematical form:

$$\mathit{PTC}=\xi T{e}^{\mathit{rt}}$$ (15)

Before receiving the products, the retailer pays σ portion of his purchase cost which is clarified in Fig. 1 and the remaining (1- σ) is expected to be paid at the receiving time. As a result, the cyclic capital cost of the advance payments is given as follows:

$$CCCP=\frac{C{e}^{rt}\sigma I_{cc}Q(n+1)L}{2n}$$ (16)

This study assumes a discount rate α is offered by the supplier on the prepayment of the purchase cost. The discount rate increases when the number of installments decreases. The supplier will provide a maximum of J % of the total purchase cost as a discount if he can pay all his purchase cost in a single installment. So, one can write mathematically, α = J/n, when, 0 ≤ J ≤ 100.

So that the discount on prepayment with inflation effect is

$$\mathit{DIS}=C\sigma Q\alpha e^{\mathit{rt}}$$ (17a)

Substituting α = J/n into (17a), one has:

$$\mathit{DIS}=\frac{C\sigma JQ{e}^{\mathit{rt}}}{n}$$ (17b)

After the receiving time, the retailer provides a delay in the payment period (M) to the customers for boosting the sales and overcome the unleashed situation. The different cases dealing with the length of M (i.e., M < L) result in some conditions which have different consequences on the earning and costs. The details for three possible inventory scenarios for Case 1 are presented in the following subsection.

4.1.1. When 0 < M ≤ t₁

The interest earned (IE_ik) is related to customer demand and interest rate I_e. Before shortage (t₂), the retailer gets compound interest, while during shortage a simple interest is applied. For this scenario, IE₁₁ is

$$I{E}_{11}=\left(1-\sigma \right)\left[p{I}_e{\int }_0^{t_2}{\int }_0^t\left(a-bp\right)e^{\mathit{rt}}dudt+\frac{p{I}_{e}D}{v}{\int }_0^{t_2}[1-e^{-v(T-t_2)}]e^{\mathit{rt}}dt\right]$$

$$=\frac{\left(1-\sigma \right)p{I}_e(a-bp)}{r}\left[t_2{e}^{r{t}_2}+\left(\frac{1}{v}-\frac{e^{-v(T-t_2)}}{v}-\frac{1}{r}\right)\left(e^{r{t}_2}-1\right)\right]$$ (18)

This represents the interest earned for the portion $\left(1-\sigma \right)$ of the total inventories.

Due to the permissible delay, the customer has no obligation to pay until M. Meanwhile, the retailer is charged for the available (positive) stock after M. Therefore, the interest charged (IC₁₁) related to the total inventory and interest rate I_c during this interval is

$$I{C}_{11}=C{I}_c{\int }_M^{t_1}{I}_1\left(t\right)e^{\mathit{rt}}dt+C{I}_c{\int }_{t_1}^{t_2}{I}_2\left(t\right)e^{\mathit{rt}}dt$$

$$=C{I}_c\left[\begin{array}{c}\left(\frac{S}{r}+\frac{a-bp}{r^2}\right)\left(e^{r{t}_1}-e^{\mathit{rM}}\right)-\frac{\left(a-bp\right)}{r}\left(t_1{e}^{r{t}_1}-M{e}^{\mathit{rM}}\right)\\ +\frac{\left(a-bp\right)}{\theta m\left(\xi \right)}\left[\frac{e^{\theta m\left(\xi \right)t_2}}{\left[r-\theta m\left(\xi \right)\right]}\left\{e^{\left[r-\theta m\left(\xi \right)\right]t_2}-e^{\left[r-\theta m\left(\xi \right)\right]t_1}\right\}-\frac{1}{r}\left(e^{r{t}_2}-e^{r{t}_1}\right)\right]\end{array}\right]$$ (19)

This equation presents the amount of interest charged at a rate I_c on the inventories depleted in [M, t₂] under the inflation rate r.

Finally, the total profit per cycle is presented as follows:

$${\mathrm{\Delta }}_{11}\left(p,\xi ,T\right)=\frac{X_{11}}{T}$$

where

$$X_{11}=\left(\mathit{SR}-OC-PC-IHC-BC-OLC-PTC-CCCP+I{E}_{11}+DIS-I{C}_{11}\right)$$

The detailed derivation is shown in Appendix A.

The subsequent problem can be written as:

Problem 4.1.1.

${\mathrm{\Delta }}_{11}\left(p,\xi ,T\right)=\frac{X_{11}}{T}$for 0 < M ≤ t₁

4.1.2. Whent₁ < M ≤ t₂

The interest earned occurs before and during the shortage. For this scenario,

$$I{E}_{12}=I{E}_{11}$$

$$=\frac{\left(1-\sigma \right)p{I}_e(a-bp)}{r}\left[t_2{e}^{r{t}_2}+\left(\frac{1}{v}-\frac{e^{-v(T-t_2)}}{v}-\frac{1}{r}\right)\left(e^{r{t}_2}-1\right)\right]$$ (20)

For this scenario, the interest charged (IC₂) considering the positive stock after M is:

$$I{C}_{12}=C{I}_c{\int }_M^{t_2}{I}_2\left(t\right)e^{\mathit{rt}}dt$$

$$=\frac{C{I}_c\left(a-bp\right)}{\theta m\left(\xi \right)}\left[\frac{e^{\theta m\left(\xi \right)t_2}}{\left[r-\theta m\left(\xi \right)\right]}\left\{e^{\left[r-\theta m\left(\xi \right)\right]t_2}-e^{\left[r-\theta m\left(\xi \right)\right]M}\right\}+\frac{1}{r}\left(e^{r{t}_2}-e^{\mathit{rM}}\right)\right]$$ (21)

Hence,

$${\mathrm{\Delta }}_{12}\left(p,\xi ,T\right)=\frac{X_{12}}{T}$$

where

$$X_{12}=\left(\mathit{SR}-OC-PC-IHC-BC-OLC-PTC-CCCP+I{E}_{12}+DIS-I{C}_{12}\right)$$

The detailed derivation is shown in Appendix A.

Accordingly, Problem 4.1.2 is:

${\mathrm{\Delta }}_{12}\left(p,\xi ,T\right)=\frac{X_{12}}{T}$for t₁ < M ≤ t₂

4.1.3. Whent₂ < M ≤ T

For this scenario,

$$I{E}_{13}=I{E}_{11}$$

$$=\frac{\left(1-\sigma \right)p{I}_e(a-bp)}{r}\left[t_2{e}^{r{t}_2}+\left(\frac{1}{v}-\frac{e^{-v(T-t_2)}}{v}-\frac{1}{r}\right)\left(e^{r{t}_2}-1\right)\right]$$ (22)

However, there is no positive stock after M. Therefore, the interest charged (IC₁₃) is

$$I{C}_{13}=0$$ (23)

Hence,

$${\mathrm{\Delta }}_{13}\left(p,\xi ,T\right)=\frac{X_{13}}{T}$$

where

$$X_{13}=\left(\mathit{SR}-OC-PC-IHC-BC-OLC-PTC-CCCP+I{E}_{13}+DIS-I{C}_{13}\right)$$

The detailed derivation is shown in Appendix A.

Hence, Problem 4.1.3 is:

${\mathrm{\Delta }}_{13}\left(p,\xi ,T\right)=\frac{X_{13}}{T}$ for t₂ < M ≤ T

Now the total profit functions for $i=1,k=1,2,3$ are expressed in the form

$${\mathrm{\Delta }}_{\mathit{ik}}\left(p,\xi ,T\right)=\left\{\begin{array}{c}{\mathrm{\Delta }}_{11}\left(p,\xi ,T\right)when0<M⩽t_1\\ {\mathrm{\Delta }}_{12}\left(p,\xi ,T\right)when{t}_1<M⩽t_2\\ {\mathrm{\Delta }}_{13}\left(p,\xi ,T\right)when{t}_2<M⩽T\end{array}\right)$$ (24)

4.2. Case 2: Without shortages

In this case, there are no shortages allowed, so the retailer will satisfy all the customer's demand within the cycle length as shown in Fig. 2. Since there are no shortages allowed in this case, there will be no backorder cost, and consequently, since there is no unsatisfied demand, the opportunity cost will also be absent. The rest of the cost factors are the same as Case 1. To avoid redundancy, we do not present the analogous calculations here.

In Case 2, the trade credit, which is offered by the retailer to its customers, occurs in two intervals. Hence, the following two inventory scenarios of Case 2 are explained in the following subsection.

4.2.1. When 0 < M ≤ t₁

In this scenario, the interest earned is the same as in section 4.1.1, except for the shortages, as shortages are not allowed in this scenario.

Then,

$$I{E}_{21}=\left(1-\sigma \right)\left[p{I}_e{\int }_0^{t_2}{\int }_0^t\left(a-bp\right)e^{\mathit{rt}}dudt\right]$$

$$=\frac{\left(1-\sigma \right)p{I}_{e}T(a-bp)e^{\mathit{rT}}}{r}$$ (25)

The interest paid is the same as in section 4.1.1, except for the second part of the interest paid. Now, if we replace t₂ = T then the total interest payment for this scenario will be:

$$I{C}_{21}=C{I}_c{\int }_M^{t_1}{I}_1\left(t\right)e^{\mathit{rt}}dt+C{I}_c{\int }_{t_1}^T{I}_2\left(t\right)e^{\mathit{rt}}dt$$

$$=C{I}_c\left[\begin{array}{c}\left(\frac{S}{r}+\frac{a-bp}{r^2}\right)\left(e^{r{t}_1}-e^{\mathit{rM}}\right)-\frac{\left(a-bp\right)}{r}\left(t_1{e}^{r{t}_1}-M{e}^{\mathit{rM}}\right)\\ +\frac{\left(a-bp\right)}{\theta m\left(\xi \right)}\left[\frac{e^{\theta m\left(\xi \right)T}}{\left[r-\theta m\left(\xi \right)\right]}\left\{e^{\left[r-\theta m\left(\xi \right)\right]T}-e^{\left[r-\theta m\left(\xi \right)\right]t_1}\right\}-\frac{1}{r}\left(e^{\mathit{rT}}-e^{r{t}_1}\right)\right]\end{array}\right]$$ (26)

This equation presents the amount of interest charged at rate I_c on the inventories depleted in [M, T] under the inflation rate r.

Therefore, the total profit per cycle is:

$${\mathrm{\Delta }}_{21}\left(p,\xi ,T\right)=\frac{X_{21}}{T}$$

where

$$X_{21}=\left(\mathit{SR}-OC-PC-IHC-PTC-CCCP+I{E}_{21}+DIS-I{C}_{21}\right)$$

The detailed derivation is shown in Appendix B.

The problem can be written in the subsequent arrangement:

Problem 4.2.1.

${\mathrm{\Delta }}_{21}\left(p,\xi ,T\right)=\frac{X_{21}}{T}$for 0 < M ≤ t₁

4.2.2. Whent₁ < M ≤ T

The interest earned also consists of before and during the shortage. For this scenario,

$$I{E}_{21}=I{E}_{22}$$

$$=\frac{\left(1-\sigma \right)p{I}_{e}T(a-bp)e^{\mathit{rT}}}{r}$$ (27)

For this scenario, the interest charged (IC₂) considering the positive stock after M is

$$I{C}_{22}=C{I}_c{\int }_M^T{I}_2\left(t\right)e^{\mathit{rt}}dt$$

$$=\frac{C{I}_c\left(a-bp\right)}{\theta m\left(\xi \right)}\left[\frac{e^{\theta m\left(\xi \right)T}}{\left[r-\theta m\left(\xi \right)\right]}\left\{e^{\left[r-\theta m\left(\xi \right)\right]T}-e^{\left[r-\theta m\left(\xi \right)\right]M}\right\}+\frac{1}{r}\left(e^{\mathit{rT}}-e^{\mathit{rM}}\right)\right]$$ (28)

Hence,

$${\mathrm{\Delta }}_{22}\left(p,\xi ,T\right)=\frac{X_{22}}{T}$$

where

$$X_{22}=\left(\mathit{SR}-OC-PC-IHC-PTC-CCCP+I{E}_{22}+DIS-I{C}_{22}\right)$$

The detailed derivation is shown in Appendix-B

Accordingly, Problem 4.2.2 is:

${\mathrm{\Delta }}_{22}\left(p,\xi ,T\right)=\frac{X_{22}}{T}$ for t₁ < M ≤ T

Now the total profit functions for $i=2,k=1,2$ are expressed in the form

$${\mathrm{\Delta }}_{\mathit{ik}}\left(p,\xi ,T\right)=\left\{\begin{array}{c}{\mathrm{\Delta }}_{21}\left(p,\xi ,T\right)when0<M⩽t_1\\ {\mathrm{\Delta }}_{22}\left(p,\xi ,T\right)when{t}_1<M⩽T\end{array}\right)$$ (29)

5. Theoretical development

In this section, we discuss the theoretical development of the mentioned two cases.

5.1. Case 1: With shortages

The objective function in equation (24) clearly shows that it is a highly non-linear equation in terms of decision variables which is almost impossible to demonstrate the joint concavity easily without implementing some terms and conditions. However, with the help of a numerical illustration, it is likely to illustrate the objective function as jointly concave with regard to the decision variables. Theoretically, by implementing some conditions, it is possible to prove the concavity of the decision variables.

From theorems 3.2.9, and 3.2.10 stated in Cambini and Martein (2009), the fractional function$\mathrm{\Delta }(x)=\frac{{\psi }_1(x)}{{\psi }_2(x)},x\in \mathfrak{R}$ is (strictly) pseudo-concave if ${\psi }_1(x)$ is non-negative, differentiable and (strictly) concave, and ${\psi }_2(x)$ is positive, differentiable and convex. With this concept for any given p and ξ, it is possible to prove that the total profit Δ_ik (p, ξ, T) where i = 1, 2 and k = 1, 2, 3 is strictly pseudo-concave in decision variable T. Consequently, for every assumed p and ξ, there occurs a distinctive universal optimal solution T_i* such that Δ_ik (p, ξ, T) where i = 1, 2 and k = 1, 2, 3 is maximized.

Consequently, one can maximize Δ_ik (p, ξ, T) where i = 1, 2 and k = 1, 2, 3 incoherently. The following theorems result:

Theorem 1.

• (a)For every fixed value of p and ξ, the profit function Δ_ik (p, ξ, T) where i = 1, 2 and k = 1, 2, 3 in terms of the decision variables T is strictly concave, and consequently, has a single maximum solution T*.

• (b)For every fixed value of ξ, the total profit function Δ_ik (p, ξ, T) where i = 1, 2 and k = 1, 2, 3 is strictly concave in terms of decision variables p and T and consequently, it produces a single maximum solution at (p*, T*).

Proof.

See Appendix A.

Theorem 2.

• (a)For every fixed value of T and ξ, the profit function Δ_ik (p, ξ, T) where i = 1, 2 and k = 1, 2, 3 in terms of decision variables p is strictly concave, and consequently, it has a single maximum solution p*.

• (b)For every fixed value of p total profit function Δ_ik (p, ξ, T) where i = 1, 2 and k = 1, 2, 3 is strictly concave in terms of decision variables T and ξ and consequently, it produces a single maximum solution at (ξ*, T*).

Proof.

Similar to Theorem 1.

Theorem 3.

• (a)For every fixed value p and T, the profit function Δ_ik (p, ξ, T) where i = 1, 2 and k = 1, 2, 3 in terms of decision variablesvξ is strictly concave, and consequently, it has a single extreme solution ${\xi }^{\ast }$.

• (b)For every fixed value of T total profit function Δ_ik (p, ξ, T) where i = 1, 2 and k = 1, 2, 3 is strictly concave in terms of decision variables ξ and p and consequently, it has a single maximum solution at (p*, ξ*).

Proof.

Similar to Theorem 1.

5.2. Case 2: Without shortages

The solution procedure is almost the same as in Case 1. To avoid the repeating, we have omitted the theoretical derivation. However, we have provided a numerical example in the latter part of the paper.

6. Special cases concerning Case 1 model

• (i)If the value of $v\to 0$ and t₂ ≈ T, i.e. R = 0, we have a fully backordered situation.
• (ii)Taking into account a constant D, when t₁ = 0, ξ = 0, r = 0, α = 0, t₂ = 0, and L = 0, then the model becomes an instantaneous deteriorating inventory model with no shortages (Zhang et al., 2014).
• (iii)If the value of t₁ = 0 then the model is similar to that of Taleizadeh et al., 2013, Wu et al., 2018 with an instantaneous deterioration.
• (iv)From the proposed model, it is also possible to deduce the model of Zia and Taleizadeh, 2015, Wu et al., 2018 when the value of t₁ = 0, ξ = 0, r = 0, α = 0, and a constant D.
• (v)If the trade-credit policy is both partial and full, with a constant D, ξ = 0, r = 0, and α = 0, then the anticipated model is similar to that of Lashgari et al. (2016).
• (vi)With the time-varying deterioration, and when D is constant, M = 0, $I_e=0$ , $I_c=0$, r = 0, α = 0, ξ = 0, then Taleizadeh et al., 2013, Teng et al., 2016’s models result.
• (vii)The projected model is generalized to the model by Shaikh et al. (2019) when the values of M = 0, $I_e=0$ , $I_c=0$, r = 0, α = 0, ξ = 0, and t₂ = 0.

7. Field study and numerical illustrations

To clarify the significance of the study, some numerical examples are considered for different trade-credit periods.

7.1. Field study

We have taken a short interview with the manager of an online-based company involved in the Bangladesh retailing business. During the current COVID-19 pandemic situation, the supplier offers advance payments to the company so that they will not cancel the order. Due to the shortages of demand, the supplier offered a discount rate which is dependent on the number of installments. The company also offers delay-in-payments for the customers Due to the pandemic, some companies are facing problems with the unavailability of transportation and goods. Data has been collected from the interview and a numerical analysis has been performed using Lingo 17 software.

7.2. Numerical illustrations

The following examples are provided from the collected data to examine the optimal decisions using the proposed model. Examples 1–3 are for Case 1.

Example 1:

The parameters are known as follows: A = 800, a = 900, b = 30, C = 5, C₁ = 0.5, C₂ = 5, C₃ = 6, θ = 0.75, r = 0.13, v = 0.7, η = 0.1, t₁ = 0.5, σ = 0.7, I_cc = 0.09, I_c = 0.09, I_e = 0.12, L = 0.2, n = 3, and trade-credit period M = 0.2 years.

Example 2:

When t₁ < M ≤ t₂ and the other parameters are the same as Example 1 except the M = 1.2 years.

Example 3:

When t₂ < M ≤ T and the other parameters are the same as Example 1 except the M = 2.0 years.

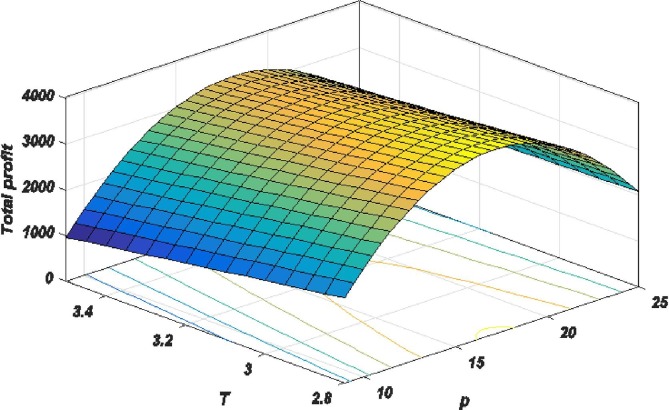
The optimal results of p*, ξ*, T*, S*, R*, and TP* are shown in Table 2 . Case 3 results in a profit of $3167.464 with respect to the decision variables. Then, the concavity of the profit function is confirmed in Fig. 3, Fig. 4, Fig. 5 . The three 3-D graphs show the concavity of the total profit for variables T-ξ, p-ξ, and T-p. They also show the approximate optimal value of the variables.

Example 4:

For Case 2

Table 2.

Outcomes for the examples that illustrate the three situations of the model with shortages.

Example	Situation	Results
		S*	R*	p*	${\xi }^{\ast }$	$T^{\ast }$	$T{P}_{\mathit{ij}}^{\ast }\left(p,\xi ,T\right)$
1	$0<M⩽t_1$	124.799	194.882	21.949	0.0	1.705	1321.443
2	$t_1<M⩽t_2$	536.049	193.339	20.586	1.640	2.432	2917.777
3	$t_2<M⩽T$	790.529	207.400	20.742	2.958	3.0567	3167.464

Fig. 3.

Total profit function vs. T and ξ.

Fig. 4.

Total profit function vs. p and ξ.

Fig. 5.

Total profit function vs. T and p.

If we consider all the parametric values in Example 1 and put t₂ = T, then the profit function of Case 1 will become the profit function of Case 2. As there are no shortages allowed in this case, we put a large value of v, i.e.: v = 99999. This results in zero shortage costs.

Table 3 presents the results where scenario 2 gives a higher total profit.

Example 5:

In this example, to examine the nature of profit, we consider different values of inflation r = (0.14, 0.18, 0.20, 0.22, 0.24). Under the pandemic situation, the exact forecasting of demands becomes difficult. Disruptions and inflation become common phenomena.

Table 3.

Outcomes of example 4 for two situations of the model without shortages.

Example	Situation	Results
		S*	R*	p*	${\xi }^{\ast }$	$T^{\ast }$	$T{P}_{\mathit{ij}}^{\ast }\left(p,\xi ,T\right)$
1	$0<M⩽t_1$	51.892	0	26.652	0.0	0.51	861.443
2	$t_1<M⩽T$	785.306	0	21.830	3.047	2.153	2247.142

The following graph presents a bar diagram showing the fluctuations in the profit of the retailer during a pandemic situation. It is clear that the increase in the inflation rate affects the retailer beneficiary in several cases. When the customer is not able to forecast the inflation rate, they will buy high amounts in bulk from the retailers. Consequently, the retailer is benefited. Sometimes, however, the retailer’s prediction on the demand of customers is inaccurate; as a result, the lower bar diagrams’ rate of growth means a decreasing total profit (Fig. 6 ). Here, we can conclude that inflation is very impactful to businesses. Furthermore, the importance of inflation increases during uncertain situations like the current pandemic. In an uncertain period, inflation might fluctuate and change abruptly. Also, the chance for receiving investments is decreased, as risk factors are increasing due to the possibility of falling customer demand. To reduce risks, investors or retailers need to find the appropriate inflation rate in which they can invest safely. This proposed model can help the investor to search for the appropriate inflation rate in these uncertain situations.

Fig. 6.

Impacts of inflation to the profit.

Next, we compare the results obtained from the cases studied in the paper. The first case considers shortages while the second one is without shortages. Three scenarios arise based on the trade-credit period for Case 1, while for Case 2, there are two scenarios. For the first case, example 3 provides the best result for the given data set (see Fig. 7 ). In contrast, example 1 provides a minimal result. However, for the case without shortages, the second example provides the best result for the retailer.

Fig. 7.

Total profit comparison based on different scenarios.

8. Sensitivity investigation

To study the consequence of the given factor regarding the decision variables, a sensitivity table is presented by changing the values of the parameters from −20% to +20% (See Table 4 ). The outcomes are accomplished by transforming each setting in turn and keeping different parameters at their unique merits.

Table 4.

Sensitivity investigation regarding various parameters.

Parameter	Variations of parameters (-20% to 20%)	Variations in TP*	Variations in
			T*	ξ*	p*
M	1.6	2989.812	2.548	1.937	20.591
	1.8	3098.887	2.793	2.476	20.643
	2.2	3201.730	3.335	3.399	20.878
	2.4	3208.068	3.536	3.682	20.989
n	2.4	3208.495	3.059	2.922	20.689
	2.7	3185.664	3.058	2.942	20.719
	3.3	3152.615	3.055	2.971	20.761
	3.6	3140.270	3.054	2.981	20.778
a	720	1235.130	3.142	2.957	17.744
	810	2107.309	3.093	2.958	19.242
	990	4415.466	3.028	2.958	22.243
	1080	5851.265	3.005	2.957	23.744
$b$	24	5232.066	3.010	2.952	24.494
	27	4069.565	3.033	2.955	22.409
	33	2454.689	3.079	2.960	19.378
	36	1883.873	3.101	2.962	18.242
C	4	3642.286	3.014	2.510	20.146
	4.5	3400.131	3.035	2.744	20.445
	5.5	2943.909	3.078	3.156	21.037
	6	2606.076	2.000	2.794	19.588
v	0.56	3316.569	3.257	3.003	20.652
	0.63	3236.411	3.148	2.979	20.698
	0.77	3107.508	2.979	2.940	20.784
	0.84	3054.876	2.912	2.925	20.823
$\sigma$	0.56	3267.459	3.045	2.982	20.688
	0.63	3217.414	3.050	2.970	20.715
	0.77	3117.612	3.062	2.946	20.770
	0.84	3067.862	3.069	2.934	20.797

Observations:

• (i)The total profit TP is proportional to the trade credit period (M); i.e., profit will upsurge for a longer trade credit period. A long trade credit period enables the retailer to earn interest for a longer time; thus the profit increases. For this nature of profit function, the retailer will try to offer a trade-credit duration as long as possible within the period during which he/she is permitted to delay payment for the supplier’s product. Total profit also increases when the basic demand (a) increases.

  Mathematically, ${\mathit{TP}}^{\ast }\propto \left\{M,a\right\}\mathrm{i}.\mathrm{e}.,{\mathit{TP}}^{\ast }=\tau \{M,a\}$; where,$\tau >0=$ $\left\{\begin{array}{c}{\tau }_{M}forM\\ {\tau }_{a}fora\end{array}\right)$ are proportional constant values for input parameters $M\mathrm{a}\mathrm{n}\mathrm{d}a$.

• (ii)On the other hand, the profit function TP is inversely proportional to n, b, C, v, and σ. So, managers should be aware of these parameters because they are responsible for profit losses when these values increase. With the intensifications of total installments, the profit decreases. This is analogous to the result of Mashud et al. (2020). In this situation, the retailer has to pay high interest due to the long installment period. So, the management needs to minimize the number of installments to restrict profit loss and receive discounts from the supplier at the same time. With a decline in the selling price coefficient parameter (b), the total profit increases. The price coefficient parameter (b) significantly affects the selling price, similar Tiwari et al. (2018). With the intensification in the portion of the purchase cost (σ), the profit decreases because the retailer needs to invest more before receiving the products. This result is similar to Mashud et al. (2020). Similarly, managers need to foresee the possible minimum values of n, b, C, v, σ.
  Mathematically one can write, ${\mathit{TP}}^{\ast }\propto \left\{\frac{1}{n},\frac{1}{b},\frac{1}{C},\frac{1}{v},\frac{1}{\sigma }\right\}$

  $$i.e.,{\mathit{TP}}^{\ast }=\lambda \{\frac{1}{n},\frac{1}{b},\frac{1}{C},\frac{1}{v},\frac{1}{\sigma }\}$$

  where $\lambda >0=$ $\left\{\begin{array}{c}{\lambda }_{n}forn\\ {\lambda }_{b}forb\\ {\lambda }_{c}forC\\ {\lambda }_{v}forv\\ {\lambda }_{\sigma }for\sigma \end{array}\right)$ is proportional constant values for different input parameters n, b, C, v, and σ.
• (iii)Total cycle length (T), preservation technology cost (ξ) and selling price (p) fluctuate with the change in the purchase cost (C). These variables increase when M increases; the results vary for other parameters.

9. Managerial insights

In business reality, some items have a temporary fresh lifetime which is known as a non-instantaneous deterioration. Furthermore, the price of the product plays a vital role for customers to choose the right kind of products, and costs are sometimes affected by the rate of inflation. In this regard, this study explores some important managerial insights which could help the managers to make decisions in view of the post Covid-19 recovery:

• (i)The effect of inflation is an important issue in this study. Hence, the manager should carefully monitor and maintain the influence of the inflation rate during this pandemic situation to be within the minimal range to get a greater profit.
• (ii)As the discount is offered for the advance payment only, the retailer always tries to use this opportunity to intensify his profit. The retailer will always try to pay the payment within the minimum number of installments because, for the greater number of installments, he will be charged higher interest and receive fewer discounts. Hence, it is highly recommended to pay the portion of the purchase cost as soon as possible.
• (iii)The retailer always seeks the perfect trade credit period for the customers as he needs to compensate purchase cost within the lead-time. A suggestion has been made for the manager which can help him in the pandemic situation to easily take his decision following the analysis of the different scenarios of the trade credit period.
• (iv)Finally, the manager will be able to know the non-deteriorating period of the products from the model which surely helps him to implement the preservation technology and create a sense of how much he needs to invest because an excessive investment may lead to a loss in profit.

10. Conclusions

The payment policies between suppliers, retailers, and customers are part of the supply chain financing strategy that affects the total costs and ordering decisions of each party. This study considers the downturn in business due to Covid-19 and provides a plan to stimulate supplier-retailer-customer business recovery. Here, an alternative strategy to sustain business relationships through a hybrid payment system and discount facility considering the inflation effect is proposed. The proposed model works for a retailer who sells a non-instantaneous deterioration product. The resulting nonlinear model is solved by Lingo 17 software, and numerical examples are presented to illustrate the model.

This study shows that the retailer can optimize the replenishment cycle, selling price, and preservation technology investment decisions. The examples show an increase in the retailer’s total profit when the delayed payment and trade credit strategies are implemented wisely. Though the total profit is extremely sensitive to the inflation rate, demand rate and purchasing price, but less sensitive to the number of prepayment installments. Furthermore, when a linear price-sensitive demand is assumed, the retailer is recommended to prepay a portion of the purchase cost as soon as possible.

This study assumes a customer demand which depends solely on selling price. Hence, future research can be done for different demand patterns. We can also investigate the impact of uncertain lead time that may arise during a pandemic.

CRediT authorship contribution statement

Abu Hashan Md Mashud: Conceptualization, Methodology, Software, Data curation, Writing - original draft. Md. Rakibul Hasan: Data curation, Writing - original draft, Visualization, Investigation, Writing - review & editing. Yosef Daryanto: Visualization, Investigation, Supervision, Software, Validation. Hui-Ming Wee: Supervision, Software, Validation, Writing - review & editing.

Appendix A.

Problem 4.1.1

${\mathrm{\Delta }}_{11}\left(p,\xi ,T\right)=X_{11}/T$ where $X_{11}=\left(\mathit{SR}-OC-PC-IHC-BC-OLC-PTC-CCCP+I{E}_{11}+DIS-I{C}_{11}\right)$

$${\mathrm{\Delta }}_{11}\left(p,\xi ,T\right)=\frac{1}{T}\left[\begin{array}{c}\left[p{t}_2\left(a-bp\right)+pR-A-\xi T-\frac{C\sigma I_{\mathit{cc}}Q(n+1)L}{2n}+\frac{C\sigma JQ}{n}\right]e^{\mathit{rt}}\\ -C_1\left[\begin{array}{c}\frac{\left(e^{r{t}_1}-1\right)}{r}\left[S+\frac{\left(a-bp\right)}{r}\right]-\frac{e^{r{t}_1}{t}_1(a-bp)}{r}\\ +\frac{(a-bp)e^{\theta m\left(\xi \right)t_2}}{\theta m\left(\xi \right)\left[r-\theta m\left(\xi \right)\right]}\left[e^{\left[r-\theta m\left(\xi \right)\right]t_2}-e^{\left[r-\theta m\left(\xi \right)\right]t_1}\right]+\frac{(a-bp)}{\theta m\left(\xi \right)r}(e^{r{t}_2}-e^{r{t}_1})\end{array}\right]\\ +\frac{e^{-vT}}{v+r}\left[e^{(v+r)T}-e^{\left(v+r\right)t_2}\right]\left[C_3\left(a-bp\right)-\frac{C_2\left(a-bp\right)}{v}\right]\\ +\left[\frac{C_2\left(a-bp\right)e^{-v\left(T-t_2\right)}}{v}-C_3\left(a-bp\right)\right]\left[\frac{1}{r}\left(e^{\mathit{rT}}-e^{r{t}_2}\right)\right]\\ -C{e}^{\mathit{rt}}\left[\left(a-bp\right)t_1+\frac{\left(a-bp\right)}{\theta m\left(\xi \right)}\left(e^{\theta m\left(\xi \right)(t_2-t_1)}-1\right)+\frac{D}{v}\left[1-e^{-v(T-t_2)}\right]\right]\\ +\frac{p\left(1-\sigma \right)I_e(a-bp)}{r}\left[t_2{e}^{r{t}_2}+\left(\frac{1}{v}-\frac{e^{-v(T-t_2)}}{v}-\frac{1}{r}\right)\left(e^{r{t}_2}-1\right)\right]\\ -C{I}_c\left[\begin{array}{c}\left(\frac{S}{r}+\frac{a-bp}{r^2}\right)\left(e^{r{t}_1}-e^{\mathit{rM}}\right)-\frac{\left(a-bp\right)}{r}\left(t_1{e}^{r{t}_1}-M{e}^{\mathit{rM}}\right)\\ +\frac{\left(a-bp\right)}{\theta m\left(\xi \right)}\left[\frac{e^{\theta m\left(\xi \right)t_2}}{\left[r-\theta m\left(\xi \right)\right]}\left\{e^{\left[r-\theta m\left(\xi \right)\right]t_2}-e^{\left[r-\theta m\left(\xi \right)\right]t_1}\right\}-\frac{1}{r}\left(e^{r{t}_2}-e^{r{t}_1}\right)\right]\end{array}\right]\end{array}\right]$$

Problem 4.1.2

${\mathrm{\Delta }}_{12}\left(p,\xi ,T\right)=X_{12}/T$ where $X_{12}=\left(\mathit{SR}-OC-PC-IHC-BC-OLC-PTC-CCCP+I{E}_{12}+DIS-I{C}_{12}\right)$

$${\mathrm{\Delta }}_{12}\left(p,\xi ,T\right)=\frac{1}{T}\left[\begin{array}{c}\left[p{t}_2\left(a-bp\right)+pR-A-\xi T-\frac{C\sigma I_{\mathit{cc}}Q(n+1)L}{2n}+\frac{C\sigma JQ}{n}\right]e^{\mathit{rt}}\\ -C_1\left[\begin{array}{c}\frac{\left(e^{r{t}_1}-1\right)}{r}\left[S+\frac{\left(a-bp\right)}{r}\right]-\frac{e^{r{t}_1}{t}_1(a-bp)}{r}\\ +\frac{(a-bp)e^{\theta m\left(\xi \right)t_2}}{\theta m\left(\xi \right)\left[r-\theta m\left(\xi \right)\right]}\left[e^{\left[r-\theta m\left(\xi \right)\right]t_2}-e^{\left[r-\theta m\left(\xi \right)\right]t_1}\right]+\frac{(a-bp)}{\theta m\left(\xi \right)r}(e^{r{t}_2}-e^{r{t}_1})\end{array}\right]\\ +\frac{e^{-vT}}{v+r}\left[e^{(v+r)T}-e^{\left(v+r\right)t_2}\right]\left[C_3\left(a-bp\right)-\frac{C_2\left(a-bp\right)}{v}\right]\\ +\left[\frac{C_2\left(a-bp\right)e^{-v\left(T-t_2\right)}}{v}-C_3\left(a-bp\right)\right]\left[\frac{1}{r}\left(e^{\mathit{rT}}-e^{r{t}_2}\right)\right]\\ -C{e}^{\mathit{rt}}\left[\left(a-bp\right)t_1+\frac{\left(a-bp\right)}{\theta m\left(\xi \right)}\left(e^{\theta m\left(\xi \right)(t_2-t_1)}-1\right)+\frac{D}{v}\left[1-e^{-v(T-t_2)}\right]\right]\\ +\frac{\left(1-\sigma \right)p{I}_e(a-bp)}{r}\left[t_2{e}^{r{t}_2}+\left(\frac{1}{v}-\frac{e^{-v(T-t_2)}}{v}-\frac{1}{r}\right)\left(e^{r{t}_2}-1\right)\right]\\ -\frac{C{I}_c\left(a-bp\right)}{\theta m\left(\xi \right)}\left[\frac{e^{\theta m\left(\xi \right)t_2}}{\left[r-\theta m\left(\xi \right)\right]}\left\{e^{\left[r-\theta m\left(\xi \right)\right]t_2}-e^{\left[r-\theta m\left(\xi \right)\right]M}\right\}+\frac{1}{r}\left(e^{r{t}_2}-e^{\mathit{rM}}\right)\right]\end{array}\right]$$

Problem 4.1.3

${\mathrm{\Delta }}_{13}\left(p,\xi ,T\right)=X_{13}/T$ where $X_{13}=\left(\mathit{SR}-OC-PC-IHC-BC-LSC-PTC-CCCP+I{E}_{13}+DIS-I{C}_{13}\right)$

$${\mathrm{\Delta }}_{13}\left(p,\xi ,T\right)=\frac{1}{T}\left[\begin{array}{c}\left[p{t}_2\left(a-bp\right)+pR-A-\xi T-\frac{C\sigma I_{\mathit{cc}}Q(n+1)L}{2n}+\frac{C\sigma JQ}{n}\right]e^{\mathit{rt}}\\ -C_1\left[\begin{array}{c}\frac{\left(e^{r{t}_1}-1\right)}{r}\left[S+\frac{\left(a-bp\right)}{r}\right]-\frac{e^{r{t}_1}{t}_1(a-bp)}{r}\\ +\frac{(a-bp)e^{\theta m\left(\xi \right)t_2}}{\theta m\left(\xi \right)\left[r-\theta m\left(\xi \right)\right]}\left[e^{\left[r-\theta m\left(\xi \right)\right]t_2}-e^{\left[r-\theta m\left(\xi \right)\right]t_1}\right]+\frac{(a-bp)}{\theta m\left(\xi \right)r}(e^{r{t}_2}-e^{r{t}_1})\end{array}\right]\\ +\frac{e^{-vT}}{v+r}\left[e^{(v+r)T}-e^{\left(v+r\right)t_2}\right]\left[C_3\left(a-bp\right)-\frac{C_2\left(a-bp\right)}{v}\right]\\ +\left[\frac{C_2\left(a-bp\right)e^{-v\left(T-t_2\right)}}{v}-C_3\left(a-bp\right)\right]\left[\frac{1}{r}\left(e^{\mathit{rT}}-e^{r{t}_2}\right)\right]\\ -C{e}^{\mathit{rt}}\left[\left(a-bp\right)t_1+\frac{\left(a-bp\right)}{\theta m\left(\xi \right)}\left(e^{\theta m\left(\xi \right)(t_2-t_1)}-1\right)+\frac{D}{v}\left[1-e^{-v(T-t_2)}\right]\right]\\ +\frac{\left(1-\sigma \right)p{I}_e(a-bp)}{r}\left[t_2{e}^{r{t}_2}+\left(\frac{1}{v}-\frac{e^{-v(T-t_2)}}{v}-\frac{1}{r}\right)\left(e^{r{t}_2}-1\right)\right]\end{array}\right]$$

Proof of Theorem 1 (a)

Let us consider for i = 1, k = 3. From the equation (24) one has

$$\begin{array}{c}{\psi }_1(T)=\left[\begin{array}{c}\left[p{t}_2\left(a-bp\right)+pR-A-\xi T-\frac{C\sigma I_{\mathit{cc}}Q(n+1)L}{2n}+\frac{C\sigma JQ}{n}\right]e^{\mathit{rt}}\\ -C_1\left[\frac{\left(e^{r{t}_1}-1\right)}{r}\left[S+\frac{\left(a-bp\right)}{r}\right]-\frac{e^{r{t}_1}{t}_1(a-bp)}{r}+\frac{(a-bp)e^{\theta m\left(\xi \right)t_2}}{\theta m\left(\xi \right)\left[r-\theta m\left(\xi \right)\right]}\left[e^{\left[r-\theta m\left(\xi \right)\right]t_2}-e^{\left[r-\theta m\left(\xi \right)\right]t_1}\right]+\frac{(a-bp)}{\theta m\left(\xi \right)r}(e^{r{t}_2}-e^{r{t}_1})\right]\\ +\frac{e^{-vT}}{v+r}\left[e^{(v+r)T}-e^{\left(v+r\right)t_2}\right]\left[C_3\left(a-bp\right)-\frac{C_2\left(a-bp\right)}{v}\right]+\left[\frac{C_2\left(a-bp\right)e^{-v\left(T-t_2\right)}}{v}-C_3\left(a-bp\right)\right]\left[\frac{1}{r}\left(e^{\mathit{rT}}-e^{r{t}_2}\right)\right]\\ -C{e}^{\mathit{rt}}\left[\left(a-bp\right)t_1+\frac{\left(a-bp\right)}{\theta m\left(\xi \right)}\left(e^{\theta m\left(\xi \right)(t_2-t_1)}-1\right)+\frac{D}{v}\left[1-e^{-v(T-t_2)}\right]\right]+\frac{\left(1-\sigma \right)p{I}_e(a-bp)}{r}\left[t_2{e}^{r{t}_2}+\left(\frac{1}{v}-\frac{e^{-v(T-t_2)}}{v}-\frac{1}{r}\right)\left(e^{r{t}_2}-1\right)\right]\end{array}\right]\\ {\psi }_2(T)=T>0\end{array}$$

Now, with respect to the decision variable T, the first order and the second-order derivative of ${\psi }_1(T)$ can be written as:

$$\begin{array}{c}{\mathrm{\Psi }}_1^{″}(T)=-D\left[{\varphi }_1\left[v^2{e}^{\left(v+r\right)t_2-vT}-r^2{e}^{\mathit{rT}}\right]+{\varphi }_2\left[C_3-C_{2}v{e}^{-v\left(T-t_2\right)}\right]+r{e}^{\mathit{rT}}\left[C_3-\frac{C_2{e}^{-v\left(T-t_2\right)}}{v}\right]+{\varphi }_{3}v{e}^{-v(T-t_2)}\right]<0\\ Where,{\varphi }_1=\frac{1}{v+r}\left[C_3-\frac{C_2}{v}\right],{\varphi }_2=\left[\frac{1}{r}\left(e^{\mathit{rT}}-e^{r{t}_2}\right)\right],{\varphi }_3=-\left(\frac{C{e}^{\mathit{rt}}}{v}+\frac{\left(1-\sigma \right)p{I}_e}{r}\left(1-e^{r{t}_2}\right)\right)\end{array}$$

which is clear from the above expression that ${\mathrm{\Psi }}_1^{″}(T)<0$. Therefore, the function ${\mathrm{\Psi }}_1(T)$becomes negative, differentiable and concave. Correspondingly, ${\mathrm{\Psi }}_2(T)=T$ is a positive, differentiable, and convex function for decision variable T. Subsequently, the total profit function Δ_ik (p, ξ, T), becomes a rigorously pseudo-concave function in terms of decision variable T, and hereafter there is a distinctive optimal solution $T^{\ast }$. This concludes the proof of theorem 1(a).

Proof of Theorem 1 (b)

Proof.

From the equation (33) if one put i = 1, k = 3 then,

$$\begin{array}{c}{\mathrm{\Psi }}_1(p,T)=\left[\begin{array}{c}\left[p{t}_2\left(a-bp\right)+pR-A-\xi T-\frac{C\sigma I_{\mathit{cc}}Q(n+1)L}{2n}+\frac{C\sigma JQ}{n}\right]e^{\mathit{rt}}\\ -C_1\left[\frac{\left(e^{r{t}_1}-1\right)}{r}\left[S+\frac{\left(a-bp\right)}{r}\right]-\frac{e^{r{t}_1}{t}_1(a-bp)}{r}+\frac{(a-bp)e^{\theta m\left(\xi \right)t_2}}{\theta m\left(\xi \right)\left[r-\theta m\left(\xi \right)\right]}\left[e^{\left[r-\theta m\left(\xi \right)\right]t_2}-e^{\left[r-\theta m\left(\xi \right)\right]t_1}\right]+\frac{(a-bp)}{\theta m\left(\xi \right)r}(e^{r{t}_2}-e^{r{t}_1})\right]\\ +\frac{e^{-vT}}{v+r}\left[e^{(v+r)T}-e^{\left(v+r\right)t_2}\right]\left[C_3\left(a-bp\right)-\frac{C_2\left(a-bp\right)}{v}\right]+\left[\frac{C_2\left(a-bp\right)e^{-v\left(T-t_2\right)}}{v}-C_3\left(a-bp\right)\right]\left[\frac{1}{r}\left(e^{\mathit{rT}}-e^{r{t}_2}\right)\right]\\ -C{e}^{\mathit{rt}}\left[\left(a-bp\right)t_1+\frac{\left(a-bp\right)}{\theta m\left(\xi \right)}\left(e^{\theta m\left(\xi \right)(t_2-t_1)}-1\right)+\frac{D}{v}\left[1-e^{-v(T-t_2)}\right]\right]+\frac{\left(1-\sigma \right)p{I}_e(a-bp)}{r}\left[t_2{e}^{r{t}_2}+\left(\frac{1}{v}-\frac{e^{-v(T-t_2)}}{v}-\frac{1}{r}\right)\left(e^{r{t}_2}-1\right)\right]\end{array}\right]\\ {\mathrm{\Psi }}_2(p,T)=T>0\end{array}$$

From Cambini and Martein (2009), to generate the Hessian matrix for the function Ψ₁(p,T), all the second-order partial derivatives must be computed with regard to the decision variables p and T.

$$\begin{array}{c}\frac{{\partial }^2{\psi }_1(p,T)}{\partial p^2}=-2b\left[t_2{e}^{\mathit{rt}}+\frac{\left(1-\sigma \right)I_e}{r}\left[t_2{e}^{r{t}_2}+\left(\frac{1}{v}-\frac{e^{-v(T-t_2)}}{v}-\frac{1}{r}\right)\left(e^{r{t}_2}-1\right)\right]\right]\\ \frac{{\partial }^2{\psi }_1(p,T)}{\partial T^2}=D\left[\begin{array}{c}\frac{1}{v+r}\left[C_3-\frac{C_2}{v}\right]\left[r^2{e}^{\mathit{rT}}-v^2{e}^{\left(v+r\right)t_2-vT}\right]+\left[C_{2}v{e}^{-v\left(T-t_2\right)}-c_3\right]\left[\frac{1}{r}\left(e^{\mathit{rT}}-e^{r{t}_2}\right)\right]+r{e}^{\mathit{rT}}\left[\frac{C_2{e}^{-v\left(T-t_2\right)}}{v}-c_3\right]\\ +\left[v{e}^{-v(T-t_2)}\right]\left(\frac{C{e}^{\mathit{rt}}}{v}+\frac{\left(1-\sigma \right)p{I}_e}{r}\left(1-e^{r{t}_2}\right)\right)\end{array}\right]\\ \frac{{\partial }^2{\psi }_1(p,T)}{\partial p\partial T}=\left[\begin{array}{c}{t}_2{e}^{\mathit{rt}}\left(a-2bp\right)-\frac{b}{v+r}\left[C_3+\frac{C_2}{v}\right]\left[r{e}^{\mathit{rT}}+v{e}^{-vT+\left(v+r\right)t_2}\right]+\left[b{C}_2{e}^{-v\left(T-t_2\right)}+b{C}_3\right]\left[\frac{1}{r}\left(e^{\mathit{rT}}-e^{r{t}_2}\right)\right]\\ +bC{e}^{-v(T-t_2)+rt}+\frac{\left(1-\sigma \right)I_e(a-2bp)}{r}\left[e^{-v(T-t_2)}\left(e^{r{t}_2}-1\right)\right]\end{array}\right]\end{array}$$

The Hessian matrix for the function ${\psi }_1(p,T)$ can be written as:

$$H_{ij}=\left[\begin{array}{cc}\frac{{\partial }^2{\psi }_1}{\partial p^2}& \frac{{\partial }^2{\psi }_1}{\partial p\partial T}\\ \frac{{\partial }^2{\psi }_1}{\partial T\partial p}& \frac{{\partial }^2{\psi }_1}{\partial T^2}\end{array}\right]$$

The first principal minor is

$$\left|H_{11}\right|=\frac{{\partial }^2{\psi }_1}{\partial p^2}=-2b\left[t_2{e}^{\mathit{rt}}+\frac{I_e\left(1-\sigma \right)}{r}\left[t_2{e}^{r{t}_2}+\left(\frac{1}{v}-\frac{e^{-v(T-t_2)}}{v}-\frac{1}{r}\right)\left(e^{r{t}_2}-1\right)\right]\right]$$

which is negative in nature.

The second principal minor is

$$\begin{array}{c}\left|H_{22}\right|=\frac{{\partial }^2{\psi }_1}{\partial p^2}\frac{{\partial }^2{\psi }_1}{\partial T^2}-{\left(\frac{{\partial }^2{\psi }_1}{\partial p\partial T}\right)}^2\\ =-2b\left[t_2{e}^{\mathit{rt}}+\left(1-\sigma \right)\left[\frac{I_e}{r}{t}_2{e}^{r{t}_2}+\left(\frac{1}{v}-\frac{1}{r}\right)\left(e^{r{t}_2}-1\right)-\frac{I_e}{r}\left(\frac{e^{-v(T-t_2)}}{v}\right)\left(e^{r{t}_2}-1\right)\right]\right]\ast \\ D\left[\begin{array}{c}\frac{1}{v+r}\left[C_3-\frac{C_2}{v}\right]\left[r^2{e}^{\mathit{rT}}-v^2{e}^{\left(v+r\right)t_2-vT}\right]+\left[C_{2}v{e}^{-v\left(T-t_2\right)}-C_3\right]\left[\frac{1}{r}\left(e^{\mathit{rT}}-e^{r{t}_2}\right)\right]+r{e}^{\mathit{rT}}\left[\frac{C_2{e}^{-v\left(T-t_2\right)}}{v}-c_3\right]\\ +\left[v{e}^{-v(T-t_2)}\right]\left(\frac{C{e}^{\mathit{rt}}}{v}+\frac{\left(1-\sigma \right)p{I}_e}{r}\left(1-e^{r{t}_2}\right)\right)\end{array}\right]\\ -{\left[\begin{array}{c}{t}_2{e}^{\mathit{rt}}\left(a-2bp\right)-\frac{b}{v+r}\left[C_3+\frac{C_2}{v}\right]\left[r{e}^{\mathit{rT}}+v{e}^{-vT+\left(v+r\right)t_2}\right]+\left[b{C}_2{e}^{-v\left(T-t_2\right)}+b{C}_3\right]\left[\frac{1}{r}\left(e^{\mathit{rT}}-e^{r{t}_2}\right)\right]\\ +bC{e}^{-v(T-t_2)+rt}+\frac{\left(1-\sigma \right)I_e(a-2bp)}{r}\left[e^{-v(T-t_2)}\left(e^{r{t}_2}-1\right)\right]\end{array}\right]}^2\\ =-2Db\left[t_2{e}^{\mathit{rt}}+\left[{\varpi }_7-{\varpi }_8{e}^{-v(T-t_2)}\right]\right]\ast \left[{\varpi }_3\left(r^2{e}^{\mathit{rT}}-v^2{e}^{\left(v+r\right)t_2-vT}\right)+\left(C_{2}v{e}^{-v\left(T-t_2\right)}-C_3\right){\varpi }_2+r{e}^{\mathit{rT}}\left(\frac{C_2{e}^{-v\left(T-t_2\right)}}{v}-C_3\right)+\left(v{e}^{-v(T-t_2)}\right){\varpi }_1\right]\\ -{\left[{\varpi }_4-{\varpi }_5\left[r{e}^{\mathit{rT}}+v{e}^{-vT+\left(v+r\right)t_2}\right]+\left[b{C}_2{e}^{-v\left(T-t_2\right)}+b{c}_3\right]\left[\frac{1}{r}\left(e^{\mathit{rT}}-e^{r{t}_2}\right)\right]+bc{e}^{-v(T-t_2)+rt}+{\varpi }_6\left[e^{-v(T-t_2)}\left(e^{r{t}_2}-1\right)\right]\right]}^2\\ \mathit{where},{\varpi }_1=\left(\frac{C{e}^{\mathit{rt}}}{v}+\frac{\left(1-\sigma \right)p{I}_e}{r}\left(1-e^{r{t}_2}\right)\right),{\varpi }_2=\left(\frac{1}{r}\left(e^{\mathit{rT}}-e^{r{t}_2}\right)\right),{\varpi }_3=\frac{1}{v+r}\left(C_3-\frac{C_2}{v}\right),{\varpi }_4=K{e}^{\mathit{rt}}\left(a-2bp\right),{\varpi }_5=\frac{b}{v+r}\left[C_3+\frac{C_2}{v}\right],\\ {\varpi }_6=\frac{\left(1-\sigma \right)I_e(a-2bp)}{r},{\varpi }_7=\frac{\left(1-\sigma \right)I_e}{r}{t}_2{e}^{r{t}_2}+\left(\frac{1}{v}-\frac{1}{r}\right)\left(e^{r{t}_2}-1\right),{\varpi }_8=\frac{\left(1-\sigma \right)I_e}{\mathit{vr}}\left(e^{r{t}_2}-1\right)\\ \end{array}$$

It is clear from the above expressions that the primary minor $\left|H_{22}\right|$ is always greater than zero. In the period in-between, it is negative and the second one is positive. Consequently, the Hessian is called a negative definite matrix. Thus, the function ${\psi }_1(p,T)$ is become a non-negative and is differentiable, and most importantly is (strictly) concave contemporaneously in connection with the decision variables p and T. Besides, as ${\psi }_2(p,T)=T$ is positive, differentiable, and convex, subsequently, the profit function Δ_ik (p, ξ, T) per unit time is pseudo-concave on selling price ‘p’ and cycle length ‘T’, and which has one maximum value. Afterward, the profit function Δ₁₃ (p, ξ, T) extends its global extreme value on the optimal point (p*, T*).

Appendix B.

Problem 4.2.1

${\mathrm{\Delta }}_{21}\left(p,\xi ,T\right)=X_{21}/T$ where $X_{21}=\left(\mathit{SR}-OC-PC-IHC-PTC-CCCP+I{E}_{21}+DIS-I{C}_{21}\right)$

$${\mathrm{\Delta }}_{21}\left(p,\xi ,T\right)=\frac{1}{T}\left[\begin{array}{c}\left[pT\left(a-bp\right)+pR-A-\xi T-\frac{C\sigma I_{\mathit{cc}}Q(n+1)L}{2n}+\frac{C\sigma JQ}{n}\right]e^{\mathit{rt}}\\ -C_1\left[\begin{array}{c}\frac{\left(e^{r{t}_1}-1\right)}{r}\left[S+\frac{\left(a-bp\right)}{r}\right]-\frac{e^{r{t}_1}{t}_1(a-bp)}{r}\\ +\frac{(a-bp)e^{\theta m\left(\xi \right)T}}{\theta m\left(\xi \right)\left[r-\theta m\left(\xi \right)\right]}\left[e^{\left[r-\theta m\left(\xi \right)\right]T}-e^{\left[r-\theta m\left(\xi \right)\right]t_1}\right]+\frac{(a-bp)}{\theta m\left(\xi \right)r}(e^{\mathit{rT}}-e^{r{t}_1})\end{array}\right]\\ -C{e}^{\mathit{rt}}\left[\left(a-bp\right)t_1+\frac{\left(a-bp\right)}{\theta m\left(\xi \right)}\left(e^{\theta m\left(\xi \right)(T-t_1)}-1\right)\right]+\frac{p\left(1-\sigma \right)I_e(a-bp)}{r}\left[T{e}^{\mathit{rT}}-\frac{1}{r}\left(e^{\mathit{rT}}-1\right)\right]\\ -C{I}_c\left[\begin{array}{c}\left(\frac{S}{r}+\frac{a-bp}{r^2}\right)\left(e^{r{t}_1}-e^{\mathit{rM}}\right)-\frac{\left(a-bp\right)}{r}\left(t_1{e}^{r{t}_1}-M{e}^{\mathit{rM}}\right)\\ +\frac{\left(a-bp\right)}{\theta m\left(\xi \right)}\left[\frac{e^{\theta m\left(\xi \right)T}}{\left[r-\theta m\left(\xi \right)\right]}\left\{e^{\left[r-\theta m\left(\xi \right)\right]T}-e^{\left[r-\theta m\left(\xi \right)\right]t_1}\right\}-\frac{1}{r}\left(e^{\mathit{rT}}-e^{r{t}_1}\right)\right]\end{array}\right]\end{array}\right]$$

Problem 4.2.2

${\mathrm{\Delta }}_{22}\left(p,\xi ,T\right)=X_{22}/T$ where $X_{22}=\left(\mathit{SR}-OC-PC-IHC-PTC-CCCP+I{E}_{22}+DIS-I{C}_{22}\right)$

$${\mathrm{\Delta }}_{22}\left(p,\xi ,T\right)=\frac{1}{T}\left[\begin{array}{c}\left[pT\left(a-bp\right)+pR-A-\xi T-\frac{C\sigma I_{\mathit{cc}}Q(n+1)L}{2n}+\frac{C\sigma JQ}{n}\right]e^{\mathit{rt}}\\ -C_1\left[\begin{array}{c}\frac{\left(e^{r{t}_1}-1\right)}{r}\left[S+\frac{\left(a-bp\right)}{r}\right]-\frac{e^{r{t}_1}{t}_1(a-bp)}{r}+\frac{(a-bp)e^{\theta m\left(\xi \right)T}}{\theta m\left(\xi \right)\left[r-\theta m\left(\xi \right)\right]}\left[e^{\left[r-\theta m\left(\xi \right)\right]T}-e^{\left[r-\theta m\left(\xi \right)\right]t_1}\right]\\ +\frac{(a-bp)}{\theta m\left(\xi \right)r}(e^{\mathit{rT}}-e^{r{t}_1})\end{array}\right]\\ -C{e}^{\mathit{rt}}\left[\left(a-bp\right)t_1+\frac{\left(a-bp\right)}{\theta m\left(\xi \right)}\left(e^{\theta m\left(\xi \right)(T-t_1)}-1\right)\right]+\frac{\left(1-\sigma \right)p{I}_e(a-bp)}{r}\left[T{e}^{\mathit{rT}}-\frac{1}{r}\left(e^{\mathit{rT}}-1\right)\right]\\ -\frac{C{I}_c\left(a-bp\right)}{\theta m\left(\xi \right)}\left[\frac{e^{\theta m\left(\xi \right)T}}{\left[r-\theta m\left(\xi \right)\right]}\left\{e^{\left[r-\theta m\left(\xi \right)\right]T}-e^{\left[r-\theta m\left(\xi \right)\right]M}\right\}+\frac{1}{r}\left(e^{\mathit{rT}}-e^{\mathit{rM}}\right)\right]\end{array}\right]$$