Epidemic and Economic Consequences of Voluntary and Request-based Lockdowns in Japan

Abstract

I examine the epidemiological and economic effects of two types of lockdowns during the COVID-19 pandemic in Japan: a voluntary lockdown by which people voluntarily stayed at home in response to the risk of infection, and a request-based lockdown by which the government requested people to stay at home without legal enforcements. I use empirical evidence on these two types of lockdowns to extend an epidemiological and economic model: the SIR-Macro model. I calibrate this extended model to Japanese data and conduct some numerical experiments. The results show that the interaction of these two types of lockdowns plays an important role in the low proportion of infectious individuals and the large decrease in consumption in Japan.

1. Introduction

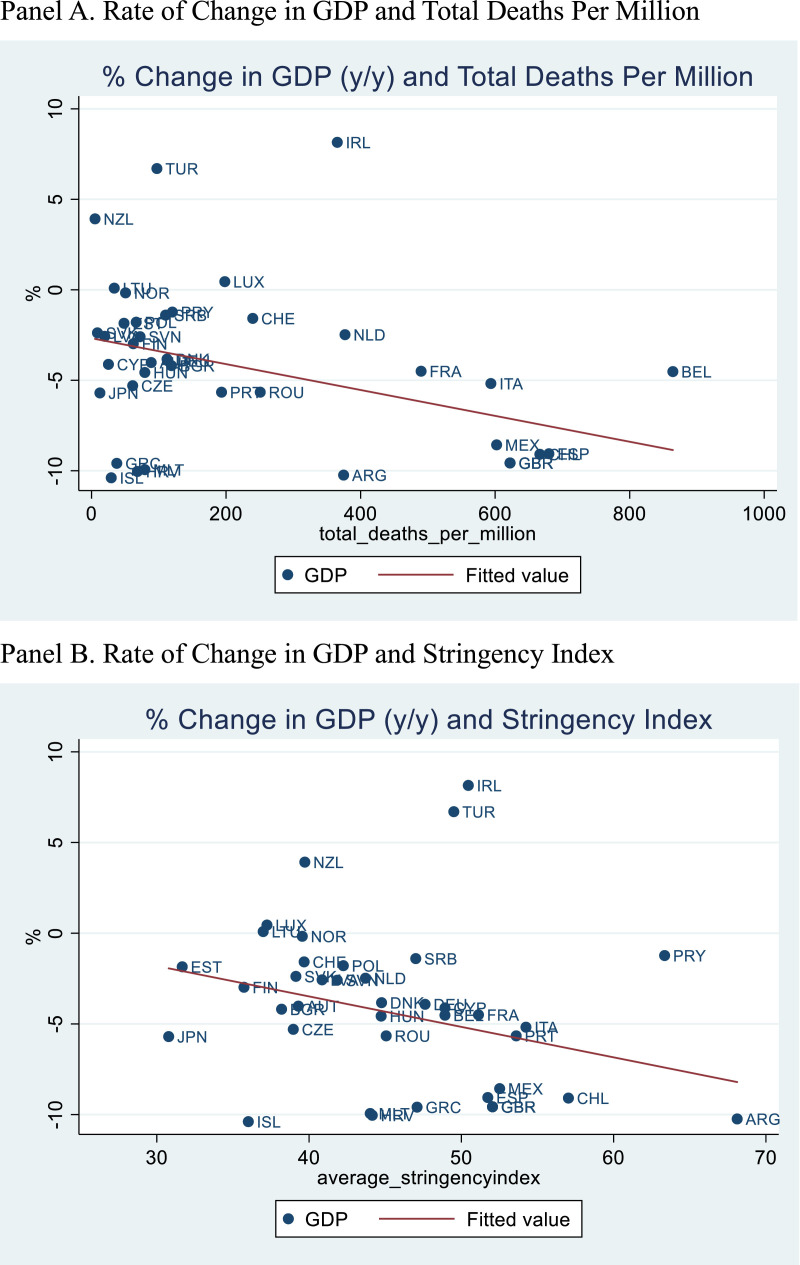
The spread of Covid-19 and non-pharmaceutical government interventions (NPIs) to contain the spread seriously damaged many economies in 2020. Panel A of Fig. 1 plots the rate of change in real GDP in the third quarter of 2020 from the previous year against the total number of deaths per million of population as of September 30.1 I use the latter as a proxy for the spread of the virus. Panel B of Fig. 1 depicts the same rate of change in real GDP against the stringency index that was averaged from January 1 to September 30.2 This index represents the strictness of lockdown-style policies that primarily restrict people's behavior. It shows that as the spread of the virus and the lockdown become severer, GDP tends to fall more. It further shows that there are large variations in the degree of the spread of the virus, the severity of the lockdown, and the decrease in GDP. In the case of Japan, the death rate was low (12.5) and the lockdown policy was loose (30.8) relative to the cross-country averages (420.7 and 51.1 for the former and the latter, respectively) while the decrease in real GDP (-5.7%) was slightly larger than the cross-country average (-4.5%).3

Fig. 1.

Rate of Change in GDP, Total Deaths Per Million, and Stringency Index. Panel A. Rate of Change in GDP and Total Deaths Per Million. Panel B. Rate of Change in GDP and Stringency Index

Notes. The rates of change in GDP are from International Financial Statistics published by International Monetary Fund and the System of National Accounts published by the Cabinet Office of Japan. They are the value in the third quarter of 2020 from the previous year. Total deaths per million are from Roser et al. (2020). They are numbers as of September 30, 2020. The stringency indexes are from Hale et al. (2020b). They are the average from January 1 to September 30, 2020. The number of countries in the sample is 42.

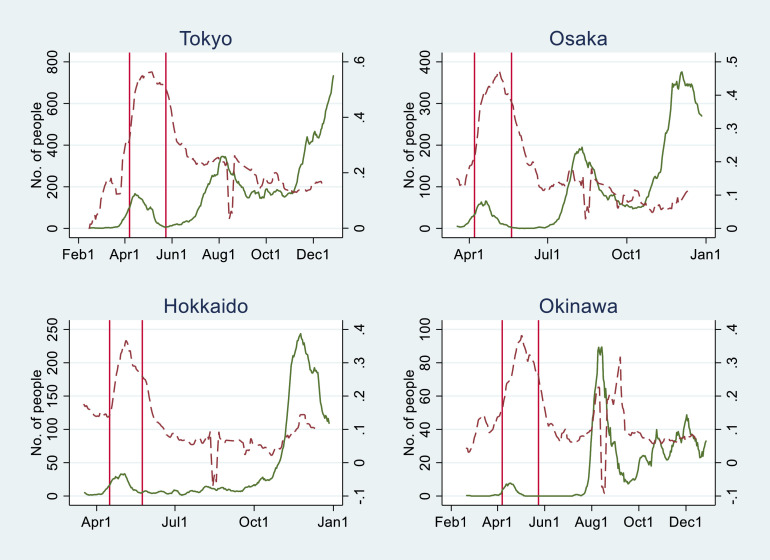
To understand such epidemiological and economic dynamics in Japan, I focus on two types of lockdowns. First, the spread of the virus made people cautious about going out. Fig. 2 shows the new cases and the stay-at-home ratios for four prefectures in Japan. Here, the stay-at-home ratio is defined as the ratio of people who stay within 500 square meters of home (Mizuno, 2020). The ratio shows that as the number of new cases increases, the stay-at-home ratio increases and that this increase is especially prominent in the first wave of Covid-19 from March to May 2020. Further, the increase is evident to some extent in the second and third waves from July to September and October to December 2020, respectively. I define a voluntary lockdown as the response of the stay-at-home ratio to an increase in the risk of infection hereafter. The presence of a voluntary lockdown can restrain the spread of new infections as the contacts between susceptible and infectious individuals are less frequent than in its absence. On the other hand, a voluntary lockdown may have adverse effects on economic activities beyond the government's behavioral restrictions, especially the consumption of goods and services that need face-to-face contact to take place.

Fig. 2.

New Cases and Stay-at-home Ratios in Four Prefectures

Note. The green solid line shows the number of new cases (left axis) and the red dashed line shows the stay-at-home ratios (%, right axis). Both series are moving averages over the past seven days. The sources of the new cases and the stay-at-home ratios are Toyo Keizai Online (2020) and Mizuno (2020), respectively.

The second type of lockdown that I focus on is the request-based lockdown that the Japanese government adopted. Although the Japanese government declared a state of emergency from April to May in 2020, it did not legally enforce or administer penalties on noncompliance with its request to stay at home.4 Thus, the government let people choose whether to go out or not. Such a request-based lockdown can have heterogeneous effects on individuals’ choice of whether to stay at home.

Voluntary and request-based lockdowns potentially affect infections and the economy during the pandemic. Moreover, they are not unique to Japan but observed in other countries.5 Nonetheless, their quantitative effects have been largely unexplored by the literature as I review in Section 2. To void this gap, I try to answer the following questions. First, do people really respond to the risk of infection in deciding whether to stay at home or not; and if so, to what extent? Second, to what extent do voluntary and request-based lockdowns, solely or interactively, constrain infections and economic activities?

To answer these questions, I first examine the existence and degree of a voluntary lockdown in Japan using daily prefecture-level data. Then, I extend an epidemiological and macroeconomic model: the SIR-Macro model that was developed by Eichenbaum, Rebelo, and Trabandt (2020) to incorporate voluntary and request- based lockdowns. In the model, susceptible individuals balance the utility from going out to consume goods that involve with the risk of infection and the disutility from the infection. Their optimization generates a feedback from the risk of infection to the voluntary lockdown, and then to the transmission rate of the virus, which, in turn, reduces the risk of infection. Moreover, the request-based lockdown decreases the utility from going out. I calibrate the model based on Japanese data and conduct some numerical experiments to examine the effects of both types of lockdowns.

My results can be summarized as follows: First, voluntary lockdowns existed in all three waves in Japan, although their degrees have declined over the three waves. Second, the interaction of these two types of lockdowns play an important role in the low proportion of infectious individuals and the large decrease in consumption in Japan.

There is a rapidly growing literature on the impacts of Covid-19 on the macroeconomy as I briefly review in Section 2. Some of them focus on the substitution from high- to low-risk consumption goods as this present study does (Farboodi, Jarosch, and Shimer, 2020; Kaplan, Moll, and Violante, 2020; Krueger, Uhlig and Xie, 2020). However, as far as I know, none of these studies focuses on the extensive margin of whether going out to purchase goods that involve the risk of infection or not. Incorporating this extensive margin has two benefits: First, I can use the actual high-frequency (i.e., daily) data about the proportion of individuals who go out to set the model's parameters. Moreover, it turns out that a voluntary lockdown can have a large negative effect on the proportion of infectious individuals with plausible parameters including the disutility from the infection and thus helps to account for their level observed in Japan.

I further contribute to the literature by incorporating a request-based lockdown and examining its epidemiological and economic effects. Request-based lockdowns are different from uniform lockdowns (examined by Eichenbaum, Rebelo, and Trabandt, 2020, among others) in that some people do not stay at home under the former. Request-based lockdowns are also different from targeted lockdowns (e.g., Acemoglu et al., 2020, among others) in that the government does not intentionally decide who stays at home under the former while the government intentionally does under the latter. Consequently, request-based lockdowns can have unique epidemiological and economic effects.

The rest of this study proceeds as follows: In Section 2, I briefly review the related literature. In Section 3, I present reduced-form evidence on the presence of a voluntary lockdown from prefecture-level daily data and its effects on the infection and consumption. In Section 4, I present the SIR-Macro model that incorporates voluntary and request-based lockdowns. In Section 5, I set the parameters. Section 6 presents numerical experiments to show the effects of voluntary and request-based lockdowns. Section 7 concludes.

2. Related Literature

Following the seminal work by Eichenbaum, Rebelo, and Trabandt (2020a), there is a growing literature on the effects of Covid-19 on economic activities. Among them, Farboodi, Jarosch, and Shimer (2020), Krueger, Uhlig and Xie (2020), Kaplan, Moll, and Violante (2020), and Aum, Lee and Shin (2020) are most closely related to the present study in that they consider people's responses to the risk of infection. Eichenbaum, Rebelo, and Trabandt (2020a) incorporate an endogenous reduction in consumption and work in response to the spread of Covid-19 in the canonical SIR model and show that such behavior decreases the proportion of infectious individuals while exacerbating the size of the recession caused by Covid-19.6 Farboodi, Jarosch, and Shimer (2020) analyze the response of social activities to the risk of infection and its effects on the transmission of the virus. Krueger, Uhlig and Xie (2020) consider heterogeneous sectors that differ in the risk of infection. Estimating the model based on Swedish health data, they show that endogenous sectoral reallocation avoids more than two-thirds of the decline in aggregate output and consumption. Kaplan, Moll, and Violante (2020) integrate an expanded SIR model into a macroeconomic model with income and wealth inequality. They also incorporate an endogenous reduction in the consumption and work that involve the risk of infection in response to an overall increase in the risk. While Kaplan, Moll, and Violante (2020) and Krueger, Uhlig and Xie (2020) analyze the sectoral shift from high- to low-risk sectors with the overall infection risk as this present study does, they consider the intensive margin of substitution of how much each type of goods to consume. In contrast, this study considers the extensive margin: whether to go out to purchase the goods with a risk of infection (“social goods”) or not. Aum, Lee and Shin (2020) build a model in which people choose occupations and whether to commute for work or to work from home. Working from home entails lower earnings due to lower productivity but curtails the risk of infection. They show that more people choose to work from home as infections rise to a high level. While they focus on the extensive margin of work, I focus on that of consumption. This is because the literature has largely left the latter unexplored, although both can play a role in the epidemiological and economic dynamics. In fact, while Brinca, Duarte, and Faria e Castro (2020) show that two-thirds of the drop in the growth rate of hours worked in April 2020 in the US was attributable to labor supply shocks, Watanabe (2020) provide evidence that the economic deterioration due to COVID-19 was largely driven by an adverse aggregate demand shock to face-to-face service industries in March 2020 in Japan.

This study is also related to the literature on the effects of various lockdown policies including overall and risk-based targeted lockdowns (Eichenbaum, Rebelo, and Trabandt, 2020a; Farboodi, Jarosch, and Shimer, 2020; Krueger, Uhlig, and Xie, 2020; Kaplan, Moll, and Violante, 2020; Kobayashi and Nutahara, 2020; Rachel, 2020; Acemoglu et al., 2020; Alvarez, Argente, and Lippi, 2020; Favero, Ichino, and Rustichini, 2020; Glover et al., 2020, among others). However, most of these studies assume that the government can coerce or induce all or targeted people to stay at home (or firms to close). In the case of the request-based lockdown that I consider, the government does not intentionally choose who follows the request, but lets people choose. Most studies have largely left the effects of such untargeted and partial characteristics of a request-based lockdown unexplored, although many countries adopt similar policies.7 I examine the epidemiological and economic effects of a request-based lockdown.

Empirical studies on the presence of a voluntary lockdown are also related to the present study. Watanabe and Yabu (2020) study the determinants of the stay-at-home ratio in Japan. They find that while the government's requests are responsible for about one quarter of the decrease in outings in Tokyo, the remaining three quarters are the result of people's voluntary response based on their awareness of the seriousness of the pandemic. Shoji et al. (2020) provide survey-based evidence that the increase in risk is associated with the likelihood of social-distancing behavior that includes infrequent dining outside. Evidence on the response of consumption to the risk of infection is not limited to Japan. Farboodi, Jarosch, and Shimer (2020) show that individuals in the US substantially reduced their social activity before state and local governments imposed the stay-at-home restrictions. Krueger, Uhlig and Xie (2020) provide evidence of the reallocation of consumption from restaurants (a typical example of goods that involves the risk of infection) to food at home in Sweden.

To focus on the roles of voluntary and request-based lockdowns, I abstract from various other important aspects that concern the relationship between the spread of the Covid-19 and economic activities that other studies focus on. These include the risk of infection at a workplace and the productivity gap between working at a workplace and from home (e.g., Aum, Lee and Shin, 2020; Jones, Philippon, and Venkateswaran, 2020), uncertainty about an individual's health status or the aggregate state of infection (e.g., Eichenbaum, Rebelo, and Trabandt, 2020b; Hamano, Katayama, and Kubota, 2020), precautionary savings against the risk of infection (e.g., Kaplan, Moll, and Violante, 2020), and heterogeneous risk of infection (.e.g., Acemoglu et al., 2020; Favero, Ichino, and Rustichini, 2020; Glover et al., 2020). These studies are all complementary to the present study in that they consider various factors other than voluntary and request-based lockdowns.

3. Reduced-form Evidence

3.1. Data

For epidemiological information, I use prefecture-level daily data compiled by Toyo Keizai Online (2020) that contain the numbers of infectious and recovered people. To derive the ratio of these people to the total prefectural population, I use the prefecture-level population as of October 1, 2019, from the Population Estimates published by the Bureau of Statistics, Japan.

Following a standard SIR model, I use these data to classify people in prefecture $i$ at date $t$ into three categories that depend on their health status: susceptible ($S$), infectious ($I$), and recovered ($R$). Then, I denote the ratio of the number of each category to the total population of the prefecture by $S_{it}$, $I_{it}$, and $R_{it}$, respectively; so that $S_{it}+I_{it}+R_{it}=1$.

Using the number of infectious people, I estimate the effective reproduction number ($E{R}_{it}$) for each prefecture by following Cori et al. (2013). I assume that the mean and standard deviation of the serial interval is 6.3 and 4.2 days, respectively, that follows Bi et al. (2020) and Yamanaka (2020). To exclude outliers, I take the following two steps: First, I drop $E{R}_{it}$ if $I_{is}=0$ for $s=-14,\dots -8$, because in such cases $E{R}_{it}$ has extraordinarily large values (typically, more than 10). Then, I drop $E{R}_{it}$ that is equal to or larger than its 99th percentile for each prefecture. From the estimated $E{R}_{it}$, I further construct the transmission rate, ${\beta }_{it}=\gamma E{R}_{it}/S_{it}$, by assuming that the recovery rate $\gamma =1/7$ as in Moll (2020).

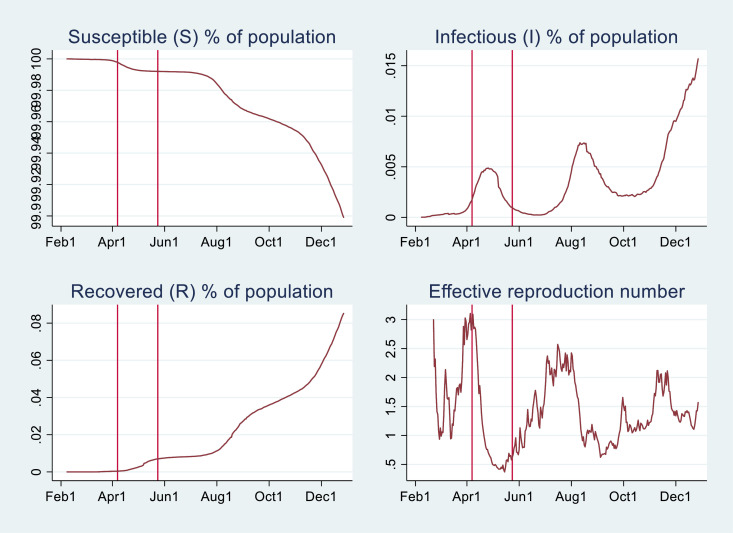
The sample period for the daily data of the epidemiological numbers runs from March 11 to December 27, 2020, for the prefectures other than Tokyo and Kanagawa; for these two prefectures, it runs from February 8 to December 27, 2020. Fig. 3 shows the average values of $S_{it}$, $I_{it}$, $R_{it}$, and $E{R}_{it}$ across the 47 prefectures. It clearly shows that Japan experienced three waves in 2020. I define the first wave as the period from February 8 to May 31, the second from July 1 to September 30, and the third from October to December 27. I exclude the period from June 1 to June 31 from any wave because there were few new cases in many prefectures that month. Moreover, the third wave was still ongoing at the end of the sample period, December 27.

Fig. 3.

Epidemiological Dynamics in Japan.

Note. The graphs show the simple averages across 47 prefectures in Japan. The effective reproduction number is the author's estimates following Cori et al., (2013). The vertical lines show the period of the state of emergency in Tokyo.

For the information on the ratio of the people who stayed at home, I use the data provided by Mizuno (2020). Using the information on the real-time population distribution that is estimated from about 78 million base stations of a major telecom company in Japan, DOCOMO, he estimates the number of outgoing people from residential areas that are defined as the difference between the daytime and nighttime population. Then he defines the stay-at-home ratio, $Sta{y}_{it}$, for prefecture $i$ on day $t$ as follows:

$$Sta{y}_{it}=1-\frac{\#ofoutgoingpeopl{e}_{it}\times averageoutoginghour{s}_{it}}{\#ofoutgoingpeopl{e}_{i0}\times averageoutoginghour{s}_{i0}}$$

Here, the 0 denotes the average of the pre-pandemic period from January 6 to January 31, 2020. “Outgoing” is defined as going outside of the 500 square meter mesh where the person's house exists. Thus, for example, if $Sta{y}_{it}$ is 60%, it means that 60% of the people stayed at home (or within the 500 square meters of the home). Please refer to Mizuno, Ohnishi, and Watanabe (2020) for details. Table 1 shows the descriptive statistics of the daily data that I use for each wave.

Table 1.

Descriptive Statistics.

Panel A. First Wave: March 11, 2020–May 31, 2020.
VARIABLES	N	mean	p50	sd	min	max
Effecitve reproduction number (ERt)	100	1.395	1.151	0.854	0.371	3.106
Transmission rate (beta)	100	0.199	0.164	0.122	0.053	0.444
Infectious (I, % of population)	114	0.00161	0.000758	0.00168	1.62E-05	0.0049
Infectious (I, day when maximum reached)						(49)
Susceptible (S, % of population)	114	100	100	0.00331	99.99	100
Recovered (R, % of population)	114	0.00181	0.000376	0.00253	0	0.00739
Stay at home ratio (Stay)	114	0.2	0.181	0.12	-0.0213	0.511
Stay at home ratio (Stay, moving average)	108	0.204	0.187	0.106	0.00898	0.407
Panel B. Second Wave: July 1, 2020–September 31, 2020.
VARIABLES	N	mean	p50	sd	min	max
Effecitve reproduction number (ERt)	92	1.465	1.148	0.634	0.624	2.571
Transmission rate (beta)	92	0.209	0.164	0.0905	0.0892	0.367
Infectious (I, % of population)	92	0.00358	0.00303	0.0022	0.000303	0.0074	1.512295	########	41
Infectious (I, day when maximum reached)						(41)
Susceptible (S, % of population)	92	99.98	99.97	0.0106	99.96	99.99
Recovered (R, % of population)	92	0.0199	0.0177	0.01	0.00826	0.0357
Stay at home ratio (Stay)	90	0.127	0.11	0.0704	-0.234	0.331
Stay at home ratio (Stay, moving average)	84	0.128	0.129	0.0198	0.0856	0.185
Panel C. Third Wave: October 1, 2020–December 27, 2020.
VARIABLES	N	mean	p50	sd	min	max
Effecitve reproduction number (ERt)	88	1.407	1.335	0.298	1.046	2.121
Transmission rate (beta)	88	0.201	0.191	0.0426	0.15	0.303
Infectious (I, % of population)	88	0.00663	0.00511	0.00443	0.00206	0.016
Susceptible (S, % of population)	88	99.94	99.95	0.0185	99.9	99.96
Recovered (R, % of population)	88	0.0519	0.0466	0.0142	0.036	0.0852
Stay at home ratio (Stay)	77	0.0885	0.0736	0.0349	0.0533	0.184
Stay at home ratio (Stay, moving average)	77	0.0888	0.0897	0.0107	0.0697	0.11

Notes. The table shows the descriptive statistics of the average numbers across 47 prefectures. For Tokyo and Kanagawa Prefectures, the first wave began on February 8, 2020. The effective reproduction number is estimated following Cori et al. (2013) and the transmission rate is estimated by${\beta }_{it}=\gamma E{R}_{it}/S_{it}$ that assumes that the recovery rate is $\gamma =1/7$ as in Moll (2020). The peak days of the infectious ratios are April 29, 2020 (49 days from March 11) and August 11, 2020 (41 days from October 1) for the first and second waves, respectively. $(I_{it},S_{it},R_{it}$) are estimated using data from Toyo Keizai Online (2020), and $Sta{y}_t$ is from Mizuno (2020).

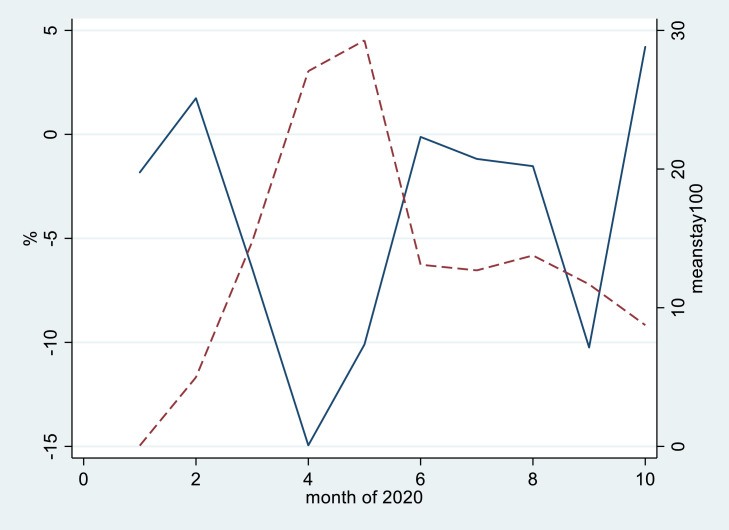
For the information on consumption, I use prefecture-level monthly data on the sales of extant department stores and supermarkets from the Monthly Report on the Current Survey of Commerce published by the Ministry of Economy, Trade, and Industry. The sample period for the monthly sales data runs from January to October 2020. Fig. 4 shows the year-on-year changes in sales and the moving average of stay-at-home ratios from January to October in 2020. They apparently move in the opposite direction.

Fig. 4.

Year-on-year Changes (%) in Sales at Department Stores and Supermarkets and Stay-at-home Ratios (%) in 2020.

Note. The blue solid line shows year-on-year changes in sales at department stores and supermarkets (%, left axis), and the red dashed line shows stay-at-home ratios (%, right axis) in 2020. Both series are simple averages across prefectures for each month. The source of year-on-year changes in sales at department stores and supermarkets is the Monthly Report on the Current Survey of Commerce published by the Ministry of Economy, Trade, and Industry and that of the stay-at-home ratios is from Mizuno (2020).

3.2. Regression results

I first examine whether the stay-at-home ratio depends on the risk of infection, ${\pi }_{it}$, that I define as the ratio of new cases to the number of susceptible people: ${\pi }_{it}=-\left(S_{it}-S_{it-1}\right)/S_{it-1}$. Specifically, I run the following fixed-effect panel regression:

$$Sta{y}_{it}=b_1{\pi }_{it-1}+b_{2}E{M}_{it}+Weekda{y}_t+f_i+{\epsilon }_{it}$$ (1)

Here, $E{M}_{it}$ denotes a dummy for the period of the state-of-emergency for prefecture $i$, $Weekda{y}_t$ is a set of dummies for Monday through Saturday, $f_i$ is a prefecture-level fixed effect, and ${\epsilon }_{it}$ is an error term. I run the regression above for each wave to consider the possibility that people's responses to the risk of infection change over the three waves. $E{M}_{it}$ is included in the regression only for the first wave because the state of emergency was declared only for that wave during my sample period.8 In the second wave, I add the summer vacation dummy that equals one for August 12 to 14.

The results shown in Columns (1) to (3) in Panel A of Table 2 provide clear evidence for the voluntary lockdown. They show that the coefficients for ${\pi }_{it-1}$ are positive and significant for all three waves that indicates that people were more likely to stay at home as the risk of infection increased. The coefficients for ${\pi }_{it}$ are the largest for the first wave (9,151), followed by the second and third waves (2,269 and 1,000, respectively). For example, an increase in new cases by 1 in 100,000 susceptible people increases the stay-at-home ratio by $9.151\%\left(=9,151\times 1/100,000\times 100\right)$ in the first wave.

Table 2.

Regression Results

Panel A. Stay-at-home Ratio
Stayhome Ratio
Wave	1st wave	2nd wave	3rd wave
Infection Risk	9,151***	2,269***	1,000***
	(11.80)	(9.140)	(10.19)
Emergency Dummy	0.140***
	(59.19)
Summer Vacation Dummy		-0.197***
		(-35.09)
Weekday dummies	yes	yes	yes
Observations	3,568	4,230	3,619
R-squared	0.658	0.44	0.451
Number of prefectures	47	47	47
model	FE	FE	FE
t-statistics in parentheses
*** p<0.01, ** p<0.05, * p<0.1
Panel B. Transmission Rate (${\beta }_t$)
Stay(t-7)	-0.213***
	(-7.803)
Wave1xTime	-0.00298***
	(-13.50)
Wave2xTIme	-0.00294***
	(-27.79)
Wave3xTime	0.00034***
	(3.20)
Wave1	65.65***
	(13.52)
Wave2	65.01***
	(27.79)
Wave3	-7.492***
	(-3.200)
Emergency Dummy (t-7)	-0.108***
	(-13.04)
Summer Vacation Dummy (t-7)	-0.0894***
	(-6.147)
Weekday dummies	yes
Observations	9,548
R-squared	0.185
Number of prefectures	47
Model	FE
t-statistics in parentheses
*** p<0.01, ** p<0.05, * p<0.1
Panel C. Year-on-year Change in Sales at Department Stores and Supermarkets
Stay	-0.228***
	(-4.519)
EM	-0.133***
	(-6.224)
Constant	0.00416
	(0.721)
Observations	470
R-squared	0.45
Number of prefectures	47
Prefecture FE	Yes

t-statistics in parentheses

*** p<0.01, ** p<0.05, * p<0.1

Next, I examine whether an increase in the stay-at-home ratio contributes to containing the spread of the virus by regressing the transmission rate on the stay-at-home ratio with the data for the whole sample period as follows:

$${\beta }_{it}=c_{1}Sta{y}_{it-7}+c_{2j}Wav{e}_j+c_{3j}Wav{e}_j\times Tim{e}_t+c_{4}E{M}_{it-7}+Weekda{y}_t+f_i+{\epsilon }_{it}$$ (2)

I take the 7-day lag of $Stay$ to consider the incubation, detection, and reporting periods. I add the three wave dummies ($Wav{e}_j$), time trend ($Tim{e}_t$), and their interaction to the explanatory variables to consider the gradual behavioral changes such as wearing a mask, social distancing, and washing hands.

Panel B of Table 2 shows that the coefficient for $Sta{y}_{it-7}$ is negative and significant. An increase in $Sta{y}_{it}$ by one percentage point decreases ${\beta }_{it}$ by 0.213 percentage points. The coefficients for the interaction of $Wave$ and $Time$ are negative for the first and second waves. This sign indicates that people gradually learned the best practices to avoid the infection. On the other hand, the coefficient for the interaction for the third wave is positive, although small. This positive sign may be because the rate of infection kept rising during the observation period of the third wave.

Third, I investigate the effect of staying at home on the rate of change in consumption from the previous year using the monthly data of sales at department stores and supermarkets, $Sale{s}_{it}$. Specifically, I run the following fixed-effect regression:

$$Sale{s}_{im}=a_{1}Sta{y}_{im}+a_{2}E{M}_{im}+f_i+{\epsilon }_{im}$$ (3)

Here, subscript $m$ denotes the month, and $Sta{y}_{im}$ and $E{M}_{im}$ are monthly averages of the daily variables, $Sta{y}_{it}$ and $E{M}_{it}$, respectively. Panel C of Table 2 shows that the coefficient for $Sta{y}_{im}$ is negative and significant. An increase in $Sta{y}_{im}$ by one percentage point decreases $Sale{s}_{im}$ by 0.228 percentage points. The coefficient for $E{M}_{im}$ is also negative and significant that indicates the request by the government to close stores had a direct and negative impact on sales after controlling for the stay-at-home ratio.

4. Model

The reduced-form evidence shows that people were more likely to stay at home as the risk of infection rose and that this voluntary lockdown mitigated the spread of the virus and decreased consumption. I formalize this idea by extending an epidemiological and macroeconomic model (SIR-Macro model) to incorporate voluntary and request-based lockdowns. First, I present a model with only a voluntary lockdown and then add a request-based lockdown.

4.1. Setup

Goods

Following Kaplan, Moll, and Violante (2020), I assume that there are three types of goods: social goods (type s) produced by firms and consumed outside of the home, regular goods (type r) produced by firms and consumed at home, and home goods (type h) produced by individuals and consumed at home. Only social goods involve the risk of infection. Both social and regular goods are sold in markets, while home goods are not. Typical examples of social, regular, and home goods are restaurants, food, and home cooking, respectively.

Firms

There is a continuum of competitive and representative firms of a sufficiently large mass that potentially produce either type s or r goods. For each type of s and r goods, a representative firm produces one unit of goods with one unit of labor. Profit maximization of each type of firm leads to the prices of type r and s goods equal to the wage rate, which I normalize to one.

Individuals

There is a continuum of competitive individuals of unit measure. Individuals are classified into three groups according to their health status: susceptible (S), infectious (I), and recovered (R).

Following the SIR model, I assume the following system of difference equations:

$$S_{t+1}=S_t-{\beta }_t{S}_t{I}_t$$ (4)

$$I_{t+1}=I_t+{\beta }_t{S}_t{I}_t-\gamma I_t$$ (5)

$$R_{t+1}=R_t+\gamma I_t$$ (6)

For simplicity, I assume no death, so that the population does not change. The parameters ${\beta }_t$ and $\gamma$ denote the transmission rate and the recovery rate, respectively. While a simple SIR model assumes that ${\beta }_t$ is constant over time, I make it endogenous and time-variant by incorporating the individuals’ behavior as in the following:

An individual is endowed with one unit of time. They can produce one unit of type h goods for their own consumption using one unit of time. Thus, the opportunity cost of consuming one unit of home goods is equal to the wage rate, that is, one.

Individuals are heterogeneous in their preference for or disutility from going out, which I denote by $\epsilon$. The $\epsilon$ is distributed according to the cumulative density function, $F\left(\epsilon \right).$ Further, $\epsilon$ can take negative values that represent disutility. Type-$\epsilon$ individual's lifetime utility is:

$$E_1\sum _{t=1}^{\infty }{\left(1-\rho \right)}^{t-1}u\left(C_{st},C_{rt},C_{ht},H_t;\epsilon \right)$$

Here, $u\left(C_{st},C_{rt},C_{ht},H_t;\epsilon \right)$ is the period utility of type-$\epsilon$ individual that depends on the consumption of social goods ($C_{st}$), regular goods ($C_{rt}$), and home goods ($C_{ht}$), their health status ($H_t$), and their time-invariant preference for going out ($\epsilon$). Health status, $H_t$, represents the status of being either susceptible ($S$), infectious ($I$), or recovered ($R$). Following Eichenbaum, Rebelo, and Trabandt (2020a), I assume that there is no way for agents to pool the risk associated with infection. Therefore, they maximize their lifetime utility under the temporal budget constraint:

$$C_{St}+C_{Rt}+C_{Ht}=1.$$ (7)

To derive budget constraint (7), I use the equilibrium conditions that the prices of all goods are equal to the wage rate of one. I specify the period utility as

$$u\left(C_{st},C_{rt},C_{ht},H_t;\epsilon \right)=v\left(C_{st},C_{rt},C_{ht}\right)+\epsilon \mathit{1}\left(C_{st}>0\right)-D\mathit{1}\left(H_t=I\right).$$ (8)

Here, $D>0$ denotes the disutility from the infection, and $\mathbf{1}(·)$ denotes an indicator function that equals one if the conditions in the parentheses are met. $v\left(·,·,·\right)$ is a well-behaved utility function from the consumption mix of $\left(C_{st},C_{rt},C_{ht}\right)$. Individuals go out and get $\epsilon$ (or incur $-\epsilon$) if and only if they consume type-s goods.

A fraction $\eta$ of infectious individuals are isolated and not allowed to consume type-s goods. The parameter $\eta$ is a measure of the effectiveness of the test-trace-isolation. Susceptible individuals take the risk of infection as given. Below I let ${\pi }_t=-\left(S_{t+1}-S_t\right)/S_t$denote the risk of infection for susceptible individuals when they go out and consume type-s goods.

4.2. Optimization of individuals

I solve for the maximization of individuals in each health status in Appendix 1. The essential part of the optimization is that of susceptible individuals, which can be summarized as

$$\begin{array}{c}\hfill (C_s,C_r,C_h)=\{\begin{array}{cc}(c_s^{*},c_r^{*},c_h^{*}),\hfill & \mathit{if}\epsilon >{\alpha }_0+{\alpha }_{1t}\left(\epsilon \right){\pi }_t\hfill \\ (0,{\overline{c}}_r,{\overline{c}}_h)\hfill & \mathit{otherwewise}\hfill \end{array}\end{array}$$ (9)

Here, $c_s^{*}$ is a positive constant, ${\alpha }_0=\overline{v}-v^{*}$, and ${\alpha }_{1t}\left(\epsilon \right)=\left(1-\rho \right)\left(V_{t+1}^S\left(\epsilon \right)-V^I\left(\epsilon \right)\right)$, where $v^{*}=v\left(c_s^{*},c_r^{*},c_h^{*}\right)$, $\overline{v}=v\left(0,{\overline{c}}_r,{\overline{c}}_h\right)$, and $V_{t+1}^S\left(\epsilon \right)$ and $V^I\left(\epsilon \right)$ are the expected life-time utilities of type-$\epsilon$ susceptible and infectious individuals, respectively.9 Importantly, $V^I\left(\epsilon \right)$, and hence ${\alpha }_{1t}\left(\epsilon \right)$, depends on $D$. Equation (9) shows that whether a susceptible individual goes out to consume type-s goods or not depends on the risk of infection, ${\pi }_t$. It further shows that as the disutility from the infection, $D$, is larger, his response to the risk of infection, ${\alpha }_{1t}\left(\epsilon \right)$, is also larger.

4.3. Equilibrium

In equilibrium, (1) each person solves their maximization problem given the risk of infection, (2) the goods and labor markets clear, and (3) the risk of infection that individuals take as given is consistent with the risk of infection that is derived from the aggregation of individual behaviors. I have already incorporated the equilibrium prices into budget constraint (7). Here I describe how aggregate output of market goods and the risk of infection evolves.

Let $Sta{y}_t$ denote the proportion of individuals who stay at home. $Sta{y}_t$ is composed of the susceptible individuals who choose $\left(0,{\overline{c}}_r,{\overline{c}}_h\right)$ at period $t$ and isolated infectious individuals. Therefore, denoting the ratio of susceptible individuals who stay at home by $p_t$, $Sta{y}_t$ can be written as:

$$Sta{y}_t=p_t{S}_t+\eta I_t$$ (10)

It is noteworthy that $p_t$ depends on ${\pi }_t$ as Equation (9) indicates. The aggregate output of market goods, $Y_t$, is equal to the aggregate consumption of market goods, which is the sum of social and regular goods:

$$Y_t=C_t=\left(1-Sta{y}_t\right)(c_s^{*}+c_r^{*})+Sta{y}_t{\overline{c}}_r=(c_s^{*}+c_r^{*})+\left({\overline{c}}_r-c_s^{*}-c_r^{*}\right)Sta{y}_t$$ (11)

The transmission rate, ${\beta }_t$, represents the ratio of susceptible individuals that an infectious individual infects over a unit of time (i.e., a day). It depends on the multiple of the share of susceptible individuals who go out and the share of infectious individuals who are not isolated. Furthermore, following Kaplan, Moll, and Violante (2020), I assume that individuals gradually change their behavior to avoid being infected such as wearing face masks at an exogenous rate over time as represented by $\omega \left(t\right)$. In sum,

$${\beta }_t=\text{max}\left\{\overline{\beta }\left(1-p_t\right)\left(1-\eta \right)-\omega \left(t\right),0\right\}$$ (12)

Here,$\overline{\beta }$ is the basic transmission rate. I impose the nonnegativity condition on ${\beta }_t$. Substituting Equation (12) into Equations (4)-(6) yields the dynamics of $S_t$ that in turn, yields ${\pi }_t=1-S_{t+1}/S_t$. In Appendix 2, I describe my algorithm for computing the equilibrium.

Equation (12) indicates that ${\beta }_t$ depends on $p_t$, which, in turn, depends on ${\pi }_t$. This generates a feedback from the risk of infection to the voluntary lockdown, and then to the transmission rate, which, in turn, reduces the risk of infection as Equation (5) indicates. Such a feedback occurs because the ratio of susceptible individuals who stay at home, $p_t$, is endogenously determined by their optimization to balance the utility from consuming type-$s$ goods and the disutility from the infection.

4.4. Request-based lockdown

I extend the basic model above by supposing that the government declares the state of emergency under which it requests people to stay at home during some span of time: from $lstart$ to $lend$. I model this request as a change in the susceptible households’ preference for going out. Specifically, susceptible individuals incur utility losses, $l$, when they go out during the state of emergency. The utility losses associated with the state of emergency reflects the sense of guilt for disobeying the government's request or social norms, and the peer effects from neighbors on staying at home. These utility losses may vary across individuals and over time. However, for the sake of analytical simplicity, we assume that the utility losses are common across individuals and constant over time.

A susceptible individual's optimization, which is described in Appendix 1, leads to

$$\begin{array}{c}\hfill (C_s,C_r,C_h)=\{\begin{array}{cc}(c_s^{*},c_r^{*},c_h^{*}),\hfill & \mathit{if}\epsilon >l_t+{\alpha }_0+{\alpha }_{1t}\left(\epsilon \right){\pi }_t\hfill \\ (0,{\overline{c}}_r,{\overline{c}}_h),\hfill & \mathit{otherwewise}\hfill \end{array}\end{array}$$ (13)

Here,

$$l_t=\{\begin{array}{cc}l,\hfill & \mathit{for}\mathit{lstart}\le t\le \mathit{lend}\hfill \\ 0,\hfill & \mathit{otherwise}\hfill \end{array}$$

Consequently, the ratio of susceptible individuals who stay at home depends on the intensity of the request-based lockdown, $l$. As $l$ is higher, the more susceptible individuals stay at home. Denoting the ratio of susceptible individuals who stay at home by $p_t^{\prime }$, $Sta{y}_t$ and ${\beta }_t$ with the request-based lockdown are the following:

$$Sta{y}_t=p_t^{\prime }{S}_t+\eta I_t$$ (14)

and

$${\beta }_t=\text{max}\left\{\overline{\beta }\left(1-p_t^{\prime }\right)\left(1-\eta \right)-\omega \left(t\right),0\right\}$$ (15)

The aggregate output and consumption of market goods are given by Equation (11).

4.5. Specification

I need to specify the functions $v\left(C_{st},C_{rt},C_{ht}\right)$, $F\left(\epsilon \right)$, and $\omega \left(t\right)$. First, I specify the period utility function from consumption, $v\left(C_{st},C_{rt},C_{ht}\right)$, as the following nested CES function:

$$v\left(C_{st},C_{rt},C_{ht}\right)={\left({({\theta }_h{C}_{ht}^{\sigma }+(1-{\theta }_h)C_{st}^{\sigma })}^{\frac{\psi }{\sigma }}+{\theta }_r{C}_{rt}^{\psi }\right)}^{\frac{1}{\psi }},\sigma ,\psi \le 1$$ (16)

Next, I specify $F\left(\epsilon \right)$ as the uniform distribution over $\left[b,b+1\right]$. Further, considering that the measured stay-at-home ratio is the change from the pre-epidemic period, I impose the restriction that the ratio of susceptible people who stay at home is zero if and only if ${\pi }_t=0$ and $l_t=0$. Thus, from Equation (13), I set $b=\overline{v}-v^{*}.$

Third, I specify the learning curve $\omega \left(t\right)$ as the following logistic curve as in Griliches (1957) and Kaplan, Moll, and Violante (2020):

$$\omega \left(t\right)=\frac{{\omega }_1\overline{\beta }}{e^{-\chi \left(t-t_0\right)}+1}$$ (17)

This specification indicates that ${\beta }_t$ eventually decreases by ${\omega }_1\times 100$%.

5. Parameterization

The unit of time is a day. To set the epidemiological parameters, I follow Moll (2020). Specifically, I set the basic reproduction number to 2.5 and the duration of the infection period to 7. These two numbers lead to $\overline{\beta }=2.5/7$ and $\gamma =1/7$. The initial conditions of $\left(S_t,I_t,R_t\right)$ are set to the average values of March 11, 2020, across prefectures in Japan.

To set the economic parameters, I first set the discount rate to $\rho =0.05/365$. Next, I set the elasticity of substitution among the three types of goods. Aguiar and Hurst (2007) estimate an elasticity of substitution between time and goods in home production at roughly 1.8. Based on this evidence, Kaplan, Moll, and Violante (2020) set the elasticity of substitution between social and home goods to 2. Following them, I set $1/\left(1-\sigma \right)=2$ that leads to $\sigma =0.5$. I set the elasticity of substitution between social and home goods and regular goods as close to one (i.e., Cobb-Douglas). Specifically, I set $\psi =0.1$.

I set the share parameters ${\theta }_h$ and ${\theta }_r$ based on the share of each type of goods. According to the 2016 Survey on Time Use and Leisure Activities published by the Statistics Bureau of Japan, the time spent on housework, caring or nursing, childcare, and shopping is 107 minutes per day, while the time spent on the secondary activities is 418 minutes per day.10 I take the ratio of the former to the latter to set the target of $c_h=0.32$. To determine the share of social goods, I rely on the 2019 Family Income and Expenditure Survey published by the Statistics Bureau of Japan. According to the survey, the share of services excluding utilities, communication, and rents to total goods and services is 0.26 for all households. Thus, I set the target to $c_s/\left(c_s+c_r\right)=0.26$. These two restrictions lead to ${\theta }_h=0.57$ and ${\theta }_r=0.95$.

Using these numbers, I calculate the rate of change in aggregate consumption of market goods in response to an increase in the stay-at-home ratio by one point, ${\overline{c}}_r/\left(c_s^{*}+c_r^{*}\right)-1$, that is based on Equation (11), to be -0.244. This is comparable to the regression coefficient for$Sta{y}_{mt}$ in Equation (3) (-0.238).

For the disutility from infection, $D$, I use the regression results from Equation (1).11 Specifically, I assume that ${\alpha }_{1t}\left(\epsilon \right)=\left(1-\rho \right)\left(V_{t+1}^S\left(\epsilon \right)-V^I\left(\epsilon \right)\right)\approx b_1$ holds for the individual with the mean $\epsilon$, that is, $\overline{\epsilon }=\overline{v}-v^{*}+0.5$. To use this relationship, I approximate $V_{t+1}^S$ as the value in the pre-and post-epidemic steady states where ${\pi }_t=0$. That is, $V_{t+1}^S\left(\overline{\epsilon }\right)\approx \left(v^{*}+\overline{\epsilon }\right)/\rho$, where $v^{*}$ is the period utility from $\left(c_s^{*},c_r^{*},c_h^{*}\right)$. Then, using this approximation, I obtain:

$$\left(1-\rho \right)\left(\frac{v^{*}+\overline{\epsilon }}{\rho }-V^I\left(\overline{\epsilon }\right)\right)=b_1$$

Substituting $\overline{\epsilon }$ into $V^I\left(\epsilon \right)$ (Equation (A4) in Appendix 1) and rearranging yield $D=\eta \left(\overline{v}-v^{*}-\overline{\epsilon }\right)+\left(\rho +\gamma -\rho \gamma \right)/\left(1-\rho \right)b_1$. Then, depending on the estimates of $b_1$ for the first, second, and third waves, I obtain three different values for $D$. I use the largest one obtained from the estimate of the first wave to obtain $D=1308.3$ as the baseline and use the other two ($D=$324.3 and 142.8) to check the sensitivity of the baseline results. The baseline, middle, and low values of $D$ correspond to 5.8, 1.4, and 0.6 times, respectively, the period utility of the susceptible individual with mean $\epsilon$ in the pre- and post-pandemic steady states (that is, $v^{*}+\overline{\epsilon }=227.5$). I further compute the no voluntary lockdown case by setting $D=0$. In this case, infectious individuals incur utility losses only from the insulation, under which they cannot consume social goods consumption. Therefore, susceptible individuals’ response to the risk of infection is quite small.12

To set the parameters ${\omega }_1,\chi ,$ and $t_0$ in Equation (17), I follow Kaplan, Moll, and Violante (2020). Specifically, I set $\chi =2/30$, ${\omega }_1=0.2$, and $t_0=120$.

To set the proportion of isolation among infectious individuals, $\eta$, I use the regression result for Equation (2). Specifically, because $S_t\approx 1$ and $I_t\approx 0$, Equations (2) and (15) lead to $\frac{\partial {\beta }_t}{\partial Sta{y}_t}\approx \frac{\partial {\beta }_t}{\partial p_t^{\prime }}=-\overline{\beta }\left(1-\eta \right)=c_1$.13 Substituting the estimated coefficient for $c_1$ and $\overline{\beta }=2.5/7$ yields $\eta =0.4036.$

Finally, to set the severity of the request-based lockdown, $l$, I use the estimated coefficient for $E{M}_{it}$ in the regression of Equation (1). Specifically, I set the lockdown severity to $l=0.323$ so that the difference in the peak levels of the simulated stay-at-home ratios between with and without the request-based lockdown is equal to the coefficient (0.14). For the sake of the sensitivity analysis, I alternatively set $l=0.108$ that is one third of the baseline value. I set the start and end dates of the request-based lockdown following the state-of-emergency during the first wave in Tokyo (from April 7 to May 24, 2020, which correspond to $lstart=27$ and $lend=27+47)$. Table 3 has a summary of the parameters.

Table 3.

Parameters

Epidemiological
Basic transmission rate	betabar	2.5/7	Moll (2020): Basic reproduction number =2.5; average duration of infectious period=7
Recovery rate	gamma	1/7	Moll (2020): Average duration of infectious period=7
Initial (S, I, R)	S1	0.9999968	Average value across prefectures as of March 11, 2020.
	I1	2.909*10-6	Average value across prefectures as of March 11, 2020.
	R1	0	Average value across prefectures as of March 11, 2020.
Countermeasures
Share of isolation of infectious	eta	0.4036	Coefficient of Stay in the regression of estimated beta
Requeset-based Lockdown (baseline: strong)	l	0.323	Coefficient of state-of-emergency dummy in the regression of Stay for 1st wave
Requeset-based Lockdown (weak)	l	0.108	one-third of the baseline
Lockdown Start	lstart	27	Start of the state of emergency in Tokyo (April 7, 2020) from day 1 (March 11, 2020)
Lockdown End	lend	27+47	End of the state of emergency in Tokyo (May 24, 2020) from day 1 (March 11, 2020)
Behavioral
Learning speed	chi	2/30	Kaplan, Moll and Violante (2020)
Upper bound of learning/basic transmission rate	omega1	0.2	Kaplan, Moll and Violante (2020)
Days at which learning srart	t0	120	Kaplan, Moll and Violante (2020)
Preference
Discount rate (per day)	rho	0.05/365
Elasticity of substitution between social and home goods	1/(1-sigma)	2	Kaplan, Moll and Violante (2020)
Elasticity of substitution between social/home and regular goods	1/(1-psi)	1/0.9	Close to Cobb-Douglas
Share of home good in total consmption	ch	0.32	Share of time spent on housework, caring or nursing, child care and shopping
Share of social goods in sum of social and regular goods	cs/(cs+cr)	0.26	Share of services excluding utilities, communication, and rents
→Share paramter of home goods in social/home aggregate	theta_h	0.57
→Share paramter of regular goods relative to social/home goods	theta_r	0.95
Disutility of infection (baseline: high)	D	1308.3	Coefficient of infection risk in the regression of the stay-at-home ratio for 1st wave
Disutility of infection (middle)	D	324.3	Coefficient of infection risk in the regression of the stay-at-home ratio for 2nd wave
Disutility of infection (small)	D	142.8	Coefficient of infection risk in the regression of the stay-at-home ratio for 3rd wave

6. Numerical Experiments

6.1. Voluntary and Request-based Lockdowns

First, I examine the effects of voluntary and request-based lockdowns separately. Fig. 5 illustrates the epidemiological and economic dynamics in the case where only the voluntary lockdown in considered.14 It shows that the risk of infection (${\pi }_t$) and the stay-at-home ratio ($Sta{y}_t$) closely comove with each other. Below I focus on the proportion of infectious individuals, $I_t$, and the rate of change in consumption, $C_t$. Table 4 has a summary of all the results for the numerical experiments.

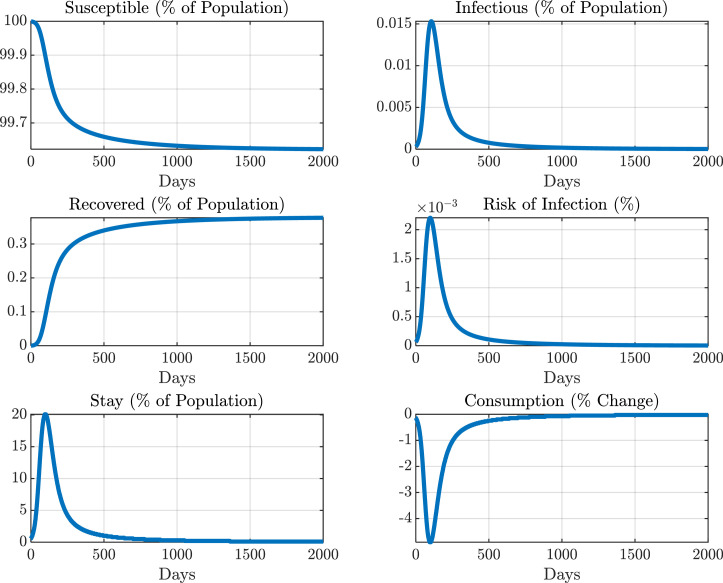
Fig. 5.

Epidemiological and Economic Dynamics with the Voluntary Lockdown

These figues show the eepidemiological and economic dynamics with only the voluntary lockdown (Case 3 in Table 4).

Table 4.

Summary of Numerical Experiments

Case	Lockdown		Infectious			Stay at home	Consumption
	Voluntary	Requested	Peak	Peak	Peak relative	Peak	Bottom
			(%)	Day	to Case 1 (%)	(%)	(% Change)
A. Baseline
Case 1	no	no	0.543	179	100.0%	0.3	-0.1
Case 2	no	yes	0.033	225	6.0%	32.3	-7.9
Case 3	yes	no	0.015	107	2.8%	20.1	-4.9
Case 4	yes	yes	0.007	150	1.2%	34.2	-8.4
B. Sensitivity Analyses
Case 5	yes (middle)	no	0.048	122	8.8%	15.6	-3.8
Case 6	yes (low)	no	0.087	133	16.1%	12.5	-3.0
Case 7	yes	yes (low)	0.012	120	2.3%	19.2	-4.7

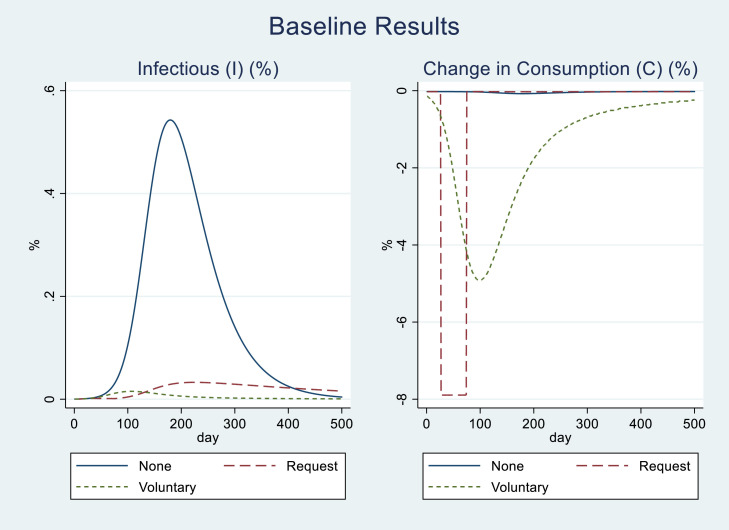
Fig. 6 depicts $I_t$ and the rate of change in $C_t$ with no, only the voluntary, and only the request-based lockdowns. For Case 1 without a voluntary or request-based lockdown, $I_t$ reaches 0.543% at the maximum while the decrease in $C_t$ is negligible (-0.1% at the bottom). The latter result is because only insulated infectious individuals reduce the consumption of social goods.

Fig. 6.

$I_t$ and $C_t$: Request-based and Voluntary Lockdowns

Note. This figure shows $I_t$ (%, in the left panel) and the rate of change in $C_t$ (%, in the right panel) for the cases with no, request-based, and voluntary lockdowns (Cases 1, 2, and 3, respectively in Table 4).

For Case 2 with only the request-based lockdown, the peak level of $I_t$ decreases to 0.033%, that is 6.0% of the peak level of $I_t$ in Case 1. The request-based lockdown delays the day when $I_t$ reaches the peak by 46 days as well (from day 179 to day 225). Meanwhile, $C_t$ decreases by 7.9% at the bottom, although $C_t$ recovers quickly after the end of the request-based lockdown.

For Case 3 with only the voluntary lockdown, the peak level of $I_t$ decreases to 0.015%, that is 2.8% of that in Case 1 and smaller than that in Case 2. The voluntary lockdown advances the day when $I_t$ reaches the peak by 72 days as compared to Case 1 (from day 179 to day 107). Thus, the effect of the voluntary lockdown on $I_t$ is substantial and larger than the request-based lockdown. Moreover, its effect on $C_t$ is also sizable: $C_t$ decreases to -4.9% at the bottom. Although this is smaller than its counterpart of the request-based lockdown, the former is more persistent than the latter: with the voluntary lockdown, $C_t$ recovers to the 99.5% of the pre-pandemic level on day 350.

6.2. Interaction of Voluntary and Request-based Lockdowns

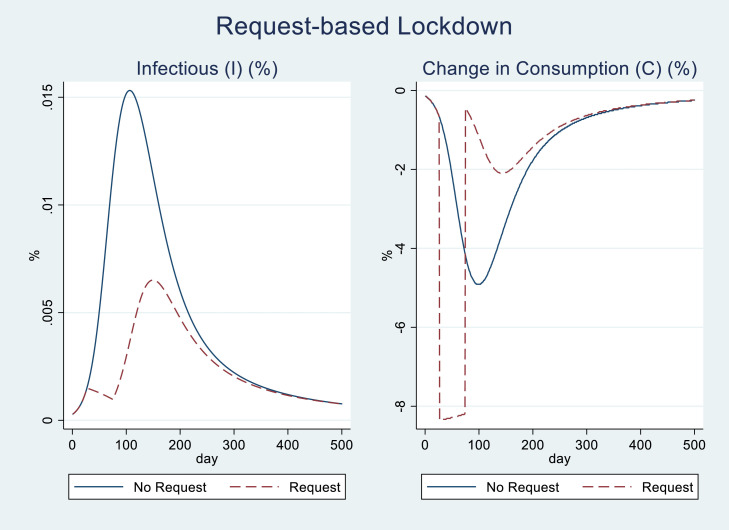
Next, I examine the interactions of voluntary and request-based lockdowns. In Case 4 of Table 4, I consider both the voluntary and request-based lockdowns. Fig. 7 depicts $I_t$ and $C_t$ in Case 3 (with only the voluntary lockdown) and Case 4 (with both the voluntary and request-based lockdown). In Case 4, the peak level of $I_t$ is 0.007%, that is only 1.2% of that in Case 1 and lower than that in Case 3. The request-based lockdown delays the day when $I_t$ reaches the peak by 43 days as compared to Case 3 (from day 107 to day 150). While the peak level of $I_t$ in Case 4 is significantly lower than that in Case 3, the decrease in $C_t$ is larger in Case 4 (-8.4%) than in Case 3 (-4.9%).

Fig. 7.

$I_t$ and $C_t$: Request-based Lockdown in the Presence of Voluntary Lockdowns

Note. This figure shows $I_t$ (%, in the left panel) and rate of change in $C_t$ (%, in the right panel) for the cases with and without the request-based lockdown (Cases 3 and 4, respectively in Table 4). The voluntary lockdown is considered in both cases.

These results show that the interaction of the voluntary and request-based lockdowns play a substantial role in the low proportion of infectious individuals and the large decrease in consumption observed in Japan. The degree of the voluntary lockdown is represented by the disutility from the infection, $D$ while the intensity of the request-based lockdown is measured by the utility losses from going out under the request, $l$. Thus, these two parameters are crucial to obtain the unique epidemiological and economic features in Japan.15

However, comparing the actual data from the first wave with the numerical experiment in Case 4, I find that the actual $I_t$ peaked at a slightly lower level (0.005% vs. 0.007%) and faster (on day 49 vs. day 150) than the simulated $I_t$ in Case 4. There are two possible reasons for these discrepancies. First, the observed number of infectious people might be underreported because of the insufficient capacity of the testing and public health system in Japan. Second, people may have responded to the risk of infection by changing their behavior in some way other than staying at home, such as wearing a face mask and washing hands, while I have assumed that such behavioral changes occurred gradually and irrespectively of the risk of infection. Moreover, the actual $C_t$ (depicted in Fig. 4) decreased more than the simulated counterpart in the first wave. This discrepancy may be because the model does not incorporate the direct effect of the state of emergency such as the requests for complete or early closures of retail shops, restaurants, bars, sports gyms, and so on.16

6.3. Sensitivity Analyses

In this subsection, I examine to what extent the baseline results so far depend on the parameters I set. Specifically, I examine the sensitivity of the results to the two key parameters: the intensities of the voluntary and request-based lockdowns.

6.3.1. Intensity of Voluntary Lockdown

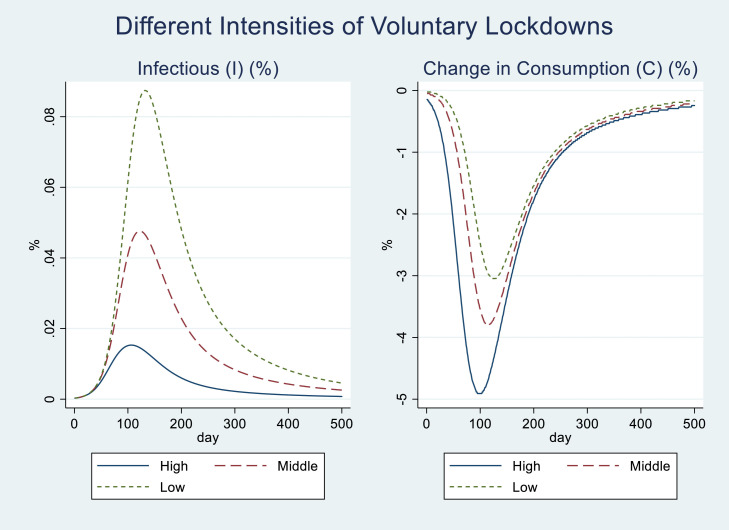
So far, I have set the intensity of the voluntary lockdown that is represented by the disutility from the disease, $D$, based on the estimation result from the first wave, which is the highest among the three waves. Here, I alternatively set the middle and small values for $D$ based on the results from the second and third waves, respectively, and examine their effects on $I_t$ and $C_t$.

In Table 4, Cases 5 and 6 show the results for the middle and low intensities of the voluntary lockdowns while Case 3 shows the results for the baseline (i.e., high) intensity case. Fig. 8 depicts $I_t$ and $C_t$ for the baseline (high), middle, and low intensities of the voluntary lockdown. I assume no request-based lockdown in Cases 3, 5 or 6. As the intensity of the voluntary lockdown is smaller, the peak level of $I_t$ is higher (0.015%, 0.048%, and 0.087% for the baseline (high), middle, and low intensities, respectively). However, even in the weak intensity case, the peak $I_t$ is 16.1% of that without no lockdown (0.543% in Case 1). Thus, a voluntary lockdown seems to be one of the key factors that account for the actual low peak levels of $I_t$ in Japan (0.005% and 0.007% in the first and second waves, respectively).17 Meanwhile, the bottom rate of the change in $C_t$ is smaller as the intensity is smaller (-4.9, -3.8, and -3.0%, for the baseline (high), middle, and low intensities, respectively) because the sensitivity of consuming social goods to the risk of infection becomes smaller.

Fig. 8.

Different Intensities of Voluntary Lockdowns

Note. This figure shows $I_t$ (%, in the left panel) and the rate of change in $C_t$ (%, in the right panel) for the cases with high (Wave 1), middle (Wave 2), and low (Wave 3) intensities of voluntary lockdowns (Cases 3, 5, and 6, respectively, in Table 4). No request-based lockdown is considered.

6.3.2. Intensity of Request-based Lockdown

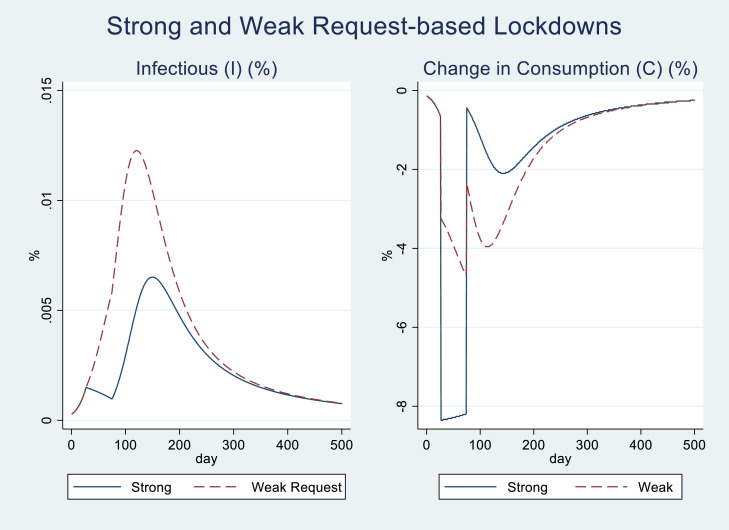
Next, I examine how the results depend on the intensity of a request-based lockdown. Specifically, I assume the one-third of the baseline intensity, $l$ (0.108). Here I assume the baseline intensity of the voluntary lockdown. Case 7 in Table 4 illustrates the results.

Fig. 9 shows $I_t$ and $C_t$ in Case 7 (with the voluntary and weak request-based lockdowns) and Case 4 (with the voluntary and baseline (i.e., strong) request-based lockdowns). In Case 7, the peak level of $I_t$ is 0.012%, which is higher than that in Case 4 by 0.006 percentage points. On the other hand, the bottom level of $C_t$ is lower than that in Case 3 (-4.7% and -8.4% in Cases 8 and 4, respectively). The weak request-based lockdown increases the proportion of infectious individuals and restrains the decrease in consumption as compared to the baseline (i.e., strong) request-based lockdown.

Fig. 9.

Strong (baseline) and Weak Request-based Lockdowns

Note. This figure shows $I_t$ (%, in the left panel) and the rate of change in $C_t$ (%, in the right panel) for the cases with the weak and strong (i.e., baseline) request-based lockdowns (Cases 7 and 4, respectively, in Table 4).

7. Conclusion

Based on the empirical evidence from Japan, I extend an epidemiological and economic model: the SIR-Macro model. In this model, I incorporate a voluntary lockdown, that is, the tendency to stay at home in response to the risk of infection. I further incorporate a request-based lockdown, that is, the government's request to stay at home without legal enforcements. My numerical experiments show that the interaction of these two types of lockdowns plays an important role in the low proportion of infectious individuals and the large decrease in consumption in Japan.

Although the numerical experiments indicate the potential role of these two types of lockdowns in mitigating infections, one needs to be careful to derive quantitative policy implications from the experiments because the parameters that represent the voluntary and request-based lockdowns may change over time and the government cannot fully control them.

The model I develop is relevant for some other countries as well because voluntary and request-based lockdowns are not limited to Japan. However, I have made various simplifying assumptions in the model to focus on the roles of voluntary and request-based lockdowns. A richer model that incorporates the risk of infection in the workplace, precautionary saving motives, and heterogeneous and uncertain risk of infection, among others, will help to give sharper quantitative estimates on the effects of voluntary and request-based lockdowns.

Appendix 1. Optimization of Individuals

In this Appendix, I solve for the maximization of individuals in each health status.

A. Recovered individuals

A recovered individual's problem can be written in the recursive form as:

$$V^R\left(\epsilon \right)=\underset{C_s,C_r,C_h}{\max }v(C_s,C_r,C_h)+\epsilon \mathbf{1}(c_s>0)+(1-\rho )V^R\left(\epsilon \right)$$

under budget constraint (7). To solve the problem, first, suppose that the individual chooses $c_s^{*}>0$, and let $\left(c_s^{*},c_r^{*},c_h^{*}\right)$ and $v^{*}$ denote the optimal consumption mix and the associated period utility, respectively. Then, $V^R\left(\epsilon \right)=\left(v^{*}+\epsilon \right)/\rho$. Next, suppose that the individual chooses $c_s^{*}=0$, and let $\left(0,{\overline{c}}_r,{\overline{c}}_h\right)$ and $\overline{v}$ denote their optimal consumption mix and the associated period utility, respectively. Then, $V^R\left(\epsilon \right)=\overline{v}/\rho$. I assume that $\epsilon >\overline{v}-v^{*}$ for all $\epsilon$. Therefore, all the recovered individuals choose $c_s^{*}>0$. Their lifetime utility is:

$$V^R\left(\epsilon \right)=\frac{v^{*}+\epsilon }{\rho }$$ (A1)

B. Infectious individuals

An uninsulated infectious individual's problem is:

$$V^{\mathit{NI}}\left(\epsilon \right)=\underset{C_s,C_r,C_h}{\max }v(C_s,C_r,C_h)+\epsilon \mathbf{1}(c_s>0)-D+(1-\rho )(\gamma V^R\left(\epsilon \right)+(1-\gamma )V^{\mathit{NI}}\left(\epsilon \right))$$

under budget constraint (7). Under the maintained assumption that $\epsilon >\overline{v}-v^{*}$, their optimal consumption mix is the same as the recovered individual, and the associated maximized lifetime utility is:

$$V^{NI}\left(\epsilon \right)=\frac{v^{*}+\epsilon -D+\left(1-\rho \right)\gamma V^R\left(\epsilon \right)}{\rho +\gamma -\rho \gamma }$$ (A2)

Infectious and isolated individuals are not allowed to consume type-s goods. Therefore, an isolated infectious individual's problem is:

$$V^{II}\left(\epsilon \right)=\underset{C_r,C_h}{max}v\left(0,C_r,C_h\right)-D+\left(1-\rho \right)\left(\gamma V^R\left(\epsilon \right)+\left(1-\gamma \right)V^{II}\left(\epsilon \right)\right)$$

under budget constraint (7). They choose $\left(C_s,C_r,C_h\right)=\left(0,{\overline{c}}_r,{\overline{c}}_h\right)$ and their lifetime utility is:

$$V^{II}\left(\epsilon \right)=\frac{\overline{v}-D+\left(1-\rho \right)\gamma V^R\left(\epsilon \right)}{\rho +\gamma -\rho \gamma }$$ (A3)

C. Susceptible individuals

C.1 No Request-based Lockdown

A susceptible individual's problem without a request-based lockdown is:

$$V_t^S\left(\epsilon \right)=\underset{C_{\mathit{st}},C_{\mathit{rt}},C_{\mathit{ht}}}{\max }v(C_{\mathit{st}},C_{\mathit{rt}},C_{\mathit{ht}})+((1-\rho )((1-{\pi }_t)V_{t+1}^S\left(\epsilon \right)+{\pi }_t{V}^I)+\epsilon )\mathbf{1}(c_{\mathit{st}}>0)+(1-\rho )V_{t+1}^S\left(\epsilon \right)\mathbf{1}(c_{\mathit{st}}=0)$$

under budget constraint (7). Here $V^I$ $\text{is}\text{the}\text{expected}\text{value}\text{of}\text{the}\text{infectious}\text{individual}:$

$$V^I\left(\epsilon \right)=\eta V^{II}\left(\epsilon \right)+\left(1-\eta \right)V^{NI}\left(\epsilon \right)=\frac{\eta \overline{v}+\left(1-\eta \right)\left(v^{*}+\epsilon \right)-D+\left(1-\rho \right)\gamma V^R\left(\epsilon \right)}{\rho +\gamma -\rho \gamma }$$ (A4)

The optimal consumption mix is

$$\begin{array}{c}\hfill (C_s,C_r,C_h)=\{\begin{array}{cc}(c_s^{*},c_r^{*},c_h^{*}),\hfill & \mathit{if}\epsilon >{\alpha }_0+{\alpha }_{1t}\left(\epsilon \right){\pi }_t\hfill \\ (0,{\overline{c}}_r,{\overline{c}}_h),\hfill & \mathit{otherwewise}\hfill \end{array}\end{array}$$ (A5)

Here, ${\alpha }_0=\overline{v}-v^{*}$ and ${\alpha }_{1t}\left(\epsilon \right)=\left(1-\rho \right)\left(V_{t+1}^S\left(\epsilon \right)-V^I\left(\epsilon \right)\right)$.

C2. Request-Based Lockdown

A susceptible individual's problem with a request-based lockdown is:

$$V_t^S\left(\epsilon \right)=\underset{C_{\mathit{st}},C_{\mathit{rt}},C_{\mathit{ht}}}{\max }v(C_{\mathit{st}},C_{\mathit{rt}},C_{\mathit{ht}})+((1-\rho )((1-{\pi }_t)V_{t+1}^S\left(\epsilon \right)+{\pi }_t{V}^I\left(\epsilon \right))+\epsilon -l_t)\mathbf{1}(c_{\mathit{st}}>0)+(1-\rho )V_{t+1}^S\left(\epsilon \right)\mathbf{1}(c_{\mathit{st}}=0)$$

Here,

$$l_t=\{\begin{array}{c}lforlstart\le l<lend\\ 0otherwise\end{array}$$

The optimal consumption mix is

$$\begin{array}{c}\hfill (C_s,C_r,C_h)=\{\begin{array}{cc}(c_s^{*},c_r^{*},c_h^{*}),\hfill & \mathit{if}\epsilon >l_t+{\alpha }_0+{\alpha }_{1t}\left(\epsilon \right){\pi }_t\hfill \\ (0,{\overline{c}}_r,{\overline{c}}_h),\hfill & \mathit{otherwewise}\hfill \end{array}\end{array}$$ (A6)

Appendix 2. Solution Method

I follow the following 7 steps to solve for the model.

1. Given $S_1$, set an initial guess of ${\left\{S_t\right\}}_{t=2}^T$.

2. Compute ${\left\{{\pi }_t\right\}}_{t=1}^T$, where ${\pi }_t=1-S_{t+1}/S_t$.

3. Because ${\pi }_t\to 0$ as $t\to \infty$, set $V_{T+1}^S=\left(v^{*}+\epsilon \right)/\rho$, and solve for a susceptible individual's period-T problem given ${\pi }_T$ (Equation 13).

4. Given ${\left\{{\pi }_t\right\}}_{t=1}^{T-1}$, solve for susceptible individuals’ problem backwardly from period T-1 to 1 (Equation 13).

5. Based on Steps 3 and 4, compute ${\left\{{\tilde{\beta }}_t\right\}}_{t=1}^T$ (Equation 15), ${\left\{({\tilde{S}}_t,{\tilde{I}}_t,{\tilde{R}}_t)\right\}}_{t=2}^T$ (Equations 4, 5, and 6, respectively), and ${\left\{{\tilde{\pi }}_t\right\}}_{t=1}^T$, where ${\tilde{\pi }}_t=1-{\tilde{S}}_{t+1}/{\tilde{S}}_t$.

6. If the maximum absolute difference in ${\left\{{\tilde{\pi }}_t\right\}}_{t=1}^T$ in Step 5 and ${\left\{{\pi }_t\right\}}_{t=1}^T$in Step 2 is larger than the tolerance level $\nu$, then, replace ${\left\{S_t\right\}}_{t=2}^T$ with ${\left\{S_t^{\prime }\right\}}_{t=2}^T$, where$S_t^{\prime }=\kappa {\tilde{S}}_t+\left(1-\kappa \right)S_t$, and iterate Steps 2 to 5. Otherwise, stop the iteration.

7. Solve for ${\left\{Sta{y}_t\right\}}_{t=2}^T$, and ${\left\{C_t\right\}}_{t=1}^T$ (Equations 14 and 11, respectively).

I set $T=2000$, $\nu ={10}^{-7}$, and $\kappa =0.1$.

Appendix 3. An Alternative Model: Exogenous Ratios of Susceptible Individuals Who Stay at Home

In this Appendix, I examine how the epidemiological and economic dynamics change if we drop the voluntary lockdowns from the model. To do so, I treat $p_t^{\prime }$ in Equation (14) as an exogenous variable that does not depend on ${\pi }_t$. Specifically, I assume that

$$p_t^{\prime }=\{\begin{array}{cc}p+l,\hfill & \mathit{for}\mathit{lstart}\le t\le \mathit{lend}\hfill \\ p,\hfill & \mathit{otherwise}.\hfill \end{array}$$

Table A1 shows the results. For the first four cases, I set $l=0$ and $p=0.0001,0.001,0.01,or0.1$. The other parameters are the same as those in the main text. In these cases, the peak levels of the proportion of infectious individuals are low and close to the actual data in the first wave (0.05%). The proportion of infectious individuals is not sensitive to the value of $p$. Meanwhile, the decreases in consumption are also quite small in all cases except for the case where $p=0.1$. In that case, $C_t$ decreases by 2.6% at the bottom, but the ratio of infectious individuals is too small (0.001%) relative to the actual data.

For the fifth case, I set $p=0.0001$ and $l=0.14$, where the latter is chosen based on the estimated coefficient $b_2$ in Equation (1). In this case, $C_t$ decreases by 3.7% at the bottom, but the proportion of infectious individuals is too small (0.001%) relative to the actual data.

These results indicate that without considering the voluntary lockdown or its interaction with the request-based lockdown, it seems difficult to account for both the low proportion of infectious individuals and the large decrease in consumption observed in Japan.

Case	Lockdown		Infectious		Stay at home	Consumption
	p	l	Peak (%)	Peak Day	Peak (%)	Bottom (% Change)
A1	0.0001	0	0.005	120	0.0	-0.003
A2	0.001	0	0.005	120	0.1	-0.03
A3	0.01	0	0.004	117	1.0	-0.3
A4	0.1	0	0.001	88	10.0	-2.6
A5	0.0001	0.14	0.001	120	14.0	-3.7