A mathematical study on a fractional COVID-19 transmission model within the framework of nonsingular and nonlocal kernel

Abstract

In this work, a mathematical model consisting of a compartmentalized coupled nonlinear system of fractional order differential equations describing the transmission dynamics of COVID-19 is studied. The fractional derivative is taken in the Atangana-Baleanu-Caputo sense. The basic dynamic properties of the fractional model such as invariant region, existence of equilibrium points as well as basic reproduction number are briefly discussed. Qualitative results on the existence and uniqueness of solutions via a fixed point argument as well as stability of the model solutions in the sense of Ulam-Hyers are furnished. Furthermore, the model is fitted to the COVID-19 data circulated by Nigeria Centre for Disease Control and the two-step Adams-Bashforth method incorporating the noninteger order parameter is used to obtain an iterative scheme from which numerical results for the model can be generated. Numerical simulations for the proposed model using Adams-Bashforth iterative scheme are presented to describe the behaviors at distinct values of the fractional index parameter for of each of the system state variables. It was shown numerically that the value of fractional index parameter has a significant effect on the transmission behavior of the disease however, the infected population (the exposed, the asymptomatic infectious, the symptomatic infectious) shrinks with time when the basic reproduction number is less than one irrespective of the value of fractional index parameter.

1. Introduction

According to the International Committee on Taxonomy of Viruses (ICTV), coronaviruses (CoVs) are enveloped, single-stranded, positive-sense and nonsegmented Ribonucleic acid (RNA) viruses which belong to the subfamily Orthocoronavirinae of the Coronaviridae family and order Nidovirales [1]. All CoVs that have affected humans are generally of animal origin, a variety of which have been isolated and identified in birds and mammals hosts [1], [2], [3], [4]. CoVs are distinctively classified into four main genera groups, namely, $\alpha -$CoVs, $\beta -$CoVs, $\gamma -$CoVs and $\delta -$CoVs [1], [3]. The $\alpha -$ and $\beta -$CoVs have mammalian hosts and are known to cause respiratory related symptoms in humans and gastroenteritis in other mammals [2], [4], while $\gamma -$ and $\delta -$CoVs are commonly found in avian hosts [3].

Before December 2019, HCoV-NL63 ($\alpha -$CoV), HCoV-229E ($\alpha -$CoV), HCoV-OC43 ($\beta -$CoV), HCoV-HKU1 ($\beta -$CoV), SARS-CoV ($\beta -$CoV) and MERS-CoV ($\beta -$CoV) where the only known pathogenic strains of human coronaviruses (HCoVs). Among these, infections due to HCoV-NL63, HCoV-229E, HCoV-OC43, HCoV-HKU1 are relatively common within the human population with varying degrees of mild flu-like symptoms typically characterized by rhinorrhea, sneezing, sore throat, nasal congestion, cough and fever [1]. However, SARS-CoV and MERS-CoV are highly pathogenic and have caused major pandemics in the last two decades [1], [2]. Towards the end of 2019, a novel viral strain of HCoVs known as Severe Acute Respiratory Syndrome Coronavirus 2 (SARS-CoV-2), which causes the disease named COVID-19, emerged from the Chinese city of Wuhan, Hubei Province [1], [5], [6], [7]. Just like SARS-CoV and MERS-CoV, genomic sequencing shows that SARS-CoV-2 belongs to the $\beta -$CoVs genera group. Although its primary origin is still shrouded in mystery, available information suggest that it is also of zoonotic origin with wild bats believed to be the primary host [8]. SARS-CoV-2 targets the respiratory tract causing common symptoms such as fever, fatigue, nasal congestion, cough, pneumonia, tiredness and loss of appetite. Within a month of its outbreak, this highly virulent disease rapidly spread to many countries throughout the world. Aside from China where the initial transmission route was claimed to be from animal host to human, the transmission route thereafter as well as to other countries were essentially human-to-human, that is, either through direct contact with already contaminated surfaces/individuals or via inhalation of minute respiratory droplets of sneezes or coughs from already infected individuals [9], [1], [7]. The risk of COVID-19 related death is high especially among the aged and imuno-compromised-COVID-19 patients as complications such as severe acute respiratory distress syndrome, multi-organ failure, septic shock, blood clots, heart failure, arrhythmias, myocarditis, seizure, encephalitis, stroke may occur [10], [11], [12]. Before the production, approval and subsequent mass availability of the current vaccines to combat and manage the spread of the virus, governments of various countries had implemented a variety of non-pharmaceutical control measures such as public campaign on the mandatory use of face masks as well as alcohol based sanitizers, imposition of total or partial lock down, observance of social distancing, ban on crowded social events/imposition of a maximum number of persons in religious gatherings, closure both public and private institutions, closure of borders, ban/restrictions on local and international flights, contact tracing of suspected infected cases and isolation of detected (asymptomatic and symptomatic) cases for prompt medical attention [13]. However, there were no total compliance to most of these measures in most of the affected countries, so that the disease which started in China gained a devastating global spread. Medical facilities became overwhelmed and doctors, nurses, health care givers and other front line staff became infected in some cases.

In existing literature there are variant notions of fractional derivatives. However, many authors have used specific fractional differential operators that best suit their interests. It is worth mentioning that mathematical models with fractional derivatives appear as natural generalizations of existing integer order models. Before 2015, all the previously used fractional differential operators incorporate singular kernels which have some setbacks in the modeling of physical phenomena. In recent times, new types of fractional differential operators with non-singular kernels have attracted the interest of many authors. To overcome some setbacks associated with singularity of kernels, Caputo and Febrizio [14] introduced the so-called Caputo-Febrizio-Caputo (CFC) fractional derivative which extends the well known Caputo fractional derivative [15] to a more general framework by incorporating non-singular kernel. However, the CFC derivative also have some associated problems due to the locality nature of its kernel. To overcome the problems associated with both singularity and locality of kernels, Atangana and Baleanu [16] introduced the so-called Atangana-Baleanu-Caputo (ABC) fractional derivative which incorporates the Mittag Leffler function as a non-local and non-singular kernel. With respect to the Mittag-Leffler function as kernel, the Atangana-Baleanu definition of the fractional derivative provides an excellent description for memory and hereditary effects present in a wide range of physical problems.

The idea of incorporating fractional order derivatives in the mathematical modeling of infectious diseases is not anything new (see, for instance [17], [18], [19], [20], [21] and the references therein). Within the past nineteen months, there have been extensive studies on COVID-19 from different mathematical perspectives. A variety of mathematical models have be constructed to better understand the transmission dynamics and optimal control of the virus. In a number of these works, the constructed models incorporate integer order derivatives [22], [23], [24], [25]. However, due to the fact that integer-order derivatives fail to adequately capture hereditary and memory effects inherent in most real life situations, some of these models have been extended by other authors to incorporate fractional (non-integer) order derivatives. Some of the earliest mathematical studies on the transmission dynamics of fractional COVID-19 models were done by Chen et al. [26] and Khan and Atangana [27]. Since then, studies on fractional COVID-19 models have attracted the interest of many authors with interesting results. For instance, in [28] the authors considered a fractional COVID-19 model incorporating the susceptible, exposed, symptomatic, asymptomatic and removed compartments. Their investigation suggests that the memory effects contained in the fractional operators apparently do not seem to play a significant role on the stability behavior of the fractional model. Verma and Kumar [29] studied a COVID-19 model with variable fractional derivative in the Caputo-Fabrizio-Caputo sense. They employed the fixed point theory to establish new existence and uniqueness results. They also obtained interesting results related to the generalized Hyers-Ulam stability and generalized Hyers-Ulam-Rassias stability of the model. Other recent works on the dynamics of fractional COVID-19 models include [9], [30], [31], [32], [33], [34].

In this paper, we contribute to existing body of works by constructing and studying a compartmentalized fractional mathematical model describing the transmission dynamics of COVID-19 using real data from Nigeria. The fractional differential operator for the constructed model is taken in the Atangana-Baleanu-Caputo sense due to its non-locality and non-singularity properties. The model considered incorporates the susceptible, exposed, asymptomatic, infectious, isolated and recovered compartments. We recall that the first case of COVID-19 in Nigeria was reported on the 27th of February 2020 with the patient being an Italian citizen who arrived Lagos [35] from Milan through the Murtala Muhammad Airport, while the second case of the disease was reported in Ewekoro, Ogun State, the patient being a Nigerian citizen who had had contact with the Italian citizen. Hence we do not take indirect transmission from animal-to-human into consideration as this is the situation for most of countries outside China. Among other things, the impact of the order of differentiation on the dynamics of the disease is investigated using a fractional two-step Adams-Bashforth scheme developed in [36].

We highlight the content of the remaining sections of this paper as follows: In Section 2, we recall some important notions and results which we will find useful in subsequent sections. In Section 3, a mathematical model incorporating the Atangana-Baleanu derivative is constructed to describe the transmission dynamics of COVID-19 in Nigeria. In view of the fact that the model describes human population, some dynamical properties such as invariant region as well as basic reproduction number are also discussed. In Section 4, we employ a fixed point argument to establish conditions under which the constructed fractional order model admits a unique solution. The stability of the model in the sense of Ulam-Hyers is investigated in Section 5. To obtain numerical solutions for the proposed model, a two-step Adems-Bashforth scheme incorporating the memory index of the fractional model is developed in Section 6. In Section 7, we do some parameter estimation and model fitting using available data from the NCDC in Nigeria. Furthermore, using these estimated parameter values as well as the iterative already developed in Section 6, we proceed further to obtain numerical simulations describing influence of distinct values of the fractional index on the dynamics of the susceptible, exposed, asymptomatic, symptomatic, isolated, and recovered individuals. Concluding remarks relevant to the present investigation are summarized in Section 8.

2. Some background materials

In this section, we collect some basic notions and results concerning the Atangana-Baleanu fractional derivatives and integrals. In the sequel, we denote by $H^1(a,b):=\{\psi \in L^2(a,b):{\psi }^{\prime }\in L^2(a,b),a<b\}$ the Sobolev space of order 1 in $(a,b)\in \mathbb{R}$, $\Gamma (·)$ the usual gamma function and ${\mathbb{E}}_{\vartheta ,\beta }(·)$, defined as

$${\mathbb{E}}_{\vartheta ,\beta }\left(z\right):=\sum _{k=0}^{\infty }\frac{z^k}{\Gamma (\vartheta k+\beta )},\vartheta ,\beta >0,z\in \mathbb{C},$$ (2.1)

the two-parameter Mittag-Leffler function [15]. If $\beta =1$, then (3.8) reduces to the one-parameter Mittag-Leffler function ${\mathbb{E}}_{\vartheta ,1}\left(z\right)\equiv {\mathbb{E}}_{\vartheta }\left(z\right)$. In particular, ${\mathbb{E}}_{1,1}\left(z\right)\equiv {\mathbb{E}}_1\left(z\right)=\exp \left(z\right)$.

Definition 2.1

[16] The Atangana-Baleanu-Caputo $\left(\mathbb{ABC}\right)$ and Atangana-Baleanu-Riemann-Liouville $\left(\mathbb{ABR}\right)$ fractional derivatives of order $\vartheta \in (0,1]$ for a function $\Theta \in H^1(a,b)$ are defined as

$${}_a^{\mathbb{ABC}}{D}_t^{\vartheta }\Theta \left(t\right)=\frac{\mathbb{ABC}\left(\vartheta \right)}{1-\vartheta }{\int }_a^t{\mathbb{E}}_{\vartheta }(-\frac{\vartheta }{1-\vartheta }{(t-s)}^{\vartheta }){\Theta }^{\prime }\left(s\right)ds,t>0,$$ (2.2)

and

$$\begin{array}{ccc}& & {}_a^{\mathbb{ABR}}{D}_t^{\vartheta }\Theta \left(t\right)\hfill \\ & & =\frac{\mathbb{ABC}\left(\vartheta \right)}{1-\vartheta }\frac{d}{dt}{\int }_a^t{\mathbb{E}}_{\vartheta }(-\frac{\vartheta }{1-\vartheta }{(t-s)}^{\vartheta })\Theta \left(s\right)ds,t>0,\hfill \end{array}$$ (2.3)

respectively, where $\mathbb{ABC}\left(\vartheta \right)$ is the normalization function satisfying the property: $\mathbb{ABC}\left(0\right)=\mathbb{ABC}\left(1\right)=1$.

Definition 2.2

[16] The fractional integral associated with the $\mathbb{ABC}$ derivative is defined as

$$\begin{array}{ccc}\hfill {}_a^{\mathbb{AB}}{I}_t^{\vartheta }\left[\Theta \left(t\right)\right]& =& \frac{1-\vartheta }{\mathbb{ABC}\left(\vartheta \right)}\Theta \left(t\right)\hfill \\ & & +\frac{\vartheta }{\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}{\int }_a^t{(t-s)}^{\vartheta -1}\Theta \left(s\right)ds,t>0.\hfill \end{array}$$ (2.4)

Lemma 2.3

Let$\vartheta \in (0,1]$and$\mathcal{H}\in C([0,T],{\mathbb{R}}_{+})$. Then the fractional initial value problem in$\mathbb{ABC}$derivative:

$$\{\begin{array}{c}{}_a^{\mathbb{ABC}}{D}_t^{\vartheta }\Theta \left(t\right)=\mathcal{H}\left(t\right),t\in [0,T],\hfill \\ \Theta \left(0\right)={\Theta }_0,\hfill \end{array}$$

has a unique solution given as

$$\Theta \left(t\right)={\Theta }_0+\frac{1-\vartheta }{\mathbb{ABC}\left(\vartheta \right)}\mathcal{H}\left(t\right)+\frac{\vartheta }{\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}{\int }_a^t{(t-s)}^{\vartheta -1}\mathcal{H}\left(s\right)ds.$$ (2.5)

Definition 2.4

[16] The Laplace transform associated with the $\mathbb{ABC}$ fractional differential operator is defined as

$$\mathcal{L}\left\{{{}^{\mathbb{ABC}}}_0{D}_t^{\vartheta }\left[\Theta \left(t\right)\right]\right\}\left(s\right)=\frac{\mathbb{ABC}\left(\vartheta \right)}{\vartheta +s^{\vartheta }(1-\vartheta )}[s^{\vartheta }\mathcal{L}\left\{\Theta \left(t\right)\right\}\left(s\right)-s^{\vartheta -1}\Theta \left(0\right)].$$ (2.6)

Definition 2.5

[37] Let $\mathcal{W}$ be a Banach space. Then the operator $\mathbf{F}:\mathcal{W}\to \mathcal{W}$ is a contraction if

$$\parallel \mathbf{F}{\Psi }_1-\mathbf{F}{\Psi }_2\parallel \le \kappa \parallel {\Psi }_1-{\Psi }_2\parallel ,\text{for}\text{all}{\Psi }_1,{\Psi }_2\in \mathcal{W},0<\kappa <1.$$

Theorem 2.6

[37]Let$\mathcal{W}$be a Banach space and$\mathcal{B}$a nonempty closed subset of$\mathcal{W}$. If the map$\mathbf{F}:\mathcal{B}\to \mathcal{B}$is a contraction, then there exists a unique fixed point of$\mathbf{F}$.

Theorem 2.7

(Krasnoselskiis fixed point theorem[38]) Let$\mathcal{B}$be a non-empty, closed, convex and bounded subset of a Banach space$\mathcal{W}$and assume that$\mathbf{F}$and$\mathbf{G}$are two operators on$\mathcal{W}$satisfying

• i)$\mathbf{F}\Psi +\mathbf{G}\Psi \in \mathcal{B}$for all$\Psi \in \mathcal{B}$;
• ii)$\mathbf{F}$is a contraction mapping;
• iii)$\mathbf{G}$is continuous and compact.

Then, there exists at least one solution$\Psi \in \mathcal{B}$such that$\mathbf{F}\Psi +\mathbf{G}\Psi =\Psi .$

Theorem 2.8

(Arzelá-Ascoli Theorem[39]) Let$\mathcal{B}$be a compact set in${\mathbb{R}}_{+}^n$$(n\ge 1)$. Then a set$\mathcal{X}\subset C\left(\mathcal{B}\right)$is relatively compact in$C\left(\mathcal{B}\right)$if and only if the functions in$\mathcal{X}$are uniformly bounded and equi-continuous on$\mathcal{B}$.

3. Construction of the proposed fractional model

Motivated by the works [26], [27], [28], we employ a compartmental approach to formulate a modified model describing the transmission dynamics of COVID-19. However, our model bears close resemblance with the the SEIAR-type model considered in [28] but differs from the ones in [26], [27] in that we do not take into account the contributions of the animal hosts population (possibly bats) and environmental reservoir (seafood market) transmission network whose dynamics accounts for the possible transmission from the source of infection to human. This is because, the initial transmission routes in other countries outside China is essentially considered to be via humam-to-human interactions. Instead, we incorporate an additional compartment accounting for the dynamics of the isolated population under medical care. More precisely, our proposed model sub-divides the total human population $N\left(t\right)$ into six mutually-exclusive compartments, namely, susceptible $\mathcal{S}\left(t\right)$, exposed $\mathcal{E}\left(t\right)$, asymptomatic $\mathcal{A}\left(t\right)$, symptomatic $\mathcal{I}\left(t\right)$, isolated $\mathcal{H}\left(t\right)$ and recovered $\mathcal{R}\left(t\right)$ compartments, such that

$$N\left(t\right)=\mathcal{S}\left(t\right)+\mathcal{E}\left(t\right)+\mathcal{A}\left(t\right)+\mathcal{I}\left(t\right)+\mathcal{H}\left(t\right)+\mathcal{R}\left(t\right).$$ (3.1)

We assume that natural mortality occur in all compartments at rate $\mu$ while disease induced mortality occur only in the $\mathcal{I}$ and $\mathcal{H}$ compartments at rate $d_1$ and $d_2$, respectively. We discuss the components of each compartment as follows:

• •
  The susceptible compartment$\mathcal{S}\left(t\right)$ consists of all individuals who are at risk of contracting the COVID-19 disease. We take into consideration direct transmission of the virus via human-to-human contact only. Recruitment of new individuals into this compartment is at a constant rate $\Pi$. Moreover, all newly recruited individuals are assumed to be susceptible. Although, some restrictive policies such as public awareness campaign, social distancing, wearing of face mask, use of alcohol based hand sanitizers and Personal Protective Equipment (PPE) as well as inter- and intra-state lock down were imposed after some weeks, compliance to these preventive regulations were not total. Let $\rho (0\le \rho \le 1)$ denote the efficacy of of the preventive measures imposed by government. Then any susceptible individual who contract the disease through effective contact with viral sources (that is, $\mathcal{A}\left(t\right)$ and $\mathcal{I}\left(t\right)$) moves into the exposed compartment at the rate $(1-\rho )\lambda \left(t\right)$ where

  $$\lambda \left(t\right):=\beta \frac{(\mathcal{I}+\tau \mathcal{A})}{N}$$ (3.2)

  denotes the force of infection. Here, $\beta$ denotes the effective contact rate for COVID-19 transmission from a viral source to a susceptible individual and $\tau \in [0,1]$ the modification parameter accounting for the relative infectiousness of individuals with COVID-19 infection in the $\mathcal{A}$ compartment in comparison to those with COVID-19 infection in the $\mathcal{I}$ compartment.
• •The exposed compartment$\mathcal{E}\left(t\right)$ consists of those who have become exposed to COVID-19. Apart from not showing any clinical symptom at this stage, exposed individuals are not also immediately infectious as the pathogen may take some time to replicate and establish itself within the new host. Between the time of exposure and development of any related symptom, COVID-19 is known to have an incubation period of 2 to 14 days. We denote by ${\theta }_1$ and ${\theta }_2$ the incubation periods for exposed individuals to become asymptomatic and symptomatic, respectively.
• •The asymptomatic infectious compartment$\mathcal{A}\left(t\right)$ consists of infected individuals who show no clinical symptoms. An asymptomatic individual is capable of infecting susceptible individuals. After the incubation period ${\theta }_1$, a proportion $\sigma$ of the exposed individuals transit to asymptomatic class at rate ${\theta }_1\sigma$. However, the number of asymptomatic individuals decreases either due to transition to isolation centers at rate ${\varphi }_1$, recovery at rate ${\phi }_1$ by overcoming the disease.
• •The symptomatic infected compartment$\mathcal{I}\left(t\right)$ consists of infected individuals with visible (or clinical) symptoms. These individual are capable of infecting susceptible individuals. After the incubation period ${\theta }_2$, the remaining $(1-\sigma )$ proportion of the exposed individuals enters the symptomatic compartment at rate ${\theta }_2(1-\sigma )$. However, the number of symptomatic individuals decreases due to transition into isolation of infectious individuals at isolation centers/hospitals at rate ${\varphi }_2$, recovery of infectious individuals at rate ${\phi }_2$.
• •The isolated compartment$\mathcal{H}\left(t\right)$ consists of COVID-19 positive individuals who are isolated at home or treatment centers for medical attention. We assume that there is that there is no viral transmission by isolated individuals to susceptible individuals (such as doctors, nurses, care givers or visitors). Individuals in this compartment increases as more asymptomatic and symptomatic cases become isolated at rate ${\varphi }_1$ and ${\varphi }_2$, respectively, and decreases due to recovery at rate ${\phi }_3$.
• •The recovered compartment$\mathcal{R}\left(t\right)$ consists of those individual who have recovered from COVID-19 infection. The recovered population increases as more asymptomatic, symptomatic and hospitalized individuals individuals recover from the infection at rate ${\phi }_1$, ${\phi }_2$ and ${\phi }_3$, respectively. Reduction of number of recovered population is only due to natural death at rate $\mu$. We assume that no infection related death occur after recovery and recovered individuals do not become susceptible again. In order words, re-infection is not taken into account due to immunity induced by COVID-19 antibodies.

Putting together the above considerations, we arrive at the following compartmental system of deterministic nonlinear ordinary differential equations:

$$\{\begin{array}{c}{D}_t\mathcal{S}\left(t\right)=\Pi -(1-\rho )\lambda \left(t\right)\mathcal{S}-\mu \mathcal{S},\hfill \\ D_t\mathcal{E}\left(t\right)=(1-\rho )\lambda \left(t\right)\mathcal{S}-({\theta }_1\sigma +{\theta }_2(1-\sigma )+\mu )\mathcal{E},\hfill \\ D_t\mathcal{A}\left(t\right)={\theta }_1\sigma \mathcal{E}-({\varphi }_1+{\phi }_1+\mu )\mathcal{A},\hfill \\ D_t\mathcal{I}\left(t\right)={\theta }_2(1-\sigma )\mathcal{E}-({\varphi }_2+{\phi }_2+d_1+\mu )\mathcal{I},\hfill \\ D_t\mathcal{H}\left(t\right)={\varphi }_1\mathcal{A}+{\varphi }_2\mathcal{I}-({\phi }_3+d_2+\mu )\mathcal{H},\hfill \\ D_t\mathcal{R}\left(t\right)={\phi }_1\mathcal{A}+{\phi }_2\mathcal{I}+{\phi }_3\mathcal{H}-\mu \mathcal{R}.\hfill \end{array}$$ (3.3)

Here, the notation $D_t$ represents the integer order time derivative. The description of the model parameters and their values are provided in Table 1 for further elucidation.

Table 1.

Parameter values.

Parameter	Description	Value	Reference	Default Value
$\Pi$	Recruitment rate of susceptible individuals	$N_0\mu$
$\beta$	Disease transmission rate	$0.2129-0.2162$	Data fitting	0.2145
$\tau$	Transmissibility multiple	$0.4251-0.4473$	Data fitting	0.43620
${\theta }_1$	Incubation rate for exposed to become asymptomatic	$\frac{1}{14}-\frac{1}{7}$ day${}^{-1}$	[44], [45]	$\frac{1}{10}$
${\theta }_2$	Incubation rate for exposed to become symptomatic	$\frac{1}{14}-\frac{1}{7}$ day${}^{-1}$	[44], [45]	$\frac{1}{8}$
${\varphi }_1$	Hospitalized rate of asymptomatic infected individuals	$0.001331-0.001391$	Data fitting	0.001361
${\varphi }_2$	Hospitalized rate of symptomatic infected individuals	$0-0.00003380$	Data fitting	$4.975\times {10}^{-6}$
$\sigma$	Fraction of exposed population that become symptomatic	$0.5725-0.6270$	Data fitting	0.5997
${\phi }_1$	Recovery rate of asymptomatic population	$\frac{1}{14}-\frac{1}{3}$ day${}^{-1}$	[42], [47]	$\frac{1}{9}$
${\phi }_2$	Recovery rate of symptomatic population	$\frac{1}{30}-\frac{1}{3}$ day${}^{-1}$	[42], [47]	$\frac{1}{14}$
${\phi }_3$	Recovery rate of hospitalized population	$0.08013-0.08594$ day${}^{-1}$	[22]	0.0815
$d_1$	Disease induced death rate for the infected class	$0.011-0.3$ day${}^{-1}$	[43]	0.015
$d_2$	Disease induced death rate for the hospitalized class	$0-0.001779$	Data fitting	0.0003629
$\mu$	Natural death rate	0.01186 year${}^{-1}$	[46], [48]
$\rho$	Efficacy of imposed control measures	$0<\rho <1$

By replacing the classical integer derivative in each equation of (3.3) with the fractional $\mathbb{ABC}$ derivative we arrive at the following generalized model:

$$\{\begin{array}{c}{}_0^{\mathbb{ABC}}{D}_t^{\vartheta }\mathcal{S}\left(t\right)=\Pi -(1-\rho )\lambda \left(t\right)\mathcal{S}-\mu \mathcal{S},\hfill \\ {}_0^{\mathbb{ABC}}{D}_t^{\vartheta }\mathcal{E}\left(t\right)=(1-\rho )\lambda \left(t\right)\mathcal{S}-({\theta }_1\sigma +{\theta }_2(1-\sigma )+\mu )\mathcal{E},\hfill \\ {}_0^{\mathbb{ABC}}{D}_t^{\vartheta }\mathcal{A}\left(t\right)={\theta }_1\sigma \mathcal{E}-({\varphi }_1+{\phi }_1+\mu )\mathcal{A},\hfill \\ {}_0^{\mathbb{ABC}}{D}_t^{\vartheta }\mathcal{I}\left(t\right)={\theta }_2(1-\sigma )\mathcal{E}-({\varphi }_2+{\phi }_2+d_1+\mu )\mathcal{I},\hfill \\ {}_0^{\mathbb{ABC}}{D}_t^{\vartheta }\mathcal{H}\left(t\right)={\varphi }_1\mathcal{A}+{\varphi }_2\mathcal{I}-({\phi }_3+d_2+\mu )\mathcal{H},\hfill \\ {}_0^{\mathbb{ABC}}{D}_t^{\vartheta }\mathcal{R}\left(t\right)={\phi }_1\mathcal{A}+{\phi }_2\mathcal{I}+{\phi }_3\mathcal{H}-\mu \mathcal{R},\hfill \end{array}$$ (3.4)

where ${}_0^{\mathbb{ABC}}{D}_t^{\vartheta }$ ($0<\vartheta \le 1$) denotes the $\mathbb{ABC}$ fractional differential operator. The model (3.4) is considered with the initial conditions:

$$\begin{array}{c}{\displaystyle \mathcal{S}\left(0\right)={\mathcal{S}}_0\ge 0,\mathcal{E}\left(0\right)={\mathcal{E}}_0\ge 0,\mathcal{A}\left(0\right)={\mathcal{A}}_0\ge 0}\hfill \\ {\displaystyle \mathcal{I}\left(0\right)={\mathcal{I}}_0\ge 0,\mathcal{H}\left(0\right)={\mathcal{H}}_0\ge 0,\mathcal{R}\left(0\right)={\mathcal{R}}_0\ge 0.}\hfill \end{array}$$ (3.5)

3.1. Positive invariant region

Since the model (3.4) describes human population, it is necessary to determine the region within which the model is epidemiologically meaningful. In this direction, we adapt the approach in [31], [18] to prove the following important result.

Lemma 3.1

The closed set

$$\Omega =\{(\mathcal{S},\mathcal{E},\mathcal{A},\mathcal{I},\mathcal{H},\mathcal{R})\in {\mathbb{R}}_{+}^6:N=\mathcal{S}+\mathcal{E}+\mathcal{A}+\mathcal{I}+\mathcal{H}+\mathcal{R}\le \frac{\Pi }{\mu }\}$$ (3.6)

is positively invariant for the fractional model(3.4).

Proof

Following similar lines of argument as in [31], [18], we sum up all equations of the fractional model (3.4) to obtain

$${}_0^{\mathbb{ABC}}{D}_t^{\vartheta }N\left(t\right)=\Pi -\mu N\left(t\right)-d(\mathcal{A}\left(t\right)+\mathcal{I}\left(t\right)+\mathcal{H}\left(t\right))\le \Pi -\mu N\left(t\right).$$

An application of the Laplace transform yields

$$\begin{array}{cc}{\displaystyle N\left(t\right)\le }\hfill & {\displaystyle [\frac{\mathbb{ABC}\left(\vartheta \right)}{\mathbb{ABC}\left(\vartheta \right)+(1-\vartheta )\mu }N\left(0\right)}\hfill \\ & {\displaystyle +\frac{(1-\vartheta )\Pi }{\mathbb{ABC}\left(\vartheta \right)+(1-\vartheta )\mu }]{\mathbb{E}}_{\vartheta ,1}(-\nu t^{\vartheta })}\hfill \\ & {\displaystyle +\frac{\vartheta \Pi }{\mathbb{ABC}\left(\vartheta \right)+(1-\vartheta )\mu }{\mathbb{E}}_{\vartheta ,\vartheta +1}(-\nu t^{\vartheta })}\hfill \end{array}$$ (3.7)

where $\nu =\frac{\vartheta \mu }{\mathbb{ABC}\left(\vartheta \right)+(1-\vartheta )\mu }$, $N\left(0\right)={\mathcal{S}}_0+{\mathcal{E}}_0+{\mathcal{A}}_0+{\mathcal{I}}_0+{\mathcal{H}}_0+{\mathcal{R}}_0$ denotes the total initial population and ${\mathbb{E}}_{\vartheta ,\beta }\left(z\right)$ is the two-parameter Mittag-Leffler function [15] defined by

$${\mathbb{E}}_{\vartheta ,\beta }\left(z\right):=\sum _{k=0}^{\infty }\frac{z^k}{\Gamma (\vartheta k+\beta )}(z,\beta \in \mathbb{C},\text{Re}\left(\vartheta \right)>0).$$ (3.8)

By invoking the following property for the two-parameter Mittag-Leffler function [15]

$${\mathbb{E}}_{\vartheta ,\beta }\left(z\right)=z{\mathbb{E}}_{\vartheta ,\vartheta +\beta }\left(z\right)+\frac{1}{\Gamma \left(\beta \right)},$$

the inequality in (3.7) simplifies to

$$N\left(t\right)\le \frac{\Pi }{\mu }+\frac{\mathbb{ABC}\left(\vartheta \right)}{\mathbb{ABC}\left(\vartheta \right)+(1-\vartheta )\mu }[N\left(0\right)-\frac{\Lambda }{\mu }]{\mathbb{E}}_{\vartheta }(-\nu t^{\vartheta }).$$

Clearly, $N\left(t\right)\le \frac{\Pi }{\mu }$ as $t\to \infty$ due to the asymptotic behaviour of the Mittag-Leffler function [15]. Thus, all solutions of the fractional model (3.4) with the non-negative initial conditions in $\Omega$ will remain in $\Omega$. Consequently, the closed set $\Omega$ is a positively invariant with regard to the fractional model (3.4). □

3.2. Model equilibrium points

The equilibrium points of the fractional model (3.4) are basically steady state solutions of the model. Clearly, by setting the left hand side of each equations in (3.4) to zero and solving the resulting algebraic system of equations, we obtain the following equilibrium points:

• i)
  Disease free equilibrium (DFE) point: In the absence of any COVID-19 infection within the population (i.e., when $\mathcal{E}=\mathcal{A}=\mathcal{I}=\mathcal{H}=0$), the the DFE, denoted by ${\mathbf{E}}^0$, is calculated as

  $${\mathbf{E}}^0=({\mathcal{S}}^0,{\mathcal{E}}^0,{\mathcal{A}}^0,{\mathcal{I}}^0,{\mathcal{H}}^0,{\mathcal{R}}^0)=(\frac{\Pi }{\mu },0,0,0,0,0).$$ (3.9)
• ii)
  Disease endemic equilibrium (DEE) point: When $\mathcal{E},\mathcal{A},\mathcal{I},\mathcal{H}\ne 0$, the DEE ${\mathbf{E}}_e$ is obtained as

  $${\mathbf{E}}_e=({\mathcal{S}}_e,{\mathcal{E}}_e,{\mathcal{A}}_e,{\mathcal{I}}_e,{\mathcal{H}}_e,{\mathcal{R}}_e)$$ (3.10)

  where

  $$\{\begin{array}{c}{\displaystyle {\mathcal{S}}_e=\frac{\Pi }{{\lambda }_e(1-\rho )+\mu },{\mathcal{E}}_e=\frac{\Pi {\lambda }_e(1-\rho )}{({\lambda }_e(1-\rho )+\mu )k_1},}\hfill \\ {\displaystyle {\mathcal{A}}_e=\frac{\Pi {\lambda }_e{\theta }_1\sigma (1-\rho )}{({\lambda }_e(1-\rho )+\mu )k_1{k}_2},{\mathcal{I}}_e=\frac{\Pi {\lambda }_e{\theta }_2(1-\sigma )(1-\rho )}{({\lambda }_e(1-\rho )+\mu )k_1{k}_3},}\hfill \\ {\displaystyle {\mathcal{H}}_e=\frac{\Pi {\lambda }_e(1-\rho )}{({\lambda }_e(1-\rho )+\mu )k_4}(\frac{{\varphi }_1{\theta }_1\sigma }{k_1{k}_2}+\frac{{\varphi }_2{\theta }_2(1-\sigma )}{k_1{k}_3})}\hfill \\ {\displaystyle {\mathcal{R}}_e=\frac{\Pi {\lambda }_e(1-\rho )}{({\lambda }_e(1-\rho )+\mu )\mu k_1{k}_4}(\frac{{\theta }_2(1-\sigma )(k_4{\phi }_2+{\varphi }_2{\phi }_3)}{k_3}+\frac{\sigma {\theta }_1(k_4{\phi }_1+{\varphi }_1{\phi }_3)}{k_2}).}\hfill \end{array}$$ (3.11)

  In (3.11), $k_1={\theta }_1(1-\sigma )+{\theta }_2\sigma +\mu ,k_2={\varphi }_1+{\phi }_1+\mu ,k_3={\varphi }_2+{\phi }_2+d_1+\mu ,k_4={\phi }_3+d_2+\mu ,$ and

  $${\lambda }_e:=\beta \left(\frac{{\mathcal{I}}_e+\tau {\mathcal{A}}_e}{N_e}\right).$$ (3.12)

  Moreover, by substituting the expressions for ${\mathcal{A}}_e$ and ${\mathcal{I}}_e$ from (3.11) into (3.12) and noting that $N_e={\mathcal{S}}_e+{\mathcal{E}}_e+{\mathcal{A}}_e+{\mathcal{I}}_e+{\mathcal{H}}_e+{\mathcal{R}}_e$, an explicit expression for ${\lambda }_e$ can be obtained.

3.3. Basic reproduction number

By using the method of next generation matrix described in [40] we find the basic reproduction number as follows: Firstly, we obtain the following Jacobian matrices at the DFE ${\mathbb{E}}_0$:

$${\mathbf{F}=J\left(\mathcal{F}\right)|}_{{\mathbb{E}}_0}=\left[\begin{array}{ccc}0& (1-\rho )\beta \tau & (1-\rho )\beta \\ 0& 0& 0\\ 0& 0& 0\end{array}\right]$$

and

$${\mathbf{V}=J\left(\mathcal{V}\right)|}_{{\mathbb{E}}_0}=\left[\begin{array}{ccc}{k}_1& 0& 0\\ -{\theta }_1\sigma & k_2& 0\\ -{\theta }_2(1-\sigma )& 0& k_3\end{array}\right]$$

where $\mathcal{F}$ and $\mathcal{V}$ are matrices consisting of the new infection terms and transmission terms, respectively, in the $\mathcal{E}$, $\mathcal{A}$ and $\mathcal{I}$ compartments. Then the expression for ${\mathcal{R}}_0$ determined next generation matrix as the spectral radius of $\mathbf{F}{\mathbf{V}}^{-1}$ (i.e., ${\mathcal{R}}_0=\rho \left(\mathbf{F}{\mathbf{V}}^{-1}\right)$) is given as

$${\mathfrak{R}}_0=\frac{\beta (1-\rho )}{k_1}(\frac{\tau \sigma {\theta }_1}{k_2}+\frac{(1-\sigma ){\theta }_2}{k_3}).$$ (3.13)

The basic reproduction number (3.13) is a non-dimensionless epidemiological quantity which reflects the average number of secondary COVID-19 cases generated by a single typical COVID-19 infective individual within a completely susceptible population. Note that we can also express the basic reproduction number (3.13) as

$${\mathfrak{R}}_0={\mathcal{R}}_{\text{asy}}+{\mathcal{R}}_{\text{sym}}$$

where

$${\mathfrak{R}}_{\text{asy}}=\frac{(1-\rho )\sigma \tau \beta {\theta }_1}{k_1{k}_2}$$

is the average number of secondary COVID-19 cases generated by a single asymptomatic COVID-19 individual within a completely susceptible population and

$${\mathfrak{R}}_{\text{sym}}=\frac{(1-\rho )(1-\sigma )\beta {\theta }_1}{k_1{k}_3}.$$

is the average number of secondary COVID-19 cases generated by a single symptomatic infected individual within a completely susceptible population.

4. Existence and uniqueness analysis

Since there exists no technique for constructing exact solutions of time-fractional system of equations of the type (3.4), we employ a fixed-point approach to investigate conditions under which the existence and uniqueness of solutions to the model is assured. To this end, we use the following notations for the right hand side of each equation in (3.4):

$$\{\begin{array}{c}{\displaystyle {\mathcal{G}}_1(t,\mathcal{S},\mathcal{E},\mathcal{A},\mathcal{I},\mathcal{H},\mathcal{R})=\Pi -(1-\rho )\lambda \left(t\right)\mathcal{S}-\mu \mathcal{S},}\hfill \\ {\displaystyle {\mathcal{G}}_2(t,\mathcal{E},\mathcal{E},\mathcal{A},\mathcal{I},\mathcal{H},\mathcal{R})=(1-\rho )\lambda \left(t\right)\mathcal{S}-({\theta }_1\sigma +{\theta }_2(1-\sigma )+\mu )\mathcal{E},}\hfill \\ {\displaystyle {\mathcal{G}}_3(t,\mathcal{A},\mathcal{E},\mathcal{A},\mathcal{I},\mathcal{H},\mathcal{R})={\theta }_1\sigma \mathcal{E}-({\varphi }_1+{\phi }_1+\mu )\mathcal{A},}\hfill \\ {\displaystyle {\mathcal{G}}_4(t,\mathcal{I},\mathcal{E},\mathcal{A},\mathcal{I},\mathcal{H},\mathcal{R})={\theta }_2(1-\sigma )\mathcal{E}-({\varphi }_2+{\phi }_2+d_1+\mu )\mathcal{I},}\hfill \\ {\displaystyle {\mathcal{G}}_5(t,\mathcal{H},\mathcal{E},\mathcal{A},\mathcal{I},\mathcal{H},\mathcal{R})={\varphi }_1\mathcal{A}+{\varphi }_2\mathcal{I}-({\phi }_3+d_2+\mu )\mathcal{H},}\hfill \\ {\displaystyle {\mathcal{G}}_6(t,\mathcal{R},\mathcal{E},\mathcal{A},\mathcal{I},\mathcal{H},\mathcal{R})={\phi }_1\mathcal{A}+{\phi }_2\mathcal{I}+{\phi }_3\mathcal{H}-\mu \mathcal{R},}\hfill \end{array}$$ (4.1)

and reformulate the model as

$$\{\begin{array}{c}{}_0^{\mathbb{ABC}}{D}_t^{\vartheta }\mathcal{U}\left(t\right)=\mathcal{G}(t,\mathcal{U}\left(t\right)),t\in \mathcal{J}:=[0,T],0<\vartheta \le 1\hfill \\ \mathcal{U}\left(0\right)={\mathcal{U}}_0\ge 0,\hfill \end{array}$$ (4.2)

where

$$\mathcal{U}\left(t\right):=\left(\begin{array}{c}\mathcal{S}\left(t\right)\\ \mathcal{E}\left(t\right)\\ \mathcal{A}\left(t\right)\\ \mathcal{I}\left(t\right)\\ \mathcal{H}\left(t\right)\\ \mathcal{R}\left(t\right)\end{array}\right),\mathcal{U}\left(0\right):=\left(\begin{array}{c}\mathcal{S}\left(0\right)\\ \mathcal{E}\left(0\right)\\ \mathcal{A}\left(0\right)\\ \mathcal{I}\left(0\right)\\ \mathcal{H}\left(0\right)\\ \mathcal{R}\left(0\right)\end{array}\right),\mathcal{G}(t,\mathcal{U}\left(t\right)):=\left(\begin{array}{c}{\mathcal{G}}_1(t,\mathcal{S},\mathcal{E},\mathcal{A},\mathcal{I},\mathcal{H},\mathcal{R})\\ {\mathcal{G}}_2(t,\mathcal{E},\mathcal{E},\mathcal{A},\mathcal{I},\mathcal{H},\mathcal{R})\\ {\mathcal{G}}_3(t,\mathcal{A},\mathcal{E},\mathcal{A},\mathcal{I},\mathcal{H},\mathcal{R})\\ {\mathcal{G}}_4(t,\mathcal{I},\mathcal{E},\mathcal{A},\mathcal{I},\mathcal{H},\mathcal{R})\\ {\mathcal{G}}_5(t,\mathcal{H},\mathcal{E},\mathcal{A},\mathcal{I},\mathcal{H},\mathcal{R})\\ {\mathcal{G}}_6(t,\mathcal{R},\mathcal{E},\mathcal{A},\mathcal{I},\mathcal{H},\mathcal{R})\end{array}\right).$$ (4.3)

Thanks to Lemma 2.3, the solution of the fractional IVP (4.2) is given by the following nonlinear Volterra-type integral representation

$$\mathcal{U}\left(t\right)=\mathcal{U}\left(0\right)+\frac{1-\vartheta }{\mathbb{ABC}\left(\vartheta \right)}\mathcal{G}(t,\mathcal{U}\left(t\right))+\frac{\vartheta }{\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}{\int }_0^t{(t-s)}^{\vartheta -1}\mathcal{G}(s,\mathcal{U}\left(s\right))ds.$$ (4.4)

Therefore, the problem of investigating the existence of a unique of solution to the fractional COVID-19 model (3.4)-(3.5) (rewritten as the fractional IVP (4.2)) is equivalent to that of investigating the existence and uniqueness of solutions to the equivalent non-linear integral Eq. (4.4). For this purpose, we introduce the Banach space $\mathcal{W}=C(\mathcal{J},{\mathbb{R}}_{+}^6)$ with respect to the supremum norm

$${\displaystyle \parallel \mathcal{U}\left(t\right)\parallel :=\underset{t\in \mathcal{J}}{\sup }\left\{\right|\mathcal{U}\left(t\right)|:\mathcal{U}\in \mathcal{W}\}}$$

where

$${\displaystyle \underset{t\in \mathcal{J}}{\sup }\left|\mathcal{U}\left(t\right)\right|=\underset{t\in \mathcal{J}}{\sup }\left[\right|\mathcal{S}\left(t\right)|+\left|\mathcal{E}\left(t\right)\right|+\left|\mathcal{A}\left(t\right)\right|+\left|\mathcal{I}\left(t\right)\right|+\left|\mathcal{H}\left(t\right)\right|+\left|\mathcal{R}\left(t\right)\right|]}$$

and $\mathcal{S}\left(t\right),\mathcal{E}\left(t\right),\mathcal{A}\left(t\right),\mathcal{I}\left(t\right),\mathcal{H}\left(t\right),\mathcal{R}\left(t\right)\in C(\mathcal{J},{\mathbb{R}}_{+})$. Clearly, by defining the operator $\Xi :\mathcal{W}⟶\mathcal{W}$ as

$$\Xi \left[\mathcal{U}\right(t\left)\right]:=\mathbf{F}\left[\mathcal{U}\right(t\left)\right]+\mathbf{G}\left[\mathcal{U}\right(t\left)\right],$$ (4.5)

where

$$\mathbf{F}\left[\mathcal{U}\left(t\right)\right]=\mathcal{U}\left(0\right)+\frac{1-\vartheta }{\mathbb{ABC}\left(\vartheta \right)}\mathcal{G}(t,\mathcal{U}\left(t\right)),$$ (4.6)

and

$$\mathbf{G}\left[\mathcal{U}\left(t\right)\right]=\frac{\vartheta }{\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}{\int }_0^t{(t-s)}^{\vartheta -1}\mathcal{G}(s,\mathcal{U}\left(s\right))ds,$$ (4.7)

the fractional integral Eq. (4.4) can be reformulated as the fixed point problem:

$$\mathcal{U}\left(t\right)=\Xi \left[\mathcal{U}\right(t\left)\right].$$ (4.8)

Furthermore, we assume that the following Lipschitz condition and linear growth bound are satisfied by the nonlinear function $\mathcal{G}:\mathcal{J}\times {\mathbb{R}}_{+}^6⟶{\mathbb{R}}_{+}^6$ appearing in (4.4):

• •
  (C1) There exists a constant $L_{\mathcal{G}}>0$ such that

  $$\parallel \mathcal{G}(t,{\mathcal{U}}^{*}\left(t\right))-\mathcal{G}(t,{\mathcal{U}}^{**}\left(t\right))\parallel \le L_{\mathcal{G}}\parallel {\mathcal{U}}^{*}\left(t\right)-{\mathcal{U}}^{**}\left(t\right)\parallel ,t\in \mathcal{J},{\mathcal{U}}^{*},{\mathcal{U}}^{**}\in \mathcal{W},$$
• •
  (C2) There exist constants $C_{\mathcal{G}}>0$ and $M_{\mathcal{G}}>0$ such that

  $$\parallel \mathcal{G}(t,\mathcal{U}\left(t\right))\parallel \le C_{\mathcal{G}}\parallel \mathcal{U}\left(t\right)\parallel +M_{\mathcal{G}},t\in \mathcal{J},\mathcal{U}\in \mathcal{W}.$$

Theorem 4.1

Consider the fractional COVID-19(3.4)in the form(4.2). Then under assumptions (C1) and (C2), the equivalent integral Eq.(4.4)admits at least one solution. As a consequence, the considered model(3.4)admits at least one solution.

Proof

Let ${\mathcal{B}}_{\gamma }:=\{\mathbb{U}\in {\mathcal{W}:\parallel \mathcal{U}\parallel }_{\mathcal{W}}\le \gamma ,\gamma >0\}$ be a closed, convex bounded subset of $\mathcal{W}$ with $\gamma \ge \frac{{\Theta }_1}{1-{\Theta }_2}$ where

$${\Theta }_1=\mathcal{U}\left(0\right)+[\frac{1-\vartheta }{\mathbb{ABC}\left(\vartheta \right)}+\frac{T^{\vartheta }}{\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}]M_{\mathcal{G}}\text{and}{\Theta }_2=[\frac{1-\vartheta }{\mathbb{ABC}\left(\vartheta \right)}+\frac{T^{\vartheta }}{\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}]C_{\mathcal{G}}.$$

We establish the result of the theorem in the following three steps.

Step I: First we show that $\Xi \left[\mathcal{U}\left(t\right)\right]=\mathbf{F}\left[\mathcal{U}\left(t\right)\right]+\mathbf{G}\left[\mathcal{U}\left(t\right)\right]\in {\mathcal{B}}_{\gamma }$ for $t\in \mathcal{J}$ and $\mathcal{U}\in {\mathcal{B}}_{\gamma }$. Indeed, by the assumption $\left(\mathit{C2}\right)$ we have

$$\begin{array}{cc}{\displaystyle \parallel \Xi \left[\mathcal{U}\right(t\left)\right]\parallel }\hfill & {\displaystyle \le \underset{t\in \mathcal{J}}{\sup }\{\mathbb{U}\left(0\right)+\frac{1-\vartheta }{\mathbb{ABC}\left(\vartheta \right)}\left|\mathcal{G}(t,\mathcal{U}\left(t\right))\right|+\frac{\vartheta }{\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}{\int }_0^t{(t-s)}^{\vartheta -1}\left|\mathcal{G}(s,\mathcal{U}\left(s\right))\right|ds\}}\hfill \\ & {\displaystyle \le \mathcal{U}\left(0\right)+\frac{1-\vartheta }{\mathbb{ABC}\left(\vartheta \right)}[C_{\mathcal{G}}\underset{t\in \mathcal{J}}{\sup }\left|\mathcal{U}\left(t\right)\right|+M_{\mathcal{G}}]+\frac{\vartheta }{\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}{\int }_0^t{(t-s)}^{\vartheta -1}[C_{\mathcal{G}}\underset{t\in \mathcal{J}}{\sup }\left|\mathcal{U}\left(t\right)\right|+M_{\mathcal{G}}]ds}\hfill \\ & {\displaystyle =\mathcal{U}\left(0\right)+\frac{1-\vartheta }{\mathbb{ABC}\left(\vartheta \right)}[C_{\mathcal{G}}\parallel \mathcal{U}\left(t\right)\parallel +M_{\mathcal{G}}]+\frac{\vartheta }{\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}{\int }_0^t{(t-s)}^{\vartheta -1}[C_{\mathcal{G}}\parallel \mathcal{U}\left(t\right)\parallel +M_{\mathcal{G}}]ds}\hfill \\ & {\displaystyle =\mathcal{U}\left(0\right)+[\frac{1-\vartheta }{\mathbb{ABC}\left(\vartheta \right)}+\frac{T^{\vartheta }}{\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}]M_{\mathcal{G}}+[\frac{1-\vartheta }{\mathbb{ABC}\left(\vartheta \right)}+\frac{T^{\vartheta }}{\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}]C_{\mathcal{G}}\gamma .}\hfill \end{array}$$

Thus we have

$$\parallel \Xi \left[\mathcal{U}\left(t\right)\right]\parallel \le {\Theta }_1+\gamma {\Theta }_2\le \gamma .$$ (4.9)

Hence, the operator $\Xi$ maps ${\mathcal{B}}_{\gamma }$ into itself.

Step II: Next, we establish that the operator $\mathbf{F}:{\mathcal{B}}_{\gamma }\to {\mathcal{B}}_{\gamma }$ is a contraction provided that $\frac{1-\vartheta }{\mathbb{ABC}\left(\vartheta \right)}{L}_{\mathcal{G}}<1$. To this end, let ${\mathcal{U}}^{*},{\mathcal{U}}^{**}\in {\mathcal{B}}_{\gamma }$ and $t\in \mathcal{J}$. Then by assumption $\left(\mathbf{C}\mathbf{1}\right)$ we have

$$\begin{array}{cc}{\displaystyle \parallel \mathbf{F}\left[{\mathcal{U}}^{*}\left(t\right)\right]-\mathbf{F}\left[{\mathcal{U}}^{**}\left(t\right)\right]\parallel }\hfill & =\underset{t\in \mathcal{J}}{\sup }\left|\frac{1-\vartheta }{\mathbb{ABC}\left(\vartheta \right)}\right(\mathcal{G}(t,{\mathcal{U}}^{*}\left(t\right))-\mathcal{G}(t,{\mathcal{U}}^{**}\left(t\right))\left)\right|\hfill \\ & {\displaystyle \le \frac{1-\vartheta }{\mathbb{ABC}\left(\vartheta \right)}{L}_{\mathcal{G}}\underset{t\in \mathcal{J}}{\sup }|{\mathcal{U}}^{*}\left(t\right)-{\mathcal{U}}^{**}\left(t\right)|}\hfill \\ & {\displaystyle =\frac{1-\vartheta }{\mathbb{ABC}\left(\vartheta \right)}{L}_{\mathcal{G}}\parallel {\mathcal{U}}^{*}\left(t\right)-{\mathcal{U}}^{**}\left(t\right)\parallel .}\hfill \end{array}$$

Clearly, under the condition that $\frac{1-\vartheta }{\mathbb{ABC}\left(\vartheta \right)}{L}_{\mathcal{G}}<1$, the operator $\mathbf{F}$ is a contraction mapping.

Step III: Lastly, we show that the operator is $\mathbf{G}$ is relatively compact (that is, continuous, uniformly bounded and equi-continuous). To prove that $\mathbf{G}$ given by (4.7) is continuous, let $\left\{{\mathcal{U}}_n\right\}$ be a sequence such that ${\mathcal{U}}_n⟶\mathcal{U}$ as $n⟶\infty$ in ${\mathcal{B}}_{\gamma }$. Then for $t\in \mathcal{J}$ we have

$$\begin{array}{cc}{\displaystyle \parallel \mathbf{G}\left[{\mathcal{U}}_n\left(t\right)\right]-\mathbf{G}\left[\mathcal{U}\left(t\right)\right]\parallel }\hfill & =\underset{t\in \mathcal{J}}{\sup }\left|\frac{\vartheta }{\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}{\int }_0^t{(t-s)}^{\vartheta -1}\right[\mathcal{G}(s,{\mathcal{U}}_n\left(s\right))-\mathcal{G}(s,\mathcal{U}\left(s\right))\left]ds\right|\hfill \\ & {\displaystyle \le \frac{\vartheta }{\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}{\int }_0^t{(t-s)}^{\vartheta -1}\underset{t\in \mathcal{J}}{\sup }|\mathcal{G}(s,{\mathcal{U}}_n\left(s\right))-\mathcal{G}(s,\mathcal{U}\left(s\right))|ds}\hfill \\ & {\displaystyle \le \frac{T^{\vartheta }}{\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}\parallel \mathcal{G}(s,{\mathcal{U}}_n\left(s\right))-\mathcal{G}(s,\mathcal{U}\left(s\right))\parallel .}\hfill \end{array}$$

Hence, since $\mathcal{G}$ is continuous and ${\mathcal{U}}_n⟶\mathbb{U}$, the operator $\mathbf{G}$ is also continuous. To establish uniform boundedness of $\mathbf{G}$ on ${\mathcal{B}}_{\gamma }$ and let $\mathcal{U}\in {\mathcal{B}}_{\gamma }$. Then for $t\in \mathcal{J}$ we have

$$\begin{array}{cc}{\displaystyle \parallel \mathbf{G}\left[\mathcal{U}\right(t\left)\right]\parallel }\hfill & =\underset{t\in \mathcal{J}}{\sup }\left|\frac{\vartheta }{\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}{\int }_0^t{(t-s)}^{\vartheta -1}\mathcal{G}(s,\mathcal{U}\left(s\right))ds\right|\hfill \\ & {\displaystyle \le \frac{\vartheta }{\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}{\int }_0^t{(t-s)}^{\vartheta -1}\underset{t\in \mathcal{J}}{\sup }\left|\mathcal{G}(s,\mathcal{U}\left(s\right))\right|ds}\hfill \\ & {\displaystyle \le \frac{\vartheta }{\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}{\int }_0^t{(t-s)}^{\vartheta -1}[C_{\mathcal{G}}\underset{t\in \mathcal{J}}{\sup }\left|\mathcal{U}\left(s\right)\right|+M_{\mathcal{G}}]ds}\hfill \\ & {\displaystyle =\frac{\vartheta }{\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}{\int }_0^t{(t-s)}^{\vartheta -1}[C_{\mathcal{G}}\parallel \mathcal{U}\left(s\right)\parallel +M_{\mathcal{G}}]ds}\hfill \\ & {\displaystyle \le \frac{T^{\vartheta }}{\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}[C_{\mathcal{G}}\gamma +M_{\mathcal{G}}].}\hfill \end{array}$$

Hence, the operator $\mathbf{G}$ is uniformly bounded on ${\mathcal{B}}_{\gamma }$. Lastly, for the equicontinuity of $\mathbf{G}$, tet $\mathcal{U}\in {\mathcal{B}}_{\gamma }$ and $t_1,t_2\in \mathcal{J}$ with $t_1<t_2$. Then

$$\begin{array}{cc}& {\displaystyle \parallel \mathbf{G}\left[\mathcal{U}\left(t_2\right)\right]-\mathbf{G}\left[\mathcal{U}\left(t_1\right)\right]\parallel }\hfill \\ & {\displaystyle =\underset{t\in \mathcal{J}}{\sup }|\frac{\vartheta }{\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}{\int }_0^{t_2}{(t_2-\tau )}^{\vartheta -1}\mathcal{G}(s,\mathcal{U}\left(s\right))ds-\frac{\vartheta }{\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}{\int }_0^{t_1}{(t_1-\tau )}^{\vartheta -1}\mathcal{G}(s,\mathcal{U}\left(s\right))ds|}\hfill \\ & {\displaystyle =\underset{t\in \mathcal{J}}{\sup }|\frac{\vartheta }{\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}{\int }_0^{t_1}{(t_2-\tau )}^{\vartheta -1}\mathcal{G}(s,\mathcal{U}\left(s\right))ds+{\int }_{t_1}^{t_2}{(t_2-\tau )}^{\vartheta -1}\mathcal{G}(s,\mathcal{U}\left(s\right))ds}\hfill \\ & {\displaystyle -\frac{\vartheta }{\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}{\int }_0^{t_1}{(t_1-\tau )}^{\vartheta -1}\mathcal{G}(s,\mathcal{U}\left(s\right))ds|}\hfill \\ & {\displaystyle \le \frac{\vartheta }{\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}{\int }_{t_1}^{t_2}{(t_2-\tau )}^{\vartheta -1}(C_{\mathcal{G}}\underset{t\in \mathcal{J}}{\sup }\left|\mathcal{U}\left(s\right)\right|+M_{\mathcal{G}})ds}\hfill \\ & {\displaystyle +\frac{\vartheta }{\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}{\int }_0^{t_1}({(t_2-\tau )}^{\vartheta -1}-{(t_1-\tau )}^{\vartheta -1})(C_{\mathcal{G}}\underset{t\in \mathcal{J}}{\sup }\left|\mathcal{U}\left(s\right)\right|+M_{\mathcal{G}})ds}\hfill \\ & {\displaystyle \le \left(\frac{(t_1^{\vartheta }-t_2^{\vartheta })+2{(t_2-t_1)}^{\vartheta }}{\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}\right)(C_{\mathcal{G}}\gamma +M_{\mathcal{G}}).}\hfill \end{array}$$

This implies that if $t_1⟶t_2$ then $\parallel \mathbf{G}\left[\mathcal{U}\left(t_2\right)\right]-\mathbf{G}\left[\mathcal{U}\left(t_1\right)\right]\parallel ⟶0$. Hence the operator $\mathbf{G}$ is equi-continuous on ${\mathcal{B}}_{\gamma }$. A direct application of the Arzelà-Ascoli Theorem ensures that the operator $\mathbf{G}$ is relatively compact. Therefore, in view of Theorem 2.7, the integral Eq. (4.4) admits at least one solution. Consequently, the considered fractional model (3.4) has at least one solution. □

Theorem 4.2

Consider the Covid-19 model(3.4)in the form(4.2). Then under the assumption that (C1) holds with

$$[\frac{1-\vartheta }{\mathbb{ABC}\left(\vartheta \right)}+\frac{T^{\vartheta }}{\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}]L_{\mathcal{G}}<1,$$ (4.10)

the fractional initial value problem(4.2)$⟺$(3.4)admits a unique solution on$\mathcal{J}$.

Proof

Considering (4.8), let ${\mathcal{U}}^{*}$ and ${\mathcal{U}}^{**}$ be two solutions of (4.2) in $\mathcal{W}$ and $t\in \mathcal{J}$. Then

$$\begin{array}{cc}{\displaystyle \parallel \Xi \left[{\mathcal{U}}^{*}\left(t\right)\right]}\hfill & {\displaystyle -\Xi \left[{\mathcal{U}}^{**}\left(t\right)\right]\parallel }\hfill \\ & {\displaystyle \le \left|\frac{1-\vartheta }{\mathbb{ABC}\left(\vartheta \right)}\underset{t\in \mathcal{J}}{\sup }\right(\mathcal{G}(t,{\mathcal{U}}^{*}\left(t\right))-\mathcal{G}(t,{\mathcal{U}}^{**}\left(t\right))\left)\right|}\hfill \\ & {\displaystyle +\left|\frac{\vartheta }{\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}\underset{t\in \mathcal{J}}{\sup }{\int }_0^t{(t-s)}^{\vartheta -1}\right(\mathcal{G}(t,{\mathcal{U}}^{*}\left(s\right))-\mathcal{G}(t,{\mathcal{U}}^{**}\left(s\right))\left)ds\right|}\hfill \\ & {\displaystyle \le \frac{1-\vartheta }{\mathbb{ABC}\left(\vartheta \right)}\parallel {\mathcal{U}}^{*}\left(t\right)-{\mathcal{U}}^{**}\left(t\right)\parallel +\frac{T^{\vartheta }}{\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}\parallel {\mathcal{U}}^{*}\left(t\right)-{\mathcal{U}}^{**}\left(t\right)\parallel }\hfill \\ & {\displaystyle =[\frac{1-\vartheta }{\mathbb{ABC}\left(\vartheta \right)}+\frac{T^{\vartheta }}{\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}]L_{\mathcal{G}}\parallel {\mathcal{U}}^{*}\left(t\right)-{\mathcal{U}}^{**}\left(t\right)\parallel .}\hfill \end{array}$$

With respect to (4.10), the operator $\Xi$ is a contraction mapping. Therefore the integral Eq. (4.4) admits a unique solution. Consequently, the fractional model (3.4) admits a unique solution. □

5. Stability (Ulam-Hyers stability)

In this section, we establish some results related to stability of Ulam-Hyers type for the proposed fractional model (3.4).

Definition 5.1

The fractional order model (3.4) considered in the form (4.2) is said to be Ulam-Hyers stable if there exist a number ${\mathcal{C}}_{\mathcal{G}}>0$ with the following property: for each $\epsilon >0$ and every solution ${\mathcal{U}}^{*}\in \mathcal{W}$ satisfying the inequality

$${\parallel }_0^{\mathbb{ABC}}{D}_t^{\vartheta }{\mathcal{U}}^{*}\left(t\right)-\mathcal{G}(t,{\mathcal{U}}^{*}\left(t\right))\parallel \le \epsilon ,t\in \mathcal{J},$$ (5.1)

there exists a unique solution $\mathcal{U}\in \mathcal{W}$ of (4.2) with initial condition $\mathcal{U}\left(0\right)={\mathcal{U}}^{*}\left(0\right)$ such that

$$\parallel {\mathcal{U}}^{*}\left(t\right)-\mathcal{U}\left(t\right)\parallel \le {\mathcal{C}}_{\mathcal{G}}\epsilon ,\text{for}\text{all}t\in \mathcal{J},$$ (5.2)

where

$${\mathcal{U}}^{*}\left(t\right):=\left(\begin{array}{c}{\mathcal{S}}^{*}\left(t\right)\\ {\mathcal{E}}^{*}\left(t\right)\\ {\mathcal{A}}^{*}\left(t\right)\\ {\mathcal{I}}^{*}\left(t\right)\\ {\mathcal{H}}^{*}\left(t\right)\\ {\mathcal{R}}^{*}\left(t\right)\end{array}\right),{\mathcal{U}}^{*}\left(0\right):=\left(\begin{array}{c}{\mathcal{S}}^{*}\left(0\right)\\ {\mathcal{E}}^{*}\left(0\right)\\ {\mathcal{A}}^{*}\left(0\right)\\ {\mathcal{I}}^{*}\left(0\right)\\ {\mathcal{H}}^{*}\left(0\right)\\ {\mathcal{R}}^{*}\left(0\right)\end{array}\right),\mathcal{G}(t,{\mathcal{U}}^{*}\left(t\right)):=\left(\begin{array}{c}{\mathcal{G}}_1(t,{\mathcal{S}}^{*},{\mathcal{E}}^{*},{\mathcal{A}}^{*},{\mathcal{I}}^{*},{\mathcal{H}}^{*},{\mathcal{R}}^{*})\\ {\mathcal{G}}_2(t,{\mathcal{S}}^{*},{\mathcal{E}}^{*},{\mathcal{A}}^{*},{\mathcal{I}}^{*},{\mathcal{H}}^{*},{\mathcal{R}}^{*})\\ {\mathcal{G}}_3(t,{\mathcal{S}}^{*},{\mathcal{E}}^{*},{\mathcal{A}}^{*},{\mathcal{I}}^{*},{\mathcal{H}}^{*},{\mathcal{R}}^{*})\\ {\mathcal{G}}_4(t,{\mathcal{S}}^{*},{\mathcal{E}}^{*},{\mathcal{A}}^{*},{\mathcal{I}}^{*},{\mathcal{H}}^{*},{\mathcal{R}}^{*})\\ {\mathcal{G}}_5(t,{\mathcal{S}}^{*},{\mathcal{E}}^{*},{\mathcal{A}}^{*},{\mathcal{I}}^{*},{\mathcal{H}}^{*},{\mathcal{R}}^{*})\\ {\mathcal{G}}_6(t,{\mathcal{S}}^{*},{\mathcal{E}}^{*},{\mathcal{A}}^{*},{\mathcal{I}}^{*},{\mathcal{H}}^{*},{\mathcal{R}}^{*})\end{array}\right),$$

and

$$\epsilon =\max \left(\begin{array}{c}{\epsilon }_1\\ {\epsilon }_2\\ {\epsilon }_3\\ {\epsilon }_4\\ {\epsilon }_5\\ {\epsilon }_6\end{array}\right),{\mathcal{C}}_{\mathcal{G}}:=\max \left(\begin{array}{c}{\mathcal{C}}_{{\mathcal{G}}_1}\\ {\mathcal{C}}_{{\mathcal{G}}_2}\\ {\mathcal{C}}_{{\mathcal{G}}_3}\\ {\mathcal{C}}_{{\mathcal{G}}_4}\\ {\mathcal{C}}_{{\mathcal{G}}_5}\\ {\mathcal{C}}_{{\mathcal{G}}_6}\end{array}\right).$$

We refer to such ${\mathcal{C}}_{\mathcal{G}}$ an Ulam-Hyers stability constant for the fractional order problem (3.4).

Definition 5.2

The aforementioned fractional problem(4.2)is said to be generalized Ulam-Hyers stable if there exists a continuous function${\Pi }_{\mathcal{G}}:\mathcal{J}\to {\mathbb{R}}_{+}$with${\Pi }_{\mathcal{G}}\left(0\right)=0$such that for each${\mathcal{U}}^{*}\in \mathcal{W}$satisfying(5.1), there exists a unique solution$\mathcal{U}\in \mathcal{W}$of(4.2)such that

$$\parallel {\mathcal{U}}^{*}\left(t\right)-\mathcal{U}\left(t\right)\parallel \le {\Pi }_{\mathcal{G}}\left(\epsilon \right),\text{for}\text{all}t\in \mathcal{J}.$$ (5.3)

Remark 5.3

Concerning the stability analysis of the model, we consider a small perturbation $\Phi \left(t\right)\in C\left(\mathcal{J}\right)$ such that $\Phi \left(0\right)=0$ and the following properties are satisfied:

• (i)$\left|\Phi \right(t\left)\right|\le \epsilon$ for $t\in \mathcal{J}$ and $\epsilon >0$;
• (ii)${}_0^{\mathbb{ABC}}{D}_t^{\vartheta }{\mathcal{U}}^{*}\left(t\right)=\mathcal{G}(t,{\mathcal{U}}^{*}\left(t\right))+\Phi \left(t\right)$, for all $t\in \mathcal{J}$,

where $\Phi \left(t\right)={({\Phi }_1\left(t\right),{\Phi }_2\left(t\right),{\Phi }_3\left(t\right),{\Phi }_4\left(t\right),{\Phi }_5\left(t\right),{\Phi }_6\left(t\right))}^{\top }$.

Lemma 5.4

The solution${\mathcal{U}}_{\Phi }^{*}\left(t\right)$of the perturbed problem

$$\{\begin{array}{c}{}_0^{\mathbb{ABC}}{D}_t^{\vartheta }{\mathcal{U}}^{*}\left(t\right)=\mathcal{G}(t,{\mathcal{U}}^{*}\left(t\right))+\Phi \left(t\right),\text{for}\text{all}t\in \mathcal{J},\hfill \\ {\mathcal{U}}^{*}\left(0\right)={\mathcal{U}}_0^{*},\hfill \end{array}$$ (5.4)

satisfies the inequality

$$|{\mathcal{U}}_{\Phi }^{*}\left(t\right)-{\mathcal{U}}^{*}\left(t\right)|\le \Theta \epsilon ,$$ (5.5)

where${\mathcal{U}}_{\Phi }^{*}$is a solution of(5.5),${\mathcal{U}}^{*}$satisfies(5.1)and$\Theta :=[\frac{1-\vartheta }{\mathbb{ABC}\left(\vartheta \right)}+\frac{T^{\vartheta }}{\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}].$

Proof

Thanks to Lemma 2.3, the solution of the fractional problem (5.5) is given by

$$\begin{array}{cc}{\displaystyle {\mathcal{U}}_{\Phi }^{*}\left(t\right)=}\hfill & {\displaystyle {\mathcal{U}}_0^{*}+\frac{1-\vartheta }{\mathbb{ABC}\left(\vartheta \right)}[\mathcal{G}(t,{\mathcal{U}}^{*}\left(t\right))+\Phi \left(t\right)]}\hfill \\ & {\displaystyle +\frac{\vartheta }{\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}{\int }_0^t{(t-s)}^{\vartheta -1}[\mathcal{G}(s,{\mathcal{U}}^{*}\left(s\right))+\Phi \left(t\right)]ds.}\hfill \end{array}$$ (5.6)

Also, we have

$${\mathcal{U}}^{*}\left(t\right)={\mathcal{U}}_0^{*}+\frac{1-\vartheta }{\mathbb{ABC}\left(\vartheta \right)}\mathcal{G}(t,{\mathcal{U}}^{*}\left(t\right))+\frac{\vartheta }{\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}{\int }_0^t{(t-s)}^{\vartheta -1}\mathcal{G}(s,{\mathcal{U}}^{*}\left(s\right))ds.$$ (5.7)

It follows from Remark 5.3 that

$$\begin{array}{cc}{\displaystyle |{\mathcal{U}}_{\Phi }^{*}\left(t\right)-{\mathcal{U}}^{*}\left(t\right)|}\hfill & \le \frac{1-\vartheta }{\mathbb{ABC}\left(\vartheta \right)}\left|\Phi \left(t\right)\right|+\frac{\vartheta }{\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}{\int }_0^t{(t-s)}^{\vartheta -1}\left|\Phi \left(t\right)\right|ds\hfill \\ & {\displaystyle \le [\frac{1-\vartheta }{\mathbb{ABC}\left(\vartheta \right)}+\frac{T^{\vartheta }}{\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}]\epsilon .}\hfill \end{array}$$ (5.8)

This implies

$$|{\mathcal{U}}_{\Phi }^{*}\left(t\right)-{\mathcal{U}}^{*}\left(t\right)|\le \Theta \epsilon .$$ (5.9)

 □

Theorem 5.5

Under the assumptions of Lemma5.4, the solution of the fractional IVP is Ulam-Hyers and also generalized Ulam-Hyers stable in$\mathcal{W}$if

$$(1-\Theta L_{\mathcal{G}})>0.$$

Consequently, the model fractional model(3.4)) is both Ulam-Hyers and generalized Ulam-Hyers stable in$\mathcal{W}$.

Proof

Suppose ${\mathcal{U}}^{*}\in \mathcal{W}$ satisfies the inequality (5.1) and ${\mathcal{U}}^{*}$ be a unique solution of the problem (4.2) with the initial condition $\mathcal{U}\left(0\right)={\mathcal{U}}^{*}\left(0\right)⟺{\mathcal{U}}_0={\mathcal{U}}_0^{*}$. Then it follows from Lemma 2.3 that

$$\mathcal{U}\left(t\right)={\mathcal{U}}_0^{*}+\frac{1-\vartheta }{\mathbb{ABC}\left(\vartheta \right)}\mathcal{G}(t,\mathcal{U}\left(t\right))+\frac{\vartheta }{\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}{\int }_0^t{(t-s)}^{\vartheta -1}\mathcal{G}(s,\mathcal{U}\left(s\right))ds.$$ (5.10)

By (5.11), assumption $\left(\mathbf{C}\mathbf{1}\right)$ and Lemma 5.4, we have

$$\begin{array}{cc}{\displaystyle \parallel {\mathcal{U}}^{*}\left(t\right)-\mathcal{U}\left(t\right)\parallel }\hfill & {\displaystyle \le \underset{t\in \mathcal{J}}{\sup }|{\mathcal{U}}^{*}\left(t\right)-{\mathcal{U}}_{\Phi }^{*}\left(t\right)|+\underset{t\in \mathcal{J}}{\sup }|{\mathcal{U}}_{\Phi }^{*}\left(t\right)-\mathcal{U}\left(t\right)|}\hfill \\ & {\displaystyle \le 2\Theta \epsilon +\frac{1-\vartheta }{\mathbb{ABC}\left(\vartheta \right)}\underset{t\in \mathcal{J}}{\sup }|\mathcal{G}(t,{\mathcal{U}}^{*}\left(t\right))-\mathcal{G}(t,\mathcal{U}\left(t\right))|}\hfill \\ & {\displaystyle +\frac{\vartheta }{\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}\underset{t\in \mathcal{J}}{\sup }{\int }_0^t{(t-s)}^{\vartheta -1}|\mathcal{G}(t,{\mathcal{U}}^{*}\left(t\right))-\mathcal{G}(t,\mathcal{U}\left(t\right))|ds}\hfill \\ & {\displaystyle \le 2\Theta \epsilon +[\frac{1-\vartheta }{\mathbb{ABC}\left(\vartheta \right)}+\frac{T^{\vartheta }}{\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}]L_{\mathcal{G}}\parallel {\mathcal{U}}^{*}\left(t\right)-\mathcal{U}\left(t\right)\parallel .}\hfill \end{array}$$ (5.11)

This implies

$$\parallel {\mathcal{U}}^{*}\left(t\right)-\mathcal{U}\left(t\right)\parallel \le \frac{2\Theta }{1-\Theta L_{\mathcal{G}}}\epsilon .$$ (5.12)

For ${\mathcal{C}}_{\mathcal{G}}:=\frac{2\Theta }{1-\Theta L_{\mathcal{G}}}$ with $1-\Theta L_{\mathcal{G}}>0$, the inequality in (5.12) implies

$$\parallel {\mathcal{U}}^{*}\left(t\right)-\mathcal{U}\left(t\right)\parallel \le {\mathcal{C}}_{\mathcal{G}}\epsilon .$$ (5.13)

Hence, the solution of the fractional IVP (4.2) is Ulam-Hyers stable. Moreover, by setting ${\mathcal{U}}_{\mathcal{G}}\left(\epsilon \right)={\mathcal{C}}_{\mathcal{G}}\epsilon$ with ${\mathcal{U}}_{\mathcal{G}}\left(0\right)=0$ such that

$$\parallel {\mathcal{U}}^{*}\left(t\right)-\mathcal{U}\left(t\right)\parallel \le {\Pi }_{\mathcal{G}}\left(\epsilon \right),$$ (5.14)

the fractional IVP (4.2) is also generalized Ulam-Hyers stable. Therefore, the proposed model (3.4) is both Ulam-Hyers stable and generalized Ulam-Hyers stable. □

6. Two-step Adams-Bashforth scheme for the considered model

Motivated by the fractional two-step Adams-Bashforth scheme introduced by Atangana and Owolabi [36], we present the corresponding numerical scheme for the approximate solutions to the fractional system of Eq. (3.4) in $\mathbb{ABC}$ derivative. The reader is referred to the work [36] for detailed treatment of the convergence and stability analysis of the scheme. To demonstrate the behaviour of the system state variables with respect to varying fractional order parameter, we also provide numerical simulations based on the aforementioned scheme. Based on the scheme developed in [36], an application of the fundamental theorem of integration in the $\mathcal{S}-$equation of (3.4) with $\mathbb{ABC}$ derivative yields the following corresponding fractional Volterrra-type integral equation

$$\mathcal{S}\left(t\right)-\mathcal{S}\left(0\right)=\frac{1-\vartheta }{\mathbb{ABC}\left(\vartheta \right)}{\mathcal{G}}_1(t,\mathcal{S}\left(t\right))+\frac{\vartheta }{\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}{\int }_0^t{(t-s)}^{\vartheta -1}{\mathcal{G}}_1(s,\mathcal{S}\left(s\right))ds.$$ (6.1)

At $t=t_k$ and $t=t_{k+1}$, $k=0,1,2,\cdots$, we have

$$\mathcal{S}\left(t_k\right)-\mathcal{S}\left(0\right)=\frac{1-\vartheta }{\mathbb{ABC}\left(\vartheta \right)}{\mathcal{G}}_1(t_{k-1},\mathcal{S}\left(t_{k-1}\right))+\frac{\vartheta }{\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}{\int }_0^{t_k}{(t_k-t)}^{\vartheta -1}{\mathcal{G}}_1(t,\mathcal{S}\left(t\right))dt$$

and

$$\mathcal{S}\left(t_{k+1}\right)-\mathcal{S}\left(0\right)=\frac{1-\vartheta }{\mathbb{ABC}\left(\vartheta \right)}{\mathcal{G}}_1(t_k,\mathcal{S}\left(t_k\right))+\frac{\vartheta }{\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}{\int }_0^{t_{k+1}}{(t_{k+1}-t)}^{\vartheta -1}{\mathcal{G}}_1(t,\mathcal{S}\left(t\right))dt.$$

respectively. Moreover,

$$\mathcal{S}\left(t_{k+1}\right)-\mathcal{S}\left(t_k\right)=\frac{1-\vartheta }{\mathbb{ABC}\left(\vartheta \right)}[{\mathcal{G}}_1(t_k,\mathcal{S}\left(t_k\right))-{\mathcal{G}}_1(t_{k-1},\mathcal{S}\left(t_{k-1}\right))]+\frac{\vartheta }{\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}(I_{\vartheta ,1}-I_{\vartheta ,2})$$ (6.2)

where

$$\begin{array}{cc}& I_{\vartheta ,1}:={\int }_0^{t_{k+1}}{(t_{k+1}-t)}^{\vartheta -1}{\mathcal{G}}_1(t,\mathcal{S}\left(t\right))dt,\hfill \\ & I_{\vartheta ,2}:={\int }_0^{t_k}{(t_k-t)}^{\vartheta -1}{\mathcal{G}}_1(t,\mathcal{S}\left(t\right))dt.\hfill \end{array}$$ (6.3)

Over the interval $[t_k,t_{k+1}]$, the function ${\mathcal{G}}_1(t,\mathcal{S})$ can be approximated by the two-point Lagrange interpolation polynomial of the form

$${\mathcal{G}}_1(t,\mathcal{S}\left(t\right))\simeq \frac{t-t_{k-1}}{t_k-t_{k-1}}{\mathcal{G}}_1(t_k,\mathcal{S}\left(t_k\right))+\frac{t-t_k}{t_{k-1}-t_k}{\mathcal{G}}_1(t_{k-1},\mathcal{S}\left(t_{k-1}\right))=\frac{t-t_{k-1}}{h}{\mathcal{G}}_1(t_k,\mathcal{S}\left(t_k\right))-\frac{t-t_k}{h}{\mathcal{G}}_1(t_{k-1},\mathcal{S}\left(t_{k-1}\right)),$$ (6.4)

so that

$$\begin{array}{c}{\displaystyle I_{\vartheta ,1}=\frac{{\mathcal{G}}_1(t_k,\mathcal{S}\left(t_k\right))}{h}[\frac{2h{t}_{k+1}^{\vartheta }}{\vartheta }-\frac{t_{k+1}^{\vartheta +1}}{\vartheta +1}]-\frac{{\mathcal{G}}_1(t_{k-1},\mathcal{S}\left(t_{k-1}\right))}{h}[\frac{h{t}_{k+1}^{\vartheta }}{\vartheta }-\frac{t_{k+1}^{\vartheta +1}}{\vartheta +1}]}\hfill \\ {\displaystyle I_{\vartheta ,2}=\frac{{\mathcal{G}}_1(t_k,\mathcal{S}\left(t_k\right))}{h}[\frac{h{t}_k^{\vartheta }}{\vartheta }-\frac{t_k^{\vartheta +1}}{\vartheta +1}]-\frac{{\mathcal{G}}_1(t_{k-1},\mathcal{S}\left(t_{k-1}\right))}{h}\frac{t_k^{\vartheta +1}}{\vartheta +1},}\hfill \end{array}$$ (6.5)

respectively. By inserting the integrals in (6.5) into (6.2) we obtain

$$\mathcal{S}\left(t_{k+1}\right)=\mathcal{S}\left(t_k\right)+{\mathcal{G}}_1(t_k,\mathcal{S}\left(t_k\right)){\Theta }_1\left(\vartheta \right)-{\mathcal{G}}_1(t_{k-1},\mathcal{S}\left(t_{k-1}\right)){\Theta }_2\left(\vartheta \right)$$ (6.6)

as the approximate solution for the $\mathcal{S}-$equation of (4.3) with fractional derivative in the $\mathbb{ABC}$ sense where

$${\Theta }_i\left(\vartheta \right)=\{\begin{array}{cc}{\displaystyle [\frac{1-\vartheta }{\mathbb{ABC}\left(\vartheta \right)}+\frac{\vartheta }{h\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}(\frac{2h{t}_{k+1}^{\vartheta }}{\vartheta }-\frac{t_{k+1}^{\vartheta +1}}{\vartheta +1}-\frac{h{t}_k^{\vartheta }}{\vartheta }+\frac{t_k^{\vartheta +1}}{\vartheta +1})]}\hfill & \text{if}i=1,\hfill \\ {\displaystyle [\frac{1-\vartheta }{\mathbb{ABC}\left(\vartheta \right)}+\frac{\vartheta }{h\mathbb{ABC}\left(\vartheta \right)\Gamma \left(\vartheta \right)}(\frac{h{t}_{k+1}^{\vartheta }}{\vartheta }-\frac{t_{k+1}^{\vartheta +1}}{\vartheta +1}+\frac{t_k^{\vartheta +1}}{\vartheta +1})]}\hfill & \text{if}i=2.\hfill \end{array}$$ (6.7)

Similarly, we obtain the the ABM scheme for the remaining state variables of the fractional model (3.4) as

$$\{\begin{array}{c}\mathcal{E}\left(t_{k+1}\right)=\mathcal{E}\left(t_k\right)+{\mathcal{G}}_2(t_k,\mathcal{E}\left(t_k\right)){\Theta }_1\left(\vartheta \right)-{\mathcal{G}}_2(t_{k-1},\mathcal{E}\left(t_{k-1}\right)){\Theta }_2\left(\vartheta \right),\hfill \\ \mathcal{A}\left(t_{k+1}\right)=\mathcal{A}\left(t_k\right)+{\mathcal{G}}_3(t_k,\mathcal{A}\left(t_k\right)){\Theta }_1\left(\vartheta \right)-{\mathcal{G}}_3(t_{k-1},\mathcal{A}\left(t_{k-1}\right)){\Theta }_2\left(\vartheta \right),\hfill \\ \mathcal{I}\left(t_{k+1}\right)=\mathcal{I}\left(t_k\right)+{\mathcal{G}}_4(t_k,\mathcal{I}\left(t_k\right)){\Theta }_1\left(\vartheta \right)-{\mathcal{G}}_4(t_{k-1},\mathcal{I}\left(t_{k-1}\right)){\Theta }_2\left(\vartheta \right),\hfill \\ \mathcal{H}\left(t_{k+1}\right)=\mathcal{H}\left(t_k\right)+{\mathcal{G}}_5(t_k,\mathcal{H}\left(t_k\right)){\Theta }_1\left(\vartheta \right)-{\mathcal{G}}_5(t_{k-1},\mathcal{H}\left(t_{k-1}\right)){\Theta }_2\left(\vartheta \right),\hfill \\ \mathcal{R}\left(t_{k+1}\right)=\mathcal{R}\left(t_k\right)+{\mathcal{G}}_6(t_k,\mathcal{R}\left(t_k\right)){\Theta }_1\left(\vartheta \right)-{\mathcal{G}}_6(t_{k-1},\mathcal{R}\left(t_{k-1}\right)){\Theta }_2\left(\vartheta \right).\hfill \end{array}$$ (6.8)

7. Parameter estimation, numerical simulations and discussion

7.1. Parameter estimation

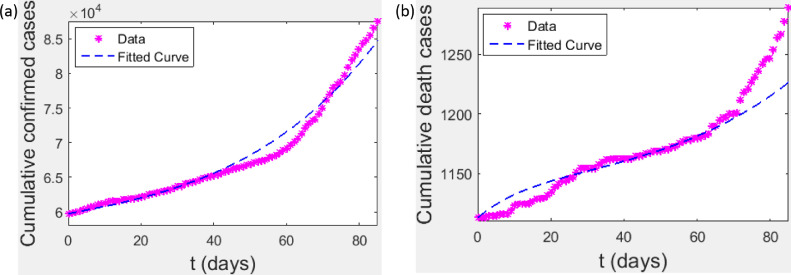
In this section, our model is fitted for $\vartheta =1$. We use the COVID-19 data provided by Nigeria Centre for Disease Control (NCDC) from 07/10/2020 through 31/12/2020 (86 days) which is publicly available at [35] for our model fitting. For the purpose of data fitting, we add to the classical model (3.3) two new compartments, namely, confirmed death cases ($\mathcal{D}\left(t\right)$) and confirmed cases ($\mathcal{C}\left(t\right)$) whose dynamics are described by the following system of equations

$$\{\begin{array}{c}{D}_t\mathcal{D}=d_2\mathcal{H},\hfill \\ D_t\mathcal{C}={\varphi }_1\mathcal{A}+{\varphi }_2\mathcal{I}.\hfill \end{array}$$ (7.1)

The confirmed cases compartment ($\mathcal{C}$) is fitted to the cumulative ”confirmed cases” while death compartment is fitted to the cumulative ”death cases”. NCDC published that 7222 individuals were quarantined, 59738 individuals were cumulative confirmed cases and 1113 cumulative death cases as of 07/10/2020 (Fig. 1 ). Adewole et al [22] estimated that about 88,000 individuals were undetected exposed $\left(\mathcal{E}\right)$, 80,000 individuals were undetected symptomatic $\left(\mathcal{I}\right)$ and 83,000 individuals were undetected asymptomatic, $\left(\mathcal{A}\right)$ as of 07/10/2020. As Nigeria is roughly a 200,000,000 population country, we therefore set $\mathcal{E}\left(0\right)=88000$, $\mathcal{A}\left(0\right)=83000$, $\mathcal{I}\left(0\right)=80000$, $\mathcal{H}\left(0\right)=7222$, $\mathcal{R}\left(0\right)=120000$, $\mathcal{S}\left(0\right)=199,600,000$. Our simulation was carried out using ”lsqcurvefit” package by MATLAB. ”lsqcurvefit” package by MATLAB solves nonlinear data-fitting problems in the least-square sense. That is, given input data $tdata$ (which could be matrices or vectors) and the observed output data $ydata$ (which could be matrices or vectors), we find coefficients $x$ that best fit the equation

$$\underset{x}{\min }{\parallel F(x,tdata)-ydata\parallel }_2^2=\underset{x}{\min }\sum _i{(F(x,tdat{a}_i)-ydat{a}_i)}^2,$$

where $F(x,tdata)$ is a matrix-valued or vector-valued function of the same size as $ydata$ [41].

Fig. 1.

(a) & (b) Data and fitted curves from 07/10/2020 through 31/12/2020.

7.2. Numerical simulations and discussion

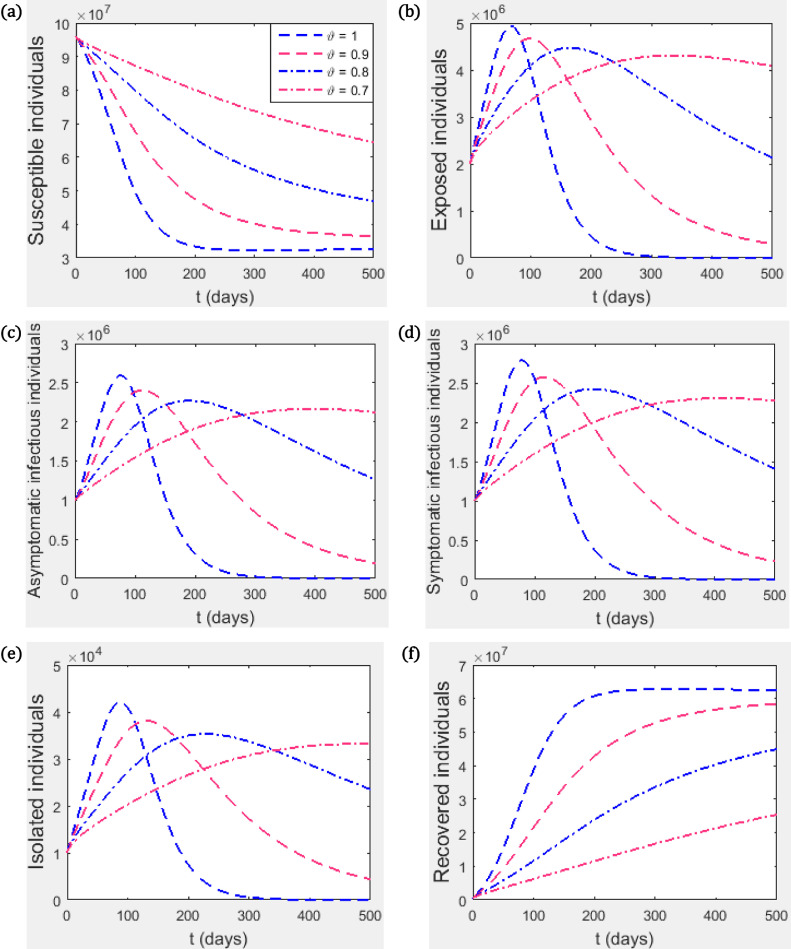
This section presents numerical simulations for our proposed fractional model (3.4) using the iterative solution scheme given by (6.6)-(6.8) as well as the numerical values of the parameters specified in Table 1. We take the time range up to 400 units. The graphical representations demonstrating the behaviour of the numerical solution for each of the system state variables $\mathcal{S}$, $\mathcal{E}$, $\mathcal{A}$, $\mathcal{I}$, $\mathcal{H}$ and $\mathcal{R}$ at various fractional orders, $\vartheta =0.7,0.8,0.9,1.0$, are given in Figs. 2 and 4. For our simulations, we take $N_0=100,000,000$, $S_0=0.96N_0$, $E_0=0.02N_0$, $A_0=0.01N_0$, $I_0=0.01N_0$, $H_0=0.0001N_0$ and $R_0=0.0049N_0$.

Fig. 2.

(a) Susceptible individuals, (b) Exposed individuals, (c) Asymptomatic infectious individuals, (d) Symptomatic infectious individuals (e) Infectious individuals in isolation, (f) Recovered individuals. We take $\rho =0$ and other parameter values as contained in Table 1 such that ${\mathfrak{R}}_0=1.5128$.

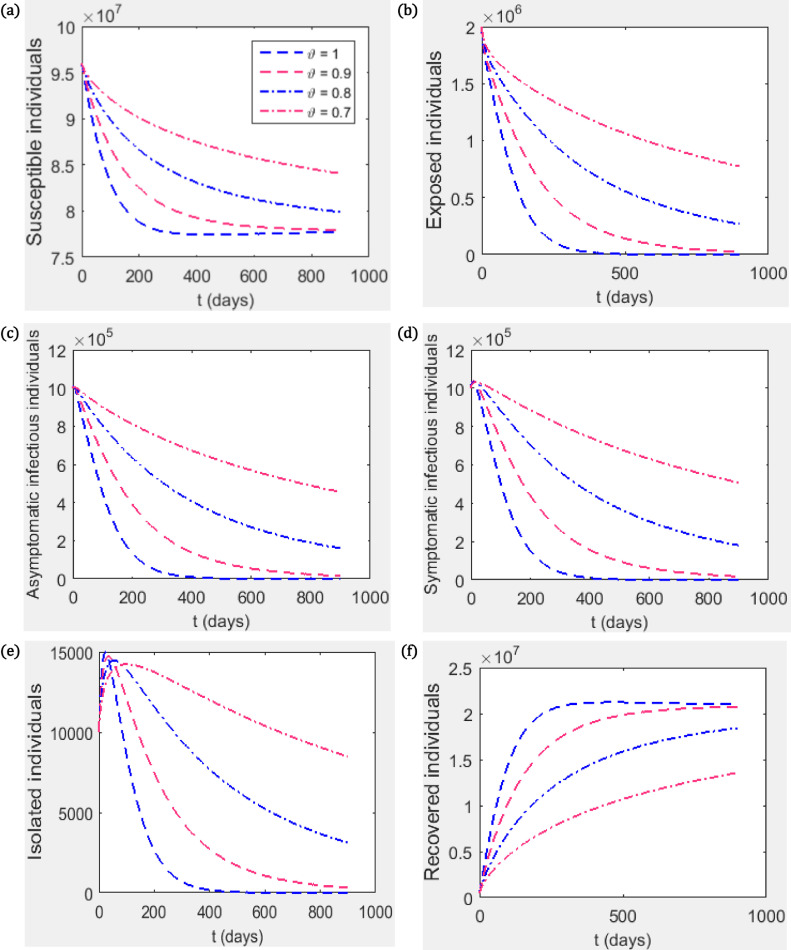
Fig. 4.

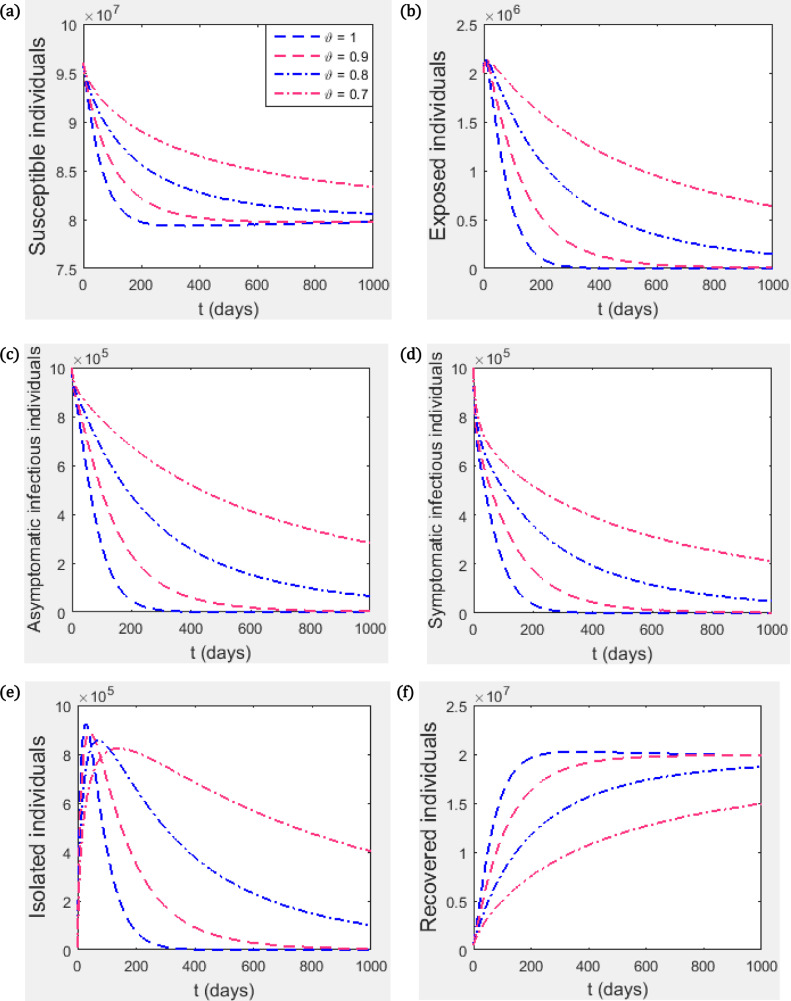
Investigating the contribution of fractional index parameter $\left(\vartheta \right)$ on the disease dynamics with reduction in transmission rate as control measure (a) Susceptible individuals, (b) Exposed individuals, (c) Asymptomatic infectious individuals, (d) Symptomatic infectious individuals (e) Infectious individuals in isolation, (f) Recovered individuals. We use the parameter values in Table 1 and take $\rho =0.4$. With these values, ${\mathfrak{R}}_0=0.9077$.

Fig. 2 shows the trajectory of the state variables for different values of the fractional index parameter $\left(\vartheta \right)$. It can be seen that the value of $\vartheta$ has a significant effect on the dynamics of the disease. For example, when $\vartheta$ reduces from 1 to 0.9, the peak of the disease is lowered but the disease stays in the population for a longer time. In general, the peak of the disease transmission is lowered as the value of $\vartheta$ reduces however, the disease stays longer in the population with reduced value of $\vartheta$. This is probably due to the memory term involved in fractional differentiation.

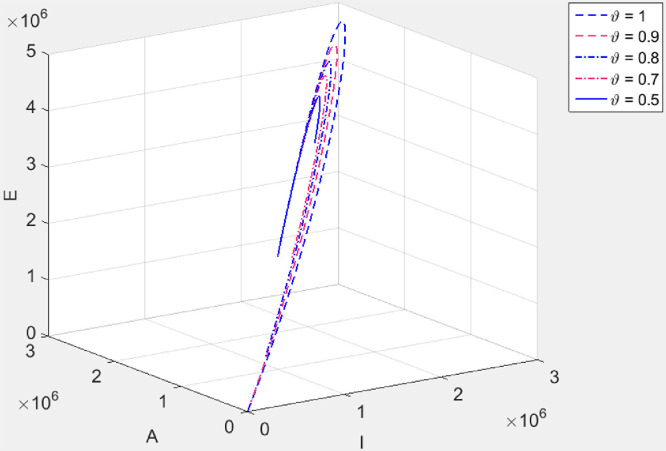
It can be seen in Fig. 3 that, irrespective of the value of the fractional index parameter $\left(\vartheta \right)$, the infected population (the exposed, the asymptomatic infectious, symptomatic infectious) approaches the disease-free equilibrium point even when ${\mathfrak{R}}_0>1$. However the infected population first increases before tending to the disease-free equilibrium. This suggests that after a certain percentage of the population is infected and recovered, the entire population has indirect immunity. This is called herd immunity.

Fig. 3.

Trajectory of disease classes when ${\mathfrak{R}}_0>1$. We use the parameter values in Table 1.

7.2.1. Reduction in transmission rate

Measures such as the use of face mask, regular hand washing using hand sanitizer, physical distancing etc. can lead to reduction in transmission rate. Suppose $50\%$ of the population is $80\%$ compliant to these measures (ie $\rho =0.4$), then ${\mathfrak{R}}_0=0.9077$. The effect of this on the dynamics of the disease is investigated and presented in Fig. 4. The isolation compartment first increases before it decreases. This is to accommodate individuals who are already infected before the initiation of the control measure. Other infected compartment (the exposed, the asymptomatic infectious, the symptomatic infectious) tend to the disease-free equilibrium. It can also be seen from Figs. 2 & 4 that the closer the value of $\vartheta$ to one the faster the state variables reach their equilibrium positions. This is probably due to the memory term involved in fractional differentiation ie the memory of the disease has great influence on the control of the disease.

7.2.2. Contact tracing

Contact tracing involves locating and quarantining individuals infected with the disease. The parameters responsible for contact tracing are ${\varphi }_1$ and ${\varphi }_2$. Suppose the average period taken to detect an asymptomatic individual is 25 days while it takes 12.5 days to detect a symptomatic individual (ie ${\varphi }_1=0.04$, ${\varphi }_2=0.08$), then ${\mathfrak{R}}_0=0.8833$. The effect of this on the dynamics of the disease is investigated and presented in Fig. 3. Isolation compartment first increases greatly before it decreases irrespective of the fractional index parameter $\left(\vartheta \right)$. This is because, with contact tracing, more people are gathered into isolation centers. Other infected compartments tend to the disease-free equilibrium. It can also be seen from Fig. 2, Fig. 4 & 5 that the closer the value of $\vartheta$ to one the faster the state variables reach their equilibrium positions. This is probably due to the memory term involved in fractional differentiation ie the memory of the disease has great influence on the control of the disease.

Fig. 5.

Investigating the contribution of fractional index parameter $\left(\vartheta \right)$ on the disease dynamics taking contact tracing as control measure (a) Susceptible individuals, (b) Exposed individuals, (c) Asymptomatic infectious individuals, (d) Symptomatic infectious individuals (e) Infectious individuals in isolation, (f) Recovered individuals. We use the parameter values in Table 1 and take ${\varphi }_1=0.04,{\varphi }_2=0.08$. With these values, ${\mathfrak{R}}_0=0.8833$.

It can be seen in Figs. 4 & 5 that, irrespective of the value of the fractional index parameter $\left(\vartheta \right)$, the infected population (the exposed, the asymptomatic infectious, symptomatic infectious) approaches the disease-free equilibrium point whenever ${\mathfrak{R}}_0<1$. In other words, the condition ${\mathfrak{R}}_0<1$ is sufficient for the disease control irrespective of the order of differentiation.

8. Conclusion

We extended a basic COVID-19 model to a fractional order model with the fractional derivative taken in the Atangana-Baleanu-Caputo sense. The model incorporate the dynamics of susceptible, exposed, asymptomatic, infectious, isolated and recovered individuals. Existence and uniqueness of solutions were established for the fractional order model via a fixed point argument while the stability of the model solutions was established in the sense of Ulam-Hyers. As part of the motivation, the influence of the distinct values of the fractional order parameter on the dynamics of the system state variables of fractional order model was also investigated. The model is calibrated using COVID-19 data provided by Nigeria Centre for Disease Control (NCDC) and important parameters were estimated. Furthermore, the two-step Adams-Bashforth method incorporating the noninteger order parameter is used for the numerical simulations of the model.

The obtained numerical simulations show that the value of fractional index parameter has effect on the dynamics of the disease status of individuals. More precisely, the peak of the disease transmission is lowered as the value of the fractional index $\vartheta$ reduces. The graphs also indicate that the equilibrium solution is stable. Moreover, the equilibrium solution is approached faster as the value of $\vartheta$ moves closer to 1. The simulations also demonstrate that the infected population (that is, the exposed, asymptomatic and symptomatic individuals) shrinks with time when the basic reproduction number is less than unity, irrespective of the value of $\vartheta$. It should also be noted that contact tracing placed a heavy burden on health care facilities irrespective of the order of differentiation.

Availability of data and materials

Data sharing is not applicable to this article. This is because the data used for parameter estimation are publicly available at [35].

CRediT authorship contribution statement

Newton I. Okposo: Conceptualization, Investigation, Methodology, Writing – original draft, Formal analysis, Validation, Writing – review & editing. Matthew O. Adewole: Methodology, Investigation, Formal analysis, Data curation, Software, Supervision, Validation, Writing – review & editing. Emamuzo N. Okposo: Methodology, Investigation, Formal analysis, Writing – review & editing. Herietta I. Ojarikre: Investigation, Visualization, Writing – review & editing. Farah A. Abdullah: Investigation, Visualization, Writing – review & editing, Validation.

Declaration of Competing Interest

The authors declare that they there exists no known competing interests that could have appeared to influence the work reported in this paper.