Optimization of supply chain networks with inclusion of labor: Applications to COVID-19 pandemic disruptions

Abstract

In this paper, we respond to the COVID-19 pandemic by constructing supply chain network optimization models, which explicitly include labor as an important variable in the network economic activity links, along with associated capacities. Labor is a critical resource in supply chains from production to transportation, storage, and distribution. In a pandemic, the availability of labor for different supply chain network activities may be disrupted due to illness, fear of contagion, morbidity, necessity of social/physical distancing, etc. The modeling framework considers first elastic demands for a product and then fixed demands, coupled with distinct types of labor capacities in order to capture the availability of this valuable resource in a pandemic, as well as possible flexibility. The supply chain network framework, which includes electronic commerce, is relevant to many different supply chain applications including protective personal and medical equipment, as well as to particular food items. Theoretical results as well as computed numerical examples are presented.

1. Introduction

The COVID-19 pandemic has transformed the world, posing great challenges to governments, businesses, medical and educational institutions, as well as citizens. Notably, the urgent need for a plethora of products and supplies, including those in healthcare, has demonstrated the criticality of supply chain networks. Indeed, with disruptions due to the pandemic, there have been shortages of numerous products from critical needs ones such as pharmaceuticals and medical equipment, including personal protective equipment (PPE) (cf. Ranney et al. (2020)) and sanitation supplies (Morrison (2020)), to even the more plebeian, yet essential ones - toilet paper (Fisher (2020)). As the pandemic progresses and evolves from country to country, newspapers around the globe are highlighting empty store shelves of certain products (Swanson (2020)).

Many of the news articles are explicitly emphasizing bottlenecks and disruptions associated with the lack of labor (Bhattarai and Reiley (2020)). For example, workers at meat processing plants in the United States are getting ill resulting in disruptions of meat products (Rosane (2020) and Reiley (2020)) and some processing plants, as a consequence, are closing (Corkery and Yaffe-Bellany (2020)). Plus, to minimize the risk of contagion through the use of physical/social distancing some facilities are being redesigned/restructures in order to space out workers (see Scheiber and Corkery (2020)). This may result in longer times for processing and, of course, fewer workers in a given facility. There are now also new challenges associated with migrant workers being unavailable to pick ripening produce on farms (Shoichet (2020), Nickel and Walljasper (2020), and Russell (2020)). Some reports, on the other hand, are noting the inability to secure inputs of material resources/supplies for production, but these also may have deficiency of labor undertones (Rabouin et al. (2020)). Many factories in China were shut down in early 2020 for weeks under a lockdown since the coronavirus that causes the COVID-19 illness in this pandemic is believed to have originated in Wuhan, China (Mistreanu (2020)). Some factories are only very gradually being reopened, resulting in shortages of pharmaceuticals, many of which are produced in China, along with face masks, etc. (cf. Harney (2020)). Furthermore, freight services have been negatively impacted as well due to workers’ illnesses, fear of contracting the coronavirus, and even border closures in certain regions resulting in transport delays (cf. Saul et al. (2020)).

In this pandemic, major electronic commerce retailers, such as Amazon, have also experienced labor shortages, due, in part, to escalating demand for online deliveries as many consumers now work from home, and are seeking many new employees (Del Ray (2020)). The pandemic is making companies completely reevaluate their supply chain networks (Shih (2020)). In fact, Amazon has even eliminated its freight division that competed with FedEx and UPS (Ziobro (2020)). At the same time, there have been reports that Amazon workers in certain distribution centers are concerned about their health and contracting the coronavirus (Heater (2020)). Clearly, this new world commercial landscape is being deeply affected by the availability of labor to contribute to each link in a supply chain network, that is, to the production, transportation, storage, and ultimate distribution of products to points of demand (Bhattarai and Reiley (2020)).

2. Literature analysis and our contributions

We now highlight some of the related and relevant literature on pandemic impacts on supply chains and on labor in supply chains.

2.1. Pandemic impacts on supply chains

The World Health Organization declared the COVID-19 pandemic on March 11, 2020 (see WHO (2020)). Given the disruptions that occurred in a spectrum of supply chain networks, researchers have been responding through relevant publications. For example, Queiroz et al. (2020) described a research agenda via a structured literature review of COVID-19 related work and supply chain research on earlier epidemics. Ivanov (2020a) overviewed simulation-based research focusing on the potential impacts on global supply chains of the COVID-19 pandemic. Ivanov and Dolgui (2020a) emphasized the importance of a novel perspective through the application of intertwined supply networks (ISNs). Currie et al. (2020) identified multiple, complex challenges due to the COVID-19 pandemic and elucidated how simulation modelling can assist in supporting enhanced decision-making. Ivanov (2020b) proposed a new concept - that of a viable supply chain (VSC), in which viability is considered as an underlying supply chain property spanning: agility, resilience, and sustainability. Such a perspective can aid firms in their decisions on the recovery and re-building of their supply chains after crises of long duration such as the COVID-19 pandemic. Ivanov and Das (2020) captured the ripple effect of an epidemic outbreak in global supply chains in their model, with the inclusion of the velocity of pandemic propagation, the duration of production, distribution and market disruption, and a demand decline. The authors analyzed pandemic supply risk mitigation measures and associated recovery paths, and included a discussion of prospective global supply chain (re)-designs.

Clearly, the pandemic has driven the importance and relevance of supply chains to the forefront in both practice and in the news and is now stimulating the investigation of theoretical as well as empirical constructs by academics. For example, Craighead et al. (2020) highlighted a spectrum of theories that they consider powerful tools for illuminating impacts of the pandemic on supply chains; how organizations responded, and also how supply chains and associated processes can be adjusted if and when another pandemic arrives. Among the theories, they highlight game theory. Nagurney et al. (2020) constructed a game theory model to capture the competition for medical supplies in the pandemic under stochastic demand. Ivanov and Dolgui (2020b), in their interesting study on Operational Research (OR) methods for coping with the ripple effect in supply chains during the pandemic provided managerial implications from the existing literature on disruption propagation in supply chains and suggested future research directions. The authors synthesized the existing knowledge on modeling the ripple effect in supply chains and its structural dynamics. van Hoek (2020), in turn, provided initial empirical exploration of supply chain risks experienced in the context of COVID-19 and approaches in practice in order to enhance supply chain resilience and argued that such research can assist in closing the gap between supply chain resilience research and efforts in industry in this domain. Paul and Chowdhury (2020), on the other hand, constructed a mathematical model that can handle both supply and demand disruptions. The model optimizes the revised production plan in the recovery window and can be solved analytically. Using a numerical example, the authors also showed how the model is capable of optimizing the recovery plan in order to better address the disruptions in the pandemic.

2.2. Labor in supply chains in the pandemic

Interestingly, the inclusion of labor as a vital resource in supply chain networks has not attained much attention in the literature. Typically, a cost associated with production, transportation, etc., is noted but the actual needs of labor for production are not explicitly quantified. This is in contrast to the economics literature on which the two major factors of production are capital and labor. For an excellent history of production functions used in economics, along with a discussion of some of the controversies, see Mishra (2007). However, in the economics literature the full richness of supply chain network topologies (see, e.g., Nagurney et al. (2013); Nagurney and Li (2016), and the references therein) and associated issues are still virgin territory. Nevertheless, it is worth noting that product assembly processes associated with multitiered supply chain networks, along with the importance of specific suppliers, have been researched (cf. Li and Nagurney (2017)). There is a literature on manpower planning and scheduling but this literature does not capture the full supply chain (see, e.g., Jaillet et al. (2019)). The COVID-19 pandemic has created novel pressures on supply chains, which include tackling potential decreases in labor resources. And, since labor is an essential input into each supply chain network economic activity, this can result in increasing costs, lower profits for firms, higher prices for consumers, and unfulfilled demand. The explicit incorporation of labor and its availability into supply chain network optimization models has yet to be deeply investigated. Hence, that is the purpose of this paper.

Since the incorporation of labor in supply chain networks has not attained much attention in the literature, the modeling of labor and impacts of availability, as revealed by the COVID-19 pandemic, is understudied and, hence, the literature on this topic is not yet well-developed. Nagurney (2020), inspired by the COVID-19 pandemic and the severe negative impacts on various food industries, in particular (see also Singh et al. (2020)), proposed a supply chain network optimization model for perishable food items that included labor. However, in contrast to the new model in this paper, labor limits were only imposed on specific links in the supply chain networks. In the model in this paper, in contrast, we allow for more flexibility and additional sets of constraints, which allow for the reallocation of labor. Furthermore, we introduce not only elastic demands for the products but also fixed demand, since in many situations the demands may be fixed since certain products may not be price-sensitive. In addition, we allow for electronic commerce in the supply chain networks, which is of special relevance in the COVID-19 pandemic.

2.3. Our contributions

In this paper, we introduce a supply chain network optimization model, in which the firm is a profit-maximizing one, and seeks to determine the optimal path flows of the product from its production sites through the supply chain network to the demand markets. The demands for the product at the demand markets are assumed to be elastic, that is, the consumers are sensitive to the price of the product. We also allow for electronic commerce, since that is a vivid feature of the commercial landscape during the COVID-19 pandemic, with emphasis on “social distancing” and, hence, the reduction of shoppers in grocery stores, pharmacies, and other essential retail outlets. The model considers three sets of labor constraints, of increasing flexibility of movement of labor for the supply chain network economic activities. In particular, in the first set, each supply chain network link has an upper bound of available labor. In this scenario, labor is not free to move to other production sites, nor to other distribution centers, or assist in freight service provision. In the second set of constraints, the labor is free to move across a supply chain set of network economic activities (such as production, or transportation, or storage, and, finally, distribution). There is a capacity of labor associated with each such “tier” of supply chain network links. Hence, those who have skills in production, or in distribution, or freight service provision may be reallocated according to their specific skills. This has been happening in freight service provision, for example, during the COVID-19 pandemic (see CBSSacramento (2020)). In the case of the third set of labor constraints, which corresponds to the most flexible scenario, labor is free to move across all the supply chain network economic activities, and there is a single capacity. Shifting employees among different tasks during the COVID-19 pandemic has been noted by McKinsey & Company as a means towards resilience and returning the supply chain to effectiveness while reenvisioning and reforming supply chain operations for enhanced performance (Aryapadi et al. (2020)).

We, subsequently, provide the fixed demand supply chain network optimization analogue for the three labor availability scenarios, which is a special case of the elastic demand model version. The variational inequality formulations of the elastic demand and fixed demand versions, under the three scenarios, are provided. In particular, the variational inequality formulations incorporate the Lagrange multipliers associated with the labor capacity constraints under each of the three scenarios. This gives us a unified formulation for computational purposes. We consider nonlinear and non separable link costs that are dependent on the product flows as well as labor costs. Our approach is that of system-optimization since we consider a firm's supply chain network which it wishes to optimize in terms of product flows and labor with the latter subject to particular capacity constraint(s). System-optimization supply chain network models have been developed for supply chain network integration in the case of mergers and acquisitions (see Nagurney (2009) and Masoumi et al. (2017)) as well as in the teaming of humanitarian organizations for disaster relief (Nagurney and Qiang (2020)). However, in those models, in contrast to the ones in this paper, it is assumed that the capacities on the supply chain network links are bounds on the link flows, and labor is not included. System-optimization models have also been constructed for supply chain network design and redesign (see Nagurney (2010)).

The paper is organized as follows. In Section 3, the supply chain network optimization modeling framework with labor is presented, along with theoretical foundations and illustrative examples. In Section 4, a computational procedure is proposed and differences in the implementation for the case of elastic demands versus fixed demands highlighted. In Section 4, we also present numerical examples and their computed solutions, which are obtained algorithmically, to further demonstrate the relevance of the modeling framework to assess needs and flexibility in supply chains in times of the COVID-19 pandemic. The numerical examples focus on life-saving healthcare supplies. Section 5 summarizes our results and presents suggestions for future research.

3. The supply chain network models with labor

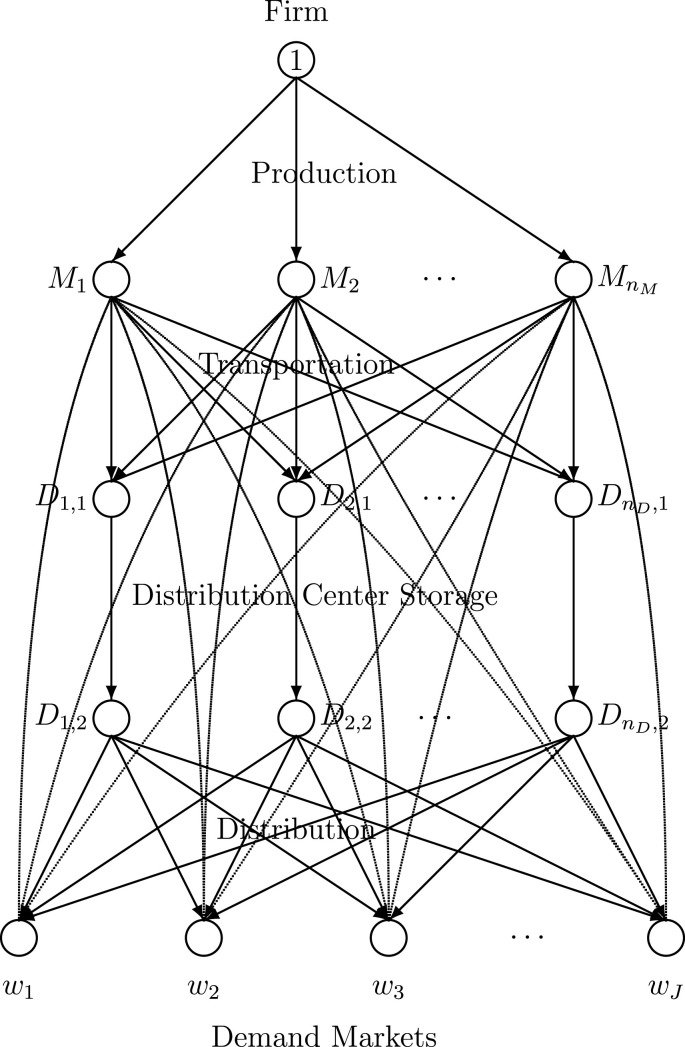
We now present the supply chain network models with labor under three different sets of labor constraints, with increasing degree of flexibility. We first consider the elastic demand case, and then the special fixed demand one. The profit-maximizing firm's supply chain network is depicted, for definiteness, in Fig. 1 . However, we emphasize that the topology can be expanded/adapted according to the specific application and, hence, the framework is not limited to such a network. The top node 1 corresponds to the firm and the bottom nodes: $w_1,\dots ,w_J$ correspond to the demand markets. The demand markets can be institutions, such as healthcare ones (depending on the specific application), retailers, and/or direct consumers. We assume that there exists one path (or more) joining node 1 with each demand node.

Fig. 1.

The supply chain network topology.

Specifically, according to Fig. 1, the firm is considering $n_M$ production sites; $n_D$ distribution centers, and must serve the J demand markets. The links from the top-tiered node 1 are connected to the possible manufacturing nodes of the firm, which are denoted, respectively, by: $M_1,\dots ,M_{n_M}$, and these links correspond to the production links. The links from the production nodes are connected to the possible distribution center nodes of the firm, and are denoted by $D_{\mathrm{1,1}},\dots ,D_{n_D,1}$. These links represent the transportation options between the production sites and the distribution centers where the product can be stored. The links joining nodes $D_{\mathrm{1,1}},\dots ,D_{n_D,1}$ with nodes $D_{\mathrm{1,2}},\dots ,D_{n_D,2}$ denote the storage options. The distribution links join the nodes $D_{\mathrm{1,2}},\dots ,D_{n_D,2}$ with the demand market nodes: $w_1,\dots ,w_J$. In order to capture electronic commerce in the form of direct shipments from the production sites to the demand points, we draw the corresponding links joining the $M_1$, $M_2$, $\dots$, $M_{n_M}$ nodes with the demand market nodes.

We denote the supply chain network consisting of the graph $G=[N,L]$, where N denotes the set of nodes and L the set of links. In the case of Scenario 2, we are interested in the possible reallocation of labor across a tier of supply chain network economic activities. We define $L^1$ as the set of links corresponding to production; $L^2$ as the set of links corresponding to transportation, and so on. Since our supply chain network modeling framework is flexible (and not limited to the topology in Fig. 1), we refer to the final (non-electronic commerce) tier of links as $L^T$ and to the electronic commerce links as $L^{T+1}$. There may be some applications where electronic commerce links are not available. They would then be removed.

A path p in the supply chain network joins node 1, which is the origin node, to a demand market node, which is a destination node. The paths are acyclic and consist of a sequence of links representing the supply chain network activities associated with producing the product and having it ultimately delivered to the demand markets. Let $P_{w_j}$ denote the set of paths, which represent alternative associated possible supply chain network processes, joining the pair of nodes $\left(1,w_j\right)$. P then denotes the set of all paths joining node 1 to the demand market nodes. There are $n_P$ paths in the supply chain network and $n_L$ links. We denote a typical demand market node by w and a typical link by a. The set of all pairs of origin and demand market nodes is denoted by W.

The additional notation for the model is given in Table 1 . All vectors are assumed to be column vectors.

Table 1.

Notation for the supply chain network models with labor.

Notation	Parameter Definition
${\alpha }_a$	positive factor relating inputs of labor to product flow on link a, $\forall a\in L$.
${\pi }_a$	the unit cost of labor at link a, $\forall a\in L$.
${\bar{l}}_a$	the upper bound on the availability of labor on link a under Scenario 1, $\forall a\in L$.
${\bar{l}}^t$	the upper bound on labor availability for tier t activities under Scenario 2, with tier $t=1$ being production; tier $t=2$ is transportation, and so on until $t=T$, which corresponds to distribution. Here, $T+1$ corresponds to the electronic commerce tiered links.
$\bar{l}$	the upper bound on labor availability under Scenario 3.
Notation	Variable Definition
$x_p$	the product flow on path p; we group all the path flows into the vector $x\in R_{+}^{n_P}$.
$f_a$	the product flow on link a; we group all the link flows into the vector $f\in R_{+}^{n_L}$.
$l_a$	the labor available for link a activity, $\forall a\in L$.
$d_{w_j}$	the demand for the product at demand market $w_j$; $j=1,\dots ,J$; we group the demands into the vector $d\in R_{+}^J$.
Notation	Function Definition
${\hat{c}}_a\left(f\right)$	the total cost associated with link a, excluding the labor cost, $\forall a\in L$.
${\rho }_{w_j}\left(d\right)$	the demand price for the product at demand market $w_j$; $j=1,\dots ,J$.

In terms of the capacities on labor we consider three different sets of constraints and we introduce the associated notation below, as it is needed.

The conservation of flow equations are as follows. The demand at each demand market must be satisfied by the product flows of the firm to each demand market, that is,

$$\sum _{p\in P_w}{x}_p=d_w,\forall w\in W.$$ (1)

Also, the product flow on a link is equal to the sum of flows on paths that contain that link, that is:

$$f_a=\sum _{p\in P}{x}_p{\delta }_{ap},\forall a\in L,$$ (2)

where ${\delta }_{ap}=1$, if link a is contained in path p, and is 0, otherwise.

The path flows must be nonnegative, that is,

$$x_p\ge 0,\forall p\in P,$$ (3)

since the product will be produced in nonnegative quantities.

In addition, here we consider the following relationship between link flows and labor:

$$f_a={\alpha }_a{l}_a,\forall a\in L.$$ (4)

According to (4), the output on each link of product is a linear function of the labor input. Hence, in terms of economics, this is a linear production function.

The firm seeks to maximize its profits, which is essential for its sustainability. The objective function faced by the firm is, hence, the difference between the revenue denoted by the sum over all the demand markets of the price the consumers are willing to pay for the product at a demand market times the demand there minus the total costs consisting of the costs associated with the links (exclusive of the labor costs) and the costs associated with labor on the links:

$$\text{Maximize}\sum _{w\in W}{\rho }_w\left(d\right)d_w-\sum _{a\in L}{\hat{c}}_a\left(f\right)-\sum _{a\in L}{\pi }_a{l}_a.$$ (5)

The optimization problem is subject to constraints (1) through (4) and the following sets of constraints depending on the labor scenarios.

Labor Scenario 1 - Bound on Labor on Each Link

The first labor scenario is the most restrictive. Labor is not transferrable from link to link, which may reflect inability and/or unwillingness to move, as well as skills geared towards a specific activity and location.

The additional constraints relevant to this scenario are:

$$l_a\le {\bar{l}}_a,\forall a\in L.$$ (6)

Labor Scenario 2 - Bound on Labor on Each Activity Tier of the Supply Chain Network

The second labor scenario, in turn, considers the following. Those involved in production may be reallocated to other production sites; the same holds for transportation service provision, since freight service providers are expected to have similar skills. Also, distribution center workers may be free to move from one distribution center to another, and, since they have similar skills, this is not unreasonable.

Hence, the additional constraints in Scenario 2 are:

$$\sum _{a\in L^1}{l}_a\le {\bar{l}}^1,$$ (7,1)

$$\sum _{a\in L^2}{l}_a\le {\bar{l}}^2,$$ (7,2)

and so on until

$$\sum _{a\in L^{T+1}}{l}_a\le {\bar{l}}^{T+1}.$$ (7,T+1)

Labor Scenario 3 - Single Bound on Labor for the Full Supply Chain Network

Finally, the third scenario offers the most flexibility. And this is being done now in practice as reported by McKinsey & Company (cf. Aryapadi et al. (2020)).

In this scenario the workers are able to do all the tasks associated with the supply chain network activities, that is, production, transportation, storage, and distribution.

In this scenario the additional constraint to (1) through (4) is:

$$\sum _{a\in L}{l}_a\le \bar{l}.$$ (8)

In view of (1), (2), and (4), we can express objective function (5) solely in terms of path flows by incorporating these constraints directly into the objective function, with the proviso that we also define the following functions: ${\tilde{c}}_a\left(x\right)\equiv {\hat{c}}_a\left(f\right)$, $\forall a\in L$; ${\tilde{\rho }}_w\left(x\right)\equiv {\rho }_w\left(d\right)$, $\forall w\in W$.

Hence, the objective function (5) now becomes the following in path flows:

$$\text{Maximize}\sum _{w\in W}{\tilde{\rho }}_w\left(x\right)\sum _{p\in P_w}{x}_p-\sum _{a\in L}{\tilde{c}}_a\left(x\right)-\sum _{a\in L}\frac{{\pi }_a}{{\alpha }_a}\sum _{p\in P}{x}_p{\delta }_{ap}.$$ (9)

Notice that we also made use in (9) of the substitution for equation (4) of: $l_a=\frac{{\sum }_{p\in P}{x}_p{\delta }_{ap}}{{\alpha }_a}$, for all $a\in L$. We assume that the objective function in (9) is concave, which will hold if the total revenue component is concave and the total link cost functions are convex. We also assume that the revenue functions and the total link cost functions are continuously differentiable.

Since (1), (2), and (4) are directly incorporated into the objective function (9), we still retain the nonnegativity assumption on the path flows (3).

We now re-express constraints (6) through (8), corresponding to scenarios 1 through 3, respectively, in path flows.

Specifically, under Scenario 1, (6), in path flows is:

$$\frac{{\sum }_{p\in P}{x}_p{\delta }_{ap}}{{\alpha }_a}\le {\bar{l}}_a,\forall a.$$ (10)

Under Scenario 2, on the other hand, the set of constraints (7) becomes:

$$\sum _{a\in L^1}\frac{{\sum }_{p\in P}{x}_p{\delta }_{ap}}{{\alpha }_a}\le {\bar{l}}^1,$$ (11,1)

$$\sum _{a\in L^2}\frac{{\sum }_{p\in P}{x}_p{\delta }_{ap}}{{\alpha }_a}\le {\bar{l}}^2,$$ (11,2)

and so on until

$$\sum _{a\in L^{T+1}}\frac{{\sum }_{p\in P}{x}_p{\delta }_{ap}}{{\alpha }_a}\le {\bar{l}}^{T+1}.$$ (11,T+1)

Finally, under Scenario 3, constraint (8) is equivalent to the following constraint in path flows:

$$\sum _{a\in L}\frac{{\sum }_{p\in P}{x}_p{\delta }_{ap}}{{\alpha }_a}\le \bar{l}.$$ (12)

3.1. Variational inequality formulations

We now provide the variational inequality (VI) formulations of the above supply chain network optimization model under the three distinct scenarios for labor availability. The solutions to the supply chain network optimization model with labor under each of the scenarios are guaranteed to exist since the feasible sets are all bounded due to capacities on the availability of labor (albeit of different forms) and, hence, the product flows are also bounded.

The proofs of the below formulations follow immediately from the classical theory of variational inequalities (Kinderlehrer and Stampacchia (1980) and Nagurney (1999)) with related applications to supply chains and derivations given in Nagurney (2006, 2010) and Nagurney and Li (2016). Indeed, we know that the feasible set underlying each of the labor scenarios is convex since the constraints are linear. Furthermore, since the objective function is concave, by assumption, the Kuhn Tucker conditions are both necessary and sufficient for optimality and these can be formulated directly as the variational inequality problems below. The variational inequality formulations enable the implementation of an effective computational procedure.

Labor Scenario 1 Variational Inequality Formulation

For Labor Scenario 1, we associate the nonnegative Lagrange multiplier ${\lambda }_a$ with the link labor constraint for each link a given by (10). We group these Lagrange multipliers into the vector $\lambda \in R_{+}^{n_L}$. We define the feasible set $K^1\equiv \{(x,\lambda )\in R_{+}^{n_P+n_L}\}$. The solution to the Scenario 1 optimization problem with objective function (9) is equivalent to the solution of the VI: determine $\left(x^{\text{*}},{\mathrm{\lambda }}^{\text{*}}\right)\in K^1$ such that

$$\sum _{w\in W}\sum _{p\in P_w}\left[\frac{\partial {\hat{C}}_p\left(x^{\text{*}}\right)}{\partial x_p}+\sum _{a\in L}\frac{{\pi }_a}{{\alpha }_a}{\delta }_{ap}-{\hat{\rho }}_w\left(x^{\text{*}}\right)-\sum _{v\in W}\frac{\partial {\hat{\rho }}_v\left(x^{\text{*}}\right)}{\partial x_p}\sum _{q\in P_v}{x}_q^{\text{*}}+\sum _{a\in L}\frac{{\mathrm{\lambda }}_a^{\text{*}}}{{\alpha }_a}{\delta }_{ap}\right]\times [x_p-x_p^{\text{*}}]+\sum _{a\in L}\left[{\bar{l}}_a-\frac{{\sum }_{p\in P}{x}_p^{\text{*}}{\delta }_{ap}}{{\alpha }_a}\right]\times [{\mathrm{\lambda }}_a-{\mathrm{\lambda }}_a^{\text{*}}]\ge 0,\forall \left(x,\mathrm{\lambda }\right)\in K^1,$$ (13)

where

$$\frac{\partial {\hat{C}}_p\left(x\right)}{\partial x_p}\equiv \sum _{a\in L}\sum _{b\in L}\frac{\partial {\hat{c}}_b\left(f\right)}{\partial f_a},\forall p\in P.$$ (14)

Labor Scenario 2 Variational Inequality Formulation

For Labor Scenario 2, we associate the nonnegative Lagrange multiplier ${\mu }^t$ with labor constraint $\left(11,t\right)$, for $t=1,\dots ,T+1$. We define the vector of Lagrange multipliers $\mu \in R_{+}^{T+1}$ and the feasible set $K^2\equiv \{(x,\mu )\in R_{+}^{n_P+T+1}\}$. The variational inequality formulation, whose solution corresponds to the supply chain network optimization problem with objective function (9) and with labor under Scenario 2 is: determine $\left(x^{\text{*}},{\mu }^{\text{*}}\right)\in K^2$, such that:

$$\sum _{w\in W}\sum _{p\in P_w}\left[\frac{\partial {\hat{C}}_p\left(x^{\text{*}}\right)}{\partial x_p}+\sum _{a\in L}\frac{{\pi }_a}{{\alpha }_a}{\delta }_{ap}-{\hat{\rho }}_w\left(x^{\text{*}}\right)-\sum _{v\in W}\frac{\partial {\hat{\rho }}_v\left(x^{\text{*}}\right)}{\partial x_p}\sum _{q\in P_v}{x}_q^{\text{*}}+\sum _{t=1}^{T+1}{\mu }^{t\ast }\sum _{a\in L^t}\frac{1}{{\alpha }_a}{\delta }_{ap}\right]\times [x_p-x_p^{\text{*}}]+\sum _{t=1}^{T+1}\left[{\bar{l}}^t-\sum _{a\in L^t}\frac{{\sum }_{p\in P}{x}_p^{\text{*}}{\delta }_{ap}}{{\alpha }_a}\right]\times [{\mu }^t-{\mu }^{t\ast }]\ge 0,\forall (x,\mu )\in K^2.$$ (15)

Labor Scenario 3 Variational Inequality Formulation

Finally, we provide the variational inequality formulation for the solution of the supply chain network optimization problem under Labor Scenario 3. Recall that this scenario is the most generous in terms of the movement of labor across the links of the supply chain network (cf. (12)). We associate the nonnegative Lagrange multiplier γ with constraint (12) and we define the appropriate feasible set $K^3\equiv \{(x,\gamma )\in R_{+}^{n_P+1}\}$. The VI for Scenario 3 with objective function (9) is then given by: determine $\left(x^{\text{*}},{\gamma }^{\text{*}}\right)\in K^3$ such that

$$\sum _{w\in W}\sum _{p\in P_w}\left[\frac{\partial {\hat{C}}_p\left(x^{\text{*}}\right)}{\partial x_p}+\sum _{a\in L}\frac{{\pi }_a}{{\alpha }_a}{\delta }_{ap}-{\hat{\rho }}_w\left(x^{\text{*}}\right)-\sum _{v\in W}\frac{\partial {\hat{\rho }}_v\left(x^{\text{*}}\right)}{\partial x_p}\sum _{q\in P_v}{x}_q^{\text{*}}+{\gamma }^{\text{*}}\sum _{a\in L}\frac{1}{{\alpha }_a}{\delta }_{ap}\right]\times [x_p-x_p^{\text{*}}]+\left[\bar{l}-\sum _{a\in L}\frac{{\sum }_{p\in P}{x}_p^{\text{*}}{\delta }_{ap}}{{\alpha }_a}\right]\times [\gamma -{\gamma }^{\text{*}}]\ge 0,\forall \left(x,\gamma \right)\in K^3.$$ (16)

3.1.1. Illustrative examples

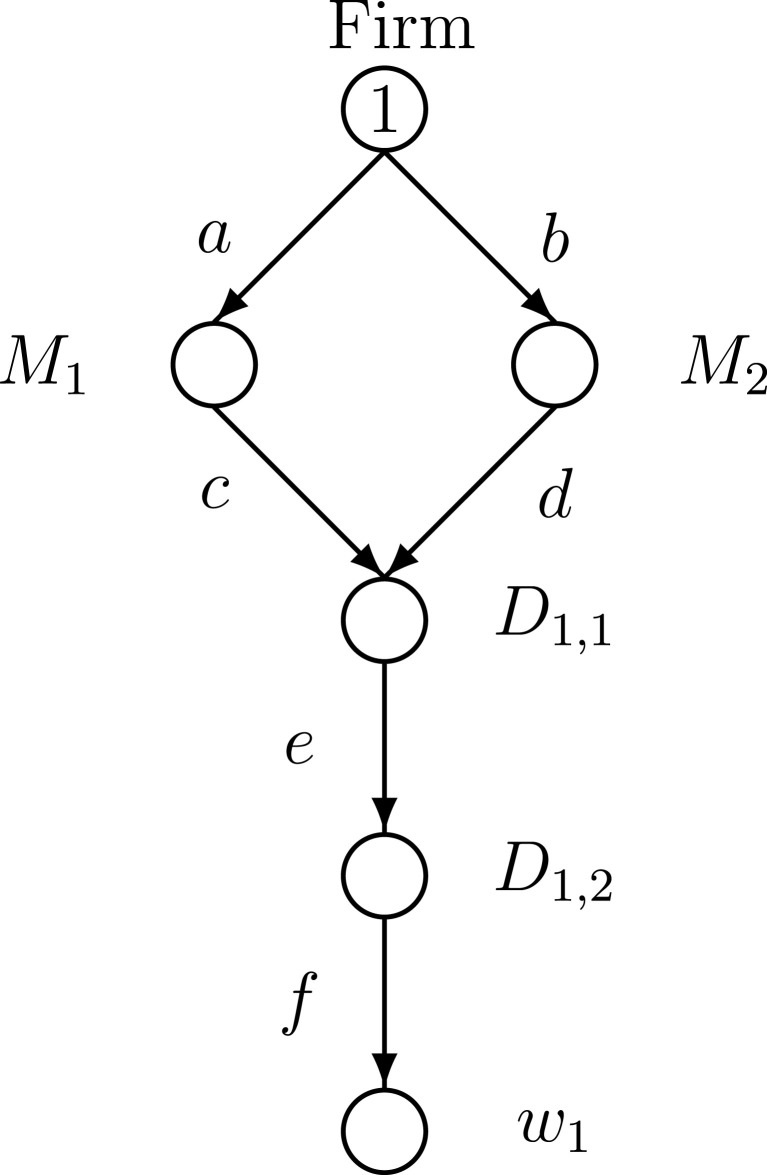
We now present small examples for illustrative purposes corresponding to Scenarios 1 and 3 above. The examples are solved algebraically. In Section 4, we solve additional, more complex numerical examples, algorithmically. The supply chain network topology is depicted in Fig. 2 and consists of the firm, its two production/manufacturing facilities, a single distribution center, and a single demand market. There is no electronic commerce. The example is inspired by an expensive item for the treatment of patients with COVID-19 and the demand point corresponds to hospitals that the firm is considering delivering the healthcare item to. The hospitals are in same metropolitan region, such as Boston or NYC, both of which have been severely impacted by the coronavirus.

Fig. 2.

Supply chain network topology for illustrative examples.

Since we want to allow for easy solution the data are as follows: the total costs on links (without the labor costs are):

$$\begin{array}{l}{\hat{c}}_a\left(f\right)=2f_a^2,{\hat{c}}_b\left(f\right)=2f_b^2,{\hat{c}}_c\left(f\right)=.5f_c^2,{\hat{c}}_d=.5f_d^2,\\ {\hat{c}}_e\left(f\right)=f_e^2+2f_e,{\hat{c}}_f\left(f\right)=.5f_f^2;\end{array}$$

the labor link costs are:

$$\begin{array}{l}{\pi }_a=10,{\pi }_b=10,{\pi }_c=4,{\pi }_d=4,\\ {\pi }_e=2,{\pi }_f=6.\end{array}$$

Here, we first consider Scenario 1, with the linear expressions relating labor to product flows being:

$$\begin{array}{l}{f}_a=l_a,f_b=l_b,f_c=10l_c,f_d=10l_d,\\ f_e=10l_e,f_f=20l_f,\end{array}$$

which corresponds to: ${\alpha }_a={\alpha }_b=1$; ${\alpha }_c={\alpha }_d=10$; ${\alpha }_e=10$, and ${\alpha }_f=20$.

The bounds on the links’ labor availability are given by:

$$\begin{array}{l}{\bar{l}}_a=20,{\bar{l}}_b=20,{\bar{l}}_c=30,{\bar{l}}_d=30,\\ {\bar{l}}_e=100,{\bar{l}}_f=120.\end{array}$$

The demand price function at the demand market is:

$${\rho }_{w_1}\left(d\right)=-d_{w_1}+80000.$$

We define path $p_1=\left(a,c,e,f\right)$ and path $p_2=\left(b,d,e,f\right)$. Due to the supply chain network topology in Fig. 2 and the fact that the cost link on a (including the labor cost) is equal to the cost on link b and, similarly, the cost on link c is equal to the cost on link d, we know that $x_{p_1}^{\text{*}}=x_{p_2}^{\text{*}}$. We can, hence, solve VI (13) algebraically, noting that the optimal path flows are positive. Furthermore, it is reasonable to assume that the optimal labor values on links a and b will be at the imposed bound, since it is low. A straightforward computation then yields:

$$x_{p_1}^{\text{*}}=20.00x_{p_2}^{\text{*}}=20.00,$$

and, hence, $d_{w_1}^{\text{*}}=40.00$ with the demand price: $\mathrm{79,960.00}$. In addition, we, thus, have that:

$$\begin{array}{l}{f}_a^{\text{*}}=f_b^{\text{*}}=f_c^{\text{*}}=f_d^{\text{*}}=20.00,\\ f_e^{\text{*}}=f_f^{\text{*}}=40.00,\end{array}$$

and

$$\begin{array}{l}{l}_a^{\text{*}}=l_b^{\text{*}}=20.00,l_c^{\text{*}}=l_d^{\text{*}}=2.00,\\ l_e^{\text{*}}=4.00,l_f^{\text{*}}=2.00.\end{array}$$

Since the upper bound on labor is met on link a, and on link b, that is, these constraint are tight, we can also compute the associated Lagrange multipliers ${\mathrm{\lambda }}_a^{\text{*}}={\mathrm{\lambda }}_b^{\text{*}}=\mathrm{79,687.10}$. All other Lagrange multipliers associated with the links and labor constraints on them are equal to 0.00. The profit of the firm corresponding to the value of the Objective Function (5); equivalently, (9), is: $\mathrm{3,195,644.00}$.

Now we consider Scenario 3. We retain the data as above except that we set $\bar{l}=\sum _{a\in L}{\bar{l}}_a=320$. This represents the situation that the firm has the same amount of available labor as in Scenario 1 but the labor is free to move among the supply chain network activities. The solution to this supply chain network optimization problem is governed by VI (16). It is easy to see that the optimal solution is now: $x_{p_1}^{\text{*}}=x_{p_2}^{\text{*}}=160$, with the optimal Lagrange multiplier being ${\gamma }^{\text{*}}=\mathrm{4,469.70}$.

The demand $d_{w_1}^{\text{*}}=320.00$ and the demand price is now: $\mathrm{79,680.00}$. In addition, we have that:

$$\begin{array}{l}{f}_a^{\text{*}}=f_b^{\text{*}}=f_c^{\text{*}}=f_d^{\text{*}}=160.00,\\ f_e^{\text{*}}=f_f^{\text{*}}=320.00,\end{array}$$

and

$$\begin{array}{l}{l}_a^{\text{*}}=l_b^{\text{*}}=160.00,l_c^{\text{*}}=l_d^{\text{*}}=16.00,\\ l_e^{\text{*}}=32.00,l_f^{\text{*}}=16.00.\end{array}$$

The firm, under much greater flexibility, now enjoys a profit of: $\mathrm{25,223,040.00}$ and the hospitals obtain 320 of the healthcare items, as opposed to only 40 in Scenario 1 above, and at a lower price. Even this simple set of illustrative examples demonstrates the need for flexibility for labor movement in a pandemic situation along with the advantages. Of course, in the case of certain products that are quite complex such a transferral of labor between/among tasks may not be possible or may require additional training, which may be costly. Interestingly, as reported by Kallingal (2020), many airlines have grounded planes and have temporarily laid-off workers, with some airlines, notably, in Sweden and the United Kingdom, encouraging flight attendants to retrain to help hospitals in the coronavirus pandemic.

These examples also provide insights under times when crisis management is not needed since a firm may be interested in evaluating the benefits of flexibility of its labor assets in its supply chain. The values of the Lagrange multipliers provide valuable information as well, since they act as shadow prices reflecting the value to profits of an additional unit of the associated labor resource with respect to the relevant constraint(s).

3.2. Variational inequality formulations of the fixed demand case

Note that the above supply chain network optimization model with labor, under different scenarios, assumes that the demand for the product at the demand markets is elastic, that is, that the consumers are sensitive to the price.

In the case of certain products during the COVID-19 pandemic, demand may be inelastic, that is, known and fixed. Observe that a special case of each of the above scenarios can be constructed for the fixed demand case. Indeed, we now have the following constraints, where, without loss of generality, $d_w$ is assumed to be known and fixed for all $w\in W$.

$$\sum _{p\in P_w}{x}_p=d_w,\forall w\in W.$$ (17)

The feasible sets for the three scenarios, respectively, in the case of fixed demands are: ${\hat{K}}^1\equiv \{(x,\lambda )\in R_{+}^{n_P+n_L}\text{such that }\left(17\right)\text{ holds}\}$; ${\hat{K}}^2\equiv \{(x,\mu )\in R_{+}^{n_P+T+1}\text{such that }\left(17\right)\text{ holds}\}$, and ${\hat{K}}^3\equiv \{(x,\gamma )\in R_{+}^{n_P+1}\text{such that }\left(17\right)\text{ holds}\}$.

In the case of fixed demands, the Objective Function (9) simplifies to:

$$\text{Minimize}\sum _{a\in L}{\tilde{c}}_a\left(x\right)+\sum _{a\in L}\frac{{\pi }_a}{{\alpha }_a}\sum _{p\in P}{x}_p{\delta }_{ap}.$$ (18)

As in the elastic demand case, each set of labor constraints corresponds to a different feasible set. Observe that, in the fixed demand case, the labor capacities may be such that the demand cannot be satisfied and, hence, the problem is infeasible. Of course, this may actually occur in the case of pandemic since demand for a product, especially a critical needs product, may exceed the availability of labor to produce it because of labor shortfalls. In order to check if the demands can be satisfied under a scenario, and, as noted in Qiang and Nagurney (2012), where a bicriteria supply chain network performance measure was introduced in the case of disasters, we can first solve the maximum flow problem (cf. Ahuja et al. (1993)), which is a well-known classical network optimization problem in operations research.

Here, we make the assumption that the demands can be satisfied. The analogous VIs for the fixed demand case under the three scenarios are now given. The results are immediate by incorporating the fixed demand constraints (17) and simplifying the respective scenarios VIs: (13), (15), and (16), accordingly, as we have done below.

Labor Scenario 1 Variational Inequality Formulation for the Fixed Demand Case

The solution to the Labor Scenario 1 supply chain network optimization problem for the fixed demand case is equivalent to the solution of the VI: determine $\left(x^{\text{*}},{\lambda }^{\text{*}}\right)\in {\hat{K}}^1$ such that

$$\sum _{w\in W}\sum _{p\in P_w}\left[\frac{\partial {\hat{C}}_p\left(x^{\text{*}}\right)}{\partial x_p}+\sum _{a\in L}\frac{{\pi }_a}{{\alpha }_a}{\delta }_{ap}+\sum _{a\in L}\frac{{\mathrm{\lambda }}_a^{\text{*}}}{{\alpha }_a}{\delta }_{ap}\right]\times [x_p-x_p^{\text{*}}]+\sum _{a\in L}\left[{\bar{l}}_a-\frac{{\sum }_{p\in P}{x}_p^{\text{*}}{\delta }_{ap}}{{\alpha }_a}\right]\times [{\mathrm{\lambda }}_a-{\mathrm{\lambda }}_a^{\text{*}}]\ge 0,\forall \left(x,\mathrm{\lambda }\right)\in {\hat{K}}^1.$$ (19)

Labor Scenario 2 Variational Inequality Formulation for the Fixed Demand Case

The variational inequality formulation for the Labor Scenario 2 supply chain network optimization problem in the case of fixed demands is, in turn: determine $\left(x^{\text{*}},{\mu }^{\text{*}}\right)\in {\hat{K}}^2$, such that:

$$\sum _{w\in W}\sum _{p\in P_w}\left[\frac{\partial {\hat{C}}_p\left(x^{\text{*}}\right)}{\partial x_p}+\sum _{a\in L}\frac{{\pi }_a}{{\alpha }_a}{\delta }_{ap}+\sum _{t=1}^{T+1}{\mu }^{t\ast }\sum _{a\in L^t}\frac{1}{{\alpha }_a}{\delta }_{ap}\right]\times [x_p-x_p^{\text{*}}]+\sum _{t=1}^{T+1}\left[{\bar{l}}^t-\sum _{a\in L^t}\frac{{\sum }_{p\in P}{x}_p^{\text{*}}{\delta }_{ap}}{{\alpha }_a}\right]\times [{\mu }^t-{\mu }^{t\ast }]\ge 0,\forall \left(x,\mu \right)\in {\hat{K}}^2.$$ (20)

Labor Scenario 3 Variational Inequality Formulation for the Fixed Demand Case

The VI for Labor Scenario 3 in the fixed demand case is, in turn: determine $\left(x^{\text{*}},{\gamma }^{\text{*}}\right)\in {\hat{K}}^3$ such that

$$\sum _{w\in W}\sum _{p\in P_w}\left[\frac{\partial {\hat{C}}_p\left(x^{\text{*}}\right)}{\partial x_p}+\sum _{a\in L}\frac{{\pi }_a}{{\alpha }_a}{\delta }_{ap}+{\gamma }^{\text{*}}\sum _{a\in L}\frac{1}{{\alpha }_a}{\delta }_{ap}\right]\times [x_p-x_p^{\text{*}}]+\left[\bar{l}-\sum _{a\in L}\frac{{\sum }_{p\in P}{x}_p^{\text{*}}{\delta }_{ap}}{{\alpha }_a}\right]\times [\gamma -{\gamma }^{\text{*}}]\ge 0,\forall \left(x,\gamma \right)\in {\hat{K}}^3.$$ (21)

Note that all of the above six VIs (three for the elastic demand case and three for the fixed demand case) can be put into standard variational inequality form. Recall (cf. Nagurney (1999)) that the finite-dimensional variational inequality problem, VI$\left(F,\mathcal{K}\right)$, is to determine a vector $X^{\text{*}}\in \mathcal{K}\subset R^{\mathcal{N}}$, such that

$$⟨F\left(X^{\text{*}}\right),X-X^{\text{*}}⟩\ge 0,\forall X\in \mathcal{K},$$ (22)

where F is a given continuous function from $\mathcal{K}$ to $R^{\mathcal{N}}$, $\mathcal{K}$ is a given closed, convex set, and $⟨\cdot ,\cdot ⟩$ denotes the inner product in $\mathcal{N}$-dimensional Euclidean space.

4. Computational procedure and numerical examples

Since the supply chain network optimization model with labor, under its realizations in the case of both elastic demands and fixed demands, and under all three labor capacity scenarios, admits a variational inequality formulation, the modified projection method of Korpelevich (1977) is proposed for computational purposes. In the case of elastic demands, each iteration of the modified projection method will yield closed form expressions for the path flows and for the associated Lagrange multipliers. This is a nice feature for implementation. On the other hand, in the case of fixed demands, in order to guarantee that the fixed demand is satisfied at each demand market, we recommend the use of the equilibration algorithm of Dafermos and Sparrow (1969), which has been used in a variety of network and supply chain settings (cf. Nagurney and Zhang (1996); Nagurney (1999)).

The conditions for convergence of the modified projection method are that the function $F\left(X\right)$ that enters the VI (cf. (22)) is Lipschitz continuous and monotone. These are reasonable conditions for the supply chain network optimization model with labor under its demand realizations as well as scenarios. In the case of fixed demands, one still has that at each iteration the relevant Lagrange multipliers can be computed exactly and in closed form.

For completeness and easy reference, we now recall the definitions of monotonicity and Lipschitz continuity of $F\left(X\right)$. The function $F\left(X\right)$ is said to be monotone, if

$$⟨F\left(X^1\right)-F\left(X^2\right),X^1-X^2⟩\ge 0,\forall X^1,X^2\in \mathcal{K},$$ (23)

and the function $F\left(X\right)$ is Lipschitz continuous, if there exists a constant $L>0$, known as the Lipschitz constant, such that

$$F\left(X^1\right)-F\left(X^2\right)\le L\left|\right|X^1-X^2\left|\right|,\forall X^1,X^2\in \mathcal{K}.$$ (24)

The steps of the modified projection method are given below, with τ denoting an iteration counter:

4.1. The modified projection method

Step 0: Initialization

Initialize with $X^0\in \mathcal{K}$. Set the iteration counter $\tau :=1$ and let β be a scalar such that $0<\beta \le \frac{1}{L}$, where L is the Lipschitz constant.

Step 1: Computation

Compute ${\bar{X}}^{\tau }$ by solving the variational inequality subproblem:

$$⟨{\bar{X}}^{\tau }+\beta F\left(X^{\tau -1}\right)-X^{\tau -1},X-{\bar{X}}^{\tau }⟩\ge 0,\forall X\in \mathcal{K}.$$ (25)

Step 2: Adaptation

Compute $X^{\tau }$ by solving the variational inequality subproblem:

$$⟨X^{\tau }+\beta F\left({\bar{X}}^{\tau }\right)-X^{\tau -1},X-X^{\tau }⟩\ge 0,\forall X\in \mathcal{K}.$$ (26)

Step 3: Convergence Verification

If $|X^{\tau }-X^{\tau -1}|\le \epsilon$, with $\epsilon >0$, a pre-specified tolerance, then stop; otherwise, set $\tau :=\tau +1$ and go to Step 1.

The modified projection method was implemented in FORTRAN and a Linux system at the University of Massachusetts Amherst used for the computation of solutions to the subsequent numerical examples. We proceeded to solve elastic demand examples, first for Scenario 1 and then for Scenario 3.

The algorithm was initialized as follows. We initialized the elastic demand for each demand market at 40 and equally distributed the demand among the paths connecting each demand market from the origin node 1 (the Firm). The Lagrange multipliers were initialized to 0. The algorithm was deemed to have converged if the absolute difference of the path flows differed by no more than ${10}^{-7}$ and the same for the Lagrange multipliers.

4.2. Scenario 1 elastic demand examples

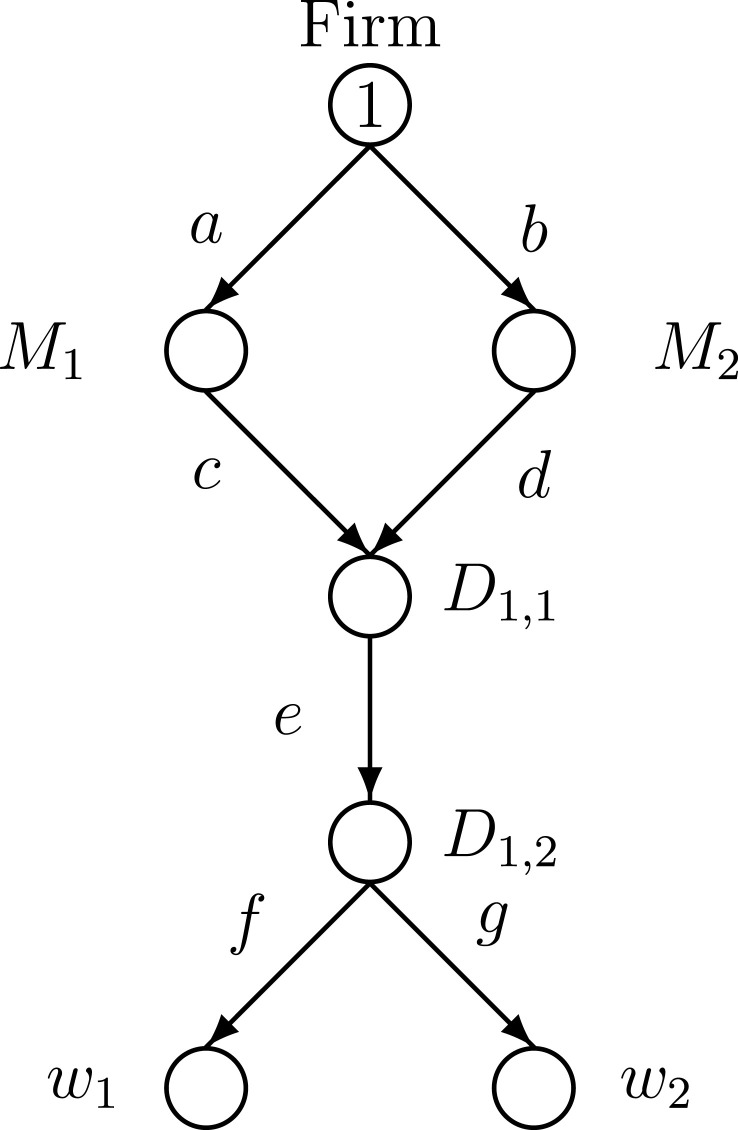
Examples 1 and 2 have the supply chain network topology given in Fig. 3 , whereas Examples 3 and 4 have electronic commerce included, and has the supply chain network topology depicted in Fig. 4 .

Fig. 3.

Supply chain network topology for examples 1 and 2.

Fig. 4.

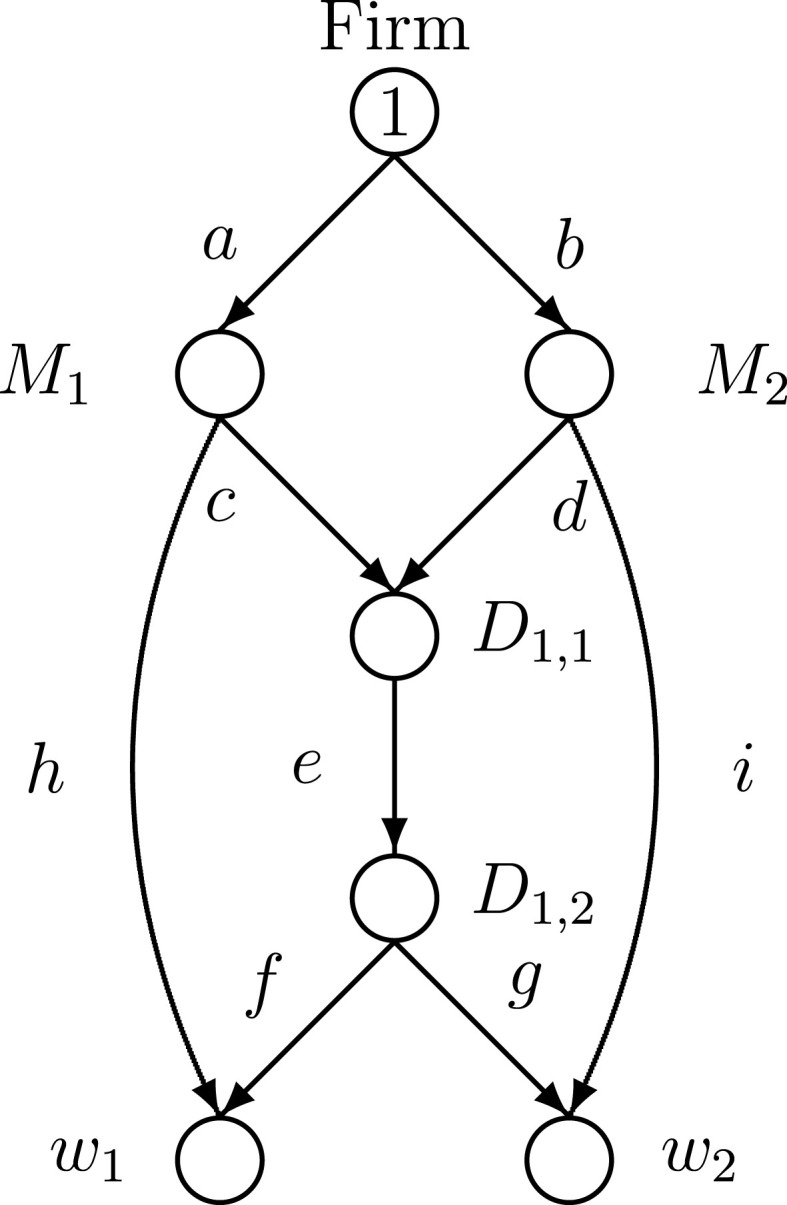
Supply chain network topology for examples 3 and 4.

4.2.1. Example 1 - baseline

Example 1 was constructed from the Scenario 1 Illustrative Example in Section 3.1.1 with the addition of a new demand market $w_2$. This example has the same data as that example with the following additions for the new link g:

$${\hat{c}}_g\left(f\right)=.5f_g^2,{\pi }_g=6.00,{\alpha }_g=20.00,$$

so that $f_g=20l_g$.

Also, the demand price function at the second demand market is: ${\rho }_{w_2}\left(d\right)=-d_{w_2}+80500$; hence, those at demand market $w_2$ are willing to pay a higher price for the healthcare product than those at demand market $w_1$.

Since Example 1 serves as the baseline for subsequent examples, we are interested in determining what would be the optimal flows and optimal levels of labor if the bounds on labor are quite high (and, thus, the associated optimal Lagrange multipliers would all be 0). Thus, we set the link labor bounds as:

$$\begin{array}{l}{\bar{l}}_a=200000.00,{\bar{l}}_b=20000.00,{\bar{l}}_c=30000.00,{\bar{l}}_d=30000.00,\\ {\bar{l}}_e=100000.00,{\bar{l}}_f=120000.00,{\bar{l}}_g=120000.00.\end{array}$$

Paths $p_1$ and $p_2$ remain as in Section 2.1.1 with the new paths $p_3$ and $p_4$ associated with the demand market $w_2$ being: $p_3=\left(a,c,e,g\right),p_4=\left(b,d,e,g\right).$

The β parameter was set to 0.005 and the modified projection method converged in 310 iterations and yielded the following solution:

$$x_{p_1}^{\text{*}}=x_{p_2}^{\text{*}}=3301.55,x_{p_3}^{\text{*}}=x_{p_4}^{\text{*}}=3384.88.$$

In terms of the optimal link labor values, we have that:

$$\begin{array}{l}{l}_a^{\text{*}}=6686.43,l_b^{\text{*}}=6686.43,l_c^{\text{*}}=668.64,l_d^{\text{*}}=668.64,\\ l_e^{\text{*}}=1337.29,l_f^{\text{*}}=330.16,l_g^{\text{*}}=338.49.\end{array}$$

As expected, all the Lagrange multipliers are equal to 0:

$${\lambda }_a^{\text{*}}={\lambda }_b^{\text{*}}={\lambda }_c^{\text{*}}={\lambda }_d^{\text{*}}={\lambda }_e^{\text{*}}={\lambda }_f^{\text{*}}={\lambda }_g^{\text{*}}=0.00.$$

The demand price at demand market $w_1$ is: $\mathrm{73,396.90}$ and at demand market $w_2$: $\mathrm{73,730.25}$ and the computed respective demands are: $\mathrm{6,603.10}$ and: $\mathrm{6,769.75}$.

The profit of the firm is: $\mathrm{536,520,192.00}$.

4.2.2. Example 2 - a much tighter labor bound on a manufacturing link

We now consider the situation where the pandemic has had an impact on labor especially in the community where the first manufacturing plant in Fig. 3 is located.

Hence, the labor bound on link a is now significantly reduced to:

$${\bar{l}}_a=5000.00.$$

The rest of the data is identical to that in Example 1.

The modified projection method converged in 13,507 iterations to the following solution:

$$x_{p_1}^{\text{*}}=2458.39,x_{p_2}^{\text{*}}=3648.73,x_{p_3}^{\text{*}}=2541.71,x_{p_4}^{\text{*}}=3732.07.$$

The optimal link labor values are:

$$\begin{array}{l}{l}_a^{\text{*}}=5000.00,l_b^{\text{*}}=7380.79,l_c^{\text{*}}=500.00,l_d^{\text{*}}=738.08,\\ l_e^{\text{*}}=1238.01,l_f^{\text{*}}=305.36,l_g^{\text{*}}=313.69.\end{array}$$

Since the bound on link a is now tight, with $l_a=5000.00$, the associated Lagrange multiplier is positive and is equal to: 11903.52. All other Lagrange multipliers are equal to 0.00.

The demand price at demand market $w_1$ is now: $\mathrm{73,892.89}$ and at demand market $w_2$ it is: $\mathrm{74,226.22}$. One can see the increase in the price for the healthcare product, as compared to the values in Example 1. The computed optimal demands at the demand markets are: $\mathrm{6,107.11}$ for $w_1$ and: $\mathrm{6,273.78}$ for $w_2$.

The firm now obtains a profit of: $\mathrm{526,483,680.00}$, a decrease of over $\mathrm{10,000,000}$ from that in Example 1.

4.2.3. Example 3 - introduction of electronic commerce

Example 3 introduces electronic commerce to Example 2 with the underlying supply chain network topology as in Fig. 4. The electronic commerce links in Fig. 4 are link h joining the first manufacturing plant node with node $w_1$ and link i joining the second manufacturing node with node $w_2$.

There are now two additional paths defined as follows:

$$p_5=\left(a,h\right),p_6=\left(b,i\right).$$

The data in Example 3 are as in Example 2 with the following additions associated with the electronic commerce links:

$${\hat{c}}_h\left(f\right)=f_h^2,{\hat{c}}_i\left(f\right)=f_i^2,$$

and

$${\pi }_h=10.00,{\pi }_i=10.00,{\alpha }_h=1.00,{\alpha }_i=1.00,$$

with labor bounds on the electronic links of:

$${\bar{l}}_h=100000.00,{\bar{l}}_i=100000.00.$$

The modified projection method with $\beta =.036$ converged in 12,952 iterations to the following solution:

$$\begin{array}{l}{x}_{p_1}^{\text{*}}=0.00,x_{p_2}^{\text{*}}=2967.86,x_{p_3}^{\text{*}}=0.00,\\ x_{p_4}^{\text{*}}=1501.03,x_{p_5}^{\text{*}}=5000.00,x_{p_6}^{\text{*}}=7450.30.\end{array}$$

The optimal link labor values are:

$$\begin{array}{l}{l}_a^{\text{*}}=5000.00,l_b^{\text{*}}=11919.19,l_c^{\text{*}}=0.00,l_d^{\text{*}}=446.89,\\ l_e^{\text{*}}=446.89,l_f^{\text{*}}=446.89,l_g^{\text{*}}=75.05,\\ l_h^{\text{*}}=5000.00,l_i^{\text{*}}=7450.30.\end{array}$$

For both demand markets, the paths $p_5$ and $p_6$ with the electronic commerce link garner the most of the healthcare product flow. Note that in the case of electronic commerce one still has freight service delivery, but in our framework there is no transportation to and from a distribution center. Paths $p_1$ and $p_3$ have zero product flow.

The demand price at demand market $w_1$ is now: $\mathrm{72,032.09}$, whereas at demand market $w_2$ it is: $\mathrm{71,548.67}$. With the introduction of electronic commerce the consumers at the demand markets enjoy lower prices. The computed optimal demands at the two demand markets are now, respectively, $\mathrm{7,967.91}$ and 8.951.33.

The firm has a profit of: $\mathrm{763,964,416.00}$, which exceeds the profits garnered in Examples 1 and 2. In Example 3, unlike in Example 1, since there is a much tighter bound on the labor available on link a (as was also the case in Example 2), the optimal labor value on link a is at the bound of 5000.00 and the Lagrange multiplier is positive and now equal to: $\mathrm{34,043.8672}$. All other Lagrange multipliers are equal to 0.00.

4.2.4. Example 4 - closure of a manufacturing plant

Example 4 has the same data as Example 3 except that now we consider an even more disruptive scenario (as is happening during the COVID-19 pandemic). Specifically, we consider the situation that due to illnesses, employee fear of contagion, etc., the first manufacturing plant is shut down. Hence, we now have that: ${\bar{l}}_a=0.00$.

The modified projection method with $\beta =.036$ converged in 13,368 iterations to the solution:

$$\begin{array}{l}{x}_{p_1}^{\text{*}}=0.00,x_{p_2}^{\text{*}}=4932.13,x_{p_3}^{\text{*}}=0.00,\\ x_{p_4}^{\text{*}}=72.47,x_{p_5}^{\text{*}}=0.00,x_{p_6}^{\text{*}}=7539.58.\end{array}$$

The computed optimal link labor values are:

$$\begin{array}{l}{l}_a^{\text{*}}=0.00,l_b^{\text{*}}=12544.18,l_c^{\text{*}}=0.00,l_d^{\text{*}}=500.46,\\ l_e^{\text{*}}=500.46,l_f^{\text{*}}=246.61,l_g^{\text{*}}=362.00,\\ l_h^{\text{*}}=0.00,l_i^{\text{*}}=7539.58.\end{array}$$

Observe that for demand point $w_1$ only path $p_2$ has positive flow with the other two paths not used, which makes sense since essentially link a is unavailable due to the closure of the manufacturing plant. The Lagrange multiplier ${\lambda }_a^{\text{*}}=\mathrm{70,114.92}$ with all other Lagrange multipliers equal to 0.00.

The demand price at demand market $w_1$ is: $\mathrm{75,067.77}$ at a computed optimal demand of: $\mathrm{4,932.23}$. At demand market $w_2$ the demand price is: $\mathrm{72,887.95}$ at a demand of: $\mathrm{7,612.06}$.

With closure of the plant, the firm's profit is only $\mathrm{503,570,432.00}$ and it suffers immense losses in profits (over $\mathrm{250,000,000.00}$) as compared to Example 3. This profit is the lowest of all the computed numerical examples to this point. This example vividly illustrates the importance of keeping operations running during the pandemic and having appropriate healthcare pandemic mitigation processes and procedures in place. With one of the two manufacturing plants closed, the prices rise at both demand markets.

4.3. Scenario 3 elastic demand examples - reduction of labor availability

We now report the computed solutions to elastic demand examples for Scenario 3. The supply chain network topology remains as in Fig. 4 and the data are identical to those in Examples 3 and 4 except that instead of having link labor bounds, there is a single upper bound on labor $\bar{l}$. Specifically, we solve three examples under this scenario. Example 5 has the upper bound $\bar{l}=50000.00$; Example 6 has $\bar{l}=\mathrm{10,000.00}$, and Example 7 has $\bar{l}=\mathrm{5,000.00}$. These examples illustrate the impact of reduction of labor availability due to a pandemic. The computed optimal product flows are reported in Table 2 .

Table 2.

Optimal product flows for examples 5, 6, and 7 representing scenario 3.

Optimal Product Flows	Ex. 5	Ex. 6	Ex. 7
$x_{p_1}^{\text{*}}$	1313.60	1785.36	958.35
$x_{p_2}^{\text{*}}$	1294.37	1766.13	958.35
$x_{p_3}^{\text{*}}$	1380.91	1852.67	1041.69
$x_{p_4}^{\text{*}}$	1361.68	1833.44	1041.69
$x_{p_5}^{\text{*}}$	7998.25	214.22	0.00
$x_{p_6}^{\text{*}}$	8046.33	262.30	0.00

We also report the computed optimal Lagrange multiplier ${\gamma }^{\text{*}}$. For Example 5, since the labor upper bound constraints was not tight, ${\gamma }^{\text{*}}=0.00$. In Example 6, on the other hand, the constraints was tight and ${\gamma }^{\text{*}}=28305.57$. In Example 7, ${\gamma }^{\text{*}}=44989.31$.

The modified projection method with $\beta =.02$ for Example 5 converged in 183 iterations; with $\beta =.2$ for Example 6, it converged in 587 iterations, and with $\beta =.02$, the modified projection method converged in 2107 iterations for Example 7. We emphasize that each iteration takes a negligible amount of CPU time since it involves explicit formulae for the path flow and Lagrange multipliers at each iteration.

The computed optimal link labor values are reported in Table 3 .

Table 3.

Optimal link labor values for examples 5, 6, and 7 representing scenario 3.

Optimal Link Labor Values	Ex. 5	Ex. 6	Ex. 7
$l_a^{\text{*}}$	10692.76	3852.25	2000.00
$l_b^{\text{*}}$	10702.38	3861.87	2000.00
$l_c^{\text{*}}$	269.45	363.80	200.00
$l_d^{\text{*}}$	265.61	359.96	200.00
$l_e^{\text{*}}$	535.06	723.76	400.00
$l_f^{\text{*}}$	130.40	177.57	95.84
$l_g^{\text{*}}$	137.13	184.31	104.17
$l_h^{\text{*}}$	7998.25	214.22	0.00
$l_i^{\text{*}}$	8046.33	262.30	0.00

In Example 5, the computed demand at demand market $w_1$ is: $\mathrm{10,606.22}$, whereas the demand at demand market $w_2$ is: $\mathrm{10,788.91}$. The computed demand in Example 6 is: 3765.71 for $w_1$ and $\mathrm{3,948.40}$ for $w_2$. In Example 7, the computed demand for the healthcare product is: $\mathrm{1,916.71}$ for $w_1$ and it is: $\mathrm{2,083.37}$ for $w_2$.

In Example 5, the demand price at demand market $w_1$ is: $\mathrm{69,393.78}$ and at demand market $w_2$ it is: $\mathrm{69,711.09}$. In Example 6, the demand price at demand market $w_1$ is: 76234.29 and at demand market $w_2$ it is: 76551.59. Finally, in Example 7, the demand price at demand market $w_1$ is: 78073.30 and at demand market $w_2$ it is: 78416.62. As the labor resources become more constrained the prices rise, which is very reasonable and we see it happening now for various products during the COVID-19 pandemic.

In terms of profits, the firm earns in Example 5 a profit of: $\mathrm{858,307,968.00}$; a profit of: $\mathrm{451,028,736.00}$ in Example 6, and a profit of: $\mathrm{272,973,568.00}$ in Example 7. The profit earned in Example 5 is the highest of all the examples and that in Example 7 is the lowest.

Interestingly, in Example 7, the paths with the electronic commerce links are not used, that is, the paths $p_5$ and $p_6$ have zero flow. At first, this may seem puzzling; however, if one looks at the cognizant variational inequality (16) and the term: ${\gamma }^{\text{*}}\sum _{a\in L}\frac{1}{{\alpha }_a}{\delta }_{ap}$ this result is clarified. In the dataset the links on the other paths, corresponding to those post the common manufacturing link(s) have ${\alpha }_a$s higher than the ${\alpha }_h$ and ${\alpha }_i$ signifying greater productivity among the storage workers and associated freight service providers.

5. Summary and conclusions and suggestions for future research

The COVID-19 pandemic has impacted the globe, causing great personal and economic strife and uncertainty. Healthcare has been one of the major sectors impacted since this sector is at the forefront of the battle against the coronavirus. In addition, the food sector, with food essential to well-being and health, has been challenged, with many reluctant to go to grocery stores and even hygiene and sanitation supplies experiencing shortages. Importantly, products for essential workers, including healthcare ones, such as PPEs, have been in short supply in the United States. This is, due, in part, to much of the manufacturing of such products (and many other, including pharmaceuticals) having been done originally in China, where the coronavirus was believed to have originated, specifically, in the city of Wuhan. With factories shut down and also the demand growing globally, prices of such products, when they can be acquired, have grown. Even states in the United States have been competing for such supplies and scrambling to acquire them for the hospital workers. With people getting sick, some tragically perishing, and others experiencing anxiety and fear, plus the acknowledgment of physical/social distancing to mitigate the spread, supply chains are trying to adapt to this new world scenario.

Critical to such supply chains is the resource of labor and during the pandemic the need for this resource has become vividly apparent. Some factories and processing plants have actually been hot spots of spread of the coronavirus since workers are in proximity to do their tasks. With labor less available, some facilities have had to shut down, creating further disruptions to needed supplies and products. Some businesses have even reallocated their workers to different tasks.

In this paper, we develop a supply chain network optimization framework that explicitly contains labor as a variable in supply chain network economics activities of production, transportation, storage, and distribution. We also allow for electronic commerce, since that has been a lifeline for many in obtaining products, with the goal of reducing exposure in grocery stores, for example. We first propose profit-maximizing models with elastic demands in the case of three labor scenarios, of increasing flexibility, as to reallocation. The first scenario has labor bounds on the links; the second scenario allows for transfer of labor across a tier of activity, whereas the third, and most flexible scenario, allows for labor reallocation across the supply chain and there is a single bound on labor. We provide illustrative examples and then construct fixed demand analogues for the three scenarios. The methodological tool for the formulation, analysis, and solution of the models is that of variational inequality theory.

In addition to the models and theoretical constructs, we also provide solutions to computed numerical examples, motivated by the healthcare disaster caused by the pandemic. Our results show the impacts on demands, product flows, prices, as well as profits of the reduction of available labor, the introduction of electronic commerce, and also a plant closure.

This work serves as the foundation for the explicit incorporation of labor, and the quantification of the impacts of labor availability in different scenarios, for other applications, with appropriate adaptations and extensions. In particular, another healthcare sector that has been gravely negatively impacted and stressed during the pandemic includes the blood supply chain. Many perishable food supply chains are also struggling now. To research the impacts of labor availability on such perishable product supply chains is most definitely worthwhile. Furthermore, with growing competition for labor among firms involved in the production of critical products, the formulation of game theory models is also promising. We leave such research for the future.

Declaration of competing interest

None.