Abstract
The COVID-19 pandemic broke the balance of oil supply and demand. Meeting these oil market challenges induced by the pandemic required a more accurate assessment of the impact of the pandemic on oil consumption. The existing measurement of the impact of the pandemic on oil consumption was based on year-over-year calculation. In this work, a new measurement approach based on a comparison of simulated and actual oil consumption was proposed. In this proposed measurement model, the actual oil consumption was from the official statistics, whereas the simulated oil demand came from business-as-usual (without pandemic) scenario simulation. In order to reduce the simulation error, three hybrid simulation approaches were developed by combining the simulation technique and machine learning technique. The mean relative errors of the proposed simulation approaches were between 1.08% and 2.51%, within the high precision level. An empirical research on the US oil consumption was conducted by running the proposed measurement model. Through analyzing the difference between the simulated and real US oil consumption, we found the impact of the epidemic on U.S. oil consumption was obvious in April–May 2020 and January–February 2021. At its worst, the oil decline in the United States reached 973 trillion British thermal units, compared to the state without the epidemic. During the entire survey period (January 2020–March 2021), the US oil consumption under the epidemic was about 18.14% lower than that under the normal epidemic-free situation, which was 5% higher than the 13% inter-annual decline rate reported. This work contributed to understand the impact of the pandemic on oil consumption more comprehensively, and also provided a new approach for analyzing the impact of the pandemic on energy consumption.
Keywords: COVID-19, U.S. petroleum, Pandemic-free scenario, Simulation
Graphical abstract
1. Introduction
The global pandemic of COVID-19 imposed serious threat to the public health of the world [1]. In order to prevent the spread of the virus, more than 187 countries around the world have adopted measures such as restricting the movement of people and city blockades, which directly brought about a substantial shrinkage of global oil demand. As one of the world's largest energy consumers and oil producers, the changes in US oil demand as a result of the pandemic affected the stability of the global oil supply chain and oil prices [2]. For a long time, petroleum was the world's main commercial energy, and it played the role of an engine in the world economy [3]. Under the circumstances that the pandemic is not yet under control, judging the future U.S. oil consumption is of key significance.
Statistical reports that assessed the impact of the pandemic on oil consumption were mostly based on inter-annual or inter-monthly measurements. As mentioned in full-year 2020 projections of the International Energy Agency [4], global oil demand was expected to be a record 9.3 mb/d lower in 2020 than in 2019. To soon, the Organization of Petroleum Exporting Countries [5] reported that world oil demand was now expected to contract by around 9.8 mb/d, year-to-year, in 2020. However, a truly effective measurement should be to compare the oil consumption under the outbreak of the 2020 epidemic with the oil consumption under the absence of the 2020 epidemic. The year-on-year measurement method assumed that the oil consumption in 2020 without a pandemic was the same as in 2019 or the historical average, which was obviously not convincing.
In this study, the true impact of the pandemic on U.S. oil consumption was re-quantified. We adopt mature forecasting technology to simulate the monthly oil consumption in 2020 under the scenario of no pandemic, with the help of data period 2015–2020 issued by Energy Information Administration [6]. Three hybrid forecasting models covering time series and machine learning ensured the credibility of simulation results. By comparing the actual U.S. oil consumption in 2020 with the simulated oil consumption in 2020 under the absence of the epidemic, the real impact on the U.S. energy industry could be assessed. Analyzing the impact of pandemics on the U.S. oil market situation from the perspective of scenario simulation could have a more comprehensive understanding of energy consumption under pandemics, so as to better respond to possible future challenges and impacts.
The remainder of this paper was organized as follows. Section 2 introduced a related literature review. Section 3 discussed the formulas and processes of several combination forecasting methods. A quantitative measure of the impact of the pandemic on US oil consumption was introduced in Section 4. Section 5 summarized the full text.
2. Literature review
2.1. Research on the impact of COVID-19 on the energy-related fields
It has become a consensus that measures taken in response to the spread of COVID-19 have a significant negative impact on the global economy [7,8]. A series of changes have taken place in the way of social operation during this period, affecting many fields such as public social interaction, transportation and energy [9]. Following this, the weakening of economic activities inevitably was reflected in changes in energy efficiency [10] and electricity demand [11]. From the perspective of different sectors of energy, the pandemic had a certain degree of impact on the industrial, commercial, and residential sectors, as well as the energy mix. Studies have shown that the pandemic would lead to an increase in residential energy demand and a decrease in industrial and commercial energy demand [12]. Zhang et al. [13] investigated the impact of the closure measures caused by the COVID-19 pandemic on the energy demand of the Swedish building portfolio. Under three restrictions, the average delivered power demand across the region increased by 14.3%–18.7%. However, the average system energy demand (the sum of heating, cooling and domestic hot water) fell by 7.1%–12.0%. The two offset each other, resulting in a small impact of the pandemic on energy demand. In addition to the above-mentioned department-focused research, scholars have also launched investigations around different types of energy. For the development of renewable energy, a significant short-term contraction was inevitable [14]. However, considering the dual threshold effect between renewable energy and financial level [15], the incentives of investment measures may also turn the crisis into an opportunity for the development of renewable energy. Naderipour et al. [16] proposed the point that the reduction of greenhouse gas emissions and pollutant gases allowed more sunlight to shine on photovoltaic panels, thereby increasing the power generation of renewable energy. Using an input-output model, Kanitkar [17] found that the daily power supply of India's thermal power plants had been reduced by nearly 26% during the blockade. Madurai Elavarasan et al. [18] investigated the impact of COVID-19 on the Indian power system. The survey results showed that during the blockade, the electricity demand for commercial loads in India had fallen the most, while the electricity demand for residential loads had increased the most. Corpus-Mendoza et al. [19] studied the overall impact of COVID-19 on electricity consumption and pollutant emissions. Studies have found that electricity consumption had dropped significantly during the pandemic. On the basis of the two-way causality between per capita carbon emissions and structural reforms, it was highly possible that the epidemic increased carbon emissions by changing energy intensity [20]. The reasons for this change were closely related to the preventive measures of various countries.
Furthermore, what was the specific impact of the epidemic on the energy industry? Norouzi et al. [21] pointed out that the oil industry was more susceptible to global crises than the power industry. The elasticity of oil and electricity demand to the number of infected persons was +0.1% and ±0.65%, respectively. Adedeji et al. [22] examined the dynamic impact of COVID-19 on the four major oil prices and found that the impact of the COVID-19 pandemic on Bonnie, Daqing, BRENT and WTI oil prices was 17%, 14%, and 7%, respectively. Studies [23] have shown that compared with 2019, the energy intensity in 2020 had obvious temporal and spatial differences, but energy demand and GDP had both declined. There were differences in the energy intensity of different regions. The United States had the highest rate of change (+29.3%), followed by Japan (+7.8%); while China (+2.8%) and the European Union (+1.03%) currently had no significant changes. Cihan [24] developed an automatic regression integrated moving average (ARIMA) and Holt-Winters model to predict the impact of the COVID-19 lockdown on electricity and natural gas consumption. The results found that in April 2020, electricity consumption fell by 72%–43%, and natural gas consumption fell by 77%–57%. Rainer et al. [25] considered the impact of the crisis on major exporters of oil and natural gas resources, with a focus on some G20 countries. The conclusion was that the COVID-19 crisis had deepened the gap between leaders and laggards in the global energy transition. Leonardo et al. [26] investigated the impact of the COVID-19-related lockdown implemented in Spain from March to June 2020 on the share of the national power sector and photovoltaics in the energy mix. The study found that the blockade reduced electricity demand by 11% and increased PV market share by nearly 1%. Some scholars have answered questions with Europe as the research object. Bahmanyar et al. [27] first compared the different control measures taken by European countries against COVID-19, and then investigated the electricity consumption in these countries. The results showed that the intensity of restrictive measures was positively correlated with the reduction in power consumption. Ruan et al. [28] confirmed that the reasons for the reduction in electricity in the United States during the pandemic were closely related to the number of cases, the degree of social distancing, and the level of commercial activities.
Through the latest literature survey, we found that the impact of the epidemic on the energy industry was mainly manifested in changes in electricity demand, residential electricity consumption patterns, and oil price. In measuring the specific impact of the epidemic on energy demand, some scholars conducted a correlation analysis by investigating the elasticity coefficient of the epidemic and energy [29]. Some scholars have analyzed the inter-annual changes in electricity demand and energy demand based on the numerical changes over the years. A few scholars have evaluated the impact of the epidemic by means of prediction and measurement. In conclusion, the impact of the epidemic on the energy sector has received extensive attention. Based on the implementation of predictive tools to assess the impact, if scenario analysis can be further taken into consideration, it will provide novel points for current research.
2.2. A review of energy simulation methods
Grasping the future development trend of energy is of vital help to the current decision-making process [30]. Therefore, energy forecasting technology has a key position in today's academic field [31]. Below we classified and sorted out the research carried out around energy forecasting in the past two years, in order to gain an understanding and mastery of popular methods.
First, the comparative study of multiple methods based on time-series forecasting methods was widely used in energy field's forecasting research. Nafil et al. [32] compared three forecasting methods (ARIMA, temporal causality modeling, and exponential smoothing) to calculate Morocco's 2020 energy demand forecast. Ye et al. [33] combined the optimized DGM (1, 1) model with interval grey numbers to predict the annual electricity consumption per capita in southern Jiangsu with an error of less than 5%. The combination of ARIMA and GM models was the same example [34]. Second, the combination of optimization and machine learning model [35,36] had become a hot topic in the field of renewable energy. Rasku et al. [37] made a random planning forecast for the variable renewable energy (VRE) in the Nordic power system. The highly nonlinear characteristics of wind energy have prompted multi-objective optimization algorithms [38] and machine learning algorithms [39,40] become a common choice in the field of clean energy. Studies [41] confirmed that models based on deep learning to predict fluctuations in power demand and power generation in a renewable energy system had significant advantages over traditional models. Third, the integration of traditional models and artificial neural networks has been proven to be robust and comprehensive in all application fields and prediction fields [42]. For example, Kazemzadeh et al. [43] proposed a combined method based on automatic regression integrated moving average (ARIMA), artificial neural network (ANN) and support vector regression technology to predict the annual peak load and total energy demand of the Iranian national power system. Ahmad and Chen [44] found that supervised learning methods could reduce noise in network formulations and control unbalanced data. Wang and Wang [45] proposed a mixed prediction model of a closed loop unit with random time effective weights (SW-GRU) and applied empirical mode decomposition (EMD) to global energy price prediction. In agreement, the combined root mean square error (CRMSE) and average absolute percentage error (CMAPE) were very suitable for evaluating model performance.
The grey forecasting method is an original pedigree forecasting method developed based on the original grey theory in China. We found that the development of the existing grey forecasting model was a closed improvement mode-self-improvement within the grey system theory. This work took a different approach and explored a new model of grey forecasting improvement-the open model, that was, the introduction of foreign forecasting methods to improve grey forecasting. Based on this, we proposed a new modeling idea of “error correction + secondary modeling”. After using the internally innovative metabolic nonlinear grey prediction to model the original data sequence, the grey prediction error sequence was modeled twice using foreign ARIMA and BP models. The ARIMA and BP models were chosen because we found that ARIMA was often used to process time-series with obvious overall trends and fluctuations in individual data points. This feature coincided with the more obvious characteristics of nonlinear fluctuations in residual series. Because of its strong self-learning ability and data processing ability, BP could dig out the complex non-linear relationship and fully capture information such as fluctuations and mutations in the sequence.
2.3. Summary of literature review
By combing the latest literature, we found that analyzing the impact of COVID-19 had become the focus of the energy sector. Research hotspots included: the comparison of inter-year changes, the comprehensive impact of clean energy, and the turnover changes of the power consumption industry. Most of these analyses started from the perspective of econometrics or statistical analysis [46]. The premise of the judgment was that the index value in 2020 was not much different from that in 2019. However, the development of energy was not a copy of historical years. Starting from this consensus, only by following the historical development trajectory to calculate the energy scale under the ideal scenario and comparing it with the energy scale under the real scenario could the true impact of the pandemic be determined.
Current energy forecasting hotspots mostly focused on the combination of traditional models and machine learning models or traditional models and artificial neural network models [47]. Almost all studies had confirmed that the prediction accuracy of the combined model was much higher than that of the single model. In addition, the combined method exhibited strong tolerance and robustness in terms of applicability to data.
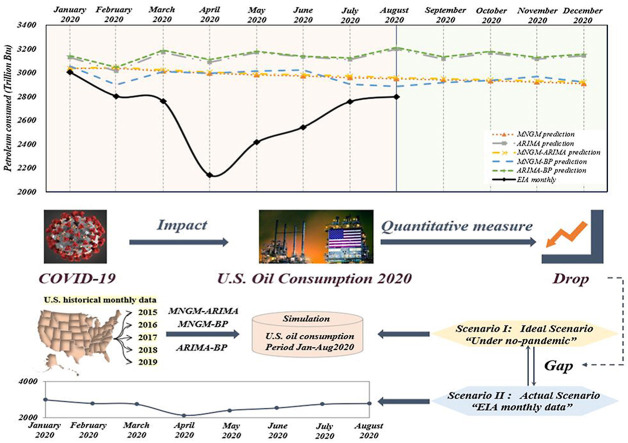
Based on this, the contribution points of this research include the following aspects. (1) This study designed a new research framework based on scenario assumptions and predictions to accurately depict the specific impact of US oil under the epidemic (as shown in Fig. 1 ). First, we used high-precision predictive models to simulate the US oil consumption under the epidemic-free scenario. Then, we calculated the error value of the fitting stage and implemented the accuracy comparison between multiple models to evaluate the prediction performance of multiple mixed models. Finally, we choose the best prediction result as the US oil consumption under the epidemic-free scenario, and compared it with the actual oil consumption. The difference between the two was regarded as the change in U.S. oil consumption caused by the epidemic. (2) This research used multiple types of combined models to simulate energy in ideal scenarios, including the combination of traditional models and artificial neural network models. Among them, MNGM-ARIMA, MNGM-BP and ARIMA-BP were all developed based on the principle of “error correction + secondary modeling”. The simultaneous use of multiple combination models was of vital help to improve the prediction performance and accurately portray the ideal scenario.
Fig. 1.
The framework of this study.
3. Methods
3.1. MNGM forecasting model
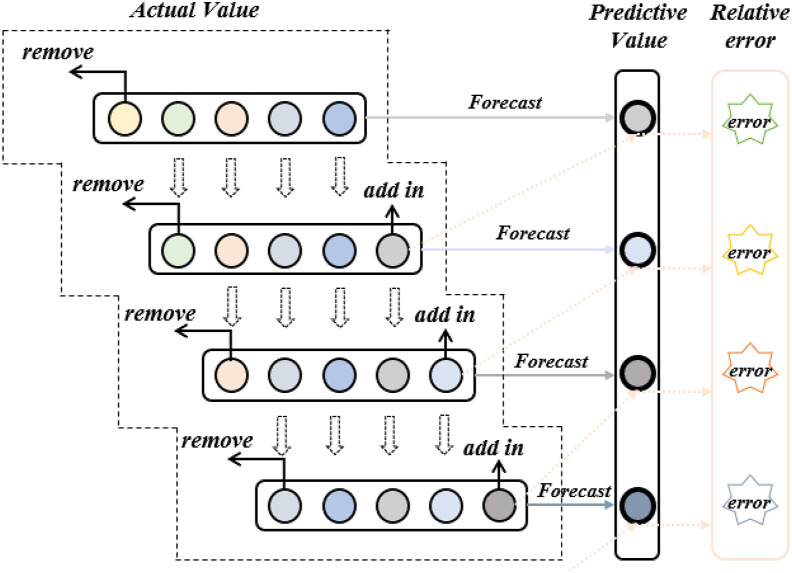
The grey prediction model (GM model for short) originated from the grey system theory proposed by Professor Deng Julong in 1982 [48]. The grey system contains both known information and unknown information. The prediction based on the grey system is to realize the purpose of prediction by treating the discrete data scattered on the time axis as a series of continuous changes, weakening the unknown factors in the grey system and strengthening the influence of the known factors. The prediction principle of the GM model is to first generate a set of new data sequences with obvious trends for a certain data sequence in an accumulative manner. Secondly, establish a model to predict according to the growth trend of the new data series. Finally, use the method of accumulation and subtraction to perform reverse calculation to restore the original data sequence and obtain the prediction result. After a period of development, scholars found that the traditional grey model has certain time constraints during its use. Specifically, as the prediction time increases, the accuracy becomes very low. To change this defect, the rolling grey forecasting model came into being. This rolling grey model is an addition mechanism for initial data replacement. The replacement of data makes the operation of each run more novel.
The metabolic nonlinear GM (1,1) prediction model (MNGM model for short) is based on this original model and improves the static model by adding metabolic ideas (that is, adding new elements and eliminating old elements). The GM model uses 5–10 data to build a set of prediction models and predict a series of future data, so a set of model parameter values are obtained during the calculation process. However, if the GM model is used for long-term forecasting, the subsequent forecast values gradually lose their validity, increasing forecast errors [49]. In order to improve this shortcoming, the metabolic GM model first uses 5–10 data to build a set of prediction models, but only predicts one data value in the future. Then, it builds the prediction model by continuously changing the data values used, so in the process, multiple module parameters are obtained. The idea of metabolism is embodied in constantly changing the data used, so it can achieve the effect of reflecting the characteristics of the system in real time. The specific principles and ideas were as Fig. 2 follows:
Fig. 2.
Flow chart of the metabolic GM (1,1) model.
During each round of calculation, the specific operating formula is introduced as follows.
First, we define the original sequence as: and the 1-AGO sequence as: , while .
Then, we define the equations of the model as Eqn 1:
| (1) |
where: is the original data sequence. is the accumulated data sequence to prepare for the construction of the next prediction equation.
The differential equation of satisfy the solutions of the following Eqn 2:
| (2) |
where: is the accumulated data sequence; “a” and “b” are constant term coefficients; “” is the power coefficient.
The constant term coefficients are solved by constructing the following matrix. We define a matrix of parameters, and satisfies the following (3), (4):
| (3) |
| (4) |
where: “a” and “b” are constant term coefficients, “B” is a matrix composed of one-time accumulated data sequence , and “Y” is a matrix composed of original data sequence .
The solution of coefficients “a”, “b” and “” can be calculated by the Runge-Kutta algorithm, which is implemented in Matlab software. Substituting the calculated three coefficients into Eqn 2, the prediction result of a cumulative sequence is calculated. According to the principle of accumulation and subtraction (as shown in Equation (5)), the predicted result is obtained:
| (5) |
3.2. MNGM-ARIMA forecasting model
Based on the principles of “error correction” and “secondary modeling”, this study used the Metabolic Nonlinear Grey Model (MNGM) as the base model and the ARIMA model as the correction model to construct a new MNGM-ARIMA combined model [50]. Firstly, the original sequence was modeled initially, and then the error sequence was modeled again to achieve the effect of reducing the prediction error.
The prediction steps of the MNGM-ARIMA model were as follows [51]:
-
(1)
Use MNGM to model the original data sequence for the first time, and calculate the initial prediction value and error sequence (as shown in Eqn 6);
| (6) |
-
(2)
Check the stationarity of the initial error series and smooth the non-stationary series using Eqn 7. The order of difference corresponds to the "d" in the model ARIMA (p, d, q). If the statistic obtained was significantly less than the critical statistic value of three confidence levels (1%, 5%, 10%), the sequence was considered to be stationary;
| (7) |
-
(3)
Establish an autoregressive AR model for stationary data series (as shown in Eqn 8);
| (8) |
-
(4)
Establish a moving average MA model for stationary data series (as shown in Eqn 9);
| (9) |
-
(5)
Combine the autoregressive AR model and moving average MA model to construct ARIMA (p, d, q).
3.3. MNGM-BP forecasting model
Based on the principles of “error correction” and “secondary modeling”, this research combined a mature time-series model with an advanced artificial neural network model to create an MNGM-BP model. Among them, the metabolic nonlinear grey model (MNGM) was the basic model, and the multi-layer feedforward network (BP) trained according to the error back propagation algorithm was the correction model.
The BP network could learn and store many input-output pattern mapping relationships without revealing the mathematical equations describing this mapping relationship in advance. Its learning rule was to use the steepest descent method to continuously adjust the weights and thresholds of the network, through backpropagation to minimize the sum of squared errors of the network. Therefore, the model could be well used to correct the errors in the prediction process, and had the effect of improving the prediction accuracy.
The prediction steps of the MNGM-BP model were as follows:
-
(1)
Select 5 data for each group and construct a nonlinear grey differential equation (as shown in Eqn 10);
| (10) |
-
(2)
Calculate and derive the unknown values of the power coefficients and constant coefficients in the equation by using the fourth-order-Runge-Kutta equation (as shown in Eqn 11);
| (11) |
-
(3)
Substitute the solved intermediate parameter values into the original differential equation, and get the initial prediction value;
-
(4)
Subtract the actual value from the initial predicted value to obtain the initial error sequence;
-
(5)
Construct a BP neural network model for the error sequence [52], and repeatedly train to obtain the corrected error sequence;
-
(6)
Combine the corrected smoothing error term with the initial prediction value to get the final prediction result.
3.4. ARIMA-BP forecasting model
Based on the principles of “error correction” and “secondary modeling”, this study used the ARIMA model as the base model and the BP model as the correction model to construct a new ARIMA-BP combined model.
The prediction steps of the ARIMA-BP model were as follows:
-
(1)
Bring the data series into the ARIMA model. The unit root test was used to judge the stationarity of the initial data series. Perform difference processing on non-stationary series to make it a stationary series.
-
(2)
Judge the order of autocorrelation and partial autocorrelation of the processed stationary series to establish the autoregressive and moving average model ARIMA (p, d, q).
-
(3)
Subtract the actual value from the initial predicted value to obtain the initial error sequence;
-
(4)
Construct a BP neural network model [53] for the error sequence, and repeatedly train to obtain the corrected error sequence;
-
(5)
Combine the corrected smoothing error term with the initial prediction value to get the final prediction result.
4. U.S. Oil consumption under pandemic-free scenario and actual scenario
4.1. Ideal oil consumption simulated according to historical trajectory
We assumed that "oil consumption under pandemic-free scenario in 2020" as an ideal scenario. In this study, we used the hybrid forecasting technique mentioned in the previous section to simulate the US oil consumption under ideal scenario. It was worth noting that all the models involved simulated the endogenous change characteristics of the data based on the historical trend of the data, and then predict the value of a specific stage in the future. Based on this, this study selected a total of 60 data sets from January 2015 to December 2019 to train the predictive model. After data training, US oil consumption at a certain stage in the future (January 2020–March 2021) was predicted. Therefore, the data value in 2020 was learned from the evolution characteristics of historical data. The result predicted from the historical data series was regarded as the 2020 U S. oil consumption in an ideal scenario (without an epidemic). According to the method flow shown in Section 3, this section focused on the specific operations of the forecasting methods.
4.1.1. Preliminary prediction: base model in two forms
The predicted principle of these hybrid models in this study was that the base model performed initial prediction, and then the modified model performed error re-prediction. Following the order of modeling, this section first introduced the calculation process of the base MNGM and ARIMA model.
The first demonstration was the MNGM model. We bring the data into the calculated equation of MNGM. With the help of the Matlab software, the intermediate parameter values of the model solution were calculated.
Then, we bring the intermediate parameters in Fig. 3 into Eqn 1. MNGM model adopted the operation mechanism of circular flow. Each round of calculation was based on the nonlinear grey model (NGM) modeling ideas. Specifically, each time we put five data into the model to solve for a set of parameters and the predicted value for the sixth year. By continuously updating the five data backwards, the forecast value of a new month was solved each time. The calculation ends until all predicted values have been solved. In this study, 15 prediction results were derived based on the law of 60 original data, which meant that the NGM formula would be circulative run for 70 times inside the model.
Fig. 3.
Intermediate parameters of MNGM model.
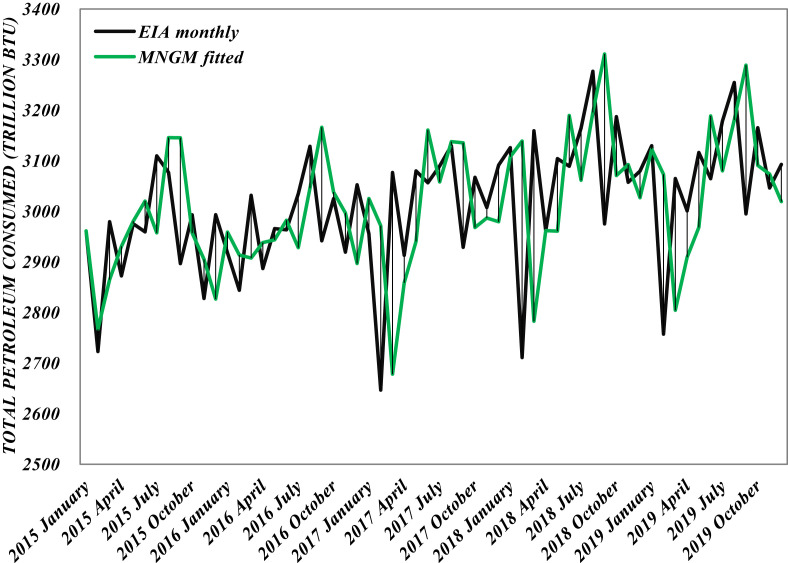
In the internal operation of the model, the MNGM model learned the changing laws of the 60-month data. On the one hand, it introduced historical fitting values, and on the other hand, it introduced multiple future forecast values. The MNGM model's prediction of the historical fit value was shown in Fig. 4 . The black curve in the picture came from EIA's monthly statistics, and the green curve was the predicted value fitted based on historical values. The gap between the two represented the predictive performance and accuracy of the model. The data in Fig. 4 showed that MNGM could simulate the trend of the original data as a whole, but the simulation at each time point had a lag. In the figure, the gap line (black thin line) between the real value and the simulated value was set. This also represented the prediction error of the model at each point in time.
Fig. 4.
Fitted result of MNGM model.
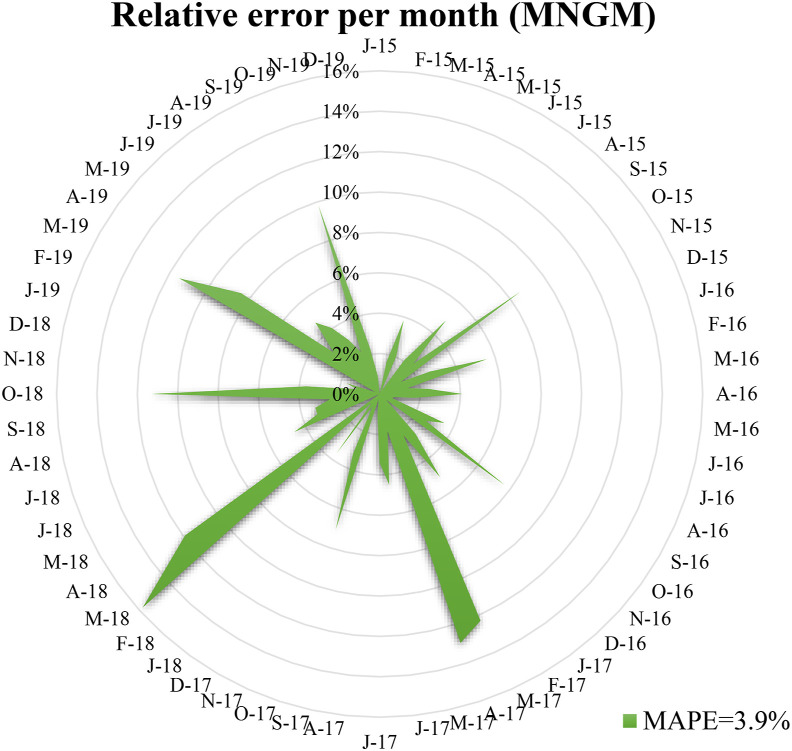
Furthermore, we quantitatively measured the forecast error of each monthly node. The indicator of quantization error was usually a relative error calculation formula. According to this formula, the relative error of each monthly node was shown in Fig. 5 . The relative error of the ring graph in the figure was 0% in the middle and 16% in the outer circle. From the distribution of the error values of each month, more than 85% of the data blocks have an error of less than 6%, and only the relative error of 4 months has reached more than 10%. Based on the number of months covered by the simulation, we averaged 60 relative errors to derive specific values for the average relative error. After calculation, the average relative error predicted by the MNGM model was 3.9%. To a certain extent, this value reflected the accuracy of the constructed model in terms of prediction. In terms of the integrity of the full text, this value has also become an exclusive measurement for the comparison and analysis of the predictive capabilities of multiple models.
Fig. 5.
Prediction result of MNGM model.
The second demonstration was the forecasting process of the ARIMA model. The ARIMA model adopted three main steps: stationarity test, parameter determination based on correlation coefficient, and model construction. The pre-judgment and analysis of the ARIMA model were introduced as follows.
The first was the unit root test. Due to the existence of the false regression problem, the stationarity of testing variables was a problem that must be solved. ADF was a strict statistical method to test the stationarity of a series. The null hypothesis of the ADF test was that the sequence had a unit root, that was, it was not stationary. For a stable time-series data, it needed to be significant at a given confidence level and reject the null hypothesis. If the statistic obtained was significantly less than the critical statistic value of 1%, 5%, 10% confidence levels, it means that the null hypothesis is rejected. In addition, it depended on whether the P-value was very close to 0 (4 decimal places were basically sufficient). Table 1 showed the value of the data after ADF inspection processing. Among them, the T-test values of the original data were all less than the test values within the confidence interval of 1%, 5%, and 10%, which means that the data reject the null hypothesis and reach a plateau.
Table 1.
Index value of ADF unit root test.
| t-Statistic |
Prob.∗ |
||
|---|---|---|---|
| Augmented Dickey-Fuller | Test Statistic | −6.069258 | 0.0000 |
| Test critical values: | 1% level | −4.137279 | |
| 5% level | −3.495295 | ||
| 10% level | −3.176618 | ||
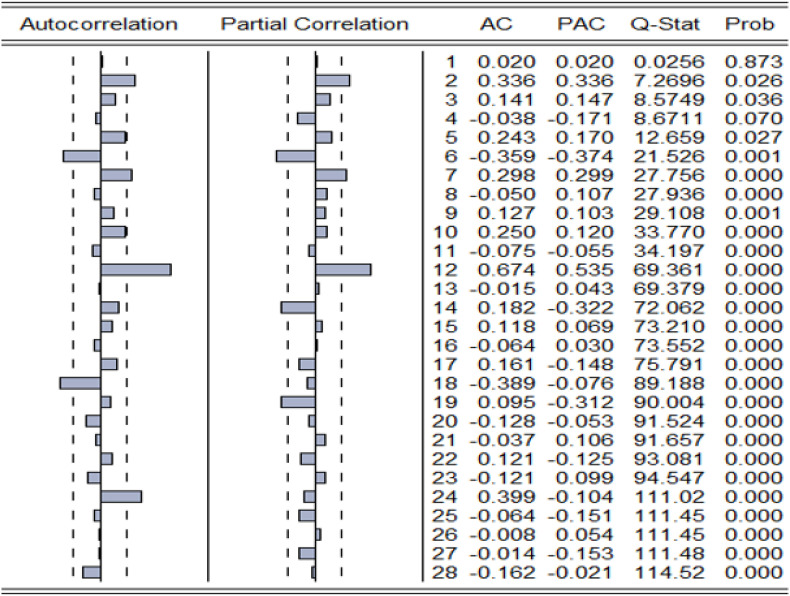
Next is the parameter determination. AC is the autocorrelation coefficient of the sequence, that is, the correlation coefficient between the t-period sequence and the t-k period sequence; PAC is the partial correlation coefficient of the sequence, that is, the partial regression coefficient when the t-period sequence is regressed to the t-1, t-2, …, t-k period sequence. In the first unit root test process, the seasonal component of the data has been removed. Therefore, the correlation coefficient graph at this stage is carried out for the data sequence that has been stationary after removing the seasonality. The main purpose of observing autocorrelation graphs and partial correlation graphs is to determine the specific form of the sequence of the ARMA (p, q) model. The autoregressive process (AR) is formed by the addition of the linear combination of the lagging variables of the sequence and the white noise (random interference term conforming to 0 mean fixed variance), and the moving average process (MA) is composed of the linear combination of white noise.
Fig. 6 showed the autocorrelation and partial autocorrelation parameters of the original data series (when the difference order = 0). On the one hand, the autocorrelation coefficient graph was truncated to within twice the standard deviation after the sixth order. On the other hand, the partial autocorrelation coefficient graph was truncated after the 6th order into the double standard deviation curve. From these two points, it could be concluded that the data was suitable for the ARIMA (6,0,6) model.
Fig. 6.
Autocorrelation/partial autocorrelation graph of stationary time series data.
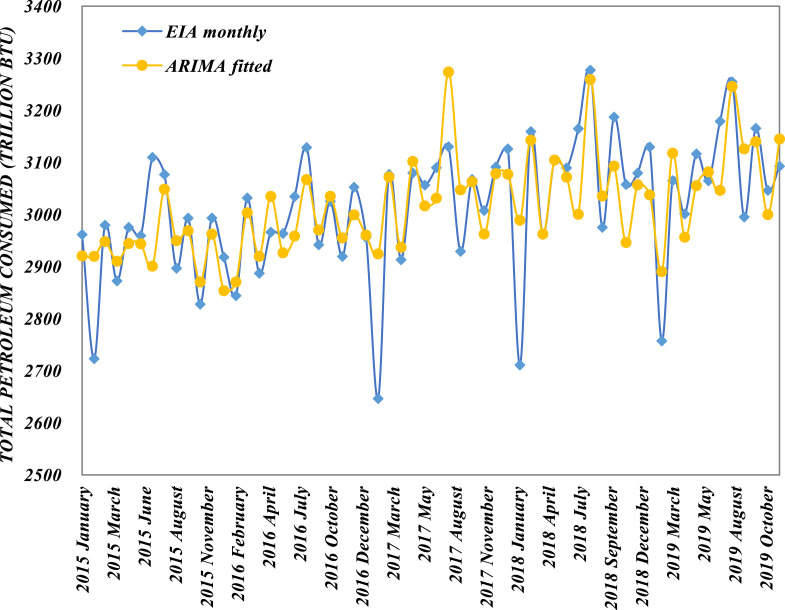
After SPSS software simulation, the initial prediction result based on the ARIMA model has been calculated. As shown in Fig. 7 , the yellow curve represents the simulation result, and the blue curve represents the real value. The close relationship between the two shows that the ARIMA model overcomes a certain degree of lag in simulating data trends compared with the MNGM model. However, the reflection of individual extreme points still has a certain degree of limitation.
Fig. 7.
Fitted result of ARIMA model.
4.1.2. Second prediction: error correction of the initial prediction
Following the combination principle of “error correction + secondary modeling”, this research further selects different models on the basis of the above two basic models (MNGM and ARIMA) to realize the error correction of the preliminary prediction process. With the help of backpropagation artificial neural network (BP for short) and the fitting characteristics of ARIMA model to volatility data, three combined models were constructed respectively. They were MNGM-ARIMA model, MNGM-BP model, and ARIMA-BP model. Among them, the MNGM-ARIMA model was based on the previous MNGM model and used the ARIMA model to correct errors. The MNGM-BP model was based on the previous MNGM model and used the BP model to correct errors. The ARIMA-BP model was based on the previous ARIMA model and used the BP model to correct errors. This section focused on the error correction process of the ARIMA and BP models in the second step of modeling.
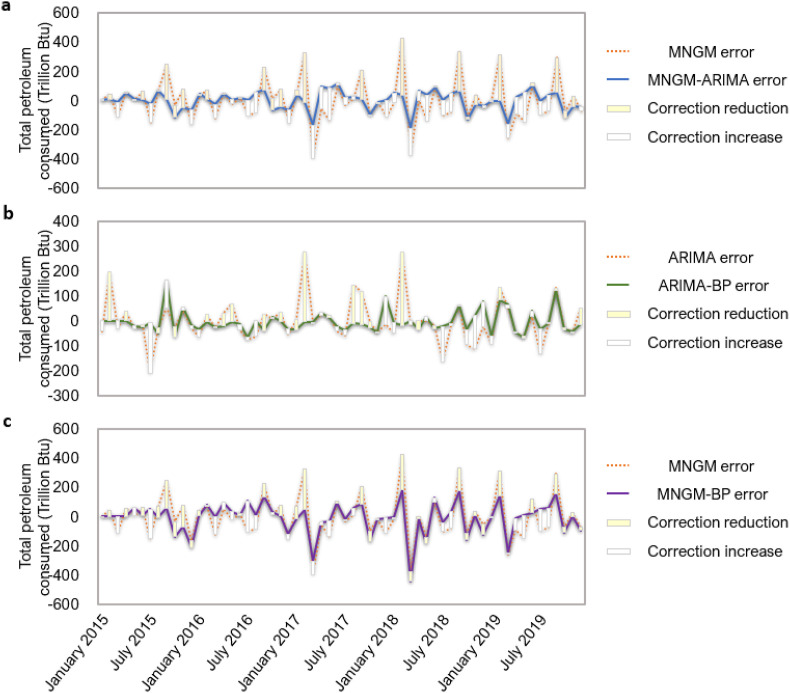
The first was the error correction process of the MNGM-ARIMA model. By calculating the difference between the predicted value of the MNGM model and the true value, we got the initial error sequence of the MNGM model. The fluctuation degree of this error sequence still has room for further reduction. We used the ARIMA model to further correct the error sequence to make its fluctuation smaller and more stable. After a series of unit root tests and related identification processes, the ARIMA (1,0,1) model was finally selected for the secondary correction of errors. Fig. 8 (a) compared the two error curves before and after the correction. Among them, the blue curve was the error sequence after ARIMA model correction, and the orange curve was the original error sequence. It could be seen from the comparison that the blue curve was smoother than the orange curve. In other words, the ARIMA model does correct the initial prediction results of the MNGM model.
Fig. 8.
Error correction diagram of corrected errors and initial errors.
The second was the error correction process of the ARIMA-BP model. Based on the calculation results of the ARIMA (6,0,6) model above, this study used the BP model to model and correct the errors obtained. Through the BP model's machine learning and repeated correction of errors, the corrected error sequence was calculated. Fig. 8(b) showed a comparison of the curves before and after error correction. From the curves in the figure, it could be seen that the green curve had an obvious error reduction effect on the basis of the orange curve.
The third was the error correction process of the MNGM-BP model. Similar to the prediction idea of the MNGM-ARIMA combined model, MNGM-BP also used the prediction principle of the quadratic model to modify the base model. The difference was that the modified model (BP neural network model) used by the MNGM-BP model was nonlinear. The residual corrected in the following two steps: (1) Set parameters. In this study, 4 input layer nodes, 1 output layer node and 10 hidden layer nodes were selected. In addition, the relevant parameters were set as follows: system accuracy , the maximum number of training times was 10,000, and the step size was 0.001. (2) Train and predict. This study used the prediction residuals of the MNGM model to train the neural network and predict the new residual sequence. This step used ‘trainRatio’, ‘valRatio’ and ‘testRatio’ to divide the sample data, of which 70% was used for training, 15% was used for verification, and 15% was used for testing. In order to improve the prediction accuracy, the BP model adds a loop statement in the network design: each prediction value is calculated based on the first four residual data. After repeated calculations by Matlab software, Fig. 8(c) showed the optimal effect after the model is run. As shown in the figure, the orange part of the curve represented the original residual value generated by the MNGM model, and the purple part represented the predicted residual value generated by the BP model. It can be seen from the figure that the new residuals obtained by the BP model were smoother than the original residuals, which also proved that the nonlinear model had a certain corrective effect in the combined model.
4.1.3. Comparison of oil consumption under ideal conditions
The above sections first introduced the prediction process of the base model, and then demonstrated the secondary modeling process of each modified model in detail, showing the intermediate parameters generated in the prediction process. This section compared and analyzed the accuracy and prediction results of each model.
In order to reflect the effectiveness of multiple mixed time series models in forecasting, this study selected the average relative error term as the evaluation index. The average relative error is the weighted average of the average absolute error. The specific formula is as follows: . Generally speaking, the average relative error can better reflect the credibility of the prediction error. The evaluation standard is that the smaller the error value, the better. The correlation between the relative error and the prediction effect is as follows: when the relative error is between 0% and 5%, the prediction effect of the model is excellent; when the relative error is between 5% and 10%, the prediction effect of the model is good; When the relative error is between 10% and 15%, the prediction effect of the model is passing; when the relative error is greater than 15%, the prediction effect of the model is unqualified. Table 2 listed the MAPE results of each model. Among them, the average relative errors of the five models were all within 4%, which belonged to the category of excellent prediction effects. Relatively speaking, the three composite models were more accurate than the two single models. Relatively speaking, better forecasting models included ARIMA-BP and MNGM-ARIMA models, with average relative errors were 1.08% and 1.63%, respectively.
Table 2.
Comparison table of mean relative error of each model.
| Single model |
Model with error-corrected |
||||
|---|---|---|---|---|---|
| MNGM | ARIMA | MNGM-ARIMA | MNGM-BP | ARIMA-BP | |
| MAPE | 3.90% | 2.06% | 1.63% | 2.51% | 1.08% |
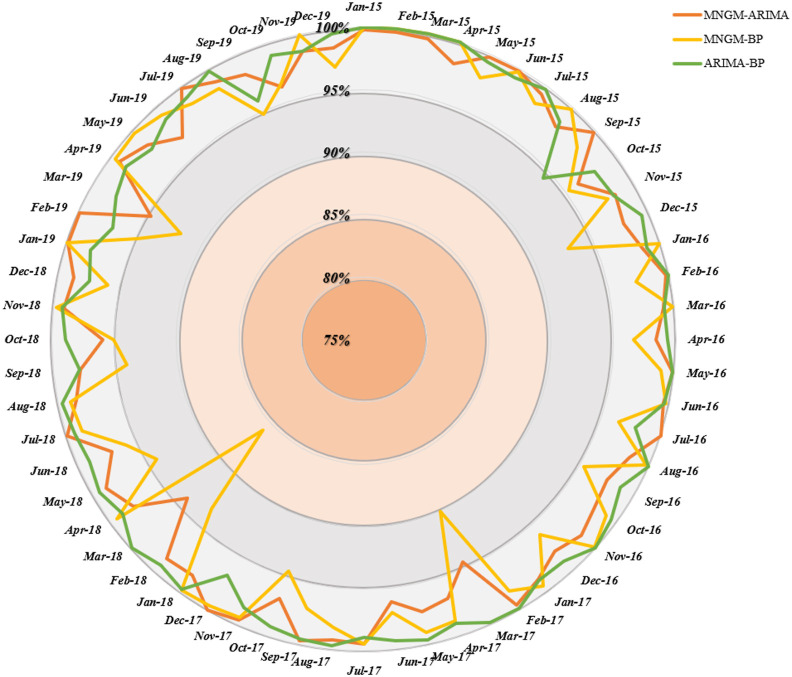
Corresponding to the relative error, this study took 1 minus the percentage value of the relative error as the prediction accuracy. Fig. 9 showed the accuracy values of each sample point. With 5% as the division unit, we used different colors to indicate different accuracy intervals. Among them, the darker the color, the lower the accuracy. It can be seen from the figure: (1) The minimum accuracy of any sample point was above 85%. (2) The average accuracy of most data points was between 95% and 100%. (3) Among the three models, the prediction accuracy of the ARIMA-BP model was slightly better than the other two models.
Fig. 9.
Prediction accuracy of the three combined models at each prediction node.
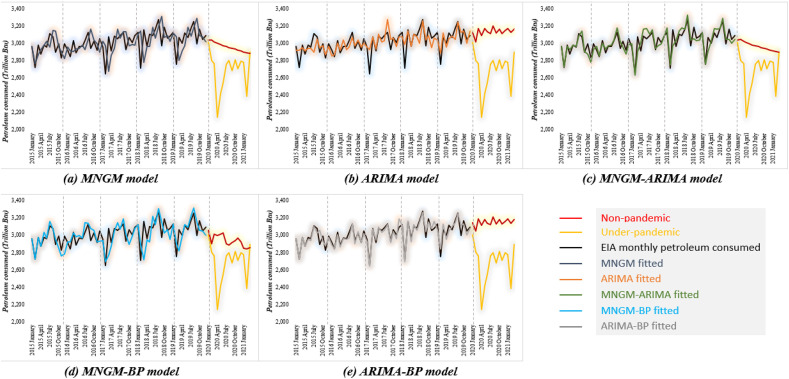
In the previous section, the above four improved models have been applied to the forecast of oil consumption. Through the calculation of the formula and the operation of the software, the prediction results of each of the five models were obtained. In addition, Fig. 10 showed the prediction results of the MNGM model, ARIMA model, MNGM-ARIMA model, MNGM-BP model and ARIMA-BP model. In Fig. 10, the entire curve was divided into two parts according to the time axis, namely the fitting part before 2020 and the forecast part after 2020. The fitting part was composed of black, purple, orange, green, and blue. Among them, black represented the true value, and color represented the predicted value of different models. In the fitting part, Fig. 10 compared the predicted results of each model with the true values one by one. The gap line between the black curve and the colored curve represented the difference between the predicted value and the true value in each year. During the January 2015 to December 2019: (1) the simulation results of the combined model were closer to the true value than the single model. (2) the three combined models could simulate the operation characteristics of the data well, and the ARIMA BP model was better than other combined models in predicting the key fluctuating months. The prediction part was uniformly composed of red and yellow. Among them, yellow represented the true value, and red represented the predicted value. The gap between red and yellow was regarded as the change in oil consumption caused by the epidemic. It can be seen from the figure that the yellow curves of different models were different. The Section 4.3 focuses on the gap between these components.
Fig. 10.
Fitting results of oil consumption of five models.
4.2. Oil consumption under real pandemic situation
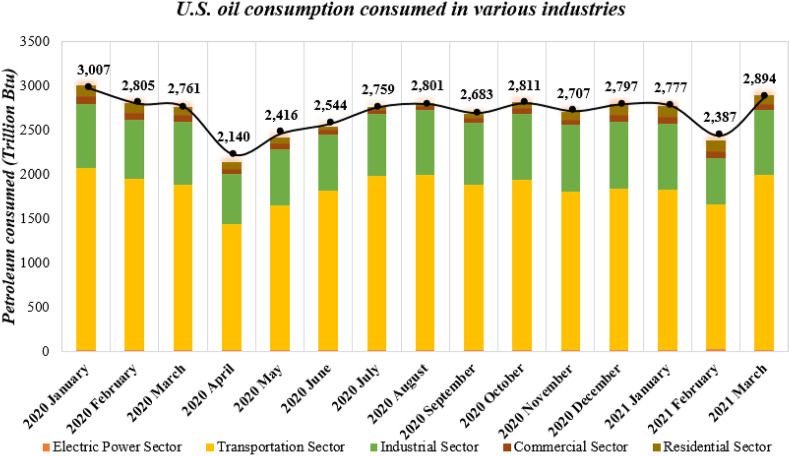
According to the monthly energy review published by the U.S. Energy Information Administration, oil is widely used in the transportation sector, industrial sector, commercial sector, residential sector and electric power sector during social operations. We have extracted U.S. oil-related consumption from the energy consumption used in different sectors. Since the data is updated to March 2021, we selected the US oil consumption during the January 2020–March 2021 pandemic. As shown in Fig. 11 , the US oil consumption peaked in January at 3006 Trillion Btu. In the following months, oil consumption did not exceed the value in January. In April 2020, U.S. oil consumption reached its lowest point in 2020 history at 2140 Trillion Btu. Since then, oil consumption has been slowly picking up, but it still has not exceeded the commanding heights at the beginning of the year. After entering 2021, US oil consumption fell into a downturn in February, reaching 2387 Trillion Btu. This situation was subsequently restored in March.
Fig. 11.
The real value of U.S. oil consumption in 2020 affected by the pandemic.
In terms of the proportion of oil consumption used in different sectors, oil demand in the transportation industry accounts for more than half of the total demand. In addition to the transportation sector, the demand for industrial sector is also above 20%. After that, the demand for oil consumption in industrial, commercial and power generation industries came at the end. This is the performance of US oil consumption in the context of the pandemic. We also regard it as oil consumption data under real scenario.
4.3. Real impact judging from the difference of the two scenarios
This study analyzed the specific performance of oil consumption in 2020 from two scenarios. Specifically, the ideal scenario was to use various forecasting tools to derive the ideal oil consumption in the absence of a pandemic from the historical trajectory. The actual scenario was the U.S. oil consumption monthly data of EIA. According to the research ideas, the difference between the two scenarios was regarded as the impact of the epidemic on the energy industry.
Based on the results of the two scenarios given in the previous two subsections, this section focused on analyzing the difference between the two. On the one hand, multiple prediction results in the ideal scenario were integrated. On the other hand, the difference/impact was analyzed based on different epidemic intervals.
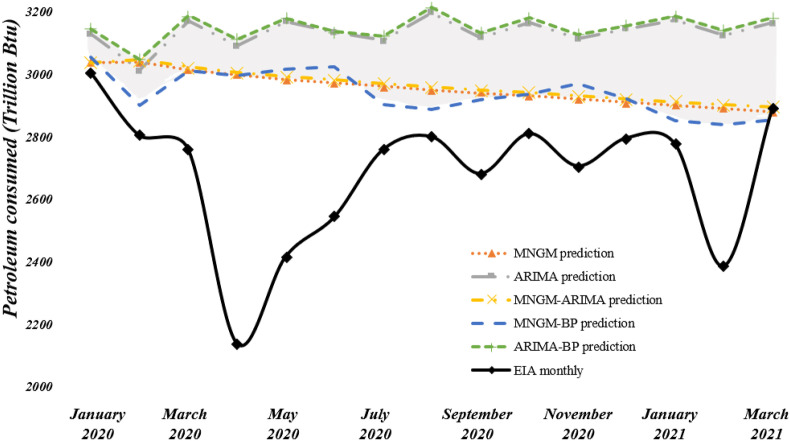
Fig. 12 showed the situation of oil consumption in the United States between January 2020 and March 2021 under the ideal situation of no epidemic situation and the actual situation. The black curve in the figure represents the ideal value of fuel consumption based on different high-precision models in the disease-free state. The yellow curve represents the true value of oil consumption under the epidemic situation. It can be further seen from the figure that an irregular area map is formed between the black curve and the shadow. This area mathematically means the gap between the ideal state and the actual state of the indicator. Applied to this study, it is regarded as the loss value of oil consumption caused by the pandemic.
Fig. 12.
Fitting results of oil consumption in pandemic year under ideal conditions.
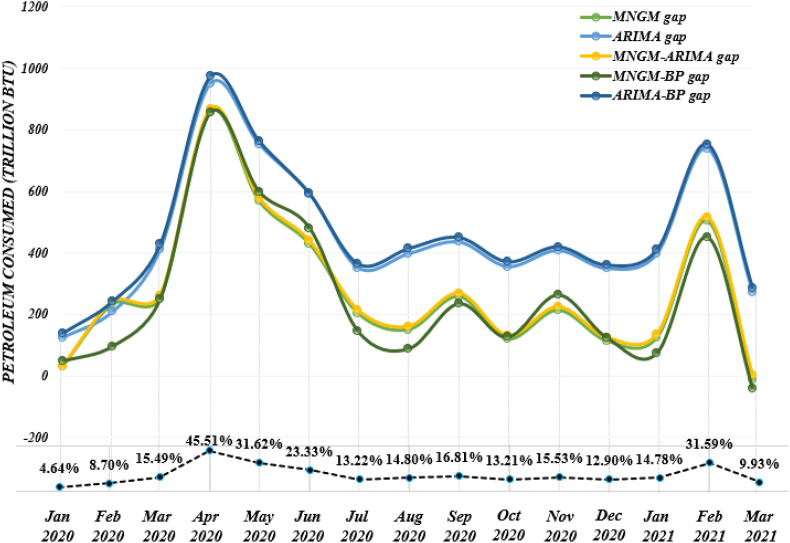
Further visualize the gap between the real scene and the ideal scene (as shown in Fig. 13 ). Among the various models, we have selected the gap between these simulations and true value as a visual difference analysis. The different curves in Fig. 13 represent the difference between the two states calculated by different prediction models. Although the curves were not completely overlapped, the overall trends were similar. In other words, there was a certain uniformity in the impact of the pandemic on oil consumption in specific months.
Fig. 13.
The quantitative impact of the pandemic on U.S. oil consumption.
From the perspective of time interval, the difference between January and March 2020 is much smaller than the rest of the time, and we set this time as a low-impact period. The difference between April and June of 2020 is significantly higher than the rest of the month, which can be judged as a period of high impact. Subsequently, the difference entered a long period of downturn from July 2020 to January 2021. In February 2021, the difference between the oil consumption under the ideal scenario and the actual scenario once again showed a small upsurge. In summary, during the epidemic cycle investigated, US oil consumption has been affected in different stages in different stages. April 2020 and February 2021 were the most severely affected months, which led to a 45% and 32% drop in U.S. oil, respectively. In the remaining months, fluctuations in U.S. oil consumption were flat, and the rate of decline remained at around 15%. In the context of the impact of the pandemic, this difference was speculated to be closely related to the confirmed cases of COVID-19. The number of confirmed cases was the best measure of the severity of a pandemic in a country. Considering the oil consumption under the influence of the pandemic, there was a certain positive correlation between the two.
4.4. Judgment of future oil consumption trends
The severe impact of the COVID-19 global pandemic on U.S. oil consumption in 2020 has become a reality. As the pandemic continues to raging, people's social isolation and economic recovery measures have gradually brought the operation of society onto the right track. So, under the dual impact of the stimulus of the epidemic and the economic recovery, how will US oil consumption change in 2021?
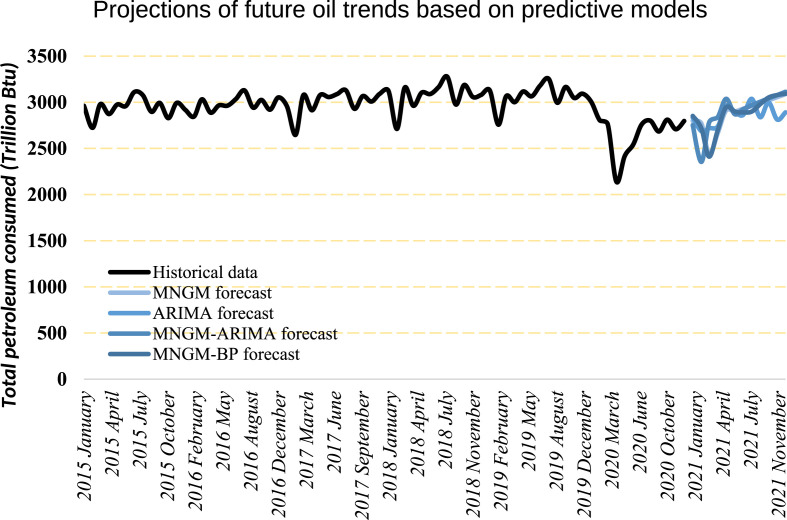
Several high-precision hybrid computing models used in this research will help clarify this problem. Using the modeling principles of the MNGM-ARIMA and MNGM-BP models, the monthly data during 2015 and 2019 were used to predict the oil trend throughout 2021. Through internal learning and modeling of 72 historical data points, the intermediate operating coefficients and future prediction results of several sets of models were solved.
Fig. 14 showed the original data values from 2015 to 2020 and the forecast trend for 2021. The black curve in the figure represented the historical data of US oil consumption, and the blue curve represented the oil forecast for 2021. It can be seen from the evolution trend that after the low tide in 2020, US oil consumption tends to show a trend of gradual recovery in 2021. Although the prediction results of the four models are slightly different, overall recovery and intermittent lows will become the characteristic keywords of US oil consumption in 2021. This result also warns us that the impact of the epidemic on U.S. oil consumption is long-term, and we should be alert to occasional oil downturns.
Fig. 14.
Projections of 2021 derived from four models based on historical trends.
5. Conclusion
This study adopted a new research framework to quantify the true impact of COVID-19 on U.S. oil consumption. We built and used three advanced hybrid forecasting models (ARIMA-BP, MNGM-ARIMA and MNGM-BP) based on the principle of “error correction + secondary modeling”. Through training on monthly data from 2015 to 2019, we simulated the U.S. oil consumption from January 2020 to March 2021 in an ideal state (no trending list occurred). After precision calculation, the MAPE of the three models in the fitting stage of the historical data were 1.08%, 1.63%, and 2.51%, respectively, which confirmed that the forecasting technology has a certain degree of credibility for the forecast results of US oil consumption. Furthermore, we compared the simulated values under this ideal scenario with real monthly energy data. The difference between the two is judged to be the decrease in U.S. oil consumption due to COVID-19. The decline in the U.S. oil industry derived from this statistical method takes into account the natural growth of oil consumption during the inter-year period. Therefore, the difference between the scenarios is more in line with the reality than the 2019–2020 rate of change mentioned in the existing report.
Through analyzing the difference between the simulated and real US oil consumption from January 2020 to March 2021, we found the following interesting conclusions. (1) The impact of the epidemic on U.S. oil consumption was most obvious in April–May 2020 and January–February 2021. When the epidemic was at its worst, the oil decline in the United States reached 973 trillion British thermal units, a decrease of about 45%, compared to the state without the epidemic. (2) During the entire survey period (January 2020–March 2021), the US oil consumption under the epidemic was about 18.14% lower than that under the normal epidemic-free situation. This value was 5% higher than the 13% inter-annual decline rate reported in the BP Statistical Yearbook 2021.
In summary, this study used advanced forecasting methods to simulate the US oil consumption in an epidemic-free state. This framework helped us quantify the true impact of COVID-19 on US oil consumption. Research contributes to assess the impact of the pandemic on the energy industry and the macro economy. In addition, the research results also have reference value for energy decision-making.
Author contribution statement
Qiang Wang: Conceptualization, Methodology, Software, Data curation, Writing- Original draft preparation, Supervision, Writing- Reviewing and Editing. Shuyu Li: Methodology, Software, Data curation, Investigation Writing- Original draft, Writing- Reviewing and Editing. Min Zhang: Software, Data curation, Investigation Writing- Original draft. Rongrong Li: Methodology, Data curation, Investigation, Writing- Reviewing and Editing.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgement
The authors would like to thank the editor and these anonymous reviewers for their helpful and constructive comments that greatly contributed to improving the final version of the manuscript. This work is supported byNational Natural Science Foundation of China (Grant No. 71874203, 71934007).
References
- 1.World Health Organization . 2020. Coronavirus disease (COVID-19) pandemic.https://www.who.int/emergencies/diseases/novel-coronavirus-2019 [Google Scholar]
- 2.Ou S., He X., Ji W., Chen W., Sui L., Gan Y., et al. Machine learning model to project the impact of COVID-19 on US motor gasoline demand. Nature Energy. 2020;5(9):666–673. doi: 10.1038/s41560-020-00711-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.OPEC . 2004. Oil and gas: the engine of the world economy.https://www.opec.org/opec_web/en/press_room/900.htm [Google Scholar]
- 4.IEA . 2020. The impacts of the Covid-19 crisis on global energy demand and CO2 emissions.https://www.iea.org/reports/global-energy-review-2020/oil#abstract [Google Scholar]
- 5.OPEC . 2020. Monthly oil market report.https://momr.opec.org/pdf-download/ [Google Scholar]
- 6.EIA . 2020. Monthly energy review.https://www.eia.gov/totalenergy/data/monthly/ [Google Scholar]
- 7.Wang J., Shao W., Kim J. Analysis of the impact of COVID-19 on the correlations between crude oil and agricultural futures. Chaos, Solit Fractals. 2020;136:109896. doi: 10.1016/j.chaos.2020.109896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wang Q., Zhang F. What does the China's economic recovery after COVID-19 pandemic mean for the economic growth and energy consumption of other countries? J Clean Prod. 2021;295:126265. doi: 10.1016/j.jclepro.2021.126265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Verma C., Alrefaee S.H., Quraishi M.A., Ebenso E.E., Hussain C.M. Environmental, safety and economic risks of Covid-19 pandemic in petroleum industries: a prospective. J Petrol Sci Eng. 2020:108161. [Google Scholar]
- 10.Wang Q., Wang S. Preventing carbon emission retaliatory rebound post-COVID-19 requires expanding free trade and improving energy efficiency. Sci Total Environ. 2020;746:141158. doi: 10.1016/j.scitotenv.2020.141158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Edomah N., Ndulue G. Energy transition in a lockdown: an analysis of the impact of COVID-19 on changes in electricity demand in Lagos Nigeria. Global Transitions. 2020;2:127–137. doi: 10.1016/j.glt.2020.07.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Mofijur M., Fattah I.M.R., Alam M.A., Islam A.B.M.S., Ong H.C., Rahman S.M.A., et al. Impact of COVID-19 on the social, economic, environmental and energy domains: lessons learnt from a global pandemic. Sustainable Production and Consumption. 2021;26:343–359. doi: 10.1016/j.spc.2020.10.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Zhang X., Pellegrino F., Shen J., Copertaro B., Huang P., Kumar Saini P., et al. A preliminary simulation study about the impact of COVID-19 crisis on energy demand of a building mix at a district in Sweden. Appl Energy. 2020;280:115954. doi: 10.1016/j.apenergy.2020.115954. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Hosseini S.E. An outlook on the global development of renewable and sustainable energy at the time of COVID-19. Energy Research & Social Science. 2020;68:101633. doi: 10.1016/j.erss.2020.101633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Wang Q., Dong Z., Li R., Wang L. Renewable energy and economic growth: new insight from country risks. Energy. 2022;238:122018. [Google Scholar]
- 16.Naderipour A., Abdul-Malek Z., Ahmad N.A., Kamyab H., Ashokkumar V., Ngamcharussrivichai C., et al. Effect of COVID-19 virus on reducing GHG emission and increasing energy generated by renewable energy sources: a brief study in Malaysian context. Environmental Technology & Innovation. 2020;20:101151. doi: 10.1016/j.eti.2020.101151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kanitkar T. The COVID-19 lockdown in India: impacts on the economy and the power sector. Global Transitions. 2020;2:150–156. [Google Scholar]
- 18.Madurai Elavarasan R., Shafiullah G.M., Raju K., Mudgal V., Arif M.T., Jamal T., et al. COVID-19: impact analysis and recommendations for power sector operation. Appl Energy. 2020;279:115739. doi: 10.1016/j.apenergy.2020.115739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Corpus-Mendoza A.N., Ruiz-Segoviano H.S., Rodríguez-Contreras S.F., Yañez-Dávila D., Hernández-Granados A. Decrease of mobility, electricity demand, and NO2 emissions on COVID-19 times and their feedback on prevention measures. Sci Total Environ. 2020:143382. doi: 10.1016/j.scitotenv.2020.143382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Li R., Wang Q., Liu Y., Jiang R. Per-capita carbon emissions in 147 countries: the effect of economic, energy, social, and trade structural changes. Sustainable Production and Consumption. 2021;27:1149–1164. [Google Scholar]
- 21.Norouzi N., Zarazua de Rubens G., Choupanpiesheh S., Enevoldsen P. When pandemics impact economies and climate change: exploring the impacts of COVID-19 on oil and electricity demand in China. Energy Research & Social Science. 2020;68:101654. doi: 10.1016/j.erss.2020.101654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Adedeji A.N., Ahmed F.F., Adam S.U. Examining the dynamic effect of COVID-19 pandemic on dwindling oil prices using structural vector autoregressive model. Energy. 2021;230:120813. doi: 10.1016/j.energy.2021.120813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Jiang P., Fan Y.V., Klemeš J.J. Impacts of COVID-19 on energy demand and consumption: challenges, lessons and emerging opportunities. Appl Energy. 2021;285:116441. doi: 10.1016/j.apenergy.2021.116441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Cihan P. Impact of the COVID-19 lockdowns on electricity and natural gas consumption in the different industrial zones and forecasting consumption amounts: Turkey case study. Int J Electr Power Energy Syst. 2022;134:107369. [Google Scholar]
- 25.Quitzow R., Bersalli G., Eicke L., Jahn J., Lilliestam J., Lira F., et al. The COVID-19 crisis deepens the gulf between leaders and laggards in the global energy transition. Energy Research & Social Science. 2021;74:101981. doi: 10.1016/j.erss.2021.101981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Micheli L., Solas Á.F., Soria-Moya A., Almonacid F., Fernández E.F. Short-term impact of the COVID-19 lockdown on the energy and economic performance of photovoltaics in the Spanish electricity sector. J Clean Prod. 2021;308:127045. [Google Scholar]
- 27.Bahmanyar A., Estebsari A., Ernst D. The impact of different COVID-19 containment measures on electricity consumption in Europe. Energy Research & Social Science. 2020;68:101683. doi: 10.1016/j.erss.2020.101683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Ruan G., Wu D., Zheng X., Zhong H., Kang C., Dahleh M.A., et al. A cross-domain approach to analyzing the short-run impact of COVID-19 on the US electricity sector. Joule. 2020;4(11):2322–2337. doi: 10.1016/j.joule.2020.08.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Wang Q., Li S. Nonlinear impact of COVID-19 on pollution – evidence from wuhan, New York, milan, madrid, bandra, london, tokyo and Mexico city. Sustainable Cities and Society. 2021;65:102629. doi: 10.1016/j.scs.2020.102629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Khan F.M., Gupta R. ARIMA and NAR based prediction model for time series analysis of COVID-19 cases in India. Journal of Safety Science and Resilience. 2020;1(1):12–18. [Google Scholar]
- 31.Duan X., Zhang X. ARIMA modelling and forecasting of irregularly patterned COVID-19 outbreaks using Japanese and South Korean data. Data in Brief. 2020;31:105779. doi: 10.1016/j.dib.2020.105779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Nafil A., Bouzi M., Anoune K., Ettalabi N. Comparative study of forecasting methods for energy demand in Morocco. Energy Rep. 2020;6:523–536. [Google Scholar]
- 33.Ye J., Dang Y., Ding S., Yang Y. A novel energy consumption forecasting model combining an optimized DGM (1, 1) model with interval grey numbers. J Clean Prod. 2019;229:256–267. [Google Scholar]
- 34.Wang Q., Li S., Li R., Jiang F. Underestimated impact of the COVID-19 on carbon emission reduction in developing countries – a novel assessment based on scenario analysis. Environ Res. 2022;204:111990. doi: 10.1016/j.envres.2021.111990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Fathi S., Srinivasan R., Fenner A., Fathi S. Machine learning applications in urban building energy performance forecasting: a systematic review. Renew Sustain Energy Rev. 2020;133:110287. [Google Scholar]
- 36.Wadhwa P., Aishwarya, Tripathi A., Singh P., Diwakar M., Kumar N. Predicting the time period of extension of lockdown due to increase in rate of COVID-19 cases in India using machine learning. Mater Today: Proceedings. 2020 doi: 10.1016/j.matpr.2020.08.509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Rasku T., Miettinen J., Rinne E., Kiviluoma J. Impact of 15-day energy forecasts on the hydro-thermal scheduling of a future Nordic power system. Energy. 2020;192:116668. [Google Scholar]
- 38.Liu H., Li Y., Duan Z., Chen C. A review on multi-objective optimization framework in wind energy forecasting techniques and applications. Energy Convers Manag. 2020;224:113324. [Google Scholar]
- 39.da Silva R.G., Ribeiro M.H.D.M., Moreno S.R., Mariani V.C., Coelho LdS. A novel decomposition-ensemble learning framework for multi-step ahead wind energy forecasting. Energy. 2020:119174. [Google Scholar]
- 40.Wang H., Lei Z., Zhang X., Zhou B., Peng J. A review of deep learning for renewable energy forecasting. Energy Convers Manag. 2019;198:111799. [Google Scholar]
- 41.Nam K., Hwangbo S., Yoo C. A deep learning-based forecasting model for renewable energy scenarios to guide sustainable energy policy: a case study of Korea. Renew Sustain Energy Rev. 2020;122:109725. [Google Scholar]
- 42.Wei N., Li C., Peng X., Zeng F., Lu X. Conventional models and artificial intelligence-based models for energy consumption forecasting: a review. J Petrol Sci Eng. 2019;181:106187. [Google Scholar]
- 43.Kazemzadeh M.-R., Amjadian A., Amraee T. A hybrid data mining driven algorithm for long term electric peak load and energy demand forecasting. Energy. 2020;204:117948. [Google Scholar]
- 44.Ahmad T., Chen H. A review on machine learning forecasting growth trends and their real-time applications in different energy systems. Sustainable Cities and Society. 2020;54:102010. [Google Scholar]
- 45.Wang B., Wang J. Energy futures and spots prices forecasting by hybrid SW-GRU with EMD and error evaluation. Energy Econ. 2020;90:104827. [Google Scholar]
- 46.Brem A., Nylund P., Viardot E. The impact of the 2008 financial crisis on innovation: a dominant design perspective. J Bus Res. 2020;110:360–369. [Google Scholar]
- 47.Wang Q., Li S., Li R. Forecasting energy demand in China and India: using single-linear, hybrid-linear, and non-linear time series forecast techniques. Energy. 2018;161:821–831. [Google Scholar]
- 48.Deng J. Grey system fundamental method. 1982;Huazhong University of Science and Technology Wuhan, China.
- 49.Selvaraj J.J., Arunachalam V., Coronado-Franco K.V., Romero-Orjuela L.V., Ramírez-Yara Y.N. Time-series modeling of fishery landings in the Colombian Pacific Ocean using an ARIMA model. Regional Studies in Marine Science. 2020;39:101477. [Google Scholar]
- 50.Zhang G.P. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing. 2003;50:159–175. [Google Scholar]
- 51.Al-Musaylh M.S., Deo R.C., Adamowski J.F., Li Y. Short-term electricity demand forecasting with MARS, SVR and ARIMA models using aggregated demand data in Queensland, Australia. Adv Eng Inf. 2018;35:1–16. [Google Scholar]
- 52.Hsu Y.-Y., Tung T.-T., Yeh H.-C., Lu C.-N. Two-stage artificial neural network model for short-term load forecasting. IFAC-PapersOnLine. 2018;51(28):678–683. [Google Scholar]
- 53.Dumitru C.-D., Gligor A. Daily average wind energy forecasting using artificial neural networks. Procedia Engineering. 2017;181:829–836. [Google Scholar]