Abstract
Inter-sectoral volatility linkages in the Chinese stock market are understudied, especially asymmetries in realized volatility connectedness, accounting for the catastrophic event associated with the COVID-19 outbreak. In this paper, we examine the asymmetric volatility spillover among Chinese stock market sectors during the COVID-19 pandemic using 1-min data from January 2, 2019 to September 30, 2020. In doing so, we build networks of generalized forecast error variances by decomposition of a vector autoregressive model, controlling for overall market movements. Our results show evidence of the asymmetric impact of good and bad volatilities, which are found to be time-varying and substantially intense during the COVID-19 period. Notably, bad volatility spillover shocks dominate good volatility spillover shocks. The findings are useful for Chinese investors and portfolio managers constructing risk hedging portfolios across sectors and for Chinese policymakers monitoring and crafting stimulating policies for the stock market at the sectoral level.
Keywords: Asymmetry, Volatility spillover, Connectedness, Chinese stock sectors, COVID-19 outbreak
1. Introduction
The COVID-19 outbreak is a human tragedy and a public health emergency. Its devastating impacts have reached the base of the global economy. The spread of this deadly virus from China in late 2019 to the rest of the world in early 2020 has led to a paralysis of economic activity and the co-called lockdown recession that is expected to be more severe than the recession experienced during the global financial crisis (GFC) of 2007–2008. COVID-19 was declared a pandemic on March 11, 2020 and some economic and financial communities refer to it as a catastrophic event. It has induced instability and sharp declines in stock markets. In China, the point of origin of COVID-19, the stock market, as measured by the CSI Index, plunged 12.50% from January 13, 2020 to February 2, 2020. Following a sharp rebound that lasted a few weeks, the CSI Index declined again by 16% over the period March 5, 2020 to March 23, 2020. Chinese stock sector indices such as energy, banks, industrials, and consumer discretionary experienced sharp declines. For example, the decline in the energy sector exceeded 20% from January 13, 2020 to February 2, 2020 and March 5, 2020 to March 23, 2020. The lockdown recession has led to a large decrease in the prices of energy, e.g., crude oil, and thus the profit margins and stock prices of energy companies. For banks, the spike in the share of non-performing loans coupled with the decrease in interest rate margins due to reductions in policy rates have crushed earnings and thus bank stock prices. Consumer discretionary spending on products and services such as travel and leisure has decreased considerably, leading to sharp decreases in the consumer discretionary index. However, increased spending on staples and survival supplies has made the consumer staples index outperform the aggregate stock market.
Under the extreme market conditions associated with the catastrophic event of the COVID-19 outbreak, it is informative to uncover the dynamics of volatility spillovers across the Chinese equity sectors for the sake of investors and policymakers. However, financial markets represent a complex and rapidly changing system characterized by an asymmetric dependency (Baruník, Kočenda, & Vácha, 2016). The correlation across large negative returns is stronger than that across large positive returns. Furthermore, the concurrent correlation between return and conditional volatility is negative. Therefore, a stronger reaction to negative shocks leads to an asymmetric price volatility that reduces the benefits of diversification (Amonlirdviman & Carvalho, 2010). Notably, investors and policymakers are concerned not only with aggregate volatility but with “good” and “bad” volatilities that exhibit opposite impacts on stock prices and market growth (Wang & Wu, 2018). Good volatility is related to positive innovation in market returns and thus enables the stock markets to be more productive. Conversely, bad volatility is related to negative innovation in market returns, and thus it has a destabilizing effect on the stock market. Notable benefits can arise from decomposing the aggregate volatility into good and bad volatility components. Gkillas et al. (2019) argue that, unlike bad volatility which is jumpy and hard to predict, good volatility is directional, persistent, and more predictable. Accordingly, detecting the spillovers of good and bad volatility across stock returns in stress periods gives insight into potential asymmetry in the propagation of risk across stock sector indices, which ultimately affects stock pricing, risk valuation, and the payoff of diversification and trading strategies (Garcia & Tsafack, 2011).
Information transmission in realized volatility and potential asymmetry in the volatility connectedness have been the subject of recent studies dealing with US equities (Baruník et al., 2016), currencies (Baruník, Kočenda, & Vácha, 2017), and commodities (Luo & Ji, 2018; Shahzad et al., 2018; Bouri, Lucey, Saeed, & Vo, 2021). However, there is a lack of evidence about what manner of volatilities, good or bad, are propagated in the Chinese stock sector markets, especially during the COVID-19 outbreak. In addition to China being the point of origin of the COVID-19 pandemic, the Chinese stock market is the fastest-growing (Xu, Ma, Chen, & Zhang, 2019) and second-largest after the US. It has a huge daily trading volume and a large number of individual and institutional investors, although market participants focus more on speculation than investment, which makes the local stock market highly sensitive (Chen, Li, & Qu, 2019). While the development of the Chinese stock market has been marked by important events such as the GFS, the European sovereign debt crisis, and the Chinese stock market turmoil of 2015 (Chen et al., 2019), there is a lack of understanding of the impact of non-financial and non-economic events, such as COVID-19, on the interconnectedness of Chinese sector indices.
In light of this discussion and the above-mentioned gap, this paper examines the asymmetric volatility connectedness among Chinese stock sector indices. We do this in static and time-varying settings using high-frequency data. Our methodological framework captures the asymmetry in the volatility spillovers accurately, given its concentration on the spillover between good volatilities and bad volatilities, as documented by Baruník et al. (2017).
We contribute to the academic literature as follows. Firstly, we add to recent studies considering the effect of COVID-19 on energy, stock, and policy uncertainty in the US economy (Sharif, Aloui, & Yarovaya, 2020) by focusing on the largest emerging market and the site of the first COVID-19 cases. Secondly, we extend previous studies dealing with stock sectoral connectedness in the Chinese stock market (e.g., Feng et al., 2018; Wu, Zhang, & Zhang, 2019) by considering the source and magnitude of volatility spillovers in static and time-varying settings, which helps detect the major sectors in the network of volatility connectedness. Thirdly, we apply the VAR-based approach to connectedness while decomposing the realized volatility into bad and good components (Baruník et al., 2016, Baruník et al., 2017; Luo & Ji, 2018; Uddin et al., 2019), which allows us to uncover evidence of asymmetric volatility spillovers among Chinese stock sector indices. This represents an extension to most previous studies that highlight the asymmetry in volatility by indicating that price volatility is larger in stress periods than calm periods. Fourthly, we apply a network typology, uncovering how spillovers of bad and good volatility are transmitted across various equity sectors during the COVID-19 outbreak. This is useful for market participants, given that the volatilities in Chinese sectors have been shown to interact with each other during crash periods, leading to an increase in the volatility of systemic risk in the stock markets.
The main results show evidence of the asymmetric impact of good and bad volatilities that are found to be time-varying and substantially intense during COVID-19. Notably, bad volatility (i.e., downside semivariance) spillover shocks dominate good volatility (i.e., upside semivariance) spillover shocks. These findings are useful for Chinese investors and portfolio managers constructing risk hedging portfolios across sectors and for Chinese policymakers monitoring and crafting stimulating policies for the stock market at the sectoral level. They are also relevant to empirical analysis which involves the predictability of the effect of tail events on volatility spillovers, which matters to financial risk management. In fact, extending our limited understanding of the pattern of extremes in the Chinese sector indices that are driven by COVID-19 can be used to improve the accuracy of predicting good and bad volatilities for risk management.
Section 2 reviews the related literature; Section 3 presents the dataset and methods; Section 4 provides the connectedness results in static and time-varying settings and offers a robustness analysis. The final section concludes.
2. Literature review
2.1. Volatility spillover
Several studies consider the volatility spillovers among stock markets using multivariate GARCH models (e.g., Li & Giles, 2015) and the asymmetric GARCH-DCC model of Cappiello, Engle, and Sheppard (2006), which allows for asymmetry in the conditional variances and correlations among stock indices, which is essential during stress periods. These models are applied to global stock sector indices to consider hedging effectiveness (Jin, Han, Wu, & Zeng, 2020). However, GARCH-based models do not sufficiently capture the dynamics of volatility spillovers. With the development of the generalized VAR framework based on forecast-error variance decomposition, total and directional volatility spillovers can be captured in a robust way in both static and time-varying settings (Diebold & Yilmaz, 2012). This approach has been used in various stock markets, to show strong cross-market volatility spillovers during and after the GFC of 2007–2008. Previous studies consider the asymmetry in volatility, which generally indicates that price volatility is larger in stress periods than calm periods, and volatility spillovers are stronger during stress periods (Do, Powell, Yong, & Singh, 2019). However, asymmetry in volatility spillovers arises from the differences between bad and good volatility. Capturing such asymmetry becomes possible thanks to the availability of intraday price data that allows for the computation of realized volatility based on 5-min price data (Andersen & Bollerslev, 1998) and decomposition of realized volatility by differentiating good from bad volatility (Barndorff-Nielsen, Kinnebrock, & Shephard, 2010). Accordingly, studies have applied such asymmetric volatility linkages based on intraday data to a wide set of assets such as currencies (Baruník et al., 2017), commodities (Luo & Ji, 2018; Uddin et al., 2019), and Asian futures markets (Yarovaya, Brzeszczyński, & Lau, 2016). In equity markets, Baruník et al. (2016) quantify asymmetries in the volatility spillovers of US equity sectors by considering the spillovers from good volatilities to bad volatilities and vice versa. The authors propose the spillover asymmetry measure (SAM).
2.2. The Chinese stock market at the sectoral level
Established in 1991, the Chinese stock market evolved rapidly to reach second place among global stock markets in terms of trading activity and market value. It involves two major exchanges containing more than 3500 listed companies spreading to various sectors. As of December 2019, the total market value of all Chinese listed companies amounted to 59.29 trillion yuan (or 9.23 trillion US dollars). The Chinese stock market plays an important role in global finance and involves many institutional investors. However, it is considered a highly volatile and risky investment scene, subject to frequent booms and busts. The market crashes around the GFC of 2007–2008, and the bubble burst of June–September 2015 are notable.
The Chinese stock market at the aggregate level is widely studied in academia, mostly in terms of its relationship with international stock markets (Yao, He, Chen, & Ou, 2018; Yu, Fang, Sun, & Du, 2018) and commodities (Hammoudeh, Nguyen, Reboredo, & Wen, 2014). However, sectors contribute to systemic risk, and the volatility contributions vary among equity sectors (Eckernkemper, 2018). As such, the volatility of one sector can transfer to another, which ultimately affects the volatility of the whole system, and thus the returns of market participants and the decisions of policymakers. Accordingly, capturing the source and magnitude of volatility is crucial to uncover sectoral volatility contributions and the network of sectoral interconnectedness in the Chinese stock market. At the sector level, few studies consider the Chinese stock market, as the focus is mainly on its relationship with crude oil prices (Huang, An, Gao, & Huang, 2015; Yang, Zhu, Wang, & Wang, 2016). Less is known about the connectedness among sector indices. Hao and He (2018) apply a copula model to the dependences between manufacturing, finance, and real estate stock sector indices. Feng et al. (2018) study risk spillover networks across Chinese sectors, considering various investment horizons. They show that the risk of one sector index has an influence on another. Wu et al. (2019) show a time-variation in the sectoral linkages in the Chinese stock markets and evidence that the industrial sector is central to the network of return spillovers.
As shown above, asymmetries in volatility spillovers among the Chinese stock sector indices at the interconnectedness level are little studied. Especially, no evidence exists of the effect of the COVID-19 outbreak on the Chinese stock sector indices in a time-varying manner using network typology, differentiating between good and bad volatilities. Accordingly, we contribute to the academic literature by examining the asymmetric volatility spillover among Chinese stock market sectors during the COVID19 pandemic using 1-min data, extending previous findings on the effects of the COVID-19 on financial markets (e.g. Shahzad et al., 2021).
3. Data and methodology
3.1. Data
We use the CSI 300 sector index series for ten sectors: energy (EN), material (MAT), industrial (IND), consumer discretionary (CD), consumer staples (CS), health care (HC), financials (FIN), information technology (IT), telecommunications (TELE), and utilities (UTL). Our sample period is January 2, 2019 to September 30, 2020, and the sampling frequency is 1 min. The component stocks contained in the sector index series are the same as the CSI 300 Index, now grouped by their industrial classifications. As a result, each index is compiled from a different number of component stocks (see the last column of Table 1 ). For each index, the base date is December 31, 2004, and the base point is 1000, denominated in RMB.
Table 1.
Sector indices of the Chinese stock market.
| Index Name | Ticker | Abbreviation | #Stocks |
|---|---|---|---|
| CSI 300 Energy Sector Index | 000908 | EN | 10 |
| CSI 300 Materials Sector Index | 000909 | MAT | 34 |
| CSI 300 Industrials Index | 000910 | IND | 53 |
| CSI 300 Consumer Discretionary Index | 000911 | CD | 30 |
| CSI 300 Consumer Staples Index | 000912 | CS | 16 |
| CSI 300 Health Care Index | 000913 | HC | 29 |
| CSI 300 Financials Index | 000914 | FIN | 77 |
| CSI 300 Information Technology Index | 000915 | IT | 34 |
| CSI 300 Telecommunication Services Index | 000916 | TELE | 8 |
| CSI 300 Utilities Sector Index | 000917 | UTL | 9 |
| total | 300 |
Notes: The CSI index series are compiled by the China Securities Index Co., Ltd. The last column (#Stocks) counts the number of component stocks included in each ETF.
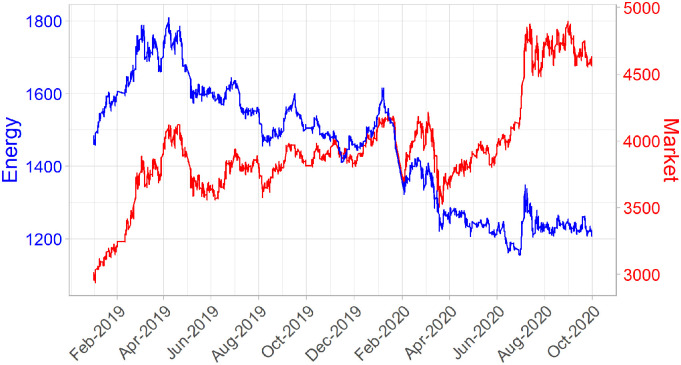
Fig. 1 plots the CSI Energy Sector Index (EN) versus the CSI Index (market). The outbreak of COVID-19 in China at the end of January 2020 has a negative effect on both indices, causing a large decline in both at the beginning of February. The market index decreases by around 12% from 4250 to around 3750, and the energy index goes down by almost 20% from 1600 to 1300. Then the energy index continues decreasing while the market index fluctuates around 3750 points.
Fig. 1.
Time series plot of the energy sector and stock market index. Note: The blue line is the CSI Energy Sector Index (EN) and the red line the CSI 300 Index (Market). The sample period is January 2, 2019 to September 30, 2020.
3.2. Realized volatility and semi-volatility
For an index price on day t, we compute its log return as r t, τ = log P t, τ − log P t, τ−1 for each minute τ. Since the Chinese stock market trades from 9:30 to 11:30 and from 13:00 to 3:00, in total, we have 4 × 60 = 240 minutes for each trading day. That is, τ = 1, …, 240. Based on these 240 1-min returns, we calculate the daily realized variance for each sectoral index as:
| (1a) |
We then follow Barndorff-Nielsen et al. (2010) to decompose RVt into two semivariances, downside semivariance, and upside semivariance, which are also known as bad volatility and good volatility, respectively:
| (1b) |
| (1c) |
It is obvious that the realized variance is the sum of the two semivariances, say, RV t = RV t − + RV t +.
The literature shows an asymmetry effect of these two semivariances. For example, Todorova (2017) examines COMEX gold futures from January 2003 to June 2016 and finds that negative semivariance relates more to the short-term dynamic of the overall volatility than positive semivariance; while the latter, on the other hand, has a stronger correlation with the overall volatility at daily, weekly, and monthly horizons. Conversely, Baruník et al. (2017) focus on the foreign exchange market 2007–2015 and show that negative semivariance dominates the spillovers. Given the disagreement on the importance of good versus bad volatility, we examine the effect of both volatilities.
3.3. Connectedness of the volatility system in the time- and frequency-domain
For the realized volatilities or semi-volatilities, we first estimate a stationary VAR model of order p:
| (2) |
where vector y t = (RV 1t, …, RV nt) is an n × 1 vector that contains the realized volatilities or semi-volatilities of sectoral index returns; Φ(L) is a lag polynomial. The vector ε t is an n × 1 vector of random errors with mean zero and variance matrix Σ; furthermore, we assume no serial correlation in ε t. Given that the VAR system specified in Eq. (2) is stationary, by the Wold representation, it can be rewritten as a moving average process with infinite order, or VMA(∞), sayy t = Ψ(L)ε t = Ψ 0 ε t + Ψ 1 ε t−1 + ⋯ + Ψ h ε t−h + ⋯. Here, Ψ h is the MA coefficient matrix corresponding to the h-th lag; when h is zero, we set Ψ 0 to the identity matrix, I.
3.3.1. Time-domain connectedness
Following Pesaran and Shin (1998), we apply a generalized forecast error variance decomposition (FEVD) to the VMA (∞) entailed by Eq. (2). By doing an H-step ahead forecast, we denote the contribution of the realized volatility of the j-th to the forecast error variance of the realized volatility of the i-th variable as follows:
| (3) |
where we denote the ij-th element of Σ as σ ij, and the j-th diagonal element as σ jj; and e j is a vector of zeros except that the j-th element is one. In our empirical studies, we choose a forecast horizon of 5 days (H = 5). By standardizing the contribution across all variables (j = 1, 2, …, n), we can compute the following connectedness measures as in Diebold and Yilmaz (2012, 2014).
3.3.2. Frequency-domain connectedness
To get the frequency-domain connectedness measures, we start with the VMA(p) model in Eq. (2). We then obtain the VMA (∞) representation, say y t = Ψ(L)ε t. We then apply the Fourier transform to the lag coefficient polynomial, and obtain Ψ(e−iω) = ∑h=0 ∞e−iωh Ψ h, where ω is a specific frequency. We then obtain the power spectrum of y t as . The contribution of the j-th variable (i.e., the realized volatility of the j-th ETF) to the forecast error variance of the i-th variable (i.e., the realized volatility of the i-th ETF) as follows:
| (4) |
3.3.3. Time-domain connectedness vs. frequency-domain connectedness
Table 2 presents the definitions of various time-domain spillover measures based on Diebold and Yilmaz (2012); Diebold and Yılmaz (2014) and the frequency-domain spillover measures based on Baruník and Křehlík (2018) and Ferrer et al. (2018). We can see that the two sets of measures differ only in their calculation of the contribution of variable j to the forecast error variance of variable i.
Table 2.
Measures of connectedness between variables in a VAR(p) system.
| Type of Connectedness | Time-Domain | Frequency-Domain |
|---|---|---|
| pairwise connectedness (j to i) | ||
| total connectedness of the system (also known as the total spillover index) | ||
| net pairwise connectedness (j to i) | ||
| from connectedness of i (from all other variables to i) | ||
| to connectedness of i (from i to all other variables) | ||
| net connectedness of i (scaled by 100) |
Note: the definitions are taken from Diebold and Yilmaz (2012, 2014) and Baruník and Křehlík (2018).
Our use of both time- and frequency-domain connectedness follows from Balli et al. (2019), Caporin et al., 2021, Liu and Hamori (2020) and Zhang, Hu, and Ji (2020). The former analyses the spillover among crude oil, natural gas, clean energy, bond, and stock index in the US and Europe, while the latter focuses on the spillover among natural gas, crude oil, and energy sector index in the US, Canada, and four European countries. As Liu and Hamori (2020) point out, the merits of this mixed approach are twofold. First, they allow us to examine directional spillovers, which we can show by a network diagram. Second, with the frequency -domain connectedness measure, we can distinguish the short- and long-term components of the spillovers. Both Liu and Hamori (2020) and Zhang, He, Nakajima, and Hamori (2020) show that the spillover based on the return system is stable during the sample horizon; meanwhile, the spillovers based on the variance system clearly identifies structural breaks due to economic and political shocks. For example, Zhang, He, et al. (2020) discover the oil crisis in late 2014 and the 2016 Brexit all lead to a sudden spike in the volatility spillover. We expect the COVID-19 brings a similar effect.
3.3.4. Spillover asymmetry measure (SAM)
Baruník et al. (2016) propose a spillover asymmetry measure (SAM) based on two semivariances:
| (5) |
where C + and C −are the total volatility spillover indices due to RV t + and RV t −. To compute SAM, we follow a three-step procedure. First, based on the positive and negative semivariances, we estimate two VAR(p) model. Second, for each VAR(p) model, we compute the two total connectedness measures, C + and C −. In this step, we refer to the formula in the second line of Table 2. Then, we compute SAM according to eq. (5). Intuitively, when SAM stays positive, the effect of upward risks dominates; when SAM is negative, the effect of down-side risks dominates.
4. Empirical findings
Our sample period covers the outbreak of COVID-19 in early 2020. Recent studies have shown that this incident has had a significant impact on crude oil prices, stock market indices, and policy uncertainty in the US (Sharif et al., 2020). Furthermore, Zhang, Hu, and Ji (2020) show that, after the outbreak in China, the connectedness of the Chinese stock market, measured by a transformed correlation, significantly increases with the stock markets of Singapore, South Korea, and Japan. Since the ten sectors of Chinese firms have a diverse degree of openness to the outside world, we expect the pandemic to have asymmetric effects, and those effects to be time-varying, depending not only on the resilience of the sector itself but also the resilience of its most connected industries.
4.1. Connectedness based on systems of daily realized variances and semi-variances
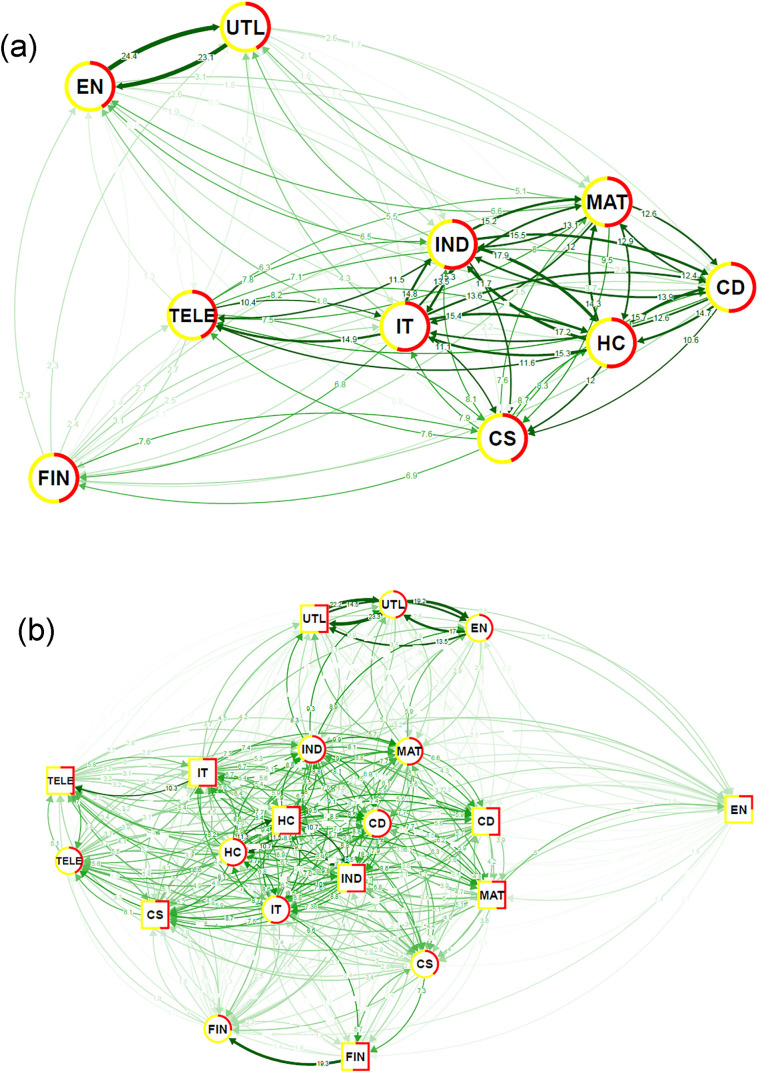
Panel (a) of Fig. 2 plots the directional connectedness based on the return variances of the ten sectoral indices. In the network graph, we can identify three clusters. First, energy (EN) and utilities (UTL) have strong spillovers to each other because the input of utility firms is the output of the energy firms, such as coal and oil. Second, the financial sector (FIN) turns to be standalone. It has weak spillovers from and to other sectors, alluding to fact that the China's financial system centers around banks rather than the securities market (Chan, Fung, & Thapa, 2007). Third, the rest eight sectors form the third and also the largest cluster. Among these sectors, consumer discretionary (CD) and consumer staples (CS) have lower “to connectedness” than the other six sectors. This finding is consistent with the consumption smoothing behavior in macroeconomics, which says that spending on daily necessities remains largely the same over time. Meanwhile, industrials (IND), materials (MAT), consumer discretionary (CD), and health care (HC) have been strong receivers of spillover. It confirms the intuition that COVID-19 has inflicted a significant negative impact on industrial production and non-food consumption due to the lock-down policy. The outbreak of the pandemic also put a heavy burden on the healthcare system, both financially and in terms of personnel (Qiu, Chen, & Shi, 2020).
Fig. 2.
Diebold-Yilmaz (DY) network diagram. (a) System of daily realized volatilities. (b) System of daily realized semivariances. The network graph illustrates the degree of pairwise weighted directional connectedness of a variance system that consists of the daily realized volatilities and daily realized semivariances (based on 1-min data) of the Chinese stock markets sectors (HC = health care; CD = consumer discretionary; UTL = utilities; CS = consumer staples; IT = information technology; IND = industrials; FIN = financials; EN = energy; MAT = materials; TELE = telecommunications) over the full sample period. Total connectedness is measured using the Diebold-Yilmaz framework. The border colour indicates the origin of connectedness. Red implies a contribution from the variable under consideration to the other variables of the system. The size of edges (indicated by the figure on the edge) shows the magnitude of pair-wise directional spillover. In Panel (b), the rectangles are positive semivariances, while the ellipses show negative semivariances. Lag = 1; forecast horizon = 5 days.
These findings, especially the second and the third points, are vastly different from those for the US. For example, Baruník et al. (2016) reaches a different conclusion when examining 21 firms from seven sectors from August 2004 to December 2011.1 They find that the financial sector (FIN) and the energy (EN) sector were the largest transmitters of net spillovers during the financial crisis. For the rest of the sample period, consumer discretionary (CD), staples (CS), telecommunications (TELE), and health care (HC) sectors display larger asymmetries in spillover than the other three sectors.
Panel (b) of Fig. 2 shows the connectedness based on the semivariances of the sectoral index returns. We use a rectangle to indicate positive semivariance and an ellipse to mark negative semivariance. The strongest spillover effect is observed in the first cluster, that is, between negative semivariance of energy (EN-) and two semivariances of utilities (UTL+ and UTL-). From the network diagram, we can discern that upward risks of the energy market (EN+)—which can be interpreted as the volatility during periods of price declines—exert two effects on the utilities index. The existence of the two effects follows from that energy products are the input of various amenities. First, when energy stocks perform weakly, energy becomes cheaper, and the profits of energy firms decrease. In this case, when other things being equal, the profit of utilities firms increases. So, there is a directional spillover from EN- to UTL+. Second, negative semivariance of energy (EN-) may be the result of a negative shock to the general economy. In this case, which transmits to the utilities sector. As a result, we also witness a spillover from EN- to UTL-. Last, negative semivariance in the energy ETF (EN-) may be the result of downside volatilities in the utilities (UTL-), so there is also connectedness from UTL- to EN-.
Another interesting spillover effect is from upward semivariance of financials (FIN+) to downside variance of financials (FIN-), which may reflect the frequent up-and-down movements in the financial sector around the pandemic outbreak. Moreover, FIN+ is a receiver of negative shocks from information technology (IT-) and consumer staples (CS-). The rationale is, the pandemic imposes negative shocks to industrial firms, pulling down the demand for IT and CS. Seeing a fall in the profitability of non-financial sectors, investors may divert funds away from the financial market. On the other hand, spillover from financials (FIN+ and FIN-) to CS is not strong, which is consistent with Luo and Ji (2018). Focusing on the spillover from US crude oil to five Chinese agricultural commodities from 2008 to 2015, Luo and Ji (2018) find that the connectedness of the volatilities of the two markets remains weak. Our findings are similar: the Chinese energy industry (EN) also has a low spillover effect on the consumer staples sectors (CS), even if we split the variances into good and bad volatilities for both sectors.
Last, the downside variance of industrials (IND-) has a spillover on the downside of materials (MAT). This spillover also has an intuitive interpretation: when there is a negative shock to the industrial sector, firms demand fewer materials to produce industrial goods. Over time, this negative impact transmits to the materials sector, resulting in large connectedness from IND- to MAT-.
4.2. Frequency-domain connectedness based on systems of daily realized semi-variances
In this section, we use the Baruník and Křehlík (BK) approach to examine the spillover among the ten sectors. Following the recent literature, such as Hasan, Arif, Naeem, Ngo, and Taghizadeh–Hesary, F. (2020) and Naeem, Peng, Suleman, Nepal, and Shahzad (2020), we focus on two horizons: short- and long-term, defined as 1 to 5 days and more than 5 days, respectively.
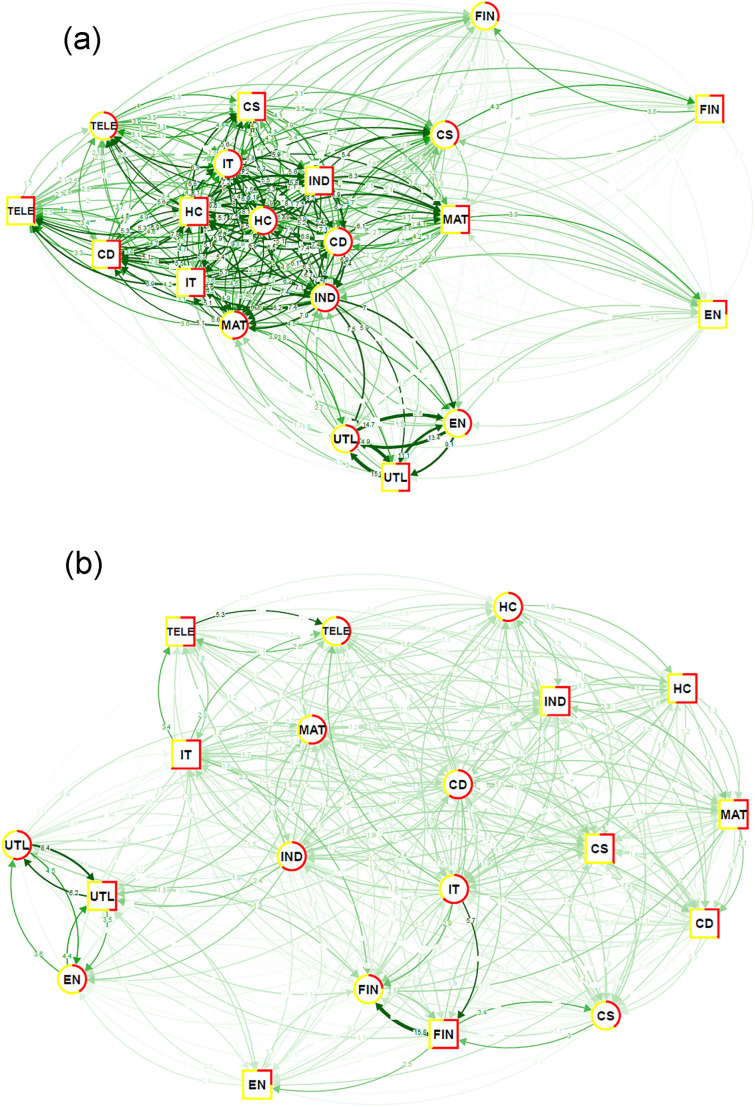
Panel (a) Fig. 3 shows the short-term spillovers. Again, we observe three clusters. The first cluster includes the negative semivariance of energy (EN-) and two semivariances of utilities (UTL+ and UTL-). At the same time, the upward semivariance of the energy sector (EN+) is a weak receiver of volatility shocks from other non-financial and non-energy sectors. These results are consistent with the Diebold-Yilmaz (DY) method—as shown in Fig. 2(b), EN- has been a receiver of volatility shocks to the utilities sectors. The second cluster includes only the financial sector (FIN+ and FIN-). Both semivariances of FIN are receivers of shocks from other sectors, yet none of them are strong. The lack of short-term spillover effect may be ascribed to the relatively slow adjustment in non-financial sectors: changing physical capital in these industries is more difficult than tuning monetary investment positions in the financial sector. The rest seven sectors form the largest cluster, where every sector functions both as a receiver and transmitter of spillovers.
Fig. 3.
Network diagram of realized semi-variances spillover using the Baruník and Křehlík (BK) approach. a). Short-run (1–5 days). b). Long-run (more than 5 days). Note: This network graph illustrates the degree of pairwise weighted directional connectedness in a system that consists of the daily realized semivariances (based on 1-min data) of Chinese stock markets sectors (HC = health care; CD = consumer discretionary; UTL = utilities; CS = consumer staples; IT = information technology; IND = industrials; FIN = financials; EN = energy; MAT = materials; TELE = telecommunications) over the full sample period. Total connectedness is measured using the generalized forecast error variance decomposition approach of Baruník and Křehlík (2018). The border colour indicates the origin of connectedness. Red implies a contribution from the variable under consideration to the other variables of the system. The size of edges (indicated by the figure on the edge) shows the magnitude of pair-wise directional spillover. The square nodes are positive semivariances, while circles show negative semivariances. Lag = 1; forecast horizon = 5 days. The sample period is from January 2, 2019 to September 30, 2020.
The long-term spillover, presented by Panel (b) of Fig. 3, deviates drastically from the short-term dynamics in Panel (a) for non-financial and non-energy sectors. There are only three pairs that have significant spillovers. (1) There is spillover from the positive semivariance of telecommunications (TELE+) to its negative counterpart (TELE+). This result may follow from the expansion-to-contraction dynamics of this sector due to the lockdown. (2) There is spillover from negative semivariance of information technology (IT-) to positive semivariance of the financial sector (FIN+). This directional connectedness might be attributed to the following mechanism: the pandemic causes a contraction in the industrials (IND-) and consumer discretionary (CD) sectors, which in turn, transmits to the IT sector. As the profitability of the IT sector tumbles, investors turn to the financial sector in a swamp, leading to a boom in the latter.
4.3. Time-varying spillover
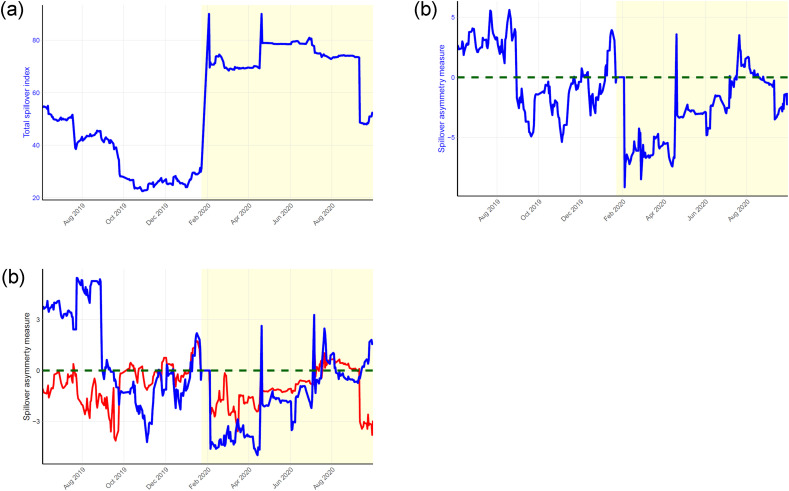
Panel (a) of Fig. 4 shows the total connectedness (or spillover) index based on the system of realized volatilities, where the forecasting horizon is 5 days (H = 5) and the window length is 100 days (w = 100). The yellow shaded area marks the period after the outbreak on February 4, 2020. Overall, the graph exhibits a time-varying pattern that has been reported by previous studies on Chinese sectors (e.g., Wu et al., 2019). As we extend our sample beyond the unprecedented outbreak of the catastrophe, we can see a sharp rise in the total connectedness measure. It indicates that the negative shock has struck the whole economic system. Towards the end of March, while the peak of the pandemic had passed, the overall connectedness index remained high. The first week of February.
Fig. 4.
Time-varying spillover. (a) Spillover based on the system of realized volatilities. (b) Spillover based on the system of asymmetry measure (SAM). (c) Spillover based on the system of frequency-domain asymmetry measure (SAM). Notes: The spillover asymmetry measure has w = 100 and h = 5 trading days. The shaded area (yellow) is the COVID-19 impact period starting on February 4, 2020. In Panel (b), negative values imply higher negative spillover, and vice versa. In Panel (c), the blue (red) line shows the short- and long-run asymmetry.
Similarly, Panel (b) of Fig. 4 shows the spillover asymmetry measure (SAM), defined as the spillover of the positive semivariance minus the spillover of the negative semivariance (Baruník et al., 2017). Before February 4, 2020, this asymmetry measure stayed within the range of [−5%, +5%]. After the COVID-19 outbreak, this measure entered the negative region and approached −10%. Nevertheless, as China gradually gets the pandemic under control around March 2020, this measure increased from its trough and reverted to its previous range.
Using frequency-domain connectedness, Panel (c) illustrates the short- and long-term asymmetry. We can see that the extreme upward and downward spikes of the total spillover index are all caused by short-term connectedness (marked in blue). The upward spike in April was owing to the removal of the lockdown. And the other two spikes in summer 2020 was also due to the removal of small-scale lockdowns.2 In contrast, the long-term SAM remain negative most of the time, indicating that continued downside risks exist our sample periods. Before the pandemic, SAM is already negative. This value can be attributed to China's economic growth decline since late 2018 (Liu, Sun, & Zhang, 2020). During the pandemic, SAM stayed within the negative realm due to the lock-down policy, under which most economic activities were put into a halt. After that, the long-term SAM decreased turned positive from July to mid-August. This decline coincides with the removal of small-scale lockdowns and travel restrictions. Entering August, long-term SAM decreases again, which may result from the second wave of lockdowns in cities like Dalian (in Liaoning Province).
4.4. Robustness checks
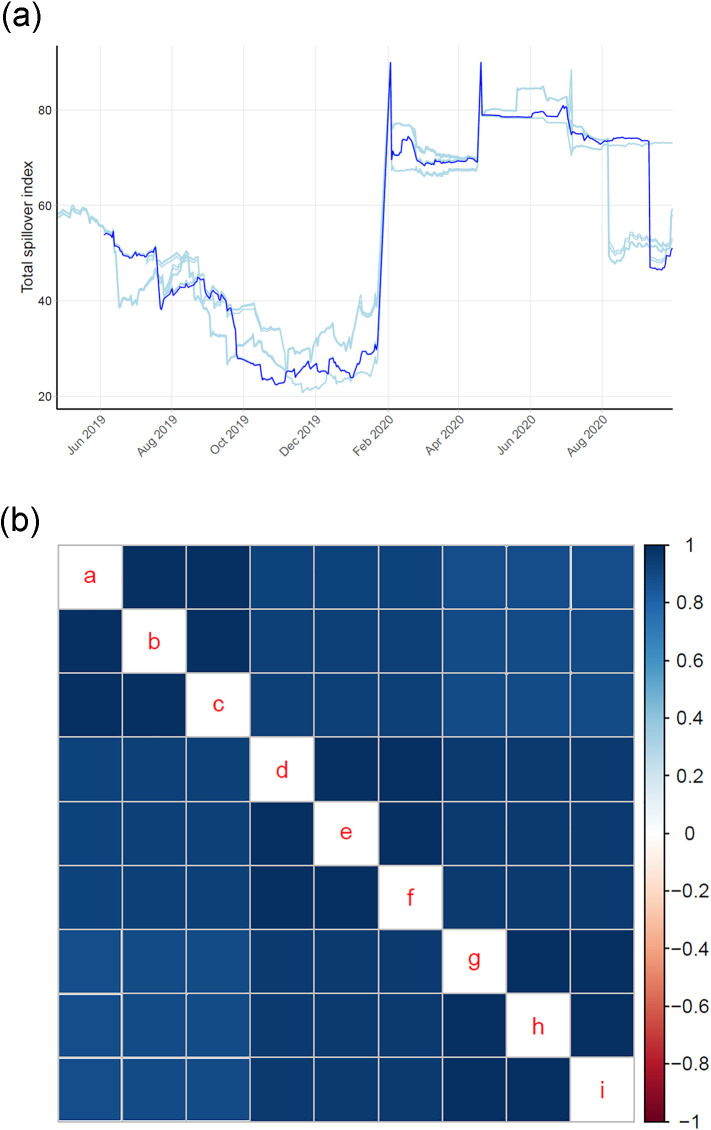
In the previous sections, our chosen forecasting horizon is 5 days (H = 5), and the window length is 100 days (w = 100). To verify that our results are not sensitive to the choice of forecasting horizon (H) or window length (w), we select all possible combinations from the following parameter sets: w ∈ {75; 100; 125} and h ∈ {3; 5; 10}. The nine combinations generated are: (a) w = 75, H = 3; (b) w = 75, H = 5; (c) w = 75, H = 10; (d) w = 100, H = 3; (e) w = 100, H = 5; (f) w = 100, H = 10; (g) w = 125, H = 3; (h) w = 125, H = 5; and (i) w = 125, H = 10.
The graph of these sets is shown in Panel (a) of Fig. 5 . In terms of the spillover index (i.e., the total connectedness of the system), all combinations of forecasting horizon (H) and window length (w) have similar trajectories and thus overlap most of the time. Moreover, all choices lead to two kink points: one situates at the beginning of February, marking the outbreak of the pandemic; and the other sits at the beginning of April, denoting the removal of the lockdown.
Fig. 5.
Robustness to the choice of rolling window and forecast horizon. (a) Spillover index. Notes: The results for our baseline setting, with window length w = 100 and forecast horizon H = 5 trading days, are shown by the dark blue line. Results for each other combination of w ∈ {75; 100; 125} and h ∈ {3; 5; 10} trading days are shown as light blue lines. (b) Correlation heatmaps of common-sample connectedness. Notes: Letters a to i in the common-sample correlation heatmap refer to combinations: (a) w = 75, h = 3; (b) w = 75, h = 5; (c) w = 75, h = 10; (d) w = 100, h = 3; (e) w = 100, h = 5; (f) w = 100, h = 10; (g) w = 125, h = 3; (h) w = 125, h = 5; and (i) w = 125, h = 10.
Panel (b) of Fig. 5 illustrates the common-sample correlation heatmap. For each square block, the darker the colour, the higher the correlation. No matter which combination of w and H we choose, the resulting spillover indexes have high, positive common-sample correlation with each other. Based on our calculations, most correlations exceed 0.8. Therefore, both panel (a) and (b) provide evidence that our results are not sensitive to the choice of forecasting window (w) and horizon (h).
5. Conclusion
In this paper, we examine the asymmetric volatility spillover among Chinese stock sector indices during the COVID19 outbreak. Using 1-min data from January 3, 2019 to September 30, 2020, we construct daily measures of realized volatility, differentiating between measures of good and bad volatilities and applying asymmetric connectedness measures in static and time-varying settings. The main results indicate an asymmetric spillover effect across the Chinese stock sector indices, which strengthens significantly during the COVID-19 outbreak. This underscores the conclusion that the catastrophic event of COVID-19 has a strong and asymmetric impact on the network of volatility spillovers among sector indices. The total volatility spillover index varies with time. Downside semivariance spillovers dominate upside semivariance spillovers during the COVID-19, suggesting an asymmetric effect. The findings are robust to the choice of forecasting horizon and window length.
Our results are useful for investors and policymakers. They give fresh insight into the dynamics of volatility spillovers among the stock sector indices and evidence of asymmetry that affects portfolio and risk choices, volatility forecasting inferences, and the payoff of trading strategies across Chinese sector indices during stress periods. Notably, market participants and policymakers should pay special attention to downside semivariance shocks more than upside semivariances during stressful periods given that downside semivariance shocks have a pressurizing effect on the system of connectedness. Therefore, vigilant monitoring of bad volatility spillovers is required for the sake of stock market stability in China. Specifically, special monitoring efforts should be given to the core sectors such as industrials, utilities, energies, and materials to maintain the overall stability of the Chinese stock market, especially given that these sectors exhibit a destabilizing effect through their bad volatility spillovers and the recent unfortunate signs that a second wave of COVID-19 is likely to emerge in China.
Future research could consider decomposition of the realized volatility into diffusive and discontinuous volatilities, to help uncover the contribution of the continuous and jump components of volatility in the network of connectedness in the Chinese stock market during COVID-19. Another contribution could involve the extension of our analysis to the asymmetric predictability of realized semivariances in the Chinese stock sector indices along the lines of Fang, Jiang, and Luo (2017).
Acknowledgements
Muhammad Abubakr Naeem gratefully acknowledges the support of Science Foundation Ireland under grant number 16/SPP/3347.
Footnotes
These sectors include financials (FIN), information technology (IT), energy (EN), consumer discretionary (CD), consumer staples (CS), telecommunications service (TELE), and health care (HC).
For example, new cases appeared in Beijing on June 11, 2020, all of which were found to relate to the Xinfadi wholesale market. Beijing was able to control the expansion of the pandemic and reopened the market on August 15. In late July, a few cities in Northeast China (e.g., Dalian in Liaoning Province) have reported imported cases, which resulted in massive COVID-19 testing and short-term lockdowns.
References
- Amonlirdviman K., Carvalho C. Loss aversion, asymmetric market comovements, and the home bias. Journal of International Money and Finance. 2010;29(7):1303–1320. [Google Scholar]
- Andersen T.G., Bollerslev T. Answering the skeptics: Yes, standard volatility models do provide accurate forecasts. International Economic Review. 1998:885–905. [Google Scholar]
- Balli F., Naeem M.A., Shahzad S.J.H., de Bruin A. Spillover network of commodity uncertainties. Energy Economics. 2019;81:914–927. [Google Scholar]
- Barndorff-Nielsen O., Kinnebrock S., Shephard N. In: Volatility and time series econometrics: Essays in Honor of Robert F. Bollerslev T., Russell J., Watson M., editors. Oxford University Press; Engle: 2010. Measuring downside risk of realized semivariance. [Google Scholar]
- Baruník J., Kočenda E., Vácha L. Asymmetric connectedness on the US stock market: Bad and good volatility spillovers. Journal of Financial Markets. 2016;27:55–78. [Google Scholar]
- Baruník J., Kočenda E., Vácha L. Asymmetric volatility connectedness on the forex market. Journal of International Money and Finance. 2017;77:39–56. [Google Scholar]
- Baruník J., Křehlík T. Measuring the frequency dynamics of financial connectedness and systemic risk. Journal of Financial Econometrics. 2018;16(2):271–296. 2018. [Google Scholar]
- Bouri E., Lucey B., Saeed T., Vo X.V. The realized volatility of commodity futures: Interconnectedness and determinants. International Review of Economics and Finance. 2021;73 139-139. [Google Scholar]
- Caporin M., Naeem M.A., Arif M., Hasan M., Vo X.V., Shahzad S.J.H. Asymmetric and time-frequency spillovers among commodities using high-frequency data. Resources Policy. 2021;70:101958. [Google Scholar]
- Cappiello L., Engle R.F., Sheppard K. Asymmetric dynamics in the correlations of global equity and bond returns. Journal of Financial Econometrics. 2006;4(4):537–572. [Google Scholar]
- Chan K.C., Fung H.G., Thapa S. China financial research: A review and synthesis. International Review of Economics and Finance. 2007;16(3):416–428. [Google Scholar]
- Chen Y., Li W., Qu F. Dynamic asymmetric spillovers and volatility interdependence on China’s stock market. Physica A: Statistical Mechanics and its Applications. 2019;523:825–838. [Google Scholar]
- Diebold F.X., Yilmaz K. Better to give than to receive: Predictive directional measurement of volatility spillovers. International Journal of Forecasting. 2012;28(1):57–66. [Google Scholar]
- Diebold F.X., Yılmaz K. On the network topology of variance decompositions: Measuring the connectedness of financial firms. Journal of Econometrics. 2014;182(1):119–134. [Google Scholar]
- Do A., Powell R., Yong J., Singh A. Time-varying asymmetric volatility spillover between global markets and China’s A, B and H-shares using EGARCH and DCC-EGARCH models. The North American Journal of Economics and Finance. 2019:101096. [Google Scholar]
- Eckernkemper T. Modeling systemic risk: Time-varying tail dependence when forecasting marginal expected shortfall. Journal of Financial Econometrics. 2018;16(1):63–117. [Google Scholar]
- Fang N., Jiang W., Luo R. Realized semivariances and the variation of signed jumps in China’s stock market. Emerging Markets Finance and Trade. 2017;53(3):563–586. [Google Scholar]
- Feng S., Huang S., Qi Y., Liu X., Sun Q., Wen S. Network features of sector indexes spillover effects in China: A multi-scale view. Physica A: Statistical Mechanics and its Applications. 2018;496:461–473. [Google Scholar]
- Ferrer R., Shahzad S.J.H., López R., Jareño F. Time and frequency dynamics of connectedness between renewable energy stocks and crude oil prices. Energy Economics. 2018;76:1–20. [Google Scholar]
- Garcia R., Tsafack G. Dependence structure and extreme comovements in international equity and bond markets. Journal of Banking & Finance. 2011;35(8):1954–1970. [Google Scholar]
- Gkillas K., Gupta R., Pierdzioch C. Forecasting (downside and upside) realized exchange-rate volatility: Is there a role for realized skewness and kurtosis? Physica A: Statistical Mechanics and its Applications. 2019;532:121867. [Google Scholar]
- Hammoudeh S., Nguyen D.K., Reboredo J.C., Wen X. Dependence of stock and commodity futures markets in China: Implications for portfolio investment. Emerging Markets Review. 2014;21:183–200. [Google Scholar]
- Hao J., He F. Univariate dependence among sectors in Chinese stock market and systemic risk implication. Physica A: Statistical Mechanics and its Applications. 2018;510:355–364. [Google Scholar]
- Hasan M., Arif M., Naeem M.A., Ngo Q.T., Taghizadeh–Hesary, F. Time-frequency connectedness between Asian electricity sectors. Economic Analysis and Policy. 2021;69:208–224. [Google Scholar]
- Huang S., An H., Gao X., Huang X. Identifying the multiscale impacts of crude oil price shocks on the stock market in China at the sector level. Physica A: Statistical Mechanics and its Applications. 2015;434:13–24. [Google Scholar]
- Jin J., Han L., Wu L., Zeng H. The hedging effectiveness of global sectors in emerging and developed stock markets. International Review of Economics and Finance. 2020;66:92–117. [Google Scholar]
- Li Y., Giles D.E. Modelling volatility spillover effects between developed stock markets and Asian emerging stock markets. International Journal of Finance and Economics. 2015;20(2):155–177. [Google Scholar]
- Liu D., Sun W., Zhang X. Is the Chinese economy well positioned to fight the COVID-19 pandemic? The financial cycle perspective. Emerging Markets Finance and Trade. 2020;56(10):2259–2276. [Google Scholar]
- Liu T., Hamori S. Spillovers to renewable energy stocks in the US and Europe: Are they different? Energies. 2020;13(12):3162. [Google Scholar]
- Luo J., Ji Q. High-frequency volatility connectedness between the US crude oil market and China's agricultural commodity markets. Energy Economics. 2018;76:424–438. [Google Scholar]
- Naeem M.A., Peng Z., Suleman M.T., Nepal R., Shahzad S.J.H. Time and frequency connectedness among oil shocks, electricity and clean energy markets. Energy Economics. 2020;91:104914. [Google Scholar]
- Pesaran H.H., Shin Y. Generalized impulse response analysis in linear multivariate models. Economics letters. 1998;58(1):17–29. [Google Scholar]
- Qiu Y., Chen X., Shi W. Impacts of social and economic factors on the transmission of coronavirus disease 2019 (COVID-19) in China. Journal of Population Economics. 2020;33:1127–1172. doi: 10.1007/s00148-020-00778-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shahzad S.J.H., Hernandez J.A., Al-Yahyaee K.H., Jammazi R. Asymmetric risk spillovers between oil and agricultural commodities. Energy Policy. 2018;118:182–198. [Google Scholar]
- Shahzad S.J.H., Bouri E., Kristoufek L., Saeed T. Impact of the COVID-19 outbreak on the US equity sectors: Evidence from quantile return spillovers. Financial Innovation. 2021;7(14) doi: 10.1186/s40854-021-00228-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharif A., Aloui C., Yarovaya L. 2020. COVID-19 pandemic, oil prices, stock market and policy uncertainty nexus in the US economy: Fresh evidence from the wavelet-based approach. (Working Paper) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Todorova N. The asymmetric volatility in the gold market revisited. Economics Letters. 2017;150:138–141. [Google Scholar]
- Uddin G.S., Shahzad S.J.H., Boako G., Hernandez J.A., Lucey B.M. Heterogeneous interconnections between precious metals: Evidence from asymmetric and frequency-domain spillover analysis. Resources Policy. 2019;64:101509. [Google Scholar]
- Wang X., Wu C. Asymmetric volatility spillovers between crude oil and international financial markets. Energy Economics. 2018;74:592–604. [Google Scholar]
- Wu F., Zhang D., Zhang Z. Connectedness and risk spillovers in China’s stock market: A sectoral analysis. Economic Systems. 2019;43(3–4):100718. [Google Scholar]
- Xu W., Ma F., Chen W., Zhang B. Asymmetric volatility spillovers between oil and stock markets: Evidence from China and the United States. Energy Economics. 2019;80:310–320. [Google Scholar]
- Yang L., Zhu Y., Wang Y., Wang Y. Multifractal detrended cross-correlations between crude oil market and Chinese ten sector stock markets. Physica A: Statistical Mechanics and its Applications. 2016;462:255–265. [Google Scholar]
- Yao S., He H., Chen S., Ou J. Financial liberalization and cross-border market integration: Evidence from China's stock market. International Review of Economics and Finance. 2018;58:220–245. [Google Scholar]
- Yarovaya L., Brzeszczyński J., Lau C.K.M. Intra-and inter-regional return and volatility spillovers across emerging and developed markets: Evidence from stock indices and stock index futures. International Review of Financial Analysis. 2016;43:96–114. [Google Scholar]
- Yu H., Fang L., Sun B., Du D. Risk contribution of the Chinese stock market to developed markets in the post-crisis period. Emerging Markets Review. 2018;34:87–97. [Google Scholar]
- Zhang D., Hu M., Ji Q. Financial markets under the global pandemic of COVID-19. Finance Research Letters. 2020;101528 doi: 10.1016/j.frl.2020.101528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang W., He X., Nakajima T., Hamori S. How does the spillover among natural gas, crude oil, and electricity utility stocks change over time? Evidence from North America and Europe. Energies. 2020;13(3):727. [Google Scholar]