Statistical methods for comparing test positivity rates between countries: Which method should be used and why?

Abstract

The test positivity (TP) rate has emerged as an important metric for gauging the illness burden due to COVID-19. Given the importance of COVID-19 TP rates for understanding COVID-related morbidity, researchers and clinicians have become increasingly interested in comparing TP rates across countries. The statistical methods for performing such comparisons fall into two general categories: frequentist tests and Bayesian methods. Using data from Our World in Data (ourworldindata.org), we performed comparisons for two prototypical yet disparate pairs of countries: Bolivia versus the United States (large vs. small-to-moderate TP rates), and South Korea vs. Uruguay (two very small TP rates of similar magnitude). Three different statistical procedures were used: two frequentist tests (an asymptotic z-test and the ‘N-1’ chi-square test), and a Bayesian method for comparing two proportions (TP rates are proportions). Results indicated that for the case of large vs. small-to-moderate TP rates (Bolivia versus the United States), the frequentist and Bayesian approaches both indicated that the two rates were substantially different. When the TP rates were very small and of similar magnitude (values of 0.009 and 0.007 for South Korea and Uruguay, respectively), the frequentist tests indicated a highly significant contrast, despite the apparent trivial amount by which the two rates differ. The Bayesian method, in comparison, suggested that the TP rates were practically equivalent—a finding that seems more consistent with the observed data. When TP rates are highly similar in magnitude, frequentist tests can lead to erroneous interpretations. A Bayesian approach, on the other hand, can help ensure more accurate inferences and thereby avoid potential decision errors that could lead to costly public health and policy-related consequences.

1. Introduction

The test positivity (TP) rate is defined as the proportion of all tested individuals who test positive for a particular illness or disease. In March of 2020, the World Health Organization [1] emphasized the importance of assessing SARS-CoV-2 test positivity. From that point forward the TP rate has emerged as a critical metric for gauging the illness burden due to COVID-19. TP rates are routinely reported by news media outlets and by many online data repositories, such as Our World in Data (ourworldindata.org). Given the importance of COVID-19 TP rates for understanding COVID-related morbidity between nations, researchers and clinicians have become increasingly interested in comparing TP rates across countries. If country A has a lower TP rate than country B, it would appear that country A has a lower disease burden. Perhaps country A mobilized a more effective public health campaign that emphasized the importance of consistent social distancing and mask use. But how do we determine whether country A truly has a lower TP rate than country B? The question is an important one that has both public health and policy-related ramifications. For example, if decision makers in country B mistakenly conclude that country A has a substantially, or significantly, lower TP rate, then country B might devote considerable resources and enact policy-related changes in order to mimic the apparent success of country A. Such efforts, however, will be in vain because in this example the TP rates for country A and country B are not meaningfully different. How then should a researcher or public health professional decide whether two TP rates are substantially different? One approach that is sometimes used, but is fraught with error and thus not recommended, is the eyeball approach (i.e., unaided human judgment). In a seminal article on this topic, Dawes and colleagues [2] discussed the issue in terms of clinical versus actuarial judgment—with actuarial methods (statistical and mathematical models) consistently outperforming human clinical judgments.

Regarding statistical and mathematical approaches, there are several methods that could be used to compare TP rates (which, statistically speaking, are proportions bounded between 0 and 1). These methods can be divided into two groups: classical or frequentist methods and Bayesian methods. Frequentist methods for comparing two proportions, such as TP rates, include the asymptotic z-test [3] and the ‘N-1’ chi-squared test [4]. One limitation of these frequentist tests is that with very large sample sizes, such as those forming the basis of TP rate calculations at the country-wide level, standard error estimates become very small which results in high statistical power and a high probability of rejecting the null hypothesis. When comparing two proportions, the null hypothesis states that there is no difference between the two values. However, when the sample size is very large, rejecting the null means that the researcher concludes there is a substantial/significant difference between the two proportions, even though the actual difference between the two values might be quite small. Related to the above point, a second limitation of frequentist methods is that results generated by these approaches are almost always interpreted from the perspective of Null Hypothesis Significance Testing (NHST). A key limitation of NHST is that the probability value (p-value) resulting from the test statistic measures the probability of the result (or one more impressive) occurring, assuming that the null hypothesis is true. The p-value does not provide direct evidence for or against the alternative hypothesis; that is, whether the two proportions (TP rates) truly differ from each other under the assumption that the null hypothesis is false. Frequentist confidence intervals don’t eliminate this concern because they, too, rely on a p-value based interpretation (e.g., if the interval excludes zero, the two proportions are statistically significantly different). A third limitation of frequentist methods concerns their emphasis on dichotomous decision making: either the null hypothesis is supported or it is not supported. In contrast to frequentist-based NHST with its focus on rejecting or retaining the null hypothesis, it is the alternative hypothesis that is almost always of interest to the researcher. Unlike frequentist methods, Bayesian approaches directly evaluate the alternative hypothesis.

Before outlining the merits of Bayesian analysis, let’s first briefly define the goal of statistical inference: the results obtained in a sample (or samples) are used to make inferences about the population (or populations) from which the sample(s) are drawn. All else being equal, the sample-based statistics are interpreted as the best single estimates of the underlying true population values (i.e., the population parameters). In the present study, the parameter of interest is the true difference between the TP rates of two different countries. In a Bayesian analysis, a key assumption is that because parameters are estimated with error (sampling error, measurement error, etc.), some parameter estimates are better, or more credible, than others. In Bayesian inference, the goal is to ascertain which parameter value, or range of values, is most credible. When performing Bayesian estimation, greater credibility is allocated toward parameter values that are consistent with the data, and less credibility is given to parameter values that are inconsistent with the data. By “data”, what is technically meant are the observed sample data combined with, or informed by, previous theory and/or research. In Bayesian estimation the previous theory and/or knowledge is codified in the form of a ‘prior distribution’. The prior distribution, which is a type of probability distribution selected by the researcher (see the Method section below for more details), combines with/informs the observed data to give rise to a posterior distribution of parameter estimates. The process is an iterative one: thousands of samples of parameter estimates are drawn and examined, using a procedure called Markov Chain Monte Carlo (MCMC) sampling, to identify the most credible parameters of interest (i.e., the values that are most likely to occur in the population of interest). The collection of credible parameter estimates constitutes the ‘posterior distribution’.

The purpose of this study was to conduct pairwise, between-country comparisons of COVID-19 TP rates using three different methods: the asymptotic z-test and the ‘N-1’ chi-squared test (both are widely used frequentist methods), and a Bayesian procedure for comparing proportions. All three methods are designed to compare statistically independent proportions. In this study, because the TP rates are derived from different countries, and because different countries contain non-overlapping populations, any pair of proportions (TP rates) are considered to be statistically independent. There were two important aims of the analyses: (1) to examine whether the results of the two methodological approaches (frequentist and Bayesian) lead to similar or different inferences, and (2) if the two approaches lead to different inferences, then which approach (frequentist or Bayesian) appears to be more accurate? By “accurate” we mean which approach seems more consistent with the observed between-country data.

2. Method

The TP rate data used in this study were obtained from Our World in Data (ourworldindata.org), which is a freely available online data repository. The database is updated frequently and the analyses performed in this study used the version of the database updated on September 18, 2020. All data were processed and analyzed using IBM SPSS and R. The z-score calculator available at www.socscistatistics.com/tests/ztest/default2.aspx was used to conduct the asymptotic z-test. To perform the ‘N-1’ chi-squared test, the online MedCalc calculator was used (available at www.medcalc.org/calc/comparison_of_proportions.php). To perform the Bayesian analysis for comparing proportions, the prop.diff.eq R function written by Reza Norouzian was used (available at raw.githubusercontent.com/izeh/i/master/i.r). For the Bayesian analysis, the prior distribution that we used was a Beta (1.2, 1.2) probability distribution. The two values of 1.2 are hyperparameters for the two probabilities being compared (i.e., the two TP rates). The specifics about hyperparameters are not important for our purposes. What is important is that this prior distribution is commonly used when comparing proportions; it is a conservative distribution that depicts most of the proportions between 0 and 1 as being fairly equally likely to occur. The exceptions are the extreme proportions near 0 and 1, which are depicted as occurring notably less frequently. A picture of the Beta (1.2, 1.2) distribution is presented in Fig. 1 .

Fig. 1.

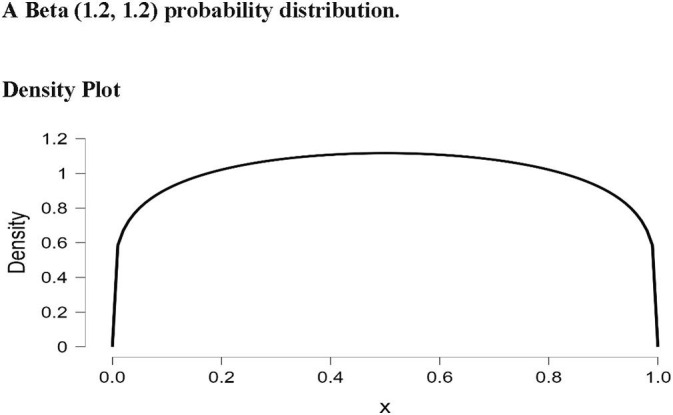
A Beta (1.2, 1.2) probability distribution.

In a Bayesian analysis, it is important to select an appropriate prior distribution. As noted above, when comparing two independent proportions, the Beta (1.2, 1.2) distribution is an appropriate choice because this distribution (a) is not biased toward (does not favor) any particular proportion value, and (b) assumes that in most real-world applications extreme proportions are, probabilistically speaking, less likely to occur. When researchers are conducting a study in which prior research has been performed and/or there is strong theory, then the past research or theory can inform the selection of a particular type of prior distribution. In contrast, for scenarios in which past research and compelling theory are lacking, the researcher can select what is known as a non-informative prior distribution. A commonly selected non-informative prior is the Uniform distribution, in which all empirical values are considered to be equally likely to occur. The Beta family of distributions is a popular choice for generating prior distributions because, depending on the particular hyperparameters selected, Beta distributions can assume the characteristics and shapes of many different distributions. To give some examples, Beta (1, 1) is the Uniform distribution, Beta (5, 5) is the Normal distribution, Beta (2, 8) is a Positively Skewed distribution, and Beta (8, 2) is a Negatively Skewed distribution. Graphs of these particular Beta distributions are presented in Fig. 2 .

Fig. 2.

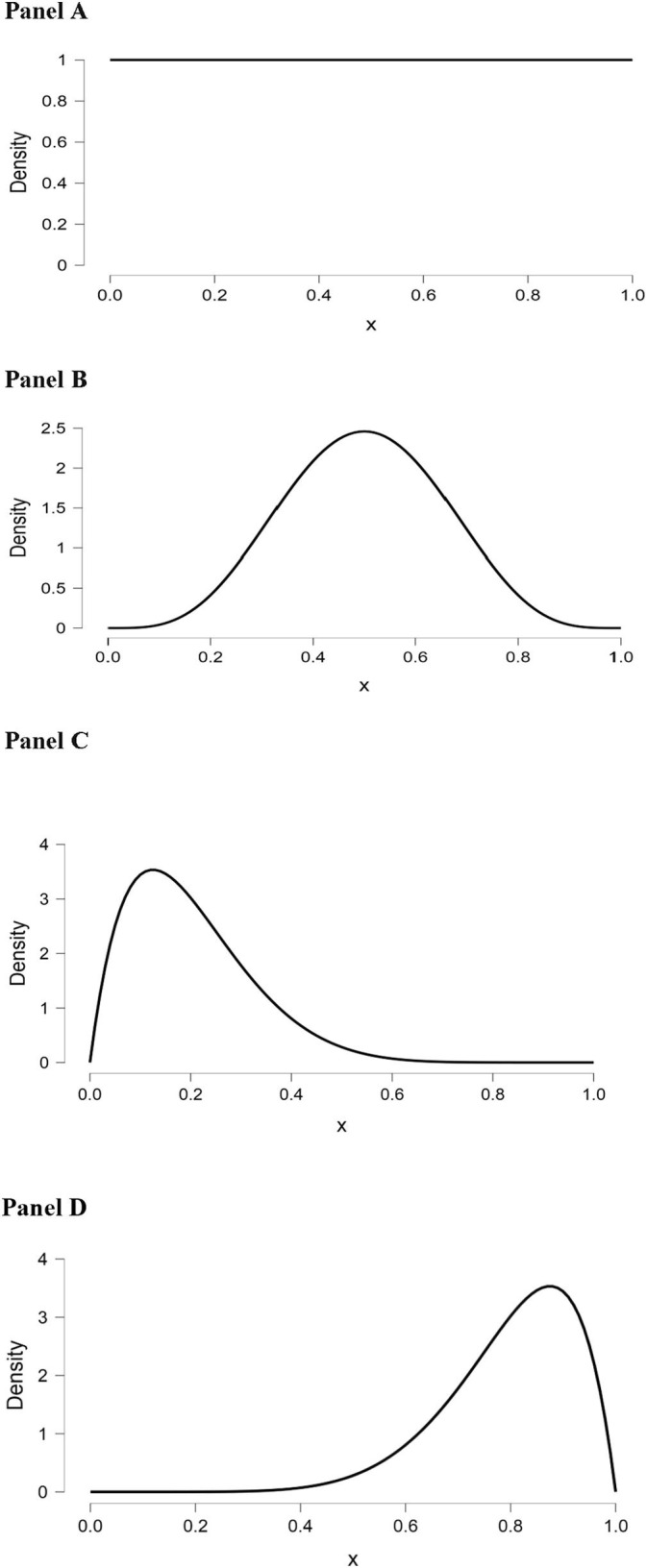
Examples of different Beta distributions. Panel A: A Uniform [Beta (1, 1)] distribution. Panel B: A Normal [Beta (5, 5)] distribution. Panel C: A Positively Skewed [Beta (2, 8)] distribution. Panel D: A Negatively Skewed [Beta (8, 2)] distribution.

3. Results and discussion

Given the large number of countries in the world, there are, obviously, a multitude of pairwise comparisons that could be conducted. Rather than performing a large number of comparisons, it is perhaps instructive to examine a few prototypical yet disparate cases. One such case involves Bolivia and the United States; these two countries have large and small-to-moderate TP rates, respectively. In the 9–18-20 update of the Our World in Data database (ourworldindata.org), the TP values for Bolivia and the United States were 0.337 and 0.045. The discrepancy between these two proportions is quite large. In such cases, where there are large between-country differences, both frequentist and Bayesian analyses will converge on the same conclusion: that there are significant/substantial differences between the two TP rates.

A second instructive case involves the scenario in which the TP rates for the two countries are quite similar. An example of this scenario involves the TP rates for South Korea and Uruguay: the values from the 9–18-20 update of the Our World in Data database were 0.009 and 0.007, respectively. These TP rates are very close together and would appear to not meaningfully differ from each other. However, despite this intuition, the p-values from both frequentist tests were highly statistically significant (z = 9.32, p < .00001; χ² = 86.94, p < .0001). Due to the extremely large sample sizes (close to 20,000 citizens in South Korea tested positive), both frequentist tests had very high statistical power and easily rejected the null hypothesis of equal TP rates.

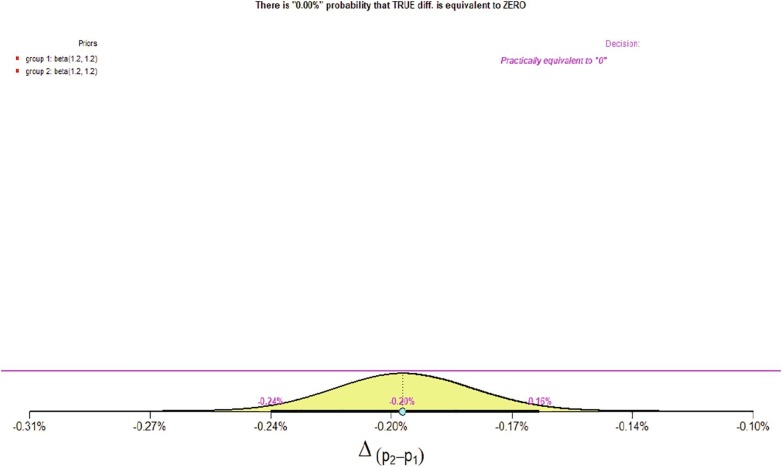
In contrast, the Bayesian procedure, which generates a distribution (a posterior distribution) of credible parameter estimates by analyzing the observed data as informed by the prior distribution, indicated that the two TP rates were practically equivalent. To be more precise, the Bayesian results showed that although the difference between the two proportions (TP rates) is not exactly equivalent to zero, the difference can be regarded as being practically equivalent to zero. This result is diametrically opposed to the frequentist findings and aligns more closely with the observation of a 0.002 difference between the two TP rates—an amount that appears to be quite trivial. A graph of the Bayesian results depicting the posterior distribution of credible parameter estimates is presented in Fig. 3 . In actuality, this graph contains several quantities of interest that warrant discussion. First, the 95% credible interval is indicated by the solid black line on the x-axis that is situated beneath the posterior distribution curve. As can be seen in the graph, the interval ranged from −0.16% to −0.24% (when converted to proportions, these values are −0.0016 and −0.0024). This credible interval can be interpreted as follows: there is a 95% probability (or, equivalently, we are 95% certain) that the true difference between the two proportions (the two TP rates) ranges between −0.0016 and −0.0024. The posterior parameter estimate, which in this case is the difference between the two TP rates, is labelled in Fig. 3 as Δ_(p2-p1). As indicated in the graph, this estimate was −0.20% (which, when converted to a proportion, equals −0.002). This estimate can be interpreted as follows: there is a 95% probability (or, equivalently, we are 95% certain) that the true difference between the two TP rates is −0.002. Note how straightforward it is to interpret the posterior parameter estimate and accompanying 95% credible interval. In contrast, if one performed a frequentist analysis and thus calculated a 95% confidence interval, the interpretation of the confidence interval would be as follows: if the researcher drew a very large number of random samples (with replacement) from South Korea and Uruguay (samples of the same size as those examined in the actual study), and for each pair of random samples the researcher calculated the difference between the two TP rates and the accompanying 95% confidence interval, then 95% of the 95% confidence intervals would contain the true difference between the two TP rates. We strongly suspect that most researchers would find the interpretation of frequentist confidence intervals to be substantially more convoluted and less illuminating than the interpretation of Bayesian credible intervals. By the way, for all of the Bayesian results discussed above, the signs of the values are irrelevant—whether they are positive or negative is merely a function of which country was labelled group 1 versus group 2 in the Bayesian analysis.

Fig. 3.

Bayesian Posterior distribution of credible parameter estimates for the difference between TP rates for South Korea and Uruguay on September 18, 2020.

There are several reasons as to why a Bayesian analysis provides richer information than frequentist tests. First, unlike NHST procedures, Bayesian approaches directly evaluate the alternative hypothesis, which in the present study is that the two TP rates are truly different. Second, a Bayesian posterior parameter estimate is accompanied by a credible interval, which can be interpreted as a range of values that contain, with a specified degree of probability, the true parameter estimate/true population value [5]. As mentioned in the previous paragraph, we believe that credible intervals are easier to interpret than frequentist confidence intervals. The major take home message from this study is that when TP rates are very similar, performing a Bayesian, rather than frequentist, analysis can avoid a potentially costly false positive decision error. Specifically, the Bayesian approach will, in all likelihood, prevent researchers and policy makers from mistakenly concluding that two TP rates of similar magnitude differ significantly from each other.

Our emphasis throughout this article has been to compare and contrast Bayesian and frequentist methods for analyzing TP rates. We did not discuss factors that could influence a test’s actual positivity rate. Although a number of factors could be relevant, we believe that two in particular deserve mention – the sensitivity of the test and the prevalence of the disease in the communities where testing is administered. A test’s sensitivity is its ability to correctly identify those individuals infected or with the disease. If a test is highly sensitive, it will have a high accuracy rate when it comes to correctly identifying those infected or with the disease. Recall that a test’s positivity rate represents the proportion of all tested individuals who test positive for a particular disease. In any group of individuals who are tested, there will be a certain number/proportion of people who have the disease. A highly sensitive test will be effective at correctly identifying such disease-positive individuals which, relative to a less sensitive test, will result in a larger proportion of the individuals testing “positive” for the disease in question. In other words, all else being equal, a test with a higher (versus lower) level of sensitivity will result in a higher test positivity rate. Another characteristic of a test is its level of specificity, which is defined as a test’s ability to correctly identify those individuals without the infection or disease. Because a test’s positivity rate is concerned solely with identifying individuals who have the disease, the concept of specificity is less relevant for TP rates. An interesting issue to consider regarding the SARS-CoV-2 virus concerns the recent variants that have been identified. To the extent that the structures and/or biomolecular properties of the variants affect the sensitivities of SARS-CoV-2 tests, then the test positivity rates of those tests could likewise be affected when the variant viruses are driving infection rates. Regarding the second influential factor that we believe deserves mention (i.e., the prevalence of disease in communities being tested), Usher-Smith and colleagues [6] found that tests developed and evaluated in communities/settings with high disease prevalence may have lower sensitivity when used in lower disease prevalence settings. The lower sensitivity in lower disease prevalence settings implies, by extension, that test positivity rates could also be affected by cross-setting differences in disease prevalence.

Finally, regarding the issue of statistical software, the Bayesian R function that we used in this study was easy to implement. However, there are other Bayesian programs for comparing two independent proportions, including the Fully Bayesian Evidence Synthesis online application (see bre-chryst.shinyapps.io/BayesApp/) and the Bayesian First Aid package for R (available at www.sumsar.net/blog/2014/01/bayesian-first-aid/). There also are other frequentist tests (see [3] for alternatives), but the two that we selected are among the most commonly used. In conclusion, although frequentist hypothesis tests for comparing proportions are widely implemented, their use for comparing between-country TP rates, when those rates are similar in magnitude, can result in erroneous interpretations which could then lead to costly public health and policy-related consequences.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.