The unprecedented reaction of equity and commodity markets to COVID-19

Abstract

Using a drifting spillover index approach (Diebold and Yilmaz, 2012) and a continuous time-frequency tool (Torrence and Webster, 1999), this paper attempts an empirical investigation of the spillovers and co-movements among commodity and stock prices in the major oil-producing and consuming countries. While our results point to the existence of a significant interdependence among the markets considered, Chinese and Saudi Arabian stock markets seem to be weakly integrated into the world market. Moreover, the spillovers are time-varying and reached their highest levels during the COVID-19 medical shock.

1. Introduction

This paper uses two complementary co-movement measures to provide some robust insights into the effect of COVID-19 pandemic developments on shaping recent stock behavior. First, we use the spillover index (Diebold and Yilmaz, 2012) which is defined in the time domain, and then implement bivariate squared cross-wavelet coherence (Torrence and Webster, 1999) which is defined in the time-frequency domain. Our investigation is motivated by the need to explain observed unprecedented financial market reactions.

Baker et al. (2020) highlight that current levels of volatility in the U.S. stock market rival or exceed those observed in October 1987, December 2008, and even as far back as late 1929 and the early 1930s. Following the latest U.S. stock market crash, stock markets in Asia and Europe also plunged. The Japanese stock market fell more than 20% from its peak in December 2019.1 On March 12, 2020, the FTSE, the U.K.'s main index, fell by more than 10%, making it its worst day since 1987.2 Baker et al. (2020) identify three main factors behind this powerful impact. A first rational explanation is the richness and speed of information dissemination possible nowadays compared to a century ago, especially news related to the Spanish flu. A second explanation is the severity of the current pandemic and its implications for public health and the global economy. The third reason is that the modern economy is characterized by interdependence and ease of long-distance travel, low communication costs, low transportation costs, etc., which has facilitated the spread of the virus worldwide. Along these lines, Goodell and Goutte (2020) apply wavelet continuous tools to daily data on world confirmed deaths from COVID-19 and daily Bitcoin prices to investigate the financial impact of the COVID-19 medical shock. Their results reveal strong out-of-phase relationships between the daily confirmed COVID-19 deaths and Bitcoin prices over almost the entire period of study (from December 31, 2019 to April 29, 2020), i.e. that the COVID-19 medical shock caused a decline in Bitcoin prices, suggesting that during extreme events Bitcoin cannot be considered a safe-haven investment.

Our results show that the COVID-19 pandemic has been producing volatility spillovers since January 2020. Almost half of the return forecast error variance in all the markets considered stems from spillovers which indicates the huge interdependence among these markets. In addition, developed countries’ stock markets tend to influence rather than to be influenced by other stock markets (positive net spillovers) whereas vice versa, developing countries’ stock markets (negative net spillovers). There seems to be a significant contagion effect between the spillover index and each of the uncertainty indices. Finally, the co-movement between the spillover index and the daily confirmed COVID-19 deaths is particularly strong and significant at high frequencies and is low and insignificant at low frequencies.

The remainder of the paper is organized as follows. Section 2 describes the empirical strategy. Section 3 presents the data and results. Section 4 concludes the paper.

2. Empirical strategy

Our empirical strategy consists of two complementary co-movement measures: the spillover index (Diebold and Yilmaz, 2012) which is defined in the time domain, and the bivariate squared cross-wavelet coherence (Torrence and Webster, 1999) which is defined in the time-frequency domain.

In the first step we use the spillover measure proposed by Diebold and Yilmaz (2012) which allows us to compute the level of interdependence among a set of financial markets. For a formal specification of spillovers, Diebold and Yilmaz (2009) consider a basic covariance stationary pth-order N-variable VAR, $y_t=\sum _{i=1}^p{\Phi }_i{y}_{t-i}+{\epsilon }_t$, where y_t = (y _1t, y _2t,…, y_Nt) is a vector of the endogenous variables, Φ_i, i = 1, …, p, are N × N parameter matrices, and $\epsilon \sim \left(0,\sum \right)$ is a N × 1 vector of the independently and identically distributed disturbances such that E(ε_t) = 0, $E\left({\epsilon }_t{\epsilon }_t^{\prime }\right)=\sum$ and E(ε_tε_t − s) = 0. The moving average (MA) representation of the VAR is given by $y_t=\sum _{i=0}^{\infty }{A}_i{\epsilon }_{t-i}$, where the N × N coefficient matrices A_i obey the recursion A_i = Φ₁ A _i − 1 + Φ₂ A _i − 2 + … + Φ_p A _i − p, with A ₀ being an N × N identity matrix and with A_i = 0 for i < 0. As the elements in ε_t are generally contemporaneously correlated, estimation of the coefficient matrix A_i requires external coefficient restrictions because the computation of the variance decompositions requires orthogonal innovations. Diebold and Yilmaz (2012) exploit the generalized VAR framework developed initially by Koop et al. (1996) and extended by Pesaran and Shin (1998) which produces generalized impulse responses invariant to the variable ordering. The generalized impulse response function is given by $A_j^G\left(i\right)=\sqrt{{\sigma }_{jj}}{A}_i\sum e_j$, where $\sqrt{{\sigma }_{jj}}$ is the standard deviation of the error term for the jth equation and e_j is a N × 1 selection vector which equals 1 for the jth element and zero otherwise. By denoting ${\theta }_{ij}^G\left(H\right)$ as the H-step-ahead forecast error variance decompositions, Pesaran and Shin (1998) show that ${\theta }_{ij}^G\left(H\right)$ is given by

$${\theta }_{ij}^G\left(H\right)=\frac{{\sigma }_{jj}^{-1}{\sum }_{h=0}^{H-1}{\left(e_i^{\prime }{A}_h\sum e_j\right)}^2}{{\sum }_{h=0}^{H-1}\left(e_i^{\prime }{A}_h\sum A_h^{\prime }{e}_i\right)},i,j=1,\dots ,N$$ (1)

Denoting the normalization of each entry of the of ${\theta }_{ij}^G\left(H\right)$ by the row sum ($\sum _{j=1}^N{\theta }_{ij}^G\left(H\right)$) asby ${\tilde{\theta }}_{ij}^G\left(H\right)$, Diebold and Yilmaz (2012) define a spillover index ($S_{DY}^G$) as

$$S_{DY}^G=\frac{{\sum }_{i,j=1,i\ne j}^N{\tilde{\theta }}_{ij}^G\left(H\right)}{N}·100$$ (2)

On average, the $S_{DY}^G$ spillover index measures the contribution of the volatility spillovers from shocks to all variables j = 1, …, N to the H-step-ahead of the total generalized forecast error variance of variables i = 1, …, N, with i ≠ j.

In the second step we use the bivariate cross-wavelet coherency measure developed by Torrence and Webster (1999) to obtain accurate frequency and time intervals where spillovers and a set of uncertainty indices move together significantly. To study the interaction between two time-series of length T, x(t) and y(t), in the time-frequency domain, Torrence and Webster (1999) define the squared cross-wavelet coherence, R²(u,s) as

$${\mathrm{R}}^2\left(\mathrm{u},\mathrm{s}\right)=\frac{{\left|{\mathrm{s}}^{-1}{\mathrm{W}}_{\text{xy}}\left(\mathrm{u},\mathrm{s}\right)\right|}^2}{{\mathrm{s}}^{-1}{\left|{\mathrm{W}}_{\mathrm{x}}^{\mathrm{y}}\left(\mathrm{u},\mathrm{s}\right)\right|}^2{\mathrm{s}}^{-1}{\left|{\mathrm{W}}_{\mathrm{y}}\left(\mathrm{u},\mathrm{s}\right)\right|}^2},{\mathrm{R}}^2\left(\mathrm{u},\mathrm{s}\right)\in \left[0,1\right]$$ (3)

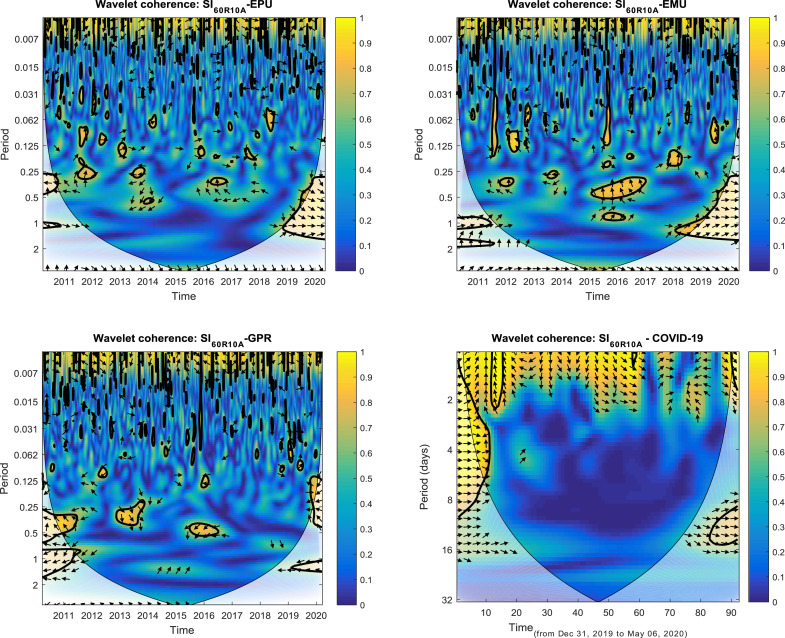
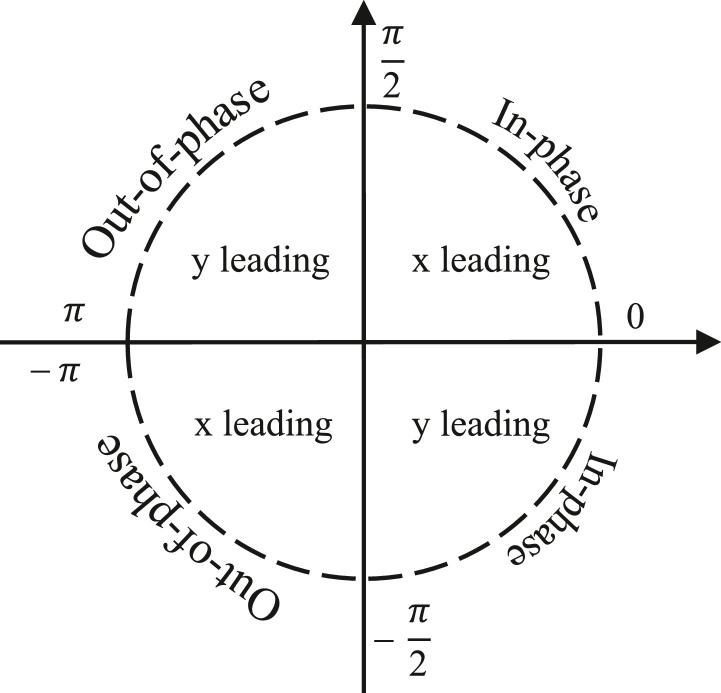
where R²(u,s) is the wavelet squared coherence which ranges between 0 and 1 and can be conceptualized as the local linear correlation coefficient between x and y,3 < • > is the smoothing operator in both time (u) and scale (s)4 , W_xy(u,s) is the cross-wavelet transform (CWT) of x(t) and y(t),5 and s⁻¹ is used to convert it to an energy density. $|{\mathrm{W}}_{\mathrm{x}}^{\mathrm{y}}\left(\mathrm{u},\mathrm{s}\right){|}^2$ and |W_y(u,s)|² are the respective wavelet power spectra of x(t) and y(t).6 We rely on Monte Carlo methods to test the statistical significance (See Grinsted et al., 2004). Since the wavelet squared coherence, R²(u,s), is an absolute value, it can take only positive values, i.e. it cannot distinguish between positive and negative co-movements. Thus, its interpretation must be associated with that of the wavelet phase-difference (See Torrence and Compo, 1998).7 The phase-differences, φ_xy(u,s), indicated by black arrows on the wavelet coherence plots (see Fig. 3), show whether the co-movement between x(t) and y(t) is positive (in-phase relationship) or negative (out-of-phase relationship), and also show the lead/lag relationship between x(t) and y(t). Fig. 1 summarizes how φ_xy(u,s) should be interpreted.

Fig. 3.

Cross-wavelet coherences. Notes: Time appears on the x-axis, while frequency on the y-axis. The cone of influence (COI) where edge effects should be considered is shown with a parabola-like lighter shade. The thick black line contours designate the 5% significance level. The color code for R²(u,s) ranges from blue (low coherency: R² close to 0) to yellow (high coherency: R² close to 1). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Fig. 1.

Phase-difference circle.

The arrows point to the right if x(t) and y(t) move in-phase, and point to the left if x(t) and y(t) move out-of-phase. Upward pointing arrows indicate that x(t) leads y(t) if they are in-phase, i.e. if ${\varphi }_{\text{xy}}\in \left(0,\frac{\pi }{2}\right)$, and that y(t) leads x(t) if they are out-of-phase, i.e. if ${\varphi }_{\text{xy}}\in \left(\frac{\pi }{2},\pi \right)$. Downward pointing arrows indicate that y(t) leads x(t) if they are in-phase, i.e. if ${\varphi }_{\text{xy}}\in \left(-\frac{\pi }{2},0\right)$, and that x(t) leads y(t) if they are out-of-phase, i.e. if ${\varphi }_{\text{xy}}\in \left(-\pi ,-\frac{\pi }{2}\right)$.

3. Data and results

3.1. Data

Our underlying data are daily local-currency stock prices in the four major oil-producing and consuming countries, the Goldman Sachs commodity index (S&P GSCI),8 the U.S. Geopolitical Risk (GPR) index,9 the U.S. Economic Policy Uncertainty (EPU) index,10 and the U.S. Equity Market-related Uncertainty (EMU) index11 and, in line with Goodell and Goutte (2020), the daily confirmed COVID-19 deaths (to proxy for the COVID-19 medical shock).12 The stock and commodity indices data were collected from Bloomberg13 and cover the period January 4, 2010 to May 6, 2020 (a total of 2697 observations); the daily confirmed COVID-19 deaths cover the period December 31, 2019 to May 6, 2020 (a total of 92 observations). Apart from the uncertainty indices and the daily confirmed deaths, all the variables are expressed as the first differences of their natural logarithms.

3.2. Spillover analysis

Table 1 shows that the value of the total return spillover index is 47.3%. This value indicates that on average and across the entire sample, almost half of the return forecast error variance in all the markets considered comes from spillovers, signaling the huge interdependence among them. While total spillovers are quite high over the entire sample period, directional spillovers display different intensities. For example, shocks to the U.S. stock market returns are responsible for 22.8% of the error variance in 10-day forecasts of Canadian returns, and are responsible for 18.3% of the error variance in forecasts of European returns.

Table 1.

Spillovers from stock market return (j) to stock market return (i).

To (i)	From (j)								From Others
	US	SA	RU	CN	CH	EU	IN	COM
US	37	2.5	6.3	23.6	1.3	17.2	5.8	6.3	63
SA	5.5	73	2.5	5.3	1.1	6	3.5	3.2	27
RU	9.6	1.3	51.4	9.8	1.7	14.4	5.5	6.2	48.6
CN	22.8	2.7	6.4	36.6	1.4	15.4	6.9	7.7	63.4
CH	4.4	1.1	3	3.9	75.7	4.9	4.2	2.8	24.3
EU	18.3	2.8	10.4	16.3	1.8	37.3	7.5	5.7	62.7
IN	10.3	2.6	6.2	10.7	3	11.2	53.4	2.6	46.6
COM	9.8	1.8	6.7	12.2	1.7	8.4	2.4	57	43
Contr. to others	80.6	14.8	41.5	81.8	12	77.5	35.8	34.5	Spillover index
Contr. incl. own	117.6	87.8	92.9	118.4	87.7	114.9	89.2	91.6	(378.5/800.1)
Net spillovers	17.6	–12.2	–7.1	18.4	–12.3	14.8	–10.8	–8.5	47.3%

Notes: Table 1 reports the total spillover index and its “input-output” decomposition for the entire sample. Its (i,j)-th elements are the estimated contributions to the forecast error variance components of the stock market return i coming from shocks to the stock market return j. The total spillover index for returns, reported in the bottom right of Table 1, is the off-diagonal column (or row) sum relative to the column (or row) sum including diagonals, expressed as a percentage. Therefore, while the off-diagonal row sums (labeled from others) or column sums (labeled contr. to others) when totaled across markets, give the numerator of the spillover index, the column sums including diagonals (labelled contr. incl. own) when totaled, give the denominator of the index.

Similarly, the directional spillovers “contribution to others” row shows that these spillovers from each of the considered markets tend to be grouped according to the country's level of development. In the case of net spillovers which is the difference between “to” and “from” directional spillovers, there are significant differences based on the country's level of development. While the stock markets of developed countries tend to influence rather than to be influenced by other markets (positive net spillover), the stock markets of developing countries tend to be influenced by rather than to influence other markets (negative net spillover). Also, the results show that Chinese and Saudi Arabian stock markets are weakly integrated into the world market.

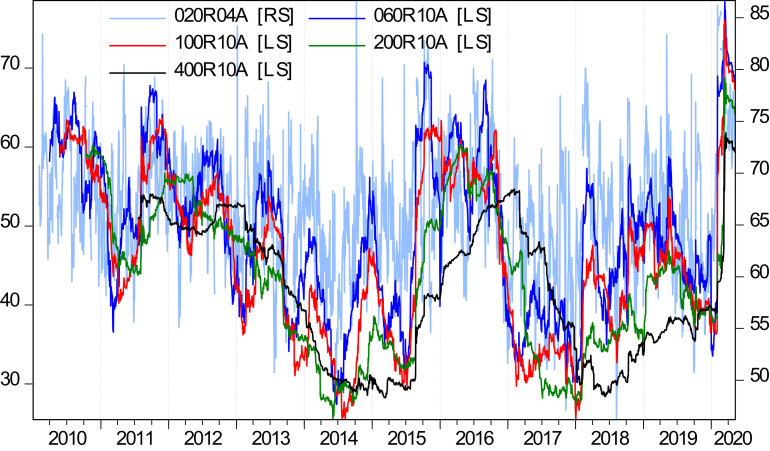
Fig. 2 presents the returns spillover plot. Although it is mainly time-varying, the spillover dynamics highlight that interactions between markets become even more intense in times of stress. The high level of spillovers that persisted until mid-2010 could be due, at least in part, to the Gulf of Mexico oil spill caused by an explosion on the Deepwater Horizon oil rig. The spillovers increase observed in 2011 is likely attributable to the uncertain environment especially related to the oil market, induced by the 2011 Arab Spring and subsequent geopolitical turbulence in the MENA region. The spillover peak recorded in 2015 is most likely explained by the collapse of the oil price which fluctuated around $50 a barrel. Given that the first confirmed COVID-19 case was reported by the Chinese authorities to the World Health Organization on December 31st, 2019, why did spillovers not exhibit a spike until the end of January 2020? According to Ramelli and Wagner (2020) and Ozili and Arun (2020), investors did not initially consider the risk of leakage of the COVID-19 outbreak beyond China too seriously. However, after January 20, when the Chinese authorities warned that SARS-CoV-2 could be transmissible between humans, attention to this virus increased dramatically.14

Fig. 2.

Spillover plot. Notes: RS – right scale; LS – left scale. To check robustness, the drifting spillover indices were estimated using different rolling windows (20, 60, 100, 200 and 400 days) and different forecast horizons (5, 10 and 15 days ahead). Results not reported here are available upon request.

3.2. Wavelet analysis

In this step, we apply the coherence methodology to accurately assess how the dependence between the time-varying spillovers and a set of uncertainty indices evolved over time and across frequencies.

Fig. 3 plots the estimated wavelet squared coherences15 , and the phase differences between the spillovers and each of the uncertainty indices. The color code for wavelet coherencies ranges from blue (weak co-movements: R²(u,s) close to 0) to red (strong co-movements: R²(u,s) close to 1). The wavelet coherencies between the spillover index and each of the uncertainty indices reveal broadly similar dependency patterns over the entire period and across the different frequencies which suggests that these co-movements are stable over time. As expected, the high coherencies apply to the entire sample period at high frequencies which highlights a significant contagion effect on the high speed of propagation between the spillover index and each of the uncertainty indices (Gallegati, 2012; Ranta, 2013). Additionally, the co-movement between the spillover index and the daily confirmed COVID-19 deaths is particularly strong (mostly yellow) and significant at high frequencies (1-2 days), and low (blue time-frequency areas) elsewhere. The phase-differences highlight a consistent positive co-movement between the spillovers and COVID-19, with COVID-19 leading the spillover index.

4. Conclusion

This paper employed two complementary co-movement measures to examine the effect of COVID-19 pandemic developments on shaping recent stock behavior. It makes two contributions to the nascent literature on the impact of COVID-19 on financial markets. First, it is one of the first papers to consider the impact of COVID-19 on financial markets by examining the contagion effect. Second, it uses recent and rich data to conduct an original statistical analysis of the impact of the COVID-19 pandemic on stock market behavior. Our results show that half of the return forecast error variance in all the markets considered comes from spillovers which demonstrates their high level of interdependence. The COVID-19 pandemic generated volatility spillovers from January 2020 to the end of the observed period and we show that the co-movement between the spillover index and the daily confirmed COVID-19 deaths is particularly strong and significant at high frequencies and vice versa at low frequencies. The phase differences highlight a consistent positive co-movement between spillovers and COVID-19, with COVID-19 leading the spillover index.

COVID-19 is having a significant impact on financial markets. Since its effects on health look likely to continue in the near future, our work needs to be extended to check the robustness of the present results to a longer period of observation. At the same time and since aggregate analyses may hide some heterogeneities between (and within) financial markets, our work could be extended by applying firm-level data.

Authors statement

With the re-submission of this manuscript we would like to undertake that:

All authors of this research paper have directly participated in the planning, execution and analysis of this study;

The contents of this manuscript have not been copyrighted or published previously;

The contents of this manuscript are not now under consideration for publication;

Our respective Institutes are fully aware of this submission.

Appendix 1. See below

Table 1.A.

Table 1.A.

Components of the S&P GSCI index.

Sub-index		Weights	Included Commodities
Energy		61.67%	Crude oil and Natural Gas
Non-energy	Agriculture	15.89%	Wheat, Corn, Soybeans, Coffee, Sugar, Cacao and Cotton
	Livestock	7.25%	Lean Hogs, Live Cattle and Feeder Cattle
	Industrial Metals	10.65%	Aluminum, Copper, Lead, Nickel and Zinc
	Precious Metals	4.5%	Gold and Silver

Notes: Weights as of May 7, 2020.

Source: www.spindices.com/documents/methodologies/methodology-sp-gsci.pdf.