VALIDATION OF RESTING ENERGY EXPENDITURE EQUATIONS IN OLDER ADULTS WITH OBESITY

Abstract

It is unclear which energy expenditure prediction equation should guide weight loss interventions in older adults with obesity. We ascertained the validity of four equations commonly used in practice in a series of weight loss studies of adults aged ≥65 with a body mass index ≥30kg/m² using indirect calorimetry data. Diagnostic accuracy was defined as <10% discrepancy between predicted and measured resting metabolic rate (RMR). Mean was 73.4 years. RMR using the ReeVue was 1,643 kCal. With 59.0% accuracy, the WHO equation demonstrated the highest accuracy while the Harris-Benedict yielded 53.5% accuracy. The Owens equation demonstrated the least variability (21.5% overprediction, 27.8% underprediction) with 50.7% accuracy. A SECA bioimpedance analyzer noted the second lowest accuracy of 49.6%. Only 43.1% of measurements were within 10% of the gold-standard indirect calorimetry value using the Mifflin equation. All equations demonstrated <60% accuracy suggesting a great need for estimating energy needs.

INTRODUCTION

Basal metabolic rate (BMR), or the minimum amount of energy needed to sustain basic metabolic function, constitutes the largest proportion of an individual’s metabolic needs, making established prediction equations important in ascertaining energy requirements.¹ The conditions required to measure BMR are often prohibitively restrictive, so resting metabolic rate (RMR) or resting energy expenditure (REE), the amount of energy burned by the body at rest, can be used as a close proxy. Calculations of energy needs are often applied in the hospital setting to ensure nutritional needs are being met adequately², but are also equally important in those requiring tube feeds³ or parenteral nutrition.⁴ In ambulatory settings, equations can also be applied during weight loss efforts to estimate the patient’s energy expenditure.⁵ Calculation of energy needs permit creation of dietary plans and caloric intake recommendations⁶ to induce net negative energy balance that can promote weight loss.

Indirect calorimetry is considered the gold standard for calculating RMR⁷; however, it is time consuming, requires specialized equipment, and is impractical in most clinical and low-resource settings with few specialized nutritional personnel. Different equations, including the Harris-Benedict⁸, Mifflin⁹, Owen^10,11, and one developed by the World Health Organization¹², derive estimates of RMR by incorporating different anthropometric and clinically available variables. In patients with obesity, the Mifflin equation has been shown to be the most accurate^13,14. However, it exhibits the greatest degree of bias¹⁵ in older adults. The Harris-Benedict equation has been shown to be within 10% of the measured RMR over 60% of the time, as opposed to the WHO, Owen, and Mifflin equations¹⁵. A systematic review by Cioffi et al suggested that the Mifflin equation had the least overall bias in older subjects at the group level, but that the Harris-Benedict equation was more accurate on an individual level.¹⁶

Changes in body composition, including lean, fat and visceral mass, that occur with aging negatively impact the sensitivity of traditional nutritional measures such as body mass index¹⁷. In fact, with increasing age, the contribution of skeletal muscle mass to total body weight decreases by as much as 50%.¹⁸ Additionally fat distribution changes, with increased deposition in the muscle and liver. As metabolic rate is impacted by age¹⁹ and obesity²⁰, it is unclear whether clinicians can assume that such equations are still valid in these subgroups. Inaccuracies of modest numbers of daily calories may cumulatively lead to unintended weight gain or loss.^21,22 RMR typically falls with age²³, further highlighting the importance of the accuracy of these equations, as weight gain may compound existing mobility impairments predisposing patients to long-term disability and morbidity²⁴. For those attempting to lose weight, greater satisfaction is associated with amount of weight lost.²⁵, Thus, inaccurate estimates could lead to greater frustration if energy needs are overestimated which can lead to an inability to lose excess weight. While some studies have evaluated the validity of these equations in older adults, others have done so only in individuals with obesity. There is a dearth of literature on the intersection of these two subgroups despite their public health significance. To address this gap, we assessed the validity of the four most commonly used equations in clinical practice using data from previously collected clinical trials in older adults with obesity.

MATERIALS AND METHODS:

Study Setting and Participants

Participants were recruited from two weight loss studies of older adults conducted in a rural region of New Hampshire and Vermont. The study population and setting have been previously described in detail.^26,27 For this study, older adults aged >65 years, with a body mass index >30kg/m² that participated and consented in two studies of three- and six-month duration, consisting of a dietary and exercise health promotion intervention were included in the analysis. We identified participants from these trials that had primary data measures to conduct our analysis which included those who dropped out of the intervention, as outlined below. Our purpose of this analysis was not to evaluate the change of a weight loss intervention on resting energy expenditure but was to ascertain validity of the equations based on available data. Individual person-level pre/post data on 85 unique participants was evaluated, for a total of 144 measurements. The study was approved by the Dartmouth-Hitchcock institutional Review Board (28905), and the University of North Carolina at Chapel Hill Institutional Review Board (20–2541).

Measured Indirect Calorimetry (Gold Standard)

Measured RMR was obtained using the ReeVue indirect calorimeter from Korr Medical Technologies, Inc. (Korr Technologies, Salt Lake City, UT). Patients were instructed to abstain from exercise on the day of the test and abstain from eating for at least eight hours prior to measurement of RMR (overnight fast). Before beginning the test, a plastic clip was placed on the patient’s nose to ensure that all exhaled breath was routed into a mouthpiece, which the patient held between their lips. The mouthpiece was connected to the MetaBreather tubing, which in turn was attached to the ReeVue. The test duration lasted approximately ten minutes to achieve steady-state. During this time, concentration of expired oxygen using a galvanic fuel cell oxygen sensor and tidal volume (mL) using a fixed orifice differential pressure pneumotach air flow sensor was measured. The volume of oxygen consumed as represented by VO₂ (mL/min) was calculated using the measured tidal volume, concentration of expired oxygen, and a correction factor derived from the humidity, atmospheric pressure, and temperature as sensed by the machine. The ReeVue then used a conversion factor of 4.813 calories/mL O₂ consumed to calculate the kcal/day of resting energy expenditure (REE). The ReeVue has been validated against the Deltatrac metabolic cart, a traditional indirect calorimeter which uses both O₂ and CO₂ concentration to measure REE in younger adults.²⁸ In a regression analysis, the two devices were found to have an R² of 0.975.²⁹

Predicted REE

Four commonly used resting energy expenditure equations, Harris-Benedict, Mifflin, Owens, and the World Health Organization/Food and Agriculture Organization/United Nations University (WHO), were evaluated against the measured RMR. Their variables and validity based on a younger adult population³⁰ are reported in Table 1. The Harris-Benedict equation was developed in 1918 based on a study of 136 men and 103 women and derived using regression formulas³¹, and it has been validated to individuals with the following characteristics: weight 25.0–124.9 kg, height 151–200 cm, and age 21–70 years. Mifflin et al derived a new equation in 1990 from a study of 498 subjects (247 females, 251 males) aged 19–78 years (mean 45±14), with BMIs ranging from normal to obese⁹. In 1986, Owen et al studied 44 healthy, lean and women with obesity in order to derive a new prediction equation. The ages of these women ranged from 18–65 years with body weights from 43–143kg.^10,11 Owen et al also conducted a reappraisal the following year of 60 healthy, lean and men with obesity, age range 18–82 years, weighing 60–181kg.^10,11 A 1985 report by the World Health Organization examined in depth the energy and nutritional needs of humans³². In this work, these authors derived RMR equations for different age groups, including the 60+ population. An additional measure of REE was obtained via the SECA bioimpedance analyzer which uses a proprietary equation.

Table 1:

Resting Metabolic Rate Prediction Equations

Equation Name	Sex	Equation	Accurate Predictions within ± 5% based on Previous Literature
Harris-Benedict	Female	RMR= 655.0955 + (9.5634 × Weight) + (1.8496 × Height) − (4.6756 × Age)	35.7%
	Male	RMR= 66.473 + (13.7516 × Weight) + (5.0033 × Height) − (6.7550 × Age)
Mifflin	Female	RMR = (9.99 × Weight) + (6.25 × Height) − (4.92 × Age) − 161	21.4%
	Male	RMR = (9.99 × Weight) + (6.25 × Height) − (4.92 × Age) + 5
Owen	Female	REE = Weight × 7.18 + 795	32.1%
	Male	REE = Weight × 10.2 + 879
WHO	Female	REE = Weight × 10.5 + 596	39.3%
	Male	REE = Weight × 13.5 + 487

Height measured in cm, age measured in years, weight measured in kg

Abbreviations: REE – Resting Energy Expenditure; RMR – Resting Metabolic Rate

Body Composition & Anthropometry

The SECA mCBA (Hamburg, Germany) is a non-invasive diagnostic tool that measures percent fat mass, fat-free mass, lean muscle mass and total body water using the 8-point method.³³ The scan begins with entering a person’s body height and weight into the apparatus. One’s shoes and socks must be removed in order to make contact with the pair of foot electrodes. The three pairs of hand electrodes are attached at different heights depending on the subject’s height (valid for a range of 1.6–2.0 m). Participants report an approximate level of physical activity which is also entered into the apparatus. The scan is performed by running a flow of low alternating current on each side of the body through the attached electrodes.

Participant height and weight were assessed by a trained research assistant. Height was measured (in cm) using a SECA stadiometer, with shoes off, back and feet against the wall, with the top of the device abutting the crown of their head. Weight was assessed (in kg) using an A+D digital scale, with shoes off and only pants and a shirt permitted.

Statistical Analysis

All continuous values are represented as means ± standard deviations or counts (%). A t-test assessed differences between both males and females, and between the measured gold standard ReeVue REE, and each of the individual equations. Percent difference was calculated as the quotient of the difference between the equation and the gold standard, and the gold standard itself. The maximum overestimation/minimum underestimation was calculated as the difference between the ReeVue gold standard value and the value generated from the question. Percent over/under-estimation was determined as the quotient of this difference and the gold standard. A spearman correlation coefficient evaluated the values between the gold standard and the specific equation. Bland-Altman plots compared each RMR estimate to measured indirect calorimetry wherein the limits of agreement are defined as two standard deviations of the difference between estimated and measured RMR.³⁴ Prediction bias was calculated as the difference between measured indirect calorimetry and estimated RMR. Equation accuracy was categorized if the equation was within ±10% of the indirect calorimetry equation. A p-value <0.05 was considered statistically significant. Data analysis was conducted with Microsoft Office 365 (Seattle, WA) and R (www.r-project.org).

RESULTS

Of the 73 unique participants, data points were available on forty males and 104 females, of whom all were white. Baseline characteristics are presented in Table 2. Average age was 74.4±5.1 and 73.1 ±4.5 years, BMI was 35.4 ±5.9 and 36.7 ±5.4 kg/m², and percent body fat was 35.4 ±5.9% and 50.3 ±4.1% for men and women, respectively. The mean RMR of the sample as determined by ReeVue indirect calorimetry was 1,643±396 kcal/day (Table 3). The mean, as estimated by each equation, was similar to the ReeVue mean (p>0.05) with the exception of Mifflin equation (p<0.001) and the value generated by SECA. There was, however, markedly more variability in the ReeVue values (standard deviation 396) versus those estimated by the equations where it ranged from 245 to 279. The discrepancy was particularly large on the lower end, with a minimum RMR of 617 as measured by ReeVue, as compared with calculated minimums which ranged from 1,100 (Mifflin) to 1,323 (WHO). Eight out of the 144 study participants had measured RMRs which were less than 1000. In six participants, RMR was overestimated between 60–100% by each of the five equations. Owen, Harris-Benedict, and the WHO formulae had the lowest % difference as compared to the gold standard.

Table 2:

Baseline Characteristics of Data Points Used (n=144)

	Males	Females	p-value
	n=40	n=104
Age, years	74.4 ±5.1	73.1 ±4.5	0.16
Weight, kg	106.4 ±19.4	93.0 ±15.5	<0.001
Height, cm	173.2 ±8.4	159.2 ±6.3	<0.001
White Race	40 (100%)	104 (100%)	—
BMI, kg/m 2	35.4 ±5.9	36.7 ±5.4	0.25
Waist Circumference, cm	119.1 ±13.4	114.5 ±30.8	0.21
Hip Circumference, cm	121.9 ±11.8	124.6 ±11.0	0.21
Waist-Hip Ratio	0.98 ±0.07	0.92 ±0.22	0.02
% Body Fat	39.2 ±6.8	50.3 ±4.1	<0.001
% Fat Free Mass	60.8 ±6.8	49.7 ±4.1	<0.001

Values reported as means +/− standard deviation or counts (%). P-values reported are the differences between sexes

Abbreviations: BMI – Body Mass Index; REE – Resting Energy Expenditure

Table 3:

Comparison of Indirect Calorimetry to Established Resting Energy Expenditure Equations

	Resting Energy Expenditure (kcal/day)		% Difference*	p-value	MUE (kcal/day)	MOE (kcal/day)	r
	Mean ± SD	Range
Indirect Calorimetry	1,643.3 ±395.9	619, 2,794	---	---	---	---	—
Equation
Harris-Benedict	1,610.0 ±278.5	1,232.1, 2,578.2	1.4%	0.41	-915.0	724.4	0.78
Mifflin	1,509.3 ±261.7	1,100.4, 2,289.9	−5.1%	<0.001	−1033.3	695.7	0.78
Owens	1,602.1 ±265.1	1,292.0, 2,415.1	1.2%	0.30	−821.3	919.7	0.75
WHO/FAU/UNU	1,670.0 ±249.9	1,322.8, 2,520.0	5.6%	0.49	−859.4	801.6	0.78
SECA	1,595.8 ±244.9	1,276, 2,703	1.4%	<0.001	−941	889	0.72

All values are represented as means ± standard deviation, range, or % difference

^*represents the difference between the gold standard (indirect calorimetry using ReeVue) and the equation used.

r – correlation coefficient

Abbreviations: MUE – Minimum Underestimation of Indirect vs. Equation; MOE – Maximum Overestimation of Indirect vs. Equation;WHO – World Health Organization; FAU – Food and Agriculture Organization of the United Nations; UNU – United Nations University

The Mifflin equation also had a strong tendency to under-predict RMR, with a prediction bias of 548 (Table 4). The other equations did not have as high of a prediction bias (Harris-Benedict: 36; Owen 41; WHO 27; SECA 40 kCal). Bland-Altman plots revealed proportional bias in all four of the other equations (Figure 1). When mean BMR was <1500 kCal, the Harris-Benedict, Owen, WHO, and SECA equations all tended to over-predict. When mean RMR was >2000 kCal, the equations each tended to under-predict. The WHO equation was the most consistent in estimating RMR within 10% of the ReeVue values, although it still failed to do so 40% of the time. The Harris-Benedict, Owen, and SECA were accurate in 54%, 51%, and 50% of the time respectively. Mifflin’s accuracy was the lowest (43%), under-predicting by >10% nearly half the time (44%).

Table 4:

Prediction Bias and Accuracy of Established Resting Energy Expenditure Equations

	Prediction Bias	±2 SD LOA	Accurate	Overpredicted	Underpredicted
Indirect Calorimetry	—	—	—	—	—
Harris-Benedict	35.8	491.4	53.5%	19.4%	27.1%
Mifflin	548.5	489.2	43.1%	12.5%	44.4%
Owens	41.2	520.3	50.7%	21.5%	27.8%
WHO/FAU/UNU	-26.7	496.3	59.0%	25.0%	16.0%
SECA	40.3	537.4	49.6%	20.9%	29.5%

Overpredicted resting metabolic rate values were defined as 10% of the value obtained from indirect calorimetry. Underpredicted resting metabolic rate values were defined as 10% of the value obtained from indirect calorimetry

Abbreviations: LOA – limits of agreement; SD – standard deviation; WHO – World Health Organization; FAU – Food and Agriculture Organization of the United Nations; UNU – United Nations University

Figure 1: Bland-Altman Plots Comparing the Indirect Calorimetry (ReeVue) and Prediction Equations listed in Table 2.

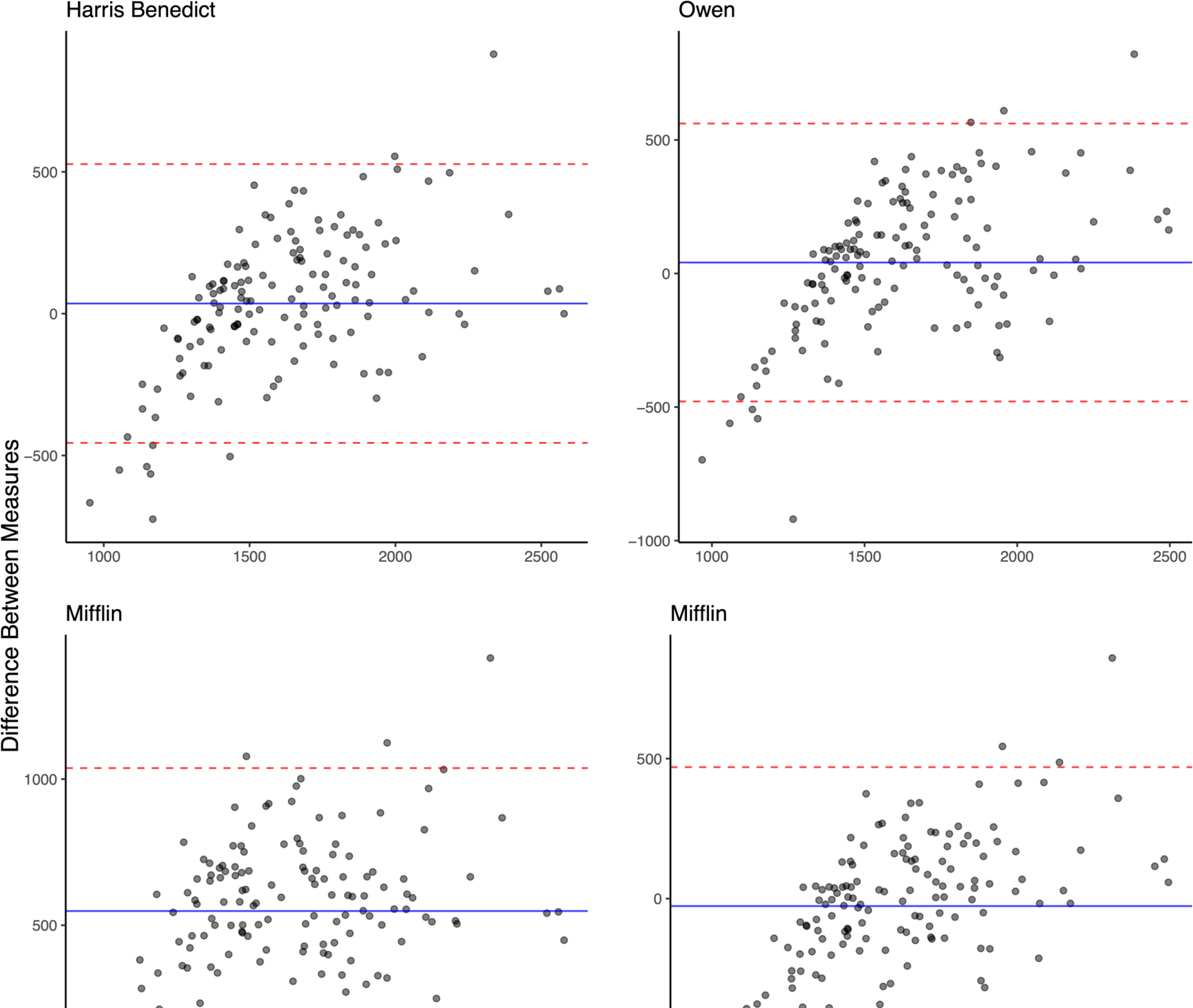
Bland-Altman plots were created by plotting the difference between the gold standard and the equation (y-axis) versus the average of both values (x-axis) for each of the five equations that were evaluated. Values on both axises are in kilocalories/day. The dotted line represents the limits of agreement (±2 standard deviations). All estimated values demonstrate bias particularly at lower levels. The positive trend of each plot suggests systematic error at low and high values wherein low values underestimate and higher values tend of overestimate ReeVue.

DISCUSSION

Our findings demonstrated that the WHO equation fared best in a population of older adults with obesity, but the Owen equation demonstrated the least under/over prediction variability in this population. In fact, none of the four equations we tested were consistently able to accurately estimate RMR in an older population with obesity with accuracy levels ≤60%. Even with a relatively modest RMR of 1000 kcal/day, a ten percent error would amount to 100 kcal/day or roughly one pound per month. These findings suggest the importance of a contact need in developing an equation that provides high diagnostic accuracy in older adults with obesity.

The WHO equation performed best in our cohort of older adults with obesity, but still failed to estimate patients BMR within 10%, forty-one percent of the time. The Mifflin equation had a prediction bias of 584, meaning that on average, it under predicted by 584 kcal/day in this population. If we use the common estimate of 3,500 calories per pound, 500 extra calories per day over seven days equates to one pound per week. For patients attempting the common target of losing a pound per week, this would completely negate any progress. For those attempting to maintain their weight, they could gain as much as fifty pounds in one year. While metabolic adaptation may prevent this from occurring³⁵, it behooves researchers to develop equations in the future that better estimate energy requirements in this at-risk population.

Part of the study population had measured RMR far below the predicted values, which may have impacted the equations’ ability to produce accurate estimates. While our measuring techniques were standardized, measurement error can potentially impact our results. These findings suggest the need for prediction equations with lower thresholds. Importantly, clinicians and researchers alike should be cautious of estimated caloric intake both at low and high values. Further research is needed to better identify these patients and produce more accurate models to estimate their energy needs.

Other studies have focused primarily either on adults with obesity or older adults separately. There have been discrepancies between the results of studies in the two populations with regards to the accuracy of the Mifflin equation. It performed among the best in patients with obesity but worst with older adults^13,15,36. Our results were consistent with the latter, as the Mifflin equation had both the lowest percent accuracy, where only 43% of patients estimated RMR was within 10% of the measured value, as well as the largest prediction bias of 548. Our findings suggest that with advanced age, the Mifflin tends to under-predict even in those with obesity. Potential areas of further investigation include examining the correlation between age and the accuracy of the Mifflin equation in more depth, to evaluate whether the degree of bias becomes more pronounced as age increases. Hasson et al did stratify patients by age and found that Mifflin under-predicted in their oldest category 50–60 year old³⁷, however it is unclear whether that trend becomes more pronounced with patients in their 60s versus 70s versus 80s. The Harris-Benedict was found to be most accurate in older adults by Siervo et al¹⁵. In our study, it performed reasonably well and may still be acceptable to use in older adults with obesity with an accuracy of 53.5%. It had the second smallest prediction bias of 36 and the second highest portion of patients accurate within ten percent. Still, it failed to estimate RMR within ten percent nearly half the time, reinforcing the need for better prediction models.

Importantly, our analysis was not meant to ascertain the impact of weight loss on resting energy expenditure. While participants did lose weight and may impact REE as a result of metabolic adaptation, the goal was to determine whether certain variables could impact the validity of the equations independent of the degree of weight loss – strictly looking at measurements within a demographic group that is often excluded in clinical trials. Still metabolic adaptation could be one factor which contributes to the inadequate performance of all of the equations this study evaluated. The variables in all four equations were limited to weight, height, and age,^{8,10,11,31,32} none of which would factor in changes due to metabolic adaptation.

There were some limitations of this study. Our population’s demographic characteristics focused on rural participants which could limit generalizability. Our values used were based on a population that was entirely white, reflecting the demographics of our region and hence, generalization to other ethnic/racial groups should be made with caution. Future research may center on other geographic areas or more racially diverse study populations. Additionally, this study was not sufficiently powered to allow multivariate analysis and our analysis was limited to a validity study. It would be worthwhile to repeat the study with a larger sample to permit stratification by sex. There is a strong likelihood that some models may be more accurate for men and others for women. In their investigation of patients with and without obesity, others found that the Harris-Benedict equation was valid for women of all BMIs, but tended to under-predict for men³⁶. Furthermore, we used the REEVue as our gold-standard in contrast to other methods with greater accuracy and validity. While we recognize the REEVue’s measurement has been challenged in the past,³⁸ this apparatus is more practical and scalable than others, including metabolic chambers or doubly-labeled water. Lastly, using newer analytical methods, such as machine learning could much improve the accuracy of calculating RMR.

This study addresses a gap in the current literature by evaluating the validity of REE equations that are commonly used in clinical practice in a specific population - older adults with obesity. These equations have been previously validated in older adults and in those with obesity, but not in the intersection between these two groups. This study highlights the need for better pragmatic clinical techniques to estimate RMR in older adults with obesity. A key first step would be identifying the populations whose RMR was not adequately estimated by the existing equations and determine if there are common variables that could be incorporated into future models. There may be additional variables that can be identified with further research in order to improve the predictive abilities of the current RMR equations. For example, thyroid function is closely correlated to RMR³⁹, and thyroid stimulating hormone and free T₄ are laboratory measures that are inexpensive and easily obtainable. Future research can also potentially evaluate the impact of body composition or hydration status on such equations. Admittedly, these types of equations are limited by the assumption that all calories are metabolized equally. This is likely not entirely accurate although some of these discrepancies may be accounted for by differences in TEE.⁴⁰ Evaluating the incremental improvement in the diagnostic accuracy of REE may require an adjustment to existing equations; in addition, their cost-effectiveness would need to be ascertained. In the interim, our findings suggest that equations may not provide reasonable substitutes for measurement by calorimetry if accuracy is required. Overall, our research highlights the gaps and areas of improvement in the RMR equations when applied to an increasingly important population, older adults with obesity. We caution clinicians in fully relying on such equations.

Older adults with obesity make up a growing part of the population that has not been adequately evaluated. Maintaining weight homeostasis has considerable value to prevent disability. Hence an equation that can easily be integrated into the health system and EMR to readily assess expenditure is key to helping providers create more individualized treatment plans. Yet, their reliability needs to be established to surmount the existing shortcomings.

ABBREVIATIONS:

BMI

body mass index

BMR

basal metabolic rate

RMR

resting metabolic rate

REE

resting energy expenditure

Biographies

Rachel Griffith is an internal medicine resident (primary care track) at Dartmouth-Hitchcock Medical Center. She has an interest in nutrition in older adults

Ryan Shean is an undergraduate student at Dartmouth College with an interest in clinical research.

Curtis Petersen is a recent graduate from the Dartmouth Institute for Health Policy and Clinical Practice. He has a Masters of Public Health and Science and has extensive data analytical experience.

Rima Al-Nimr is a registered dietitian and nutritionist at the Geisel School of Medicine at Dartmouth. She is a research dietitian and has extensive experience in conducting clinical trials in older adults.

Tyler Gooding and Meredith Roderka are both research assistants at Dartmouth-Hitchcock Medical Center.

JOHN A. BATSIS, MD, FACP, FTOS, AGSF, FGSA is an Associate Professor at the University of North Carolina at Chapel Hill in the Division of Geriatric Medicine, School of Medicine, with a joint appointment in the Department of Nutrition in the Gillings School of Global Public Health, in Chapel Hill, NC. Dr. Batsis provides clinical care in the outpatient and nursing home setting to older adults with multimorbidity and frailty. He is a fellow of the American College of Physicians, American Geriatrics Society, Gerontological Society of America, and the Obesity Society

Dr. Batsis is board certified in Internal Medicine, Geriatrics and Obesity Medicine. He received his Medical Degree with Honors from the University of Dublin, Trinity College, in Dublin, Ireland, and completed a medical-surgical internship in Dublin at St. James’ Hospital. He completed his residency training in Internal Medicine and fellowship in Geriatrics at the Mayo Clinic College of Medicine. He also holds a Certificate in Translational Science Activities from the Mayo Graduate School of Medical Education.

Dr. Batsis’ research explores the association of obesity, sarcopenia and impaired function in older adults and has 130 peer reviewed publications. He is funded by the National Institute on Aging (National Institutes of Health) for projects focusing on strategies of improving Wellness in Older Adults with Obesity using mobile health technologies in rural areas. He is actively involved in developing, testing and implementing novel mobile health based technologies (including remote monitoring and video-conferencing) in patient populations. He has received a number of clinical and research accolades and is an active member on the Research Committees of the Gerontological Society of America and the American Geriatrics Society, and the Clinical Committee of The Obesity Society