How do government subsidies promote new energy vehicle diffusion in the complex network context? A three-stage evolutionary game model

Abstract

In order to cope with the impact of current coronavirus disease 2019 (COVID-19), the continued extension of financial subsidy period for new energy vehicles at the national level is a strong measure to support the sustainable development of new energy vehicle (NEV) industry. This paper further explores the promotion impact of government subsidies on NEV diffusion, and establishes a three-stage evolutionary game model. Based on the actual application, the NEV diffusion process is simulated in four kinds of authoritative networks. Results show that: (1) in the scale-free network, the subsidy rate must be high enough to promote full NEV diffusion, and the larger the network scale, the higher the threshold of subsidy rate; (2) in the small-world network, the larger the network scale, the more beneficial it is for full NEV diffusion; (3) for the small-scale network, topological characteristics have little effect on NEV diffusion depth, and only affect the speed when NEV diffusion reaches the stable state; (4) for the large-scale network, NEV diffusion in the scale-free network is more sensitive to the subsidy rate than that in the small-world network; (5) network topologies influencing NEV diffusion can be divided into two priorities. Finally, relevant policy recommendations are presented.

Nomenclature

Sets and indices

$i=\left\{\mathrm{1,2}\right\}$

the individuals from Group 1 and 2

$G\left(V,E\right)$

the NEV diffusion network

$G_1\left(V,E\right)$

the NEV diffusion network with scale-free characteristics

$G_2\left(V,E\right)$

the NEV diffusion network with small-world characteristics

$V$

all nodes in the NEV diffusion network

$E$

all edges in the NEV diffusion network

NN

Strategy combination NEV-NEV

NF

Strategy combination NEV-FV

FN

Strategy combination FV-NEV

FF

Strategy combination FV-FV

$S^{\ast },S$

the strategy $S^{\ast }$ and $S$

$\Phi$

the payoff function

$m,n,l$

the node $m$, $n$ and $l$

Parameters

$M$

the number of auto manufacturers in the population

$P$

the market-clearing price

$a$

the basic price

$b$

the elasticity coefficient

$q_i$

the production volume of auto manufacturer $i$

$c_i$

the basic cost of auto manufacturer $i$ producing a NEV

$c_i^N$

the cost of auto manufacturer $i$ producing a NEV

$c_i^F$

the cost of auto manufacturer $i$ producing a FV

$s$

the subsidy rate

$F$

the government's penalty for FV manufacturers

$\delta$

the emission reduction rate of NEVs relative to FVs in the production process

$s_1,s_2$

two thresholds of the subsidy rate

$s_3$

the government's optimal subsidy rate under the decision criterion of NEV target output

$s_4$

the government's optimal subsidy rate under the decision criterion of NEV manufacturers target number

$q_0$

the NEV target output

$Q_0$

the target number of NEV manufacturers in the population

$M_1,M_2$

the numbers of individuals in Groups 1 and 2

${\Pi }_m$

probability of a newly added node connected to an existing node $m$ in scale-free network

$k_m,k_n$

the degree of nodes $m$ and $n$

$p$

probability of random reconnection in the small-world network

$p{r}_m,p{r}_n,p{r}_l$

the payoff of nodes $m,n,l$

$A_m,A_n$

the strategy choices of the node $m$ and $n$

$\tau \left(A_m\to A_n\right)$

probability of node $m$ imitating node $n$ strategy

$k$

the noise intensity of the external environment

${\gamma }_{m\to l}$

probability of node $m$ connecting to node $l$

$\beta$

the preference tendency

Variables

$x$

the proportion of auto manufacturers who choose NEV strategy in Group 1

$y$

the proportion of auto manufacturers who choose NEV strategy in Group 2

Acronyms

COVID-19

the epidemic of coronavirus disease 2019

NEV(s)

new energy vehicle(s)

IoT

Internet-of-Things

FV(s)

fossil vehicle(s)

EV(s)

electric vehicle(s)

PHEV(s)

plug-in hybrid electric vehicle(s)

FCEV(s)

fuel cell electric vehicle(s)

(I)EGT

(indirect) evolutionary game theory

GSCM

green supply chain management

ESS

evolutionary stable strategy

1. Introduction

In the face of the dual challenges of transportation energy and environmental issues, integrating electric vehicles, smart grids, and Internet-of-Things (IoT) technologies, using renewable energy resources towards green smart transportation will become the main direction of the future development of transportation field [1]. At present, the new energy vehicle (NEV) industry is developing rapidly around the world, especially in China. In 2018, China's production and sales of NEVs reached 1.271 million and 1.256 million respectively, up 60.0% and 61.7% year-on-year, and up 238.7% and 240.6% from 2009 [2]. However, affected by phasing out subsidies, the production and sales of NEVs in China in 2019 were 1.242 million and 1.206 million, down 2.2% and 4.0% year-on-year, which was the first year-on-year decline in the past decade [3] (see Fig. 1 ). To cope with the impact of the current epidemic of coronavirus disease 2019 (COVID-19), the continued extension of the financial subsidy period for NEVs at the national level is a strong measure to incentivize the sustainable development of NEV industry [4].

Fig. 1.

China's production and sales of NEVs from 2009 to 2019.

The government subsidies aim at promoting the choice and spread of NEV production strategies. This paper considers the NEVs including all electric vehicles (EVs), plug-in hybrid electric vehicles (PHEVs), and fuel cell electric vehicles (FCEVs). According to Rogers' classic definition for diffusion of innovation theory [5], this paper define NEV diffusion as the process in which NEV production strategies are spread among auto manufacturers over time through diffusion networks. Promoting NEV diffusion is the key to increase the market share of NEVs (technologies and products) [6]. However, in practice, the intensity of government subsidies has not brought us the expected effect in promoting NEV diffusion [7]. Therefore, it is urgent to prove the influence mechanism of government subsidies on NEV diffusion and whether subsidies can really achieve the desired effect, which is the theme and focus of this paper.

Compared with the hypothesis of perfect rationality in classical game theory, the hypothesis of bounded rationality in evolutionary game theory (EGT) has more practical significance. EGT is a used tool to solve multiple Nash equilibriums and population decision-making problems [8]. The NEV diffusion model based on EGT can effectively describe the evolution process of NEV diffusion and reveal its evolution law. However, with the rapid development of the Internet and IoT, many industries present typical complex network characteristics [6]. Due to different research perspectives and starting points, most of the existing NEV diffusion researches focus on the two-dimensional operation level and largely ignores the complex relationships among node enterprises in the diffusion network. The NEV diffusion network is a systematic topology abstraction connected by many node enterprises and has typical complex network characteristics. Considering the consistency of network characteristics between the complex network and NEV diffusion network, this paper builds the three-stage evolutionary game model and networked evolutionary dynamics model based on networked evolutionary game method. The purpose of this paper is to simulate the real influence of government subsidies on NEV diffusion in the actual network to the greatest extent, so as to make decisions on government regulation and enterprise operation.

The diffusion of NEV production strategies among auto manufacturers is a typical group dynamic decision-making problem, and the essence of subsidies involves periodical adjustments by government. How to promote the stable NEV diffusion and ease the fiscal pressure faced by government is the key issue of this paper. The paper helps to answer the following questions: (1) What are the influences of government subsidies on the development of the NEV industry? (2) How do the network topology and scale of the external diffusion network affect NEV diffusion: the diffusion depth vs. speed? (3) How to evaluate the priority levels of network characteristics that affect NEV diffusion? (4) Which network structure exhibits optimum performance in NEV diffusion?

The NEV diffusion mechanism includes the choice of NEV production strategies within auto manufacturers, government subsidy policies and other external drivers, and external diffusion networks. By means of the networked evolutionary game, this paper considers the dynamics and complexity of the system and the bounded rationality of the players. The main contributions of this paper are as follows: (1) A three-stage evolutionary game theoretical model for NEV diffusion is developed. (2) The NEV diffusion process is simulated in four kinds of authoritative networks constructed at the present stage. (3) The influence of government subsidies on NEV diffusion in different topology characteristics and scale of the network is analyzed from the diffusion depth and speed. (4) Network topologies influencing NEV diffusion are divided into two priorities, and the network structure exhibiting the best performance in NEV diffusion is found.

The rest is structured as follows: Section 2 reviews relevant research. Sections 3 builds the three-stage evolutionary game theoretical model and networked evolutionary dynamics model. Moreover, the rules of network evolution dynamics are presented in Section 3. In Section 4, the NEV diffusion process is simulated in four authoritative networks, and the simulation results are analyzed from the diffusion depth and speed. Concludes, policy recommendations and limitations are given in Section 5.

2. Related literature

This paper considers that each node enterprise in the auto manufacturer population is faced with the choice of two production strategies, namely NEV production and FV production, which correspond to two low-carbon technologies with different unit production costs and emission reduction levels. The literature highly relevant to this study can be divided into the following two streams.

2.1. The impact of government subsidies on NEV diffusion

As NEV diffusion is faced with a multi-participant and complex environment, in order to understand its quantitative law scientifically, the influence of government subsidies and other external drivers on NEV diffusion should be analyzed first. For this research issue, scholars at home and abroad mainly focuses on the macro policy level and micro-operation level.

At the macro policy level, Thiel et al. [9] found that in the early stage of the development of the NEV industry, the high cost of R&D and batteries was the main factor restricting its development, and government's incentive policies could effectively solve the problem of high cost. Ma et al. [10] demonstrated that there was a positive co-integration relationship between the NEV market share and subsidies for NEVs. Sierzchula and Nemet [11] confirmed that a series of legislation and regulatory measures provided by the government of California in the United States, such as zero-emission vehicles, low-carbon fuel standard supervision and subsidies, are conducive to NEV diffusion. Zhang and Bai [12] examined the incentive policies from 2006 to 2016 and the NEV adoption from 2010 to 2020 in China, they indicated that government policies are the main driving force in terms of NEV adoption. Liu and Xiao [13] analyzed the development of China's EV industry under policy incentives through scenario analysis, and pointed out that the penetration of China's EV market is mainly dominated by national policies, especially financial supports. Santos and Rembalski [14] analyzed the total cost of ownership of petrol, diesel, hybrid electric vehicles, plug-in hybrid electric vehicles and battery electric vehicles in the UK over 2017–2029. They found that plug-in hybrid and battery electric vehicles need subsidies. Some scholars reviewed the influences of China's phasing out subsidies and dual credit policy on NEV diffusion [[15], [16], [17], [18]]. For example, Li et al. [17] considered both dual credit policy and subsidy policy. They found that the dual credit policy could significantly raise the amounts of new energy vehicles to two times as much as those of current subsidy level, and subsidy policy was not optimal. The research at the macro policy level can provide reference for governments in the decision-making process of NEV industry dynamics, but ignores the characteristics and differences between regions.

The micro-operation level involves the policy measures designed of promoting NEV diffusion among auto manufacturers. For example, Krass et al. [19] believed that different low-carbon technologies were different in terms of environmental efficiency, fixed cost, and variable cost, etc., and studied the influence of carbon tax policies and subsidy policies on guiding enterprises to choose low-carbon production strategies. Masiero et al. [20] used government support in the form of subsidies combined with effective strategies implemented by BYD to explain why this emerging industry had expanded successfully in China. Liu et al. [21] estimated the influence of governmental subsidies on the decision making of auto manufacturers and the development of EV industry. They found that the probability of auto manufacturers to produce EV is negatively correlated with the ceiling of subsidies. Chen and Hu [22] found that manufacturers' behavioral strategies are mainly affected by government policies, and examined manufacturers' behavioral strategies in response to subsidies and carbon taxes. Fan and Dong [7] through a case of NEV diffusion, discussed how the government selected subsidy strategy in low-carbon diffusion. Through theoretical models and empirical analysis, Ji et al. [23] confirmed that subsidy policy phase-outs can promote NEV diffusion and contribute to develop the NEV industry, and they obtained the optimal phase-out rate. Mo et al. [24] formulated duopoly competition between two non-cooperative heterogeneous ride-sourcing platforms considering the adoption of electric vehicles (EV) and government subsidies on EVs. Fang et al. [25] prove the advantages of the balanced dynamic subsidy and taxation policies on the promotion of electric charging infrastructures. From the existed studies, few researches focus on NEV diffusion considering the industry's network characteristics, and only Ref. [25] considers the competitive connections between the charging stations.

Considering that NEV production strategy spreads among auto manufacturers through diffusion networks, this paper further extends the two-dimensional level to the network level, and reveals the network evolution process and law of NEV diffusion, which will provide a new perspective to explain the impact of government subsidies on NEV diffusion.

2.2. The research methods of diffusion problem

Domestic and foreign scholars have used different theories and analytical methods to study the diffusion problem, including: (1) Innovation diffusion. Rogers [5] first proposed the concept of innovation diffusion in 1995. The traditional diffusion theory of innovation provides an important theoretical basis for related research of diffusion problem. For example, Jacobsson and Johnson [26], Kemp and Volpi [27] and Iyer et al. [28] respectively studied renewable energy diffusion, clean technology diffusion and low-carbon diffusion. (2) Empirical analysis. Some scholars have used empirical analysis methods to conduct pioneering research on the influencing factors of diffusion problem. Among them, Weyant [29] discussed the role of policy tools in promoting the development and diffusion of new energy technologies. West et al. [30] believed that public perception was the main obstacle to the development of renewable energy in England and several other European countries. Scholars also considered the influence of network embedding [31], technology interaction [32], carbon price [33,34], credit conditions [35] and other factors on diffusion problem. (3) Game theory. Some scholars incorporated influencing factors into the modeling system to conduct game analysis on the relationship among stakeholders in diffusion problem. Among them, Zhu and Dou [36] established an evolutionary game model between the government and core enterprises, and proposed that GSCM (green supply chain management) diffusion among core enterprises was affected by the costs and benefits of implementing GSCM, as well as government subsidies and penalties. Chen et al. [37] established an evolutionary game model between hospitals and patients. They believed that with government incentives, more hospitals would tend to provide mHealth. (4) System dynamics. Based on the system dynamics model, some scholars further reveal the complex relationship among stakeholders in diffusion problem. Jeon et al. [38] established a dynamics model of the energy subsidy system and applied the model to the Korean photovoltaic subsidy problem. Zhu et al. [39] studied the impact of government intervention on the diffusion of low-carbon production strategies with the help of system dynamics, and found that dynamic punishment or subsidies could promote the choice and spread of enterprises' low-carbon production strategies.

The existing research work is based on a variety of theories and methods to model, solve and analyze the diffusion problem, which provides a scientific methodological basis and guidance for the study of this paper. However, the existing researches on diffusion are not dynamic and complex enough, that is, the empirical analysis and classical game theory fail to reveal how the game achieves equilibrium and equilibrium stability; the pure evolutionary game analysis and system dynamics fail to consider the process of information exchange and mutual learning between players through network connections. Therefore, according to the characteristics of the research problem, this paper designs and develops a model framework combining indirect evolutionary game with complex network theory.

3. Proposed model and method

By utilizing the theory of indirect evolutionary game and complex network, this paper proposes a new NEV diffusion model, including the three-stage evolutionary game model and networked evolutionary dynamics model. For the market with special network characteristics, the model framework is still applicable. The evolutionary game of complex network is composed of three elements: game model, network structure and evolutionary rules. The following descriptions are expanded for the corresponding element.

3.1. Problem description

Considering that the market contains a population of auto manufacturers with a size of $M$. All auto manufacturers in the population meet the production qualification of NEVs and face the choice of two production strategies, that is, the production of NEVs and FVs, which are recorded as NEV strategy and FV strategy. The choice of different production strategies will affect the carbon emission and production cost in the production process, but will not affect the price level and basic functional characteristics of the final product. This paper randomly divides the auto manufacturer population into two groups, Group 1 and Group 2, with inter-group heterogeneity, and studies a two-population model. Assuming that the entire market contains multiple identical and independent small markets in different geographic locations, and each specific small market contains only two competing auto manufacturers, that is, individuals from Groups 1 and 2, referred to as auto manufacturer 1 and 2, are randomly matched to play a one-shot game. This assumption is commonly found in the literature of one/two-population evolutionary game models [[40], [41], [42], [43], [44], [45], [46]]. In a specific small market, the linear inverse demand function of the market is $P=a-b\left(q_1+q_2\right)$. The cost function of auto manufacturer $i$ who chooses the NEV strategy is $c_i^N=\left(1-s\right)c_i$, the cost function of auto manufacturer $i$ who chooses the FV strategy is $C_i^F=\delta c_i+F$, where $c_i$ is the basic cost of auto manufacturer $i$ producing a NEV, such as the battery cost, motor cost and electric control cost, etc., supposing $a>c_i$. $s$($0<s<1$) is the subsidy rate provided by the government to NEV manufacturers (hereinafter referred to as NEV manufacturers who choose the NEV strategy for short), such as subsidies for NEV manufacturers' R&D. $F$ is the government's penalty for FV manufacturers (hereinafter referred to as FV manufacturers who choose the FV strategy for short), such as the consumption tax, value-added tax and corporate income tax, etc. Nomenclature details other notations.

Thus, the profit function of auto manufacturer $i$ with the NEV strategy is

$${\pi }_i\left(q_1,q_2\right)=\left[a-b\left(q_1+q_2\right)-\left(1-s\right)c_i\right]q_i$$ (1)

The profit function of auto manufacturer $i$ with the FV strategy is

$${\pi }_i\left(q_1,q_2\right)=\left[a-b\left(q_1+q_2\right)-\delta c_i-F\right]q_i$$ (2)

3.2. The three-stage evolutionary game model

According to the problem studied in this paper, there is a three-stage evolutionary game between the government and auto manufacturer population. The game sequence is: in the first stage, the government first chooses the subsidy decision-making target and subsidy rate; in the second stage, individual manufacturers competing with each other in the population choose their production strategies, namely NEV strategy and FV strategy, and the selection results and the average income of the population change over time; in the third stage, in a specific market, two randomly matched individuals determine the production volume according to their selected production strategy.

In this paper, backward induction is used to solve the problem. First, a Cournot duopoly model is used to obtain the production volume of the Cournot equilibrium in the third stage, then the evolutionary stable strategy (ESS) of the auto manufacturer population in the second stage is analyzed, and finally the indirect evolutionary game method is used to determine the government's subsidy rate in the first stage. The diagram of the three-stage evolutionary game for NEV diffusion is shown in Fig. 2 .

Fig. 2.

Diagram of the three-stage evolutionary game for NEV diffusion.

3.2.1. One-shot duopoly game between auto manufacturers

According to the above analysis, in a given market, auto manufacturers 1 and 2 have a one-shot duopoly game, and there are four strategy combinations between them, namely, NEV-NEV, NEV-FV, FV- NEV, FV-FV, which are abbreviated as NN, NF, FN and FF successively.

Given the government subsidy rate, if both auto manufacturers 1 and 2 choose NEV production strategy, according to equation (1), the Cournot equilibrium outputs of auto manufacturers 1 and 2 under the NN strategy combination are

$$q_1^{NN}\left(s\right)=\frac{a+\left(1-s\right)\left(c_2-2c_1\right)}{3b}$$ (3)

$$q_2^{NN}\left(s\right)=\frac{a+\left(1-s\right)\left(c_1-2c_2\right)}{3b}$$ (4)

Furthermore, the equilibrium profits of auto manufacturers 1 and 2 are

$${\pi }_1^{NN}\left(s\right)=\frac{{\left[a+\left(1-s\right)\left(c_2-2c_1\right)\right]}^2}{9b}$$ (5)

$${\pi }_2^{NN}\left(s\right)=\frac{{\left[a+\left(1-s\right)\left(c_1-2c_2\right)\right]}^2}{9b}$$ (6)

An analytical derivation for the other three strategy combinations is noted in Appendix A of Supplementary materials. As an important component in the evolutionary game, payoff matrix can measure the income of players for selecting the strategies [8]. Furthermore, this paper is able to establish the payoff matrix of auto manufacturers 1 and 2 accordingly to describe the dynamic evolution of production strategies over time in the auto manufacturer population, as shown in Table 1 .

Table 1.

The payoff matrix of both players.

		Auto manufacturers in Group 2
		NEV	FV
Auto manufacturers in Group 1	NEV	${\pi }_1^{NN}\left(s\right)$; ${\pi }_2^{NN}\left(s\right)$	${\pi }_1^{NF}\left(s\right)$; ${\pi }_2^{NF}\left(s\right)$
	FV	${\pi }_1^{FN}\left(s\right)$; ${\pi }_2^{FN}\left(s\right)$	${\pi }_1^{FF}\left(s\right)$; ${\pi }_2^{FF}\left(s\right)$

3.2.2. Evolutionary stable strategy of auto manufacturers

This section first defines the proportion of the players choosing different strategies, and then describes the problem from the perspective of indirect evolutionary game theory (IEGT). Based on the payoff matrix, this paper gives replicator dynamic equations, calculates the equilibriums, and obtains the ESSs of the game. Suppose that the proportion of auto manufacturers who choose NEV production strategy in Group 1 is $x$, and the proportion of auto manufacturers who choose FV production strategy is $1-x$; the proportion of auto manufacturers who choose NEV production strategy in Group 2 is $y$, and the proportion of auto manufacturers who choose FV production strategy is $1-y$. In this part, an indirect evolutionary game model is constructed based on one-shot duopoly game, in which individual behaviors evolve over time based on Table 1. IEGT does not deny rational decision-making, assuming that decision-makers' behaviors under given preferences are rational, but their preferences will evolve over time [47,48]. The indirect evolutionary game in this paper is expressed as follows: the auto manufacturers in the market first choose production strategies based on their own preferences, and then continuously modify their preferences based on the behavior of competitors. Through replicated and dynamical adjustments, low-margin auto manufacturers will imitate the behavior of high-margin auto manufacturers in order to obtain higher profits, and eventually the low-margin auto manufacturers in the population will be replaced by high-margin auto manufacturers.

The payoff matrix of auto manufacturers in Group 1 is

$$\mathit{A}=\left(\begin{array}{ll}{\pi }_1^{NN}\left(s\right)\hfill & {\pi }_1^{NF}\left(s\right)\hfill \\ {\pi }_1^{FN}\left(s\right)\hfill & {\pi }_1^{FF}\left(s\right)\hfill \end{array}\right)$$ (7)

The payoff of auto manufacturers in Group 1 choosing NEV strategy is

$$\begin{array}{l}\mathit{eA}{\mathit{y}}^T=\left(\begin{array}{ll}1\hfill & 0\hfill \end{array}\right)\left(\begin{array}{ll}{\pi }_1^{NN}\left(s\right)\hfill & {\pi }_1^{NF}\left(s\right)\hfill \\ {\pi }_1^{FN}\left(s\right)\hfill & {\pi }_1^{FF}\left(s\right)\hfill \end{array}\right)\left(\begin{array}{l}y\hfill \\ 1-y\hfill \end{array}\right)\\ =y{\pi }_1^{NN}\left(s\right)+\left(1-y\right){\pi }_1^{NF}\left(s\right)\end{array}$$ (8)

The average payoff of auto manufacturers in Group 1 is

$$\begin{array}{l}\mathit{xA}{\mathit{y}}^T=\left(\begin{array}{ll}x\hfill & 1-x\hfill \end{array}\right)\left(\begin{array}{ll}{\pi }_1^{NN}\left(s\right)\hfill & {\pi }_1^{NF}\left(s\right)\hfill \\ {\pi }_1^{FN}\left(s\right)\hfill & {\pi }_1^{FF}\left(s\right)\hfill \end{array}\right)\left(\begin{array}{l}y\hfill \\ 1-y\hfill \end{array}\right)\\ =xy{\pi }_1^{NN}\left(s\right)+x(1-y){\pi }_1^{NF}\left(s\right)+(1-x)y{\pi }_1^{FN}\left(s\right)+(1-x)(1-y){\pi }_1^{FF}\left(s\right)\end{array}$$ (9)

According to the Malthusian equation, the growth of auto manufacturers in Group 1 choosing NEV strategy should be equal to the payoff $\mathit{eA}{\mathit{y}}^T$, minus the average payoff $\mathit{xA}{\mathit{y}}^T$. Therefore, the replicator dynamic equation of auto manufacturers in Group 1 is as follows, which is an efficient tool to analyze the evolutionary process of the strategies [49].

$$\begin{array}{l}F\left(x\right)=\frac{dx}{dt}=x[\mathit{eA}{\mathit{y}}^T-\mathit{xA}{\mathit{y}}^T]\\ =x\left(1-x\right)\left[y\left({\pi }_1^{NN}\left(s\right)-{\pi }_1^{FN}\left(s\right)\right)+\left(1-y\right)\left({\pi }_1^{NF}\left(s\right)-{\pi }_1^{FF}\left(s\right)\right)\right]\end{array}$$ (10)

Similarly, the replicator dynamic equation of auto manufacturers in Group 2 can be obtained as:

$$\begin{array}{l}F\left(y\right)=\frac{dy}{dt}=y[\mathit{eB}{\mathit{x}}^T-\mathit{yB}{\mathit{x}}^T]\\ =y\left(1-y\right)\left[x\left({\pi }_2^{NN}\left(s\right)-{\pi }_2^{NF}\left(s\right)\right)+\left(1-x\right)\left({\pi }_2^{FN}\left(s\right)-{\pi }_2^{FF}\left(s\right)\right)\right]\end{array}$$ (11)

Combining equations (10), (11) obtains the replicator dynamic system (I), which is a two-dimensional nonlinear dynamic system for auto manufacturers 1 and 2 as follows [23]:

$$\{\begin{array}{c}F\left(x,s\right)=x\left(1-x\right)\left[y\left({\pi }_1^{NN}\left(s\right)-{\pi }_1^{FN}\left(s\right)\right)+\left(1-y\right)\left({\pi }_1^{NF}\left(s\right)-{\pi }_1^{FF}\left(s\right)\right)\right]\\ F\left(y,s\right)=y\left(1-y\right)\left[x\left({\pi }_2^{NN}\left(s\right)-{\pi }_2^{NF}\left(s\right)\right)+\left(1-x\right)\left({\pi }_2^{FN}\left(s\right)-{\pi }_2^{FF}\left(s\right)\right)\right]\end{array}$$ (12)

Proposition 1

According to the replicator dynamic system (I) of the auto manufacturer population, it can be obtained

• (1)Points$\left(0,0\right)$, $\left(0,1\right)$, $\left(\mathrm{1,0}\right)$, and$\left(1,1\right)$are the equilibrium points of system (I) evolution;
• (2)When$\left({\pi }_1^{NN}\left(s\right)-{\pi }_1^{FN}\left(s\right)\right)\left({\pi }_1^{NF}\left(s\right)-{\pi }_1^{FF}\left(s\right)\right)<0$and$\left({\pi }_2^{NN}\left(s\right)-{\pi }_2^{NF}\left(s\right)\right)\left({\pi }_2^{FN}\left(s\right)-{\pi }_2^{FF}\left(s\right)\right)<0$, $\left(x^{\text{∗}},y^{\text{∗}}\right)$is also an equilibrium point of system (I),

where$x^{\ast }=\frac{a+\delta c_1-\left(1-s+\delta \right)c_2}{F-\left(1-s-\delta \right)c_1}$, $y^{\ast }=\frac{a+\delta c_2-\left(1-s+\delta \right)c_1}{F-\left(1-s-\delta \right)c_2}$.

Proof

See Appendix B of Supplementary materials.

Note that not all equilibrium points are the ESSs of the game. ESS is an EGT equilibrium satisfying the Lyapunov asymptotically stable conditions [8]. Furthermore, the Jacobian matrix is used to evaluate the asymptotic stability of equilibrium strategy pairs. According to Friedman's proposal, ‘describe (co)evolution of population(s) with dynamics defined by differential equations' [40]. According to equation (12), the Jacobian matrix $\mathit{J}$ of auto manufacturers in Groups 1 and 2 can be obtained as follows:

$$\mathit{J}=\left[\begin{array}{ll}\partial F\left(x\right)/\partial x\hfill & \partial F\left(x\right)/\partial y\hfill \\ \partial F\left(y\right)/\partial x\hfill & \partial F\left(y\right)/\partial y\hfill \end{array}\right]$$ (13)

where $\partial F\left(x\right)/\partial x=\left(1-2x\right)\left[y\left({\pi }_1^{NN}\left(s\right)-{\pi }_1^{FN}\left(s\right)\right)+\left(1-y\right)\left({\pi }_1^{NF}\left(s\right)-{\pi }_1^{FF}\left(s\right)\right)\right]$;$\partial F\left(x\right)/\partial y=x\left(1-x\right)\left({\pi }_1^{NN}\left(s\right)-{\pi }_1^{FN}\left(s\right)-{\pi }_1^{NF}\left(s\right)+{\pi }_1^{FF}\left(s\right)\right)$; $\partial F\left(y\right)/\partial x=y\left(1-y\right)\left({\pi }_2^{NN}\left(s\right)-{\pi }_2^{NF}\left(s\right)-{\pi }_2^{FN}\left(s\right)+{\pi }_2^{FF}\left(s\right)\right)$; $\partial F\left(y\right)/\partial y=\left(1-2y\right)\left[x\left({\pi }_2^{NN}\left(s\right)-{\pi }_2^{NF}\left(s\right)\right)+\left(1-x\right)\left({\pi }_2^{FN}\left(s\right)-{\pi }_2^{FF}\left(s\right)\right)\right]$.

ESS is the core concept of EGT [50], which can be defined as a strategy $S^{\ast }$ satisfying two conditions: (1) $\Phi \left(S^{\ast },S^{\ast }\right)\ge \Phi \left(S,S^{\ast }\right)$ for all $S\ne S^{\ast }$ and (2) $\Phi \left(S^{\ast },S\right)>\Phi \left(S,S\right)$ , where $\Phi$ denotes the payoff function and $S$ represents the possible strategy other than $S^{\ast }$ [51]. By analysing the local stability of the five equilibrium points, the evolutionary stable results of replicator dynamic system (I) are obtained when the subsidy rate is in different intervals. The ESS analysis for both players is listed in Table 2 , where $s_1=\left[\left(1-\delta \right)c_2-F\right]/c_2$ and $s_2=\left[\left(1-\delta \right)c_1-F\right]/c_1$.

Proposition 2

There are two thresholds of$s_1$and$s_2$in the evolution of replicator dynamic system (I). When the subsidy rate is in different threshold intervals, the ESS of the system is different, as follows.

• (1)When$s>\max \left\{s_1,s_2\right\}$, the ESS of the system is$\left(1,1\right)$;
• (2)When$\mathit{min}\left\{s_1,s_2\right\}<s<\mathit{max}\left\{s_1,s_2\right\}$, the ESS of the system is$\left(1,0\right)$or$\left(\mathrm{0,1}\right)$, where$s_1<s_2$is$\left(0,1\right)$ and $s_1>s_2$ is $\left(1,0\right)$ ;
• (3)When$s<\mathit{min}\left\{s_1,s_2\right\}$, the ESS of the system is$\left(0,0\right)$.

Proof

See Table 2.

Table 2.

ESS analysis for both players.

	Strategy	$\det J$	$trJ$	Result
$s>\mathit{max}\left\{s_1,s_2\right\}$	$\left(\mathrm{0,0}\right)$	+	+	Instability point
	$\left(\mathrm{0,1}\right)$	－		Saddle point
	$\left(\mathrm{1,0}\right)$	－		Saddle point
	$\left(\mathrm{1,1}\right)$	+	－	ESS
	$\left(x^{\ast },y^{\ast }\right)$			Not equilibrium point
$s_1<s<s_2$	$\left(\mathrm{0,0}\right)$	－		Saddle point
	$\left(\mathrm{0,1}\right)$	+	－	ESS
	$\left(\mathrm{1,0}\right)$	+	+	Instability point
	$\left(\mathrm{1,1}\right)$	－		Saddle point
	$\left(x^{\ast },y^{\ast }\right)$			Not equilibrium point
$s_2<s<s_1$	$\left(\mathrm{0,0}\right)$	－		Saddle point
	$\left(\mathrm{0,1}\right)$	+	+	Instability point
	$\left(\mathrm{1,0}\right)$	+	－	ESS
	$\left(\mathrm{1,1}\right)$	－		Saddle point
	$\left(x^{\ast },y^{\ast }\right)$			Not equilibrium point
$s<\min \left\{s_1,s_2\right\}$	$\left(\mathrm{0,0}\right)$	+	－	ESS
	$\left(\mathrm{0,1}\right)$	－		Saddle point
	$\left(\mathrm{1,0}\right)$	－		Saddle point
	$\left(\mathrm{1,1}\right)$	+	+	Instability point
	$\left(x^{\ast },y^{\ast }\right)$			Not equilibrium point

The phase diagrams of system (I) evolutionary process for different subsidy rates $s$ are shown in Fig. 3 .

Fig. 3.

Dynamic phase diagrams of system (I) evolution.

Proposition 2 shows that when the subsidy rate is moderate, both NEV and FV strategies will be adopted simultaneously in the population as expected. In reality, the government's intention is to promote NEV diffusion, but due to financial pressure, the subsidy rate is limited. Taking the case of $s_2<s<s_1$ as an example, the subsidy rate is set as $s$. From the expression of the threshold $s_1$, it can be seen that when the subsidy rate is limited, the government can also achieve the purpose of promoting NEV diffusion by increasing penalties for FV manufacturers, or by means of technological support and promoting technological innovation to reduce production costs and strengthen the emission reduction advantage of NEVs over FVs.

3.2.3. Decision analysis of government subsidy rate

Suppose that the government has two decision-making criteria for subsidies to NEV manufacturers. One is to promote the NEV output to reach a target value, and the other is to promote the number of NEV manufacturers to reach a target value. The following is the discussion of the government's subsidy rate to NEV manufacturers under these two decision criteria.

• (1)Target NEV output decision: set the NEV target output as $q_0$.

In one-shot duopoly game, the average output of each auto manufacturer in Group 1 to produce NEV is

$$\left(\begin{array}{ll}x\hfill & 0\hfill \end{array}\right)\left(\begin{array}{ll}{q}_1^{NN}\left(s\right)\hfill & q_1^{NF}\left(s\right)\hfill \\ q_1^{FN}\left(s\right)\hfill & q_1^{FF}\left(s\right)\hfill \end{array}\right)\left(\begin{array}{l}y\hfill \\ 1-y\hfill \end{array}\right)=x\left[y{q}_1^{NN}\left(s\right)+\left(1-y\right)q_1^{NF}\left(s\right)\right]$$ (14)

In one-shot duopoly game, the average output of each auto manufacturer in Group 2 to produce NEV is

$$\left(\begin{array}{ll}x\hfill & 1-x\hfill \end{array}\right)\left(\begin{array}{ll}{q}_2^{NN}\left(s\right)\hfill & q_2^{NF}\left(s\right)\hfill \\ q_2^{FN}\left(s\right)\hfill & q_2^{FF}\left(s\right)\hfill \end{array}\right)\left(\begin{array}{l}y\hfill \\ 0\hfill \end{array}\right)=y\left[x{q}_2^{NN}\left(s\right)+\left(1-x\right)q_2^{FN}\left(s\right)\right]$$ (15)

Therefore, the average output of NEVs produced by each auto manufacturer in the population in one-shot duopoly game is

$$\stackrel{-}{q}\left(x,y,s\right)=x\left[y{q}_1^{NN}\left(s\right)+\left(1-y\right)q_1^{NF}\left(s\right)\right]+y\left[x{q}_2^{NN}\left(s\right)+\left(1-x\right)q_2^{FN}\left(s\right)\right]$$ (16)

Since the number of individuals in the auto manufacturer population is $M$, let $M\cdot \stackrel{-}{q}\left(x,y,s_3\right)=q_0$, the government's optimal subsidy rate $s_3$ under the decision criterion of NEV target output can be obtained.

• (2)Target NEV manufacturers number decision: set the target number of NEV manufacturers in the population as $Q_0$($0<Q_0<M$).

According to the replicator dynamic equations (10), (11) of Groups 1 and 2, combined with the stability theory, it can be known that when $y=y^{\ast }$, any $x$($0\le x\le 1$) is in a stable state, that is, any production strategy of Group 1 is a stable strategy; when $x=x^{\ast }$, any $y$($0\le y\le 1$) is in a stable state, that is, any production strategy of Group 2 is a stable strategy. Therefore, $x^{\ast }$ and $y^{\ast }$ are the only co-existing unilateral stable strategies in the evolutionary game between Groups 1 and 2 (but not the evolutionary stable strategy of the system. Weibull pointed out that the mixed equilibrium under the asymmetric condition is not ESS [52], which can also be explained by Table 2 in this paper).

Assuming that the numbers of individuals in Groups 1 and 2 are $M_1$ and $M_2$, and $M_1+M_2=M$, let $x^{\ast }\left(s_4\right)M_1+y^{\ast }\left(s_4\right)M_2=Q_0$, the government's optimal subsidy rate $s_4$ under the decision criterion of NEV manufacturers target number can be obtained.

3.3. Networked evolutionary dynamics model

In the real world, many systems are embedded in social systems and have topological and statistical characteristics. There is a close relationship between the evolutionary game process and the network structure [53]. Scholars have studied the structure of social networks from different perspectives and found that the social network in the initial stage of formation is random. With the continuous development of the network, it gradually presents the characteristics of scale-free or small-world network [54]. In order to fully reveal the influence of government subsidies on NEV diffusion, this paper studies the network evolution law of NEV diffusion with BA scale-free network and WS small-world network as the carriers.

3.3.1. Model building

Build the NEV diffusion network $G\left(V,E\right)$, which is a heterogeneous complex network, where $V$ represents the set of all nodes in the NEV diffusion network, that is, all auto manufacturers in the network; $E=\left\{e_{mn}\right\}$ represents the set of all edges. If $e_{mn}=1$ indicates that there is a game relationship between two nodes $m$ and $n$; if $e_{mn}=0$ indicates that there is no game relationship between the two. Assuming that the player in the NEV diffusion network chooses only one neighbor node to play the game at a time, that is, the game radius is 1, and whether it simulates the strategy of the neighbor node will depend on the expected payoff obtained from Table 1. At the same time, all auto manufacturers in the network adopt the same strategy update rules, and strategy choice each time depends only on the result of the previous game, that is, the memory length is 1. The following generates NEV diffusion networks with scale-free characteristics and small-world characteristics.

BA scale-free network starts from a connected network of $m_0$ nodes, and in each time step, an auto manufacturer with a connection degree of $m_1$ ($m_1\le m_0$) is added [55]. The newly added nodes are connected to existing $m_1$ nodes in the network in accordance with equation (17), and there is no repeated connection. Finally, a diffusion network $G_1$ with scale-free characteristics is generated. Fig. 4 (a) and (b) respectively show the two-dimensional schematic diagrams of a small-scale BA network with 30 nodes and a large-scale BA network with 50 nodes randomly generated at the beginning of the evolution.

$${\Pi }_m=\frac{k_m}{{\displaystyle \sum _n}{k}_n}$$ (17)

Fig. 4.

Two-dimensional schematic diagrams for BA network.

Equation (17) shows that the probability ${\Pi }_m$ of a newly added node connected to an existing node $m$ is proportional to the degree $k_m$ of node $m$.

WS small-world network is given a nearest-neighbor coupled network containing $N$ nodes, each node is connected to its left and right neighboring $k/2$ nodes ($k$ is an even number, and $N>>k$), randomly reconnect each edge of the original network with probability $p$ (no heavy edges and self-loops) [56]. Finally, a diffusion network $G_2$ with small-world characteristics is generated. Fig. 5 (a) and (b) respectively show the two-dimensional schematic diagrams of a small-scale WS network with 30 nodes and a large-scale WS network with 50 nodes randomly generated at the beginning of the evolution.

Fig. 5.

Two-dimensional schematic diagrams for WS network.

3.3.2. Rulemaking of network evolution dynamics

The auto manufacturer population is in the NEV diffusion network with a certain topology. According to Femi rule [57,58], after the first game, the player $m$ will randomly select a neighbor player $n$ for a payoff comparison. If its own payoff $p{r}_m$ is less than the neighbor's payoff $p{r}_n$, it will imitate the neighbor's strategy in the next round of the game with probability $\tau$.

$$\tau \left(A_m\to A_n\right)=\frac{1}{1+\exp [\left(p{r}_n-p{r}_m\right)/k]}$$ (18)

Among it, $k$($k>0$) represents the noise intensity of the external environment where the auto manufacturer population is located. The noise involved in this paper mainly refers to the uncertainty of the external environment, including the dynamics and the complexity of the environment. The greater the $k$, the greater the interference of the uncertainty of the external environment on the player's strategy imitation or learning. This paper takes the neutral noise intensity $k=0.5$.

After the strategy imitation, player $m$ will reconnect with other neighbor players in the network with random probability $\gamma$. The probability ${\gamma }_{m\to l}$ of player $m$ connecting to player $l$ is

$${\gamma }_{m\to l}=\sum _{m\in G}\frac{p{r}_l^{\beta }}{p{r}_m^{\beta }}$$ (19)

Among it, $\beta$ represents the preference tendency, and the larger $\beta$ is, the more obvious the preference tendency is. In this paper, $\beta =1$ is used for experimental analysis.

When all auto manufacturers in the diffusion network learn and adjust their strategies according to the above rules, with the increase of iteration times, the strategy distribution of the auto manufacturer population will gradually tend to a stable state, and finally NEV diffusion will be realized. This paper takes the proportion of the number of NEV manufacturers in the total number of auto manufacturers in the stable state as the NEV diffusion depth, in order to explore the network evolution law of NEV diffusion.

4. Simulation analysis

This paper presents an actual application to simulate. This paper uses public data related to BYD officials, regulatory announcements and similar studies. The unified simulation time is 100 months, and the time unit is one month. Simulation analysis reveals the potential law of NEV diffusion under different topologies.

4.1. Data and parameters

As the leader in China's NEV industry, BYD has been the world's NEV sales champion for four consecutive years since 2015 [59]. In April 2016, BYD launched the ‘dynasty’ series of NEVs. In 2019, BYD successively released Tang DM, Tang EV, Qin Pro DM, Qin Pro EV, Song MAX DM and Yuan EV535. Taking the standard version of Qin Pro EV as an example, its official guiding price is 172,400 Yuan per vehicle, and the actual purchase price after deducting subsidies is 149,900 Yuan per vehicle. According to the propaganda data of Qin's ‘one cost price’ sales, the theoretical cost per vehicle is estimated to be about 155,160 Yuan, which is marked with $c_1$. In order to reflect the heterogeneity between Groups 1 and 2, this paper sets $c_2$ to 160,000 Yuan. The most popular traditional FVs at the same level, such as Volkswagen Lavida, Honda Civic and Toyota Corolla, are also in this price range. Thus, the unit price of traditional FVs is set as 150,000 Yuan. According to the studies in Ref. [60], this paper assumes that the government's penalty for FV manufacturers is 10% of the selling price, and $F$ is set as 15,000 Yuan. According to Ref. [61], this paper assumes that the emission reduction rate of NEVs compared to FVs during the production process is 25%, i.e., $\delta =25\text{\%}$. Combined with the problem description, this paper assumes that other parameter values are as follows: $a=200\text{,}000Yuan$, $b=1Yuan/vehicle$, $M=50manufacturers$, $M_1=20manufacturers$, $M_2=30manufacturers$. Simulation steps are listed in Appendix C of Supplementary materials.

Fig. 6(a) shows that when the subsidy rate is in different threshold intervals, the NEV diffusion depth presents a segmented distribution, which is consistent with Proposition 2. Fig. 6(b) shows that the NEV diffusion depth presents a linear relationship with the subsidy rate under the decision-making criteria of the target NEV manufacturers number.

Fig. 6.

Simulation results of the NEV diffusion depth.

In reality, the auto manufacturer population realizes NEV diffusion through nonlinear mechanism of interaction, coordination, competition and promotion among individuals under a certain socio-economic background. According to the simulation results in Fig. 6, let the subsidy rate $s$ change over interval $\left[0.636,0.696\right]$ in incremental steps of 0.02, which covers the thresholds $s_1$ and $s_2$($s_1>s_2$). Taking the NEV diffusion depth as a measurement index, this paper further studies the following influences of different network scales and topologies on the production strategies of auto manufacturers over time. In order to prevent the influence of instability on the simulation results, each group of parameters is run 50 times, and finally the average value of the measurement indexes is taken.

4.2. Simulation analysis of NEV diffusion in scale-free networks

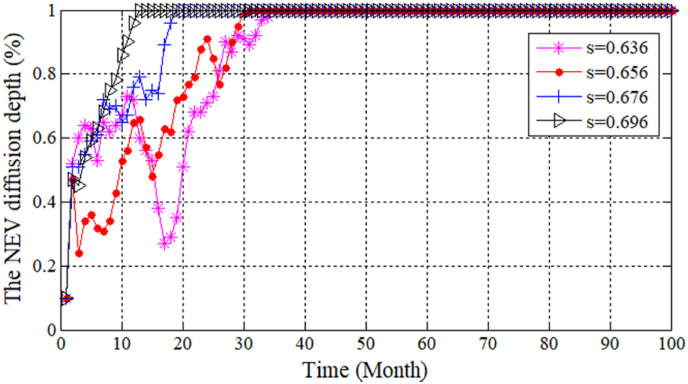
This paper simulates the NEV diffusion process in scale-free networks, and compare the diffusion depth and speed in the small-scale scale-free network and large-scale scale-free network.

It can be seen from Fig. 7 that when the subsidy rate of the government is 0.636, the NEV diffusion depth finally degenerates to 0 due to the low subsidy rate ($0.636<s_2$, see Fig. 6(a)), which is not enough to counter the advantage of the production cost of traditional FVs. When the subsidy rate is 0.656–0.696, the NEV diffusion depths all evolve to 1, and the higher the subsidy rate within a certain threshold range, the shorter the time consumed by a full diffusion. This is because the scale-free network has a small average path length, and the transmission efficiency of information in the network is high. The higher the subsidy rate faced by individuals with the goal of maximizing their own interests, the greater the motivation of producing NEVs. The news of their profit can spread rapidly in the network, thus driving the NEV diffusion speed in the overall network.

Fig. 7.

The NEV diffusion depth in a BA network of 30 nodes.

However, when the subsidy rate is 0.696, it takes the longest time for the NEV strategy to be fully diffused, and there is a large fluctuation in the initial stage of evolution. Possible reasons are as follows: the subsidy rate is too high, and the production technology requirements for the pure electric range and battery energy density will be increasingly strict; the NEV industry is still in early stage of development, and the production technology of most auto manufacturers is not yet mature; at this time, some outstanding individuals with a strong exemplary role choose the NEV strategy; the ‘choose the strongest’ mechanism of the scale-free network enables other individuals to follow the strategy; at the same time, in the early stage of development of NEV industry, there were no effective supervision mechanisms and punishment measures for potential cheat subsidy of some auto manufacturers, so that the NEV strategy in the network could finally achieve complete diffusion after a period of fluctuation.

The large-scale diffusion network is developed from the small-scale diffusion network. It can be seen from Fig. 8 that when the government subsidy rate is 0.656, the NEV diffusion depth finally converges to 0 after a small amplitude fluctuation. This is because when the size of the auto manufacturer population expands to 50 and the market share is fixed, the competition intensity among individuals increases and the subsidy rate is relatively low ($s_2<0.656<s_1$, see Fig. 6(a)), and the profit space of most individuals becomes smaller or even no profit. Some individuals with strong guiding ability based on their own interests, first respond and adopt the FV strategy. While the node degree distribution of the scale-free network presents a power-law distribution (also known as fat-tailed distribution [62]), showing a strong ‘Matthew effect’, and a small amount of hub nodes with a high degree affect the connection trend of other nodes in the network, making the NEV network diffusion depth eventually degenerate to 0.

Fig. 8.

The NEV diffusion depth in a BA network of 50 nodes.

By comparing and analyzing Fig. 7, Fig. 8, it can also be found that when individuals' production technology level and market competition intensity are not taken into account ($s=0.636$ and $s=0.676$), the speed at which the NEV diffusion depth reaches a stable state in a large-scale scale-free network is significantly lower than that in a small-scale scale-free network. This is because from the perspective of network characteristics, the clustering coefficient of the scale-free network is generally inversely proportional to $N$, that is, the larger the scale of scale-free network is, the lower the clustering coefficient is. The low clustering coefficient makes the connection among the auto manufacturers looser, the information asymmetry in the network is significant, and the information transmission speed and accuracy are relatively weakened, which eventually leads to a longer time of the NEV diffusion depth achieving steady state.

4.3. Simulation analysis of NEV diffusion in small-world networks

This paper further simulates the NEV diffusion process in small-world networks, and compare the diffusion depth and speed in small-world networks and scale-free networks, as well as in the small-scale small-world network and large-scale small-world network. Fig. 9 shows that in the small-scale small-world network, the effect of subsidy rate on the NEV diffusion depth is similar to that in the small-scale scale-free network (see Fig. 7). The differences between the two are as follows:

• (1)When the subsidy rate is 0.636, it takes longer for the NEV diffusion depth to reach a stable state, and there is a large amplitude of fluctuations in the initial stage of evolution. This is because the individuals in the diffusion network not only consider their own interests, but also observe the decision-making behavior of other individuals. In the network with small-world characteristics, the connection mechanism among the individuals is more complex. In addition to the connection relationship of ‘choose the strongest’, there is no lack of ‘choose the well-connected’, which leads to the diversification of social relations in the diffusion network. Individuals will continuously seek the best strategy imitation target for their own interests until the maximum benefit and the NEV diffusion depth reaches the stable state.
• (2)When the subsidy rate is 0.656–0.696, the speed of full diffusion of NEV strategy in the small-scale small-world network decreases with the increase of the subsidy rate, which is different from the case in scale-free network. This is because during this period, the number of individuals in the auto manufacturer population decreases gradually with the production technology from low to high. The small-world network has a larger clustering coefficient, and the individuals are more closely connected. Therefore, in the iteration range, when the links between individuals in the network are closer and the connection mechanism is more complex, the time of the number-dominant situation evolving to a stable state is the shortest. Therefore, when the subsidy rate is 0.656, the NEV strategy achieves full diffusion at the fastest speed, followed by 0.676 and 0.696.

Fig. 9.

The NEV diffusion depth in a WS network of 30 nodes.

Fig. 10 shows that when the subsidy rate is 0.636–0.696, the NEV diffusion depth will all converge to 1. This is because, compared with the situation in the scale-free diffusion network (see Fig. 8), the connection among individuals in the small-world diffusion network is more complicated. When the subsidy rate is low, the behavior of choosing the NEV strategy has certain risks. However, due to the bounded rationality of game players, when the NEV industry is in the growth stage, they are more likely to perceive the tendency of government policy, and with the increase of popularity pressure, some individuals with social responsibility first choose the NEV strategy. The inherent high clustering coefficient of the small-world network enhances the degree of aggregation among individuals, and other individuals will choose the NEV strategy based on the ‘herding effect’. Finally, the diffusion depth of the NEV network reaches 100% steady state.

Fig. 10.

The NEV diffusion depth in a WS network of 50 nodes.

According to the relevant data in Section 4.1 of this paper, the production cost of the standard version of Qin Pro EV is 155,160 yuan, and the central subsidy in 2019 is 22,500 yuan. It is estimated that the subsidy rate should be 12.7%. Here, this paper does not consider the micro impact of the actual size of the auto manufacturer population in the market on the magnitude of the subsidy rate. Similar to the official propaganda of Qin, the lower subsidy rate leads to no cost advantage compared with traditional FVs at the same level. However, BYD still chooses the NEV strategy for the purpose of expanding the market.

4.4. Extensions

In order to standardize the research work, this paper further introduces the regular network and random network as extensions to examine the influence of network topology on NEV diffusion. This section conducts a comprehensive study of authoritative networks constructed at the present stage.

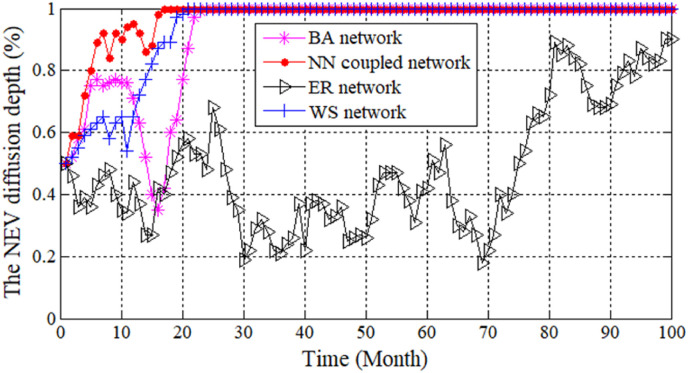
The nearest-neighbor coupled network contains a total of $N$ nodes. It is stipulated that each node in the network is only connected with neighboring nodes around it, and each node is connected with $k/2$ adjacent nodes on its left and right ($k$ is an even number) [63]. ER random network is given $N$ isolated nodes with marks, and all possible $N\left(N-1\right)/2$ connections are connected with a certain random probability [64]. Take the network scale $N$ as 50 and the subsidy rate $s$ as 0.696 to observe the influence of different network topologies on the NEV diffusion depth, as shown in Fig. 11 .

Fig. 11.

The NEV diffusion depth with different network topologies.

It can be seen from Fig. 11 that the speed of full NEV diffusion in the nearest-neighbor coupled network is the largest, followed by WS small-world network and BA scale-free network. In ER random network, the NEV strategy does not achieve full diffusion within the experimental iteration range. From the perspective of network topology characteristics, the nearest-neighbor coupled network has a large clustering coefficient, and the information can be quickly spread among closely connected ‘kinship networks', thus speeding up NEV full diffusion. However, ER random network has a small clustering coefficient, the individuals are widely connected, and the information asymmetry is prominent, which leads to the insufficient diffusion of the NEV strategy within the iteration range. Because the average path length of WS small-world network and BA scale-free network is smaller than that of ER random network, and the clustering coefficient is smaller than that of the nearest-neighbor coupled network, the information propagation path in WS small-world network and BA scale-free network is more concise than that of ER random network, and the connection between nodes is looser than that of the nearest-neighbor coupled network. Therefore, trends of NEV diffusion are between the nearest-neighbor coupled network and ER random network. At the same time, the clustering coefficient of BA scale-free network is smaller than that of WS small-world network, so the speed of full NEV diffusion in WS small-world network is higher.

5. Conclusions and policy recommendations

The research on NEV diffusion under different network topologies is a new proposition. For the market with special network characteristics, the model framework based on the indirect evolutionary game and complex network proposed in this paper is still applicable. The following innovative conclusions are summarized: (1) in a scale-free diffusion network, the subsidy rate provided by the government must be high enough to promote the full NEV diffusion, and the larger the network scale, the higher the threshold of subsidy rate; (2) for the small-scale network, topological characteristics have little effect on the NEV diffusion depth, and only affect the speed when NEV diffusion reaches the stable state; (3) for the large-scale diffusion network, NEV diffusion in the scale-free network is more sensitive to the change of the subsidy rate than that in the small-world network; (4) in a diffusion network with small-world characteristics, the larger the network scale, the more conducive to the full NEV diffusion; (5) network topologies influencing NEV diffusion can be divided into two priority levels, that is, the first priority is the clustering coefficient and the second priority is the average path length.

In the market with scale-free characteristics, most ‘normal’ auto manufacturers have very few connections, while a few ‘hot’ manufacturers have extremely many connections; in the market with small-world characteristics, the links between auto manufacturers are closer and the connection mechanism is more complex. The large-scale market is developed from the small-scale market. Government designers should take specific measures according to the characteristics of different markets.

Firstly, when the amount of subsidies is limited, for the small-scale market with scale-free characteristics, the government should not rush to expand the market scale, but should first cultivate it into a market with small-world characteristics by strengthening the network connection, such as organizing the auto manufacturer association and establishing the auto manufacturer alliance, and improving the network environment, such as reducing monopoly and building multiple information sharing platforms, and then appropriately expand the market scale by reducing market barriers, so that the measure cost is lower and the promotion effect is better. The implications and recommendations are in agreement with the innovative conclusions (1), (4) and (5).

Secondly, for the small-scale market with small-world characteristics, the government's direction of efforts is to appropriately expand the market scale. In addition, the supervision mechanism should be improved to effectively avoid potential cheat subsidy of auto manufacturers. The implications and recommendations are in agreement with the innovative conclusion (4) and the simulation analysis.

The following important limitations are identified, which may be useful for future research. First, the topology and scale of the network will change over time due to the influence of the external environment. The authors believe that coupling the dynamics of NEV diffusion with the dynamics of network evolution is a promising method to solve this problem. Second, this paper considers only inter-group heterogeneity. A completely different model is needed to explain intra-group's competition. Third, in the application simulation, the theoretical cost of the standard version of Qin Pro EV is evaluated based on the promotion of Qin's ‘one cost price’ sales. There is a certain gap between this study and reality.

CRediT author statement

Dan Zhao: Conceptualization, Methodology, Data curation, Software, Writing - original draft. Shou-feng Ji: Validation, Writing - review & editing. He-ping Wang: Supervision, Writing - review & editing. Li-wen Jiang: Software, Validation.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following is the Supplementary data to this article: