Work-loop contractions reveal that the afterload-dependent time course of cardiac Ca²⁺ transients is modulated by preload

Abstract

Preload and afterload dictate the dynamics of the cyclical work-loop contraction that the heart undergoes in vivo. Cellular Ca²⁺ dynamics drive contraction, but the effects of afterload alone on the Ca²⁺ transient are inconclusive. To our knowledge, no study has investigated whether the putative afterload dependence of the Ca²⁺ transient is preload dependent. This study is designed to provide the first insight into the Ca²⁺ handling of cardiac trabeculae undergoing work-loop contractions, with the aim to examine whether the conflicting afterload dependency of the Ca²⁺ transient can be accounted for by considering preload under isometric and physiological work-loop contractions. Thus, we subjected ex vivo rat right-ventricular trabeculae, loaded with the fluorescent dye Fura-2, to work-loop contractions over a wide range of afterloads at two preloads while measuring stress, length changes, and Ca²⁺ transients. Work-loop control was implemented with a real-time Windkessel model to mimic the contraction patterns of the heart in vivo. We extracted a range of metrics from the measured steady-state twitch stress and Ca²⁺ transients, including the amplitudes, time courses, rates of rise, and integrals. Results show that parameters of stress were afterload and preload dependent. In contrast, the parameters associated with Ca²⁺ transients displayed a mixed dependence on afterload and preload. Most notably, its time course was afterload dependent, an effect augmented at the greater preload. This study reveals that the afterload dependence of cardiac Ca²⁺ transients is modulated by preload, which brings the study of Ca²⁺ transients during isometric contractions into question when aiming to understand physiological Ca²⁺ handling.

NEW & NOTEWORTHY This study is the first examination of Ca²⁺ handling in trabeculae undergoing work-loop contractions. These data reveal that reducing preload diminishes the influence of afterload on the decay phase of the cardiac Ca²⁺ transient. This is significant as it reconciles inconsistencies in the literature regarding the influence of external loads on cardiac Ca²⁺ handling. Furthermore, these findings highlight discrepancies between Ca²⁺ handling during isometric and work-loop contractions in cardiac trabeculae operating at their optimal length.

INTRODUCTION

The heart in vivo undergoes a cyclical work-loop contraction pattern where the venous pressures upstream (preload) and arterial pressures downstream (afterload) dictate the pressure development and, therefore, the shortening and lengthening dynamics of ventricular muscle fibers. Over the past century, it has become apparent that cardiac stress-length mechanics are contraction mode dependent. For a given length, the isometric stress production is greater than the end-systolic stress produced at the end of the shortening phase in a work-loop, and this discrepancy is augmented at lower afterloads (1) but eliminated at reduced preloads (2).

Ca²⁺ transients, the primary driver of cardiac contraction, are commonly studied within isometric contractions, where an external load prevents isolated muscle fibers from shortening. No study has measured Ca²⁺ transients in cardiac trabeculae undergoing work-loop contractions. A handful of investigations, in both multicellular (3–5) and single cellular (6, 7) preparations, have examined the influence of afterloaded shortening on the Ca²⁺ transient but using isotonic contraction modes. The general finding was that, at low afterloads, the twitch duration reduced, whereas the Ca²⁺ transient amplitude did not change and the transient duration extended.

Ca²⁺ transients have been measured during work-loop contractions in whole hearts (8), but the study was limited to a single afterload at the mid-range of isovolumic pressure. Under these conditions, Ca²⁺ transients demonstrated no contraction-mode dependency. That is, the Ca²⁺ transient under isovolumic and work-loop conditions was indistinguishable. This sets a precedent for an equivalency of work-loop and isometric Ca²⁺ handling that may be unfounded over a greater range of afterloads.

Mode-dependency of Ca²⁺ handling has not been resolved in silico. Mathematical models of isotonic shortening have predicted that the Ca²⁺ transient duration either increases (9) or decreases (10) at reduced afterloads. Modeling studies focused on work-loop contractions, where the muscle is allowed to fully relax before restretch occurs, predict a morphological change to the decay of the Ca²⁺ transient but little to no change to the duration with changing afterload (11, 12).

The preload dependence of Ca²⁺ handling in cardiac muscle has been studied in isometrically contracting trabeculae (13–15) and auxotonically contracting myocytes (16), but it has not yet been examined in isolated cardiac muscle undergoing work-loop contractions. From a mechanistic standpoint, preload has a major role in modulating the ability of cardiac muscle to relax under afterloaded isotonic contractions in trabeculae (17) and myocytes (10, 18), as well as on the mechano-Ca²⁺ feedback as recently shown in silico (19). Hence, it is possible that preload modulates the afterload-dependent Ca²⁺ handling observed in the literature.

The aim of conducting the experiments in this study is to gain an understanding of the Ca²⁺ handling of cardiac trabeculae performing work-loops. The experiments involved subjecting isolated ventricular trabeculae to work-loops at two preloads and a range of afterloads in the custom-built cardiomyometer. Preload was set by prestretching the muscle to 95% or 100% optimal length. Steady-state twitch stress and Ca²⁺ transient data were measured and analyzed to assess their responses to these loading conditions. By collecting these data, we provide the first insight into the influence of preload on Ca²⁺ handling during work-loop contractions over a wide range of afterloads, thereby reconciling a literature inconsistency.

MATERIALS AND METHODS

Ethical Approval

The Animal Ethics Committee of The University of Auckland approved protocols for animal handling and euthanasia (AEC No. 2722).

Work-Loop Control

All experiments were conducted on isolated ventricular trabeculae from male Wistar rats in the cardiomyometer (20, 21). In this device, trabeculae developed force-length work loops by contracting against a mechanical admittance computed in real time in a field-programmable gate array (FPGA) and imposed by a linear actuator based on a voice coil motor (22). The mechanical admittance (velocity per unit force) experienced by the muscle was scaled from the instantaneous solution of a three-element “Windkessel” model of the vasculature impedance (Z_wk) as follows. Briefly, the force generated by the muscle upon stimulation was scaled in the FPGA to an equivalent ventricular pressure using measured muscle dimensions and applying Laplace’s law (23). This scaling technique approximates the ventricle as a sphere due to the timing and hardware constraints of the FPGA used. Although a different geometrical model would likely change the morphology of the stress-length loops, the model used was sufficient to test the hypothesis that the Ca²⁺ transient is load-dependent, without introducing bias.

The muscle contracted isometrically until the pressure exceeded Pa(s), the Laplace domain expression of the arterial pressure stored in the vascular network. As in the heart, ejection/muscle shortening could only occur when ventricular pressure exceeded that of the arterial network. Once this condition was met, the flow rate of blood out of the ventricle was computed from

$$\begin{array}{c}Q\left(s\right)=\frac{Pa\left(s\right)}{Z_{Wk}\left(s\right)}\end{array}$$ (1)

where Z_Wk(s) is the Laplace-domain transfer function of a Windkessel model of the vasculature defined as

$$Z_{Wk}\left(s\right)=\frac{\left(Z_c{R}_{p}C\right)s+\left(Z_c+R_p\right)}{\left(R_{p}C\right)s+1}$$ (2)

Z_c is the characteristic impedance, R_p is the peripheral resistance, and C is the arterial compliance. Q(s) was then scaled into its one-dimensional equivalent (rate of shortening) and used to control the rate of length change of the muscle. The ejection phase continued until the arterial pressure exceeded the ventricular pressure, whereupon the trabecula relaxed isometrically. As the rate of stress change approached zero, the trabecula was restretched back to its initial length. The restretch rate was user defined by a constant volumetric refill rate and scaled into the equivalent muscle length.

The FPGA calculated these parameter values at a rate of 20 kHz and applied the predicted rate of shortening to the trabecula in real time. The afterload generated during work-loops was adjusted by modifying R_p within the range from 5 kPa·s/mL to 1,000 kPa·s/mL_, while C and Z_c were held constant at 0.032 mL/kPa and 5 kPa·s/mL, respectively. These values were adapted from a previous study (22). The volumetric flow rate was set to 0.6 mL/s as this was sufficient for the restretch phase to complete within the diastolic period of each stress twitch at a stimulus frequency of 2 Hz and a temperature of 32°C.

Preparing Trabeculae

To obtain trabeculae, 8- to 10-wk-old male Wistar rats were anesthetized with gaseous isoflurane (5% in O₂) before being injected with heparin (1,000 IU/kg). The rats were killed via cervical dislocation and their hearts removed within 30 s. Each excised heart was immediately submerged in ice-cold 2,3-butanedione monoxime (BDM)-Tyrode’s solution consisting of (in mM): 130 NaCl, 6 KCl, 1.5 MgCl₂, 0.5 NaH₂PO₄, 0.3 CaCl₂, 10 glucose, and 20 2,3-butanedione monoxime (BDM). The heart was then transferred to a dissection bath, and Langendorff perfused with the BDM-Tyrode’s solution at room temperature with the pH adjusted to 7.4. The atria were removed and the ventricles opened by cutting along the septum. Trabeculae used within this study were excised from the right ventricle.

Each dissected trabecula was mounted between two platinum hooks in the cardiomyometer (20). Voice-coil motors mechanically coupled to each hook set the slack length of the trabecula. Platinum electrodes upstream and downstream of the measurement chamber were used to stimulate the trabecula electrically. The resultant stress produced by the trabecula was inferred from the deflection of a steel cantilever, with a known stiffness, attached to the downstream hook. When mounted in the cardiomyometer, the trabecula was superfused with Krebs-Henseleit (K-H) solution (in mM): 118 NaCl, 4.75 KCl, 1.18 MgSO₄, 1.18 KH₂PO₄, 24.8 NaHCO₃, 1.5 CaCl₂, and 10 glucose. The superfusate was bubbled with carbogen (95% O₂, 5% CO₂) to maintain the pH at 7.4 and supply the muscle with ample oxygen throughout the protocol. The stimulus frequency was set to 1 Hz throughout an hour-long equilibration period for the acclimatization of the trabecula.

Determining L₁₀₀

After the stress generated by the trabecula had stabilized, when the diastolic and peak stress production had remained constant over a 10-min window, the muscle was considered to have acclimatized. It was then stretched to optimal length (L₁₀₀). A central window was imaged with a ×20 objective lens, and the average sarcomere length was calculated using a two-dimensional (2-D)-fast Fourier transform algorithm (24). Trabeculae were discarded if it was not possible to image sarcomeres in a central region.

For each experiment, L₁₀₀ was defined as the muscle length corresponding to an average measured sarcomere length of ∼2.3 μm in the central region of each trabecula. L₉₅ was defined as 95% of the L₁₀₀ muscle length. Muscle length was maintained throughout each contraction using proportional-integral-derivative-controlled voice-coil motors informed by continuous measurement via laser interferometry.

Ca²⁺ Transient Measurements

Fura-2 was used to measure intracellular Ca²⁺ dynamics in the trabeculae. Briefly, the broadband light produced by a 300 W xenon arc lamp was cyclically switched at 600 Hz between three different central wavelengths of 340 nm, 365 nm, and 380 nm, each with a bandwidth of 10 nm. The filtered light was projected onto a central portion of the trabecula via the bright-field microscope objective. The resultant fluorescent emission passed through a 510-nm bandpass filter before the intensity was measured using a photomultiplier tube. Before loading the trabecula with Fura-2, the background fluorescence of the trabecula was recorded. These autofluorescence measurements were subtracted from the fluorescence signals before calculating the ratio of the emission associated with the 340-nm and 380-nm excitation light (F₃₄₀/F₃₈₀). During loading, the stimulation frequency was set to 0.2 Hz, and the muscle superfused with a loading solution comprised K-H solution with 10 μM of cell-permeable Fura-2/AM and 1 mM probenecid. Loading was considered complete when F₃₆₅ had reached 10 times the background fluorescence measurement or the loading period had reached 2 h. Following loading, the superfusate was switched back to the standard K-H solution with 1 mM probenecid, and the stimulus frequency increased to 2 Hz. Intracellular Ca²⁺ dynamics were taken as F₃₄₀/F₃₈₀.

Experimental Protocol

Following the achievement of a steady state of both stress production and the fluorescence ratio (unchanged diastolic and peak measurements over a 10-min period), the bath temperature was increased to 32°C using a thermoelectric heat pump in combination with a temperature controller. The experiment was performed at 32°C as a compromise between physiological temperature (37^oC) and the Fura-2 leak rate. At 37°C, the leak rate of Fura-2 is substantial even in the presence of probenecid (25), an inhibitor of the anion transporters that drive the leakage. Lowering the experimental temperature to 32°C provided confidence that the entire preload-afterload protocol could be completed before extensive Fura-2 leakage occurred. This choice of temperature meant that the stimulation frequency had to be reduced to 2 Hz to provide an adequate diastolic period within which restretch could be completed before the start of the subsequent contraction.

After the temperature stabilized, the experiment commenced by setting the muscle to one of two preloads, achieved by setting the muscle length to either L₉₅ or L₁₀₀. The selection of the first preload used was randomized for each trabecula. The trabecula was then stimulated to contract isometrically while the deflection of the force transducer was compensated for using the upstream motor, thereby maintaining muscle length. Once the isometric stress transient reached a beat-to-beat steady state, the muscle was subjected to FPGA-driven three-element Windkessel work-loops until stable loops were achieved. This process was repeated for six R_p values ranging from 5 kPa·s/mL to 1,000 kPa·s/mL to characterize the afterload-dependent behavior between close to minimal (isotonic) and maximal (isometric) stress. The order in which R_p values were used was randomized to mitigate the introduction of fatigue basis into the measurements. The muscle length was changed to L₁₀₀ or L₉₅ depending on the starting length, and the process was repeated until data for all afterloads had been collected. Force and Ca²⁺ data were collected for the duration of this protocol.

Trabecula Dimension

At the end of the experiment, muscle geometry was measured at L₁₀₀ with the trabecula at quiescence. In total, seven trabeculae were studied. Their cross-sectional area was measured using spectral-domain optical coherence tomography as described previously (26). Briefly, a broadband (100 nm) low-coherence superluminescent diode with a central wavelength of 840 nm was split into a measurement and reference path. The reference path contained only a mirror, and the measurement path had a 2-D galvanometer that directed and focused the light onto the trabecula. The superposition of the back reflections from each optical path was passed through a spectrometer. The frequency domain encodes depth information in spectral-domain optical coherence tomography (27). After subtracting the background image, the interference pattern was inverse fast Fourier transformed. Steering the measurement arm along a single axis enabled the imaging of muscle cross section, and using a second axis, enabled the imaging of muscle volume. The resultant images were segmented, and the cross-sectional area was calculated by scaling the pixel area by the lateral and depth resolutions of the optical coherence tomography (OCT) (20). The seven trabeculae had an average cross-sectional area of 0.06 ± 0.04 mm², an average length at L₁₀₀ of 2.2 ± 0.5 mm, and a major:minor width ratio of 1.2 ± 0.3 (values expressed as means ± SD). From the OCT images, we approximated the major and minor diameters of the trabeculae that represented the way an experimentalist may have been able to measure using a microscope and an angled mirror. These major and minor diameters averaged 300 ± 100 µm and 260 ± 40 µm, respectively.

Possible Influence of Motion

It is important to consider the possibility that any changes to the Ca²⁺ transient may be a consequence of motion artifacts, as has been considered previously (7). Here, motion artifacts were investigated in a separate experiment using a gated imaging protocol (20). The imaging systems of the cardiomyometer are fixed at the center of the measurement chamber and have limited fields of view. Hence, to capture imaging data for the entire trabecula, it must be moved relative to the imaging systems. The upstream and downstream hooks can move in synchrony to achieve such a movement. By moving the trabecula to five different positions within the measurement chamber each 50 μm apart, we were able to perform gated imaging on an actively contracting trabecula (20). At each position, the trabecula performed work-loop contractions with the same loading conditions (i.e., preload and afterload) while bright-field images (100 fps) and stress and fluorescence data (20 kHz) were captured.

Following the experiment, the bright-field and fluorescence images were analyzed using a weighted averaging technique. First, the bright-field images from each window were stitched together and a central point in the most upstream imaging window was tracked using a subpixel registration algorithm (28). A measured Gaussian function of the regional fluorescence signal intensity was aligned with each bright-field imaging window. The tracking information was used to determine the relative signal intensity of the tracked point for each window at each time point. These signal intensities were normalized to the total sum to generate weighting factors and applied to the fluorescence signal from each window. The closer the tracked point was to the center of an imaging window, the greater the weighting factor for the fluorescence signal of that window. There was less than a 0.5% difference in the Ca²⁺ transient amplitude between the motion-compensated and uncompensated signals. Hence, the Ca²⁺ fluorescence signals reported here were not compensated for motion.

Data Analysis

Data were acquired using custom-written LabVIEW (National Instruments) software and analyzed offline using a series of custom-written MATLAB (MathWorks) programs. Muscle-specific averages of 10 steady-state force twitches and Ca²⁺ transients were computed for each preload and afterload, and various parameters describing active stress and Ca²⁺ dynamics were extracted (Fig. 1). Data would have been discarded if a trabecula experienced stress rundown of more than 20% for a single preload (29). However, no trabecula that underwent the entire protocol exhibited rundown to this extent. Active stress rundown per preload was 6.9% ± 5.3% (mean ± SD).

Figure 1.

Twitch stress and Ca²⁺ transient parameters. Each panel shows a transient computed by averaging 10 steady-state stress twitches or Ca²⁺ transients. The passive component of stress twitches has been accounted for and only the active stress is shown. A: twitch duration measurements for an averaged isometric stress profile. t_durx refers to the time that stress remained greater than X % of the peak active stress and was calculated for 10% (t_dur10), 25% (t_dur25), 50% (t_dur50), and 75% (t_dur75) of the stress amplitude. The shaded area represents the stress-time integral (STI). B: twitch duration measurements for an averaged work-loop contraction. For this work-loop twitch, the afterload was 0.31 (decimal fraction of the peak isometric stress) as achieved by setting R_p to 50 kPa·s/mL. Four measures of twitch duration (as in A) were assessed, but only t_dur10 and t_dur75 have been included on the panel to mitigate visual clutter. The shaded area represents the integral of the twitch. C: twitch duration measurements for an averaged Ca²⁺ transient. t_durx here refers to the time that the fluorescence signal remained greater than X % of the peak signal and was calculated for 10% (t_dur10), 25% (t_dur25), 50% (t_dur50), and 75% (t_dur75) of the Ca²⁺ transient amplitude. The F₃₄₀/F₃₈₀-time integral (CTI) is represented by the shaded area. D: decay time measurements for an averaged Ca²⁺ transient. t_X equates to the time to X % decay from the peak fluorescence and was calculated for 25% (t₂₅), 50% (t₅₀), 75% (t₇₅), and 90% decay (t₉₀). The maximum rate of rise for stress and Ca²⁺ transients was also computed but have not been included on any panels.

Muscle force was converted to stress using the measured cross-sectional area. Active twitch stress under the isometric contraction was revealed by subtracting the constant passive force from the total twitch stress (Fig. 1A). For work-loop contractions, the dynamic nature of the passive component of total stress during work-loop contractions meant that it was necessary to account for this dynamic effect when extracting parameters pertaining to active stress dynamics. This was achieved by first fitting a third-order polynomial to the passive stress-length trajectory of the lowest afterloaded work-loop. In combination with the fit results, the stored length information for a work-loop twitch was then used to estimate the dynamic passive force. Subtracting the resultant passive estimate from the total force isolated the active component for analysis (Fig. 1B).

The dynamics of stress were analyzed using the following parameters: stress-time integral (STI), maximum rate of stress development (dS/dt), and various twitch durations (t_dur75, t_dur50, t_dur25, and t_dur10). The twitch durations represent the time that stress remained greater than X % of active stress, where X is the subscript number (e.g., 25 in t_dur25). Equivalent parameters were extracted to analyze the Ca²⁺ dynamics in the form of F₃₄₀/F₃₈₀ time integral (CTI), maximum rate of F₃₄₀/F₃₈₀ rise (dF₃₄₀/F₃₈₀/dt), and transient durations (t_dur75, t_dur50, t_dur25, and t_dur10). In addition, various decay timings (t₂₅, t₅₀, t₇₅, and t₉₀), time to peak (t_peak), diastolic, peak, and F₃₄₀/F₃₈₀ amplitude were calculated. The decay timings represent the time the Ca²⁺ signal takes to decay by X % from the peak (e.g., t₂₅ represents the time for the Ca²⁺ transient to decay by 25% from the peak F₃₄₀/F₃₈₀ signal). With the exception of the rate of rise of stress and F₃₄₀/F₃₈₀, all parameters are illustrated in Fig. 1.

These parameters were plotted against relative end-systolic stress (ESS). ESS was defined as the stress at the time point where muscle length stopped reducing at the end of the shortening phase and represents the afterload experienced by the muscle. This was expressed relative to the isometric stress of the associated initial length. Hence, relative ESS was equal to 1 for isometric contractions.

Statistical Analysis

An F test was performed for each parameter to determine whether a first- or second-order polynomial was sufficient to describe the relationship. The relationship included the parameters pertaining to twitch stress, and those pertaining to the Ca²⁺ transient, as functions of relative ESS. Statistical regression between the independent and dependent variables was performed using SAS software (Copyright 2021 SAS Institute Inc.). Linear mixed-effect models in SAS were used with muscle number treated as a random effect, and the initial muscle length (preload) and relative ESS (afterload) treated as fixed effects. A compound symmetry covariance structure was used in the model statement as this corresponded with the model with the smallest Akaike information criterion value. Afterload dependence was considered significant for each preload if the P value associated with either the linear term or, when applicable, the quadratic term, in the fixed effect between independent and dependent variables was <0.05. The effect of preload was considered significant if the P value associated with the “Contrast” statement in SAS output between the two regression lines for L₁₀₀ and L₉₅ was <0.05.

RESULTS

Data were obtained to elucidate the effects of preload and afterload on the Ca²⁺ handling of cardiac muscle during isometric (Fig. 1A) and work-loop (Fig. 1B) contractions. These data consist of stress (Fig. 1, A and B) and Ca²⁺ (Fig. 1, C and D) information collected from seven right-ventricular trabeculae, each exposed to a series of work-loops at six different afterloads and two different initial muscle lengths of L₁₀₀ and L₉₅. Several parameters were quantified from these average twitches and Ca²⁺ transients, including the timings annotated in Fig. 1. The average minimum relative ESS across the seven muscles determined the plotting range used for the linear regression for each preload.

The stress, length, and F₃₄₀/F₃₈₀ profiles from an exemplar trabecula at each preload are superimposed in Fig. 2, with the stress-length work-loops presented in Fig. 2, D and H. Increasing R_p increased afterload and thereby increased ESS. Afterload did not appear to affect the amplitude of the Ca²⁺ transient but had effects on the duration of the Ca²⁺ transient (Fig. 2, C and G). The afterload-induced effects on the duration of Ca²⁺ transient appeared to be less pronounced at the reduced preload (Fig. 2G vs. Fig. 2C). A secondary component of the Ca²⁺ transient relaxation phase, or “bump,” appeared to be more pronounced during isometric contractions (Fig. 2, C and G) and at the greater preload (Fig. 2C vs. Fig. 2G). The isometric active stress at L₁₀₀ was 37 ± 17 kPa and the resting tension was 7 ± 4 kPa, which were significantly greater (P < 0.01) than those at L₉₅ (the isometric active stress was 23 ± 10 kPa and the resting tension was 3 ± 1 kPa; each presented as means ± SD).

Figure 2.

Stress-length work loops and Ca²⁺ transients of a representative trabecula at two different preloads. Steady-state twitch stress (A and E), muscle length (B and F), and Ca²⁺ transient (C and G) for a set of work loops over a range of afterloads at fixed preloads set by holding the muscle at L₁₀₀ (A–D) and L₉₅ (E–H). In all panels, twitches are overlaid. The solid dark line represents the isometric twitch. The dashed line represents the work-loop twitch at the lowest afterload. D and H: steady-state stress-length work loops are revealed when stress and length traces are plotted parametrically for each preload.

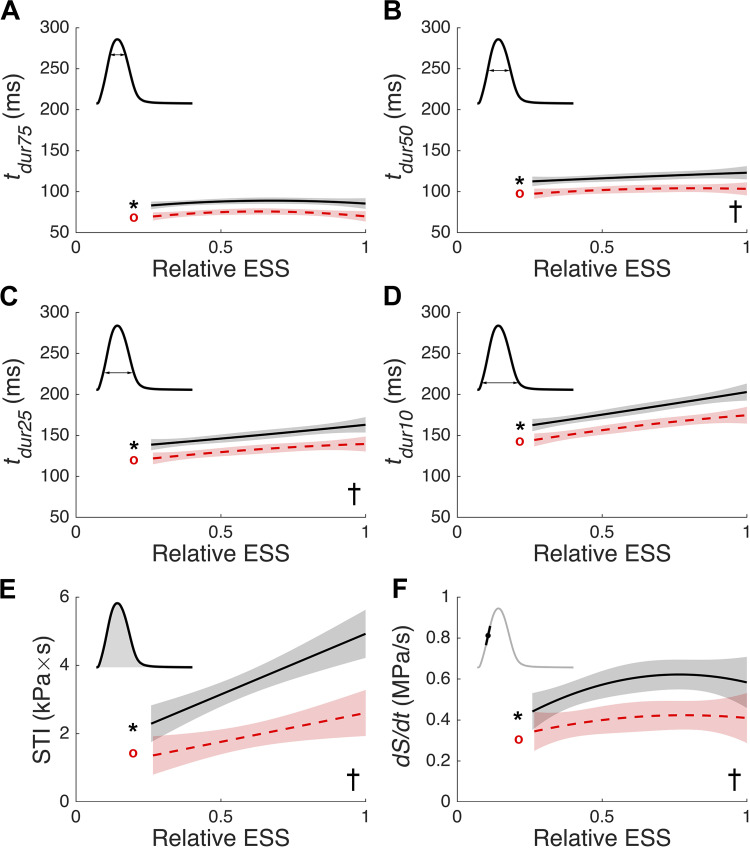
Figure 3 shows the effects of preload and afterload on stress production. At both preloads, all twitch duration metrics (t_dur75, t_dur50, t_dur25, and t_dur10) increased with increasing afterload (Fig. 3, A–D). The regression line between duration and relative ESS at L₁₀₀ was significantly different from that at L₉₅, only for t_dur50 (Fig. 3B) and t_dur25 (Fig. 3C). Both the stress-time integral (STI) and maximum rate of rise of stress were afterload and preload dependent (Fig. 3, E and F). The afterload dependence of the maximum rate of rise of stress (dS/dt) reached a plateau at higher afterloads (Fig. 3F). Similarly, the time that peak dS/dt occurred followed a comparable trajectory to the afterload-dependence of maximal dS/dt (not shown). It is worth noting that the time at which dS/dt occurred always preceded the commencement of shortening in work-loop contractions.

Figure 3.

Preload and afterload dependence of the steady-state stress production. Data from 14 different experimental conditions on n = 7 muscle samples were analyzed to extract the following parameters: twitch durations (A–D), stress-time integral (STI; E), and the maximum rate of rise of stress development (dS/dt; F). The fixed-effect results of the linear mixed-effects model fitting are indicated for each of the two muscle lengths: L₁₀₀ is indicated with a solid black line, and L₉₅ is indicated with a dashed red line. The pale shading surrounding each fitted line indicates the 95% confidence band, calculated from the covariance matrix [as described previously (30)]. STI against relative ESS was fitted with a first-order polynomial; all other stress parameters were fitted with a second-order polynomial. These data are plotted against afterload, expressed as “relative ESS.” Each panel contains an inset that indicates how the respective metric was calculated. Data were analyzed using linear mixed-effect models implemented in SAS with muscle number treated as a random effect, and the initial muscle length (preload) and relative ESS (afterload) treated as fixed effects. *Significant afterload dependence at L₁₀₀; red ^osignificant afterload dependence at L₉₅; †significant preload dependence. ESS, end-systolic stress.

No statistically significant afterload or preload dependence was observed in the F₃₄₀/F₃₈₀-time integral (CTI), peak, diastolic, amplitude, or the maximum rate of rise of the F₃₄₀/F₃₈₀ signal (Fig. 4, A–D, respectively).

Figure 4.

Preload and afterload dependence of Ca²⁺ transient. Data from 14 different experimental conditions on n = 7 muscle samples were analyzed to extract the following parameters: F₃₄₀/F₃₈₀ time integral (CTI; A), peak (upper lines) and diastolic (lower lines) F₃₄₀/F₃₈₀ signal (B), the F₃₄₀/F₃₈₀ signal amplitude (C), and the maximum rate of rise of the F₃₄₀/F₃₈₀ signal (D). The fixed-effect results of the linear mixed-effects model fitting for each of the two muscle lengths, L₁₀₀ is indicated with a solid black line and L₉₅ is indicated with a dashed red line. The pale shading surrounding each fit indicates the 95% confidence band, calculated from the covariance matrix [as described previously (30)]. These data are plotted against afterload, expressed as relative ESS. ESS, end-systolic stress. Data were analyzed using linear mixed-effect models implemented in SAS with muscle number treated as a random effect, and the initial muscle length (preload) and relative ESS (afterload) treated as fixed effects.

However, as suggested by the representative data in Fig. 2, C and G, some of the Ca²⁺ transient durations were afterload and preload dependent. Like the twitch duration metric, t_dur25 (Fig. 5C) increased with increasing afterload at L₁₀₀. Yet, unlike in the stress case, both t_dur75 (Fig. 5A) and t_dur50 (Fig. 5B) correlated negatively with afterload, but t_dur10 was afterload independent (Fig. 5D). At L₉₅, only t_dur75 was significantly afterload dependent. There was no significant preload dependence for t_dur75 or t_dur10, but significant preload dependence for t_dur50 and t_dur25. There was neither preload nor afterload dependence in the time to the peak of the Ca²⁺ transient (Fig. 5E). t_dur50 and t_dur25 and the equivalent decay parameters, t₅₀ and t₂₅, aligned well with the start and end of the “bump” in the relaxation phase of the Ca²⁺ transient, respectively.

Figure 5.

Preload and afterload dependence of the time course of Ca²⁺ transient. Data from 14 different experimental conditions on n = 7 muscle samples were analyzed to extract the following parameters: Ca²⁺ transient durations (A–D), time to F₃₄₀/F₃₈₀ signal Ca²⁺ (E), and the time to X % decay from the peak F₃₄₀/F₃₈₀ (F–I). The fixed-effect results of the linear mixed-effects model fitting for each of the two muscle lengths, L₁₀₀ is indicated with a solid black line and L₉₅ is indicated with a dashed red line. The pale shading surrounding each fit indicates the 95% confidence band, calculated from the covariance matrix [as described previously (30)]. These data are plotted against afterload (“relative ESS”). Each panel contains an inset that indicates how each metric was calculated. Data were analyzed using linear mixed-effect models implemented in SAS with muscle number treated as a random effect, and the initial muscle length (preload) and relative ESS (afterload) treated as fixed effects. *Significant afterload dependence at L₁₀₀, red ^osignificant afterload dependence at L₉₅, †significant preload dependence. ESS, end-systolic stress.

The timings associated with the decay of intracellular Ca²⁺ (t₂₅, t₅₀, t₇₅, and t₉₀) were plotted in Fig. 5, F–I. At L₁₀₀, afterload dependence was obtained at the three earlier decay timings (Fig. 5, F–H) only. At L₉₅, afterload dependence was obtained at t₂₅, but not at t₅₀, t₇₅, or t₉₀. Preload dependence was significant at all Ca²⁺ decay timings with the exception at t₂₅. The initial negative relationship between Ca²⁺ decay timing and relative ESS became positive and eventually flat later within the decay phase.

DISCUSSION

To our knowledge, this is the first study to have measured Ca²⁺ transients in isolated cardiac trabeculae under a work-loop contraction mode that mimics the contraction pattern of the whole heart. This represents the first novelty of this study, which has extended the contraction modes studied previously in understanding cardiac Ca²⁺ handling: afterloaded isotonic contraction (5), unloaded shortening (7), and sinusoidal length perturbation (31). The second novelty is the finding that the afterload dependence of the cardiac Ca²⁺ transient is preload dependent, which serves to reconcile conflicting afterload-dependent Ca²⁺ handling results in the literature. We evaluated the effects of preload and afterload on stress and Ca²⁺ dynamics by deriving various morphological and time course parameters (Fig. 1) as functions of relative ESS (Figs. 3, 4, and 5). Reducing preload from L₁₀₀ to L₉₅ diminished the afterload dependence of the Ca²⁺ transient timing, particularly during the decay phase.

Experimental Design Considerations

In these experiments, the work-loop contraction mode was designed to simulate the pressure-volume loop typically observed in vivo (22), with the ability to vary the hemodynamic parameters governing the arterial impedance, the aortic compliance, and peripheral resistance. Isolated right-ventricular trabeculae were made to perform isometric and work-loop contractions over a range of afterloads at two preloads (Fig. 2) to assess their effects on the twitch stress and Ca²⁺ independently and simultaneously. The model parameters for the Windkessel work-loop contractions (R_p, Z_c, and C) were adapted from a previous study (22), in line with the in vivo measurements on the rat (32). Only R_p, which represents the peripheral resistance, was changed in this study as previous work showed its dominant effect on afterload (22). We selected the range of R_p values to encapsulate much of the afterload range between unloaded isotonic and isometric contractions.

Effect of Preload and Afterload on Stress Production

Under Windkessel work-loop loading conditions, the measured stress dynamics aligned well with the existing literature. Twitch stress duration (Fig. 3, A–D) increased with afterload (3, 33, 34). STI (Fig. 3E), an index of cardiac energy expenditure, was enhanced for twitches at greater preloads and afterloads (35, 36). The maximum rate of rise of the stress (dS/dt; Fig. 3F) was greater at longer muscle lengths and higher afterloads for both muscle lengths. As afterload increases, dS/dt reached a plateau at both preloads. This suggests that the limiting factor for dS/dt is the timing of the onset of shortening, which increases with afterload. These results are unsurprising as, for a given preload, the twitch profile will follow the same isometric upstroke until the stress produced is sufficient to overcome the external afterload and initiate muscle shortening. Existing studies unequivocally support this preload (37, 38) and afterload dependence (36, 37, 39). Therefore, using Windkessel work loops did not modify the expected preload- and afterload-dependent stress dynamics consistently observed in the literature.

Effect of Preload and Afterload on Ca²⁺ Handling

Confirming the consistency between our data on the stress dynamics with the literature outlined above enables the consideration of the effects of preload and afterload on Ca²⁺ transients. With the use of an isometric contraction protocol, a length-independent Ca²⁺ amplitude reminiscent of our data (Fig. 4C) has been reported previously (40, 41). However, such a result is not ubiquitous (13, 42, 43). The measurement of length-dependent Ca²⁺ transients may be confounded by the slow-force response of cardiac muscle to sudden length changes, which can induce a transitory modification of the Ca²⁺ transient (44, 45).

The afterload dependence of the Ca²⁺ transient is contentious. Although numerous studies observed a null effect of afterload on the Ca²⁺ transient (6, 8, 31), two studies have reported a negative dependence of Ca²⁺ transient amplitude on afterload (5, 7). The substantial afterload-dependent augmentation of the Ca²⁺ transient seen in trabeculae from failing hearts was much smaller in healthy human trabeculae (5). In addition, Yasuda et al. (7), the other study that observed an acute modification phenomenon, performed a unique experimental protocol of switching between isotonic and isometric every few twitches (7). In our experiment, contraction mode was changed after the stress development and Ca²⁺ amplitude had reached a steady state.

Considering the afterload dependence of Ca²⁺ dynamics at L₁₀₀, only the timing of the transients displayed significant dependence, particularly in the decay phase (Fig. 5). Afterload-dependent Ca²⁺ decay aligns well with both modeling (10–12) and experimental (5, 7, 40) work that studied afterload-dependent Ca²⁺ handling only.

The afterload-dependent behavior observed in the Ca²⁺ transient is well explained by force-modulated cooperativity of Ca²⁺-TnC binding (40, 46). T₂₅ represents the initial decay of the Ca²⁺ transient, and it increased as the afterload decreased (Fig. 5F). Initial Ca²⁺ decline occurs during the upstroke of the force twitch (Fig. 2), where free intracellular Ca²⁺ concentration decreases due to sequestering mechanisms and Ca²⁺ binding to TnC. If the phosphorylation state of the myofilaments is constant with afterload, the reduction of free intracellular Ca²⁺ associated with TnC binding would be proportional to force; the greater the force, the more Ca²⁺ bound to TnC, i.e., cooperativity. Hence, the slower initial decay of Ca²⁺ transients observed at lower afterloads was as expected, largely in line with the force-modulated cooperativity mechanism.

The plateau in the Ca²⁺ transient decay phase, or “bump,” is a morphological feature that has been observed in several animal studies (16, 46, 47) and predicted, to some extent, in silico (12). The bump is thought to be caused by Ca²⁺ dissociation from troponin-C (TnC) during relaxation at a faster rate than it can be sequestered into the sarcoplasmic reticulum (SR) (46). Jiang et al. (46) confirmed that the amplitude of the bump is correlated with the number of bound cross bridges and that the start time of the bump depends on the stress twitch duration. As the twitch duration increased, the bump occurred later in the Ca²⁺ transient. Our results at L₁₀₀ are consistent with the proposed mechanism. At higher afterloads, the overall duration (t_dur10) of the twitch stress increased. As expected, t₅₀, which aligns approximately with the bump onset, decreased with increasing afterload, reflecting the delayed bump onset. Further, t₇₅, which aligns with the bump region, was longer with increasing afterload, reflecting the enhanced bump amplitude. The final metric of the Ca²⁺ decay, t₉₀, is not afterload dependent, and thus it appears that the afterload-induced TnC binding affinity does not affect the overall decay phase of the Ca²⁺ transient.

This is the first study to show, experimentally, some preload-induced modification of Ca²⁺ transient afterload dependency. We found that the decay-related timing metrics t₅₀, t₇₅, and t₉₀ had preload-informed modulation of their afterload dependency. The underlying molecular basis for this warrants further study, but we speculate that it too can be explained by the force-dependent Ca²⁺-TnC cooperativity. This speculation stems from two of our findings. First, the preload was more influential on the overall duration of the Ca²⁺ transient than afterload, as t₉₀ and t_dur10 (Ca²⁺) were shorter at the lower preload while being afterload independent (Fig. 5I). On initial inspection, the preload dependency of the Ca²⁺ transient duration measured within this study directly contradicts preexisting observations that greater muscle lengths are associated with shorter Ca²⁺ transients (48, 49) and with those reporting no length dependence (13). However, the observed behavior seems to align with a force-based binding affinity of TnC (50, 51). At the greater preload, more cross bridges can form, increasing the binding affinity of TnC for Ca²⁺, slowing the eventual Ca²⁺ dissociation (52), thereby extending the duration of the Ca²⁺ transient. Second, greater muscle lengths are associated with an augmented bump area (47) as preload modulates the amount of Ca²⁺ that will bind to TnC due to a greater number of strong-binding, force-producing, cross bridges. At lower preloads, the maximum area of the bump would be reduced, and therefore the previously described afterload-dependent modification of the bump would be less detectable. Hence, we suggest that the preload- and afterload-dependent modifications to the Ca²⁺ transient can be explained by force-dependent TnC binding affinity for Ca²⁺.

Given that the proposed mechanism for contraction-mode-dependent behavior relies solely on a dynamic Ca²⁺-TnC binding affinity, it follows that metrics describing Ca²⁺ release would not demonstrate mode dependence. As expected, the maximum rate of rise of the Ca²⁺ transient was unaffected by preload and afterload (Fig. 4D), as observed previously (6, 33). The time to peak Ca²⁺ was also independent of preload and afterload (Fig. 5E). In the literature, the time to peak Ca²⁺ is length independent in healthy cardiac muscle (13, 47, 48), and the afterload independence is also consistent with data collected from small- to medium-sized mammalian heart tissues (3, 4, 8). We found that the integral of the Ca²⁺ transient (CTI), which provides an insight into the exposure of internal structures to Ca²⁺, was independent of afterload and preload (Fig. 4A). This finding aligns well with data collected under similar experimental conditions (6, 8, 31).

Our results reconcile literature findings wherein the cases that observed no afterload dependence used equivalent muscle lengths much shorter than L₁₀₀ (6, 8) or only exposed preparations to high afterloads where the difference would be difficult to detect (31).

Ca²⁺-Stress Decoupling

Stress and Ca²⁺ dynamics had distinct dependences on preload and afterload (Fig. 3 vs. Fig. 5). Cardiac Ca²⁺-stress decoupling is well known, even in systems with sudden reductions of muscle length (40, 46). Mechanistically, this is unsurprising given that the intracellular Ca²⁺ and the myofilaments only reach dynamic equilibrium at the end of diastole (53). Stress production is enhanced at L₁₀₀ from L₉₅ due to myofilament length-dependent activation underlined by various interactions including, but not limited to, more optimal myofilament overlap (54), reduced interfilament lattice spacing (55, 56), and enhanced sensitivity of the myofilament to Ca²⁺ (57, 58) that is associated with reduced phosphorylation state of TnI (59). Ca²⁺ transients, on the other hand, are dictated by the release and reuptake rates of Ca²⁺, which are dependent on intracellular Ca²⁺ concentration (60). A limitation of fluorescent dyes is that they measure the free intracellular Ca²⁺ (i.e., not bound to TnC). When the muscle shortens during contractions, the affinity for Ca²⁺ decreases and causes some Ca²⁺ to unbind from TnC and “slow” the Ca²⁺ transient decay (61). The complex interplay between the two dynamic systems of the Ca²⁺ transient and the force-producing cross-bridge cycle means that only a minor deviation in the Ca²⁺ transient is necessary to result in the substantial preload- and afterload-dependent twitch stress durations observed.

Ca²⁺ Indicator Considerations

To measure intracellular Ca²⁺ handling in this study, we used the ratiometric fluorescent dye Fura-2 (62). An improper fluorescence loading procedure can result in incomplete acetyl-methyl ester (AM) hydrolysis of Fura-2/AM (63, 64) and subcompartmental loading of the dye into organelles (65, 66). Each of these issues can lead to erroneous fluorescence signals that are not correlated with cytosolic Ca²⁺ concentration. In this study, loading was performed at room temperature and Pluronic F-127 was included in the loading solution to ameliorate these issues, the success of which has been shown previously (67).

It has been suggested that, even at low intracellular concentrations, the rate constants of Fura-2 (k_on and k_off) are too low for the binding reaction of Fura-2 and Ca²⁺ to be at equilibrium during a Ca²⁺ transient (68). Should this be the case, one would expect some distortion of the Ca²⁺ transient morphology, beyond the nonlinear scaling required to transform F₃₄₀/F₃₈₀ to [Ca²⁺]_i (62). As each muscle was exposed to every combination of loading (seven afterloads each at the two preloads) and the order was randomized, these distortions could not have introduced bias into the investigation of load dependence.

The development of novel thin-filament localized sensors has created a new pathway for studying intracellular mechanisms. Sparrow et al. (69) describe the development of a genetically encoded fluorescent Ca²⁺ sensor that is localized to the thin filament. Similar to the fluorescent dyes outlined above, this sensor introduces buffering effects, which may disrupt force production, but has the major advantage of specifically targeting the troponin complex. Should our hypothesis hold true, force-dependent binding rates of Ca²⁺ to Tn should be observed. In addition, Vetter et al. (70) describe a genetically encoded fluorescent sensor that detects, in real time, the distance between TnI and TnC, which can be used to infer when the thin filament is active. Aligned with our hypothesis, loading their samples changed the Tn complex activation twitch, particularly in the duration of the activated period. Their preliminary findings align well with our proposed mechanism and it would be interesting to test explicitly using these technologies.

Contraction-Mode Dependence

The end-systolic stress-length relation under the work-loop contraction mode is lower than that obtained under the isometric contraction mode (1, 2). Whereas recent modeling work predicts some afterload-dependent modifications of the Ca²⁺ transient decay phase (10–12), Shimizu et al. (8) replicated the stress-length profile for isometric and work-loop contractions using a contraction-mode-independent Ca²⁺ transient without including length-dependent myofilament Ca²⁺ sensitivity. This study, therefore, provides the required experimental data for modeling work to reconcile the Ca²⁺ transient with the contraction-mode dependence observed in the stress-length domain.

The Physiological Relevance of Isometric Ca²⁺

It is more common for cardiac physiologists to study Ca²⁺ handling under isometric contraction conditions at L₁₀₀ than contraction modes that allow muscle shortening. Our results comparing these contraction modes raise questions regarding the suitability of using Ca²⁺ measurements under isometric conditions to infer those underlying work-loop contractions. At L₁₀₀, there were significant differences in the decay phase of the Ca²⁺ transients when comparing work-loop and isometric contractions (Fig. 5, F–H). Thus, the isometric and work-loop Ca²⁺ transients at L₁₀₀ are not equivalent. The afterload dependence of the Ca²⁺ decay is modulated by preload, and, at L₉₅, only t₂₅ was afterload dependent. With the results presented in this study, it would seem reasonable to discourage the study of Ca²⁺ handling under isometric conditions for muscle lengths greater than L₉₅.

Limitations

The working range of sarcomeres in an ex vivo heart can range from 1.9 µm to 2.4 µm (71–73). Here, trabeculae were studied at and near the optimal muscle length (sarcomere length of 2.3 µm) to replicate conditions under which ex vivo tissue experiments are commonly performed. As the afterload dependence of Ca²⁺ transients was assessed at only two preloads at L₁₀₀ (sarcomere length of 2.3 µm) and L₉₅, it is difficult to extrapolate the afterload dependence to even lower preloads. At muscle lengths shorter than L₈₅, we have observed that work-loop contractions result in out-of-plane motion where the distance between the trabecula and the microscope objective varied. To avoid this out-of-plane motion confounding the fluorescence signals, we limited the shortest muscle length to L₉₅ as the muscle shortening was ∼10% of the initial muscle length at the lowest afterload (Fig. 2D). Previous mechanistic studies have shown a substantial change in the contraction-mode dependence of the stress-length relation between L₁₀₀ and L₉₅ (2). Hence, we were confident that, should the Ca²⁺ handling be preload dependent, any dependency would be detectable with the two selected preloads. Extrapolating the contraction-mode dependence of the stress-length relation, one could speculate that the afterload dependence of Ca²⁺ transients would continue to diminish as preload is reduced. Perhaps the afterload dependence would be eliminated at the muscle lengths corresponding to the functional sarcomere length in vivo of 2.1 μm (74) or 90% to 95% of the optimal length at physiological end-diastolic pressures (71). A future study may involve the investigation of muscle lengths greater than L₁₀₀ or under interventions that mimic conditions of physiological stress and exercise.

Isometric force control in this study was achieved by maintaining muscle length rather than sarcomere length. We did not measure internal shortening explicitly during this study, though a previous study indicates that sarcomere length may not be homogenous during fixed-end contraction at L₁₀₀ (28). To control the muscle length such that the sarcomere length in the central region is fixed would require stretching the sarcomeres at each end of the trabecula. Furthermore, Janssen and de Tombe (75) showed that uncontrolled sarcomere shortening during isometric contractions, as is the case in muscle length-based control, changes the amplitude of the Ca²⁺ transient but not the timing of Ca²⁺ transients. Thus, we believe that muscle-length control during the isometric phases of the implemented work-loop contraction protocol has negligible impacts on the parameters quantifying the time course of the Ca²⁺ transient, which we found were afterload and preload dependent.

Conclusions

These experiments exploiting work-loop contractions demonstrate that the parameters associated with Ca²⁺ transients display a mixed dependence on afterload and preload. Whereas the amplitude, integral and rates are independent of afterload and preload, the decay-phase time courses are afterload dependent, an effect augmented at the greater preload. These results show a preload dependence to the afterload dependence of the cardiac Ca²⁺ transient and serve to reconcile conflicting literature conclusions regarding whether Ca²⁺ transient is afterload dependent. This study provides ample evidence to discourage the common use of Ca²⁺ transients under isometric conditions to infer those under work-loop contractions.

GRANTS

This study was funded by Doctoral Scholarships from The University of Auckland (awarded to J.M.D. and A.S.G.), Sir Charles Hercus Health Research Fellowships (20/011 and 21/116) from the Health Research Council of New Zealand (awarded to J-C.H. and K.T., respectively), a Doctoral Scholarship awarded by the Heart Foundation of New Zealand (awarded to A.A.), Marsden Fast-Start grants (UOA1504 and UOA1703) from the Royal Society of New Zealand (awarded to J-C.H. and K.T., respectively), and a James Cook Research Fellowship from the Royal Society of New Zealand (awarded to A.J.T.). The original development of this instrument was funded by a Marsden grant (11-UOA-199) from the Royal Society of New Zealand (awarded to A.J.T. and P.M.F.N.).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

J.M.D., K.T., A.S.G., A.J.A., P.M.F.N., A.J.T., and J-C.H. conceived and designed research; J.M.D. performed experiments; J.M.D. and J-C.H. analyzed data; J.M.D. interpreted results of experiments; J.M.D. prepared figures; J.M.D. drafted manuscript; J.M.D., K.T., A.S.G., A.J.A., P.M.F.N., A.J.T., and J-C.H. edited and revised manuscript; J.M.D., K.T., A.S.G., A.J.A., P.M.F.N., A.J.T., and J-C.H. approved final version of manuscript.