Abstract
The increasing consumption of ducks and chickens in China demands characterizing carcasses of domestic birds efficiently. Most existing methods, however, were developed for characterizing carcasses of pigs or cattle. Here, we developed a noncontact and automated weighing method for duck carcasses hanging on a production line. A 2D camera with its facilitating parts recorded the moving duck carcasses on the production line. To estimate the weight of carcasses, the images in the acquired dataset were modeled by a convolution neuron network (CNN). This model was trained and evaluated using 10-fold cross-validation. The model estimated the weight of duck carcasses precisely with a mean abstract deviation (MAD) of 58.8 grams and a mean relative error (MRE) of 2.15% in the testing dataset. Compared with 2 widely used methods, pixel area linear regression and the artificial neural network (ANN) model, our model decreases the estimation error MAD by 64.7 grams (52.4%) and 48.2 grams (45.0%). We release the dataset and code at https://github.com/RuoyuChen10/Image_weighing.
Key words: machine learning, duck carcasses weighing, convolutional neural networks, image-based weighing
INTRODUCTION
As the world economy develops, the production and consumption of meat have been increasing significantly. From 1961 to 2018, the production of meat increased 4 folds worldwide and more than 34 folds in China (Ritchie et al., 2017). Though most meat from pigs and cattle, China consumes and produces most of the chickens and ducks in the world (Li et al., 2017). In 2018, China produces 20.12 million tons of poultry and more than 3 million tons of ducks (Ritchie et al., 2017).
For quality control and monitory evaluation, the factories characterize the animal carcasses during production. Among all the characteristics of animal carcasses, weight is a key feature for daily management (Brown et al., 2014; Jones and Dawkins, 2010). According to its weight, the carcass is processed using, different methods for a better economic outcome (Adamczak et al., 2018). However, most production lines for handling duck carcasses do not have an automated section for automatic weighing. Factories often require manual weighing or use an additional conveyor to assist in weighing. The widely used conveyor scales require transferring carcasses between the conveyor scale and the production line (Jørgensen et al., 2019), which is labor-intensive and time-consuming. While some modern systems enable efficient carcass quality grading, for most factories, upgrading existing production lines is cumbersome and costly. It is important to develop a low-cost and efficient weighing method.
Noncontact weighing methods were developed to improve the weighing efficiency (Scollan et al., 1998; Oviedo-Rondón et al, 2007; Jørgensen et al., 2019). Oviedo-Rondón et al. (2007) developed a real-time ultrasound system to estimate the breast muscle weight of broiler chickens. Scollan et al. (1998) developed a nuclear magnetic resonance imaging (MRI) system to estimate the weight of the Pectoralis muscle of chickens. These methods require cumbersome instruments and hard to fit into the production line.
In contrast, cameras can be easily installed and suitable for the production line. Two types of computer-vision enabled noncontact weighing methods have also been extensively studied: classification and regression (Lotufo et al., 1999; Nyalala et al., 2021; Teimouri et al., 2018). In classification methods, the carcass weight is classified into one of the evenly divided grades (weight ranges) (Chen et al., 2017; Koodtalang and Sangsuwan, 2019; Qi et al., 2019). The prediction accuracy of this method, however, was limited by the size of the weight range. For example, Qi et al. (2019) divided the carcass of chickens into 5 grades each with 300 grams range.
The current image weighing methods are based on regression models using 3D images (Adamczak et al., 2018; Jørgensen et al., 2019) or 2D images (Lotufo et al., 1999; Nyalala et al., 2021). In these methods, a weight prediction model was built based on several manually extracted features. Based on machine vision, Lotufo et al. (1999) proposed a real-time broiler carcasses weighing system. They split an image of a chicken into 5 parts and used their pixel area to estimate the weight of this chicken. Teimouri et al. (2018) separated and sorted the chicken body parts using geometrical, color, and texture features. Integrating 2D and 3D features, Jørgensen et al. (2019) predicted the weight of a single carcass better than the ones using 2D features. Obtaining 3D features of carcasses, however, requires multiple cameras and more facilitating devices; meanwhile, simultaneous 3D reconstruction algorithms are often computational and time consuming. It thus is still attractive to estimate the weight of small animals using 2D images. Nyalala et al. (2021) segmented the depth images of broiler carcass into 5 parts, extract 2D features, and estimated the weights of different parts using different regression models. We found that most methods require handcrafted features which will determine the upper bound of the model performance (Chen et al., 2021). Because of the hidden relationship between the weight and features, it's difficult to manually design high-quality features. Though the rising consumption of ducks, most methods were developed for estimating the weights of the chicken carcasses. Few methods have been developed to predict the weights of duck carcasses.
In this paper, we proposed a convolutional neural networks (CNN) regression model to estimate the weights of white Pekin duck carcasses. Using CNN, our method avoids the biases caused by human-involved feature selection. We developed an image acquisition system integrated with the duck carcasses production line. Using this system, we further collected a dataset including 150 images from 50 ducks. The developed CNN regression model was trained and validated using 10-fold cross-validation. For the testing dataset, our model achieved a MAD of 58.8 grams and a MRE of 2.15%, decrease the estimation error compared to the pixel area linear regression model (MAD of 123.5 grams and MRE of 4.60%) and the artificial neural network (Kashiha et al., 2014) model (MAD of 107.0 grams and MRE of 3.79%).
To sum up, our method is mainly oriented to duck carcass production lines without an automatic weighing function. These production lines can easily incorporate our measurement methods at a low cost. Our method can also be a powerful tool for facilitating carcass sorting by weight, which is a routine procedure in duck processing lines. This was achieved by a new image-based weighing method. Compared with previous methods, our method automatically abstracts features and greatly improves the accuracy of white Peking duck weight estimation.
MATERIALS AND METHODS
Data Collection
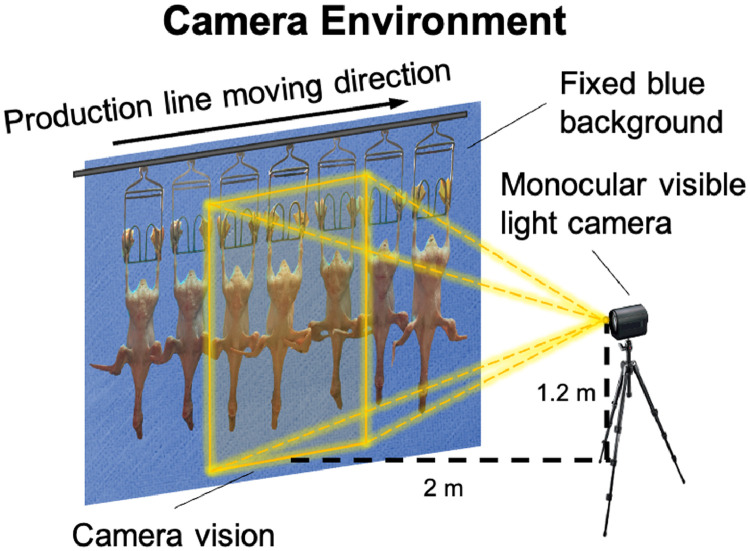
The dataset was collected in the food processing department of a duck husbandry factory (Shandong Hongye Food Co. Ltd., Shandong, China). The working environment and camera setting are shown in Figure 1. A monocular visible-light camera was mounted on a tripod two meters away from the production line. The camera was set to keep the white Pekin ducks in its focal plane and the center of its vision. To reduce noise, the background of the production line was set to blue by a piece of cloth. The production line ran at 0.5 meters per second. To ensure image quality, the camera shot at 30 frames per second. These ducks were weighed using an electronic balance to evaluate our model.
Figure 1.
The image acquisition setting and site environment.
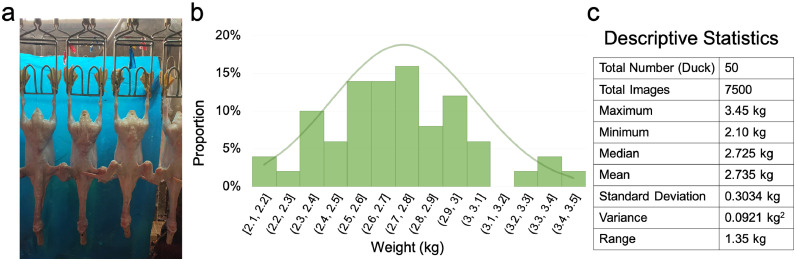
The dataset included 50 ducks, each with 150 images from different angles (Approximately ±30 degrees), the shooting scene of the photo is shown in Figure 2A. The bodyweight distribution of 50 duck carcasses is shown in Figures 2B and 2C depicts the statistics of the dataset. Images of 45 randomly selected ducks were set as the training set. For the remaining 5 ducks, 20% of their images were randomly selected as the validation set, and the remaining 80% of images were used as the test set. The training set was used to optimize the parameters of the network, the validation set was used to validate the accuracy and generalization ability of the network in the training process, and the test set was used to test the accuracy of the network after training and to ultimately evaluate the accuracy and generalization ability of the network.
Figure 2.
Description of the collected dataset. (A) Photos taken from a real camera perspective. (B) Weight distribution map of 50 collected white Pekin duck carcasses. (C) The descriptive statistics of the measured weight of white Pekin duck carcasses.
Data Preprocessing
To weigh individual ducks, the shapes of the ducks were extracted from their images. This step, however, was limited by several characteristics of the images, such as background noises and overlap between ducks. To accurately estimate the weight of ducks, the images were preprocessed as follows. As shown in Figure 7 in the appendix, the R (red) channel of the images had the best contrast between the ducks and the blue background (see Figure 7 in the appendix). The R channel of each image was thus extracted for further analysis to reduce the computing level in our model. To reduce the low-level background noise, pixel values below 40 were set to 0, and those above 40 were set to 255, the maximum value. The information other than that in the duck area was removed by an open operation using a 5 × 5 kernel with the value of 1. The ducks’ feet were of essentially the same weight, so their feet were excluded from the images (additional experimental results are shown in in Figure 9 in the appendix). The section of 300 pixels below the iron frame was used as the duck images. To reduce the computational cost and the number of parameters to optimize, the extracted images of individual ducks were scaled from 1,015 × 321 down to 253 × 80 pixels and labeled with their weights. The pixel values were further normalized to [0, 1].
CNN Regression Model
Our model was developed using Python (Version 3.7) and TensorFlow (Version 1.15.0) on a computer with a GTX 1080Ti graphics card. The two comparative models, the area-based linear regression model, and the artificial neural network (Kashiha et al., 2014) model were developed using MATLAB (Version 2019A).
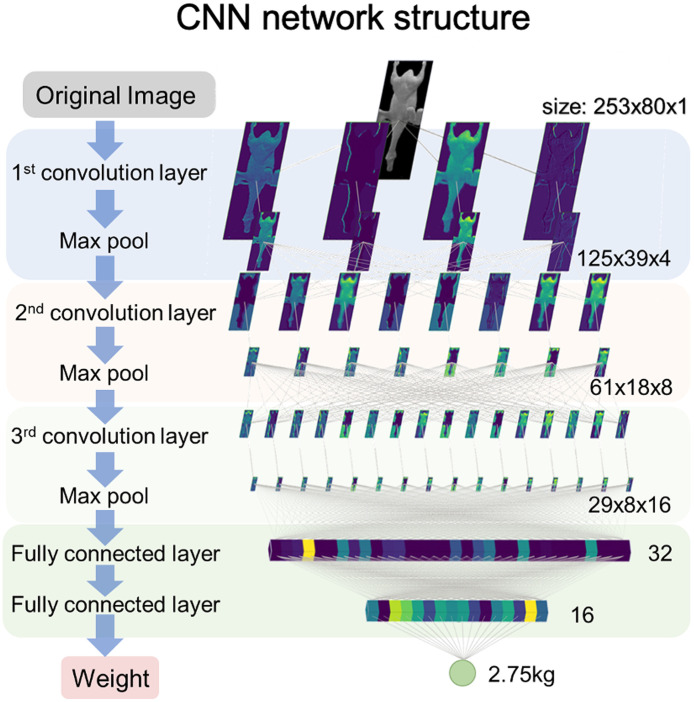
Our model was built based on CNN for regression tasks. The architecture of this CNN model is illustrated in Figure 3. The input of this model was an image with 253 × 80 pixels. The model included three convolutional layers, 2 fully connected layers, and one output layer. The kernel size of each convolutional layer was 3 × 3, and the convolution stride was set to 1 without padding. Each convolution operation was followed by a softplus activation function (Dugas et al., 2000) and a pooling layer with a 2 × 2 pooling window and 2 strides with no padding. The two fully connected layers contained 32 nodes and 16 nodes, respectively. Both layers had a dropout rate of 10% during training and were equipped with the softplus activation function. The output layer had no activation function. During the validation and testing process, no dropout was performed.
Figure 3.
The scheme of the convolutional neural network for white Pekin duck carcass weight estimating.
The model was trained using mini-batch gradient descent with the Adam optimization method (Kingma and Ba, 2015), and the loss function for the optimizer was a mean squared error (MSE), as given in the following formula:
| (1) |
where and denote the predicted and real weight of the duck in the ith image, respectively, and refers to the batch size. To converge faster during training, the decay learning rate was used as described in the following formula:
| (2) |
where denotes the initial learning rate (), denotes the decay rate (0.99), and and denote the decay steps (1,000) and global steps, respectively. The initial learning rate and decay rate were selected based on the authors’ experiences.
RESULTS AND DISCUSSION
Estimating the Weight of Ducks
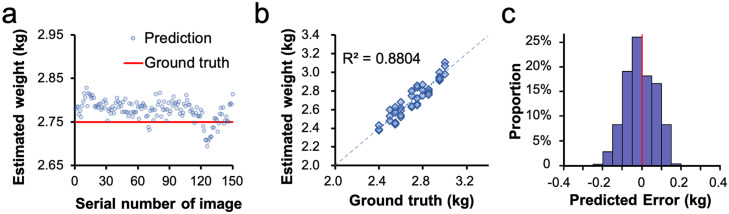
We evaluated the proposed CNN model for estimating the weight of ducks. The input images were grouped based on ducks. In each test set of the 10-cross-validation, we randomly selected 45 ducks as the training set and the remaining 5 ducks as the testing set (20% of images for the ducks from the testing set were selected as the validation set). In this way, the different images of the same duck will not exist in the training set and the testing set at the same time. The estimated weights from each of the 150 images of the same duck are shown in Figure 4A. For a stable and accurate estimation of the weight, the mean of these 150 results was used as the final estimation weight (Luo et al., 2018). The predicted error was defined as the difference between the estimated and the true weight of the duck. The relative error (Teimouri et al., 2018) was defined as the ratio of the predicted error to the ground truth y. Mean Relative Error (MRE) was defined by the average of RE in the test set. The accuracy of the model was evaluated by the Mean Absolute Deviation (Kashiha et al., 2014) and Mean Relative Error (MRE), as represented by the following formula,
| (3) |
| (4) |
where refers to the number of weighed ducks, is the estimated weight, and is the true weight of the i-th duck. The MAD of the proposed model was 58.8 g. The MRE was 2.15%. The estimated results of the 50 ducks against the ground truth are shown in Figure 4B. The distribution of the predicted error (Picouet et al., 2010) of all the testing images is shown in Figure 4C.
Figure 4.
Result of the model test. (A) The estimated weight of one duck in different angles. (B) The estimated results against the original weight of 50 samples. (C) PE distribution of the individual images of 50 samples, 7,500 images in total.
We also evaluate our model on some other metrics including , RMSE, and CVe (coefficient of variation of the residual standard), as shown below,
| (5) |
| (6) |
| (7) |
where is the estimated weight, and is the ground true weight of the i-th animal carcass. , RMSE and CVe were 0.8804, 63.6 grams, and 2.33%, respectively.
Comparison With Other 2D Based Methods
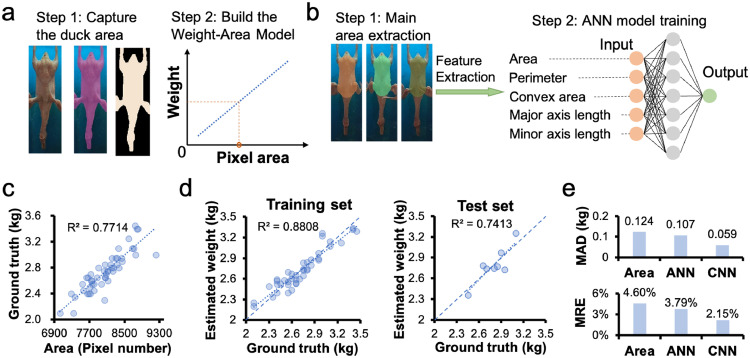
To accurately evaluate the performance of our CNN model, we compared it with the other 2 image-based weighing methods. The first was a linear regression model between the weight and the 2D pixel area of a duck (Mollah et al., 2010; Balaban et al., 2010a,b; Kashiha et al., 2014). The process of capturing the duck area and building the model is illustrated in Figure 5A. To reduce the complexity caused by different imaging angles, the ducks’ images in the center of the camera field of view were captured. These images were used to extract features in this section, which contribute to high weighing accuracy for the method (Lotufo et al., 1999). After the 50 ducks’ areas were extracted, we estimated the weights of the ducks from their area using linear regression. As shown in Figure 5C, The MAD was 123.5 grams, the MRE was 4.60%, and the was 0.7714. These results suggested that the accuracy of this method is less than optimal for weighing ducks on the production line.
Figure 5.
(A) The linear regress model by pixel area. (B) The ANN model. Five features were extracted from the duck's back area and the weight was regressed with ANN. (C) The linear regress results from the linear regress model. (D) The estimated results against the original weight of the training set and testing set in Bayesian regulation training algorithm. (E) Comparison among the three methods.
The second method compared was an artificial neural network (Kashiha et al., 2014) model. The ANN model regressed the weight through features extracted from the duck's image, as illustrated in Figure 5B. This method has been used by Amraei et al. (2017) for estimating the weights of broilers. In their work, the limb, neck, and head were not included in the area to capture the main features of the broiler's weight. Here, we similarly captured the area for the convenience of comparison. The circular kernel of 1 value in size of was used by a morphological open operation to segment the back of the duck as a binarized image. Five features, including area, perimeter, convex area, major axis length, and minor axis length, were captured from the segmented image. The ANN model with one hidden layer was trained using the nntool toolbox in MATLAB. Default parameters were adopted for the training: sigmoid as the transfer function for the hidden layer, MSE as the loss function, and learn gradient descent with momentum backpropagation as the adaption learning function. Table 1 shows the configuration and the estimated weight results of the ducks and the broilers. The model with nine hidden neurons and a Bayesian regulation training algorithm achieved the lowest MAD of 107.0 grams and an MRE of 3.79%. Figure 5D shows the estimated results against the original weight of the training set and testing set in the Bayesian regulation training algorithm. This is similar to the performance of this ANN method in estimating the weight of broilers.
Table 1.
Results in different configurations and training algorithms.
| Training algorithm | Number of neurons | Training MAD (gram) | Training RMSE (gram) |
Broilers training RMSE (gram) (Amraei, et al., 2017) |
Testing MAD (gram) | Testing RMSE (gram) | Broilers testing RMSE (gram) (Amraei, et al., 2017) |
|---|---|---|---|---|---|---|---|
| Gradient descent | 7 | 129.4 | 161.76 | 150.66 | 183.7 | 217.87 | 157.12 |
| Levenberg–Marquardt | 10 | 70.9 | 89.65 | 89.63 | 149.7 | 209.87 | 91.59 |
| Scaled conjugate gradient | 11 | 114.4 | 137.59 | 115.10 | 113.6 | 131.55 | 121.63 |
| Bayesian regulation | 9 | 88.5 | 109.48 | 80.68 | 107.0 | 121.59 | 82.37 |
Comparing the results of these three methods, the CNN model outperformed the other methods in estimating the weight of ducks from 2D images, as shown in Figure 5E. The estimation error of the ANN method was about 2 times higher than that of the CNN model. In addition, the CNN model could automatically extract features, avoiding the insufficiency of features due to artificial extraction while offering more convenience.
Hyperparameter Optimization
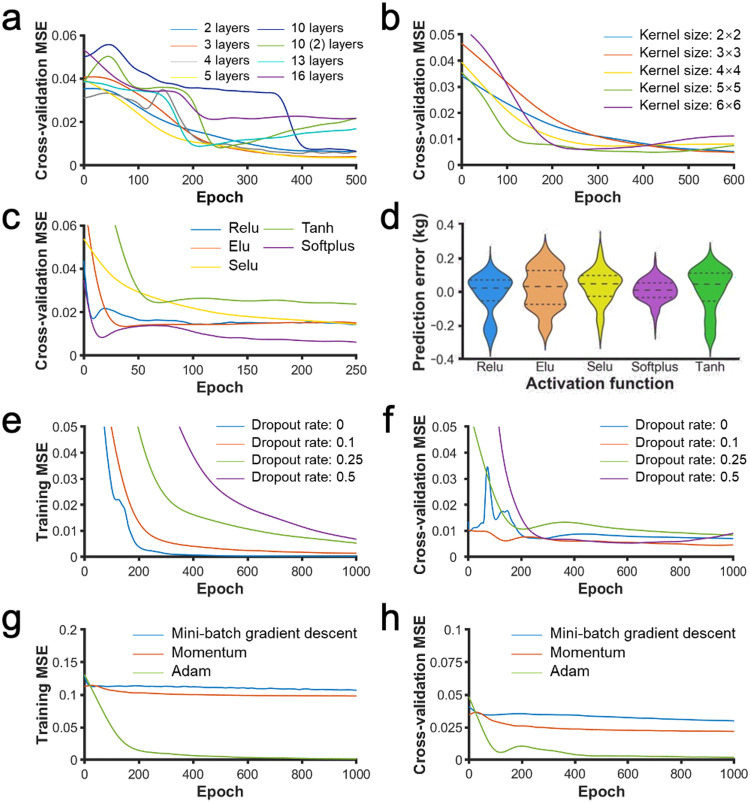
Here, we discuss the effects of hyperparameters on the performance of the model. The hyperparameters included depth of layers, kernel size, activation function, dropout rate, and optimization method. We found that activation function and optimization method are the most influential factors. The effects of activation function were demonstrated using the error distribution on the test dataset. The Adam optimization method was the only method that fits the training dataset well. Its effects on model accuracy were demonstrated using learning curves. We found that softplus (Dugas et al., 2000) activation function and Adam (Kingma and Ba, 2015) optimization method can fit the datasets effectively. The effects of depth of layers, kernel size, and dropout rate on model accuracy were presented using learning curves. The learning curves shown in Figure 6 were smoothed by smooth spline method.
Figure 6.
The learning curves (smoothed by smooth spline method) and the predicted error distribution of the CNN models with different hyperparameters. (A) The cross-validation MSE in different convolution layers. (B) The cross-validation MSE in different kernel sizes. (C) The cross-validation MSE in different activation functions. (D) The predicted error distribution for different activation functions. (E) The training MSE and (F) the cross-validation MSE in different dropout rates. (G) The training MSE and (H) the cross-validation MSE in different optimization methods.
Depth of Convolutional Layers
The number of convolutional layers is a crucial factor for the CNN model (Simonyan and Zisserman, 2015). To optimize the regression results, we tested eight different CNN structures (Table 2). The first convolutional layer had 4 kernels. For the following convolutional layers, this number doubled relative to the previous one. The normal distribution initialization method was used for the initial convolution kernel. All the convolutional layers were activated using a softplus activation function. Max-pooling was performed on these layers. In all these 8 models, the fully connected layers had the same structure. The learning curves for the training dataset, as shown in Figure 8A in the appendix, demonstrated that all networks fit the training dataset well. The learning curves for the validation dataset were shown in Figure 6A. The 3-layer CNN model and 5-layer CNN model achieved the lowest MSE on the validation set (Figure 6A). Though the 3-layer and 5-layer CNN models converged at a similar number of epochs, the 3-layer CNN model converged faster because its epoch is shorter than that of the 5-layer model. Meanwhile, the 3-layer model has fewer parameters. We thus selected the 3-layer CNN model.
Table 2.
The structure of eight types of CNN models. Each convolution layer and fully connected layer followed a softplus activation function, except the output layer. The size of each convolution kernel was 3 × 3, and the stride was 1 without padding. For the max-poolling operation, the pool window was 2 × 2, and the stride was 2 without padding. The convolutional layer parameters are denoted as “Conv-(numbers of kernels)”, and the fully connected layer parameters are denoted as “Dense-<number of nodes>”.
| 2 layers | 3 layers | 4 layers | 5 layers | 10 layers | 10 (2) layers | 13 layers | 16 layers |
|---|---|---|---|---|---|---|---|
| Input (253×80×1) | |||||||
| Conv-4 | Conv-4 | Conv-4 | Conv-4 | Conv-4 Conv-4 |
Conv-4 Conv-4 |
Conv-4 Conv-4 |
Conv-4 Conv-4 Conv-4 Conv-4 |
| Max Pool | |||||||
| Conv-8 | Conv-8 | Conv-8 | Conv-8 | Conv-8 Conv-8 |
Conv-8 Conv-8 |
Conv-8 Conv-8 Conv-8 |
Conv-8 Conv-8 Conv-8 Conv-8 |
| Max Pool | |||||||
| \ | Conv-16 | Conv-16 | Conv-16 | Conv-16 Conv-16 Conv-16 |
Conv-16 Conv-16 Conv-16 |
Conv-16 Conv-16 Conv-16 Conv-16 |
Conv-16 Conv-16 Conv-16 Conv-16 |
| Max Pool | |||||||
| \ | Conv-32 | Conv-32 | Conv-32 Conv-32 Conv-32 |
Conv-32 Conv-32 Conv-32 |
Conv-32 Conv-32 Conv-32 Conv-32 |
Conv-32 Conv-32 Conv-32 Conv-32 |
|
| Max Pool | |||||||
| Max Pool | |||||||
| Conv-64 | |||||||
| Max Pool | Max Pool | ||||||
| Dense-32 (dropout rate 0.1) | |||||||
| Dense-16 (dropout rate 0.1) | |||||||
| Dense-1 | |||||||
Kernel Size
The kernel size of CNN is crucial for model performance. Therefore, we evaluated 5 kernel sizes based on the accuracy of weight estimation. During the experiment, the number of convolution kernels was fixed and the kernel size was set to be the same across all the convolutional layers in a model. The learning curves for the training dataset, as shown in Figure 8B in the appendix, demonstrated that all networks fit the training dataset well. Figure 6B shows the learning curves of models with different kernel sizes on the validation dataset. We selected the 3 × 3 kernel, as it had the lowest MSE in the validation dataset (Figure 6B).
Activation Function
The activation function affects the backpropagation of the CNN model. We tested 5 activation functions: tanh, relu, elu (Clevert et al., 2016), selu (Klambauer et al., 2017), and softplus (Dugas et al., 2000). The learning curves for the training dataset, as shown in Figure 8C in the appendix, demonstrated that all networks fit the training dataset well. The model using softplus got the lowest MSE in the validation dataset (Figure 6C) as well as the smallest predicted error (Picouet et al., 2010) (Figure 6D). We thus selected softplus as the activation function.
Dropout
To avoid overfitting, 4 dropout rates were examined using models having the same parameters and structure. The learning curves of these dropout rates were compared in Figures 6E and 6F. In Figure 6E, only the dropout rates of 0 and 0.1 fit the training dataset well, so we only considered these dropout rates. In Figure 6F, the dropout rate of 0.1 got the lowest MSE on the validation dataset. Therefore, the dropout rate was set to 0.1 during training.
Optimization Method
Adam optimizer has been viewed as the default for overall choices (Ruder, 2016). Here, using the same model, we compared three optimization methods: Mini-batch gradient descent (Ruder, 2016), Momentum (Qian, 1999), and Adam (Kingma and Ba, 2015). In the Momentum optimization method, the momentum term was set to 0.9. Figures 6G and 6H show the learning curves of the three optimization methods in the training dataset and the validation dataset. For both datasets, the Adam optimization method achieved the lowest MSE. We, thus, selected Adam as the optimization method.
CONCLUSIONS
Here, we proposed a low-cost 2D image weighing method to estimate the weight of ducks based on end-to-end deep learning methods. Since most factories do not have automatic carcass weighing devices like modern systems, our method enables low-cost weighing of existing production lines. Our image weighing method can accurately estimate the body weight of white Peking duck carcasses on a working production line. It thus significantly increases the efficiency of meat processing. By using a 10-fold cross-validation method to estimate the model, we achieved a testing MAD of 58.8 grams and an MRE of 2.15%. We also compared our CNN model with a pixel area linear regression model and an ANN model based on the same dataset. The results demonstrated that the CNN model outperformed the other 2D image weighing methods. The ability to estimate the weight of white Pekin duck carcasses in a noncontact and accurate manner makes our proposed CNN method a suitable solution for weighing duck carcasses on the production line of slaughter factories.
ACKNOWLEDGMENTS
This work was supported by the National Natural Science Foundation of China (Grant No. 61873307, 62273338), the Hebei Natural Science Foundation (Grant No. F2020501040, F2021203070, F2021501021), the Fundamental Research Funds for the Central Universities (Grant No. N2123004, 2022GFZD014), the Administration of Central Funds Guiding the Local Science and Technology Development (Grant No. 206Z1702G) and in part by the Chinese Academy of Sciences (CAS)-Research Grants Council (RGC) Joint Laboratory Funding Scheme under Project JLFS/E-104/18.
Data availability statements: The datasets analyzed during the current study are available in the repository1, and the original dataset is available on reasonable request.
DISCLOSURES
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Footnotes
https://github.com/RuoyuChen10/Image_weighing
Supplementary material associated with this article can be found (Visualization of real-time image weighing), in the online version, at doi:10.1016/j.psj.2022.102348.
Appendix. Supplementary materials
Fig. 7. Extract images of ducks from video frames. The section of 300 pixels below the iron frame was used as the duck images. These images were scaled from 1015×321 to 253×80 pixels and spliced into R, G, B channels. The R channel of the images was used, and the pixel values were normalized from [0, 255] to [0, 1].
Fig. 8. The learning curves (smoothed by smooth spline method) of the CNN models with different hyperparameters. a. The training MSE in different convolution layers. b. The training MSE in different kernel sizes. c. The training MSE in different activation functions.
Fig. 9: Discussion of remove the feet area of duck carcasses a. The area which light brightness to change greatly. b. The estimated result of one duck based on the images from different angles. The PE distribution of the weight estimation. c. with feet, the MAD is 76.5 grams and d. without feet, the MAD is 54.6 grams.
REFERENCES
- Adamczak L., Chmiel M., Florowski T., Pietrzak D., Witkowski M., Barczak T. The use of 3D scanning to determine the weight of the chicken breast. Comput. Electr. Agric. 2018;155:394–399. [Google Scholar]
- Amraei S., Abdanan Mehdizadeh S., Salari S. Broiler weight estimation based on machine vision and artificial neural network. Br. Poult. Sci. 2017;58:200–205. doi: 10.1080/00071668.2016.1259530. [DOI] [PubMed] [Google Scholar]
- Balaban M.O., Chombeau M., Cirban D., Gumus B. Prediction of the weight of Alaskan pollock using image analysis. J. Food Sci. 2010;75:E552–E556. doi: 10.1111/j.1750-3841.2010.01813.x. [DOI] [PubMed] [Google Scholar]
- Balaban M.O., Unal Sengor G.F., Gil Soriano M., Guillen Ruiz E. Using image analysis to predict the weight of Alaskan salmon of different species. J. Food Sci. 2010;75:E157–E162. doi: 10.1111/j.1750-3841.2010.01522.x. [DOI] [PubMed] [Google Scholar]
- Brown D.J., Savage D.B., Hinch G.N. Repeatability and frequency of in-paddock sheep walk-over weights: implications for flock-based management. Anim. Produc. Sci. 2014;54:582–586. [Google Scholar]
- Chen K., Li H., Yu Z., Bai L. Grading of chicken carcass weight based on machine vision. Transac. Chin. Soc. Agric. Mach. 2017;48:290–295. [Google Scholar]
- Chen Y., Liu L., Tao J., Chen X., Xia R., Zhang Q., Xiong J., Yang K., Xie J. The image annotation algorithm using convolutional features from intermediate layer of deep learning. Multimedia Tools Appl. 2021;80:4237–4261. [Google Scholar]
- Clevert D.-A., Unterthiner T., Hochreiter S. Pages 1–14 in International Conference on Learning Representations. 2016. Fast and accurate deep network learning by exponential linear units (ELUs) [Google Scholar]
- Dugas C., Bengio Y., Bélisle F., Nadeau C. In: Advances in Neural Information Processing Systems. Leen Todd K., Dietterich Thomas G., Tresp Volker., editors. MIT Press; Denver, CO: 2000. Incorporating second-order functional knowledge for better option pricing; pp. 472–478. [Google Scholar]
- Jones T.A., Dawkins M.S. Environment and management factors affecting Pekin duck production and welfare on commercial farms in the UK. Br. Poult. Sci. 2010;51:12–21. doi: 10.1080/00071660903421159. [DOI] [PubMed] [Google Scholar]
- Jørgensen A., Dueholm J.V., Fagertun J., Moeslund T.B. Pages 221–232 in Scandinavian Conference on Image Analysis. 2019. Weight estimation of broilers in images using 3D prior knowledge. [Google Scholar]
- Kashiha M., Bahr C., Ott S., Moons C.P.H., Niewold T.A., Ödberg F.O., Berckmans D. Automatic weight estimation of individual pigs using image analysis. Comput. Electr. Agric. 2014;107:38–44. [Google Scholar]
- Kingma D.P., Ba J. Pages 1–15 in International Conference on Learning Representations. 2015. Adam: a method for stochastic optimization. [Google Scholar]
- Klambauer G., Unterthiner T., Mayr A., Hochreiter S. Pages 971–980 in Advances in Neural Information Processing Systems. Curran Associates, Inc.; Long Beach, CA: 2017. Self-normalizing neural networks. [Google Scholar]
- Koodtalang W., Sangsuwan T. Proc. 2019 First International Symposium on Instrumentation, Control, Artificial Intelligence, and Robotics (ICA-SYMP) 2019. The chicken's legs size classification using image processing and deep neural network. [Google Scholar]
- Li P., Zhang R., Chen J., Sun D., Lan J., Lin S., Song S., Xie Z., Jiang S. Development of a duplex semi-nested PCR assay for detection of classical goose parvovirus and novel goose parvovirus-related virus in sick or dead ducks with short beak and dwarfism syndrome. J. Virol. Methods. 2017;249:165–169. doi: 10.1016/j.jviromet.2017.09.011. [DOI] [PubMed] [Google Scholar]
- Lotufo R.A., Taube-Netto M., Conejo E., Hoyos F.J. Pages 43–49 in Machine Vision Applications in Industrial Inspection VII. SPIE, Bellingham, WA; 1999. Using machine vision to estimate bird weight in the poultry industry. [Google Scholar]
- Luo G., Dong S., Wang K., Zuo W., Cao S., Zhang H. Multi-views fusion CNN for left ventricular volumes estimation on cardiac MR images. IEEE Transact. Biomed. Eng. 2018;65:1924–1934. doi: 10.1109/TBME.2017.2762762. [DOI] [PubMed] [Google Scholar]
- Mollah M.B.R., Hasan M.A., Salam M.A., Ali M.A. Digital image analysis to estimate the live weight of broiler. Comput. Electr. Agric. 2010;72:48–52. [Google Scholar]
- Nyalala I., Okinda C., Makange N., Korohou T., Chao Q., Nyalala L., Jiayu Z., Yi Z., Yousaf K., Chao L., Kunjie C. On-line weight estimation of broiler carcass and cuts by a computer vision system. Poult. Sci. 2021;100 doi: 10.1016/j.psj.2021.101474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oviedo-Rondón E.O., Parker J., Clemente-Hernández S. Application of real-time ultrasound technology to estimate in vivo breast muscle weight of broiler chickens. Br. Poult. Sci. 2007;48:154–161. doi: 10.1080/00071660701247822. [DOI] [PubMed] [Google Scholar]
- Picouet P.A., Teran F., Gispert M., Font i Furnols M. Lean content prediction in pig carcasses, loin and ham by computed tomography (CT) using a density model. Meat Sci. 2010;86:616–622. doi: 10.1016/j.meatsci.2010.04.039. [DOI] [PubMed] [Google Scholar]
- Qi C., Xu J., Liu C., Wu M., Chen K. Automatic classification of chicken carcass weight based on machine vision and machine learning technology. J. Nanjing Agric. Univ. 2019;42:551–558. [Google Scholar]
- Qian N. On the momentum term in gradient descent learning algorithms. Neural Networks. 1999;12:145–151. doi: 10.1016/s0893-6080(98)00116-6. [DOI] [PubMed] [Google Scholar]
- Ritchie, H., P. Rosado, and M. Roser. 2019. Meat and dairy production. Version 2. Accessed Aug. 2017. https://ourworldindata.org/meat-production.
- Ruder, S. 2016. An overview of gradient descent optimization algorithms. arXiv preprint arXiv:1609.04747.
- Scollan N., Caston L., Liu Z., Zubair A., Leeson S., McBride B. Nuclear magnetic resonance imaging as a tool to estimate the mass of the pectoralis muscle of chickens in vivo. Br. Poult. Sci. 1998;39:221–224. doi: 10.1080/00071669889150. [DOI] [PubMed] [Google Scholar]
- Simonyan K., Zisserman A. Pages 1–14 in International Conference on Learning Representations. 2015. Very deep convolutional networks for large-scale image recognition. [Google Scholar]
- Teimouri N., Omid M., Mollazade K., Mousazadeh H., Alimardani R., Karstoft H. On-line separation and sorting of chicken portions using a robust vision-based intelligent modelling approach. Biosyst. Eng. 2018;167:8–20. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Fig. 7. Extract images of ducks from video frames. The section of 300 pixels below the iron frame was used as the duck images. These images were scaled from 1015×321 to 253×80 pixels and spliced into R, G, B channels. The R channel of the images was used, and the pixel values were normalized from [0, 255] to [0, 1].
Fig. 8. The learning curves (smoothed by smooth spline method) of the CNN models with different hyperparameters. a. The training MSE in different convolution layers. b. The training MSE in different kernel sizes. c. The training MSE in different activation functions.
Fig. 9: Discussion of remove the feet area of duck carcasses a. The area which light brightness to change greatly. b. The estimated result of one duck based on the images from different angles. The PE distribution of the weight estimation. c. with feet, the MAD is 76.5 grams and d. without feet, the MAD is 54.6 grams.