Abstract
The consequences of crowding on the dynamic conformational ensembles of intrinsically disordered proteins (IDPs) remain unresolved because of their ultrafast motion. Here, we report crowder-induced interactions and conformational dynamics of a prototypical multistimuli-responsive IDP, Rec1-resilin. The effects of a range of crowders of varying sizes, forms, topologies, and concentrations were examined using spectroscopic, spectrofluorimetric, and contrast-matching small- and ultrasmall-angle neutron scattering investigation. To achieve sufficient neutron contrast against the crowders, deuterium-labeled Rec1-resilin was biosynthesized successfully. Moreover, the ab initio “shape reconstruction” approach was used to obtain three-dimensional models of the conformational assemblies. The IDP revealed crowder-specific systematic extension and compaction with the level of macromolecular crowding. Last, a robust extension-contraction model has been postulated to capture the fundamental phenomena governing the observed behavior of IDPs. The study provides insights and fresh perspectives for understanding the interactions and structural dynamics of IDPs in crowded states.
In the push and pull of crowds, environment-sensitive, intrinsically disordered protein dances precariously.
INTRODUCTION
Macromolecular crowding is a fundamental and universal feature that governs a variety of vital activities in all living organisms. For example, eukaryotic cellular environments are highly crowded, where the estimated total concentration of soluble and insoluble macromolecules, including proteins, nucleic acids, ribosomes, and carbohydrates in the cytoplasm ranges from 50 to 400 mg/ml and may occupy 30 to 40% of the total cell volume (1). Such “macromolecular crowding” conditions can affect the conformational dynamics, molecular diffusion, stability, and functional properties of proteins (2, 3). The influence of crowding on protein packing is dominated by two phenomena: (i) hard nonspecific steric effects that can reduce the space available for protein dynamics via excluded volume and (ii) soft (or chemical) repulsive or attractive interactions, such as electrostatic, hydrophobic, and van der Waals interactions that can encourage dynamics (3, 4). Steric repulsion can provide a stabilizing effect on the native state of the protein indirectly because of compaction of the denatured states [i.e., entropic (3)], whereas a large number of attractive or repulsive interactions can overcome steric stabilization, causing unfolding and exposure of new protein surfaces [i.e., enthalpic (4)]. The effects of different crowding agents, such as polyethylene glycol, Ficoll, and dextran, on the kinetics and thermodynamics of ordered (globular) proteins have been reported in the literature through both theoretical and experimental methods (5, 6). However, there have been very limited studies on the impact of macromolecular crowding on the dynamic conformational ensembles and stability of intrinsically disordered proteins (IDPs).
IDPs are abundant in eukaryotic proteomes and have emerged as a functionally important family of proteins involved in a wide range of biological tasks, including cell signaling, regulation (7), transcription elongation (8), membrane-less organelles (9), and homoeostasis (10). They also play critical roles in different pathological states, including Alzheimer’s, Parkinson’s, and Huntington’s disease (11). The pathogenicity and infectivity of viruses like SARS-CoV-2 are also associated with IDPs/intrinsic disordered regions (IDRs) in viral proteins. IDPs/IDRs confer viral proteins the ability to easily and promiscuously bind to the host proteins and play a crucial role in their antigenic flexibility, immunological evasion, and antibody escape (12).
IDPs lack stable tertiary structures and are flexible in nature, with a large ensemble of rapidly interconverting conformations under nondenaturing conditions. Their corresponding free energy landscape is thus characterized by multiple minima. Because of this spatiotemporal heterogeneity and conformational polymorphism, the study of crowder-dependent conformational dynamics in IDP is very challenging (13). Computational modeling, using an ensemble of a coarse-grained IDP, has predicted substantial decreases in the radius of gyration (Rg) of IDPs under crowding conditions, and repulsive interactions due to crowding agents are suggested to cause chain compaction (14). Soft interaction effects of crowding agents on IDPs are more complex because of the conformational freedom of amino acid sequences and the length of IDPs. Soft interaction effects on dynamic conformational ensembles of IDPs are largely unexplored. On the basis of a limited number of available reports, the structural responses of IDPs under experimental crowding conditions can be grouped into three broad categories, namely, foldable (at least partially), nonfoldable (does not fold), and unfoldable (extends) (13, 15, 16). The compiled data on extension and compaction of IDPs under crowding conditions (fig. S1) indicate the following: (i) most studies report no effect or monotonic compaction due to crowding, (ii) the degree of compaction can reach 40% while the degree of extension can reach 20%, (iii) compaction may not occur until the crowder volume fraction exceeds 5 to 10%, and (iv) the compaction and preservation pathways do not have to be monotonic. The experimental data for each crowding fraction represent a snapshot, based on the measurement method, of the most populated lowest energy state for the IDP ensemble of states.
Measuring conformational change of the IDP of interest in dilute to concentrated solutions/dispersions of macromolecular crowding agents relevant to cellular environments is an experimental challenge. The presence of a large ensemble of rapidly interconverting structures in IDPs precluded the use of conventional structural biological techniques, such as x-ray crystallography and nuclear magnetic resonance (NMR), for resolving their structures (17). As a result, molecular dynamics simulations have been proposed to probe structure, dynamics, and interaction-driven change in conformational landscape of IDPs (18, 19). NMR relaxation studies have been advanced to identify dynamic modes and assess dynamic interaction profile and molecular recognition trajectory of IDPs (20, 21). Although challenging, experimental identification of the conformational ensembles of IDPs is of great interest since they establish the link between their sequences and functions. This challenge has been previously approached using advanced low-resolution techniques, including single-molecule fluorescence resonance energy transfer spectroscopy (16) and small-angle x-ray scattering (SAXS) measurement (22). SAXS and small-angle neutron scattering (SANS) are very powerful complementary techniques for determining size, shape, aggregation, and/or hierarchical arrangements of protein complexes in dilute to concentrated solutions at a mesoscopic scale (22). Particularly, SANS is useful for the study of biological macromolecules in close to native solutions and their aggregation behavior in concentrated solution and gel phases (23, 24). The different interaction of neutrons with hydrogen and its isotope deuterium provides different neutron scattering length density (SLD) and thereby offers contrast-matching capability, which can be applied to specifically study the conformation and stability of proteins in the presence of crowding agents through masking the signal of the crowders (25). Moreover, SANS can be used to identify the conformational changes of proteins due to soft attraction and/or steric repulsion with crowding agents (17). In addition, the ultrasmall-angle neutron scattering (USANS) technique can measure the elastic scattering from nuclei of molecules and can be used to characterize structures with dimensions of about 0.1 to 50 μm (26). In the present work, we use a combination of contrast-matching SANS and USANS to explore the effects of a variety of crowding agents with varying sizes (1 to 14 nm), forms (spherical to ribbon), topologies (linear to network), and concentrations (up to 40%) on the evolution of conformational ensembles of a multistimuli-responsive resilin-mimetic IDP, Rec1-resilin, over four decades of length scale.
Resilin is an elastomeric protein found in many insects and is currently considered as the most resilient (97%) protein known (27). In recent years, several resilin-mimetic proteins (RMPs) and polypeptides, with exquisite control over the amino acid sequence comprising repeat resilin motifs, have been successfully designed and synthesized. RMPs have been the subject of significant research interest for their potential applications in the areas of biotechnology, medicine, and nanotechnology (28). Rec1-resilin is the first genetically engineered RMP derived from exon-1 of the fruit fly Drosophila melanogaster (CG15920 gene), which compositionally comprises 18 repeats of a 15–amino acid sequence: GGRPSDSYGAPGGGN (fig. S2) with a molecular weight of 28.5 kDa (28). Over the past decade, we and others have extensively investigated the structure and properties of RMPs (28) and have established Rec1-resilin to be an IDP (23, 29) exhibiting multistimuli responsiveness, including unusual dual phase transition behavior and pH-responsive photophysical properties (30). Studies using SAXS have shown that Rec1-resilin can alter its packing to achieve several reversible states as a function of its environment, including compacted and extended states, with Rg values ranging from 2.9 nm [42% compaction at 30 weight % (wt %) self-crowding], 3.6 nm [27% compaction at lower critical solution temperature (LCST) of 75°C], 4.9 nm (equilibrium state), up to 6.2 nm [27% extension at upper critical solution temperature (UCST) of 4°C] in 10 mM phosphate-buffered saline (PBS) (23). We have also demonstrated patterned surfaces (31), responsive interfaces (32), photocrosslinked hydrogels (33, 34), and multifunctional soft templates to generate designer nanobioconjugates and/or metallic nanoclusters (sub-nano to nanoscale) using Rec1-resilin as a directing agent (35–39). Such IDPs have markedly altered the structure-function paradigm of proteins. However, the conformational ensembles and the dynamics of such multistimuli-responsive IDPs under physiologically relevant crowded conditions remain unexplored despite their critical importance (28). To achieve this goal, in this work, we synthesized deuterated Rec1-resilin (D-Rec1) in vitro to perform SANS and USANS experiments at the crowder contrast-matching point, which rendered only the protein visible to the neutron beam. Such a study offers a rare opportunity to examine the conformational dynamics of a prototypical multistimuli-responsive IDP, even at a very highly crowded condition. In addition, crowder-directed interactions, conformational dynamics, and secondary structural evolution have also been examined using spectrofluorimetric and circular dichroism (CD) spectroscopy. To obtain three-dimensional (3D) models of the IDP structure that exhibited crowder-specific systematic extension and compaction with the level of macromolecular crowding, an ab initio “shape reconstruction” approach was used. Last, for modeling IDP structures that agree with the experimental data and represent the basic principles governing the observed behavior of the IDP, we proposed a new extension-contraction model.
RESULTS
Size and surface charge of crowding agents
In this work, the crowding experiments were performed using a small carbohydrate molecule, glucose (GLU; molecular weight, 180 g/mol); a small peptide molecule, glutathione (GSH; molecular weight, 307 g/mol); and small-to-medium size synthetic macromolecules, polyethylene glycol (PEG3; molecular weight, 3 kDa), Ficoll (FIC70; molecular weight, 70 kDa), and dextran (DEX70; molecular weight, 70 kDa) dispersed in 10 mM PBS (pH 7.4) at concentrations in the range of 1 to 40 wt % (i.e., 10 to 400 mg/ml). These crowding molecules are of significant relevance in biochemistry and cell biology (section S3 and fig. S3). As the estimated neutron SLDs of GLU (~1.5 × 10−6 Å−2), GSH (~1.9 × 10−6 Å−2), PEG3 (~0.6 × 10−6 Å−2), FIC70 (~2.3 × 10−6 Å−2), and DEX70 (~1.8 × 10−6 Å−2) are close to that of Rec1-resilin (2.8 × 10−6 Å−2), D-Rec1 was synthesized and used at 3.0 wt % concentration to provide sufficient scattering and neutron contrast against the crowding agents. Both GLU and GSH have been reported to exhibit open chain or linear form conformation in an aqueous medium (6). On the other hand, PEG is a polyether compound that exhibits a mesh-like structure (above the semi-dilute regime), whereas FIC and DEX are copolymers of sucrose-epichlorohydrin and GLU, which exhibit compact spherical-like (relatively less flexible) and ribbon-like (relatively more flexible) morphologies, respectively, in an aqueous medium (6). The zeta (ζ) potential and hydrodynamic diameter (Dh) of D-Rec1 and crowding agents at 0.5 wt % concentration in 10 mM PBS were measured using the dynamic light scattering (DLS) technique (section S4 and fig. S4). All the samples exhibited a negative net surface charge (ζ potential), which indicates good aqueous solubility of the molecules and mutually repulsive intermolecular forces. Such repulsive interactions have been theoretically predicted to cause chain compaction of IDPs under crowding conditions (12). D-Rec1 exhibited ζ potential and Dh values of −8.5 ± 0.4 mV and 10.8 ± 0.2 nm, respectively, in 10 mM PBS, which are in good agreement with values previously reported for hydrogenated Rec1-resilin at physiological pH (23, 30). The GLU, GSH, PEG3, FIC70, and DEX70 exhibited Dh values of 1.1 ± 0.1, 4.3 ± 0.1, 5.8 ± 0.1, 9.8 ± 0.2, and 13.4 ± 0.4 nm, respectively, which are in general agreement with literature reports (2).
SANS intensity profile of D-Rec1 under different contrast-matching conditions
The SANS data of 3.0 wt % D-Rec1 in 10 mM PBS under different contrast-matching conditions are shown in Fig. 1A. As expected, the characteristic scattering profile of D-Rec1 is observed to be similar to that of Rec1-resilin (23), exhibiting a Porod (0.02 < q < 0.5 Å−1; high q) and a Guinier (0.006 < q < 0.02 Å−1; low q) region, where q is the scattering vector (22). The unsuppressed scattering profile of D-Rec1 exhibiting both Porod and Guinier regions in 48% deuterium oxide (D2O) [solvent with neutron SLD matching Rec1-resilin (23)] demonstrates successful deuteration in the protein. In contrast-matching SANS experiments, the concentration (C) normalized scattering intensity at zero angles, I(0), calculated using the Guinier approximation, decreases with the decrease in the contrast between the solute molecules and the solvent. The I(0)/C plot as a function of % of D2O in the solvent (Fig. 1B) provides an experimental estimate of the protein’s match point at around 75% D2O, which indicates about 70% deuteration on nonexchangeable hydrogen positions in the protein. The Porod region in SANS intensity profiles fundamentally describes the nature of the interface and structure of the scattering unit, whereas the Guinier region describes the size in terms of the Rg (40). A Porod slope of 1.85 ± 0.01 obtained for D-Rec1 using a power-law fit at high q region (0.06 < q < 0.22 Å−1) is a signature of swollen polymer coils in theta solvents and is consistent with values previously reported for Rec1-resilin (23). The intrinsically disordered nature of D-Rec1 was also established using the Kratky plot (Fig. 1C), which demonstrates an initial monotonic increase in I(q)*q2 at low q followed by a plateau at high q, a typical characteristic of IDPs (23). The shape-independent Gaussian coil model function (40), which describes the scattering from polymer chains in theta solvents, was fitted to the D-Rec1 scattering data (Fig. 1D) to obtain the Rg value. Moreover, Guinier approximations (40) also allow us to estimate (from small q values at low q) the overall size (Rg) of randomly oriented macromolecules. The Gaussian coil fit revealed an Rg of 6.2 ± 0.1 nm for D-Rec1, which is close to the value (6.5 ± 0.3 nm) estimated by Guinier approximation. The Rg values of D-Rec1 obtained from SANS data are in general agreement with values previously reported for Rec1-resilin (23). Moreover, the theoretical structure profile of Rec1-resilin (Fig. 1E) generated using a database of disordered protein predictions (D2P2) platform (comprising some of the commonly available tools for predicting intrinsic disorder propensity) also provides evidence for Rec1-resilin to be predominantly disordered in nature (41).
Fig. 1. SANS results of synthesized pure D-Rec1.
(A) SANS intensity profile of D-Rec1 at 3.0 wt % and (B) concentration normalized zero scattering intensity as a function of D2O%. (C) Corresponding Kratky plot. (D) Model fits to SANS data presented with intensity offset for clarity. (E) Intrinsic disorder profile of Rec1-resilin generated by a database of disordered protein predictions (D2P2) platform. The nine color bars at the top represent disordered regions in Rec1-resilin sequence predicted by different disorder predictors (Espritz, IUPred, etc.). The green bar at the bottom represents predicted disorder region agreement between the nine predictors. The yellow bar at the bottom corresponds to disorder-based binding sites known as molecular recognition features (MoRFs).
SAXS and SANS intensity profile of crowding agents
Figure S5 (A to D) shows the SAXS data of 0.5 wt % crowding agents in 10 mM PBS. The structural information of the GLU could not be measured as the size of the molecule falls below the SAXS instrument measurement range (1.6 to 62.8 nm). The size of the GLU molecule can be estimated from the kinetic diameter, σ, of 0.86 nm (42). The scattering profile of other crowding agents exhibited both Porod and Guinier regions in the measured experimental range. A power-law fit in the high q (0.1 < q < 0.25 Å−1) scattering region of GSH, PEG3, FIC70, and DEX70 revealed Porod slope values of 1.71 ± 0.05, 2.00 ± 0.04, 2.61 ± 0.01, and 1.89 ± 0.01, respectively, which correspond to polymer coils for GSH, PEG3, and DEX70 (slope between 1.65 and 2.00) and mass fractal for FIC70 (slope between 2 and 3) (40). The degree of flexibility of the crowding agents was further analyzed using the Kratky plot (fig. S5E), which showed an unfolded structure for GSH, PEG3, and DEX70 and a partially folded/compact structure for FIC70 (43). On the basis of the above details, a shape-independent Gaussian coil model function was used to fit the GSH, PEG3, and DEX70 scattering data (44). Conversely, a shape-independent polymer-excluded volume model function, which describes the scattering from polymer chains as mass fractals, was fitted to the FIC70 scattering data (44). The model function fits (fig. S5, A to D), with all parameters set free, returned Rg values of 1.1 ± 0.1, 2.2 ± 0.2, 4.4 ± 0.2, and 6.5 ± 0.2 nm for the GSH, PEG3, FIC70, and DEX70, respectively, which is marginally higher than values estimated by Guinier approximation (section S4). The different sizes, ζ potential, structure, morphology, and concentration or volume fraction of crowding agents are expected to affect the packing of D-Rec1.
Figure S6 shows the SANS intensity profiles of pristine crowding agents at their maximum tested concentration (40 wt %) in 10 mM PBS with and without solvent contrast matching. The GLU and GSH exhibited very poor or no scattering at low q, suggesting a lack of clustering or network formation for these small molecules. Conversely, the scattering intensity upturn observed at low q for the PEG3, FIC70, and DEX70 can be attributed to clustering or network structures formed at 40 wt % for these macromolecules (45). The structure of the formed network was determined to be that of a mass fractal with a power-law fit at extended low q (0.0007 < q < 0.005 Å−1), returning a Porod slope value in the range of 2.46 to 2.79 (40). However, it can be observed that under contrast-matching conditions, the scattering intensity from the crowding agents was effectively suppressed or masked (fig. S6) and markedly lower than pristine D-Rec1 in 48% D2O (Fig. 1A), thereby providing the opportunity to measure/study scattering from D-Rec1 in the presence of the crowding agents even at high concentrations. The crowding agents under contrast-matching conditions exhibited very poor or no scattering for q < 0.006 (fig. S6).
Crowder-directed conformational dynamics of D-Rec1
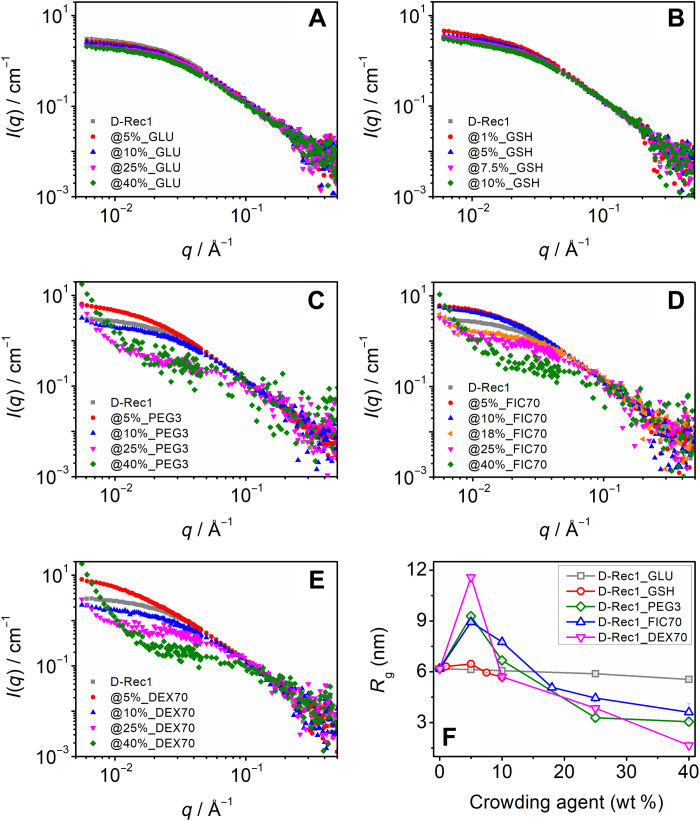
Figure 2 (A to E) shows the SANS intensity profiles of 3.0 wt % D-Rec1 with different types and levels (1 to 40 wt %) of contrast-matched crowding agents. The scattering profiles of the samples crowded with GLU (Fig. 2A) and GSH (Fig. 2B) are observed to be similar or close to that of pristine D-Rec1 over all the tested concentration levels. The presence of up to 5 wt % concentration of PEG3 (Fig. 2C), FIC70 (Fig. 2D), and DEX70 (Fig. 2E) also exhibited pristine D-Rec1–like scattering profiles with distinctive Porod and Guinier regions. However, in these systems, with an increase in crowder concentration beyond 5% (i.e., 10 to 40 wt %), the turnover point of the respective Guinier region was observed to shift toward a higher q value, concurrent with a decrease in the scattering intensity in the Guinier region. A further increase in the scattering intensity at low q to form a new Porod-like region is also evident. The Kratky plots of the samples (fig. S7) show a plateau region in the high q regime, suggesting that the protein retains its disordered structure even under highly crowded conditions (23). As the protein is subjected to excluded volume effects under crowding conditions, a shape-independent polymer-excluded volume model function was fitted to the scattering data (fig. S8) to obtain the respective Porod slope and Rg values. The fits revealed Porod slope values between 1.85 and 2.0 (the signature of a swollen polymer Gaussian coil) for all the samples, which further confirms that the disordered or random-coil nature of the protein is conserved even in highly crowded environments (40). The Rg values of D-Rec1 estimated from the excluded-volume effects model function fit are presented in Fig. 2F. The fit revealed an Rg of 6.2 ± 0.1 nm for D-Rec1, which is consistent with the value obtained from the Gaussian coil fit (Fig. 1D). A systematic decrease in the Rg of D-Rec1 is observed in the presence of GLU. An initial net 4.7% increase in the Rg of D-Rec1 is observed at lower GSH concentrations (1 to 5 wt %), which is followed by a net 8.1% decrease in the Rg at relatively higher GSH concentrations (5 to 10 wt %). In the presence of macromolecular crowders PEG3, FIC70, and DEX70, the Rgs of D-Rec1 are observed to increase significantly (by 50.2, 44.5, and 87.4%, respectively) at lower crowder concentrations (5 to 10 wt %), whereas with further increase in concentration (10 to 40 wt %), a systematic decrease in the Rg values to net 50.5, 41.6, and 73.1%, respectively, at 40 wt % crowding agent is observed.
Fig. 2. SANS results of D-Rec1 under macromolecular crowding conditions.
SANS intensity (normalized) profile of D-Rec1 at 3.0 wt % as a function of different crowding agents (contrast matched to solvent) at different concentrations: (A) glucose (GLU), (B) glutathione (GSH), (C) polyethylene glycol (PEG3), (D) Ficoll (FIC70), and (E) dextran (DEX70). (F) Estimated radius of gyration (Rg) of D-Rec1 (using the polymer excluded volume model fit) as a function of crowding agent concentration.
For IDPs, single Rg values obtained from Guinier approximation or model function fits (Fig. 2F) are often reported to be an underestimation, or inaccurate, because of the presence of conformational heterogeneity in IDPs (46). Therefore, to establish the trend in Rg distribution of D-Rec1 in the presence of crowders, a model-independent pair-distance distribution function, P(r), fit was also performed (40). The P(r) function estimates the real-space Rg by inverse Fourier transform of the I(q) taking a histogram of all of the interatomic distances (r) within the molecule. Figure 3 (A to E) represents the P(r) distribution curves of 3.0 wt % D-Rec1 in the presence of GLU, GSH, PEG3, FIC70, and DEX70 at different concentrations (1 to 40 wt %). The asymmetric nature of all the curves indicates an elongated shape of D-Rec1, which is consistent with previously reported profiles of Rec1-resilin (23). The real-space Rg of D-Rec1 in the presence of crowders estimated from the P(r) fit is presented in Fig. 3F. The Rg of D-Rec1 (in the absence of crowder) obtained from the P(r) fit was 7.4 nm, which is larger than the values estimated from the Gaussian coil fit and Guinier approximation (Fig. 2F). The observed trend in Rg of D-Rec1 with increase in crowding agent concentration is similar to that of polymer-excluded volume model fit results (Fig. 2F). The change in Rg of D-Rec1 in the presence of GLU and GSH is more prominent for the P(r) fit results (compare Fig. 3F and Fig. 2F). A systematic decrease in the Rg of D-Rec1 is observed up to 31.2% in the presence of 40 wt % GLU. An initial net 26.1% increase in the Rg of D-Rec1 at lower GSH concentrations (1 to 5 wt %) followed by a net 20.2% decrease in the Rg at relatively higher GSH concentrations (5 to 10 wt%) is observed. In the presence of macromolecular crowders PEG3, FIC70, and DEX70, the Rg of D-Rec1 is observed to increase substantially (by 46.0, 31.6, and 91.8%, respectively) at lower crowder concentrations (5 to 10 wt %), whereas with further increase in concentration (10 to 40 wt %), a systematic decrease with Rg values to net 60.3, 66.4, and 59.4%, respectively, at 40 wt % crowding agent is observed. In addition, the P(r) fits (fig. S9A) revealed real-space Rg values of 1.8, 4.3, and 6.3 nm for neat PEG3, FIC70, and DEX70, respectively. The P(r) function did not produce a satisfactory fit for the GSH data. However, the Gaussian coil fit and the Guinier approximation yielded an identical Rg value of 1.1 nm for GSH, and a value of 0.43 nm can be estimated for the Rg of GLU (which is half the kinetic diameter) (42). These P(r) fit results for Rg and best Rg estimates (for GLU and GSH) will be used for further analysis in this work.
Fig. 3. Distance distribution results of D-Rec1 under macromolecular crowding conditions.
P(r) curve of D-Rec1 at 3.0 wt % as a function of different crowding agents (contrast matched to solvent) at different concentrations: (A) GLU, (B) GSH, (C) PEG3, (D) FIC70, and (E) DEX70. (F) Estimated Rg of D-Rec1 (using the polymer excluded volume model fit) as a function of crowding agent concentration.
Evolution of 3D conformation ensembles of D-Rec1 with crowding environment
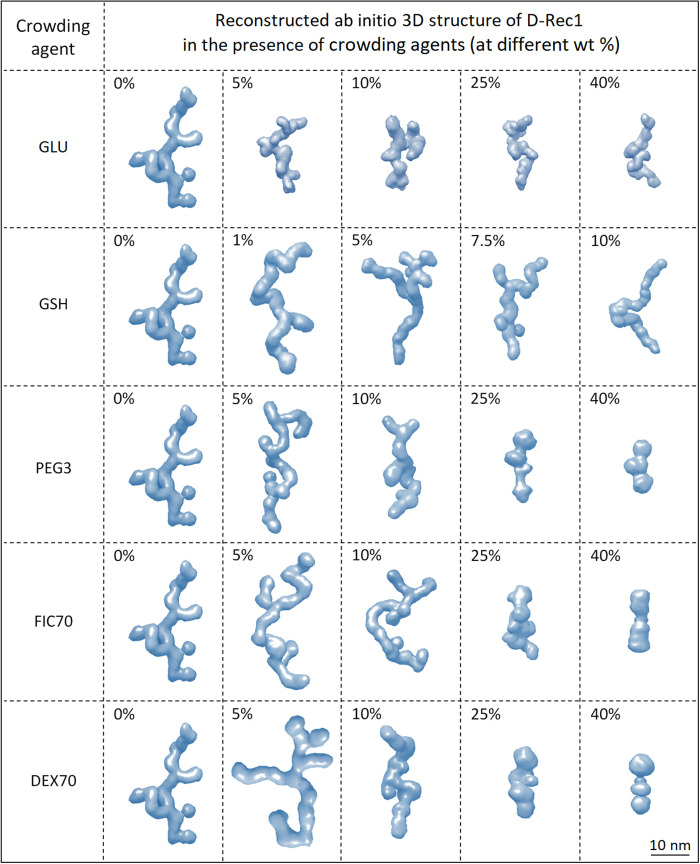
To assess the change in domain structure of D-Rec1 with crowding environment, ab initio 3D structures were reconstructed from the P(r) fit results using the GASBOR program (47). About 310 dummy residues (representing the total number of amino acid residues in Rec1-resilin) were used to fit the data to create chain-like ensemble structures (one among an infinite possible ensemble), which are presented in Fig. 4 in the form of an envelope structure using the Chimera program (48). Ab initio envelope structures of PEG3, FIC70, and DEX70 are also shown in fig. S9B.
Fig. 4. Ab initio shape simulations of D-Rec1 under macromolecular crowding conditions.
One among infinite possible ensemble shapes of D-Rec1 as a function of different crowding agents, such as GLU, GSH, PEG3, FIC70, and DEX70 at different concentrations, is presented. Reconstruction was performed using the GASBOR program with the pair-distance distribution output and visualized using the Chimera program. The results of 20 independent simulations were averaged and filtered to give the most probable shape shown as an envelope structure.
Crowder-induced aggregation behavior beyond SANS length scale
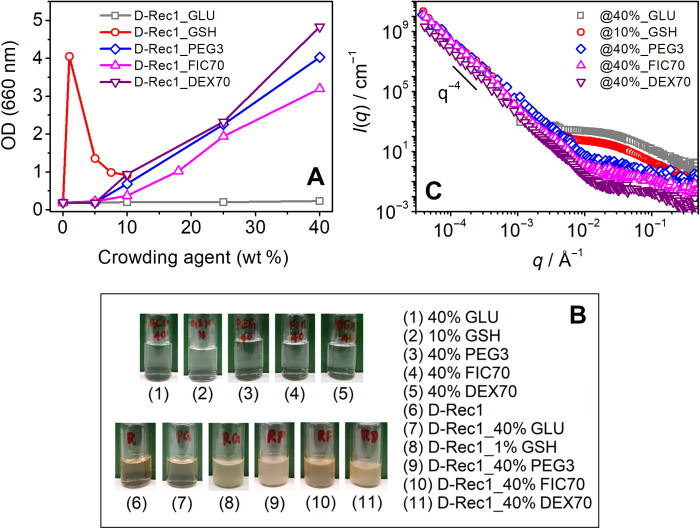
To gain insight into crowder-induced aggregation in the system, low q SANS data (0.00004 < q < 0.001 Å−1) of D-Rec1 were acquired in the presence of crowders and combined with the respective SANS data. Crowding environment–dependent optical density (OD) fluctuations were also studied to assess microaggregate formation. The crowder concentration–dependent increase in the OD of D-Rec1 aggregates is presented in Fig. 5A. No significant change in OD of D-Rec1 was observed in the presence of GLU at all concentrations, whereas a peak in OD was observed in the presence of GSH at 1 wt %. No significant change in OD of D-Rec1 was observed in the presence of PEG3, FIC70, and DEX70 up to 5 wt %, whereas a systematic increase in OD was observed with further increase in crowding agent concentration (10 to 40 wt %). These results are supported by optical observation of turbid dispersions (Fig. 5B), whereas pristine D-Rec1 (3.0 wt %) and pristine crowding agents (at the highest concentrations used) showed clear solutions. The observations indicate that crowding agents as small as GSH induce aggregation of D-Rec1 with optical observation of turbid dispersions, which could scatter neutrons beyond the above measured SANS q-range. The size of the aggregates could not be estimated using DLS as they were beyond the instrument measurement range (0.3 nm to 10.0 μm). Figure 5C shows the extended low q SANS data (0.0007 < q < 0.006 Å−1) of D-Rec1 in the presence of PEG3, FIC70, and DEX70 at 40 wt % (highest OD measured), which reveals a new Porod-like region with increased scattering intensity and no apparent Guinier region, supporting the presence of large structures/aggregates in the sample on length scales extending beyond the measured SANS range. Such a feature was also observed for D-Rec1 in the presence of 1 wt % GSH, but not for GLU, even at 40 wt % (Fig. 5C). Moreover, the observed strong upturn in extended low q SANS data of D-Rec1 in the presence of GSH, PEG3, FIC70, and DEX70 does not reach a Guinier region, suggesting the size of aggregates to be beyond the measured SANS length scale range. The very low q USANS data (0.00004 < q < 0.001 Å−1) of D-Rec1 in the presence of GSH, PEG3, FIC70, and DEX70 were measured and combined with respective SANS data (Fig. 5C) that expand the total experimental q range over four decades. All USANS data exhibited a power law behavior of ∼q−4, which is a characteristic of spherical morphology and/or smooth interface (40).
Fig. 5. Crowder-induced aggregation results of D-Rec1.
(A) Optical density (OD), (B) optical images, and (C) combined SANS and USANS intensity profile of pristine D-Rec1 at 3.0 wt %, crowding agents (GLU, GSH, PEG3, FIC70, and DEX70), and their mixtures as a function of crowding agent concentration.
Spectrofluorimetric assessment of the crowder-directed interactions and conformational dynamics
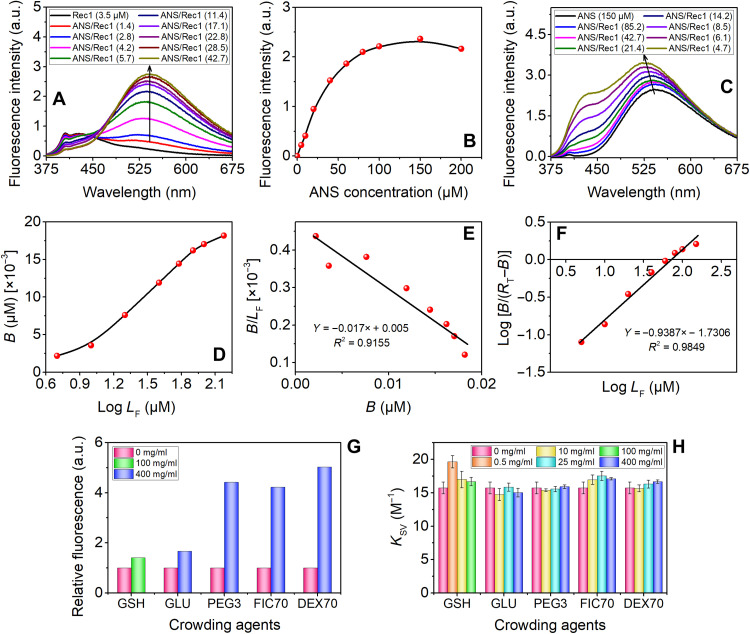
The changes in the exposed surface hydrophobicity of Rec1-resilin in the presence of crowder were assessed using 8-anilino-1-naphthalenesulfonic acid (ammonium salt) (ANS) as an extrinsic fluorescence probe. ANS displays a distinct absorption maximum at ~355 nm (fig. S10), which is not affected by the presence of Rec1-resilin and was used as the excitation wavelength for all the experiments. When the unbound ANS dye is excited at 355 nm, a minimally fluorescent spectrum with an emission maximum at ~543 nm is produced. Figure 6A displays a typical fluorescence titration curve of Rec1-resilin with ANS, and an enhancement in the fluorescence quantum yield due to ligand-substrate interaction (ANS-Rec1-resilin) is observed. The progressive change in fluorescence peak intensity (λmax at ~543 nm) with an increase in ANS concentration is shown in Fig. 6B. The distinctive hyperbolic shape of the titration curve suggests the saturation of ligand binding sites on Rec1-resilin with increasing ANS content. The maximum fluorescence was observed at a dye-to-protein ratio of ~42.7. With a further increase in dye concentration, the peak intensity is reduced, which is related to the self-aggregation of ANS. Figure 6C displays the ANS fluorescence emission spectra when a fixed amount of ANS is titrated with an increasing amount of Rec1-resilin. The binding of ANS to the hydrophobic surface cavity of Rec1-resilin results in an enhanced λmax, along with a progressive blue shift in the wavelength of peak emission (543 to 523 nm with an increase in Rec1-resilin) and a broadening of the emission curves (spectral full width at half maximum). The index of surface hydrophobicity of Rec1-resilin appears to be very low (fig. S11A). This is also reflected from the Kyte-Doolittle hydrophobicity plot of amino acid sequence of Rec1-resilin (fig. S11B). A double reciprocal plot (fig. S11C) of λmax with protein concentration was used to establish a quantitative relationship between fluorescence intensity change and bound ANS (49). A smooth, inflection-free, plateaued plot of the bound ligand (B) versus total free ligand (LF) (fig. S11D) indicates the presence of minimal nonspecific binding component. To define the ligand-receptor interactions, we attempted a number of data analysis techniques. A sigmoidal curve with an inflexion point that corresponds to the Kd (dissociation constant) and the upper asymptote RT (the total receptor concentration) is obtained from the Klotz plot (Fig. 6D), which indicates the sufficiency of the data range and the quality.
Fig. 6. Spectrofluorimetric assessment of the effect of crowders on conformational adjustment and surface hydrophobicity change using ANS as the extrinsic fluorescence probe and Tyr as the intrinsic fluorescence probe.
(A) Steady-state fluorescence emission spectra of pure Rec1-resilin and ANS/Rec1-resilin complexes at various molar ratios. (B) Change in λmax with increase in concentration of ANS in fixed Rec1-resilin. The maximum fluorescence intensity for the complex was observed at approximately ~42.7:1 ANS/Rec1-resilin ratio. (C) Fluorescence spectra of pure ANS and ANS/Rec1 complex with increasing Rec1 concentration. (D) Klotz plot: binding isotherm representing the number of moles of ANS bound per mole of protein. (E) Scatchard treatment of the ANS binding data. (F) Hill plot of the binding data. (G) Enhancement in fluorescence intensity (ΔF) due to ANS bound to Rec1-resilin. (H) Effect of type and level of crowder on the Stern-Volmer quenching constants, KSV. a.u., arbitrary units.
The Scatchard equation (section S11 and eq. S1) was used to calculate the affinity of the receptor (hydrophobic cavity of Rec1-resilin) for ligand ANS. The Scatchard plot B/LF versus B (Fig. 6E) provides a straight line with RT/Kd as the Y intercept, RT as the X intercept, and −1/Kd as the slope. The Kd value of 58.82 μM and an RT of 0.02941 μM are obtained for the binding between the ANS and Rec1-resilin. The Kd value obtained for the binding between the Rec1-resilin and ANS reflects a low-affinity interaction under the experimental condition compared to other proteins, such as human αB (n = 0.97, Kd = 1.78 μM) (50), bovine serum albumin (n = 10, Kd = 1.085 μM), ovalbumin (n = 1, Kd = 1.321 μM), lysozyme (n = 3, Kd = 13.003 μM), and porcine somatotrophin (n = 10, Kd = 1.219 μM) (49). The linear regression value obtained was 0.91, indicating a non-perfect data fit, and initially, a concave-up followed by a concave-down trend is reflected from the plot (Fig. 6E). A Hill plot (Fig. 6F) of the data was used for the assessment of the cooperativity (section S11 and eq. S2). Such plot returns a Kd value of 53.77 and Hill’s coefficient n = 0.9387. The ANS binding sites per molecule of Rec1-resilin are indicated by the n value of Hill’s plot, and the associated negative cooperativity (n < 1) indicates that the occupancy of some of the sites affects the ligand’s affinity for open sites. Hydrophobic exposure of Rec1-resilin in the presence of the crowder was also probed by fluorescence titration of Rec1-resilin by ANS both in the presence and in the absence of different types and levels of crowders (fig. S12). Figure 6G shows the enhancement in fluorescence spectra due to ANS bound to Rec1-resilin in the absence and presence of a different crowder in a very high concentration level of 400 mg/ml. Even at very high crowder concentrations, Rec1-resilin exhibits modest surface modifications in the presence of GLU and GSH (100 mg/ml), while macromolecular crowders PEG, Dextran, and Ficoll are observed to be more effective.
Quenching studies of the intrinsic fluorescence properties of Tyr amino acid residue in proteins/peptides are strongly dependent on the internal changes of the buried Tyr group and can be used as a sensitive probe of the conformational state. Rec1-resilin lacks the Trp amino acid residue, and the fluorescence emission in Rec1-resilin is entirely due to Tyr (section S13). A typical fluorescence quenching experiment of Rec1-resilin using Ficoll (25 mg/ml) as a crowder is shown in fig. S13A. We quantified the fluorescence quenching of Rec1-resilin by acrylamide in the presence and absence of the crowders to identify the change. The data were analyzed using the Stern-Volmer equation (51), which enabled us to calculate the quenching constant (KSV) (eq. S3). Stern-Volmer plots of the acrylamide quenching of Tyr in Rec1-resilin in the absence of a crowder (fig. S13B) and in the presence of a crowder (fig. S13C) were linear, and KSV values were calculated from the linear fits of the data. Figure 6H shows that, except for GSH-0.5, the presence and absence of crowders have no significant impact on KSV (within ≤10%), confirming the notion that the buried Tyr environment remains unaffected. An appreciable difference in the solvent exposure of Tyr is observed only in GSH-0.5, which displays a ~25% increase of the KSV value, reflecting less shielding of Tyr from the polar but noncharged water-soluble acrylamide quencher. The time-resolved fluorescence of ANS and Tyr can offer a more thorough description of the complex systems with hydrophobic sites or Tyr associated with different degrees of solvent exposure; however, this is outside the scope of the current work and will be a subject of future study.
CD spectroscopic assessment of the effect of crowders on the secondary structural dynamics
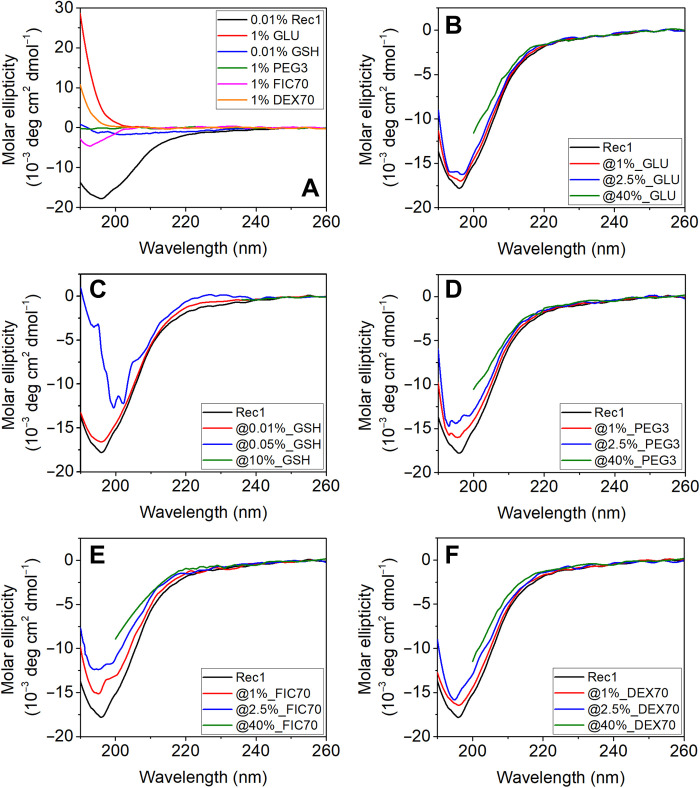
To fully comprehend the secondary structural nature of Rec1-resilin as well as the impact of the type and concentration of crowders on the secondary structure of Rec1-resilin, neat Rec1-resilin and crowded Rec1-resilin solutions were experimentally studied using CD spectroscopy. The secondary structure of proteins can be identified using CD spectra in which α helices, β sheets, and random coils exhibit distinctive spectra at wavelengths between 190 and 250 nm (52). The CD spectra of neat Rec1-resilin resemble those of unfolded global proteins, and the pure crowders exhibit no unique conformation (Fig. 7A). Irrespective of the type and the level of the crowders' presence, the CD spetrum of Rec1-reslin essentially exhibits the characteristics of an unfolded protein(Fig. 7 B to F ). The results corroborate the SANS observation and support the theoretical assessments obtained via protein secondary structure prediction routines (Fig. 1E) and confirm that Rec1-resilin is largely disordered in aqueous solution at physiological pH with marginal contributions from the helix and modest contribution from β sheets. The CD spectrum of a typical protein is assumed to be a unique structural fingerprint made up of all of its constituent secondary structural components. Thus, secondary structure deconvolution fits were used to attempt quantitative estimation of the secondary structure(s) from the CD spectra using the Dicroweb online tool (53), and the results are shown in table S1. The results confirm that the overall secondary structural nature of Rec1-resilin is marginally affected by the presence of the type and the quantity of experimental crowders, and only GSH at higher concentration (~10%) reflects marginal change in the secondary structural organization.
Fig. 7. Effect of crowders on the CD spectrum of Rec1-resilin.
(A) CD spectrum of pure Rec1-resilin and pure crowding agents. CD spectra of Rec1-resilin as a function of different crowding agents at different concentrations: (B) GLU, (C) GSH, (D) PEG3, (E) FIC70, and (F) DEX70. High concentrations of crowding agents (10% GSH and 40% others) resulted in high tension (HT) signal greater than 800 V (i.e., the noise becomes disproportionate to the signal) in the middle-UV range (<240 nm) for GSH and in the far-UV range (<200 nm) for GLU, PEG3, FIC70, and DEX70.
DISCUSSION
The aqueous solubility, molecular geometry, and surface chemistry of proteins depend on their amino acid composition and sequence, as well as on the solution environment, including pH, temperature, ion concentration, and presence of crowders. Rec1-resilin is a multistimuli-responsive IDP whose amino acid sequence is composed of 54.5 mole percent (mol %) nonpolar, 33.5 mol % uncharged polar, and 11.9 mol % charged polar amino acid residues (table S2). The solubility of Rec1-resilin in aqueous solutions is a complex phenomenon as the protein exhibits an experimental isoelectric point (where net surface charge is zero) at pH 4.9 compared to the theoretical value of pH 9.2 (30). At physiological pH, Rec1-resilin exhibits an IDP structure with negative ζ potential (large number of polar groups exposed to the surface and nonpolar groups mostly buried in the core) stabilizing the protein (29). It has previously been established that in addition to the frequently reported excluded volume effects, inert molecular crowders also play an essential role in solvent characteristics and molecular diffusion via physical and soft chemical interactions with proteins (54, 55). The soft interactions can be nonspecific and/or native-state interactions, and it has been shown that they can fully compensate for the effects of excluded volume (56). Therefore, both hard-core steric repulsions and soft interactions (attractive and repulsive), along with molecular diffusion, need to be carefully taken into account when attempting a complete assessment of molecular crowding effects on proteins (57). Spectrofluorimetric assessment of the crowder-directed interactions and conformational dynamics, and (CD) spectroscopic analyses of the effect of crowders on the secondary structural dynamics confirm that Rec1-resilin largely remains an IDP even at a highly crowded state.
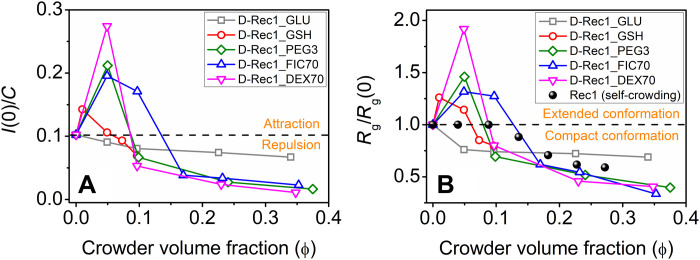
The present work reveals SANS evidence of both extension and compaction of D-Rec1 under crowding conditions. To compare D-Rec1 behavior with that reported in other IDPs (13), the SANS intensity normalized data from Fig. 2 (A to E) can be plotted as a function of crowder volume fraction (ϕ), as shown in Fig. 8A, where ϕ was calculated from table S3. Similarly, the SANS data of Fig. 3F can be plotted as the Rg scaled to the pristine protein [i.e., Rg/Rg] as a function of ϕ, as shown in Fig. 8B. The Rg/Rg(0) data of Rec1-resilin (protonated Rec1-resilin) from self-crowding experiments [from our previous work (23)] are also presented in Fig. 8B for comparison. In the absence of crowders, D-Rec1 exhibited an I(0)/C value of 0.038 liters cm−1 g−1. Figure 8 indicates initial increases in I(0)/C and Rg/Rg(0) of D-Rec1 at low ϕ of crowding agents (GSH, PEG3, FIC70, and DEX70) followed by decreases at higher ϕ to I(0)/C and Rg/Rg(0) values lower than that of the pristine D-Rec1 protein. The I(0)/C values of D-Rec1 observed above >0.038 liters cm−1 g−1 at lower crowder ϕ indicate soft attraction between the protein and crowding agents (GSH, PEG3, FIC70, and DEX70), whereas a repulsion [I(0)/C < 0.038 liters cm−1 g−1] at higher crowder ϕ is evident (Fig. 8A). D-Rec1 exhibits only compact conformations with an increase in ϕ of the crowding agent GLU. When Rec1-resilin crowds itself, the Rg/Rg(0) of Rec1-resilin does not change up to a self-crowding ϕ of 0.09; it then systematically decreases with a further increase in ϕ, as shown in Fig. 8B.
Fig. 8. Crowder-induced conformational dynamics of D-Rec1.
(A) Concentration normalized zero scattering intensity of D-Rec1 as a function of crowder volume fraction and (B) Rg scaled to the pristine D-Rec1 protein [i.e., Rg/Rg(0)] as a function of crowder volume fraction. Self-crowding conformations for Rec1-resilin protein reported elsewhere (23) are given to indicate known packing regions.
It is tempting to hypothesize that GLU is so small and has such a small negative ζ potential in 10 mM PBS (fig. S4B) that it is unable to extend the conformation of D-Rec1; however, Rec1-resilin (and D-Rec1) are larger molecules with substantial negative ζ potential and are unable to cause self-extension on self-crowding. For the moment, it can be postulated that on initial introduction of crowding molecules, with some combination of relative size and interaction parameter, long-range soft attractive interactions between the protein and the crowding agent begin to cause extension of the IDP conformation (55, 56). Such attractive interactions overcome the stabilizing charge-charge repulsion of the protein molecules, providing an enthalpic contribution to the free energy of the system, which has been previously reported for other proteins and inert crowding agents (58, 59). At pH 7.4, three amino acids of D-Rec1 are positively charged: lysine (Lys, 0.6 mol %), arginine (Arg, 5.2 mol %), and histidine (His, 1.9 mol %), and thus, the hydrophilic surface is expected to be Arg-rich. Attractive (electrostatic) long-range interactions between the positively charged amino acids (Lys, Arg, and His; 7.7 mol % in total) of the protein and the negatively charged surfaces of the crowding agents in PBS extends the molecular geometry of D-Rec1, resulting in an increase of the Rg. At higher concentrations of crowders, excluded volume effects provide an entropic contribution to the system free energy as the volume packing fraction continues to increase. The increase in concentration of GSH, PEG3, FIC70, and DEX70 means the protein and crowding molecules are eventually pushed inside each other’s excluded volume regions via the osmotic pressure. The progressive decrease in I(0)/C and Rg/Rg(0) of D-Rec1 at higher concentrations of crowders, along with the increase in OD (aggregation), can be attributed to the excluded volume effects and solvent depletion around protein molecules (55, 60). With the increase in concentration of a crowding agent, the solvent surrounding the D-Rec1 molecules gets depleted (because of the volume being taken up by crowding agents), which forces the protein molecules to decrease their Rg by changing their conformation with more hydrophilic groups pushed toward the inside (core) and hydrophobic groups exposed outside (shell). Moreover, hydrophobic interactions between neighboring protein molecules may lead to protein coacervation or phase separation [consistent with the resulting increased scattering at very low q in USANS (Fig. 5C) and increased turbidity (Fig. 5A)] evidenced by the observed USANS power law behavior of ∼q−4 (hydrophilic-hydrophobic interface). These results allow the postulation of rules of engagement that can be tested by modeling and further experimentation.
It is likely that the crossover point [Rg/Rg(0) = 1] for each crowding agent, ϕcrossover, occurs when the entropic-excluded volume effects (osmotic pressure) begin to balance and then overcome the long-range enthalpic soft interactions (extension) as a function of increasing crowder ϕ. The amount of protein compaction achievable for each crowder in our study appears to be limited. Our previous work (23) has shown that Rec-1 in solution can crowd itself, resulting in compaction up to 42% of its original size, Rg(0), as a function of concentration to 30 wt % (or ϕ to 0.27), as shown in Fig. 8B. The measured contractions of the D-Rec1 IDP in Fig. 8A are larger than those predicted by the theory of Miller for IDPs of varying hydrophobicity and crowder molecules of a similar size or smaller than the protein (61). Miller et al. (61) predicted a maximum contraction of 40% for a crowder fraction ϕ = 0.4 for proteins with a hydrophobicity of 0.2 to 0.3, with smaller crowders being more effective. Kang et al. (62) predict that the osmotic pressure begins to reduce Rg when the average distance between crowding agents, 〈D〉, is less than or equal to Rg(0) of the protein. The 〈D〉 value can be calculated using the relationship provided by Bansal and Ardell (63). The volume fraction at the peak, ϕpeak, or the volume fraction at the crossover point [Rg/Rg(0) = 1], ϕcrossover, for each crowding agent in the present work occurs when the 〈D〉 values are 1.2 to 4.7 nm, much smaller than Rg(0) = 7.4 nm, supporting the notion of the osmotic pressure as the driving force for compaction. For GLU, the 〈D〉 values are 0.53 to 0.11 nm over the range of GLU ϕ, indicating osmotic pressure as the driving force for compaction. Kang et al. (62) have developed a scaling theory to predict crowding-induced protein compaction, where the parameter Rg(0)/Rg(crowder) varies, for example, from 0.9 to 6.9, predicting a protein compaction, Rg/Rg(0), of 0.95 to 0.75 (or 5 to 25%), respectively, as the crowder molecules become smaller; i.e., smaller is more effective. Our results do not follow the predictions of the scaling theory of Kang et al (62). Our examination of the available models (7, 12, 61, 62,64) has led us to develop a new model to predict the dominant contributions to free energy that drive extension and compaction in IDPs as shown in Fig. 8B.
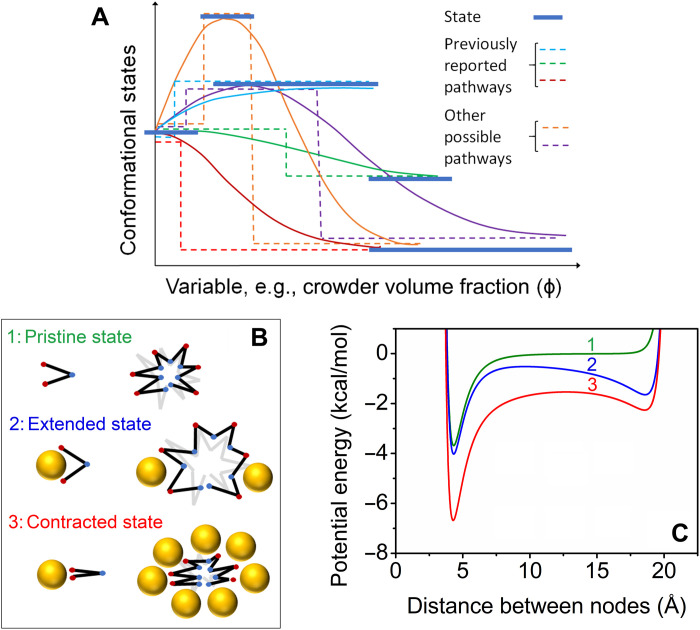
Figure 9A shows a schematic illustration of energy landscapes and several potential pathways of conformational response to the environmental variable of interest, which could be crowder volume fraction, temperature, pH, degree of protein hydration, etc. Two of the monotonic compaction pathways and one of the extension pathways mimic the global property, Rg, measured or modeled in previous studies (fig. S1). However, other pathways involving both extension and compaction are also shown to be possible in this schematic map of an IDP energy landscape, portending further experiment and modeling. In this context, an extension-contraction model has been developed to capture the fundamental phenomena governing the observed extension and contraction behavior of the D-Rec1 molecules under varying concentrations of crowder molecules. The model was inspired by three publications: first, Kobayashi and Winkler (65), who developed a node-to-node mechanical model to understand the expansion and contraction of hydrogels; second, Zhou et al. (66), who developed the free energy model by combining enthalpic and entropic terms; and third, Baowan and Hill (67), who developed the approach of nanomechanics for predicting the motion of molecular structures under the influence of van der Waals and electrostatic forces. The elements of the model are shown in Fig. 9B. The resilin molecule is represented as a long chain of nodes linked by rigid segments. A node can represent a single amino acid or a cluster of amino acids. Nodes interact with each other via van der Waals and electrostatic forces. The crowder molecule is represented as a uniform sphere that interacts with the resilin nodes via van der Waals forces. On the basis of these elements, the contracted and extended state of the resilin can be modeled as a balance of forces between the nodes and the crowder molecules. If the attractive forces between the nodes are stronger than the attractive forces between the nodes and the crowders, then resilin will tend toward the contracted state. Vice versa, if the attractive forces between the nodes and the crowder molecules are stronger than the attractive forces between the nodes, then the resilin will tend toward the extended state.
Fig. 9. Energy landscape, schematic of model elements, and potential energy for predicted scenarios.
(A) Schematic of energy landscape showing known and possible routes of conformational change in response to the environment. Dotted lines indicate uniform path of discrete jumps between minimum energy states, and solid lines indicate ensemble behavior. (B) Depiction of the elements of the model used. The resilin molecule is represented as a long chain of nodes linked by rigid segments. A node can represent a single amino acid or a cluster of amino acids. Nodes interact with each other via van der Waals and electrostatic forces. The crowder molecule is represented as a uniform sphere that interacts with the resilin nodes via van der Waals forces. (C) Potential energy between two nodes of a segment for three scenarios: (1) pristine state with no crowders, (2) extended state with few crowders, and (3) contracted state with many crowders.
Node-node interactions consist of van der Waals forces and electrostatic forces, which result in a potential energy (Un-n). The Lennard-Jones 12-6 potential (68) is used to calculate the potential energy of the van der Waals forces, while the electrostatic forces are calculated using Coulomb’s law, as follows
| (1) |
where ρ is the distance between the nodes, A (=4εσ6) and B (=4εσ12) are the Lennard-Jones constants (where ε is the well depth and σ is the van der Waals diameter), q is the elementary charge of the node, and ϵ(ϕ) is the dielectric constant of the surrounding medium. The dielectric constant is a decreasing function of crowder ϕ. Node-crowder interactions consist of van der Waals forces, which result in a potential energy (Un-c). Baowan and Hill (67) calculated the interactions between a molecule and a sphere by integrating the van der Waals forces across the surface of the sphere, resulting in the following expression
| (2) |
| (3) |
where η is the surface density of atoms for the crowder molecule, a is the radius of the crowder molecule, and δ is the distance between the resilin node and the center of the crowder molecule, which can be expressed as a function of ρ using geometric principles. The total potential energy (Utot) is then calculated as a sum of node-node and node-crowder interactions, as follows
| (4) |
where f (ϕ) is a weighting function of crowder ϕ. Figure 9C depicts the total potential energy between two nodes of a segment for three scenarios: (1) in the absence of crowder molecules, (2) in the presence of few crowder molecules, and (3) in the presence of many crowder molecules. For scenario (1), there is an attractive potential energy well at a node-node distance near to 5 Å, followed by the repulsive forces around 4 and 20 Å due to the interatomic repulsive forces between the nodes at close distances and the covalent bond restriction at the fully extended state, respectively. Ignoring kinetic motion and other forces, the potential energy for scenario (1) suggests that the segment will prefer the natural state, where many nodes will sit at a distance of around 5 Å. For scenario (2), the introduction of crowder molecules results in an attractive potential energy well ~19 Å. This means that a number of segments will extend as a result of the attractive forces offered by the crowder molecules. For scenario (3), both potential wells remain at higher crowder ϕ; however, the attractive electrostatic interactions between nodes become stronger as the crowder molecules reduce the dielectric constant of the surrounding medium. The Rg of the resilin molecule is a function of the weighted average of all node-node distances (ρav), as follows
| (5) |
| (6) |
| (7) |
where N is the number of nodes, ω is a geometric factor related to the shape and density of the resilin molecule, G is the Gibbs free energy, k is the Boltzmann constant, T is the temperature, and S(ϕ) is entropy that decreases with ϕ. The functions for the dielectric constant ϵ(ϕ), weighting function f (ϕ), and entropic function S(ϕv) are based on the logistic-type equations in the form
| (8) |
where k is the rate constant and ϕmax is the maximum limit of the function.
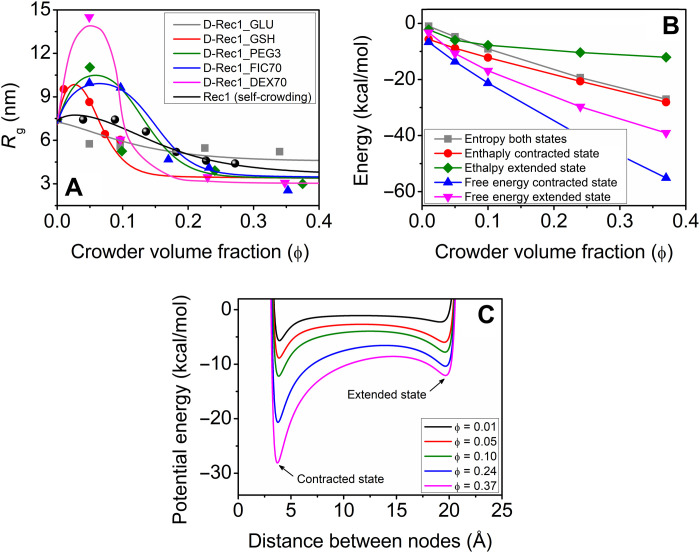
Figure 10A depicts the model results and experimental data for the Rg of D-Rec1 molecules as a function of ϕ of the crowder of interest (GLU, GSH, PEG3, FIC70, and DEC70). Quantitative agreement is found between the model and the experimental data. The model is capable of capturing the important features including the nonlinear extension and contraction behavior of the D-Rec1 molecules. Intuitively, the model highlights the balancing forces between the intermolecular and intramolecular interactions. The parameters for crowder radius (a) were taken from table S4 (0.43 nm for GLU, 1.1 nm for GSH, 1.8 nm for PEG3, 4.3 nm for FIC70, and 6.3 nm for DEX70), while the other parameters were fitted. The key parameters were found to be the crowder radius and the resilin-crowder interaction parameter captured by η (0.05 for GLU, 0.75 for GSH, 1.3 for PEG3, 0.93 for FIC70, and 0.6 for DEX70). The resilin-resilin interaction parameter for Rec1 self-crowding, ηs-c, is 0.35 for comparison. As can be seen in Fig. 10A, the measured and modeled extension and compaction behaviors show that D-Rec1 extends by 92% and compacts by 66% depending on the size of the crowder and the IDP-crowder interaction approximated using van der Waals forces. The limit of compaction is governed by the equilibrium distance between the nodes within the resilin molecule. The equilibrium distance is a function of the van der Waals radii of the atoms and the electrostatic interactions. If the dielectric constant of the surrounding medium is low, then the electrostatic potential between the atoms can increase, which can result in a larger equilibrium distance.
Fig. 10. Crowder-induced conformation and energy changes in Rec1-resilin.
(A) Rg of D-Rec1 as a function of crowder volume fraction for different crowders (GLU, GSH, PEG3, FIC70, and DEX70). Solid color lines represent the model predictions and open symbols represent the respective experimental data. Self-crowding conformations for Rec1-resilin protein reported elsewhere (23) are given to further test the model. (B) Model results for an ensemble of states, a snapshot at each crowder volume fraction, for the crowder PEG3. The enthalpy and entropy are calculated for the extreme cases (i.e., contracted and extended states). (C) Corresponding potential energy of the system obtained from the model.
Figure 10B shows the calculated free energy, enthalpy, and entropy for the PEG3 crowding conditions. The model predicts that the system wants to minimize its free energy at each step, and the IDP preference is always the contracted state, but the extended state offers a reasonable alternative, especially at the lower crowder volume fractions. Additional work can be performed on the model, where the geometry of the resilin molecule can be improved by using a variety of segment lengths, and the functions for dielectric constants and entropy could be improved on the basis of experimental results. The goodness of fit as measured by R2 is largest for the crowder molecule that causes the largest extension (DEX70), which is also the only crowder that is larger than the IDP. R2 values for fits shown in Fig. 10B are as follows: 0.51 for GLU, 0.80 for GSH, 0.55 for PEG3, 0.95 for FIC70, 0.96 for Rec1 (self-crowding), and 0.99 for DEX70. See table S5 for a complete list of parameters, including root mean square error for the model. Figure 10C shows the corresponding total potential energy between two nodes of a segment of resilin molecule for PEG3 crowding conditions. With an increase in crowder ϕ, both attractive potential energy wells around 5 and 19 Å, corresponding to the interatomic forces (attractive electrostatic interactions) between the nodes and covalent bond restriction, respectively, remain. However, the attractive electrostatic interactions between nodes become stronger with an increase in crowder ϕ as the crowder molecules reduce the dielectric constant of the surrounding medium. The extension-contraction model relies on interactions as a driving force of protein conformation. Protein-water interactions and crowder-water interactions can vary the conformation and dynamics of macromolecules. In the extension-contraction model, the crowder molecules can act as shuttles delivering or removing water from the local protein environment, as driven by the interactions. The model does not consider the role of water in isolation, rather the whole system coming to a state of lowest free energy. Moreover, the values of energy in kilocalories per mole can be translated to equivalent thermal driving force, indicating that the LCST/UCST window is available at ambient temperature for D-Rec1 for the various crowding conditions: UCST at low volume fraction of crowder and LCST at high volume fraction of crowder. The results presented suggest additional experimental studies to measure the variation in USCT and LCST as a function of crowder volume fraction and to confirm the reversibility of the states or, in other words, to confirm that the energy landscape pathways are reversible.
In summary, we have investigated conformational dynamics and stability of D-Rec1 under physiologically relevant macromolecular crowding conditions, using contrast-matching SANS and USANS. A variety of crowding agents with a wide range of sizes, shapes, and structures were examined. Compaction of D-Rec1 by 31% was observed with the small monosaccharide GLU molecule as crowder, whereas the small GSH peptide and the macromolecular crowders PEG3, FIC70, and DEX70 systematically extended (up to 92%) and compacted (up to 66%) the conformational ensemble. The increase in size of D-Rec1 for initial crowding agent packing fraction (0.01 to 0.13) for GSH, PEG3, DEX70, and FIC70, respectively, was attributed to soft attraction between protein and crowding agents. A systematic decrease in size with a further increase in crowding agent packing fraction up to 0.375 demonstrated compaction of the conformation attributed to excluded volume effects and depletion interactions between protein molecules. Combined spectrofluorimetric and CD spectroscopic assessment of the crowder-directed interactions, conformational dynamics, and secondary structural evolution revealed the capacity of Rec1-resilin to evade crowder-induced folding and retain its overall IDP character. A computer-generated simulation and visualization of the change in domain structure of D-Rec1 in the crowding environment has been successfully attempted using ab initio 3D structure modeling. An extension-compaction model has been developed to understand the observed behavior of the IDP as a function of crowding agent packing fraction. The presented results and model contribute to a more detailed understanding of the conformational dynamics of stimulus-responsive IDPs in crowded physiological environments and elucidate the rules of engagement that govern the packing of such IDPs in crowded conditions. The technique has great potential in drug therapy, in terms of gaining an in-depth understanding of the pharmacokinetic and pharmacodynamic profiles of encapsulated/conjugated small molecular drugs, proteins, or nanoparticles under crowded conditions.
MATERIALS AND METHODS
Expression and purification of D-Rec1
To achieve sufficient neutron contrast against the crowding agents, D-Rec1-resilin was biosynthesized. D-Rec1 was overexpressed in BL21*(DE3) pLysS Escherichia coli strain containing the Rec1-resilin gene sequence in pET28a plasmid. The cells from single colonies were gradually adapted to D2O-based minimal “Mod C1” media (69) with kanamycin, containing a stepwise increasing concentration of D2O from 0 to 100%, and stored as glycerol stock at −80°C until needed. The starter culture of 100 ml of 90% D2O minimal medium, OD600 between 0.9 and 1.1, was used to inoculate 2 liters of RTF-5 fermenter bioreactors (Real Time Engineering) containing 1 liter of the same medium. Cells were cultured at 37°C with automatically regulated pH and dissolved oxygen. Cultures were fed with 20 ml of 66% glycerol in D2O solution about 1 hour before induction, and when the OD600 reached 17 to 18, they were induced to express the desired protein with 1 mM isopropyl β-d-1-thiogalactopyranoside, and the temperature was lowered to 30°C. After 15 hours, the biomass was harvested and stored at −80°C or on dry ice until purification. The obtained cell paste was resuspended in homogenization/lysis buffer containing 1.7% sodium chloride, 0.6% tris base, 6.2 mM benzamidine, 10.6 mM β-mercaptoethanol, 0.01% Triton X-100, 0.04% deoxyribonuclease I (10 mg/ml), and 0.016% lysozyme. The suspension was passed through the homogenizer (three times with cooling between passes) at a pressure of 700 bar. The obtained homogenate was clarified by centrifugation (70). Saturated ammonium sulfate was slowly added to the supernatant to a final concentration of 20% and stirred at 4°C overnight. The suspension was centrifuged to pellet the protein. The protein pellet was resuspended in PBS and stirred overnight to dissolve. The resulting protein solution was dialyzed overnight at 4°C against PBS. The dialysate was clarified, and the supernatant was heated at 80°C for 15 min. The heat-treated protein solution was centrifuged at 11,419g for 15 min at 20°C to remove the denatured proteins. The supernatant was concentrated using an Amicon stirred concentrator cell with a 10K MWCO (molecular weight cut-off) membrane. The protein was stored at 4°C, and a coacervate formed with the lower layer containing the pure D-Rec1. The bicinchoninic acid assay was performed, and the concentration of protein in the lower layer was estimated at 240 mg/ml. The molecular mass of D-Rec1 measured using electrospray ionization time-of-flight mass spectrometry was 29.4 kDa (fig. S14), which is slightly larger than Rec1-resilin (28.5 kDa) (29) and indicates ~70% deuteration on nonexchangeable hydrogen positions in the protein.
Dynamic light scattering
The ζ potential and Dh of pristine D-Rec1 and crowding agents in 10 mM PBS were experimentally determined using a Zetasizer (NanoZS, Malvern Instruments Ltd.). The measurements were performed at a fixed temperature of 25°C. The ζ potential values were determined from the measured electrophoretic mobility (μ) using the Smoluchowski approximation in the DTSNano software, which runs an algorithm based on a nonnegative least-squares fit, as follows
| (9) |
where V is the applied voltage, D is the electrode separation, and ε and η are the dielectric constant and viscosity of PBS, respectively. The measured Dh and ζ potential values were calculated from cumulative analysis of three cycles.
Small-angle x-ray scattering
SAXS analysis was performed using the bench-top NanoSTAR II SAXS instrument (Bruker) with a rotating anode Cu Kα radiation source (1.54 Å) and a 2D detector. The scattering intensity of samples was collected as a function of the scattering vector q in the range of 0.01 to 0.39 Å−1 using the below relation (40)
| (10) |
where θ is the angle of scattering and λ is the wavelength of neutrons. The samples were loaded in a quartz capillary with temperature maintained at 25°C. In all the cases, the scattering data of the buffer background were subtracted from the sample for analysis.
Contrast-matching SANS and USANS
SANS analysis was performed using the Quokka SANS instrument (71). Three detector distances of 1.3 m (with 300-mm offset), 12 m, and 20 m, respectively, with an incident neutron wavelength of 5 and 8.1 Å−1 (for 20-m lens optics) were used. The scattering intensity of samples was collected in the q range of 0.0007 to 0.5 Å−1. For contrast-matching experiments, D2O/H2O mixtures matching neutron SLD of crowding agents were used as the dispersion medium. The neutron SLD estimations/calculations were made using the National Institute of Standards and Technology (NIST) online neutron activation and scattering calculator (https://ncnr.nist.gov/resources/activation/). For sample analysis, the prepared dispersions were loaded into demountable Quokka cells of 20-mm diameter and 1-mm path length. The cell temperature was maintained at 25°C for all measurements. The collected SANS data were reduced using NIST Center for Neutron Research SANS reduction macros (modified for the Quokka instrument) using the IGOR Pro software package with data corrected for empty cell scattering and transmission (72). The data collected were transformed to absolute scale using an attenuated direct beam transmission measurement. In all the cases, the appropriate dispersion medium background was subtracted from the sample scattering using the PRIMUS program (73). Moreover, the incoherent background scattering from the systems were determined with a high q power law fit using the SasView program and subtracted from the respective data for analysis (74). The structural parameters of the samples were determined by fitting the data with selective shape-independent model functions using the SasView program. The ab initio 3D structures of the samples were obtained from P(r) outputs using the GASBOR program (47) and visualized as envelope structures using the UCSF Chimera program (48). The concentration normalized I(0) was obtained using Guinier approximation (in the PRIMUS program), as follows
| (11) |
USANS analysis was performed using the Kookaburra USANS instrument (75) with the long neutron wavelength configuration (λ = 4.74 Å). The scattering data were collected at 25°C in the q range of 0.00004 to 0.001 Å−1. For sample analysis, the prepared dispersions were loaded into demountable Kookaburra cells of 40 diameter and 0.5-mm path length. The raw USANS data of samples were reduced using scattering collected from the empty cell and converted to absolute scale using python scripts based on the standard procedure (75). The obtained data were desmeared using the Lake algorithm, incorporated in NIST USANS macros using the IGOR Pro software package (72). The structural parameters of the samples were determined by fitting the data with a shape-independent power law model function using the SasView computer program.
UV-Vis absorption spectroscopy
The absorbance value (at 660 nm) of pristine D-Rec1 and the D-Rec1/crowding agent mixture in 1 mM PBS was experimentally measured using a UV-2700 spectrophotometer (Shimadzu Scientific Instruments). The OD values were calculated from the absorbance values (A) using the below relation
| (12) |
where α is the absorption coefficient and t is the thickness or cuvette path length (in centimeters). The ultraviolet-visible (UV-Vis) absorbance spectrum of pristine Rec1, Rec1/ANS, and Rec1/acrylamide complexes in the absence and presence of crowders (in 1 mM PBS) was also recorded in the wavelength range 200 to 500 nm. The measurements were performed at a fixed temperature of 25°C.
Fluorescence spectroscopy
Crowder-directed change in the surface hydrophobicity of Rec1-resilin was measured using spectrofluorimetric assessment. The interaction of the fluorescent dye (ANS) and fluorescent quencher (acrylamide) with protein was analyzed using a Cary Eclipse fluorescence spectrophotometer (Varian Inc., USA). The ANS/Rec1-resilin and Rec1-resilin/acrylamide complexes and their mixtures with different crowders were equilibrated in the dark for ~1 hour before fluorescence measurements. Samples were equilibrated at 25°C and loaded in a quartz cuvette of 1-cm path length for fluorescence measurement. The excitation wavelength was fixed at 355 nm for samples with ANS and 275 nm for samples with acrylamide. The emission spectrum was collected in the wavelength range of 370 to 800 nm for samples with ANS and 290 to 350 nm for samples with acrylamide. The emission spectra were recorded at 1-nm increments with excitation and emission slit widths of 5 nm and a scan rate of 60 nm/min. The fluorescence measurements were corrected for primary absorbance effects. Sample spectra were also corrected for the background fluorescence of ANS and acrylamide in the absence of Rec1-resilin.
CD spectroscopy
The secondary structure of Rec1-resilin in the crowding environment was measured using CD spectroscopy. CD spectra were recorded (at 25°C) in the wavelength range 190 to 260 nm using a JASCO spectropolarimeter (Jasco J-150, Jasco, Japan) connected to a Jasco MCB-100 Mini Circulation Bath. A UV quartz cuvette with a path length of 1 mm was used for all the measurements. The protein concentration used was 0.1 mg/ml, and CD spectra were measured in 1 mM PBS buffer and crowded conditions (at concentrations comparable to those used in the SANS experiment). Before measurements, all systems were stirred (30 min), centrifuged (12,000g for 2 min), and left to equilibrate for 1 hour. The data pitch was set at 0.2 nm, at a scanning speed of 20 nm/min, a bandwidth of 0.2 nm, a digital integration time (DIT) of 1 s, and an accumulation of 10 scans. CD data were analyzed using the CDPro software package. The online fitting program interface Dichroweb was used to extract secondary structure information from CD spectra (53).
Acknowledgments
We are thankful to R. Knott for support in performing all the SAXS experiment and data analyses. We acknowledge the facilities and the scientific and technical assistance of the RMIT Micro Nano Research Facility. This work benefited from the use of the free protein scattering length density calculator (http://psldc.isis.rl.ac.uk/Psldc/) database of Disordered Protein Predictions resource (https://d2p2.pro/), DichroWeb (http://dichroweb.cryst.bbk.ac.uk/html/home.shtml), and SasView (https://sasview.org/) applications.
Funding: This work was supported by the Australian Research Council’s Discovery Projects funding scheme (project DP160101267). Biosynthesis of D-Rec1 and access to the SANS and USANS facility were supported by ANSTO beamtime awards (proposal NDF6169 and P6170). N.W.’s visit to ANSTO was supported by the Australian Institute of Nuclear Science and Engineering Postgraduate Research award. The National Deuteration Facility at ANSTO is partly supported by the National Collaborative Research Infrastructure Strategy, an initiative of the Australian Government.
Author contributions: R.B., N.R.C., and N.K.D. conceived the project. A.R. synthesized and S.B. and G.D. purified the D-Rec1-resilin. R.B. performed the SANS and USANS experiments and respective data analysis under the guidance of J.P.M. N.W. performed the CD, UV-Vis, and fluorescence spectroscopy experiments under the guidance of N.K.D., and R.B. performed the respective data analysis under the guidance of N.K.D. A.W.T. performed the energy landscape modeling under the guidance of A.J.H. and in discussion with N.R.C. and N.K.D. R.B. wrote the draft manuscript. N.R.C. and N.K.D. supervised the project. All the authors contributed to discussions of the results and revisions of the manuscript.
Competing interests: The authors declare that they have no competing interests.
Data and materials availability: The Rec1-plasmid that has been used to express the resilin protein in this work can be provided by CSIRO, Australia pending scientific review and a completed material transfer agreement. Requests for the Rec1-plasmid should be submitted to CSIRO, Clayton South 3169, Victoria, Australia. All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials.
Supplementary Materials
This PDF file includes:
Supplementary Text
Figs. S1 to S14
Tables S1 to S5
References
REFERENCES AND NOTES
- 1.K. A. Sharp, Unpacking the origins of in-cell crowding. Proc. Natl. Acad. Sci. U.S.A. 113, 1684–1685 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.I. M. Kuznetsova, K. K. Turoverov, V. N. Uversky, What macromolecular crowding can do to a protein. Int. J. Mol. Sci. 15, 23090–23140 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Y. Wang, M. Sarkar, A. E. Smith, A. S. Krois, G. J. Pielak, Macromolecular crowding and protein stability. J. Am. Chem. Soc. 134, 16614–16618 (2012). [DOI] [PubMed] [Google Scholar]
- 4.Y. Phillip, G. Schreiber, Formation of protein complexes in crowded environments—From in vitro to in vivo. FEBS Lett. 587, 1046–1052 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.H.-X. Zhou, S. Qin, Simulation and modeling of crowding effects on the thermodynamic and kinetic properties of proteins with atomic details. Biophys. Rev. 5, 207–215 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.S. Shahid, M. I. Hassan, A. Islam, F. Ahmad, Size-dependent studies of macromolecular crowding on the thermodynamic stability, structure and functional activity of proteins: In vitro and in silico approaches. Biochim. Biophys. Acta Gen. Subj. 1861, 178–197 (2017). [DOI] [PubMed] [Google Scholar]
- 7.P. E. Wright, H. J. Dyson, Intrinsically disordered proteins in cellular signalling and regulation. Nat. Rev. Mol. Cell Biol. 16, 18–29 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.J. Liu, N. B. Perumal, C. J. Oldfield, E. W. Su, V. N. Uversky, A. K. Dunker, Intrinsic disorder in transcription factors. Biochemistry 45, 6873–6888 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.A. L. Darling, Y. Liu, C. J. Oldfield, V. N. Uversky, Intrinsically disordered proteome of human membrane-less organelles. Proteomics 18, 1700193 (2018). [DOI] [PubMed] [Google Scholar]
- 10.H. Popelka, Dancing while self-eating: Protein intrinsic disorder in autophagy. Prog. Mol. Biol. Transl. Sci. 174, 263–305 (2020). [DOI] [PubMed] [Google Scholar]
- 11.V. N. Uversky, C. J. Oldfield, A. K. Dunker, Intrinsically disordered proteins in human diseases: Introducing the D2 concept. Annu. Rev. Biophys. 37, 215–246 (2008). [DOI] [PubMed] [Google Scholar]
- 12.R. Tenchov, Q. A. Zhou, Intrinsically disordered proteins: Perspective on COVID-19 infection and drug discovery. ACS Infect. Dis. 8, 422–432 (2022). [DOI] [PubMed] [Google Scholar]
- 13.A. V. Fonin, A. L. Darling, I. M. Kuznetsova, K. K. Turoverov, V. N. Uversky, Intrinsically disordered proteins in crowded milieu: When chaos prevails within the cellular gumbo. Cell. Mol. Life Sci. 75, 3907–3929 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.S. Qin, H.-X. Zhou, Effects of macromolecular crowding on the conformational ensembles of disordered proteins. J. Phys. Chem. Lett. 4, 3429–3434 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.E. A. Cino, M. Karttunen, W.-Y. Choy, Effects of molecular crowding on the dynamics of intrinsically disordered proteins. PLOS ONE 7, e49876 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.A. Soranno, I. Koenig, M. B. Borgia, H. Hofmann, F. Zosel, D. Nettels, B. Schuler, Single-molecule spectroscopy reveals polymer effects of disordered proteins in crowded environments. Proc. Natl. Acad. Sci. U.S.A. 111, 4874–4879 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.A. Banks, S. Qin, K. L. Weiss, C. B. Stanley, H.-X. Zhou, Intrinsically disordered protein exhibits both compaction and expansion under macromolecular crowding. Biophys. J. 114, 1067–1079 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.K. Lindorff-Larsen, N. Trbovic, P. Maragakis, S. Piana, D. E. Shaw, Structure and dynamics of an unfolded protein examined by molecular dynamics simulation. J. Am. Chem. Soc. 134, 3787–3791 (2012). [DOI] [PubMed] [Google Scholar]
- 19.R. E. Ithuralde, A. E. Roitberg, A. G. Turjanski, Structured and unstructured binding of an intrinsically disordered protein as revealed by atomistic simulations. J. Am. Chem. Soc. 138, 8742–8751 (2016). [DOI] [PubMed] [Google Scholar]
- 20.W. Adamski, N. Salvi, D. Maurin, J. Magnat, S. Milles, M. R. Jensen, A. Abyzov, C. J. Moreau, M. A. Blackledge, A unified description of intrinsically disordered protein dynamics under physiological conditions using NMR spectroscopy. J. Am. Chem. Soc. 141, 17817–17829 (2019). [DOI] [PubMed] [Google Scholar]
- 21.E. Delaforge, J. Kragelj, L. Tengo, A. Palencia, S. Milles, G. Bouvignies, N. Salvi, M. Blackledge, M. R. Jensen, Deciphering the dynamic interaction profile of an intrinsically disordered protein by NMR exchange spectroscopy. J. Am. Chem. Soc. 140, 1148–1158 (2018). [DOI] [PubMed] [Google Scholar]
- 22.J.-B. Guilbaud, A. Saiani, Using small angle scattering (SAS) to structurally characterise peptide and protein self-assembled materials. Chem. Soc. Rev. 40, 1200–1210 (2011). [DOI] [PubMed] [Google Scholar]
- 23.R. Balu, J. P. Mata, R. Knott, C. M. Elvin, A. J. Hill, N. R. Choudhury, N. K. Dutta, Effects of crowding and environment on the evolution of conformational ensembles of the multi-stimuli-responsive intrinsically disordered protein, Rec1-resilin: A small-angle scattering investigation. J. Phys. Chem. B 120, 6490–6503 (2016). [DOI] [PubMed] [Google Scholar]
- 24.J. L. Whittaker, R. Balu, R. Knott, L. de Campo, J. P. Mata, C. Rehm, A. J. Hill, N. K. Dutta, N. Roy Choudhury, Structural evolution of photocrosslinked silk fibroin and silk fibroin-based hybrid hydrogels: A small angle and ultra-small angle scattering investigation. Int. J. Biol. Macromol. 114, 998–1007 (2018). [DOI] [PubMed] [Google Scholar]
- 25.W. T. Heller, Small-angle neutron scattering and contrast variation: A powerful combination for studying biological structures. Acta Crystallogr. D Struct. Biol. Crystallogr. 66, 1213–1217 (2010). [DOI] [PubMed] [Google Scholar]
- 26.D. W. Schaefer, M. M. Agamalian, Ultra-small-angle neutron scattering: A new tool for materials research. Curr. Opin. Solid State Mater. Sci. 8, 39–47 (2004). [Google Scholar]
- 27.E. Appel, J. Michels, S. N. Gorb, Native resilin: Properties, occurrence and biological functions of a remarkable bio-elastomer, in Biomimetic Protein Based Elastomers: Emerging Materials for the Future, N. Roy Choudhury, J. C. Liu, N. K. Dutta, Eds. (RSC, 2022), pp. 8–44. [Google Scholar]
- 28.R. Balu, N. K. Dutta, A. K. Dutta, N. R. Choudhury, Resilin-mimetics as a smart biomaterial platform for biomedical applications. Nat. Commun. 12, 149 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.R. Balu, R. Knott, N. P. Cowieson, C. M. Elvin, A. J. Hill, N. R. Choudhury, N. K. Dutta, Structural ensembles reveal intrinsic disorder for the multi-stimuli responsive bio-mimetic protein Rec1-resilin. Sci. Rep. 5, 10896 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.N. K. Dutta, M. Y. Truong, S. Mayavan, N. Roy Choudhury, C. M. Elvin, M. Kim, R. Knott, K. M. Nairn, A. J. Hill, A genetically engineered protein responsive to multiple stimuli. Angew. Chem. Int. Ed. 50, 4428–4431 (2011). [DOI] [PubMed] [Google Scholar]
- 31.N. K. Dutta, N. R. Choudhury, M. Y. Truong, M. Kim, C. M. Elvin, A. J. Hill, Physical approaches for fabrication of organized nanostructure of resilin-mimetic elastic protein rec1-resilin. Biomaterials 30, 4868–4876 (2009). [DOI] [PubMed] [Google Scholar]
- 32.M. Y. Truong, N. K. Dutta, N. R. Choudhury, M. Kim, C. M. Elvin, A. J. Hill, B. Thierry, K. A. Vasilev, A pH-responsive interface derived from resilin-mimetic protein Rec1-resilin. Biomaterials 31, 4434–4446 (2010). [DOI] [PubMed] [Google Scholar]
- 33.M. Y. Truong, N. K. Dutta, N. R. Choudhury, M. Kim, C. M. Elvin, K. M. Nairn, A. J. Hill, The effect of hydration on molecular chain mobility and the viscoelastic behavior of resilin-mimetic protein-based hydrogels. Biomaterials 32, 8462–8473 (2011). [DOI] [PubMed] [Google Scholar]
- 34.R. Balu, P. Dorishetty, J. P. Mata, A. J. Hill, N. K. Dutta, N. R. Choudhury, Tuning the hierarchical structure and resilience of resilin-like polypeptide hydrogels using graphene oxide. ACS Appl. Bio Mater. 3, 8688–8697 (2020). [DOI] [PubMed] [Google Scholar]
- 35.S. Mayavan, N. K. Dutta, N. R. Choudhury, M. Kim, C. M. Elvin, A. J. Hill, Self-organization, interfacial interaction and photophysical properties of gold nanoparticle complexes derived from resilin-mimetic fluorescent protein rec1-resilin. Biomaterials 32, 2786–2796 (2011). [DOI] [PubMed] [Google Scholar]
- 36.N. K. Dutta, N. Roy Choudhury, S. Mayavan, R. Balu, J. Whittaker, C. Elvin, A. J. Hill, Template directed formation of metal nanoparticles and uses thereof, WO Patent 2014071463A1 (2014).
- 37.R. Balu, L. Bourgeois, C. M. Elvin, A. J. Hill, N. R. Choudhury, N. K. Dutta, A multi-responsive intrinsically disordered protein (IDP)-directed green synthesis of fluorescent gold nanoclusters. J. Mater. Chem. B 3, 6580–6586 (2015). [DOI] [PubMed] [Google Scholar]
- 38.N. K. Dutta, N. Roy Choudhury, R. Balu, C. Elvin, A. J. Hill, Formation of sub-nano metal particles, WO Patent 20150240631A1 (2015).
- 39.R. Balu, R. Knott, C. M. Elvin, A. J. Hill, N. Roy Choudhury, N. K. Dutta, A sustainable biomineralization approach for the synthesis of highly fluorescent ultra-small Pt nanoclusters. Biosensors 9, 128 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.D. I. Svergun, M. H. J. Koch, P. A. Timmins, R. P. May, Small Angle X-Ray and Neutron Scattering from Solutions of Biological Macromolecules (Oxford Univ. Press, 2013). [Google Scholar]
- 41.M. E. Oates, P. Romero, T. Ishida, M. Ghalwash, M. J. Mizianty, B. Xue, Z. Dosztányi, V. N. Uversky, Z. Obradovic, L. Kurgan, A. K. Dunker, J. Gough, D2P2: Database of disordered protein predictions. Nucleic Acids Res. 41, D508–D516 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.S. Li, V. A. Tuan, J. L. Falconer, R. D. Noble, Separation of 1,3-propanediol from glycerol and glucose using a ZSM-5 zeolite membrane. J. Membr. Sci. 191, 53–59 (2001). [Google Scholar]
- 43.C. D. Putnam, M. Hammel, G. L. Hura, J. A. Tainer, X-ray solution scattering (SAXS) combined with crystallography and computation: Defining accurate macromolecular structures, conformations and assemblies in solution. Q. Rev. Biophys. 40, 191–285 (2007). [DOI] [PubMed] [Google Scholar]
- 44.B. Hammouda, SANS from homogeneous polymer mixtures: A unified overview, in Polymer Characteristics (Springer, 1993), pp. 87–133. [Google Scholar]
- 45.V. Petrenko, L. Bulavin, M. Avdeev, V. Garamus, M. Koneracka, P. Kopcansky, Structure and interaction of poly(ethylene glycol) in aqueous solutions. Small-angle neutron scattering data. Macromol. Symp. 335, 20–23 (2014). [Google Scholar]
- 46.P. Bernadó, Effect of interdomain dynamics on the structure determination of modular proteins by small-angle scattering. Eur. Biophys. J. 39, 769–780 (2010). [DOI] [PubMed] [Google Scholar]
- 47.D. I. Svergun, M. V. Petoukhov, M. H. J. Koch, Determination of domain structure of proteins from X-ray solution scattering. Biophys. J. 80, 2946–2953 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng, T. E. Ferrin, UCSF Chimera—A visualization system for exploratory research and analysis. J. Comput. Chem. 25, 1605–1612 (2004). [DOI] [PubMed] [Google Scholar]
- 49.M. Cardamone, N. K. Puri, Spectrofluorimetric assessment of the surface hydrophobicity of proteins. Biochem. J. 282, 589–593 (1992). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.A. Biswas, K. P. Das, Zn2+ enhances the molecular chaperone function and stability of α-crystallin. Biochemistry 47, 804–816 (2008). [DOI] [PubMed] [Google Scholar]
- 51.M. R. Eftink, C. A. Ghiron, Fluorescence quenching studies with proteins. Anal. Biochem. 114, 199–227 (1981). [DOI] [PubMed] [Google Scholar]
- 52.N. J. Greenfield, Using circular dichroism spectra to estimate protein secondary structure. Nat. Protoc. 1, 2876–2890 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.A. J. Miles, S. G. Ramalli, B. A. Wallace, DichroWeb, a website for calculating protein secondary structure from circular dichroism spectroscopic data. Protein Sci. 31, 37–46 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Y. C. Kim, J. Mittal, Crowding induced entropy-enthalpy compensation in protein association equilibria. Phys. Rev. Lett. 110, 208102 (2013). [DOI] [PubMed] [Google Scholar]
- 55.I. M. Kuznetsova, B. Y. Zaslavsky, L. Breydo, K. K. Turoverov, V. N. Uversky, Beyond the excluded volume effects: Mechanistic complexity of the crowded milieu. Molecules 20, 1377–1409 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.M. Sarkar, C. Li, G. J. Pielak, Soft interactions and crowding. Biophys. Rev. 5, 187–194 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.G. Rivas, A. P. Minton, Macromolecular crowding in vitro, in vivo, and in between. Trends Biochem. Sci. 41, 970–981 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.A. Christiansen, P. Wittung-Stafshede, Synthetic crowding agent dextran causes excluded volume interactions exclusively to tracer protein apoazurin. FEBS Lett. 588, 811–814 (2014). [DOI] [PubMed] [Google Scholar]
- 59.J. Rosen, Y. C. Kim, J. Mittal, Modest protein−crowder attractive interactions can counteract enhancement of protein association by intermolecular excluded volume interactions. J. Phys. Chem. B 115, 2683–2689 (2011). [DOI] [PubMed] [Google Scholar]
- 60.N. Kozer, Y. Y. Kuttner, G. Haran, G. Schreiber, Protein-protein association in polymer solutions: From dilute to semidilute to concentrated. Biophys. J. 92, 2139–2149 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.C. M. Miller, Y. C. Kim, J. Mittal, Protein composition determines the effect of crowding on the properties of disordered proteins. Biophys. J. 111, 28–37 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.H. Kang, P. A. Pincus, C. Hyeon, D. Thirumalai, Effects of macromolecular crowding on the collapse of biopolymers. Phys. Rev. Lett. 114, 068303 (2015). [DOI] [PubMed] [Google Scholar]
- 63.P. P. Bansal, A. J. Ardell, Average nearest-neighbor distances between uniformly distributed finite particles. Metallography 5, 97–111 (1972). [Google Scholar]
- 64.L. Sapir, D. Harries, Is the depletion force entropic? Molecular crowding beyond steric interactions. Curr. Opin. Colloid Interface Sci. 20, 3–10 (2015). [Google Scholar]
- 65.H. Kobayashi, R. G. Winkler, Universal conformational properties of polymers in ionic nanogels. Sci. Rep. 6, 19836 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.H.-X. Zhou, G. Rivas, A. P. Minton, Macromolecular crowding and confinement: Biochemical, biophysical, and potential physiological consequences. Annu. Rev. Biophys. 37, 375–397 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.D. Baowan, J. M. Hill, Mathematical modeling of interaction energies between nanoscale objects: A review of nanotechnology applications. Adv. Mech. Eng. 8, 1–16 (2016). [Google Scholar]
- 68.X. Wang, S. Ramírez-Hinestrosa, J. Dobnikar, D. Frenkel, The Lennard-Jones potential: When (not) to use it. Phys. Chem. Chem. Phys. 22, 10624–10633 (2020). [DOI] [PubMed] [Google Scholar]
- 69.A. P. Duff, K. L. Wilde, A. Rekas, V. Lake, P. J. Holden, Robust high-yield methodologies for 2H and 2H/15N/13C labeling of proteins for structural investigations using neutron scattering and NMR. Methods Enzymol. 563, 3–25 (2015). [DOI] [PubMed] [Google Scholar]
- 70.M. Kim, C. Elvin, A. Brownlee, R. Lyons, High yield expression of recombinant pro-resilin: Lactose-induced fermentation in E. coli and facile purification. Protein Expr. Purif. 52, 230–236 (2007). [DOI] [PubMed] [Google Scholar]
- 71.K. Wood, J. P. Mata, C. J. Garvey, C.-M. Wu, W. A. Hamilton, P. Abbeywick, D. Bartlett, F. Bartsch, P. Baxter, N. Booth, W. Brown, J. Christoforidis, D. Clowes, T. d’Adam, F. Darmann, M. Deura, S. Harrison, N. Hauser, G. Horton, D. Federici, F. Franceschini, P. Hanson, E. Imamovic, P. Imperia, M. Jones, S. Kennedy, S. Kim, T. Lam, W. T. Lee, M. Lesha, D. Mannicke, T. Noakes, S. R. Olsen, J. C. Osborn, D. Penny, M. Perry, S. A. Pullen, R. A. Robinson, J. C. Schulz, N. Xiong, E. P. Gilbert, QUOKKA, the pinhole small-angle neutron scattering instrument at the OPAL Research Reactor, Australia: Design, performance, operation and scientific highlights. J. Appl. Cryst. 51, 294–314 (2018). [Google Scholar]
- 72.S. R. Kline, Reduction and analysis of SANS and USANS data using IGOR Pro. J. Appl. Cryst. 39, 895–900 (2006). [Google Scholar]
- 73.P. V. Konarev, V. V. Volkov, A. V. Sokolova, M. H. J. Koch, D. I. Svergun, PRIMUS: A Windows PC-based system for small-angle scattering data analysis. J. Appl. Cryst. 36, 1277–1282 (2003). [Google Scholar]
- 74.R. Balu, N. Roy Choudhury, J. P. Mata, L. de Campo, C. Rehm, A. J. Hill, N. K. Dutta, Evolution of the interfacial structure of a catalyst Ink with the quality of the dispersing solvent: A contrast variation small-angle and ultrasmall-angle neutron scattering investigation. ACS Appl. Mater. Interfaces 11, 9934–9946 (2019). [DOI] [PubMed] [Google Scholar]
- 75.A. Brûlé, F. Darmann, F. Bartsch, A. Berry, Design and performance of the variable-wavelength Bonse–Hart ultra-small-angle neutron scattering diffractometer KOOKABURRA at ANSTO. J. Appl. Cryst. 51, 1–8 (2018). [Google Scholar]
- 76.J. F. Comesaña, J. J. Otero, E. García, A. Correa, Densities and viscosities of ternary systems of water + glucose + sodium chloride at several temperatures. J. Chem. Eng. Data 48, 362–366 (2003). [Google Scholar]
- 77.A. Eliassi, H. Modarress, G. A. Mansoori, Densities of poly(ethylene glycol) + water mixtures in the 298.15−328.15 K temperature range. J. Chem. Eng. Data 43, 719–721 (1998). [Google Scholar]
- 78.O. Mach, L. Lacko, Density gradient in a dextran medium. Anal. Biochem. 22, 393–397 (1968). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Text
Figs. S1 to S14
Tables S1 to S5
References