Abstract
We describe the generalized weighted thermodynamic perturbation (gwTP) method for estimating the free energy surface of an expensive “high-level” potential energy function from the umbrella sampling performed with multiple inexpensive “low-level” reference potentials. The gwTP method is a generalization of the weighted thermodynamic perturbation (wTP) method developed by Li and co-workers [J. Chem. Theory Comput. 2018, 14, 5583–5596] that uses a single “low-level” reference potential. The gwTP method offers new possibilities in model design whereby the sampling generated from several low-level potentials may be combined (e.g., specific reaction parameter models that might have variable accuracy at different stages of a multistep reaction). The gwTP method is especially well suited for use with machine learning potentials (MLPs) that are trained against computationally expensive ab initio quantum mechanical/molecular mechanical (QM/MM) energies and forces using active learning procedures that naturally produce multiple distinct neural network potentials. Simulations can be performed with greater sampling using the fast MLPs and then corrected to the ab initio level using gwTP. The capabilities of the gwTP method are demonstrated by creating reference potentials based on the MNDO/d and DFTB2/MIO semiempirical models supplemented with the “range-corrected deep potential” (DPRc). The DPRc parameters are trained to ab initio QM/MM data, and the potentials are used to calculate the free energy surface of stepwise mechanisms for nonenzymatic RNA 2′-O-transesterification model reactions. The extended sampling made possible by the reference potentials allows one to identify unequilibrated portions of the simulations that are not always evident from the short time scale commonly used with ab initio QM/MM potentials. We show that the reference potential approach can yield more accurate ab initio free energy predictions than the wTP method or what can be reasonably afforded from explicit ab initio QM/MM sampling.
Keywords: phosphoryl transfer, reaction mechanism, free energy profile, thermodynamic perturbation, combined QM/MM, neural network
Graphical Abstract
Introduction
The study of chemical mechanisms of complex systems1 has broad application to areas of heterogeneous, homogeneous and enzyme catalysis,2 synthetic chemistry3 and chemical education.4 Chemical mechanism is often explored through calculation of a free energy surface (FES) in a reduced set of collective variables referred to as reaction coordinates.5 The FES is used to characterize the location and free energy values of competitive reactive pathways connecting the reactant and product states. Numerous methods have been developed to calculate free energy surfaces from combined quantum mechanical/molecular mechanical (QM/MM) simulation. The approaches have been classified into 3 categories:6 methods based on the work of Jarzynski7 which analyze nonequilibrium statistics,8–10 methods that analyze equilibrium statistics generated from biased simulations (umbrella sampling),11–14 and methods which introduce and integrate auxiliary degrees of freedom, such as λ-dynamics15–18 and metadynamics.19,20
Umbrella sampling is a technique that applies an artificial bias to improve sampling efficiency. That is to say, a bias can be chosen to enhance the sampling in the high energy regions of the FES that would otherwise be difficult to sample on a reasonable time scale. If the FES was known a priori, then uniform sampling could be achieved by introducing a bias that exactly canceled the free energy. In practice, one instead performs a series of biased simulations that restrain the sampling to a particular region of reaction coordinates. The umbrella potentials are often chosen to be uncoupled harmonic oscillators, and the biased simulations differ by the choice of biasing force constants and equilibrium positions; however, the methods presented in the present work are general and do not assume a specific functional form for the biasing potential. For relatively simple mechanisms, the umbrella potentials can be chosen to span a predetermined range of reaction coordinates; however, methods have been developed to adaptively focus the sampling21–30 and locate minimum free energy pathways.31–38 There are several analysis techniques that can be used to reconstruct the FES from the biased simulations, including: the weighted histogram analysis method (WHAM),39,40 and unbinned weighted histogram analysis method (UWHAM),41,42 the multistate Bennett acceptance ratio method (MBAR),43 the variational free energy profile (vFEP) method,44–46 and umbrella integration.47–49
A series of recent works have introduced the weighted thermodynamic perturbation (wTP) method.50–55 This method estimates the FES of an expensive target potential from the umbrella sampling performed with a cost-effective reference potential. One can view the wTP method as being analogous to the reference potential method encountered in alchemical free energy applications,56–59 and the accuracy of the wTP method similarly relies on close agreement between the target and reference potentials.60 By performing simulations with an inexpensive reference potential, much greater sampling can be achieved through longer and/or more numerous independent simulations. Therefore, the wTP method is complimentary to other approaches that extend the sampling, such as multiple timestep integration.61 Analysis of the extended simulations is useful for identifying unequilibrated sampling, and extended simulations become necessary in situations where multiple structural conformations are thermally accessible.
In the present work, we describe the generalized weighted thermodynamic perturbation (gwTP) method. The gwTP method estimates the FES of an expensive target potential from the aggregate umbrella sampling performed with multiple reference potentials. By combining the sampling, one no longer relies on a single reference potential to obtain good phase space overlap with the target potential throughout the entire FES.59,62,63 Instead, only one of the reference potentials must have good phase space overlap in each region of the FES. If all of the potentials poorly overlapped with the target, then no reweighting strategy is likely to succeed from a limited number of target potential evaluations. Thus, it is important to have a quantitative measure of agreement between the reference and target potentials to gauge the reliability of the approach. The “reweighting entropy” is an index developed specifically for this purpose,64 and we shall discuss it in more detail in subsequent sections. We were motivated to develop the gwTP method by the growing interest in supplementing semiempirical QM/MM Hamiltonians with machine learning potentials (MLP) that are trained to reproduce ab initio QM/MM energies and forces.51,65–75 If one had a priori confidence in the trained MLP, then one obviously can use it to estimate free energy surfaces without additional correction; however, if one is applying a MLP to a system that was not explicitly included in the training, then a MLP-corrected model naturally serves as an excellent reference potential to estimate the ab initio FES from reweighting. Furthermore, the active learning procedure used to train MLPs produces several neural network parameter sets (several potentials),76,77 and the gwTP method provides a means to estimate the ab initio FES from the aggregate sampling performed with each potential. As multiple independent simulation runs are typically performed in order to produce robust averages and error estimates, the use of different reference potentials can often be accommodated for no added computational cost. The gwTP framework further offers new possibilities in model design. Because the gwTP method can combine the sampling from several “specific reaction parameter” (SRP) models,78–80 one can design several potentials that specialize their training to reproduce different chemical events embodied within a complex chemical mechanism, such as the general acid, general base, and phosphoryl transfer steps in RNA cleavage reactions.81 Alternatively, one could parametrize several potentials that are trained to model the 2′-O-transesterification reaction in different RNA environments, and then perform sampling with each potential when exploring the mechanism in an RNA environment not included in the training. In the above discussion, the trained MLPs are used to perform the sampling; however, MLPs can also be utilized in another strategy whereby an uncorrected reference potential is sampled, and a MLP is trained to a small number of configurations to estimate the target potential energies required for thermodynamic perturbation.68,82–84
We apply the gwTP method to two non-enzymatic RNA 2′-O-transesterification model reactions shown in Figure 1. The mechanism of closely related non-enzymatic phosphoryl transfer reactions have been explored with linear free energy relationships85,86 and through the calculation of free energy surfaces.87,88 These previous works found that the pathway is correlated to the pKa of the leaving group. Leaving groups with a pKa < 11 (“enhanced” leaving groups) proceed through a concerted mechanism containing a single, “early” (ξPT < 0) transition state, whereas leaving groups with a pKa > 12 (“poor” leaving groups) proceed through two distinct barriers separated by a minimum. The methoxide and ethoxide leaving groups shown in Figure 1 are “poor” leaving groups, so the FESs are expected to contain an early transition state characterized by partial formation of the O2′-P bond and a second rate-controlling transition state characterized by partial cleavage of the O5′-P bond.
Figure 1:
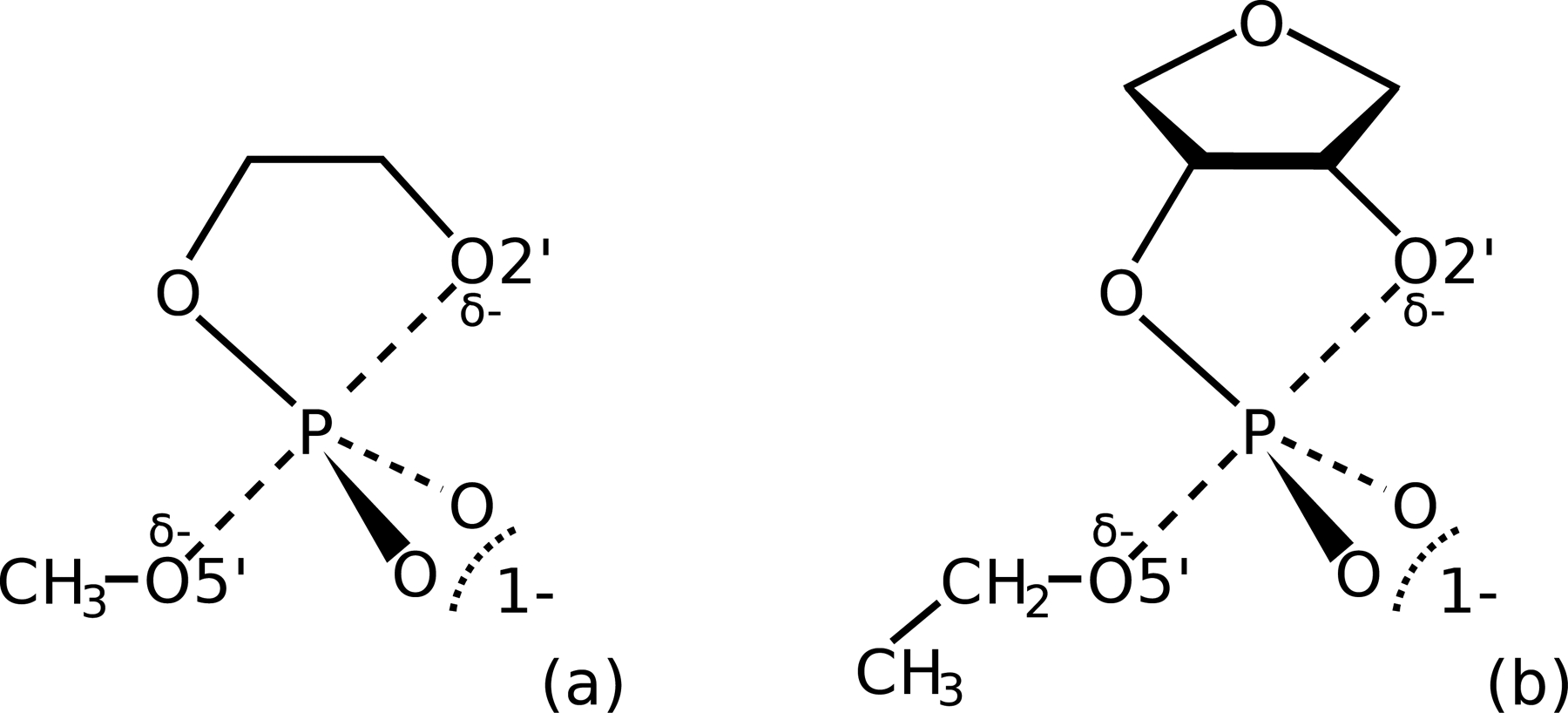
Non-enzymatic RNA 2′-O-transesterification model reactions explored in this work (atomic numbering of 2′ and 5′ positions in the model systems reflect their analogous positions in RNA). (a) The ethylene phosphate model reaction with a methoxide leaving group. (b) The native model reaction used in ref. 88 with an ethoxide leaving group. The reaction coordinate used in this work is ξPT = RP-O5’ − RP-O2’.
The ethylene phosphate reaction (Figure 1a) is used to demonstrate the gwTP method’s ability to reconstruct a PBE0/6–31G* target FES from the sampling obtained from 4 disparate reference potentials. For the purpose of providing a stringent test case for demonstration, the 4 reference potentials were specifically designed such that none of them accurately reproduce the target FES throughout the entire range of ξPT values. The reference potentials use the MNDO/d semiempirical Hamiltonian supplemented with a range-corrected deep potential76,88 (DPRc) MLP. We trained 4 ad hoc MNDO/d QM/MM+DPRc potentials using different target data to yield significantly different reference potentials. Each MNDO/d QM/MM+DPRc potential was trained to reproduce the PBE0/6–31G* target energies and forces at different stages along the reaction coordinate (i.e., different subdomains of the ξPT reaction coordinate) such that the reference potentials disagree with each other and the target in the regions they were not trained. We will show that the wTP estimates of the target FES (based on a single reference potential) are inaccurate in the untrained regions, whereas the gwTP analysis of the aggregate sampling from all reference potentials accurately reproduces the PBE0/6–31G* surface.
The native model reaction (Figure 1b) is used as a case study to emphasize the benefits offered by the reference potential approach. This reaction was one of 6 nonenzymatic models used to parametrize the DFTB2/MIO QM/MM+DPRc potentials in ref. 88. Free energy surfaces of the PBE0/6–31G* QM/MM, DFTB2/MIO QM/MM, and DFTB2/MIO QM/MM+DPRc potentials were obtained from identical simulation protocols. The DPRc correction was shown to improve the comparison with the ab initio results; however, some discrepancies between the PBE0/6–31G* QM/MM and DFTB2/MIO QM/MM+DPRc native model profiles remained. In the present work, we revisit the calculation of the native model FES. We show that gwTP analysis of the DFTB2/MIO QM/MM+DPRc sampling performed in ref. 88 results in excellent agreement with the PBE0/6–31G* FES. Furthermore, we extend the DFTB2/MIO QM/MM+DPRc sampling from 100 ps/window to 1.2 ns/window of aggregate sampling – an amount of sampling well beyond what is routinely affordable using ab initio QM/MM simulation. The extended sampling made possible by the reference potential approach allows us to demonstrate that the native model reaction ab initio QM/MM free energy profiles presented in ref. 88 are not converged. We show that a better estimate of the ab initio FES can be made using reference potentials with extended sampling than what can reasonably be afforded from ab initio QM/MM simulation.
Theory
Multistate Bennett Acceptance Ratio (MBAR) Method
In this section, we introduce our notation by reviewing the MBAR approach for calculating free energy surfaces. The description also serves to aid the reader’s understanding of the differences between the MBAR, wTP, and gwTP methods. The FES of a system composed of 3N atomic coordinates r is typically expressed in a reduced set of relevant collective variables ξ(r), called reaction coordinates. Umbrella sampling is used to enhance the statistics in the high-energy regions of the FES by performing a series of Kh simulations of biased potential energy (PE) functions Uhk(r) that differ only by varying the bias Whk(r) applied to the unbiased potential Uh(r).
| (1) |
The subscripts h and k denote the unbiased PE function and biasing potential, respectively, and one can interpret (hk) as a combined-index of biased states. The goal is to use MBAR to analyze the biased sampling performed with Uhk(r) to estimate the unbiased FES of Uh(r). One could write the MBAR expressions without introducing the h subscript because only a single unbiased PE function is ever considered; however, the utility of its inclusion will become apparent when describing the wTP and gwTP methods in the ensuing sections. A simulation performed with Uhk(r) at temperature Thk produces an ensemble of Nhk structures. The 3N array of atomic coordinates of sample n in the ensemble of state hk is denoted rhkn. Our description of the methods shall write the PE and biasing potential in reduced energy units: uhk(rh′k′n) = βh′k′Uhk(rh′k′n), uh(rh′k′n) = βh′k′Uh(rh′k′n), and whk(rh′k′n) = βh′k′Whk(rh′k′n) where βhk = (kBThk)−1 and kB is the Boltzmann constant.
The unbiased free energy surface Fh(ξ) is, to within an additive constant, related to the probability of observing a sample at ξ, ρh(ξ).
| (2) |
In practice, the probability is approximated by discretizing ξ into histogram bins consisting of centers ξm and widths Δξ. Let δ(ξm − ξ(rhkn)) denote the indicator function, which is 1 only if the sample is contained within bin m.
| (3) |
The probability of observing a sample in bin m is then given by eq. 4, where ωh(rhkn) is the weight of sample rhkn (see eq. 6).
| (4) |
The MBAR expression for the FES of uh(r) within histogram m is given by inserting eq. 4 into eq. 2.
| (5) |
If the sampling was performed with an unbiased PE, then the sample weights would be uniform and eqs. 4–5 would merely count the fraction of samples observed within each bin. The situation is more complicated when umbrella sampling is performed because the distributions are skewed by the artificial bias. Reference 43 developed the equations to reweight trajectories using MBAR, and ref. 50 specialized those equations to combine the biased sampling in FES applications. The result of these previous developments is shown in eq. 6.
| (6) |
The fhk values are the free energies (in reduced energy units) of the Kh biased states obtained from solution to the MBAR/UWHAM equations.
| (7) |
The fh value is the free energy of unbiased PE uh(r). The numerator of eq. 6 includes the factor ; this factor is the inverse of the unbiased state’s partition function, which formally normalizes the weights.43,50 In practice, the normalization constant shifts the entire FES by a constant.
| (8) |
Weighted Thermodynamic Perturbation (wTP) Method
The wTP method has been developed over a series of recent articles.50–55 The purpose of the method is to predict the FES of an expensive “target” PE function from the umbrella sampling performed with an inexpensive “reference” PE function. The unbiased target ut(rhkn) and reference uh(rhkn) PE functions of each sample are evaluated, and the energy differences Δuth(rhkn) = ut(rhkn) − uh(rhkn) are used to predict the target FES. In this sense, the wTP method is analogous to a “reference potential method” often encountered in alchemical free energy applications.
The wTP FES estimate of the unbiased target potential is given by eqs. 9–10.
| (9) |
| (10) |
The ft quantity is the free energy of the unbiased target potential.
| (11) |
Multiplying the numerator and denominator of eq. 10 by exp[uh(rhkn)] allows one to rewrite the expression in terms of the energy difference.
| (12) |
The second line of eq. 12 suggests that one can interpret the wTP method as effectively performing “exponential averaging” between the reference and target potentials in each histogram bin upon reweighting the biased simulations. The exp(ft − fh) factor is a ratio of partition functions that merely shifts the FES by a constant.
Generalized Weighted Thermodynamic Perturbation (gwTP) Method
The gwTP method extends the wTP approach by considering situations where umbrella sampling has been performed with NPE reference potentials. We place no restrictions on the relationship between the sets of biasing potentials used to enhance the sampling of each reference potential; that is, Kh does not need to be the same as any other Kh′, and whk(r) does not need to be the same as any other wh′k′(r). It is for this precise reason why the biasing potentials are written with both h and k subscripts. With this freedom, there are a total of biased states, and expressions which sum all biased states must now be written either as a double summation or by viewing hk as a combined-index of biased simulations . The MBAR/UWHAM equations for the solution of the Nsim biased free energies is shown in eq. 13.
| (13) |
The target potential free energy (eq. 14) and the target FES (eq. 15) are similarly rewritten to account for the additional umbrella sampling.
| (14) |
| (15) |
All that remains is to generalize the wTP expression for the target potential sample weights (eq. 12). As previously stated, the wTP method can be interpreted as a weighted exponential averaging procedure within each histogram bin, so it may be perplexing how this could be adapted to treat multiple reference potentials because exponential averaging has traditionally been applied to the calculation of free energy differences between pairs of potentials. Our approach is to reinterpret the biased potentials as using a single reference (the “selected reference”) perturbed by an effective bias that accounts for the difference in unbiased energies. This is more clearly described by eq. 16 which re-expresses the biased PE uh′k′(r) in terms of the selected reference uh(r) and the effective bias wk′(r) + Δuh′h(r), where Δuh′h(r) = uh′(r) − uh(r).
| (16) |
The decision of which potential to select as the reference is arbitrary; it has no effect on the predicted FES. Our convention is to select the potential which produced the sample. That is to say, the sample rhkn is a member of the ensemble generated from uhk(r), whose reference potential is uh(r), thus we choose uh(r) to be the selected reference. The gwTP expression for the sample weights (eq. 17) differs from eq. 12 only by considering the additional simulated states and by replacing the biasing potential with the effective bias.
| (17) |
Multiplying the numerator and denominator by exp[−uh(rhkn)] yields an expression that illustrates more clearly that the weights are independent of the selected reference.
| (18) |
The weights shown in eqs. 6, 10, and 18 are very similar because they are all specialized forms of the general expressions for the MBAR weights developed by Shirts and Chodera.43 In their work, an ensemble average of a target thermodynamic state is expressed using the samples obtained from a collection of explicitly-simulated states (which may or may not include the target state). To apply the MBAR approach in a novel way, one must define the target and sampled potentials in the context of the new application and describe how the weights are used. In the context of umbrella sampling, the target state corresponds to an unbiased potential, the sampled states are the biased simulations, and the weights are used to approximate the spatial distribution of the density (eq. 4). The methods described in the present work differ only in their choice of target and sampled potentials.
The reweighting entropy is a useful index to gauge the reliability of a calculated FES.64 It can be interpreted as being a measure of “flatness” in the sample weights, such that it is 1 when the distribution of weights in a bin are uniform, and it approaches 0 when the sum of weights is dominated by only a few samples. The gwTP expression for the reweighting entropy is given by eqs. 19–20.
| (19) |
| (20) |
Computational Models and Methods
All simulations described below were performed with a development version of SANDER.89 The simulations were propagated with a 1 fs time step. All production sampling was performed in the canonical ensemble using the Langevin thermostat with a 5 ps−1 collision frequency to maintain a temperature of 298 K.90 The equilibration of the system densities were performed in the isothermal-isobaric ensemble using the Berendsen barostat to maintain an external pressure of 1 atm.91 The long-range electrostatics were calculated with a particle mesh Ewald (PME) method using a 1 Å3 regular grid spacing, 8 Å real-space cutoffs, and tinfoil boundary conditions.92 Specifically, the semiempirical QM/MM simulations performed PME with Mulliken charges,93,94 whereas the ab initio QM/MM calculations used the ambient-potential composite Ewald method.87 The ab initio QM/MM simulations were performed with the HFDF software package developed within our group, which we interfaced to SANDER and described in ref. 87. The Lennard-Jones potential was truncated at 8 Å, and a tail correction was applied to model the interactions beyond the cutoff.95 The solute structures were initially prepared with the GAFF force field,96 and the solvent was modeled with the TIP4P-Ew water model.97 The MNDO/d QM/MM+DPRc and DFTB2/MIO98–100 QM/MM+DPRc potentials include a nonelectrostatic MLP correction to the underlying QM/MM energy and forces. The DPRc potential is an extension of the DeepPot-SE model101 that includes corrections for both the QM-QM and QM-MM interactions, and the neural network parameters are optimized to reproduce the target QM/MM energies and forces. The DPRc model has been previous described,76,88 and additional details are provided in the Supporting Information.
Simulations of the ethylene phosphate reaction.
The ethylene phosphate (Figure 1a) FES was calculated from umbrella sampling performed at 48 values of ξPT ranging from −3.1 to 1.6 Å in steps of 0.1 Å that bias the PE with a spring force constant of 200 kcal mol−1 Å−2. An initial structure for the unimolecular reactant state was prepared by solvating the system in a truncated octahedron containing 2974 TIP4P-Ew water molecules. A 100 ps MNDO/d QM/MM simulation was performed in the NPT ensemble to equilibrate the system density, and the final real-space lattice vector lengths were 49.03 Å. A series of 3 ps NVT simulations were conducted to slowly progress the structure along the reaction coordinate (that is, the brief simulation of window i + 1 was restarted from simulation i) to generate initial structures for each window. Each window was then equilibrated with MNDO/d QM/MM for 100 ps in the NVT ensemble. This was followed by an additional 20 ps of NVT equilibration with PBE0/6–31G* QM/MM. Production sampling was performed with PBE0/6–31G* QM/MM to obtain a target FES used to validate the wTP and gwTP reference potential methods. The PBE0/6–31G* QM/MM production simulations were performed for 80 ps/(window·trial) and repeated 4 times to analyze the uncertainty in the FES values. The 4 trials differed only by changing the thermostat random number seed value. The aggregate amount of PBE0/6–31G* sampling corresponds to 320 ps/window or 15.36 ns of sampling for the entire FES. The coordinates were saved every 10 fs for analysis.
The parametrization of MLPs often involves the use of an active learning procedure that results in several network parameter sets that produce similar corrections to the energies and forces for the data they were trained against. If the training data adequately represents the ensemble of structures observed in production sampling, then the trial network parameter sets can lead to similar FES values. For illustrative purposes, we’ve chosen to construct 4 ad hoc MNDO/d QM/MM+DPRc potentials that yield disparate FES values. These potentials were trained to reproduce different regions of the ethylene phosphate FES rather than the entire surface. Each potential well-reproduces the ab initio FES in the region where it was parametrized, but the FES values disagree with each other and the ab initio target elsewhere. We will show that the gwTP analysis from the combined sampling of all 4 potentials reproduces the ab initio FES over the full range. The MNDO/d QM/MM+DPRc potentials will be referred to as ML0, ML1, ML2, and ML3. The potentials were trained to reproduce different sets of target PBE0/6–31G* energies and forces. Specifically, the ML0 potential was trained only using the sampling obtained from −0.1 Å ≤ ξPT ≤ 1.6 Å, the ML1 potential was trained to −1.3 Å ≤ ξPT ≤ 1.0 Å, the ML2 potential was trained to −2.5 Å ≤ ξPT ≤ −0.2 Å, and the ML3 potential was trained to −3.1 Å ≤ ξPT ≤ −1.4 Å. In the present work, we are making comparison with a FES obtained from explicit ab initio sampling; therefore, we’ve reused the sampling to serve as initial training data for each potential. Specifically, 2.5% of the PBE0/6–31G* trajectory frames in the desired range was chosen at random to parametrize each potential. The optimization of the network parameters was performed with the DeePMD-kit and DP-GEN software.102,103 The optimization consisted of 200k steps with initial and final learning rates of 10−3 and 5·10−8 respectively. The initial optimization was followed by 9 cycles of active learning to search for additional training data.76 Each active learning cycle performs 4 parameter optimizations to yield 4 trial parameter sets. One of the parameter sets is used to generate 20 ps of MNDO/d QM/MM+DPRc sampling for each window in the selected range of ξPT values. The atomic forces are then computed with each of the 4 trial parameter sets, and if the maximum standard deviation of atomic forces is within the range 0.08 to 0.25 eV/Å, then the candidate structure is included in the next round of optimization. Upon completion of the active learning procedure, the “DP Compress” compression algorithm was applied to the MLP to improve computational performance during inference.104 The production sampling of each potential, described below, was performed using only 1 of the 4 parameter sets. In hindsight, the initial parameterization to the ab initio sampling would have been sufficient for our purpose; each round of active learning only labeled 6 candidate structures, on average.
The MNDO/d QM/MM+DPRc production sampling of the ethylene phosphate system was performed for 250 ps/(window·potential·trial), and the coordinates were saved to a trajectory file every 50 fs. Three trials were performed with different random number seed values for error analysis. From these simulations, one can use MBAR or wTP to evaluate 12 surfaces corresponding to the 3 trials of the 4 MNDO/d QM/MM+DPRc potentials. One can further obtain 4 trial-averaged surfaces. Each of the 12 surfaces is analyzed from 12 ns/(potential·trial) of sampling, and each of the 4 trial-averaged surfaces are produced from 36 ns/potential of sampling. We use the notation ΔA(target;reference) to distinguish between the surfaces. This notation signifies that the curve is the FES of the target PE function estimated from the sampling performed with reference. When the target and reference are the same PE function, then the FES is calculated from the MBAR method. If the target FES is calculated from the sampling performed with a single reference other than the target, then the wTP method is used. If the target FES is estimated from multiple reference potentials, then the gwTP method is used. The trial-averaged estimates of the ML0, ML1, ML2, and ML3 potentials calculated from the MBAR method shall be labeled ΔA(MLi;MLi) (where i ∈ [0,3]). The trial-averaged estimates of the PBE0/6–31G* FES obtained from wTP analysis of the individual potentials are denoted ΔA(PBE0;MLi). The gwTP method analyzes the combined sampling from the 4 MNDO/d QM/MM+DPRc potentials. Therefore, one obtains 3 gwTP surfaces corresponding to the 3 trials; each surface consists of 48 ns/trial of sampling, and the trial-averaged gwTP FES includes 144 ns of aggregate sampling. The trial-averaged gwTP FES is referred to as ΔA(PBE0;ML*). One can further make a “best estimate” of the ab initio FES by using gwTP to analyze the 144 ns of MNDO/d QM/MM+DPRc sampling and the 15.36 ns of PBE0/6–31G* sampling. The best estimate is denoted ΔA(PBE0;All).
Simulations of the native model reaction.
The native model reaction (Figure 1b) was previously examined in ref. 88. It was one of 6 nonenzymatic transesterification model reactions used to develop 4 DFTB2/MIO QM/MM+DPRc potentials trained to reproduce PBE0/6–31G* QM/MM energies and forces. The 4 potentials were generated from an active learning procedure described in that work.88 In the present work, we reuse the DFTB2/MIO QM/MM+DPRc potentials without modification. The 5 analogous systems included within the training differ from the native model by having replaced one-or-more oxygens with sulfurs at key positions. We do not reconsider the sulfur substituted systems in the present work; instead, our interest in the native model reaction arises from noticeable discrepancies between the ab initio and DFTB2/MIO QM/MM+DPRc FES values. We will show that the native model reaction profiles presented in ref. 88 are not fully converged. The high computational cost of ab initio QM/MM calculations, however, places practical limitations on the amount of sampling that can be reasonably achieved. We will demonstrate that gwTP analysis of extended sampling performed with the reference potentials produces a better estimate of the ab initio FES than what can be afforded from ab initio QM/MM simulation.
An initial structure for the native model unimolecular reactant state was prepared by solvating the system in a box of 1510 TIP4P-Ew waters and performing 200 ps of DFTB2/MIO QM/MM simulation in the NPT ensemble to equilibrate the system density. The final unit cell lattice vectors were approximately 35.8 Å. This was followed by a series of 2 ps DFTB2/MIO QM/MM simulations in the NVT ensemble that slowly incremented the value of the reaction coordinate to obtain initial structures for each window in the range −3.5Å ≤ ξPT ≤ 5Å in steps of 0.1 Å. The umbrella potentials biased the simulations with a spring force constant of 100 kcal mol−1 Å−2. Each of the 86 windows were equilibrated with DFTB2/MIO QM/MM for 100 ps in the NVT ensemble, and this was followed by an additional 25 ps of PBE0/6–31G* QM/MM NVT equilibration. The 25 ps/window of PBE0/6–31G* equilibration is not included in the analysis presented in this work nor ref. 88.
PBE0/6–31G* production sampling of the native model reaction was run for 25 ps/(window·trial), and the coordinates were saved every 25 fs. Each simulation was repeated 4 times using different thermostat random number seed values to yield 4 FES estimates. Each surface is the analysis of 2.15 ns/trial of sampling. The trial-averaged FES, denoted “ΔA(PBE0;PBE0) 100 ps”, includes all 8.6 ns of production sampling (100 ps/window of aggregate sampling).
DFTB2/MIO QM/MM+DPRc production sampling of the native model reaction proceeded similarly. However, the active learning procedure yields 4 neural network parameter sets, so we performed 25 ps/(window·potential) of sampling with each potential. Therefore, the average DFTB2/MIO QM/MM+DPRc FES does not correspond to a single potential; instead, it is the mean of the 4 reference potentials. The average DFTB2/MIO QM/MM+DPRc FES includes 100 ps/window of aggregate sampling, and it is denoted “〈ΔA(ML;ML)〉 100 ps”. The gwTP method can be used to estimate the PBE0/6–31G* from the combined sampling of the DFTB2/MIO QM/MM+DPRc potentials, referred to as “ΔA(PBE0;ML*) 100 ps”.
To examine the behavior of the predicted native model reaction FES on a longer timescale, we extended the DFTB2/MIO QM/MM+DPRc simulations and performed multiple trials with each potential. The extended simulations were sampled for 100 ps/(window·potential·trial), and we performed 3 trials of each simulation with different random number seed values. The 3 trials of the 4 potentials yield 12 surfaces. Each surface is the analysis of 8.6 ns/(potential·trial) of sampling. The average FES is the mean of the 12 estimates, such that it considers 103.2 ns (1.2 ns/window) of aggregate sampling. The average DFTB2/MIO QM/MM+DPRc FES from the extended sampling shall be labeled “〈ΔA(ML;ML)〉 1.2 ns”. The sampling from the 3 trials produce 3 gwTP estimates of the ab initio surface. The PBE0/6–31G* FES from the extended sampling is labeled “ΔA(PBE0;ML*) 1.2 ns”. An analogous set of profiles labeled “〈ΔA(ML;ML)〉 last 600 ps” and “ΔA(PBE0;ML*) last 600 ps” were analyzed from the last 50 ps/(window·potential·trial) of sampling from each simulation. Finally, we shall refer to a profile labeled “ΔA(PBE0;All)”. This FES includes all 103.2 ns of DFTB2/MIO QM/MM+DPRc sampling and the 8.6 ns of PBE0/6–31G* sampling.
Error Analysis.
The uncertainties in the free energy values can be estimated from the MBAR calculation of the sample weight covariance43 between spatial bins, as was done in ref. 52. This approach uses the fluctuations of the statistically independent samples within the observed ensembles to assign error values. Another strategy for estimating errors is the “ensemble average approach” which estimates the standard errors from the distribution of calculated results produced from independent simulations.105–108 The ensemble average approach can be viewed as a strategy to gauge the uncertainty arising from limited finite sampling. In the present work, we incorporate the ideas that motivate both strategies by analyzing multiple trials with bootstrap analysis. Let be the free energy of target potential t in spatial histogram m from trial i (i ∈ [1, Ntrial]). The uncertainty of the FES value is estimated from circular moving block bootstrap error analysis,109 where the block size of each simulation is chosen from the autocorrelation of the biasing potential time series whk(rhkn). The aggregate sampling from all trials can similarly be analyzed to yield free energy values and uncertainties . To compute a trial-average , we choose a set of constants Ci that uniformly shift each surface to minimize the weighted sum of squared differences with the values.
| (21) |
The weights are chosen to be inversely proportional to the bootstrap uncertainties.
| (22) |
The average value and its standard error are then given by eqs. 23 and 24, respectively.
| (23) |
| (24) |
The first and second terms in eq. 24 correspond to the unbiased sample variance between trials and the average bootstrap variance, respectively. The error bars shown in the figures are 95% confidence intervals .
Results and Discussion
Ethylene Phosphate Reaction Profiles
Figure 2 displays free energy profiles of the ethylene phosphate reaction calculated with the MBAR and wTP methods using each of the 4 MNDO/d QM/MM+DPRc reference potentials (ML0, ML1, ML2, and ML3). As previously mentioned, the reference potentials were specifically designed to disagree with each other and the PBE0/6–31G* target in various regions of the FES. The surfaces estimated with the gwTP method are shown in figure 3. These figures demonstrate that the gwTP method can improve upon the wTP estimate by combining the sampling from multiple reference potentials.
Figure 2:
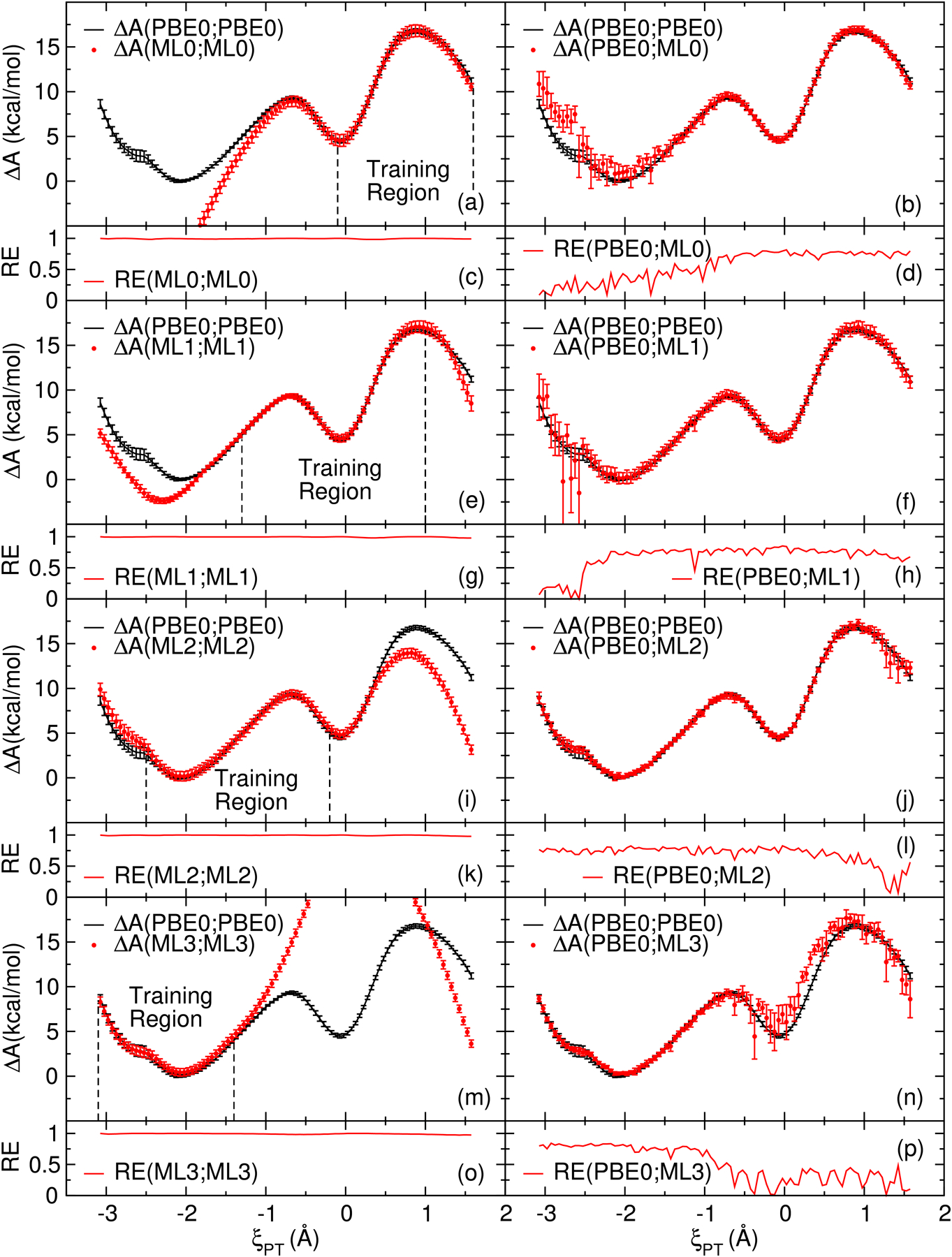
Free energy surfaces (ΔA) of the ethylene phosphate model reaction (Figure 1a) calculated with MBAR and wTP analysis. Reweighting entropies (RE) are shown in the subplots below each FES. Parts (a), (e), (i), and (m) are the 4 MNDO/d QM/MM+DPRc potentials (ML0, ML1, ML2 and ML3) evaluated from MBAR analysis. Parts (b), (f), (j), and (n) are their corresponding wTP estimates of the PBE0/6–31G* FES. Parts (c), (d), (g), (h), (k), (l), (o), and (p) are the reweighting entropy of the corresponding MBAR and wTP analysis. The error bars are 95% confidence intervals.
Figure 3:
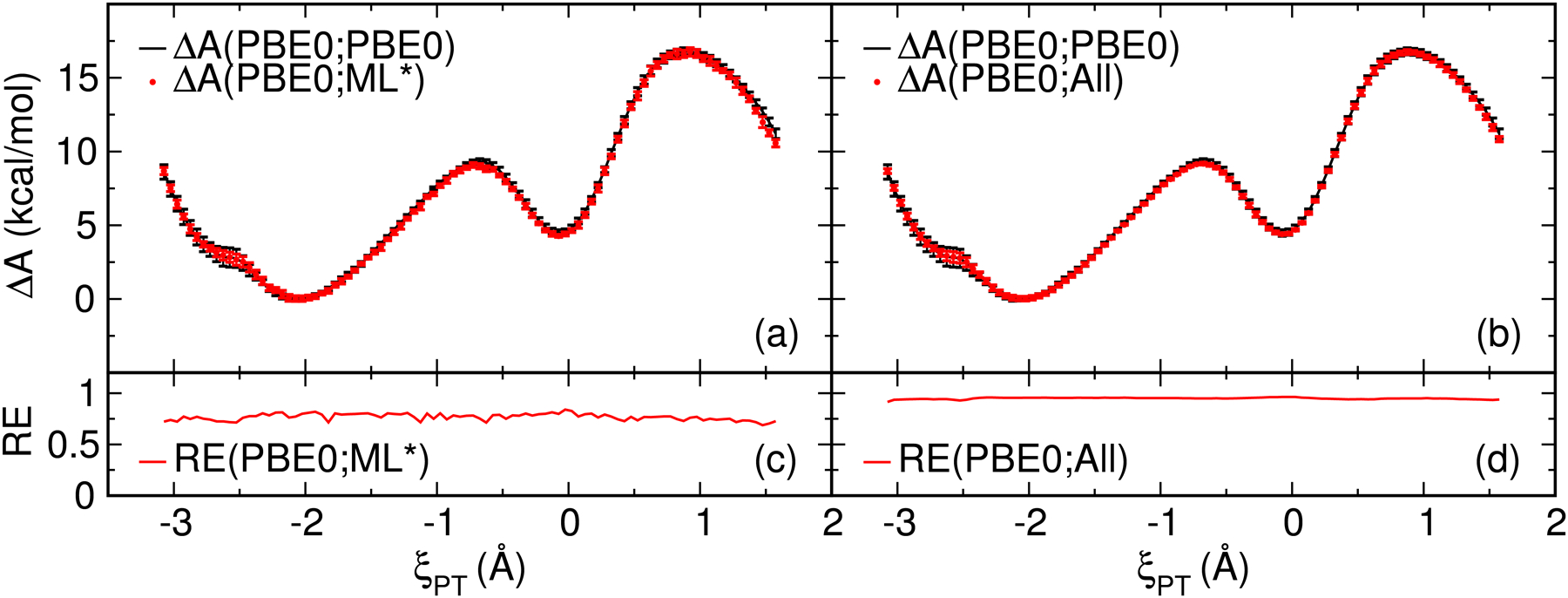
Free energy surfaces (ΔA) of the ethylene phosphate model reaction (Figure 1) calculated with gwTP analysis. Reweighting entropies (RE) are shown in the subplots below each FES. (a) The gwTP FES estimated from the combined umbrella sampling produced from the 4 MNDO/d QM/MM+DPRc potentials (ML0, ML1, ML2 and ML3). (b) The PBE0/6–31G* surface estimated from gwTP analysis of all available PBE0/6–31G* and MNDO/d QM/MM+DPRc umbrella sampling. Parts (c) and (d) are the reweighting entropy of the corresponding MBAR and gwTP analysis. The error bars are 95% confidence intervals.
Figure 2 parts a, e, i, and m show that the 4 MNDO/d QM/MM+DPRc potentials agree with PBE0/6–31G* in the regions they were trained to reproduce the target energies and forces. Outside of these regions, the profiles disagree with ab initio and each other. Figure 2 parts b, f, j, and n are the wTP estimates of the target FES from each reference potential. The wTP surfaces generally improve the agreement with the target; however, they suffer from numerical noise and large uncertainties in the untrained regions. This is further emphasized by a corresponding decrease in the reweighting entropies shown in parts d, h, l, and p. The results shown in figure 2 are consistent with previous work which found that reliable free energies are produced by the wTP method when the reweighting entropy is larger than 0.6, but the results become questionable when the reweighting entropy decreases below 0.3.50 Every MNDO/d QM/MM+DPRc potential shown in figure 2 exhibits reweighting entropies below 0.3 for some ξPT values.
The gwTP estimate of the ab initio FES is shown in figure 3. Figure 3a uses the combined sampling from each MNDO/d QM/MM+DPRc potential, and the resulting FES agrees with the MBAR analysis of the ab initio sampling to within the uncertainties of the calculations throughout the entire range of ξPT values. Similarly, the reweighting entropies shown in 3c consistently remain above 0.6. The gwTP FES shown in Figure 3b includes sampling from both the ab initio and MNDO/d QM/MM+DPRc potentials and represents our best estimate of the surface. The inclusion of sampling from the target potential increases the reweighting entropy values, but the FES values do not significantly change.
An approach for smoothing the density-of-states (DoS) in wTP calculations was presented in ref. 52. The motivation for DoS smoothing is to effectively remove statistically unlikely samples from a distribution that are over-represented within the limited amount of finite sampling. We generalized the DoS smoothing procedure in the Supporting Information. Figures S1 and S2 are analogous to figures 2 and 3, but include DoS smoothing. The use of DoS smoothing does not significantly improve the wTP estimates of the ab initio surface, because the failure is produced from the large differences in reference and target potentials, not from the presence of a few, unlikely samples. The gwTP formalism does not introduce any mechanism to prevent the occurrence of over-represented samples. Although the DoS smoothing procedure is unnecessary in the present applications, we continue to regard it as a valuable technique which can help eliminate numerical noise from the predicted free energies. Application of DoS smoothing to the MBAR and gwTP analysis yield profiles that are indistinguishable from those shown in Figures 2 and 3.
Native Model Reaction Profiles
Free energy surfaces of the native model reaction (Figure 1b) are shown in figures 4 and 5. These figures illustrate that the extended sampling made possible by using an affordable reference potential can result in a more accurate FES than what can be estimated from limited sampling performed with an expensive target potential.
Figure 4:
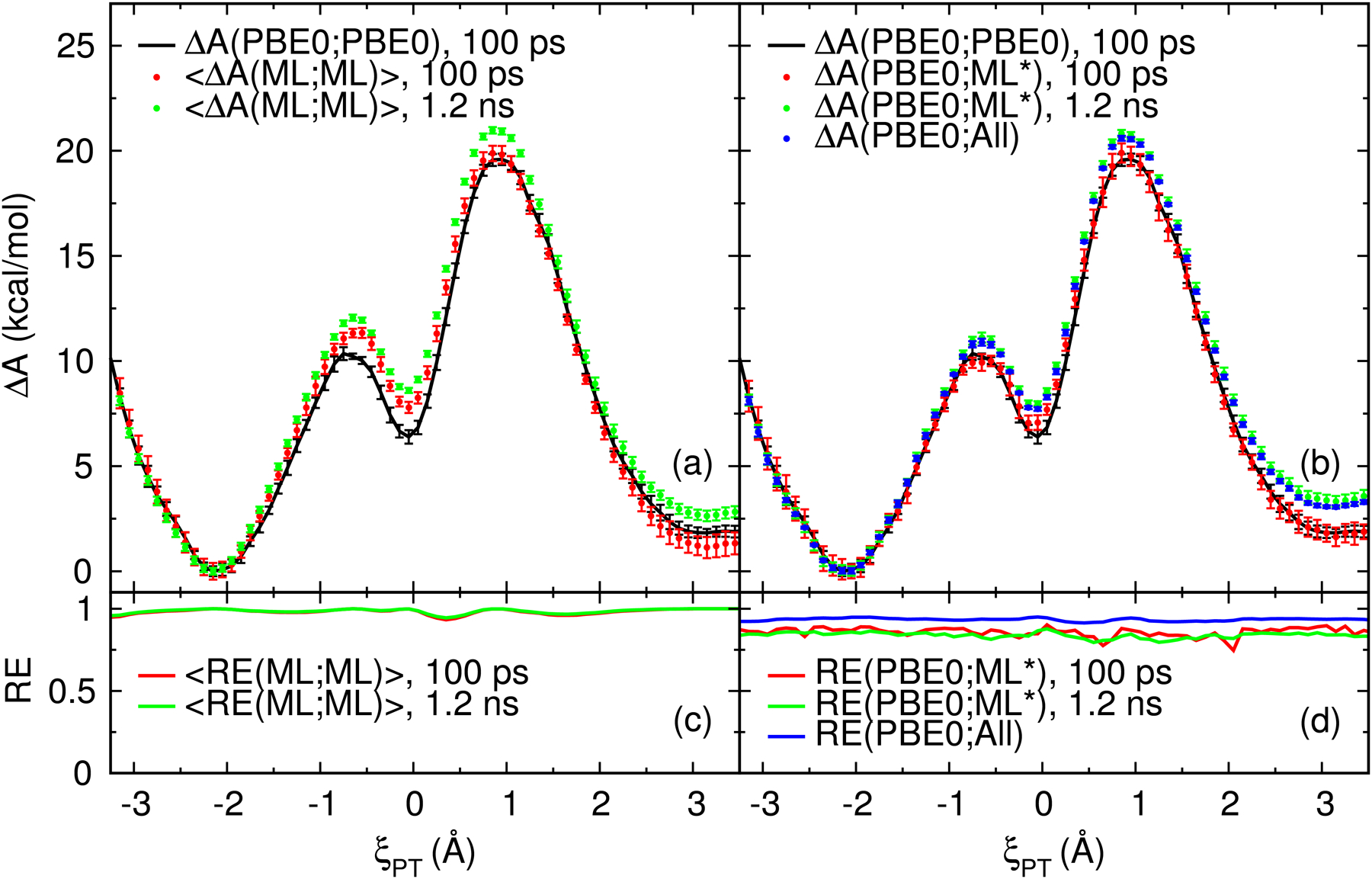
Free energy surfaces (ΔA) of the native model reaction (Figure 1). (a) Comparison of the PBE0/6–31G* FES to the average FES of the 4 DFTB2/MIO QM/MM+DPRc potentials (ML0, ML1, ML2 and ML3). The listed times are the total amount of sampling per umbrella window used in the FES calculation. (b) Comparison of the PBE0/6–31G* FES to those predicted from gwTP analysis. The ΔA(PBE0;ML*) gwTP surfaces are evaluated using the sampling from all 4 DPRc potentials. The ΔA(PBE0;All) surface is calculated from the 1.2 ns/window of DPRc sampling and the 100 ps/window PBE0/6–31G* sampling. The error bars are 95% confidence intervals. The RE values shown in parts (c) and (d) are the reweighting entropies.
Figure 5:
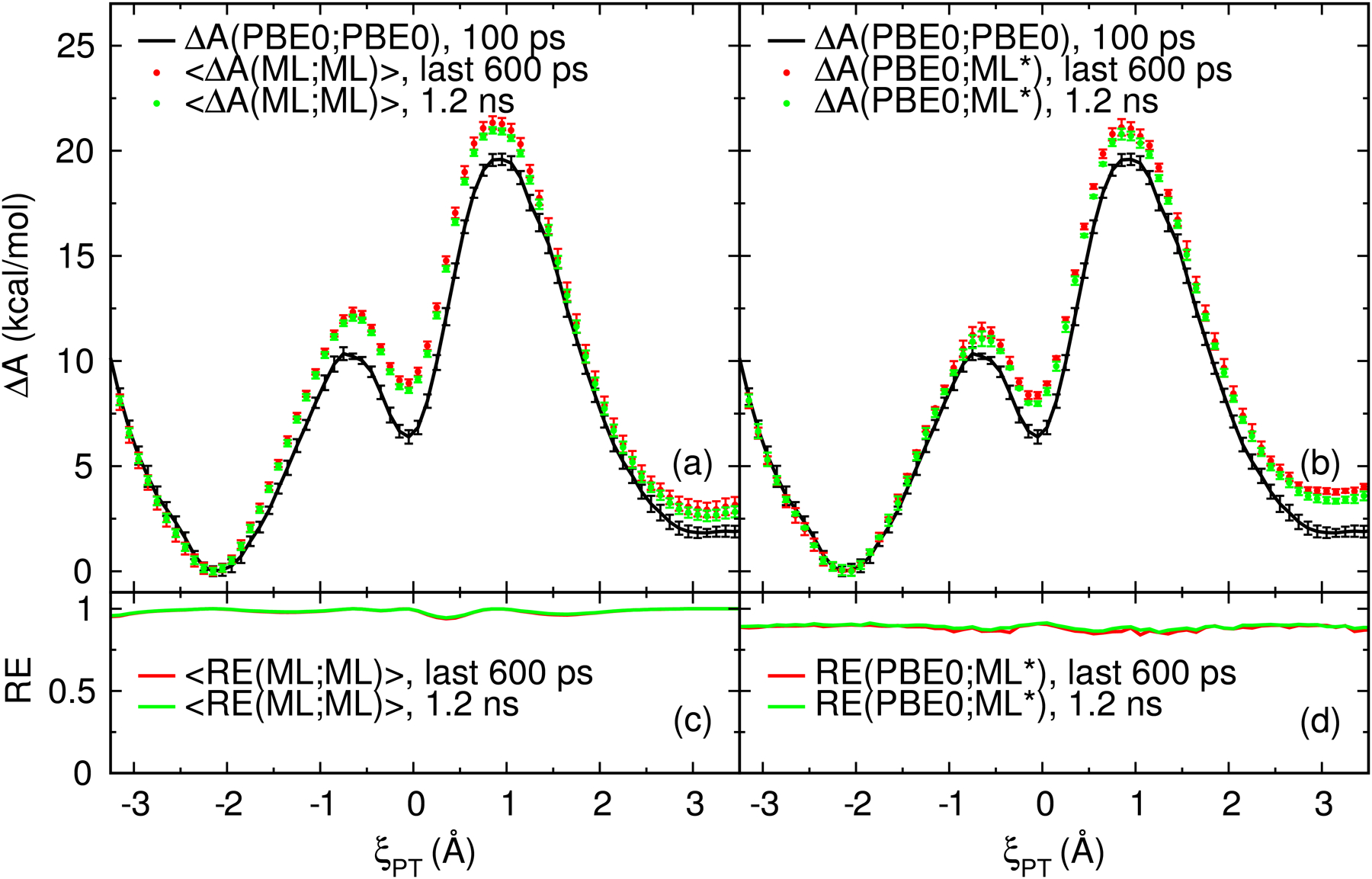
Free energy surfaces (ΔA) of the native model reaction (Figure 1). (a) Comparison of the PBE0/6–31G* FES to the average FES of the 4 DFTB2/MIO QM/MM+DPRc potentials (ML0, ML1, ML2 and ML3). (b) Comparison of the PBE0/6–31G* FES to those predicted from gwTP analysis. The surfaces labeled “last 600 ps” refer to aggregate sampling taken from the last 50 ps of the 12 DFTB2/MIO QM/MM+DPRc simulations. The error bars are 95% confidence intervals. The RE values shown in parts (c) and (d) are the reweighting entropies.
The PBE0/6–31G* and average DFTB2/MIO QM/MM+DPRc surfaces (the black and red surfaces, respectively) shown in figure 4a were originally presented in ref. 88. These surfaces include 100 ps/window of aggregate production sampling. Additional ab initio sampling was deemed too costly to extend, and the DFTB2/MIO QM/MM+DPRc sampling was chosen to mimic the protocol used to perform the ab initio simulations. The ab initio and reference potentials generally agree except in the range ξPT ≈ [−1 Å, 0.5 Å], where the reference potential FES is noticeably higher in energy.
We used the gwTP method to estimate the ab initio FES from the 100 ps/window of DFTB2/MIO QM/MM+DPRc sampling, and the result is labeled “ΔA(PBE0;ML*), 100 ps” in figure 4b. This gwTP estimate agrees with the MBAR analysis of the ab initio sampling to within the uncertainties of the calculations, and the reweighting entropy is larger than 0.6. This suggests there is a small discrepancy in the reference potentials’ ability to reproduce the ab initio QM/MM energies and forces which is corrected by reweighting the samples. However, if the reference potential simulations are extended to include 1.2 ns/window of aggregate sampling (the green surfaces shown in figures 4a and 4b), the predicted activation energy increases by 1 kcal/mol even though the reweighting entropies remain largely unchanged. The large reweighting entropies suggest that there is good phase space overlap between the reference and target potentials in both the 100 ps/window and 1.2 ns/window simulations. Similarly, the gwTP ab initio FES values are nearly 1 kcal/mol higher near the transition state when analyzing the combined sampling from both the PBE0/6–31G* and extended DFTB2/MIO QM/MM+DPRc simulations (the blue surface in 4b). These results suggest that another reason for the observed discrepancies between PBE0/6–31G* and the DFTB2/MIO QM/MM+DPRc potentials may due to the limited amount of sampling. In other words, the ab initio simulations may not represent converged equilibrium ensembles. Consequently, the ΔA(PBE0;PBE0) MBAR estimate should not be trusted, and the ΔA(PBE0;All) gwTP result does not represent a “best estimate” of the FES because it is potentially skewed by nonequilibrium sampling.
We performed forward and reverse analysis of the sampling110,111 to examine the convergence of the extended simulations. The forward analysis generates a hΔA(ML;ML)i FES from the first P% of samples, whereas reverse analysis calculates a FES from the last P% of the simulations. From these surfaces, we monitor the free energy values (and uncertainties) of the two transition states and intermediate relative to the unimolecular reactant state as a function of P%. The convergence behavior of these properties is shown in Figure S3 within the Supporting Information. In summary, the reverse analysis is stable with respect to P%, but the forward analysis display drifts in the free energy values. The forward and reverse analysis do not agree to within their estimated uncertainties until the first 50% of the simulations are discarded. It is difficult to ascertain if the simulations have converged without having extended the sampling (see Figure S4 in the Supporting Information); when the data contains a slight drift, the reverse analysis artificially agrees with the forward analysis simply because it hasn’t been given ample opportunity to approach an equilibrium value. The assertion that the ab initio simulations are not converged is further supported by umbrella integration analysis47–49 (see Figure S5 in the Supporting Information). The extended simulations yield a smooth free energy gradient profile, whereas the gradient profiles obtained from the limited sampling are contaminated with noise. Figure 5 displays the 〈ΔA(ML;ML)〉 and ΔA(PBE0;ML*) surfaces after discarding the first half of each simulation. These surfaces represent our best estimate of the profiles. It is notable that the best estimate of the ab initio FES does not include any of the available PBE0/6–31G* QM/MM sampling, and the best estimate of the rate-limiting transition state barrier is 1.5 kcal/mol higher in energy than the MBAR analysis of the PBE0/6–31G* QM/MM simulations (see Table 1).
Table 1:
Native model reaction free energies (kcal/mol) of the first transition state ΔA(ξTS1), the intermediate ΔA(ξint), the rate-limitingtransition state ΔA‡, and the reaction product ΔA. The uncertainties are standard errors.
| Target | Ref. | Sampling | ΔA(ξTS1) | ΔA(ξint) | ΔA‡ | ΔA |
|---|---|---|---|---|---|---|
| PBE0 | PBE0 | 100 ps | 10.4 ± 0.2 | 6.4 ± 0.2 | 19.6 ± 0.2 | 1.5 ± 0.3 |
| PBE0 | ML* | 100 ps | 10.0 ± 0.2 | 7.0 ± 0.2 | 19.9 ± 0.3 | 1.2 ± 0.3 |
| PBE0 | ML* | last 600 ps | 11.5 ± 0.2 | 8.3 ± 0.1 | 21.1 ± 0.2 | 3.6 ± 0.1 |
To reduce the number of target potential evaluations, one should identify correlation within the simulations and only consider the statistically independent samples. The “〈ΔA(ML;ML)〉, last 600 ps” and “ΔA(PBE0;ML*), last 600 ps” surfaces displayed in Figure 5 where analyzed from the correlated samples, and the errors were estimated from block bootstrap analysis. Figure S6 in the Supporting Information compares these surfaces to the analysis performed with uncorrelated samples from the last half of each simulation. The uncorrelated data is the subset of samples extracted with a stride equal to the statistical inefficiency of the biasing energy time series. In summary, analysis of the uncorrelated samples produce surfaces that are visually indistinguishable from the results shown in Figure 5.
The obvious benefit of using gwTP (or wTP) is the reduced computational effort associated with performing the sampling with an affordable reference potential. The total cost of performing MBAR and gwTP estimates of the target FES are given by eqs. 25 and 26, respectively.
| (25) |
| (26) |
T is the aggregate simulation time (ps) of all windows, trials, and potentials (if applicable). νt and νh are the simulation rates (ps/day) using the target and reference potentials. Equation 25 is, therefore, the net cost of performing the sampling with the target potential, and the first term in eq. 26 is the cost of performing the reference simulations. The second term in eq. 26 is the additional cost of performing target potential evaluations of the saved samples. feq and ffile are the fraction of simulation steps excluded as equilibration and the fraction of samples written to file for analysis, respectively. findep is the fraction of statistically independent samples, and feval is the fraction of the statistically independent samples used to perform target potential evaluations. The ratio C(t;t)/C(t;h) is the computational savings from using the reference potential approach. If one assumes the methods are performed with equal sampling, then the ratio is given by eq. 27.
| (27) |
In practice, the goal is to use the information provided by the reference simulations to reduce the number of target potential evaluations, thus maximizing the savings. First, one should estimate feq by verifying that the reference simulations are converged to avoid unnecessary evaluations of unequilibrated data. In the present work, we chose feq by monitoring the energies of relevant stationary points from forward and reverse analysis of the time series.110,111 Second, one should estimate the correlation in the time series so only the statistically independent samples are evaluated with the target potential. In principle, one could estimate the correlation from the energy differences Δut,h, but that approach would defeat the purpose of reducing the number of target potential evaluations. Instead, we’ve chosen to estimate the correlation from the biasing potential whk time series. Finally, the value of ffile should generally by chosen such that the statistical inefficiency of the saved frames is close to 1 to avoid storing unnecessarily large files.
To estimate the time savings of the native model reaction, we measured the performance of the PBE0/6–31G* QM/MM (νt = 1.565 ps/day) and DFTB2/MIO QM/MM+DPRc (νh = 392.7 ps/day) simulations on a single 2.10 GHz Intel Xeon Gold 6230 CPU core. We further note that the first half (feq = 1/2) of each simulation was discarded as equilibration, the samples were saved every 50 steps (ffile = 1/50), and the fraction of statistically independent samples was found to be findep = 0.763. Equation 27 suggests that the gwTP method is 86 times faster than performing an equivalent amount of ab initio QM/MM sampling for this system even if the full set of uncorrelated samples were used to evaluate the target potential (feval = 1).
One may question how many of the uncorrelated samples are necessary to obtain a reasonable estimate of the target FES. The required number of target evaluations will generally depend on the agreement between the target and reference potentials. In the limit that the reference was the target potential, then an accurate target FES would require the minimum number of samples needed to construct the reference FES. If the target potential differed from the reference, then one would expect this limit to be a lower bound on the number of target evaluations. Furthermore, the required number of samples will depend on the acceptable level of uncertainty. If one is comparing different mechanistic pathways, for example, then a high degree of certainty is not necessary to rule out a path exhibiting a large rate-limiting transition state. Table 2 shows how the free energy values, uncertainties, and reweighting entropies behave when gwTP analysis is performed with a varying amount of uncorrelated samples. When feval = 1, the analysis is performed with all available uncorrelated samples (after removing the unequilibrated portion of simulations). On average, there are 381.4 samples/(trial·potential·window). In the remaining rows, we perform the analysis using the first Neval uncorrelated samples from each simulation. For example, Neval = 15 signifies that the target potential was evaluated using the first 15 uncorrelated samples/(trial·potential·window), on average. In the present application, we have 4 reference potentials and each simulation was performed 3 times, so this corresponds to 15 × 4 × 3 = 180 evaluations/window. As feval increases, the value of Neval ceases to be integer because there are one-or-more simulations that had fewer samples than requested. From a practical perspective, we cannot recommend a precise value of Neval that the reader should use, for reasons already discussed. Instead, we can offer guidance for a procedure that the reader can follow. First, perform evaluations with a small number of samples and evaluate the FES. If the reweighting entropy is less than some tolerance (e.g., 0.6) or the uncertainty in the free energy values are unacceptably large, then one should increase Neval accordingly. One could even focus the evaluations in the particular region(s) of the FES where the reweighting entropy was low. Table 2 suggests that Neval = 15 samples/simulation are required for the minimum observed entropy to exceed 0.6. If the activation energy must be estimated to within an uncertainty of 0.2 kcal/mol, then the number of samples must be increased to Neval = 50. The surfaces evaluated with Neval = 15 and Neval = 50 are compared in Figure S7 within the Supporting Information.
Table 2:
Relative energies of the native model reaction free energy surfaces estimated from gwTP analysis as a function of the number of target potential evaluations.a
| N eval | f eval | min RE | 〈RE〉 | ΔA(ξTS1) | ΔA(ξint) | ΔA‡ | ΔA |
|---|---|---|---|---|---|---|---|
| 5.0 | 0.013 | 0.42 | 0.78 | 12.0 ± 0.5 | 8.3 ± 0.4 | 21.2 ± 0.4 | 3.1 ± 0.4 |
| 10.0 | 0.026 | 0.56 | 0.80 | 11.7 ± 0.4 | 8.2 ± 0.4 | 21.0 ± 0.3 | 3.2 ± 0.3 |
| 15.0 | 0.039 | 0.64 | 0.81 | 11.7 ± 0.4 | 8.2 ± 0.4 | 21.1 ± 0.3 | 3.5 ± 0.2 |
| 25.0 | 0.066 | 0.70 | 0.83 | 11.8 ± 0.4 | 8.3 ± 0.3 | 21.2 ± 0.3 | 3.6 ± 0.2 |
| 49.7 | 0.130 | 0.75 | 0.85 | 11.7 ± 0.2 | 8.4 ± 0.2 | 21.5 ± 0.2 | 3.6 ± 0.1 |
| 97.9 | 0.257 | 0.71 | 0.86 | 11.5 ± 0.2 | 8.3 ± 0.2 | 21.1 ± 0.2 | 3.5 ± 0.1 |
| 381.4 | 1.000 | 0.82 | 0.88 | 11.5 ± 0.2 | 8.3 ± 0.2 | 21.1 ± 0.2 | 3.6 ± 0.1 |
Neval is the number of statistically independent samples per simulation used to evaluate the target potential energies. feval is the fraction of the statistically independent samples selected for target potential evaluation. The uncertainties are the standard errors. “min RE” and 〈RE〉 are the minimum and average reweighting entropy observed during the gwTP analysis of the aggregate sampling.
The reader may question if MLPs are required for their application or if it would suffice to perform wTP from uncorrected semiempirical QM/MM sampling. After all, the idea of training a MLP and also performing target potential evaluations to analyze the results may seem formidable. The gwTP method allows one to combine the MLP training and analysis so that all of the target potential evaluations used to train the MLP can also be used to estimate the target FES. For example, one could first perform standard semiempirical QM/MM sampling and estimate the target FES with the wTP method from a limited number of target potential evaluations. If the reweighting entropy is high, then no refinement is necessary. If the entropy is low, one may deem it worthwhile to reuse the target evaluations to train a MLP correction. The trained MLP is then sampled, and a limited number of target potential evaluations are made to estimate the FES; however, the gwTP method allows one to analyze the FES using the combined sampling from the uncorrected and MLP-corrected simulations. This process can be iterated, such that one performs “active learning” in a manner which reuses the aggregate sampling from previous iterations to improve the predicted target FES while also generating new training data for the next iteration.
Conclusion
We described a new reference potential approach for calculating free energy surfaces called the generalized weighted thermodynamic perturbation (gwTP) method. The gwTP method extends the formulation of weighted thermodynamic perturbation (wTP) to include sampling from multiple reference potentials. This work was motivated by the growing interest in the use of MLPs being trained to correct semiempirical QM/MM energies and forces to match target ab initio values. The active learning procedure often employed to train these corrections results in several neural network parameter sets. Each parameter set corresponds to a different reference potential, and the gwTP method can be used to analyze the aggregate sampling from each potential to estimate the target free energies.
We envision other strategies where gwTP analysis may be useful. One could train separate MLPs for different systems, such as RNA catalysis reactions in different enzyme environments, or create a single MLP that tries to model all systems. One can perform sampling with all of these potentials and use gwTP to make a best estimate of another system not included in the training. Alternatively, one could construct potentials that specialize their parametrizations to have high accuracy at different stages of a multistep enzyme reaction. In this way the gwTP method can be used to combine the sampling from several “specific reaction parametrizations”78–80 and thus provide new opportunities in model design.
To this end, we created 4 ad hoc MNDO/d QM/MM+DPRc neural network parameter sets to calculate the free energy surface of an ethylene phosphate model reaction. Each parametrization limited the training data such that the potentials well-reproduced PBE0/6–31G* energies and forces in the regions they were trained, but the potentials disagree with each other and the ab initio target in all other regions. We showed that the wTP method fails to accurately predict the target free energies in the untrained regions. We further demonstrated that the gwTP method accurately reconstructs the ab initio surface from the aggregate sampling.
We used the gwTP method to examine the free energy surface of a non-enzymatic RNA 2′-O-transesterification model with an ethoxide leaving group. This system was used as a case study to emphasize the benefits offered by the reference potential approach. Because the reference potentials are much more affordable, the sampling could be extended. The extended simulations allowed us to determine that the ab initio QM/MM sampling was not converged. Excluding the first half of each simulation from the analysis produced a rate limiting transition state 1.5 kcal/mol higher than the value predicted from ab initio QM/MM sampling; however, the reweighting entropy remained high. In other words, we made a better estimate of the ab initio free energy surface using gwTP analysis than what direct ab initio QM/MM simulation can reasonably afford. For this system, the computational cost of estimating the ab initio surface from gwTP analysis of the DFTB2/MIO QM/MM+DPRc sampling was found to be 86 times faster than an equivalent amount of PBE0/6–31G* QM/MM simulation. The cost savings is expected to increase for systems with larger QM regions due to the inherent differences in the formal computational scaling behaviors of ab initio and semiempirical Hamiltonians. The computational cost is minimized by choosing an efficient reference potential and reducing the number of target potential evaluations. The number of target potential evaluations is reduced by analyzing the reference potential simulations to identify and eliminate the unequilibrated portions of the simulations and by extracting the statistically independent samples.
Supplementary Material
Acknowledgments
The authors are grateful for financial support provided by the National Institutes of Health (No. GM62248 and GM107485), and also early-stage seed support from the Grossman Innovation Prize established by Alan Grossman. Computational resources were provided by the Office of Advanced Research Computing (OARC) at Rutgers, The State University of New Jersey (specifically, the Amarel cluster and associated research computing resources), the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation Grant ACI-1548562.112 (specifically, the resources COMET and EXPANSE at SDSC through allocation TG-CHE190067). The authors also acknowledge the Texas Advanced Computing Center (TACC, http://www.tacc.utexas.edu) at The University of Texas at Austin for providing HPC resources, specifically the Frontera Supercomputer, that have contributed to the research results reported within this paper.
Footnotes
Supporting Information Available
Additional descriptions of the DPRc correction and the density-of-states smoothing procedure. Comparison of the forward and reverse analysis, and the analysis of statistically independent samples. This material is available free of charge via the Internet at http://pubs.acs.org/.
References
- (1).Klippenstein SJ; Pande VS; Truhlar DG Chemical Kinetics and Mechanisms of Complex Systems: A Perspective on Recent Theoretical Advances. J. Am. Chem. Soc 2014, 136, 528–46. [DOI] [PubMed] [Google Scholar]
- (2).Wüthrich K, Grubbs RH, de Bocarmé TV, De Wit A, Eds. Catalysis in Chemistry and Biology; World Scientific, 2018. [Google Scholar]
- (3).Cheng G-J; Zhang X; Wa Chung L; Xu L; Wu Y-D Computational Organic Chemistry: Bridging Theory and Experiment in Establishing the Mechanisms of Chemical Reactions. J. Am. Chem. Soc 2015, 137, 1706–1725. [DOI] [PubMed] [Google Scholar]
- (4).Talanquer V Importance of Understanding Fundamental Chemical Mechanisms. J. Chem. Educ 2018, 95, 1905–1911. [Google Scholar]
- (5).Christ C; Mark A; van Gunsteren W Basic Ingredients of Free Energy Calculations: A Review. J. Comput. Chem 2010, 31, 1569–1582. [DOI] [PubMed] [Google Scholar]
- (6).Kästner J Umbrella sampling. WIREs Comput. Mol. Sci 2011, 1, 932–942. [Google Scholar]
- (7).Jarzynski C Nonequilibrium equality for free energy differences. Phys. Rev. Lett 1997, 78, 2690–2693. [Google Scholar]
- (8).Adib AB Free energy surfaces from nonequilibrium processes without work measurement. J. Chem. Phys 2006, 124, 144111. [DOI] [PubMed] [Google Scholar]
- (9).Hummer G Fast-growth thermodynamic integration: Error and efficiency analysis. J. Chem. Phys 2001, 114, 7330–7337. [Google Scholar]
- (10).Zuckerman DM; Woolf TB Theory of a Systematic Computational Error in Free Energy Differences. Phys. Rev. Lett 2002, 89, 180602. [DOI] [PubMed] [Google Scholar]
- (11).Torrie GM; Valleau JP Monte Carlo free energy estimates using non-Boltzmann sampling: Application to the sub-critical Lennard-Jones fluid. Chem. Phys. Lett 1974, 28, 578–581. [Google Scholar]
- (12).Torrie GM; Valleau JP Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella sampling. J. Comput. Phys 1977, 23, 187–199. [Google Scholar]
- (13).McDonald IR; Singer K Machine Calculation of Thermodynamic Properties of a Simple Fluid at Supercritical Temperatures. J. Chem. Phys 1967, 47, 4766–4772. [Google Scholar]
- (14).McDonald IR; Singer K Examination of the Adequacy of the 12–6 Potential for Liquid Argon by Means of Monte Carlo Calculations. J. Chem. Phys 1969, 50, 2308–2315. [Google Scholar]
- (15).Knight JL; Brooks CL 3rd Lambda-dynamics free energy simulation methods. J. Comput. Chem 2009, 30, 1692–1700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (16).Kong X; Brooks CL III λ-dynamics: A new approach to free energy calculations. J. Chem. Phys 1996, 105, 2414–2423. [Google Scholar]
- (17).Liu Z; Berne BJ Method for accelerating chain folding and mixing. J. Chem. Phys 1993, 99, 6071–6077. [Google Scholar]
- (18).Tidor B Simulated annealing on free energy surfaces by a combined molecular dynamics and Monte Carlo approach. J. Phys. Chem 1993, 97, 1069–1073. [Google Scholar]
- (19).Laio A; Parrinello M Escaping free-energy minima. Proc. Natl. Acad. Sci. USA 2002, 99, 12562–12566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (20).White AD; Dama JF; Voth GA Designing Free Energy Surfaces That Match Experimental Data with Metadynamics. J. Chem. Theory Comput 2015, 11, 2451–2460. [DOI] [PubMed] [Google Scholar]
- (21).Grubmüller H; Heymann B; Tavan P Ligand Binding: Molecular Mechanics Calculation of the Streptavidin-Biotin Rupture Force. Science 1996, 271, 997–999. [DOI] [PubMed] [Google Scholar]
- (22).Izrailev S; Stepaniants S; Balsera M; Oono Y; Schulten K Molecular dynamics study of unbinding of the avidin-biotin complex. Biophys. J 1997, 72, 1568–1581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (23).Evans E; Ritchie K Dynamic strength of molecular adhesion bonds. Biophys. J 1997, 72, 1541–1555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (24).Mezei M Adaptive umbrella sampling: Self-consistent determination of the non-Boltzmann bias. J. Comput. Phys 1987, 68, 237–248. [Google Scholar]
- (25).Hooft RWW; van Eijck BP; Kroon J An adaptive umbrella sampling procedure in conformational analysis using molecular dynamics and its application to glycol. J. Chem. Phys 1992, 97, 6690–6694. [Google Scholar]
- (26).Bartels C; Karplus M Multidimensional adaptive umbrella sampling: applications to main chain and side chain peptide conformations. J. Comput. Chem 1997, 18, 1450–1462. [Google Scholar]
- (27).Bartels C; Karplus M Probability distributions for complex systems: adaptive umbrella sampling of the potential energy. J. Phys. Chem. B 1998, 102, 865–880. [Google Scholar]
- (28).Huber T; Torda AE; van Gunsteren WF Local elevation: A method for improving the searching properties of molecular dynamics simulation. J. Comput.-Aided Mol. Des 1994, 8, 695–708. [DOI] [PubMed] [Google Scholar]
- (29).Hansen HS; Hünenberger PH Using the local elevation method to construct optimized umbrella sampling potentials: calculation of the relative free energies and interconversion barriers of glucopyranose ring conformers in water. J. Comput. Chem 2010, 31, 1–23. [DOI] [PubMed] [Google Scholar]
- (30).Rjamani R; Naidoo KJ; Gao J Implementation of an adaptive umbrella sampling method for the calculation of multidimensional potential of mean force of chemical reactions in solution. J. Comput. Chem 2003, 24, 1775–1781. [DOI] [PubMed] [Google Scholar]
- (31).Vanden-Eijnden E Some recent techniques for free energy calculations. J. Comput. Chem 2009, 30, 1737–1747. [DOI] [PubMed] [Google Scholar]
- (32).E W; Ren W; Vanden-Eijnden E String method for the study of rare events. Phys. Rev. B 2002, 66, 052301. [DOI] [PubMed] [Google Scholar]
- (33).Peters B; Heyden A; Bell AT; Chakraborty A A growing string method for determining transition states: comparison to the nudged elastic band and string methods. J. Chem. Phys 2004, 120, 7877–7886. [DOI] [PubMed] [Google Scholar]
- (34).E W; Ren W; Vanden-Eijnden E Finite temperature string method for the study of rare events. J. Phys. Chem. B 2005, 109, 6688–6693. [DOI] [PubMed] [Google Scholar]
- (35).E W; Ren W; Vanden-Eijnden E Simplified and improved string method for computing the minimum energy paths in barrier-crossing events. J. Chem. Phys 2007, 126, 164103. [DOI] [PubMed] [Google Scholar]
- (36).Maragliano L; Fischer A; Vanden-Eijnden E; Ciccotti G String method in collective variables: minimum free energy paths and isocommittor surfaces. J. Chem. Phys 2006, 125, 024106. [DOI] [PubMed] [Google Scholar]
- (37).Sheppard D; Terrell R; Henkelman G Optimization methods for finding minimum energy paths. J. Chem. Phys 2008, 128, 134106. [DOI] [PubMed] [Google Scholar]
- (38).Crehuet R; Field MJ A temperature-dependent nudged-elastic-band algorithm. J. Chem. Phys 2003, 118, 9563–9571. [Google Scholar]
- (39).Kumar S; Bouzida D; Swendsen RH; Kollman PA; Rosenberg JM The weighted histogram analysis method for free-energy calculations on biomolecules. I. The method. J. Comput. Chem 1992, 13, 1011–1021. [Google Scholar]
- (40).Souaille M; Roux B Extension to the weighted histogram analysis method: Combining umbrella sampling with free energy calculations. Comput. Phys. Commun 2001, 135, 40–57. [Google Scholar]
- (41).Tan Z; Gallicchio E; Lapelosa M; Levy RM Theory of binless multi-state free energy estimation with applications to protein-ligand binding. J. Chem. Phys 2012, 136, 144102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (42).Zhang BW; Xia J; Tan Z; Levy RM A Stochastic Solution to the Unbinned WHAM Equations. J. Phys. Chem. Lett 2015, 6, 3834–3840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (43).Shirts MR; Chodera JD Statistically optimal analysis of samples from multiple equilibrium states. J. Chem. Phys 2008, 129, 124105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (44).Lee T-S; Radak BK; Pabis A; York DM A new maximum likelihood approach for free energy profile construction from molecular simulations. J. Chem. Theory Comput 2013, 9, 153–164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (45).Lee T-S; Radak BK; Huang M; Wong K-Y; York DM Roadmaps through free energy landscapes calculated using the multidimensional vFEP approach. J. Chem. Theory Comput 2014, 10, 24–34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (46).Giese TJ; Ekesan Ş; York DM Extension of the Variational Free Energy Profile and Multistate Bennett Acceptance Ratio Methods for High-Dimensional Potential of Mean Force Profile Analysis. J. Phys. Chem. A 2021, 125, 4216–4232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (47).Kästner J; Thiel W Bridging the gap between thermodynamic integration and umbrella sampling provides a novel analysis method: “Umbrella integration”. J. Chem. Phys 2005, 123, 144104. [DOI] [PubMed] [Google Scholar]
- (48).Kästner J; Thiel W Analysis of the statistical error in umbrella sampling simulations by umbrella integration. J. Chem. Phys 2006, 124, 234106. [DOI] [PubMed] [Google Scholar]
- (49).Kästner J Umbrella integration in two or more reaction coordinates. J. Chem. Phys 2009, 131, 034109. [DOI] [PubMed] [Google Scholar]
- (50).Li P; Jia X; Pan X; Shao Y; Mei Y Accelerated Computation of Free Energy Profile at ab Initio Quantum Mechanical/Molecular Mechanics Accuracy via a Semi-Empirical Reference Potential. I. Weighted Thermodynamics Perturbation. J. Chem. Theory Comput 2018, 14, 5583–5596. [DOI] [PubMed] [Google Scholar]
- (51).Pan X; Li P; Ho J; Pu J; Mei Y; Shao Y Accelerated computation of free energy profile at ab initio quantum mechanical/molecular mechanical accuracy via a semi-empirical reference potential. II. Recalibrating semi-empirical parameters with force matching. Phys. Chem. Chem. Phys 2019, 21, 20595–20605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (52).Hu W; Li P; Wang J-N; Xue Y; Mo Y; Zheng J; Pan X; Shao Y; Mei Y Accelerated Computation of Free Energy Profile at Ab Initio Quantum Mechanical/Molecular Mechanics Accuracy via a Semiempirical Reference Potential. 3. Gaussian Smoothing on Density-of-States. J. Chem. Theory Comput 2020, 16, 6814–6822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (53).Wang J-N; Liu W; Li P; Mo Y; Hu W; Zheng J; Pan X; Shao Y; Mei Y Accelerated Computation of Free Energy Profile at Ab Initio Quantum Mechanical/Molecular Mechanics Accuracy via a Semiempirical Reference Potential. 4. Adaptive QM/MM. J. Chem. Theory Comput 2021, 17, 1318–1325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (54).Jin S; Wang J-N; Xue Y; Li P; Mei Y Selectivity of parvalbumin B protein binding to Ca2+ and Mg2+ at an ab initio QM/MM level using the reference-potential method. Chinese J. Chem. Phys 2021, 34, 741–750. [Google Scholar]
- (55).Xue Y; Wang J-N; Hu W; Zheng J; Li Y; Pan X; Mo Y; Shao Y; Wang L; Mei Y Affordable Ab Initio Path Integral for Thermodynamic Properties via Molecular Dynamics Simulations Using Semiempirical Reference Potential. J. Phys. Chem. A 2021, 125, 10677–10685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (56).Gao J Absolute Free Energy of Solvation from Monte Carlo Simulations Using Combined Quantum and Molecular Mechanical Potentials. J. Phys. Chem 1992, 96, 537–540. [Google Scholar]
- (57).Gao J; Xia X A priori evaluation of aqueous polarization effects through Monte Carlo QM-MM simulations. Science 1992, 258, 631–635. [DOI] [PubMed] [Google Scholar]
- (58).Luzhkov V; Warshel A Microscopic models for quantum mechanical calculations of chemical processes in solutions: LD/AMPAC and SCAAS/AMPAC calculations of solvation energies. J. Comput. Chem 1992, 13, 199–213. [Google Scholar]
- (59).Giese TJ; York DM Development of a Robust Indirect Approach for MM → QM Free Energy Calculations That Combines Force-Matched Reference Potential and Bennett’s Acceptance Ratio Methods. J. Chem. Theory Comput 2019, 15, 5543–5562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (60).Cave-Ayland C; Skylaris C-K; Essex JW Direct validation of the single step classical to quantum free energy perturbation. J. Phys. Chem. B 2015, 119, 1017–1025. [DOI] [PubMed] [Google Scholar]
- (61).Pan X; Van R; Epifanovsky E; Liu J; Pu J; Nam K; Shao Y Accelerating Ab Initio Quantum Mechanical and Molecular Mechanical (QM/MM) Molecular Dynamics Simulations with Multiple Time Step Integration and a Recalibrated Semiempirical QM/MM Hamiltonian. J. Phys. Chem. B 2022, 126, 4226–4235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (62).Piccini G; Parrinello M Accurate Quantum Chemical Free Energies at Affordable Cost. J. Phys. Chem. Lett 2019, 10, 3727–3731. [DOI] [PubMed] [Google Scholar]
- (63).Ito S; Cui Q Multi-level free energy simulation with a staged transformation approach. J. Chem. Phys 2020, 153, 044115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (64).Wang M; Li P; Jia X; Liu W; Shao Y; Hu W; Zheng J; Brooks BR; Mei Y Efficient Strategy for the Calculation of Solvation Free Energies in Water and Chloroform at the Quantum Mechanical/Molecular Mechanical Level. J. Chem. Inf. Model 2017, 57, 2476–2489. [DOI] [PubMed] [Google Scholar]
- (65).Ramakrishnan R; Dral PO; Rupp M; von Lilienfeld OA Big Data Meets Quantum Chemistry Approximations: The Δ-Machine Learning Approach. J. Chem. Theory Comput 2015, 11, 2087–2096. [DOI] [PubMed] [Google Scholar]
- (66).Pan X; Yang J; Van R; Epifanovsky E; Ho J; Huang J; Pu J; Mei Y; Nam K; Shao Y Machine-Learning-Assisted Free Energy Simulation of Solution-Phase and Enzyme Reactions. J. Chem. Theory Comput 2021, 17, 5745–5758. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (67).Kim B; Snyder R; Nagaraju M; Zhou Y; Ojeda-May P; Keeton S; Hege M; Shao Y; Pu J Reaction Path-Force Matching in Collective Variables: Determining Ab Initio QM/MM Free Energy Profiles by Fitting Mean Force. J. Chem. Theory Comput 2021, 17, 4961–4980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (68).Bučko T; Gešvandtnerová M; Rocca D Ab Initio Calculations of Free Energy of Activation at Multiple Electronic Structure Levels Made Affordable: An Effective Combination of Perturbation Theory and Machine Learning. J. Chem. Theory Comput 2020, 16, 6049–6060. [DOI] [PubMed] [Google Scholar]
- (69).Ruth M; Gerbig D; Schreiner PR Machine Learning of Coupled Cluster (T)-Energy Corrections via Delta (Δ)-Learning. J. Chem. Theory Comput 2022, 18, 4846–4855. [DOI] [PubMed] [Google Scholar]
- (70).Lu F; Cheng L; DiRisio RJ; Finney JM; Boyer MA; Moonkaen P; Sun J; Lee SJR; Deustua JE; Miller TF 3rd et al. Fast Near Ab Initio Potential Energy Surfaces Using Machine Learning. J. Phys. Chem. A 2022, 126, 4013–4024. [DOI] [PubMed] [Google Scholar]
- (71).Liu Y; Li J Permutation-Invariant-Polynomial Neural-Network-Based Δ-Machine Learning Approach: A Case for the HO2 Self-Reaction and Its Dynamics Study. J. Phys. Chem. Lett 2022, 13, 4729–4738. [DOI] [PubMed] [Google Scholar]
- (72).Pham CH; Lindsey RK; Fried LE; Goldman N High-Accuracy Semiempirical Quantum Models Based on a Minimal Training Set. J. Phys. Chem. Lett 2022, 13, 2934–2942. [DOI] [PubMed] [Google Scholar]
- (73).Dettmann MA; Cavalcante LSR; Magdaleno C; Masalkovaite K; Vong D; Dull JT; Rand BP; Daemen LL; Goldman N; Faller R et al. Comparing the Expense and Accuracy of Methods to Simulate Atomic Vibrations in Rubrene. J. Chem. Theory Comput 2021, 17, 7313–7320. [DOI] [PubMed] [Google Scholar]
- (74).Böselt L; Thürlemann M; Riniker S Machine Learning in QM/MM Molecular Dynamics Simulations of Condensed- Phase Systems. J. Chem. Theory Comput 2021, 17, 2641–2658. [DOI] [PubMed] [Google Scholar]
- (75).Unzueta PA; Greenwell CS; Beran GJO Predicting Density Functional Theory-Quality Nuclear Magnetic Resonance Chemical Shifts via Δ-Machine Learning. J. Chem. Theory Comput 2021, 17, 826–840. [DOI] [PubMed] [Google Scholar]
- (76).Zeng J; Giese TJ; Ekesan Ş; York DM Development of Range-Corrected Deep Learning Potentials for Fast, Accurate Quantum Mechanical/Molecular Mechanical Simulations of Chemical Reactions in Solution. J. Chem. Theory Comput 2021, 17, 6993–7009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (77).Dral PO; Owens A; Dral A; Csányi G Hierarchical machine learning of potential energy surfaces. J. Chem. Phys 2020, 152, 204110. [DOI] [PubMed] [Google Scholar]
- (78).Nam K; Cui Q; Gao J; York DM Specific reaction parametrization of the AM1/d Hamiltonian for phosphoryl transfer reactions: H, O, and P atoms. J. Chem. Theory Comput 2007, 3, 486–504. [DOI] [PubMed] [Google Scholar]
- (79).Tejero I; González-Lafont Àngels,; LLuch JM A PM3/s specific reaction parameterization for iron atom in the hydrogen abraction catalyzed by soybean lipoxygenase-1. J. Comput. Chem 2007, 28, 997–1005. [DOI] [PubMed] [Google Scholar]
- (80).Giese TJ; Sherer EC; Cramer CJ; York DM A semiempirical quantum model for hydrogen-bonded nucleic acid base pairs. J. Chem. Theory Comput 2005, 1, 1275–1285. [DOI] [PubMed] [Google Scholar]
- (81).Bevilacqua PC; Harris ME; Piccirilli JA; Gaines C; Ganguly A; Kostenbader K; Ekesan Ş; York DM An Ontology for Facilitating Discussion of Catalytic Strategies of RNA-Cleaving Enzymes. ACS Chem. Biol 2019, 14, 1068–1076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (82).Chehaibou B; Badawi M; Bučko T; Bazhirov T; Rocca D Computing RPA Adsorption Enthalpies by Machine Learning Thermodynamic Perturbation Theory. J. Chem. Theory Comput 2019, 15, 6333–6342. [DOI] [PubMed] [Google Scholar]
- (83).Rizzi A; Carloni P; Parrinello M Targeted Free Energy Perturbation Revisited: Accurate Free Energies from Mapped Reference Potentials. J. Phys. Chem. Lett 2021, 12, 9449–9454. [DOI] [PubMed] [Google Scholar]
- (84).Herzog B; Chagas da Silva M; Casier B; Badawi M; Pascale F; Bučko T; Lebègue S; Rocca D Assessing the Accuracy of Machine Learning Thermodynamic Perturbation Theory: Density Functional Theory and Beyond. J. Chem. Theory Comput 2022, 18, 1382–1394. [DOI] [PubMed] [Google Scholar]
- (85).Huang M; York DM Linear free energy relationships in RNA transesterification: theoretical models to aid experimental interpretations. Phys. Chem. Chem. Phys 2014, 16, 15846–15855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (86).Chen H; Giese TJ; Huang M; Wong K-Y; Harris ME; York DM Mechanistic Insights into RNA Transphosphorylation from Kinetic Isotope Effects and Linear Free Energy Relationships of Model Reactions. Chem. Eur. J 2014, 20, 14336–14343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (87).Giese TJ; York DM Ambient-Potential Composite Ewald Method for ab Initio Quantum Mechanical/Molecular Mechanical Molecular Dynamics Simulation. J. Chem. Theory Comput 2016, 12, 2611–2632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (88).Giese TJ; Zeng J; Ekesan Ş; York DM Combined QM/MM, Machine Learning Path Integral Approach to Compute Free Energy Profiles and Kinetic Isotope Effects in RNA Cleavage Reactions. J. Chem. Theory Comput 2022, 18, 4304–4317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (89).Case DA; Aktulga HM; Belfon K; Ben-Shalom IY; Berryman JT; Brozell SR; Cerutti DS; Cheatham TE I.; Cisneros GA; Cruzeiro VWD et al. Amber 2022. University of California, San Francisco, 2022. [Google Scholar]
- (90).Loncharich RJ; Brooks BR; Pastor RW Langevin dynamics of peptides: the frictional dependence of isomerization rates of N-acetylalanyl-N’-methylamide. Biopolymers 1992, 32, 523–535. [DOI] [PubMed] [Google Scholar]
- (91).Berendsen HJC; Postma JPM; van Gunsteren WF; Dinola A; Haak JR Molecular dynamics with coupling to an external bath. J. Chem. Phys 1984, 81, 3684–3690. [Google Scholar]
- (92).Essmann U; Perera L; Berkowitz ML; Darden T; Lee H; Pedersen LG A smooth particle mesh Ewald method. J. Chem. Phys 1995, 103, 8577–8593. [Google Scholar]
- (93).Nam K; Gao J; York DM An efficient linear-scaling Ewald method for long-range electrostatic interactions in combined QM/MM calculations. J. Chem. Theory Comput 2005, 1, 2–13. [DOI] [PubMed] [Google Scholar]
- (94).Kubař T; Welke K; Groenhof G New QM/MM implementation of the DFTB3 method in the gromacs package. J. Comput. Chem 2015, 36, 1978–89. [DOI] [PubMed] [Google Scholar]
- (95).Giese TJ; York DM A GPU-Accelerated Parameter Interpolation Thermodynamic Integration Free Energy Method. J. Chem. Theory Comput 2018, 14, 1564–1582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (96).Wang J; Wolf RM; Caldwell JW; Kollman PA; Case DA Development and testing of a general amber force field. J. Comput. Chem 2004, 25, 1157–1174. [DOI] [PubMed] [Google Scholar]
- (97).Horn HW; Swope WC; Pitera JW; Madura JD; Dick TJ; Hura GL; HeadGordon T Development of an improved four-site water model for biomolecular simulations: TIP4P-Ew. J. Chem. Phys 2004, 120, 9665–9678. [DOI] [PubMed] [Google Scholar]
- (98).Elstner M; Porezag D; Jungnickel G; Elsner J; Haugk M; Frauenheim T; Suhai S; Seifert G Self-consistent-charge density-functional tight-binding method for simulations of complex materials properties. Phys. Rev. B 1998, 58, 7260–7268. [Google Scholar]
- (99).Niehaus TA; Elstner M; Frauenheim T; Suhai S Application of an approximate density-functional method to sulfur containing compounds. J. Mol. Struct. (Theochem) 2001, 541, 185–194. [Google Scholar]
- (100).Gaus M; Cui Q; Elstner M DFTB3: Extension of the seld-consistent-charge density-functional tight-binding method (SCC-DFTB). J. Chem. Theory Comput 2011, 7, 931–948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (101).Zhang L; Han J; Wang H; Saidi W; Car R; E W End-to-end Symmetry Preserving Inter-atomic Potential Energy Model for Finite and Extended Systems. In Advances in Neural Information Processing Systems 31; Bengio S, Wallach H, Larochelle, Grauman K, Cesa-Bianchi N, Garnett R, Eds.; Curran Associates, Inc., 2018; pp 4436–4446. [Google Scholar]
- (102).Wang H; Zhang L; Han J; E W DeePMD-kit: A deep learning package for many-body potential energy representation and molecular dynamics. Comput. Phys. Commun 2018, 228, 178–184. [Google Scholar]
- (103).Zhang Y; Wang H; Chen W; Zeng J; Zhang L; Han W; E W DP-GEN: A concurrent learning platform for the generation of reliable deep learning based potential energy models. Comput. Phys. Commun 2020, 253, 107206. [Google Scholar]
- (104).Lu D; Jiang W; Chen Y; Zhang L; Jia W; Wang H; Chen M DP Compress: A Model Compression Scheme for Generating Efficient Deep Potential Models. J. Chem. Theory Comput 2022, 18, 5559–5567. [DOI] [PubMed] [Google Scholar]
- (105).Caves LS; Evanseck JD; Karplus M Locally accessible conformations of proteins: multiple molecular dynamics simulations of crambin. Protein Sci. 1998, 7, 649–666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (106).Loccisano AE; Acevedo O; DeChancie J; Schulze BG; Evanseck JD Enhanced sampling by multiple molecular dynamics trajectories: carbonmonoxy myoglobin 10 μs A0 → A1–3 transition from ten 400 picosecond simulations. J. Mol. Graph. Model 2004, 22, 369–376. [DOI] [PubMed] [Google Scholar]
- (107).Likic VA; Gooley PR; Speed TP; Strehler EE A statistical approach to the interpretation of molecular dynamics simulations of calmodulin equilibrium dynamics. Protein Sci. 2005, 14, 2955–2963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (108).Elofsson A; Nilsson L How consistent are molecular dynamics simulations? Comparing structure and dynamics in reduced and oxidized Escherichia coli thioredoxin. J. Mol. Biol 1993, 233, 766–780. [DOI] [PubMed] [Google Scholar]
- (109).Lahiri SN Comparison of Block Bootstrap Methods. In Resampling Methods for Dependent Data; Springer; New York, 2003; pp 115–144. [Google Scholar]
- (110).Klimovich PV; Shirts MR; Mobley DL Guidelines for the analysis of free energy calculations. J. Comput.-Aided Mol. Des 2015, 29, 397–411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (111).Yang W; Bitetti-Putzer R; Karplus M Free energy simulations: Use of reverse cumulative averaging to determine the equilibrated region and the time required for convergence. J. Chem. Phys 2004, 120, 2618–2628. [DOI] [PubMed] [Google Scholar]
- (112).Towns J; Cockerill T; Dahan M; Foster I; Gaither K; Grimshaw A; Hazlewood V; Lathrop S; Lifka D; Peterson GD et al. XSEDE: Accelerating Scientific Discovery. Comput. Sci. Eng 2014, 16, 62–74. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


