Addendum: A dispersive analysis of ${\mathit{\eta }}^{\mathbf{\prime }}\mathbf{\to }{\mathit{\pi }}^{\mathbf{+}}{\mathit{\pi }}^{\mathbf{-}}\mathit{\gamma }$ and ${\mathit{\eta }}^{\mathbf{\prime }}\mathbf{\to }{\mathit{\ell }}^{\mathbf{+}}{\mathit{\ell }}^{\mathbf{-}}\mathit{\gamma }$

Abstract

In this addendum to Ref. [1] we show that the mismatch between the $\rho$–$\omega$ mixing parameter ${ϵ}_{\rho \omega }$ as extracted from ${\eta }^{\prime }\to {\pi }^{+}{\pi }^{-}\gamma$ and $e^{+}{e}^{-}\to {\pi }^{+}{\pi }^{-}$ can be resolved by including higher orders in the expansion in $e^2$ in the description of the ${\eta }^{\prime }\to {\pi }^{+}{\pi }^{-}\gamma$ decay. We repeat the analysis in this extended framework and update the numerical results accordingly.

Addendum to: Eur. Phys. J. C 10.1140/epjc/s10052-022-10247-7

Extended formalism

Following the notation from Ref. [1] throughout, the spectrum for $P\to {\pi }^{+}{\pi }^{-}\gamma$ can be expressed as

$$\begin{array}{cc}\hfill \frac{\text{d}\Gamma (P\to {\pi }^{+}{\pi }^{-}\gamma )}{\text{d}s}& =16\pi \alpha {\Gamma }_0{|F_{\pi }^V(s)|}^2|P(s)(1+{\Pi }_{\pi }(s))\hfill \\ \hfill & -\frac{e^2{F}_{P\gamma \gamma }}{s}-\frac{g_{P\omega \gamma }}{g_{\omega \gamma }}\frac{{ϵ}_{\rho \omega }-e^2{g}_{\omega \gamma }^2}{M_{\omega }^2-s-i{M}_{\omega }{\Gamma }_{\omega }}{|}^2,\hfill \end{array}$$ 1.1

generalizing Eq. (D.14) in Ref. [1] by the next order in the expansion in $e^2$ (the sign convention is such that $g_{P\omega \gamma }<0$). The most important change, numerically, concerns ${ϵ}_{\rho \omega }\to {ϵ}_{\rho \omega }-e^2{g}_{\omega \gamma }^2$ in the numerator of the $\omega$ propagator, corresponding to the photon contribution in ${ϵ}_{\rho \omega }$ as defined in resonance chiral perturbation theory [2–4]. In our formalism, ${ϵ}_{\rho \omega }$, determined from a fit to the bare cross section for $e^{+}{e}^{-}\to {\pi }^{+}{\pi }^{-}$, does not include this VP effect, in line with the definition in Ref. [5] (numerically, it evaluates to $e^2{g}_{\omega \gamma }^2=0.34(1)\times {10}^{-3}$). This shift removes the tension observed between ${\eta }^{\prime }\to {\pi }^{+}{\pi }^{-}\gamma$ and $e^{+}{e}^{-}\to {\pi }^{+}{\pi }^{-}$ in Ref. [1].

The coefficients appearing in Eq. (3.9) of Ref. [1] are generalized according to Eq. (1.1):

$$\begin{array}{cc}\hfill {\mathcal{A}}_2& =-\Gamma ({\eta }^{\prime }\to {\pi }^{+}{\pi }^{-}\gamma )+16\pi \alpha {\int }_{4M_{\pi }^2}^{M_{{\eta }^{\prime }}^2}\text{d}s{\Gamma }_0{|F_{\pi }^V(s)|}^2\hfill \\ \hfill & \times {\left|\frac{g_{{\eta }^{\prime }\omega \gamma }}{g_{\omega \gamma }},\frac{{ϵ}_{\rho \omega }-e^2{g}_{\omega \gamma }^2}{M_{\omega }^2-s-i{M}_{\omega }{\Gamma }_{\omega }},+,\frac{e^2{F}_{{\eta }^{\prime }\gamma \gamma }}{s}\right|}^2,\hfill \\ \hfill {\mathcal{A}}_1& =32\pi \alpha {\int }_{4M_{\pi }^2}^{M_{{\eta }^{\prime }}^2}\text{d}s{\Gamma }_0{|F_{\pi }^V(s)|}^2\text{Re}[P_{\text{ev}}(s)(1+{\Pi }_{\pi }^{\ast }(s))\hfill \\ \hfill & \times (\frac{g_{{\eta }^{\prime }\omega \gamma }}{g_{\omega \gamma }}\frac{e^2{g}_{\omega \gamma }^2-{ϵ}_{\rho \omega }}{M_{\omega }^2-s-i{M}_{\omega }{\Gamma }_{\omega }}-\frac{e^2{F}_{{\eta }^{\prime }\gamma \gamma }}{s})],\hfill \\ \hfill {\mathcal{A}}_0& =16\pi \alpha {\int }_{4M_{\pi }^2}^{M_{{\eta }^{\prime }}^2}\text{d}s{\Gamma }_0{|F_{\pi }^V(s)|}^2{P}_{\text{ev}}^2(s)|1+{\Pi }_{\pi }(s){|}^2.\hfill \end{array}$$ 1.2

In the following, we provide the updated numerical results when including the additional $e^2$ effects as given in Eq. (1.1), implemented in the fit via Eq. (1.2).

Numerical results

The updated fit parameters are collected in Table 1, Fig. 1, and Table 2. The main difference to the results presented in Ref. [1] is that the shift ${ϵ}_{\rho \omega }\to {ϵ}_{\rho \omega }-e^2{g}_{\omega \gamma }^2$ removes the tension between $e^{+}{e}^{-}\to {\pi }^{+}{\pi }^{-}$ and the ${\eta }^{\prime }\to {\pi }^{+}{\pi }^{-}\gamma$ spectrum, markedly improving the quality of the combined fit.

Table 1.

Comparison of the fit outcome of the differential decay width in Eq. (1.1) to the BESIII ${\eta }^{\prime }\to {\pi }^{+}{\pi }^{-}\gamma$ spectrum [6] of the binned maximum likelihood and minimum ${\chi }^2$ strategies. The ${\chi }^2/\text{dof}$ is 1.30 and 1.31, respectively, with the one of the Likelihood method extracted by means of the approximation described in App. C of Ref. [7]

Quantity	Likelihood	${\chi }^2$
$A[{\text{GeV}}^{-3}]$	17.12(35)	17.09(32)
$\beta [{\text{GeV}}^{-2}]$	0.714(55)	0.723(45)
$\gamma [{\text{GeV}}^{-4}]$	$-0.412(55)$	$-0.420(45)$
${ϵ}_{\rho \omega }\times {10}^3$	1.998(67)	1.997(54)
$M_{\omega }[\text{MeV}]$	782.99(33)	783.00(27)

Fig. 1.

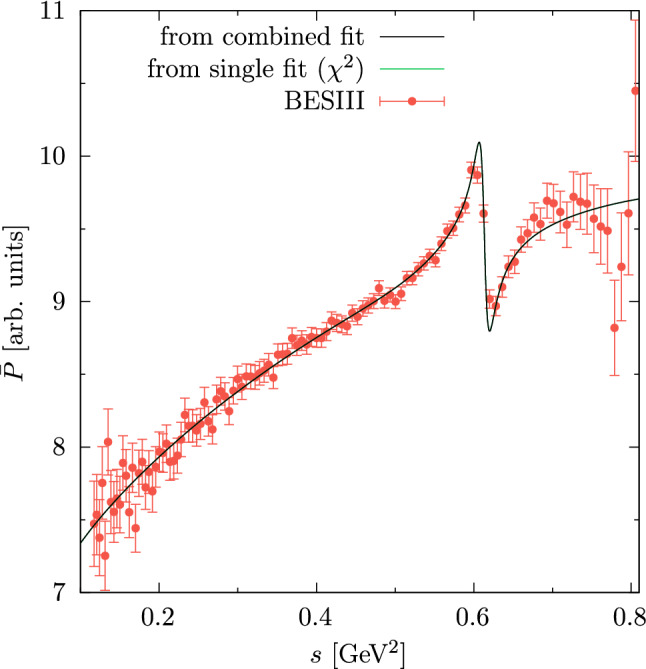
Fit to the differential decay rate of ${\eta }^{\prime }\to {\pi }^{+}{\pi }^{-}\gamma$ (individually or combined with the VFF). To highlight potential differences in the $\rho$–$\omega$ region, we show the associated function $\overline{P}$, as defined in Eq. (3.11) of Ref. [1], compared to the experimental data from BESIII [6]. The two fits cannot be distinguished on this scale

Table 2.

Combined fit to several pion VFF data sets (BaBar, KLOE, CMD-2, SND) and ${\eta }^{\prime }\to {\pi }^{+}{\pi }^{-}\gamma$ spectrum (BESIII) with overall ${\chi }^2/\text{dof}=1.46$. In the row for KLOE, the three values for $M_{\omega }$ refer to the combinations of the global KLOE $\omega$ mass and the corresponding mass shifts of the three underlying data sets from 2008, 2010, 2012, respectively

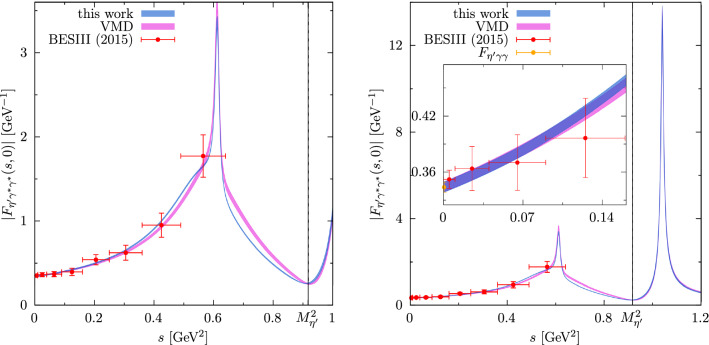
The updated results for the TFF are shown in Fig. 2 and Table 3. In particular, the prediction for the slope parameter

$$\begin{array}{c}\hfill b_{{\eta }^{\prime }}=1.431(23){\text{GeV}}^{-2}\end{array}$$ 2.1

is reduced by about $1\sigma$, which traces back not to the change in ${ϵ}_{\rho \omega }$ (which is marginal given the fact that the fit is dominated by $e^{+}{e}^{-}\to {\pi }^{+}{\pi }^{-}$), but to a stronger curvature in the polynomial P(s) (the coefficient $\gamma$ of the quadratic term increases by a factor 3).

Fig. 2.

Determination of the ${\eta }^{\prime }$ TFF in comparison to data from BESIII [8] (statistical and systematic errors added in quadrature) scaled with $F_{{\eta }^{\prime }\gamma \gamma }$ and the VMD model from Ref. [1] for the $\varphi$ resonance; for the kinematic range accessible in ${\eta }^{\prime }$ decays (left) and a larger time-like region including the $\varphi$ resonance with inset magnifying the low-s region (right)

Table 3.

Contributions from the various components of the TFF to the sum rules of the normalization and the slope parameter

	${(I=1)}_{{ϵ}_{\rho \omega }=0}$	$\Delta {(I=1)}_{{ϵ}_{\rho \omega }\ne 0}$	${(I=0)}_{{ϵ}_{\rho \omega }=0}^{\omega }$	$\Delta {(I=0)}_{{ϵ}_{\rho \omega }\ne 0}^{\omega }$	${(I=0)}^{\varphi }$	Total
Norm $[\%]$	69.18(86)	$-0.1388(19)$	7.06(22)	$-0.1397(47)$	15.85(61)	91.9(1.1)
$b_{{\eta }^{\prime }}[{\text{GeV}}^{-2}]$	1.160(23)	0	0.1176(32)	0	0.1526(53)	1.431(23)