Comparisons of Fit Factors Between Two Quantitative Fit Testers (PortaCount vs. MT)

Abstract

This study evaluated the consistency between two quantitative fit test devices with different methods of ambient aerosol counting. Three types of respirators (N95, half mask, and full facepiece) were worn by 50 participants (male, n = 25; female, n = 25), PortaCount (Pro+ 8038) and MT (05U) were connected to one probe to one mask, and fit factors (FFs) were measured simultaneously with the original and modified protocols. As a result of comparing MT FFs with PortaCount FFs as references and by applying for the pass/fail criteria (FF = 100), the consistency between the two devices for half masks and full facepieces was very high. N95 was somewhat weaker than the two type of respirators in the consistency; however, the correlation between the two devices was very strong (p < 0.0001). The results showed that an FF of 100 as measured by PortaCount was likely to be measured as 75 by the MT. Therefore, when performing the fit test for N95 using the MT and pass level of FF 100, a certain level of adjustment is necessary, whether end-user or putting a scaling factor by manufacturer.

1. Introduction

Facial leakage occurs because respirators do not match with the wearer's face. It is now taken as a serious problem not only for industrial health but also for health care workers. Moreover, in the Republic of Korea, where wearing a mask has become mandatory due to the coronavirus disease 2019 (COVID-19), many people complain of leakage even after wearing a mask and realize that the effectiveness of wearing a mask is very low with severe facial leakage. Developed industrial health countries such as the United States and Japan are trying to minimize facial leakage by enforcing fit tests [1,2]. Because the fit test is a very important for the health of workers wearing respirators, the International Organization for Standardization also recommends fit tests [3]. In the Republic of Korea, fit testing is not stipulated by law; however, some large companies and large hospitals are currently conducting fit tests. To support this, the Korea Safety and Health Agency strongly recommend conducting fit tests when selecting and wearing respiratory protective equipment [4] and is preparing for legalization [5].

Methodologies of quantitative fit tests (QNFTs) using aerosols from ambient air as a challenge agent include currently the PortaCount series of TSI in the United States and MT series of SIBATA in Japan.

In PortaCount, when fine aerosol is passed through a saturated isopropyl alcohol vapor, the aerosol nuclei begin to grow through condensation to a critical size that is easily counted by the instrument, and this process is so-called condensation nuclear counting [6]. Therefore, even very small particles that are barely recognized by any device that measures aerosol can be counted. This is the main characteristic of this device; Very high numbers of particles are counted because particles of 0.02 to 1 μm or larger are counted. By contrast, the MT series follows the optical particle counting method by emitting laser light to particles dried in the air and counting scattered light [7]. Unlike condensation nuclear counting, a very small number of particles are counted because of the relatively large particles with sizes of 0.3 μm or ≥0.5 μm. Although the same counting principle is followed, that is, counting particles in the air, the counting methods are different.

The fit factor (FF) compares the concentration of aerosols inside and outside the respirator when wearing respirators and conducting QNFT; generally, a respirator with large FF value fits better on the wearer's face. In the United States, FF ≥ 100 is designated as “pass” for half masks and FF ≥ 500 for full facepieces [1], and most other countries also apply this standard.

Even if the same number of aerosol is counted in the air, it will not be easy to match the measured values between two devices if the counting methods are different. Wu et al compared FFs between two devices, with PortaCount as the reference and MT as the new method [8]. In this study, the FFs of MT were generally lower than those of PortaCount; however, the sensitivity between FFs of the two devices was 0.98 for the P100 and 1.00 for the full facepiece. The consistency for FFs between the two devices was therefore very high. In another study, the pass and fail match rate between the two devices was defined as the rate to determine the pass as pass and the fail as fail, which was 93% (181 of 194 times) for N95, when FF 100 was applied as pass level [9]. In full facepiece, when FF 500 was applied with the same pass standard as occupational safety and health administration (OSHA), the match rate between the two devices was very high at 95% (79 of 83 times).

In the Republic of Korea, the COVID-19 outbreak has increased the demand for fit performance of masks for health care workers, and QNFT is actually being performed in many hospitals with two devices, PortaCount or MT. However, when measured with two devices at the same time, a difference in FFs occurred, and a clear scientific explanation of these different data was required.

This study aimed to provide important data when using two devices by comparing FFs of two QNFT devices, that is, TSI PortaCount and SIBATA MT.

2. Subjects and methods

2.1. Research design

One probe was inserted into the participant's mask, and to calculate the FF simultaneously, a Teflon tube was connected in a Y-shape outside the mask, where one end was connected to PortaCount (Model 8038, TSI, USA), and the other was connected to MT (Model 05U, SIBATA, Japan).

2.2. Participants

Participants were recruited from volunteer college students without age limit. Patients with current or past lung disease who cannot wear a mask or with severe facial deformities that may significantly reduce the fit performance of the mask were excluded.

When the effect size was set to a large value of 0.5, significance level of 0.05, and power (1-α error) of 0.95 in consideration of the results of previous studies [8], the total sample size in G-power was 42 [10]. To leave a sufficient margin, approximately 20% was added to increase the total number of participants to 50 (male, n = 25; female, n = 25).

This study was conducted after obtaining approval from the Institute Review Board Committee of Inje University (INJE 2021-04-017-003).

2.3. Respirators

The participant wore full facepiece (3M, 6800-medium, USA), half mask (3M, 7502-medium, USA), and N95 (Dobu Life Tech Co., Korea).

2.4. Fit test

The entire process of the fit test was performed according to the OSHA QNFT protocol of 29CFR1910.134 [1]. The original (requires eight exercise regimens before modification) and modified (requires only four exercise regimens after modification) protocols were performed. As a pass/fail criterion, full facepieces should have ≥500, whereas half masks and filtering facepiece respirator (FFRs) should have ≥100 to gain a pass status.

If the aerosol concentration in the laboratory is too low (<2,000 particles/cc), the fit test is not possible, so the aerosol concentration was stabilized by operating the aerosol generator 1 hour before the test. After wearing respirators, the participant shook the mask vigorously from side to side, and the user's seal was checked. If the participants failed to pass the user's seal check, they repeatedly wore the respirator again and performed fit test after passing the user's seal check. For the order of measurements, the test mask was selected randomly to avoid selection bias.

2.5. Statistical analysis

As descriptive statistics, the geometric mean and geometric standard deviation for the FFs were calculated, and the correlation between the FFs of the two devices was analyzed. Pearson linear correlation coefficient was used to measure how strong linearity is between two FFs. The statistical package of SPSS was used.

Consistency is defined as a proportion in which FFs determined by two devices yield the same result compared with pass or fail criteria in the study. In general, quantitative values for consistency are the five statistics specified by ANSI. To determine the consistency between the two devices, a continuity table of ANSI 2010 was used [11]. In a previous study [8], the FFs calculated using two PortaCount were very consistent, so the PortaCount method was also used as a reference method in this study. The FF, which was determined by the PortaCount, was indicated as FF_PC, and the FF determined by MT was FF_MT in Table 1. The number of fit tests with passing and failing FFs were compared for both devices and placed into one of four categories as shown in Table 1. The test statistics, that is, sensitivity, predictive value of a pass (PVP), specificity, predictive value of a fail (PVF), and Kappa statistic, were calculated and compared (Table 1). For example, sensitivity is the proportion of the number of fit tests to which PortaCount FFs and MT FFs are both below the target FF, OSHA pass/fail criterion (reference fit factor). The proportion to which less than half mask FF 100 or full facepiece FF 500 by PortaCount is also less than 100 or 500 by MT is sensitivity, and it is mandatory.

Table 1.

Contingency table and test statistics from ANSI (2010)

Result	Failed PortaCount (FFPC < RFF∗)	Passed PortaCount (FFPC > RFF)
Passed MT (FFMT > RFF)	A	B
Failed MT (FFMT < RFF)	C	D

Statistics	Equation	Value	Level of endorsement
Test sensitivity	C/(A + C)	≥0.95	Mandatory
Predictive value of a pass	B/(A + B)	≥0.95	Advised
Test specificity	B/(B + D)	≥0.50	Advised
Predictive value of a fail	C/(C + D)	≥0.50	Advised
Kappa statistics	(Po† − Pe‡)/(1 − Pe‡)	>0.7	Recommended

^∗RFF (Reference Fit Factor) means OSHA's pass/fail criterion; half mask FF = 100, full facepiece FF = 500. FF_PC means FF determined by PortaCount, and FF_MT means FF determined by MT.

^†P_o = (B + C)/(A + B + C + D).

^‡P_e = [(A + B) (B + D) + (C + D) (A + C)]/(A + B + C + D)².

Among the five statistics in the Table, sensitivity is the most important statistic to find out the consistency of the two devices. The reason is that only sensitivity is specified as “mandatory.”

3. Results

3.1. Descriptive statistics of FFs

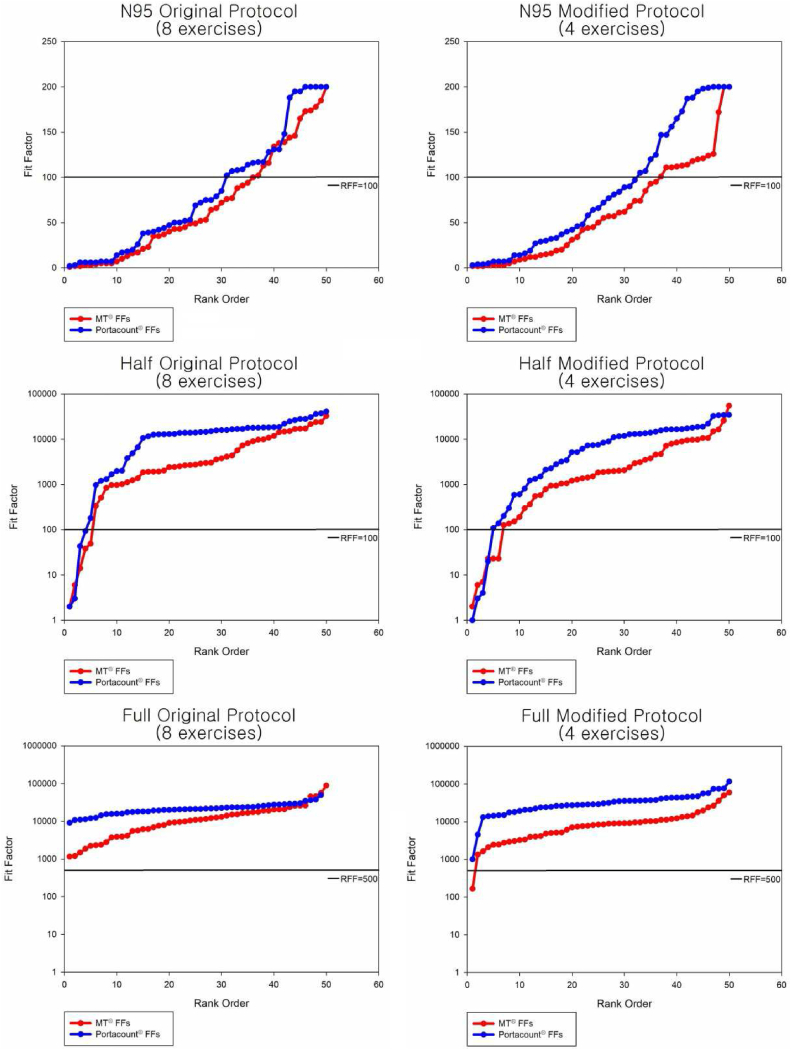
Fig. 1 shows the FFs between the two devices in a graph according to the size order of FFs by mask and test protocol. Two FFs measured by MT and PortaCount for one sample are not paired matched; this graph simply illustrated the FFs for 50 samples in order. Therefore, Fig. 1 shows that the FFs from each device in rank order help to show the difference in FF values, but it shows no the difference within a specific test with the exact same fit. At a glance, the FFs of MT were lower than those of PortaCount in all masks, which agreed with the results of previous studies [8,9]. This occurs because the aerosol counting methods of the two devices are different. MT can only count aerosols greater than approximately 0.3 μm (>0.5 μm in N95 test); however, PortaCount can broadly count up to 20–100 nm or more. Thus, the number of particles outside the mask, the denominator of FF, is much higher in PortaCount measurements than in MT measurements. Inside the mask, the number of smaller particles measured by PortaCount is less than the number of larger particles measured by MT because diffusional losses occur at the leak site and within the mask [12,13]. Therefore, it is thought that the FF measured by PortaCount may be higher than the FF measured by MT under the same ambient particles.

Fig. 1.

Comparison of the FFs of respirator-type devices and protocol according to rank order. FFs measured by MT and PortaCount for one sample were not paired matched. FF: fit factor.

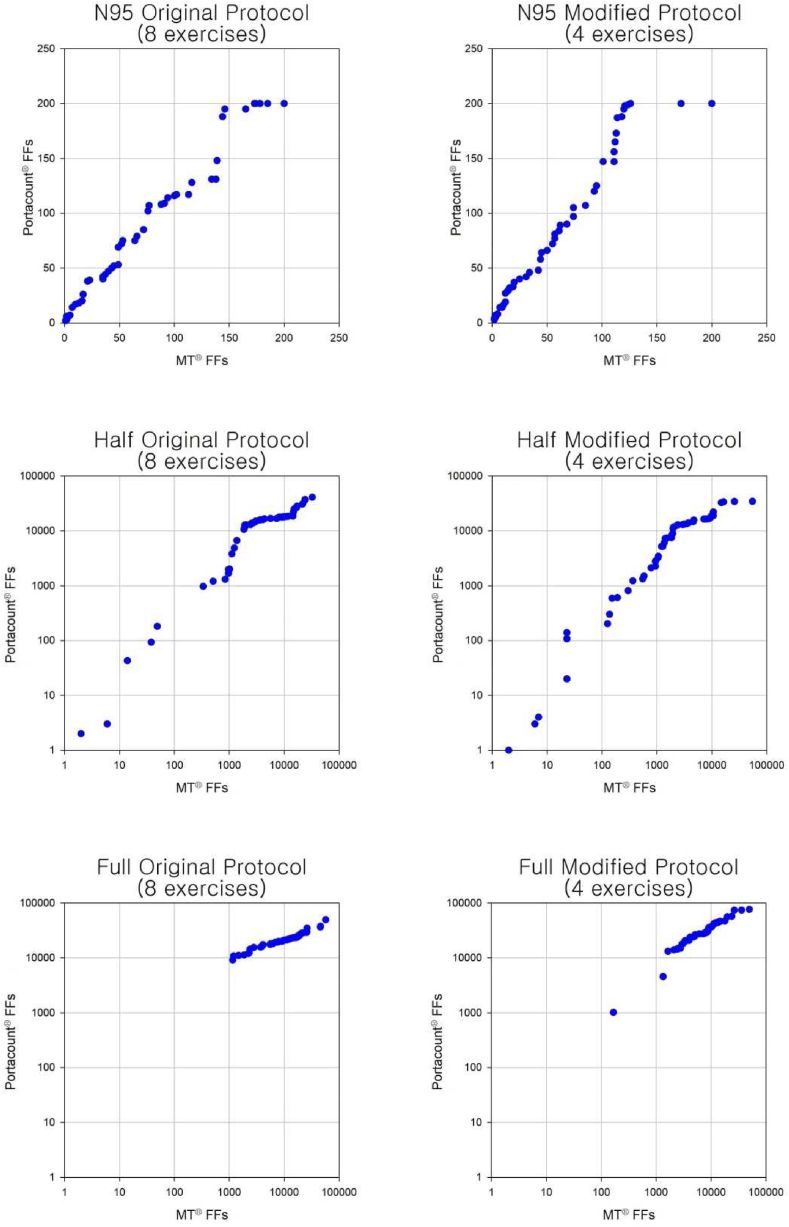
Fig. 2 is a graph of the FFs of MT (x-axis) and PortaCount (y-axis) to determine approximately the extent of FF difference between the two devices. For example, in N95, the FF by MT corresponding to FF 100 by PortaCount in the original protocol (8 exercises) or the modified protocol (4 exercises) is approximately between 70 and 80 (Fig. 3).

Fig. 2.

Comparison of FFs of two respirator-type devices and protocol according to differences. FF: fit factor.

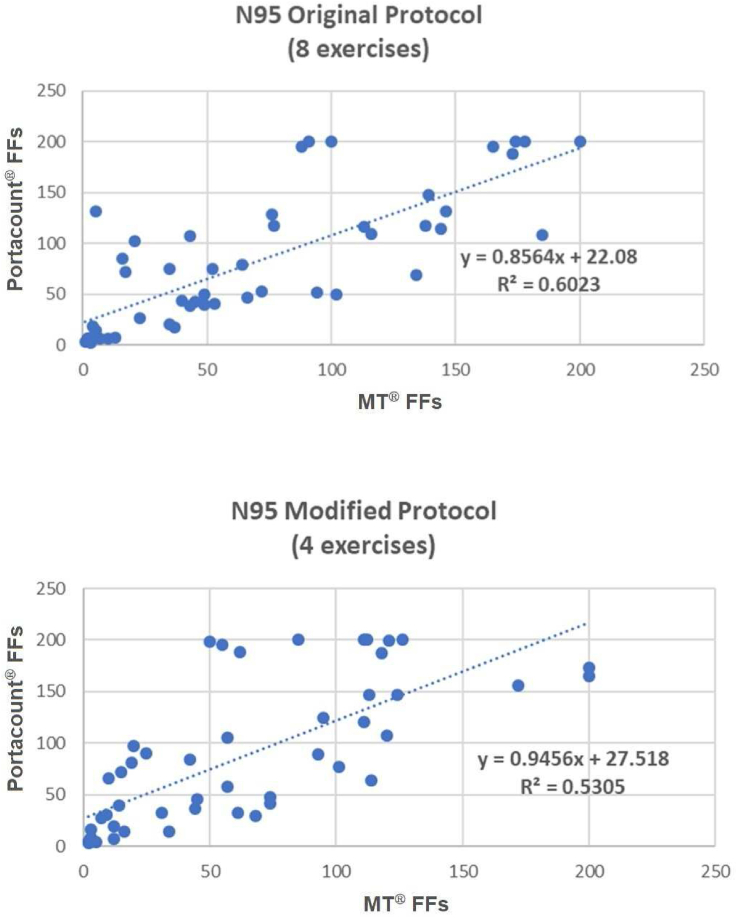
Fig. 3.

Correlation of FFs for N95 FFR between two devices by protocols. FF: fit factor.

The geometric mean and geometric standard deviation of overall FFs measured by protocols are presented. As mentioned earlier, the FFs measured by MT were much lower than those measured by PortaCount, the differences in two devices were significant in both half mask and full facepiece, and the extent of significance was higher in the full facepiece. Meanwhile, in N95, the measured values by MT were lower than those by PortaCount; however, no significant difference was observed between the two devices.

Moreover, no significant differences in the FFs were noted between the original and modified protocol, but the FFs by the modified protocol were slightly lower overall than those by the original protocol in half masks.

3.2. Consistency between the two devices

Table 2 presents the results of analyzing the consistency between the two devices by test protocols. Regardless of the test protocols, both the half mask and full facepiece showed a very high consistency in sensitivity, PVP, specificity, and PVF at the level of endorsement specified by ANSI [11]. In N95, both specificity and PVF satisfied ANSI's level of endorsements specified; however, the sensitivity and PVP were not reached. ANSI specifies Kappa statistics >0.70, which appears to be 0.88 and 0.78 in half masks, indicating that the observation class would be quite consistent with the prediction class. However, the values were 0.61 and 0.64 in N95, so the level specified by ANSI [11] was not satisfied.

Table 2.

Statistics summary along with ANSI requirements/recommendations by test protocols

Test protocols	Respirator	Sensitivity	PVP	Specificity	PVF	Kappa statistics
Original protocol	N95	0.93	0.87	0.65	0.80	0.61
	Half mask	1.00	1.00	0.98	0.80	0.88
	Full mask	−∗	1.00	1.00	−∗	−∗
Modified protocol	N95	0.94	0.86	0.67	0.83	0.64
	Half mask	1.00	1.00	0.96	0.67	0.78
	Full mask	−∗	1.00	0.98	−∗	−∗
ANSI requirement/recommendation		≥0.95	≥0.95	≥0.50	≥0.50	>0.70

PVP, predictive value of a pass; PVF, predictive value of a fail.

^∗Full mask is not calculated because the cell value is zero.

Compared with the results of a previous study [8], where the statistical analytical methods were the same, the half mask and full facepiece showed comparable results. Although direct comparison was difficult because different statistical analysis methods were used, the full facepiece showed higher consistency than those in another study [9], but N95 was slightly lower.

Consequently, the consistency between the two devices for the half mask and full facepiece sufficiently satisfied the values specified by ANSI in both protocols. But in N95, the sensitivity and Kappa statistics in both protocols were not met the ANSI's specified levels. Therefore, further statistical analysis was needed to supplement this finding, and it is presented in the discussion section.

4. Discussion

4.1. Consistency between the two devices

The size of influenza aerosols that can spread COVID-19 was found to be <1 μm for 42% of coughing, 87% of exhalation air, 1 to ∼4 μm for 23% of coughing, 13% of exhalation air, and >4 μm for 35% of coughing only. Influenza virus in exhaled breath is contained in smaller particles than in cough [13]. Since the size of the influenza aerosol is included in the aerosol size measured by the two devices, it would not affect the results of fit testing [14]. Therefore, even if the size of the particles used for measurement is different, it cannot be said that either method is better.

Half masks and full facepieces demonstrated very high consistency between the two devices; thus, the pass/fail by MT would be almost the same as that by PortaCount.

The authors expect that as in a previous study [7], if P100 or FFP3 had been used instead of N95, the consistency between the two devices would have been much better than these results. However, N95 was used in the present study because N95 was actually widely used in Korean hospitals, and the certification criteria for N95 were similar to those of KF94 masks for the general public to prevent COVID-19.

For the N95 mask, the sensitivity between the two devices (the proportion to which PortaCount is determined to fail and MT also failed) was very close to 0.95 specified by ANSI (original protocol 0.93 vs. modified protocol 0.94), which was unlikely to be a major problem. However, both the protocols did not satisfy the Kappa statistics >0.70 (0.61 vs. 0.64). Therefore, a correlation analysis was conducted; as a result, the correlation coefficients were 0.78 and 0.73 for the original and modified protocols, respectively, which were significant (p < 0.0001). These results provide a strong logical basis for inferring what MT FF corresponds to FF 100, the pass criterion for N95, measured by PortaCount.

4.2. Suggestion on pass level of FFs for N95 by MT-05U

MT FF corresponding to OSHA's pass level of FF 100 for N95 measured by PortaCount was obtained by the correlation equation. As a result, PortaCount FF 100 corresponds to MT FF 91 in the original protocol and 77 in the modified protocol. At present, because fit testing prefers the modified protocol (4 exercises) over the original protocol (8 exercises), the statistics for the modified protocol were calculated based on the ANSI criteria (2010) [11].

Statistical analysis was performed to find out which FF measured by MT corresponds to FF of 100 by PortaCount. The five statistics specified by ANSI [11] were used for statistical analysis, and sensitivity of them was the first considered. The cutoff value of MT FF of 75 was adjusted to PortaCount FF of 100, and the sensitivity was 0.96, satisfying the mandatory value of ≥0.95 while the PVP was 0.94, almost the same as ≥0.95. Both specificity and PVF are satisfied. When FF measured by MT was 75, the Kappa statistic >0.7 specified by ANSI [11] was not satisfied. However, the Kappa statistic of 0.64 is generally considered reasonable.

When the MT FFs were 106 and 107, the Kappa statistic exceeded 0.7. However, in this case, not only did the PVP fall to 0.92 but also the descriptive statistics described earlier showed that the MT FFs were lower than the PortaCount FFs, which makes it logically inconsistent.

Consequently, the results show that a FF of 100 as measured by PortaCount is likely to be measured as 75 by the MT. But this does not demonstrate that a new pass criterion should be established. At this point, when performing the fit test for N95 using the MT and pass level of FF 100, a certain level of adjustment is absolutely necessary. Of course, a larger number of fit test studies should be followed to clearly determine “a certain level of adjustment.” Another suggestion is that the MT manufacturer should consider inputting a scaling factor to apply a pass level of FF 100 when fit testing N95 using it.

Ethical statement

The study practice was approved the Institutional Review Board of the Inje University (approval ID: INJE 2021-04-017-003).

Conflicts of interest

All authors declare that there are no conflicts of interest. There are no conflicts of interest with commercial products regarding the devices and materials used in this study.