Abstract
We introduce a Gaussian accelerated molecular dynamics (GaMD), Deep Learning (DL) and free energy prOfiling Workflow (GLOW) to predict molecular determinants and map free energy landscapes of biomolecules. All-atom GaMD enhanced sampling simulations are first performed on biomolecules of interest. Structural contact maps are then calculated from GaMD simulation frames and transformed into images for building DL models using convolutional neural network. Important structural contacts are further determined from DL models of attention maps of the structural contact gradients, which allow us to identify the system reaction coordinates. Finally, free energy profiles are calculated for the selected reaction coordinates through energetic reweighting of the GaMD simulations. We have also successfully demonstrated GLOW on characterization of activation and allosteric modulation of a GPCR, using the adenosine A1 receptor (A1AR) as a model system. GLOW findings are highly consistent with previous experimental and computational studies of the A1AR, while also provide further mechanistic insights into the receptor function. In summary, GLOW provides a systematic approach to mapping free energy landscapes of biomolecules. The GLOW workflow and its user manual can be downloaded at http://miaolab.org/GLOW.
Keywords: GLOW, Gaussian accelerated molecular dynamics (GaMD), Deep Learning (DL), free energy, GPCR, activation, allosteric modulation
Graphical Abstract
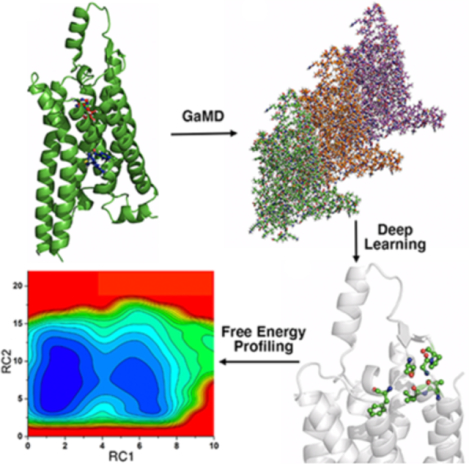
GLOW integrates a Gaussian accelerated molecular dynamics (GaMD), Deep Learning (DL) and free energy prOfiling Workflow to predict molecular determinants and map free energy landscapes of biomolecules. GaMD simulations are performed on biomolecules. DL identifies important system reaction coordinates. Free energy profiles are finally calculated to characterize biomolecular dynamics.
Introduction
Molecular dynamics (MD) is a powerful computational technique for simulating biomolecular dynamics at an atomistic level1. Longer and cheaper MD simulations can now be achieved due to remarkable advances in computing hardware (e.g., the Anton supercomputer and GPUs) and software developments2, 3. Even so, conventional MD (cMD) is typically limited to hundreds of nanoseconds to tens of microseconds3–10. Many biological processes of interest, however, occur over milliseconds or even longer timescales, due to high energy barriers (e.g., 8–12 kcal/mol)3–10. Consequently, sufficient sampling of different conformations and accurate calculations of free energy profiles of biomolecules remain challenging for cMD simulations3.
Enhanced sampling techniques have been developed to overcome the above challenges. Many enhanced sampling techniques have been developed during the last several decades11–15. Overall, these techniques greatly improve the sampling of biomolecular dynamics and the accuracy of free energy calculations. One class of these methods use predefined collective variables (CVs) or reaction coordinates (RCs), including umbrella sampling16, 17, metadynamics18, 19, adaptive biasing force20, 21 and steered MD22. It is, however, rather challenging to define proper CVs in prior because the system needs to be studied in detail beforehand3. In addition, predefining CVs could significantly limit sampling of the conformational space during simulations. Another class of enhanced sampling techniques do not require predefined CVs, including replica exchange MD (REMD)23, 24 or parallel tempering25, self-guided Langevin MD26–28 and accelerated MD (aMD)29, 30. In aMD, a boost potential is added to sample different low-energy conformational states by smoothing the system potential energy surface and reducing the energy barriers29, 31. Despite the advantage of unconstrained enhanced sampling, aMD suffers from high energetic noise and difficulties in recovering the original statistical ensemble3, 32. This issue can be severe for large biomolecular systems, such as proteins and nucleic acids, where proper energetic reweighting has often been prohibitive33.
Gaussian accelerated molecular dynamics (GaMD) is developed based on aMD for simultaneous unconstrained enhanced sampling and free energy calculations of large biomolecules34. GaMD adds a harmonic boost potential to reduce the system energy barriers34. This boost potential usually exhibits a Gaussian distribution. Cumulant expansion to the second order (“Gaussian approximation”) can be applied to achieve proper energetic reweighting33. GaMD resolves the energetic noise problem encountered in the previous aMD method29, 35, and allows for recovery of the original free energy profiles34. GaMD has been successfully demonstrated on enhanced sampling of ligand binding34, 36–40, protein folding34, 36, protein conformational changes37, 41–43, protein-membrane44, protein-protein41, 45, 46 and protein-nucleic acid47, 48 interactions, etc. Furthermore, GaMD has been combined with REMD49, 50 to further improve conformational sampling and free energy calculations3. Recently developed “selective GaMD” algorithms, including Ligand GaMD (LiGaMD)51 and Peptide GaMD (Pep-GaMD)52, have enabled repetitive binding and dissociation of small-molecule ligands and highly flexible peptides within microsecond simulations, which allow for highly efficient and accurate calculations of ligand/peptide binding free energies and kinetic rate constants3.
Machine Learning (ML) has been applied to enhance MD simulations and facilitate the simulation analysis of biomolecules53, 54, particularly G-protein-coupled receptors (GPCRs). GPCRs are the largest family of human membrane proteins and represent primary targets of ~34% of currently marketed drugs55. For class A (rhodopsin-like) GPCRs, activation is often triggered by binding of an agonist to the orthosteric pocket located within the receptor seven transmembrane (TM) domain56. However, complete activation of GPCRs usually requires additional coupling of the intracellular G proteins. GPCR activation has been characterized by structural rearrangements of the TM5, TM6 and TM7 helices, notably outward tilting of the TM6 cytoplasmic end, inward movement of the NPxxY motif in the TM7 intracellular domain and close interaction of Tyr5.58 and Tyr7.53 in the G protein-coupling site57–64. GPCR residues are numbered according to the Ballesteros-Weinstein scheme65. In addition to orthosteric ligands, GPCR structural dynamics can be modulated by allosteric ligands, compounds that bind to topographically distant (“allosteric”) sites66–68. For example, binding of a positive allosteric modulator (PAM) in the M2 muscarinic receptor led to sidechain rotation of residue W7.35 and slight contraction of the receptor extracellular pocket, which was pre-formed in the active agonist-bound structure57, 69. Binding of a muscarinic toxin negative allosteric modulator (NAM) to the antagonist bound M1 muscarinic receptor resulted in conformational changes in the extracellular loop 2 (ECL2), TM1, TM2, TM6 and TM7 extracellular domains, as well as the TM2 and TM6 intracellular domains70. In the free fatty acid receptor GPR40, PAM binding in a lipid-facing pocket induced conformational changes in the intracellular loop 2 (ICL2), TM4 and TM5 of the active receptor71. The ICL2 adopted a short helical conformation and the TM5 was shifted along its helical axis towards the extracellular side relative to the TM471. A similar allosteric site was identified for binding of NAMs between TM3-TM4-TM5 on the lipid-exposed surface of the C5a receptor72. Recently, binding of a PAM to an extrahelical lipid-facing pocket formed by TM1-TM6-TM7 helices of adenosine A1 receptor (A1AR) stabilized the receptor-G protein complex by increasing agonist binding affinity and reducing receptor-G protein mobility42. Notably, ECL2 has been suggested to play an important role in the activation and allosteric modulation of A1AR and other GPCRs42, 73–77.
Weinstein and co-workers developed an ML approach for analysis of cMD simulations to classify inverse, partial and full agonists of class A GPCRs and predict their molecular determinants78. It was based on transforming MD trajectories into image representations recognizable by Deep Neural Networks (DNNs). The X, Y and Z coordinates of an atom in each simulation frame were converted to the red, green and blue (RGB) color values of a pixel in an image. They also developed a Rare Event Detection (RED) protocol to investigate ligand-dependent conformational transitions in cMD simulations of the serotonin 5-HT2AR receptor79. RED was able to identify rare transition events in residue contacts of the GPCR in response to binding of the agonist and inverse agonist. Another ML approach was developed to cluster MD simulations of the dopamine D3 receptor (D3R) for rationalizing the efficacy change induced by binding of four orthosteric ligands80. The analysis revealed that increase in ligand flexibility progressively destabilized the D3R, which was validated in experiments. Furthermore, supervised and unsupervised ML methods were used to create interpretable maps of important features from MD simulations to analyze signal transduction, ligand binding and voltage sensing of the β2-adrenoceptor81. ML was also combined with infrequent metadynamics simulations to predict the kinetic rates and mechanisms of orthosteric ligand dissociation from the μ opioid receptor (μOR)82. Supervised ML classifiers have been built on molecular features to distinguish active orthosteric ligands from the inactive or random compound and allosteric modulators from orthosteric ligands in the CB1 and CB2 cannabinoid receptors83. However, ML has not been combined with MD for modeling of GPCR allosteric modulation.
In this work, we introduce a GaMD, deep Learning and free energy prOfiling Workflow (GLOW) for biomolecular simulations. First, GaMD simulations are performed on biomolecular systems of our interest. A Deep Learning (DL) model is then trained with residue contact maps of GaMD trajectories transformed into image representations. The DL model allows us to classify the systems of interest and predict their molecular determinants, from which important residues will be identified by pixel-attributed backpropagation84 to select the system reaction coordinates (RCs). Free energy profiles of the RCs are finally calculated from GaMD simulations to enable detailed characterization of target biomolecular systems. GLOW provides a systematic approach to mapping free energy landscapes of systems of interest. Furthermore, we demonstrate GLOW on characterization of both activation and allosteric modulation of a model GPCR.
Methods
Overview of GLOW
In GLOW, GaMD and DL are integrated to identify important reaction coordinates and map free energy profiles of biomolecules. First, GaMD simulations were performed on the target biomolecules (Figure 1A). Since simulation trajectories are collections of static PDB snapshots, the residue contact map of each simulation frame can be calculated and transformed into images (Figure 1B). The specialized type of neural network for image classification, two-dimensional (2D) convolutional neural network (CNN), is employed to classify the residue contact maps of target biomolecules, from which important residue contacts are identified by classic gradient-based pixel attribution84 (Figure 1C). Finally, the free energy profiles of these RCs are calculated through reweighting of GaMD simulations to characterize the biomolecular systems of interest (Figure 1D). Related theories and application of GLOW are described in detail below.
Figure 1. Overview of the Gaussian accelerated molecular dynamics (GaMD), Deep Learning (DL) and Free Energy PrOfiling Workflow (GLOW).
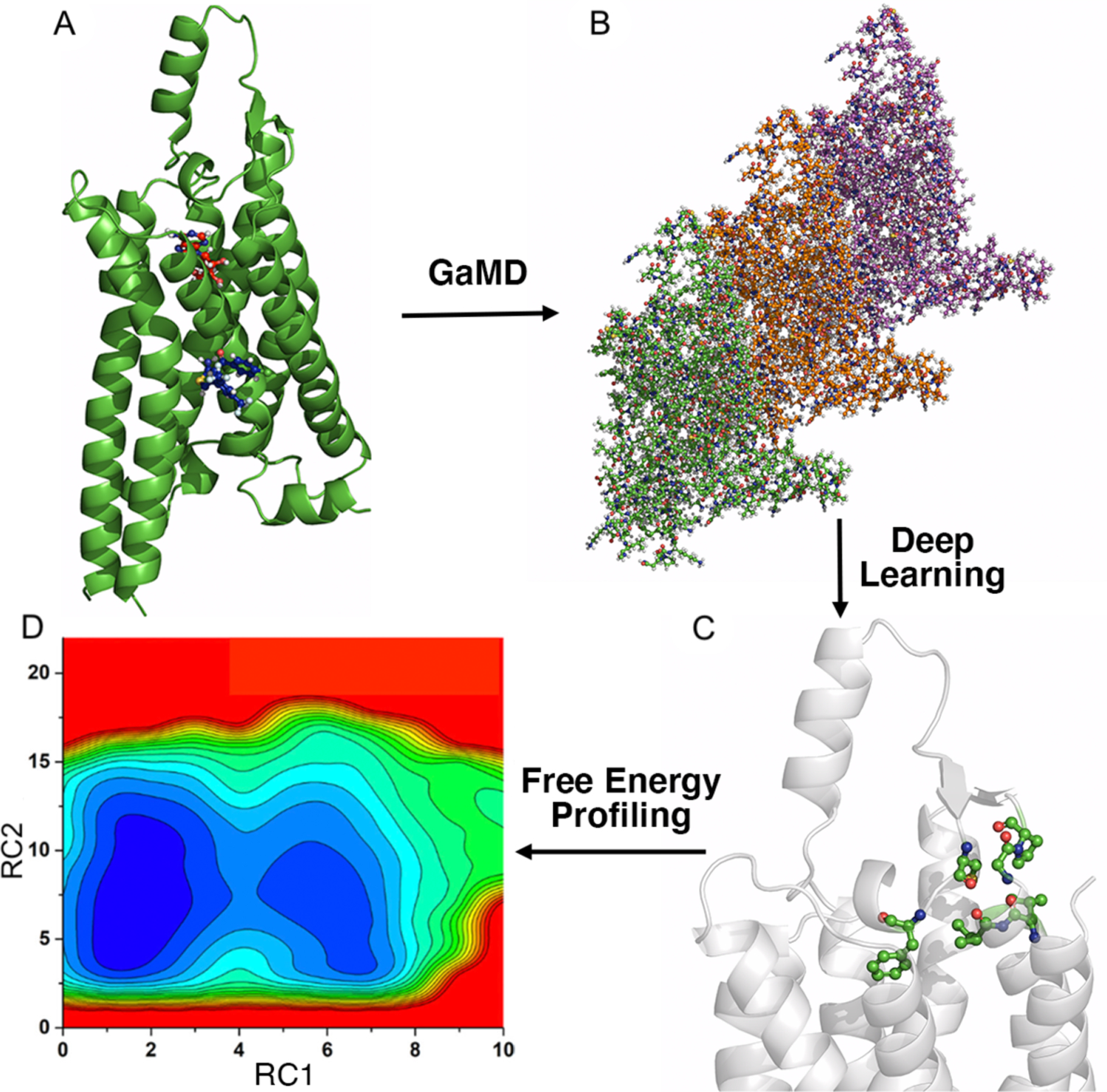
(A) With structures of our interest, GaMD simulations are applied for enhanced sampling of the system dynamics. (B) DL models are then built with GaMD trajectories of residue contact maps transformed into image representations. (C) The DL analysis allows us to identify important residue contacts and system reaction coordinates (RCs). (D) Free energy profiles of the RCs are finally calculated through reweighting of GaMD simulations to characterize the system dynamics.
Gaussian accelerated molecular dynamics
GaMD works by adding a harmonic boost potential to smooth the potential energy surface when the system potential drops below a reference energy E:
| (1) |
where k is the harmonic force constant. The two adjustable parameters E and k can be determined based on three enhanced sampling principles. First, for any two arbitrary potential values and found on the original energy surface, if , ΔV should be a monotonic function that does not change the relative order of the biased potential values; i.e., . Second, if , the potential difference observed on the smoothed energy surface should be smaller than that of the original, i.e., . The reference energy needs to be set in the following range:
| (2) |
where Vmax and Vmin are the system minimum and maximum potential energies. To ensure that equation (2) is valid, k must satisfy: . Let us define , then 0 ≤ k0 ≤ 1. Third, the standard deviation of ΔV needs to be small enough (i.e., narrow distribution) to ensure proper energetic reweighting33: σΔV = k(E − Vavg)σV ≤ σ0, where Vavg and σV are the average and standard deviation of the system potential energies, σΔV is the standard deviation of ΔV with σ0 as a user-specified upper limit (e.g., 10kBT) for proper reweighting. When E is set to the lower bound E = Vmax, k0 can be calculated as:
| (3) |
Alternatively, when the threshold energy E is set to its upper bound , k0 is set to:
| (4) |
if is found to be between 0 and 1. Otherwise, k0 is calculated using equation (3).
Similar to aMD, GaMD provides options to add only the total potential boost ΔVp, only dihedral potential boost ΔVD, or the dual potential boost (both ΔVp and ΔVD). The dual-boost GaMD generally provides higher acceleration than the other two types of simulations31.
Simulation protocol
The X-ray crystal structure of human A1AR in complex with PSB36 antagonist (PDB: 5N2S)85 and cryo-EM structures of the A1AR bound by the adenosine (ADO) and Gi2 protein (PDB: 6D9H)86 and A1AR bound by ADO, Gi2 protein and MIPS521 PAM (PDB: 7LD3)42 were used to set up the simulation systems. The Gi2 protein was removed from the 6D9H structure to prepare the A1AR – ADO system. While GaMD simulations of the A1AR-ADO-Gi2, A1AR-ADO-Gi2-MIPS521 and A1AR-ADO systems were obtained from a previous study42, we additionally performed GaMD simulations on the A1AR-PSB36 system. All chain termini were capped with neutral patches (acetyl and methylamide). The receptor was then embedded in POPC membrane lipid bilayers and complex structures were solvated in 0.15 M NaCl solutions. The CHARMM36m force field parameter set87 was used for the simulations. The systems were energetically minimized for 5000 steps using the steepest-descent algorithm and equilibrated with the constant number, volume, and temperature (NVT) ensemble with 310 K. They were further equilibrated for 375 ps at 310 K with the constant number, pressure, and temperature (NPT) ensemble. The cMD simulations were then performed for 10 ns using the NPT ensemble with constant surface tension at 1 atm pressure and 310 K temperature. GaMD implemented in GPU version of AMBER 2034, 88, 89 was applied to simulate the A1AR systems. The simulation involved an initial short cMD of 10 ns to calculate GaMD acceleration parameters and GaMD equilibration of added boost potential for 40 ns. Three independent GaMD production simulations with randomized initial atomic velocities were performed at the “dual-boost” level, with one boost potential applied to the dihedral energetic term and the other to the total potential energetic term. 500-ns simulations were performed on the experimental structure complexes, and 1000-ns simulations were performed on the A1AR-ADO system. The reference energy was set to the lower bound, and the upper limit of the boost potential standard deviation, σ0, was set to 6.0 kcal/mol for both the dihedral and total potential energetic terms. The GaMD simulations are summarized in Table S1.
Deep Learning
Deep learning was applied to analyze GaMD simulations of the A1AR systems. The residue contact map of each GaMD simulation frame was computed using Python packages MDTraj90 and contact map explorer90. A contact definition of ≤4.5 Å between any heavy atoms was used. The resulting 287 × 287 – residue contact maps were transformed into 287 × 287 – pixel grayscale images for analysis by a 2D CNN (Figure 1B). In total, 150,000 images were obtained for each A1AR system, 80% of which were randomly selected for training, while the rest were used for validation. We built our 2D CNN using the Keras module91 embedded in Python TensorFlow package92. The best fit model consisted of four convolutional layers of 3 × 3 kernel size, with 32, 32, 64 and 64 filters, respectively, followed by three fully connected (dense) layers, the first two of which included 512 and 128 filters with a dropout rate of 0.5 each. The final fully connected layer was the classification layer. We used “ReLu” activation for all layers in the 2D CNN, except the classification layer, in which “softmax” activation was used. A maximum pooling layer of 2 × 2 kernel size was added after each convolutional layer. Finally, the saliency (attention) map of residue contact gradients was calculated through backpropagation by vanilla gradient-based pixel attribution84 using the residue contact map of the most populated structural cluster of each A1AR system. The hierarchical agglomerative clustering algorithm was used to cluster snapshots of receptor conformations with all GaMD production simulations combined for each system.
Free energy profiling
Important residue contacts were identified from the DL model based on the following: (1) the contact gradients were above 0.4 in the saliency (attention) maps (see Figs. 2 and 5, Tables S2 and S3), (2) the residue contacts were from different receptor domains, and (3) they showed distinct features in different forms of the simulation system. RCs associated with the important residues were then selected to compute free energy profiles by reweighting the GaMD simulations using the PyReweighting toolkit33, 34. A bin size of 0.5 Å was used, and the cutoff was set to 500 – 1000 frames in one bin for reweighting. The probability distribution of selected RCs can be calculated from simulations as p*(A). Given the boost potential ΔV(r) of each frame in GaMD simulations, p*(A) can be reweighted to recover the canonical ensemble distribution, p(A), as:
| (5) |
where M is the number of bins, β = kBT and 〈eβΔV(r)〉j is the ensemble-averaged Boltzmann factor of ΔV(r) for simulation frames found in the jth bin. The ensemble-averaged reweighting factor can be approximated using cumulant expansion33, 34:
| (6) |
where the first two cumulants are given by:
| (7) |
The boost potential obtained from GaMD simulations usually shows near-Gaussian distribution93. Cumulant expansion to the second order thus provides a good approximation for computing the reweighting factor33, 34. The reweighted free energy F(A) = −kBT ln p(A) is calculated as:
| (8) |
where F*(A) = −kBT ln p*(A) is the modified free energy obtained from GaMD simulation and Fc is a constant.
Figure 2. Demonstration of GLOW on characterization of GPCR activation using adenosine A1 receptor (A1AR) as a model system.
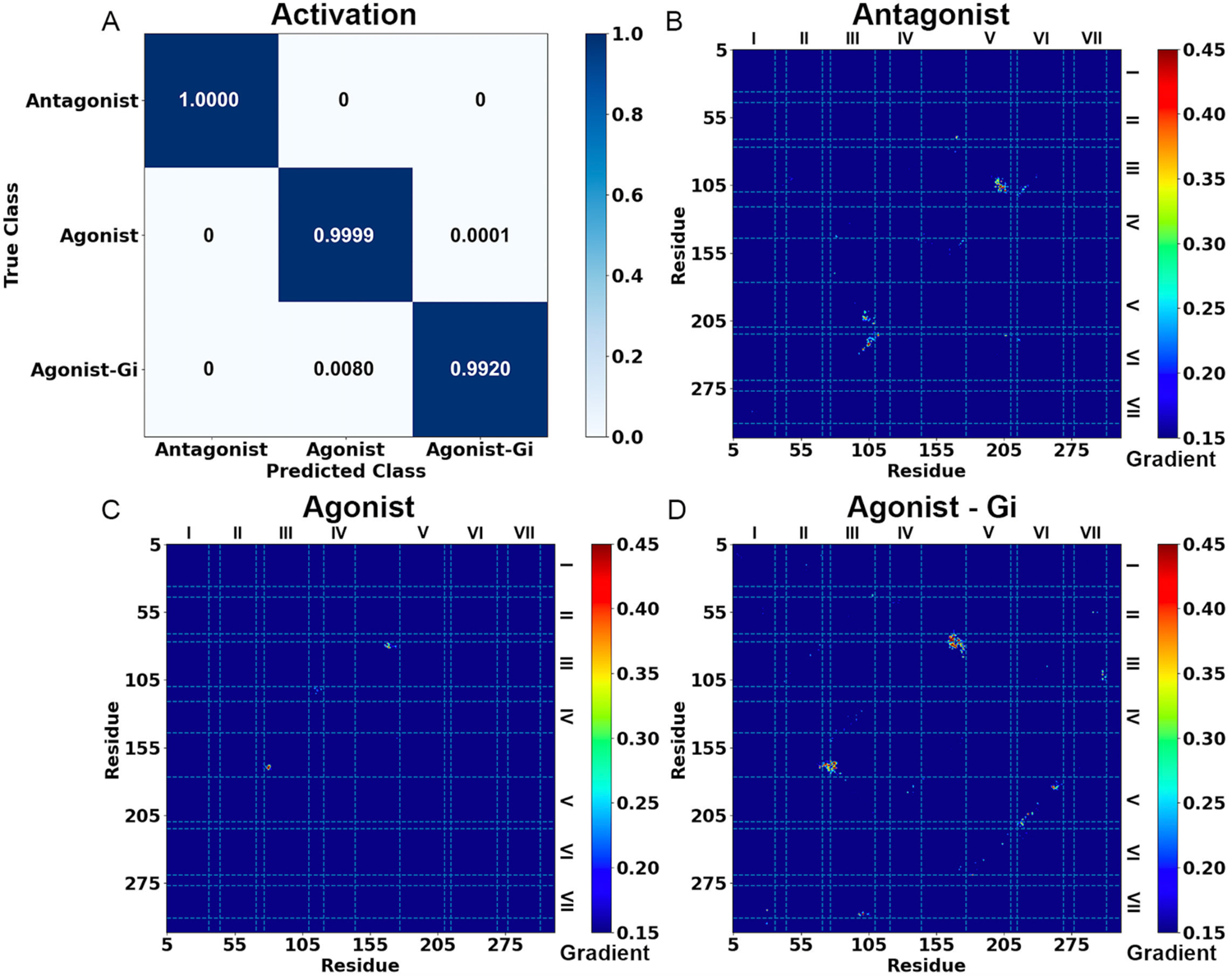
(A) Classification of different A1AR systems bound by the “Antagonist”, “Agonist” and “Agonist – Gi”. (B-D) Saliency (attention) maps of residue contact gradients of the A1AR bound by (B) “Antagonist”, (C) “Agonist” and (D) “Agonist – Gi”. The seven transmembrane helices are labeled from I to VII. The gradient of each residue contact is shown in a 0.15 (blue) to 0.45 (red) color scale.
Figure 5. Demonstration of GLOW on characterization of GPCR allosteric modulation using adenosine A1 receptor (A1AR) as a model system.
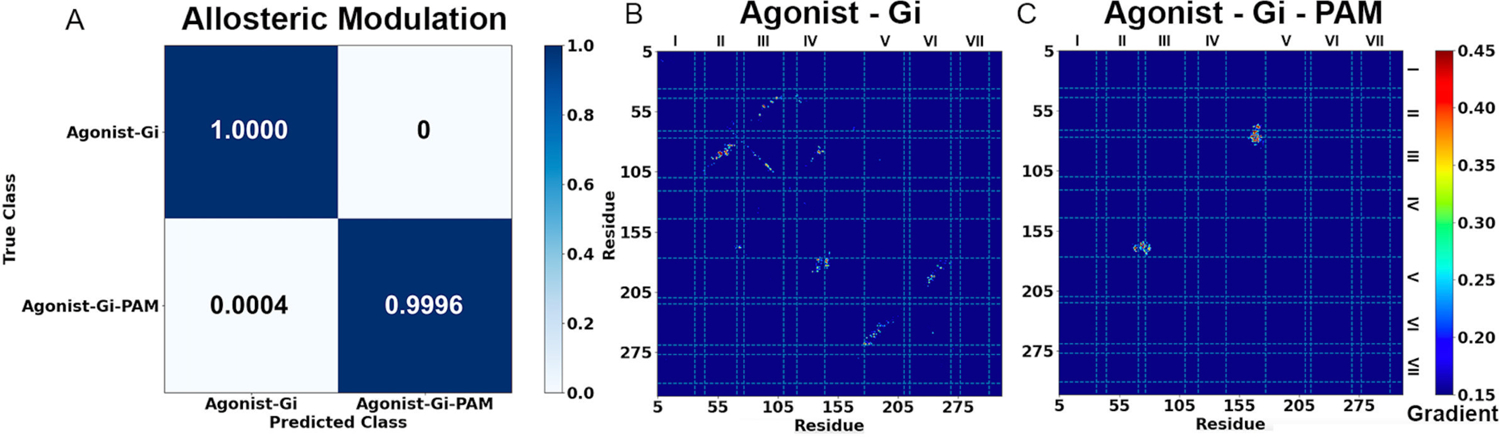
(A) Classification of different A1AR systems bound by the “Agonist – Gi” and “Agonist – Gi – PAM”. (B-C) Saliency (attention) maps of residue contact gradients of the A1AR bound by (B) “Agonist – Gi” and (C) “Agonist – Gi – PAM”. The seven transmembrane helices are labeled from I to VII. The gradient of each residue contact is shown in a 0.15 (blue) to 0.45 (red) color scale.
Results
We obtained dual-boost GaMD simulations on four systems of the A1AR bound by the “Antagonist”, “Agonist”, “Agonist – Gi” and “Agonist – Gi – PAM” (Table S1). GaMD simulations recorded similar averages and standard deviations (SDs) of the added boost potentials, i.e., 15.07 ± 4.53 kcal/mol for the Antagonist – A1AR, 17.07 ± 5.01 kcal/mol for the Agonist – A1AR, 18.32 ± 6.29 kcal/mol for the Agonist – A1AR – Gi and 20.53 ± 6.54 kcal/mol for the Agonist – A1AR – Gi – PAM complex, respectively. The residue contact map of every 10 simulation frames was extracted and transformed into an image. We then built a 2D CNN for each system. The saliency (attention) maps of residue contact gradients of the most populated structural clusters were used to infer characteristic residue contacts in activation and allosteric modulation of the A1AR. The complete lists of important residue contacts (whose gradients were ≥0.4 from pixel backpropagation) are summarized in Table S2 for activation and Table S3 for allosteric modulation.
Characterization of GPCR activation with GLOW
Classification of the A1AR bound by “Antagonist”, “Agonist” and “Agonist – Gi” by GLOW is depicted in Figure 2. The overall accuracy achieved on the validation set after 15 epochs was 0.9934, while the overall loss was 0.0185 (Figure S1). Among the 30,000 frames for validation of each system, GLOW accurately classified most of them, including all 30,000 frames of “Antagonist” bound A1AR, 29,997 frames of “Agonist” bound A1AR and 29,760 frames of “Agonist – Gi” bound A1AR, respectively. Only a marginal portion of the frames were inaccurately categorized. Specifically, ~0.01% (3 frames) of “Agonist” bound A1AR were predicted to be “Agonist – Gi” bound A1AR, and ~0.8% (240 frames) of “Agonist – Gi” bound A1AR were predicted to be “Agonist” bound A1AR (Figure 2A).
The pixel-attributed residue contact gradient maps of the most populated A1AR clusters bound by “Antagonist”, “Agonist” and “Agonist – Gi” are shown in Figures 2B – 2D, respectively, and S2. Overall, the characteristic residue contacts of “Antagonist” bound A1AR were located between TM2 – ECL2, TM3 – TM5, TM3 – TM6 and ICL2 – TM6 (Figures 2B and S2A). The characteristic residue contacts of “Agonist” bound A1AR were between TM3 – ECL2 (Figures 2C and S2B), whilst of “Agonist – Gi” bound A1AR were between TM1 – TM7, TM2 – ECL2, ECL1 – ECL2, TM3 – ECL2, TM3 – TM7 and TM5 – TM6 (Figures 2D and S2C, and Table S2). We selected 5 pairs of characteristic residues from different receptor domains as RCs for 2D free energy profiling, including G2.67 – K168ECL2, Y3.21 – I167ECL2, R3.53 – E6.30, R3.50 – Y7.53 and E5.60 – Y7.53 (Figures 3 and S3). Their distances in available experimental structures (PDB: 5N2S, 5UEN and 6D9H)85, 86, 94 are summarized in Table S4 for reference. The time courses of characteristic residue contacts in the A1AR activation are plotted in Figure S4.
Figure 3. 2D free energy profiles of characteristic residue contacts in the A1AR activation.
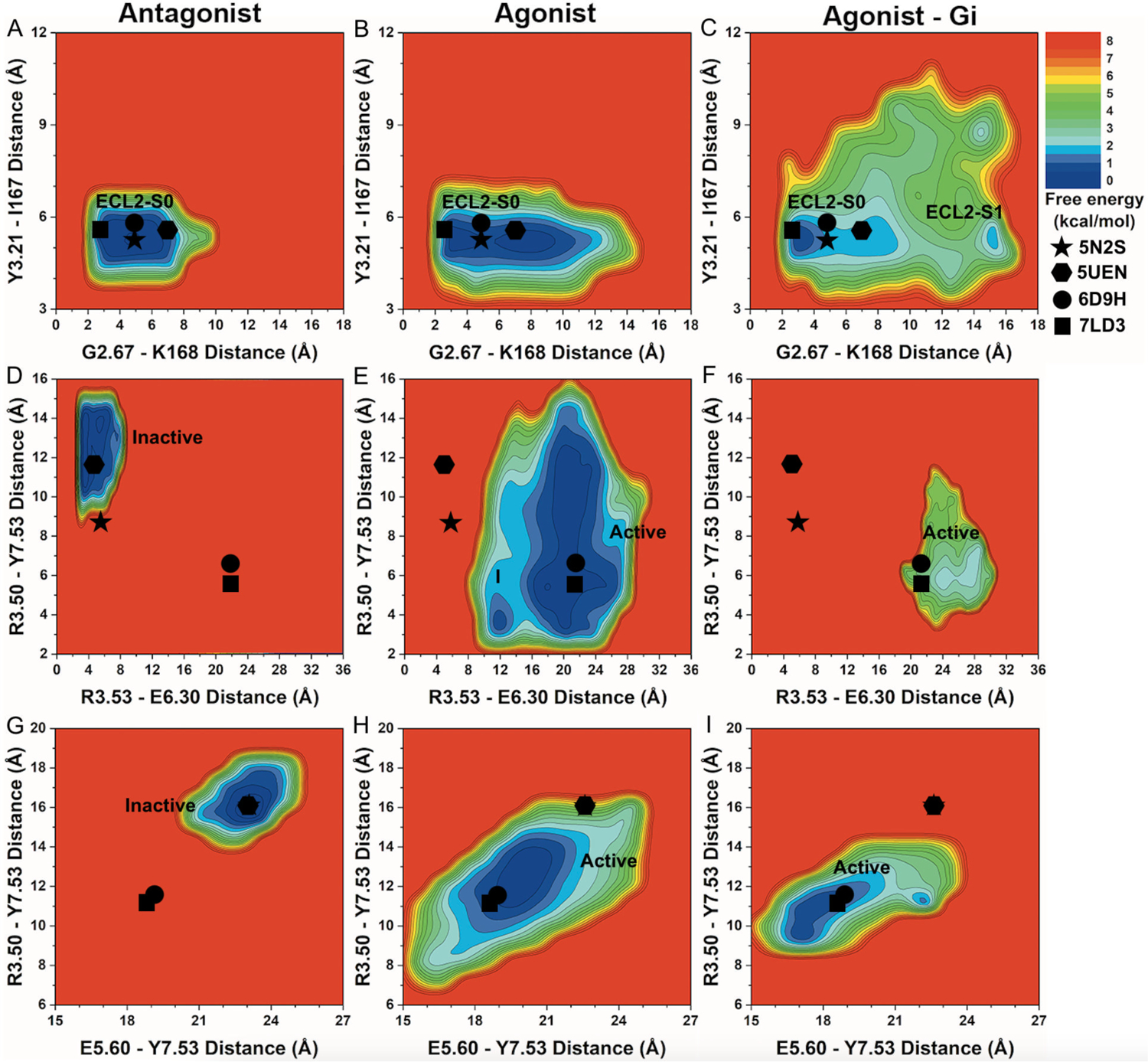
(A-C) 2D free energy profiles of the distance between residue G2.67 atom O and residue K168ECL2 atom NZ and distance between residue Y3.21 atom O and residue I167ECL2 atom N of the A1AR bound by (A) “Antagonist”, (B) “Agonist” and (C) “Agonist – Gi”. (D-F) 2D free energy profiles of the distance between charge centers of residue R3.53 (atom CZ) and residue E6.30 (atom CD) and distance between residue R3.50 atom CZ and residue Y7.53 atom OH of the A1AR bound by (D) “Antagonist”, (E) “Agonist” and (F) “Agonist – Gi”. (G-I) 2D free energy profiles of the distance between residue E5.60 atom CA and residue Y7.53 atom CA and distance between residue R3.50 atom CA and residue Y7.53 atom CA of the A1AR bound by (G) “Antagonist”, (H) “Agonist” and (I) “Agonist – Gi”. The low-energy ECL2 conformational state corresponding to the 5N2S, 5UEN, 6D9H and 7LD3 PDB structures is labeled “ECL2-S0”. The low-energy TM intracellular state corresponding to the inactive 5N2S and 5UEN PDB structures is labeled “Inactive” and “Active” for the active 6D9H and 7LD3 PDB structure. New low-energy receptor conformational states are labeled “ECL2-S1” in (C) and “I” in (E). The 5N2S, 5UEN, 6D9H and 7LD3 PDB structures of the A1AR are mapped to the free energy surface as star, hexagon, circle and rectangle, respectively.
Free energy calculations showed that the low-energy “ECL2 – S0” conformational state in the A1AR bound by “Antagonist” was located at ~3–7Å distance between G2.67 – K168ECL2 and ~5–6Å distance between Y3.21 – I167ECL2 (Figure 3A). In the A1AR bound by “Agonist”, the distance between residues G2.67 – K168ECL2 sampled a broader energy well (Table 1). In the A1AR bound by “Agonist – Gi”, the conformational space of receptor ECL2 expanded significantly (Figure 3B and Table 1). One low-energy conformational state was identified at ~3–4Å distance between G2.67 – K168ECL2 and ~5–6Å distance between Y3.21 – I167ECL2, being similar to the experimental structures. A new low-energy state, namely “ECL2 – I1”, was uncovered at ~15–16Å distance between G2.67 – K168ECL2 and ~5–6Å distance between Y3.21 – I167ECL2 (Figure 3C).
Table 1.
Distances between selected characteristic residue pairs in the A1AR bound by “Antagonist”, “Agonist” and “Agonist-Gi” for the A1AR activation.
| Residue contacts | “Antagonist” (Å) | “Agonist” (Å) | “Agonist-Gi” (Å) |
|---|---|---|---|
| G2.67 – K168ECL2 | 2 – 10 | 2 – 15 | 2 – 17 |
| Y3.21 – I167ECL2 | 4 – 7 | 3 – 7 | 3 – 11 |
| R3.53 – E6.30 | 2 – 8 | 8 – 30 | 18 – 30 |
| R3.50 – Y7.53 sidechains | 9 – 15 | 2 – 16 | 3 – 12 |
| R3.50 – Y7.53 backbone | 14 – 19 | 7 – 16 | 9 – 14 |
| E5.60 – Y7.53 | 20 – 25 | 15 – 25 | 15 – 24 |
In addition, the “Inactive” low-energy conformational state in the A1AR bound by “Antagonist” was restricted at ~4–8Å distance between residues R3.53 – E6.30 and ~10–15Å distance between residues R3.50 – Y7.53 (Figure 3D). In the A1AR bound by “Agonist – Gi”, the “Active” low-energy state was identified at ~20–30Å distance between R3.53 – E6.30 and ~4–12Å distance between R3.50 – Y7.53 (Figure 3F). Upon removal of the Gi protein, the “Agonist” bound A1AR underwent deactivation with large conformational changes in the TM6 and TM7 intracellular domains. A new intermediate low-energy conformational state “I” was revealed at ~12Å distance between R3.53 – E6.30 and ~3–4Å distance between R3.50 – Y7.53 (Figure 3E).
Finally, a distance of ~22–24 Å between residues E5.60 – Y7.53 and ~15–17 Å between residues R3.50 – Y7.53 constituted the “Inactive” low-energy conformational state in the A1AR bound by “Antagonist” (Figure 3G). In the A1AR bound by “Agonist – Gi”, the “Active” low-energy conformational state was identified at ~17–19Å distance between E5.60 – Y7.53 and ~9–12Å distance between R3.50 – Y7.53 (Figure 3I). The A1AR bound by “Agonist” after removal of the Gi2 protein, again, transitioned towards the “Inactive” state (Figure 3H and Table 1). The “Active” low-energy conformational state was identified at ~19–21Å distance between E5.60 – Y7.53 and ~11–14Å distance between R3.50 – Y7.53.
Low-energy conformational states identified for GPCR activation
Two new low-energy conformational states, namely “ECL2 – S1” (Figure 3C) and “I” (Figure 3E), were uncovered for the A1AR bound by “Agonist – Gi” and “Agonist”, respectively. The low-energy conformational state “ECL2 – S1” was compared to the cryo-EM structure of active agonist – Gi – bound A1AR (PDB: 6D9H) (Figure 4A). In this state, the distance between residues Y3.21 – I167ECL2 was ~4 Å and comparable to the “Active” conformational state in the 6D9H cryo-EM structure, whilst the distance between residues G2.67 – K168ECL2 increased from ~5.0 Å in the “Active” state to ~16.0 Å due to significant outward movement of the TM2 extracellular domain. In the intermediate low-energy conformational state “I” (Figure 4B), the distance between residues R3.53 – E6.30 decreased from ~21.5 Å in the “Active” state to ~12 Å due to inward movement of the TM6 intracellular domain, whereas the distance between residues R3.50 – Y7.53 only decreased slightly from ~6.3 Å in the “Active” state to ~4.0 Å in the intermediate state “I” (Figures 4B and 3E).
Figure 4. Low-energy conformational states of the A1AR during activation uncovered by GLOW.
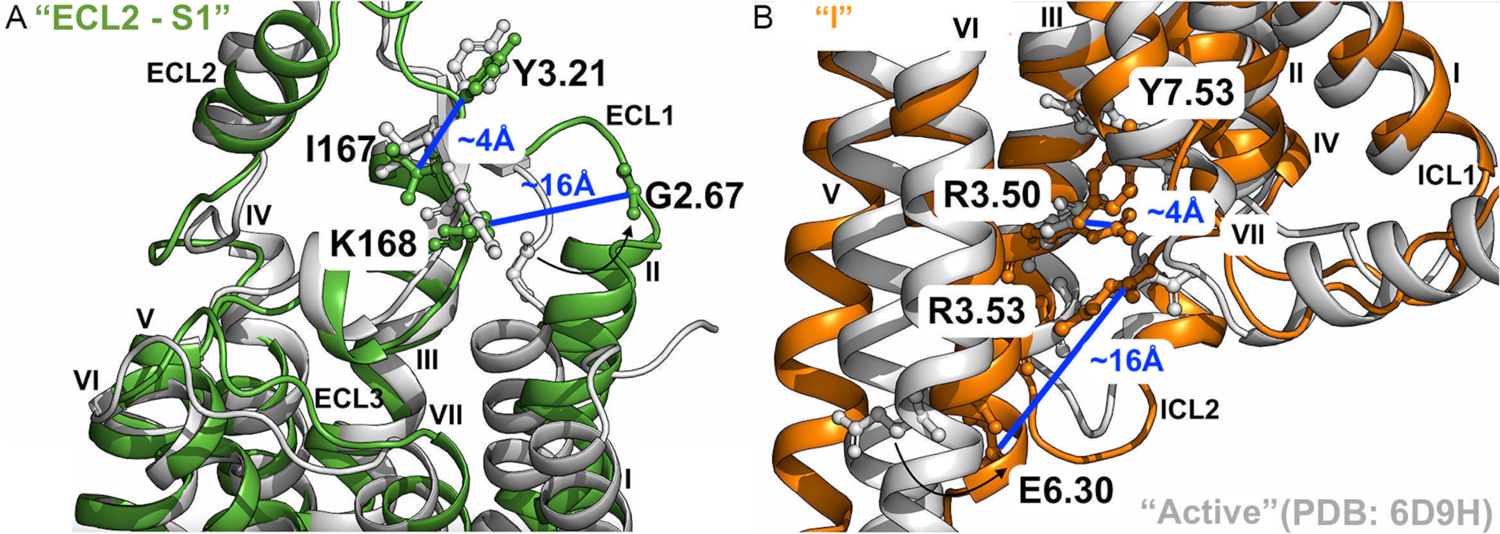
(A) Low-energy conformational state “ECL2 – S1” (Figure 3C) compared to the active 6D9H PDB structure. The distance between residues G2.67 and K168ECL2 is ~16Å, and ~4Å between residues Y3.21 and I167ECL2. (B) Low-energy conformational state “I” (Figures 3E) compared to the active 6D9H PDB structure. The distance between residues R3.53 and E6.30 is ~12Å, and ~4Å between residues R3.50 and Y7.53. The A1AR bound by “Agonist” and “Agonist – Gi” are colored orange and green, respectively, and the 6D9H PDB structure is colored gray.
Characterization of the GPCR allosteric modulation with GLOW
Classification of the A1AR bound by “Agonist – Gi” and “Agonist – Gi – PAM” by GLOW is shown in Figure 5A. The overall accuracy and loss reached 0.9927 and 0.0178, respectively (Figure S1). All 30,000 frames and 29,988 frames of the A1AR bound by “Agonist – Gi” and “Agonist – Gi – PAM” were correctly classified, respectively. Only 12 frames (~0.04%) of the A1AR bound by “Agonist – Gi – PAM” were wrongly predicted to be A1AR bound by “Agonist – Gi” (Figure 5A).
The pixel-attributed residue contact gradient maps of A1AR bound by “Agonist – Gi” and “Agonist – Gi – PAM” are shown in Figures 5B – 5C, respectively, and S5. In the A1AR bound by “Agonist – Gi”, characteristic residue contacts were identified between TM2 – TM3, ECL1 – ECL2, TM3 – TM4, ECL2 – ECL2, ECL2 – TM5 and TM5 – TM6 (Figures 5B and S5A), while in the A1AR bound by “Agonist – Gi – PAM”, the characteristic residue contacts were located between TM2 – ECL2, ECL1 – ECL2 and TM3 – ECL2 (Figures 5C and S5B, and Table S3). We selected 5 characteristic residue contacts from different receptor domains as RCs to calculate free energy profiles from GaMD simulations, including G2.67 – K168ECL2, Y3.21 – I167ECL2, P23.50ECL1 – K168ECL2, N148ECL2 – V152ECL2 and W146ECL2 – E5.36 (Figures 6 and S6). Their distances in the experimental PDB structures (PDB: 5N2S, 5UEN, 6D9H and 7LD3)85, 86, 94 are summarized in Table S5 for reference. The time courses of characteristic residue contacts in the A1AR allosteric modulation are plotted in Figure S7.
Figure 6. 2D free energy profiles of characteristic residue contacts in A1AR allosteric modulation.
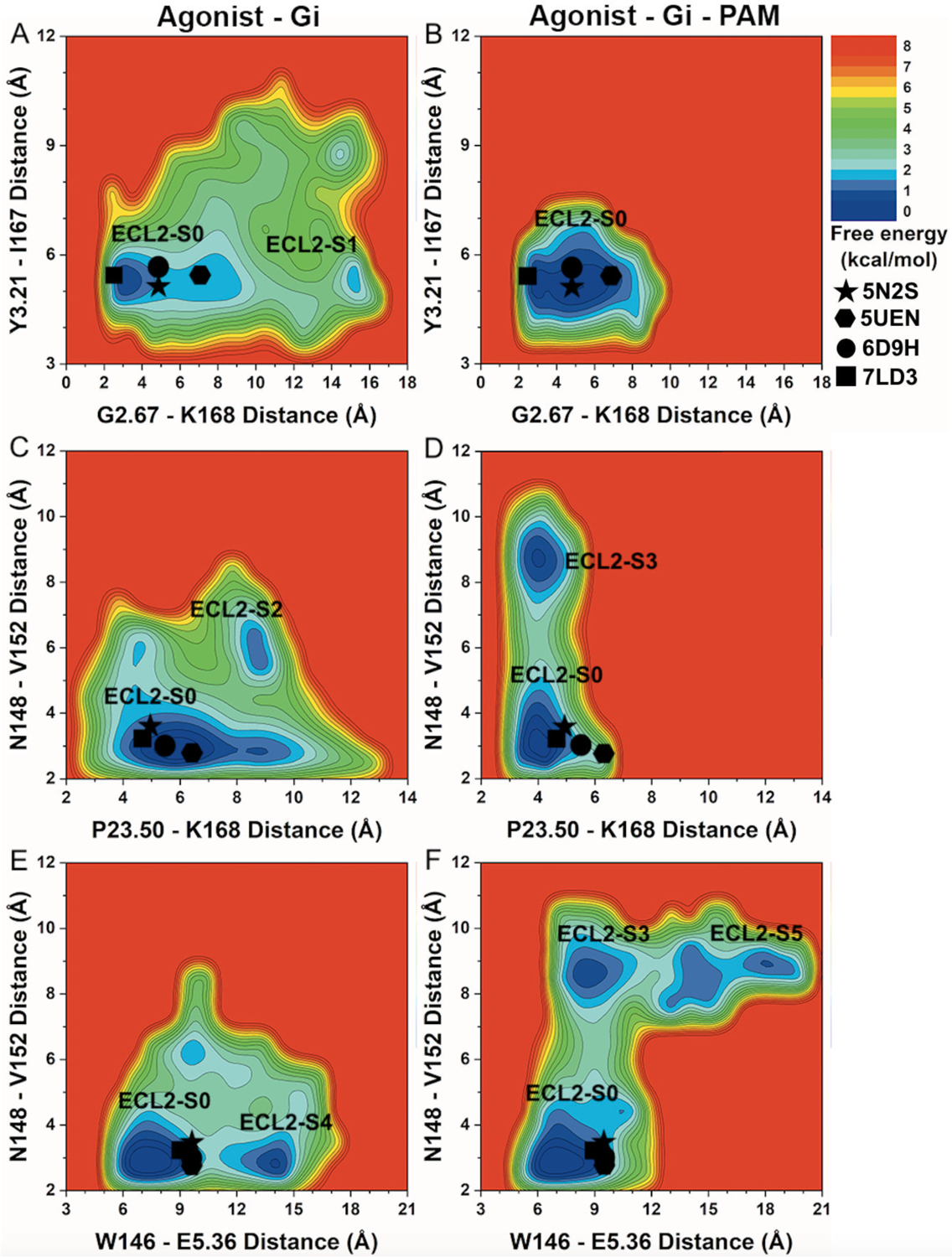
(A-B) 2D free energy profiles of the distance between residue G2.67 atom O and residue K168ECL2 atom NZ and distance between residue Y3.21 atom O and residue I167ECL2 atom N of the A1AR bound by (A) “Agonist – Gi” and (B) “Agonist – Gi – PAM”. (C-D) 2D free energy profiles of the distance between residue P23.50ECL1 atom O and residue K168ECL2 atom N and distance between residue N148ECL2 atom O and residue V152ECL2 atom N of the A1AR bound by (C) “Agonist – Gi” and (D) “Agonist – Gi – PAM”. (E-F) 2D free energy profiles of the distance between residue W146ECL2 atom CA and residue E5.36 atom CA and distance between residue N148ECL2 atom O and residue V152ECL2 atom N of the A1AR bound by (E) “Agonist – Gi” and (F) “Agonist – Gi – PAM”. The low-energy ECL2 conformational state corresponding to the 5N2S, 5UEN, 6D9H and 7LD3 PDB structures is labeled “ECL2-S0”. New low-energy receptor conformational states are labeled “ECL2-S1” in (A), “ECL2-S2” in (C), “ECL2-S3” in (D and F), “ECL2-S4” in (E), and “ECL2-S5” in (F). The 5N2S, 5UEN, 6D9H and 7LD3 PDB structures of the A1AR are mapped to the free energy surface as star, hexagon, circle and rectangle, respectively.
PAM binding greatly reduced conformational space of the agonist – Gi bound A1AR in 2D free energy profiles of the distances between residues G2.67 – K168ECL2 and Y3.21 – I167ECL2 (Figures 6A and 6B, and Table 2). Two low-energy conformational states were observed in the A1AR bound by “Agonist – Gi”, including “ECL2 – S0” and “ECL2 – S1” (Figure 6A), whereas the A1AR bound by “Agonist – Gi – PAM” adopted only one low-energy conformational state (“ECL2 – S0”), at ~3–7Å distance between residues G2.67 – K168ECL2 and ~5–6Å distance between residues Y3.21 – I167ECL2 (Figure 6B).
Table 2.
Distances between selected characteristic residue pairs in the A1AR bound by “Agonist-Gi” and “Agonist-Gi-PAM” for the A1AR allosteric modulation.
| Residue contacts | “Agonist-Gi” (Å) | “Agonist-Gi-PAM” (Å) |
|---|---|---|
| G2.67 – K168ECL2 | 2 – 17 | 2 – 10 |
| Y3.21 – I167ECL2 | 3 – 11 | 3 – 7 |
| P23.50ECL1 – K168ECL2 | 2 – 13 | 3 – 7 |
| N148ECL2 – V152ECL2 | 2 – 9 | 2 – 11 |
| W146ECL2 – E5.36 | 5 – 18 | 4 – 21 |
Further free energy profiling showed that the distance range between P23.50ECL1 – K168ECL2 decreased from the A1AR bound by “Agonist – Gi” to the A1AR bound by “Agonist – Gi – PAM” (Figures 6C and 6D, and Table 2). However, the distance range between residues N148ECL2 – V152ECL2 increased (Table 2). The low-energy conformational state “ECL2 – S0” was identified in the A1AR bound by “Agonist – Gi” and “Agonist – Gi – PAM”, respectively. Two new low-energy conformational states, namely “ECL2 – S2” and “ECL2 – S3”, were uncovered in the A1AR bound by “Agonist – Gi” and “Agonist – Gi – PAM”, respectively. The low-energy state “ECL2 – S2” of the A1AR exhibited ~9Å distance between P23.50ECL1 – K168ECL2 and ~5–7Å distance between N148ECL2 – V152ECL2 (Figure 6C). The low-energy state “ECL2 – S3” of the A1AR induced by PAM binding showed ~3–5Å and ~8–9Å distances between P23.50ECL1 – K168ECL2 and N148ECL2 – V152ECL2, respectively (Figure 6D).
Finally, the distance range between W146ECL2 – E5.36 increased upon PAM binding (Figures 6E and 6F, and Table 2). Besides the low-energy conformational state “ECL2 – S0”, new low-energy states “ECL2 – S4” and “ECL2 – S5” were revealed in the A1AR bound by “Agonist – Gi” and “Agonist – Gi – PAM”, respectively. The low-energy state “ECL2 – S0” showed ~6–9Å and ~2.5–3.5Å distances between W146ECL2 – E5.36 and N148ECL2 – V152ECL2, respectively, in the A1AR bound by “Agonist – Gi” and “Agonist – Gi – PAM”. In the A1AR bound by “Agonist – Gi”, the low-energy state “ECL2 – S4” showed ~13–14Å and ~2.5–3Å distances between residues W146ECL2 – E5.36 and N148ECL2 – V152ECL2, respectively (Figure 6E). The “ECL2 – S3” state of the A1AR bound by “Agonist – Gi – PAM” (Figure 6D) showed ~8–9Å distance between W146ECL2 – E5.36 and ~8–9Å distance between N148ECL2 – V152ECL2 (Figure 6F). While the distance between residues N148ECL2 – V152ECL2 remained similar, the distance between residues W146ECL2 – E5.36 increased to ~17–20 Å in the “ECL2 – S5” state of the A1AR induced by PAM binding (Figure 6F).
Low-energy conformational states relevant to GPCR allosteric modulation
Apart from the “ECL2 – S1” conformational state shown in Figure 4A, four additional low-energy states of the ECL2 were found relevant to allosteric modulation of the A1AR, including “ECL2 – S2” (Figure 6C), “ECL2 – S3” (Figure 6D), “ECL2 – S4” (Figure 6E) and “ECL2 – S5” (Figure 6F). In the absence of PAM, the receptor was able to sample the “ECL2 – S1”, “ECL2 – S2” and “ECL2 – S4” conformational states (Figures 6A, 6C and 6E). Binding of the MIPS521 PAM, however, biased the receptor to sample distinct conformational states, including the “ECL2 – S3” and “ECL2 – S5” (Figures 6D and 6F). These conformations were compared to the 6D9H cryo-EM structure of agonist – Gi bound A1AR and 7LD3 cryo-EM structure of agonist – Gi – PAM bound A1AR (“ECL2 – S0”) in Figure 7. In the “ECL2 – S2” state of the A1AR bound by “Agonist – Gi”, the receptor ECL1 and ECL2 exhibited significant conformational changes relative to the 6D9H structure. The distance between residues P23.50ECL1 – K168ECL2, N148ECL2 – V152ECL2 and W146ECL2 – E5.36 shifted to ~9 Å, ~6 Å and ~7 Å, respectively (Figure 7A). In the “ECL2 – S3” state induced by PAM binding, the distance between residues P23.50ECL1 – K168ECL2 and W146ECL2 – E5.36 were comparable to those in the “ECL2 – S0” structure, whereas the distance between N148ECL2 – V152ECL2 increased to ~9 Å (Figures 7B and 6D). In the “ECL2 – S4” state of the A1AR without PAM, the distances between P23.50ECL1 – K168ECL2 and N148ECL2 – V152ECL2 were similar to those in the 6D9H PDB structure, but the distance between W146ECL2 – E5.36 increased to ~13 Å (Figures 7C and 6E). In the “ECL2 – S5” state of the A1AR with PAM bound, the distances between residues P23.50ECL1 – K168ECL2 and N148ECL2 – V152ECL2 were the same as in the “ECL2 – S3” state, but the distance between residues W146ECL2 – E5.36 increased to ~19 Å (Figures 7D and 6F). Therefore, the highly flexible ECL2 appeared to play an important role in allosteric modulation of the A1AR.
Figure 7. Low-energy conformational states of the A1AR induced by PAM binding uncovered by GLOW.
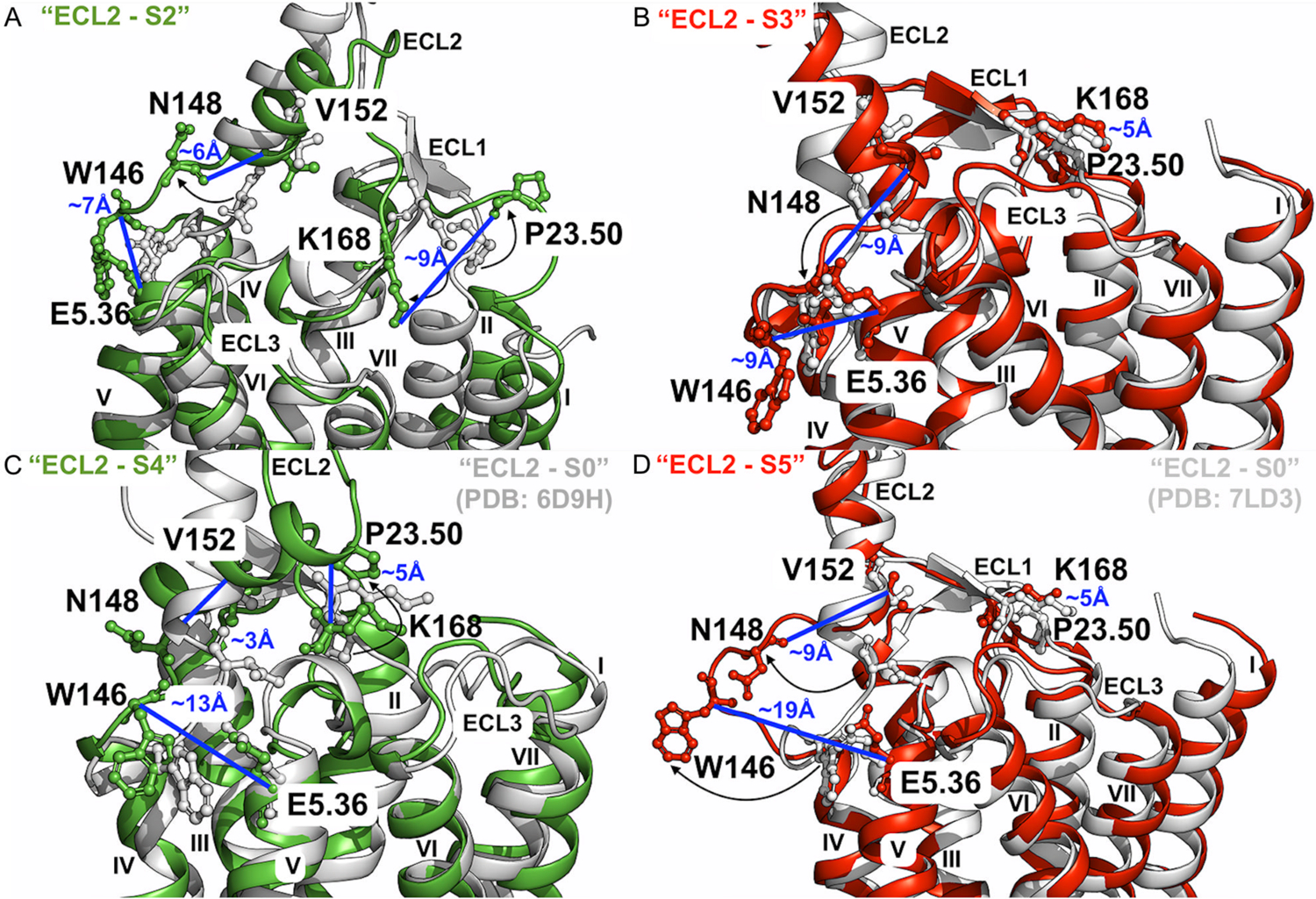
(A) Low-energy conformational state “ECL2 – S2” (Figure 6C) compared to the active 6D9H PDB structure. The distance between residues P23.50ECL1 and K168ECL2 is ~9Å, ~6Å between residues N148ECL2 and V152ECL2, and ~7Å between residues W146ECL2 and E5.36. (B) Low-energy conformational state “ECL2 – S3” (Figures 6D and 6F) compared to the active 7LD3 PDB structure. The distance between residues P23.50ECL1 and K168ECL2 is ~5Å, ~9Å between residues N148ECL2 and V152ECL2, and ~9Å between residues W146ECL2 and E5.36. (C) Low-energy conformational state “ECL2 – S4” (Figure 6E) compared to the active 6D9H PDB structure. The distance between residues P23.50ECL1 and K168ECL2 is ~5Å, ~3Å between residues N148ECL2 and V152ECL2, and ~13Å between residues W146ECL2 and E5.36. (D) Low-energy conformational state “ECL2 – S5” (Figure 6F) compared to the active 7LD3 PDB structure. The distance between residues P23.50ECL1 and K168ECL2 is ~5Å, ~9Å between residues N148ECL2 and V152ECL2, and ~19Å between residues W146ECL2 and E5.36. The A1AR bound by “Agonist – Gi” and “Agonist – Gi – PAM” are colored green and red, and the 6D9H and 7LD3 PDB structure are colored gray and silver, respectively.
Discussion
In this study, we have presented GLOW – a workflow that integrated GaMD and DL for free energy profiling of biomolecules. The residue contact maps of GaMD trajectories have been successfully classified by DL to identify RCs for mapping free energy profiles. In addition, we have demonstrated the ability of GLOW to characterize both activation and allosteric modulation of a GPCR. GLOW has, for the first time, enabled combining ML and MD for modeling of GPCR allosteric modulation. GLOW has allowed us to map free energy landscapes and identify important low-energy conformational states of the A1AR model system.
We performed two additional, independent Deep Learning analyses, where residue contact maps were randomly selected for model training and validation of each A1AR system to determine the precision of GLOW. GLOW classified most of the simulation frames in validation of each system with closely similar accuracies in the two new models (“Model 2” and “Model 3”) compared with the original “Model 1”. For the characterization of the A1AR activation, GLOW accurately classified 100% of the simulation frames of the A1AR bound by “Antagonist” in all three models. For the A1AR bound by “Agonist”, the corresponding accuracies were 99.99%, 99.91% and 99.87% in the three DL models. The accuracies were 99.20%, 99.73% and 96.73% for the A1AR bound by “Agonist-Gi-PAM”. For the characterization of the A1AR allosteric modulation, GLOW accuracies were 100%, 100% and 99.99% for the A1AR bound by “Agonist-Gi”, and 99.96%, 99.90% and 99.69% for the A1AR bound by “Agonist-Gi-PAM” (Figure S8). The saliency (attention) maps of residue contact gradients obtained from the three independent DL models were also mostly similar for each A1AR system (Figure S8), despite certain variations in attention maps of the “Agonist” and “Agonist-Gi” bound A1AR due to residue conformational changes during GaMD simulations of these systems (Figures S4 and S7). Therefore, independent DL analyses with random assignment of residue contact maps to training and validation datasets does not result in significantly different model accuracies and attention maps.
Removal of the Gi2 protein from the A1AR bound by “Agonist – Gi protein” led to the deactivation of the A1AR. The intracellular halves of TM3, TM5, TM6 and TM7 underwent significant conformational changes. TM6 drew closer to TM3, while TM7 moved away from TM3 and TM5 (Figures 3E – 3F and 3H – 3I). The receptor TM5 and TM6 intracellular domains and helix 8 also became more flexible in the absence of Gi2 protein (Figure S9). Furthermore, an intermediate state “I” was sampled during deactivation, being consistent with previous studies of activation and deactivation of class A GPCRs43, 59, 95–98. Deactivation of the class A GPCR upon removal of the G protein was found to involve conformational changes of TM6, the R3.50 – E6.30 ionic lock and the NPxxY motif in the TM7 intracellular domain96. This was consistent with previous MD simulation findings43, 59, 95–98. The intermediate state “I” of “Agonist” bound A1AR revealed by GLOW was only different from the 6D9H cryo-EM structure in the position of TM6 intracellular end, which shifted inwards by ~12 Å (Figures 4B and 3E). Replacement of the “Agonist” with “Antagonist” in A1AR led to the complete closure of the intracellular pocket, in which TM3 formed intracellular residue contacts with TM6 with the R3.53 – E6.30 distance reduced to ~5 Å, and the NPxxY motif in TM7 moved away from TM3 and TM5 (Figures 3D and 3G).
The ligand-binding extracellular domains and intracellular G-protein binding domains were found to be loosely coupled in GPCR activation59. The ECL2 was revealed to be flexible in the active “Agonist – Gi” bound A1AR and played an important role in activation of the A1AR73, 74, 77, 99 (Figure 3C). A1AR even sampled a more “open” conformational state (“ECL2 – S1”) of the extracellular mouth in the “Agonist-Gi” bound system during GaMD simulations, due to mostly increased flexibility of the ECL1 and ECL2 (Figure S9). The “ECL2 – S1” conformation was similar to the cryo-EM structure of “ECL2 – S0” state, with the difference of ~11Å outward movement of the TM2 extracellular domain (Figures 4A and 3C). In comparison, removal of the Gi2 protein from the Agonist-Gi-A1AR complex reduced conformational space of the receptor ECL2 (Figure 3B). Finally, replacement of “Agonist” by “Antagonist” stabilized ECL2 in a narrow energy well corresponding to the X-ray and cryo-EM structures of the A1AR (Figure 3A).
The focus of this study was to determine conformational changes of the A1AR during activation and allosteric modulation. Therefore, we included only residues from the receptor in the contact maps for analysis, not the ligands such as the PAM. The PAM interacting residues apparently formed similar contacts with the surrounding receptor residues in the absence and presence of the PAM, and thus were not picked in the ML model. Notably, binding of the PAM did not change the structure of agonist-Gi-bound A1AR as shown in the previous study42. Structural dynamics of the GPCR-G protein interface has been analyzed in our previous study42. With the DL analyses, characteristic residue contacts such as T2.39-D3.49 (“Model 1”), A12.49ICL1-Y3.51, R12.51ICL1-R3.53, D2.37-R3.50, A2.38-D3.49, T2.39-T4.38 (“Model 2”) and T2.39-R3.53 (“Model 3”) were also identified in the intracellular domains at the G protein-coupling interface of the A1AR during allosteric modulation (Figures 5 and S8). In addition, GLOW showed that ECL2 played a critical role in the allosteric modulation of A1AR, being consistent with previous mutagenesis, structure and molecular modeling studies42, 73–76. Structural analysis alone could not tell the differences in this region between the A1AR bound by “Agonist – Gi” and “Agonist – Gi – PAM” (Table S5 and Figure 6). GLOW revealed that the binding of a PAM to the agonist-Gi-A1AR complex biased the receptor conformational ensemble, especially in the ECL2 and ECL1 regions (Figures 6 and 7). Indeed, mutations in ECL2 were found to influence binding affinity and efficacy of both the orthosteric and allosteric ligands, as well as their binding and functional cooperativities42, 73–77. PAM binding stabilized agonist binding within the orthosteric pocket of A1AR, thus leading to the observed confined states of the extracellular mouth. Furthermore, PAM binding was able to disrupt the N148ECL2 – V152ECL2 α-helical hydrogen bond and distort this portion of the ECL2 helix. The tri-alanine mutation of NLL(147–149)ECL2 by Peeters et al.74 increased the EC50 of an agonist by more than 100 folds, suggesting the critical role of this particular region in the activation and allosteric modulation of A1AR. Nguyen et al.75 also found that mutation of N148ECL2 significantly changed the binding affinity and efficacy of an allosteric ligand to A1AR. The distortion of ECL2 helix resulted in formation of the “ECL2 – S3” and “ECL2 – S5” conformational states (Figures 6D and 6F). These two states were similar to each other, with the only difference in the relative position of ECL2 to the TM5 extracellular domain. Whilst the receptor sampled a complete closure of the extracellular mouth in the “ECL2 – S3” state with ECL2 in proximity with TM5 extracellular domain76 (Figures 7B and 6D), a small pocket was formed in the ECL2 – TM5 – ECL3 region because of the conformational change of ECL2 in the “ECL2 – S5” state (Figures 7D and 6F). These observations were consistent with the finding by Nguyen et al.75 that mutation of W146ECL2 decreased the cooperativity between the allosteric and orthosteric ligands, illustrating the importance of this particular residue in the allosteric modulation of A1AR. A number of other “intermediate” low-energy conformational states, including “ECL2 – S1”, “ECL2 – S2” and “ECL2 – S4, were also identified by GLOW. The “intermediate” low-energy conformational states identified from free energy profiles appeared to result from binding of Gi2 protein and MIPS521 to the A1AR. As described in the previous study42, binding of the MIPS521 PAM to the extrahelical lipid-facing pocket formed by TM1-TM6-TM7 helices of the A1AR stabilized the receptor-G protein complex by increasing agonist binding affinity and reducing receptor-G protein mobility42. Furthermore, since ECL2 was previously suggested to play an important role in agonist binding and allosteric modulation of A1AR, the “intermediate” states identified from this study have provided further mechanistic insights into the functional mechanism of ECL2. In general, GLOW findings were consistent with previous experimental and computational studies, while also provided further insights into the mechanisms of activation and allosteric modulation of a model GPCR.
In summary, we have integrated GaMD enhanced sampling and DL in GLOW, a workflow that enables calculations of free energy profiles for DL-predicted RCs with high accuracy. The GLOW workflow and its user manual can be downloaded at http://miaolab.org/GLOW. GLOW provides a systematic approach to mapping free energy landscapes of biomolecules.
Supplementary Material
Acknowledgements
We thank Anh Nguyen and Lauren May for valuable discussions. This work used supercomputing resources with allocation award TG-MCB180049 through the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI-1548562, and project M2874 through the National Energy Research Scientific Computing Center (NERSC), which is a U.S. Department of Energy Office of Science User Facility operated under Contract No. DE-AC02-05CH11231, and the Research Computing Cluster at the University of Kansas. This work was supported in part by the National Institutes of Health (R01GM132572) and the startup funding in the College of Liberal Arts and Sciences at the University of Kansas.
Footnotes
Supporting Information
Figures S1–S9 and Table S1–S5 are provided in the Supporting Information. This information is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.Karplus M; McCammon JA, Molecular dynamics simulations of biomolecules. Nature Structural Biology 2002, 9 (9), 646–652. [DOI] [PubMed] [Google Scholar]
- 2.Hollingsworth S; Dror R, Molecular dynamics simulation for all. Neuron 2018, 99, 1129–43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Wang J; Arantes P; Bhattarai A; Hsu R; Pawnikar S; Huang Y.-m.; Palermo G; Miao Y, Gaussian accelerated molecular dynamics: principles and applications. WIREs Computational Molecular Science 2021, e1521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Henzler-Wildman K; Kern D, Dynamic personalities of proteins. Nature 2007, 450, 964–72. [DOI] [PubMed] [Google Scholar]
- 5.Harvey MJ; Giupponi G; Fabritiis GD, ACEMD: accelerating biomolecular dynamics in the microsecond time scale. Journal of Chemical Theory and Computation 2009, 5, 1632–9. [DOI] [PubMed] [Google Scholar]
- 6.Johnston JM; Filizola M, Showcasing modern molecular dynamics simulations of membrane proteins through G protein-coupled receptors. Current Opinions in Structural Biology 2011, 21, 552–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Shaw DE; Maragakis P; Lindorff-Larsen K; Piana S; Dror RO; Eastwood MP; Bank JA; Jumper JM; Salmon JK; Shan Y; Wriggers W, Atomic-level characterization of the structural dynamics of proteins. Science 2010, 330, 341–6. [DOI] [PubMed] [Google Scholar]
- 8.Lane TJ; Shukla D; Beauchamp KA; Pande VS, To milliseconds and beyond: challenges in the simulation of protein folding. Current Opinions in Structural Biology 2013, 23, 58–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Vilardaga J-P; Bünemann M; Krasel C; Castro M; Lohse MJ, Measurement of the milisecond activation switch of G protein-coupled receptors in living cells. Nature Biotechnology 2008, 21, 807–12. [DOI] [PubMed] [Google Scholar]
- 10.Miao Y; Ortoleva PJ, Viral structural transitions: an all-atom multiscale theory. Journal of Chemical Physics 2006, 125, 214901. [DOI] [PubMed] [Google Scholar]
- 11.Spiwok V; Sucur Z; Hosek P, Enhanced sampling techniques in biomolecular simulations. Biotechnology Advances 2015, 33, 1130–40. [DOI] [PubMed] [Google Scholar]
- 12.Gao YQ; Yang LJ; Fan YB; Shao Q, Thermodynamics and kinetics simulations of multi-timescale processes for complex systems. International Reviews in Physical Chemistry 2008, 27, 201–227. [Google Scholar]
- 13.Liwo A; Czaplewski C; Oldziej S; Scheraga HA, Computational techniques for efficient conformational sampling of proteins. Current Opinion in Structural Biology 2008, 18, 134–139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Christen M; van Gunstere W, On searching in, sampling of, and dynamically moving through conformational space of biomolecular systems: a review. Journal of Computational Chemistry 2008, 29, 157–66. [DOI] [PubMed] [Google Scholar]
- 15.Miao Y; McCammon JA, Unconstrained enhanced sampling for free energy calculations of biomolecules: a review. Molecular Simulation 2016, 42, 1046–55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Torrie G; Valleau J, Nonphysical sampling distributions in Monte Carlo free-energy estimation: umbrella sampling. Journal of Computational Physics 1977, 23, 187–199. [Google Scholar]
- 17.Kumar S; Rosenberg J; Bouzida D; Swendsen R; Kollman P, THE weighted histogram analysis method for free-energy calculations on biomolecules. I. THE method. Journal of Computational Chemistry 1992, 13, 1011–21. [Google Scholar]
- 18.Laio A; Gervasio F, Metadynamics: a method to simulate rare events and reconstruct the free energy in biophysics, chemistry and material science. Reports on Progress in Physics 2008, 71, 126601. [Google Scholar]
- 19.Besker N; Gervasio F, Using metadynamics and path collective variables to study ligand binding and induced conformational transitions. In Computational drug discovery and design, Berlin: Springer: 2012; pp 501–13. [DOI] [PubMed] [Google Scholar]
- 20.Darve E; Rodriguez-Gomez D; Pohorille A, Adaptive biasing force method for scalar and vector free energy calculations. Journal of Chemical Physics 2008, 128, 144120. [DOI] [PubMed] [Google Scholar]
- 21.Darve E; Wilson M; Pohorille A, Calculating free energies using a scaled-force molecular dynamics algorithm. Molecular Simulation 2002, 28, 113–44. [Google Scholar]
- 22.Isralewitz B; Baudry J; Gullingsrud J; Kosztin D; Schulten K, Steered molecular dynamics investigations of protein function. Journal of Molecular Graphics and Modelling 2001, 19, 13–25. [DOI] [PubMed] [Google Scholar]
- 23.Sugita Y; Okamoto Y, Replica-exchange molecular dynamics method for protein folding. Chemical Physics Letters 1999, 314, 141–51. [Google Scholar]
- 24.Okamoto Y, Generalized-ensemble algorithms: enhanced sampling techniques for Monte Carlo and molecular dynamics simulations. Journal of Molecular Graphics and Modelling 2004, 22, 425–39. [DOI] [PubMed] [Google Scholar]
- 25.Hansmann U, Parallel tempering algorithm for conformational studies of biological molecules. Chemical Physics Letters 1997, 281, 140–50. [Google Scholar]
- 26.Wu X; Brooks B, Self-guided Langevin dynamics simulation method. Chemical Physics Letters 2003, 381, 512–8. [Google Scholar]
- 27.Wu X; Brooks B; Vanden-Eijnden E, Self-guided Langevin dynamics via generalized Langevin equation. Journal of Computational Chemistry 2016, 37, 595–601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Wu X; Wang S, Self-guided molecular dynamics simulation for efficient conformational search. Journal of Physcial Chemistry B 1998, 102, 7238–50. [Google Scholar]
- 29.Hamelberg D; Mongan J; McCammon JA, Accelerated molecular dynamics: a promising and efficient simulation method for biomolecules. Journal of Chemical Physics 2004, 120, 11919–11929. [DOI] [PubMed] [Google Scholar]
- 30.Voter AF, Hyperdynamics: Accelerated Molecular Dynamics of Infrequent Events. Physical Review Letters 1997, 78, 3908. [Google Scholar]
- 31.Hamelberg D; de Oliveira CAF; McCammon JA, Sampling of slow diffusive conformational transitions with accelerated molecular dynamics. J Chem Phys 2007, 127 (15), 155102. [DOI] [PubMed] [Google Scholar]
- 32.Shen TY; Hamelberg D, A statistical analysis of the precision of reweighting-based simulations. J Chem Phys 2008, 129 (3), 034103. [DOI] [PubMed] [Google Scholar]
- 33.Miao Y; Sinko W; Pierce L; Bucher D; Walker RC; McCammon JA, Improved reweighting of accelerated molecular dynamics simulations for free energy calculation. Journal of Chemical Theory and Computation 2014, 10, 2677–2689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Miao Y; Feher VA; McCammon JA, Gaussian accelerated molecular dynamics: unconstrained enhanced sampling and free energy calculation. Journal of Chemical Theory and Computation 2015, 11, 3584–3595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Shen T; Hamelberg D, A statistical analysis of the precision reweighting-based simulations. Journal of Chemical Physics 2008, 129, 034103. [DOI] [PubMed] [Google Scholar]
- 36.Pang Y; Miao Y; McCammon JA, Gaussian accelerated molecular dynamics in NAMD. Journal of Chemical Theory and Computation 2017, 13, 9–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Bhattarai A; Pawnikar S; Miao Y, Mechanism of ligand recognition by human ACE2 receptor. Journal of Physcial Chemistry Letters 2021, 12, 4814–4822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Tang Z; Akhter S; Ramprasad A; Wang X; Reibarkh M; Wang J; Aryal S; Thota S; Zhao J; Douglas J; Gao P; Holmstrom E; Miao Y; Wang J, Recognition of single-stranded nucleic acids by small-molecule splicing modulators. Nucleic Acids Research 2021, 49 (14), 7870–7883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Do H; Akhter S; Miao Y, Pathways and Mechanism of Caffeine Binding to Human Adenosine A2A Receptor. Frontiers in Molecular Biosciences 2021, 8, 242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Pawnikar S; Miao Y, Pathway and Mechanism of Drug Binding to Chemokine Receptors Revealed by Accelerated Molecular Simulations. Future Medicinal Chemsitry 2020, 12 (13), 1213–1225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Bhattarai A; Devkota S; Bhattarai S; Wolfe MS; Miao Y, Mechanisms of gamma-secretase activation and substrate processing. ACS Central Science 2020, 6 (6), 969–983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Draper-Joyce C; Bhola R; Wang J; Bhattarai A; Nguyen A; Cowie-Kent I; O’Sullivan K; Venugopal H; Valant C; Thal D; Wootten D; Panel N; Carlsson J; Christie M; Scammells P; May L; Sexton P; Danev R; Miao Y; Glukhova A; Wendy L; Christopoulos A, Positive allosteric mechanisms of adenosine A1 receptor-mediated analgesia. Nature 2021, In Press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Miao Y; McCammon JA, Graded activation and free energy landscapes of a muscarinic G-protein–coupled receptor. Proc Natl Acad Sci 2016, 113 (43), 12162–12167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Bhattarai A; Wang J; Miao Y, G-protein-coupled receptor-membrane interactions depend on the receptor activation state. Journal of Computational Chemistry 2020, 41, 460–471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Miao Y; McCammon JA, Mechanism of the G-protein mimetic nanobody binding to a muscarinic G-protein-coupled receptor. Proceedings of the National Academy of Sciences of the United States of America 2018, 115, 3036–3041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Wang J; Miao Y, Mechanistic insights into specific G protein interactions with adenosine receptors. Journal of Physcial Chemistry B 2019, 123, 6462–6473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Ricci CG; Chen JS; Miao Y; Jinek M; Doudna JA; McCammon JA; Palermo G, Deciphering Off-Target Effects in CRISPR-Cas9 through Accelerated Molecular Dynamics. ACE Central Science 2019, 5 (4), 651–662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.East KW; Newton JC; Morzan UN; Narkhede YB; Acharya A; Skeens E; Jogl G; Batista VS; Palermo G; Lisi GP, Allosteric Motions of the CRISPR-Cas9 HNH Nuclease Probed by NMR and Molecular Dynamics. Journal of American Chemical Society 2020, 142 (3), 1348–1358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Huang Y.-m.; McCammon JA; Miao Y, Replica exchange Gaussian accelerated molecular dynamics: improved enhanced sampling and free energy calculation. Journal of Chemical Theory and Computation 2018, 14, 1853–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Oshima H; Re S; Sugita Y, Replica-exchange umbrella sampling combined with Gaussian accelerated molecular dynamics for free-energy calculation of biomolecues Journal of Chemical Theory and Computation 2019, 15, 5199–208. [DOI] [PubMed] [Google Scholar]
- 51.Miao Y; Bhattarai A; Wang J, Ligand Gaussian accelerated molecular dynamics (LiGaMD): characterization of ligand binding thermodynamics and kinetics. Journal of Chemical Theory and Computation 2020, 16, 5526–47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Wang J; Miao Y, Peptide Gaussian accelerated molecular dynamics (Pep-GaMD): enhanced sampling and free energy and kinetics calculations of peptide binding. Journal of Chemical Physics 2020, 153, 154109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Noe F; Tkatchenko A; Muller KR; Clementi C, Machine Learning for Molecular Simulation. Annu Rev Phys Chem 2020, 71, 361–390. [DOI] [PubMed] [Google Scholar]
- 54.Wang Y; Lamim Ribeiro JM; Tiwary P, Machine learning approaches for analyzing and enhancing molecular dynamics simulations. Curr Opin Struct Biol 2020, 61, 139–145. [DOI] [PubMed] [Google Scholar]
- 55.Hauser AS; Chavali S; Masuho I; Jahn LJ; Martemyanov KA; Gloriam DE; Babu MM, Pharmacogenomics of GPCR Drug Targets. Cell 2018, 172 (1–2), 41–54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Ye L; Van Eps N; Zimmer M; Ernst OP; Prosser RS, Activation of the A2A adenosine G-protein-coupled receptor by conformational selection. Nature 2016, 533, 265–268. [DOI] [PubMed] [Google Scholar]
- 57.Kruse AC; Ring AM; Manglik A; Hu J; Hu K; Eitel K; Hubner H; Pardon E; Valant C; Sexton PM; Christopoulos A; Felder CC; Gmeiner P; Steyaert J; Weis WI; Garcia KC; Wess J; Kobilka BK, Activation and allosteric modulation of a muscarinic acetylcholine receptor. Nature 2013, 504 (7478), 101–106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Nygaard R; Zou Y; Dror RO; Mildorf TJ; Arlow DH; Manglik A; Pan AC; Liu CW; Fung JJ; Bokoch MP; Thian FS; Kobilka TS; Shaw DE; Mueller L; Prosser RS; Kobilka BK, The dynamic process of β2-adrenergic receptor activation. Cell 2013, 152, 532–542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Dror RO; Arlow DH; Maragakis P; Mildorf TJ; Pan AC; Xu H; Borhani DW; Shaw DE, Activation mechanism of the β2-adrenergic receptor. Proceedings of the National Academy of Sciences of the United States of America 2011, 108 (46), 18684–18689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Miao Y; Nichols SE; Gasper PM; Metzger VT; McCammon JA, Activation and dynamic network of the M2 muscarinic receptor. Proceedings of the National Academy of Sciences of the United States of America 2013, 110, 10982–10987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Hilger D; Kumar KK; Hu H; Pedersen MF; O’Brien ES; Giehm L; Jennings C; Eskici G; Inoue A; Lerch M; Mathiesen JM; Skiniotis G; Kobilka BK, Structural insights into differences in G protein activation by family A and family B GPCRs. Science 2020, 369 (6503), eaba3373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Zhou Q; Yang D; Wu M; Guo Y; Guo W; Zhong L; Cai X; Dai A; Jang W; Shakhnovich EI; Liu Z-J; Stevens RC; Lambert NA; Babu MM; Wang M-W; Zhao S, Common activation mechanism of class A GPCRs. eLife 2019, 8, e50279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Do H; Haldane A; Levy R; Miao Y, Unique Features of different classes of G-protein-coupled receptors revealed from sequence coevolutionary and structural analysis. Proteins 2021, 1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Hauser AS; Kooistra AJ; Munk C; Heydenreich FM; Veprintsev DB; Bouvier M; Babu MM; Gloriam DE, GPCR activation mechanisms across classes and macro/microscales. Nature Structural and Molecular Biology 2021, 28, 879–888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Ballesteros JA; Weinstein H, Integrated methods for the construction of three-dimensional models and computational probing of structure-function relations in G protein-coupled receptors. In Methods in Neurosciences, Stuart CS, Ed. Academic Press: New York, 1995; Vol. Volume 25, pp 366–428. [Google Scholar]
- 66.Christopoulos A, Allosteric binding sites on cell-surface receptors: Novel targets for drug discovery. Nat Rev Drug Discov 2002, 1 (3), 198–210. [DOI] [PubMed] [Google Scholar]
- 67.Jeffrey Conn P; Christopoulos A; Lindsley CW, Allosteric modulators of GPCRs: a novel approach for the treatment of CNS disorders. Nat Rev Drug Discov 2009, 8 (1), 41–54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Thal D; Glukhova A; Sexton P; Christopoulos A, Structural insights into G-protein-coupled receptor allostery. Nature 2018, 559, 45–53. [DOI] [PubMed] [Google Scholar]
- 69.Maeda S, Qu Q, Robertson MJ, Skiniotis G, Kobilka BK, Structures of the M1 and M2 muscarinic acetylcholine receptor/G-protein complexes. Science 2019, 364 (6440), 552–557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Maeda S; Xu J; FM NK; Clark MJ; Zhao J; Tsutsumi N; Aoki J; Sunahara RK; Inoue A; Garcia KC; Kobilka BK, Structure and selectivity engineering of the M1 muscarinic receptor toxin complex. Science 2020, 369 (6500), 161–167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Lu J, Byrne N, Wang J, Bricogne G, Brown FK, Chobanian HR, Colletti SL, Di Salvo J, Thomas-Fowlkes B, Guo Y, Hall DL, Hadix J, Hastings NB, Hermes JD, Ho T, Howard AD, Josien H, Kornienko M, Lumb KJ, Miller MW, Patel SB, Pio B, Plummer CW, Sherborne BS, Sheth P, Souza S, Tummala S, Vonrhein C, Webb M, Allen SJ, Johnston JM, Weinglass AB, Sharma S, Soisson SM, Structural basis for the cooperative allosteric activation of the free fatty acid receptor GPR40. Nature Structural and Molecular Biology 2017, 24 (7), 570–577. [DOI] [PubMed] [Google Scholar]
- 72.Liu H; Kim HR; Deepak R; Wang L; Chung KY; Fan H; Wei Z; Zhang C, Orthosteric and allosteric action of the C5a receptor antagonists. Nat Struct Mol Biol 2018, 25 (6), 472–481. [DOI] [PubMed] [Google Scholar]
- 73.Avlani V; Gregory K; Morton C; Parker M; Sexton P; Christopoulos A, Critical role for the second extracellular loop in the binding of both orthosteric and allosteric g protein-coupled receptor ligands. Journal of Biological Chemistry 2007, 282 (35), 25677–25686. [DOI] [PubMed] [Google Scholar]
- 74.Peeters M; Wisse L; Dinaj A; Vroling B; Vriend G; IJzerman A, The role of the second and third extracellular loops of the adenosine A1 receptor in activation and allosteric modulation. Biochemical Pharmacology 2012, 84 (1), 76–87. [DOI] [PubMed] [Google Scholar]
- 75.Nguyen A; Vecchio E; Thomas T; Nguyen T; Aurelio L; Scammells P; White P; Sexton P; Gregory K; May L; Christopoulos A, Role of the Second Extracellular Loop of the Adenosine A1 Receptor on Allosteric Modulator Binding, Signaling, and Cooperativity. Molecular Pharmacology 2016, 90 (6), 715–725. [DOI] [PubMed] [Google Scholar]
- 76.Miao Y; Bhattarai A; Nguyen A; Christopoulos A; May L, Structural Basis for Binding of Allosteric Drug Leads in the Adenosine A1 Receptor. Scientific Reports 2018, 8 (1), 16836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Nguyen AT; Baltos JA; Thomas T; Nguyen TD; Munoz LL; Gregory KJ; White PJ; Sexton PM; Christopoulos A; May LT, Extracellular Loop 2 of the Adenosine A1 Receptor Has a Key Role in Orthosteric Ligand Affinity and Agonist Efficacy. Mol Pharmacol 2016, 90 (6), 703–714. [DOI] [PubMed] [Google Scholar]
- 78.Plante A; Shore DM; Morra G; Khelashvili G; Weinstein H, A Machine Learning Approach for the Discovery of Ligand-Specific Functional Mechanisms of GPCRs. Molecules 2019, 24 (11). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Plante A; Weinstein H, Ligand-Dependent Conformational Transitions in Molecular Dynamics Trajectories of GPCRs Revealed by a New Machine Learning Rare Event Detection Protocol. Molecules 2021, 26 (10). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Ferraro M; Decherchi S; De Simone A; Recanatini M; Cavalli A; Bottegoni G, Multi-target dopamine D3 receptor modulators: Actionable knowledge for drug design from molecular dynamics and machine learning. Eur J Med Chem 2020, 188, 111975. [DOI] [PubMed] [Google Scholar]
- 81.Fleetwood O; Kasimova M; Westerlund A; Delemotte L, Molecular Insights from Conformational Ensembles via Machine Learning. Biophysical Journal 2019, 118, 765–780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Lamim Ribeiro JM; Provasi D; Filizola M, A combination of machine learning and infrequent metadynamics to efficiently predict kinetic rates, transition states, and molecular determinants of drug dissociation from G protein-coupled receptors. J Chem Phys 2020, 153 (12), 124105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Bian Y; Jing Y; Wang L; Ma S; Jun JJ; Xie XQ, Prediction of Orthosteric and Allosteric Regulations on Cannabinoid Receptors Using Supervised Machine Learning Classifiers. Mol Pharm 2019, 16 (6), 2605–2615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Kotikalapudi R Keras-Vis, GitHub: 2017. [Google Scholar]
- 85.Cheng R; Segala E; Robertson N; Deflorian F; Dore A; Errey J; Fiez-Vandal C; Marshall F; Cooke R, Structures of Human A1 and A2A Adenosine Receptors with Xanthines Reveal Determinants of Selectivity Structure 2017, 25 (e4), 1275–1285. [DOI] [PubMed] [Google Scholar]
- 86.Draper-Joyce CJ; Khoshouei M; Thal DM; Liang YL; Nguyen ATN; Furness SGB; Venugopal H; Baltos JA; Plitzko JM; Danev R; Baumeister W; May LT; Wootten D; Sexton PM; Glukhova A; Christopoulos A, Structure of the adenosine-bound human adenosine A1 receptor-Gi-complex. Nature 2018, 558, 559–563. [DOI] [PubMed] [Google Scholar]
- 87.Huang J; Rauscher S; Nawrocki G; Ran T; Feig M; de Groot BL; Grubmuller H; MacKerell AD Jr, CHARMM36m: an improved force field for folded and intrinscially disordered proteins. Nature Methods 2017, 14, 71–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Salomon-Ferrer R; Gotz AW; Poole D; Le Grand S; Walker RC, Routined microsecond molecular dynamics simulations with AMBER on GPUs. 2. Explicit solvent Particle Mesh Ewald. Journal of Chemical Theory and Computation 2013, 9, 3878–3888. [DOI] [PubMed] [Google Scholar]
- 89.Case DA; Aktulga HM; Belfon K; Ben-Shalom IY; Brozell SR; Cerutti DS; Cheatham TE I.; Cruzeiro VWD; Darden TA; Duke RE; Giambasu G; Gilson MK; Gohlke H; Goetz AW; Harris R; Izadi S; Izmailov SA; Jin C; Kasavajhala K; Kaymak MC; King E; Kovalenko A; Kurtzman T; Lee TS; LeGrand S; Li P; Lin C; Liu J; Luchko T; Luo R; Machado M; Man V; Manathunga M; Merz KM; Miao Y; Mikhailovskii O; Monard G; Nguyen H; O’Hearn KA; Onufriev A; Pan F; Pantano S; Qi R; Rahnamoun A; Roe DR; Roitberg A; Sagui C; Schott-Verdugo S; Shen J; Simmerling CL; Skrynnikov NR; Smith J; Swails J; Walker RC; Wang J; Wei H; Wolf RM; Wu X; Xue Y; York DM; Zhao S; Kollman PA Amber 2021, University of California, San Francisco: 2021. [Google Scholar]
- 90.McGibbon RT; Beauchamp KA; Harrigan MP; Klein C; Swails JM; Hernandez CX; Schwantes CR; Wang L-P; Lane TJ; Pande VS, MDTraj: A Modern Open Library for the Analysis of Molecular Dynamics Trajectories. Biophysical Journal 2015, 109 (8), 1528–1532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Gulli A; Pal S, Deep Learning with Keras. Packt Publishing Ltd: 2017. [Google Scholar]
- 92.Abadi M; Barham P; Chen J; Chen Z; Davis A; Dean J; Devin M; Ghemawat S; Irving G; Isard M; Kudlur M; Levenberg J; Monga R; Moore S; Murray DG; Steiner B; Tucker P; Vasudevan V; Warden P; Wicke M; Yu Y; Zheng X In TensorFlow: A System for Large-Scale Machine Learning, Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI’ 16), 2016; pp 265–283. [Google Scholar]
- 93.Miao Y; McCammon JA, Gaussian Accelerated Molecular Dynamics: Theory, Implementation and Applications. Annu Rep Comp Chem 2017, 13, 231–278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Glukhova A; Thal DM; Nguyen ATN; Vecchio EA; Jorg M; Scammells PJ; May LT; Sexton PM; Christopoulos A, Structure of the Adenosine A1 Receptor Reveals the Basis for Subtype Selectivity. Cell 2017, 168 (e13), 867–877. [DOI] [PubMed] [Google Scholar]
- 95.Niesen M; Bhattacharya S; Vaidehi N, The Role of Conformational Ensembles in Ligand Recognition in G-Protein Coupled Receptors. Journal of American Chemical Society 2011, 133 (33), 13197–13204. [DOI] [PubMed] [Google Scholar]
- 96.Shan J; Khelashvili G; Mondal S; Mehler E; Weinstein H, Ligand-Dependent Conformations and Dynamics of the Serotonin 5-HT2A Receptor Determine Its Activation and Membrane-Driven Oligomerization Properties. PLOS Computational Biology 2012, 8 (4), e1002473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Li J; Jonsson A; Beuming T; Shelley J; Voth G, Ligand-Dependent Activation and Deactivation of the Human Adenosine A2A Receptor. Journal of American Chemical Society 2013, 135 (23), 8749–8759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Provasi D; Artacho M; Negri A; Mobarec J; Filizola M, Ligand-Induced Modulation of the Free Energy Landscape of G Protein-Coupled Receptors Explored by Adaptive Biasing Techniques. PLOS Computational Biology 2011, 7 (10), e1002193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Peeters M; Li Q; van Westen G; IJzerman A, Three “hotspots” important for adenosine A(2B) receptor activation: a mutational analysis of transmembrane domains 4 and 5 and the second extracellular loop. Purinergic Signalling 2012, 8 (1), 23–38. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


