Abstract
We present a two-headed approach called Bayesian Integrated Coalescent Epoch PlotS (BICEPS) for efficient inference of coalescent epoch models. Firstly, we integrate out population size parameters, and secondly, we introduce a set of more powerful Markov chain Monte Carlo (MCMC) proposals for flexing and stretching trees. Even though population sizes are integrated out and not explicitly sampled through MCMC, we are still able to generate samples from the population size posteriors. This allows demographic reconstruction through time and estimating the timing and magnitude of population bottlenecks and full population histories. Altogether, BICEPS can be considered a more muscular version of the popular Bayesian skyline model. We demonstrate its power and correctness by a well-calibrated simulation study. Furthermore, we demonstrate with an application to SARS-CoV-2 genomic data that some analyses that have trouble converging with the traditional Bayesian skyline prior and standard MCMC proposals can do well with the BICEPS approach. BICEPS is available as open-source package for BEAST 2 under GPL license and has a user-friendly graphical user interface.[Bayesian phylogenetics; BEAST 2; BICEPS; coalescent model.]
Knowledge of population size dynamics can be of interest, for example, for the study of megafauna extinctions (Campos et al. 2010), conservation biology (Shapiro et al. 2004), reconstructing human settlement history (Pedro et al. 2020), impact of viral ecology on public health (Rambaut et al. 2008), or the influence of climate events on population sizes (Miller et al. 2012). Here, we will infer population size dynamics using a phylogeny with sequence data on a single gene, for example, mitochondrial sequences, or full genome viral data, based on coalescent theory in a Bayesian setting. We do not assume any structure, that is, we assume there is a single population, and we assume there is random mating and no admixture. Coalescent theory links phylogenies with population sizes through tree priors based on Kingman’s theory (Kingman 1982). These tree priors are driven by a population function that defines the effective population size through time. A population function can be parametric, like exponential or constant (Kuhner et al. 1998), but nonparametric methods that split up the time frame spanning a tree into epochs allow a population function to be constant in an epoch but vary over time. Nonparametric methods allow the representation of a much wider range of population functions than parametric methods and can capture one or more population bottlenecks and expansions without a priori having to commit to the number of such bottlenecks or expansions. So, nonparametric models offer a flexible alternative to parametric models and allow more wide range of population size dynamics estimates. Even when population size dynamics is of no interest, these models provide a flexible tree prior allowing a broad range of tree shapes and sizes.
The classic skyline model (Pybus et al. 2000), introduced in a maximum likelihood framework, is based on epochs for every coalescent event. It assumes that the phylogeny is fully resolved and divergence time estimates are reliable, so can only be applied when the data exhibit a strong phylogenetic signal. The classic skyline model was later generalized to epochs grouping coalescent events in the generalized skyline model (Strimmer and Pybus 2001), making it possible to estimate population histories when little divergence information is available, for instance, when the alignment contains identical sequences. The Bayesian skyline plot (Drummond et al. 2005) generalized this to a Bayesian setting, where epochs span multiple coalescent events, and the number of coalescent events as well as population sizes for an epoch are sampled during Markov chain Monte Carlo (MCMC). Furthermore, a smoothing prior is employed that links population sizes in consecutive epochs. Linking population sizes reduces stochastic noise and makes biological sense in that consecutive population sizes will usually be of a similar order of magnitude as preceding ones. Other popular epoch based coalescent models with different smoothing priors include the skyride prior (Minin et al. 2008), which takes the amount of time between epochs in account, the skygrid prior (Gill et al. 2013; Hill and Baele 2019), which allows users to define epoch boundaries, and the besp model (Parag et al. 2020), which takes sampling times in account.
All the above Bayesian methods sample the population function parameters. By assuming an inverse gamma prior distribution on population size, we demonstrate that the population size can be integrated out during MCMC. The technique is used in the multispecies coalescent models StarBeast2 (Ogilvie et al. 2017) and STACEY (Jones 2017), where a constant population size is associated with each branch of the species tree. Here, we generalize this method to the case where we have a single tree, potentially with sampled tip dates, and assume a piecewise constant population for each epoch under an inverse gamma prior. The mean for the population size of the youngest epoch can be sampled but for consecutive epochs the posterior mean of the previous epoch can be used, providing us with a smoothing prior. Even though population sizes are integrated out, they can still be sampled from the posterior population sizes for the epochs conditioned on the tree. This allows us to reconstruct population size history including uncertainty intervals in a similar fashion as for the Bayesian skyline plot as follows. At regular intervals during the MCMC, we log the tree, group sizes, and sample for each group a population size from the posterior. Each such sample defines a demographic history where the length of each epoch is defined by the tree and group sizes, a so-called skyline plot (Fig. 1, Drummond et al. 2005). So, for each point in time, the skyline plot defines a population size for a particular tree and its parameters. By considering all the trees and other parameters in the posterior, we get a distribution of population sizes for each point in time, which we can use to find the confidence intervals of the distribution (Fig. 5).
Figure 1.
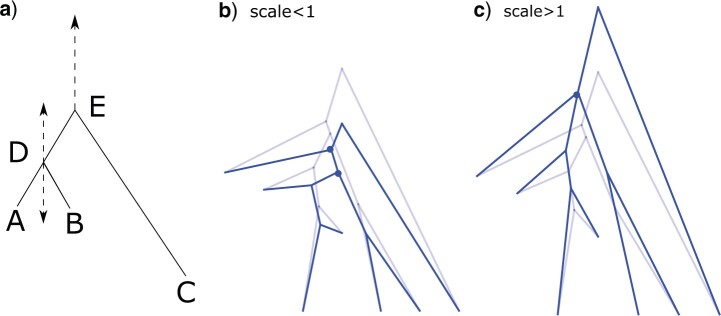
The traditional scale operator that gets often rejected when there are many tip data
(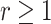 ) because of high probability of
negative branch lengths when scaling down or inappropriately stretching short branches
into older tips when scaling up. Tree stretch proposal moves nodes near tips (e.g., node
D) less far than nodes away from tips (e.g., node E), b) for scale factor
) because of high probability of
negative branch lengths when scaling down or inappropriately stretching short branches
into older tips when scaling up. Tree stretch proposal moves nodes near tips (e.g., node
D) less far than nodes away from tips (e.g., node E), b) for scale factor
 where lighter trees are the original
state and darker trees are proposals, and c) for scale factor larger than one.
where lighter trees are the original
state and darker trees are proposals, and c) for scale factor larger than one.
Figure 5.
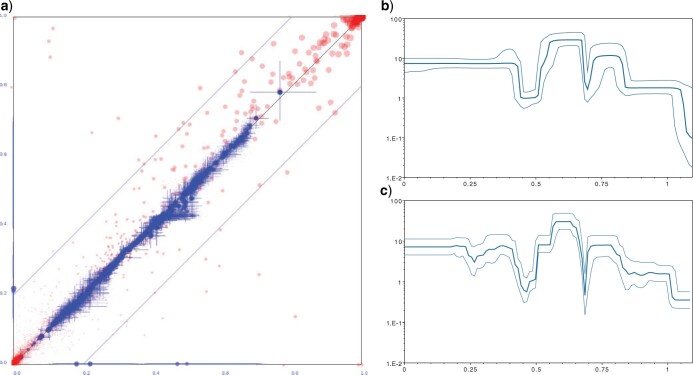
BSP and BICEPS compared. a) Difference in clade support and clade heights for the Bayesian skyline analysis from Douglas et al. (2021) and the same analysis with a BICEPS prior. Red dots indicate clade support between 0 and 1 on both axis, blue dots indicate mean clade heights with cross hairs showing the 95% HPD intervals of height estimates. The axis are scaled between zero and the highest tree height found in either tree set. b) Population history for COVID-19 inferred with the BSP model and c) BICEPS model. Dark middle line indicates the median, lighter outer lines cover the 95%HPD intervals. The x-axis shows time in years going backward from left to right, the y-axis shows population size on a log scale. BSP and BICEPS analyses largely agree.
Apart from introducing a more efficient way to infer population size histories at different epochs, we also consider a number of new MCMC proposals that can lift a large number of nodes in a tree simultaneously. Observing that tree priors tend to be highly correlated with the length of a tree, we target tree length changes by moving nodes in randomly chosen time intervals (not necessarily the ones used for the tree prior). Note that we are considering rooted time trees only, so the tree length is defined as the sum of branch lengths in units of time of the tree. The likelihood is also correlated with the length of the tree, but only after scaling it with a clock rate.
Furthermore, noting that scaling of trees tends to be hampered by serially sampled tips, we design a new scale proposal that moves all nodes in a tree simultaneously but with better exploratory powers than standard scalers. Both proposals move tree length, and since clock rates tend to be inversely correlated with the tree length (Douglas et al. 2021c), we designed proposals that simultaneously move the clock rate to compensate for a changing tree length. We demonstrate the effectiveness of these MCMC proposals for improving the mixing of tree lengths, and thus tree priors.
Together, integrating out population sizes and employing more sophisticated MCMC proposals allow us to do inference efficiently and make it possible to perform larger analyses, as we demonstrate using SARS-CoV-2 data. In the next section, we consider the technical details around integrating out parameters and new MCMC proposals. We continue with validating the method and presenting results. In Conclusions (final section), we consider ways to generalize the approach and in particular point out how to integrate out parameters for an epoch version of the Yule prior (Appendices B and C of the Supplementary material).
Methods
First, we consider integrating out population size parameters, then we design a set of new MCMC proposals.
BICEPS Model: Integrating Out parameters
Let 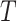 be a rooted binary tree with
be a rooted binary tree with
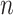 taxa sampled at
taxa sampled at 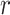 different times.1 So,
different times.1 So,
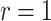 when all taxa are sampled at the same
time and
when all taxa are sampled at the same
time and 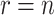 when all taxa are sampled at different
times. Then, there are
when all taxa are sampled at different
times. Then, there are 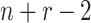 times
times 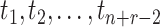 that are either
sampling times or coalescent times ordered from youngest tip (
that are either
sampling times or coalescent times ordered from youngest tip (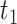 ) to
the coalescent time at the root (
) to
the coalescent time at the root (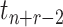 ) and let
) and let
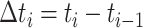 denote the length of
an interval. Let
denote the length of
an interval. Let 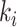 be the number of lineages at event
be the number of lineages at event
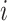 , so
, so 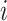 decreases by one at a coalescent event, but increases at a sampling event. Let
decreases by one at a coalescent event, but increases at a sampling event. Let
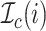 be an indicator function
that indicates whether the
be an indicator function
that indicates whether the 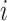 th event is a coalescent event
(
th event is a coalescent event
(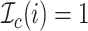 ) or a sampling event
(
) or a sampling event
(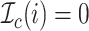 ).
).
Consider 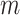 epochs defined by groups of coalescent
events, and let
epochs defined by groups of coalescent
events, and let 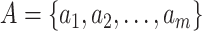 be the number of
coalescent events in each of the
be the number of
coalescent events in each of the 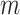 epochs that cover the
whole tree (so
epochs that cover the
whole tree (so 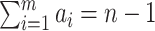 ). (Parag and Pybus, 2019) show that having a similar
number of coalescent events per epoch increases accuracy of population size estimates, so
in practice we keep group sizes constant and evenly spread. The number of epochs is a
parameter to be provided by the user, but by default 10 epochs will be used unless the
epoch sizes become less than 6 (
). (Parag and Pybus, 2019) show that having a similar
number of coalescent events per epoch increases accuracy of population size estimates, so
in practice we keep group sizes constant and evenly spread. The number of epochs is a
parameter to be provided by the user, but by default 10 epochs will be used unless the
epoch sizes become less than 6 (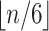 groups
will be used) or larger than 30 (
groups
will be used) or larger than 30 (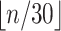 groups
will be used).
groups
will be used).
Let 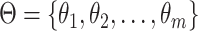 be the effective population sizes for the
be the effective population sizes for the 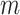 epochs, that define a
piecewise constant population function for the
epochs, that define a
piecewise constant population function for the 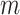 epochs. Let
epochs. Let
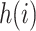 be a function
be a function
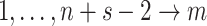 that map the coalescent
and sampling events
that map the coalescent
and sampling events 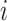 to epochs (Drummond et al. 2005, Eq. (4)). Then, the log likelihood
to epochs (Drummond et al. 2005, Eq. (4)). Then, the log likelihood 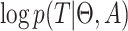 of the
tree
of the
tree 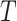 given
given 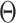 and
and 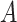 is (Drummond et al. 2005, Eq. (3)):
is (Drummond et al. 2005, Eq. (3)):
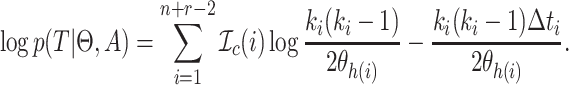 |
(1) |
Taking the exponent, gives the density
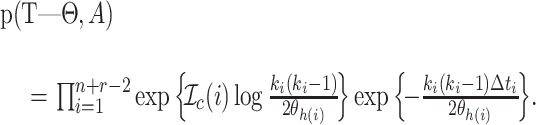 |
(2) |
Let 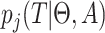 denote the contribution for
a single epoch
denote the contribution for
a single epoch 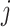 so
so 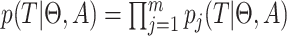 ,
and let
,
and let 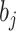 be the index of event
be the index of event
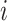 at the start of the
at the start of the
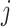 th epoch (so,
th epoch (so, 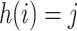 for
for 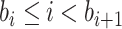 ), then
), then
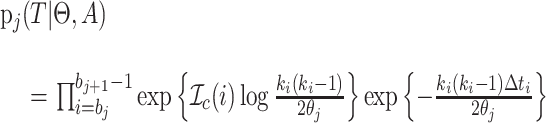 |
(3) |
which can be simplified to
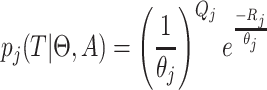 |
(4) |
with 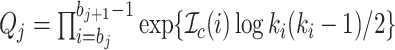 and
and 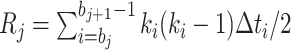 .
Following (Liu et al., 2008), we note that the
inverse gamma distribution
.
Following (Liu et al., 2008), we note that the
inverse gamma distribution 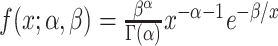 is conjugate for
is conjugate for 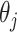 , in other words, the posterior is
, in other words, the posterior is
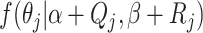 and
integrating out
and
integrating out 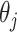 gives
gives
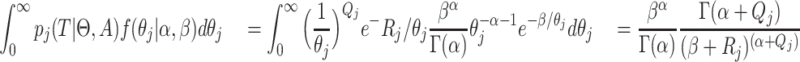 |
(5) |
thus we get a closed form density for the contribution of epoch
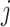 that has the population size
that has the population size
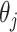 integrated out. Since
integrated out. Since
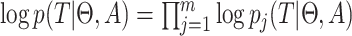 and
and 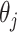 independent, we can do this for
each of the intervals.
independent, we can do this for
each of the intervals.
This leaves us to choose the parameters for the inverse gamma prior on population sizes.
If no further information about population sizes, this prior ideally has little influence
on the distribution of population sizes (Liu et al.
2008). By default, the shape value of 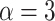 is fixed as
suggested elsewhere (Ogilvie et al. 2017; Liu et al. 2008), which has the special property that
the standard deviation is identical to the mean (Ogilvie
et al. 2017), so the coefficient of variation is 1, providing a wide ranging
distribution. If there is some information about possible values of
is fixed as
suggested elsewhere (Ogilvie et al. 2017; Liu et al. 2008), which has the special property that
the standard deviation is identical to the mean (Ogilvie
et al. 2017), so the coefficient of variation is 1, providing a wide ranging
distribution. If there is some information about possible values of
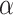 , these can be changed. The
population mean
, these can be changed. The
population mean 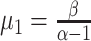 estimated
during the MCMC run with a lognormal
estimated
during the MCMC run with a lognormal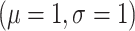 by
default.
by
default.
Smoothing priors
Epoch models can show abrupt changes in population size estimates when population sizes
for the epochs are assumed to be independent. For that reason, smoothing priors are
applied (Drummond et al. 2005; Minin et al. 2008; Gill et al. 2013), which suppress large fluctuations of population sizes in
consecutive epochs. One way to do this is to sample only the population mean for the
first epoch, and for consecutive epochs, the posterior mean of the previous epoch
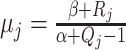 can
be used to set
can
be used to set 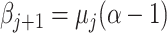 .
.
Inferring skyline plots
While models that explicitly sample population sizes of each epoch store population
sizes and epoch information during MCMC, we do not have population size information
available when integrating them out. However, given that for each epoch
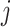 we have a posterior distribution
we have a posterior distribution
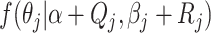 we can
just sample a value from that posterior and approximate the population size distribution
for each epoch, and this allows us to perform demographic reconstruction. A sample from
an inverse gamma distribution can be obtained by sampling a gamma distribution with
shape
we can
just sample a value from that posterior and approximate the population size distribution
for each epoch, and this allows us to perform demographic reconstruction. A sample from
an inverse gamma distribution can be obtained by sampling a gamma distribution with
shape 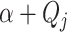 and scale
and scale
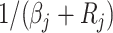 and taking the reciprocal
value of the sample.
and taking the reciprocal
value of the sample.
BICEPS Operators
To help convergence of the MCMC algorithm, we introduce a number of new proposals that move a large number of heights of internal nodes in the tree while keeping leaf node heights constant. These proposals have a large effect on the length of a tree, and thus indirectly on the tree prior. Note that the methods introduced are applicable to all phylogenetic tree priors and are not restricted to the epoch model discussed above.
New tree stretch proposal
The standard tree scale proposal in BEAST 2 simply multiplies all internal node heights
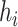 (for node
(for node 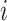 ) with
the same randomly chosen scale factor
) with
the same randomly chosen scale factor 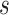 , but leaf node heights
remain unchanged. This can lead to negative branch lengths if an internal node is scaled
down below a tip height of a descendant, at which point the scale proposal is instantly
rejected (see node D in Fig. 1a when scaled down).
When there are many dated tips over a large time range, and there is little variation in
sequence data resulting in short terminal branches, scaling up can make relatively short
terminal branches stretch out a lot causing a marked reduction in tree likelihood
causing the proposal to be rejected (see node D in Fig.
1a when scaled up).
, but leaf node heights
remain unchanged. This can lead to negative branch lengths if an internal node is scaled
down below a tip height of a descendant, at which point the scale proposal is instantly
rejected (see node D in Fig. 1a when scaled down).
When there are many dated tips over a large time range, and there is little variation in
sequence data resulting in short terminal branches, scaling up can make relatively short
terminal branches stretch out a lot causing a marked reduction in tree likelihood
causing the proposal to be rejected (see node D in Fig.
1a when scaled up).
To remedy such low acceptance, the range from which the scale factor is sampled can be reduced, but that leads to smaller overall changes to the tree. Note that when scaling all nodes in the tree the pruning algorithm (Felsenstein 1981) for calculating the tree likelihood needs to recalculate all so called partials for internal nodes, which is a computationally expensive task (see Felsenstein 1981 for details). So, ideally we would like to make bold proposals to justify this computationally costly operation.
Instead of simply multiplying internal node heights, as the standard scale operator
does, we can do a postorder traversal where we scale branch lengths and add them to the
height of the left and right child, then take the average of these heights to set the
height of the current node in the traversal. Formally, let 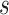 be a
randomly chosen scale factor from a Bactrian kernel (Yang and Rodríguez 2013; Thawornwattana et al.
2018), that is, we randomly sample a value from a standard Gaussian
be a
randomly chosen scale factor from a Bactrian kernel (Yang and Rodríguez 2013; Thawornwattana et al.
2018), that is, we randomly sample a value from a standard Gaussian
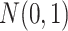 scaled with
scaled with
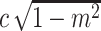 , and randomly add or
subtract
, and randomly add or
subtract 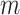 . Here,
. Here, 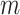 determines the shape of the Bactrian distribution and is set to 0.95 by default, and
determines the shape of the Bactrian distribution and is set to 0.95 by default, and
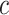 is a tuning parameter. The tuning
parameter is automatically optimized (Drummond and
Bouckaert 2015) during MCMC to obtain optimal balance between better acceptance
(at lower values of
is a tuning parameter. The tuning
parameter is automatically optimized (Drummond and
Bouckaert 2015) during MCMC to obtain optimal balance between better acceptance
(at lower values of 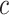 ) and boldness (at larger values of
) and boldness (at larger values of
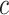 ). A target acceptance probability of
0.4 suggested in (Yang and Rodríguez, 2013)
appears to give good results. Automatic tuning of operators ensures that for models with
high rejection rate, the size of the proposed changes will be reduced, so subsequent
proposals will be less bold. Let
). A target acceptance probability of
0.4 suggested in (Yang and Rodríguez, 2013)
appears to give good results. Automatic tuning of operators ensures that for models with
high rejection rate, the size of the proposed changes will be reduced, so subsequent
proposals will be less bold. Let 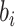 be the branch length
above node
be the branch length
above node 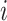 , so
, so 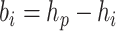 when
when 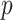 is
the parent of node
is
the parent of node 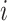 . We traverse the tree and do not change
leaf node heights, but for a node
. We traverse the tree and do not change
leaf node heights, but for a node 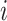 with children
with children
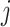 and
and 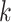 (assuming they were already visited), we set the new height
(assuming they were already visited), we set the new height 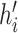 of
node
of
node 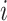 to
to 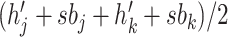 . When all tips
are contemporary, this proposal is the same as the traditional tree scale operator
(because
. When all tips
are contemporary, this proposal is the same as the traditional tree scale operator
(because 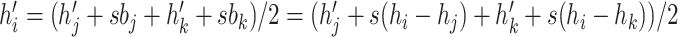 under induction assumption
under induction assumption 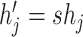 and
and 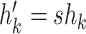 , giving
, giving 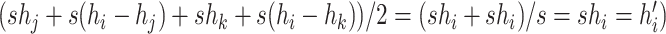 .
But, with dated tips, nodes closer to dated tips move less than nodes farther away from
tips.
.
But, with dated tips, nodes closer to dated tips move less than nodes farther away from
tips.
The probability of acceptance of an MCMC proposal (Green 1995; Holder et al. 2005) is
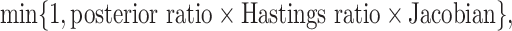 |
where the posterior ratio is the posterior of the proposed state
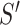 divided by that of the current state
divided by that of the current state
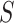 , the Hastings ratio the probability of
moving from
, the Hastings ratio the probability of
moving from 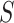 to
to 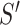 divided by the probability of moving back from
divided by the probability of moving back from 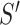 to
to
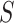 , and the Jacobian is the determinant of
the matrix of partial derivatives of the parameters in the proposed state with respect
to that of the current state. The Hastings ratio has a contribution of
, and the Jacobian is the determinant of
the matrix of partial derivatives of the parameters in the proposed state with respect
to that of the current state. The Hastings ratio has a contribution of
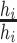 for each node that is
moved, so the Hastings ratio works out as
for each node that is
moved, so the Hastings ratio works out as 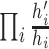 . By using a Bactrian
kernel, the Jacobian is 1. Note that down stretching can lead to increased branch
lengths, and up stretching to reduced branch lengths, for example in the internal branch
below the left branch below the root marked with dots on the nodes in Figure 1b and c, respectively. In Figure 1c, the dots overlap due to the branch length being reduced to
close to zero. While it is still possible for node heights to be proposed that result in
negative branch lengths, if this happens often, automatic tuning parameter optimization
ensures that boldness of the move is reduced, and still a good number of proposals will
be accepted.
. By using a Bactrian
kernel, the Jacobian is 1. Note that down stretching can lead to increased branch
lengths, and up stretching to reduced branch lengths, for example in the internal branch
below the left branch below the root marked with dots on the nodes in Figure 1b and c, respectively. In Figure 1c, the dots overlap due to the branch length being reduced to
close to zero. While it is still possible for node heights to be proposed that result in
negative branch lengths, if this happens often, automatic tuning parameter optimization
ensures that boldness of the move is reduced, and still a good number of proposals will
be accepted.
New epoch flex proposal
The epoch flex-operator randomly selects a lower bound 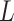 and
upper bound
and
upper bound 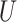 in the range between the root height of
the tree and the youngest leaf (enforcing
in the range between the root height of
the tree and the youngest leaf (enforcing 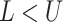 by swapping values
if
by swapping values
if 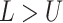 ), then scales the interval with a
random scale value
), then scales the interval with a
random scale value 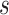 drawn from a Bactrian distribution
(Yang and Rodríguez 2013; Thawornwattana et al. 2018) with respect to the lower bound. Internal
nodes above the upper bound
drawn from a Bactrian distribution
(Yang and Rodríguez 2013; Thawornwattana et al. 2018) with respect to the lower bound. Internal
nodes above the upper bound 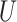 are moved to
accommodate the scaled height of the interval. Internal nodes below
are moved to
accommodate the scaled height of the interval. Internal nodes below
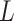 and leaf nodes do not have their
heights changed, which allows caching of the partial calculations for the tree
likelihood for at least the nodes below
and leaf nodes do not have their
heights changed, which allows caching of the partial calculations for the tree
likelihood for at least the nodes below 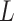 (Fig. 2), making it a more time efficient operator that the tree
stretch operator.
(Fig. 2), making it a more time efficient operator that the tree
stretch operator.
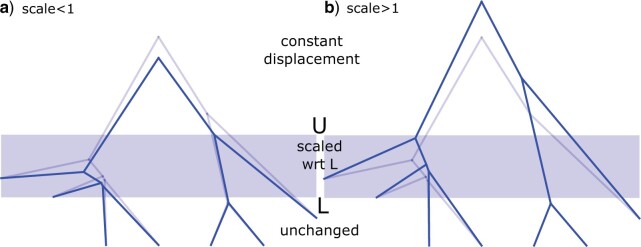
Figure 2.
Epoch operator selects lower bound L, upper bound L, and scale factor s and scale all nodes between L and U. Nodes above U are moved to make space for the newly scaled epoch. a) applied to light tree giving dark tree when scale factor less than one, and b) when scale factor larger than one.
More formally, for every node 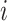 with height
with height
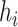 the proposed height
the proposed height
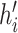 is
is
| (6) |
The Hastings ratio requires taking into account selecting 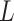 and
and
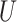 and since these are chosen uniform in
the interval
and since these are chosen uniform in
the interval 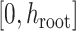 and we have a new root
height
and we have a new root
height 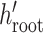 after the proposal the
contribution is
after the proposal the
contribution is 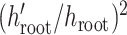 for these
two random values. Furthermore, let there be
for these
two random values. Furthermore, let there be  nodes with heights in
between
nodes with heights in
between 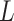 and
and  ,
then the contribution of scaling these
,
then the contribution of scaling these  nodes is
nodes is
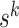 , making the log Hastings ratio
, making the log Hastings ratio
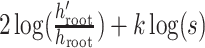 .
.
Like for the tree stretch operator, a tuning parameter  is
used for sampling
is
used for sampling 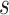 to obtain an optimal acceptance
probability of 0.4. The proposal can result in direct rejection if any of the scaled
nodes are assigned heights below a tip. One way to prevent this from happening is to
enforce the lower bound to be older than the oldest tip, so only part of the tree above
the oldest tip is scaled. Since that part of the tree tends to be less constrained by
tips, bolder proposals are possible, so having both the restricted and unrestricted
version of the operator in the mix can lead to better proposals overall. Note that this
is only an effective strategy if there are a sufficiently large number of internal nodes
above the oldest tip. This is not always the case, for example, influenza data sets can
be sampled over a large duration of an outbreak, and most internal nodes may end up
younger than the oldest sample.
to obtain an optimal acceptance
probability of 0.4. The proposal can result in direct rejection if any of the scaled
nodes are assigned heights below a tip. One way to prevent this from happening is to
enforce the lower bound to be older than the oldest tip, so only part of the tree above
the oldest tip is scaled. Since that part of the tree tends to be less constrained by
tips, bolder proposals are possible, so having both the restricted and unrestricted
version of the operator in the mix can lead to better proposals overall. Note that this
is only an effective strategy if there are a sufficiently large number of internal nodes
above the oldest tip. This is not always the case, for example, influenza data sets can
be sampled over a large duration of an outbreak, and most internal nodes may end up
younger than the oldest sample.
New up/down proposal
Mean clock rate, tree prior parameters, and tree height tend to be highly correlated,
so moving them at the same time (but in opposite direction) can help mixing. The so
called up/down operator in BEAST randomly picks a scale factor 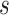 and
scales up the tree with factor
and
scales up the tree with factor 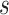 while scaling down
the clock by scaling with factor
while scaling down
the clock by scaling with factor 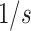 . Tree prior
parameters like birth rate or population size can be scaled in the appropriate direction
at the same time.
. Tree prior
parameters like birth rate or population size can be scaled in the appropriate direction
at the same time.
The new tree stretch and epoch flex operators also change tree height, so we can use
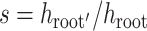 as scale
factor in a similar fashion as for the up/down operator and scale clock rates and tree
prior parameters. For each scaled parameter, a contribution of
as scale
factor in a similar fashion as for the up/down operator and scale clock rates and tree
prior parameters. For each scaled parameter, a contribution of 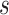 when
scaling up (or
when
scaling up (or 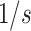 when scaling down) must be added to
the Hasting ratio.
when scaling down) must be added to
the Hasting ratio.
Validation
We performed a well-calibrated simulation study in order to make sure our implementation is correct and performed an analysis of SARS-CoV-2 for community outbreaks in New Zealand.
The Implementation is Correct
To establish correct implementation of BICEPS, we performed a well-calibrated simulation
study sampling 50 tip dates randomly from the interval 0 to 1. To establish correctness of
the new operators, we use a coalescent tree prior with constant population size
(log-normal(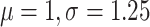 ) distributed), a HKY
model with kappa log-normal(
) distributed), a HKY
model with kappa log-normal(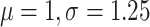 ) distributed and gamma
rate heterogeneity with four categories with shape parameter exponentially distributed
with mean=1, and frequencies Dirichlet(1,1,1,1) distributed. Further, gamma is lower
bounded by 0.1 to give reasonable range of rates (Bouckaert
2020) and frequencies lower bounded by 0.2 to prevent atypical parameter values.
We use a strict clock where the clock rate times tree height has a tight
normal(
) distributed and gamma
rate heterogeneity with four categories with shape parameter exponentially distributed
with mean=1, and frequencies Dirichlet(1,1,1,1) distributed. Further, gamma is lower
bounded by 0.1 to give reasonable range of rates (Bouckaert
2020) and frequencies lower bounded by 0.2 to prevent atypical parameter values.
We use a strict clock where the clock rate times tree height has a tight
normal(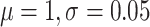 ) prior. Sampling 100
instances from this distribution using MCMC in BEAST 2 (Bouckaert et al. 2019), we get a range of tree heights from 1.03 to 8.8 with
mean 1.6 (note that due to the tips being sampled from 0 to 1, the tree height is lower
bounded by 1) and a clock rate range of 0.1 to a fraction over 1 in our study. With these
trees, we sample sequences of 1000 sites using the sequence generator in BEAST 2.
) prior. Sampling 100
instances from this distribution using MCMC in BEAST 2 (Bouckaert et al. 2019), we get a range of tree heights from 1.03 to 8.8 with
mean 1.6 (note that due to the tips being sampled from 0 to 1, the tree height is lower
bounded by 1) and a clock rate range of 0.1 to a fraction over 1 in our study. With these
trees, we sample sequences of 1000 sites using the sequence generator in BEAST 2.
Tables 1 and 2 show the coverage of true parameter values (and some other statistics) used to
simulate the sequence data by the 95% highest probability density (HPD) intervals
estimated after running MCMC. With 100 experiments, the 95% HPD of the binomial
distribution with 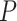 = 0.95 ranges from 91 to 99 inclusive.
All analyzes were run for 20 million samples, which was sufficient to obtain effective
sample sizes of at least 200 for each of the parameters shown in Tables 1 and 2. All coverages
observed are in the expected range, suggesting no problems with the implementation.
= 0.95 ranges from 91 to 99 inclusive.
All analyzes were run for 20 million samples, which was sufficient to obtain effective
sample sizes of at least 200 for each of the parameters shown in Tables 1 and 2. All coverages
observed are in the expected range, suggesting no problems with the implementation.
Table 1.
Coverage of the true value by 95 %HPD estimates from 100 independent runs of BICEPS for various parameters in the model and for different operators added to the standard set of operators.
| Parameter | Epoch flexer | Tree stretcher | Up/down |
|---|---|---|---|
| Tree height | 91 | 95 | 94 |
| Tree length | 94 | 91 | 92 |
| Kappa | 96 | 99 | 99 |
| Gamma shape | 99 | 98 | 96 |
| Population parameter | 97 | 94 | 93 |
| Clock rate | 96 | 99 | 98 |
| Tree prior | 98 | 92 | 93 |
| Frequencies A | 95 | 91 | 92 |
| Frequencies C | 97 | 94 | 95 |
| Frequencies G | 95 | 93 | 95 |
| Frequencies T | 96 | 96 | 96 |
Notes: All coverage is in the expected 91–99 range, providing confidence there are not errors in the operator implementation.
Table 2.
Results for 100 BICEPS analysis with 50 taxa, 250 sites, and unlinked and linked population sizes with standard operators and with the new operators added in
| Coverage | Average ESS | Minimum ESS | |||||
|---|---|---|---|---|---|---|---|
| Linked | Linked | Linked | |||||
| Parameter | Unlinked | Standard | New | Standard | New | Standard | New |
| Tree height | 97 | 93 | 94 | 1640 | 1709 | 116 | 1219 |
| Tree length | 99 | 97 | 94 | 1540 | 1669 | 113 | 1200 |
| Population size | 94 | 97 | 96 | 1709 | 1736 | 783 | 1250 |
| Coalescent prior | 98 | 98 | 94 | 1547 | 1690 | 121 | 1216 |
| Pop size epoch 1 | 97 | 96 | 98 | 1721 | 1731 | 969 | 1358 |
| Pop size epoch 2 | 97 | 96 | 93 | 1704 | 1728 | 250 | 1401 |
| Pop size epoch 3 | 99 | 96 | 95 | 1711 | 1731 | 232 | 1285 |
| Pop size epoch 4 | 97 | 96 | 97 | 1695 | 1711 | 364 | 1343 |
| Pop size epoch 5 | 94 | 95 | 96 | 1693 | 1716 | 289 | 1035 |
| Kappa | 97 | 96 | 93 | 1530 | 1536 | 1114 | 1132 |
| Gamma shape | 92 | 99 | 93 | 1532 | 1543 | 644 | 741 |
| Frequencies A | 91 | 95 | 97 | 790 | 778 | 213 | 342 |
| Frequencies C | 94 | 96 | 94 | 750 | 752 | 390 | 349 |
| Frequencies G | 91 | 93 | 98 | 787 | 760 | 425 | 369 |
| Frequencies T | 92 | 89 | 95 | 789 | 761 | 293 | 228 |
| Clock rate | 96 | 92 | 94 | 1622 | 1690 | 125 | 1182 |
Notes: Coverage as in Table 1 for unlinked BICEPS with standard operators, linked BICEPS with and without new operators. Effective sample size (ESS) shown compares the standard with new operators, where bold numbers indicate the better ESS. Coverage is in the expected 91–99 range for all cases but ESS increase for tree related parameters, in particular the minimum ESS of the 100 runs increases significantly. Coverage of the true value by 95% HPD estimates from 100 independent runs of BICEPS for various parameters in the model and for different operators added to the standard set of operators.
COVID-19 in New Zealand
We use the 887 full genome sequence data from (Douglas et
al., 2021a) containing samples from the 11 community outbreaks in New Zealand
plus closely related sequences from the rest of the world. Further, we use a subsample of
all taxa sampled up to 31 August 2020 consisting of 257 taxa for performance comparison.
The data were analyzed as follows. Genomic sites were partitioned into the three codon
positions, plus noncoding, as described by (Douglas et al.,
2021b). For each partition, we model evolution with an HKY substitution model
with log-normal(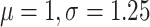 ) prior on kappa,
frequencies estimated with Dirichlet(1,1,1,1) prior, and relative substitution rates with
Dirichlet(1,1,1,1). We use a strict clock model with log-normal(
) prior on kappa,
frequencies estimated with Dirichlet(1,1,1,1) prior, and relative substitution rates with
Dirichlet(1,1,1,1). We use a strict clock model with log-normal(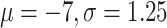 ) prior on mean clock rate
as in (Douglas et al., 2021a,b), and for tree prior we use a Bayesian skyline model (Drummond et al. 2005) with Markov chain distribution on
population sizes and log-normal(
) prior on mean clock rate
as in (Douglas et al., 2021a,b), and for tree prior we use a Bayesian skyline model (Drummond et al. 2005) with Markov chain distribution on
population sizes and log-normal(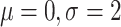 ) on first
population size and compare this with a BICEPS tree prior. MCMC analyses were initialized
with a neighbor joining tree.
) on first
population size and compare this with a BICEPS tree prior. MCMC analyses were initialized
with a neighbor joining tree.
Results
Operator Performance Analysis
Figure 3a–c shows violin plots for effective sample sizes (ESS) obtained with the 100 runs for the posterior, prior, and tree length where the first item was done with standard operators, the second with the epoch flex operator added, and the the third with tree stretch operator added as well. There was some beneficial effect from these operators on the posterior, more so on the prior, as well as the tree length. Site model parameters were practically unaffected by adding these operators, but there was some beneficial effect on the ESS for the clock rate. Note these ESSs were obtained under similar run times, so the plots suggest the operators are moderately beneficial for data simulated under the model, or at least no detrimental to mixing. However, for empirical data, we observed more marked differences (see below).
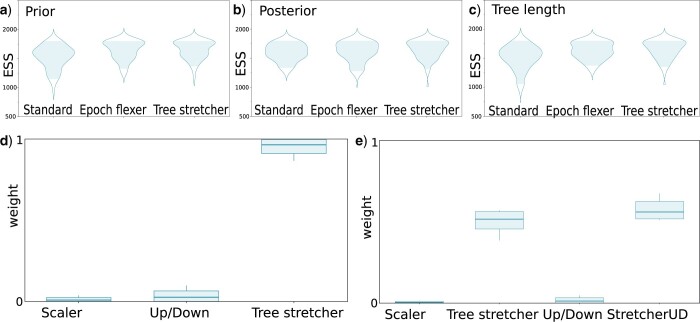
Figure 3.
Performance of epoch flexer and tree stretch operators. Operator are weighted such that run times of various combinations are similar, so ESSs are comparable. ESSs improve a little, and weights favor the new operators over standard ones. a) ESSs on a scale of 500–2500 of the prior for different operator combinations—classic, with epoch operator and with epoch operator and scaler. b) ESSs for posterior, c) ESSs for tree length. d) Weights on a scale of 0–1 assigned to operators by the adaptable operator sampler for standard tree scaler, up/down operator and tree stretcher. e) Weights for standard tree scaler, tree stretcher, up/down operator, and tree stretcher with up/down combination.
Another way to get a sense of the performance of the BICEPS operators compared to standard operators is by employing the adaptable operator sampler (Douglas et al. 2021c). This is an operator that selects among a set of operators by keeping track of relevant performance indicators of the various operators, namely amount of change in node heights, amount of time required to calculate the new state, and probability of acceptance. Together, these factors are used by the adaptable operator sampler to reweigh sets of operators for optimal amount of node height change per unit of time.
Figure 3d and e shows the end weight distribution over the 100 runs of the well-calibrated simulation study for the case where the tree scaler, up/down operator, and tree stretcher were reweighted by an adaptable operator sampler, and Figure 3e the case where a new up/down operator was added. In the first case shown in Figure 3d, an overwhelming amount of weight is distributed towards the tree stretcher. In the second case shown in Figure 3e, about standard operators hardly get any weight assigned, while most of the weight is distributed almost evenly between tree stretcher and new up/down operator, with a slight preference for the up/down operator. This illustrates the new tree stretch and up/down variant perform well when balancing the size of change, the time to recalculate the posterior, and how often the operator is accepted. Since there is no directly comparable version of the epoch flexer, we omitted it from the mix.
COVID-19 Analysis
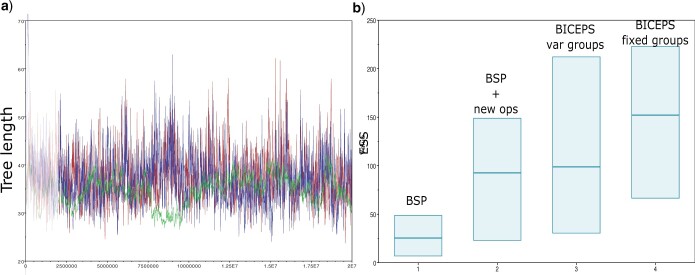
For the 10 runs of the 257 taxa SARS-CoV-2 analysis, MCMC convergences (all parameters having ESSs larger than 200) around 20 million samples for the BICEPS analysis while the BSP analysis still struggles to achieve mixing. In particular, the tree length only achieves single digit ESSs or ESSs less than 20 when taking favorable burn-in values for the 10 runs in Tracer. Figure 4a shows a typical trace of the tree length for one of the BSP and one of the BICEPS analyses, highlighting how BICEPS achieves convergence much faster. Figure 4b displays the poster ESSs over 10 runs and shows that adding the BICEPS operators helps mixing with the BSP model. Further, integrating out parameters as done in the BICEPS model improves ESSs a bit more and fixing group sizes instead of estimating them improves ESSs even more.
Figure 4.
MCMC efficiency a) Trace of tree length for BSP (green line with very low period),
BSP with new operators (blue line with higher period) and BICEPS analysis (red line
forming a satisfying hairy caterpillar pattern). The BSP analysis typically does not
reach an ESS of 10 when the BICEPS analysis already has ESSs around 200. b) Posterior
ESS for 10 runs of BSP, BSP  new operators, and
BICEPS with variable and fixed group sizes. Both new operators and the BICEPS prior
contribute to improving ESSs.
new operators, and
BICEPS with variable and fixed group sizes. Both new operators and the BICEPS prior
contribute to improving ESSs.
The COVID-19 analysis from (Douglas et al., 2021a) required eight chains running 1 billion samples each and were combined to obtain satisfactory ESSs over 200. In contrast, for the same analysis with BICEPS prior and new operators a single run converged in 1 billion samples to ESSs over 200, a factor 8 speed up. Since these analyses use a different though related tree prior, we compare the tree posteriors (see Fig. 5a) and conclude these tree priors lead to very similar results in posterior tree distributions. Clade support is very similar (red dots in Fig. 5a) except for a handful of clades, which may be due to imperfect mixing of the trees, something not unexpected with this many taxa and sequences with relatively little variation (some sequences are even identical).
The estimate of most clade ages and in particular the root ages are consistent with each other. However, the BSP analysis puts the root age a fraction lower (at 1.24 year) than the BICEPS analysis (at 1.25). This can be explained when considering the demographic reconstruction, shown for BSP in Figure 5b, and for BICEPS in Figure 5c. Over all, the reconstructions are quite similar, but note that the population size estimates near the root (right-hand side of plots) are lower and with higher uncertainty for the BSP reconstruction. The BICEPS reconstruction assumes a constant population size for each epoch and number of coalescent intervals are fixed to 29 or 30 (making 30 groups for 887 taxa). Therefore, the last 29 coalescent events to the root are assumed to be under a constant population. The BSP analysis on the other hand estimates group sizes, and it is 22 on average with 95% credible range of 11 to 35, resulting in a smaller population size estimate, hence a slightly reduced root age estimate. When running the BICEPS with 10 epochs instead of 30, the effect is enlarged (giving a root age estimate of 1.29 year).
A general rule of thumb in statistics is that 30 observations are sufficient to estimate the mean of a parameter. Given that epochs can be linked through posterior mean population size estimates in BICEPS, using epochs that cover more than 30 observations does not seem necessary. By default, the model uses 10 groups unless group sizes are larger than 30, then the group count is set to the number of taxa divided by 30. However, if group sizes are less than 6 then group count is set to the number of taxa divided by 6.
HCV Analysis
To demonstrate BICEPS does not only perform well with serially sampled data, we analyzed
a data set of 63 hepatitis-C virus sequences sampled in Egypt in 1993, which was earlier
analyzed in Drummond et al., 2005 and (Stadler et al., 2013). We analyzed with a GTR
substitution model with gamma rate heterogeneity with four categories and fixed the clock
rate at 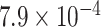 substitutions per site
per year.
substitutions per site
per year.
Where BSP requires 30 million samples for MCMC to converge, BICEPS requires only 5 million samples, demonstrating that BICEPS can be considerably faster. A comparison similar to shown in Figure 5 for SARS-CoV-2 can be found in Appendix A of the Supplementary material. It demonstrates that the BSP and BICEPS models result in very similar tree sets, but the BICEPS analysis can be performed more efficiently, both when tips are sampled through time as in the case of the SARS-CoV-2 data, or when tips are sampled at the same time as for the HCV data. This suggests that we can analyze larger data sets using the BICEPS model than the BSP model. So, the primary benefit of using this model is being able to analyze more sequences and allowing us to investigate processes such as demographic reconstructions in more refined detail.
Generalization to Other Tree Priors
The efficiency of the BICEPS tree prior relies on integrating out population sizes, so that fewer parameters need to be inferred. Here, we used an inverse gamma distribution over population sizes, but a gamma distribution would be a suitable alternative. For models with more parameters, like the besp tree prior which takes sampling in account (Parag et al. 2020), integrating out parameters analytically if possible at all would require nonstandard techniques. Regardless, coalescent models assume that the samples represent a small number of individuals from a much larger population. When this assumption does not hold, birth–death models may be more appropriate. However, it is more challenging to extend the idea of integrating out parameters to birth death sampling models.
For the Yule model (Yule et al. 1924; Aldous 2001), a pure birth model, this is straightforward (Appendix B of the Supplementary material). An epoch version of the Yule model assuming death and sample rates of zero and sampling all extant taxa at the same time (i.e., rho-sampling with rho = 1) can be found in Appendix C of the Supplementary material. The latter is available as “Yule skyline” model in BEAST in the BICEPS package. This provides a flexible prior for the case where tips are not sampled through time, but are all taken at the same time. The model is implemented in BEAST 2 and a well calibrated simulation study (Appendix C of the Supplementary material) passed. For more general cases this approach is hampered by the large number of parameters (birth, death, sampling rate, etc.), and because the tree likelihood is of a form that does not appear to lend itself for integrating out parameters.
The BICEPS and Yule skyline tree priors put coalescent events in approximately equally sized groups in order to reduce noise and provide estimates of population sizes and birth rates respectively with tight uncertainty bounds. An alternative is to split the tree height into equally sized time intervals and use the coalescent and lineage count information in these same sized epochs. Though most epoch boundaries do not coincide with coalescent events any more, this has little impact in the way the mathematics works out but will impact the distribution of coalescent events in the intervals: usually, there will be fewer near the root and more near sampling times. Consequently, uncertainty bounds will become larger near the root and smaller in epochs containing larger numbers of coalescent events.
Primates Analysis
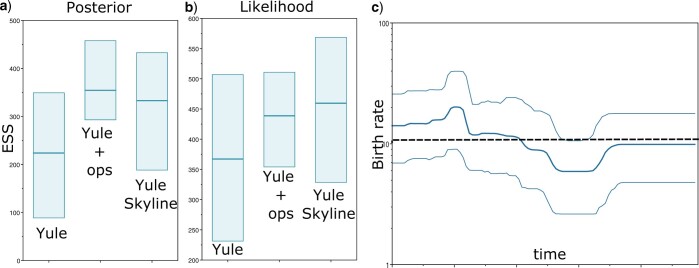
A primate alignment of full mitochondrial genomes with 87 taxa and 19,220 sites (Finstermeier et al. 2013) was analyzed using a GTR substitution model with estimated frequencies, optimized relaxed clock model (Douglas et al. 2021c) and Yule tree prior (see Supplementary material for BEAST 2 XML files for this and associated analyses). Due to the very informative sequence data, this analysis tends to mix slowly because the posterior is very peaked making it hard for standard operators to make bold moves (Zhang and Drummond 2020). Figure 6 shows how adding the BICEPS operators does help mixing of the posterior and the likelihood, demonstrating that adding BICEPS operators allows analyses to run more efficiently. A Yule skyline analysis with the same data shows significant improvements in mixing for both posterior and likelihood compared to the Yule analyses with standard operators, but slight degradation of the posterior ESS though still improved likelihood ESS compared to Yule analyses with BICEPS operators. A birth rate skyline reconstruction through time shows that there is only small variation through time. In fact, Figure 6c shows the mean birth rate under the Yule model, which assumes a constant birth rate throughout the whole tree, as dashed horizontal line. The line fits inside the whole 95% HPD trajectory, which suggests a constant rate of speciation of primates cannot be ruled out.
Figure 6.
Primate analysis. a) ESS over 10 runs for posterior when using Yule with standard operators, Yule with BICEPS operators and Yule skyline with BICEPS operators. b) ESSs for the likelihood. Note the change in scale. c) Reconstruction of birth rates with Yule Skyline showing median and 95% HPD intervals. The dashed line shows the mean birth rate for a Yule analysis.
Conclusions
We introduced a two-headed approach for improving the efficiency of Bayesian inference under epoch models: a flexible tree prior based coalescent epoch model that integrates out population size parameters and a set of new MCMC proposals directly targeting tree lengths. Both these elements contribute to more efficient inference, in particular with SARS-CoV-2 data and with serially sampled sequence data. The behavior of BICEPS tree prior is very similar to that of the popular Bayesian skyline plot and allows for reconstruction of demographic histories through time making it possible to estimate timing and magnitude of population bottlenecks as well as track population expansions through time.
A generalization to a pure birth prior under an epoch model that integrates out birth rate parameters, the Yule skyline model, is detailed in Appendix C of the Supplementary material. Other generalizations integrating out tree prior parameters appear to be mathematically challenging. The benefit of integrating out parameters instead of estimating them through MCMC as well as the more efficient tree operators is that it becomes possible to analyze larger data sets and infer more detailed population histories. Even if the population history is of no interest, but for example the tree topology, timing of origins of clades or evolutionary rate estimates are the topic of investigation, the BICEPS model provides a flexible tree prior that caters for a wide range of tree shapes and sizes with little requirements in terms of prior knowledge, unlike many birth death based priors.
The application of the new tree operators is not limited to the BICEPS tree prior, but can be used in combination with any tree prior. These operators can be expected to contribute to more efficient inference under a wide range of models, and make it possible to include more taxa than is possible with the currently available standard set of operators. This is especially important with the growing amount of sequence data, and allows for more detailed post hoc analyses by techniques such as lineage through time plots, or when location information for taxa is available, introduction through time plots (see Douglas et al. 2020b for an example applied to COVID-19). Most tree operators in BEAST either move a very small number of nodes (often just one), or move all nodes. The tree stretch operators introduced here moves all nodes, while the epoch flex operator moves a large subset of nodes. A tree operator that randomly selects a single node proposes a new height and moves surrounding nodes to accommodate the node height change by minimizing changes in evolutionary distances did not prove to be effective in that it did not increase effective sample sizes per unit of time. It is an open question whether tree operators for Bayesian inference under MCMC that move a small subset of nodes can contribute to the efficiency of MCMC.
The BICEPS tree prior and operators are implemented in BEAST 2 (Bouckaert et al. 2019) and can be used in combination with a large range of different data types, substitution and site models as well, a number of clock models, sampled ancestor trees and in combination with various types of data, including geographical locations, morphological characters, micro satellite, etc.
Acknowledgments
I thank Alexei Drummond and Jordan Douglas for stimulating discussions, Jordan Douglas and Cinthy Jimenez-Silva for proofreading the manuscript and anonymous reviewers for providing useful comments that helped improve the manuscript.
Footnotes
Though the notation of Drummond et al., 2005 is
mostly followed here, we use 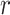 instead of
instead of 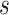 since
later
since
later 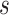 will be used to denote scale factors for
MCMC proposals.
will be used to denote scale factors for
MCMC proposals.
Availability
The open source BICEPS package for BEAST 2 (Bouckaert et al. 2019) is available under GPL at https://github.com/rbouckaert/biceps. An analysis can be set up through BEAUti, the user friendly GUI for BEAST, both for the BICEPS and Yule Skyline models.
Funding
The work was supported by a Marsden [18-UOA-096] from the Royal Society of New Zealand, a contract from the Health Research Council of New Zealand (20/1018), and Te Punaha Matatini COVID Modelling Programme via the COVID-19 Innovation Acceleration Fund managed by the Ministry of Business, Innovation, and Employment.
Supplementary material
BEAST XML files used in the experiments are available at https://github.com/rbouckaert/biceps/releases/tag/v0.0.1.
References
- Aldous D.J. 2001. Stochastic models and descriptive statistics for phylogenetic trees, from Yule to today. Stat. Sci. 16(1):23–34. [Google Scholar]
- Bouckaert R., Vaughan T.G., Barido-Sottani J., Duchêne S., Fourment M., Gavryushkina A., Heled J., Jones G., Kühnert D., De Maio N., Matschiner M., Mendes F., Müller N., Ogilvie H., du Plessis L., Popinga A., Rambaut A., Rasmussen D., Siveroni I., Suchard M., Wu C.-H., Xie D., Zhang C., Stadler T., Drummond A.. 2019. BEAST 2.5: an advanced software platform for Bayesian evolutionary analysis. PLoS Comput. Biol. 15(1):e1006650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bouckaert R.R. 2020. OBAMA: OBAMA for Bayesian amino-acid model averaging. PeerJ 8:e9460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Campos P.F., Willerslev E., Sher A., Orlando L., Axelsson E., Tikhonov A., Aaris-S⊘rensen K., Greenwood A.D., Kahlke R.-D., Kosintsev P., et al. 2010. Ancient DNA analyses exclude humans as the driving force behind late Pleistocene musk ox (Ovibos moschatus) population dynamics. Proc. Natl. Acad. Sci. USA 107(1):5675–5680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Douglas J., Geoghegan J.L., Hadfield J., Bouckaert R., Storey M., Ren X., de Ligt J., French N., Welch D.. 2021a. Real-time genomics for tracking severe acute respiratory syndrome coronavirus 2 border incursions after virus elimination, New Zealand. Emerg. Infect. Dis. 27(1):2361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Douglas J., Mendes F.K., Bouckaert R., Xie D., Jiménez-Silva C.L., Swanepoel C., de Ligt J., Ren X., Storey M., Hadfield J., Simpson C.R., Geoghegan J.L., Drummond A.J., Welch D.. 2021b. Phylodynamics reveals the role of human travel and contact tracing in controlling the first wave of COVID-19 in four island nations. Virus Evol. 7. veab052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Douglas J., Zhang R., Bouckaert R.. 2021c. Adaptive dating and fast proposals: revisiting the phylogenetic relaxed clock model. PLoS Comput. Biol. 17(1):e1008322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drummond A.J., Bouckaert R.R.. 2015. Bayesian evolutionary analysis with BEAST. Cambridge University Press. [Google Scholar]
- Drummond A.J., Rambaut A., Shapiro B., Pybus O.G.. 2005. Bayesian coalescent inference of past population dynamics from molecular sequences. Mol. Biol. Evol. 22(1):1185–1192. [DOI] [PubMed] [Google Scholar]
- Felsenstein J. 1981. Evolutionary trees from DNA sequences: a maximum likelihood approach. J. Mol. Evol. 17(1):368–376. [DOI] [PubMed] [Google Scholar]
- Finstermeier K., Zinner D., Brameier M., Meyer M., Kreuz E., Hofreiter M., Roos C.. 2013. A mitogenomic phylogeny of living primates. PLoS One 8(1):e69504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gill M.S., Lemey P., Faria N.R., Rambaut A., Shapiro B., Suchard M.A.. 2013. Improving Bayesian population dynamics inference: a coalescent-based model for multiple loci. Mol. Biol. Evol. 30(1):713–724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Green P. 1995. Reversible jump Markov chain Monte Carlo computation and Bayesian model determination. Biometrika 82: 711–732. [Google Scholar]
- Hill V., Baele G.. 2019. Bayesian estimation of past population dynamics in BEAST 1.10 using the Skygrid coalescent model. Mol. Biol. Evol. 36(1):2620–2628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holder M.T., Lewis P.O., Swofford D.L., Larget, B.. 2005. Hastings ratio of the local proposal used in Bayesian phylogenetics. Syst. Biol. 54(1):961–965. [DOI] [PubMed] [Google Scholar]
- Jones G. 2017. Algorithmic improvements to species delimitation and phylogeny estimation under the multispecies coalescent. J. Math. Biol. 74(1-2):447–467. [DOI] [PubMed] [Google Scholar]
- Kingman J.F.C. 1982. The coalescent. Stoch. Process. Appl. 13(1):235–248. [Google Scholar]
- Kuhner M.K., Yamato J., Felsenstein J.. 1998. Maximum likelihood estimation of population growth rates based on the coalescent. Genetics 149(1):429–434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu L., Pearl D.K., Brumfield R.T., Edwards S.V.. 2008. Estimating species trees using multiple-allele DNA sequence data. Evolution 62(1):2080–2091. [DOI] [PubMed] [Google Scholar]
- Miller W., Schuster S.C., Welch A.J., Ratan A., Bedoya-Reina O.C., Zhao F., Kim H.L., Burhans R.C., Drautz D.I., Wittekindt N.E., et al. 2012. Polar and brown bear genomes reveal ancient admixture and demographic footprints of past climate change. Proc. Natl. Acad. Sci. USA 109(1):E2382–E2390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Minin V.N., Bloomquist E.W., Suchard M.A.. 2008. Smooth skyride through a rough skyline: Bayesian coalescent-based inference of population dynamics. Mol. Biol. Evol. 25(1):1459–1471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ogilvie H.A., Bouckaert R.R., Drummond A.J.. 2017. StarBEAST2 brings faster species tree inference and accurate estimates of substitution rates. Mol. Biol. Evol. 34(1):2101–2114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parag K.V., du Plessis L., Pybus O.G.. 2020. Jointly inferring the dynamics of population size and sampling intensity from molecular sequences. Mol. Biol. Evol. 37(1):2414–2429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parag K.V., Pybus O.G.. 2019. Robust design for coalescent model inference. Syst. Biol. 68(1):730–743. [DOI] [PubMed] [Google Scholar]
- Pedro N., Brucato N., Fernandes V., André M., Saag L., Pomat W., Besse C., Boland A., Deleuze J.-F., Clarkson C., Sudoyo H., Metspalu M., Stoneking M., Cox M.P., Leavesley M., Pereira L., Ricaut F.-X.. 2020. Papuan mitochondrial genomes and the settlement of Sahul. J. Hum. Genet. 65(1):875–887. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pybus O.G., Rambaut A., Harvey P.H.. 2000. An integrated framework for the inference of viral population history from reconstructed genealogies. Genetics 155(1):1429–1437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rambaut A., Pybus O.G., Nelson M.I., Viboud C., Taubenberger J.K., Holmes E.C.. 2008. The genomic and epidemiological dynamics of human influenza A virus. Nature 453(1):615–619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shapiro B., Drummond A.J., Rambaut A., Wilson M.C., Matheus P.E., Sher A.V., Pybus O.G., Gilbert M.T.P., Barnes I., Binladen J., Willerslev E., Hansen A.J., Baryshnikov G.F., Burns J. A., Davydov S., Driver J.C., Froese D.G., Harington C.R., Keddie G., Kosintsev P., Kunz M.L., Martin L.D., Stephenson R.O., Storer J., Tedford R., Zimov S., Cooper A.. 2004. Rise and fall of the Beringian steppe bison. Science 306(1):1561–1565. [DOI] [PubMed] [Google Scholar]
- Stadler T., Kühnert D., Bonhoeffer S., Drummond A.J.. 2013. Birth–death skyline plot reveals temporal changes of epidemic spread in HIV and hepatitis C virus (HCV). Proc. Natl. Acad. Sci. USA 110(1):228–233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strimmer K., Pybus O.G.. 2001. Exploring the demographic history of DNA sequences using the generalized skyline plot. Mol. Biol. Evol. 18(1):2298–2305. [DOI] [PubMed] [Google Scholar]
- Thawornwattana Y., Dalquen D., Yang Z.. 2018. Designing simple and efficient Markov chain Monte Carlo proposal kernels. Bayesian Anal. 13(1):1037–1063. [Google Scholar]
- Yang Z., Rodríguez C.E.. 2013. Searching for efficient Markov chain Monte Carlo proposal kernels. Proc. Natl. Acad. Sci. USA 110(1): 19307–19312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yule G.U. 1924. A mathematical theory of evolution, based on the conclusions of Dr. JC Willis. Philos. Trans. R. Soc. Lond. Ser. B 213(402-410):21–87. [Google Scholar]
- Zhang R., Drummond A.. 2020. Improving the performance of Bayesian phylogenetic inference under relaxed clock models. BMC Evol. Biol. 20:1–28. [DOI] [PMC free article] [PubMed] [Google Scholar]