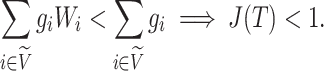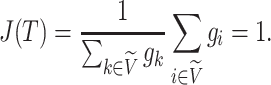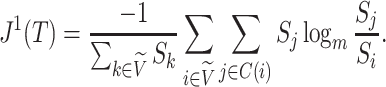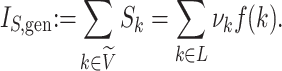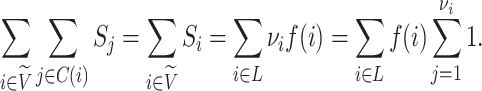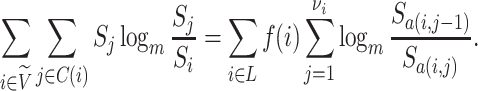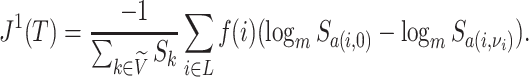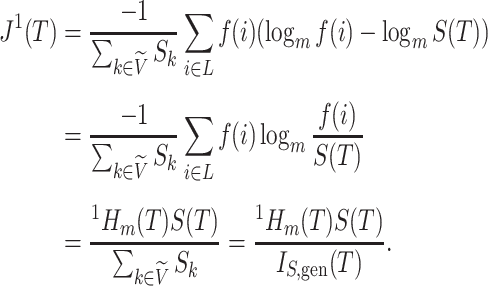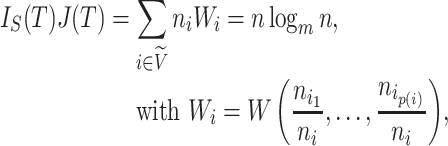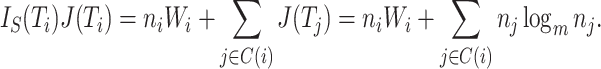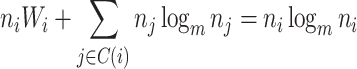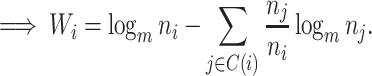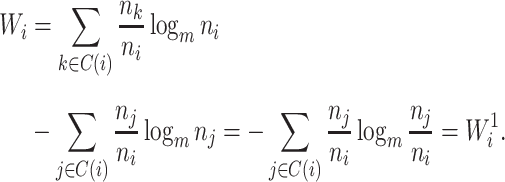Abstract
Balance indices that quantify the symmetry of branching events and the compactness of trees are widely used to compare evolutionary processes or tree-generating algorithms. Yet, existing indices are not defined for all rooted trees, are unreliable for comparing trees with different numbers of leaves, and are sensitive to the presence or absence of rare types. The contributions of this article are twofold. First, we define a new class of robust, universal tree balance indices. These indices take a form similar to Colless’ index but can account for population sizes, are defined for trees with any degree distribution, and enable meaningful comparison of trees with different numbers of leaves. Second, we show that for bifurcating and all other full m-ary cladograms (in which every internal node has the same out-degree), one such Colless-like index is equivalent to the normalized reciprocal of Sackin’s index. Hence, we both unify and generalize the two most popular existing tree balance indices. Our indices are intrinsically normalized and can be computed in linear time. We conclude that these more widely applicable indices have the potential to supersede those in current use. [Cancer; clone tree; Colless index; Sackin index; species tree; tree balance.]
Tree balance indices—most notably those credited to Sackin (1972) and Colless (1982)—are widely used to describe speciation processes, compare cladograms, and assert the correctness of tree reconstruction methods (Shao and Sokal 1990; Mooers and Heard 1997; Fischer et al. 2021). Existing tree balance indices have several important flaws. First, they cannot be applied to any tree in which any node has only one descendant. Second, existing indices are unreliable for comparing trees with different numbers of leaves. Third, because they do not account for population sizes, these indices are sensitive to the omission or inclusion of rare types. The latter issue is, for example, a problem in oncology (Chkhaidze et al. 2019; Scott et al. 2020), where methods for determining and classifying evolutionary modes have clinical value (Davis et al. 2017; Maley et al. 2017).
Here, we develop a new class of robust, universal tree balance indices. Our definitions not only extend the tree balance concept and open up new applications but also unify the two main approaches to quantifying balance as proposed by Sackin and Colless. We describe several general advantages of our indices compared to those in current use.
Materials and Methods
Rooted Trees
We consider exclusively rooted trees in which all edges are oriented away from the root (which will be topmost in our figures). This orientation defines a natural order on the tree, from top to bottom: edges descend from the root to the other internal nodes and finally to the terminal nodes or leaves. The out-degree of a node 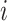 , written
, written 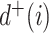 , is the number of direct descendants, ignoring any subtrees in which all nodes have zero size. Internal nodes have out-degree at least one, whereas leaves have out-degree zero. If all internal nodes have out-degree 1, then the tree is called linear. If all internal nodes have out-degree
, is the number of direct descendants, ignoring any subtrees in which all nodes have zero size. Internal nodes have out-degree at least one, whereas leaves have out-degree zero. If all internal nodes have out-degree 1, then the tree is called linear. If all internal nodes have out-degree 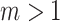 then the tree is a full
then the tree is a full 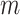 -ary tree, and if
-ary tree, and if 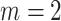 then it is also called bifurcating (such as Fig. 1a,b).
then it is also called bifurcating (such as Fig. 1a,b).
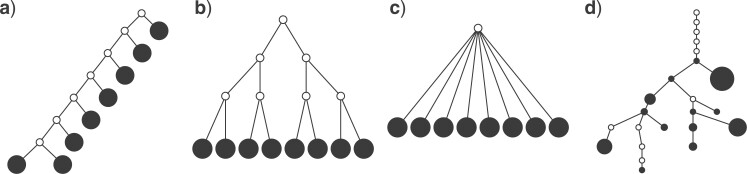
Figure 1.
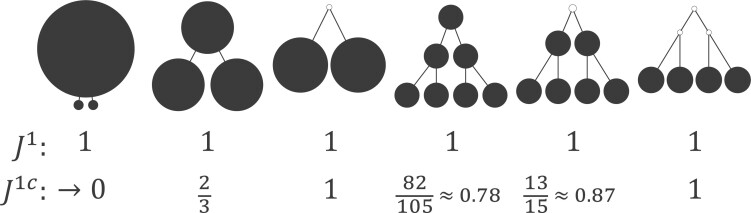
Contrasting trees. a) Caterpillar tree with 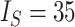 ,
, 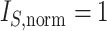 ,
, 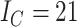 ,
, 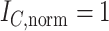 ,
,  ,
, 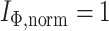 . b) Fully symmetric bifurcating tree with
. b) Fully symmetric bifurcating tree with 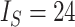 ,
, 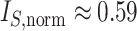 ,
, 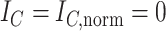 ,
,  ,
, 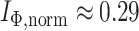 . c) Star tree with
. c) Star tree with 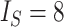 ,
, 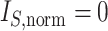 ,
, 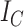 and
and 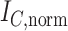 undefined,
undefined, 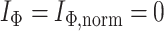 . d) Clone tree of the lung tumor CRUK0065 in the TRACERx cohort (Jamal-Hanjani et al. 2017). In the clone tree, nodes represented by empty circles correspond to extinct clones, and the diameters of other nodes are proportional to the corresponding clone population sizes.
. d) Clone tree of the lung tumor CRUK0065 in the TRACERx cohort (Jamal-Hanjani et al. 2017). In the clone tree, nodes represented by empty circles correspond to extinct clones, and the diameters of other nodes are proportional to the corresponding clone population sizes.
Some other tree topologies have particular names. A caterpillar tree (Fig. 1a) is a bifurcating tree in which every internal node except one has exactly one leaf. A fully symmetric tree (Fig. 1b) is such that every internal node with the same depth has the same degree or, equivalently, for each internal node 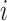 all the subtrees rooted at
all the subtrees rooted at 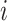 are identical. A star tree (Fig. 1c) is a tree whose leaves are all attached to the root, which is the only internal node.
are identical. A star tree (Fig. 1c) is a tree whose leaves are all attached to the root, which is the only internal node.
Node Sizes, Tree Magnitudes, and Leafy Trees
Although our definitions can be applied in other contexts, we will assume that nodes correspond to biological taxa or clones, and on this basis, we assign non-negative node sizes. If we know (or care) only whether each type is extant or extinct—as is typical in taxonomy—then we assign size zero to every node representing an extinct type, and size one otherwise. If nodes represent clones with known population sizes—as is often the case in studies of cancer and microbial evolution—then each node size is equal to the population size of the corresponding clone. The magnitude of a tree or subtree is then defined as the sum of its node sizes (we use magnitude here because a tree’s size is conventionally defined as its number of nodes). We define a leafy tree as a rooted tree in which all internal nodes have size zero.
Cladograms, Taxon Trees, and Clone Trees
Tree types can also be defined in terms of what they represent. Following Podani (2013), we distinguish between two representations used in systematic biology.
We define a cladogram as a rooted tree in which internal nodes represent hypothetical extinct ancestors, leaves represent extant biological taxa, and edges represent evolutionary relationships. This is equivalent to the synchronous cladogram definition of Podani (2013). Every cladogram is by definition a leafy tree, with a magnitude equal to its number of leaves. A common conception is that only bifurcating cladograms can be considered fully resolved. However, the linear two-node cladogram is appropriate for representing serial anagenesis (in which each descendant replaces its ancestor), while budding (in which an ancestor produces a descendant and remains extant) can give rise to cladogram nodes with an out-degree greater than two (Podani 2013). Hence, there is no restriction on cladogram node degrees. An extant ancestor is represented in a cladogram by a leaf stemming from the internal ancestor node, in which case, as Podani notes, “an ancestor is identical to an extant taxon connected directly to it.”
Alternatively, extant or known ancestors may be represented uniquely by internal nodes (like in a genealogy with overlapping generations). Such diagrams are known to organismal biologists as species trees or taxon trees, and to oncologists as clone trees. We define a taxon tree as a rooted tree in which all nodes represent biological taxa, and edges represent ancestor-descendant relationships. Similarly, a clone tree is defined as a rooted tree in which each node represents a clone (a set of cells that share alterations of interest due to common descent), and edges represent the chronology of alterations. Both taxon tree and clone tree fit the achronous tree definition of Podani (2013). Clone tree nodes can have any out-degree, including 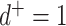 , and each node—including internal nodes—can be associated with a non-negative size, as illustrated in Figure 1d.
, and each node—including internal nodes—can be associated with a non-negative size, as illustrated in Figure 1d.
When nodes are associated with sizes, the addition of subtrees comprising even vanishingly small nodes can change leaves into internal nodes and so substantially change the value of existing tree balance indices. This behavior is unsatisfactory because relatively small nodes typically represent either newly created types that have yet to experience evolutionary forces or types on the verge of extinction, and in either case convey negligible information about the mode of evolution. Data sets may also omit rare types due to sampling error or because genetic sequencing methods have imperfect sensitivity (Turajlic et al. 2018).
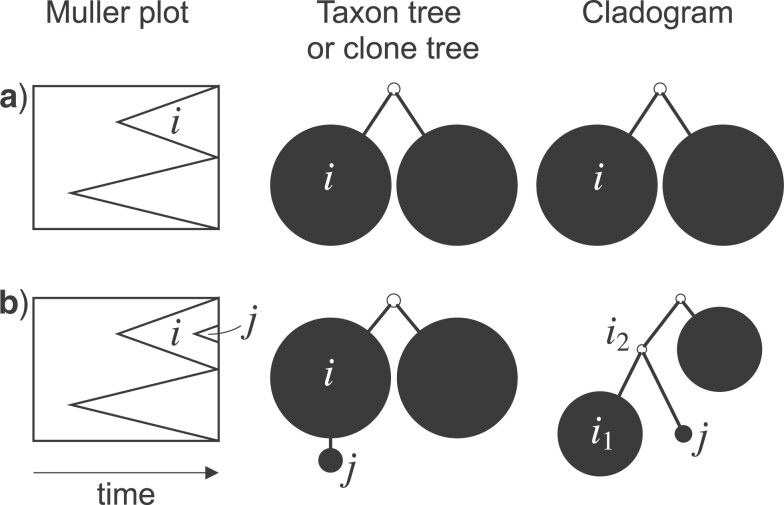
The change due to the addition of terminal nodes is greater when the tree is a cladogram rather than a taxon or clone tree. For example, when a three-node, two-leaf tree (Fig. 2a) is augmented by adding a node 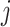 to a leaf
to a leaf 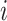 (Fig. 2b), the three original nodes retain their positions in the clone tree (middle column of Fig. 2), but in the cladogram (right column) node
(Fig. 2b), the three original nodes retain their positions in the clone tree (middle column of Fig. 2), but in the cladogram (right column) node 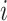 becomes two nodes (
becomes two nodes (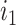 and
and 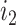 ), the larger of which is now further from the root (see Podani (2013) for further illustrations of this difference). As the size of the new node
), the larger of which is now further from the root (see Podani (2013) for further illustrations of this difference). As the size of the new node 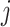 is continuously reduced to zero, the clone tree changes continuously, whereas the cladogram undergoes an abrupt change of topology when the size of node
is continuously reduced to zero, the clone tree changes continuously, whereas the cladogram undergoes an abrupt change of topology when the size of node 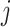 reaches zero. We conclude that the taxon tree or clone tree representation is more robust than the cladogram representation in the general case in which nodes are associated with sizes and ancestors can be extant. Also, an index that accounts for nonzero internal node sizes can be made more robust than one that does not. Accordingly, we will define indices for the more general domain of clone trees and then obtain results for cladograms as a special case.
reaches zero. We conclude that the taxon tree or clone tree representation is more robust than the cladogram representation in the general case in which nodes are associated with sizes and ancestors can be extant. Also, an index that accounts for nonzero internal node sizes can be made more robust than one that does not. Accordingly, we will define indices for the more general domain of clone trees and then obtain results for cladograms as a special case.
Figure 2.
Muller plots (left column), taxon or clone trees (middle column), and cladograms (right column) representing evolution by splitting only (a) and both splitting and budding (b). In a Muller plot, polygons represent proportional subpopulation sizes (vertical axis) over time (horizontal axis), and each descendant is shown emerging from its parent polygon. In the trees, nodes represented by empty circles correspond to extinct types.
Existing Tree Balance Indices
The most widely used tree balance indices are in fact imbalance indices, such that more balanced trees are assigned smaller values. These indices were introduced to study cladograms; they take no account of node size, and, even after applying standard normalizations, they are appropriate only for comparing trees with equal numbers of leaves. The most popular are Sackin’s index and Colless’ index.
Sackin’s index
Let 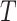 be a tree with a set of leaves
be a tree with a set of leaves 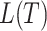 . For a leaf
. For a leaf 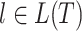 , let
, let 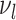 be the number of internal nodes between
be the number of internal nodes between 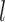 and the root, which is included in the count. Then, the index credited to Sackin (1972) is
and the root, which is included in the count. Then, the index credited to Sackin (1972) is
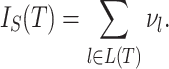 |
For two bifurcating trees with the same number of leaves, a less balanced tree has higher values of 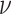 as the tree is in a sense less compact (compare trees a and b in Fig. 1).
as the tree is in a sense less compact (compare trees a and b in Fig. 1).
Since the value tends to increase with the number of nodes, Shao and Sokal (1990) proposed normalizing 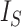 with respect to trees on
with respect to trees on 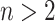 leaves by subtracting its minimum possible value for such trees and then dividing by the difference between the maximum and minimum possible values. The minimal
leaves by subtracting its minimum possible value for such trees and then dividing by the difference between the maximum and minimum possible values. The minimal 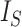 is reached on the star tree, such as tree c in Figure 1, and hence
is reached on the star tree, such as tree c in Figure 1, and hence 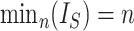 . The maximum is attained on the caterpillar tree, such as tree a:
. The maximum is attained on the caterpillar tree, such as tree a:
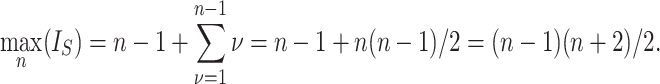 |
The normalized index is then
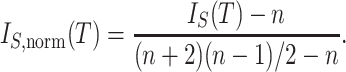 |
This normalized index is not very satisfactory as a balance index because it fails to capture an intuitive notion of balance. For example, it is not obvious why a fully symmetric tree (b) should be considered less balanced than the star tree (c) in Figure 1, yet its 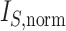 value is much larger. To address this issue, Shao and Sokal (1990) further suggested normalizing
value is much larger. To address this issue, Shao and Sokal (1990) further suggested normalizing 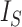 relative to its extremal values among trees with the same number of internal nodes as well as the same number of leaves. But even then the index remains unreliable for comparing trees with different numbers of leaves. For example, the index is 1 for every caterpillar tree, yet long caterpillar trees are intuitively less balanced than short ones. The conventional
relative to its extremal values among trees with the same number of internal nodes as well as the same number of leaves. But even then the index remains unreliable for comparing trees with different numbers of leaves. For example, the index is 1 for every caterpillar tree, yet long caterpillar trees are intuitively less balanced than short ones. The conventional 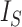 normalizations are not defined for trees containing linear parts. Moreover, since
normalizations are not defined for trees containing linear parts. Moreover, since 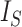 does not account for node size, it is sensitive to the addition or removal of subtrees comprising relatively small nodes.
does not account for node size, it is sensitive to the addition or removal of subtrees comprising relatively small nodes.
Colless’ index
For an internal node 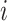 of a bifurcating tree
of a bifurcating tree 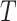 , define
, define 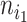 as the number of leaves of the left branch of the subtree rooted at
as the number of leaves of the left branch of the subtree rooted at 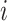 , and
, and 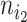 as the number of leaves of the right branch. Then, the index defined by Colless (1982) is
as the number of leaves of the right branch. Then, the index defined by Colless (1982) is
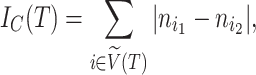 |
where 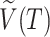 is the set of all internal nodes of
is the set of all internal nodes of 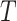 . The index can be normalized for the set of trees on
. The index can be normalized for the set of trees on 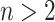 leaves by dividing by its maximal value,
leaves by dividing by its maximal value, 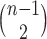 , which is reached on the caterpillar tree (as in Fig. 1a).
, which is reached on the caterpillar tree (as in Fig. 1a).
Because Colless’ index cannot be applied to multifurcating trees, Mir et al. (2018) recently introduced a family of Colless-like balance indices, including 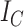 as a special case. Each of these indices
as a special case. Each of these indices 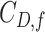 is determined by a weight function
is determined by a weight function 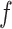 , which assigns a size to each subtree as a function of its out-degree, and a dissimilarity function
, which assigns a size to each subtree as a function of its out-degree, and a dissimilarity function 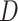 . By definition of
. By definition of 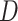 , Colless-like indices are zero if and only if each internal node divides its descendants into subtrees of equal size. But since these indices are normalized by dividing by the maximal value for trees on the same number of leaves, they are unreliable for comparing trees with different numbers of leaves. In common with Sackin’s index, the total cophenetic index
, Colless-like indices are zero if and only if each internal node divides its descendants into subtrees of equal size. But since these indices are normalized by dividing by the maximal value for trees on the same number of leaves, they are unreliable for comparing trees with different numbers of leaves. In common with Sackin’s index, the total cophenetic index 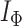 (Mir et al. 2013) (see Appendix), and other existing indices (surveyed by Fischer et al. (2021)), the Colless-like indices so far defined do not account for node sizes and can be applied only to trees in which all nodes have out-degree greater than one.
(Mir et al. 2013) (see Appendix), and other existing indices (surveyed by Fischer et al. (2021)), the Colless-like indices so far defined do not account for node sizes and can be applied only to trees in which all nodes have out-degree greater than one.
Desirable Properties of a Universal, Robust Tree Balance Index
Our aim is to derive a tree balance index 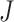 that is useful for classifying and comparing rooted trees that can have any distributions of node degrees and node sizes. Here, we specify four desirable properties that such an index should have. The first two axioms relate to extrema. We will call an index universal if it is defined for trees with any degree distribution and obeys these first two axioms. An index that conforms to the other three axioms—which are relevant only when nodes can have arbitrary sizes—will be called robust.
that is useful for classifying and comparing rooted trees that can have any distributions of node degrees and node sizes. Here, we specify four desirable properties that such an index should have. The first two axioms relate to extrema. We will call an index universal if it is defined for trees with any degree distribution and obeys these first two axioms. An index that conforms to the other three axioms—which are relevant only when nodes can have arbitrary sizes—will be called robust.
We will begin by introducing some additional notation (see also Table 1). For a tree 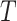 , we will use
, we will use 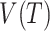 to denote the set of all nodes of
to denote the set of all nodes of 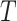 , which we will abbreviate to
, which we will abbreviate to 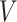 when the identity of the tree is unambiguous. Let
when the identity of the tree is unambiguous. Let 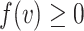 denote the size of node
denote the size of node 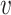 . Then,
. Then, 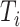 denotes the subtree rooted at node
denotes the subtree rooted at node 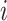 (i.e., the subtree that contains node
(i.e., the subtree that contains node 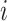 and all its descendants);
and all its descendants); 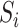 is the magnitude of
is the magnitude of 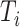 ; and
; and 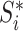 is the magnitude of
is the magnitude of 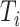 excluding its root:
excluding its root:
Table 1.
Notation used throughout this article
Properties of a node 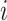
|
|
|---|---|
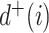
|
Out-degree |
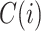
|
Set of children |
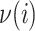
|
Depth |
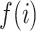
|
Size |
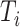
|
Subtree rooted at 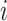
|
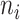
|
Number of leaves of 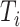
|
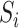
|
Magnitude of 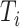 (sum of node sizes) (sum of node sizes) |
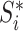
|
Magnitude of 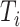 excluding its root excluding its root |
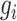
|
Importance factor |
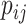
|
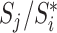 , where
, where 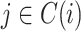
|
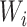
|
Balance score |
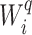
|
Balance score based on 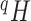
|
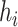
|
Nonroot dominance factor |
| Sets of nodes | |
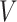
|
All nodes |
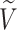
|
Internal nodes 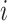 such that such that 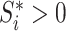
|
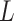
|
Leaves |
| Entropies and tree balance indices | |
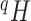
|
Generalized entropy with parameter 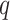
|
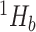
|
Shannon entropy with base 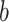
|
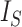
|
Sackin’s index |
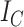
|
Colless’ index |
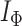
|
Total cophenetic index |
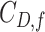
|
Colless-like index |
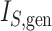
|
Generalized Sackin’s index |
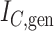
|
Generalized Colless’ index |
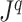
|
Tree balance index based on 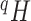
|
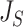
|
Normalized inverse Sackin index |
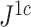
|
A conservative tree balance index |
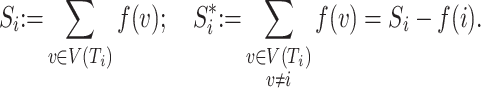 |
We will use 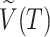 or simply
or simply 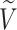 to denote the set of all internal nodes such that
to denote the set of all internal nodes such that 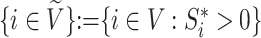 .
.
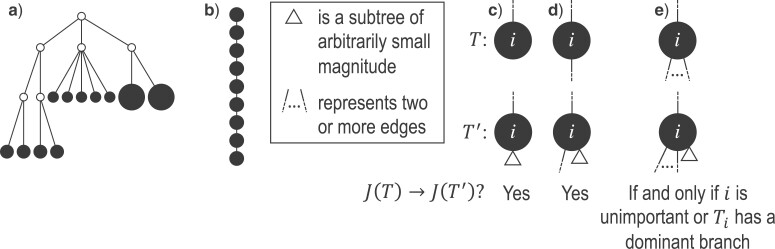
Conventionally, a tree is considered maximally balanced only if every internal node splits its descendants into subtrees on the same number of leaves (Shao and Sokal 1990). We generalize this concept by requiring that every internal node splits its descendants into at least two subtrees of equal magnitude, as in Figure 3a. We call this the equal splits property, and we make it a necessary and sufficient condition for maximal balance.
Figure 3.
a) A tree in which each internal node has null size and splits its descendants into subtrees of equal magnitude, and hence 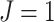 . This tree can be considered balanced only according to an index that accounts for node size. b) A linear tree, for which
. This tree can be considered balanced only according to an index that accounts for node size. b) A linear tree, for which 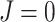 . c–e) A robust, universal tree balance index
. c–e) A robust, universal tree balance index 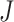 is insensitive to the addition of a subtree of arbitrarily small magnitude if it is added to a leaf (a) or a nonroot node with out-degree 1 (b), but not necessarily if the subtree is added to a nonroot node with greater out-degree (c).
is insensitive to the addition of a subtree of arbitrarily small magnitude if it is added to a leaf (a) or a nonroot node with out-degree 1 (b), but not necessarily if the subtree is added to a nonroot node with greater out-degree (c).
Axiom 1 (Maximum value).
for all trees
, and
if and only if
has equal splits.
Another convention is that trees with relatively many internal nodes are considered highly imbalanced. According to this convention, linear trees (i.e., trees in which every node 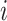 has
has 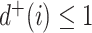 , as in Fig. 3b) should be considered even less balanced than caterpillar trees. Also, given that balance implies branching, the most imbalanced split is one that assigns all descendants to one branch and none to any other branches. Hence our second desirable property:
, as in Fig. 3b) should be considered even less balanced than caterpillar trees. Also, given that balance implies branching, the most imbalanced split is one that assigns all descendants to one branch and none to any other branches. Hence our second desirable property:
Axiom 2 (Minimum value).
for all trees
, and
if and only if
is a linear tree.
Our third desirable property ensures that our index is insensitive to the properties of nodes that have relatively few descendants.
Axiom 3 (Insensitivity).
Let
be a tree and
be one of its leaves. If we create a new tree
from
by adding a subtree with finitely many nodes rooted at
then
as
.
Our fourth axiom ensures that a linear section of a tree is regarded as a maximally unequal split.
Axiom 4 (Linear limit).
Let
be a tree and
with
. Let
be the unique child of
. If we create a new tree
from
by adding additional subtrees with finitely many nodes rooted at
then
as
.
Lastly, we require continuity with respect to varying node size:
Axiom 5 (Continuity).
Suppose we create a new tree
by selecting a node of tree
and changing the node’s size from
to
. Then
as
.
Alternative axioms are considered in the Appendix.
Sensitivity to Changes in Out-degree of Nonroot Nodes
By design, our definition of a robust tree balance index does not require insensitivity to the addition or removal of rare types in all cases. To see why, suppose we transform a tree 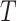 into
into 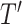 by adding one or more subtrees of arbitrarily small magnitude, attached to a nonroot node
by adding one or more subtrees of arbitrarily small magnitude, attached to a nonroot node 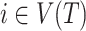 . As illustrated in Figure 3c–e, there are three topologically distinct cases to consider. If
. As illustrated in Figure 3c–e, there are three topologically distinct cases to consider. If 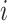 is a leaf of
is a leaf of  (Fig. 3c) or
(Fig. 3c) or 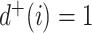 in
in  (Fig. 3d) then
(Fig. 3d) then 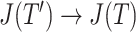 due to Axioms 3 or 4. In the first case,
due to Axioms 3 or 4. In the first case, 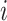 is an unimportant node, which we define to mean that
is an unimportant node, which we define to mean that 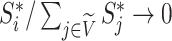 . In the second case, if
. In the second case, if 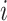 is not an unimportant node in
is not an unimportant node in 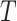 then
then 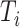 must have a dominant branch, meaning that
must have a dominant branch, meaning that 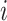 has a child
has a child 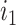 such that
such that 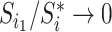 . The third case, when
. The third case, when 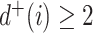 in
in 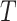 (Fig. 3e), is more complicated. If
(Fig. 3e), is more complicated. If  is an unimportant node in
is an unimportant node in 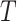 then
then 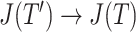 as
as 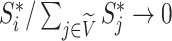 in
in 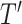 , by Axiom 3. If
, by Axiom 3. If 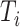 in
in 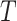 has a dominant branch
has a dominant branch  in
in 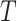 then
then 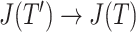 as
as 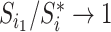 in
in 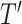 , by Axiom 4. But if neither of those conditions hold then our axioms do not specify the size of the effect on
, by Axiom 4. But if neither of those conditions hold then our axioms do not specify the size of the effect on 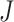 .
.
Although we could modify Axiom 4 so that 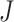 is always insensitive to the addition of relatively low-magnitude subtrees—thus increasing the index’s robustness—we argue that this would undermine its utility as a tree balance index. The balance of a node can be conventionally defined as the extent to which it splits its descendants into multiple subtrees of equal magnitude. By this definition, the attachment of a new, relatively low-magnitude subtree to a perfectly balanced node will create an imbalance even as—in fact especially as—the magnitude of this new subtree, relative to the magnitude of the node’s pre-existing descendants, approaches zero. Therefore, it is desirable for a tree balance index to be sensitive to certain changes in node degree, such that in the third scenario considered above,
is always insensitive to the addition of relatively low-magnitude subtrees—thus increasing the index’s robustness—we argue that this would undermine its utility as a tree balance index. The balance of a node can be conventionally defined as the extent to which it splits its descendants into multiple subtrees of equal magnitude. By this definition, the attachment of a new, relatively low-magnitude subtree to a perfectly balanced node will create an imbalance even as—in fact especially as—the magnitude of this new subtree, relative to the magnitude of the node’s pre-existing descendants, approaches zero. Therefore, it is desirable for a tree balance index to be sensitive to certain changes in node degree, such that in the third scenario considered above, 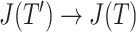 if and only if
if and only if 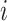 is an unimportant node or
is an unimportant node or  has a dominant branch (Fig. 3e).
has a dominant branch (Fig. 3e).
Results
General Definition of Universal, Robust Tree Balance Indices
Our general definition depends on two continuous functions of subtree magnitudes:
An importance factor
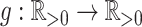 with
with 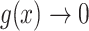 as
as 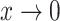 ;
;A balance score
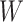 that assigns
that assigns 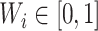 to each internal node
to each internal node 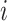 such that
such that 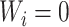 if and only if
if and only if 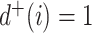 , and
, and 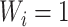 if and only if
if and only if 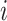 splits its descendants into at least two equal-magnitude subtrees.
splits its descendants into at least two equal-magnitude subtrees.
To allow us to define  more rigorously, let
more rigorously, let  denote the set of vectors with positive components that sum to unity:
denote the set of vectors with positive components that sum to unity:
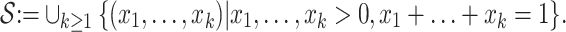 |
Then, 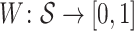 is such that, for all
is such that, for all 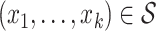 :
:
(Associativity) For every permutation
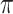 ,
, 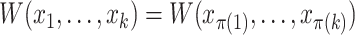 ;
;(Maximum value)
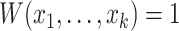 if and only if
if and only if 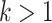 and
and 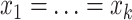 ;
;(Minimum value)
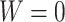 if and only if
if and only if 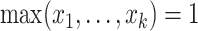 ;
;(Continuity)
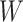 is a continuous function with respect to each of its arguments.
is a continuous function with respect to each of its arguments.
We then define a balance index in terms of subtree magnitudes as
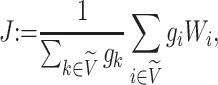 |
(1) |
where
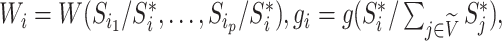 and
and 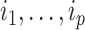 are the children of node
are the children of node 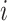 (see Table 1 for a recap of notation). A short proof that this type of index satisfies our five axioms for robustness and universality (Axioms 1–5) is presented in the Appendix.
(see Table 1 for a recap of notation). A short proof that this type of index satisfies our five axioms for robustness and universality (Axioms 1–5) is presented in the Appendix.
The balance score 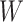 in Equation 1 measures the extent to which an internal node splits its descendants into equal-magnitude subtrees. The importance factor
in Equation 1 measures the extent to which an internal node splits its descendants into equal-magnitude subtrees. The importance factor 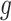 assigns more weight to nodes that are the roots of large subtrees. In biological terms, this means giving more weight to types that have more descendants. Sackin’s and Colless’ indices similarly assign more weight to nodes that have more descendant leaves or are closer to the root. Mooers and Heard (1997) have argued that it is reasonable to put more weight on nodes deeper within the tree because “those nodes are the most informative, as the subclades they define are older and therefore sample longer periods of evolutionary time.”
assigns more weight to nodes that are the roots of large subtrees. In biological terms, this means giving more weight to types that have more descendants. Sackin’s and Colless’ indices similarly assign more weight to nodes that have more descendant leaves or are closer to the root. Mooers and Heard (1997) have argued that it is reasonable to put more weight on nodes deeper within the tree because “those nodes are the most informative, as the subclades they define are older and therefore sample longer periods of evolutionary time.”
A Specific Index Based on the Shannon Entropy
In defining a specific index, we start by opting for the simplest importance factor function: 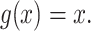 The role of the balance score function
The role of the balance score function 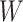 is to quantify the extent to which a set of objects (specifically subtrees) have equal magnitude. A well-known index that satisfies the necessary conditions is the normalized Shannon entropy.
is to quantify the extent to which a set of objects (specifically subtrees) have equal magnitude. A well-known index that satisfies the necessary conditions is the normalized Shannon entropy.
Assume a population is partitioned into 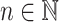 types, with each type
types, with each type 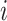 accounting for a proportion
accounting for a proportion 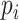 . Then, the Shannon entropy with base
. Then, the Shannon entropy with base 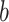 is defined as
is defined as 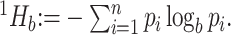 If all types have equal frequencies
If all types have equal frequencies 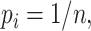 then
then 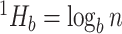 . If the types have unequal sizes, then
. If the types have unequal sizes, then 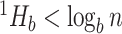 . And if the abundance is mostly concentrated on one type
. And if the abundance is mostly concentrated on one type 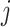 , such that
, such that 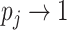 , then
, then 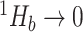 .
.
Let 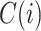 denote the set of children (immediate descendants) of a node
denote the set of children (immediate descendants) of a node 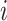 , and for
, and for  let
let 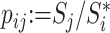 denote the relative magnitude of subtree
denote the relative magnitude of subtree 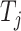 compared to all subtrees attached to
compared to all subtrees attached to 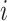 .
.
A balance score based on the normalized Shannon entropy is then
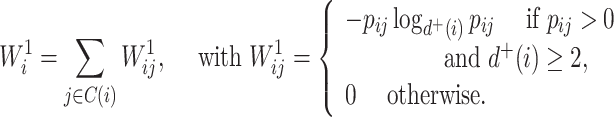 |
(2) |
For every internal node 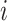 , the number of frequencies
, the number of frequencies 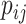 is equal to
is equal to 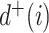 , and if all these frequencies are equal then
, and if all these frequencies are equal then 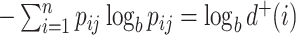 , for any base
, for any base 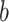 . Changing the base of the logarithm from
. Changing the base of the logarithm from 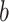 to
to 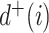 is equivalent to dividing the sum by
is equivalent to dividing the sum by 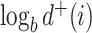 , which implies that
, which implies that 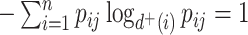 when all the
when all the 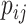 are equal. From aforementioned properties of the Shannon entropy, it then follows that
are equal. From aforementioned properties of the Shannon entropy, it then follows that 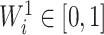 , with
, with 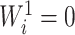 if and only if
if and only if 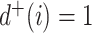 , and
, and 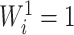 if and only if
if and only if 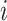 splits its descendants into at least two equal-magnitude subtrees. Therefore, the following specific balance index satisfies our robustness and universality axioms:
splits its descendants into at least two equal-magnitude subtrees. Therefore, the following specific balance index satisfies our robustness and universality axioms:
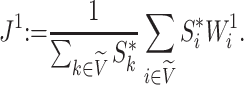 |
(3) |
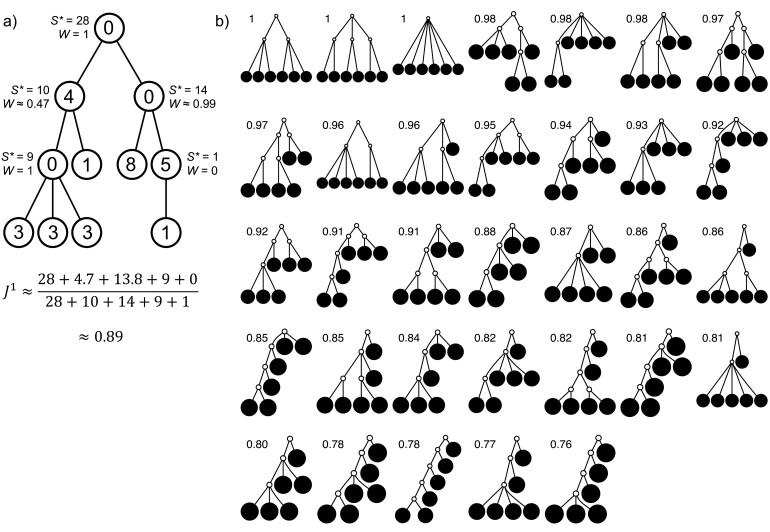
The calculation of 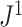 is illustrated in Figure 4a.
is illustrated in Figure 4a.
Figure 4.
a) An example calculation of 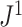 . Numbers shown inside nodes are the node sizes. b) All multifurcating leafy trees on six leaves without linear parts and with equally sized leaves, sorted and labelled by
. Numbers shown inside nodes are the node sizes. b) All multifurcating leafy trees on six leaves without linear parts and with equally sized leaves, sorted and labelled by 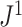 value.
value.
The definition simplifies when we restrict the domain to the set of multifurcating leafy trees in which all leaves have equal size 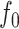 . This includes cladograms in which internal nodes represent extinct ancestors and leaves correspond to equally important extant types. For all internal nodes
. This includes cladograms in which internal nodes represent extinct ancestors and leaves correspond to equally important extant types. For all internal nodes 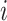 in such trees,
in such trees, 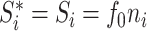 , where
, where 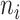 is the number of leaves of the subtree rooted at node
is the number of leaves of the subtree rooted at node 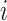 . The general definition of Equation 1 can then be expressed in terms of node balance scores and leaf counts:
. The general definition of Equation 1 can then be expressed in terms of node balance scores and leaf counts:
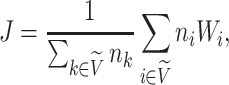 |
(4) |
and the specific definition of Equation 3 becomes
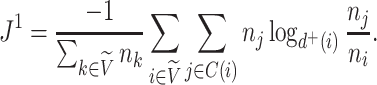 |
(5) |
For example, Figure 4b shows the 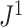 values of all leafy trees on six equally sized leaves without linear parts. Unlike Sackin’s and Colless’ indices,
values of all leafy trees on six equally sized leaves without linear parts. Unlike Sackin’s and Colless’ indices, 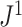 does not consider the caterpillar tree the least balanced of these trees.
does not consider the caterpillar tree the least balanced of these trees.
There are of course many alternative options for 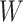 . For example, Colless’ index can be generalized to define a robust, though not universal, tree balance index on the domain of bifurcating trees (see Appendix). Since the Shannon entropy belongs to families of generalized entropies (Rényi 1961; Chao et al. 2014) parameterized by
. For example, Colless’ index can be generalized to define a robust, though not universal, tree balance index on the domain of bifurcating trees (see Appendix). Since the Shannon entropy belongs to families of generalized entropies (Rényi 1961; Chao et al. 2014) parameterized by 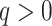 , the above reasoning can be generalized to define a balance score
, the above reasoning can be generalized to define a balance score 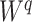 , and hence a robust, universal balance index
, and hence a robust, universal balance index 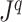 , for every
, for every 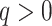 (see Appendix). Other candidates for
(see Appendix). Other candidates for 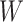 include one minus the variance of the proportional subtree magnitudes or one minus the mean deviation from the median (Mir et al. 2018). We prefer
include one minus the variance of the proportional subtree magnitudes or one minus the mean deviation from the median (Mir et al. 2018). We prefer 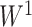 mostly because, as we shall show, it is the only function for which Equation 4 is a generalization of the normalized inverse Sackin index.
mostly because, as we shall show, it is the only function for which Equation 4 is a generalization of the normalized inverse Sackin index.
Relationship with Colless’ Index
Like Colless’ index and Colless-like indices as previously defined, our new family of tree balance indices is based on the intuitive idea of assigning a value to each internal node, summing these values, and then normalizing the sum. A Colless-like index in the sense of Mir et al. (2018) depends on a function 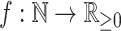 , which assigns node sizes, and a dissimilarity score
, which assigns node sizes, and a dissimilarity score 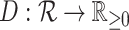 , where
, where 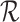 is the set of non-null real vectors. Before normalization, such an index has the form
is the set of non-null real vectors. Before normalization, such an index has the form
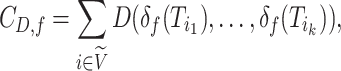 |
where 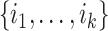 are the children of node
are the children of node 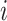 . The function
. The function 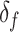 assigns a size to each subtree by summing the node sizes:
assigns a size to each subtree by summing the node sizes: 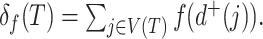 Neglecting the initial normalizing factor, our general definition (Equation 1) has a similar form and can be considered Colless-like in only a slightly broader sense. Our definition nevertheless differs in two important ways.
Neglecting the initial normalizing factor, our general definition (Equation 1) has a similar form and can be considered Colless-like in only a slightly broader sense. Our definition nevertheless differs in two important ways.
First, whereas the unbounded dissimilarity index 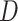 measures both node imbalance and importance and is undefined for nodes with out-degree one, we split these two roles into a normalized balance score
measures both node imbalance and importance and is undefined for nodes with out-degree one, we split these two roles into a normalized balance score 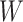 and an unbounded importance factor
and an unbounded importance factor 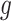 , and we assign a
, and we assign a  value (specifically zero) to nodes with out-degree one. This difference enables us to extend the balance index definition to trees with any degree distribution. It also makes it easy to normalize our indices for any tree, simply by dividing by the sum of the important factors. Furthermore, our normalization is universal, rather than being based on comparison with other trees with the same number of leaves. For example, our
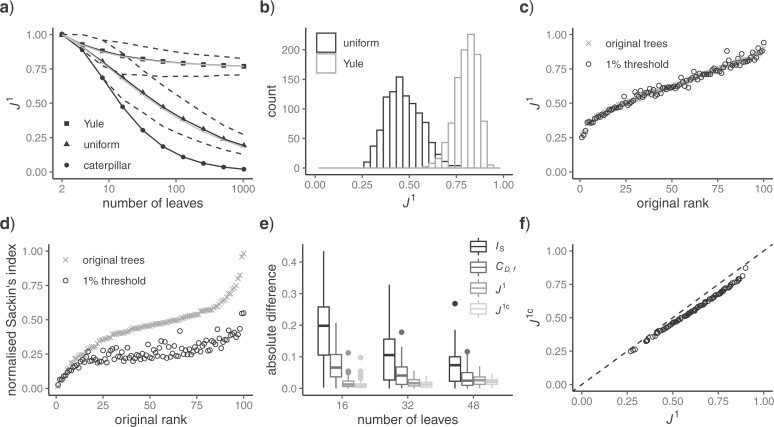
value (specifically zero) to nodes with out-degree one. This difference enables us to extend the balance index definition to trees with any degree distribution. It also makes it easy to normalize our indices for any tree, simply by dividing by the sum of the important factors. Furthermore, our normalization is universal, rather than being based on comparison with other trees with the same number of leaves. For example, our 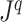 indices judge long caterpillar trees less balanced than short ones (Fig. 5a), whereas Sackin’s index, Colless’ index, and the total cophenetic index consider all caterpillar trees on more than two leaves equally imbalanced.
indices judge long caterpillar trees less balanced than short ones (Fig. 5a), whereas Sackin’s index, Colless’ index, and the total cophenetic index consider all caterpillar trees on more than two leaves equally imbalanced.
Figure 5.
a) 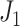 values for caterpillar trees and random trees generated from the Yule and uniform models (1000 trees per data point). All internal nodes have null size and all leaves have equal size. Solid black curves are the means; dashed curves are the 5th and 95th percentiles; and gray curves are
values for caterpillar trees and random trees generated from the Yule and uniform models (1000 trees per data point). All internal nodes have null size and all leaves have equal size. Solid black curves are the means; dashed curves are the 5th and 95th percentiles; and gray curves are 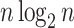 divided by the corresponding expectation of
divided by the corresponding expectation of 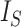 (where
(where 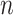 is the number of leaves). b)
is the number of leaves). b) 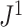 distributions for random trees on 64 leaves generated from the Yule and uniform models (1000 trees per model). c)
distributions for random trees on 64 leaves generated from the Yule and uniform models (1000 trees per model). c) 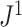 values for 100 random trees on 16 leaves, before and after applying a 1
values for 100 random trees on 16 leaves, before and after applying a 1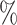 sensitivity threshold. These random trees were generated from the alpha-gamma model with
sensitivity threshold. These random trees were generated from the alpha-gamma model with 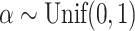 and
and 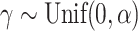 . d)
. d) 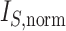 values for the same set of random trees. e) Absolute change in normalized index values due to applying a 1
values for the same set of random trees. e) Absolute change in normalized index values due to applying a 1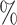 sensitivity threshold. Results are based on 100 random trees for each number of leaves, generated as in (c) and (d).
sensitivity threshold. Results are based on 100 random trees for each number of leaves, generated as in (c) and (d). 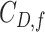 here is the Colless-like index with
here is the Colless-like index with 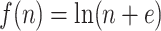 and
and 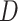 is the mean deviation from the median, as recommended by Mir et al. (2018). f) Values of
is the mean deviation from the median, as recommended by Mir et al. (2018). f) Values of 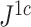 versus
versus 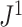 for random multifurcating trees on 16 leaves, with node sizes drawn from a continuous uniform distribution. The dashed reference line has slope 1.
for random multifurcating trees on 16 leaves, with node sizes drawn from a continuous uniform distribution. The dashed reference line has slope 1.
Second, instead of assigning a size to each node as a function of its out-degree, we associate a node’s size with the size of the biological population it represents. This ensures that our indices can be made reliably robust by including population size data.
Relationship with Sackin’s Index
The sum 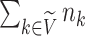 is just another way of expressing Sackin’s index (summing over internal nodes instead of leaves). Therefore,
is just another way of expressing Sackin’s index (summing over internal nodes instead of leaves). Therefore, 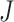 in Equation 4 is essentially a weighted Sackin index (with each term in the sum weighted by the balance score
in Equation 4 is essentially a weighted Sackin index (with each term in the sum weighted by the balance score 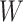 ) divided by the unweighted Sackin index. In the special, important case of full
) divided by the unweighted Sackin index. In the special, important case of full 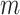 -ary leafy trees (including full
-ary leafy trees (including full 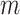 -ary cladograms), the weighted sum in
-ary cladograms), the weighted sum in 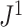 (Equation 5) simplifies yet further. Let
(Equation 5) simplifies yet further. Let 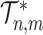 denote the set of all trees on
denote the set of all trees on 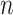 leaves such that all internal nodes have the same out-degree
leaves such that all internal nodes have the same out-degree 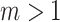 , every internal node has null size, and all leaf sizes are equal. Then, we obtain a remarkably simple relationship between
, every internal node has null size, and all leaf sizes are equal. Then, we obtain a remarkably simple relationship between 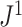 and Sackin’s index:
and Sackin’s index:
Proposition 6.
Let
be a tree on
leaves with
and
for every internal node
. Then
where
is the Shannon entropy (base
) of the proportional node sizes,
is the magnitude of
, and
. If additionally all leaves of
have the same size (so
) then
(6) where
is the minimum
value of trees in
.
The above result is somewhat surprising as it unifies our Colless-like index, which can be viewed as a weighted average of internal node balance scores, and Sackin’s index, which is the sum of all leaf depths. A short proof of Proposition 6 is presented in the Appendix. The converse result, which is also proved in the Appendix, justifies our choice of 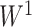 instead of alternative balance score functions:
instead of alternative balance score functions:
Proposition 7.
Let
be a tree balance index such that
where
are the children of node
, and
is a balance score satisfying the conditions stated before Equation 1. Suppose that for all trees
,
Then,
.
The right-hand side of Equation 6 incidentally provides an alternative way of normalizing Sackin’s index on full 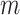 -ary leafy trees, including the bifurcating cladograms on which the index was originally defined. This normalized inverse Sackin index, which we can define as
-ary leafy trees, including the bifurcating cladograms on which the index was originally defined. This normalized inverse Sackin index, which we can define as 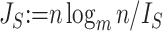 , provides a more satisfactory way of comparing trees that differ in their node degrees or leaf counts.
, provides a more satisfactory way of comparing trees that differ in their node degrees or leaf counts. 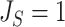 if and only if the tree has minimal depth given
if and only if the tree has minimal depth given 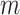 , which is equivalent to being fully symmetric, and so
, which is equivalent to being fully symmetric, and so 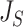 is a sound tree balance index in the sense defined by Mir et al. (2018) (see Appendix for a proof). For
is a sound tree balance index in the sense defined by Mir et al. (2018) (see Appendix for a proof). For 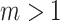 , we have
, we have 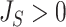 but
but 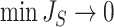 as
as 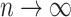 , which makes sense because trees with more leaves can be made less balanced. In particular, when
, which makes sense because trees with more leaves can be made less balanced. In particular, when 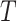 is a caterpillar tree on
is a caterpillar tree on 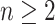 leaves,
leaves,
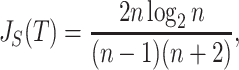 |
as illustrated in Figure 5a. The definition of 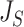 can be naturally extended to the case
can be naturally extended to the case 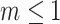 by setting
by setting 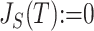 if
if 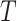 is linear or has only one node. From this point of view,
is linear or has only one node. From this point of view, 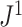 (a Colless-like index) is a generalization of
(a Colless-like index) is a generalization of 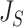 (the normalized reciprocal of Sackin’s index) to the domain of trees with arbitrary degree distributions and arbitrary node sizes.
(the normalized reciprocal of Sackin’s index) to the domain of trees with arbitrary degree distributions and arbitrary node sizes.
Distributions under the Yule and Uniform Models
An immediate corollary of Proposition 6 is that 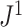 can be used to test whether a set of full
can be used to test whether a set of full 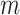 -ary cladograms is consistent with a particular tree-generating model, with exactly the same sensitivity as Sackin’s index. For example, Figure 5a,b shows
-ary cladograms is consistent with a particular tree-generating model, with exactly the same sensitivity as Sackin’s index. For example, Figure 5a,b shows 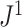 distributions for random bifurcating trees in
distributions for random bifurcating trees in 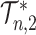 generated from the Yule and uniform models. These two distributions have insignificant overlap when the trees have at least a few dozen leaves.
generated from the Yule and uniform models. These two distributions have insignificant overlap when the trees have at least a few dozen leaves.
Kirkpatrick and Slatkin (1993) showed that the expectation of 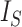 for the Yule model is
for the Yule model is
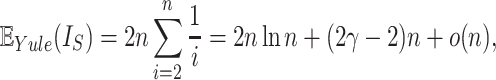 |
where 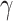 is Euler’s constant and
is Euler’s constant and 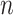 is the number of leaves. Mir et al. (2013) have shown that the expectation of
is the number of leaves. Mir et al. (2013) have shown that the expectation of 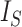 for the uniform model is
for the uniform model is
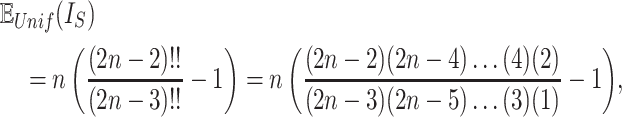 |
which approaches 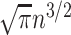 as the number of leaves
as the number of leaves  approaches infinity (Blum et al. 2006; King and Rosenberg 2021). Consistent with Proposition 6, we find that for random trees in
approaches infinity (Blum et al. 2006; King and Rosenberg 2021). Consistent with Proposition 6, we find that for random trees in 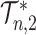 generated by either the Yule or the uniform model, a good approximation to the
generated by either the Yule or the uniform model, a good approximation to the 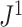 mean is
mean is 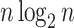 divided by the corresponding expectation of
divided by the corresponding expectation of 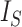 (gray curves in Fig. 5a). As
(gray curves in Fig. 5a). As 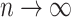 , these approximations approach
, these approximations approach 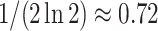 and zero for the Yule and uniform models, respectively.
and zero for the Yule and uniform models, respectively.
Robustness when Applied to Random Trees
To test the robustness of 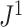 , we generated random multifurcating trees with node sizes drawn from a continuous uniform distribution and then compared
, we generated random multifurcating trees with node sizes drawn from a continuous uniform distribution and then compared 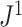 values for these trees before and after applying a 1
values for these trees before and after applying a 1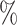 sensitivity threshold. In the latter case, whenever the combined frequency of a clone and its descendants was below 1
sensitivity threshold. In the latter case, whenever the combined frequency of a clone and its descendants was below 1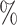 , we merged the corresponding subtree with the clone’s parent, to simulate imperfect detection of rare types. As expected, the
, we merged the corresponding subtree with the clone’s parent, to simulate imperfect detection of rare types. As expected, the 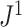 values for the two sets of trees were highly similar, with a median absolute difference of only 0.01 for trees that initially had 16 leaves (Fig. 5c). In contrast, the median absolute difference in the normalized Sackin’s index for the same two sets of trees (after resolving any linear parts in the manner of Fig. 2) was 0.20 (Fig. 5d), confirming that
values for the two sets of trees were highly similar, with a median absolute difference of only 0.01 for trees that initially had 16 leaves (Fig. 5c). In contrast, the median absolute difference in the normalized Sackin’s index for the same two sets of trees (after resolving any linear parts in the manner of Fig. 2) was 0.20 (Fig. 5d), confirming that 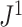 is much more robust to the omission of rare types.
is much more robust to the omission of rare types.
As the number of leaves per tree increases, indices such as Sackin’s index and the Colless-like index recommended by Mir et al. (2018) become more robust to the removal of rare types (Fig. 5e). Like 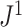 , these previously defined indices give more weight to nodes nearer the root. In larger trees, the nodes near the root tend to have large numbers of descendant leaves. It follows that removing a random sample of nodes from near the tips of the tree is likely to have only a modest effect on balance, as the tree’s core structure is preserved. In our results, this effect outweighs an increase in the proportion of nodes removed (a median of 7
, these previously defined indices give more weight to nodes nearer the root. In larger trees, the nodes near the root tend to have large numbers of descendant leaves. It follows that removing a random sample of nodes from near the tips of the tree is likely to have only a modest effect on balance, as the tree’s core structure is preserved. In our results, this effect outweighs an increase in the proportion of nodes removed (a median of 7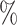 , 19
, 19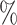 , and 24
, and 24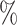 of nodes were removed from trees that originally had 16, 32, and 48 leaves, respectively, by applying the 1
of nodes were removed from trees that originally had 16, 32, and 48 leaves, respectively, by applying the 1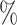 sensitivity threshold). Therefore the robustness benefit of
sensitivity threshold). Therefore the robustness benefit of 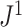 is more pronounced in trees with fewer leaves.
is more pronounced in trees with fewer leaves.
Comparison with a Conservative Tree Balance Index
We additionally investigated the robustness of an alternative new tree balance index 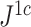 , defined as
, defined as
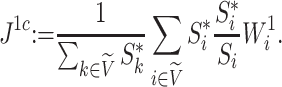 |
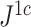 —which we denoted
—which we denoted 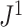 in a previous paper (Noble et al. 2022)—conforms to an alternative set of axioms that define what we call a conservative tree balance index. This index is maximal not for all trees with equal splits, but only for leafy trees with equal splits (see Appendix for details).
in a previous paper (Noble et al. 2022)—conforms to an alternative set of axioms that define what we call a conservative tree balance index. This index is maximal not for all trees with equal splits, but only for leafy trees with equal splits (see Appendix for details).
An advantage of 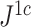 is that, unlike
is that, unlike 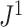 , it is always insensitive to adding relatively low-magnitude subtrees to the root of the tree. Nevertheless, as the number of nodes increases, the difference between
, it is always insensitive to adding relatively low-magnitude subtrees to the root of the tree. Nevertheless, as the number of nodes increases, the difference between 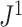 and
and 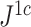 rapidly diminishes, unless the root node is disproportionately large (Fig. 6). For example, when
rapidly diminishes, unless the root node is disproportionately large (Fig. 6). For example, when 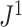 and
and 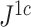 are applied to random multifurcating trees on 16 leaves, with node sizes drawn from a continuous uniform distribution, the linear correlation between the two indices is 0.998 (
are applied to random multifurcating trees on 16 leaves, with node sizes drawn from a continuous uniform distribution, the linear correlation between the two indices is 0.998 (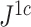 is approximately 10
is approximately 10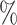 smaller than
smaller than 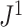 in this case; Fig. 5f). Accordingly, we find that
in this case; Fig. 5f). Accordingly, we find that 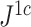 is only slightly more robust than
is only slightly more robust than 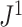 to the removal of rare types when applied to reasonably large random trees (Fig. 5e). For most practical purposes, we see no strong reason to favor
to the removal of rare types when applied to reasonably large random trees (Fig. 5e). For most practical purposes, we see no strong reason to favor 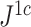 over the simpler index
over the simpler index 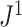 .
.
Figure 6.
Example values of 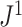 versus the conservative tree balance index
versus the conservative tree balance index 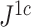 . The latter index takes account of the size of each internal node, relative to the sum of its descendant node sizes.
. The latter index takes account of the size of each internal node, relative to the sum of its descendant node sizes.
Resolution Power
Mir et al. (2013) have argued that a useful tree balance index should have good resolution power, meaning a low probability of assigning the same value to two trees with the same number of leaves, chosen uniformly at random. Proposition 6 implies that, when applied to full 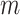 -ary leafy trees with equally sized leaves,
-ary leafy trees with equally sized leaves, 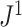 has the same resolution power as Sackin’s index.
has the same resolution power as Sackin’s index.
Correlations with Pre-existing Indices
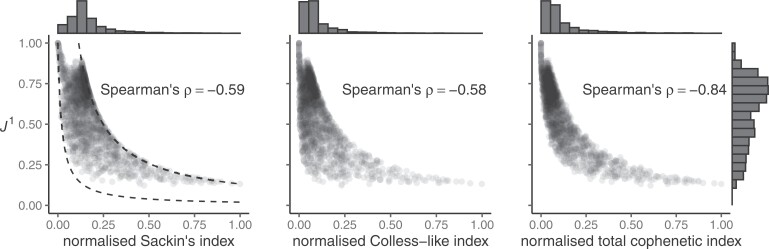
To compare 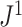 to Sackin’s index, a Colless-like index, and the total cophenetic index (defined in the Appendix) on a diverse set of trees, we generated 2000 random multifurcating leafy trees on 100 equally sized leaves using the alpha-gamma model (Chen et al. 2009) via the R package CollessLike (Mir et al. 2018). As shown in Figure 7, our new balance index correlates negatively with the previously defined imbalance indices on this set of random trees, indicating that it captures a similar notion of balance. The strongest correlation is between
to Sackin’s index, a Colless-like index, and the total cophenetic index (defined in the Appendix) on a diverse set of trees, we generated 2000 random multifurcating leafy trees on 100 equally sized leaves using the alpha-gamma model (Chen et al. 2009) via the R package CollessLike (Mir et al. 2018). As shown in Figure 7, our new balance index correlates negatively with the previously defined imbalance indices on this set of random trees, indicating that it captures a similar notion of balance. The strongest correlation is between 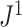 and the total cophenetic index (Spearman’s
and the total cophenetic index (Spearman’s 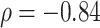 for all trees, and
for all trees, and 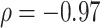 for trees with a mean out-degree greater than 3). The marginal histograms in Figure 7 additionally show that more than 85
for trees with a mean out-degree greater than 3). The marginal histograms in Figure 7 additionally show that more than 85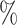 of these random trees have balance values less than 0.25 according to the previously defined indices, whereas
of these random trees have balance values less than 0.25 according to the previously defined indices, whereas 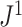 values are more evenly distributed between zero and one, with mean and median approximately equal to 0.6.
values are more evenly distributed between zero and one, with mean and median approximately equal to 0.6.
Figure 7.
Scatter plots of 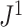 versus normalized Sackin’s, Colless-like, and total cophenetic indices for 2000 random multifurcating leafy trees with 100 equally sized leaves. Histograms in the margins show the marginal distributions. Dashed reference curves in the first panel are obtained by substituting
versus normalized Sackin’s, Colless-like, and total cophenetic indices for 2000 random multifurcating leafy trees with 100 equally sized leaves. Histograms in the margins show the marginal distributions. Dashed reference curves in the first panel are obtained by substituting 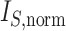 into Equation 6 with
into Equation 6 with 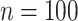 and
and 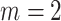 (upper curve) or
(upper curve) or 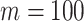 (lower curve). We use the Colless-like index with
(lower curve). We use the Colless-like index with 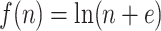 and
and 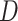 the mean deviation from the median, as recommended by Mir et al. (2018). Normalization of each index other than
the mean deviation from the median, as recommended by Mir et al. (2018). Normalization of each index other than 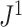 depends only on the number of leaves and so does not affect correlations. Trees were generated from the alpha-gamma model with
depends only on the number of leaves and so does not affect correlations. Trees were generated from the alpha-gamma model with 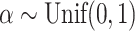 and
and 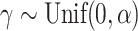 .
.
Sensitivity to Certain Changes in Node Degree
As explained in the Methods section, we consider it desirable for tree balance indices to be sensitive to certain changes in node degree. In 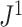 this sensitivity arises because, in the calculation of the node balance score, the node out-degree features as the base of the logarithm. For example, consider a star tree
this sensitivity arises because, in the calculation of the node balance score, the node out-degree features as the base of the logarithm. For example, consider a star tree 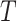 with
with 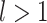 leaves each of size
leaves each of size 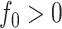 . Suppose we add to the root another
. Suppose we add to the root another 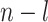 leaves, each of size
leaves, each of size 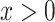 . If
. If 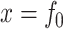 then
then 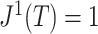 since all the leaves have the same size. Otherwise
since all the leaves have the same size. Otherwise
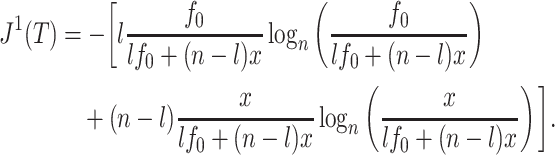 |
As 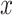 decreases from
decreases from 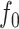 towards zero,
towards zero, 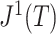 decreases monotonically to account for the growing loss of balance. And as
decreases monotonically to account for the growing loss of balance. And as 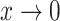 , so
, so 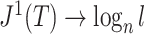 . If we then remove these vanishingly small leaves, the value of
. If we then remove these vanishingly small leaves, the value of 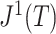 will jump from
will jump from 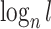 back to 1 because the remaining leaves are of equal size. The sensitivity of
back to 1 because the remaining leaves are of equal size. The sensitivity of 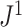 to such changes in node degree is thus a straightforward consequence of the conventional notion of node balance. The size of the jump in
to such changes in node degree is thus a straightforward consequence of the conventional notion of node balance. The size of the jump in 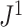 is at most
is at most 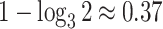 , and it approaches zero as
, and it approaches zero as 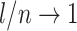 (i.e., when the new nodes are relatively few). The analyses shown in Figure 5e,f show that such discontinuities do not compromise the overall robustness of
(i.e., when the new nodes are relatively few). The analyses shown in Figure 5e,f show that such discontinuities do not compromise the overall robustness of 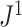 to the removal of rare types.
to the removal of rare types.
Implementation and Algorithmic Complexity
Assuming the identity of the root is known, our new indices can be computed from an adjacency matrix in 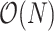 time, where
time, where 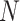 is the number of nodes (or the number of edges plus one). Subtree magnitudes are computed via depth-first search, which takes linear time, and the computation of the balance index takes at most
is the number of nodes (or the number of edges plus one). Subtree magnitudes are computed via depth-first search, which takes linear time, and the computation of the balance index takes at most 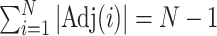 steps, where
steps, where 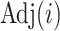 is the adjacency list of node
is the adjacency list of node 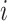 . Efficient R code for calculating
. Efficient R code for calculating 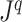 is shared in an online repository (Noble and Lemant 2021).
is shared in an online repository (Noble and Lemant 2021).
Discussion
Here, we have defined a new class of tree balance index that unifies, generalizes, and in various ways improves upon previous definitions. Even when restricted to the tree types on which pre-existing indices are defined, our indices enable a more meaningful comparison of trees with different degree distributions or different numbers of leaves. Due to these advantages, our indices have the potential to supersede those in current use.
Our indices also enable important new applications. A challenge in comparing simulated phylogenies and trees inferred from data is that the former are exact, whereas the latter are often incomplete (Scott et al. 2020). In oncology, for example, it has been shown that whether or not a rare tumor clone is detected depends on both methodology and chance (Turajlic et al. 2018). Our balance indices largely solve this problem as they are insensitive to the omission of rare types, as demonstrated briefly here and more comprehensively in a companion paper (Noble et al. 2022).
Because of its unique relationship with Sackin’s index, we especially recommend 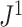 —a weighted average of the normalized entropies of the internal nodes—as defined in general by Equation 3 and more simply for cladograms by Equation 5. Given that Sackin’s index has been well studied, it is convenient that
—a weighted average of the normalized entropies of the internal nodes—as defined in general by Equation 3 and more simply for cladograms by Equation 5. Given that Sackin’s index has been well studied, it is convenient that 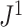 inherits some of the properties of that index when applied to full
inherits some of the properties of that index when applied to full 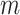 -ary cladograms, including its relatively high sensitivity in distinguishing between alternative tree-generating models (Kirkpatrick and Slatkin 1993; Agapow and Purvis 2002). Within our framework, Sackin’s index is seen not as a general balance index but rather as a normalizing factor, which works as a balance index only in the special case of full
-ary cladograms, including its relatively high sensitivity in distinguishing between alternative tree-generating models (Kirkpatrick and Slatkin 1993; Agapow and Purvis 2002). Within our framework, Sackin’s index is seen not as a general balance index but rather as a normalizing factor, which works as a balance index only in the special case of full 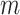 -ary leafy trees (for which the numerator of
-ary leafy trees (for which the numerator of 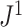 is independent of tree topology).
is independent of tree topology).
Proposition 6 implies that determining the precise moments of 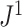 for a model that generates full
for a model that generates full 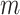 -ary leafy trees is equivalent to determining the moments of the reciprocal of Sackin’s index. Figure 7 suggests that
-ary leafy trees is equivalent to determining the moments of the reciprocal of Sackin’s index. Figure 7 suggests that 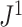 has interesting relationships with other indices such as the total cophenetic index. These are promising areas for further investigation.
has interesting relationships with other indices such as the total cophenetic index. These are promising areas for further investigation.
Acknowledgments
We thank Laura Keller, Lisa Lamberti, Niko Beerenwinkel, Francesco Marass, Jack Kuipers, and Katharina Jahn for helpful conversations, and János Podani for advice on terminology.
Appendix
Definition of the Total Cophenetic Index
The cophenetic value 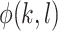 of a pair of leaves
of a pair of leaves 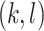 is the depth of their lowest common ancestor. The total cophenetic index (Mir et al. 2013) is then the sum of the cophenetic values over all pairs of leaves:
is the depth of their lowest common ancestor. The total cophenetic index (Mir et al. 2013) is then the sum of the cophenetic values over all pairs of leaves:
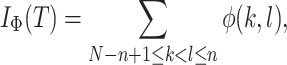 |
where 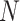 is the number of nodes and
is the number of nodes and 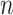 the number of leaves. As in Sackin’s index, the principle is that an unbalanced tree stretches more than a balanced tree. Being explicitly defined for all multifurcating trees, the total cophenetic index permits meaningful comparison of any two multifurcating trees on the same number of leaves.
the number of leaves. As in Sackin’s index, the principle is that an unbalanced tree stretches more than a balanced tree. Being explicitly defined for all multifurcating trees, the total cophenetic index permits meaningful comparison of any two multifurcating trees on the same number of leaves.
For trees on 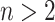 leaves, the minimum of the total cophenetic index is reached on the star tree, with
leaves, the minimum of the total cophenetic index is reached on the star tree, with 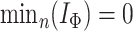 . The maximum is attained on the caterpillar tree:
. The maximum is attained on the caterpillar tree:
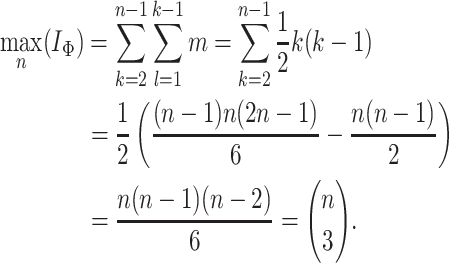 |
Hence, a normalized version of the total cophenetic index is  This normalized imbalance index is not minimal for all fully symmetric trees. For example, the cophenetic value of the two leftmost leaves of the fully symmetric tree in Figure 1b is two, and so both the un-normalized and normalized cophenetic indices of this tree will be nonzero.
This normalized imbalance index is not minimal for all fully symmetric trees. For example, the cophenetic value of the two leftmost leaves of the fully symmetric tree in Figure 1b is two, and so both the un-normalized and normalized cophenetic indices of this tree will be nonzero.
Conservative Tree Balance Indices
Our axioms permit  to change discontinuously when we add rare types to the root. This is because Axioms 3 and 4 consider the addition of subtrees that have vanishingly small magnitude relative to other subtrees excluding their roots, whereas the relative size of the root of the entire tree is immaterial. For example, consider a two-node linear tree
to change discontinuously when we add rare types to the root. This is because Axioms 3 and 4 consider the addition of subtrees that have vanishingly small magnitude relative to other subtrees excluding their roots, whereas the relative size of the root of the entire tree is immaterial. For example, consider a two-node linear tree  in which the nonroot node has size
in which the nonroot node has size  , relative to the size of the root. Then
, relative to the size of the root. Then 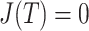 by Axiom 4. But if we add another child to the root of
by Axiom 4. But if we add another child to the root of 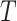 , also of relative size
, also of relative size 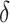 , then the
, then the 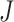 value of the new tree will be 1 (by Axiom 1), even as
value of the new tree will be 1 (by Axiom 1), even as 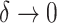 . To make our index robust in such cases, we can add another axiom:
. To make our index robust in such cases, we can add another axiom:
Axiom A.1 (Root limit).
Let
be a tree with root
. Then,
as
.
But this new axiom conflicts with Axiom 1, which we must then modify, such that equal splits are no longer sufficient for maximal balance:
Axiom A.2 (Alternative maximum value).
for all trees
, and
only if
has equal splits. Furthermore, if
has equal splits and is a leafy tree then
.
We will call a tree balance index conservative if it conforms to these two alternative axioms in addition to Axioms 2, 3, 4, and 5. This name is appropriate because Axiom A.1 implies that a tree will be considered imbalanced unless there is strong evidence to the contrary (in the form of a relatively small root node). Every conservative index is both universal and robust.
One way to define a class of conservative indices is to add to Equation 1 a nonroot dominance factor 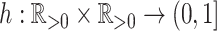 with
with 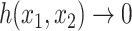 as
as 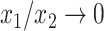 , and
, and  if and only if
if and only if 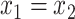 . We then obtain
. We then obtain
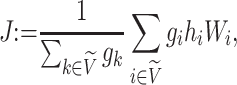 |
with 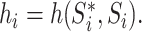 The role of
The role of 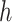 is to quantify the extent to which a node should be considered a leaf (which does not contribute to the index’s value) as opposed to an internal node (which does). Adding this factor has no effect on the balance values assigned to leafy trees, including cladograms, because if an internal node
is to quantify the extent to which a node should be considered a leaf (which does not contribute to the index’s value) as opposed to an internal node (which does). Adding this factor has no effect on the balance values assigned to leafy trees, including cladograms, because if an internal node 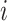 has zero size then
has zero size then 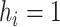 . Setting
. Setting 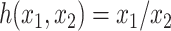 , we can modify Equation 3 to obtain the specific conservative index
, we can modify Equation 3 to obtain the specific conservative index
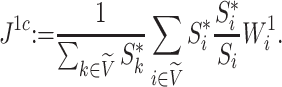 |
We previously used  instead of
instead of  to denote the above index (Noble et al. 2022).
to denote the above index (Noble et al. 2022).
Alternative Axioms Proposed by Fischer et al. (2021)
Shortly after we posted a preprint version of the current article, Fischer et al. (2021) posted a preprint in which they proposed two alternative axioms for nonrobust, nonuniversal tree balance indices, such as Sackin’s and Colless’ indices. In these axioms,  denotes the set of rooted bifurcating trees with
denotes the set of rooted bifurcating trees with  leaves,
leaves, 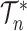 is the set of all rooted trees with
is the set of all rooted trees with 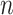 leaves such that
leaves such that 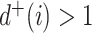 for all internal nodes
for all internal nodes 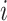 , and the tree balance index is denoted
, and the tree balance index is denoted 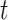 .
.
Axiom A.3 (Fischer et al. minimum value).
The caterpillar tree with
leaves is the unique tree minimizing
on
(if
is defined on multifurcating trees) or on
(if
is defined only on bifurcating trees) for all
.
Axiom A.4 (Fischer et al. maximum value).
The fully symmetric bifurcating tree with
leaves is the unique tree maximizing
on
for all
with
.
These axioms can be compared with our axioms if we consider only leafy trees in which all leaves have equal size (such as cladograms). Axiom A.4 is then just a special case of our more general Axiom 1 because the fully symmetric bifurcating tree with 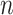 leaves is the only tree in
leaves is the only tree in 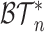 that has equal splits. But Axiom A.3 is not necessarily consistent with our Axiom 2. In particular, as shown in Figure 4b, our index
that has equal splits. But Axiom A.3 is not necessarily consistent with our Axiom 2. In particular, as shown in Figure 4b, our index 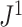 does not comply with Axiom A.3 in the case of multifurcating leafy trees. We can resolve this incompatibility with the following simplification:
does not comply with Axiom A.3 in the case of multifurcating leafy trees. We can resolve this incompatibility with the following simplification:
Axiom A.5 (Alternative Fischer et al. minimum value).
The caterpillar tree with
leaves is the unique tree minimizing
on
for all
(whether or not
is defined on multifurcating trees).
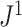 is consistent with Axiom A.5 because, when we consider only bifurcating leafy trees in which all leaves have equal size,
is consistent with Axiom A.5 because, when we consider only bifurcating leafy trees in which all leaves have equal size, 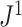 is equal to
is equal to 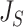 (by Proposition 6), which is inversely proportional to
(by Proposition 6), which is inversely proportional to 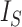 by definition, and the caterpillar tree is the unique bifurcating tree that maximizes
by definition, and the caterpillar tree is the unique bifurcating tree that maximizes 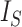 (Fischer et al. 2021). Although Axiom 1 does not necessarily imply Axiom A.5, it is reasonable to expect useful universal tree balance indices to satisfy both conditions.
(Fischer et al. 2021). Although Axiom 1 does not necessarily imply Axiom A.5, it is reasonable to expect useful universal tree balance indices to satisfy both conditions.
Proof that the Index of Equation 1 Satisfies Our Five Axioms
Proof. (Axiom 1 (Maximum value):
We have
since
and
lie between zero and one by definition. Also if any internal node
of tree
does not split its descendants into at least two equal-magnitude subtrees then
by definition and so
Now, let
be a tree such that every internal node splits its descendants into at least two equal-magnitude subtrees. Then
for all
by definition. Hence,
Axiom 2 (Minimum value): We have
since
and
are always non-negative by definition. Also if
is a linear tree then
for all
by definition, and hence
. Conversely, if some internal node
has
then
by definition and, because
must be positive by definition, we must have
.
Axiom 3 (Insensitivity): Adding a subtree to a leaf
changes the tree balance value via the contributions of two sets of nodes: the internal nodes of
(including
), and all other internal nodes. For each internal node,
, as
so also
(because
), which implies
by definition, and hence all such contributions approach zero. The contribution of all other internal nodes also approaches zero because
and
are continuous by definition.
Axiom 4 (Linear limit): Let
with
. Without loss of generality, let
denote the original child of
, and
denote the newly added children of
. Adding subtrees to
changes the tree balance value via the contributions of the newly added nodes and of node
. As
, so
for all
. This implies that
and hence
by definition for all
. Therefore, the first contribution approaches zero. Also as
, we have
, and so
by definition. Therefore, the second contribution also approaches zero.
Axiom 5 (Continuity): The continuity of
follows immediately from the continuity of
and
. □
New Generalizations of Sackin’s and Colless’ Indices
The number of distinct subtrees that contain a given leaf 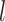 is equal to its number of ancestors, which is the same as
is equal to its number of ancestors, which is the same as 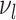 , the depth of
, the depth of 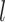 . Hence, Sackin’s index is equivalent to the sum of the leaf counts of the subtrees rooted at each internal node. By extension, we can define a new, more general form of Sackin’s index that accounts for node sizes:
. Hence, Sackin’s index is equivalent to the sum of the leaf counts of the subtrees rooted at each internal node. By extension, we can define a new, more general form of Sackin’s index that accounts for node sizes:
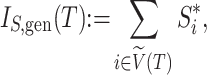 |
where 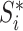 is the magnitude of the subtree rooted at node
is the magnitude of the subtree rooted at node 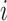 , excluding the root. In the special case of leafy trees in which all leaves have size one, we recover
, excluding the root. In the special case of leafy trees in which all leaves have size one, we recover 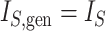 . This new index is not very useful for assessing tree balance because it increases with the total tree magnitude, but in our framework, it performs an important role as a normalizing factor.
. This new index is not very useful for assessing tree balance because it increases with the total tree magnitude, but in our framework, it performs an important role as a normalizing factor.
If we let 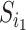 denote the magnitude of the left branch of the subtree rooted at
denote the magnitude of the left branch of the subtree rooted at 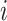 , and
, and 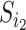 denote the magnitude of the right branch, then we can generalize Colless’ index to account for node sizes in bifurcating trees:
denote the magnitude of the right branch, then we can generalize Colless’ index to account for node sizes in bifurcating trees:
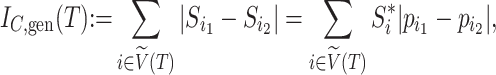 |
where 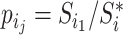 . This definition reduces to
. This definition reduces to  in the case of leafy trees in which all leaves have size one. The right-hand expression above clarifies that the contribution of each node to Colless’ index is the product of the node’s importance (i.e., its number of descendants) and its balance (the degree to which the node splits its descendants into two equal-magnitude subtrees). We further see that
in the case of leafy trees in which all leaves have size one. The right-hand expression above clarifies that the contribution of each node to Colless’ index is the product of the node’s importance (i.e., its number of descendants) and its balance (the degree to which the node splits its descendants into two equal-magnitude subtrees). We further see that  for all trees
for all trees  (because
(because 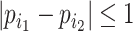 for all
for all 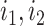 ), which suggests the normalization
), which suggests the normalization
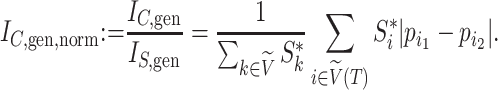 |
This new generalization of Colless’ index is more robust than the conventional form, in the sense that its value is insensitive to the addition or removal of relatively small nodes.  also enables meaningful comparison of trees with different numbers of leaves. But, the problem remains that
also enables meaningful comparison of trees with different numbers of leaves. But, the problem remains that 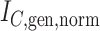 applies only to bifurcating trees.
applies only to bifurcating trees.
Other Balance Indices Based on Generalized Entropies
As defined by Chao et al. (2014), generalized entropies for 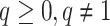 are
are
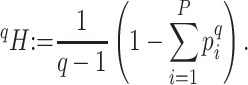 |
Parameter 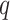 determines the sensitivity to the type frequencies.
determines the sensitivity to the type frequencies. 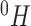 is simply the richness (minus 1) of the population, which corresponds to ignoring the frequencies and just counting the types. For
is simply the richness (minus 1) of the population, which corresponds to ignoring the frequencies and just counting the types. For 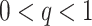 , rare types are given more weight than implied by their proportion, whereas for
, rare types are given more weight than implied by their proportion, whereas for 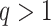 abundant types matter more.
abundant types matter more. 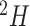 is the Gini–Simpson coefficient. In the limit
is the Gini–Simpson coefficient. In the limit  we recover the Shannon entropy
we recover the Shannon entropy 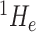 .
.
For 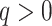 ,
, 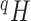 attains its maximum value if and only if all types have equal frequency
attains its maximum value if and only if all types have equal frequency 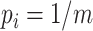 :
:
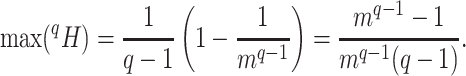 |
We can therefore define a normalized balance score  for
for  and
and  :
:
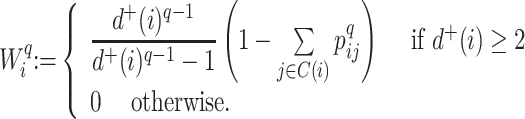 |
Similarly, one can define 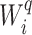 for
for 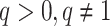 based on the entropy defined by Rényi (1961):
based on the entropy defined by Rényi (1961):
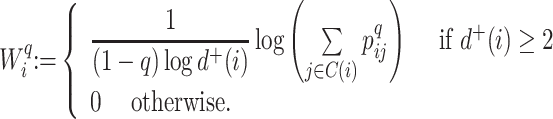 |
In either case, a balance index 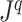 satisfying our axioms is
satisfying our axioms is
 |
for any  . And in either case,
. And in either case,  as
as  .
.
Proof of Proposition 6
Proof.
By definition of
, if
is a tree on
leaves with
and
for every internal node
then
The sum of subtree magnitudes over the set of all internal nodes is equal to the sum of
multiplied by leaf size over the set of all leaves:
Summing first over the internal nodes and then over their children gives the same result:
Let
denote the ancestor of node
at distance
, with
and
(the root) for all
. Then by extension,
for any function
. In particular, we have
Substituting this result into the expression for
, we find
The right-hand sum is a telescoping series that collapses to give
Now since
is a leaf,
. Also
. Hence,
If additionally all leaves
of
have the same size
then
,
, and
, which implies
□
Proof of Proposition 7
Proof.
Since
, the conditions are equivalent to
where
are the children of
. Let
be a tree in
and
be an internal node of
. Then,
and
for every child
of
. Therefore
Also,
, so we have
Since
, this implies
□
Proof that 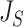 is a Sound Tree Balance Index
is a Sound Tree Balance Index
Proof.
By the definition of Mir et al. (2018), a sound tree balance index
is such that
is maximal if and only if
is fully symmetric. The fully symmetric full
-ary tree on
leaves is the unique tree that minimizes
among full
-ary trees on
leaves. This minimum value is
(since every leaf
has the same depth
). Because
is defined only on full
-ary trees, if follows that
is maximal if and only if
is fully symmetric. □
Contributor Information
Jeanne Lemant, Department of Biosystems Science and Engineering, ETH Zurich, Mattenstrasse 26, 4058 Basel, Switzerland; Department of Epidemiology and Public Health, Swiss Tropical and Public Health Institute, Kreuzstrasse 2, 4123 Allschwil, Switzerland; University of Basel, Petersplatz 1, 4001 Basel, Switzerland.
Cécile Le Sueur, Department of Biosystems Science and Engineering, ETH Zurich, Mattenstrasse 26, 4058 Basel, Switzerland.
Veselin Manojlović, Department of Mathematics, City, University of London, Northampton Square, London EC1V 0HB, UK.
Robert Noble, Department of Biosystems Science and Engineering, ETH Zurich, Mattenstrasse 26, 4058 Basel, Switzerland; Department of Mathematics, City, University of London, Northampton Square, London EC1V 0HB, UK.
Funding
This work was supported by the National Cancer Institute at the National Institutes of Health [U54CA217376 to R.N. and V.M.]. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
References
- Agapow P.M., Purvis A. 2002. Power of eight tree shape statistics to detect nonrandom diversification: a comparison by simulation of two models of cladogenesis. Syst. Biol. 51(6): 866–872. [DOI] [PubMed] [Google Scholar]
- Blum M.G.B., François O., Janson S. 2006. The mean, variance and limiting distribution of two statistics sensitive to phylogenetic tree balance. Ann. Appl. Prob. 16(4): 2195–2214. [Google Scholar]
- Chao A., Chiu C.-H., Jost L. 2014. Unifying species diversity, phylogenetic diversity, functional diversity, and related similarity and differentiation measures through hill numbers. Annu. Rev. Ecol. Evol. Syst. 45 (1): 297–324. [Google Scholar]
- Chen B., Ford D., Winkel M. 2009. A new family of Markov branching trees: the alpha-gamma model. Electron. J. Prob. 14: 400–430. [Google Scholar]
- Chkhaidze K., Heide T., Werner B., Williams M.J., Huang W., Caravagna G., Graham T.A., Sottoriva A. 2019. Spatially constrained tumour growth affects the patterns of clonal selection and neutral drift in cancer genomic data. PLoS Comput. Biol. 15(7):e1007243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colless D.H. 1982. Review of phylogenetics: the theory and practice of phylogenetic systematics. Syst. Zool. 31(1):100–104. [Google Scholar]
- Davis A., Gao R., Navin N. 2017. Tumor evolution: linear, branching, neutral or punctuated? Biochim. Biophys. Acta 1867 (2): 151–161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischer M., Herbst L., Kersting S., Kühn L., Wicke K. 2021. Tree balance indices: a comprehensive survey. arXiv preprint arXiv:2109.12281. [Google Scholar]
- Jamal-Hanjani M., Wilson G.A., McGranahan N., Birkbak N.J., Watkins T.B.K., Veeriah S., Shafi S., Johnson D.H., Mitter R., Rosenthal R., Salm M., Horswell S., Escudero M., Matthews N., Rowan A., Chambers T., Moore D.A., Turajlic S., Xu H., Lee S.-M., Forster M.D., Ahmad T., Hiley C.T., Abbosh C., Falzon M., Borg E., Marafioti T., Lawrence D., Hayward M., Kolvekar S., Panagiotopoulos N., Janes S.M., Thakrar R., Ahmed A., Blackhall F., Summers Y., Shah R., Joseph L., Quinn A.M., Crosbie P.A., Naidu B., Middleton G., Langman G., Trotter S., Nicolson M., Remmen H., Kerr K., Chetty M., Gomersall L., Fennell D.A., Nakas A., Rathinam S., Anand G., Khan S., Russell P., Ezhil V., Ismail B., Irvin-Sellers M., Prakash V., Lester J.F., Kornaszewska M., Attanoos R., Adams H., Davies H., Dentro S., Taniere P., O’Sullivan B., Lowe H.L., Hartley J.A., Iles N., Bell H., Ngai Y., Shaw J.A., Herrero J., Szallasi Z., Schwarz R.F., Stewart A., Quezada S.A., Le Quesne J., Van Loo P., Dive C., Hackshaw A., Swanton C. 2017. Tracking the evolution of non–small-cell lung cancer. N. Engl. J. Med. 376 (22): 2109–2121. [DOI] [PubMed] [Google Scholar]
- King M.C., Rosenberg N.A. 2021. A simple derivation of the mean of the Sackin index of tree balance under the uniform model on rooted binary labeled trees. Math. Biosci. 342:108688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirkpatrick M., Slatkin M. 1993. Searching for evolutionary patterns in the shape of a phylogenetic tree. Evolution 47 (4):1171–1181. [DOI] [PubMed] [Google Scholar]
- Maley C.C., Aktipis A., Graham T.A., Sottoriva A., Boddy A.M., Janiszewska M., Silva A.S., Gerlinger M., Yuan Y., Pienta K.J., Anderson K.S., Gatenby R., Swanton C., Posada D., Wu C.-I., Schiffman J. D., Shelley Hwang E., Polyak K., Anderson A.R.A., Brown J.S., Greaves M., Shibata D. 2017. Classifying the evolutionary and ecological features of neoplasms. Nat. Rev. Cancer 17 (10): 605–619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mir A., Rosselló F., Rotger L.A. 2013. A new balance index for phylogenetic trees. Math. Biosci. 241 (1): 125–136. [DOI] [PubMed] [Google Scholar]
- Mir A., Rotger L., Rosselló F. 2018. Sound Colless-like balance indices for multifurcating trees. PLoS One 13 (9):e0203401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mooers A.O., Heard S.B. 1997. Inferring evolutionary process from phylogenetic tree shape. Q. Rev. Biol. 72 (1): 31–54. [Google Scholar]
- Noble R., Lemant J. 2021. RUtreebalance: robust, universal tree balance indices, 2021. https://zenodo.org/badge/latestdoi/399934945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noble R., Burri D., Le Sueur C., Lemant J., Viossat Y., Kather J.N., Beerenwinkel N. 2022. Spatial structure governs the mode of tumour evolution. Nat. Ecol. Evol. 6(2):207–217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Podani J. 2013. Tree thinking, time and topology: comments on the interpretation of tree diagrams in evolutionary/phylogenetic systematics. Cladistics 29(3):315–327. [DOI] [PubMed] [Google Scholar]
- Rényi A. 1961. On measures of entropy and information. Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Contributions to the Theory of Statistics, vol. 4; University of California Press. p. 547–562. [Google Scholar]
- Sackin M.J. 1972. “Good” and “bad” phenograms. Syst. Biol. 21 (2): 225–226. [Google Scholar]
- Scott J.G., Maini P.K., Anderson A.R.A.A., Fletcher A.G. 2020. Inferring tumor proliferative organization from phylogenetic tree measures in a computational model. Syst. Biol. 69 (4):623–637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shao K.-T., Sokal R.R. 1990. Tree balance. Syst. Zool. 39 (3): 266. [Google Scholar]
- Turajlic S., Xu H., Litchfield K., Rowan A., Horswell S., Chambers T., O’Brien T., Lopez J.I., Watkins T.B.K., Nicol D., Stares M., Challacombe B., Hazell S., Chandra A., Mitchell T.J., Au L., Eichler-Jonsson C., Jabbar F., Soultati A., Chowdhury S., Rudman S., Lynch J., Fernando A., Stamp G., Nye E., Stewart A., Xing W., Smith J.C., Escudero M., Huffman A., Matthews N., Elgar G., Phillimore B., Costa M., Begum S., Ward S., Salm M., Boeing S., Fisher R., Spain L., Navas C., Grönroos E., Hobor S., Sharma S., Aurangzeb I., Lall S., Polson A., Varia M., Horsfield C., Fotiadis N., Pickering L., Schwarz R.F., Silva B., Herrero J., Luscombe N.M., Jamal-Hanjani M., Rosenthal R., Birkbak N.J., Wilson G.A., Pipek O., Ribli D., Krzystanek M., Csabai I., Szallasi Z., Gore M., McGranahan N., Van Loo P., Campbell P., Larkin J., Swanton C. 2018. Deterministic evolutionary trajectories influence primary tumor growth: TRACERx renal. Cell 173 (3): 595–610.e11. [DOI] [PMC free article] [PubMed] [Google Scholar]