A fractional-order mathematical model based on vaccinated and infected compartments of SARS-CoV-2 with a real case study during the last stages of the epidemiological event

Abstract

In 2020 the world faced with a pandemic spread that affected almost everything of humans’ social and health life. Regulations to decrease the epidemiological spread and studies to produce the vaccine of SARS-CoV-2 were on one side a hope to return back to the regular life, but on the other side there were also notable criticism about the vaccines itself. In this study, we established a fractional order differential equations system incorporating the vaccinated and re-infected compartments to a $SIR$ frame to consider the expanded and detailed form as an $SVI{I}_{v}R$ model. We considered in the model some essential parameters, such as the protection rate of the vaccines, the vaccination rate, and the vaccine’s lost efficacy after a certain period. We obtained the local stability of the disease-free and co-existing equilibrium points under specific conditions using the Routh–Hurwitz Criterion and the global stability in using a suitable Lyapunov function. For the numerical solutions we applied the Euler’s method. The data for the simulations were taken from the World Health Organization (WHO) to illustrate numerically some scenarios that happened.

1. Introduction

Many deaths occur daily worldwide due to the epidemiological disease SARS-CoV-2, which appeared in Wuhan, China, in 2019 and affected the whole world in an unexpectedly short time. The rapid spread of the virus, it is strengthening through mutations, people’s lack of adequate attention, and the fact that no permanent medicine for disease prevention has been found yet, continue to raise concerns of all humanity.

Undoubtedly, the epidemiological event that appeared with SARS-CoV-2 is closely related to some sensitive parameters that had a dominant effect on the spread of the virus worldwide. Therefore, the mathematical models based on these parameters are among the most reliable methods for monitoring and controlling the current situation and possible scenarios.

Well-known and most frequently used models for infectious diseases are models created by ordinary differential equation systems such as SI, SIR, SIRD, and SEIRD. Each model variable represents the number of individuals in a different compartment.

It is known that integer order differential equations cannot always manage complex problems in nature. Nevertheless, the applications of fractional models can be seen in many fields such as physics, medicine, chemistry, and engineering [1], [2], [3], [4], [5], [6], [7], [8], [9], [10], [11]. Specifically, fractional modeling is a perfect tool for problems with complex mechanisms such as disease pandemics [12], [13], [14], [15], [16], [17], [18], [19], [20].

The high interest in modeling dynamics of the novel coronavirus SARS-CoV-2, also defined as COVID-19, disease via fractional derivatives can be reflected in the literature. A dynamical SEIRS model that includes the vaccine rate is investigated by Kumar et al. [21]. In [22], authors introduced a fractional order approach to modeling and simulations of the novel COVID-19 by including transmission rate, testing rates, and transition rate from asymptomatic to symptomatic population groups. In [23], authors considered a model with the help of the Atangana Baleanu Caputo (ABC) fractal-arbitrary order derivative for studying the outbreaks of COVID-19 in the three cities of Brazil by using the real raw data-based parameter values. Atangana [24] proposed a fractal-fractional mathematical model and presented some basic statistical figures to indicate the spread profile using data from Italy. Chen et al. [25] reviewed the fractional epidemic model and proposed a general fractional-order epidemic models system and a multi-term fractional-order SEIAR Model based on the Caputo fractional derivative. Bozkurt et al. [26] considered a model of differential equations with piecewise constant arguments that explores the outbreak of Covid-19 including the control mechanisms. A new nonlinear fractional order model in the Caputo sense to analyze and simulate the dynamics of this viral disease with a case study of Algeria was introduced in [27]. Researchers in [28] created a model of differential equations with piecewise constant arguments that explore the outbreak of COVID-19, including the control mechanisms. Bozkurt et al. [29] introduced a fractional SEIR+D model for COVID-19, and they investigated the fear effect of the community spread through the media, social networks, and health organizations.

Different from the models mentioned above and in the literature, the following innovations are considered in this study:

• •It was assumed that the virus could not be transmitted to vaccinated individuals. However, later studies showed that SARS-CoV-2 can still infect vaccinated individuals. Therefore, we include the $I_v$ compartment in our system to emphasize the vaccine’s minor efficiency if regular vaccination is not repeated. However, some facts also emerge with the progress in the course of pandemics. Considering that the virus can be transmitted to vaccinated individuals as well, one should underline the reality that depending on the vaccine’s protection rate; these individuals would be able to overcome the disease with low complications. In other words, following the completed incubation period, these individuals will either switch to the compartment of infected individuals showing symptoms or to the compartment of recovered individuals, depending on the protective rate of the vaccine. Besides this, there is the fact that vaccinated and infected individuals can also transmit the virus to susceptible individuals. However, recent research studies illustrated that transmission rates of vaccinated–infected individuals are much lower than unvaccinated–infected individuals [30], [31], [32], [33], [34].
• •It has been seen from previously implemented models that all vaccinated individuals were evaluated within an equal category. However, the situation is somewhat different in reality. Apart from the vaccine’s protection rate, the protection period is also to be considered. In a certain period, the vaccinated individuals switch from the vaccinated compartment to the susceptible individuals’ compartment. The same is true for individuals who have previously had the disease. In our study, all these situations were integrated into the model.
• •Different protection rates of existing or developed vaccines on the virus, changing by mutation, are also relevant. Therefore, the vaccine’s protection rate was also considered in this study. Thus, this paved the way for determining the effects of vaccinations made with different types in different countries around the world on the pandemic scenario of that country.
• •Numerous prediction models for the SARS-CoV-2 pandemic were proposed. However, unknown parameters of these models are often estimated based on observational data. Therefore, the model parameters were formulated for pandemic scenarios in further studies.

In addition to the stability analysis of the model, numerical solutions were obtained using the fractional Euler’s method.

The rest of this paper is organized as follows: Section 1 includes relevant literature. Some preliminaries of Caputo fractional calculus and the established model $SVI{I}_{v}R$ are introduced in Section 2. The numerical solution method of the model is given in Section 3. Section 4 presents a series of samples to validate the $SVI{I}_{v}R$ model. Finally, the conclusions of this study are given in Section 5.

2. The fractional $SVI{I}_{v}R$ model with vaccinated–infected and susceptible vaccinated compartments

As mentioned in the previous section, fractional differential equations are preferred in real-life modeling problems despite the difficulties in calculations. The most important reason for this is that fractional-order models have memory properties [35]. For instance, there is no difference in applying the integer-order model created for a pandemic disease in different regions where the pandemic continues. However, it is probable to have different conditions and parameters in each region where the pandemic continues. This leads to the understanding that the model works in the same structure in every region, which may be unrealistic. Notwithstanding, if the model is of fractional order, the optimum derivative order can be determined for each region. This way, the created model is reduced to a sub-model specific to the studied region. In this way, more realistic and accurate results are ensured to be obtained. There are various definitions of fractional derivatives. Riemann–Liouville, Caputo, Atangana–Baleanu, and Conformable are the most frequently used ones. In this study, Caputo derivative operator was preferred and utilized for modeling for easy implementation of classical initial conditions and ease of calculations. Caputo’s fractional derivative definition is given below:

Definition 1

The fractional differential of order $\alpha >0$ for a function $f:{\mathbb{R}}^{+}\to \mathbb{R}$ is defined by

$$D^{\alpha }f\left(t\right)=\left\{\begin{array}{c}\frac{1}{\Gamma (n-\alpha )}{\int }_0^t\frac{f^n\left(\xi \right)}{{(t-\xi )}^{\alpha +1-n}}d\xi ,\text{if}n-1<\alpha \le n\in \mathbb{N},\hfill \\ \hfill \\ \frac{d^{n}f\left(t\right)}{d{t}^n},\alpha =n\in \mathbb{N},\hfill \end{array}\right)$$ (2.1)

where $\Gamma (.)$ is a gamma function. Also, the Caputo fractional integral of order $\alpha$ is defined as

$$I^{\alpha }f\left(t\right)=\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^t{\left(t-\xi \right)}^{\alpha -1}f\left(\xi \right)d\xi .$$ (2.2)

In this study, we have developed a new compartment model based on the epidemiological characteristics of SARS-CoV-2 with current information about the pandemic event. The total population $N\left(t\right)$ was divided into five compartments. These compartments include susceptible, vaccinated, unvaccinated–infected, vaccinated–infected, and recovered individuals. These sub-populations are symbolized as $S\left(t\right),V\left(t\right),I\left(t\right),I_v\left(t\right)$ and $R\left(t\right)$, respectively. The expanded form of a SIR model can be seen, considering the added compartments, as a $SVI{I}_{v}R$ mathematical model. The vaccinated–infected compartment $I_v\left(t\right)$ will be included in the literature for the first time. Moreover, the interactions between the compartments are designed according to new information regarding the pandemic. The compartment of the deceased individuals was not taken into account. This is because there is no transition from this compartment to any other compartments, so it has no effect on the pandemic mechanism.

The compartment of susceptible $S\left(t\right)$ denotes individuals who were not infected but could get infected with the virus. In this study, the compartment $V\left(t\right)$ represents the individuals who completed at least two vaccinations in the last 6 months. Unfortunately, none of the produced vaccines show permanent residence to the virus. After the determined 6 months any individual would be considered as non-vaccinated, which means that the infection and transmission cycle starts again. Therefore, the study recommend re-vaccinations to avoid the epidemiological event. Individuals in both compartments, $S\left(t\right)$ and $V\left(t\right)$, can get infected, while those in the vaccinated compartment would show mainly minor symptoms. When individuals in compartments $S\left(t\right)$ and $V\left(t\right)$ are infected, they pass through the compartments $I\left(t\right)$ and $I_v\left(t\right)$, respectively. Individuals in these two compartments also can transmit the virus to the susceptible class. At the end of the incubation period, most individuals in the $I_v\left(t\right)$ compartment move to the recovered compartment, depending on the vaccine’s protection rate. These individuals either show no symptoms or show mild symptoms. Individuals remaining in the $I_v\left(t\right)$ compartment (i.e., the rate excluding the protection rate of the vaccine) move to the $I\left(t\right)$ compartment and may face serious symptoms due to the disease.

The $SVI{I}_{v}R$ model is defined as a system of fractional-order differential equations as following;

$$\frac{d^{\alpha }S\left(t\right)}{d{t}^{\alpha }}=bN-{\mu }_{1}S\left(t\right)-{\beta }_1\frac{I\left(t\right)S\left(t\right)}{N}-{\beta }_2\frac{I_v\left(t\right)S\left(t\right)}{N}-\sigma S\left(t\right)+cR\left(t\right)+dV\left(t\right),$$

$$\frac{d^{\alpha }V\left(t\right)}{d{t}^{\alpha }}=\sigma S\left(t\right)-dV\left(t\right)-{\beta }_1\frac{I\left(t\right)V\left(t\right)}{N}-{\mu }_{1}V\left(t\right)-{\beta }_2\frac{I_v\left(t\right)V\left(t\right)}{N},$$

$$\frac{d^{\alpha }I\left(t\right)}{d{t}^{\alpha }}={\beta }_1\frac{I\left(t\right)S\left(t\right)}{N}+{\beta }_2\frac{I_v\left(t\right)S\left(t\right)}{N}+m(1-p)I_v\left(t\right)-(w+{\mu }_1+{\mu }_2)I\left(t\right),$$ (2.3)

$$\frac{d^{\alpha }{I}_v\left(t\right)}{d{t}^{\alpha }}={\beta }_1\frac{I\left(t\right)V\left(t\right)}{N}+{\beta }_2\frac{I_v\left(t\right)V\left(t\right)}{N}-m{I}_v\left(t\right)-{\mu }_1{I}_v\left(t\right),$$

$$\frac{d^{\alpha }R\left(t\right)}{d{t}^{\alpha }}=mp{I}_v\left(t\right)+wI\left(t\right)-cR\left(t\right)-{\mu }_{1}R\left(t\right).$$

The parameters in system (2.3) are positive real numbers, where $b$ denotes the birth rate, ${\mu }_1$ is the natural death rate, ${\mu }_2$ is the disease-related death, ${\beta }_1$ is the transmission coefficient of the virus from unvaccinated–infected individuals to susceptible and vaccinated individuals (i.e., the transmission rate from $S$ to $I$ and from $V$ to $I_v$), ${\beta }_2$ is the transmission coefficient from vaccinated–infected individuals to susceptible (and vaccinated) individuals (i.e., from $S$ to $I$ and from $V$ to $I_v$ owing to vaccinated–infected individuals). Here, $d$ represents the proportion of individuals who were vaccinated, but the vaccine lost the effect, $\sigma$ represents the vaccination rate, $c$ is the immunity loss rate of the recovered individuals, $p$ is the protection rate of the vaccine, and $m$ is the incubation period. The order of the derivative is represented as $0<\alpha \le 1$ and $\frac{d^{\alpha }}{d{t}^{\alpha }}$ denotes the Caputo fractional derivative of order $\alpha$. All compartments and the description of the parameters are given in Table 1 and Table 2, respectively. The flow diagram of the system is represented in Fig. 1 to describe the interaction and transmissions among the compartments.

Table 1.

Compartment variables and their meanings.

Compartments	Meaning
$S\left(t\right)$	Susceptible individuals at time $t$
$V\left(t\right)$	Vaccinated individuals at time $t$
$I\left(t\right)$	Unvaccinated–Infected individuals at time $t$
$I_v\left(t\right)$	Vaccinated–Infected individuals at time $t$
$R\left(t\right)$	Recovered individuals at time $t$
$V\left(0\right)$	Vaccinated individuals in the last 6 months
$I\left(0\right)$	Unvaccinated–Infected individuals in the last 14 days
$I_v\left(0\right)$	Vaccinated–Infected individuals in the last 14 days
$R\left(0\right)$	Recovered individuals in the last 6 months
$S\left(0\right)$	$N-(I_0+V_0+I_{v0}+R_0)$

Table 2.

Parameters and their meanings.

Parameters	Meaning
$b$	Natural birth rate per unit time
$d$	The rate at which vaccinated individuals but they lose their immunity per unit time
${\mu }_1$	Natural death rate per unit time
${\mu }_2$	Disease induced death rate per unit time
${\beta }_1$	Disease transmission rate from unvaccinated–infected to susceptible per unit time
${\beta }_2$	Disease transmission rate from vaccinated–infected to susceptible per unit time
$\sigma$	Vaccination rate per unit time
$c$	The rate at which recovered individuals lose their immunity per unit time
$p$	The protection rate of vaccine
$w$	Recovery rate per unit time
$m$	The incubation period

Fig. 1.

A schematic diagram of the model.

In addition, the initial conditions are described as follows: $S\left(0\right)=S_0,V\left(0\right)=V_0,I\left(0\right)=I_0,I_v\left(0\right)=I_{v0}$ and $R\left(0\right)=R_0$.

The total number of actively infected people is $I_{act}=I_0+I_{v0}$. There are also individuals in the population that are infected and whose treatment continues for more than 14 days. However, the treatment of these individuals after 14 days is usually due to the damage left by the virus in their bodies, and these individuals can no longer transmit the virus after 14 days. Moreover, infected individuals may receive positive PCR (Polymerase Chain Reaction) test results for about 40 days after they are infected, but the transmission characteristic of the virus disappears after 14 days. Infected individuals who were kept isolated and completed the 14 days are considered recovered and moved to the $R$ compartment. Both compartments, $I$ and $I_v$, contain infected individuals who can transmit the virus. Besides, it is known that the adequate protection period of the vaccine is six months for individuals who have received a total dosage, and the vaccine’s protection rate drops significantly after the sixth month. It is stipulated that this drop in protection may be rather severe in Delta, Nu, Omicron, BA.4/5, and Deltacron variants that have emerged lately. Similarly, it is stated that the individuals who overcame the disease and gained natural immunity would still not show permanent immunity; therefore, they would lose their immunity within six months. Thus, the $V$ compartment shows the individuals who have been vaccinated within the last six months and not the total number of vaccinated individuals in the population. It was assumed that an equal number of individuals had been vaccinated daily in the last six months. Therefore, every day, people who were vaccinated $180$ days ago moved from compartment $V$ to compartment $S$. A similar case is also proper for recovered individuals.

According to the data of the World Health Organization (WHO), of the total number of actively infected individuals ($I_{act}$) within a region, the segregation between vaccinated–infected and unvaccinated–infected individuals has not been reached. Therefore, in order to determine the initial conditions of $I_0$ and $I_{v0}$, the ratio of the actively vaccinated individuals within the total population (i.e., within the last six months) was calculated and considered valid for $I_{act}$ as well. Thus, we have

$$\frac{V_0}{N}=\frac{I_{v0}}{I_{act}}$$

and from here it can be derived that

$$I_{v0}=\frac{I_{act}{V}_0}{N}.$$ (2.4)

One of the critical points in modeling a pandemic is the correct definition and calculation of the parameters in the model. These parameters do not alter with time and are the same values as when solutions are prepared. The section below demonstrates the definitions and formulations of the parameters in the model given with the system (2.3).

2.1. Parametric relations and parametric values

One of the most critical parameters in the model (2.3) is $\beta$ parameter, which shows the transmission rate of the disease. In case of a decrease in this parameter, the pandemic stage would shift significantly in a positive direction. As much as we know, no concrete study in the literature would demonstrate this parameter’s calculation. Therefore, we devised a simple and effective formulation for the parameter $\beta$. In one day, infected individuals engage with people so that the disease can be transmitted to $a$ number of people. From these contacts, $S/N$ amount are susceptible people infected with the probability of $P$. According to this, $\beta$ parameter in the model can be calculated as follows,

$$\beta =aP.$$ (2.5)

The parameter denoted as $a$ is determined differently in every society where the pandemic continues. Generally, infected people do not show any symptoms during the incubation period. Therefore, they can transmit the virus to many people with whom they have been in close contact during the day without realizing it. Since they are quarantined after showing symptoms at the end of the incubation period, the number of their daily active contacts, $a$, decreases significantly. Therefore, when calculating the number $a$, the average number of people with whom a symptomatic person can come in daily active contact should be taken, on average, for the duration of the incubation period, from the days before the incubation period until the completion of the quarantine. For example, let the total number of active cases in the last 14 days be $I_{act}=I_0+I_{v0}$. In this case, the number of not infected individuals at that moment is $S_0+V_0+R_0$. According to this, the probability of an uninfected individual in the community getting the disease from an infected individual is given as follows:

$$P=\frac{I_{act}}{S_0+V_0+R_0}.$$ (2.6)

Thus, according to Eq. (2.5), the parameter $\beta$ can be calculated as follows,

$$\beta =a\frac{I_{act}}{S_0+V_0+R_0}=a\frac{I_0+I_{v0}}{N-(I_0+I_{v0})}.$$ (2.7)

In the fractional model given by system (2.3), the $\beta$ parameter is divided into two parts ${\beta }_1$ and ${\beta }_2$. So we can write that $\beta ={\beta }_1+{\beta }_2$. Here ${\beta }_1$ and ${\beta }_2$ parameters depend on the transmission probabilities of unvaccinated–infected and vaccinated–infected, respectively. Clinical studies implemented at the time of this article are prepared to show that vaccinated–infected individuals spread the virus at a much lower rate than unvaccinated–infected people [30], [31], [32], [33], [34], [36], [37]. However, since these ratios have not yet been scientifically determined clearly, it is assumed that ${\beta }_1>{\beta }_2$, and the parameter $\beta$ is allocated to ${\beta }_1$ and ${\beta }_2$, such as

$${\beta }_1=0.8\beta ,{\beta }_2=0.2\beta .$$ (2.8)

The first equation in the system (2.3) illustrated the change concerning time in the $S$ (susceptible individuals) compartment. Positive signs indicate those entering compartment $S$, and negative ones indicate those leaving this compartment. $bN$ indicates the number of people born daily, and newborns are considered susceptible individuals. The rate of people leaving compartment $S$ is the same as the number of natural deaths. Individuals in compartment $I$ represent unvaccinated–infected persons. They can transmit the virus to healthy people in compartments $S$ and $V$. The number of susceptible individuals will decrease as the number of infected individuals increases. In one day, infected individuals engage with people so that the disease can be transmitted to $a$ number of people (therefore $aI$ number of people are under daily risk). From these contacts, $S/N$ amount is healthy people infected with the probability of $P$. Thus, the rate of decrease of $S$ depends on both $I$ and $S$. In that case, ${\beta }_1\frac{I\left(t\right)S\left(t\right)}{N}$ amount of people are infected daily by individuals in compartment $I$ and pass from compartment $S$ to $I$. Individuals in compartment $I_v$ represent vaccinated–infected persons. They can also transmit the virus to healthy individuals in compartment $S$. Thus, daily ${\beta }_2\frac{Iv\left(t\right)S\left(t\right)}{N}$ amount of people are infected by individuals in $I_v$, and pass from compartment $S$ to compartment $I$. Individuals in compartment $S$ have not completed their vaccinations yet (or are considered unvaccinated because they have completed it more than six months ago), so those who leave this compartment pass directly to compartment $I$.

One of the significant parameters of this model is $w$, which represents the daily recovery rate. As mentioned above, the meaning of recovery from SARS-CoV-2 is loss of transmitting the disease upon the termination of 14 days. That is to say, according to the current information, an individual cannot transmit the virus 14 days after being infected. However, the treatment may last longer due to the side effects of the disease. Even during the treatment, the cause of death is attributed to diseases other than COVID-19 (heart failure, permanent lung damage, deterioration in brain functions, etc.). In this case, who are the recovered individuals today? The answer to this question is people who were infected on the 15th day before today. Similarly, those who recovered yesterday were infected on the 16th day before today. Considering this, the total number of people recovered during the last 14 days, $R_m$, is calculated. From the total number of infected people, these individuals are those who have recovered between 15–28 days before today. The total number of infected people between 15–28 days before today was shown as $I_m^{\ast }$. Thus, the daily recovery rate can be calculated as follows,

$$w=\frac{1}{14}\frac{R_m}{I_m^{\ast }}.$$ (2.9)

The vaccination rate is yet another significant parameter regarding the model regarding vaccination. In the model given in the system (2.3), the daily vaccination rate was expressed as $\sigma$. As indicated in the previous section, for individuals vaccinated within the last six months, the vaccine’s protective effect continues to be strong. The vaccine does not only protect the infected individuals. It protects the whole society, as individuals who are fully vaccinated transmit the virus at a lower rate than those who are not vaccinated. Let us show the number of individuals vaccinated in the last six months and whose reminder doses have been given as $V_0$. In this case, the number of individuals in the population considered unvaccinated is $V_{uv}=N-V_0$. If we take the average number of people vaccinated daily in the last month as $V_m$, we can calculate the daily vaccination rate as follows,

$$\sigma =\frac{V_m}{V_{uv}}.$$ (2.10)

The reason for choosing one month instead of 14 days, contrary to previous calculations, is to prevent setbacks that may occur in a short time due to vaccine supply or other reasons, causing errors in the calculations of this parameter.

Parameters $c$ and $d$, included in the model defined as a fractional differential equation system (2.3), represent the proportion of people who have been re-infected and show symptoms. However, they have recently recovered from the disease or recently completed their vaccinations. Therefore, the number of these people in the population is relatively low. Due to the inability to produce enough antibodies despite meeting the vaccine or virus, the immune systems of these people cannot prevent the individual from getting sick. Additionally, these parameters represent the proportion of individuals who recovered before six months or who completed all their vaccinations more than six months ago and who re-transfer to compartment $S$ from the compartments that consist of the individuals who recovered and were vaccinated, respectively. In this case, the total number of individuals recovered within the last six months can be shown as $c=1/180$ assuming an equal daily recovery rate. Similarly, the total number of individuals who have completed their vaccinations in the last six months can be taken as $d=1/180$ assuming an equal daily vaccination rate. Thus, every day from today, the individuals who have recovered or completed their vaccinations $180$ days ago leave compartments $R$ and $V$ respectively and pass to the compartment $S$, which consists of susceptible individuals.

Nevertheless, another parameter in the model is ${\mu }_2$, which is the daily death rate from COVID-19. If we show the total number of people who died due to COVID-19 in the last month with $D_m$, the daily death rate can be calculated as follows,

$${\mu }_2=\frac{D_m}{I_s}.$$ (2.11)

where $I_s$ is the total number of people infected in the last month. The incubation period is the time between the transmission of the virus to a person and the appearance of the signs of infection. Although the incubation period varies from one person to another between $2\text{–}14$ days, the average period is $5$ days. This period also depends on the amount of virus a person has been exposed to [38]. Since the infected individuals do not show any symptoms during the incubation period, the potential to transmit the virus is high. The incubation period is $m=1/T$ where $T$ represents the incubation time. As it can be seen from the last three equations in the model given in the system (2.3), as much as the daily incubation period of the individuals in the compartment $I_v$, they either pass into compartment $I$ or $R$. The protection rate of the vaccine is very effective in this transfer.

The rest of the parameters in our model $b,{\mu }_1$, and $p$, are daily birth, daily natural death, and protection rate of the vaccine, respectively. Of these ratios, $b$ and ${\mu }_1$ can be determined according to official sources for the studied region. The protection rate of the vaccine, $p$, varies according to each vaccine brand and virus mutation and can be taken according to current

2.2. Local stability analysis of the disease-free and co-existing equilibrium points

One of the most important problems to deal with in mathematical epidemiology models is to determine the disease-free equilibrium point and study the stability of the system at this point. To evaluate equilibrium points of system (2.3), we set $D^{\alpha }S\left(t\right)=0,D^{\alpha }V\left(t\right)=0,D^{\alpha }I\left(t\right)=0,D^{\alpha }{I}_v\left(t\right)=0,D^{\alpha }R\left(t\right)=0$. Hence, we can write the system as follows:

$$bN-{\mu }_{1}S\left(t\right)-{\beta }_1\frac{I\left(t\right)S\left(t\right)}{N}-{\beta }_2\frac{I_v\left(t\right)S\left(t\right)}{N}-\sigma S\left(t\right)+cR\left(t\right)+dV\left(t\right)=0$$ (2.12)

$$\sigma S\left(t\right)-dV\left(t\right)-{\beta }_1\frac{I\left(t\right)V\left(t\right)}{N}-{\mu }_{1}V\left(t\right)-{\beta }_2\frac{I_v\left(t\right)V\left(t\right)}{N}=0$$ (2.13)

$${\beta }_1\frac{I\left(t\right)S\left(t\right)}{N}+{\beta }_2\frac{I_v\left(t\right)S\left(t\right)}{N}+m(1-p)I_v\left(t\right)-(w+{\mu }_1+{\mu }_2)I\left(t\right)=0$$ (2.14)

$${\beta }_1\frac{I\left(t\right)V\left(t\right)}{N}+{\beta }_2\frac{I_v\left(t\right)V\left(t\right)}{N}-m{I}_v\left(t\right)-{\mu }_1{I}_v\left(t\right)=0$$ (2.15)

$$mp{I}_v\left(t\right)+wI\left(t\right)-cR\left(t\right)-{\mu }_{1}R\left(t\right)=0$$ (2.16)

The above system has a disease-free equilibrium when $I\left(t\right)=0$ and $I_v\left(t\right)=0$. According to this, the disease-free equilibrium point is obtained as,

$${\stackrel{\text{\_}}{E}}_0=\left({\stackrel{\text{\_}}{S}}_0,{\stackrel{\text{\_}}{V}}_0,{\stackrel{\text{\_}}{I}}_0,{\stackrel{\text{\_}}{I_v}}_0,{\stackrel{\text{\_}}{R}}_0\right)=\left(\frac{\left(d+{\mu }_1\right)bN}{{\mu }_1\left(d+\sigma +{\mu }_1\right)},\frac{\sigma bN}{{\mu }_1\left(d+\sigma +{\mu }_1\right)},0,0,0\right).$$ (2.17)

The Jacobian matrix $J\left({\stackrel{\text{\_}}{E}}_0\right)$ for the above system at the disease-free equilibrium point ${\stackrel{\text{\_}}{E}}_0$ is as follows:

$$J\left({\stackrel{\text{\_}}{E}}_0\right)=\left[\begin{array}{ccccc}\hfill -{\mu }_1-\sigma \hfill & \hfill d\hfill & \hfill \frac{-{\beta }_1\left(d+{\mu }_1\right)b}{{\mu }_1\left(d+\sigma +{\mu }_1\right)}\hfill & \hfill \frac{-{\beta }_2\left(d+{\mu }_1\right)b}{{\mu }_1\left(d+\sigma +{\mu }_1\right)}\hfill & \hfill c\hfill \\ \hfill \sigma \hfill & \hfill -d-{\mu }_1\hfill & \hfill \frac{-{\beta }_1\sigma b}{{\mu }_1\left(d+\sigma +{\mu }_1\right)}\hfill & \hfill \frac{-{\beta }_2\sigma b}{{\mu }_1\left(d+\sigma +{\mu }_1\right)}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{{\beta }_1\left(d+{\mu }_1\right)b}{{\mu }_1\left(d+\sigma +{\mu }_1\right)}\hfill & \hfill m(1-p)+\frac{{\beta }_2\left(d+{\mu }_1\right)b}{{\mu }_1\left(d+\sigma +{\mu }_1\right)}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{{\beta }_1\sigma b}{{\mu }_1\left(d+\sigma +{\mu }_1\right)}\hfill & \hfill -m-{\mu }_1+\frac{{\beta }_2\sigma b}{{\mu }_1\left(d+\sigma +{\mu }_1\right)}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill w\hfill & \hfill mp\hfill & \hfill -c-{\mu }_1\hfill \end{array}\right].$$ (2.18)

Theorem 1

Consider the following fractional-order system

$$D_t^{\alpha }x\left(t\right)=f(t,x\left(t\right)),x\left(t_0\right)=x_0,0<\alpha \le 1,$$

where $D^{\alpha }$ is the Caputo derivative of the order $\alpha$ , $f(t,x\left(t\right)):{\mathbb{R}}^{+}\times {\mathbb{R}}^n\to {\mathbb{R}}^n$ is a vector field. The disease-free equilibrium point ${\stackrel{\text{\_}}{E}}_0$ is locally asymptotically stable if all eigenvalues, ${\lambda }_i$ , of the Jacobian matrix $J\left({\stackrel{\text{\_}}{E}}_0\right)$ at the equilibrium point satisfy following condition: $\left|Arg\left({\lambda }_i\right)\right|>\frac{\pi \alpha }{2}$ .

The eigenvalues obtained from the Jacobian matrix (2.18) are calculated as

$$\begin{array}{cc}\hfill {\lambda }_1=\hfill & -c-{\mu }_1\hfill \\ \hfill {\lambda }_2=\hfill & -{\mu }_1\hfill \\ \hfill {\lambda }_3=\hfill & -d-{\mu }_1-\sigma \hfill \\ \hfill {\lambda }_4=\hfill & G_1(G_2+\sqrt{G_3})\hfill \\ \hfill {\lambda }_5=\hfill & G_1(G_2-\sqrt{G_3})\hfill \end{array}$$

where

$$\begin{array}{cc}{G}_1=\hfill & \frac{1}{2{\mu }_1\left(\sigma +d+{\mu }_1\right)}\hfill \\ G_2=\hfill & -2{\mu }_1^3+\left(-2\sigma -2d-m-w-{\mu }_2\right){\mu }_1^2+\left[\left(-m-w-{\mu }_2\right)\left(\sigma +d\right)+{\beta }_{1}b\right]{\mu }_1+b\left({\beta }_{1}d+{\beta }_2\sigma \right)\hfill \\ G_3=\hfill & b^2{\left(d+{\mu }_1\right)}^2{\beta }_1^2-2b\left[{\mu }_1\left(\sigma +d+{\mu }_1\right)\left(\left(d+{\mu }_1\right){\mu }_2-\left(d+{\mu }_1+2\sigma -2\sigma p\right)m+w\left(d+{\mu }_1\right)\right)\right)\hfill \\ \hfill & -\left(\left(d+{\mu }_1\right){\beta }_2\sigma b\right]{\beta }_1\hfill \\ \hfill & +{\left[\left(\sigma +d+{\mu }_1\right)\left({\mu }_2-m+w\right){\mu }_1+{\beta }_2\sigma b\right]}^2.\hfill \end{array}$$

Because the parameters $c,d,{\mu }_1$ and $\sigma$ are definitely positive real numbers, it is clear that ${\lambda }_1<0,{\lambda }_2<0$ and ${\lambda }_3<0$. In addition, it can be easily seen that $G_1>0$ and the other eigenvalues ${\lambda }_{4,5}<0$ when $G_2<0$ and

$$\left|G_2\right|>\sqrt{G_3}.$$ (2.19)

Hence, $\left|Arg\left({\lambda }_i\right)\right|=\pi >\frac{\pi \alpha }{2}$ for each $i=1,2,3,4,5$.

The number $R_0$, represents the average number of secondary cases transmitted from a typical patient for infectious disease in a fully susceptible population. Even though $R_0$ is specified as a single number or a number distribution. It may vary according to many factors such as epidemiological characteristics of the infection (transmission route, incubation period, infectious period, immunity rate gained by the population, vaccination rate, vaccine protection rate, etc.), biological characteristics of the infectious agent, socio-demographic variables (the environment between infected and sensitive people, risk of contact, intensity, and duration, etc.). So, $R_0$ can be considered an epidemiological summary of many factors [39]. If $R_0$ is greater than $1$, it is predicted that an infected person can transmit the disease to more than one person, and the disease will gradually spread in the population over time. Suppose $R_0$ is less than $1$. In that case, it means that with each case, the disease cannot be transmitted to another person proportionally. The disease is gradually self-limiting, and the cases decrease rapidly. However, in the lack of necessary precautions, the number of $R_0$ can grow again. Diseases with a high $R_0$ value have a higher potential to spread and cause a pandemic in society than diseases with a low $R_0$ value. If adequate precautions are not taken in society, this rate of spread can reach dangerous levels. In general, it can be said that the $R_0$ value of SARS-CoV-2, which causes the current COVID-19 pandemic, is about 2.6 on average. This value is higher than other severe coronavirus infections, SARS and MERS. Therefore, it can be said that the COVID-19 disease has the potential to spread much faster [39]. As discussed above, the value of $R_0$ depends on many parameters related to the pandemic. Local governments and individuals can play an active role in many of these parameters. Thus, reaching the parameters (such as vaccination rate and quarantine) that will reduce the number of $R_0$ is significant for the termination of the pandemics.

According to Eq. (2.19), we conclude that the basic reproduction number, $R_0$, is given by

$$R_0=\frac{\sqrt{G_3}}{\left|G_2\right|}$$ (2.20)

under the assumption that $G_2<0$. So, if $R_0<1$, the disease-free equilibrium of the model (2.3) is locally asymptotically stable and if $R_0>1$ then ${\stackrel{\text{\_}}{E}}_0$ is unstable. In this case, we can analyze an endemic (positive) equilibrium point $\tilde{E}=\left(\tilde{S},\tilde{V},\tilde{I},\widetilde{I_v},\tilde{R}\right)$ of the system in the next sub-section.

The endemic equilibrium is obtained by solving the system of equations $D^{\alpha }S\left(t\right)=0,D^{\alpha }V\left(t\right)=0,D^{\alpha }I\left(t\right)=0,D^{\alpha }{I}_v\left(t\right)=0,D^{\alpha }R\left(t\right)=0$. According to system (2.12)–(2.16), the endemic equilibrium can be obtained by the following methodology.

From Eq. (2.15), it is clear that

$$I=I_{v}f\left(v\right),$$ (2.21)

where $f\left(v\right)=\frac{N}{{\beta }_{1}V}(m+{\mu }_1-\frac{{\beta }_{2}V}{N})$.

Substituting Eq. (2.21) into Eq. (2.14) and using the symbolic computation, we have

$$S=g\left(v\right)$$ (2.22)

where $g\left(v\right)=N\frac{\left(w+{\mu }_1+{\mu }_2\right)f\left(v\right)+m(p-1)}{{\beta }_{1}f\left(v\right)+{\beta }_2}$.

Considering the Eqs. (2.21), (2.22) in Eq. (2.13), we have

$$I_v=h\left(v\right),$$ (2.23)

where $h\left(v\right)=\frac{N}{V}\frac{\sigma g\left(v\right)-(d+{\mu }_1)V}{{\beta }_{1}f\left(v\right)+{\beta }_2}$. From the Eqs. (2.21), (2.23), it is obvious that

$$I=h\left(v\right)f\left(v\right).$$ (2.24)

Thus, by using Eqs. (2.23), (2.24) into Eq. (2.16), we get

$$R=k\left(v\right),$$ (2.25)

where $k\left(v\right)=\frac{mph\left(v\right)+wh\left(v\right)f\left(v\right)}{c+{\mu }_1}$.

Finally, substituting the Eqs. (2.22)–(2.25) into Eq. (2.12), we obtain the following quadratic equation:

$$A{V}^2+BV+C=0.$$ (2.26)

Here, the coefficients $A,B$ and $C$ are depend on the parameters of the model, ${\beta }_1,{\beta }_2,b,{\mu }_1,\dots$,etc. We obtained the proper form of these coefficients using the MAPLE software, but we did not include it in this paper because it was rather long. However, since the parameters of the model will be known numerically for a real application, the coefficients $A$, $B$ and $C$ can be easily calculated by hand with the help of Eqs. (2.12)–(2.16). Thus, the positive variable $V$ to be obtained is written in the Eqs. (2.12)–(2.16) and the pandemic equilibrium point $\tilde{E}=\left(\tilde{S},\tilde{V},\tilde{I},\widetilde{I_v},\tilde{R}\right)$ is obtained. Stability analysis of the endemic balance point can be done through MAPLE or similar software.

2.3. Global stability of the disease-free and co-existing equilibrium points

In this part, we want to apply the discretization process to analyze the global stability of system (2.3) since the compartments’ dynamical behavior show affects of discrete-time. The discretization of system (2.3) is as follows, where $z=\left[\frac{t}{x}\right]x$;

$$\left\{\begin{array}{cc}{D}^{\alpha }S\left(t\right)=\hfill & bN-{\mu }_{1}S\left(z\right)-\left(\frac{{\beta }_1}{N}I\left(z\right)+\frac{{\beta }_2}{N}{I}_v\left(z\right)\right)S\left(z\right)-\sigma S\left(z\right)+cR\left(z\right)+dV\left(z\right)\hfill \\ D^{\alpha }V\left(t\right)=\hfill & \sigma S\left(z\right)-dV\left(z\right)-\left(\frac{{\beta }_1}{N}I\left(z\right)+\frac{{\beta }_2}{N}{I}_v\left(z\right)\right)V\left(z\right)-{\mu }_{1}V\left(z\right)\hfill \\ D^{\alpha }I\left(t\right)=\hfill & \left(\frac{{\beta }_1}{N}I\left(z\right)+\frac{{\beta }_2}{N}{I}_v\left(z\right)\right)S\left(z\right)+m(1-p)I_v\left(z\right)-(w+{\mu }_1+{\mu }_2)I\left(z\right)\hfill \\ D^{\alpha }{I}_v\left(t\right)=\hfill & \left(\frac{{\beta }_1}{N}I\left(z\right)+\frac{{\beta }_2}{N}{I}_v\left(z\right)\right)V\left(z\right)-\left(m+{\mu }_1\right)I_v\left(z\right)\hfill \\ D^{\alpha }R\left(t\right)=\hfill & mp{I}_v\left(z\right)+wI\left(z\right)-\left(c+{\mu }_1\right)R\left(z\right).\hfill \end{array}\right)$$ (2.27)

For $t\in \left[0,h\right)$, $\frac{t}{h}\in \left[0,1\right)$, we have

$$\left\{\begin{array}{cc}{D}^{\alpha }S\left(t\right)=\hfill & bN-{\mu }_{1}S\left(0\right)-\left(\frac{{\beta }_1}{N}I\left(0\right)+\frac{{\beta }_2}{N}{I}_v\left(0\right)\right)S\left(0\right)-\sigma S\left(0\right)+cR\left(0\right)+dV\left(0\right)\hfill \\ D^{\alpha }V\left(t\right)=\hfill & \sigma S\left(0\right)-dV\left(0\right)-\left(\frac{{\beta }_1}{N}I\left(0\right)+\frac{{\beta }_2}{N}{I}_v\left(0\right)\right)V\left(0\right)-{\mu }_{1}V\left(0\right)\hfill \\ D^{\alpha }I\left(t\right)=\hfill & \left(\frac{{\beta }_1}{N}I\left(0\right)+\frac{{\beta }_2}{N}{I}_v\left(0\right)\right)S\left(0\right)+m(1-p)I_v\left(0\right)-(w+{\mu }_1+{\mu }_2)I\left(0\right)\hfill \\ D^{\alpha }{I}_v\left(t\right)=\hfill & \left(\frac{{\beta }_1}{N}I\left(0\right)+\frac{{\beta }_2}{N}{I}_v\left(0\right)\right)V\left(0\right)-\left(m+{\mu }_1\right)I_v\left(0\right)\hfill \\ D^{\alpha }R\left(t\right)=\hfill & mp{I}_v\left(0\right)+wI\left(0\right)-\left(c+{\mu }_1\right)R\left(0\right).\hfill \end{array}\right)$$ (2.28)

The solution of (2.28) reduces to

$$\left\{\begin{array}{cc}S\left(1\right)=\hfill & S\left(0\right)+\frac{t^{\alpha }}{\Gamma \left(\alpha +1\right)}\left\{bN-{\mu }_{1}S\left(0\right)-\left(\frac{{\beta }_1}{N}I\left(0\right)+\frac{{\beta }_2}{N}{I}_v\left(0\right)\right)S\left(0\right)-\sigma S\left(0\right)+cR\left(0\right)+dV\left(0\right)\right\}\hfill \\ V\left(1\right)=\hfill & V\left(0\right)+\frac{t^{\alpha }}{\Gamma \left(\alpha +1\right)}\left\{\sigma S\left(0\right)-dV\left(0\right)-\left(\frac{{\beta }_1}{N}I\left(0\right)+\frac{{\beta }_2}{N}{I}_v\left(0\right)\right)V\left(0\right)-{\mu }_{1}V\left(0\right)\right\}\hfill \\ I\left(1\right)=\hfill & I\left(0\right)+\frac{t^{\alpha }}{\Gamma \left(\alpha +1\right)}\left\{\left(\frac{{\beta }_1}{N}I\left(0\right)+\frac{{\beta }_2}{N}{I}_v\left(0\right)\right)S\left(0\right)+m(1-p)I_v\left(0\right)-(w+{\mu }_1+{\mu }_2)I\left(0\right)\right\}\hfill \\ I_v\left(1\right)=\hfill & I_v\left(0\right)+\frac{t^{\alpha }}{\Gamma \left(\alpha +1\right)}\left\{\left(\frac{{\beta }_1}{N}I\left(0\right)+\frac{{\beta }_2}{N}{I}_v\left(0\right)\right)V\left(0\right)-\left(m+{\mu }_1\right)I_v\left(0\right)\right\}\hfill \\ R\left(1\right)=\hfill & R\left(0\right)+\frac{t^{\alpha }}{\Gamma \left(\alpha +1\right)}\left\{mp{I}_v\left(0\right)+wI\left(0\right)-\left(c+{\mu }_1\right)R\left(0\right)\right\}.\hfill \end{array}\right)$$ (2.29)

For $t\in \left[h,2h\right)$, $\frac{t}{h}\in \left[1,2\right)$, we get

$$\left\{\begin{array}{cc}S\left(2\right)=\hfill & S\left(1\right)+\frac{{(t-h)}^{\alpha }}{\Gamma \left(\alpha +1\right)}\left\{bN-{\mu }_{1}S\left(1\right)-\left(\frac{{\beta }_1}{N}I\left(1\right)+\frac{{\beta }_2}{N}{I}_v\left(1\right)\right)S\left(1\right)-\sigma S\left(1\right)+cR\left(1\right)+dV\left(1\right)\right\}\hfill \\ V\left(2\right)=\hfill & V\left(1\right)+\frac{{(t-h)}^{\alpha }}{\Gamma \left(\alpha +1\right)}\left\{\sigma S\left(1\right)-dV\left(1\right)-\left(\frac{{\beta }_1}{N}I\left(1\right)+\frac{{\beta }_2}{N}{I}_v\left(1\right)\right)V\left(1\right)-{\mu }_{1}V\left(1\right)\right\}\hfill \\ I\left(2\right)=\hfill & I\left(1\right)+\frac{{(t-h)}^{\alpha }}{\Gamma \left(\alpha +1\right)}\left\{\left(\frac{{\beta }_1}{N}I\left(1\right)+\frac{{\beta }_2}{N}{I}_v\left(1\right)\right)S\left(1\right)+m(1-p)I_v\left(1\right)-(w+{\mu }_1+{\mu }_2)I\left(1\right)\right\}\hfill \\ I_v\left(2\right)=\hfill & I_v\left(1\right)+\frac{{(t-h)}^{\alpha }}{\Gamma \left(\alpha +1\right)}\left\{\left(\frac{{\beta }_1}{N}I\left(1\right)+\frac{{\beta }_2}{N}{I}_v\left(1\right)\right)V\left(1\right)-\left(m+{\mu }_1\right)I_v\left(1\right)\right\}\hfill \\ R\left(2\right)=\hfill & R\left(1\right)+\frac{{(t-h)}^{\alpha }}{\Gamma \left(\alpha +1\right)}\left\{mp{I}_v\left(1\right)+wI\left(1\right)-\left(c+{\mu }_1\right)R\left(1\right)\right\}.\hfill \end{array}\right)$$ (2.30)

Repeating the process $n$ times, we obtain

$$\left\{\begin{array}{cc}S\left(n+1\right)=\hfill & S\left(n\right)+\frac{{(t-nh)}^{\alpha }}{\Gamma \left(\alpha +1\right)}\left\{bN-{\mu }_{1}S\left(n\right)-\left(\frac{{\beta }_1}{N}I\left(n\right)+\frac{{\beta }_2}{N}{I}_v\left(n\right)\right)S\left(n\right)-\sigma S\left(n\right)+cR\left(n\right)+dV\left(n\right)\right\}\hfill \\ V\left(n+1\right)=\hfill & V\left(n\right)+\frac{{(t-nh)}^{\alpha }}{\Gamma \left(\alpha +1\right)}\left\{\sigma S\left(n\right)-dV\left(n\right)-\left(\frac{{\beta }_1}{N}I\left(n\right)+\frac{{\beta }_2}{N}{I}_v\left(n\right)\right)V\left(n\right)-{\mu }_{1}V\left(n\right)\right\}\hfill \\ I\left(n+1\right)=\hfill & I\left(n\right)+\frac{{(t-nh)}^{\alpha }}{\Gamma \left(\alpha +1\right)}\left\{\left(\frac{{\beta }_1}{N}I\left(n\right)+\frac{{\beta }_2}{N}{I}_v\left(n\right)\right)S\left(n\right)+m(1-p)I_v\left(n\right)-(w+{\mu }_1+{\mu }_2)I\left(n\right)\right\}\hfill \\ I_v\left(n+1\right)=\hfill & I_v\left(n\right)+\frac{{(t-nh)}^{\alpha }}{\Gamma \left(\alpha +1\right)}\left\{\left(\frac{{\beta }_1}{N}I\left(n\right)+\frac{{\beta }_2}{N}{I}_v\left(n\right)\right)V\left(n\right)-\left(m+{\mu }_1\right)I_v\left(n\right)\right\}\hfill \\ R\left(n+1\right)=\hfill & R\left(n\right)+\frac{{(t-nh)}^{\alpha }}{\Gamma \left(\alpha +1\right)}\left\{mp{I}_v\left(n\right)+wI\left(n\right)-\left(c+{\mu }_1\right)R\left(n\right)\right\}.\hfill \end{array}\right)$$ (2.31)

For $t\in \left[nh,(n+1)h\right)$, while $t⟶(n+1)h$ and $\alpha ⟶1$, we have

$$\left\{\begin{array}{cc}S\left(n+1\right)=\hfill & S\left(n\right)+\frac{h^{\alpha }}{\Gamma \left(\alpha +1\right)}\left\{bN-{\mu }_{1}S\left(n\right)-\left(\frac{{\beta }_1}{N}I\left(n\right)+\frac{{\beta }_2}{N}{I}_v\left(n\right)\right)S\left(n\right)-\sigma S\left(n\right)+cR\left(n\right)+dV\left(n\right)\right\}\hfill \\ V\left(n+1\right)=\hfill & V\left(n\right)+\frac{h^{\alpha }}{\Gamma \left(\alpha +1\right)}\left\{\sigma S\left(n\right)-dV\left(n\right)-\left(\frac{{\beta }_1}{N}I\left(n\right)+\frac{{\beta }_2}{N}{I}_v\left(n\right)\right)V\left(n\right)-{\mu }_{1}V\left(n\right)\right\}\hfill \\ I\left(n+1\right)=\hfill & I\left(n\right)+\frac{h^{\alpha }}{\Gamma \left(\alpha +1\right)}\left\{\left(\frac{{\beta }_1}{N}I\left(n\right)+\frac{{\beta }_2}{N}{I}_v\left(n\right)\right)S\left(n\right)+m(1-p)I_v\left(n\right)-(w+{\mu }_1+{\mu }_2)I\left(n\right)\right\}\hfill \\ I_v\left(n+1\right)=\hfill & I_v\left(n\right)+\frac{h^{\alpha }}{\Gamma \left(\alpha +1\right)}\left\{\left(\frac{{\beta }_1}{N}I\left(n\right)+\frac{{\beta }_2}{N}{I}_v\left(n\right)\right)V\left(n\right)-\left(m+{\mu }_1\right)I_v\left(n\right)\right\}\hfill \\ R\left(n+1\right)=\hfill & R\left(n\right)+\frac{h^{\alpha }}{\Gamma \left(\alpha +1\right)}\left\{mp{I}_v\left(n\right)+wI\left(n\right)-\left(c+{\mu }_1\right)R\left(n\right)\right\}.\hfill \end{array}\right)$$ (2.32)

Theorem 2

Let ${\left\{S\left(n\right),V\left(n\right),I\left(n\right),I_v\left(n\right),R\left(n\right)\right\}}_{n=0}^{\infty }$ be the solutions of system (2.32) that are monotonic decreasing. Moreover, let the conditions of Theorem 1 hold. If

$$h<{\left(\frac{2\left(S\left(n\right)-\overline{S_0}\right)\Gamma \left(\alpha +1\right)}{-bN+{\mu }_{1}S\left(n\right)+\left(\frac{{\beta }_1}{N}I\left(n\right)+\frac{{\beta }_2}{N}{I}_v\left(n\right)\right)S\left(n\right)+\sigma S\left(n\right)-cR\left(n\right)-dV\left(n\right)}\right)}^{\frac{1}{\alpha }}\text{ for }S\left(n\right)>\overline{S_0}$$

$$h<{\left(\frac{2\left(V\left(n\right)-\overline{V_0}\right)\Gamma \left(\alpha +1\right)}{-\sigma S\left(n\right)+dV\left(n\right)+\left(\frac{{\beta }_1}{N}I\left(n\right)+\frac{{\beta }_2}{N}{I}_v\left(n\right)\right)V\left(n\right)+{\mu }_{1}V\left(n\right)}\right)}^{\frac{1}{\alpha }}\text{ for }V\left(n\right)>\overline{V_0},$$

$$h<{\left(\frac{2I\left(n\right)\Gamma \left(\alpha +1\right)}{-\left(\frac{{\beta }_1}{N}I\left(n\right)+\frac{{\beta }_2}{N}{I}_v\left(n\right)\right)S\left(n\right)-m(1-p)I_v\left(n\right)+(w+{\mu }_1+{\mu }_2)I\left(n\right)}\right)}^{\frac{1}{\alpha }},$$

$$h<{\left(\frac{2I_v\left(n\right)\Gamma \left(\alpha +1\right)}{-\left(\frac{{\beta }_1}{N}I\left(n\right)+\frac{{\beta }_2}{N}{I}_v\left(n\right)\right)V\left(n\right)+\left(m+{\mu }_1\right)I_v\left(n\right)}\right)}^{\frac{1}{\alpha }},$$

and

$$h<{\left(\frac{2R\left(n\right)\Gamma \left(\alpha +1\right)}{-mp{I}_v\left(n\right)-wI\left(n\right)+\left(c+{\mu }_1\right)R\left(n\right)}\right)}^{\frac{1}{\alpha }}.$$

Then the disease-free equilibrium point $\overline{E_0}$ of system (2.32) is global asymptotically stable.

Proof

To prove the global stability of the disease free-equilibrium point, we choose a suitable Lyapunov function. Let us consider a Lyapunov function $L\left(n\right)$ defined by

$$L\left(n\right)={\left(X\left(n\right)-E_0\right)}^2,n=0,1,2,\dots$$ (2.33)

where $X\left(n\right)=\left(S\left(n\right),V\left(n\right),I\left(n\right),I_v\left(n\right),R\left(n\right)\right)$ and $E_0=\left(\overline{S_0},\overline{V_0},0,0,0\right)$. The change along the solutions of the system is

$$\begin{array}{cc}\hfill \Delta L\left(n\right)\hfill & =L(n+1)-L\left(n\right)\hfill \\ \hfill \hfill & ={\left(X\left(n+1\right)-E_0\right)}^2-{\left(X\left(n\right)-E_0\right)}^2\hfill \\ \hfill \hfill & =\left(X\left(n+1\right)-X\left(n\right)\right)\left(X\left(n+1\right)+X\left(n\right)-2E_0\right)\hfill \end{array}$$ (2.34)

From the first equation of system (2.32), we have

$$\Delta L_1\left(n\right)=\left(S\left(n+1\right)-S\left(n\right)\right)\left(S\left(n+1\right)+S\left(n\right)-2\overline{S_0}\right).$$ (2.35)

For a monotonic decrease of the compartment $S$, we have $S(n+1)<S\left(n\right)$, such that

$$bN-{\mu }_{1}S\left(n\right)-\left(\frac{{\beta }_1}{N}I\left(n\right)+\frac{{\beta }_2}{N}{I}_v\left(n\right)\right)S\left(n\right)-\sigma S\left(n\right)+cR\left(n\right)+dV\left(n\right)<0.$$ (2.36)

Thus, we need to show only that

$$S\left(n+1\right)+S\left(n\right)-2\overline{S_0}>0,$$ (2.37)

which holds for

$$h<{\left(\frac{2\left(S\left(n\right)-\overline{S_0}\right)\Gamma \left(\alpha +1\right)}{-bN+{\mu }_{1}S\left(n\right)+\left(\frac{{\beta }_1}{N}I\left(n\right)+\frac{{\beta }_2}{N}{I}_v\left(n\right)\right)S\left(n\right)+\sigma S\left(n\right)-cR\left(n\right)-dV\left(n\right)}\right)}^{\frac{1}{\alpha }}\text{ and }S\left(n\right)>\overline{S_0}.$$ (2.38)

Thus, we obtain $\Delta L_1\left(n\right)<0$. The monotonic decrease of the compartments $V,I,I_v$ and $R$ show in similar way the following conditions to obtain $\Delta L_2\left(n\right)<0,\Delta L_3\left(n\right)<0,\Delta L_4\left(n\right)<0$ and $\Delta L_5\left(n\right)<0$. Here, we have

$$\sigma S\left(n\right)-dV\left(n\right)-\left(\frac{{\beta }_1}{N}I\left(n\right)+\frac{{\beta }_2}{N}{I}_v\left(n\right)\right)V\left(n\right)-{\mu }_{1}V\left(n\right)<0$$ (2.39)

such that

$$h<{\left(\frac{2\left(V\left(n\right)-\overline{V_0}\right)\Gamma \left(\alpha +1\right)}{-\sigma S\left(n\right)+dV\left(n\right)+\left(\frac{{\beta }_1}{N}I\left(n\right)+\frac{{\beta }_2}{N}{I}_v\left(n\right)\right)V\left(n\right)+{\mu }_{1}V\left(n\right)}\right)}^{\frac{1}{\alpha }}\text{ and }V\left(n\right)>\overline{V_0}.$$ (2.40)

Moreover, straightforward computations let us obtain

$$h<{\left(\frac{2I\left(n\right)\Gamma \left(\alpha +1\right)}{-\left(\frac{{\beta }_1}{N}I\left(n\right)+\frac{{\beta }_2}{N}{I}_v\left(n\right)\right)S\left(n\right)-m(1-p)I_v\left(n\right)+(w+{\mu }_1+{\mu }_2)I\left(n\right)}\right)}^{\frac{1}{\alpha }},$$ (2.41)

$$h<{\left(\frac{2I_v\left(n\right)\Gamma \left(\alpha +1\right)}{-\left(\frac{{\beta }_1}{N}I\left(0\right)+\frac{{\beta }_2}{N}{I}_v\left(0\right)\right)V\left(0\right)+\left(m+{\mu }_1\right)I_v\left(0\right)}\right)}^{\frac{1}{\alpha }},$$ (2.42)

$$h<{\left(\frac{2R\left(n\right)\Gamma \left(\alpha +1\right)}{-mp{I}_v\left(n\right)-wI\left(n\right)+\left(c+{\mu }_1\right)R\left(n\right)}\right)}^{\frac{1}{\alpha }}.$$ (2.43)

This completes the proof. □

Theorem 3

Let ${\left\{S\left(n\right),V\left(n\right),I\left(n\right),I_v\left(n\right),R\left(n\right)\right\}}_{n=0}^{\infty }$ be the solutions of system (2.32) that are monotonic decreasing. Moreover, let the conditions of local asymptotic stability hold. If

$$h<{\left(\frac{2\left(S\left(n\right)-\overline{S_1}\right)\Gamma \left(\alpha +1\right)}{-bN+{\mu }_{1}S\left(n\right)+\left(\frac{{\beta }_1}{N}I\left(n\right)+\frac{{\beta }_2}{N}{I}_v\left(n\right)\right)S\left(n\right)+\sigma S\left(n\right)-cR\left(n\right)-dV\left(n\right)}\right)}^{\frac{1}{\alpha }}\text{ for }S\left(n\right)>\overline{S_1}$$

$$h<{\left(\frac{2\left(V\left(n\right)-\overline{V_1}\right)\Gamma \left(\alpha +1\right)}{-\sigma S\left(n\right)+dV\left(n\right)+\left(\frac{{\beta }_1}{N}I\left(n\right)+\frac{{\beta }_2}{N}{I}_v\left(n\right)\right)V\left(n\right)+{\mu }_{1}V\left(n\right)}\right)}^{\frac{1}{\alpha }}\text{ for }V\left(n\right)>\overline{V_1},$$

$$h<{\left(\frac{2\left(I\left(n\right)-\overline{I_1}\right)\Gamma \left(\alpha +1\right)}{-\left(\frac{{\beta }_1}{N}I\left(n\right)+\frac{{\beta }_2}{N}{I}_v\left(n\right)\right)S\left(n\right)-m(1-p)I_v\left(n\right)+(w+{\mu }_1+{\mu }_2)I\left(n\right)}\right)}^{\frac{1}{\alpha }}\text{ for }I\left(n\right)>\overline{I_1},$$

$$h<{\left(\frac{2\left(I_v\left(n\right)-\overline{I_{v1}}\right)\Gamma \left(\alpha +1\right)}{-\left(\frac{{\beta }_1}{N}I\left(n\right)+\frac{{\beta }_2}{N}{I}_v\left(n\right)\right)V\left(n\right)+\left(m+{\mu }_1\right)I_v\left(n\right)}\right)}^{\frac{1}{\alpha }}\text{ for }{I}_v\left(n\right)>\overline{I_{v1}},$$

and

$$h<{\left(\frac{2\left(R\left(n\right)-\overline{R_1}\right)\Gamma \left(\alpha +1\right)}{-mp{I}_v\left(n\right)-wI\left(n\right)+\left(c+{\mu }_1\right)R\left(n\right)}\right)}^{\frac{1}{\alpha }}\text{ for }R\left(n\right)>\overline{R_1}.$$

Then the co-existing positive equilibrium point $\overline{E_1}$ of system (2.32) is global asymptotically stable.

Proof

The proof is similar to Theorem 2 and is omitted. □

2.4. Non-negative solutions

This section studied the existence and uniqueness of non-negative solutions of the fractional $SVI{I}_{v}R$ model. For biological reasons, the compartments forming model (2.3) are functions with non-negative values. Firstly, let us show that all system solutions (2.3) are positive.

Theorem 4

All of the solutions of the system (2.3) belong to ${\mathbb{R}}_{+}^5$ . Where ${\mathbb{R}}_{+}^5$ is defined as ${\mathbb{R}}_{+}^5=x=(x_1,x_2,x_3,x_4,x_5):x_k\ge 0$ for each $k=1,2,\dots ,5$ .

Proof

$$\begin{array}{ccccc}\hfill & D_t^{\alpha }S{\left(t\right)}_{{\mid }_{S\left(t\right)=0}}\hfill & =\hfill & bN+cR\left(t\right)+dV\left(t\right)\ge 0,\hfill & \text{ since }R\left(t\right)\ge 0,V\left(t\right)\ge 0\text{ and }N>0,b>0,c>0,d>0.\hfill \\ \hfill & D_t^{\alpha }V{\left(t\right)}_{{\mid }_{V\left(t\right)=0}}\hfill & =\hfill & \sigma S\left(t\right)\ge 0,\hfill & \text{ since }S\left(t\right)\ge 0\text{ and }\sigma >0.\hfill \\ \hfill & D_t^{\alpha }I{\left(t\right)}_{{\mid }_{I\left(t\right)=0}}\hfill & =\hfill & m(1-p)I_v\left(t\right)\ge 0,\hfill & \text{ since }{I}_v\left(t\right)\ge 0,0<p\le 1\text{ and }m>0.\hfill \\ \hfill & D_t^{\alpha }{I}_v{\left(t\right)}_{{\mid }_{I_v\left(t\right)=0}}\hfill & =\hfill & {\beta }_1\frac{I\left(t\right)V\left(t\right)}{N}\ge 0,\hfill & \text{ since }I\left(t\right)\ge 0,V\left(t\right)\ge 0\text{ and }N>0,{\beta }_1>0.\hfill \\ \hfill & D_t^{\alpha }R{\left(t\right)}_{{\mid }_{R\left(t\right)=0}}\hfill & =\hfill & mp{I}_v\left(t\right)+wI\left(t\right)\ge 0,\hfill & \text{ since }I\left(t\right)\ge 0,I_v\left(t\right)\ge 0,0<p\le 1\text{ and }m>0,w>0.\square \hfill \end{array}$$

One of the critical steps in the fractional model is the concept of the existence of solutions in a dynamic system. In this part, we prove the existence and uniqueness of the solution for the proposed nonlinear model (2.3). Here, we write the above fractional model in a short form by following the generality. The compact form of the model (2.3) is given as follows:

$$\begin{array}{ccc}{D}_t^{\alpha }S\left(t\right)\hfill & =\hfill & H_1(t,S\left(t\right)),\hfill \\ D_t^{\alpha }V\left(t\right)\hfill & =\hfill & H_2(t,V\left(t\right)),\hfill \\ D_t^{\alpha }I\left(t\right)\hfill & =\hfill & H_3(t,I\left(t\right)),\hfill \\ D_t^{\alpha }{I}_v\left(t\right)\hfill & =\hfill & H_4(t,I_v\left(t\right)),\hfill \\ D_t^{\alpha }R\left(t\right)\hfill & =\hfill & H_5(t,R\left(t\right)).\hfill \end{array}$$ (2.44)

where

$$\begin{array}{ccc}{H}_1(t,S\left(t\right))\hfill & =\hfill & bN-({\mu }_1+\sigma )S\left(t\right)-{\beta }_1\frac{I\left(t\right)S\left(t\right)}{N}-{\beta }_2\frac{I_v\left(t\right)S\left(t\right)}{N}+cR\left(t\right)+dV\left(t\right)\hfill \\ H_2(t,V\left(t\right))\hfill & =\hfill & \sigma S\left(t\right)-(d+{\mu }_1)V\left(t\right)-{\beta }_1\frac{I\left(t\right)V\left(t\right)}{N}-{\beta }_2\frac{I_v\left(t\right)V\left(t\right)}{N}\hfill \\ H_3(t,I\left(t\right))\hfill & =\hfill & {\beta }_1\frac{I\left(t\right)S\left(t\right)}{N}+{\beta }_2\frac{I_v\left(t\right)S\left(t\right)}{N}+m(1-p)I_v\left(t\right)-(w+{\mu }_1+{\mu }_2)I\left(t\right)\hfill \\ H_4(t,I_v\left(t\right))\hfill & =\hfill & {\beta }_1\frac{I\left(t\right)V\left(t\right)}{N}+{\beta }_2\frac{I_v\left(t\right)V\left(t\right)}{N}-(m+{\mu }_1)I_v\left(t\right)\hfill \\ H_5(t,R\left(t\right))\hfill & =\hfill & mp{I}_v\left(t\right)+wI\left(t\right)-(c+{\mu }_1)R\left(t\right).\hfill \end{array}$$ (2.45)

In addition, $H_1,H_2,H_3,H_4$ and $H_5$ are the contraction for $S$, $V$, $I$, $I_v$ and $R$, respectively. To show the existence and uniqueness requirements, we use fixed point theory and Picard–Lindelof techniques. Using initial conditions and fractional integral operator (2.2), the given system in (2.3), becomes the following Volterra-type integral equations

$$\begin{array}{ccc}S\left(t\right)\hfill & =\hfill & S\left(0\right)+\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^t{\left(t-\xi \right)}^{\alpha -1}{H}_1(\xi ,S\left(\xi \right))d\xi \hfill \\ V\left(t\right)\hfill & =\hfill & V\left(0\right)+\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^t{\left(t-\xi \right)}^{\alpha -1}{H}_2(\xi ,V\left(\xi \right))d\xi \hfill \\ I\left(t\right)\hfill & =\hfill & I\left(0\right)+\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^t{\left(t-\xi \right)}^{\alpha -1}{H}_3(\xi ,I\left(\xi \right))d\xi \hfill \\ I_v\left(t\right)\hfill & =\hfill & I_v\left(0\right)+\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^t{\left(t-\xi \right)}^{\alpha -1}{H}_4(\xi ,I_v\left(\xi \right))d\xi \hfill \\ R\left(t\right)\hfill & =\hfill & R\left(0\right)+\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^t{\left(t-\xi \right)}^{\alpha -1}{H}_5(\xi ,R\left(\xi \right))d\xi .\hfill \end{array}$$ (2.46)

Now, we get the subsequent Picard iterative algorithm

$$\begin{array}{ccc}{S}^{n+1}\left(t\right)\hfill & =\hfill & \frac{1}{\Gamma \left(\alpha \right)}{\int }_0^t{\left(t-\xi \right)}^{\alpha -1}{H}_1(\xi ,S^n\left(\xi \right))d\xi \hfill \\ V^{n+1}\left(t\right)\hfill & =\hfill & \frac{1}{\Gamma \left(\alpha \right)}{\int }_0^t{\left(t-\xi \right)}^{\alpha -1}{H}_2(\xi ,V^n\left(\xi \right))d\xi \hfill \\ I^{n+1}\left(t\right)\hfill & =\hfill & \frac{1}{\Gamma \left(\alpha \right)}{\int }_0^t{\left(t-\xi \right)}^{\alpha -1}{H}_3(\xi ,I^n\left(\xi \right))d\xi \hfill \\ I_v^{n+1}\left(t\right)\hfill & =\hfill & \frac{1}{\Gamma \left(\alpha \right)}{\int }_0^t{\left(t-\xi \right)}^{\alpha -1}{H}_4(\xi ,I_v^n\left(\xi \right))d\xi \hfill \\ R^{n+1}\left(t\right)\hfill & =\hfill & \frac{1}{\Gamma \left(\alpha \right)}{\int }_0^t{\left(t-\xi \right)}^{\alpha -1}{H}_5(\xi ,R^n\left(\xi \right))d\xi \hfill \end{array}$$ (2.47)

It is clear that, Eq. (2.46) can be rewritten as follows,

$$X\left(t\right)=X\left(0\right)+\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^t{\left(t-\xi \right)}^{\alpha -1}H(\xi ,X\left(\xi \right))d\xi$$ (2.48)

where

$$X\left(t\right)={\left(S\left(t\right),V\left(t\right),I\left(t\right),I_v\left(t\right),R\left(t\right)\right)}^T,$$ (2.49)

$$H(\xi ,X\left(\xi \right))=\left(\begin{array}{c}\hfill H_1(\xi ,S\left(\xi \right))\hfill \\ \hfill H_2(\xi ,V\left(\xi \right))\hfill \\ \hfill H_3(\xi ,I\left(\xi \right))\hfill \\ \hfill H_4(\xi ,I_v\left(\xi \right))\hfill \\ \hfill H_5(\xi ,R\left(\xi \right))\hfill \end{array}\right),$$ (2.50)

and

$$X\left(0\right)={\left(S\left(0\right),V\left(0\right),I\left(0\right),I_v\left(0\right),R\left(0\right)\right)}^T.$$ (2.51)

Lemma 5

The function$H(t,X\left(t\right))$defined in Eq. (2.48) satisfies the Lipschitz condition given by

$$\Vert H(t,X_1\left(t\right))-H(t,X_2\left(t\right))\Vert \le \Omega \Vert X_1\left(t\right)-X_2\left(t\right)\Vert ,$$ (2.52)

where

$$\Omega =max\left({\mu }_1+{\beta }_1+{\beta }_2+\sigma ;d+{\mu }_1+{\beta }_1+{\beta }_2;w+{\mu }_1+{\mu }_2+{\beta }_1;m+{\mu }_1+{\beta }_2;c+{\mu }_1\right)$$

and the norm $∥.∥$ corresponds to the space $C\left(\left[0,T\right],{\mathbb{R}}^5\right)$ .

Proof

From the first component of $H_1(t,X\left(t\right))$, we may write the following inequality,

$$\begin{array}{ccc}\hfill \Vert H_1(t,S_1\left(t\right))-H_1(t,S_2\left(t\right))\Vert \hfill & \hfill =\hfill & \Vert \left({\mu }_1+{\beta }_1\frac{I}{N}+{\beta }_2\frac{I_v}{N}+\sigma \right)\left(S_2-S_1\right)\Vert \hfill \\ \hfill \hfill & \hfill \le \hfill & \left({\mu }_1+{\beta }_1+{\beta }_2+\sigma \right)\Vert S_2-S_1\Vert .\hfill \\ \hfill \hfill & \hfill \le \hfill & \Omega \Vert S_2-S_1\Vert .\hfill \end{array}$$

For the remaining components of $H(t,X\left(t\right))$, it holds

$$\begin{array}{ccc}\Vert H_2(t,V_1\left(t\right))-H_2(t,V_2\left(t\right))\Vert \hfill & \le \hfill & \left(m+{\mu }_1+{\beta }_2\right)\Vert V_2-V_1\Vert \le \Omega \Vert V_2-V_1\Vert \hfill \\ \Vert H_3(t,I_1\left(t\right))-H_3(t,I_2\left(t\right))\Vert \hfill & \le \hfill & \left(d+{\mu }_1+{\beta }_1+{\beta }_2\right)\Vert I_2-I_1\Vert \le \Omega \Vert I_2-I_1\Vert \hfill \\ \Vert H_4(t,I_{V1}\left(t\right))-H_4(t,I_{V2}\left(t\right))\Vert \hfill & \le \hfill & \left(w+{\mu }_1+{\mu }_2+{\beta }_1\right)\Vert I_{V2}-I_{V1}\Vert \le \Omega \Vert I_{V2}-I_{V1}\Vert \hfill \\ \Vert H_5(t,R_1\left(t\right))-H_5(t,R_2\left(t\right))\Vert \hfill & \le \hfill & \left(c+{\mu }_1\right)\Vert R_2-R_1\Vert \le \Omega \Vert R_2-R_1\Vert .\square \hfill \end{array}$$

Theorem 6

Let the result of Lemma 5 holds and $\Lambda =\frac{T^{\alpha }}{\alpha \Gamma \left(\alpha \right)}$ . If $\Omega \Lambda <1$ then there exists a unique solution of model (2.3) on $t\in [0,T]$ .

Proof

We consider the Picard operator, $P:C\left(\left[0,T\right],{\mathbb{R}}^5\right)\to C\left(\left[0,T\right],{\mathbb{R}}^5\right)$ defined as follows:

$$P\left(X\left(t\right)\right)=X\left(0\right)+\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^t{\left(t-\xi \right)}^{\alpha -1}H(\xi ,X\left(\xi \right))d\xi$$ (2.53)

where $X\left(t\right)$, $X\left(0\right)$ and $H(\xi ,X\left(\xi \right))$ are given in Eqs. (2.48), (2.51), (2.50), respectively. In addition

Using the result of Lemma 5 we have,

$$\begin{array}{ccc}\Vert P\left(X_1\left(t\right)\right)-P\left(X_2\left(t\right)\right)\Vert \hfill & =\hfill & \Vert \frac{1}{\Gamma \left(\alpha \right)}{\int }_0^t{\left(t-\xi \right)}^{\alpha -1}\left(H(\xi ,X_1\left(\xi \right))-H(\xi ,X_2\left(\xi \right))\right)d\xi \Vert \hfill \\ \hfill & \le \hfill & \frac{1}{\Gamma \left(\alpha \right)}{\int }_0^t{\left(t-\xi \right)}^{\alpha -1}\Vert H(\xi ,X_1\left(\xi \right))-H(\xi ,X_2\left(\xi \right))\Vert d\xi \hfill \\ \hfill & \le \hfill & \frac{\Omega }{\Gamma \left(\alpha \right)}{\int }_0^t{\left(t-\xi \right)}^{\alpha -1}\Vert X_1\left(t\right)-X_2\left(t\right)\Vert d\xi \hfill \\ \hfill & \le \hfill & \frac{\Omega T^{\alpha }}{\alpha \Gamma \left(\alpha \right)}\Vert X_1\left(t\right)-X_2\left(t\right)\Vert .\hfill \end{array}$$ (2.54)

From Eqs. (2.48), (2.53), it can be seen that $P\left(X\left(t\right)\right)=X\left(t\right)$ and so $\Vert P\left(X_1\left(t\right)\right)-P\left(X_2\left(t\right)\right)\Vert =\Vert X_1\left(t\right)-X_2\left(t\right)\Vert$. Therefore, from Eq. (2.54) we have,

$$\Vert X_1\left(t\right)-X_2\left(t\right)\Vert \le \frac{\Omega T^{\alpha }}{\alpha \Gamma \left(\alpha \right)}\Vert X_1\left(t\right)-X_2\left(t\right)\Vert .$$ (2.55)

Then

$$\Vert X_1\left(t\right)-X_2\left(t\right)\Vert \left(1-\Omega \Lambda \right)\le 0$$ (2.56)

where $\Lambda =\frac{T^{\alpha }}{\alpha \Gamma \left(\alpha \right)}$.

Thus, if $\Omega \Lambda <1$ then we conclude that $\Vert X_1\left(t\right)-X_2\left(t\right)\Vert =0$, so we obtain $X_1\left(t\right)=X_2\left(t\right)$. Therefore, $P$ is a contraction mapping, and consequently by the Banach contraction mapping principle, $P$ has a unique fixed point on $[0,T]$, which is solution of the given fractional model (2.3). □

3. Numerical solutions of the model

Obtaining exact solutions to a system of fractional differential equations with initial conditions is one of the problems of computational and applied mathematics, which, as far as we know, has not yet been completely overcome. The difficulty here is that such systems of equations that usually govern actual events are nonlinear. Thus, popular numerical calculation methods such as Euler, Runge–Kutta, Adam–Bashford, and predictor–corrector are frequently used to obtain approximate solutions to systems of fractional differential equations.

In this section, approximate solutions of the system (2.3) were obtained using a discretization method based on Euler’s method developed by Agarwal et al. [3]. When $\alpha \to 1$, this discretization method turns into the Euler discretization method. Thus, the fractional Euler method is a generalization of the classical Euler method. Here, the definition range of a variable consisting of a range is converted into a discrete set of nodes [40]. Firstly, let us summarize the formulation of this discretization.

Consider the initial value problem,

$$D_t^{\alpha }g\left(t\right)=h(t,g\left(t\right)),g\left(t_0\right)=g_0,0<\alpha \le 1,c\le t\le d,$$ (3.1)

where $c=t_0<t_1<\cdots <t_n=d$ such that $t_k=c+k\Delta$, $k=0,1,\dots ,n$ and $\Delta =\frac{d-c}{n}$. Here, it is assumed that $D_t^{\alpha }g\left(t\right)$ and the other derivatives are continuous on interval $[c,d]$. By using Taylor’s expansion for Eq. (3.1) and making the necessary operations (see the Refs. [3], [41] for details), the numerical solution formulation can be written as,

$$g\left(t_{k+1}\right)=g\left(t_k\right)+\frac{{\Delta }^{\alpha }}{\Gamma (\alpha +1)}h(t_k,g\left(t_k\right)).$$ (3.2)

For the fractional differential equations of the model (2.3) it can be written that

$$\begin{array}{c}\hfill D_t^{\alpha }S\left(t_k\right)=h_1(t_k,S\left(t_k\right)),\hfill \\ \hfill D_t^{\alpha }V\left(t_k\right)=h_2(t_k,V\left(t_k\right)),\hfill \\ \hfill D_t^{\alpha }I\left(t_k\right)=h_3(t_k,I\left(t_k\right)),\hfill \\ \hfill D_t^{\alpha }{I}_v\left(t_k\right)=h_4(t_k,I_v\left(t_k\right)),\hfill \\ \hfill D_t^{\alpha }R\left(t_k\right)=h_5(t_k,R\left(t_k\right)),\hfill \end{array}$$ (3.3)

for $0<\alpha \le 1,t>0$. Where

$$\begin{array}{cc}{h}_1(t_k,S\left(t_k\right))=\hfill & bN-{\mu }_{1}S\left(t_k\right)-{\beta }_1\frac{I\left(t_k\right)S\left(t_k\right)}{N}-{\beta }_2\frac{I_v\left(t_k\right)S\left(t_k\right)}{N}-\sigma S\left(t_k\right)+cR\left(t_k\right)+dV\left(t_k\right)\hfill \\ h_2(t_k,V\left(t_k\right))=\hfill & \sigma S\left(t_k\right)-dV\left(t_k\right)-{\beta }_1\frac{I\left(t_k\right)V\left(t_k\right)}{N}-{\mu }_{1}V\left(t_k\right)-{\beta }_2\frac{I_v\left(t_k\right)V\left(t_k\right)}{N}\hfill \\ h_3(t_k,I\left(t_k\right))=\hfill & {\beta }_1\frac{I\left(t_k\right)S\left(t_k\right)}{N}+{\beta }_2\frac{I_v\left(t_k\right)S\left(t_k\right)}{N}+m(1-p)I_v\left(t_k\right)-(w+{\mu }_1+{\mu }_2)I\left(t_k\right)\hfill \\ h_4(t_k,I_v\left(t_k\right))=\hfill & {\beta }_1\frac{I\left(t_k\right)V\left(t_k\right)}{N}+{\beta }_2\frac{I_v\left(t_k\right)V\left(t_k\right)}{N}-m{I}_v\left(t_k\right)-{\mu }_1{I}_v\left(t_k\right)\hfill \\ h_5(t_k,R\left(t_k\right))=\hfill & mp{I}_v\left(t_k\right)+wI\left(t_k\right)-cR\left(t_k\right)-{\mu }_{1}R\left(t_k\right).\hfill \end{array}$$ (3.4)

Now, applying the numerical solution procedure described at Eq. (3.2) for the system equations in (3.3) we have

$$\begin{array}{cc}\hfill S\left(t_{k+1}\right)=\hfill & \hfill S\left(t_k\right)+\frac{{\Delta }^{\alpha }}{\Gamma (\alpha +1)}{h}_1(t_k,S\left(t_k\right))\hfill \\ \hfill V\left(t_{k+1}\right)=\hfill & \hfill V\left(t_k\right)+\frac{{\Delta }^{\alpha }}{\Gamma (\alpha +1)}{h}_2(t_k,V\left(t_k\right))\hfill \\ \hfill I\left(t_{k+1}\right)=\hfill & \hfill I\left(t_k\right)+\frac{{\Delta }^{\alpha }}{\Gamma (\alpha +1)}{h}_3(t_k,I\left(t_k\right))\hfill \\ \hfill I_v\left(t_{k+1}\right)=\hfill & \hfill I_v\left(t_k\right)+\frac{{\Delta }^{\alpha }}{\Gamma (\alpha +1)}{h}_4(t_k,I_v\left(t_k\right))\hfill \\ \hfill R\left(t_{k+1}\right)=\hfill & \hfill R\left(t_k\right)+\frac{{\Delta }^{\alpha }}{\Gamma (\alpha +1)}{h}_5(t_k,R\left(t_k\right))\hfill \end{array}$$ (3.5)

for $k=0,1,\dots ,n-1$. In the next section, an actual application of the proposed model will be given using sample case studies in Türkiye. Undoubtedly, the proposed method can be utilized for other applications as well.

4. An application of the model using real case studies

In this section, the model and all the steps described above will be applied to the example of Türkiye. Thus, in the absence of extraordinary changes, the course of COVID-19 in Türkiye will be illustrated. In this application, all parameters and data were calculated with the help of Eqs. (2.4)–(2.11) based on the official information received from the World Health Organization (WHO) and the Ministry of Health of the Republic of Türkiye. Apart from the current situation in Türkiye, good and bad scenarios have been put forward and interpreted. We want to point out that the mathematical model established in this study is not for a particular country or region but can be applied to any part of the world.

4.1. Model parameters

According to the data derived from the sources of WHO, Turkish Statistical Institute (TUIK), and the Ministry of Health of the Republic of Türkiye, we consider specifically the date 29th of July 2022 in Türkiye (see Table 3).

Table 3.

Physical parameter values used in the model.

Parameters	Values	Source
$S\left(0\right)$	21999069	[42], [43]
$V\left(0\right)$	56820928	[42], [43]
$I\left(0\right)$	279750	[42], [43]
$I_v\left(0\right)$	593268	Calculated with Eq. (2.4)
$R\left(0\right)$	3921347	[42], [43]
$b$	0,0000364	[44]
$d$	$1/180$	From Section 2.1
${\mu }_1$	0,0000299	[44]
${\mu }_2$	0,004	Calculated with Eq. (2.11)
${\beta }_1$	0,27011	Calculated with Eq. (2.8)
${\beta }_2$	0,06752	Calculated with Eq. (2.8)
$\sigma$	0,00929	Calculated with Eq. (2.10)
$c$	$1/180$	From Section 2.1
$p$	0.88	[43]
$w$	0,0899	Calculated with Eq. (2.9)
$m$	1/5	[43]

According to the official data given in Table 3, a large proportion of Türkiye’s population has been vaccinated. However, any individual who do not continue with periodic vaccinations returns back to the susceptible compartment and can get infected or can also transmit the disease. On the other side, vaccinated individuals who are within the vaccination period or repeat the vaccination in proper time have residence against the virus.

This study analyzed the last stages of the epidemiological spread, where the majority of the individuals in Türkiye took the vaccine. However, many of them avoid later on to continue to be vaccinated again. Therefore, $I_v$ shows a greater value than $I$, since those are the individuals who were vaccinated but exceeded the vaccination period. It is a fact that even if the entire population is vaccinated, the virus will continue to transmit the disease in a form of influenza, which satisfies the simulation result that Iv has to be greater than the compartment $I$. This information is included to the manuscript to clarify the biological interpretation.

The number $a$ in Eq. (2.7) shows an average number of people per day with whom infected individuals have had close contact during their illness. Considering that public places such as schools, cinemas, restaurants, and public transportation are also risk areas, the number can be estimated as $a=32$. The most important reason for this high number is that individuals show symptoms on an average of $5$ days after infection and usually have PCR tests after the symptoms appear. Applying to Eq. (2.20) a specific determined day (29th of July 2022), the basic reproduction number for Türkiye is obtained as,

$$R_0=2.3245$$ (4.1)

$R_0>1$ is a sign that the epidemiological level in Türkiye might continue to exist with periodic waves. We will show and discuss this scenario in the next section.

According to Eq. (2.17), the disease-free equilibrium point is determined as

$${\stackrel{\text{\_}}{E}}_0=\left({\stackrel{\text{\_}}{S}}_0,{\stackrel{\text{\_}}{V}}_0,{\stackrel{\text{\_}}{I}}_0,{\stackrel{\text{\_}}{I_v}}_0,{\stackrel{\text{\_}}{R}}_0\right)=\left(38202723,63588674,0,0,0\right).$$ (4.2)

This shows the total population of Türkiye with based on susceptible and vaccinated compartments. In this scenario, the infection approaches extinction.

The endemic equilibrium points exist in the environment if and only if the basic reproduction number exceeds 1, where it represents asymptotically stable behavior [45].

From the Eq. (2.26),

$$-0.4704419887\times 10^{-9}{V}^2+0.2162866394\times V-0.6155340444\times 10^7=0.$$ (4.3)

By solving Eq. (4.3), we have

$$V=\left\{30479885,429272102\right\}.$$ (4.4)

It is clear that, the second solution of $V$ is very obvious. Hence, if we take $V=30479887$ and by using Eqs. (2.22)–(2.25), the endemic equilibrium point can be written as

$$\tilde{E}=\left(\tilde{S},\tilde{V},\tilde{I},\widetilde{I_v},\tilde{R}\right)=(21843811,30479887,292498,164168,9880822).$$ (4.5)

It is clear that, $\tilde{E}=\left(\tilde{S},\tilde{V},\tilde{I},\widetilde{I_v},\tilde{R}\right)\ne (0,0,0,0,0)$ because the disease is persist in the population.

4.2. Some numerical solution

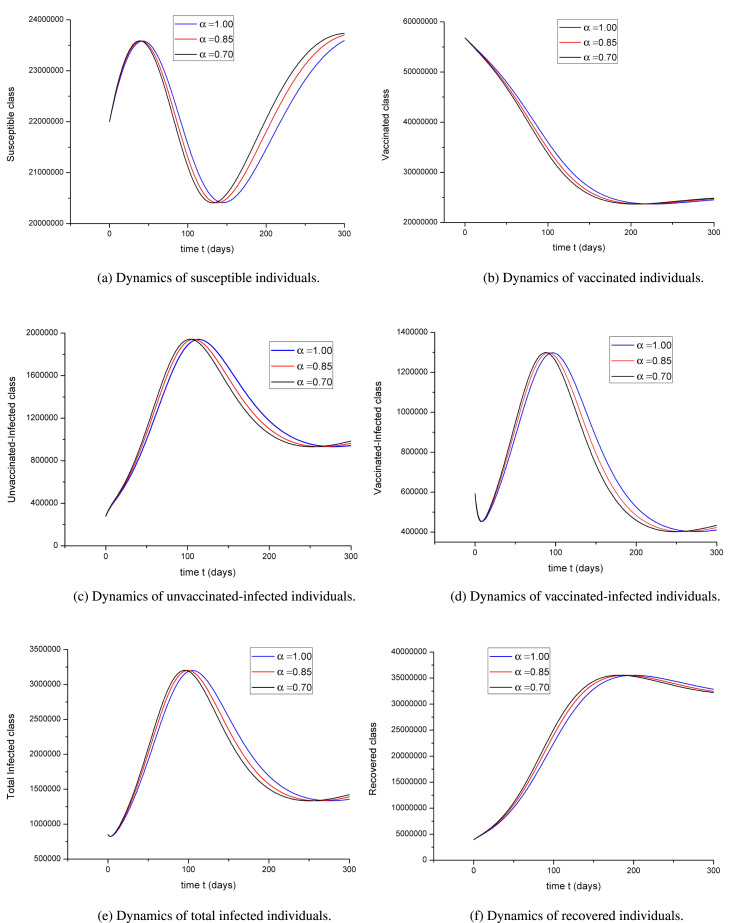
In this sub-section, we used MATLAB to illustrate the dynamic process of actual data in Türkiye. We focus on a specific date, the 29th of July 2022, to discuss the results. In Fig. 2(a), one can notice the wave of the susceptible compartment in the further months. This might be related to the change of the season from summer to autumn, letting people get infected again. However, since the re-vaccination period would start frequently, we expect an increase of the susceptible population again. Therefore, we expect that approximately after 50 days, the number of susceptible individuals will decrease and reach the minimum value after 140 days, which is almost the month from the end of November to December. However, the worry of returning to epidemiological life would push many susceptible individuals to be re-vaccinated and be isolated from the community so that beginning of Spring 2023, the number of susceptible compartments would increase. Although the amount of this increase varies for each value of $\alpha$, the dynamic structure of the relevant compartment is similar. This study aims not to estimate the number of people in the compartments depending on time but to reveal the course of the pandemic depending on time. Therefore, we were not interested in calculating the optimum value of $\alpha$.

Fig. 2.

Dynamics of the compartments for various values of $\alpha$.

It can be seen from Fig. 2(b) that according to the current vaccination policy, the total number of vaccinated individuals within the last six months will decrease over time. In the first months, when the vaccination started to become widespread worldwide, the number of daily vaccinations in Türkiye was over one hundred thousand. Although most of the population has completed all vaccinations, the rate of taking the reminder dose (i.e., the third dose) after six months, as recommended by the relevant authorities, is low. In this case, according to our model given in the system (2.3), individuals who complete their vaccinations leave compartment $V$ and move to compartment $S$ after six months. It is known that under normal conditions, the protection rate of existing vaccines decreases significantly after six months, but it is not finished. However, it is unknown precisely how long the current vaccines will keep the immunity against the mutated variants SARS-CoV-2. Therefore, even if the total number of actively vaccinated individuals decreases, it is seen that this number will not be zeroized in the long term. There are still reminder doses, and the vaccination of people in compartment $S$ who have not yet been vaccinated (see figure Fig. 2(b)).

The overtime alteration of the most crucial compartment of the mathematical model and the pandemics, $I$, according to the usual course of the pandemic in Türkiye, will be as shown in Fig. 2(c). Compartment $I$, unlike many other models in the literature, shows only the number of infected individuals within the last 14 days, not the total number of infected individuals since the beginning of the pandemic in our model. This represents actively infected, i.e., unvaccinated individuals who can transmit the virus, recover or die. In Fig. 2(c), it is seen that there has been an increase in the number of unvaccinated–infected individuals for about 120 days from today (29 July 2022. This number is expected to increase within 4 months. The most important reason for this is the decrease in immunity of currently vaccinated individuals and the decrease in the rate of new vaccinations. Thus, there is a possibility of a new big wave. On the other hand, if the daily vaccination rate is increased, rules such as social distancing are followed, and people who are against the vaccine are persuaded, an upsurge in the number of individuals in the compartment $I$ can be prevented.

Completing vaccinations does not mean an individual will not contract the disease. However, even if these people are infected, depending on the protection rate of their vaccine, their immune systems have gained resistance to the virus, so they will recover to a great extent or survive the disease with mild symptoms. As can be seen from Fig. 2(d), it is expected that the total number of individuals in the compartment $I_v$ will increase for a long time. However, an increase in the population of this compartment is expected with the increase in the previous compartment $I$. When figures Fig. 2, Fig. 2 are examined together, in case of a peak that can be seen in the future, the compartment $I_v$ will be less affected than $I$. In addition, the total number of actively infected individuals, $I+I_v$, can be seen in Fig. 2(e).

It is clear that as the number of infected individuals increases, the number of recovered individuals will also increase. Because the more sick individuals there are, the more people recover. It can be seen from Fig. 2(f) that with the increase in the number of infected individuals, there will be an increase in the number of those who recovered in parallel.

According to the results, the number of infected individuals seems relatively high. However, official statements regarding the daily number of infected individuals will remain below these numbers despite this. This situation depends on two main reasons: some infected individuals do not show symptoms, and some infected individuals do not have a PCR test even though they show symptoms.

4.3. Some predictions of SARS-CoV-2 infections and beyond

In this part, it is aimed to show the effects of the parameters on the model and to reveal possible good and bad scenarios for Türkiye.

4.3.1. An optimistic scenario

Considering the same case study of Türkiye, we assumed some parametric changes in the system to show up an optimistic scenario to manage the spread Therefore,if we reduce the values of ${\beta }_1$ and ${\beta }_2$, such that ${\beta }_1=0.05541$ and ${\beta }_2=0.0139$, and the daily vaccination rate increases to $\sigma =0.00345$, then the expected situations in the compartments in the last six months can be seen in the Figs. 3(a)–3(e).

Fig. 3.

Dynamics of the compartments for various values of $\alpha$ according to the good scenario.

According to Eq. (2.20), the number of basic reproductions for Türkiye would be

$$R_0=0.718.$$ (4.6)

Some suggestions can be given to reduce the ${\beta }_1$ and ${\beta }_2$ to reach the desired levels. One of these suggestions is to reduce the number $a$ in Eq. (2.7). In order to reach the new values of ${\beta }_1$ and ${\beta }_2$, a must decrease to $a=20$. For this, all infected or uninfected individuals need to be aware of health protection rules such as keeping social distancing and being isolated during the infection period. Another suggestion is to reduce the $P$ value in Eq. (2.6), which is the transmission probability of the disease. This is also related to properly implementing measures such as social distance and masks. Thus, it is expected to follow permanent protection rules during the seasonal changes when the temperature moves to cold to avoid the increase of SARS-CoV-2.

4.3.2. A pessimistic scenario

In this part, a pessimistic scenario was created regarding the course of the SARS-CoV-2 in Türkiye. This scenario can be encountered if the parameters change slightly from the current state. This means that unfavorable developments in the fight against the pandemic will cause new negativities, and thus, the pandemic may grow out of control.

According to the model, if parameters ${\beta }_1$ and ${\beta }_2$ increase to ${\beta }_1=0.304$ and ${\beta }_2=0.0760$, and the vaccination rate drops to $\sigma =0.0011$, the expected situations in the compartments formed by susceptible individuals, active vaccinated individuals, active unvaccinated infected individuals and total recoveries in the last six months are shown in Figs. 4(a)–4(e).

Fig. 4.

Dynamics of the compartments for various values of $\alpha$ according to the bad scenario.

According to Eq. (2.20), the number of basic reproductions in this scenario for Türkiye was calculated as

$$R_0=14.11.$$ (4.7)

The increase of ${\beta }_1$ and ${\beta }_2$ parameters to the levels in the scenario can occur when the number $a$ in Eq. (2.7) increases from $32$ to $36$. This is possible even with a slight decrease in respecting the social distance rule. Another reason for the increase in ${\beta }_1$ and ${\beta }_2$ parameters is the increase in the $P$ value in Eq. (2.6), which is the probability of disease transmission. This will only happen if measures such as social distancing, masks, and cleaning are not followed correctly. If these two situations occur together, the pandemic may grow out of control in a short time.

5. Conclusions

One of the primary purposes of this study was to show the effect of vaccination in the SARS-CoV-2 pandemic. Contrary to popular opinion, it was reflected in the model that the virus can also be transmitted to vaccinated individuals. However, depending on the vaccine’s protection rate, these individuals can easily overcome the disease. Furthermore, based on the current information that vaccinated and infected individuals can also transmit the virus, but their rate of infectivity is different from unvaccinated–infected individuals, $I_v$ the compartment was added to the model marking the first in the literature. Unlike other models, the necessary parameters were defined in the model in which vaccinated or recovered individuals were considered susceptible after six months. Formulas were developed for each parameter, and the obtainment method was shown. Stability analyses showed the attainment of endemic and disease-free equilibrium points. The importance and formulation of the number of reproductions were given.

The mathematical model was established as a fractional derivative in the Caputo sense. The aim was to take advantage of the precision and memory effect of fractional modeling. Obtaining numerical solutions using the generalized Euler method is given.

We used Türkiye’s case study data to analyze the spread and illustrate optimistic and pessimistic scenarios. Both scenarios depended on the health rules determined by health institutions and the re-vaccination period. We want to point out that the model we have created, in line with the latest information about SARS-CoV-2, can be used for Türkiye and any region worldwide. Numerical solutions were performed for different values of the derivative order of $\alpha$, and how the population in each compartment would change over time was analyzed. It was seen that the course of the pandemic is parallel to each other for different values of $\alpha$. However, in this parallelism seen in the graphs, although the curves are thought to be very close to each other, considering that the vertical axis illustrates vast numbers (millions), it can be said that the numerical results are very different at different derivative orders. We pointed out that in this study, we did not aim to estimate the number of individuals in the compartments over time but to examine the variation in compartments during the dynamic process. Since these changes are similar for different values of $\alpha$, we were not interested in determining the optimum value of $\alpha$. Finally, we obtained the good and bad scenarios results to show the effects of essential parameters in the model, such as the vaccination rate and the infectivity coefficient. These results were presented as a recommendation that can be targeted for Türkiye (good scenario) and the contrary (pessimistic scenario) by revealing the importance of vaccination and the factors affecting the infectivity coefficient.

A mathematical model can be developed as a follow-up study by adding different compartments, such as quarantine, to this model and defining new parameters based on more up-to-date information. Furthermore, appropriate optimization studies can obtain the optimum $\alpha$ value.

Data availability

No data was used for the research described in the article.