Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2022 Dec 8;7(50):47156–47164. doi: 10.1021/acsomega.2c06302

Comparison of the Silhouette of Virtual Clothes by Fabric Characteristics of Nylon Fabric for the Utilization of Virtual Clothes

Euijin Shim 1, Da Som Koo 1, Jae Sang An 1, Hye Jun Yoon 1,*
PMCID: PMC9773953  PMID: 36570184

Abstract

graphic file with name ao2c06302_0008.jpg

In this study, various nylon fabrics were investigated to measure the physical properties of the actual fabric using Kawabata systems and CLO fabric kits, and the correlation between the physical and drape properties of the fabric was statistically analyzed. Subsequently, the CLO fabric kit results were used as basic data for the CLO three-dimensional (3D) virtual clothing program, and the drapeability of the virtual fabrics was measured. The factors with the most significant effect on the drape properties were analyzed by comparing the drape measurement of the real fabrics through the variable measurement of various fabrics and correlation analysis with the drape properties, and attempts were made to reduce the difference between real fabrics and their virtual implementations. The correlation analysis results revealed that both the Kawabata system and CLO fabric kit results indicated that the bending and shear properties exhibited the highest correlation with the drape ratio. In addition, the comparison of the real and virtual fabric images revealed that they exhibited a similar morphology. Furthermore, the results confirmed that the difference between the real and virtual fabrics could be reduced as much as possible when the values measured using the Kawabata system and CLO fabric kit were converted into a database. Subsequently, the differences between virtual fabrics with various thicknesses were confirmed through CLO 3D simulation. The findings of this study are expected to be used as basic data for building fabric database.

1. Introduction

Recently, the widespread use of IT has expanded the fashion industry via the construction of design libraries, expansion of online platforms, improvement of consumer convenience, and provision of shopping information using AI through the convergence of three-dimensional (3D) technology. In addition, the commercialization of digital technology has exerted various economic effects, such as expense reduction and simplification of the design processes owing to reduced design, manufacturing, and production processes. Accordingly, 3D virtual wear technology has emerged as one of the important factors for reducing the design process of fabrics and creating competitiveness in the fashion industry.1,2

In addition to the fashion industry, the attitude of consumers is changing. For example, consumer consumption patterns have changed from the typical offline shopping behavior to online shopping behavior owing to the activation of nonface-to-face interaction due to the COVID-19 pandemic. Metaverse has attracted attention as a 3D immersive next-generation platform that can replace e-learning, web portals, and e-commerce.3,4 Therefore, online marketing using 3D virtual clothing has emerged as an important part of metaverse, and examples include metaverse marketing of luxury brands, virtual fashion shows, and marketing using virtual influencers.5,6 Consequently, research on the virtual expression of fabrics and clothing is considered essential.

The application of virtual reality in the clothing industry began in the 1980s. For example, 3D clothing virtual display technology based on virtual reality and digital simulation technology can be used in the design and production processes of clothing samples.7−9 In addition, 3D simulation enables the implementation of various designs within a short time, as well as the evaluation of the look and fit of an apparel product without manufacturing a sample. However, the high dependence of this technology on traditional manual work and the difference in the characteristics of real fabric and its 3D implementation have limited the effective application of this technology. It is crucial to ensure that the drape and silhouette of a 3D simulation program are similar to those of a real fabric.10,11 Particularly, the virtual fabric should accurately reflect the properties of the real fabric for the realistic expression of the silhouette of virtual garments.10

Lim and Istook investigated the change in the silhouette of a virtual costume applied to a virtual avatar with a change in the virtual fabric property.12 Yang investigated and correlated the drape properties of seam fabrics using experimental and hypothetical approaches.13 Lee et al. verified the objectivity and validity of the 3D virtual fabric simulation method by comparing the similarity between a real and virtual fabric when the 3D virtual fabric parameters obtained in a previous study were applied to the 3D virtual clothing simulation.14 Numerous studies have been conducted on virtual fabrics, clothing implementations, and the drape performance of clothing, which are the largest factors affecting the silhouette of clothing. However, studies that reflect changes in material properties are few compared to studies comparing the similarities of real and virtual clothes. In addition, comparative studies on images according to the physical characteristics of various materials are insufficient.15,16

Various 3D virtual programs have been widely employed, such as “CLO 3D” by CLO, which is a representative example used in Korea. Overseas, examples of 3D virtual programs include Israel’s Opitex’s “3D Runway Designer,” Browzwear’s “V-stitcher,” France’s Lectra’s “3D-Fit,” and Japan’s Technoa’s “i-Designer”.17−21 To increase the similarity between CLO 3D-designed fabric and real clothes, the approximate physical properties of the fabric are measured using the CLO fabric kit provided by CLO, after which the properties are applied to the 3D virtual clothes to achieve a more similar appearance to the real clothes.11,22 However, there is a gap between actual fabrics and virtual fabrics created using the CLO fabric kit owing to the unnatural characteristics of virtual fabrics. Therefore, various emotional characteristics for e-commerce, such as clothing shopping in metaverse and virtual clothing fashion shows of virtual models, are insufficient. In addition, as the use of the CLO fabric kit for the measurement of the physical properties of fabrics is a simple test, accurate test results cannot be obtained.2,23

The Kawabata evaluation system (KES) is the first advanced and unique solution for the user-friendly testing of the mechanical properties of fabrics and has attracted tremendous attention in numerous countries owing to its highly precise and reproducible measurement.24−26

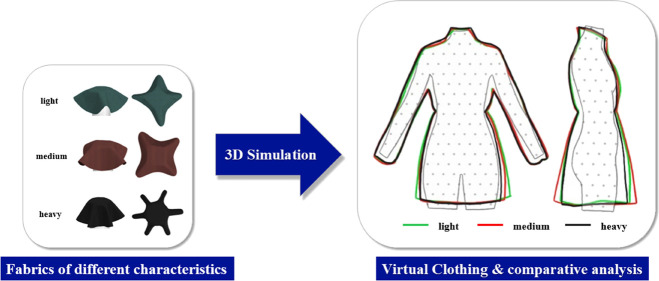
In this study, to verify the objectivity and validity of 3D virtual fabric simulations for a nylon fabric, the physical properties of the real fabric and the basic properties of the virtual fabric to be implemented were measured using KES and CLO fabric kit and the factors affecting the drape of the fabric were analyzed. Thereafter, the weight per unit area, thickness, bending stiffness, and tensile stiffness of synthetic fibers used for wind protection in real fabrics were measured, and their correlation with the drape performance of the fabric was derived from the analysis results. In addition, as drapes are visually classified,27,28 the appearances of the virtual fabrics were compared by wearing windproof jackets made of various virtual fabrics with different physical properties on virtual avatars. This increased the similarity and reliability of the virtual fabric with the real fabric, and the result was used as the basic data for a new 3D virtual clothing simulation technique.

2. Methods and Materials

2.1. Materials

To obtain information on the drape performance of fabrics after building a woven fabric property database, approximately 280 woven fabrics were collected by receiving fabric information and samples from various fabric companies in Korea. Among the collected fabrics, 57 fabrics (weight: 30–150 gsm, average weight: 82 gsm; and thickness: 0.07–0.41, average thickness: 0.21 mm) with a mixing ratio of at least 70% nylon, which are mainly used in windproof jackets, were selected and used in this study.

2.2. Objective Sensory Properties

2.2.1. KES-FB Properties

In this study, the bending properties of the real fabrics were measured using a fabric rating (FAST) system (CSIRO) based on Kawabata’s fabric rating system (KES-FB; KATO TECH). A square sample with a size of 20 × 20 cm was used as the test sample. After measuring the weight of the sample, the sample was subjected to compression, surface, bending, shear, and tensile tests, which are less damaging to the fabric.

To measure the weight of the sample, the average weight in the warp, weft, and bias directions was measured using an electronic scale, and the weight per unit area was obtained by dividing the measured weight by the fabric area. The sample thickness was determined using a thickness tester (No. 20465, Mitutoyo Co., Kawasaki, Japan) according to the ASTM D 5729-9 standard.29 The bending distance and length were measured using a bending test kit, and the bending stiffness was derived using eq 1 according to the KS K ISO 9073-7 standard.30Table 1 summarizes the KES-FB test conditions.

2.2.1. 1
Table 1. KES-FB Test Condition.
property test condition
compression sensitivity: 2 × 5
velocity: 50 s/min
stroke: 5 mm/10 V
compression area: 2 cm2
maximum load: 50 gf/cm2
surface friction sensitivity: 2 × 5
roughness sensitivity: 2 × 5
roughness static load: 10 g
friction static load: 50 g
velocity: 1.0 mm/s
initial tension: 400 g
bending sensitivity: 2 × 1
sample width: 20 cm
curvature: 2.5 cm–1 (one cycle)
shear sensitivity: 2 × 5
sample width: 20 cm
constant tension: 10 gf/cm
shear angle: ±8°
tensile sensitivity: 5 × 5
velocity: 0.2 mm/s
sample width: 20 cm
clamp interval: 5.0 cm
elongation sensitivity: 25 mm/10 V
maximum load: 500 gf/cm2
tensile-preset dial: 2
Open in a new tab

G: Bending stiffness.

M: Mass of specimen per unit area (g/m2).

C: Overall average bending length of the specimen (cm).

2.2.2. Drapeability

The drapeability was evaluated according to the KS K ISO 9073-0:2008 standard. The drape performance was evaluated using an acrylic cylinder with a diameter of 7.5 cm and a height of 30 cm, and a drape performance measuring device was designed to obtain the drooping appearance of a fabric at a certain location. For this experiment, circular-shaped samples with a diameter of 25 cm were prepared. During the experiment, after aligning the center of the cylinder with the center of the sample, images were taken using a high-resolution camera from the top and side directions to capture the sagging image of the fabric when naturally placed on the cylinder. To evaluate the drape performance, the area ratio of the top-view image was calculated using eq 2, and the drape ratio was obtained and digitized. In this case, the drape performance increased with a decrease in the drape ratio and vice versa.

2.2.2. 2

2.3. Sensory Images of 3D Virtual Fabrics

2.3.1. Physical Property Evaluation Using the CLO Fabric Kit

To evaluate the physical properties using the CLO fabric kit, the fabric was cut into a rectangular shape with a size of 22 × 3 cm. Samples were prepared in three directions: warp, weft, and bias. The experiments were conducted sequentially on the weight, thickness, bending stiffness, and tensile stiffness, which are less damaging to the fabric.31 To measure the weight, the average weight in the warp, weft, and bias directions was measured using an electronic scale, and the weight per unit area was obtained by dividing this by the fabric area. The thickness of the samples was measured using the thickness tester of the CLO kit according to the CLO fabric kit manual, and the bending distance and length were measured using a bending tester.

2.3.2. Virtual Image Implementation

The 3D virtual drape of the fabric was simulated using the CLO CAD program. 3D virtual simulation can accurately represent the shape of a drape and the physical properties of a fabric by inputting the mechanical property data values measured by the CLO fabric kit. Therefore, the 57 fabrics selected for the analysis of the windproof jackets were sorted based on their weight, and nine fabrics were used for this analysis, including three light-weight, three medium-weight, and three heavy-weight fabrics, to compare the differences in the drapes and appearance of the fabrics. Subsequently, the windbreak jacket pattern was worn on a virtual avatar, the virtual fabric was applied, and the CLO 3D virtual closing program was simulated.

2.4. Statistical Analysis

Statistical analysis was performed using SPSS Win 18.0 program, and the scores of the real and virtual fabric evaluation were compared using the t-test. The relationships between the real and virtual evaluation modes, and the difference in the image of the subjective sensation of real clothing and virtual clothing, were evaluated using Pearson correlation coefficients.32

3. Results and Discussion

3.1. KES and Drapeability Correlation Analysis Results

The correlation between the drape ratio and the weight, thickness, bending, shear, and tensile properties of the fabric in the warp–weft directions was analyzed using KES, and the regression model was summarized using multiple correlation analysis. The r2 value (Table 2) indicated that approximately 85% of the drape ratio of the fabric can be expressed by the model, in which the independent variable is the dependent variable. Although the significance of the p-value was less than 0.05, the Durbin–Watson value was 1.771, and the residual independence was uncertain. The regression equation of this regression model is expressed in eq 3 as follows:

3.1. 3

Table 2. Regression Analysis Results of KES Variables.

r 0.922
r2 0.850
Durbin–Watson 1.771
F 25.993
p 0.000
Open in a new tab

Table 3 shows the correlation between KES measurements and the drape ratio. The variance inflation factor (VIF) check revealed that the KES-FB shear stiffness (WARP and WEFT) was above 10, indicating the multicollinearity of the two independent variables (i.e., variables that were very similar were included in the independent variables).33 However, other variables that were very similar were not included as independent variables. In addition, the p-value value was greater than 0.05, indicating that the KES-FB thickness, elasticity (WEFT), and tensile properties (WARP, WEFT) had no significant effect on the dependent variable. In contrast, the weight, KES-FB bending stiffness (WARP, WEFT), KES-FB resilience, and KES-FB shear stiffness (WARP, WEFT) with a p-value of less than 0.05 significantly affected the dependent variables.

Table 3. Correlation between KES Measurements and the Drape Ratio.

dependent variable independent variable B SE β t P-value tolerance VIF
drape ratio constant 0.191 0.044   4.382 0.000    
KES-FB weight –0.009 0.002 –0.560 –3.913 0.000 0.160 6.256
KES-FB thickness 0.109 0.070 0.189 1.562 0.125 0.224 4.460
KES-FB bending stiffness (WARP) 0.600 0.226 0.281 2.652 0.011 0.290 3.444
KES-FB resilience (WARP) 0.853 0.335 0.277 2.548 0.014 0.277 3.615
KES-FB bending stiffness (WEFT) 0.217 0.104 0.263 2.083 0.043 0.205 4.885
KES-FB resilience (WEFT) 0.503 0.260 0.238 1.935 0.059 0.215 4.642
KES-FB shear stiffness (WARP) 0.028 0.019 0.570 1.472 0.148 0.022 45.902
KES-FB shear stiffness (WEFT) –0.018 0.022 –0.347 –0.858 0.395 0.020 50.074
KES-FB tensile strength (WARP) 0.028 0.039 0.060 0.735 0.466 0.492 2.034
KES-FB tensile strength (WEFT) 0.029 0.043 0.062 0.672 0.505 0.385 2.594
Open in a new tab

3.2. CLO Fabric Kit Measurement Result and Drape Ratio Correlation Analysis

The correlation between the drape ratio and CLO fabric kit measurements was analyzed by measuring the weight, thickness, bending, shear, and tensile properties in the warp–weft direction using the CLO fabric kit. The r2 value (Table 4) indicated that this model can express approximately 75.3% of the drape ratio, in which the independent variable is the dependent variable. The Durbin–Watson value was 1.868, confirming the satisfaction of the residual independence, and the significance p value was less than 0.05, indicating the suitability of the regression model.34

Table 4. Regression Analysis of CLO Fabric Kit Variables.

r 0.868
r2 0.753
Durbin–Watson 1.868
F 31.100
p 0.000
Open in a new tab

The regression equation of this regression model is expressed in eq 4, as follows.

3.2. 4

Table 5 shows the correlation between KES measurements and the drape ratio. The VIF check results were less than 10, indicating that there was no multicollinearity problem (Multicollinearity: when variables that are too similar are included in the independent variable).35 The p-values of the CLO weight per unit area, thickness, and shear stiffness were greater than 0.05, indicating that these variables did not significantly affect the dependent variable. In contrast, the p-value of the CLO bending stiffness (WARP and WEFT) was less than 0.05, indicating that they significantly affected the dependent variable.36

Table 5. Correlation between CLO Fabric Kit Measurements and the Drape Ratio.

dependent variable independent variable B SE β t P-value tolerance VIF
drape ratio constant 0.266 0.12   22.940 0.000    
CLO weight –0.004 0.04 –0.209 –0.959 0.342 0.102 9.759
CLO thickness –0.189 0.121 –0.311 –1.568 0.123 0.123 8.106
CLO bending stiffness (WARP) 7.408 × 10–6 0.000 0.222 1.838 0.072 0.333 3.007
CLO bending stiffness (WEFT) 1.190 × 10–5 0.000 0.638 4.400 0.000 0.230 4.346
CLO shear stiffness 0.021 0.022 0.130 0.971 0.336 0.270 3.696
Open in a new tab

3.3. Comparison of the Correlation between the KES-FB and CLO Fabric Kit Measurement Values

3.3.1. Weight and Thickness

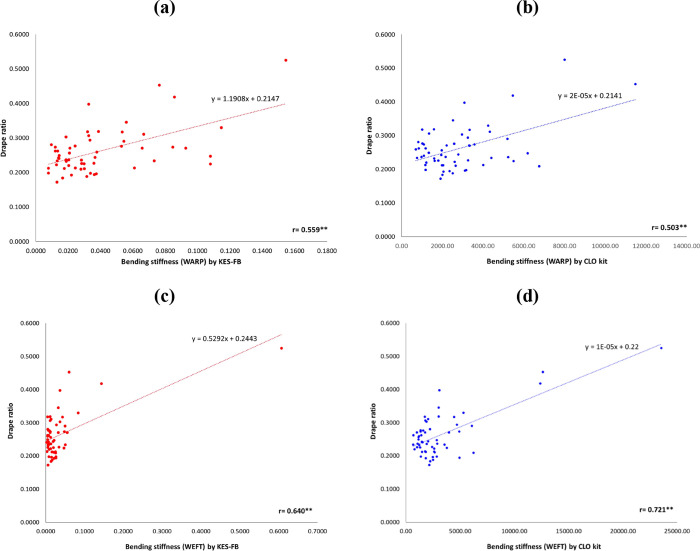
The correlation between the drape ratio of KES-FB and CLO weight and the thickness values was below the expected value (Figure 1). However, the correlation analysis revealed that the absolute values of “r” were similar in (a) and (b), and in (c) and (d). This indicates that although the KES-FB and CLO fabric kit instruments utilized different measurement principles, they exhibited similar effects on the drape ratio.37 This indicated that the CLO fabric kit and KES-FB equipment fabrics can be effectively utilized to measure the mechanical properties.

Figure 1.

Figure 1

Open in a new tab

Comparison of the correlation between the drape coefficient and weight and the thickness: (a) Kawabata evaluation system (KES)-FB weight, (b) CLO fabric kit weight, (c) KES-FB thickness, and (d) CLO fabric kit thickness.

3.3.2. Bending Stiffness and Shear Stiffness

The drape property is a complex attribute of fabrics, and it mostly depends on the mechanical and physical properties of the fabric. Among the physical factors, the bending and shearing stiffness are considered as the most important and are known as the main dependent properties of fabric drapes. This study revealed a high correlation between the bending and shear properties of the fabric and their drape ratio, which is consistent with the findings of a previous study.27 In addition, the correlation between the drape coefficient and the bending and shear stiffness properties was high (Figures 2 and 3). The correlation coefficient between the KES-FB bending (WEFT) and CLO bending (WEFT) parameters and the drape ratios were 0.640 and 0.721, respectively. In addition, the correlation coefficient between the KES-FB shear (WEFT) and CLO bending parameters and the drape ratio was 0.626 and 0.761, respectively. The correlation coefficients of the bending and shear stiffness parameters with the drape ratio of the KES-FB and CLO analysis were very similar. This confirmed the high correlation between the drape of the fabric and the shear stiffness and bendability of the fabric. In addition, as the correlation coefficients of KES-FB and the CLO fabric kit exhibited a similar trend, it was expected that the virtual fabric can be implemented in the CLO 3D using the physical properties of the real fabric.

Figure 2.

Figure 2

Open in a new tab

Comparison of the correlation coefficient between the drape ratio and bending stiffness: (a) KES-FB (WARP direction), (b) CLO fabric kit (WARP direction), (c) KES-FB (WEFT direction), and (d) CLO fabric kit (WEFT direction).

Figure 3.

Figure 3

Open in a new tab

Comparison of the correlation coefficient of the drape and shear stiffness: (a) KES-FB (WARP direction), (b) KES-FB (WEFT direction), and (c) CLO fabric kit.

3.3.3. Virtual Image Implementation Using CLO 3D Virtual Fabric

The weight and drape characteristics of the selected fabric are shown in Table 6. The comparison of the weight and number of nodes revealed that the number of nodes tended to increase with an increase in the weight. This was consistent with the findings of Carrera et al., Hu and Chung, and Kenkare and May-Plumlee, which reported that the number of nodes is an important factor in drape sensitivity and that the drape performance increases with an increase in the number of nodes.27,38,39 The comparison of the drape properties of real and virtual fabrics indicated that there was no external difference (Table 7). We believe that this may be related to the high correlation between KES-FB and the CLO fabric kit drape ratio, which was observed in this study, and further verifies the feasibility of implementing virtual fabrics in CLO 3D. Therefore, a windproof jacket pattern (Figure 4) was used to compare the appearance of fabrics with different weights but similar drape ratios after virtual wear, and the results are shown in Table 8. The weights of the two fabrics with similar drape ratios of 0.32 and 0.33 were 3.74 and 7.07, respectively, which were approximately two times different. In addition, the virtual fitting of the windproof jacket pattern confirmed that the heavy fabric exhibited a softer silhouette. In the case of two fabrics with similar drape ratios of 0.24 and 0.25, their weight was 7.17 and 14.44, respectively, which was approximately two times different. Similarly, the heavier fabric was closer to the body of the avatar and exhibited a softer silhouette. This result indicated that even if the fabrics exhibit a similar drape ratio, the silhouette appearance differs with a change in the weight. In addition, the possibility of making a clothing prototype using a virtual fabric implemented with the physical properties of the fabric was confirmed.

Table 6. Physical Properties of Real and Virtual Fabrics.
  weight per unit area (mg/cm2)
 drape ratio number of nodes
CLO KES-FB
light 3.74 3.65 0.23 4
3.74 3.77 0.28 4
3.74 3.81 0.32 3
medium 7.02 7.11 0.35 4
7.07 7.42 0.24 5
7.17 7.21 0.33 4
heavy 14.44 14.42 0.20 6
14.44 14.99 0.25 6
14.85 14.31 0.21 5
Open in a new tab
Table 7. Comparison of the Drape Properties of Real and Virtual Fabrics.

3.3.3.

Open in a new tab
Figure 4.

Figure 4

Open in a new tab

Windproof jacket patterns for the comparison of the silhouette of different virtual fabrics.

Table 8. Comparison of the CLO 3D Virtual Clothes Implemented Using Virtual Fabrics with Different Weights.

3.3.3.

Open in a new tab

4. Conclusions

In this study, to reduce the difference between the appearance of a real fabric and its virtual implementation, the correlation between the physical properties of the fabric and the drape was analyzed. Although the KES-FB and CLO 3D virtual clothing program utilize different measuring instruments, they exhibited similar correlations between each parameter. Statistical analysis revealed a high correlation between the drape thickness and multiple regression models of the drape tensile properties. In addition, a high correlation was observed between the drape bending stiffness and the drape shear stiffness, which was the main parameter that affected the drape.

After the correlation analysis, a virtual prototype with the pattern of an actual commercially available women’s windbreaker jacket implemented using the virtual fabric was created using the CLO 3D program. The results confirmed the application of the virtual fabric to a single item in various ways by implementing clothes with the same shape as the real one. However, one of the limitations of this study is that it did not derive the effect of fabric processing. As a follow-up study, we intend to conduct research on the effect and correlation of fabric processing on drape characteristics and garment silhouette.

As the textile industry researches ways to increase the possibility of realizing virtual fabrics and clothing in the 4th industrial revolution era, objective evaluation systems, such as KES-FB and CLO, will continue to be used as basic systems and play an important role in the future. In addition, it is believed that the virtual fabrication of clothing prototypes using virtual fabrics will also play an important role.

Acknowledgments

This research was supported by the Technology Innovation Program (Grant No.: 20000806) and the development of AR-VR cloud platform for fashion product funded by the Ministry of Trade, Industry & Energy (MOTIE, Korea).

The authors declare no competing financial interest.

References

  1. Shin H. K. A study on Design of Casual wear utilizing 3D Virtual Clothing Technology-focus on Generation Z. J Converg. Cult. Technol. 2021, 7, 75–81. 10.17703/JCCT.2021.7.1.75. [DOI] [Google Scholar]
  2. Ju K.; Jeong Y. Usage & education of the CLO 3D virtual clothing program in the development office & academic. Fash. Inf. Technol. 2016, 13, 51–59. [Google Scholar]
  3. Lee J. Y. A study on metaverse hype for sustainable growth. Int. J. Adv. Smart Converg. 2021, 10, 72–80. 10.7236/IJASC.2021.10.3.72. [DOI] [Google Scholar]
  4. Koch J.; Frommeyer B.; Schewe G. Online shopping motives during the COVID-19 pandemic—lessons from the crisis. Sustainability 2020, 12, 10247. 10.3390/su122410247. [DOI] [Google Scholar]
  5. Brienza M. V.Technological evolution in the luxury and fashion industry: focus on the metaverse and NFT, 2022.
  6. de Carvalho Godim C.; Cunha J.. A Look into Fashion Shows During and After the Covid-19 Pandemic: Are Digital Fashion Shows Here to Stay?. In International Conference on Design and Digital Communication; Springer: Cham, 2023; pp 406–414. [Google Scholar]
  7. Lai H.; Lee S. The application of artificial intelligence and VR technology in clothing store display design. IEEE Access. 2020, 1. 10.1109/ACCESS.2020.3020551. [DOI] [Google Scholar]
  8. Lee E.; Park H. 3D Virtual fit simulation technology: strengths and areas of improvement for increased industry adoption. Int. J. Fash. Des. Technol. Educ. 2017, 10, 59–70. 10.1080/17543266.2016.1194483. [DOI] [Google Scholar]
  9. Tatsiopoulos I. P.; Ponis S. T.; Hadzilias E. A.; Panayiotou N. A. Realization of the virtual enterprise paradigm in the clothing industry through e-business technology. Prod. Oper. Manage. 2022, 11, 516–530. 10.1111/j.1937-5956.2002.tb00475.x. [DOI] [Google Scholar]
  10. Kim H. S.; Na M. H. Effects of bending properties and drapability on the hand and appearance of wool-blended Fabrics: Comparison of real clothing with online and 3D virtual garments. Fibers Polym. 2013, 14, 2148–2156. 10.1007/s12221-013-2148-2. [DOI] [Google Scholar]
  11. Jang H.; Chen J. A Study on the Analysis and Comparison of DC Suite and CLO3D. J. Fash. Bus. 2017, 21, 87–105. 10.12940/jfb.2017.21.6.87. [DOI] [Google Scholar]
  12. Lim H.; Istook C. L. Drape simulation of three-dimensional virtual garment enabling fabric properties. Fibers Polym. 2011, 12, 1077–1082. 10.1007/s12221-011-1077-1. [DOI] [Google Scholar]
  13. Yang Y. Investigating seamed woven fabric drape using experimental and virtual approaches. Fibers Polym. 2014, 15, 2217–2224. 10.1007/s12221-014-2217-1. [DOI] [Google Scholar]
  14. Lee M. J.; Sohn H. S.; Kim J. J. A Study on Representation of 3D Virtual Fabric Simulation with Drape Image Analysis II-Focus on the Comparison between Real Clothing and 3D Virtual Clothing. J. Fash. Bus. 2011, 15, 97–111. 10.12940/jfb.2011.15.3.097. [DOI] [Google Scholar]
  15. Kim H. A.; Ryu H. S.; Lee J. H.; Nam Y. J. A study on the comparing visual images between the real garment and the 3D garment simulation of flare skirts. Sci. Emot. Sensibility 2011, 14, 385–394. [Google Scholar]
  16. Lee H.; Hong K. Comparison Between Actual and 3D Virtual Skirts of Different Front and Back Silhouette with Regard to the Evaluation of Subjective Appearance and Shape Characteristics. J. Fash. Bus. 2017, 21, 91–108. 10.12940/jfb.2017.21.5.91. [DOI] [Google Scholar]
  17. Sayem A. S. M.; Kennon R.; Clarke N. 3D CAD systems for the clothing industry. Int. J. Fash. Des. Technol. Educ. 2010, 3, 45–53. 10.1080/17543261003689888. [DOI] [Google Scholar]
  18. Power J. Fabric objective measurements for commercial 3D virtual garment simulation. Int. J. Cloth. Sci. Technol. 2013, 25, 423. 10.1108/IJCST-12-2012-0080. [DOI] [Google Scholar]
  19. Liu Y. M.; Jang H.. K. In: Advanced Materials Research; Trans Tech Publications Ltd, 2013; pp 501–505. [Google Scholar]
  20. Kim Y. S.; Yin S. Y.; Song H. K. A comparison of fit and appearance between real torso length sloper with 3D virtual torso length sloper. Res. J. Costume Cult. 2014, 22, 911–929. 10.7741/rjcc.2014.22.6.911. [DOI] [Google Scholar]
  21. Lage A.; Ancutiene K. Virtual try-on technologies in the clothing industry. Part 1: investigation of distance ease between body and garment. J. Text. Inst. 2017, 108, 1787–1793. 10.1080/00405000.2017.1286701. [DOI] [Google Scholar]
  22. Wang H.; Cho J. H. Research on Virtual Display of Wetsuit Based on CLO3D. Sci. Program. 2021, 2021, 1052510 10.1155/2021/1052510. [DOI] [Google Scholar]
  23. Kwak Y. A study on the 3D simulation system improvement through comparing visual images between the real garment and the 3D garment simulation of women’s Jacket. J. Converg. Cult. Technol. 2016, 2, 15–22. 10.17703/JCCT.2016.2.3.15. [DOI] [Google Scholar]
  24. Tsukada M.; Khan M. M. R.; Miura T.; Postle R.; Sakaguchi A. Mechanical performance of wool fabrics grafted with methacrylamide and 2-hydroxyethyl methacrylate by the Kawabata Evaluation System for Fabric method. Text. Res. J. 2013, 83, 1242–1250. 10.1177/0040517512458338. [DOI] [Google Scholar]
  25. Chan C. K.; Jiang X. Y.; Liew K. L.; Chan L. K.; Wong W. K.; Lau M. P. Evaluation of mechanical properties of uniform fabrics in garment manufacturing. J. Mater. Process. Technol. 2006, 174, 183–189. 10.1016/j.jmatprotec.2006.01.002. [DOI] [Google Scholar]
  26. Harwood R. J.; Weedall P. J.; Carr C. The use of the Kawabata Evaluation System for product development and quality control. J. Soc. Dyers Colour. 1990, 106, 64–68. 10.1111/j.1478-4408.1990.tb01244.x. [DOI] [Google Scholar]
  27. Carrera-Gallissà E.; Capdevila X.; Valldeperas J. Evaluating drape shape in woven fabrics. J. Text. Inst. 2017, 108, 325–336. 10.1080/00405000.2016.1166804. [DOI] [Google Scholar]
  28. Yuan W.; Wang S.; Dong S.; Adelson E.. Connecting look and feel: Associating the visual and tactile properties of physical materials. In Proc. IEEE Conf. Comput. Vis. Pattern Recognit.; 2017; pp 5580–5588.
  29. Ju E.; Choi M. G. Estimating Cloth Simulation Parameters From a Static Drape Using Neural Networks. IEEE Access 2020, 8, 195113–195121. 10.1109/ACCESS.2020.3033765. [DOI] [Google Scholar]
  30. Shim E.; Jang J. P.; Moon J. J.; Kim Y. Improvement of Polytetrafluoroethylene Membrane High-Efficiency Particulate Air Filter Performance with Melt-Blown Media. Polymer 2021, 13, 4067. 10.3390/polym13234067. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Owczarek M.; Szkopiecka M.; Jagodzińska S.; Dymel M.; Kudra M.; Gzyra-Jagieła K.; Miros-Kudra P. Biodegradable Nonwoven of an Aliphatic-Aromatic Copolyester with an Active Cosmetic Layer. Fibres Text. East. Eur. 2019, 27, 102–109. 10.5604/01.3001.0013.4475. [DOI] [Google Scholar]
  32. Moon H. S.; Yoon H. J.; Park S. W.; Kim C. Y.; Jeong M. S.; Lim S. M.; Ryu J. H.; Heo H. Usefulness of virtual reality-based training to diagnose strabismus. Sci. Rep. 2021, 11, 5891. 10.1038/s41598-021-85265-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Salmerón Gómez R.; García Pérez J.; López Martín M. D. M.; García C. G. Collinearity diagnostic applied in ridge estimation through the variance inflation factor. J. Appl. Stat. 2016, 43, 1831–1849. 10.1080/02664763.2015.1120712. [DOI] [Google Scholar]
  34. Atsalis A.; Mirasgedis S.; Tourkolias C.; Diakoulaki D. Fuel poverty in Greece: Quantitative analysis and implications for policy. Energy Build. 2016, 131, 87–98. 10.1016/j.enbuild.2016.09.025. [DOI] [Google Scholar]
  35. Curto J. D.; Pinto J. C. The corrected vif (cvif). J. Appl. Stat. 2011, 38, 1499–1507. 10.1080/02664763.2010.505956. [DOI] [Google Scholar]
  36. Vannarath S.; Vilaichone R. K.; Rasachak B.; Mairiang P.; Yamaoka Y.; Shiota S.; Binh T. T.; Mahachai V. Virulence genes of Helicobacter pylori in gastritis, peptic ulcer and gastric cancer in Laos. Asian Pac. J. Cancer Prev. 2014, 15, 9027–9031. 10.7314/APJCP.2014.15.20.9027. [DOI] [PubMed] [Google Scholar]
  37. Akaydin M.; Can Y. Pilling performance and abrasion characteristics of selected basic weft knitted fabrics. Fibres Text. East. Eur. 2010, 18, 79. [Google Scholar]
  38. Hu J.; Chung S. Drape behavior of woven fabrics with seams. Text. Res. J. 1998, 68, 913–919. 10.1177/004051759806801206. [DOI] [Google Scholar]
  39. Kenkare N.; May-plumlee T. Fabric drape measurement :A modified method using digital image processing. JTATM 2005, 4, 1–8. [Google Scholar]

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES