Abstract
Quantitative phase microscopies (QPMs) enable label-free, non-invasive observation of living cells in culture, for arbitrarily long periods of time. One of the main benefits of QPMs compared with fluorescence microscopy is the possibility to measure the dry mass of individual cells or organelles. While QPM dry mass measurements on neural cells have been reported this last decade, dry mass measurements on their neurites has been very little addressed. Because neurites are tenuous objects, they are difficult to precisely characterize and segment using most QPMs. In this article, we use cross-grating wavefront microscopy (CGM), a high-resolution wavefront imaging technique, to measure the dry mass of individual neurites of primary neurons in vitro. CGM is based on the simple association of a cross-grating positioned in front of a camera, and can detect wavefront distortions smaller than a hydrogen atom (∼0.1 nm). In this article, an algorithm for dry-mass measurement of neurites from CGM images is detailed and provided. With objects as small as neurites, we highlight the importance of dealing with the diffraction rings for proper image segmentation and accurate biomass measurements. The high precision of the measurements we obtain using CGM and this semi-manual algorithm enabled us to detect periodic oscillations of neurites never observed before, demonstrating the sufficient degree of accuracy of CGM to capture the cell dynamics at the single neurite level, with a typical precision of 2%, i.e., 0.08 pg in most cases, down to a few fg for the smallest objects.
1. Introduction
Quantitative phase microscopies (QPMs) are optical imaging techniques capable of mapping the phase of a light wave after passing the object plane of a microscope [1]. Most of the applications of QPMs are related to biology, for the observation of cells in vitro. In this context, the measured phase image reads
| (1) |
| (2) |
where h is the thickness profile of the imaged object, n its refractive index (supposed here to be uniform for the sake of simplicity) and the refractive index of the environment. In Eq. (2), has been replaced with , called the optical path difference (OPD) image, or equivalently the optical wavefront profile.
QPMs have the great advantage, compared with fluorescence microscopies, to be label-free and to not require the use of UV-blue light. For these reasons, they are non-invasive, do not suffer from photobleaching, and can be conducted for arbitrarily long periods of time, without decay of the signal and without perturbing the imaged cells. Moreover, the quantitative nature of the measurements provides QPMs with the ability to measure the bio-mass of the imaged cells [2]. Indeed, the refractive index is in direct relation with dry mass density and the total dry mass of an imaged object can be calculated by summing all the pixels values of the OPD image:
| (3) |
where is the dry mass of the entire cell, p the pixel size of the image at the sample plane, and is the dry mass volumetric density. For the sake of simplicity, we consider here that the background is uniform and set to . In practice, when the background is non-uniform, image treatment may be required, as done in Ref. [3]. Equation (3) can be recast using the optical volume difference :
| (4) |
An interesting physical quantity to deal with is the dry mass areal density (dry mass per unit area), directly proportional to the OPD image [4]:
| (5) |
Although the use of (a volumetric dry mass density) seems more natural in this context, the QPM community rather uses the so-called refractive index increment , as originally introduced in 1954, leading to expressions such as . The value has been considered rather constant for biological media, ranging from to µm3·pg-1. We used in this study µm3·pg-1, i.e., pg·µm-3 or g·ml-1.
Although the idea of measuring biomass using light dates from 1952 [5], one had to wait around 50 years for the development of CCD cameras and effective QPMs to observe the first optical measurements of dry mass at high resolution, independently by Popescu et al. [6] and Rappaz et al. [7] in 2008 and 2009. Since then, dry mass measurements using QPM have been reported by several groups for the study of mammalian cells [8,9,3,10,11,12], cancer cells [4,13,14,15], red blood cells [16], bacteria [17], yeast [18], and neurons [19,20]. More recently, masses of single molecules were reported using iScat by the group of Kukura, a technique called mass photometry [21].
Cross-grating wavefront microscopy is a QPM based on the use of a two-dimensional grating (aka a cross-grating) positioned around 1 mm from the sensor of a camera [22]. This simple association enables the mapping of the wavefront profile of a light wave (Eq. (2)). When implemented on a microscope, this wavefront imaging technique can be used as a QPM technique, according to Eq. (2) that establishes the equivalence between phase and wavefront profiles [23,24]. Interestingly, because the dry mass directly depends on , CGM does not require the knowledge of the illumination wavelength to measure dry masses [3,12,20], unlike the other QPM techniques based on interferometry, which rather measure . Moreover, unlike Shack-Hartmann wavefront sensing, which has been very rarely used in bio-imaging because of its low spatial resolution [25], CGM is a wavefront imaging technique that can reach a diffraction-limited spatial resolution. In 2020, the group of Zangle reported the first observation of neural cells using CGM [20]. Using a home-made Matlab segmentation algorithm, they performed ensemble measurements of the dry masses of the somas and neurites separately, averaged over the field of view of a microscope. This work was the occasion to highlight the ability of QPM to follow the developments of cells in vitro for days, without perturbation or loss of the signal. However, this work only reported ensemble measurements.
In this article, we report the observation of neural cells in vitro using CGM, and present an image segmentation method for the precise estimation of the dry mass of individual neurites, from their birth until they connect. We highlight the importance of taking into account diffraction rings to achieve quantitative measurements, and the benefit of using CGM over other existing QPMs for the analysis of such tenuous biological objects. We evidence a precision of 2% on the dry mass measurements, i.e., around 0.08 pg. As a means to demonstrate the interest of conducting experiments at the single cell level, we present the observation of periodic oscillations of neurite outgrowth, in the pg range.
2. Material and methods
2.1. Cross-grating wavefront microscopy
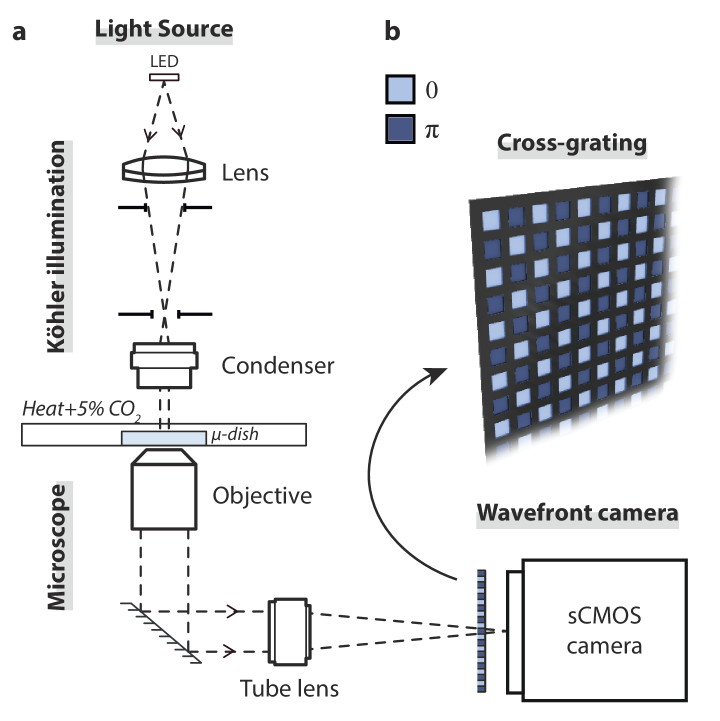
All the experiments were conducted on a home-made microscope (Fig. 1), endowed with a 60 , 1.25 NA oil immersion objective lens (Olympus UPLFLN60XOI), a 200 mm tube lens (leading to a 66 total magnification), a Köhler illumination using a mounted LED at 625 nm (Thorlabs M625L2-C1), and a heating stage (Tokai Hit, WSKMX) maintaining the cells at 37°C and regulating CO2 at 5%. For CGM measurements, we used a Zyla 5.5 sCMOS camera with a quadriwave lateral shearing interferometry (QLSI) cross-grating positioned at 0.86 mm from the camera. The pitch of the grating was µm, 6 times the camera pixel size p. This configuration gives a zeta-factor [26] equal to . Another common value of the zeta-factor is 4, but higher values of reduce the spatial resolution.
Fig. 1.
(a) Schematic of the experimental setup. (b) Representation of the cross-grating used in CGM, characterized by a checkerboard pattern of phase shifts.
To postprocess the raw images (called interferograms), we used a home-made algorithm that we detail in Ref. [24], and provide on a github repository [27]. Unlike more common algorithms, our algorithm does not yield a reduction of the number of pixels of the image by a factor of . The number of pixels of the OPD image is the same as the number of pixels of the camera sensor ( ), because we perform a demodulation in the Fourier space, instead of an image crop by a factor of . This common -reduction in the number of pixels enables faster computation, and thus faster live acquisition. Note that it does not yield a reduction of the resolution, only of the image definition, i.e. of the number of pixels (Fig. S4). However, avoiding this image reduction is a benefit for data visualization, especially on objects as tenuous and small as neurites. To provide a visual comparison of these low- and high-definition algorithms, Fig. 2 shows the same image of a neurite processed with both types of algorithms. Figure 2 is also the occasion to show that OPD images can be considered as dry mass density images as well, according to Eq. (5).
Fig. 2.

(a) OPD image of a neurite processed with a full-pixel algorithm. (b) OPD image from the same measurement, processed with the more common pixel-reduction algorithm. The color bar shows the equivalence between OPD and dry mass density.
2.2. Cell preparation
All procedures were in agreements with the guidelines established by the European Animal Care and Use Committee (86/609/CEE) and was approved by the local ethics committee (agreement G13O555). We used primary neural cell cultures from embryonic rat hippocampus. Pregnant female Wistar rats were obtained from Janvier labs. The plug date of the female rats was marked E0. All embryos staged at E18 from the female rats were used in the experiments. For cell culture and observation, we used 35-mm µ-Dishes, high Glass Bottom, 170 µm thick (Ibidi, 81158). µ-dishes were first incubated for 24 h with a PEI solution (1 ml, 20 µg/ml) and then rinsed 3 times with mQ water, leading to a PEI coating favouring cell adhesion. 150,000 to 200,000 cells were plated on the µ-dishes, with 1 ml of culture medium composed of Neurobasal/B27/L-glutamin with antifungal/antibiotics (Gibco 15240062), and let 1h30min in the incubator at 37°C, 5% CO2, before being placed on the microscope stage. The cells were gently washed before imaging to reduce the number of debris commonly found in primary cultures, and to ease the measurements of dry mass of neurites.
3. Results
3.1. Image processing method for single neurite dry-mass measurement
To measure the dry mass of a single neurite using Eq. (3), the OPD background value has to be precisely set. Indeed, CGM primarily measures wavefront gradients and the wavefront profile is obtained by integration of the gradients, to within a constant. For proper estimation of the dry mass, this constant has to be set such that the OPD of the background area is zero, defined as the part of the image where there is no object. However, this background may not be perfectly uniform, especially for long neurites covering a large part of the field of view, which makes precise dry mass estimation not as straightforward as what Eq. (3) suggests.
To circumvent this problem, the neurite to be measured was segmented, defining an area , and the background value was calculated as the averaged OPD value over a few-pixel thick boundary ( ) outlining the segmented area:
| (6) |
| (7) |
The complexity of the problem comes down to automatically determine . There exist many image segmentation methods but for objects as tenuous as neurites, and surrounded by complex objects such a soma and debris, it was hard to find an automated algorithm that could approach human performance. Machine learning (ML) could be an effective method for this task, but ML algorithms need to be trained on a set of trustful data obtained by more common human-guided algorithms anyway.
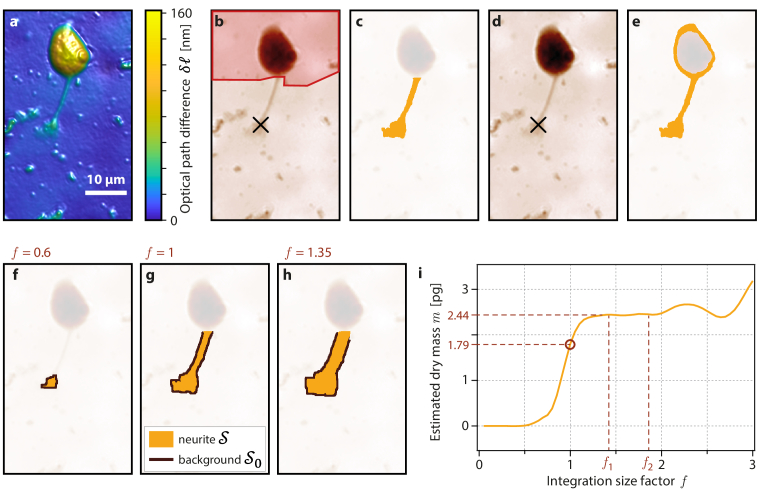
We developed a semi-manual segmentation algorithm based on a magic-wand selection. The four-step procedure is described in Fig. 3, and the related Matlab code is provided in Suppl. Mater. and on github [28]. Here is a description of the four steps of the segmentation algorithm illustrated with a particular neuron image (Fig. 3(a)):
-
1.
Exclusion. The soma and any other unwanted objects at the vicinity of the neurite (like debris) have to be manually outlined to avoid their inclusion during the integration step (Fig. 3(b), red area). This step has to be performed mostly for the first image, because all these objects (soma and debris) usually do not move (or very little) during the acquisition. Outlining the soma is important to avoid the natural capture of its boundary by the magic wand, as represented in Fig. 3(d),(e). For most cells, the demarcation between the soma and the neurite is straightforward to define. However, in some cases, the demarcation with the soma is less abrupt, or neurites can arise from a lamellipodium (bottom cell of Fig. 4), making the onset of the neurite less easy to define. In such a case, the exclusion line can be drawn arbitrarily further along the neurite. Part of the dry mass may be missed, but any missing constant offset won't affect measurements of growth dynamics and velocity, which is what essentially matters.
-
2.
Magic-wand selection. The neurite of interest has to be clicked, ideally on the highest pixel value (Fig. 3(b), cross marker). Several clicks on several locations on the neurites may be necessary to properly capture the whole neurite.
-
3.
Adjustment. The magic-wand sensitivity has to be adjusted so that the whole neurite is properly captured, which defines the initial segmentation area (Fig. 3(c)).
-
4.Inflation. The initial area is dilated by a factor of f, ranging typically from 0.5 to 2 (Fig. 3(f),(g),h). The optical volume as a function of f, , defined by Eq. (9), normally reaches a plateau from , corresponding to the true value of the dry mass (Fig. 3(i)).
(8)
This inflation of the area above the apparent outline of the neurites actually captures the diffraction rings that we barely see in the image and that would not be captured by standard segmentation algorithms. However, they notably contribute in the total dry mass. To ascertain that diffraction are actually responsible for this missing dry mass, numerical simulations have been conducted using IF-DDA [29] and shown in SI (Fig. S6).(9) -
5.Plateau selection. To obtain more accurate measurement, the retained value of does not only correspond to one selected value on the plateau, but to the average value over the plateau. For this purpose, two f values are selected, and , such that the dry mass equals.
Above a certain value of f, around in Fig. 3(i), the estimated value of becomes unstable due to debris and even tends to diverge due to image noise. One neurite segmentation (steps 1 to 5) takes around 30 s.(10)
Fig. 3.
(a) OPD image of a neuron and its unique neurite. (b) Same OPD image as (a). The red area corresponds to the manual exclusion of the soma. The cross indicates where the magic wand was subsequently applied. (c) Area (orange area) captured by the magic wand after adjustment of the magic-wand sensitivity. (d) Representation of a magic-wand application, without soma removal, and (e) corresponding area captured by the same magic-wand application. A problem of capture of the soma boundary is evidenced. (f, g, h) OPD images of the same neurite along with segmented areas for 3 values of the inflation factor f, namely , , and . (i) Dry mass of the neurite measured as a function of the inflation factor f, featuring a plateau above . Two dry mass values are highlighted: pg, corresponding to the properly estimated value, and pg, an underestimated value corresponding to , highlighting the importance of inflating the initial segmented area.
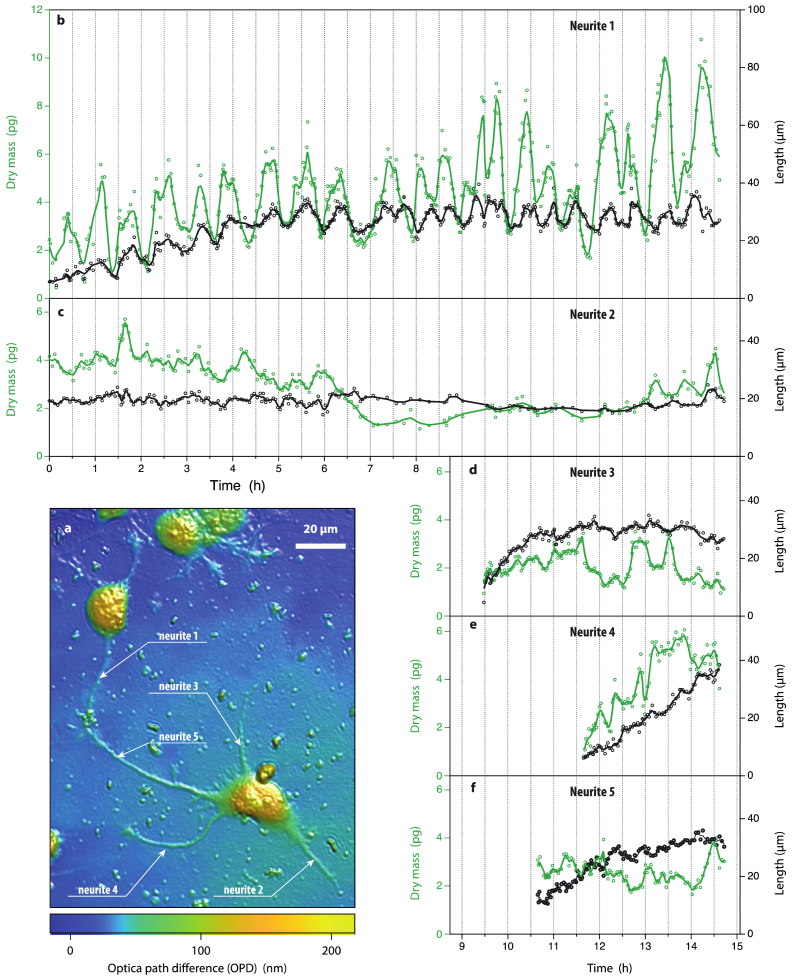
Fig. 4.
(a) OPD image of neural cells, corresponding to time h. The 5 neurites are indicated and numbered. (b – f) Dry mass and length as a function of time for the 5 neurites indicated in (a).
This algorithm has been tested and intensively used by 3 different users. Figure S3 plots dry mass measurements performed by two different users on the exact same series of data, demonstrating a very good reproducibility.
The interest of measuring the OV on a plateau of , rather than at , is not only to obtain a value closer to reality. Note that the true dry mass is anyway biased by the arbitrary choice of the coefficient within the range to µm3·pg-1. The other, and more important, interest of avoiding is rather that the slope of at is abrupt, leading to a much larger variation of the measured OV, and thus of the dry mass. To illustrate this statement, Figure S2c plots the measured dry masses over 30 successive frames of a neurite of fixed neurons with the two modalities: at and on the plateau. While the standard deviation of the measurement is 1.3% on the plateau, it is 11% at .
In Ref. [30], The authors introduce a segmentation algorithm to measure dry masses of red blood cells from QPM images. To quantify the efficiency of the measurements, they introduced a metrics, named the segmentation accuracy, defined as “the absolute value of correlation between segmented RBCs image and reference image, which is manually obtained”. We cannot apply such a metrics because the segmentations we perform are already obtained semi-manually, i.e., they are already visually checked individually. However, our algorithm could be the basis for the generation of a ground truth for training a deep learning algorithm for neurite segmentation. In this case, such a metrics could be advantageously used.
3.2. Illustration of the numerical procedure on experimental CGM images
To illustrate the efficiency and the degree of accuracy of the algorithm, Fig. 4 presents dry mass measurements of neurites stemming from a 15-h long image acquisition, one image per minute, of two nearby neurons. Figure 4(a) displays the OPD image of the field of view at the end of the data acquisition, where all the neurites of interest are indicated. The full movie is provided in Suppl. Mater (Visualization 1 (78.6MB, avi) and Fig. S7 for a time lapse of 16 images). Of particular interest are neurites 1 and 5, which eventually connect, just at the end of the acquisition. Figure 4(b)–(f) plots both the dry mass and the length of the neurites.
All the neurites are a few pg in mass. Rare are the dry mass measurements reaching such small values. Common dry mass measurements using QPM rather report values around a few 100s of pg (mass of eukaryotic cells). The precision of neurite dry mass measurements was 0.08 pg, calculated as the standard deviation of series of dry mass measurements for which the dry mass of the neurite was constant (see Fig. S1). The precision of other QPMs is rather in the 1 pg range [31,32]. CGM recently confirmed its ability to yield highly precise OPD measurements, better than other conventional QPM technique such as DHM [33]. We recently dedicated an article on the precision and accuracy of CGM, and demonstrated that the OPD precision can typically reach 0.1 nm, i.e. a fraction of hydrogen atom, corresponding to a precision in of 0.55 fg·µm-1 (Eq. (5)) [26]. This high precision comes from the fact that CGM does not require the use of a reference arm, like other QPMs based on interferometry measurements for which it makes the setup highly sensitive to environmental perturbation, such as air flow, mechanical drift, thermal variation, etc. The common-path configuration also ensures a perfectly flat background. No image treatment has been performed in our data, except the correction of a tilt on the OPD images. With CGM, all the optical metrology happens within a distance of around 1 mm, between the camera sensor and the cross-grating, a volume that can be made particularly solid, robust and isolated from any perturbation. Thanks to this high precision, we recently could characterize for the first time the optical properties of small objects and 1-atom-thick 2D-materials using QPM [34,35].
In the case of the data presented in Fig. 4, this high precision, along with the magic-wand algorithm, enabled us to observe fine variations of neurite masses, in the sub-pg range. Most of the time, the evolution looks chaotic, with succeeding periods of activity, inactivity, regression, growth. Interestingly, neurite lengths do not necessarily correlate with their dry mass. In many occasions, neurites thicken without elongation, and reciprocally, change length without mass increase.
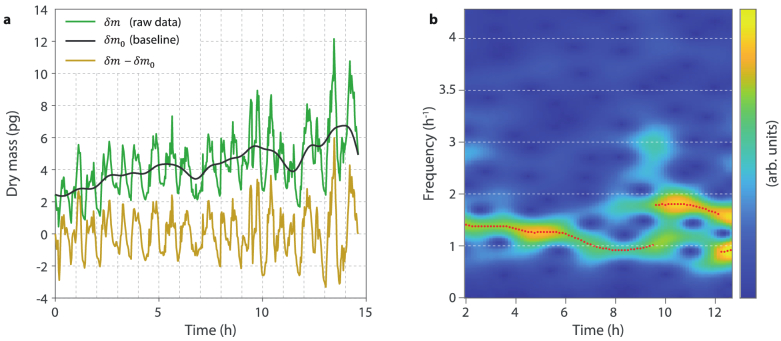
Of particular interest with this set of data is neurite 1, which featured a periodic oscillation of its dry mass, a behavior that has never been reported in the literature. This behavior is not systematic, only this neurite shows this effect in this set of data. During these oscillations, the neurite length also demonstrates an oscillation, correlated with the dry mass, but much weaker. To determine the oscillation frequency, we conducted a short-time Fourier transform analysis: from the dry mass profile of neurite 1, the baseline is estimated with a low-pass filter and then subtracted (green line in Fig. 5(a)). This operation is aimed to remove the low spatial frequencies of the signal that would have masked the signal of interest in Fig. 5(b). Then, a spectrogram (modulus of the short-time Fourier transform with a Gaussian window of size 4 h) of this baseline-free signal is computed to provide a time-frequency representation (Fig. 5(b)). Finally, the ridge of the time-frequency pattern is calculated (red dotted line if Fig. 5(b)) giving an estimation of the instantaneous frequency of the neurite oscillation as a function of time. We can see that the oscillation frequencies lie around to h-1 at the beginning of the acquisition, and then splits, or maybe becomes more chaotic from h. Let us notice that this time corresponds to neurite 5 arriving is close proximity to neurite 1 (see Visualization 1 (78.6MB, avi) in Suppl. Info.). We show another event of neurite oscillation in Suppl. Mater (Fig. S5), with the same period of around 1 h.
Fig. 5.
(a) Dry mass of neurite 1 as a function of time , sampled at h-1 (green line) and its baseline (black line). Subtraction of these two profiles (yellow line). (b) Spectrogram (estimated instantaneous frequency of as a function of time) calculated with a time window of 4 h. The dotted red line is the calculated ridge of the image, giving the estimated frequency of the oscillation as a function of time.
To date, we did not elucidate the origin of this oscillation, although we believe it may be correlated with the dynamics of actin waves. Because the aim of this article is primarily to demonstrate the possibility of CGM to investigate single neurites with high precision, and give the tool to do it, we will leave this question for a future work.
4. Discussion and summary
We show in this article that cross-grating wavefront microscopy (CGM) can be used to monitor the dynamics of single neurites in vitro, via measurements of dry mass with a sub-pg sensitivity. For this purpose, we developed a semi-manual segmentation algorithm, suited for neurite segmentation. Previously reported CGM measurements on neurons only investigated ensemble measurements of soma and neurite dry masses, an approach that naturally erases any particular behaviour at the single cell level. We show that imaging such tenuous objects implies two requirements: First, the neurite segmentation has to take into account the diffraction rings that are barely visible on the OPD images in order to achieve precise measurements. Second, a highly sensitive QPM has to be used, the neurite OPD being only around 10 to 20 nm. CGM performs very well, with its typical noise amplitude of 0.1 nm, and because it yields images with a particular flat background over the field of view, being insensitive to environmental perturbation, unlike common QPM technique based on interferometry. CGM is also simple (no modification of the microscope), cost-effective (only involves the addition of a cross-grating). Moreover, CGM offers easy fluorescence/phase correlation measurements because it can be easily implemented on any standard fluorescence microscope. For all these reasons, CGM has the potential for becoming a major QPM technique in the near future, and in particular in the field of neurobiology.
Acknowledgments
The authors thank Christophe Leterrier and Fanny Boroni-Rueda for providing the primary neural cells, and for helpful discussion; Frédéric Galland and Maëlle Bénéfice for helpful discussion; and the ANRT for financial support.
Funding
Association Nationale de la Recherche et de la Technologie10.13039/501100003032.
Disclosures
The authors declare no conflicts of interest.
Data availability
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.
Supplemental document
See Supplement 1 (5.3MB, pdf) for supporting content.
References
- 1.Park Y., Depeursinge C., Popescu G., “Quantitative phase imaging in biomedicine,” Nat. Photonics 12(10), 578–589 (2018). 10.1038/s41566-018-0253-x [DOI] [Google Scholar]
- 2.Zangle T. A., Teitell M. A., “Live-cell mass profiling: an emerging approach in quantitative biophysics,” Nat. Methods 11(12), 1221–1228 (2014). 10.1038/nmeth.3175 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Aknoun S., Savatier J., Bon P., Galland F., Abdeladim L., Wattellier B., Monneret S., “Living cell dry mass measurement using quantitative phase imaging with quadriwave lateral shearing interferometry: an accuracy and sensitivity discussion,” J. Biomed. Opt. 20(12), 126009 (2015). 10.1117/1.JBO.20.12.126009 [DOI] [PubMed] [Google Scholar]
- 4.Girshovitz P., Shaked N. T., “Generalized cell morphological parameters based on interferometric phase microscopy and their application to cell life cycle characterization,” Biomed. Opt. Express 3(8), 1757–1773 (2012). 10.1364/BOE.3.001757 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Barer R., “Interference microscopy and mass determination,” Nature 169(4296), 366–367 (1952). 10.1038/169366b0 [DOI] [PubMed] [Google Scholar]
- 6.Popescu G., Park Y., Lue N., Best-Popescu C., Deflores L., Dasari R. R., Feld M. S., Badizadegan K., “Optical imaging of cell mass and growth dynamics,” American Journal of Physiology-Cell Physiology 295(2), C538–C544 (2008). 10.1152/ajpcell.00121.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Rappaz B., Cano E., Colomb T., Kühn J., Depeursinge C., Simanis V., Magistretti P. J., Marquet P., “Noninvasive characterization of the fission yeast cell cycle by monitoring dry mass with digital holographic microscopy,” J. Biomed. Opt. 14(3), 034049 (2009). 10.1117/1.3147385 [DOI] [PubMed] [Google Scholar]
- 8.Cooper K. L., Oh S., Sung Y., Dasari R. R., Kirschner M. W., Tabin C. J., “Multiple phases of chondrocyte enlargement underlie differences in skeletal proportions,” Nature 495(7441), 375–378 (2013). 10.1038/nature11940 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Sung Y., Tzur A., Oh S., Choi W., Li V., Dasari R. R., Yaqoob Z., Kirschner M. W., “Size Homeostasis in Adherent Cells Studied by Synthetic Phase Microscopy,” Proc. Natl. Acad. Sci. 110(41), 16687–16692 (2013). 10.1073/pnas.1315290110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kandel M. E., Lu W., Liang J., Aydin O., Saif T. A., Popescu G., “Cell-to-Cell Influence on Growth in Large Populations,” Biomed. Opt. Express 10(9), 4664 (2019). 10.1364/BOE.10.004664 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Sandoz P. A., Tremblay C., van der Goot F. G., Frechin M., “Image-Based Analysis of Living Mammalian Cells Using Label-Free 3D Refractive Index Maps Reveals New Organelle Dynamics and Dry Mass Flux,” PLoS Biol 17(12), e3000553 (2019). 10.1371/journal.pbio.3000553 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Aknoun S., Yonnet M., Djabari Z., Graslin F., Taylor M., Pourcher T., Wattellier B., Pognonec P., “Quantitative Phase Microscopy for Non-Invasive Live Cell Population Monitoring,” Sci. Rep. 11(1), 4409 (2021). 10.1038/s41598-021-83537-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Tolde O., Gandalovičová A., Křížová A., Veselý P., Chmelík R., Rosel D., Brábek J., “Quantitative Phase Imaging Unravels New Insight into Dynamics of Mesenchymal and Amoeboid Cancer Cell Invasion,” Sci. Rep. 8(1), 12020 (2018). 10.1038/s41598-018-30408-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ayyappan V., Chang A., Zhang C., Paidi S. K., Bordett R., Liang T., Barman I., Pandey R., “Identification and Staging of B-Cell Acute Lymphoblastic Leukemia Using Quantitative Phase Imaging and Machine Learning,” ACS Sens. 5(10), 3281–3289 (2020). 10.1021/acssensors.0c01811 [DOI] [PubMed] [Google Scholar]
- 15.Su Y., Fu R., Du W., Yang H., Ma L., Luo X., Wang R., Lin X., Jin X., Shan X., Lv W., Huang G., “Label-Free and Quantitative Dry Mass Monitoring for Single Cells during In Situ Culture,” Cells 10(7), 1635 (2021). 10.3390/cells10071635 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Phillips K. G., Jacques S. L., McCarty O. J. T., “Measurement of Single Cell Refractive Index, Dry Mass, Volume, and Density Using a Transillumination Microscope,” Phys. Rev. Lett. 109(11), 118105 (2012). 10.1103/PhysRevLett.109.118105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Mir M., Wang Z., Shen Z., Bednarz M., Bashir R., Golding I., Prasanth S. G., Popescu G., “Optical Measurement of Cycle-Dependent Cell Growth,” Proc. Natl. Acad. Sci. U.S.A. 108(32), 13124–13129 (2011). 10.1073/pnas.1100506108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Midtvedt D., Olsén E., Höök F., Jeffries G. D. M., “Label-Free Spatio-Temporal Monitoring of Cytosolic Mass, Osmolarity, and Volume in Living Cells,” Nat. Commun. 10(1), 340 (2019). 10.1038/s41467-018-08207-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Cintora P., Arikkath J., Kandel M., Popescu G., Best-Popescu C., “Cell Density Modulates Intracellular Mass Transport in Neural Networks,” Cytometry 91(5), 503–509 (2017). 10.1002/cyto.a.23111 [DOI] [PubMed] [Google Scholar]
- 20.Pradeep S., Tasnim T., Zhang H., Zangle T. A., “Simultaneous Measurement of Neurite and Neural Body Mass Accumulation via Quantitative Phase Imaging,” Analyst 146(4), 1361–1368 (2021). 10.1039/D0AN01961E [DOI] [PubMed] [Google Scholar]
- 21.Young G., Hundt N., Cole D., Fineberg A., Andrecka J., Tyler A., Olerinyova A., Ansari A., Marklund E. G., Collier M. P., Chandler S. A., Tkachenko O., Allen J., Crispin M., Billington N., Takagi Y., Sellers J. R., Eichmann C., Selenko P., Frey L., Riek R., Galpin M. R., Struwe W. B., Benesch J. L. P., Kukura P., “Quantitative Mass Imaging of Single Molecules,” Science 360(6387), 423–427 (2018). 10.1126/science.aar5839 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Primot J., Guerineau N., “Extended Hartmann Test Based on the Pseudoguiding Property of a Hartmann Mask Completed by a Phase Chessboard,” Appl. Opt. 39(31), 5715–5720 (2000). 10.1364/AO.39.005715 [DOI] [PubMed] [Google Scholar]
- 23.Bon P., Maucort G., Wattellier B., Monneret S., “Quadriwave Lateral Shearing Interferometry for Quantitative Phase Microscopy of Living Cells,” Opt. Express 17(15), 13080–13094 (2009). 10.1364/OE.17.013080 [DOI] [PubMed] [Google Scholar]
- 24.Baffou G., “Quantitative Phase Microscopy Using Quadriwave Lateral Shearing Interferometry (QLSI): Principle, Terminology, Algorithm and Grating Shadow Description,” J. Phys. D: Appl. Phys. 54(29), 294002 (2021). 10.1088/1361-6463/abfbf9 [DOI] [Google Scholar]
- 25.Gong H., Agbana T. E., Pozzi P., Soloviev O., Verhaegen M., Vdovin G., “Optical Path Difference Microscopy with a Shack–Hartmann Wavefront Sensor,” Opt. Lett. 42(11), 2122 (2017). 10.1364/OL.42.002122 [DOI] [PubMed] [Google Scholar]
- 26.Marthy B., Baffou G., “Cross-Grating Phase Microscopy (CGM): In Silico Experiment (Insilex) Algorithm, Noise and Accuracy,” Opt. Commun. 521, 128577 (2022). 10.1016/j.optcom.2022.128577 [DOI] [Google Scholar]
- 27.Baffou G.,, CGM Process, Github, 2022, Github.Com/Baffou/CGMprocess.
- 28.Baffou G., CGM_magicWandSegmentation, Github, 2022, Github.Com/Baffou/CGM_magicWandSegmentation.
- 29.Chaumet P. C., Sentenac D., Maire G., Rasedujjaman M., Zhang T., Sentenac A., “IFDDA, an Easy-to-Use Code for Simulating the Field Scattered by 3D Inhomogeneous Objects in a Stratified Medium: Tutorial,” J. Opt. Soc. Am. A 38(12), 1841 (2021). 10.1364/JOSAA.432685 [DOI] [Google Scholar]
- 30.Yi F., Moon I., Javidi B., Boss D., Marquet P., “Automated Segmentation of Multiple Red Blood Cells with Digital Holographic Microscopy,” J. Biomed. Opt. 18(2), 026006 (2013). 10.1117/1.JBO.18.2.026006 [DOI] [PubMed] [Google Scholar]
- 31.Park K., Millet L. J., Kim N., Li H., Jin X., Popescu G., Aluru N. R., Hsia K. J., Bashir R., “Measurement of Adherent Cell Mass and Growth,” Proc. Natl. Acad. Sci. 107(48), 20691–20696 (2010). 10.1073/pnas.1011365107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Popescu G., Park K., Mir M., Bashir R., “New Technologies for Measuring Single Cell Mass,” Lab Chip 14(4), 646–652 (2014). 10.1039/C3LC51033F [DOI] [PubMed] [Google Scholar]
- 33.Allier C., Hervé L., Mandula O., Blandin P., Usson Y., Savatier J., Monneret S., Morales S., “Quantitative Phase Imaging of Adherent Mammalian Cells: A Comparative Study,” Biomed. Opt. Express 10(6), 2768 (2019). 10.1364/BOE.10.002768 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Khadir S., Bon P., Vignaud D., Galopin E., McEvoy N., McCloskey D., Monneret S., Baffou G., “Optical Imaging and Characterization of Graphene and Other 2D Materials Using Quantitative Phase Microscopy,” ACS Photonics 4(12), 3130–3139 (2017). 10.1021/acsphotonics.7b00845 [DOI] [Google Scholar]
- 35.Khadir S., Andrén D., Chaumet P. C., Monneret S., Bonod N., Käll M., Sentenac A., Baffou G., “Full optical characterization of single nanoparticles using quantitative phase imaging,” Optica 7(3), 243 (2020). 10.1364/OPTICA.381729 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.