Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2022 Jul 22;2(6):461–476. doi: 10.1021/acsengineeringau.2c00025

Modeling of Hydrodynamic Cavitation Reactors: Reflections on Present Status and Path Forward

Vivek V Ranade 1,*
PMCID: PMC9782368  PMID: 36573175

Abstract

graphic file with name eg2c00025_0012.jpg

Hydrodynamic cavitation (HC) is finding ever increasing applications in water, energy, chemicals, and materials sectors. HC generates intense shear, localized hot spots, and hydroxyl radicals, which are harnessed for realizing desired physicochemical transformations. Despite identification of HC as one of the most promising technology platforms, its potential is not yet adequately translated in practice. Lack of appropriate models for design, optimization, and scale-up of HC reactors is one of the primary reasons for this. In this work, the current status of modeling of HC reactors is presented. Various prevailing approaches covering empirical, phenomenological, and multiscale models are critically reviewed in light of personal experience of their application. Use of these approaches for different applications such as biomass pretreatment and wastewater treatment is briefly discussed. Some comments on extending these models for other applications like emulsions and crystallization are included. The presented models and discussion will be useful for practicing engineers and scientists interested in applying HC for a variety of applications. Some thoughts on further advances in modeling of HC reactors and outlook are shared, which may stimulate further research on improving the fidelity of computational models of HC reactors.

Keywords: Per-pass models, Data-driven models, CFD models, Multilayer models, Ensemble approach

1. Introduction

Hydrodynamic cavitation is realized by generating a low pressure region in a fluidic device where vaporous cavities (microbubbles) are formed. These cavities travel with the flow and experience pressure fluctuations. Under certain conditions, this leads to catastrophic collapse of cavities and generation of intense shear, localized high pressure and temperature zones, and hydroxyl radicals.1−4 These locally extreme conditions are being harnessed for realizing numerous beneficial physicochemical transformations, intensifying a wide range of processes, and developing innovative products. A schematic of the hydrodynamic cavitation phenomenon and its application is shown in Figure 1. A large number of applications of hydrodynamic cavitation have been explored and investigated (see, for example, reviews by Carpenter et al.;5 Holkar et al.6).

Figure 1.

Figure 1

Open in a new tab

Hydrodynamic cavitation—phenomenon and applications.

Most of these applications harness the following key physicochemical effects of cavitation or their combination:

  • Low-pressure region: degassing

  • Local evaporation: descaling

  • Localized high pressure–temperature: pyrolysis, thermal cracking based processes

  • Intense shear: processes based on breakage of bubbles, drops, particles, and microbial cells—aeration, flotation, disinfection, emulsions, and crystallization

  • Hydroxyl radicals: processes based on oxidation, depolymerization, and other radical based reactions—water treatment, biodiesel, organic reaction in and on water, biomass pretreatment

In many applications, such as wastewater treatment;7−11 ozonation;12 microbial disinfection;13−15 desulfurization of fuels;16,17 biomass pretreatment;18,19 and biodiesel synthesis;20,21 the combined influence of all of these physicochemical effects controls the overall performance.

A typical implementation of the hydrodynamic cavitation based application process in practice is shown schematically in Figure 2. The design of the hydrodynamic cavitation device is a key aspect of any such process. Several different types of cavitation devices have been used which may be broadly grouped in two categories: without moving parts and with moving parts. Devices with moving parts like high-speed rotors are typically used for high value products and relatively smaller scale operations. Devices without moving parts are more widely used so far. The devices without moving parts may be further classified into those based on linear or axial flows and those based on swirling flows. Simpson and Ranade22 have discussed these different types of hydrodynamic cavitation devices in detail and have presented their key flow characteristics. In this work, we will not be discussing any specific cavitation device. The focus is on interpreting and modeling overall performance of hydrodynamic cavitation based processes.

Figure 2.

Figure 2

Open in a new tab

Schematic of typical hydrodynamic cavitation based application process.

For a specific hydrodynamic cavitation device and holding tank configuration, overall performance of the hydrodynamic cavitation based process mainly depends on:

  • For batch system: net flow, q is zero, and key parameters are flow through cavitation device, Q, and batch time, t.

  • For continuous system: key parameter is flow through cavitation device, Q, and net flow rate, q.

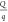The flow rate through the hydrodynamic cavitation device will control the extent of cavitation, and the resulting physicochemical transformations per pass through the device and batch time or net flow will determine the collective influence of the number of passes through the device (Inline graphic or Inline graphic). Besides, these may affect other system-specific parameters such as pH, temperature, downstream pressure, reactivity of chemical species with hydroxyl radicals, and so on. It is essential to develop an appropriate modeling framework to interpret the experimental results and use for optimization and translation to practice. Various approaches used so far are briefly reviewed and analyzed based on personal experience of applying those for different applications of hydrodynamic cavitation processes. Some comments on the path forward and a desirable (yet speculative at this point of time) approach of combining real-time data and phenomenological models is outlined at the end. The discussion will be useful to researchers and engineers interested in harnessing hydrodynamic cavitation based processes and may stimulate further research toward developing high-fidelity computational models for simulating hydrodynamic cavitation reactors.

2. Current Status of Modeling of Hydrodynamic Cavitation Reactors/Processes

The extreme conditions realized by cavitation and resulting physicochemical transformations encompass a very wide range of spatiotemporal scales: from molecular length and time scales to micron scales of cavity up to reactor/cavitation device scale processes. For these multiple scales spanning orders of magnitude and complexity of underlying physics of phase change and high temperature chemical reactions, predictive models based on first-principles are not yet available. In the absence of such predictive models, process engineers have used myriad different approaches and models for designing hydrodynamic cavitation based processes. The approaches used so far may be broadly classified into three groups: (a) semiempirical models, (b) data-driven models, and (c) physics-based models (see Figure 3). The relative merits and demerits of models falling in these three categories are briefly discussed in the sections 2.1, 2.2 and 2.3 respectively. Some suggestions on improving these models are included.

Figure 3.

Figure 3

Open in a new tab

Alternative modeling approaches used for simulating performance of cavitation reactors.

2.1. Semiempirical Models

In this approach, complex physicochemical transformations occurring in a hydrodynamic cavitation reactor are modeled by using a lumped parameter model. Mainly, two approaches are used for this purpose. In the first approach, all physicochemical transformations are represented by a first order reaction, and a simple pseudo-first order kinetics is used to describe the observed data. Although, in principle, it is possible to use pseudo-nth order kinetics, most of the reports describing experimental data on pollutant degradation using hydrodynamic cavitation have used pseudo-first order kinetics. Several studies are published using this approach.23−26 This approach of using a pseudo-first order rate constant for describing the hydrodynamic cavitation process has been shown to not be appropriate by Ranade et al.27 They had clearly shown that this approach would predict two different values of the effective rate constant for the same hydrodynamic cavitation reactors under the same operating conditions for different volume of the holding tank (kapp = 1.06 × 10–3 min–1 for 0.005 m3 volume in the holding tank and kapp = 2.41 × 10–4 min–1 for 0.024 m3 volume in the holding tank). It is unphysical to expect dependence of the effective rate constant on the volume of the holding tank! It therefore preferrable to use a per-pass performance factor to characterize the hydrodynamic cavitation reactor which will solely depend on the design of the reactor and operating conditions. The per-pass performance factor was used by Sarvothaman et al.9 in which an empirical parameter, Φ, was used to represent per-pass performance of the hydrodynamic cavitation reactor. The process described schematically in Figure 2 can then be described using the per-pass factor as

2.1. 1

where V is the volume of liquid in the holding tank, q is net flow rate, Q is flow rate through the hydrodynamic cavitation reactor and C is characteristic of interest–like concentration for water treatment or extraction application, particle or drop size for size reduction applications and so on (with appropriate units). The value of Φ is obtained from experimental data and used for interpretation, design, and optimization. Generally, eq 1 is rewritten in terms of number of passes through cavitation reactor rather than time by using 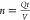Inline graphic where n is number of passes. Assuming the per-pass performance factor remains constant over the range of number of passes, for batch system, a simple relationship like the following is obtained:

2.1. 2

For a continuous mode of operation, at a steady state, performance equation becomes

2.1. 3

where Cin is the inlet concentration and β is a ratio of flow rate through cavitation device (Q) and net flow rate (q). The β in a continuous process is approximately analogous to the number of passes, n in the batch process. Using eq 3, the flow rate through the cavitation reactor can be estimated from the desired extent of transformation (C/Cin) and system specific value of per pass performance factor (for a given device and operating conditions). Experimental data obtained with the batch system and eq 2 may be used to estimate per-pass performance factor. The approach has been extended for non-isothermal operation (Sarvothaman et al.9) or varying per-pass performance factor (Ranade et al.27). It was shown to be useful to describe the experimentally observed performance data. As an example, the results presented by Ranade et al.27 where they used the per-pass performance factor for describing pollutant degradation by hydrodynamic cavitation over four different scales of hydrodynamic cavitation reactor are shown in Figure 4. In this work, Ranade et al.27 used vortex diode as a hydrodynamic cavitation device for treating water containing 2,4-dichloroaniline (DCA)—an aromatic compound with multiple functional groups, as a model pollutant. Degradation of DCA in water was performed over four different scales of cavitation reactors with characteristic throat dimension, d, as 3, 6, 12, and 38 mm with scale-up of almost 200 times based on the flow rates (1.3 to 247 LPM). The per-pass factor was found to vary with the number of passes and with the scale of the hydrodynamic cavitation reactor. Ranade et al.27 developed the suitable per-pass factor model and showed that the following equation describes the experimental data over four scales adequately:

2.1. 4

where Φ0 is the initial per-pass degradation factor and φ∞ is the per-pass factor for the infinitely large cavitation device. The β is a fitted parameter. For the case of DCA, Ranade et al.27 have reported the value of Φ∞ as 1.5 × 10–4 and β as 10.85. It can be seen that the model is able to describe the experimental data reasonably well.

Figure 4.

Figure 4

Open in a new tab

Per-pass model for describing data over four different scales (from Ranade et al.27). Devices—D1:3 mm, 1.2 LPM; D2:6 mm, 5 LPM; D3:12 mm, 20 LPM; D4:38 mm, 200 LPM. Reprinted from ref (27), copyright 2021, with permission from Elsevier.

Following the methodology presented here, the approach may be extended to cases where other mechanisms like pyrolysis or intense shear are predominant. The per-pass performance factor allows comparison of various hydrodynamic cavitation devices on a uniform basis and is recommended. The approach requires experimental data to obtain quantitative estimation of per-pass performance factor. Once the relevant per-pass performance factor is obtained from the data, it allows a possibility of developing correlations of per-pass performance factor with key operating parameters and thereby opens up an opportunity for process optimization. More importantly, the per-pass performance approach also opens up a possibility of developing physics based models for estimating per-pass performance factors. The physics based models may not be as accurate as data-driven or semiempirical models for describing experimental data. However, such models will enhance our understanding and can provide new insights beyond available experimental data. Physics based models are briefly discussed in section 2.3.

2.2. Data-Driven Models

Considering the complexity of various physicochemical processes occurring in hydrodynamic cavitation reactors, attempts have been made to use purely data-driven approaches to describe the performance of hydrodynamic cavitation reactors. While several data-driven modeling formalisms are available, the artificial neural network (ANN) appears to be suitable for describing performance of hydrodynamic cavitation based processes (see, for example, recent application by Ranade et al.28).

ANNs are capable of describing complex relationships.29,30 Typical applications of ANNs use large data sets.31 However, experiments based on hydrodynamic cavitation are complex, require larger quantities of materials, are time-consuming, and are therefore expensive. Naturally the data available from hydrodynamic cavitation based experiments is rather limited. This may lead to overfitting where the ANN model captures relationships that do not exist and often leads to unphysical interpolation and extrapolation results. To avoid overfitting, it is advisable to start with as simple an ANN architecture as possible. Typically ANN models with a single hidden layer provide a good starting point.32 A general rule of thumb for deciding the maximum number of neurons in a hidden layer (assuming 70% of the available data is used for training) may be written as

2.2. 5

Here Ndata is the number of experimental data points available and Nin and Nout are the number of input and output variables. It is recommended that several ANN models with variable numbers of neurons be developed using this guidance. The performance of these models can be evaluated using the test data (30% data which was not used for training). Various statistical parameters may be used for quantifying the performance. Typically, the coefficient of determination, R2, and mean square error, MSE, of test data are used for performance evaluation (Himmelblau31). It should be highlighted here that appropriate data cleaning and conditioning techniques may have to be used before the experimental data can be used for training. It is also recommended to use prior knowledge or known initial and boundary conditions relevant to hydrodynamic cavitation based applications to artificially augment the experimental data for reinforcing training of ANN models to ensure that limiting cases are well captured.

Ranade et al.28 have recently presented development of the ANN model for describing results for two very different applications of hydrodynamic cavitation: pretreatment of waste biomass for enhancing biogas yield and degradation of organic pollutants in water. ANN models with a single hidden layer were used. The developed ANN models were shown to capture the experimental data quite well (see Figure 5). While the experimental data was captured quite well within its range, the extrapolated biomethane generation with respect to time showed unphysical trends. The ANN model however showed excellent performance and the ability to interpolate within the range of experimental data. While such models can be used for effective interpolation, the models cannot provide insights beyond the available experimental data and are not very useful for extrapolation. This is not surprising considering the black box nature of the ANN approach. Semiempirical models may be used to complement such fully data-driven models.

Figure 5.

Figure 5

Open in a new tab

Comparison of simulated (lines) and experimental (symbols) data. (a) Simulated bio-methane generation at four different numbers of passes (n). (b) Simulated DCA degradation profiles at four scales of HC reactor Cavitation device: Vortex diode; d is a throat diameter of the vortex diode. Reprinted from ref (27), copyright 2021, with permission from Elsevier.

The data-driven approach was also shown recently to be useful for scale-up of vortex based cavitation devices.33 In this example, Ranade et al.33 extracted key features from the acquired acoustic signals emanating from the vortex based cavitation devices and related these extracted features with the observed performance at different scales. The approach of per-pass performance factor was used for establishing the relationship between the performance and extracted features as follows:

The per-pass degradation factor (Φ) was related to extracted feature, flatness (F):

2.2. 6

where Φ is per-pass performance factor and F is flatness of acquired acoustic signals (see Ranade et al.33 for more details). The subscript ∞ denotes infinite scale-up. The approach was able to capture the influence of the device scale via extracted feature F, from acquired acoustic signals from different scales. While such semiempirical or fully data-driven models are useful, rigorous mathematical models based on first-principles are necessary for gaining better insight into underlying processes and making “a priori” predictions. Attempts to develop such physics-based models are briefly discussed in the following section.

2.3. Physics-Based Models

The processes based on hydrodynamic cavitation essentially use generated shear, localized hot spots, and hydroxyl radicals for realizing various physicochemical transformations. It is therefore essential to develop an ability to make “a priori” predictions of these as a function of device design and operating parameters. Despite attempts for more than a century (may be starting with Rayleigh34), quantitative simulations of overall performance of hydrodynamic cavitation devices/processes are still elusive without the use of adjustable parameters. The main reason for this is the coexistence of relevant time scales and length scales spanning several orders of magnitude ranging from radicals and molecules to micron-size cavities and tens of centimeters scale cavitation devices. Performance of any hydrodynamic cavitation reactor or process depends on a variety of subprocesses such as

  • Location, rate of generation, and trajectories of cavities: these depend on design of cavitation reactor, flow rate, pressure, temperature, dissolved gases, etc.

  • Collapse of cavities and associated physicochemical effects: as cavities are generated and carried away by flowing fluid, cavities experience pressure fluctuations, and under certain circumstances, these cavities violently collapse. The collapse generates localized very high pressures and temperatures as well as very intense shear, high velocity jets, and shocks. The location, number, and intensity of collapsing cavities will be a crucial factor determining the reactor performance.

  • Contact of collapsing cavities and application process of interest: Depending upon the application of interest, the effectiveness of this contact may depend on variety of factors like pH, hydrophobicity, and time scales of contact in addition to the factors mentioned in the above two points.

A wide range of spatiotemporal scales, from a single cavity (∼10–6 m, ∼10–4 s), cluster of cavities (10–3 m scale, ∼10–3 s), and cavitation reactor scale (∼100 m, ∼10–1 s), coexist. Therefore, a single comprehensive model to simulate the overall performance of hydrodynamic cavitation-based processes is very difficult to realize. More often than not, individual components are modeled separately and applied collectively to draw useful results, typically called multilayer models. Unlike multiscale models where information exchange across different scales occurs via a formal framework (see, for example, Vlachos;35 van den Akker;36 Ge et al.;37 and a more recent one by Radhakrishnan38 and references cited therein), the multilayer models (Ranade;39 Ranade and Utikar40) employ ad-hoc and heuristic based ways for exchanging information across different scales. For complex physicochemical processes like hydrodynamic cavitation, at present, it is more pragmatic to develop a multilayer modeling strategy for design, optimization, and scale-up of hydrodynamic cavitation reactors. The overall approach to develop such a multilayer model is shown in Figure 6.

Figure 6.

Figure 6

Open in a new tab

Multilayer modeling approach to simulate performance of hydrodynamic cavitation reactor.

The microscale flow processes of cavity collapse need to be combined with device/reactor scale flow processes to develop a model for simulating the overall performance of cavitation processes. Cavity dynamics models use boundary conditions in terms of concentrations, temperature, turbulent pressure fluctuations for calculating a localized high temperature and pressure zone, intense shear, hydroxyl radicals, as well as pyrolysis products produced during the collapse event. The cavity collapse models provide source terms for device scale flow models which may then be used for estimating the number of cavitation events (per unit volume, per unit time). The combined information about number of cavitation events and physicochemical transformations associated with an individual cavitation event can then be used for estimating an overall per-pass performance factor for the cavitation device/reactor under consideration. These individual modeling layers are briefly discussed in the following.

2.3.1. Cavity Dynamics Models

Several different approaches may be used for simulating a collapse of a single cavity. Key approaches may be broadly grouped as (a) one-dimensional models based on Rayleigh-Plasset equations or their variants (for example, Pandit et al.4); (b) multidimensional CFD based models. Several different approaches like volume of fluid (for example, Orthaber et al.41), smooth particle hydrodynamics (for example, Patiño-Nariño et al.42), and lattice Boltzman (for example, Shan et al.43) have been used for simulating multidimensional cavity collapse simulations. Some attempts are also made using molecular dynamics (Wei et al.44). Considering the extreme pressure and temperature generated during cavity collapse and associated uncertainties in estimating physicochemical properties, one-dimensional models of cavity collapse based on the Rayleigh-Plasset type of equations appear to be a pragmatic choice at the moment.

Recently, Pandit et al.4 have critically reviewed different variants of the Rayleigh-Plasset type of equations used for simulating cavity dynamics and have presented simulated results on jet velocity, hammer pressure, and hydroxyl radicals over the wide parameter space covering ambient temperature, pressure, amplitude, and frequency of pressure fluctuations and initial cavity radius. A sample of their results on hydroxyl radicals are reproduced in Figure 7. The Blake threshold showed in this figure defines a minimum pressure amplitude ratio (with respect to ambient pressure) required for the onset of cavitation. This is a function of various parameters such as frequency of pressure fluctuations and initial size of the cavity. OHG stands for generation rate of OH radicals. Figure 7a,b shows the contours of OHG as a function of driving frequency and initial bubble radius, respectively, for a range of pressure amplitude ratio (with an emphasis on the region above the Blake threshold). It should be noted that the driving frequency and pressure amplitude relevant for hydrodynamic cavitation are not externally set like in ultrasonic cavitation. Instead, the driving frequency and pressure amplitude depend on the realized turbulent flow field and may vary within the hydrodynamic cavitation reactor/device. The amplitude and frequency of turbulent pressure fluctuations can be estimated by solving the appropriate turbulence model. For example, Sarvothaman et al.45 have used averaged values of turbulent kinetic energy (kR) and turbulent frequency (ωR) in the cavity collapse region R for estimating pressure fluctuations experienced by cavities (see discussion in section 2.3.2 and eq 7). Kanthale et al.46,47 have developed an approach to account for the influence of neighboring cavities on the collapsing cavity cluster. By combining the estimated active volume of cavitation and physicochemical effects realized by collapsing cavities (like generation of hydroxyl radicals or shear), the overall macroscopic performance such as degradation of organic pollutants or size reduction might be estimated. The physicochemical effects of cavity collapse (like generation of hydroxyl radicals or shear) can be used for estimating the macroscopic performance such as degradation of organic pollutants or size reduction. Attempts have been made to develop empirical correlations based on the results of detailed cavity dynamic models. For example, Gogate and Pandit48 have presented an empirical correlation for cavity collapse pressure as a function of orifice configuration and inlet pressure. Kanthale et al.47 presented correlations of collapse pressure and active cavitation volume. Tao et al.49 have reported a correlation of generated hydroxyl radicals. Though these studies showed promise, their applicability was rather restricted. Considering strong nonlinearities and complex underlying physics, artificial neural network (ANN) based models may be more suitable for developing useful relationships among the key design and operating parameters and the realized performance of HC based applications.

Figure 7.

Figure 7

Open in a new tab

Contour plots (plotted with Blake threshold) of the logarithm of •OH generation for hydrodynamic cavitation as a function of the pressure amplitude ratio (from Pandit et al.4). Reprinted with permission under a Creative Commons CC BY 4.0 License from ref (4). Copyright 2021 Elsevier.

Either the full RP-like equations or ANN-like models constructed based on simulated results may be used for developing a full multilayer model indicated in Figure 6. That kind of implementation however requires inputs from computational flow models, which are discussed in the following.

2.3.2. Device Scale Flow Models

Computational fluid dynamics (CFD) models allow detailed simulation of three-dimensional, transient flow field of hydrodynamic cavitation devices. Several studies report simulations of turbulent cavitating flows in different cavitation devices. These flow modeling studies may be broadly divided into two groups: the first group focuses on detailed flow characteristics using sophisticated computational fluid dynamics (CFD) models (for example, Ma et al.,50 Hsiao et al.51). However, such studies mainly focus on fluid dynamics and are not concerned with the simulation of overall performance of a cavitation based transformation process. The second group uses rather simplified CFD models but focuses on simulating performance of cavitation reactors. For example, Capocelli et al.52 used a simplified one-dimensional CFD model for flow in cavitating venturi for qualitatively capturing the trend observed in the performance of the cavitation reactor. Pawar et al.53 have used single phase flow simulations at a single operating condition for four hydrodynamic cavitation devices. It is often necessary to choose an intermediate approach between these two broad categories like the one adapted by Sarvothaman et al.45

It is also essential to note that, intricacies of CFD models may have to account for specific designs and their peculiarities while selecting appropriate CFD models. Broadly, there are three types of hydrodynamic cavitation devices:

  • (a)

    Devices based on constriction and linear flows—orifice/venturi: It is essential to capture all the minute geometric details of orifice and venturi configuration. Small geometric changes like sharp versus smooth edge may significantly influence simulated results. Examples of studies reporting flow characteristics of this type of devices are Simpson and Ranade22,54 and Abbasi et al.55

  • (b)

    Devices based on rotor-stator configuration: It is essential to use either a multiple reference frame or sliding mesh approach for simulating flows in rotor-stator devices. See for example, recent attempts to model cavitating flows in rotor–stators: Sun et al.56 and Fu et al.57

  • (c)

    Devices based on swirling flows without any moving parts: Strong swirling flow generated without any moving parts offers additional challenges of potential relaminarization and nonisotropic eddy viscosity to CFD modelers. The advantage of this type of device is that device walls are shielded from collapsing cavities. See, for example, studies by Ranade and co-workers22, 58, and 59.

Such CFD models may be used for obtaining key flow parameters required for estimating the performance of hydrodynamic cavitation devices. The flow field obtained from the CFD models may be used to simulate the inception of cavities and their trajectories by examining turbulent pressure fluctuations, mean pressure field, and vapor pressure at prevailing ambient temperature. The pressure fluctuations and environment experienced by cavities can then be used for solving cavity dynamics models. For the purpose of illustration, some flow results obtained for the case of vortex based cavitation devices considered by Sarvothaman et al.45 are shown in Figure 8. The flow in the vortex based cavitation device was simulated by following the Eulerian–Eulerian model of Simpson and Ranade.22 For the sake of brevity, the discussion is restricted to outlining the approach of Sarvothaman et al.45 rather than presenting the detailed steps. The original paper may be referred for a more detailed explanation. Please note that the Eulerian–Eulerian approach was used by Sarvothaman et al. and coalescence of cavities forming a gas core was not explicitly modeled. Considering this, it is unavoidable to use an approximation for identifying a boundary of the gas core. Ranade39 had reviewed these approximations which have assumed the volume fraction threshold in the range of 0.5–0.66. The choice is rather arbitrary, and Sarvothaman et al.45 had used 0.5 as a threshold. The choice is not expected to change the qualitative behavior of the model.

Figure 8.

Figure 8

Open in a new tab

Sample of simulated results using the CFD model from Sarvothaman et al.45 6 mm cavitation device, throat velocity = 3 m/s, pressure drop = 250 kPa. Reprinted from ref (45). Copyright 2019, with permission from Elsevier.

It can be seen that formation of the gas core is captured correctly by the CFD models. The cavities are generated in this low pressure region at the core of the vortex. These cavities then travel away from the core following the turbulent fluctuations of the flow. The cavity dynamics models indicate that the typical lifetime of cavities is of the order of 10–4 s. This means cavities travel quite a short distance before collapsing (of the order of 10–3 m). The simulated results of the gas volume fraction within the cavitation device can be used to quantify the relevant region for generation and collapse of cavities. Some further assumptions are needed to estimate the volume fraction/number of cavities. Sarvothaman et al.45 used a volume fraction threshold of 0.5 to identify a boundary of gas core and dispersion. Cavities were assumed to be generated on the surface of this identified gas core. The outer boundary of the cavity collapse region was estimated by taking cutoff values of the gas volume fraction as 0.1. These boundaries of the gas core and cavity collapse region based on this assumed cutoff in the gas volume fraction can then be used to estimate the volume fraction of cavities, ϵGR, required for estimating the number of cavitation events.

For estimating the fate of generated cavities, the Lagrangian approach may be used to simulate the motion of cavities within the considered device. The information on pressure fluctuations experienced by such moving cavities obtained from the Lagrangian simulations can then be used with the cavity dynamics models to estimate the collapse of cavities and subsequent generation of shear, hammer pressure, local temperature and pressure, as well as hydroxyl radicals. As seen in Section 2.1, the results of the cavity dynamics model are quite sensitive to the initial size of the cavity. There have been attempts to include the distribution of initial cavity sizes instead of considering a single size cavity. For example, Capocelli et al.52 used a size distribution of initial cavity size, R0, in the range of 20–250 μm. Attempts have been made to qualitatively relate the results of cavity dynamics models with the performance of the cavitation reactor. Sharma et al.60 have developed an empirical correlation for temperature, pressure, and radical generation at collapse as a function of the initial radius of the cavity, the inlet pressure to the HC device, and the diameter of an orifice hole. Unfortunately, the applicability of such correlations is quite restricted and different HC devices are seldom directly comparable (Šarc et al.61). Other potential ways of coupling cavity dynamics models with device scale flow were used by Sarvothaman et al.45 where they have approximated the fluctuations in the bulk pressure experienced by the cavity as

2.3.2. 7

where PB is the pressure experienced by a cavity, Pv is vapor pressure of the liquid, f is an empirical parameter, and kR and ωR are average turbulent kinetic energy and turbulent frequency in the cavity collapse region, R. The rationale behind this approximation was that the cavity collapse time scales are usually quite small, and considering the typical mean velocities in cavitation devices, the distance traveled by cavities until their collapse is rather small. It is therefore reasonable to approximate the values of turbulent kinetic energy and turbulent frequency averaged over the small cavity collapse region, R. It can be seen that the amplitude of pressure fluctuations is proportional to the liquid density and turbulent kinetic energy, and the frequency of pressure fluctuations is directly related to turbulent frequency. These device scale flow results can provide the number of cavities generated in the hydrodynamic cavitation reactor and the subsequent cavitation effect generated via collapsing cavities.

2.3.3. Overall Performance Models

In order to develop a model for simulating overall performance of the hydrodynamic cavitation device/process, it is essential to develop a per-pass performance model for the overall products (hydroxyl radicals/shear) generated within the cavitation reactor. Sarvothaman et al.45 have presented such a model for estimating per-pass pollutant degradation performance. The approach is however quite general and can be extended for other desired transformation process. In this approach, the net change occurring within one pass through cavitation device may be written as

2.3.3. 8

where G is the generation rate of the relevant cavitation effect (for example, hydroxyl radicals for oxidation of organic pollutants or local energy dissipation rate for breakage of suspended particles) and δ is the effectiveness factor measuring the utilization efficiency of cavitation effects in realizing desired transformations.

For degradation of organic pollutants, the source term appearing in eq 1 is related to phyisco-chemical effects of collapsing cavities, and therefore the per-pass degradation factor may be written as

2.3.3. 9

Considering that a typical lifetime of radicals is much smaller than the residence time of the cavitation device, it is reasonable to assume that all the hydroxyl radicals generated in the cavitation device are consumed within the device and the downstream pipe. It should be noted that hydroxyl radicals are highly reactive and react unselectively with organic pollutants as well as any other reactive species including water itself. Therefore, only a fraction of generated radicals (say, δ) will be used for degrading the pollutant. This fraction may be written as

2.3.3. 10

where k2 and kS are rate constants of reactions between pollutant, C, and other scavengers, CS, with hydroxyl radicals, respectively. The per-pass degradation factor can then be related to the generation rate as

2.3.3. 11

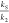For low concentrations of pollutant (C ≪ CS), the value of per-pass degradation factor will depend on G and the ratio (Inline graphic). It will not depend on pollutant concentration. Increase in the relative rate constants of scavengers and pollutant (Inline graphic) leads to reduction in the per-pass degradation factor.

The radical generation rate, G, depends on the number density of cavitation events and the generation of hydroxyl radicals per collapsing cavity (which will be function of intensity of cavity collapse). Number density and collapse intensity of generated cavities are determined by flow characteristics of the cavitation device. The generation rate of hydroxyl radicals, G (typically expressed in micromoles per second) may be written as

2.3.3. 12

where n is the number of cavities collapsing per second in the cavitation device and mOH is hydroxyl radicals generated per collapse. The value of mOH depends on variety of parameters such as initial radius of the cavity and bulk pressure fluctuations experienced by the cavity. In order to account for the distribution of initial radii of cavities and varied pressure fluctuations experienced by all the cavities, a proportionality factor needs to be introduced in eq 12. Assuming that the number density of cavities is proportional to the volume fraction of vapor, one may write the per-pass factor as

2.3.3. 13

where α is a proportionality constant. The concentration of scavangers may be assumed as constant and may be lumped with the proportionality constant. For the sake of dimensional consistency, CS may be assumed to be 1 kmol/m3. Equation 13 provides a direct link between the key flow characteristics of the cavitation device/reactor and the overall performance of the cavitation reactor. The values of vapor volume fractions appearing in eq 13 may be obtained from CFD models of the cavitation device. COH may be estimated by solving cavity dynamics models. It should be noted that the mathematical modeling framework described here still requires information about initial cavity size for estimating values of the per-pass degradation factor! The value of initial cavity size (or size distribution) is rather difficult to estimate. It may therefore be practical to treat the initial cavity size as an adjustable parameter. With such an approach, Sarvothaman et al.45 were able to simulate influence of pressure drop across the vortex based cavitation device on the degradation performance of the device. Their results are shown in Figure 9 for illustrating the potential of this approach.

Figure 9.

Figure 9

Open in a new tab

Influence of throat velocity on performance of cavitation reactor. Reprinted from ref (45). Copyright 2019, with permission from Elsevier.

Most of the discussion on modeling so far was focused on degradation of organic effluents using hydrodynamic cavitation with an exception of the ANN based modeling of biomass pretreatment data. New applications of hydrodynamic cavitation are continuously evolving. For example, hydrodynamic cavitation is used for making emulsions (Ramisetty et al.,62 Thaker and Ranade59), for enhancing liquid–liquid reactions and extractions (Surywanshi et al.16), controlling particle size distribution in crystallization (Madane and Ranade63), and enhancing extraction of bioactives from algae (Mittal and Ranade, unpublished work). It is important to extend the modeling approaches discussed here to such a variety of applications. Hydrodynamic cavitation is used either for reducing some characteristic variable (such as pollutant concentration or droplet size) or for enhancing some characteristic variable (such as concentration of extractant or biogas generation rate). Overall performance behavior of a typical hydrodynamic cavitation based application is shown schematically in Figure 10; where R is a desired result which either needs to be reduced or enhanced via hydrodynamic cavitation, φ is per-pass performance factor and n is number of passes. As shown in Figure 10, performance of any typical hydrodynamic cavitation based application can be analyzed by using suitable normalization. When HC is used for reducing certain characteristics, it is recommended to use normalized performance variable as 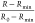Inline graphic. The subscripts 0, min, and max denote initial, minimum, and maximum value of expected result R. When HC is used for enhancing certain characteristics, it is recommended to use the normalized performance variable as Inline graphic. It can be seen that the proposed normalization facilitates relating the normalized performance with number of passes.

Figure 10.

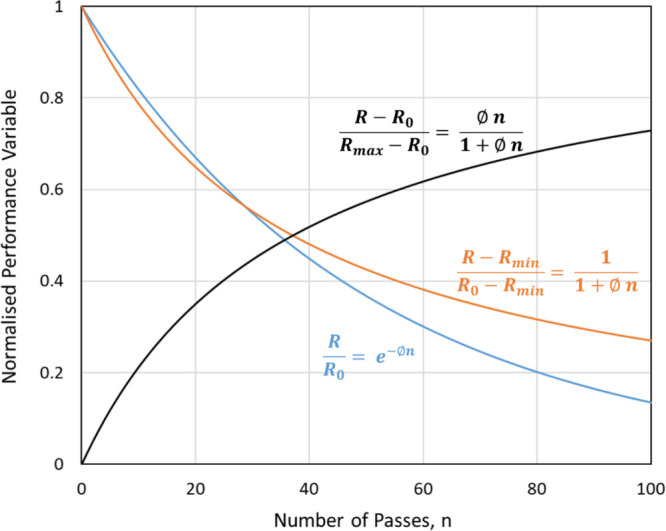
Figure 10

Open in a new tab

Typical behavior of a normalized performance variable of HC application R is a desired result; subscripts 0, min, and max denote initial, minimum, and maximum value of R.

When per-pass performance factor is small, simplified linear approximations indicated in Figure 10 may be used to describe the observed performance. When applying to pollutant degradation, theoretical minimum concentration for a pollutant may be considered as zero (Rmin = 0). This assumes that all the subsequent degradation products are also degraded via HC. In some pollutants, the degradation products may not be susceptible to further degradation. In such cases, Rmin will have a finite value. For droplet size reduction, typically, there will be a minimum achievable droplet size for a given system and intensity of cavitation. In such a case, typically the following equation may be used for describing droplet size reduction via hydrodynamic cavitation:

2.3.3. 14

In some cases, where cavitation as well as other mechanisms of droplet breakage are active, additional factors and parameters may have to be included in eq 14.

When HC is used for enhancing interphase mass transfer in multiphase processes (such as liquid–liquid extraction), the enhanced extractant concentration may be described as

2.3.3. 15

where C is the concentration of extractant and subscripts 0 and e denote initial and equilibrium (which is a maximum concentration) concentration of extractant.

Once the per-pass performance factor based equations are formulated for the application under consideration (like eq 14 or 15), the approach discussed in section 2.3.3 can be extended for the performance characteristic under consideration. Instead of relating the per-pass performance factor to the generation rate of hydroxyl radicals as in eq 11, the corresponding physical mechanisms controlling the process can be estimated from the device scale flow models and cavity dynamics models. For the case of droplet breakage, the per-pass breakage performance may be related to the number of cavities generated, the probability of collision between collapsing cavities and droplets, and the intensity of collapse (shear and hammer pressure generated via collapse). Thus, the combination of the per-pass performance model, cavity dynamics model, and device scale flow models may allow simulation of the overall performance of HC-based application. In some cases, direct formulation of the phenomenological model for estimating the per-pass performance factor is difficult; the use of physics informed machine learning might be used. The approach described here is quite powerful and has the potential to make high-fidelity computational models for simulating and optimizing hydrodynamic cavitation devices and processes. Significant further work on improving our ability to simulate cavitating flows and particularly developing “performance” models relating observable performance with cavity collapse conditions is needed. Some of these needs are briefly discussed in the following section.

3. Modeling of Hydrodynamic Cavitation Reactors/Processes: Path Forward

Application of semiempirical models based on pseudo rate constant or per-pass performance factor approach are commonly used in published studies of hydrodynamic cavitation. As discussed in section 2.1, the per-pass performance factor approach is recommended over the pseudo rate constant approach, since it provides a framework to capture the per-pass performance of the cavitation device without any extraneous influences of the holding tank, etc. However, use of the per-pass performance factor approach alone is not very useful for gaining insights or extrapolation of results. It has been observed that the per-pass performance factor is influenced by the design of the cavitation device, the pressure drop across the cavitation device, the downstream pressure, the operating temperature, the pH, and many other process parameters (see, for example, Ranade et al.64). Wu et al.65,66 presented results of degradation of chlorocarbons with hydrodynamic cavitation and highlight the role of solubility and hydrophobicity of organics on effectiveness of degradation. Their results showed that species which are more soluble and hydrophobic tend to accumulate at the cavity surface and are therefore more susceptible for degradation. The per-pass performance factor exhibits an optimum behavior (see, for example, Figure 9) with respect to many operating parameters (for example, pressure drop or flow rate, and temperature). Increase in flow rate (or pressure drop) and temperature results in the increase in the number density of generated cavities. However, the enhanced volume fraction of the gas phase leads to enhanced compressibility of the gas–liquid mixture, which leads to reduced intensity of collapse (lower collapse temperature and hydroxyl radical generation) and therefore lower degradation performance. The per-pass performance factor of geometrically similar devices often decreases with an increase in scale of the cavitation device (Ranade et al.27). It is therefore essential to augment the simplified semiempirical models with data-driven and physics-based models.

The data-driven approaches, which are briefly discussed in section 2.2, look promising. The approach and examples illustrated in Figure 5 can be adapted for many other applications of hydrodynamic cavitation. Thaker and Ranade59 used a vortex-based cavitation device for producing liquid–liquid emulsions. Madane and Ranade63 recently showed potential applications of hydrodynamic cavitation for manipulating the crystal size distribution in antisolvent crystallization. The droplet or crystal size distribution data from such applications may be related to key design and operating parameters using standard machine learning tools. Ranade et al.64 summarized the influence of various parameters such as the chemical nature of pollutants, pH, pKa, operating temperature and pressure, cavitation device design, etc., on the per-pass performance for degradation of organic pollutants. Machine learning approaches are best suited for such compiled data and for extracting useful features from it for establishing useful relationships for guiding the design and operation. However, it should be highlighted that not all the published studies report all the relevant parameters so as to connect observed results with per-pass performance of the considered cavitation device. It is important to insist on reporting all the relevant design and operating parameters for facilitating and realizing the potential of machine learning approaches for enhancing hydrodynamic cavitation based applications. Availability of data (quality and quantity) often constrains widespread applications of the surrogate models discussed in section 2.2. It should be noted that the surrogate models generally fail to extrapolate beyond the training data. One potential way to overcome these limitations is to use real-time data from online sensors for developing data-driven models. Recent advances in nonlinear data processing and machine learning open entirely new opportunities to analyze and extract useful information from the real-time spatiotemporal data. Ranade et al.33 were able to identify the inception and extent of cavitation using acoustic data emanating from cavitation devices. Though the data-driven machine learning approaches are having a transformative impact on the sciences, for making further progress toward development of predictive models, it is essential to develop physics-based models.

The overall approach for developing physics-based models to simulate applications based on hydrodynamic cavitation is shown in Figure 6 (in section 2.3). There is significant scope to develop improved models of various components shown in this approach. Apart from an appropriate formulation of model equations based on first-principles, further work on quantifying the influence of numerical issues such as grid spacing, time step, degree of convergence, and so on, simulated results are also needed for high-fidelity simulations of real-life applications of hydrodynamic cavitation. In this section, we will restrict the discussion to potential improvements on physical aspects of modeling and will leave out numerical aspects.

The current understanding of a variety of physicochemical transformations occurring via inception, growth, and collapse of cavities (and their interaction with the surroundings) is inadequate. Most of the cavity dynamics models are still based on the classical Rayleigh–Plesset (RP) cavity dynamics model (Pandit et al.4) which assumes a cavity in an infinite medium (that is symmetric expansion and collapse). In reality, most cavities will undergo asymmetric collapse because of surrounding cavities and other disturbances. It is therefore essential to develop quantitative models for simulating asymmetric cavity collapse and subsequent physicochemical transformations. Recently, Orthaber et al.67 used a volume of fluid (VOF) method for simulating asymmetric collapse of a cavity near a liquid droplet. These simulations were two-dimensional and axis-symmetric. It is essential to develop fully asymmetric, three-dimensional transient flow models necessary for quantitative predictions of physicochemical transformations caused by asymmetric cavity collapse. One of the promising options for this appears to be a Pseudophase Lattice Boltzmann (PPLB) approach. The PPLB approach naturally captures phase separation and interface formation/collapse without requiring front tracking methods (Chen et al.68) and therefore may have the potential to realize a breakthrough in understanding inception, growth, and collapse of cavities. Su et al.69 and Shan et al.43 have used the PPLB approach to carry out three-dimensional simulations of collapsing cavities. Recently, Trummler et al.70 used full 3D CFD simulations using the VOF approach to understand the influence of nearby surfaces (either rigid or flexible) on cavity collapse. Rasthofer et al.71 simulated a collapse of a cluster of cavities. Such VOF or PPLB based approaches with full 3D simulations will hopefully provide better insights and quantitative information on asymmetric cavity collapse and resulting physicochemical transformations.

Besides such microscale simulations of cavities, several attempts have been made to develop new cavitation models. For example, a new cavitation model based on intercavity interactions has recently been presented by Shi et al.72 For improving the state of the art on modeling hydrodynamic cavitation devices, further research and better models are necessary in the following areas:

  • Source terms for modeling extent of cavitation: The models used in most of the CFD simulations of hydrodynamic cavitation devices use overly simplified cavity dynamics models for formulating source terms representing mass of liquid evaporated or condensed during cavitation. Better models to represent complex phase change processes are needed, and a unified framework to reconcile differences and similarities of different cavitation models is needed.

  • Turbulence modeling: State of the art understanding and models representing influence of turbulence, vortices, and other coherent structures on inception and extent of cavitation is not adequate. This is especially relevant in the presence of dissolved gases or dispersed phase particles (solid, liquid, or gas).

  • Models for representing physical effects of collapsing cavities: As mentioned earlier, collapsing cavities generate high-speed jets, shear, and hammer pressure, which may be harnessed for particle breakage, cleaning, and other applications. The currently available cavity dynamics models are mostly restricted to collapse of a single cavity. Further work on extending these models to account for influence of neighboring cavities, dispersed phase particle, or wall is important and essential. More importantly, further work on representing such local effects generated by collapsing cavities in device scale simulations is needed.

  • Models for representing chemical effects of collapsing cavities: In addition to physical effects mentioned above, collapsing cavities generate localized hot spots, which may cause radical formation, pyrolysis, and a multitude of radical based reactions in gas phase as well as in surrounding liquid phase. Currently, there are no rigorous models available to represent such local chemical transformations caused by collapsing cavities into device scale flow models. New ways and new models are needed to reasonably represent physicochemical transformations caused by collapsing cavities into macro or device scale models.

The list is merely suggestive. The complexity of reactive multiphase flows occurring in hydrodynamic cavitation devices may greatly expand the list of issues on which further research is needed.

Despite significant research efforts, the quest for developing an adequate understanding and description of transport processes occurring in hydrodynamic cavitation devices/ reactors through models still continues, since the state of the art requires many flow regime and system dependent empirical (or “ad-hoc”) adjustments for adequately representing complex multiscale interactions. The use of such regime and system-dependent ad-hoc models severely restricts our ability to use the models for optimizing hydrodynamic cavitation based applications. A completely different approach is needed to realize a breakthrough in our ability to accurately predict, manipulate, and control multiphase transport processes occurring in different applications of hydrodynamic cavitation. Here we would like to suggest a radically different approach which synergistically combines real-time spatiotemporal data, machine learning, and physics based models to provide a new and significantly improved methodology for predicting and optimizing the performance of hydrodynamic cavitation devices and applications. The suggested approach is shown in Figure 11.

Figure 11.

Figure 11

Open in a new tab

Conceptual framework for combining data, machine learning, and physics based models for simulating hydrodynamic cavitation based applications.

The approach is based on a key hypothesis that the real-time spatiotemporal data captures key multiscale interactions and therefore can be deciphered to discover closure models, which will allow simulation of multiphase reacting systems over a wide variety of flow and reaction regimes without any regime or system dependent ad-hoc adjustments. The approach is speculative at the moment. However, several indications may make this approach successful. Recent advances in nonlinear data processing and machine learning open new opportunities to analyze and extract useful information from real-time spatiotemporal data. Several inexpensive and noninvasive sensors such as acoustic sensors or pressure sensors are now available which may be harnessed for acquiring real-time spatiotemporal data. Such data captures all the relevant information about flow regimes, turbulence, dispersed phase particles, interphase transport, and inherent system characteristics. Ranade et al.33 have recently shown a feasibility of relating features extracted from such a data to performance of hydrodynamic cavitation process. The data-driven machine learning approaches are making a transformative impact on the sciences. Though many of these approaches are based on surrogate models which may fail to extrapolate beyond the training data, these may be synergistically combined with the physics based models (with governing equations in the form of differential equations) to gain new insights and understanding as well as to accurately predict and optimize dynamical systems. The real breakthrough may be achieved if we can extract high-fidelity closure models from such spatiotemporal data which do not require ad-hoc flow regime and system dependent adjustments. Some efforts have been made to use detailed microscale simulations or direct numerical simulations and machine learning approaches to identify parameters of the assumed closure models.73−77 None of the approaches includes the discovery of appropriate forms of closure equations; instead, they focus on estimation of parameters. There have been some attempts to extract governing equations from data using machine learning approaches.78−81 Such machine learning based approaches which are informed via rigorous interface-resolved microscale models discussed earlier in this section may allow us to develop the desired high-fidelity models for simulating applications based on hydrodynamic cavitation over a wide range of operating conditions and systems under consideration. Such an ambitious ensemble approach is now possible because of the recent advances in (1) GPU based solvers that allow extensive particle resolved simulations within tractable times (Petrone82), (2) feature extraction methods that may enable unraveling of multiscale signatures embedded in the spatiotemporal data (Sharma et al.83), and (3) machine learning methods including symbolic manipulation (Sivaram and Venkatasubramanian84). Time is now ripe for the development of such a new methodology, which has the potential to bridge the gaps in the current state of the art and enable process innovations to accelerate realization of the full potential of hydrodynamic cavitation in a variety of sectors.

4. Closing Remarks

State of the art computational models are still found to be inadequate for quantitative a priori predictions of complex physicochemical transformations occurring in a hydrodynamic cavitation reactor. In this article, semiempirical, data-driven, and physics based models are briefly reviewed. Data-driven or semiempirical approaches are not useful for scale-up and developing new hydrodynamic cavitation devices/reactors. The state of the art physics based models still require ad-hoc adjustable parameters for describing the observed performance and are not really predictive. We hope that the presented review provides a useful perspective for selecting an appropriate approach for the design and optimization of applications of hydrodynamic cavitation. A potentially promising approach, though speculative at the moment, is outlined here which suggests anchoring of physics based models with real-time data via machine learning. Such truly linked multiscale models may lead to the desired breakthrough in the fundamental understanding of hydrodynamic cavitation reactors.

Acknowledgments

V.R. wishes to acknowledge funding support by Science Foundation Ireland (Grant number: 20/FFP-A/8518) for supporting the work.

Glossary

Notations

C

Characteristic of interest, e.g., concentration

d

Throat diameter of cavitation device, droplet diameter

H

Number of hidden neurons

F

Flatness of acoustic signal

G

Generation rate of desired cavitation effect, e.g., hydroxyl radicals

k

Rate constant

kR

Average turbulent kinetic energy in the cavity collapse region

mOH

Hydroxyl radicals generated per collapse

n

Number of passes through cavitation device

Ndata

Number of data points

Nin

Number of input variables

Nout

Number of output variables

PB

Pressure experienced by a cavity

Pv

Vapor pressure

q

Net flow rate

Q

Flow rate through cavitation device

R

Cavity collapse region, desired performance result

t

Time

V

Volume of liquid in the holding tank

Greek symbols

β

Ratio of flow rate through cavitation device and net flow rate

δ

Effectiveness factor for utilizing generated cavitation effect

ϵGR

Volume fraction of gas phase in cavity collapse region

Φ

Per-pass performance factor

ρ

Density

ωR

Average turbulent frequency in the cavity collapse region

Subscripts

0

At time = 0

2

Second order rate constant between hydroxyl radicals and targeted reacting species

∞

At infinite scale-up

in

Inlet

out

Outlet

S

Scavenger

Acronyms

DCA

Dichloro aniline

HC

Hydrodynamic cavitation

Author Contributions

CRediT: Vivek V. Ranade conceptualization (lead), data curation (lead), formal analysis (lead), funding acquisition (lead), methodology (lead), writing-original draft (lead), writing-review & editing (lead).

The author declares no competing financial interest.

References

  1. Suslick K. S.; Mdleleni M. M.; Ries J. T. Chemistry Induced by Hydrodynamic Cavitation. J. Am. Chem. Soc. 1997, 119 (39), 9303–4. 10.1021/ja972171i. [DOI] [Google Scholar]
  2. Shah Y. T.; Pandit A. B.; Moholkar V. S.. Cavitation reaction engineering; Springer Science & Business Media, 1999. [Google Scholar]
  3. Brennen C. E.Cavitation and bubble dynamics; Cambridge University Press, 2014. [Google Scholar]
  4. Pandit A. V.; Sarvothaman V. P.; Ranade V. V. Estimation of chemical and physical effects of cavitation by analysis of cavitating single bubble dynamics. Ultrasonics Sonochemistry 2021, 77, 105677. 10.1016/j.ultsonch.2021.105677. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Carpenter J.; Badve M.; Rajoriya S.; George S.; Saharan V. K.; Pandit A. B. Hydrodynamic cavitation: an emerging technology for the intensification of various chemical and physical processes in a chemical process industry. Reviews in Chemical Engineering 2017, 33 (5), 433–68. 10.1515/revce-2016-0032. [DOI] [Google Scholar]
  6. Holkar C. R.; Jadhav A. J.; Pinjari D. V.; Pandit A. B. Cavitationally driven transformations: A technique of process intensification. Ind. Eng. Chem. Res. 2019, 58 (15), 5797–819. 10.1021/acs.iecr.8b04524. [DOI] [Google Scholar]
  7. Ranade V. V.; Bhandari V. M. Preface. Industrial wastewater treatment, recycling and reuse 2014, xi. 10.1016/B978-0-08-099968-5.09994-3. [DOI] [Google Scholar]
  8. Ga̧gol M.; Przyjazny A.; Boczkaj G. Wastewater treatment by means of advanced oxidation processes based on cavitation–a review. Chemical Engineering Journal 2018, 338, 599–627. 10.1016/j.cej.2018.01.049. [DOI] [Google Scholar]
  9. Sarvothaman V. P.; Nagarajan S.; Ranade V. V. Treatment of Solvent-Contaminated Water Using Vortex-Based Cavitation: Influence of Operating Pressure Drop, Temperature, Aeration, and Reactor Scale. Ind. Eng. Chem. Res. 2018, 57 (28), 9292–304. 10.1021/acs.iecr.8b01688. [DOI] [Google Scholar]
  10. Joshi S. M.; Gogate P. R. Intensification of industrial wastewater treatment using hydrodynamic cavitation combined with advanced oxidation at operating capacity of 70 L. Ultrasonics Sonochemistry 2019, 52, 375–381. 10.1016/j.ultsonch.2018.12.016. [DOI] [PubMed] [Google Scholar]
  11. Patil P. B.; Bhandari V. M.; Ranade V. V. Wastewater Treatment and Process Intensification for Degradation of Solvents using Hydrodynamic Cavitation. Chemical Engineering and Processing-Process Intensification 2021, 166, 108485. 10.1016/j.cep.2021.108485. [DOI] [Google Scholar]
  12. Gogate P. R.; Mededovic-Thagard S.; McGuire D.; Chapas G.; Blackmon J.; Cathey R. Hybrid reactor based on combined cavitation and ozonation: From concept to practical reality. Ultrasonics Sonochemistry 2014, 21, 590–598. 10.1016/j.ultsonch.2013.08.016. [DOI] [PubMed] [Google Scholar]
  13. Jain P.; Bhandari V. M.; Balapure K.; Jena J.; Ranade V. V.; Killedar D. J. Hydrodynamic cavitation using vortex diode: An efficient approach for elimination of pathogenic bacteria from water. Journal of environmental management 2019, 242, 210–9. 10.1016/j.jenvman.2019.04.057. [DOI] [PubMed] [Google Scholar]
  14. Mane M. B.; Bhandari V. M.; Balapure K.; Ranade V. V. Destroying antimicrobial resistant bacteria (AMR) and difficult, opportunistic pathogen using cavitation and natural oils/plant extract. Ultrasonics Sonochemistry 2020, 69, 105272. 10.1016/j.ultsonch.2020.105272. [DOI] [PubMed] [Google Scholar]
  15. Mane M. B.; Bhandari V. M.; Ranade V. V. Safe water and technology initiative for water disinfection: Application of natural plant derived materials. Journal of Water Process Engineering 2021, 43, 102280. 10.1016/j.jwpe.2021.102280. [DOI] [Google Scholar]
  16. Suryawanshi N. B.; Bhandari V. M.; Sorokhaibam L. G.; Ranade V. V. Developing techno-economically sustainable methodologies for deep desulfurization using hydrodynamic cavitation. Fuel 2017, 210, 482–90. 10.1016/j.fuel.2017.08.106. [DOI] [Google Scholar]
  17. Uebe J.; Kryževičius Ž; Januteniene J.; Žukauskaite A.; Bertašius E.; Rapolavičius R.; et al. Desulfurizing of Pyrolysis Oil of Used Tires Using a 3D-Printed Vortex Diode and Modeling of Process. Journal of Marine Science and Engineering. 2021, 9 (8), 876. 10.3390/jmse9080876. [DOI] [Google Scholar]
  18. Teran Hilares R.; Ramos L.; da Silva S. S.; Dragone G.; Mussatto S. I.; Santos J. C. d. Hydrodynamic cavitation as a strategy to enhance the efficiency of lignocellulosic biomass pretreatment. Critical reviews in biotechnology 2018, 38 (4), 483–93. 10.1080/07388551.2017.1369932. [DOI] [PubMed] [Google Scholar]
  19. Nagarajan S.; Ranade V. V. 2019, Pretreatment of lignocellulosic biomass using vortex-based devices for cavitation: influence on biomethane potential. Ind. Eng. Chem. Res. 2019, 58 (35), 15975–88. 10.1021/acs.iecr.9b00859. [DOI] [Google Scholar]
  20. Maddikeri G. L.; Gogate P. R.; Pandit A. B. Intensified synthesis of biodiesel using hydrodynamic cavitation reactors based on the interesterification of waste cooking oil. Fuel 2014, 137, 285–92. 10.1016/j.fuel.2014.08.013. [DOI] [Google Scholar]
  21. Malani R. S.; Shinde V.; Ayachit S.; Goyal A.; Moholkar V. S. Ultrasound–assisted biodiesel production using heterogeneous base catalyst and mixed non–edible oils. Ultrasonics sonochemistry 2019, 52, 232–43. 10.1016/j.ultsonch.2018.11.021. [DOI] [PubMed] [Google Scholar]
  22. Simpson A.; Ranade V. V. 110th Anniversary: Comparison of Cavitation Devices Based on Linear and Swirling Flows: Hydrodynamic Characteristics. Ind. Eng. Chem. Res. 2019, 58 (31), 14488–509. 10.1021/acs.iecr.9b02757. [DOI] [Google Scholar]
  23. Braeutigam P.; Franke M.; Schneider R. J.; Lehmann A.; Stolle A.; Ondruschka B. Degradation of carbamazepine in environmentally relevant concentrations in water by Hydrodynamic-Acoustic-Cavitation (HAC). Water research 2012, 46 (7), 2469–77. 10.1016/j.watres.2012.02.013. [DOI] [PubMed] [Google Scholar]
  24. Raut-Jadhav S.; Saini D.; Sonawane S.; Pandit A. Effect of process intensifying parameters on the hydrodynamic cavitation based degradation of commercial pesticide (methomyl) in the aqueous solution. Ultrasonics sonochemistry 2016, 28, 283–93. 10.1016/j.ultsonch.2015.08.004. [DOI] [PubMed] [Google Scholar]
  25. Yi C.; Lu Q.; Wang Y.; Wang Y.; Yang B. Degradation of organic wastewater by hydrodynamic cavitation combined with acoustic cavitation. Ultrasonics sonochemistry 2018, 43, 156–65. 10.1016/j.ultsonch.2018.01.013. [DOI] [PubMed] [Google Scholar]
  26. Ye Y.-F.; Zhu Y.; Lu N.; Wang X.; Su Z. Treatment of rhodamine B with cavitation technology: comparison of hydrodynamic cavitation with ultrasonic cavitation. RSC Adv. 2021, 11 (9), 5096–106. 10.1039/D0RA07727E. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Ranade V. V.; Prasad Sarvothaman V.; Simpson A.; Nagarajan S. Scale-up of vortex based hydrodynamic cavitation devices: A case of degradation of di-chloro aniline in water. Ultrasonics Sonochemistry 2021, 70, 105295. 10.1016/j.ultsonch.2020.105295. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Ranade N. V.; Nagarajan S.; Sarvothaman V.; Ranade V. V. ANN based modelling of hydrodynamic cavitation processes: Biomass pre-treatment and wastewater treatment. Ultrasonics sonochemistry 2021, 72, 105428. 10.1016/j.ultsonch.2020.105428. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Panerati J.; Schnellmann M. A.; Patience C.; Beltrame G.; Patience G. S. Experimental methods in chemical engineering: Artificial neural networks–ANNs. Canadian Journal of Chemical Engineering 2019, 97 (9), 2372–82. 10.1002/cjce.23507. [DOI] [Google Scholar]
  30. Venkatasubramanian V. The promise of artificial intelligence in chemical engineering: Is it here, finally. AIChE J. 2019, 65 (2), 466–78. 10.1002/aic.16489. [DOI] [Google Scholar]
  31. Himmelblau D. M. Applications of artificial neural networks in chemical engineering. Korean journal of chemical engineering. 2000, 17 (4), 373–92. 10.1007/BF02706848. [DOI] [Google Scholar]
  32. Heaton J.Introduction to neural networks with Java; Heaton Research, Inc.; 2008. [Google Scholar]
  33. Ranade N. V.; Sarvothaman V.; Ranade V. V. Acoustic Analysis of Vortex-based Cavitation Devices: Inception and extent of cavitation. Ind. Eng. Chem. Res. 2021, 60, 8255–8268. 10.1021/acs.iecr.1c01005. [DOI] [Google Scholar]
  34. Rayleigh L. VIII On the pressure developed in a liquid during the collapse of a spherical cavity. London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 1917, 34 (200), 94–8. 10.1080/14786440808635681. [DOI] [Google Scholar]
  35. Vlachos D. G. A review of multiscale analysis: examples from systems biology, materials engineering and other fluid-surface interacting systems. Advances in Chemical Engineering 2005, 30, 1–61. 10.1016/S0065-2377(05)30001-9. [DOI] [Google Scholar]
  36. Van den Akker H. E. A. Toward A Truly Multiscale Computational Strategy For Simulating Turbulent Two-Phase Flow Processes Ind. Eng. Chem. Res. 2010, 49, 10780–10797. 10.1021/ie1006382. [DOI] [Google Scholar]
  37. Ge; et al. Meso-scale oriented simulation towards virtual process engineering (VPE) the EMMS Paradigm. Chem. Eng. Sci. 2011, 66 (19), 4426–4458. 10.1016/j.ces.2011.05.029. [DOI] [Google Scholar]
  38. Radhakrishnan R. A survey of multiscale modeling: Foundations, historical milestones, current status, and future prospects. AIChE J. 2021, 67, 1–21. 10.1002/aic.17026. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Ranade V. V.Computational Flow Modelling for Chemical Reactor Engineering; Academic Press: London, 2002. [Google Scholar]
  40. Ranade V. V.; Utikar R. P., Ed. Multiphase Flow for Process Industires: Fundamentals and Applications; Wiley, 2022. [Google Scholar]
  41. Orthaber U.; Zevnik J.; Dular M. Cavitation bubble collapse in a vicinity of a liquid-liquid interface-Basic research into emulsification process. Ultrasonics sonochemistry 2020, 68, 105224. 10.1016/j.ultsonch.2020.105224. [DOI] [PubMed] [Google Scholar]
  42. Patiño-Nariño E. A.; et al. Numerical study of single bubble rising dynamics for the variability of moderate Reynolds and sidewalls influence: A bi-phase SPH approach,. Engineering Analysis with Boundary Elements 2021, 129, 1–26. 10.1016/j.enganabound.2021.04.011. [DOI] [Google Scholar]
  43. Shan M.; Zhu Y.; Yao C.; Han Q.; Zhu C. Modeling for Collapsing Cavitation Bubble near Rough Solid Wall by Mulit-Relaxation-Time Pseudopotential Lattice Boltzmann Model. Journal of Applied Mathematics and Physics 2017, 5 (6), 1243–56. 10.4236/jamp.2017.56106. [DOI] [Google Scholar]
  44. Xu W.; Zhu R.; Fu Q.; Wang X.; Zhao Y.; Wang J. Effect of Bubble Collapse Combined with Oxidants on the Benzamide by Molecular Dynamics Simulation. Ind. Eng. Chem. Res. 2022, 61 (17), 5984–5993. 10.1021/acs.iecr.1c05026. [DOI] [Google Scholar]
  45. Sarvothaman V. P.; Simpson A. T.; Ranade V. V. Modelling of vortex based hydrodynamic cavitation reactors. Chemical Engineering Journal 2019, 377, 119639. 10.1016/j.cej.2018.08.025. [DOI] [Google Scholar]
  46. Kanthale P. M.; Gogate P. R.; Pandit A. B.; Wilhelm A. M. Cavity cluster approach for quantification of cavitational intensity in sonochemical reactors. Ultrason. Sonochem. 2003, 10, 181–189. 10.1016/S1350-4177(03)00088-9. [DOI] [PubMed] [Google Scholar]
  47. Kanthale P. M.; Gogate P. R.; Pandit A. B.; Wilhelm A. M. Dynamics of cavitational bubbles and design of a hydrodynamic cavitational reactor: cluster approach. Ultrasonics Sonochemistry 2005, 12 (6), 441–452. 10.1016/j.ultsonch.2004.05.017. [DOI] [PubMed] [Google Scholar]
  48. Gogate P. R.; Pandit A. B. Engineering design methods for cavitation reactors II: hydrodynamic cavitation. AIChE journal 2000, 46 (8), 1641–9. 10.1002/aic.690460815. [DOI] [Google Scholar]
  49. Tao Y.; Cai J.; Huai X.; Liu B. Global Average Hydroxyl Radical Yield throughout the Lifetime of Cavitation Bubbles. Chem. Eng. Technol. 2018, 41 (5), 1035–42. 10.1002/ceat.201700153. [DOI] [Google Scholar]
  50. Ma J.; Hsiao C.-T.; Chahine G. L. A physics based multiscale modeling of cavitating flows. Computers & fluids 2017, 145, 68–84. 10.1016/j.compfluid.2016.12.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Hsiao C.-T.; Ma J.; Chahine G. L. Multiscale tow-phase flow modeling of sheet and cloud cavitation. International Journal of Multiphase Flow 2017, 90, 102–17. 10.1016/j.ijmultiphaseflow.2016.12.007. [DOI] [Google Scholar]
  52. Capocelli M.; Musmarra D.; Prisciandaro M.; Lancia A. Chemical effect of hydrodynamic cavitation: simulation and experimental comparison. AIChE J. 2014, 60 (7), 2566–72. 10.1002/aic.14472. [DOI] [Google Scholar]
  53. Pawar S. K.; Mahulkar A. V.; Pandit A. B.; Roy K.; Moholkar V. S. Sonochemical effect induced by hydrodynamic cavitation: Comparison of venturi/orifice flow geometries. AIChE J. 2017, 63 (10), 4705–16. 10.1002/aic.15812. [DOI] [Google Scholar]
  54. Simpson A.; Ranade V. V. Modelling of hydrodynamic cavitation with orifice: Influence of different orifice designs. Chem. Eng. Res. Des. 2018, 136, 698–711. 10.1016/j.cherd.2018.06.014. [DOI] [Google Scholar]
  55. Abbasi E.; Saadat S.; Jashni A. K.; Shafaei M. H. A novel method for optimization of slit Venturi dimensions through CFD simulation and RSM design. Ultrasonics sonochemistry 2020, 67, 105088. 10.1016/j.ultsonch.2020.105088. [DOI] [PubMed] [Google Scholar]
  56. Sun X.; You W.; Xuan X.; Ji L.; Xu X.; Wang G.; Zhao S.; Boczkaj G.; Yoon J. Y.; Chen S. Effect of the cavitation generation unit structure on the performance of an advanced hydrodynamic cavitation reactor for process intensifications. Chemical Engineering Journal 2021, 412, 128600. 10.1016/j.cej.2021.128600. [DOI] [Google Scholar]
  57. Fu S.; Lu J.; Zhou F.; Yuan H.; Wang Y.; Dai C. (2022), Study on the performance of a novel hydrodynamic cavitation device for treatment of wastewater. Asia-Pacific J. Chem. Eng. 2022, 17, e2752 10.1002/apj.2752. [DOI] [Google Scholar]
  58. Pandare A.; Ranade V. V. Flow in vortex diodes. Chemical engineering research and design 2015, 102, 274–85. 10.1016/j.cherd.2015.05.028. [DOI] [Google Scholar]
  59. Thaker A. H.; Ranade V. V. Drop breakage in a single-pass through vortex-based cavitation device: Experiments and modeling. AIChE J. 2021, 1–19. 10.1002/aic.17512. [DOI] [Google Scholar]
  60. Sharma A.; Gogate P. R.; Mahulkar A.; Pandit A. B. Modeling of hydrodynamic cavitation reactors based on orifice plates considering hydrodynamics and chemical reactions occurring in bubble. Chemical Engineering Journal 2008, 143 (1–3), 201–209. 10.1016/j.cej.2008.04.005. [DOI] [Google Scholar]
  61. Šarc A.; Stepišnik-Perdih T.; Petkovšek M.; Dular M. The issue of cavitation number value in studies of water treatment by hydrodynamic cavitation. Ultrasonics sonochemistry 2017, 34, 51–9. 10.1016/j.ultsonch.2016.05.020. [DOI] [PubMed] [Google Scholar]
  62. Ramisetty K. A.; Pandit A. B.; Gogate P. R. Novel Approach of Producing Oil in Water Emulsion Using Hydrodynamic Cavitation Reactor. Ind. Eng. Chem. Res. 2014, 53 (42), 16508–16515. 10.1021/ie502753d. [DOI] [Google Scholar]
  63. Madane K. R.; Ranade V. V.. Anti-solvent Crystallization: Particle Size Distribution with different Devices. Chem. Eng. J., accepted for publication, 2002. [Google Scholar]
  64. Ranade V. V.; Bhandari V. M.; Nagarajan S.; Simpson A.; Sarovothaman V.. Hydrodynamic Cavitation: Devices, Design and Applications; Wiley-VCH: Beijing. 2022. [Google Scholar]
  65. Wu Z.; Ondruschka B.; Bräutigam P. Degradation of chlorocarbons driven by hydrodynamic cavitation. Chem. Eng. Technol. 2007, 30 (5), 642–648. 10.1002/ceat.200600288. [DOI] [Google Scholar]
  66. Wu Z.; Ondruschka B.; Zhang Y.; Bremner D. H.; Shenb H.; Franke M. Chemistry driven by suction. Green Chem. 2009, 11 (7), 1026–1030. 10.1039/b902224d. [DOI] [Google Scholar]
  67. Orthaber U.; Zevnik J.; Petkovšek R.; Dular M. Cavitation bubble collapse in a vicinity of a liquid-liquid interface - Basic research into emulsification process. Ultrason - Sonochemistry 2020, 68, 105224. 10.1016/j.ultsonch.2020.105224. [DOI] [PubMed] [Google Scholar]
  68. Chen L.; Kang Q.; Mu Y.; He Y.-L.; Tao W.-Q. A critical review of the pseudopotential multiphase lattice Boltzmann model: Methods and applications. International journal of heat and mass transfer 2014, 76, 210–36. 10.1016/j.ijheatmasstransfer.2014.04.032. [DOI] [Google Scholar]
  69. Su Y.; Tang X.; Wang F.; Li X.; Shi X. Three-dimensional cavitation bubble simulations based on lattice Boltzmann model coupled with Carnahan-Starling equation of state. Commun. Comput. Phys. 2017, 22 (2), 473–93. 10.4208/cicp.OA-2016-0112. [DOI] [Google Scholar]
  70. Trummler T.; Schmidt S. J.; Adams N. A. Effect of stand-off distance and spatial resolution on the pressure impact of near-wall vapor bubble collapses. International Journal of Multiphase Flow 2021, 141, 103618. 10.1016/j.ijmultiphaseflow.2021.103618. [DOI] [Google Scholar]
  71. Rasthofer U.; Wermelinger F.; Karnakov P.; Šukys J.; Koumoutsakos P. Computational study of the collapse of a cloud with 12 500 gas bubbles in a liquid. Physical Review Fluids 2019, 4 (6), 063602. 10.1103/PhysRevFluids.4.063602. [DOI] [Google Scholar]
  72. Shi Y.; Luo K.; Chen X.; Li D.; Jia L. A new cavitation model considering inter-bubble action. International Journal of Naval Architecture and Ocean Engineering 2021, 13, 566. 10.1016/j.ijnaoe.2021.05.005. [DOI] [Google Scholar]
  73. Brunton S. L.; Noack B. R.; Koumoutsakos P. Machine Learning for Fluid Mechanics. Annu. Rev. Fluid Mech. 2020, 52, 477–508. 10.1146/annurev-fluid-010719-060214. [DOI] [Google Scholar]
  74. Kochkov D.; Smith J. A.; Alieva A.; Wang Q.; Brenner M. P.; Hoyer S. Machine learning-accelerated computational fluid dynamics. Proceedings of the National Academy of Sciences USA 2021, 118, 1–13. 10.1073/pnas.2101784118. [DOI] [PMC free article] [PubMed] [Google Scholar]
  75. Novati G.; de Laroussilhe H. L.; Koumoutsakos P. Automating turbulence modelling by multi-agent reinforcement learning. Nature Machine Intelligence 2021, 3, 87–96. 10.1038/s42256-020-00272-0. [DOI] [Google Scholar]
  76. Sadrehaghighi I.Artificial Intelligence (AI) and Deep Learning For CFD. CFD Open Series: Technical Report, 2021; pp 1–131.
  77. Wang B.; Wang J. Application of Artificial Intelligence in Computational Fluid Dynamics. Ind. Eng. Chem. Res. 2021, 60, 2772–2790. 10.1021/acs.iecr.0c05045. [DOI] [Google Scholar]
  78. Rudy S. H.; Brunton S. L.; Proctor J. L.; Kutz J. N. Data-driven discovery of partial differential equations. Sci. Adv. 2017, 3, 1–6. 10.1126/sciadv.1602614. [DOI] [PMC free article] [PubMed] [Google Scholar]
  79. Raissi M.; Karniadakis G. E. Hidden physics models: Machine learning of nonlinear partial differential equations. J. Comput. Phys. 2018, 357, 125–141. 10.1016/j.jcp.2017.11.039. [DOI] [Google Scholar]
  80. Champion K.; Lusch B.; Kutz J. N.; Brunton S. L. Data-driven discovery of coordinates and governing equations. Proceedings of the National Academy of Sciences USA 2019, 116, 22445–22451. 10.1073/pnas.1906995116. [DOI] [PMC free article] [PubMed] [Google Scholar]
  81. Lejarza F.; Baldea M. Discovering governing equations via moving horizon learning: The case of reacting systems. AIChE J. 2022, 1–15. 10.1002/aic.17567. [DOI] [PMC free article] [PubMed] [Google Scholar]
  82. Petrone G.Unleashing the Power of Multiple GPUs for CFD Simulations, 2022. https://www.ansys.com/blog/unleashing-the-power-of-multiple-gpus-for-cfd-simulations.
  83. Sharma G.; Umapathy K.; Krishnan S. Trends in audio signal feature extraction methods. Applied Acoustics 2020, 158, 107020. 10.1016/j.apacoust.2019.107020. [DOI] [Google Scholar]
  84. Sivaram A.; Venkatasubramanian V. XAI-MEG: Combining symbolic AI and machine learning to generate first-principles models and causal explanations. AIChE J. 2022, 1–11. 10.1002/aic.17687. [DOI] [Google Scholar]

Articles from ACS Engineering Au are provided here courtesy of American Chemical Society

RESOURCES