Abstract
Population forecasts are used by governments and the private sector for planning, with horizons up to about three generations (around 2100) for different purposes. The traditional methods are deterministic using scenarios, but probabilistic forecasts are desired to get an idea of accuracy, assess changes, and make decisions involving risks. In a significant breakthrough, since 2015, the United Nations has issued probabilistic population forecasts for all countries using a Bayesian methodology that we review here. Assessment of the social cost of carbon relies on long-term forecasts of carbon emissions, which in turn depend on even longer-range population and economic forecasts, to 2300. We extend the UN method to very-long range population forecasts by combining the statistical approach with expert review and elicitation. While the world population is projected to grow for the rest of this century, it will likely stabilize in the 22nd century and decline in the 23rd century.
Keywords: Bayesian hierarchical model, Cohort-component method of population projection, Expert elicitation, Scenario, Social cost of carbon
1. Introduction
Governments use population forecasts at all levels (national, regional, city, international) for planning purposes, broadly defined. The basic purpose of government is to provide services for citizens, and this requires knowing how many people there will in the future, often broken down by age, sex and other characteristics, such as race and geography.1 Population forecasts are also widely used in the private sector for strategic planning, and by academics and other researchers, particularly in the health and social sciences.
Here we focus on national and international population forecasts by age and sex. For some countries, these are produced by national governments. The United Nations is the main organization that produces regularly updated estimates and forecasts of the population; it produces estimates of the population since 1950 and forecasts to 2100 for all countries by age and sex. These have been published since 1953 in a publication called the World Population Prospects, updated every two years to incorporate the most recent data and improved methods, most recently in 2019 (United Nations, 2019a). These estimates and forecasts are used throughout the UN system, including as part of the process for monitoring development goals, notably the Sustainable Development Goals (SDGs), which are targets for 2030 agreed by all countries, succeeding the Millennium Development Goals (MDGs) for 2015. The forecasts are used as inputs to global modeling, such as for food security and climate change. Many countries also use them for their national planning.
At first sight, it may seem absurd to issue forecasts of the population to 2100, when forecasting other quantities such as unemployment or inflation over much shorter periods is so difficult. However, population is a system with considerable inertia, making it possible to make reasonable forecasts over long time horizons. The effective time unit for population forecasting is the generation, which is about 27 years, so forecasts to 2100 are for about three time units ahead, which no longer seems so hopeless.
National governments typically forecast about 40–50 years into the future; for example, as of 2020, the US Census Bureau projects the population of the USA 40 years into the future (Vespa, Medina, & Armstrong, 2020), while the Japanese government projects 50 years into the future (National Institute of Population and Social Security Research, 2017). This is about the longest forecast lag needed for major national questions of infrastructure and personnel planning. The US Social Security Administration forecasts its budget up to 75 years into the future, which involves mortality and other population forecasts for that forecast horizon (Social Security Administration, 2020).
Multinational organizations often project farther into the future; for example, the EU projects its population to 2100 (Eurostat, 2020). The UN also forecasts to 2100, to be able to assess the implications of population change for other long-term trends influenced by population, such as food security and climate change.
The UN’s population forecasting track record is surprisingly good. For example, in 1958, the UN issued some first-world population forecasts for 2000 or later. This period of 42 years turned out to be one of considerable population volatility, with life expectancy increasing and fertility rates declining dramatically, and the world population roughly doubling. Population forecasting over this period was thus exceptionally difficult. Nevertheless, the UN’s 1958 forecast of the world population in 2000 was accurate to within 4% (Keilman, 2019). Even more strikingly, the UN’s 1963 forecast of the world population in 2000 was 6,130 million (Keyfitz, 1972), while the actual number was 6143 million (United Nations, 2019a), an error of just 0.2%.
For assessing the social cost of carbon, much longer forecast horizons are needed, and here we develop methods for probabilistic population projection up to 2300 for this purpose. Note that we use ‘‘projection’’ rather than ‘‘forecast’’ when referring to times after 2100, as for such long time horizons projections depend critically on assumptions whose validity cannot be verified empirically and is more a matter of expert review and elicitation. For going this far into the future, we develop a method that combines statistical models with expert review and elicitation.
Population forecasts have traditionally been produced by a deterministic mathematical method called the cohort-component method, which has been the dominant method since the 1940s. Uncertainty has usually been communicated, not by statistical measures such as standard errors and confidence intervals, but by subjectively determined scenarios. These are hard to interpret, and they lack statistical or probabilistic validity.
The demand for probabilistic population forecasts is driven by the desire for a general sense of forecast accuracy, the need to assess the reality of changes in population forecasts and estimates over time, and to make decisions taking account of risks. In recent decades, probabilistic forecasts have become standard in other fields such as economics and infectious disease epidemiology. The continued use of scenarios in demography may be because it was one of the first disciplines to produce rigorous quantitative forecasts and needed to assess uncertainty before statistical uncertainty assessment had fully matured. The use of scenarios became the standard way of doing things in demography starting in the 1940s (Whelpton, 1936) and probabilistic methods for uncertainty in population estimates and forecasts have only begun to make inroads in practice in the past decade, although academics have been calling for them for far longer (Bongaarts & Bulatao, 2000; Keyfitz, 1972).
The purpose of our article is two-fold: first to provide a self-contained review of recently developed methods for probabilistic population projections, and second to develop new methods that extend these to very long time horizons. We start by providing an overview of the dominant methods of demographic forecasting over the past 80 years, and a discussion of their limitations, notably their strong reliance on expert forecasts and their lack of a statistically-based assessment of uncertainty. We then review the development of practical statistically-based probabilistic population projection methods over the past decade that overcome these limitations and are now used by the UN for their official population projections for all countries to 2100. Finally, we develop new methods that extend the probabilistic projections to 2300 for use in assessing the social cost of carbon. This is done by combining the statistical methods with expert review and elicitation, by incorporating probabilistic forecasts of international migration, and by including constraints that avoid unrealistic outcomes over such a long time horizon.
The article is organized as follows. In Section 2 we review the standard deterministic and scenario-based methods for population forecasting, along with some of the associated issues. In Section 3 we describe the Bayesian probabilistic population forecasting method now used by the UN. In Section 4 we describe our extension of these methods for very long-term probabilistic population projections to 2300, motivated by the problem of assessing the social cost of carbon, while in Section 5 we give results of these methods. We conclude with a discussion in Section 6.
2. Population projections
We now outline some of the basic concepts of population projections. The cohort-component method of population projection (CCMPP) was first outlined by Canann (1895), and developed in more detail by Whelpton (1928, 1936). It became the standard method used by the U.S. Census Bureau starting in the 1940s, and subsequently spread around the world. It is now used by most national agencies producing population forecasts. It is a deterministic (i.e., non-probabilistic) method, but, as we will see, it is nevertheless at the root of the probabilistic method that we describe here. The accounts of Canann and Whelpton were largely descriptive and numerical. At the same time, the method was formalized mathematically by Leslie (1945), using what became known as the Leslie matrix as its basic concept.
Here we give a brief and simplified overview of the method. For a fuller account, see Preston, Heuveline, and Guillot (2001). The three components of population change are births, deaths and migration. These happen in continuous time, but they are typically aggregated to time periods. As a result, most demographic data (counts of births, deaths and migration events) refer to discrete-time such as years or five-year periods. The mathematics of the underlying continuous-time processes are relatively simple and elegant (Pollard, 1969; Sharpe & Lotka, 1911). Methods for analyzing the discrete-time data available to demographers, however, unavoidably involve approximations that can be somewhat complicated and inelegant.
2.1. Mortality rates
We first consider the situation where survival probabilities and fertility rates are assumed known and constant over time for a population. For simplicity, we consider only one sex (female). Suppose the probability that a woman aged x survives to age x +n is nsx. The cases most considered are n = 1 and n = 5, where death data are reported in one-year or five-year time periods and the age groups considered are one year or five years of age.
An important related concept is the mortality rate between ages x and x + n, denoted by nmx and defined as the expectation of the number of deaths between ages x and x + n divided by the number of person-years lived from age x to age x + n. If the mortality rate is constant within the age interval, then nsx = exp(−n × nmx). The mortality rate is never actually constant with respect to age, so this relationship is only approximate, but the approximation is usually good. In demography, a rate is defined as the expected or actual number of events during a period, divided by the number of person-years at risk of the event during the period.
The life expectancy at birth can be derived as a function of either nsx or nmx for all age groups [x, x + n). Life expectancy at birth is an important summary of mortality at all ages, and has the advantage that when estimated from a population it does not depend on the population’s age structure.
2.2. Fertility rates
The age-specific fertility rate for ages x to x + n, nFx, is defined as the expected number of births to women aged x to x + n divided by the number of person-years lived by women aged x to x + n. An important summary measure is the total fertility rate (TFR), defined as
| (1) |
The TFR is interpreted as the number of children a woman would bear if she survived the reproductive interval (i.e. typically to age 49), and experienced at each age interval, x to x + n, the current age-specific fertility rate nFx. It has the advantage that it is age-standardized and so does not depend on the age distribution of the population.
2.3. International migration
We now turn to migration. For national population projections, what matters is international migration, rather than internal migration. The definition of an international migration event is not uniform. Still, the most used definition is one that has been given by the UN, namely that it happens when a migrant moves from one country to another and stays there for at least 12 months (UN Department of Economic and Social Affairs, 1998, p. 10). International migration is an issue that gives rise to strong feelings in many countries and generates a great deal of political discussion and policy analysis. Despite this, it is a relatively rare event and only about 3.5% of the world’s population are currently living in a country other than their country of birth (UN Population Division, 2019). Nevertheless, it can have a significant impact on the population in the long term.
A difficulty with international migration flows is that much of the data on them is of poor quality (Azose & Raftery, 2019). Official estimates of migration flows often have large biases and measurement errors, resulting in considerable uncertainty that is sometimes not fully acknowledged in official publications. This uncertainty makes it difficult to use more refined quantities in forecasts, such as immigration and emigration separately, or bilateral flows between specific pairs of countries.
Net migration can be estimated with some reliability for many countries for intercensal periods from the so-called residual method, which consists of taking the population distribution by age and sex from a census, projecting it forward to the next census using measured or estimated births and deaths (for example, from vital registration records), and comparing the resulting projected age distribution to the one measured in the next census. The difference is attributed to international migration, and yields an estimate of the net migration flow by age in the intercensal period (Siegel & Hamilton, 1952). Immigration and emigration are harder to estimate separately, which has been another motivation for using net migration.
Because of these data issues, the UN uses net migration flows in producing their population forecasts for all countries. The UN defines the net migration rate for a country in a five-year period as the number of immigrants minus the number of emigrants over the period, divided by the average population. Note that, strictly speaking, this is not a rate by some demographic definitions, since the denominator is not the population at risk of the event. However, this definition has been useful in analysis, since more populous countries tend to have larger numbers of both immigrants and emigrants than less populated countries.
It has been pointed out that net migration can have difficulties for some purposes, such as setting migration policy, and also has the analytical issue that the age structure of immigration can be different from that of emigration (Rogers, 1990). However, for the specific purpose of population forecasts, these issues have not generally been viewed as serious enough to require sacrificing the analytic simplicity of net migration. This is partly because the age structure of international migration is very concentrated, with most of it happening between 15 and 35 years of age, so overall results tend not to be too sensitive to fine-grained differences in the age structure. In the context of subnational migration forecasting, Pittenger (1974) and Shroeder and Pittenger (1983) developed model age schedules for net migration and showed them to be useful in practice.
Estimating migration is one of the biggest outstanding problems in demography, and some progress has been made recently (Raymer, Guan, & Ha, 2019; Raymer, Wiśniowski, Forster, Smith, & Bijak, 2013). Generally, the most reliable direct measures of international migration are stocks from the census, namely the number of people born in one country currently living in another. However, these stocks do not give us direct, reliable estimates of bilateral flows. A method has been developed that leverages stocks using censuses from all countries, and not just the country of interest, to give minimum estimates of bilateral flows (Abel, 2010, 2013; Abel & Sander, 2014). This was a big step forward, but sometimes resulted in significant underestimates. A pseudo-Bayes method was developed more recently that gives more accurate estimates (Abel & Cohen, 2019; Azose & Raftery, 2019). Also, some promising results have been found using email, mobile phone, social media and other Big Data to estimate international migration (Alexander, Polimis, & Zagheni, 2020; Zagheni, Garimella, Weber, & State, 2014; Zagheni & Weber, 2012; Zagheni, Weber, & Gummadi, 2017).
2.4. The cohort-component method of population projection
We now introduce the cohort-component method of population projection (CCMPP). We simplify notation by giving results for one-year age groups and one-year time periods. Thus the subscript n in nsx and nFx will be taken to be n = 1 and suppressed. This will work with no change if projections are in n-year periods for n-year age groups. Then everything is in terms of the n-year periods. For example, the UN generally produces projections for five-year periods and five-year age groups. There are two exceptions, for the youngest and oldest age groups, so that the UN often uses the age group set 0, 1–4, 5–9, …, 100+, where the latter refers to people aged 100 or more. This leads to some solvable technical complications.
The key concept underlying the CCMPP is the demographic balancing equation, namely:
| (2) |
where Nt is the population at time t, Bt is the number births, Dt is the number of deaths, and Gt is net migration, defined by Gt = It − Et, where It is the number of immigrants and Et is the number of emigrants, all in the time interval (t, t + 1]. Unlike most equations in social science, Eq. (2) is exact, giving a potentially physics-like rigor to some of the calculations underlying population forecasts.
To be able to make projections based on Eq. (2), we need to introduce age. To do this, let Nx,t denote the population of age x = 0, 1, …, (A − 1)+ in year t, and Nt = (N0,t, N1,t, …, NA−1,t )T. Initially, consider only one sex (female), and assume that the population is closed to migration. Then
| (3) |
where is the expected number of female births to a woman aged x last birthday, who survive to time t + 1. Note that is an adjusted version of the age-specific fertility rate Fx, which refers to female births only, and takes account of the fact that some women aged x may die before time t + 1, and so may not contribute a full person-year of exposure, and that some babies may die before time t + 1.
We can then project the number of women aged x + 1 at the next time period using the relationship
| (4) |
with an adjustment for the highest age group. Eqs. (3) and (4) can then be written in matrix form as
| (5) |
where
| (6) |
In Eq. (6), L is the Leslie matrix (Leslie, 1945).
This leads to remarkably simple expressions for the complicated business of projecting populations by age. We have seen that Eq. (5) can be used to project one period ahead. To project k periods ahead, we use the equally simple equation
| (7) |
Eq. (7) is the CCMPP in its simplest form.
To account for migration in the CCMPP, let be the vector of age-specific net numbers of female migrants in the period (t, t+1]. Migration is a continuous process over the time period, and incorporating it generally requires a discrete-time approximation. One such approximation is to assume that half the net migration happens at the beginning of the interval, and half at the end. Then
| (8) |
It is possible to account for the continuous nature of migration using Integral Projection Models (Easterling, Ellner, & Dixon, 2000), but this is much more complicated than the CCMPP.
2.5. Issues with the CCMPP
Overall, the CCMPP has worked well over time. However, there are issues with the CCMPP, some of which are important, while others do not matter much in practice.
The CCMPP, as we have described it, is a one-sex model. Explicitly accounting for both sexes complicates formalism, but the basic approach still applies. Instead of A age groups, there are 2A age-sex categories, and the fertility rates are coded as zero for males. The Leslie matrix is then a 2A × 2A matrix. The additional key quantity is the sex ratio at birth, and given that, births are distributed between males and females, and survived as before.
A second issue is that the CCMPP is deterministic, but the reality is stochastic. In particular, in the CCMPP, the numbers of births and deaths are taken as deterministic and equal to their expectations, whereas these numbers have at least binomial variation. The CCMPP ignores this. However, the human populations analyzed by demographers are usually large, and then the binomial or Poisson variation is very small relative to other sources of uncertainty, so the deterministic model is a reasonable approximation. In practice, the stochastic variation makes little difference when the total population analyzed is over 100,000, but can be important to consider when the total population is under 20,000.
A third, and much more consequential issue, is that fertility and mortality rates vary over time. If future fertility and mortality rates vary, but are assumed known, then the Leslie matrix L depends on time and becomes Lt for time period t. Then the simplest projection equation (7) becomes
| (9) |
However, in practice, future fertility and mortality rates are unknown and uncertain. Indeed, this is the largest source of uncertainty in real-life population forecasts, and will be the major focus of our work here.
Another issue is that in many countries, the numbers of births and deaths in the past are not known accurately. Of the world’s 201 countries with populations over 100,000 in 2019, only about 50 have long-standing high-quality vital registration systems, and for these, the estimated numbers of births and deaths can be viewed as highly accurate. For the other countries, the numbers of births and deaths have been far less accurate. For most countries, even including those with good vital registration systems, direct estimates of international migration have not been of good quality. There are various demographic methods for improving estimates of births, deaths and migration by reference to the full range of available demographic information (Abel, 2013; Azose & Raftery, 2019; Preston et al., 2001; Wheldon, Raftery, Clark, & Gerland, 2013, 2015, 2016). Thus uncertainty about past estimates is a component of uncertainty about future population quantities and is rarely taken into account; an exception is Liu and Raftery (2020). Here we won’t focus on this issue and will consider forecasts conditional on past estimates of fertility, mortality, migration and population by age and sex.
An additional issue is that the HIV/AIDS epidemic has changed, not just the level of mortality, but also the pattern of age-specific mortality in many countries. Most causes of death primarily affect the very young and the old, but HIV/AIDS is different because it primarily affects young to middle-aged adults. Again, we won’t dwell on this issue here; probabilistic population forecasting methods that account for it have been proposed by Godwin and Raftery (2017) and Sharrow, Godwin, He, Clark, and Raftery (2018).
Issues such as these motivate statistical demography, which attempts to use modern statistical methods to estimate and forecast population quantities, and to take account of uncertainty about them.
3. Probabilistic population forecasting
3.1. Background
The standard method of population forecasting by national governments since the 1940s has been deterministic, based on the CCMPP. The UN used this approach up to 2008 for its official population projections for all countries, and then shifted progressively to the probabilistic approach that we describe here, which it adopted fully in 2015 (United Nations, 2015).
A major weakness of the CCMPP is that it requires specification of future fertility and mortality rates by the user. These are usually produced subjectively by in-house experts or panels of experts. The forecasting literature suggests that, while experts are good at assessing the relevant science, assembling the required data and evaluating its quality, and designing models for forecasts, they are not as good at producing forecasts subjectively from scratch.
Meehl (1954) was the first to document this, showing that for many clinical outcomes, simple statistical models or rules of thumb beat expert forecasts from reputed clinicians in various medical or paramedical fields. His results were greeted initially with disbelief and outrage, and many tried to disconfirm them, only to find them supported by their own studies; Meehl (1986) reviews some of this subsequent literature. Medicine has now fully integrated these results, and medical prognoses now rely on statistical analyses of relevant data, as interpreted by the practitioner rather than purely on subjective expert forecasts.
Oeppen and Vaupel (2002) reviewed 70 years of subjective expert forecasts of life expectancy, and found that they uniformly performed poorly, systematically underestimating future life expectancy. Tetlock (2005) considered expert political forecasts by respected political scientists, pundits and analysts, and found that they performed poorly, famously summarizing his findings by saying that political pundits performed no better than dart-throwing chimpanzees. In follow-up research, Tetlock and Gardner (2016) found that a subset of forecasters do produce good subjective forecasts from scratch. They are the ones who monitor their forecast performance most closely and are most prepared to revise their forecasts in light of new information. In a sense, therefore, they are the forecasters who behave most like statistical models.
The CCMPP approach does not account for uncertainty using standard statistical methods such as standard errors or confidence intervals. Instead, it uses scenarios or variants. For example, the UN traditionally has published High, Medium and Low variants. The Medium variant corresponds to the expert best guess of future fertility, mortality and migration rates. The High variant corresponds to the Medium variant, with half a child per woman, added to all the future total fertility rates (TFR), while the Low variant is similar, but with half a child subtracted.
This has the disadvantage of having no probabilistic basis and thus being hard to interpret. In addition, it leads to uncertainty statements that are implausible over multiple projection periods or for projections aggregated over multiple countries. For example, the UN’s High variant adds half a child to all the TFR values, and indeed it is plausible that a future TFR in a given country and a given time period could be half a child higher than the best guess in the Medium variant. However, that’s not what the High variant says. Instead, it says that TFR will be half a child higher in all countries and future time periods considered, a total of over 3000 country-period combinations. If one thinks probabilistically, it is clear that this is highly unlikely. Overall, even if the High variant is realistic for each country-period combination individually, it is implausible for multiple countries and periods, including aggregated quantities over multiple countries, such as regions, continents, and trading blocs.
Probabilistic forecasts may be desired for several reasons (Raftery, 2016). One is to provide a general assessment of accuracy, which has become a standard expectation in recent decades for estimates and forecasts in many fields. Population forecasts became widespread in the 1940s, long before statistical assessment of uncertainty became standard, and the lack of them for many population forecasts to this day may be due to inertia. Estimates and forecasts that started being produced more recently typically do come with standard errors or confidence intervals.
This is illustrated by the US Census Bureau, three of whose main activities are the US decennial Census started in 1790, population projections started in the 1930s, and the American Community Survey (ACS) started in 2005. Census population estimates and population projections are generally published without statistical assessments of uncertainty, while in contrast, results from the much more recent ACS are usually published with statistical confidence intervals.
A second reason is that probabilistic forecasts provide a basis for assessing changes over time. For example, if the reported TFR goes down by 0.1 children, is it a real change, or just the kind of fluctuation expected in the normal run of things?
A third reason is that probabilistic forecasts allow one to assess differences between outcomes and expectations. For example, from 2014 to 2018, US life expectancy declined by 0.2 years of life in a four-year period, while from 1950 to 2014, it increased by 0.17 years per calendar year on average (Bastian, Tejada, Arias, et al., 2020). Is the virtual lack of change between 2014 and 2020 out of line with the range of possibilities that might have been expected?
A fourth reason for producing probabilistic forecasts is that they can be an input to decision-making that attempts to limit the risk of an adverse outcome, or to balance these risks against future benefits. For example, when deciding whether to close a school, we may want to be sure (for example, with probability 90%) that there will still be enough space for the children in the area in the future. A deterministic forecast is not adequate because it will give only a best guess; if this is the median of likely outcomes, for example, it will yield a 50% probability of not having enough space for the children. Adding a rough ‘‘safety margin’’ is a blunt instrument that may lead to more capacity than is needed and waste resources. In this case, one wants the 90th percentile of the forecast distribution of the number of children in the future, and a probabilistic forecast can give this while a deterministic one cannot.
3.2. Probabilistic population forecasting methods
The main approaches to producing probabilistic population forecasts include ex-post analysis, time series methods and expert-based approaches (Bongaarts & Bulatao, 2000; Booth, 2006). Ex-post analysis is based on the errors in past forecasts (Alders, Keilman, & Cruijsen, 2007; Alho, et al., 2006; Alho, Jensen, & Lassila, 2008; Keyfitz, 1981; Stoto, 1983). The time-series analysis approach uses past time series of forecast inputs, such as fertility and mortality, to estimate a statistical time series model, which is then used to simulate a large number of random possible future trajectories. Simulated trajectories of forecast inputs are combined via the CCMPP to produce predictive distributions of forecast outputs (Lee & Tuljapurkar, 1994; Tuljapurkar & Boe, 1999). In the expert-based method (Lutz, Sanderson, & Scherbov, 1996, 1998, 2004; Pflaumer, 1988), experts are asked to provide distributions for each forecast input. These are then used to construct predictive distributions of forecast outputs using a stochastic method similar to the time series method.
Here we will focus on the approach now used by the UN as part of the basis for its official population forecasts for all countries. It is most closely related to the time series approach. It produces probabilistic forecasts of each of the three components of population change: fertility, mortality and migration. The first step is to develop statistical models for the evolution of the total fertility rate (TFR), life expectancy (e0), and the net migration rate in a country. Then a large number of trajectories of future values of the Total Fertility Rate (TFR) for all countries and future time periods are simulated. Each one is then converted to age-specific fertility rates using model fertility schedules. We simulate an equal number of trajectories of life expectancy at birth for females and males, and convert them to age-specific mortality rates using a variant of the Lee–Carter method (Lee & Carter, 1992). Finally, an equal number of trajectories of future net migration in each country are simulated. We convert each of these trajectories to a future trajectory of all age- and sex-specific population quantities using the CCMPP. For any future population quantity of interest, the resulting set of values is viewed as a sample from the sought predictive distribution.
We will give more detail about the model for TFR in Section 3.3, as fertility is the most important component of population change for long-term global population forecasts (Raftery, Alkema, & Gerland, 2014). The methods for converting TFR to age-specific fertility rates are described by Ševčíková, Li, Kantorová, Gerland, and Raftery (2016).
The model for life expectancy was described by Raftery, Chunn, Gerland, and Ševčíková (2013) for one-sex life expectancy, while the model for forecasting the sex gap in life expectancy, and hence the joint distribution of female and male life expectancy, was described by Raftery, Lalic, and Gerland (2014). For our illustrative results here, life expectancy for countries with generalized HIV/AIDS epidemics was projected using the same model as used for other countries (Raftery et al., 2013), but these countries were not used to help estimate the model. This differs from the procedure used by the UN for countries with generalized HIV/AIDS epidemics in their 2019 projections, which was more complicated (United Nations, 2019b). Finally, male life expectancy was projected using the gap model (Raftery, Lalic, & Gerland, 2014). Each simulated value of future period life expectancy at birth was broken down into age-specific mortality rates using a rotated, coherent version of the Lee–Carter method (Lee & Carter, 1992; Li & Lee, 2005; Li, Lee, & Gerland, 2013; Ševčíková et al., 2016). More recent updates to the life expectancy model are described by Castanheira, Pelletier, and Ribeiro (2017) and United Nations (2019b).
The UN currently uses a deterministic approach to forecasting net migration. However, we have developed a probabilistic approach, described by Azose and Raftery (2015) and Azose, Ševčíková, and Raftery (2016). We will illustrate it in the very long-term forecasting example results we give later in the paper.
All methods that we use to generate probabilistic population projections are available as R packages for anyone to use. The bayesTFR R package implements the TFR model (Ševčíková, Alkema, & Raftery, 2011), the bayesLife package implements the forecasting model for female and male life expectancy at birth (Ševčíková, Raftery, & Chunn, 2019), and the MortCast package can be used to project age-specific mortality rates (Ševčíková, Li, & Gerland, 2020). Finally, the bayesPop package combines the demographic components into overall probabilistic population forecasts (Ševčíková & Raftery, 2016).
3.3. Probabilistic forecasting of the total fertility rate
Over the past 150 years, the evolution of TFR in most countries has followed a similar pattern, albeit starting at different times and proceeding at different speeds. In 1870, the TFR in most countries was high, typically between 4 and 8 children per woman. Then, at times that differed by country, the TFR started to decline steadily. This point typically followed the start of industrialization and improvement in child mortality. Eventually, the TFR reached a point below the replacement level of slightly above two children per woman, after which it plateaued and fluctuated, often increasing slightly. The replacement level is often taken to be 2.1, although the precise value depends on the mortality level. This evolution is illustrated in Fig. 1 by the historical data on TFR in the Netherlands from 1850 to 2020. In that case, the fertility transition from high to low fertility lasted about 100 years.
Fig. 1.
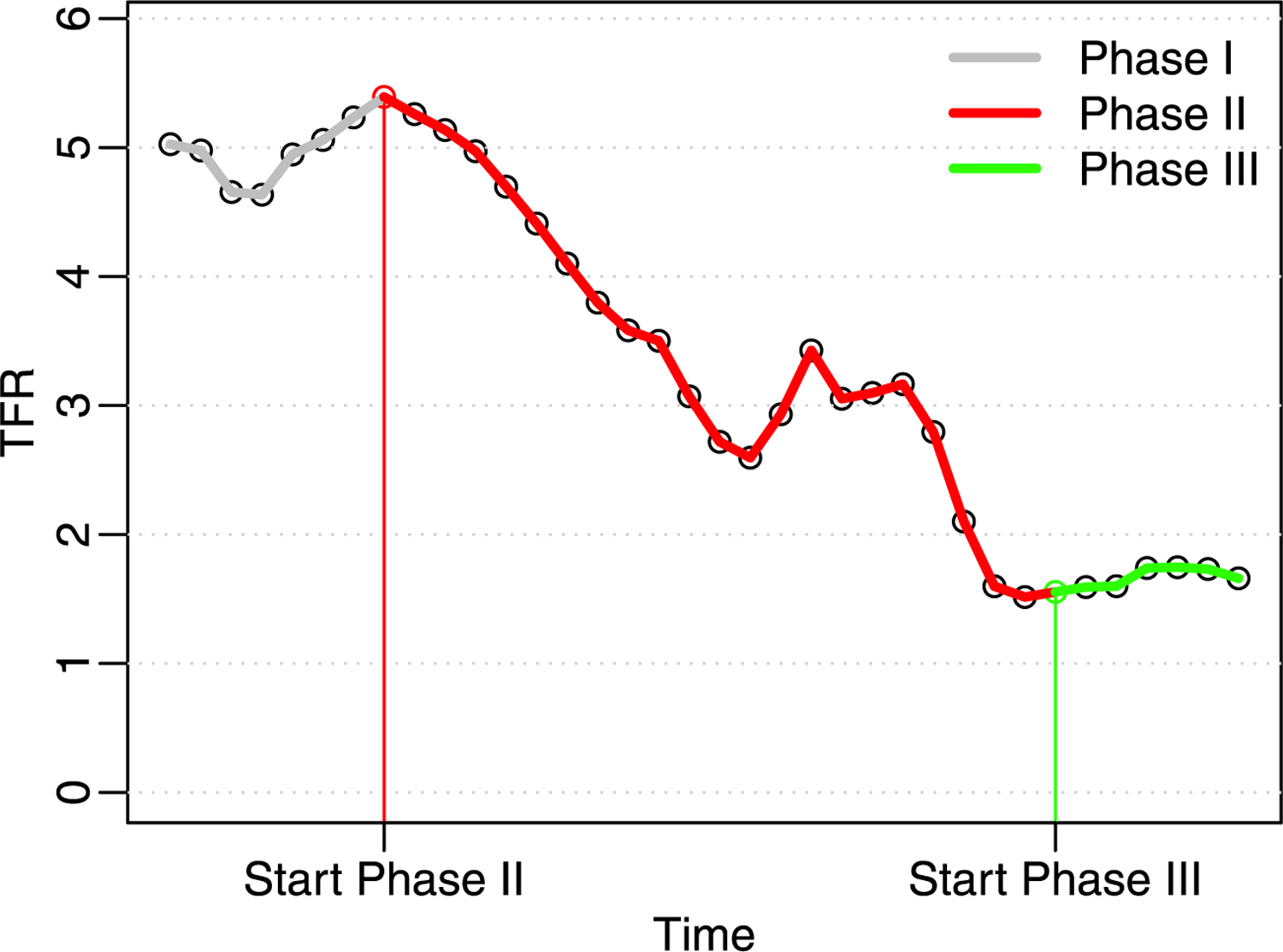
The three phases of the fertility transition, illustrated by historical data on TFR for the Netherlands from 1850 to 2020. Phase I, in grey, is the pre-transition phase, Phase II, in red, is the fertility transition from high to low fertility, which took about 100 years, and Phase III, in green, is the post-transition phase of leveling off and fluctuations.
The period of decline is usually called the fertility transition. The overall phenomenon of which it is part, including the reduction in mortality and the resulting population changes, is called the demographic transition. By now, the fertility transition is generally agreed to have started in all or almost all countries.
We divide this evolution into three phases: Phase I, the high-fertility pre-transition phase; Phase II, the fertility transition itself, during which fertility declines to below replacement level; and Phase III, the low fertility period of fluctuations, and in some cases turnaround. The fertility transition has started in all countries, so Phase I is now entirely in the past and is not of interest for forecasting. It is therefore not modeled.
3.3.1. Model for TFR during the fertility transition
Empirically, based on the historical experience of 200 countries, the fertility transition follows a common pattern. The fertility decline starts slowly, then accelerates as the decline gains momentum, then continues to decline at a fairly constant rate, then decelerates as TFR approaches the replacement level and finally stops at a point below the replacement level.
This is a somewhat complicated pattern, but its commonality across countries suggests representing its expectation by a parametric function. Considerable success has been found using a double logistic function, or a sum of two logistic functions, to model the changes in the TFR. For our purposes, the general form of this is
| (10) |
where f is the current TFR level, g(f ) is the expected decline in the TFR in the next time period, and d > 0, ai > 0 for i = 1, 2, 3, 4 are the model parameters, with a4 > a2. The parameter d is an upper bound on the expected rate of change, a1 represents the time taken for the upswing, a2 is the middle of the upswing, a3 represents the time taken for the downswing, and a4 is the middle of the downswing. The length of the plateau at the top is largely determined by the difference a4 − a2. This is a flexible five-parameter functional form that nevertheless has the general characteristics of the historical change in TFR observed in all countries.
For modeling the evolution of the TFR, it turns out that a more interpretable parameterization is as follows (Alkema et al., 2011, Appendix). It is motivated by the fact that if we write a single logistic function as
| (11) |
the parameters have the following interpretations. The function increases from 0 to d, the midpoint of the increase is at f50%, defined as the value of f such that , and ∆ is the length of the interval in which L(·) increases from to . Thus setting p = 9 gives ∆ = f90% − f10%, called the 80% range of the logistic function.
Motivated by this, we write the expected decline in TFR as a function of current TFR, as follows:
| (12) |
| (13) |
where θ = (d, △1, △2, △3, △4). The parameters then have the following interpretation. The parameter d is still an upper bound of the expected decline, the midpoint of the first logistic function is 0.5∆3 +∆4, ∆3 is the 80% range of the first logistic function, and the midpoint of the second logistic function is 0.5∆1 + ∆2 + ∆3 + ∆4. Then ∆1 is the 80% range of the second logistic function. This is plotted in Fig. 2.
Fig. 2.
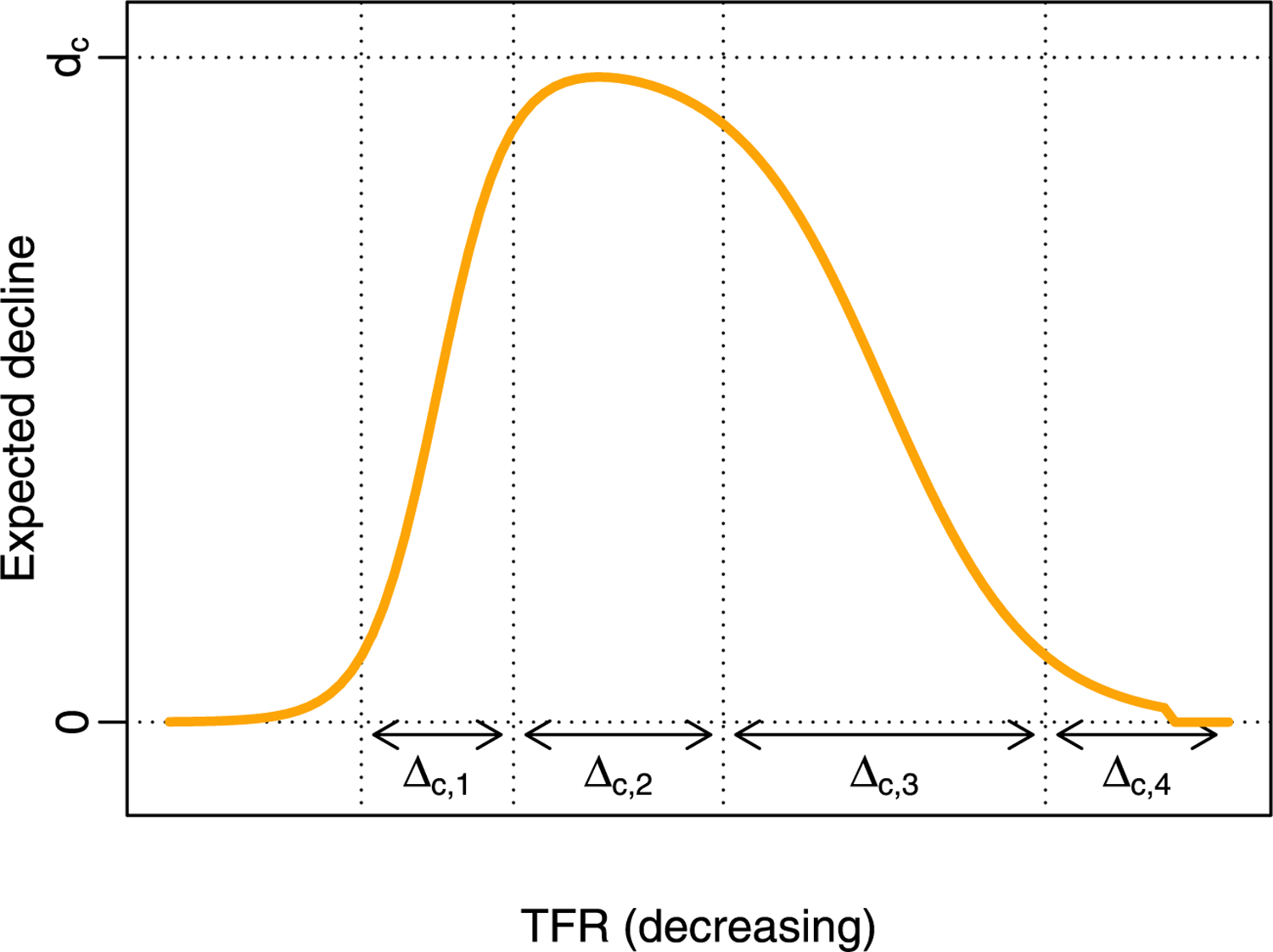
The double logistic function for modeling the expected change in the TFR, g(f ), as a function of the current TFR level, f. The TFR level is shown decreasing, since during the transition, the TFR is typically decreasing, and with this choice, time is generally moving from left to right. The parameters of the function are country-specific, denoted by the subscript c.
The model is made probabilistic by adding a random error term. The model for the evolution of the TFR over time in a given country during the fertility transition thus becomes a random walk with a non-constant drift given by the double logistic function. Least-squares double logistic fits to the changes in TFR for several countries are shown in Fig. 3. Although the evolutions are quite different, with a slow decline in India, a fast decline in Thailand, and an incomplete decline to date in Mali, the double logistic function fits each one well.
Fig. 3.
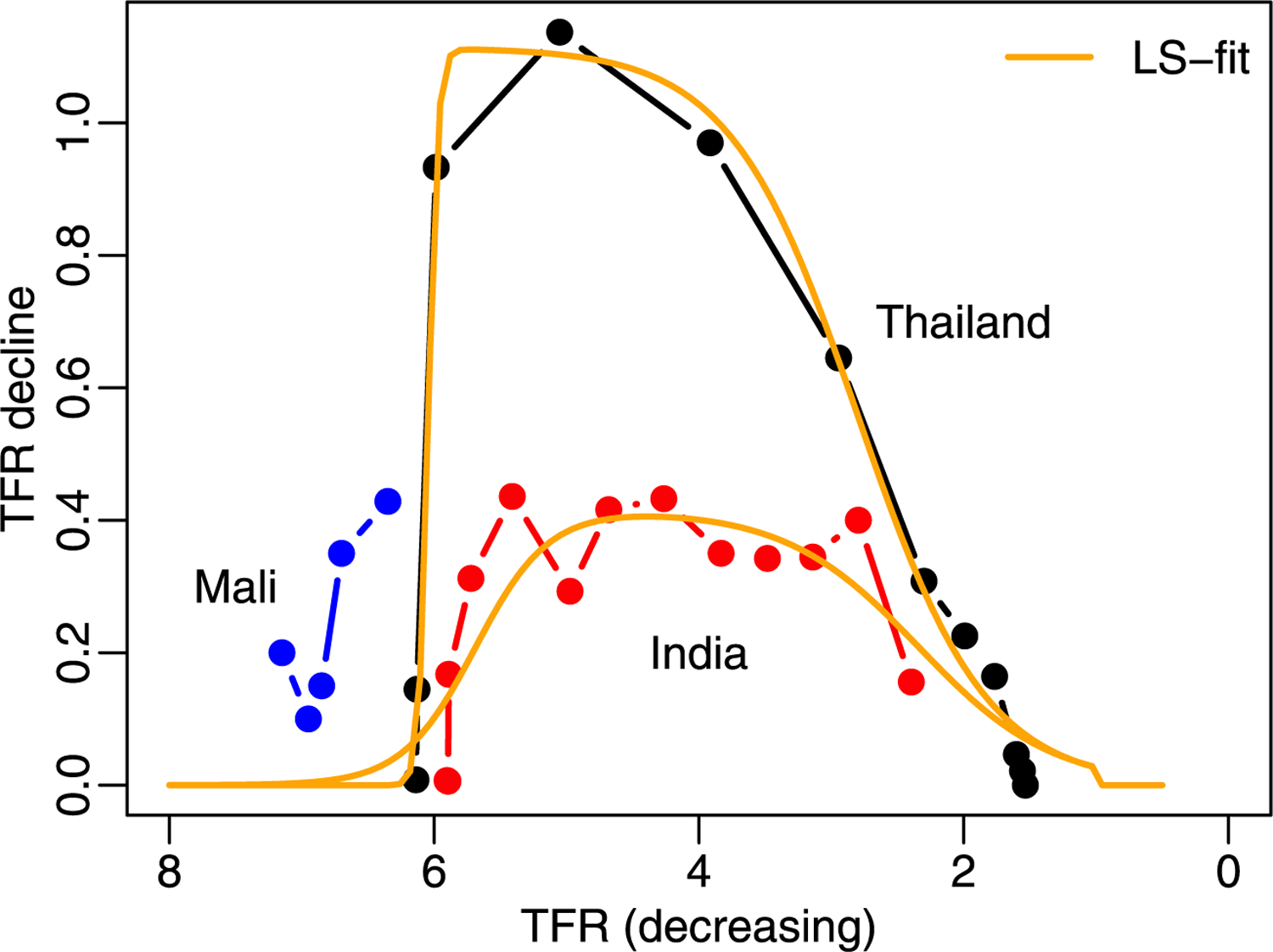
The least squares fits of the double logistic function to the TFR declines in Thailand and India. Data from Mali are also shown, but the least-squares fit of the double-logistic function is not, as there were only five relevant data points.
Ideally, if we had a complete record of the fertility transition for each country, we would estimate the model separately for each country, for example, using nonlinear least squares, as in Fig. 3. However, for high-fertility countries, such as Mali, only the early part of the fertility transition has taken place. The number of data points to inform the model is very small. As a result, for these countries, any estimate based on data from that country alone would be very uncertain.
The solution is, for each country, to draw on information from other countries, leveraging the fact that the patterns for different countries are similar, differing mainly in the speed of the transition. We do this by building a hierarchical model. Conceptually, this works as follows. The evolution of TFR for each country is assumed to follow a random walk with a drift that is a double logistic function of the current level. Each country has its own set of five parameters for the double logistic function. These sets of parameters are assumed to be drawn from a world distribution.
In this way, the world experience of which patterns of fertility decline are possible is refined by the country’s own historical experience to date. Also, the point estimate for a given country is approximately equal to a weighted average of an estimate based on its data only, and the world average. Typically, for countries where the fertility transition is complete or almost complete, such as Thailand in Fig. 3, the country’s historical experience will dominate. But for countries where the fertility transition is at an early stage, such as Mali in Fig. 3, the world experience will play a more prominent role.
Specifically, the model has three levels. In summary, Level 1 is the observation distribution,
| (14) |
where fc,t is the TFR for country c in time period t, g(fc,t ) is the expected decline, given by
| (15) |
| (16) |
and the error term, εc,t has a nonconstant variance that depends on the current TFR level, so that
Level 2 specifies the world distribution, namely θc ∼ h(·|ϕ), where θc = (△c,1, △c,2, △c,3, △c,4, dc ) is the vector of the five double logistic parameters for country c. Level 3 specifies the prior distribution on the world parameters, or hyperparameters ϕ, namely ϕ ∼ π(·). The distribution π (·) is chosen to be diffuse relative to the data distribution. The Level 2 and Level 3 distributions are given in detail in Alkema et al. (2011, Appendix).
The overall model is estimated by Bayesian estimation using Markov chain Monte Carlo (MCMC) sampling from the posterior distribution. With 201 countries, there are slightly over 1000 parameters to be estimated. The parameters are updated one at a time, some using a Gibbs sampling step, some a Metropolis step, and some with a slice sampling step (Neal, 2003). Convergence and the number of iterations are determined using trace plots and standard MCMC convergence and run-length diagnostics (Gelman, Rubin, et al., 1992; Raftery & Lewis, 1996).
3.3.2. Model for TFR after the fertility transition
The start of Phase III is defined algorithmically by two consecutive five-year increases below a TFR of 2. This was chosen because it corresponds intuitively to the notion of the end of the fertility transition, and also because it turns out to satisfy the definition of phases. Phases should be sequential, with one after the other. When the process moves from one phase to the next, it should not move back again later to an earlier phase. Empirically, with this definition of Phase III, we found that once a country has moved from Phase II to Phase III by this definition, it has never moved back to Phase II. Phase III has started in 40 countries or territories so far, including most European countries and the USA, many of those with Chinese culture (China, Singapore, Hong Kong, Taiwan, Macao), and also Japan, Vietnam, Barbados and Aruba (United Nations, 2019a).
Phase III is characterized by movement towards and fluctuations around a country-specific ultimate fertility level, µc; see the green points in Fig. 1 for an example of the general pattern. This is modeled by a first-order autoregressive model:
| (17) |
| (18) |
where 0 ≤ ρc ≤ 1.
As was done for the model for Phase II, this is estimated using a Bayesian hierarchical model. For each country there is a vector of two parameters, (µc, ρc ). At the second level of the model, the world level, these two parameters are modeled as follows:
| (19) |
| (20) |
where represents the world mean parameter for the country-specific asymptotes, their variance, and TN[0,∞) denotes a truncated normal distribution. In (20), ρc is restricted to satisfy |ρc | < 1 to guarantee stationarity of the time series process, and hence projection intervals that do not expand indefinitely with forecast horizon. Also, we assume that ρc ≥ 0, in line with the intuition and empirical observation that fertility rates in a country tend to change incrementally over time, and hence are positively correlated.
Reasonably spread out prior distributions are used for the parameters σµ, and σρ. However, an informative prior distribution is used for the world mean parameter, , namely
| (21) |
Thus the maximum for the ultimate world mean parameter is set at approximate replacement total fertility. This reflects an expert consensus that in the long run, over a long period, overall average world fertility is unlikely to significantly exceed the replacement level indefinitely. It could, however, exceed it for periods because fertility for many countries is still in Phase II and above this level, and because this is a constraint on the average of the distribution of fertility rates, not on the world average fertility rate itself. Indeed, the average world TFR currently is about 2.5 (United Nations, 2019a), well above the replacement level. In fact, it is likely to remain so for a long period, until most or all countries have reached Phase III.
3.4. Results: Probabilistic TFR forecasts
We first show example results for fertility, focusing on France. France had entered Phase III by 2005, following a steady decline since the 1950s. The TFR in France stopped declining in the early 1990s, and by the early 2000s, it was clear that the fertility transition had been completed.
Fig. 4(a) shows three trajectories simulated from the posterior predictive distribution of TFR for France. It can be seen that these fluctuate, but they show that it is possible that TFR could remain fairly steady close to the current level, that it could remain largely below the current level, or that it could rise somewhat above the current level.
Fig. 4.
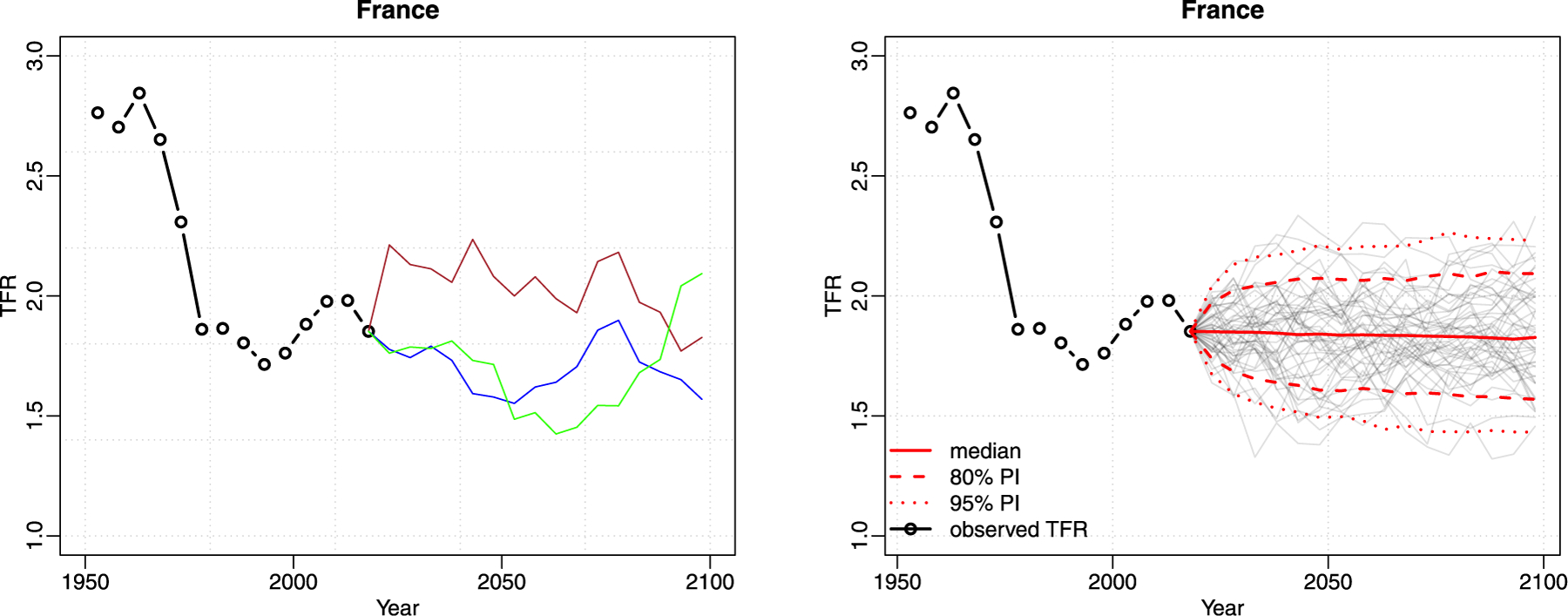
Probabilistic forecast of TFR for France. (a) Left: Three trajectories from the posterior predictive distribution for 2020–2100. (b) Right: Predictive median, 80% and 95% predictive intervals, with 50 trajectories shown in grey.
Fig. 4(b) shows the posterior predictive median and 80% and 95% intervals, along with 50 trajectories shown in grey. The median is effectively constant at the estimated long-term asymptote of about 1.85 children per woman, close to the current level. The limits of the pointwise 95% intervals are about 0.4 children above and below the median, respectively.
Comparing the left and right panels of Fig. 4 points to an issue in communicating probabilistic forecasts like this, particularly Bayesian ones that take the form of a large number of simulated possible future trajectories. Both the historical data and the trajectories in the left panel show that the evolution of TFR in France has had quite a bit of jerky stochastic variation in the past. This is likely to continue in the future. However, the median, or ‘‘best’’ forecast in the right panel is extremely smooth, with almost no stochastic variation, as indeed are the predictive quantiles. Thus the ‘‘best’’ forecast looks unlike all the trajectories that make up the predictive distribution as a whole.
Mathematically, of course, this is not a puzzle: the median forecast is a median of a large number of fluctuating trajectories, and is smooth because averaging (or taking medians) smooths out stochastic variation. But from a cognitive point of view, it can present a challenge. Users often focus on the ‘‘best’’ forecast, and can misunderstand this forecast to mean that future TFR will converge to a single value with little variation around it. A more sophisticated, but still incorrect, reading of Fig. 4(b) views the time series of limits of the pointwise predictive intervals as plausible trajectories or scenarios. In fact, a smooth trajectory that looked qualitatively like, say, the upper limit of the 80% predictive interval for the 80 years from 2020–2100 would be very unlikely.
We have tried to overcome this by first presenting a small number of trajectories, as in Fig. 4(a), and only then presenting the summary results in Fig. 4(b). This seems to improve understanding somewhat, but how best to present such results to users remains an open issue.
3.5. Results: Probabilistic population forecasts
Fig. 5 shows the Bayesian probabilistic projections of fertility, mortality and population for Nigeria using the methodology described in this section. Nigeria is the most populous country in Africa, and its population is likely to grow substantially, so the demography of Nigeria is important for the future population of Africa, and indeed the world as a whole.
Fig. 5.
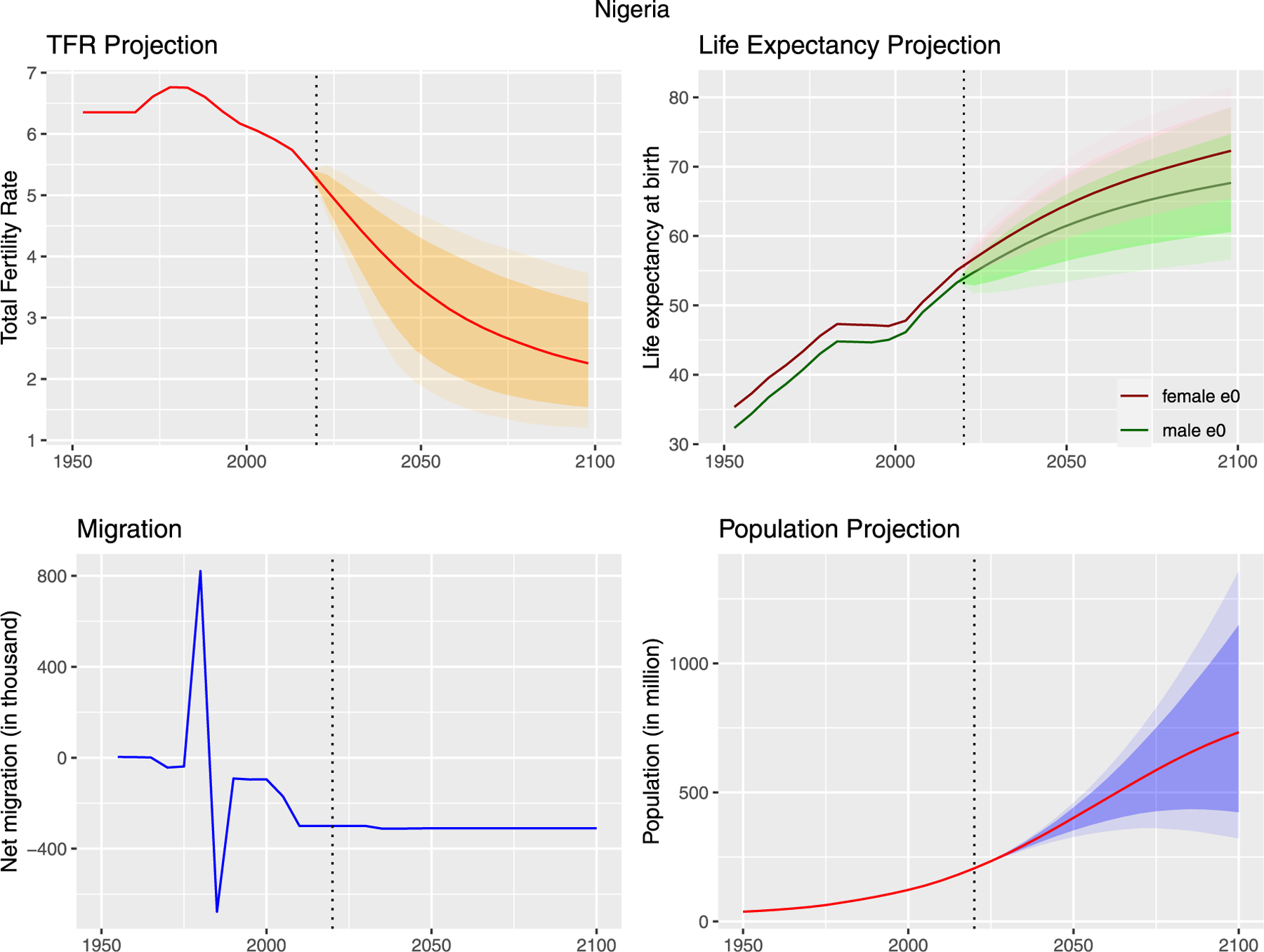
Probabilistic Bayesian projection of vital rates and population for Nigeria, 2020–2100, based on data from 1950–2020. (a) Top left: TFR projection. The red line shows the historical data and the median projection. The dark shaded area is the pointwise 80% forecast interval, and the light shaded area is the pointwise 95% forecast interval. (b) Top right: Life expectancy projection. The dark red line shows the historical data and the median projection for females, while the dark green line shows the same for males. The pink (green) dark/light shaded areas show the 80%/95% pointwise prediction intervals for females (males). (c) Bottom left: Net migration (in thousands), historical data and UN deterministic projection (United Nations, 2019a). (d) Bottom right: Population projection. The red line shows the historical data and the median projection. The dark/light shaded areas show the 80%/95% pointwise prediction intervals.
Fig. 5(a) shows that fertility is likely to decline in Nigeria over the remainder of the century, but there is considerable uncertainty about how fast that will happen. This uncertainty is highly consequential for the population as a whole, because in Nigeria, fertility is the biggest driver of population growth. The fertility transition is well underway but is less than one-third complete. By the end of the century, the predictive median is that TFR will be close to the replacement level of 2.1, but it could still be close to 4. Indeed, it could reach the very lowest levels of around 1.2 seen in Europe or East Asia.
Fig. 5(b) shows that life expectancy is likely to increase substantially, but again there is considerable uncertainty about the speed of the increase. This is less important than uncertainty about future fertility for the overall population, because changes in life expectancy influence population less than fertility over the forecast horizon of three generations (a generation is often considered to be about 27 years). Changes in female and male life expectancy are highly correlated in Nigeria, as in all other countries, and so we modeled the sex gap in life expectancy, which is expected not to change too much over time (Raftery, Lalic, & Gerland, 2014).
We used the deterministic net migration projections used by the UN (United Nations, 2019a). These usually amount to assuming that net migration will stay at the same level in the future as now. Fig. 5(c) shows this projection for Nigeria.
The trajectories from these projections are combined using the CCMPP to give a probabilistic population projection for Nigeria, shown in Fig. 5(d). This shows that the population of Nigeria is likely to increase dramatically from its current level of 206 million, with a median projection of 733 million, 80% prediction interval 423–1149 million, and 95% prediction interval 322–1358 million. This projected increase is despite the likely decline in fertility, and reflects both the fact that fertility will possible stay above the replacement level for several decades, and that the current population is young.
Fig. 6 shows the results for China, currently the world’s most populous country. These contrast strongly with those from Nigeria. China completed its fertility transition several decades ago, and its population is projected to peak in about ten years. It is then projected to decline from its current level of 1.44 billion by 26% to 1.06 billion. By 2100 its population could be as high as 1.34 billion or as low as 820 million (95% prediction interval).
Fig. 6.
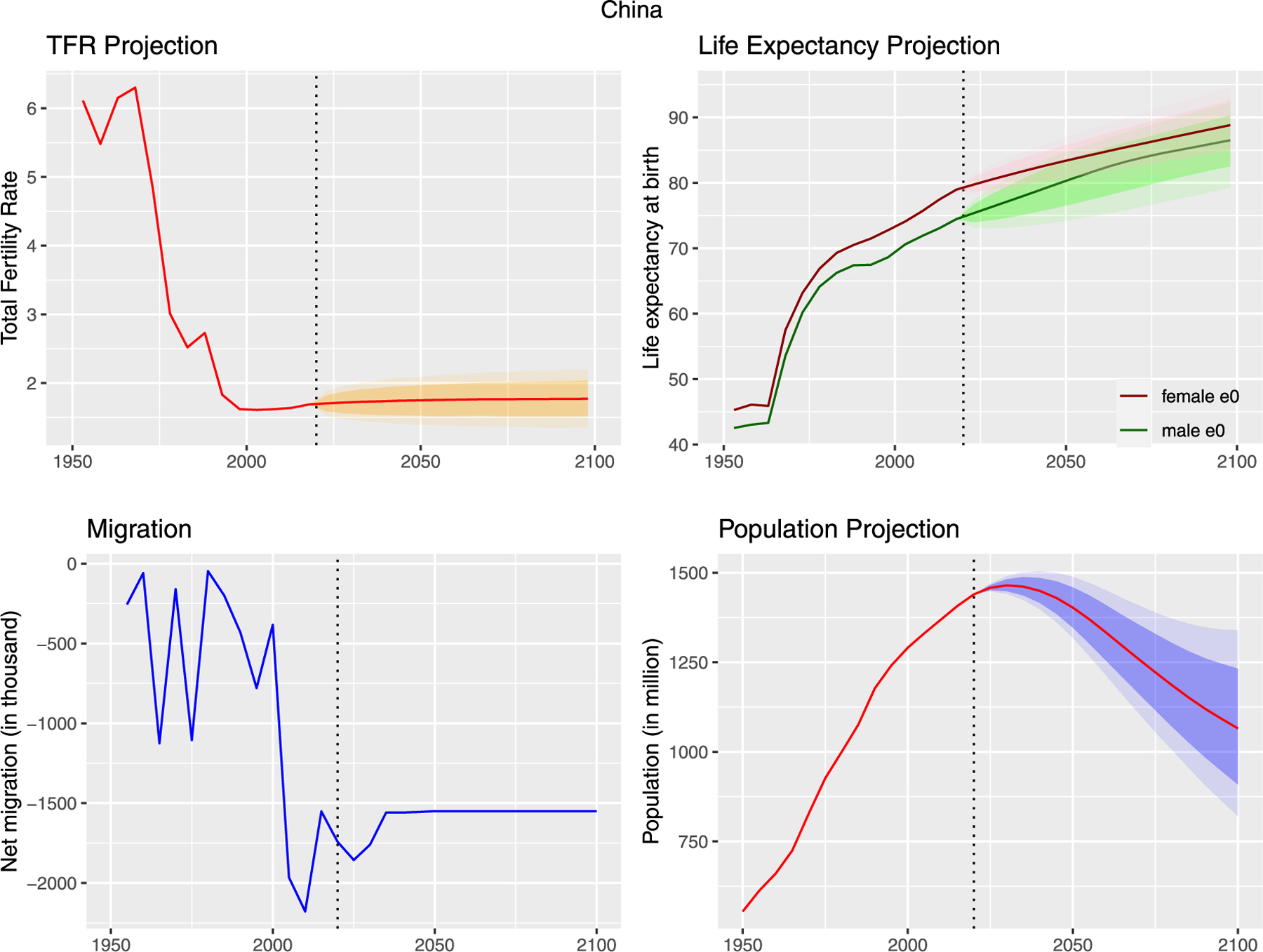
Probabilistic Bayesian projection of vital rates and population for China, 2020–2100, based on data from 1950–2020. (a) Top left: TFR projection. The red line shows the historical data and the median projection. The dark shaded area is the pointwise 80% forecast interval, and the light shaded area is the pointwise 95% forecast interval. (b) Top right: Life expectancy projection. The dark red line shows the historical data and the median projection for females, while the dark green line shows the same for males. The pink (green) dark/light shaded areas show the 80%/95% pointwise prediction intervals for females (males). (c) Bottom left: Net migration (in thousands), historical data and UN deterministic projection (United Nations, 2019a). (d) Bottom right: Population projection. The red line shows the historical data and the median projection. The dark/light shaded areas show the 80%/95% pointwise prediction intervals.
Fig. 7(a) shows the resulting projection for the world as a whole. The world population is projected to increase from its current 7.8 billion to 10.9 billion in 2100, with 95% prediction interval 9.4 to 12.7 billion. There is very little uncertainty up to 2050, with uncertainty growing fast in the second half of the century. Indeed, the growth of the prediction error variance is superlinear, much faster even than the linear growth that would be expected with a nonstationary random walk process. This reflects that most of the uncertainty comes from births after 2020, accounting for a minority of the world’s population in 2050, but most of it in 2100.
Fig. 7.
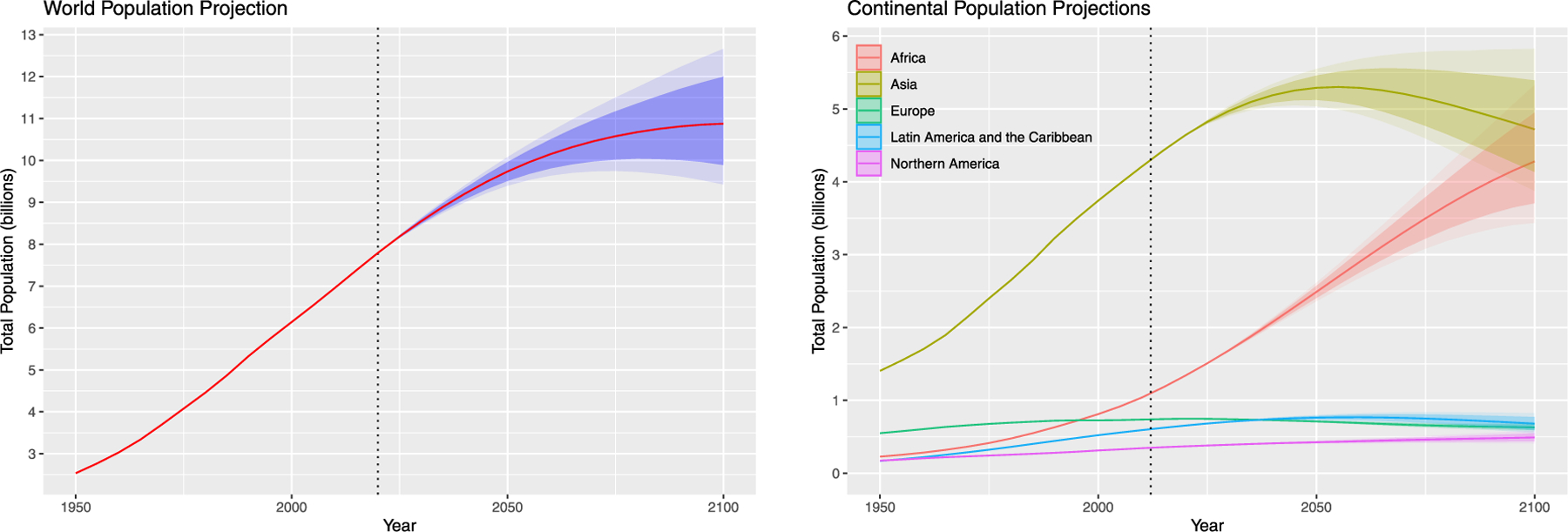
Aggregate Bayesian probabilistic population projections. (a) Left: Projection of world population, 2020–2100. The red line shows the historical data and the predictive median. The dark/light shaded areas show the pointwise 80%/95% prediction intervals. (b) Right: Projections for each continent.
Fig. 7(b) shows the projections for the continents. The population of four of the five continents is expected to peak and then decline. The exception is Africa, which is expected to roughly quadruple this century. These results update those of Gerland, et al. (2014), but the results remain qualitatively similar.
4. Very long-term probabilistic population projections for assessing the social cost of carbon
4.1. Background
The social cost of carbon is a tool for quantifying the societal damage from emitting a given amount of carbon in the atmosphere, and informs billions of dollars of policy decisions. The U.S. government has developed a methodology for estimating the social cost of carbon, and has used it to assess the effect of its regulatory measures on climate change; its methodology is used by several other governments.
In 2017, the National Research Council (NRC) of the National Academies of Science, Engineering and Medicine carried out a comprehensive review of options for updating the methodology for estimating the social cost of carbon (National Research Council, 2017). Resources For the Future (RFF), a Washington, D.C.-based think tank, is leading a multidisciplinary research initiative to advance the NRC recommendations.
Any assessment of the social cost of carbon depends on future economic and population trends, which drive economic activity, and hence carbon emissions. One of the objectives of the RFF initiative is to revise projections of population growth to reflect key uncertainties better. Because the impact of carbon emissions is so long-lasting, it is desirable to project them far into the future. The most widely used current projections are those by the Intergovernmental Panel on Climate Change (IPCC) (Intergovernmental Panel on Climate Change, 2014), and these go to 2100. However, the National Research Council (2017) has suggested that projections to 2300 are needed.
The IPCC projections are based on expert opinion-based scenarios for future economic and population growth, but these do not provide a full assessment of the relevant uncertainties, and do not have a probabilistic interpretation (National Research Council, 2017). The IPCC projections were produced in 2014, at which point there were no official probabilistic population projections for the world and its countries, which may partly explain why it did not produce probabilistic projections of carbon emissions.
However, in 2015 for the first time, the UN produced official probabilistic population projections for all countries to 2100 (United Nations, 2015), using the Bayesian methodology described in Section 3. Raftery, Zimmer, Frierson, Startz, and Liu (2017) developed probabilistic projections of carbon emissions and global temperature increase to 2100. The methodology was used by Liu and Raftery (2021) to address the question of what emissions reductions would be needed to meet the objective of keeping global average temperature increase to below 1.5 or 2 °C with a given probability.
We now consider how to extend the UN probabilistic population projections to 2300 to use as inputs to the assessment of the social cost of carbon. There are few extant population projections beyond 2100. We are aware of three, all of which are deterministic and not probabilistic, and do not include an assessment of uncertainty (Basten, Lutz, & Scherbov, 2013; United Nations, 2004; Vallin & Caselli, 1997).
As a first step, we extended the UN’s current statistical model for projecting to 2100 (United Nations, 2019a) to 2300 without substantial methodological modification. In a second step, the results were reviewed by a panel of demographers convened by the RFF. In a third step, the projections were modified in light of their opinions.
The resulting methodology is a combination of statistical modeling and expert review and elicitation in a particular way that seems to be successful in this case. A statistical model is developed, the resulting forecasts are reviewed by experts and are then modified in light of the expert opinions. This is different from purely subjective expert forecasts from scratch, and has the potential to combine the strengths of both approaches, particularly for very long-term forecasts where purely statistical methods are harder to validate.
Three of the panel’s critiques of the first version of our methodology were particularly salient. The first was that the predictive distribution of world average total fertility rate (TFR) from the purely statistical model was too narrow for projections so far into the future. To reflect this, we added a variance component, modeled as an additional country-invariant random walk, to the simulated values of TFR for all countries.
The second critique was that the UN’s deterministic international migration assumption was inadequate and that international migration should also be modeled probabilistically. In response to this, we incorporated a previously developed probabilistic model for international net migration (Azose & Raftery, 2015; Azose et al., 2016). However, this models total net migration without reference to population age structure. For the period from 2020 to 2100 this works reasonably well as an approximation, but by 2300 we can expect substantial population aging. Since international migration tends to be concentrated at younger ages, broadly between 15 and 35, this population aging is likely to lead to a long-term reduction in migration. We further modified the method to account for this.
The third critique was that some trajectories from the Bayesian predictive distribution led to populations for some countries that were too large. Our first-step method already incorporated an upper limit on population density, but the comment was made that this was not low enough for some countries with larger geographic areas. In response, we modified our method to include an upper limit on population that depends on both population density and geographic area.
4.2. Projecting total fertility to 2300: Bayesian hierarchical model with expert review and elicitation
In our first step, a Bayesian hierarchical model for TFR was estimated as in the standard UN approach described above, using the bayesTFR R package (Ševčíková et al., 2011). The same MCMC-sampled values of the model parameters were used as for the standard 2100 projections. Using 2300 as the end year, TFR was projected by generating 1000 trajectories of future values for all countries. Spatial correlation between countries was taken into account (Fosdick & Raftery, 2014).
The RFF’s panel of expert demographers felt that the resulting uncertainty about long-term future world average TFR was understated. The 95% interval from the model for world average TFR in 2300 was 1.66–2.23, and the panel felt that the lower bound was too high, as lower values were possible. They thought that the upper bound was reasonable. Here we first lay out a rationale for a specific lower bound, based primarily on comments from one member of the expert panel. We then describe the modified statistical method used to achieve it.
4.2.1. Lower bound on world average TFR in 2300
In the context of the review, a lower bound was proposed based on the observation that several countries, especially in Southern Europe and Eastern Asia, have had a sustained TFR lower than 1.66 for some decades, and the argument that this is one possible path for world average TFR in the very long term (Basten, 2013; Basten et al., 2013; Lutz, Skirbekk, & Testa, 2006; Reher, 2019).
There are several countries or territories (Italy, Spain, Ukraine, Taiwan, South Korea, Singapore, Hong Kong) where period TFR has been below 1.5 since 2000 and the TFR recovery has been either absent or shallow so far. This raises the possibility that some countries and regions may experience deeper and more protracted fertility declines followed by a slow and shallow TFR recovery, with the resulting long-term TFR below 1.6, and possibly between 1.2 and 1.5. Italy and Spain have now recorded more than 30 years with a period TFR below 1.5.
Further evidence is provided by considering the countries with the lowest cohort TFR, measured as the completed fertility rates among women born in 1976. For sixteen countries, this is below 1.66 (Human Fertility Database, 2019; Vienna Institute of Demography, 2018; Yoo & Sobotka, 2018). Hong Kong is the lowest with 1.15 children, and Spain is the second-lowest with 1.35, while a further five countries had completed fertility below 1.5 (among the 201 countries with a population above 100,000 in 2019). This again suggests that a lower bound of 1.66 is too high, but it also suggests that a lower bound of 1.2 is likely low enough to encompass most realistic possibilities.
In addition, a world average TFR of 1.2 from 2250, by when the demographic transition would likely be complete in all or almost all countries, implies a reduction of the world population by about 40% per generation. This would produce a reduction of 85% in one century and 98% in two centuries, a rapidly aging population and an inverted age pyramid. The human species would then be on a path to extinction. It seems at least plausible that humanity would act collectively or individually well before that point to avoid such an outcome, and that TFR would not stay as low as 1.2 for very long. This is a further argument for 1.2 being low enough to serve as a lower bound for world average TFR in the very long term.
4.2.2. Projection of TFR to 2300
The unmodified Bayesian hierarchical model gives a 95% prediction interval for world average (population-weighted) TFR, or WTFR, in 2300 of [1.66, 2.23]. As we have noted, the RFF’s panel of demographers agreed that the upper bound of 2.23 is reasonable, but felt that the lower bound of 1.66 is too high over the period of about ten generations into the future to 2300.
We, therefore, developed a method for modifying the projections for the period 2100–2300. It consists of adding a globally defined and simulated random walk to all country-specific trajectories for the period 2100–2300. The basic idea is to add to all TFR trajectories a global random walk (the same for all countries, but different for each MCMC trajectory). The unmodified posterior predictive distribution of WTFR stabilizes around 2250 and remains stable from 2250 to 2300. This corresponds to the projection that the fertility transition is likely to be largely complete around the world by 2250. Thus the random walk would operate between 2100 and 2250, a 150-year time interval consisting of 30 five-year time periods. The mean and variance of the random walk are defined so that the uncertainty in 2250 would be inflated to the desired extent, and the mean would also change accordingly.
Note that, if a random walk is given by Y0 = 0, and
Yt = Yt−1 + µ + εt,
where , then its expectation at time t is E[Yt ] = tµ, and its variance at time t is Var[Yt ] = tσ2. Since we want the distribution to stabilize in 2250, we would set Yt = Yt−1 for years between 2250 and 2300.
We find µ and σ as follows. Let ft be WTFR in year t, and let fj,t be simulation j of WTFR in year t from the initial MCMC run, for j = 1, …, J, where J is the number of MCMC samples. Also, let f¯ = E(f2245−2250) and V = Var(f2245−2250) from the initial MCMC run. Suppose the target (lower and upper) .025 and .975 quantiles for f2245−2250 are L* = 1.20 and U* = 2.23.
We use the following iterative algorithm for determining µ and σ:
Set initial values for µ and σ. We chose these as µ = −0.00575, σ = 0.0353.
Compute L′ and U′ by running the population model with the random walk added to the country-specific TFRs for each trajectory.
Set µnew = µ + [(L* + U*)/2 − (L′ + U′)/2]/30.
Set .
Set µ ← µnew and σ ← σnew.
If |L′ − L*| < .005 and |U′ − U*| < .005, stop.
Otherwise, go to step 2.
To generate the probabilistic projections of TFR for all countries to 2300, we proceed as follows. Let fj,c,t denote the simulated TFR for country c in time period t in trajectory j of the MCMC algorithm. Let t here denote five-year time periods starting at 2100. Thus t = 1 corresponds to the time period 2095–2100, t = 2 corresponds to 2100–2105, and t = 41 corresponds to 2295–2300.
In summary, our algorithm is as follows. For each trajectory j from the MCMC algorithm, and for t spanning the period 2100–2300, replace fj,c,t by , where is simulated as follows:
- Simulate the global random walk Yj,t:
- Let Yj,1 = 0, corresponding to the period 2095–2100.
-
For t = 2, …, 31 (with t = 31 corresponding to 2245–2250), simulate Yj,t as follows:Yj,t = Yj,t−1 + µ + εj,t,where
- For t = 32, …, 41, let Yj,t = Yj,t−1.
Calculate the replaced simulated TFR, as follows: For each country c and each time period from 2100–2105 to 2295–2300, let = fj,c,t + Yj,t.
Finally, the sex ratio at birth was assumed to be constant at the 2100 level from United Nations (2019b) until 2300.
4.3. Projecting Net International Migration to 2300
For projecting net migration to 2100, the UN uses a deterministic approach that assigns values for the first few five-year periods after 2020 using available information, and then assumes that net migration remains constant thereafter. This was used in the first version of our method. This approach was criticized by the RFF’s panel of demographers as understating uncertainty in a way that may be particularly important for assessing future carbon emissions, since carbon emissions per capita are much higher in more developed than less developed countries. Migration does not make much difference to the future total world population. However, migration flows from less developed to more developed countries tend to be higher than in the other direction, so the UN’s deterministic assumption may lead to an inadequate assessment of the proportion of people in more developed countries in the future. This, in turn, has important implications for future carbon emissions.
Instead, we used a probabilistic method for net migration rates (Azose & Raftery, 2015; Azose et al., 2016). The model is a Bayesian hierarchical first-order autoregressive model for five-year rates, where each country has its own long-term mean and variance and autoregressive parameter.
This method does not take account of population age distribution. This is reasonable for projections three generations ahead, to 2100, because population age distribution typically changes slowly enough that it doesn’t dramatically affect likely migration numbers over this period. However, there are about ten generations to 2300, and these are likely to see significant population aging throughout the world. Since international migration is largely concentrated in young ages, mostly between 15 and 35, this population aging is likely to lead to substantial reductions in migration over such a long period.
We modified the method to take account of this. We first consider negative simulated values of net migration and treat them as if they were entirely made up of out-migration. We used a Rogers-Castro-like schedule for age-specific out-migration, taken from the schedule used for China and other countries by the UN for 2020–2025 (Rogers & Castro, 1981; United Nations, 2019b). Using this schedule and the age breakdown of the population in 2020, we converted the simulated net migration rate to the corresponding Gross Migraproduction Rate (GMR), which is an age-standardized measure of out-migration and is independent of the population age structure (Rogers & Castro, 1981). We then reconverted it to an adjusted net migration rate for the future year.
More specifically, let a denote age group, for a = 1, …, A, and let Ra denote the assumed age-specific migration rate from the Rogers-Castro-like schedule. Note that here Ra is taken to be constant over time and countries, for convenience; the results are unlikely to be sensitive to this assumption. We let πa,c,t be the proportion of the population of the sending country c at time t that was in age group a, so that for each c and t. Let rc,t be the net migration rate for country c at time T. Let . The age-adjusted net migration rate is then rc,tKc,t/Kc,2020.
Similarly, we treat positive simulated values of net migration as if they were entirely made up of in-migration. In that case, the relevant denominator population for the migration rate is the population of the rest of the world, which we will approximate by the population of the world as a whole. Let wa,t be the projected proportion of the world’s population in age group a at the beginning of time period t for the simulated trajectory being constructed, and define . Then the age-adjusted net migration rate is rc,tWt/W2020.
In summary, our age-adjusted net migration rate is
| (22) |
Qualitatively, this will tend to reduce numbers of migrants, both for individual countries and worldwide, as the population ages.
Finally, when this is incorporated into the population projections in the form we have described, migration will not sum to zero across the world. In practice, the difference between the sum of net migration by country and zero is generally small, so this is not a major problem in practical terms, but it is nevertheless unrealistic. To address this, we rebalanced migration in each time period and for each age and sex by reallocating any excess to countries in proportion to their population, as described by Azose et al. (2016). Special treatment is required for the six countries of the Gulf Coordinating Council or GCC and the primary countries that supply them with migrant labor, as described by Azose et al. (2016).
4.4. Population density constraints
In a probabilistic projection, some trajectories may produce unrealistically high or low populations for some countries. This is essentially unavoidable, and we deal with it by imposing constraints on the population density that can be attained.
Intuitively, small countries will have a larger density constraint than big countries. This is because high-density small countries tend to consist largely of a dense metropolitan area and its hinterland. On the other hand, countries with large geographic areas may have dense metropolitan areas, but they also have large rural areas, so they tend to have lower population densities. For example, it is unlikely that a large country like Niger would reach the same population density as much smaller countries or territories like Hong Kong or Singapore, which are essentially city-states.
Fig. 8 shows the current relationship between population (in thousands) and land area (in km2) on the log–log scale as black dots. The blue dashed line is the corresponding regression line with a slope of 0.771; below 1 supports our claim that average population density tends to decline with the area. In addition to a few countries marked in the plot, we also included Dhaka, which is by some measures the densest major city in the world, with a population density of 41,000 inhabitants per square kilometer (Demographia, 2019). Our constraint is defined as the red line in Fig. 8, which has the same slope as the blue regression line, and the intercept is chosen such that it intersects the data point corresponding to Dhaka, namely 5.118. This restriction yields a different maximum density for each country that depends on its area. For example, the limit is 5300 people per km2 for India and 37,360 for Singapore.
Fig. 8.
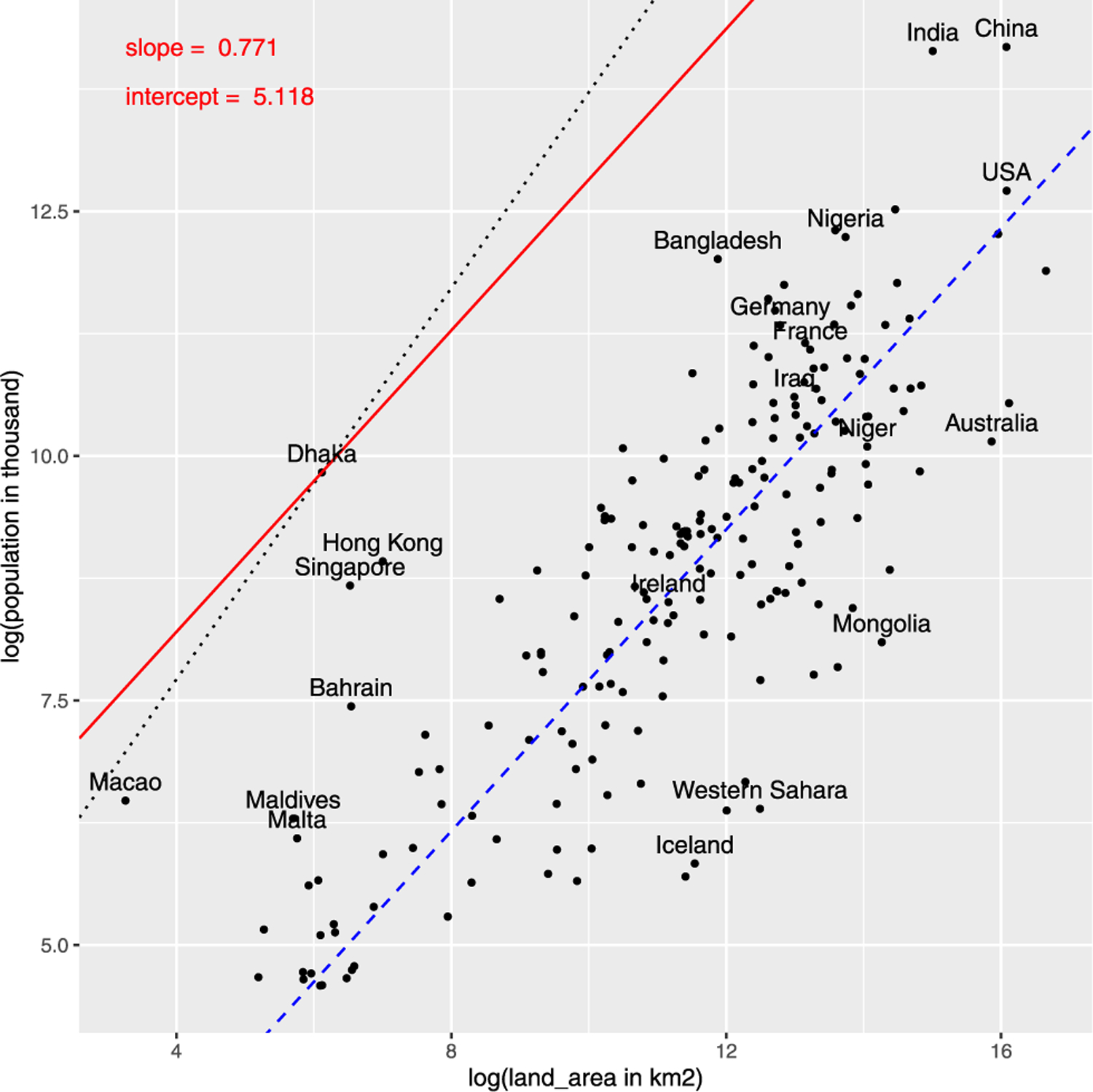
Log–log plot of population (in thousands) and land area (in km2). Black dots show the current data, while the blue dashed line is the regression line. The red line depicts our density constraint defined as log(population) < 5.118 + 0.771· log(land area). The black dotted line is a line with slope 1 that intersects Dhaka.
This density limit is imposed by restricting the maximum number of in-migrants for the particular country in each time period. We pose a similar limit on the number of out-migrants, which is such that the density does not fall below the current density of Mongolia (1.9 persons per km2) or the historical lowest observed density of the country since 1950, whichever is smaller. Note that Mongolia is currently the country with the lowest population density globally (among the 201 countries with a population of over 100,000 in 2019).
5. Very long-term population projections: Results
The country-specific projections to 2300 are shown in the Appendices in the Supplementary Material. The fertility results are shown in Appendix A, the life expectancy results in Appendix B, the migration results in Appendix C, and the total population results in Appendix D.
5.1. Total fertility
The fertility results show the total fertility rate in all countries eventually fluctuating around a country-specific level that is below the replacement level of 2.1. For current high-fertility countries, there is considerable uncertainty about when that is likely to occur. The plots also show the UN’s probabilistic TFR projections to 2100 (United Nations, 2019a); these agree closely with our projections up to that point, as expected.
For countries that currently have high fertility, uncertainty about future TFR first widens, then shrinks, and finally stabilizes as we move farther into the future. This may seem surprising at first sight, since in most situations, we expect uncertainty to increase steadily as we go farther into the future. However, for high-fertility countries, overall uncertainty about future fertility is produced by the combination of several trends that go in different directions, producing the pattern seen.
In the short term, uncertainty is low because fertility changes slowly over time, due to the inherent inertia in human population dynamics. In the medium term, uncertainty is dominated by uncertainty about the future pace of the fertility decline, which is considerable. Eventually, however, our model implies that the fertility transition will be complete and fertility will stabilize. It is uncertain precisely when the fertility transition will be complete in these countries, but there is a point that differs by country but is no later than 2250 for any country, by which we can be fairly sure that it will be complete everywhere.
As we approach that point, uncertainty about the pace of the fertility decline becomes less relevant and contributes less to overall uncertainty, thus reducing it. Once that point has been reached, uncertainty is dominated by the expected stochastic fluctuations around the country-specific long-term mean. The combination of these trends produces the unusual widening-shrinking-stabilizing pattern that we observe in the prediction intervals.
Percentiles of the distribution of world TFR (weighted by countries’ populations) for the 2245–2250 and 2295–2300 periods are shown in Table 1. It can be seen that the95% intervals are the same as the desired interval elicited from the RFF expert panel.
Table 1.
Percentiles of the posterior predictive distribution of world TFR (weighted by the countries’ populations) for the 2245–2250 and 2295–2300 periods.
| Year | Percentile |
||||
|---|---|---|---|---|---|
| 2.5 | 10 | 50 | 90 | 97.5 | |
| 2245–2250 | 1.20 | 1.41 | 1.72 | 2.07 | 2.23 |
| 2295–2300 | 1.20 | 1.37 | 1.72 | 2.07 | 2.23 |
The evolution of world TFR in 2100–2300 is shown in Fig. 9. It can be seen that fertility declines steadily until 2250, after which it stabilizes, as desired. The width of the interval increases over time up to the point of likely stabilization by 2250, also as desired.
Fig. 9.
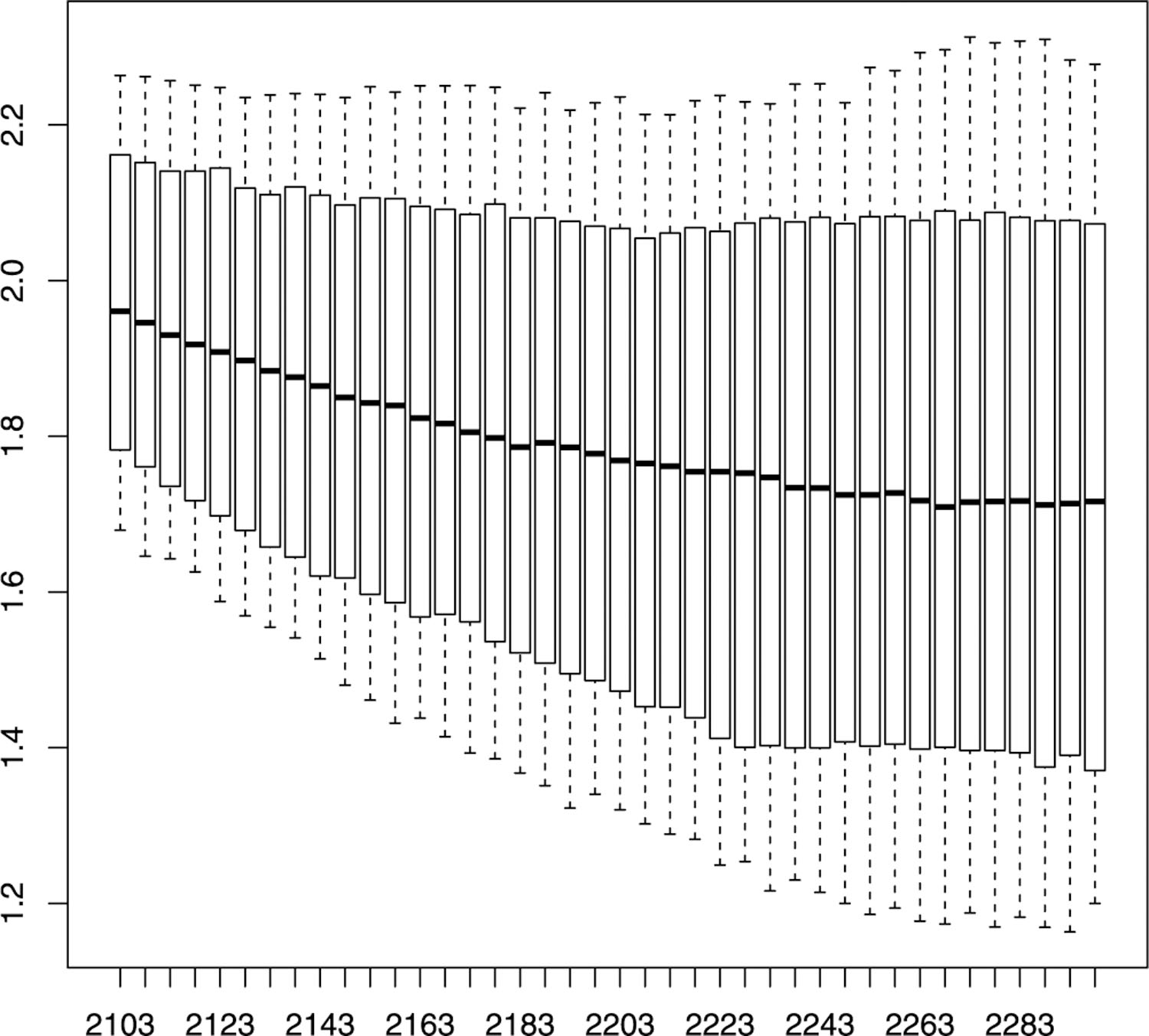
Predictive distribution of world TFR (weighted by countries’ populations) from 2100–2300. The line in the middle of the box is the predictive median, the box shows the 80% prediction interval, and the dashes show the 95% prediction interval.
5.2. Life expectancy
The life expectancy results show life expectancy continuing to improve in expectation in all countries, but with many trajectories showing considerable fluctuations, including temporary declines. By 2300, it is anticipated that life expectancy in most countries will have reached the high 90s.
5.3. Migration
The probabilistic projections of net migration counts reflect several countervailing long-term trends. The model for net migration rates, defined as net migration divided by population, says that each country has a long-term mean and that the net migration rate fluctuates around it according to a first-order autoregressive process (Azose & Raftery, 2015). This leads to prediction intervals that are narrow for short-term predictions, then widen and finally stabilize as the forecast horizon increases. This is a standard pattern for stationary time series models.
The net migration rate is multiplied by a factor reflecting the projected population age structure, as described in Section 4.3. Since the population is projected to show a general aging trend in almost every country over the next 280 years, this factor is generally below 1 and declines as time goes forward, leading to a narrowing of the intervals. The combination of these two trends yields a pattern of widening and then shrinking for the uncertainty intervals for net migration numbers for most countries.
The plots in Appendix C also show the UN’s projections of migration to 2100 (United Nations, 2019a). For most countries, these combine expert opinion for the first few time periods past 2020 with an assumption of constant migration after that. Our predictive medians tend to shrink towards zero and thus be smaller than the UN’s projections in absolute value. This reflects two factors. First, our method accounts for the tendency of net migration to shrink towards a long-term estimated mean which is usually less extreme (i.e. closer to zero) than the current value. Second, our method accounts for population aging, which is also likely to shrink net migration towards zero.
5.4. Population
Quantiles of the predictive distribution of total world population to 2300 are shown in Fig. 10 and Table 2. They show that the world population is likely to level off in the 22nd century, and to decline slightly in the 23rd century. Uncertainty for 2300 is considerable, appropriately, reflecting the very long forecast time horizon, with a median forecast of 7.5 billion, but a likely range (90% interval) of 2.8 to 20.5 billion.
Fig. 10.
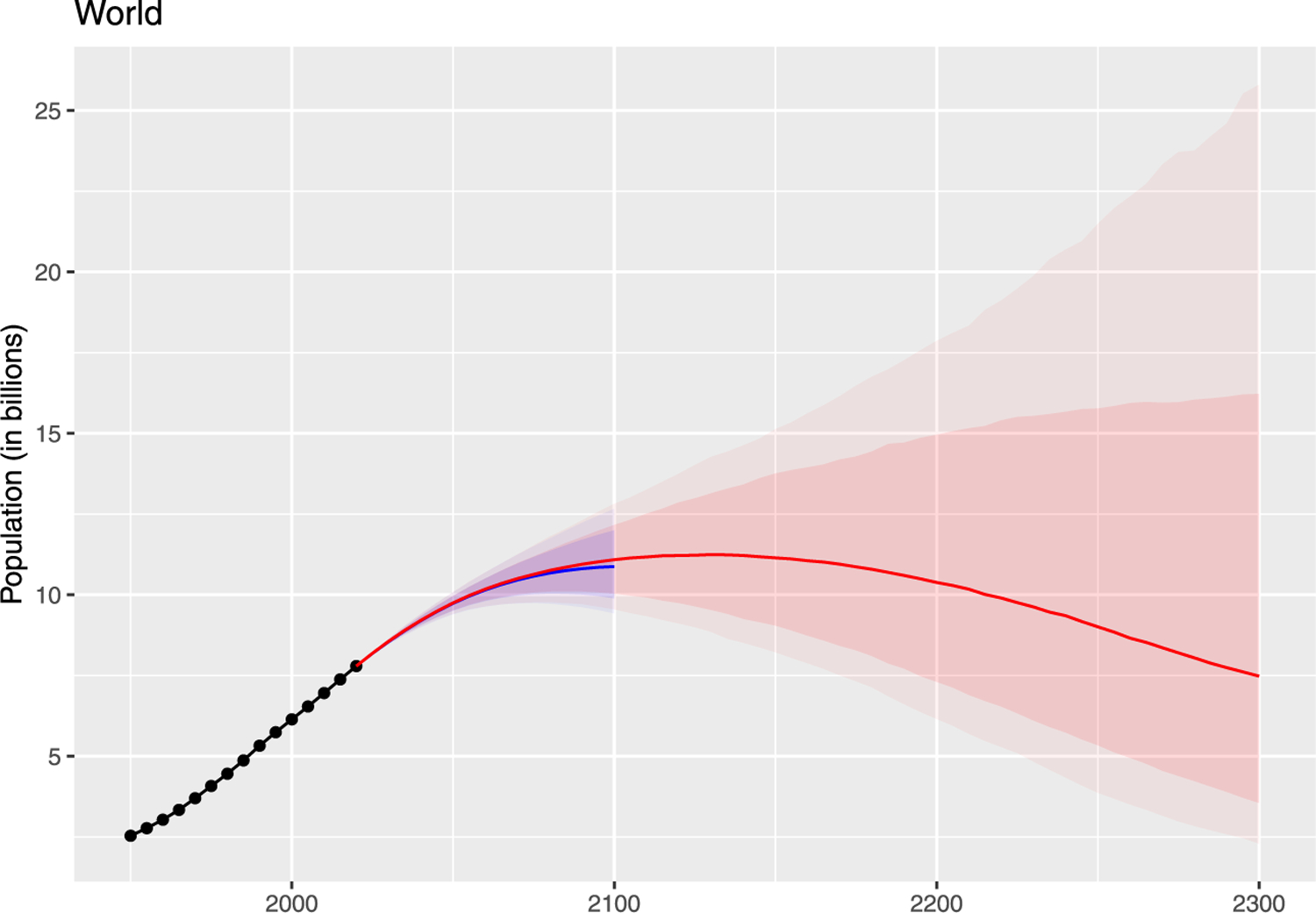
Predictive distribution of total world population to 2300, in billions. The circles show UN 2019 estimates of past population. The red curve shows our predictive median to 2300, the darker shaded area shows the 80% predictive interval, and the lighter shaded area shows the 95% predictive interval. The blue lines and shaded areas show the UN’s probabilistic forecasts of world population to 2100 (United Nations, 2019a).
Table 2.
Predictive distributions of total population for the world and the major continental regions in 2100, 2200 and 2300, in thousands. The predictive median, 80% intervals, 90% intervals (‘‘likely range’’) and 95% intervals are shown.
| Name | Year | Median | low80 | high80 | low90 | high90 | low95 | high95 |
|---|---|---|---|---|---|---|---|---|
| World | 2020 | 7,793,665 | ||||||
| World | 2100 | 11,087,401 | 10,038,154 | 12,163,649 | 9,757,003 | 12,548,652 | 9,549,781 | 12,818,071 |
| World | 2200 | 10,381,900 | 7,305,100 | 14,956,607 | 6,643,463 | 16,545,674 | 6,156,100 | 17,863,299 |
| World | 2300 | 7,479,886 | 3,554,617 | 16,223,973 | 2,793,983 | 20,510,688 | 2,293,425 | 25,801,229 |
|
| ||||||||
| Africa | 2020 | 1,340,592 | ||||||
| Africa | 2100 | 4,290,987 | 3,686,547 | 4,972,991 | 3,542,387 | 5,211,465 | 3,435,249 | 5,401,694 |
| Africa | 2200 | 5,323,541 | 3,278,622 | 9,210,068 | 2,924,092 | 10,585,450 | 2,747,030 | 11,514,647 |
| Africa | 2300 | 3,982,297 | 1,671,097 | 10,586,376 | 1,250,330 | 13,696,038 | 995,185 | 17,667,505 |
|
| ||||||||
| Latin America | 2020 | 653,561 | ||||||
| Latin America | 2100 | 686,138 | 596,425 | 795,440 | 571,759 | 830,258 | 552,256 | 862,167 |
| Latin America | 2200 | 432,221 | 302,055 | 629,780 | 276,232 | 709,607 | 252,908 | 780,968 |
| Latin America | 2300 | 256,177 | 123,485 | 579,450 | 102,446 | 734,926 | 83,261 | 936,212 |
|
| ||||||||
| Northern America | 2020 | 368,745 | ||||||
| Northern America | 2100 | 432,649 | 342,876 | 517,695 | 319,832 | 541,262 | 291,137 | 570,309 |
| Northern America | 2200 | 389,732 | 224,336 | 640,079 | 183,844 | 764,334 | 153,865 | 888,621 |
| Northern America | 2300 | 300,657 | 112,286 | 792,596 | 80,708 | 1,066,054 | 66,708 | 1,341,687 |
|
| ||||||||
| Europe | 2020 | 747,279 | ||||||
| Europe | 2100 | 614,387 | 554,549 | 682,457 | 537,381 | 705,422 | 523,280 | 728,253 |
| Europe | 2200 | 467,211 | 353,597 | 646,902 | 323,876 | 711,139 | 306,563 | 769,195 |
| Europe | 2300 | 323,045 | 165,330 | 650,339 | 136,827 | 817,130 | 112,740 | 1,023,016 |
|
| ||||||||
| Oceania | 2020 | 42,433 | ||||||
| Oceania | 2100 | 63,786 | 48,794 | 81,787 | 45,638 | 88,995 | 41,729 | 95,792 |
| Oceania | 2200 | 57,509 | 32,762 | 104,733 | 28,100 | 122,283 | 24,636 | 147,899 |
| Oceania | 2300 | 40,186 | 16,791 | 113,117 | 14,416 | 160,667 | 12,905 | 207,300 |
|
| ||||||||
| Asia | 2020 | 4,641,055 | ||||||
| Asia | 2100 | 4,938,621 | 4,354,567 | 5,633,480 | 4,207,749 | 5,857,253 | 4,076,522 | 6,070,905 |
| Asia | 2200 | 3,420,825 | 2,363,271 | 4,793,465 | 2,182,077 | 5,464,810 | 1,989,421 | 5,890,026 |
| Asia | 2300 | 2,142,945 | 998,585 | 4,456,487 | 792,596 | 5,804,237 | 627,913 | 6,972,282 |
Fig. 10 also shows the UN’s estimates of past world population from 1950 to 2020, and the UN probabilistic forecasts of world population to 2100. These agree closely with our forecasts to 2100. The slight differences are due to minor differences in methodology, most notably in terms of migration and modeling mortality in countries with generalized HIV/AIDS epidemics.
Fig. 11 shows the results for each major continental region. They show that the populations of Asia, Europe, and Latin America are likely to peak well before the end of this century and then decline substantially. The populations of Africa and Northern America are also likely to peak and then decline, but much later, in the 22nd century. In the case of Africa, this is due to population momentum (with a high fraction of the population currently in reproductive ages) and current high fertility. In the case of Northern America, it is due to a combination of modest population momentum, fertility that is closer to replacement level than in other continents, and immigration. Uncertainty for each region in 2300 is high.
Fig. 11.
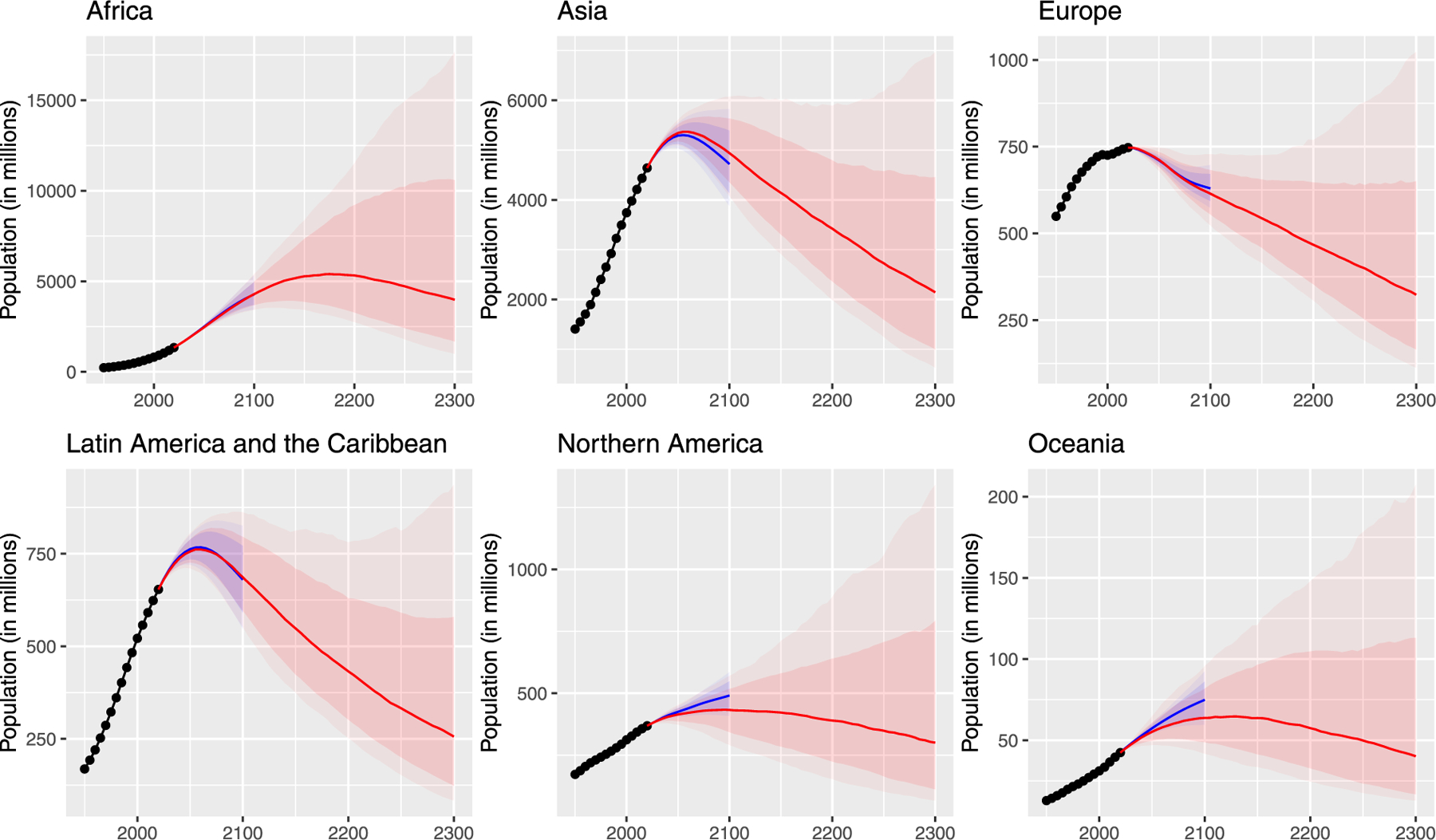
Predictive distribution of total population to 2300 for the major continental regions. The circles show UN 2019 estimates of past population. The red curve shows our predictive median to 2300, the darker shaded area shows the 80% predictive interval, and the lighter shaded area shows the 95% predictive interval. The blue lines and shaded areas show the UN’s probabilistic population forecasts to 2100 (United Nations, 2019a).
Fig. 11 also shows the UN’s probabilistic population projections for the major continental regions, from United Nations (2019a). For Africa, Asia, Europe and Latin America and the Caribbean, these agree closely with our projections to 2100. For Northern America, however, we project lower population growth to 2100 than the UN does. This reflects that population growth in this region is driven to a significant extent by immigration to the US and Canada. The UN projects (deterministically) that net migration to these countries will continue at essentially its current level until 2100. We project lower migration, however, mainly due to the projected population aging in the rest of the world for the remainder of this century. This translates to lower population growth in Northern America, which is projected to continue to draw immigrants from all over the world.
Fig. 12 shows the results for each of the UN’s major groupings of countries by the current level of development — more developed, less developed and least developed. These are important in the context of projecting carbon emissions, since more developed countries are likely to emit relatively large amounts of carbon, while the least developed countries are currently emitting very low levels of carbon. Until 2100 the projections agree fairly closely with those of the UN, although they are somewhat lower for the more developed regions, due to our lower projections of migration. Our migration projections are for continued net migration towards the most developed countries and away from most of the least developed countries. However, this is not enough to completely cancel out the lower population decline in the least developed countries due to population momentum (i.e. a currently young population), and current high (albeit declining) fertility.
Fig. 12.
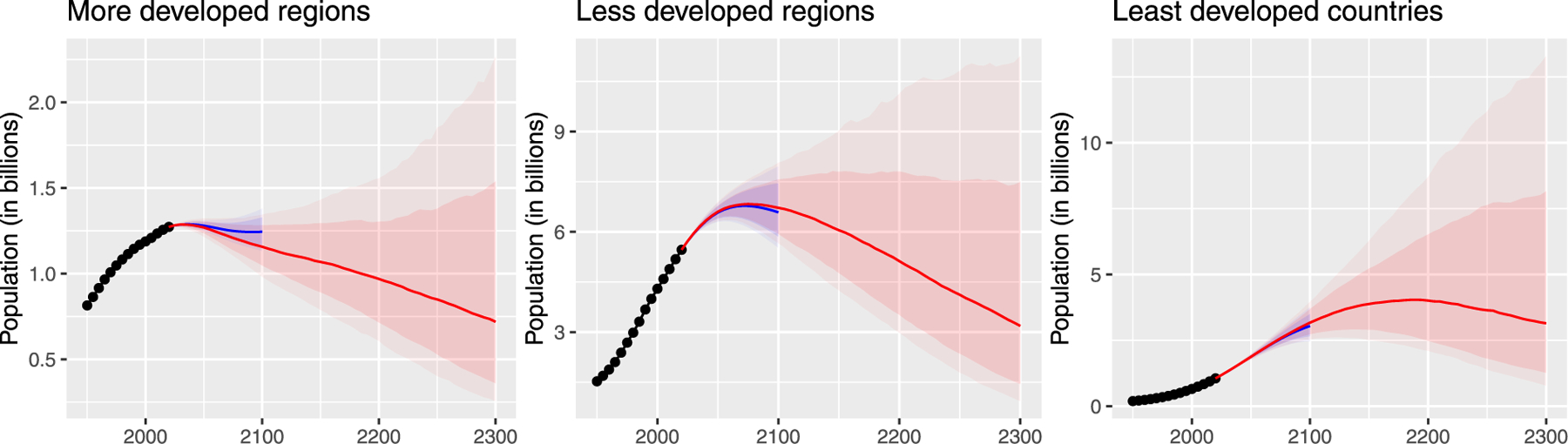
Predictive distribution of total population to 2300 for the UN’s major developmental groupings of countries. The circles show UN 2019 estimates of the past population. The red curve shows our predictive median to 2300, the darker shaded area shows the 80% predictive interval, and the lighter shaded area shows the 95% predictive interval. The blue lines and shaded areas show the UN’s probabilistic population forecasts to 2100 (United Nations, 2019a).
Appendix D shows our population projections for each country, along with those of the UN. The two sets of projections are very close for most countries up to 2100. There are some countries for which there are notice-able differences, however, due to the different migration treatment. In some cases (e.g. Norway, Switzerland), we project lower in-migration because of long-term population aging, which the UN does not consider. In others (e.g. Zimbabwe, Botswana, Eswatini, Syria, Venezuela) there has been substantial recent out-migration, often due to conflicts, and the UN projects large positive return migration. Our method instead has a median projection of continued out-migration from these countries, although with substantial uncertainty that does allow for the possibility of large return migration. In each of these cases, the UN’s deterministic projection of net migration is contained within our prediction interval.
6. Discussion and conclusion
We have reviewed the UN’s methodology for probabilistic population forecasts to 2100, using Bayesian hierarchical models. We have extended this to produce probabilistic population projections for all countries of the world to 2300 for use in assessing the social cost of carbon. The method combines an extension of the UN’s current probabilistic population projections from 2100 to 2300 with expert review, elicitation and modification. The results show a likely stabilization of the world population in the 22nd century, with a slight decline in the 23rd century. There is, appropriately, considerable uncertainty about the population at these distant time horizons.
We are aware of only three other detailed efforts to project the world population to 2300. One was carried out by United Nations (2004) and was deterministic, but containing several scenarios. The range of these projections for 2300 from the different scenarios went from 2.3 to 36.4 billion, compared with our 95% prediction interval of 2.3 to 25.8 billion. Although using very different method-ologies and carried out over 15 years apart, the two sets of projections give results that are compatible with one another, perhaps to a surprising extent. The very high upper bound for the United Nations (2004) projections is likely an artefact due to the perfect correlation implied by the deterministic scenarios and the aggregation of such results.
Another such exercise was carried out by Vallin and Caselli (1997), also deterministic with scenarios. They presented three scenarios corresponding to different long-term trajectories of world TFR. Two of the scenarios led to the world population stabilizing at around 9 billion, while the other resulted in 4.3 billion people in 2300. All three of these scenarios give world population in 2300 well within our 80% interval. The range is much narrower than either ours or that of United Nations (2004).
Basten et al. (2013) also performed a projection exercise to 2300. This was also deterministic but with a very wide range of scenarios for long-term world TFR. In their tables of results, they showed projections of global population yielding anything from zero to 86 billion in 2300. They emphasized scenarios in which the global level of fertility converges to the then-current European TFR of 1.5, or that of Southeast Asia or Central America, of around 2.5. According to their analysis, the former would lead to a world population of about 1.1 billion, while the latter would lead to 86 billion in 2300. As with the United Nations (2004) projections, these very extreme outcomes are likely in part due to the perfect correlation between countries implied by the deterministic scenarios and the aggregation of such results.
The UN’s 2019 projections to 2100 use a complicated compartmental model for mortality for the 20 or so countries, they were assessed as needing special analytic treatment because of the presence of generalized HIV/AIDS epidemics (United Nations, 2019b). It would not have been feasible for us to extend this model to 2300. Instead, we applied the same model for mortality to all countries, but we did not use the HIV/AIDS countries in estimating the parameters of the mortality model. As can be seen from Appendix B, this leads to only very small differences between the UN projections and ours for life expectancy, even in the countries with the highest HIV prevalences.
A much simpler method for projecting mortality and hence population in countries with generalized HIV/AIDS epidemics, that does take explicit account of the demographic impact of the epidemic, was developed by Godwin and Raftery (2017) and Sharrow et al. (2018). The UN Population Division is considering using this method in future revisions of the World Population Prospects, and doing so could also improve the very long-range projections. It is generally thought, however, that HIV prevalence will have declined to low levels by 2100, so this might not have much impact on projections of population change between 2100 and 2300.
A significant limitation of our work is that we do not explicitly model climate and other population feedback. In principle, doing this would be a good idea, but at this stage, it does not seem that the science needed to do this defensibly is yet in place. A great deal of the relevant climate science to 2014 is contained in the IPCC Fifth Assessment Report (Intergovernmental Panel on Climate Change, 2014). While there has been some progress since then, we do not believe that there is enough consensus about the likely extent of global impacts of climate change on the components of population change to support a detailed modeling exercise.
Consider the three main components of population change: fertility, mortality and migration. There is no clear evidence of a major impact of climate change on fertility, the most important component at the world level, much less of its direction and extent. In contrast, there is evidence of an impact on mortality. The most widely cited assessment is that climate change will cause approximately 250,000 additional deaths per year from malnutrition, malaria, diarrhea and heat stress (World Health Organization, 2014). While this is large from a humanitarian point of view, its global demographic impact is relatively small.
Finally, it is known that climate change is likely to cause migration, but most of it will be either internal migration or migration from small islands or other nations at risk of flooding. Thus its impact on national populations is unlikely to be large for most countries.
However, we would argue that our approach does implicitly incorporate some effects of future climate change on the population. The climate has already warmed by about 1 °C, with most of the change happening since 1950, i.e. during the period from which the data on which our model is built come. Thus, our model has been estimated using data from a warming planet. More specifically, the mortality impact of climate change to date is likely already included in the life expectancy data used to estimate our model. Thus our projected changes in future life expectancy are already lower because of the effect of climate change.
The same is true for international migration. Our model for migration anticipates a continuation of existing trends, which already reflect emigration from the countries most affected by climate change, to the extent that it is occurring. For example, one of the countries most threatened by climate change is the small Pacific Island nation of Kiribati. Our method projects continuing sustained out-migration from Kiribati, indeed to a greater extent than the UN projections. As a result, our median projection calls for a 77% decline in the population of Kiribati from 2100 to 2300, mainly because of out-migration caused by climate change.
As another example, among countries with large populations, Bangladesh is perhaps the most at risk of climate-driven international migration due to increasing floods. Our method projects likely sustained out-migration from Bangladesh over the coming centuries, likely in large part driven by climate change. Our method translates this to a projected reduction of 84% in the population of Bangladesh from its peak in 2050 to 2300, again due in large part to climate change.
Our method also implicitly incorporates climate and other feedbacks through the density-dependent constraints, as well as the continuing international migration, particularly from developing countries to rich countries. The global density-dependent constraints ensure that if countries approach particular thresholds on population density, their population growth is likely to slow. In practice, the mechanisms for this are likely to be climate and other feedbacks. Also, the fact that we model out-migration as proportional to the age-adjusted population of a country means that the method does capture the likelihood of population growth leading to increased migration out of developing countries, at least approximately.
Finally, these projections are for use in assessing the social cost of carbon, for which a 3% discounting rate has been proposed (National Research Council, 2017). Under such a discounting rate, impacts over from 2100 to 2300 would account for only about 10% of the impacts over the entire period from 2020 to 2300. On the other hand, the effect of climate feedback on population is likely to be most keenly felt in the period after 2100. Thus it seems unlikely that the assessment of the social cost of carbon would be very sensitive to reasonable changes in the precise way climate feedback effects are incorporated into the analysis.
Thus overall, we would argue that our approach implicitly captures likely feedbacks from climate to population, at least approximately. We feel that the science does not yet lend itself to more detailed modeling that would command consensus. However, continuing research to include climate feedbacks more explicitly in long-term population projections should be pursued.
An even more fundamental question is whether projecting population to 2300 makes sense at all, given the possibility of major disruptions due to technological, environmental and other changes. The underlying assumption here is that the basic demographic patterns that have prevailed over the past century and a half, since the spread of the Industrial Revolution beyond Britain, will continue. Very broadly, these are a continuation of the fertility transition for countries with above-replacement fertility, continued fluctuations of fertility levels not too far from current or replacement levels in countries once their fertility transition is complete, and continued steady improvement in life expectancy of the kind that has prevailed over the past 170 years.
One argument for making long-term population forecasts is that population is a system with a great deal of inertia that changes more slowly than most other social systems. The natural time unit in demography is the generation (roughly 27 years), and projecting to 2100 involves forecasting three generations into the future; assuming reasonable stability over three time units does not seem unreasonable. However, the year 2300 is about ten generations into the future, which makes the assumption of historic trends continuing more questionable.
One can think of various ways in which such an assumption might not be appropriate. For fertility, Warren (2015) has argued that a small subpopulation might become dominant over time if its members had consistently very high fertility, eventually leading to much higher than replacement fertility for the world population as a whole. His simulations showed, however, that it would require in the region of seven centuries for something like this to have a major global demographic impact, and its effect would likely still be modest in 2300, even if it started to happen immediately.
For mortality, our method is based on the assumption that life expectancy will continue to increase incrementally in all countries. de Grey and Rae (2007) have argued, however, that it will soon be possible for people to live much longer than they do now; for example, Aubrey de Grey has conjectured that the first person to live to 1000 years has already been born. We have not taken into account explicitly of such possibilities.
However, our results allow for the possibility of high life expectancies in some countries by 2300, with the upper bounds of our predictive intervals exceeding 120 years in some cases. Dong, Milholland, and Vijg (2016) have argued that there is a natural limit to the life expectancy of around 115 years. There does not seem to be a consensus in favor of this view in the demographic community. If there were, however, it could warrant a modest modification of our mortality model to take it into account. We do not expect that such a modification would change our results dramatically.
A different set of statistically-based probabilistic population projections for all countries to 2100 has recently been published by Vollset, et al. (2020). These have been criticized by Gietel-Basten and Sobotka (2020) and Gietel-Basten et al. (2020) (the latter a letter signed by over 100 population scientists) because they suffer from numerous issues with the underlying data, models and scenarios as well as over-simplistic interpretations of their results. The most significant differences between the results of Vollset et al. and those of the UN (United Nations, 2019a) lie in their different forecasts of fertility in high-fertility countries. Alkema (2020) has pointed out that the Vollset et al. results are based on unvalidated assumptions about increasing met need for contraception and may overestimate decreases in fertility in countries with low levels of modern contraceptive use, and also that the way they assessed their method’s performance is questionable.
Supplementary Material
Acknowledgments
This work was supported by NIH grant R01 HD070936 from the Eunice Kennedy Shriver National Institute of Child Health and Human Development. We thank Rob Hyndman for the initial suggestion to develop this paper when he was IJF Editor-in-Chief, and to the editor, associate editor and two anonymous reviewers for constructive comments. We are grateful to Kevin Rennert of Resources For the Future (RFF) for suggesting the development of a very long-term probabilistic population projections and for many helpful discussions, and to Cora Kingdon for her work on the RFF project. We are also extremely grateful to the nine discussants who made up the RFF expert panel that reviewed and discussed the first version of this work: Juha Alho, Leontine Alkema, Jakub Bijak, Patrick Gerland, Nico Keilman, Ronald Lee, Jim Oeppen, Warren Sanderson, and Tomáš Sobotka. Their written discussions and verbal comments were of exceptionally high quality, and led us to make many substantial improvements to our work; notably the inclusion of additional uncertainty in world TFR, the probabilistic treatment of migration, the area-dependent bounds on population density, and the discussion of climate and other feedbacks.
Footnotes
This is a invited paper.
Demographers often use the term population projections rather than forecasts. Projections are made under specific assumptions, and forecasts are projections made under assumptions designed to be realistic (Keyfitz, 1972). The distinction is blurry at best (except when projections are not designed to be realistic).
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Appendix A. Supplementary data
Supplementary material related to this article can be found online at https://doi.org/10.1016/j.ijforecast.2021.09.001. It includes country-specific projections to 2300: fertility (Appendix A), life expectancy (Appendix B), migration (Appendix C), population (Appendix D).
References
- Abel GJ (2010). Estimation of international migration flow tables in Europe. Journal of the Royal Statistical Society: Series A (Statistics in Society), 173, 797–825. [Google Scholar]
- Abel GJ (2013). Estimating global migration flow tables using place of birth data. Demographic Research, 28, 505–546. [Google Scholar]
- Abel GJ, & Cohen JE (2019). Bilateral international migration flow estimates for 200 countries. Scientific Data, 6, 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abel GJ, & Sander N (2014). Quantifying global international migration flows. Science, 343, 1520–1522. [DOI] [PubMed] [Google Scholar]
- Alders M, Keilman N, & Cruijsen H (2007). Assumptions for long-term stochastic population forecasts in 18 European countries. European Journal of Population, 23, 33–69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alexander M, Polimis K, & Zagheni E (2020). Combining social media and survey data to nowcast migrant stocks in the united states. Population Research and Policy Review, 39, 1–28. [Google Scholar]
- Alho JM, Alders M, Cruijsen H, Keilman N, Nikander T, & Pham DQ (2006). New forecast: Population decline postponed in Europe. Statistical Journal of the United Nations Economic Commission for Europe, 23, 1–10. [Google Scholar]
- Alho JM, Jensen SEH, & Lassila J (2008). Uncertain demographics and fiscal sustainability. Cambridge University Press. [Google Scholar]
- Alkema L (2020). The global burden of disease fertility forecasts: Summary of the approach used and associated statistical concerns. 10.31219/osf.io/3m6va, OSF Preprints. (Accessed 7 March 2021). [DOI]
- Alkema L, Raftery AE, Gerland P, Clark SJ, Pelletier F, Buettner T, et al. (2011). Probabilistic projections of the total fertility rate for all countries. Demography, 48, 815–839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Azose JJ, & Raftery AE (2015). Bayesian probabilistic projection of international migration. Demography, 52, 1627–1650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Azose JJ, & Raftery AE (2019). Estimation of emigration, return migration, and transit migration between all pairs of countries. Proceedings of the National Academy of Sciences, 116, 116–122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Azose JJ, Ševčíková H, & Raftery AE (2016). Probabilistic population projections with migration uncertainty. Proceedings of the National Academy of Sciences, 113, 6460–6465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Basten S (2013). Comparing projection assumptions of fertility in six advanced Asian economies; or ‘thinking beyond the medium variant’. Asian Population Studies, 9, 322–331. [Google Scholar]
- Basten S, Lutz W, & Scherbov S (2013). Very long range global population scenarios to 2300 and the implications of sustained low fertility. Demographic Research, 28, 1145–1166. [Google Scholar]
- Bastian B, Tejada VB, Arias E, et al. (2020). Mortality trends in the United States, 1900–2018. National Center for Health Statistics, Center for Disease Control and Prevention, Atlanta, Ga. https://www.cdc.gov/nchs/data-visualization/mortality-trends/index.htm. (Accessed 9 March 2021). [Google Scholar]
- Bongaarts J, & Bulatao R (2000). Beyond six billion: forecasting the world’s population. Washington, D.C.: National Academy Press. [Google Scholar]
- Booth H (2006). Demographic forecasting: 1980 to 2005 in review. International Journal of Forecasting, 22, 547–581. [Google Scholar]
- Canann E (1895). The probability of a cessation of the growth of population in England and Wales during the next century. The Economic Journal, 5, 505–515. [Google Scholar]
- Castanheira H, Pelletier F, & Ribeiro I (2017). A sensitivity analysis of the Bayesian framework for projecting life expectancy at birth. Technical Paper 7, United National Population Division, New York, NY. [Google Scholar]
- de Grey A, & Rae M (2007). Ending aging: the rejuvenation break-throughs that could reverse human aging in our lifetime. New York: Saint Martin’s Press. [Google Scholar]
- Demographia (2019). Demographia World Urban Areas. 15th annual edition, URL: http://www.demographia.com/db-worldua.pdf.
- Dong X, Milholland B, & Vijg J (2016). Evidence for a limit to human lifespan. Nature, 538, 257–259. [DOI] [PubMed] [Google Scholar]
- Easterling MR, Ellner SP, & Dixon PM (2000). Size-specific sensitivity: applying a new structured population model. Ecology, 81, 694–708. [Google Scholar]
- Eurostat (2020). Population projections. https://ec.europa.eu/eurostat/web/population-demography-migration-projections/population-projections-data. (Accessed 6 March 2021).
- Fosdick BK, & Raftery AE (2014). Regional probabilistic fertility forecasting by modeling between-country correlations. Demographic Research, 30, 1011–1034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gelman A, Rubin DB, et al. (1992). Inference from iterative simulation using multiple sequences. Statistical Science, 7, 457–472. [Google Scholar]
- Gerland P, Raftery AE, Ševčíková H, Li N, Gu D, Spoorenberg T, et al. (2014). World population stabilization unlikely this century. Science, 346, 234–237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gietel-Basten S, & Sobotka T (2020). Uncertain population futures: Critical reflections on the IHME scenarios of future fertility, mortality, migration and population trends from 2017 to 2100. 10.31235/osf.io/5syef, SocArXiv. (Accessed 7 March 2021). [DOI]
- Gietel-Basten SA, et al. (2020). Letter on ‘Fertility, mortality, migration, and population scenarios for 195 countries and territories from 2017 to 2100: A forecasting analysis for the global burden of disease study’ by S.E. Vollset, others. [DOI] [PMC free article] [PubMed]
- Godwin J, & Raftery AE (2017). Bayesian projection of life expectancy accounting for the HIV/AIDS epidemic. Demographic Research, 37, 1549–1610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Human Fertility Database (2019). Human fertility database, 2019. period total fertility rates and completed cohort fertility rates. Max Planck Institute for Demographic Research (Germany) and Vienna Institute of Demography (Austria). Website: www.humanfertility.org. (Accessed November 2019). [Google Scholar]
- Intergovernmental Panel on Climate Change (2014). Climate Change 2013: The Physical Science Basis: Working group I contribution to the fifth assessment report of the intergovernmental panel on climate change, WMO/UNEP. [Google Scholar]
- Keilman N (2019). Erroneous population forecasts. In Bengtsson T, & Keilman N (Eds.), Old and new perspectives on mortality forecasting (pp. 95–112). Cham, Switzerland: Springer Open. [Google Scholar]
- Keyfitz N (1972). On future population. Journal of the American Statistical Association, 67, 347–363. [DOI] [PubMed] [Google Scholar]
- Keyfitz N (1981). The limits of population forecasting. Population and Development Review, 7, 579–593. [Google Scholar]
- Lee RD, & Carter L (1992). Modeling and forecasting the time series of US mortality. Journal of the American Statistical Association, 87, 659–671. [Google Scholar]
- Lee RD, & Tuljapurkar S (1994). Stochastic population forecasts for the United States: Beyond high, medium, and low. Journal of the American Statistical Association, 89, 1175–1189. [PubMed] [Google Scholar]
- Leslie PH (1945). On the use of matrices in certain population dynamics. Biometrika, 33, 183–212. [DOI] [PubMed] [Google Scholar]
- Li N, & Lee RD (2005). Coherent mortality forecasts for a group of populations: An extension of the Lee-Carter method. Demography, 42, 575–594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li N, Lee RD, & Gerland P (2013). Extending the Lee-Carter method to model the rotation of age patterns of mortality decline for long-term projections. Demography, 50, 2037–2051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu PR, & Raftery AE (2020). Accounting for uncertainty about past values in probabilistic projections of the total fertility rate for most countries. Annals of Applied Statistics, 14, 685–705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu PR, & Raftery AE (2021). Country-based rate of emissions reductions should increase by 80% beyond nationally determined contributions to meet the 2°C target. Communications Earth & Environment, 2, 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lutz W, Sanderson WC, & Scherbov S (1996). Probabilistic population projections based on expert opinion. In The future population of the world: what can we assume today? (Revised 1996 ed.). (pp. 397–428). London: Earthscan Publications Ltd.. [Google Scholar]
- Lutz W, Sanderson WC, & Scherbov S (1998). Expert-based probabilistic population projections. Population and Development Review, 24, 139–155. [Google Scholar]
- Lutz W, Sanderson WC, & Scherbov S (2004). The end of world population growth in the 21st century: new challenges for human capital formation and sustainable development. Sterling, VA: Earthscan. [Google Scholar]
- Lutz W, Skirbekk V, & Testa MR (2006). The low fertility trap hypothesis. forces that may lead to further postponement and fewer births in Europe. Vienna Yearbook of Population Research, 2006, 167–192. [Google Scholar]
- Meehl PE (1954). Clinical versus statistical prediction: A theoretical analysis and a review of the evidence. University of Minnesota Press. [Google Scholar]
- Meehl PE (1986). Causes and effects of my disturbing little book. Journal of Personality Assessment, 50, 370–375. [DOI] [PubMed] [Google Scholar]
- National Institute of Population and Social Security Research (2017). Population projections for Japan (2016–2065). http://www.ipss.go.jp/pp-zenkoku/e/zenkoku_e2017/pp_zenkoku2017e_gaiyou.html. (Accessed 6 March 2021).
- National Research Council (2017). Valuing climate damages: updating estimation of the social cost of carbon dioxide. Washington, D.C.: The National Academies Press. [Google Scholar]
- Neal RM (2003). Slice sampling. The Annals of Statistics, 31, 705–767. [Google Scholar]
- Oeppen J, & Vaupel JW (2002). Broken limits to life expectancy. Science, 296, 1029–1031. [DOI] [PubMed] [Google Scholar]
- Pflaumer P (1988). Confidence intervals for population projections based on Monte Carlo methods. International Journal of Forecasting, 4, 135–142. [DOI] [PubMed] [Google Scholar]
- Pittenger DB (1974). A typology of age-specific net migration rate distributions. Journal of the American Institute of Planners, 40, 278–283. [Google Scholar]
- Pollard J (1969). Continuous-time and discrete-time models of population growth. Journal of the Royal Statistical Society: Series A (General), 132, 80–88. [Google Scholar]
- Preston SH, Heuveline P, & Guillot M (2001). Demography: measuring and modeling population processes. Malden, Mass.: Blackwell. [Google Scholar]
- Raftery AE (2016). Use and communication of probabilistic forecasts. Statistical Analysis and Data Mining, 9, 397–410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raftery AE, Alkema L, & Gerland P (2014). Bayesian population projections for the United Nations. Statistical Science, 29, 58–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raftery AE, Chunn JL, Gerland P, & Ševčíková H (2013). Bayesian probabilistic projections of life expectancy for all countries. Demography, 50, 777–801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raftery AE, Lalic N, & Gerland P (2014). Joint probabilistic projection of female and male life expectancy. Demographic Research, 30, 795–822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raftery AE, & Lewis SM (1996). Implementing MCMC. In Gilks WR, Richardson S, & Spiegelhalter DJ (Eds.), Markov chain Monte Carlo in practice (pp. 115–130). Boca Raton, Fla.: Chapman and Hall. [Google Scholar]
- Raftery AE, Zimmer A, Frierson DMW, Startz R, & Liu P (2017). Less than 2°C warming by 2100 unlikely. Nature Climate Change, 7, 637–641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raymer J, Guan Q, & Ha JT (2019). Overcoming data limitations to obtain migration flows for ASEAN countries. Asian and Pacific Migration Journal, 28, 385–414. [Google Scholar]
- Raymer J, Wiśniowski A, Forster JJ, Smith PW, & Bijak J (2013). Integrated modeling of European migration. Journal of the American Statistical Association, 108, 801–819. [Google Scholar]
- Reher DS (2019). The aftermath of the demographic transition in the developed world: Interpreting enduring disparities in reproductive behavior. Population and Development Review, 30, 1–29. [Google Scholar]
- Rogers A (1990). Requiem for the net migrant. Geographical Analysis, 22, 283–300. [Google Scholar]
- Rogers A, & Castro LJ (1981). Model migration schedules: Report RR-81–030, Laxenberg, Austria: International Institute for Applied Systems Analysis. [Google Scholar]
- Ševčíková H, Alkema L, & Raftery AE (2011). bayesTFR: An R package for probabilistic projections of the total fertility rate. Journal of Statistical Software, 43, 1–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ševčíková H, Li N, & Gerland P (2020). MortCast: Estimation and projection of age-specific mortality rates. R package version 2.3–0, https://CRAN.R-project.org/package=MortCast. (Accessed 15 March 2021).
- Ševčíková H, Li N, Kantorová V, Gerland P, & Raftery AE (2016). A ge-specific mortality and fertility rates for probabilistic population projections. In Schoen R (Ed.), Dynamic demographic analysis chapter 15 (pp. 285–310). New York: Springer. [Google Scholar]
- Ševčíková H, & Raftery AE (2016). bayesPop: Probabilistic population projections. Journal of Statistical Software, 75(5). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ševčíková H, Raftery AE, & Chunn JL (2019). bayesLife: Bayesian projection of life expectancy. R package version 4.1–0, URL: https://CRAN.R-project.org/package=bayesLife. (Accessed March 2021).
- Sharpe FR, & Lotka AJ (1911). A problem in age distribution. Philosophical Magazine, 21, 435–438. [Google Scholar]
- Sharrow DJ, Godwin J, He YJ, Clark SJ, & Raftery AE (2018). Probabilistic population projections for countries with generalized HIV/AIDS epidemics. Population Studies, 72, 1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shroeder EC, & Pittenger DB (1983). Improving the accuracy of migration age detail in multiple-area population forecasts. Demography, 20, 235–248. [PubMed] [Google Scholar]
- Siegel JS, & Hamilton CH (1952). Some considerations in the use of the residual method of estimating net migration. Journal of the American Statistical Association, 47, 475–500. [Google Scholar]
- Social Security Administration (2020). The 2020 annual report of the board of trustees of the federal old-age and survivors insurance and federal disability insurance trust funds, https://www.ssa.gov/oact/TR/2020/tr2020.pdf. (Accessed 6 March 2021).
- Stoto MA (1983). The accuracy of population projections. Journal of the American Statistical Association, 78, 13–20. [DOI] [PubMed] [Google Scholar]
- Tetlock PE (2005). Expert political judgment: how good is it? how can we know?. Princeton University Press. [Google Scholar]
- Tetlock PE, & Gardner D (2016). Superforecasting: the art and science of prediction. Random House. [Google Scholar]
- Tuljapurkar S, & Boe C (1999). Validation, probability-weighted priors, and information in stochastic forecasts. International Journal of Forecasting, 15, 259–271. [Google Scholar]
- UN Department of Economic and Social Affairs (1998). Recommendations on statistics of international migration (Revision 1 ed.). New York, NY: United Nations, https://unstats.un.org/unsd/publication/seriesm/seriesm_58rev1e.pdf. (Accessed 6 March 2021). [Google Scholar]
- UN Population Division (2019). International Migration 2019 Report, New York, NY: United Nations. [Google Scholar]
- United Nations (2004). World population to 2300. New York: United Nations. [Google Scholar]
- United Nations (2015). World population prospects: the 2015 revision. New York: United Nations. [Google Scholar]
- United Nations (2019a). World population prospects: the 2019 revision. New York: United Nations. [Google Scholar]
- United Nations (2019b). World population prospects. In The 2019 Revision: Methodology of the United Nations Population Estimates and Projections. New York: United Nations. [Google Scholar]
- Vallin J, & Caselli G (1997). Towards a new horizon in demographic trends: The combined effects of 150 years life expectancy and new fertility models. In Robine J-M, Vaupel JW, Jeune B, & Allard M (Eds.), Longevity: to the limits and beyond (pp. 29–68). Berlin/Heidelberg: Springer-Verlag. [Google Scholar]
- Vespa J, Medina L, & Armstrong DM (2020). Demographic turning points for the United States: population projections for 2020 to 2060: Current population reports P25–1144, Washington, D.C.: U.S. Census Bureau. [Google Scholar]
- Vienna Institute of Demography (2018). European demographic datasheet 2018. Vienna: Vienna Institute of Demography (VID) and International Institute for Applied Systems Analysis (IIASA), Wittgenstein Centre (IIASA, VID/OEAW, WU, Available at www.populationeurope.org. [Google Scholar]
- Vollset SE, Goren E, Yuan C-W, Cao J, Smith AE, Hsiao T, et al. (2020). Fertility, mortality, migration, and population scenarios for 195 countries and territories from 2017 to 2100: a forecasting analysis for the Global Burden of Disease study. The Lancet, 396, 1285–1306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warren SG (2015). Can human populations be stabilized? Earth’s Future, 3, 82–94. [Google Scholar]
- Wheldon MC, Raftery AE, Clark SJ, & Gerland P (2013). Estimating demographic parameters with uncertainty from fragmentary data. Journal of the American Statistical Association, 108, 96–110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wheldon MC, Raftery AE, Clark SJ, & Gerland P (2015). Bayesian reconstruction of two-sex populations by age: estimating sex ratios at birth and sex ratios of mortality. Journal of the Royal Statistical Society. Series A (Statistics in Society), 178, 977–1007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wheldon MC, Raftery AE, Clark SJ, & Gerland P (2016). Bayesian population reconstruction of female populations for less developed and more developed countries. Population Studies, 70, 21–37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whelpton PK (1928). Population of the United States, 1925–1975. American Journal of Sociology, 31, 253–270. [Google Scholar]
- Whelpton PK (1936). An empirical method for calculating future population. Journal of the American Statistical Association, 31, 457–473. [Google Scholar]
- World Health Organization (2014). Quantitative risk assessment of the effects of climate change on selected causes of death, 2030s and 2050s: Technical Report, Geneva, Switzerland: World Health Organization, https://apps.who.int/iris/handle/10665/134014. [Google Scholar]
- Yoo SH, & Sobotka T (2018). Ultra-low fertility in South Korea: The role of the tempo effect. Demographic Research, 38, 549–576. [Google Scholar]
- Zagheni E, Garimella VRK, Weber I, & State B (2014). Inferring international and internal migration patterns from Twitter data. In Proceedings of the 23rd international conference on world wide web (pp. 439–444). [Google Scholar]
- Zagheni E, & Weber I (2012). You are where you e-mail: using e-mail data to estimate international migration rates. In Proceedings of the 4th annual ACM web science conference (pp. 348–351). [Google Scholar]
- Zagheni E, Weber I, & Gummadi K (2017). Leveraging facebook’s advertising platform to monitor stocks of migrants. Population and Development Review, 43, 721–734. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


