Abstract
A generalized pathway model, with time-dependent parameters, is applied to describe the mortality curves of the COVID-19 disease for several countries that exhibit multiple waves of infections. The pathway approach adopted here is formulated explicitly in time, in the sense that the model’s growth rate for the number of deaths or infections is written as an explicit function of time, rather than in terms of the cumulative quantity itself. This allows for a direct fit of the model to daily data (new deaths or new cases) without the need of any integration. The model is applied to COVID-19 mortality curves for ten selected countries and found to be in very good agreement with the data for all cases considered. From the fitted theoretical curves for a given location, relevant epidemiological information can be extracted, such as the starting and peak dates for each successive wave. It is argued that obtaining reliable estimates for such characteristic points is important for studying the effectiveness of interventions and the possible negative impact of their relaxation, as it allows for a direct comparison of the time of adoption/relaxation of control measures with the peaks and troughs of the epidemic curve.
Keywords: COVID-19, Epidemic wave, Growth model, Public health
Introduction
The pandemic of the novel coronavirus disease (COVID-19), caused by the SARS-CoV2 virus, has proven to be one of the most serious health crises in recent human history. As of this writing, over half a billion of infection cases have been confirmed [1], with millions more probably having gone undetected owing to a myriad of reasons, from a lack of sufficient testing to asymptomatic infections to poor reporting practices. Sadly, more than 6.3 millions lives worldwide have thus far been lost to the disease. The global fight against COVID-19 has been made more difficult by the resurgence of infections after periods of relative control of the disease spread, thus giving rise to successive ‘epidemic waves’ [2, 3] in most countries.
Several epidemics, especially those caused by respiratory viruses, are known to occur in repeated, seasonal patterns [4–6]. The COVID-19 pandemic has shown a much more complex behavior in that the successive waves of infections in a given population group stem not so much from seasonal effects but rather from the intricate interaction between the virus propagation dynamics and the population behavior in response to interventions (or lack thereof) by the local health authorities [7]. Indeed, when restrictions are lifted (or poorly adhered to), transmission tends to increase; and, conversely, when control measures are reintroduced, the transmission rate declines. It is thus important to be able to identify, in a quantitative and reliable manner, the occurrence of distinct waves in a given epidemic dataset, as this information can help researchers and health authorities to surmise the impact of control measures (and their relaxation) on the overall epidemic evolution. Having reliable mathematical models and numerical algorithms to describe epidemic curves with multiple waves is therefore an important step in this endeavor. Several models have been considered in the literature to describe COVID-19 curves with multiple waves, such as compartmental [8–10] and growth [7, 11] models with time-dependent parameters, among others. These models, albeit satisfactory in many cases, have the disadvantage that their defining ordinary differential equations (ODE) need to be integrated numerically, which makes fitting the model to empirical data more cumbersome.
In this paper, we consider a different class of models—called the pathway approach—where the growth rate for the quantity of interest, say, the total number of cases or deaths, is given as a known, explicit function of time. The pathway approach was originally introduced to describe, in a unified manner, a large family of probability distributions [12, 13], but recently it has been applied to one-wave COVID-19 curves of cases and deaths [14]. Here, we extend the model to multiwave epidemic curves by assuming that the model parameters become time dependent, so as to reflect the changes in the underlying epidemiological conditions associated with the successive waves of infection. The specific time dependency of the model parameters is given by a multistep logistic-like function with N plateaus, where N is the number of waves, whereby each plateau represents the parameter value during the corresponding wave. We apply our time-dependent pathway model to COVID-19 mortality curves from ten selected countries, exhibiting from two up to five waves and show that the model is in excellent agreement with the empirical data for all countries considered.
The pathway approach considered here has several advantages. First, the model turns out to be quite flexible and capable of capturing the various distinct wave-like patterns present in empirical data. Second, it allows us to perform numerical fits directly on the daily data without any ODE integration involved, as the theoretical daily curve is written as an explicit function of time. This is particularly relevant for multiwave epidemics, as fittings based on numerical integration of ODEs for such cases are more computationally demanding and more prone to parameter uncertainties. Third, from the fitted theoretical curve, it is an easy matter to determine its maxima and minima and thus locate the starting and peak dates for each wave. Furthermore, the model is able to describe not only the main waves of a given epidemic curve but also smaller dynamical structures (e.g., sub-waves and ‘shoulders’) inside a main wave, as will been seen later.
Data
Here, we focus exclusively on mortality data from COVID-19, instead of infection cases. The reason for this choice is the difficulty to estimate the actual number of infected people by the SARS-CoV-2, since the confirmed cases represent only an unknown fraction of the total number of infections. In this scenario, the number of deaths attributed to COVID-19 is a somewhat more reliable measure to describe the dynamics of the epidemic [15].
As our main aim here is to analyze the successive waves of the COVID-19 epidemic in different countries, we have selected a representative set of countries that have undergone, until the maximum date considered here, namely March 3, 2022, from two up to five waves of infections. More specifically, we have analyzed the COVID-19 mortality curves for the following ten countries: Austria, Brazil, Bulgaria, Canada, Croatia, Italy, Netherlands, Slovakia, South Africa, and USA. The data used in this study were obtained from the database made publicly available by the Johns Hopkins University [16], which lists in automated fashion the number of the confirmed cases and deaths per country.
Methods
In this section, we introduce the pathway model and discuss its main mathematical aspects. We begin with the case where the model parameters are constant in time, which applies to single-wave epidemic curves. Then, we allow the model parameters to become time dependent, so as to capture multiple-wave effects.
Standard pathway model
We describe the time evolution of the daily number of cases or deaths (dD/dt) in the epidemic by means of the pathway model (PM), defined by the following ordinary differential equation:
| 1 |
where t is the time elapsed since the last day prior to the first death, such that represents the day before the first death occurred. As indicated above, the aggregated quantity D(t) could represent the cumulative number of either detected infection cases or deaths attributed to COVID-19. But here, we shall focus exclusively on death curves, for they are less affected by under reporting [15] and hence present a more reliable measure to study multiple waves of infections, which is our main goal here. The dynamical role played by the different parameters in (1) will be discussed later on. For now, it suffices to say that in order to ensure that D(t) reaches a finite value for (rather than growing indefinitely which is not epidemiologically sensible), we must require that
| 2 |
It is worth noting that the right-hand side of (1), with , corresponds to the generalized type-2 beta density function, which is one of the limiting cases of the so-called pathway approach to describe certain complex systems [12, 13]. In the pathway approach, the parameter q can be varied so as to produce a rather extensive family of probability distributions, ranging from the generalized type-1 beta functions () to the generalized type-2 beta functions (), while also recovering in the limit the generalized gamma distribution and other related distributions [13]. In epidemic dynamics, which is our main focus here, the relevant range is . It is nonetheless worth noting that the generalized type-1 beta functions () also find applications in the context of mathematical epidemiology. In this case, however, the pathway approach is formulated as a generalized logistic model, where the growth rate is written in terms of the cumulative variable D itself (rather than explicitly in terms of the time t). In other words, replacing t with D in the right-hand side of (1) and considering , one obtains the so-called beta logistic model, which has been applied to epidemic COVID-19 curves with one and multiple epidemic waves [7, 17].
Viewing the right-hand side of (1) as a probability density function can be useful to understand the underlying epidemic growth process. In this perspective, Eq. (1) says that the growth rate of the disease, , where dot denotes time derivative, counted in number of cases or deaths at a given time t, can be viewed as proportional to the probability that a new case or death may occur at time t. For a typical epidemic outbreak, one then expects that the probability is quite low in the beginning of the outbreak, then it increases rather sharply until reaching a peak, after which the probability of infection should decrease, possibly with a long tail. The PM, as defined in (1), provides a flexible approach to describe this generic behavior of an epidemic outbreak. Another noteworthy aspect of the pathway approach is the fact that its probability density function can be derived by optimizing a generalized entropy measure [18], which provides an interesting way to justify the PM as an effective macroscopic description of an underlying agent-based dynamics.
A direct integration of (1) yields the following analytic expression for the cumulative number of deaths up to time t:
| 3 |
where is the Gauss hypergeometric function. The fact that the PM has an explicit analytic solution is an important property, especially for applications in one-wave epidemic curves, for it allows a direct fit of the model to cumulative curves, where fluctuations are smaller in comparison with daily curves; see Sect. 4.1.
Figure 1a shows a plot of the function , as given by the right-hand side of (1) for the following parameter values: , , , and . Note that the shape of the curve has the expected behavior described above. One important feature of the curve defined by (1) is its asymmetry around the peak, which reflects the fast initial growth of the epidemics, followed by a slower decay of the daily number of deaths/cases after the peak, as seen in Fig. 1a. In terms of the cumulative curve D(t), shown in Fig. 1b, this dynamics translates as follows: The curve displays a rapid early rise, followed by a nearly linear growth regime around the inflection point (which corresponds to the peak of the daily curve), after which the growth profile decelerates and starts to approach a plateau, which corresponds to the total number of cases/deaths at the end of the epidemics (assuming there is only one wave of infections). The different regimes of the growth dynamics mentioned above are governed by the different parameters of the model, as discussed next.
Fig. 1.
Plots of the daily (a) and cumulative (b) curves for the pathway model with the following (constant) parameters: , , , , and
First, taking the limit in (1) yields
| 4 |
so that the cumulative curve has a polynomial early growth:
| 5 |
where and . Incidentally, Eq. (4) can be used to estimate the order of magnitude of the constant C, which as we shall see is the smallest parameter in the model. If we define as the approximate day of the beginning of the fully developed epidemic growth (roughly 2 weeks), then , where is the number of daily deaths at time . Setting and , we can see that for values of . Similar analysis shows that the parameter is also rather small, being comparable to or sometimes even smaller than C, while the exponents , q, and are typically of the order of unity. Controlling the numerical errors associated with such small values of C and (in comparison with the other parameters) is one of the challenges of our fitting algorithm; see below. Now, differentiating (1) and setting it to zero, one finds that the inflection point of the cumulative curve (corresponding to the peak of the daily curve), defined by , is given by
| 6 |
In view of (6), we can alternatively write (1) as
| 7 |
Let us now analyze the large-time behavior of D(t), i.e., for . First, we compute the final plateau, K, of the cumulative epidemic curve, where . Writing , where is as in (1), and performing the integration yields
| 8 |
Now taking the limit in (1), one obtains
| 9 |
which upon integration yields
| 10 |
where
| 11 |
and
| 12 |
with condition (2) ensuring that .
Equation (10) thus shows that the PM has the important property that the cumulative curve approaches the plateau as a power law, rather than exponentially fast as would be predicted by, say, the standard compartmental models of the SIR type. Recent analyses [17] have shown that the COVID-19 fatality curves for many countries do indeed display such a polynomially slow approach to the plateau (during the first wave of the disease). Hence it is important to consider theoretical models with power-law behavior. Several such models have been discussed in the literature, including generalized logistic models [17] and compartmental models with nonlinear incidence rate [19]. One advantage of the pathway approach, as already mentioned, is that it is formulated explicitly in time, making its power-law behavior rather manifest.
For completeness, we note that in the limit , Eq. (1) becomes
| 13 |
showing that in this limit, the daily curve has a stretched-exponential decay after the peak, whereas in the general case (), it has a power-law tail, as shown in (9).
From the preceding analysis, a few words can be said about the role that each parameter plays in defining the overall shape of the curve D(t). First, it is obvious from (4) that the parameter controls the early growth regime, as it defines the exponent of the polynomial growth at the beginning of the outbreak. Second, note that, although the parameter enters into the expression for the exponent in (12), it is clear that is more sensitive to variations in the parameter q. Besides, the power-law behavior shown in (10) is only possible for , with yielding a stretched-exponential behavior, as mentioned above. It can thus be said that q is mainly responsible for controlling the power-law saturation regime, while adds flexibility to the model as it contributes to the asymmetry of the cumulative (daily) curve around the inflection point (peak). Third, one sees from (6) that the parameter sets the time scale for the location of the inflection point . Finally, let us consider the role of the pre-factor C in (1). In statistical applications of the pathway approach, where the right-hand side of (1) is a probability density function, C is a normalizing constant which can be obtained in terms of the other parameters. In a similar vein, as the ‘area’ under the daily curve yields the total number of deaths/cases at the end of the epidemic, it is natural to expect that C should relate to the value of the plateau K of the cumulative curve, which is indeed the case as shown in (8). As the value of K is not known a priori, we must therefore take C as a free parameter to be estimated from the numerical fit of the model to the data.
As described above, the set of parameters of the pathway model can capture a rich class of dynamical behaviors and therein lies the model’s power and flexibility. The pathway approach has, however, the drawback that the model parameters are not easily interpreted in terms of standard epidemiological concepts, as in the case of compartmental models. In this context, it should be noted that some logistic-like growth models can be ‘mapped’ onto respective compartmental models [7, 20, 21], whereby the parameters of the former models can be put into correspondence (albeit in a coupled and nonlinear manner) with the parameters of the latter. A similar comparative study between the pathway approach and compartmental models is therefore an interesting topic for future research.
The pathway approach in its probabilistic version has been applied to a great variety of physical phenomena, for instance in astrophysics and statistical mechanics [13]. More recently, this approach was also used to model epidemic dynamics in the context of the COVID-19 pandemic [14], where the main idea was to predict the day in which the peak of the curves of active cases and daily deaths would be achieved in various countries. Here, we shall pursue further the epidemiological application of the PM by extending it to the case of multiple waves of infections, as described next.
Multiple-wave model
To describe epidemic curves with multiple waves of infections, we shall continue to use the PM, as given by (1), but now we assume that all model parameters are time dependent, which we indicate by writing C(t), , q(t), , and . Furthermore, to capture the distinct growth regimes corresponding to the successive waves, we propose that these parameters evolve in time according to the following generalized logistic function
| 14 |
where stands for any of the model parameters, that is, , and N is the number of waves. The function given in (14) describes a curve with N plateaus, whose values are denoted by the constants , , where each plateau represents the corresponding parameter value during the i-th infection wave. The constants , , determine the transition times between successive waves; whereas the constants characterize how rapid this transition takes place, so that the larger the value of , the faster the transition to the next wave regime. The transition times, , and transition rates, , are assumed to be the same for all model parameters. This is justified because an overall change in the epidemic dynamics, as a result, say, of the adoption or relaxation of control measures, is expected to affect simultaneously all epidemiological parameters [17]. Thus, in effective models based on a single ODE, such as the pathway approach or growth models, changes in the epidemic dynamics as result of both pharmacological and non-pharmacological interventions are reflected in time variations in the model parameters. Conversely, one may mimic the implementation of control measures by introducing a priori changes in the model parameters at some point in time and studying their impact in the future evolution of the epidemic curve [15].
In the case of time-dependent parameters, an analytical solution for the PM is no longer possible. Thus, in order to obtain the cumulative curve D(t), one must resort to a numerical integration of (1), with the parameters described by their respective transition functions as given in (14).
Figure 2a shows an example plot of a daily curve obtained from the PM (1) for three waves, i.e., , with the corresponding cumulative curve being shown in Fig. 2b. The time dependencies of the model parameters for the example given in Fig. 2 are shown in Fig. 3, where the specific plateau values entering function (14) for each model parameter are given in the figure caption. In Fig. 3, one clearly sees the three plateaus for each of the model parameters, where each such plateau gives origin to a corresponding wave in the epidemic curves shown in Fig. 2. Also indicated in Fig. 3 are the corresponding transition times , for , between i-th and the -th waves. The temporal width, , of each transition region is dictated by the corresponding transition rate (assuming that the transition times are well separated apart). An estimate of the width can be obtained by using a linear approximation for each transition region centered at the mid point between the two consecutive plateaus, in which case one finds that [7].
Fig. 2.
Plots of the daily (a) and cumulative (b) curves for the pathway model with waves, where the time-dependent parameters are as shown in Fig. 3
Fig. 3.
Plots of the model parameters used in the example with three waves () shown in Fig. 2. The respective plateau parameters entering function (14) are as follows: , , , , , , , , , , , , , , , , , , and . The plot of C(t) in the upper left panel is shown in a semi-log scale
One sees from (14) that, for a given N, the N-wave model has free parameters, corresponding to the N plateaus for each of the five model parameters , together with the ) parameters and , , describing the transition regions between successive waves. In applying a model with such a large number of parameters to empirical data, one must be careful to avoid excessive overfitting. Below we describe a fitting procedure that aims at minimizing this risk.
Data analysis
In all numerical fits reported here, we employed the Levenberg-Marquardt algorithm to solve the nonlinear least square optimization problem, as implemented in the scipy package of the Python language. In the case of single-wave epidemic curves, the empirical data can be fitted with the PM with constant parameters. Since in this case the model can be integrated exactly for the cumulative number D(t), we prefer to fit the analytic solution given in (3) to the cumulative data, where the level of noise is considerably smaller than that in the daily curve. For this reason, the fits presented in Sect. 4.1 for one-wave curves were performed on the respective cumulative empirical data using the exact solution (3). In such cases, for each given dataset, we need to determine five parameters, namely .
For epidemic curves with multiple waves, which is our main focus of interest here, the model parameters become time dependent, as discussed in Sect. 3.2, and the model no longer admits an explicit solution for the cumulative count D(t). In such cases, it is more convenient to perform the fits on the empirical data for the daily number of deaths, as the function is given explicitly by (1) and (14), thus rendering the numerical analysis easier to apply to the daily data (rather than to the cumulative counts). Thus, all numerical fits presented in Sects. 4.2–4.5 for COVID-19 curves with multiple waves were performed on the daily curves.
Owing to the large number of parameters for the multiwave model (we recall that there are free parameters for N waves), the parameter estimates returned by the fitting procedure are quite sensitive to their respective initial guesses. In particular, we noticed that the fitting procedure is particularly sensitive to the initial guesses for the transition times between successive waves. For instance, in some cases, one obtains a visually good fit to the data, but with high errors in some of the parameters, possibly indicating overfitting. We have therefore implemented some control measures to reduce overfitting, as discussed below.
First, we have imposed some range restrictions on the parameters , such that their respective lower bounds are as in (1), with an additional upper bound for equal to 3. Second, in the fitting procedure, we require that condition (2) be satisfied for the parameters of the last wave, namely
| 15 |
As discussed in Sect. 3.1, this is necessary to ensure that D(t) reaches a finite value as . Third, we have carefully selected the initial guesses for the fitting parameters, as follows. As mentioned before, the quality of the fits is quite sensitive on the choice of the initial guesses for the transitions times but less so for the other parameters. In view of this fact, we have chosen to fix the initial guesses for the parameters , for , as well as the initial guesses for the transitions rates at , for ; whereas the initial guesses for the transition times are randomly selected in intervals whose bounds are chosen a priori by visual inspection of the empirical curve. This manner to select the parameter initial guesses has proven quite satisfactory and in general yields very good fits. As already mentioned, because of the large discrepancy in orders of magnitude of the parameters and relatively to the other parameters, the errors in the fitting parameters are not reliably estimated by our routine. Nonetheless, the excellent agreement between the theoretical curves and the empirical data in all fits presented here indicates that our numerical procedure yields dependable results.
Results
As of this writing, most countries around the world have exhibited at least three or more waves of COVID-19 [22], with just a few countries having only two major waves, and hardly any with merely a single wave. As our main aim in this paper is to illustrate the application of the PM to epidemic curves with multiple waves, we have chosen a representative sample of COVID-19 fatality curves from countries that exhibit up to five waves. More specifically, we have selected a total of 10 countries, as follows: one country (Slovakia) with two waves; two countries (Brazil and Bulgaria) with three waves; three countries (Croatia, Netherlands, and South Africa) with four waves; and four countries (Austria, Italy, Portugal, and USA) with five waves. For all selected countries above, we have analyzed data up to March 3, 2022.
For completeness, we have also included examples of applications of the PM to single-wave epidemic curves. Since to this day practically every country has experienced at least a second wave of COVID-19 infections, in order to obtain single-wave curves we need to truncate the empirical data at a suitable date before the second wave had started. To exemplify such cases, we have selected three countries and respective maximum dates, as follows: Brazil, up to October 22, 2020; Italy, up to August 10, 2020; and the USA, up to June 27, 2020. Below, we start by showing model fits for one-wave curves, after which we present results for multiple waves.
Examples with one wave
In the left panels of Fig. 4, we show as green circles the empirical data for the cumulative number of COVID-19 deaths in Brazil (up to October 22, 2020), Italy (up to August 10, 2020), and the USA (up to June 27, 2020); while the black solid lines correspond to the fitted curves obtained from the exact solution (3) for the PM. The right panels in Fig. 4 show the empirical daily counts of deaths in green circles, while the solid curves represent the theoretical daily curves given by the right-hand side of (1). The black dots on the theoretical daily curves indicate the peaks of the first wave. In all fits shown, one sees a remarkable agreement between the theoretical model and the empirical data. The fit parameters for the plots shown in Fig. 4 are given in Table 2. In the remainder of this section, we present examples of recent COVID-19 epidemic curves for several countries where multiple waves of infections developed.
Fig. 4.
Left panels: cumulative number of deaths (green circles) attributed to COVID-19 for a Brazil, up to October 20, 2020, c Italy, up to August 10, 2020, and e USA, up to June 27, 2020. The solid curves are the best fits by the standard pathway model with one wave. Right panels: Daily number of deaths for the same countries as in the corresponding left panels, where the empirical data are indicated by green circles and the solid curve represents the time derivative of the respective theoretical curve in the left panels. The peaks of the daily curves are indicated by the black dots
Table 2.
Parameter estimates of the one-wave model for the selected countries shown in Fig. 4
| Parameters | Brazil | Italy | USA |
|---|---|---|---|
| C | |||
| 3.61 | 4.23 | 7.51 | |
| q | 1.10 | 1.28 | 1.27 |
| 0.0353 | |||
| 1.07 | 2.52 | 2.87 |
Example with two waves
We recall that for curves with multiple waves, the PM no longer admits an exact solution for the cumulative curve D(t). In such cases, it is more convenient to fit the daily data with the theoretical daily curve , as it is given explicitly by the right-hand side of (1), with the model parameters as in (14). In Fig. 5a, we show the empirical data (green circles) of the daily number of COVID-19 deaths for Slovakia, which has thus far developed only two main waves of COVID-19. The black solid line in this figure corresponds to the fitted curve obtained from the multiwave PM with , where the fitted parameters are given in the figure caption. In Fig. 5b, we show the corresponding cumulative curves, where the empirical data are indicated by green circles and the solid black curve was obtained by numerical integration of Eqs. (1) and (14), using the parameter values obtained from the fit in the left panel.
Fig. 5.
a Daily number of deaths (green circles) attributed to COVID-19 for Slovakia up to March 3, 2022. The solid curve is the best fit by the pathway model with three waves (), yielding the following parameters: , and . The black dots indicate the maxima and minima of the daily theoretical curve. b Cumulative number of deaths, where the empirical data are indicated by green circles and the solid curve represents the curves obtained by numerically integrating the theoretical curve in the left panel
It is interesting to notice that the first main wave in Slovakia came to almost a complete stop, before a resurgence of the disease. This is indicated by the near-zero ‘trough’ separating the two main waves in Fig. 5a, which corresponds to a near-horizontal, extended intermediate plateau in the cumulative curve in Fig. 5b. Capturing such a wide flat trough with an overall smooth curve is not an easy task, nonetheless the PM does a remarkable job in fitting Slovakia’s daily curve, as seen in Fig. 5a. The agreement between theory and data in the cumulative curves, see Fig. 5b, is also very good.
From the best-fit model, one can obtain relevant information about the epidemic evolution, such as the peak and starting dates of each wave, as represented by the maxima and minima of the theoretical daily curve, which are indicated by black dots in Fig. 5a. The calendar dates for such important characteristic points of the COVID-19 epidemic in Slovakia are given in Table 1.
Table 1.
Peak and starting dates of the main epidemic waves for all countries studied, as obtained from the maxima and minima of the respective theoretical daily curves shown in Figs. 5, 6, 7, 8
| Dynamical points | Slovakia | Brazil | Bulgaria | Croatia | Netherlands | South Africa | Austria | Italy | USA | Portugal |
|---|---|---|---|---|---|---|---|---|---|---|
| Peak of 1st wave | 02/28/21 | 06/26/20 | 12/04/20 | 12/15/20 | 04/06/20 | 08/04/20 | 04/07/20 | 03/30/20 | 04/19/20 | 04/08/20 |
| Start of 2nd wave | 08/26/21 | 11/24/20 | 01/28/21 | 02/24/21 | 07/06/20 | 11/09/20 | 09/11/20 | 09/11/20 | 06/24/20 | 08/24/20 |
| Peak of 2nd wave | 12/13/21 | 04/07/21 | 04/07/21 | 04/24/21 | 11/09/20 | 01/14/21 | 12/05/20 | 11/29/20 | 08/02/20 | 12/05/20 |
| Start of 3rd wave | – | 12/27/21 | 07/14/21 | 08/01/21 | 12/08/20 | 04/24/21 | 03/07/21 | 02/26/21 | 10/13/20 | 12/26/20 |
| Peak of 3rd wave | – | 02/10/22 | 11/03/21 | 12/01/21 | 01/06/21 | 07/28/21 | 04/08/21 | 03/31/21 | 01/17/21 | 01/29/21 |
| Start of 4th wave | – | – | – | 01/02/22 | 09/17/21 | 11/20/21 | 08/07/21 | 07/11/21 | 07/02/21 | 05/02/21 |
| Peak of 4th wave | – | – | – | 02/15/22 | 12/05/21 | 02/01/22 | 12/04/21 | 09/09/21 | 09/21/21 | 08/20/21 |
| Start of 5th wave | – | – | – | – | – | – | 01/13/22 | 10/25/21 | 11/18/21 | 10/22/21 |
| Peak of 5th wave | – | – | – | – | – | – | 02/28/22 | 01/27/22 | 01/30/22 | 03/03/22 |
Countries with three waves
In Fig. 6, we show the empirical data (green circles) of the daily number of COVID-19 deaths for Brazil and Bulgaria, two countries that have experienced three major waves of the pandemic. The black solid lines in this figure correspond to the fitted curves obtained from the multiwave PM (1), where the time dependency of the parameters is as given in (14) for . (The parameter values of the theoretical curve for the fits shown in Fig. 6 are given in Table 3.)
Fig. 6.
Left panels: daily number of deaths (green circles) attributed to COVID-19 for a Brazil and c Bulgaria, up to March 3, 2022. The solid curves are the best fits by the pathway model with three waves (). The black dots indicate the maxima and minima of the daily theoretical curve that correspond to the peak and starting dates of the main waves. Right panels: Cumulative number of deaths for the same countries as in the corresponding left panels, where the empirical data are indicated by green circles and the solid curve represents the curves obtained by numerically integrating the theoretical curves in the left panels
Table 3.
Parameter estimates of the fitted daily curves for the selected countries with three waves shown in Fig. 6
| Parameters | Brazil | Bulgaria |
|---|---|---|
| 3.51 | 1.75 | |
| 1.35 | 2.98 | |
| 2.00 | 1.44 | |
| 2.36 | 7.76 | |
| 1.00 | 3.00 | |
| 1.67 | 15.3 | |
| 0.0700 | 0.0648 | |
| 336 | 294 | |
| 2.02 | ||
| 9.21 | 8.21 | |
| 1.02 | 1.16 | |
| 1.74 | 2.23 | |
| 0.0666 | 0.0946 | |
| 651 | 541 |
One sees from the left panels of Fig. 6 that in spite of large fluctuations in the empirical daily data, the theoretical curves give a very good description of the data evolution. This, in turn, translates into an excellent agreement between theory and data for the cumulative curves, as shown in the right panels of Fig. 6, where the green data are the cumulative death counts and the black solid lines are obtained by numerical integration of the theoretical curves in the corresponding left panels. The starting and peak dates for the successive epidemic waves in each country shown in Fig. 6, corresponding to the black dots indicated in the left panels of the figure, are given in Table 1.
Countries with four waves
In the left panels of Fig. 7, we show the empirical data (green circles) for the daily number of COVID-19 deaths for Croatia, Netherlands, and South Africa, superimposed with the fitted curves (black solid lines) obtained using the four-wave version of the model given by (1), with the parameters varying in time according to (14) with . (The parameter values of the theoretical curves are shown in Table 4.) As before, the right panels of Fig. 7 show the empirical (green circles) and theoretical (black solid lines) cumulative curves obtained from the daily curves shown in corresponding left panels. Once again, one sees a very good agreement between theory and data for both daily and cumulative curves. The peak and starting dates for the successive epidemic waves in each country shown in Fig. 7 are again given in Table 1.
Fig. 7.
Left panels: Daily number of deaths (green circles) attributed to COVID-19 for a Croatia, and c Netherlands, and e South Africa, up to March 3, 2022. The solid curves are the best fits by the pathway model with four waves (), while the black dots indicate the maxima and minima corresponding to the peak and starting dates of the main waves. Right panels: Cumulative number of deaths for the same countries as in the corresponding left panels, where the empirical data are indicated by green circles and the solid curve represents the curves obtained by numerically integrating the theoretical curves in the left panels
Table 4.
Parameter estimates of the fitted daily curves for the selected countries with four waves shown in Fig. 7
| Parameters | Croatia | Netherlands | South Africa |
|---|---|---|---|
| 4.23 | 7.76 | 4.34 | |
| 1.34 | 1.43 | 1.30 | |
| 3.26 | 3.86 | 3.40 | |
| 5.59 | 8.84 | 4.17 | |
| 1.08 | 1.65 | 1.23 | |
| 2.72 | 4.77 | 3.37 | |
| 0.0471 | 0.160 | 0.0904 | |
| 370 | 77.6 | 301 | |
| 3.84 | 9.70 | 4.60 | |
| 1.24 | 1.10 | 1.10 | |
| 3.20 | 1.69 | 2.98 | |
| 0.0794 | 0.0976 | 0.0644 | |
| 638 | 302 | 521 | |
| 3.77 | 10.6 | 3.44 | |
| 1.31 | 1.03 | 1.50 | |
| 3.14 | 1.43 | 3.12 | |
| 0.306 | 0.118 | 0.0344 | |
| 698 | 612 | 662 |
Countries with five waves
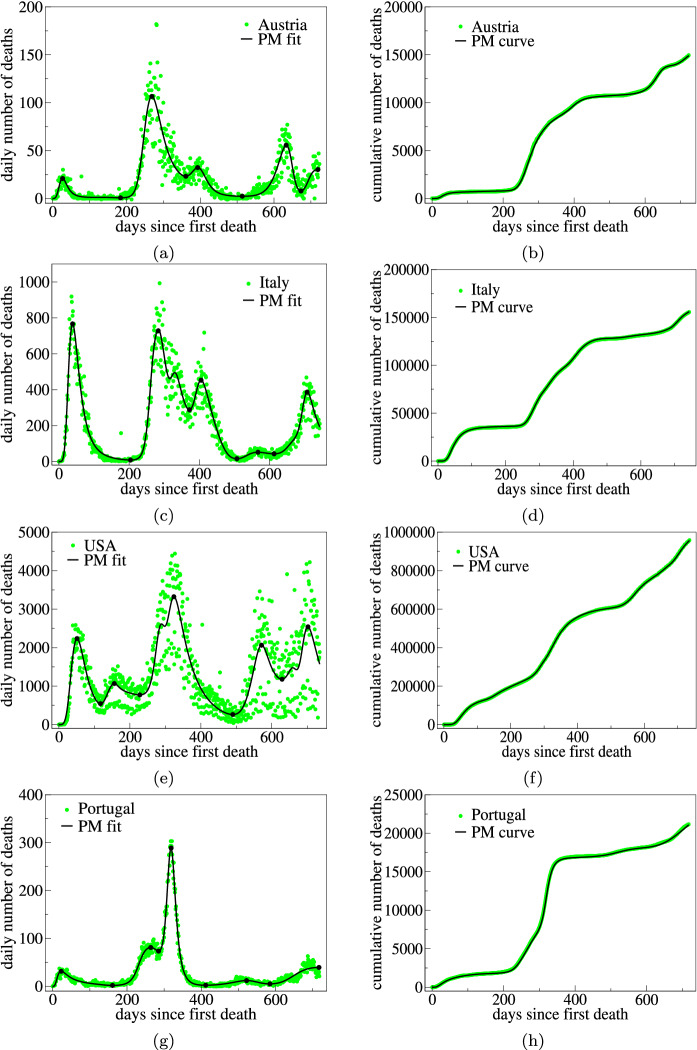
In the left panels of Fig. 8, we show the empirical data (green circles) and theoretical fits (solid black lines) of the multiwave PM with for the daily number of COVID-19 deaths for Austria, Italy, Portugal, and USA. (The parameter values of the theoretical curve are shown in Table 5.) The right panels in the figure show the empirical and theoretical cumulative curves for the corresponding daily curves in the left panels. Again, the same conclusions as before can be drawn about the efficiency of our model in fitting the empirical data, even for epidemic curves with complex evolution patterns and a larger number of waves of infections, such as those shown in Fig. 8. The peak and starting dates of the epidemic waves for the countries seen in Fig. 8 are all shown in Table 1.
Fig. 8.
Left panels: Daily number of deaths (green circles) attributed to COVID-19 for a Austria, c Italy, e USA, and g Portugal, up to March 3, 2022. The solid curves are the best fits by the pathway model with five waves (). The black dots indicate the maxima and minima that correspond to the peak and starting dates of the main waves. Right panels: Cumulative number of deaths for the same countries as in the corresponding left panels, where the empirical data are indicated by green circles and the solid curve represents the curves obtained by numerically integrating the theoretical curves in the left panels
Table 5.
Parameter estimates of the fitted daily curves for the selected countries with five waves shown in Fig. 8
| Parameters | Austria | Italy | USA | Portugal |
|---|---|---|---|---|
| 3.73 | 5.10 | 4.36 | 3.92 | |
| 1.32 | 1.36 | 1.40 | 1.37 | |
| 2.93 | 3.18 | 3.23 | 2.10 | |
| 4.06 | 3.81 | 3.72 | 3.95 | |
| 1.10 | 1.32 | 1.76 | 1.60 | |
| 2.76 | 2.64 | 3.33 | 2.84 | |
| 0.0503 | 0.129 | 0.123 | 0.0884 | |
| 174 | 271 | 156 | 154 | |
| 3.18 | 3.88 | 3.94 | 4.06 | |
| 1.25 | 2.24 | 1.25 | 1.43 | |
| 3.14 | 4.53 | 2.91 | 3.09 | |
| 0.0633 | 0.113 | 0.0986 | 0.0987 | |
| 356 | 325 | 288 | 286 | |
| 4.78 | 2.82 | 3.63 | 2.86 | |
| 1.49 | 1.24 | 1.46 | 1.22 | |
| 2.73 | 2.62 | 3.23 | 2.46 | |
| 0.0150 | 0.0580 | 0.0744 | 0.0598 | |
| 509 | 490 | 529 | 332 | |
| 3.73 | 4.53 | 3.84 | 4.90 | |
| 1.37 | 1.12 | 1.14 | 1.45 | |
| 2.66 | 2.50 | 3.06 | 3.45 | |
| 0.0950 | 0.0811 | 0.101 | 0.0343 | |
| 663 | 693 | 664 | 593 |
Discussion
We have seen above that the PM, as defined in (1) and (14), is a versatile model that is able to capture with a considerable degree of fidelity the complex patterns of COVID-19 epidemic curves with multiple waves of infection. An important advantage of the pathway approach to bear in mind is that it yields an explicit model, meaning that the expression for the daily curve, represented by in (1), is written explicitly in terms of the time variable, which makes it quite convenient for direct fits to the daily empirical data. Contrast this with the usual growth and compartmental models, where the respective differential equations are given in terms of the accumulated variables, thus requiring a numerical integration of the model before it can be fitted to the data [7]. A minor conceptual downside of the pathway formulation is that it cannot be formally rewritten as a standard growth model, since the dependency of the growth rate on the cumulative quantity D is not known a priori nor can it be easily obtained (if possible at all), although it could be easily computed numerically. This makes the epidemiological interpretation of the parameters of the PM less direct than, say, those of compartmental and growth models [7, 17]; see Sect. 3.1. Nonetheless, the PM has proven very effective in describing epidemics with complex multiwave behavior, as shown here, and as such it contributes an important tool to the mathematical epidemiology toolbox.
Another important aspect of the PM is that it has an in-built complexity that stems from the multistep logistic function (14) used for the time dependency of the parameters. This allows for a rich behavior that is not easily anticipated from the model’s equation of motion. For example, in addition to the N main peaks (for a given N), the model is also able to capture ‘subwaves’ (i.e., smaller peaks) and ‘shoulders’ (i.e., flatter portions) near a main peak. Examples of these interesting features can be seen, for instance, in Figs. 6a, c, 8c, and e.
As already mentioned, from the fitted theoretical curve for a given location, one can extract relevant information about the dynamical evolution of the disease in the chosen location. For example, from the fitted theoretical daily curve, it is a simple matter to determine its maxima and minima, where the former points correspond to the waves’ peaks, when the epidemic was at its worst periods; while the latter indicate periods when an epidemic wave has subsided, meaning that some control of the disease spread had by then been attained, after which a resurgence of infections takes place (probably owing to relaxation of control measures), thus characterizing the beginning of a new wave. Obtaining reliable estimates for the starting and peak dates for each successive wave is important for researchers and health authorities [23–25], as it allows for a direct comparison of the occurrence of peaks and troughs in an epidemic curve with the timing of containment measures, thus making it possible to study in a more quantitative fashion the efficacy of interventions and the (possibly negative) impact of their relaxation.
It is important to point out that the type of information extracted from mathematical models, such as the PM, cannot be easily obtained—at least not with the same degree of accuracy—from a mere visual inspection of neither the raw empirical data nor its moving-average smoothed version [11, 26]. Indeed, the large fluctuations in the daily data make usual smoothing procedures less reliable for such purposes. Mathematical models are therefore required to obtain a sound quantitative description of the epidemic dynamics. Another important aspect of the PM that we would like to point out is its applicability to the daily number of both deaths and infection cases. For instance, a combined analysis of cases and deaths within the pathway approach was performed for the first COVID-19 wave in several countries [14]. Similar analysis could in principle be extended to multiple waves, albeit it is more numerically demanding and hence will be left for future studies.
Conclusion
In this paper, we have studied the dynamics of multiple waves of COVID-19 infections by means of a generalized pathway model with time-dependent parameters. The pathway approach used here is formulated explicitly in time by writing the growth rate of the relevant epidemic variable (in our case, number of deaths attributed to COVID-19) as a prescribed function of time—more specifically, a type-2 beta function [12]. The explicit timewise nature of the model allows it to be fitted directly to daily data without the need of any ODE integration [14].
Here, we have extended the pathway model to the case of epidemic curves with multiple waves by assuming that the original model parameters are time dependent, so as to capture the successive acceleration-deceleration-reacceleration regimes (waves) of the disease. More concretely, in order to describe an epidemic curve with N waves, we assumed that the parameters vary in time according to a multistep logistic function with N plateaus, where each plateau represents the parameter value during the respective wave [7]. We have applied the model to the daily number of COVID-19 deaths for ten selected countries—all exhibiting multiple waves of infections (ranging from two to five). Our results show that the model is very efficient in modeling such complex epidemic data.
From the fitted model, important characteristic points of the epidemic evolution, such as the starting and peak dates for each wave, can be easily obtained. We have argued that this type of information should be helpful in analyzing the effectiveness of both pharmacological and non-pharmacological interventions. For instance, it is expected that the time for an epidemic wave to reach a peak should correlate positively with the delay to adopt control measures and negatively with their strength [15]. Conversely, it is reasonable to expect that the beginning of a reacceleration regime (new wave) is in part due to relaxation of control measures or perhaps to the appearance of new pathogen variant or both. Similarly, the start of vaccination should help to tame an epidemic wave. As the main goal of the present paper was to introduce the pathway approach for multiwave epidemics and show its efficiency in describing COVID-19 data, a more detailed study about the effectiveness of intervention measures along the lines outlined above is left for future work. As a concluding remark, we note that although the pathway approach presented here was focused on the COVID-19 pandemic, the model can be readily applied to any infectious disease, old and new, thus opening new possibilities of applications.
A Tables of fitted parameters
Author Contributions
The study was conceived and designed by GV, AM, and UT. Material preparation, data collection, and numerical analysis were performed by NP and NS. AB and RO provided additional data analysis. All authors contributed to the discussion of the results. The first draft of the manuscript was written by GV and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.
Funding
This work was supported in part by the following Brazilian agencies: Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), under Grants No. 312985/2020-7 (GLV), No. 312612/2019-2 (AMSM), No. 305305/2019-0 (RO) and No. 167348/2018-3 (AAB), and Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES). GLV also acknowledges partial funding from UFPR through the COVID-19/PROIND-2020 Research Program. U.T. is a member of the Science Academy, Bilim Akademisi, Turkey.
Data availability
The data used in this study are available in the public repository maintained by the Center for Systems Science and Engineering at the Johns Hopkins University, https://coronavirus.jhu.edu/map.html.
Declarations
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Humanitariam Data Exchange. Novel Coronavirus (COVID-19) Cases Data. https://data.humdata.org/dataset/novel-coronavirus-2019-ncov-cases (2020). Accessed 26 Aug 2022
- 2.Jefferson, T., Heneghan, C.: Covid 19 – Epidemic ‘waves’. The Centre for Evidence-Based Medicine, University of Oxford. https://www.cebm.net/covid-19/covid-19-epidemic-waves (2020). Accessed 20 Jun 2022
- 3.Wagner, A.L.: What makes a ‘wave’ of disease? An epidemiologist explains. TheConversation, July 6, 2020.https://theconversation.com/what-makes-a-wave-of-disease-an-epidemiologist-explains-141573 (2020). Accessed 20 Jun 2022
- 4.Grassly NC, Fraser C. Seasonal infectious disease epidemiology Proceedings. Biol. Sci. 2006;273(1600):2541. doi: 10.1098/rspb.2006.3604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Fisman D. Seasonality of viral infections: mechanisms and unknowns. Clin. Microbiol. Infect. 2012;18(10):946. doi: 10.1111/j.1469-0691.2012.03968.x. [DOI] [PubMed] [Google Scholar]
- 6.Moriyama M, Hugentobler WJ, Iwasaki A. Seasonality of respiratory viral infections. Annu. Rev. Virol. 2020;7(1):83. doi: 10.1146/annurev-virology-012420-022445. [DOI] [PubMed] [Google Scholar]
- 7.Vasconcelos GL, Brum AA, Almeida FAG, Macêdo AMS, Duarte-Filho GC, Ospina R. Standard and anomalous waves of COVID-19: a multiple-wave growth model for epidemics. Braz. J. Phys. 2021;51(6):1867. doi: 10.1007/s13538-021-00996-3. [DOI] [Google Scholar]
- 8.Friston, K.J., Parr, T., Zeidman, P., Razi, A., Flandin, G., Daunizeau, J., Hulme, O.J., Billig, A.J., Litvak, V., Price, C.J., Moran, R.J., Lambert, C.: Second waves, social distancing, and the spread of COVID-19 across America. arXiv preprint arXiv:2004.13017 (2020) [DOI] [PMC free article] [PubMed]
- 9.Friston, K., Parr, T., Zeidman, P., Razi, A., Flandin, G., Daunizeau, J., Hulme, O., Billig, A., Litvak, V., Moran, R., Price, C., Lambert, C.: Dynamic causal modelling of COVID-19. Wellcome Open Res. 5(89), (2020) [DOI] [PMC free article] [PubMed]
- 10.Cacciapaglia, G., Cot, C., Sannino, F.: Second wave COVID-19 pandemics in Europe: a temporal playbook. Sci. Rep. 10(1), 1 (2020) [DOI] [PMC free article] [PubMed]
- 11.Brum, A.A., Vasconcelos, G.L., Duarte-Filho, G.C., Ospina, R., Almeida, F.A.G., Macêdo, A.M.S.: ModInterv COVID-19: An online platform to monitor the evolution of epidemic curves. medRxiv 10.1101/2022.01.31.22270192. https://www.medrxiv.org/content/early/2022/06/06/2022.01.31.22270192 (2022) [DOI] [PMC free article] [PubMed]
- 12.Mathai A. A pathway to matrix-variate gamma and normal densities. Linear Algebra Appl. 2005;396:317. doi: 10.1016/j.laa.2004.09.022. [DOI] [Google Scholar]
- 13.Sebastian N, Nair SS, Joseph DP. An overview of the pathway idea and its applications in statistical and physical sciences. Axioms. 2015;4(4):530. doi: 10.3390/axioms4040530. [DOI] [Google Scholar]
- 14.Tsallis C, Tirnakli U. Predicting COVID-19 peaks around the world. Frontiers Phys. 2020;8:217. doi: 10.3389/fphy.2020.00217. [DOI] [Google Scholar]
- 15.Vasconcelos GL, Macêdo AM, Ospina R, Almeida FA, Duarte-Filho GC, Brum AA, Souza IL. Modelling fatality curves of COVID-19 and the effectiveness of intervention strategies. PeerJ. 2020;8:e9421. doi: 10.7717/peerj.9421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hopkins, Johns: University. Coronavirus COVID-19 Global Cases by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University (JHU) Coronavirus COVID-19 Global Cases by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University (JHU). https://coronavirus.jhu.edu/map.html (2021). Accessed 26 Aug 2022
- 17.Vasconcelos GL, Macêdo AMS, Duarte-Filho GC, Brum AA, Ospina R, Almeida FAG. Power law behaviour in the saturation regime of fatality curves of the COVID-19 pandemic. Sci. Rep. 2021;11(1):4619. doi: 10.1038/s41598-021-84165-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Mathai A, Haubold H. On generalized entropy measures and pathways. Physica A. 2007;385(2):493. doi: 10.1016/j.physa.2007.06.047. [DOI] [Google Scholar]
- 19.Tirnakli, U., Tsallis, C.: Epidemiological model with anomalous kinetics: early stages of the COVID-19 pandemic. Front. Phys. 8, 613168 (2020). 10.3389/fphy
- 20.Wang XS, Wu J, Yang Y. Richards model revisited: Validation by and application to infection dynamics. J. Theor. Biol. 2012;313:12. doi: 10.1016/j.jtbi.2012.07.024. [DOI] [PubMed] [Google Scholar]
- 21.Macêdo AM, Brum AA, Duarte-Filho GC, Almeida FA, Ospina R, Vasconcelos GL. A comparative analysis between a SIRD compartmental model and the Richards growth model. Trends Comput. Appl. Math. 2021;22(4):1. doi: 10.5540/tcam.2021.022.04.00545. [DOI] [Google Scholar]
- 22.Hopkins, J.: Mortality analyses. Coronavirus resource center. Mortality analyses. https://data.humdata.org/dataset/novel-coronavirus-2019-ncov-cases (2021). Accessed 02 Mar 2022
- 23.de Lima Gianfelice PR, Sovek Oyarzabal R, Cunha A, Vicensi Grzybowski JM, da Conceição Batista F, Macau EEN. The starting dates of COVID-19 multiple waves. Chaos Interdiscip. J. Nonlinear Sci. 2022;32(3):031101. doi: 10.1063/5.0079904. [DOI] [PubMed] [Google Scholar]
- 24.Li Z, Lin S, Rui J, Bai Y, Deng B, Chen Q, Zhu Y, Luo L, Yu S, Liu W, Zhang S, Su Y, Zhao B, Zhang H, Chiang YC, Liu J, Luo K, Chen T. An easy-to-use public health-driven method (the generalized logistic differential equation model) accurately simulated COVID-19 epidemic in wuhan and correctly determined the early warning time. Frontiers Public Health. 2022 doi: 10.3389/fpubh.2022.813860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Jang SY, Hussain-Alkhateeb L, Rivera Ramirez T, Al-Aghbari AA, Chackalackal DJ, Cardenas-Sanchez R, Carrillo MA, Oh IH, Alfonso-Sierra EA, Oechsner P, Kibiwott Kirui B, Anto M, Diaz-Monsalve S, Kroeger A. Factors shaping the COVID-19 epidemic curve: a multi-country analysis. BMC Infect. Dis. 2021;21(1):1032. doi: 10.1186/s12879-021-06714-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Vasconcelos, G.L., Duarte-Filho, G.C., Brum, A.A., Ospina, R., Almeida, F.A., Macêdo, A.: Situation of COVID-19 in Brazil in August 2020: An Analysis via Growth Models as Implemented in the ModInterv System for Monitoring the Pandemic. J Control Autom Electr Syst pp. 1–19 (2022)
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data used in this study are available in the public repository maintained by the Center for Systems Science and Engineering at the Johns Hopkins University, https://coronavirus.jhu.edu/map.html.