Summary
Brain‐state‐dependent stimulation during slow‐wave sleep is a promising tool for the treatment of psychiatric and neurodegenerative diseases. A widely used slow‐wave prediction algorithm required for brain‐state‐dependent stimulation is based on a specific amplitude threshold in the electroencephalogram. However, due to decreased slow‐wave amplitudes in aging and psychiatric conditions, this approach might miss many slow‐waves because they do not fulfill the amplitude criterion. Here, we compared slow‐wave peaks predicted via an amplitude‐based versus a multidimensional approach using a topographical template of slow‐wave peaks in 21 young and 21 older healthy adults. We validate predictions against the gold‐standard of offline detected peaks. Multidimensionally predicted peaks resemble the gold‐standard regarding spatiotemporal dynamics but exhibit lower peak amplitudes. Amplitude‐based prediction, by contrast, is less sensitive, less precise and – especially in the older group – predicts peaks that differ from the gold‐standard regarding spatiotemporal dynamics. Our results suggest that amplitude‐based slow‐wave peak prediction might not always be the ideal choice. This is particularly the case in populations with reduced slow‐wave amplitudes, like older adults or psychiatric patients. We recommend the use of multidimensional prediction, especially in studies targeted at populations other than young and healthy individuals.
Keywords: acoustic stimulation, aging, amplitude, slow‐wave prediction, slow‐wave sleep, topographic maps
1. INTRODUCTION
Brain‐state‐dependent stimulation (BSDS) during slow‐wave sleep (SWS) is a non‐invasive method to increase or disrupt slow‐wave activity (SWA) of SWS (Fehér et al., 2021). The method enjoys growing scientific interest due to the health‐promoting role of SWS across many domains, such as memory, clearance of metabolic waste or mental health (Léger et al., 2018). Particularly, BSDS is discussed as a preventative and therapeutic tool to counteract cognitive decline in aging (Wunderlin et al., 2020).
Brain‐state‐dependent stimulation relies on algorithms that monitor brain activity via electroencephalogram (EEG) measurements, detect a specific phase of the oscillatory waveform, most commonly the slow‐wave (SW) peak, and apply acoustic stimuli following either a fixed time‐interval or when certain criteria inherent to the signal are met (Ngo et al., 2013). A widely used method to detect SW‐peaks is to wait for the EEG signal at a frontal location to undercut an amplitude threshold with the expectation that a sufficiently strong signal valley is followed by a signal peak (Ngo et al., 2013; Figure 1). By continuously hitting SW‐peaks, BSDS can be used to increase the amplitude of endogenous SWs as well as inducing new trains of SWs.
FIGURE 1.
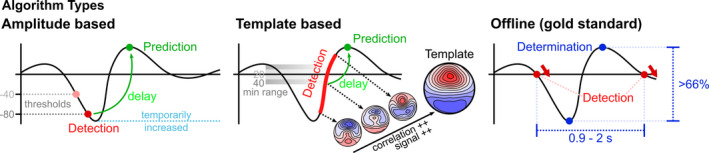
Types of slow‐wave (SW)‐peak prediction/detection algorithms. Left panel: The amplitude‐based online prediction algorithm is based on the detection of specific negative thresholds (grey) corresponding to a valley of a SW. The two thresholds used here are indicated (conservative: −80 µV; liberal: −40 µV). Whenever the signal in one frontal electrode (Fz) passed the threshold, a prediction was scored and a peak was marked after a pre‐calibrated post‐prediction delay (green). The threshold is perpetually set to the lowest point in the most recent 2 s of data if this point is lower than the chosen default threshold. Centre panel: The template‐based online prediction algorithm is based on detecting amplitude‐independent signal increases and magnitude‐independent increases in the correlation of the ongoing signal with a canonical template map (“Template”) of a SW‐peak. The map “Template” is a visualization of the actual template used. The higher the correlation, the closer the signal is to a SW‐peak. Additionally, the most recent 500 ms of data need to exceed a minimum range (grey highlights) for predictions to be allowed. Indicated are two of the three minimum ranges used here (conservative: 40 µV; liberal: 20 µV). Whenever both the correlation towards the canonical template as well as overall signal amplitude were increasing in more than 75% of the most recent 120 ms of data, a prediction was scored and a peak was marked after a pre‐calibrated post‐prediction delay (green). Right panel: Offline detection of SW‐peaks using a well‐established algorithm (Mölle et al., 2009). First, consecutive positive‐to‐negative zero‐crossings are detected in SW‐filtered data. The lowest and highest samples within those zero‐crossings are marked, and a peak‐sample is determined to be a SW‐peak if the interval between zero‐crossings is within 0.9 and 2 s, and if the amplitude between the lowest and highest sample is greater than 66% of the average amplitudes of all candidate waves
Slow‐waves serve a key role in the overnight consolidation of memory traces (Rasch & Born, 2013). One goal of BSDS is to promote memory consolidation by creating more windows of opportunity for consolidation through entrainment of SWs. Several studies show that overnight memory consolidation is increased in a BSDS versus a sham‐controlled condition (Wunderlin et al., 2021), although this effect is not consistently found (Schneider et al., 2020). So far, most experiments were conducted in young adults and only few in older adults. However, due to natural and pathological memory decline in aging, older individuals could arguably profit the most from an intervention boosting SWs and memory performance. In a recent meta‐analysis, we found a more robust effect of BSDS on memory consolidation in a subgroup model focusing on young individuals compared with a model including all age groups (Wunderlin et al., 2021). We argue that some specifics of older adults’ sleep physiology may render it more difficult to successfully apply BSDS. Schneider et al. (2020) found that BSDS entrained SWs in both younger and older groups, but the magnitude of the effect was drastically impeded in the older group. Furthermore, overnight memory consolidation was only increased in the younger, but not in the older group. A different BSDS study found an increase in overnight memory consolidation in healthy elderlies (Papalambros et al., 2017). A potential reason for the discrepancy in memory effects could be due to the arbitrary amplitude thresholds in SW‐prediction algorithms (Wunderlin et al., 2021). While Papalambros et al. (2017) used an amplitude threshold of −40 µV, Schneider et al. (2020) used a threshold of −70 µV (adapted in some cases). SW‐amplitudes are reduced in older compared with younger adults (Colrain et al., 2010). Consequently, an amplitude‐dependent SW‐prediction algorithm might miss many SWs in older individuals, missing critical windows of opportunity for BSDS, resulting in insufficient stimulation for effects on memory consolidation to unfold.
Canonically, SW‐peaks are represented by a topographic state that shows frontal dominance (Dang‐Vu et al., 2008; Züst et al., 2019). This topographical representation is preserved in aging irrespective of decreased amplitudes (Muehlroth & Werkle‐Bergner, 2019). Therefore, a prediction approach focusing on the topographic representation of a SW‐peak, rather than amplitude thresholds, might be more adequate, especially in populations with decreased amplitudes, such as in aging or psychiatric patients.
Here, we compare the performance of two distinct algorithms in 21 young versus 21 old individuals: (1) a one‐dimensional algorithm imposing amplitude thresholds in a frontal channel (Ngo et al., 2013); and (2) a multidimensional, largely amplitude‐independent algorithm based on the correlation of the ongoing signal with a topographical template representing a canonical SW‐peak (topographic targeting of slow oscillations; Ruch et al., 2021). We analyse the number of predictions and spatiotemporal dynamics of the predicted peaks and compare them with a well‐established offline detection algorithm (Mölle et al., 2009). Our goal is to reliably detect SW‐peaks with a method that generalizes to settings outside of young and healthy individuals.
2. METHODS
2.1. Sample
The data consist of whole‐night polysomnographic measurements of 21 healthy younger adults (mean age: 22.3 years, 6 male) and 21 healthy older adults (mean age: 69.1 years, 3 male). All participants underwent a screening and adaptation night to ensure the absence of sleep pathologies such as apnea or restless legs syndrome. None of the participants exhibited subjective or objective sleep abnormalities. The data constitute baseline recordings (no interventions) of ongoing studies at the University Hospital of Psychiatry and Psychotherapy (UPD), Bern. EEG was recorded using a 128‐channel MicroCel Geodesic Sensor net (400 series Geodesic EEG SystemTM) from Electrical Geodesics (EGI). The data were recorded at 500 Hz referenced to Cz. Polysomnographic scoring of sleep stages according to the American Academy of Sleep Medicine (AASM; Iber, 2007) was performed by an experienced and certified rater.
2.2. SW‐peak prediction algorithms
Two types of online SW‐peak prediction algorithms were compared. One is based on detecting a specific negative amplitude in the online EEG signal in one frontal electrode, Fz (amplitude‐based algorithm, A), and the other is based on the correlation of the online signal in all 128 electrodes with a canonical topographic representation of a SW‐peak (template‐based algorithm, T). Both algorithms were implemented in MATLAB (version R2019a, The MathWorks, Natick, Massachusetts, USA) and were run on pre‐recorded data lightly pre‐processed using the PREP‐pipeline (Bigdely‐Shamlo et al., 2015) implemented in the EEGLAB environment (v2019.1; Delorme & Makeig, 2004) for MATLAB. The main purpose of applying the PREP pipeline before running the algorithms was bad channel control, mimicking supervision and quality assurance by an experimenter while still maintaining realistic conditions of an online setting including sporadic artefacts, for example due to movement. Both online algorithms used a set of internal artefact gates to prevent predictions if the streamed signal exceeded artefact‐like amplitudes or signal‐jumps. After each prediction, a refractory period of 800 ms was applied to prevent further predictions. See Supplementary Material (Section 1) for a more detailed description of these implementations.
2.2.1. Amplitude‐based algorithm
The amplitude‐based (A) algorithm was implemented according to previous descriptions (Harrington et al., 2021; Ngo et al., 2013). This is one of the most widely used BSDS algorithms, and has remained conceptually largely unchanged since its original documentation (Ngo et al., 2013). The SW‐passband filtered (0.25–4 Hz) EEG signal at electrode Fz, referenced to pooled mastoids, was streamed into a 5‐s buffer. If the most recent data sample was below a continuously updating detection threshold, the occurrence of a SW‐peak was predicted (Figure 1). Every 2 s, the 5‐s buffer was scanned for its minimum value. If this minimum was smaller than a default threshold, the detection threshold was updated to this new minimum value. The algorithm was run using previously reported default thresholds of −80 µV (conservative; Harrington et al., 2021; Ngo et al., 2013) and −40 µV (liberal; Garcia‐Molina et al., 2018; Papalambros et al., 2017), in the following sections referred to as “A‐80” and “A‐40”. After a prediction, a per‐subject fixed delay was applied before scoring a peak prediction (see Section 2.2.4 ‘Peak prediction’ for a detailed description of how this delay was determined).
2.2.2. Template‐based algorithm
The template‐based (T) algorithm is an adaptation of a novel algorithm described elsewhere in more detail (Ruch et al., 2021; https://zenodo.org/record/5661989). The broadly filtered (0.25–45 Hz) EEG signal of all 128 channels, referenced to the global average, was streamed into a 2‐s buffer. During each iteration of the algorithm loop, the most recent data of the buffer were analysed in three parts, all of which needed to be Boolean “true” for a SW‐peak prediction (Figure 1): (1) analysis for rising voltage in frontal channels within the most recent 120 ms of data; (2) analysis for topographic correlation with a canonical template map of a SW‐peak within the most recent 120 ms of data; and (3) analysis of minimum range within the most recent 500 ms of data. For part 1, the signals of four frontal channels (F3, F4, AF1, AF2) were averaged, then the sign of the approximate derivative was calculated, then averaged again. This resulted in an amplitude‐independent measure of how many consecutive samples within the most recent 120 ms were rising or falling, respectively, ranging from −1 (all samples were falling) to 1 (all samples were rising). If this value was larger than 0.75, part 1 of the signal analysis was set to “true”. For part 2, the same procedure was applied to the Pearson correlation of the channels in the empirical data with the channels in the canonical template at each sample, returning one Pearson r‐value per sample. Of these 120 consecutive r‐values, the average of the sign of the approximate derivative was calculated. Analogously to part 1, this yields a magnitude‐free measure of how many consecutive correlation r‐values were rising or falling (−1 to 1). If this value was larger than 0.75, the algorithm assumed the signal was developing towards a SW‐peak and part 2 of the signal analysis was set to “true”. The canonical template was provided by the original creators of this algorithm (Ruch et al., 2021), and is based on the post hoc detection of SWs in 39 datasets of SWS. Part 3 of the signal analysis was set to “true” if the range of the data was equal or above a pre‐determined threshold (minimum range criterion). As the other two parts of signal analysis are completely amplitude‐independent, part 3 was needed to reduce spurious predictions in very‐low‐amplitude data. We used three values for the minimum range criterion based on observations of algorithm performance in pilot data: 40 µV (conservative), 30 µV (intermediate) and 20 µV (liberal), referred to as “T40”, “T30” and “T20” in the following sections.
2.2.3. Offline detection algorithm and visual detection
While the A‐ and T‐based algorithms are used to predict the occurrence of a SW‐peak while data are being live‐streamed, we needed an offline gold‐standard to test their performance against. For this purpose, we implemented a widely used offline detection algorithm for SWs (Mölle et al., 2009; Staresina et al., 2015) described in the Supplementary Material (Section 2) and referred to as “offline” henceforth. In short, all consecutive positive‐to‐negative zero‐crossings that are 0.9–2 s apart were marked as SWs if the absolute valley amplitude, as well as valley‐to‐peak amplitude range was above two‐thirds of the average absolute valley amplitude and the average amplitude range, respectively (Figure 1). Furthermore, five files per age group (~25%) were manually scored for SW‐peaks by a trained and experienced rater to validate the offline detection approach. The validation showed that SW‐peaks of the offline algorithm and manually marked SW‐peaks are morphologically and topographically almost indistinguishable, but manually scored peaks tended to exhibit a higher amplitude (see Supplementary Material, Section 3).
2.2.4. Peak prediction
To align stimulations in real‐world settings with SW‐peaks, a post‐prediction delay is applied. This delay is highly dependent on the software, hardware and individual SW‐frequency. Usually, after general system‐calibrations, a baseline‐night is used to calibrate the system for every participant. Here, we assume that these calibrations are achieved with the best possible accuracy for each individual. This allows us to analyse the spatiotemporal properties of predicted SW‐peaks while controlling for circumstantial factors (like system delays or individual variability in SW‐frequency) that do not pertain to the algorithms conceptually. See Section 4 of the Supplementary Material for the peak alignment procedure.
2.3. Statistical analysis
All analyses were performed in R (version 4.1.1, R Core Team, 2021) and MATLAB (version R2019a, The MathWorks, Natick, Massachusetts, USA) using the toolboxes FieldTrip (Oostenveld et al., 2010), EEGLAB (Delorme & Makeig, 2004), Ragu (Koenig et al., 2011), CircStat (Berens, 2009) and Cocor (Diedenhofen & Musch, 2015). After SW‐peak prediction/detection was completed, the data were preprocessed (see Supplementary Material Section 5). All analyses focus on sleep stages N2 and N3 only. Markers for the different peaks as detected by A‐based, T‐based and offline approaches were written into the same full‐spectrum EEG‐file, which was subsequently preprocessed and analysed using unified settings.
The number of peaks and peak amplitudes were compared using an analysis of variance (ANOVA). The grand mean event‐related potentials (ERPs) were calculated for each algorithm type and each age group. For that purpose, the data were epoched around the peak predictions/detections between −1.5 s and 3.5 s. No baseline correction was applied to avoid biasing the signal based on existent or non‐existent SWA prior to the event. For the phase analysis, the data were filtered between 0.25 and 2 Hz before instantaneous phases of peak predictions (i.e. angle of Hilbert‐transform) and their resultant vectors were calculated. A multivariate approach using randomization statistics to analyse the topographic representation of ERPs was used. We performed a topographical outlier analysis, calculated a topographic analysis of variance (TANOVA) as well as a microstate analysis (Koenig et al., 2014). Microstate analyses allow for an investigation of how the voltage distribution across electrodes develops over time in the ERPs, and how specific temporal sections of the ERP might be represented by similar underlying neuronal sources (Koenig et al., 2014; see Supplementary Material Section 6 for more details).
3. RESULTS
All participants were normal sleepers (see Table 1 for polysomnographic and subjective sleep data). Compared with the young group, the older group exhibited a lower sleep efficiency, spent less time asleep, especially in stages N2, N3 and rapid eye movement (REM), and spent relatively more time in stage N1 (all p < 0.001).
TABLE 1.
Sleep parameters
| Young adults | Older adults | t‐value | p‐value | |
|---|---|---|---|---|
| TST a | 432 (28.4) | 325 (60.7) | −7.32 | < 0.001* |
| SE b | 85% (5.5) | 67% (10.8) | −6.98 | < 0.001* |
| WASO c | 46.2 (24.3) | 142 (51) | 7.80 | < 0.001* |
| N1 d | 44.9 (23) | 85.4 (39.1) | 4.06 | < 0.001* |
| N2 d | 200 (40.5) | 151 (35.4) | −4.20 | < 0.001* |
| N3 d | 95.5 (32.3) | 36.8 (22.7) | −6.80 | < 0.001* |
| REM e | 92.3 (24.3) | 52.3 (15.2) | −6.38 | < 0.001* |
| Subj. sleep quality f | 3.57 (1.43) | 3.67 (1.91) | 0.18 | 0.85 |
The mean values and standard deviations of relevant sleep parameters are displayed per age group.
Total sleep time (TST).
Sleep efficiency (SE) describes the percentage of sleep relative to the time spent in bed.
Wake time after sleep onset (WASO).
The times spent in each sleep stage (N1–N3) are displayed in minutes.
REM, rapid eye movement.
Subjective sleep quality was rated on an eight‐point Likert scale, where 1 indicated very good and 8 very bad sleep quality. The t‐ and p‐values for the analysis of group differences are displayed.
3.1. Number of predicted peaks
An outlier analysis was performed using the toolbox Ragu (Koenig et al., 2011) revealing one outlier in the old age group, which was removed from all analyses (see red highlight in Figure 5). The final sample contained 41 participants (n old = 20; n young = 21). The mean number of peaks during sleep stages N2/N3 differed between algorithm types. In both age groups, all algorithm types except for A‐80 predicted significantly more peaks compared with the offline algorithm (Figure 2).
FIGURE 5.
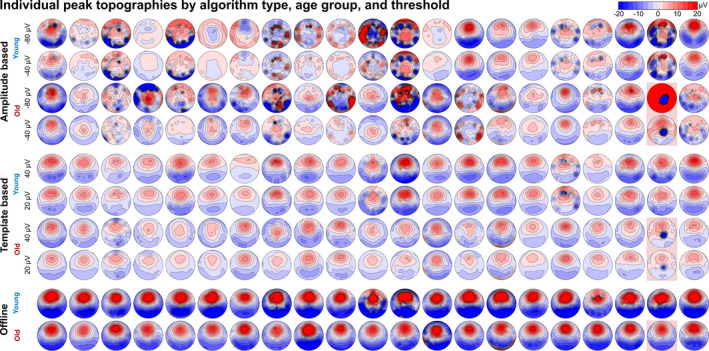
Variance of peak topographies in individual maps. Topographic maps of the predicted/detected peaks are displayed for each of the 42 study participants. The topographies are plotted for the two amplitude‐based prediction approaches (A‐40 [liberal] and A‐80 [conservative]), two of the three template‐based prediction approaches (T20 [liberal] and T40 [conservative]) and for the offline detection approach. The five marked topographies (second to last column, red highlights) represent the outlier who was excluded from all analyses
FIGURE 2.
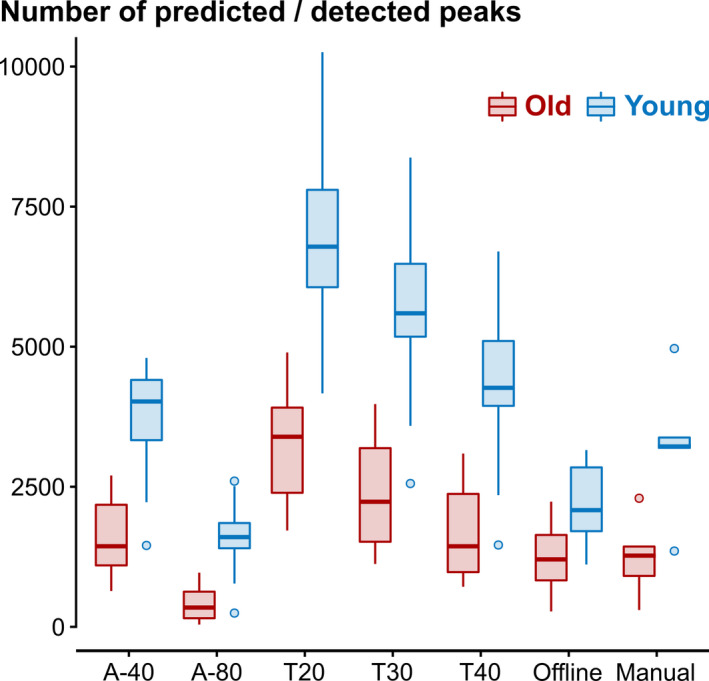
Histogram of mean predicted/detected peaks per age group and algorithm type. A‐40 and T20 represent the liberal criterion, A‐80 and T40 the conservative criterion of the amplitude (A)‐ and template (T)‐based algorithm approaches, respectively. T30 represents an intermediate criterion of the template algorithm. The two offline detection approaches were either based on a widely used slow wave (SW)‐detection approach ("Offline"; Mölle et al., 2009) or manually scored peaks by a trained rater (“Manual”; a subset of five datasets per age group [~25%])
The template‐based prediction generally predicted more peaks than the amplitude‐based prediction, which was seen in both age groups but was more pronounced in the younger group. Table 2 shows the mean number of predicted/detected peaks during N2/N3 as well as the mean peak amplitudes for all algorithm types and age groups. The mean number of predicted peaks for A‐based algorithms was 1006 for the older group and 2686 for the younger group. T‐based algorithms predicted 2453 peaks in the older group and 5594 peaks in the younger group. Offline determination detected 1236 peaks in the older group and 2189 peaks in the younger group. An ANOVA implementing a Greenhouse–Geisser correction revealed significant main effects of age (F 1,39 = 82.5, p < 0.001) and algorithm types (F 1.59,61.99 = 218.8, p < 0.001) as well as a significant interaction (F 1.59,61.99 = 40.3, p < 0.001). Bonferroni‐corrected pairwise comparisons showed that all comparisons were significant (p < 0.02), with the exception of A versus offline in the older group (p = 0.063).
TABLE 2.
Number and amplitudes of predicted/detected peaks
| Algorithm approach | Number of peaks | Amplitudes of peaks | ||
|---|---|---|---|---|
| Young adults | Older adults | Young adults | Older adults | |
| A‐40 | 3776 (843) | 1608 (682) | 6.97 µV (4.13) | 7.47 µV (4.37) |
| A‐80 | 1597 (541) | 404 (275) | 10.9 µV (7.26) | 13.4 µV (6.96) |
| T20 | 6884 (1393) | 3276 (939) | 11.1 µV (2.9) | 8.43 µV (2.89) |
| T30 | 5602 (1434) | 2436 (943) | 12.5 µV (3.21) | 9.73 µV (3.16) |
| T40 | 4298 (1326) | 1651 (787) | 14.0 µV (3.82) | 11.1 µV (3.7) |
| OFFLINE | 2189 (675) | 1236 (538) | 37.7 µV (7.36) | 25.5 µV (7.18) |
| Manual (subset n = 5) | 3223 (1281) | 1242 (732) | 40.7 µV (9.04) | 28.5 µV (9.04) |
The number of predicted/detected peaks during sleep stages N2/N3 and their respective peak amplitudes are displayed per algorithm type and age group. A‐40 and A‐80 represent the amplitude‐based algorithm types with detection thresholds of −40 µV (liberal) and −80 µV (conservative), respectively. T20, T30 and T40 represent template‐based algorithm types with a minimal range criterion of 20 µV (liberal), 30 µV (intermediate) and 40 µV (conservative). The offline detection algorithm (OFFLINE) is based on a widely used SW‐detection approach (Mölle et al., 2009). In the last column the number and amplitude of manually scored peaks by a trained rater are displayed. Manual ratings were performed for a subset of five files per age group (~25%).
The Greenhouse–Geisser‐corrected ANOVA for the mean peak amplitudes (Aold = 10.4 µV, Ayoung = 8.94 µV, Told = 9.76 µV, Tyoung = 12.5 µV, OFFLINEold = 25.5 µV, OFFLINEyoung = 37.7 µV) revealed significant main effects of age (F 1,39 = 10.5, p = 0.002) and algorithm types (F 1.64,63.79 = 344, p < 0.001), as well as a significant interaction (F 1.64,63.79 = 28.2, p < 0.001). All Bonferroni‐corrected pairwise comparisons were significant (p < 0.009), except for Aold versus Ayoung (p = 0.402) and Aold versus Told (p = 0.527).
3.2. ERPs, phase and topographies of predicted peaks
Because the number and amplitude of predicted peaks does not allow for an evaluation of the quality of SO‐peaks, the ERPs as well as peak topographies were analysed. Figure 3 displays ERPs and peak topographies for the A‐, T‐ and offline approaches. The rose plots display phase variance within the SW (0.25–2 Hz) filtered signal for predicted/detected peaks, with 0 radians representing a peak and ± π radians representing a valley. All algorithm types showed a preferred phase (resultant vector, red line, Figure 3) – close to 0° (A = −1.6521°; T = −0.0027°; offline = 0.0031°). This indicates that prediction delay calibration was successful, and the peaks are comparable across algorithm types in relation to their phase (see Supplemental Material Section 4 for information on peak alignment). The resultant vector length is an indicator for the variability of the observed phase distribution, with longer vectors indicating less phase variability. A Wilcoxon signed‐rank test revealed that the vector length for A‐based predictions (v len = 0.32) was significantly shorter than the vector length for T‐based predictions (v len = 0.39; p = 0.002). This result indicates that A‐based predictions are less phase‐precise than T‐based predictions. Both vector lengths were significantly shorter than the resultant vector length for offline detected peaks (v len = 0.93, p < 0.001).
FIGURE 3.
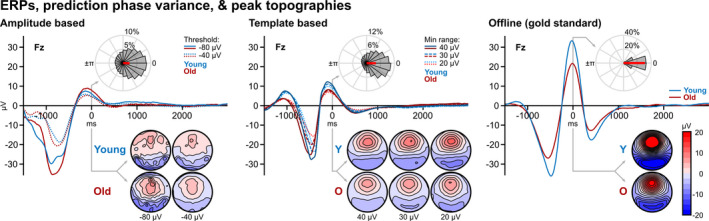
Event‐related potentials (ERPs), peak topographies and phase variance. t = 0 on the x‐axis represents the timing of the mean peak predictions/detections. Blue lines show the mean signal for younger adults, and red lines display the mean signal for older adults. Different line types represent different implementations of the respective algorithm types (A‐based: solid = −80 µV, dotted = −40 µV threshold; T‐based: solid = 40 µV, dashed = 30 µV, dotted = 20 µV minimum range). The peak topographic maps are displayed per age group and algorithm type. Rose plots show that the preferred phase of the peaks (resultant vector plotted in red) was about 0° for all algorithm types (collapsed across thresholds and age groups), confirming that all of the algorithms predicted/detected true peaks of the wave form
In order to investigate whether individual rank orders for the peak counts, peak amplitudes and resultant vector lengths correlate across methods, we performed a rank order analysis. Spearman's rank correlation coefficients between each online algorithm, threshold levels collapsed, and the offline prediction algorithm were calculated (Table 3). Overall, there was a high rank order similarity across algorithms for peak counts, i.e. all algorithms agreed which individuals exhibited high versus low numbers of peaks. For peak amplitudes, only T‐based prediction and offline detection exhibited significant rank order similarity. Phase resultant vector lengths, a measure for phase‐precision, exhibited the least amount of similarity. Only T‐based prediction and offline detection reached significant similarity, but the correlation was rather low (Table 3).
TABLE 3.
Rank correlation coefficients (Spearman's ρ) of selected peak metrics across algorithms
| Peak counts | Peak amplitude | Phase resultant vector length | |
|---|---|---|---|
| Corr(A,T) | 0.94*** | 0.25 | 0.27† |
| Corr(A, offline) | 0.75*** | 0.10 | 0.11 |
| Corr(T, offline) | 0.78*** | 0.78*** | 0.37* |
FDR‐corrected critical p = 0.028.
Abbreviations: A, amplitude‐based approach, collapsed across thresholds and age groups; T, template‐based approach, collapsed across thresholds and age groups; offline, gold‐standard for detecting peaks post hoc, collapsed across age groups.
*p = 0.017, ***p < 0.001, † p = 0.086.
The ERPs for offline detections showed a distinct negative deflection before the peak (t = 0) and a following positive deflection, with higher amplitudes found in younger adults compared with older adults. The peak topographical maps show a distinct frontal localization. The negative to positive deflection of the signal can also be observed for the A‐ and T‐based approaches. Notably, for A‐based prediction, ERP morphology and peak topography diverge compared with both T‐ and offline approaches. T‐ and offline, on the other hand, exhibit similar spatiotemporal dynamics except for differences in amplitude.
To analyse the differences in peak topographies across algorithm types and age groups, a topographic analysis of variance (TANOVA) was calculated at t = 0 (on‐peak) using randomization statistics. The two factors age (young versus old) and algorithm type (A‐40 versus A‐80 versus T20 versus T30 versus T40 versus OFFLINE) were used. To specifically test for differences of the topographical distribution of predicted peaks independent of signal amplitude, we normalized the data with respect to its global field power (GFP). Figure 4a displays normalized topographies per algorithm approach and age group. There was a significant main effect for both the factors age (p = 0.003) and algorithm type (p < 0.001) at t = 0, but no interaction. Figure 4b displays the map similarities among the conditions at t = 0 using multidimensional scaling (MDS). In this state‐space approach (Habermann et al., 2018), each point represents a condition's mean topographic map, with the distance between points indicating topographic similarity. The maps can be considered relatively similar if two conditions are close together, and different if they are further apart. The topographies of T‐based predictions cluster around the offline detection approach (especially for younger participants), while A‐based predictions are further away. To quantify the differences in topographies between the algorithm types and the offline approach, we calculated correlation coefficients for each of the 128 channel's amplitudes at t = 0 between the offline approach and all implementations of the online algorithms. Both amplitude‐based algorithms displayed lower mean correlations (r A‐40.old = 0.83 [R 2 A‐40.old = 0.75], r A‐80.old = 0.85 [R 2 A‐80.old = 0.74], r A‐40.young = 0.76 [R 2 A‐40.young = 0.66], r A‐80.young = 0.78 [R 2 A‐80.young = 0.66]) with the offline approach than the template‐based algorithms (r T20.old = 0.99 [R 2 T20.old = 0.99], r T30.old = 0.99 [R 2 T30.old = 0.99], r T40.old = 0.99 [R 2 T40.old = 0.98], r T20.young = 0.98 [R 2 T20.young = 0.98], r T30.young = 0.99 [R 2 T30.young = 0.98], r T40.young = 0.99 [R 2 T40.young = 0.98]). We compared the correlations collapsed over age groups and algorithm threshold levels using the R package Cocor (Diedenhofen & Musch, 2015). This analysis showed a significant difference between A‐based (r = 0.83) and T‐based (r = 0.99) algorithm types (Pearson and Filon's z = −3.4127, p < 0.001, Zou's 95% CI: [−0.30 −0.09]). The correlations remained different when analysing the age groups separately (young: r A = 0.78 versus r T = 0.99, Pearson and Filon's z = 2.5131, p = 0.01, Zou's 95% CI: [−0.4637 −0.0893]; old: r A = 0.87 versus r T = 0.99, Pearson and Filon's z = −2.3212, p < 0.001, Zou's 95% CI: [−0.2888 −0.0482]). Hence, T‐based algorithms predicted peaks that are highly correlated with the peaks found with the offline gold‐standard, whereas A‐based algorithms predicted peaks that are significantly less correlated with the offline gold‐standard.
FIGURE 4.
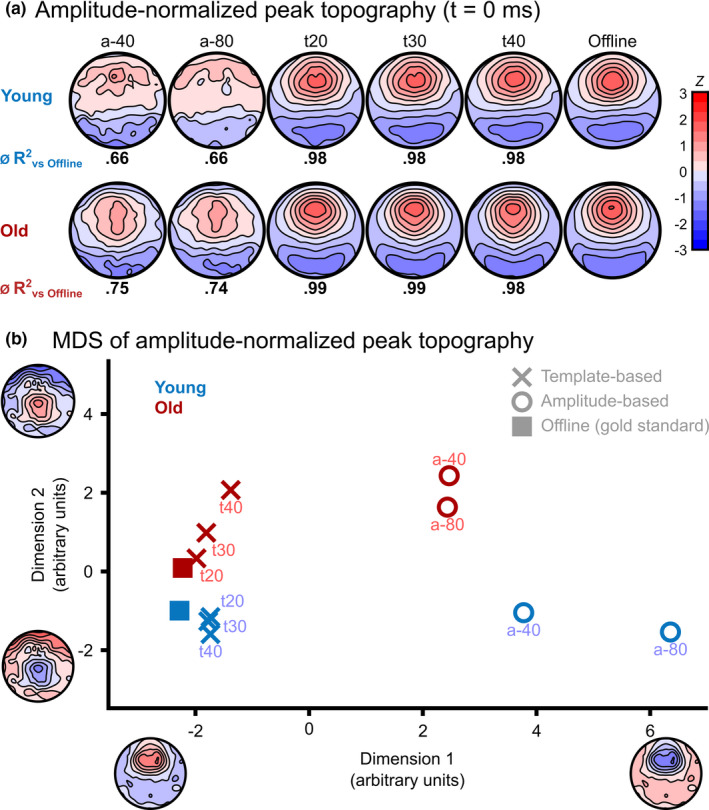
Normalized topographical maps and how they differ. (a) The displayed topographies per age group and algorithm type were normalized with respect to their global field power (GFP). Below each topography, the mean explained variance (R 2) for the channel‐by‐channel correlation between the A‐ and T‐algorithm types and the offline approach is displayed. (b) Multidimensional scaling (MDS) for topographic differences shows the mean topographic maps of each algorithm type and age group. The axes represent the principal virtual topographic features explaining most of the variance between algorithm types. The distance between two data points indicates how similar or dissimilar the respective maps are. The different algorithm types are represented by X (template‐based), O (amplitude‐based) and squares (offline gold‐standard). Older adults are displayed in red, and younger adults in blue. The maps of template‐based predictions are highly similar to the gold‐standard, as is visible by the close clustering of these data points, while amplitude‐based predictions result in relatively dissimilar maps. For template‐based predictions, similarity numerically scales with liberality of thresholds, indicating the smaller the remaining amplitude‐restriction, the more similar the maps become to the gold‐standard
These analyses indicated that the topographic representation of the predicted peaks might be different between amplitude‐ and template‐based approaches, and might not represent the same physiological state. To further investigate this, peak topographies were plotted individually for each subject and each algorithm type. The offline detection approach showed consistent topographies for all participants with differences only seen in individual amplitudes but not in the overall pattern of the surface distribution (Figure 5). Template‐based predictions displayed some level of variance, but overall showed a distinct SW‐topography in every subject – albeit with lower overall GFP owing to the fact that predictions showed higher phase variance compared with offline detection (see rose plots in Figure 3). Critically, amplitude‐based predictions showed a large variance in peak topographies, in some cases exhibiting almost the inverse (a negative frontal signal deflection) of the expected positive frontal signal deflection (Figure 5).
3.3. Microstate analysis
To investigate the temporal evolution of the topographic signal around peak predictions/detections, a microstate analysis was performed. For this analysis, we collapsed all threshold levels within the A‐ and T‐based approaches. The number of microstates in the data was determined using cross‐validation with 45 runs testing a range of 4 to 10 microstates. This procedure determined that the data were best explained with eight microstates (Figure 6). Two of these states represent “valley” states (blues in Figure 6) and three represent “peak” states (red/yellow/orange in Figure 6) corresponding to peaks and valleys in the ERP (Figure 3). The remaining three microstates resemble transitional states predominantly found as the signal drifts away from clear peak/valley states (greys in Figure 6). For all algorithm types, a peak state was present at t = 0 (states 3 and 4 in Figure 6). The peak state was identical for most approaches (state 3, red), i.e. a topography resembling a SW‐peak as found in the literature (Dang‐Vu et al., 2008; Züst et al., 2019), our own TANOVA (see previous section), and manually detected peaks (see Supplemental Material). Only A‐based prediction in the old age group did not produce this state, but rather a more centrally located and less focused peak (state 4, see yellow arrow in Figure 6). This suggests that for old individuals, the amplitude‐based prediction finds a peak state with statistically different signal sources compared with T‐based prediction and offline determination. Permutation tests (5000 permutations) were calculated to compare the area under the curve (AUC) of peak and valley states between algorithm types and age groups.
FIGURE 6.
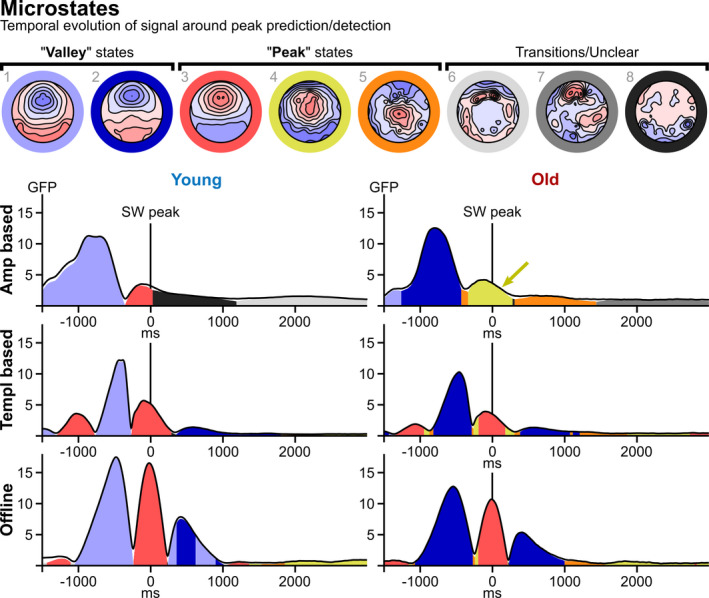
Microstate analysis. The top row displays eight identified microstates representing different predominant topographical maps with distinct underlying neuronal sources reflecting continuous periods within the event‐related potentials (ERPs). Two microstates represent valley states (blues) and three represent peak states (red/yellow/orange) and transitional states (greys), respectively. The six diagrams below the microstate maps depict the microstate time‐courses for each algorithm approach and age group. The black curves illustrate total global field power (GFP) of the data, while the coloured areas represent GFP explained by the corresponding microstates. While the peak states (t = 0) were identical for T‐ and offline approaches in both groups, the peak state in the amplitude‐based approach differed for older adults (yellow arrow). In both T‐based and offline approaches, the states oscillate between peak and valley states, while for A‐based prediction there is only a singular transition from valley to peak state. Compared with T‐based and offline approaches, the valley states in the A‐based approach are lengthier in the pre‐prediction window for both age groups, and the post‐prediction window shows a transition into an unclear state directly following the peak in the young group and a transition into a different peak state instead of a valley state in the older group. Additionally, younger and older adults exhibit different predominant valley states irrespective of algorithm type (young: light blue, state 1, relatively more centrally localized; older: dark blue, state 2, relatively more frontally localized)
For peak states, AUC for state 3 (canonical peak, red in Figure 6) is significantly different across both algorithm types and age groups (both p < 0.001), with no interaction (p = 0.544). Pair‐wise comparisons of AUC between algorithm types indicated that AUC was larger in offline‐ (4404 ms × µV ) versus T‐ (2505 ms × μV) and A‐ (527 ms × μV) approaches (all p < 0.001). In accordance with the literature (Muehlroth & Werkle‐Bergner, 2019), the younger age group exhibited larger AUC for state 3 (red, canonical peak) than the older age group (2227 versus 1306 ms × μV, p < 0.001). Conversely, for state 4 (yellow, non‐canonical peak found only for A‐based prediction in older age group) there was a significant effect of algorithm type (p = 0.047), but not age group (p = 0.196), with a significant interaction term (p < 0.001), indicating that the isolated occurrence of this state for A‐based prediction in the old age group is remarkable.
There was a dissociation of valley states among age groups. Older adults exhibit a valley state that is more frontally localized (state 2 in Figure 6) compared with younger adults (state 1 in Figure 6) across all algorithm types (see Supplementary Materials Section 6 for an analysis of valley states across algorithm types in a split group model).
Regarding the temporal structuring of states, an oscillatory back‐and‐forth between peak and valley states is apparent for both T‐based prediction and offline determination, starting with a peak at −1000 ms, oscillating twice and ending with a valley at about +800 ms. No such oscillation is apparent for A‐based predictions, where the pre‐prediction window consists of a single valley state, briefly transitioning into a low‐powered peak at about 0 ms, then quickly decaying into a transitional state (young age group) or an even more centrally localized peak state (older age group) before tapering off. The temporal GFP‐mass centre of the respective valley states was significantly different across algorithm types in both age groups (young: p = 0.012; old: p < 0.001). Pair‐wise comparisons in the younger age group indicated that mass centre was significantly earlier for A (−882 ms) versus offline (−399 ms, p = 0.025), and A versus T (−507 ms, p = 0.030). Analogously, in the older age group, mass centre was significantly earlier for A (−903 ms) versus offline (−271 ms), and A versus T (−319 ms) (both p < 0.001). There was no difference in mass centre for T versus Offline in either age group (both p > 0.19). Taken together, these results indicate that, especially in the older group, amplitude‐based prediction does not find peaks that correspond to the expected morphology and topography of SWs (Dang‐Vu et al., 2008; Züst et al., 2019).
4. DISCUSSION
A currently widely used SW‐detection algorithm is dependent on a hard amplitude threshold (Ngo et al., 2013). We show that this one‐dimensional approach may not be optimal: its predictions produced states that are different from what was determined through manually validated, automatized offline SW‐detection (Mölle et al., 2009). This was especially true for older participants. In contrast to the A‐based prediction, T‐based prediction was highly similar to the offline gold‐standard, irrespective of age group. We recommend the usage of this largely amplitude‐independent, multidimensional approach based on a topographical template (Ruch et al., 2021), especially when amplitudes are decreased, such as in aging and psychiatric conditions.
While the two online‐SW‐prediction approaches are technically different, conceptually they have the same goal: detecting SW‐peaks. All peaks – irrespective of how they were predicted – should elicit activation of a common set of neuronal sources. We tested this assumption using a topographic ANOVA and a microstate analysis. Each microstate is considered to reflect predominant and distinct activation of contributing sources and therefore distinct underlying processes (Koenig et al., 2014). Based on the temporal evolution of the signal, our analyses suggest that A‐predicted peaks might be different from T‐ and offline‐based approaches. This was particularly the case in older adults, where peaks exhibited a less frontally and more centrally shifted localization compared with the other approaches. However, the frontal dominance of SWs has been shown to be preserved in aging (Muehlroth & Werkle‐Bergner, 2019). We conclude that A‐based prediction might not be ideal for finding SW‐peaks in older adults.
Considering the number of predictions, we found that the T‐based approaches predicted more but lower‐amplitude peaks than the offline approach in both age groups. This may reflect that the offline detection approach is also amplitude‐dependent – albeit not by using a hard threshold. Only the upper 33% of detected waves in any individual are scored as valid peaks, while the lower 66% of detected waves are sorted out. Because SWs are specifically decreasing in amplitude with age (Colrain et al., 2010), the gold‐standard – just like the A‐based algorithms – might sort out many valid, lower‐amplitude SWs in older participants. The same is true for manual scoring according to AASM standards, which also employs a fixed and fundamentally arbitrary threshold. Our results illustrate that, for the purpose of detecting SWA in populations with decreased SW‐amplitudes – like aging or psychiatric populations – amplitude criteria might be detrimental.
4.1. Recommendations for algorithm usage
The A‐based algorithm is more economical as it works with a small number of electrodes. This might be particularly important in the application of easy to use mobile devices, which is an emerging interest in the field of BSDS. Furthermore, its computational requirements are lower and it is well tested in the literature (Harrington et al., 2021; Ngo et al., 2013; Schneider et al., 2020). However, its economic advantage also renders the approach more prone to artefacts and false‐positive predictions. One potential reason for the discrepancy between A‐ and T‐based approaches might owe to differences in their generalizability. We found large differences in the algorithms’ performance in individual subjects, with high inter‐individual differences seen in A‐based prediction. Notably, in some individuals, A‐based prediction topographies did not resemble the canonical SW‐pattern (Figure 5), suggesting off‐target predictions. An analysis of phase‐precision confirmed that there was a more focused phase distribution for T‐based versus A‐based prediction. Overall, A‐based algorithms can be a good and preferred tool if one is interested in group‐level effects in healthy younger individuals with high SWAs, where individual divergence is less of a concern. Also, it is the better algorithm when limited to low electrode numbers.
The T‐based algorithm is more complex, both computationally and regarding its practical implementation (see Supplementary Material Section 7 for the computational profiling of both prediction algorithms). The T‐based algorithm should be applied with a sufficiently high‐density EEG system. If the goal of a study is to stimulate as many SW‐peaks as possible, T‐based prediction has the advantage over A‐based prediction due to higher detection counts (Figure 2). If one is worried about off‐target stimulations, T‐based prediction is advantageous as it is more temporally precise (see phase diagrams in Figure 3) and reliable (see individual predicted peak topographies in Figure 5 and rank correlation analysis in Table 3). One‐dimensional A‐based prediction is more susceptible to off‐target effects compared with a multidimensional T‐based approach, which is more robust against artefactual or false‐positive signals in one channel. The topographical correlation between the streamed signal and the template will be increasing towards a peak even in the presence of bad channels. Furthermore, the T‐based predicted peaks better resemble the gold‐standard regarding spatiotemporal dynamics, especially in older adults (see microstates analysis in Figure 6). Taken together, T‐based approaches provide significant benefits when one is interested in single‐subject level effects and in populations with reduced SWAs (e.g. older individuals or psychiatric patients).
4.2. Limitations
The goal of the current report was to analyse what the different algorithm types claim to be SW‐peaks. Our analyses are limited to the comparison of unstimulated SO peaks as predicted via A‐ and T‐based algorithms. Therefore, we cannot make any statements about how physiological responses after peak‐locked stimulus delivery might be affected by the difference in predictive performance of the tested algorithms. This is an important question that needs to be addressed in future research.
Both A‐ and T‐based algorithms were run on previously recorded data simulating real‐time streaming. The algorithms might perform differently in real world settings. Furthermore, sleep acoustic stimulation studies usually require a trained experimenter to manually stop the algorithm when arousals or changes in sleep stages are indicated. As an alternative to manual supervision, some SW‐prediction algorithms automatically detect sleep stages and pause the stimulation whenever participants are in non‐desired sleep stages (Santostasi et al., 2016). Our analyses focused on sleep stages N2 and N3, and we therefore cannot comment on off‐target stimulations. However, we recommend that some form of sleep stage control is implemented, be that a vigilant experimenter or a robust automatized staging algorithm.
Our analyses are limited to the comparison of two online SW‐prediction algorithm approaches. While there are other algorithms that are used in acoustic stimulation studies, for example phase‐locked loop (Santostasi et al., 2016) or sine fitting approaches (Cox et al., 2014), we intended to specifically address the limitations of amplitude thresholds in SW‐prediction approaches. While comparisons to other SW‐prediction approaches would be interesting, it is beyond the scope of this report.
Lastly, our findings are limited to theoretical assumptions about the underlying neurophysiology of the differently predicted peaks. Future research should implement similar protocols in animal models, use intracranial recordings in epileptic patients, or perform EEG‐functional magnetic resonance imaging recordings in healthy participants.
4.3. Conclusion and future directions
Our results suggest that – although being more complex in its practical and programmatical implementation – T‐based prediction is more valid, reliable and sensitive than A‐based prediction. Arguably, this is because a multidimensional T‐based approach incorporates as much information as possible into SW‐peak prediction instead of relying on a hard threshold on one dimension of the data. Importantly, A‐based prediction might not be ideal when detecting SWs in older adults as it finds peak states that differ from canonical SW‐peaks. T‐based prediction is better suited for older adults’ sleep physiology: relatively decreased amplitudes notwithstanding, detected peaks exhibit qualitative aspects of canonical SW‐peaks like the expected spatiotemporal representation, suggesting identical signal generators in the brain. On top of superior validity and reliability, T‐based prediction is more sensitive than A‐based prediction. With more predicted SW‐peaks, more windows of opportunity arise for acoustic stimulation to aim at. This might not only prove relevant for therapeutic applications in cognitively impaired older adults (Rauchs et al., 2008; Westerberg et al., 2012), but also in other patient groups exhibiting reduced SW‐amplitudes, for example when using SW‐peak prediction in studies mimicking the effect of sleep deprivation in major depression (Wolf et al., 2016). A multidimensional‐ and largely amplitude‐independent SW‐prediction approach might do justice to the more complex sleep physiology found outside of young and healthy sleepers.
CONFLICT OF INTEREST
The authors have no conflict of interest to declare.
AUTHOR CONTRIBUTIONS
MW, CN and MZ conceptualized the current work. MW and MZ drafted the outline and first version of the manuscript. MZ implemented the algorithms. MW and MZ analysed the data. TK provided methodological support. All of the authors discussed the results, and provided critical revision of the manuscript and final approval.
Supporting information
Supplementary Material
ACKNOWLEDGEMENTS
The authors thank their collaborators, Simon Ruch, Flavio Schmidig and Katharina Henke, for sharing code of the original implementation of the T‐based algorithm, and Hong‐Viet Ngo for his helpful comments on the implementation of the A‐based algorithm. This work was supported by the Synapsis Foundation, the Peter Bockhoff Foundation, the Heidi Seiler Foundation [2018‐PI02], and the Interfaculty Research Cooperation “Decoding sleep” at the University of Bern. Open Access Funding provided by Universitat Bern.
Wunderlin, M. , Koenig, T. , Zeller, C. , Nissen, C. , & Züst, M. A. (2022). Automatized online prediction of slow‐wave peaks during non‐rapid eye movement sleep in young and old individuals: Why we should not always rely on amplitude thresholds. Journal of Sleep Research, 31, e13584. 10.1111/jsr.13584
[Corrections added on 11 and 21 April 2022, after first online publication: Three instances of the unit "ms μV‐1" was corrected to "ms × μV" under the Microstate Analysis subsection. The Ruch et al. reference was updated. CSAL funding statement has been added.]
DATA AVAILABILITY STATEMENT
The data that support the findings of this study are available from the corresponding author upon reasonable request.
REFERENCES
- Berens, P. (2009). CircStat: A MATLAB toolbox for circular statistics. Journal of Statistical Software, 31, 1–21. [Google Scholar]
- Bigdely‐Shamlo, N. , Mullen, T. , Kothe, C. , Su, K.‐M. , & Robbins, K. A. (2015). The PREP pipeline: Standardized preprocessing for large‐scale EEG analysis. Frontiers in Neuroinformatics, 9, 16. 10.3389/fninf.2015.00016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colrain, I. M. , Crowley, K. E. , Nicholas, C. L. , Afifi, L. , Baker, F. C. , Padilla, M. , Turlington, S. R. , & Trinder, J. (2010). Sleep evoked delta frequency responses show a linear decline in amplitude across the adult lifespan. Neurobiology of Aging, 31, 874–883. 10.1016/j.neurobiolaging.2008.06.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox, R. , Korjoukov, I. , de Boer, M. , & Talamini, L. M. (2014). Sound asleep: Processing and retention of slow oscillation phase‐targeted stimuli. PLoS One, 9, e101567. 10.1371/journal.pone.0101567 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dang‐Vu, T. T. , Schabus, M. , Desseilles, M. , Albouy, G. , Boly, M. , Darsaud, A. , Gais, S. , Rauchs, G. , Sterpenich, V. , Vandewalle, G. , Carrier, J. , Moonen, G. , Balteau, E. , Degueldre, C. , Luxen, A. , Phillips, C. , & Maquet, P. (2008). Spontaneous neural activity during human slow wave sleep. Proceedings of the National Academy of Sciences USA, 105, 15160–15165. 10.1073/pnas.0801819105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delorme, A. , & Makeig, S. (2004). EEGLAB: an open source toolbox for analysis of single‐trial EEG dynamics including independent component analysis. Journal of Neuroscience Methods, 134, 9–21. 10.1016/j.jneumeth.2003.10.009 [DOI] [PubMed] [Google Scholar]
- Diedenhofen, B. , & Musch, J. (2015). cocor: A comprehensive solution for the statistical comparison of correlations. PLoS One, 10, e0121945. 10.1371/journal.pone.0121945 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fehér, K. D. , Wunderlin, M. , Maier, J. G. , Hertenstein, E. , Schneider, C. L. , Mikutta, C. , Züst, M. A. , Klöppel, S. , & Nissen, C. (2021). Shaping the slow waves of sleep: A systematic and integrative review of sleep slow wave modulation in humans using non‐invasive brain stimulation. Sleep Medicine Reviews, 58, 101438. 10.1016/j.smrv.2021.101438 [DOI] [PubMed] [Google Scholar]
- Garcia‐Molina, G. , Tsoneva, T. , Jasko, J. , Steele, B. , Aquino, A. , Baher, K. , Pastoor, S. , Pfundtner, S. , Ostrowski, L. , Miller, B. , Papas, N. , Riedner, B. , Tononi, G. , & White, D. P. (2018). Closed‐loop system to enhance slow‐wave activity. Journal of Neural Engineering, 15, 066018. 10.1088/1741-2552/aae18f [DOI] [PubMed] [Google Scholar]
- Habermann, M. , Weusmann, D. , Stein, M. , & Koenig, T. (2018). A student’s guide to randomization statistics for multichannel event‐related potentials using Ragu. Frontiers in Neuroscience, 12, 355. 10.3389/fnins.2018.00355 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harrington, M. O. , Ngo, H.‐V.‐V. , & Cairney, S. A. (2021). No benefit of auditory closed‐loop stimulation on memory for semantically‐incongruent associations. Neurobiology of Learning and Memory, 183, 107482. 10.1016/j.nlm.2021.107482 [DOI] [PubMed] [Google Scholar]
- Iber, C. (2007). The AASM manual for the scoring of sleep and associated events: Rules. Terminol. Tech. Specif. [Google Scholar]
- Koenig, T. , Kottlow, M. , Stein, M. , & Melie‐García, L. (2011). Ragu: A free tool for the analysis of EEG and MEG event‐related scalp field data using global randomization statistics. Computational Intelligence and Neuroscience, 2011, 1–14. 10.1155/2011/938925 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koenig, T. , Stein, M. , Grieder, M. , & Kottlow, M. (2014). A tutorial on data‐driven methods for statistically assessing ERP topographies. Brain Topography, 27, 72–83. 10.1007/s10548-013-0310-1 [DOI] [PubMed] [Google Scholar]
- Léger, D. , Debellemaniere, E. , Rabat, A. , Bayon, V. , Benchenane, K. , & Chennaoui, M. (2018). Slow‐wave sleep: From the cell to the clinic. Sleep Medicine Reviews, 41, 113–132. 10.1016/j.smrv.2018.01.008 [DOI] [PubMed] [Google Scholar]
- Mölle, M. , Eschenko, O. , Gais, S. , Sara, S. J. , & Born, J. (2009). The influence of learning on sleep slow oscillations and associated spindles and ripples in humans and rats. European Journal of Neuroscience, 29, 1071–1081. 10.1111/j.1460-9568.2009.06654.x [DOI] [PubMed] [Google Scholar]
- Muehlroth, B. E. , & Werkle‐Bergner, M. (2019). Understanding the interplay of sleep and aging: Methodological challenges. Neuroscience. [DOI] [PubMed] [Google Scholar]
- Ngo, H.‐V.‐V. , Martinetz, T. , Born, J. , & Mölle, M. (2013). Auditory closed‐loop stimulation of the sleep slow oscillation enhances memory. Neuron, 78, 545–553. 10.1016/j.neuron.2013.03.006 [DOI] [PubMed] [Google Scholar]
- Oostenveld, R. , Fries, P. , Maris, E. , & Schoffelen, J.‐M. (2010). FieldTrip: Open source software for advanced analysis of MEG, EEG, and invasive electrophysiological data. Computational Intelligence and Neuroscience, 2011, e156869. 10.1155/2011/156869 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Papalambros, N. A. , Santostasi, G. , Malkani, R. G. , Braun, R. , Weintraub, S. , Paller, K. A. , & Zee, P. C. (2017). Acoustic enhancement of sleep slow oscillations and concomitant memory improvement in older adults. Frontiers in Human Neuroscience, 11. 10.3389/fnhum.2017.00109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Core Team . (2021). R Core Team R: A Language and Environment for Statistical Computing. R Foundation for Statistical. [Google Scholar]
- Rasch, B. , & Born, J. (2013). About sleep’s role in memory. Physiological Reviews, 93, 681–766. 10.1152/physrev.00032.2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rauchs, G. , Schabus, M. , Parapatics, S. , Bertran, F. , Clochon, P. , Hot, P. , Denise, P. , Desgranges, B. , Eustache, F. , Gruber, G. , & Anderer, P. (2008). Is there a link between sleep changes and memory in Alzheimer’s disease? NeuroReport, 19, 1159–1162. 10.1097/WNR.0b013e32830867c4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruch, S. , Schmidig, F. J. , Knüsel, L. , & Henke, K. (2021). Closed‐loop modulation of local slow oscillations in human NREM sleep. Zenodo. 10.5281/zenodo.5661989 [DOI] [PubMed] [Google Scholar]
- Santostasi, G. , Malkani, R. , Riedner, B. , Bellesi, M. , Tononi, G. , Paller, K. A. , & Zee, P. C. (2016). Phase‐locked loop for precisely timed acoustic stimulation during sleep. Journal of Neuroscience Methods, 259, 101–114. 10.1016/j.jneumeth.2015.11.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneider, J. , Lewis, P. A. , Koester, D. , Born, J. , & Ngo, H.‐V.‐V. (2020). Susceptibility to auditory closed‐loop stimulation of sleep slow oscillations changes with age. Sleep, 43, zsaa111. 10.1093/sleep/zsaa111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Staresina, B. P. , Bergmann, T. O. , Bonnefond, M. , van der Meij, R. , Jensen, O. , Deuker, L. , Elger, C. E. , Axmacher, N. , & Fell, J. (2015). Hierarchical nesting of slow oscillations, spindles and ripples in the human hippocampus during sleep. Nature Neuroscience, 18, 1679–1686. 10.1038/nn.4119 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Westerberg, C. E. , Mander, B. A. , Florczak, S. M. , Weintraub, S. , Mesulam, M.‐M. , Zee, P. C. , & Paller, K. A. (2012). Concurrent impairments in sleep and memory in amnestic mild cognitive impairment. Journal of the International Neuropsychological Society, 18, 490–500. 10.1017/S135561771200001X [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolf, E. , Kuhn, M. , Normann, C. , Mainberger, F. , Maier, J. G. , Maywald, S. , Bredl, A. , Klöppel, S. , Biber, K. , van Calker, D. , Riemann, D. , Sterr, A. , & Nissen, C. (2016). Synaptic plasticity model of therapeutic sleep deprivation in major depression. Sleep Medicine Reviews, 30, 53–62. 10.1016/j.smrv.2015.11.003 [DOI] [PubMed] [Google Scholar]
- Wunderlin, M. , Züst, M. A. , Fehér, K. D. , Klöppel, S. , & Nissen, C. (2020). The role of slow wave sleep in the development of dementia and its potential for preventative interventions. Psychiatry Res. Neuroimaging, 306, 111178. 10.1016/j.pscychresns.2020.111178 [DOI] [PubMed] [Google Scholar]
- Wunderlin, M. , Züst, M. A. , Hertenstein, E. , Fehér, K. D. , Schneider, C. L. , Klöppel, S. , & Nissen, C. (2021). Modulating overnight memory consolidation by acoustic stimulation during slow‐wave sleep: a systematic review and meta‐analysis. Sleep, 44, zsaa296. 10.1093/sleep/zsaa296 [DOI] [PubMed] [Google Scholar]
- Züst, M. A. , Ruch, S. , Wiest, R. , & Henke, K. (2019). Implicit vocabulary learning during sleep is bound to slow‐wave peaks. Current Biology, 29, 541–553.e7. 10.1016/j.cub.2018.12.038 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Material
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.


