Abstract
Feature selection is indispensable in microbiome data analysis, but it can be particularly challenging as microbiome data sets are high dimensional, underdetermined, sparse and compositional. Great efforts have recently been made on developing new methods for feature selection that handle the above data characteristics, but almost all methods were evaluated based on performance of model predictions. However, little attention has been paid to address a fundamental question: how appropriate are those evaluation criteria? Most feature selection methods often control the model fit, but the ability to identify meaningful subsets of features cannot be evaluated simply based on the prediction accuracy. If tiny changes to the data would lead to large changes in the chosen feature subset, then many selected features are likely to be a data artifact rather than real biological signal. This crucial need of identifying relevant and reproducible features motivated the reproducibility evaluation criterion such as Stability, which quantifies how robust a method is to perturbations in the data. In our paper, we compare the performance of popular model prediction metrics (MSE or AUC) with proposed reproducibility criterion Stability in evaluating four widely used feature selection methods in both simulations and experimental microbiome applications with continuous or binary outcomes. We conclude that Stability is a preferred feature selection criterion over model prediction metrics because it better quantifies the reproducibility of the feature selection method.
Keywords: classification, feature selection, microbiome, prediction, reproducible, stability
1. INTRODUCTION
Reproducibility is imperative for any scientific discovery, but there is a growing alarm about irreproducible research results. According to a survey by Nature Publishing Group of 1576 researchers in 2016, more than 70% of researchers have tried and failed to reproduce another scientist's experiments, and more than half have failed to reproduce their own experiments (Baker, 2016). This “reproducibility crisis” in science affects microbiome research as much as any other areas, and microbiome researchers have long struggled to make their research reproducible (Schloss, 2018). Great efforts have been made toward setting protocols and standards for microbiome data collection and processing (Thompson et al., 2017), but more could be achieved using statistical techniques for reproducible data analysis. Microbiome research findings rely on statistical analysis of high‐dimensional data, and feature selection is an indispensable component for discovering biologically relevant microbes. In this field, it is a common practice to use predictive models as a way to infer disease biomarkers or more generally phenotype markers for variables like age, vitamin D metabolism, and human disease status such as cancer and IBD (Gevers et al., 2014; Huang et al., 2020; Poore et al., 2020; Thomas et al., 2020). As discussed in Duvallet et al. (2017), when comparing cases versus controls, the identification of microbial features uniquely associated with a phenotype, shared among phenotypes, or uniquely associated with healthy controls can have vastly different implications for probiotic or drug development. As such in this context researchers are often interested in identifying the most relevant microbial features associated with a given outcome. This task can be particularly challenging in microbiome analyses, as the datasets are typically high dimensional, underdetermined (the number of features far exceeds the number of samples), sparse (a large number of zeros are present), and compositional (the relative abundance of taxa in a sample sum to one). Current methodological research has been focusing on developing and identifying the best methods for feature selection that handle the above characteristics of microbiome data, however, methods are typically evaluated based on overall performance of model prediction, such as Mean Squared Error (MSE), R‐squared, or Area Under the Curve (AUC). Although prediction accuracy is important, another possibly more biologically relevant criterion for choosing an optimal feature selection method is reproducibility, that is, how reproducible are all discovered features in unseen (independent) samples? If a feature selection method is identifying true signals in a microbiome dataset, then we would expect those discovered features to be found in other similar datasets using the same method, indicating high reproducibility of the method. If a feature selection method yields a good model fit yet poor reproducibility, then its discovered features will mislead related biological interpretation. The notion of reproducibility for evaluating feature selection method seems intuitive and sensible, yet in reality we neither have access to multiple similar datasets to estimate reproducibility, nor have a well‐defined mathematical formula to define reproducibility. The many available resampling techniques (Efron and Tibshirani, 1994) enable us to utilize well‐studied methods, for example, bootstrapping, to create replicates of real microbiome datasets for estimating reproducibility. Moreover, given the burgeoning research in reproducibility estimation in the field of computer science (Kalousis et al., 2005, 2007; Nogueira, 2018), we can borrow their concept of Stability to approximate the reproducibility of feature selection methods in microbiome data analysis.
In this paper, we investigate the performance of popular model prediction metrics MSE or AUC and the proposed feature selection criterion Stability in evaluating four widely used feature selection methods in microbiome analysis (lasso, elastic net, random forests, and compositional lasso) (Tibshirani, 1996; Breiman, 2001; Zou and Hastie, 2005; Lin et al., 2014; Lu et al., 2019). We evaluate both extensive simulations and experimental microbiome applications, with a focus of feature selection analysis in the context of continuous or binary outcomes. We find that Stability is a superior feature selection criterion to MSE or AUC as it is more reliable in discovering true and biologically meaningful signals. We thus suggest that microbiome researchers incorporate a reproducibility criterion such as Stability into model prediction performance metric such as MSE or AUC for feature selection in microbiome data analysis in order to achieve both high stability and low prediction error.
2. METHODS
2.1. Estimation of stability
The Stability of a feature selection method was defined as the robustness of the feature preferences it produces to differences in training sets drawn from the same generating distribution (Kalousis et al., 2005). If the subsets of chosen features are nearly static with respect to data changes, then this feature selection method is a stable procedure. Conversely, if small changes to the data result in significantly different feature subsets, then this method is considered unstable, and we should not trust the output as reflective of the true underlying structure influencing the outcome being predicted. In biomedical fields, this is a proxy for reproducible research, in the latter case indicating that the biological features the method has found are likely to be a data artifact, not a real clinical signal worth pursuing with further resources (Lee et al., 2013). Goh and Wong (2016) recommend augmenting statistical feature selection methods with concurrent analysis on stability and reproducibility to improve the quality of selected features prior to experimental validation (Sze and Schloss, 2016; Duvallet et al., 2017).
Although the intuition behind the concept of stability is simple, there is to date no single agreed‐upon measure for precisely quantifying stability. Up to now, there have been at least 16 different measures proposed to quantify the stability of feature selection algorithms in the field of computer science (Nogueira et al., 2017). Given the variety of stability measures published, it is sensible to ask: which stability measure is most valid in the context of microbiome research? A multiplicity of methods for stability assessment may lead to publication bias in that researchers may be drawn toward the metric that extracts their hypothesized features or that reports their feature selection algorithm as more stable (Boulesteix and Slawski, 2009). Under the perspective that a useful measure should obey certain properties that are desirable in the domain of application, and provide capabilities that other measures do not, Nogueira and Brown aggregated and generalized the requirements of the literature into a set of five properties (Nogueira et al., 2017). The first property requires the stability estimator to be fully defined for any collection of feature subsets, thus allowing a feature selection algorithm to return a varying number of features. The second property requires the stability estimator to have a negative relationship with the variances in feature selections. The third property requires the stability estimator to be bounded by constants not dependent on the overall number of features or the number of features selected. The fourth property states that a stability estimator should achieve its maximum if and only if all chosen feature sets are identical. The fifth property requires that under the null model of feature selection, where we independently draw feature subsets at random, the expected value of a stability estimator should be constant. These five properties are desirable in any reasonable feature selection scenario, and are critical for useful comparison and interpretation of stability values. Among all the existing measures, only Nogueira's stability measure (defined below) satisfies all five properties, thus we adopted this measure in the current work.
We assume a data set of n samples , where each is a p‐dimensional feature vector and is the associated biological outcome. The task of feature selection is to identify a feature subset, of size , that conveys the maximum information about the outcome . An ideal approach to measure stability is to first take M data sets drawn randomly from the same underlying population, to apply feature selection to each data set, and then to measure the variability in the M feature sets obtained. The collection of the M feature sets can be represented as a binary matrix of size , where a row represents a feature set (for a particular data set) and a column represents the selection of a given feature over the M data sets as follows:
Let denote the column of the binary matrix , indicating the selection of the feature among the M data sets. Then follows a Bernoulli distribution with mean , and variance . Moreover, is the average number of selected features over the M data sets. Under the null model of feature selection H 0 when feature subsets are drawn independently at random, . Nogueira then defined the stability estimator as
| (1) |
This proposed measure is undefined when contains all 0s or all 1s. Nogueira's stability is asymptotically bounded by 0 and 1. It reaches maximum 1 when each column of contains either all 1s or all 0s, indicating the selection of each feature is consistent across all M data sets. It reaches minimum 0 when selection of each feature alternatives between 0 and 1, suggesting highly unstable feature selection results.
In practice, we usually only have one data sample (not M), so a typical approach to measure stability is to first take M bootstrap samples of the provided data set, and apply the procedure described in the previous paragraph. Other data sampling techniques can be used as well, but due to the well‐understood properties and familiarity of bootstrap to the community, we adopt the bootstrap approach.
2.2. Four selected feature selection methods
Lasso, elastic net, compositional lasso, and random forests were chosen as benchmarked feature selection methods in this paper due to their wide application in microbiome community (Knights et al., 2011). Lasso is a penalized least squares method imposing an L 1‐penalty on the regression coefficients (Tibshirani, 1996). Owing to the nature of the L 1‐penalty, lasso does both continuous shrinkage and automatic variable selection simultaneously. One limitation of lasso is that if there is a group of variables among which the pairwise correlations are very high, then lasso tends to select one variable from the group and ignore the others. Elastic net is a generalization of lasso, imposing a convex combination of the L 1 and L 2 penalties, thus allowing elastic net to select groups of correlated variables when predictors are highly correlated (Zou and Hastie, 2005). Compositional lasso is an extension of lasso to compositional data analysis for continuous outcome (Lin et al., 2014) and general outcome (Lu et al., 2019), and it is one of the most highly cited compositional feature selection methods in microbiome analysis (Kurtz et al., 2015; Li, 2015; Shi et al., 2016; Silverman et al., 2017). Compositional lasso, or the sparse log‐contrast model, considers variable selection via L 1 regularization. The log‐contrast regression model expresses the continuous outcome of interest as a linear combination of the log‐transformed compositions subject to a zero‐sum constraint on the regression vector, which leads to the intuitive interpretation of the response as a linear combination of log‐ratios of the original composition. Suppose an matrix consists of n samples of the composition of a mixture with p components, and suppose is a response variable depending on . The nature of composition makes each row of lie in a ‐dimensional positive simplex . This compositional lasso model for continuous outcome is then expressed as
| (2) |
where is the design matrix and is the p‐vector of regression coefficients. Applying the L 1 regularization approach to this model is then
| (3) |
where is a regularization parameter, and and denote the L 2 and L 1 norms, respectively. For general outcome, the linear model (2) is extended to the generalized linear model with its density function specified as
| (4) |
where , and satisfies , with C as the orthonormal constraint matrix (Shi et al., 2016). For binary outcome, , and the l 1 penalized estimates of is
| (5) |
subject to , where λ is a tuning parameter.
Random forests is regarded as one of the most effective machine learning techniques for feature selection in microbiome analysis (Statnikov et al., 2013; Liu et al., 2017; Belk et al., 2018; Santo et al., 2019; Namkung, 2020). Random forests is a combination of tree predictors such that each tree depends on the values of a random vector sampled independently and with the same distribution for all trees in the forest (Breiman, 2001). As random forests do not select features but only assign importance scores to features, we choose features from random forests using Altmann's permutation test (Altmann et al., 2010), where the response variable is randomly permuted S times to construct new random forests and new importance scores computed. The S importance scores are then used to compute the p‐value for the feature, which is derived by computing the fraction of the S importance scores that are greater than the original importance score. In our applications, we set the number of permutations S to be 100, and chose those features with permuted p‐values less or equal to 0.05.
2.3. Simulation settings
We compared the performance of the popular model prediction metrics MSE or AUC and the proposed criterion Stability in evaluating four widely used feature selection methods for different data scenarios. We simulated features with Independent, Toeplitz, and Block correlation structures for data sets with the number of samples and features in all possible combinations of (50, 100, 500, 1000), resulting in the ratio of p (number of features) over n (number of samples) ranging from 0.05 to 20. Our simulated compositional microbiome data are an extension of the simulation settings from Lin et al. (2014) as follows:
-
(1)
Generate tan data matrix from a multivariate normal distribution . To reflect the fact the components of a composition in metagenomic data often differ by orders of magnitude, let with for and otherwise. To describe different types of correlations among the components, we generated three general correlation structures: Independent design where covariates are independent from each other, Toeplitz design where with , and Block design with five blocks, where the intra‐block correlations are 0.1, 0.3, 0.5, 0.7, 0.9, and the inter‐block correlation is 0.09.
-
(2)
Obtain the covariate matrix by the transformation , and the log‐ratio matrix , which follows a logistic normal distribution (Aitchison, 1982). Note that does not follow the exact same correlation structures specified in step (1) due to the compositional data transformation, hence the correlation designs of Independent, Toeplitz, and Block refer to the data matrix rather than the log‐ratio matrix .
-
(3)
Generate the continuous responses according to the model , , where , and , indicating that only six features are real signals. To generate binary responses, we convert the continuous responses into classes 0 or 1 by the cutoff of the median value.
-
(4)
Repeat steps 1–3 for 100 times to obtain 100 simulated datasets for each simulation setting, and apply the desired feature selection algorithm with 10‐fold cross‐validation on the 100 simulated datasets, which allows the optimal hyperparameters to vary for each simulation scenario. Specifically, each simulated data set is separated into training and test sets in the ratio of 8:2, 10‐fold cross‐validation is applied to the training set (80% of the data) for parameter tuning (e.g., the value of tuning parameter λ in lasso and compositional lasso, α and λ in elastic net, and the number of variables randomly sampled as candidates at each split in random forests) and variable selection, and then model prediction (i.e., MSE or AUC) is evaluated on the test set (20% of the data). Hence, stability is measured according to Nogueira's definition based on the 100 subsets of selected features. Average MSE or AUC is calculated as the mean of the MSEs or AUCs across the 100 simulated data sets, and the average false positive or false negative rate denotes the mean of the false positive or false negative rates across the 100 simulated data sets.
In summary, a total of 176 simulation scenarios were generated, with 16 for Independent design, 80 for Toeplitz or Block design, and 100 replicated data sets were simulated for each simulation setting, resulting in 17,600 simulated data sets in total.
3. SIMULATION RESULTS
Given that the true numbers of false positive and false negative features are known in simulations, we can utilize their relationships with prediction metrics (MSE for continuous outcome or AUC for binary outcome) and Stability to compare the reliability of MSE or AUC and Stability in evaluating feature selection methods. In theory, we would expect to see a positive correlation between MSE and false positive or false negative rates, while a negative correlation between AUC or Stability and false positive or false negative rates. This is because when the real signals are harder to select (i.e., increasing false positive or false negative rates), a feature selection method would perform worse (i.e., increasing MSE or decreasing AUC and Stability). The first column in Figure 1 shows the relationship between MSE and false positive rate in three correlation designs for continuous outcome, and the second column in Figure 1 shows the relevant relationship between Stability and false positive rate. In contrast to the random pattern in MSE versus false positive rate (Figure 1A, E, and I), where drastic increase in false positive rate could lead to little change in MSE (e.g. random forests), or big drop in MSE corresponds to little change in false positive rate (e.g. elastic net), we see a clear negative correlation pattern between Stability and false positive rate (Figure 1B, F, and J). This clear relationship of false positive rate with Stability versus a vague pattern with predictive metric are consistently observed for binary outcome (shown in the third and fourth columns of Figure 1). Regarding false negative rate, we also observe a random pattern in MSE or AUC and a meaningful negative correlation relationship in Stability (Supplementary Figure 1). These results suggest that Stability is a more reliable evaluation criterion than MSE or AUC due to its closer reflection of the ground truth in the simulations (i.e., false positive & false negative rates), and this is true irrespective of feature selection method used, features‐to‐sample size ratio (), correlation structure among the features, or types of outcome.
FIGURE 1.
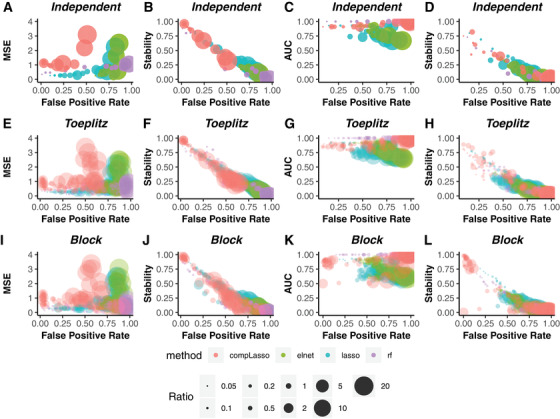
Comparing the relationship between MSE or AUC and False Positive Rate versus Stability and False Positive Rate in three correlation structures for continuous or binary outcomes. The first two columns denote the results for continuous outcome, and the last two columns are the results for binary outcome. Colored dots represent values from different feature selection methods: compositional lasso (red), elastic net (green), lasso (blue) and random forests (purple). Size of dots indicate features‐to‐sample size ratio .
Using the more reliable criterion Stability, we now investigate the best feature selection method in different simulation scenarios. Figure 2A–C shows that for continuous outcome, compositional lasso has the highest stability in “easier” correlation settings based on Stability (Toeplitz 0.1–0.7 in Supplementary Figure 2A–D, represented by Toeplitz 0.5 in Figure 2A due to their similar results; Block 0.9–0.3 in Supplementary Figure 3A–D, represented by Block 0.5 in Figure 2C) for all combinations of n (number of samples) and p (number of features). Across all “easier” correlation scenarios, compositional lasso has an average stability of 0.76 with its minimum at 0.21 and its maximum close to 1 (0.97), while the second‐best method Lasso has an average stability of only 0.44 with the range from 0.09 to 0.89, and the average stabilities of random forests and Elastic Net hit as low as 0.24 and 0.17, respectively. In “extreme” correlation settings (Toeplitz 0.9 in Figure 2B or Block 0.1 in Figure 2D), compositional lasso no longer maintains the highest stability across all scenarios, but it still has the highest average stability of 0.42 in Toeplitz 0.9 (surpassing the second‐best Lasso by 0.09), and the second highest average stability in Block 0.1 (only 0.03 lower than the winner Lasso). Regarding specific scenarios in “extreme” correlation settings, compositional lasso, lasso, or random forests can be the best in different combinations of p and n. For example, in both Toeplitz 0.9 and Block 0.1, with small p (when p = 50 or 100), random forests has highest stability (≥0.8) when n is largest (), but Lasso or compositional lasso surpasses random forest when n is smaller than 1000, although all methods have poor stability (⩽0.4) when . Similarly, for binary outcome, compositional lasso achieves the highest stability in most scenarios (Figure 2E–G and Supplementary Figure 3E–H), and lasso surpasses it in some Toeplitz cases and scenario of Block 0.1 (Figure 2E–H and Supplementary Figure 2E–H). This indicates that best feature selection method based on Stability depends on the correlation structure among features, the number of samples, and the number of features in each particular data set; thus there is no single omnibus best, that is, most stable, feature selection method.
FIGURE 2.
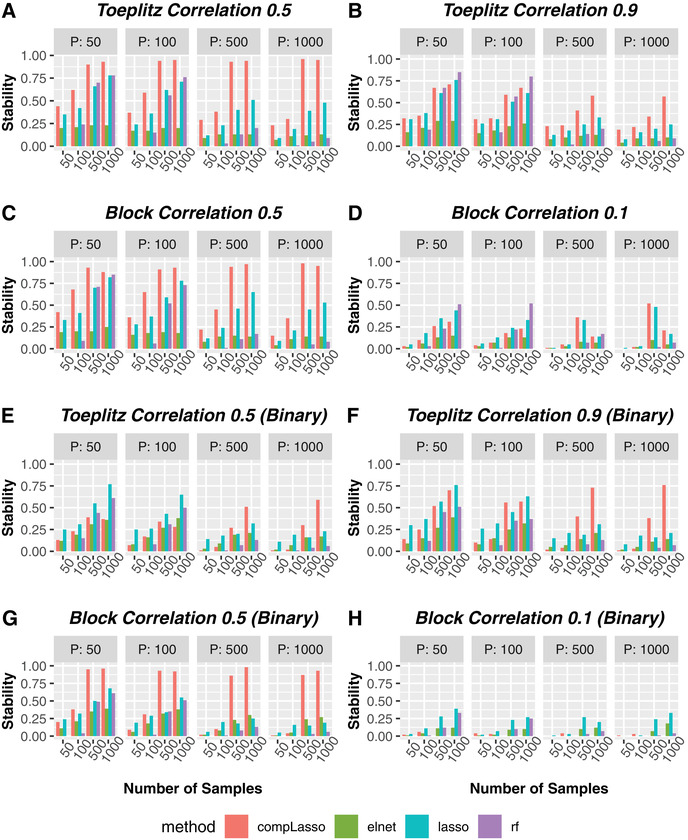
Method comparisons based on Stability in representative correlation structures for continuous or binary outcomes. The first two rows denote the results for continuous outcome, and the last two rows are the results for binary outcome. Colored bars represent Stability values corresponding to specific number of samples (x‐axis) and number of features (p) for different feature selection methods: compositional lasso (red), elastic net (green), lasso (blue) and random forests (purple). Note that Toeplitz 0.1‐0.7 has similar results as Toeplitz 0.5 (see Supplementary Figure 2), and Block 0.9‐0.3 has similar results as Block 0.5 (see Supplementary Figure 3). Moreover, Stability equals to zero when no features were selected by methods (e.g. random forests chooses nothing when the number of samples equals 50). (A) Toeplitz Correlation 0.5 (Continuous). (B) Toeplitz Correlation 0.9 (Continuous). (C) Block Correlation 0.5 (Continuous). (D) Block Correlation 0.1 (Continuous). (E) Toeplitz Correlation 0.5 (Binary). (F) Toeplitz Correlation 0.9 (Binary). (G) Block Correlation 0.5 (Binary). (H) Block Correlation 0.1 (Binary).
To further examine the effect of high correlation on stability, we investigated the large p small n case () for continuous outcomes, which is common in microbiome data, under two correlation structures: independence and high correlation (Toeplitz 0.9) for continuous outcome. We extracted selection probabilities for each feature for each of the four each feature selection methods. The results (Supplementary Figure 4) suggest that while it is true that high correlation leads to instability in feature selection, this issue is most pronounced for random forest. According to the simulation settings, , suggesting that all six real signals are concentrated among the first 10 features, with features 1, 6, and 8 having largest effect sizes. For lasso, elastic net, and compositional lasso, features with large effects have high selection probabilities (>0.75 in Supplementary Figure 4A–F). Also, for lasso, elastic net, and composition lasso, while features with moderate‐low effects have lower selection probabilities, and in some cases “wrong” features that are not the true signals are selected, the selection probabilities of the wrongly selected features (potentially due to high correlation with true signals) are mostly low (<0.3). For random forests, all the selection probabilities, whether true or false signals and irrespective of effect‐size are much lower (⩽0.55) than the other methods (Supplementary Figure 4G and H). Of note, when we examined simulations with independence correlation structure (Supplementary Figure 4G), random forest still had low selection probabilities for all features, suggesting that stability is more intrinsic to the feature selection method than correlation structure of the features.
If we use MSE or AUC as the evaluation criterion, how will results differ with regards to the best feature selection method? Using the extreme correlation settings (Toeplitz 0.9 and Block 0.1) as examples, for continuous outcome, random forest has lowest MSEs for all combinations of p and n (Figure 3A and B). However, Figure 3E and F unveils that random forests has highest false negative rates in all scenarios of Toeplitz 0.9 and Block 0.1, and its false negative rates can reach as high as the maximum 1, indicating that random forests fails to pick up any real signal despite its low prediction error. Moreover, Figure 3I and J shows that random forests can have highest false positive rates when p is as large as 500 or 1000. For binary outcome, random forests also performs the best in terms of prediction metric (AUC), in fact it achieves the perfect AUC score of 1 in all cases (Figure 3C and D). However, it has the highest false negative rates in most cases (Figure 3G and H), and highest false positive rates when in Toeplitz 0.9, or when and in Block 0.1 (Figure 3K and L). These highlight the danger of choosing inappropriate feature selection method based on MSE or AUC, where the merit of high predictive power masks high errors in false positives and false negatives. On the other hand, the method with lowest false positive rates (compositional lasso) was rather often found to have the worst performance by MSE or AUC, suggesting another pitfall of missing the optimal method when using prediction performance as the evaluation criterion. It is possible that high false negative or false positive rates of highly predictive method were due to its selecting the highly correlated yet wrong features. However, Toeplitz 0.9 and Block 0.1 serve as two extreme scenarios of the correlation structures, where features are highly correlated in Toeplitz 0.9 while weakly correlated in Block 0.1. Hence, we expect our conclusion here to be true regardless of the strength of correlation among features.
FIGURE 3.
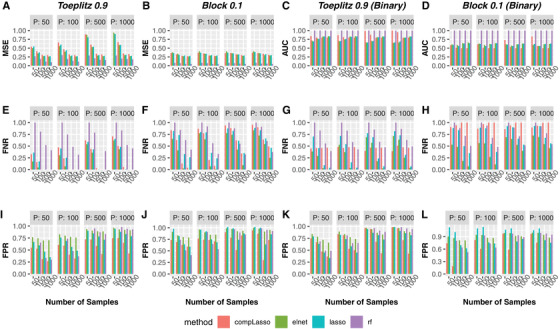
Method comparisons based on MSE in extreme correlation structures (Toeplitz 0.9 and Block 0.1) for continuous or binary outcomes. The first two columns denote the results for continuous outcome, and the last two columns are the results for binary outcome. Colored bars represent MSE (first row), False Negative Rates (second row), and False Positive Rates (third row) corresponding to a specific number of samples (x‐axis) and features (p) for different feature selection methods: compositional lasso (red), elastic net (green), lasso (blue), and random forests (purple). Note that false positive rates are not available for random forests when number of samples equals 50 because it chooses zero features.
The use of point estimates alone to compare feature selection methods, without incorporating variability in these estimates, could be misleading. Hence, as a next step, we evaluate reliability of prediction metrics and Stability across methods using a hypothesis testing framework. Specifically, we evaluate compositional lasso (which generally had the highest stability) and random forests (which generally had the best prediction metrics, i.e., lowest MSE or highest AUC). We consider the cases of & for Toeplitz 0.5 and Block 0.5 and use the continuous outcome for illustration purpose. We use bootstrap to construct 95% confidence intervals to compare compositional lasso versus random forests based on Stability or prediction metrics (MSE). For each simulated data (100 in total for Toeplitz 0.5 or Block 0.5), we generate 100 bootstrapped data sets and apply feature selection methods to each bootstrapped data set. Then for each simulated data, Stability is calculated based on the 100 subsets of selected features from the bootstrapped replicates, and the variance of Stability is measured as its variability across the 100 simulated data. As MSE can be obtained for each simulated data without bootstrapping, we use the variability of MSE across the 100 simulated data as its variance. Based on the 95% CI for the difference in Stability between compositional lasso and random forest methods (Table 1), we see that compositional lasso is superior to random forest in terms of Stability index, and not statistically inferior to random forests in terms of MSE despite its lower point estimate. This suggests that Stability has higher precision (i.e., lower variance). Conversely, MSE has higher variance, which results in wider confidence intervals and its failure to differentiate methods.
TABLE 1.
Hypothesis testing using Bootstrap to compare compositional lasso (CL) with random forests (RF) based on Stability or prediction metric (MSE) using two simulation scenarios (*indicate statistically significant)
| Example (N = 100 & P = 1000)(Continuous) | Estimated mean difference (CL‐RF) in Stability index with 95% CI | Estimated mean difference (CL‐RF) in MSE with 95% CI |
|---|---|---|
| Toeplitz 0.5 | 0.22 (0.19, 0.28)* | 0.23 (‐0.62, 1.36) |
| Block 0.5 | 0.23 (0.17, 0.29)* | 0.44 (‐0.27, 1.57) |
4. EXPERIMENTAL MICROBIOME DATA APPLICATIONS
To compare the reliability of prediction metrics (MSE or AUC) and Stability in choosing feature selection methods in microbiome data applications, two experimental microbiome data sets were chosen to cover common sample types (human gut and environmental soil samples) and the scenarios of and (where p is the number of features and n is the number of samples). The human gut data set represents a cross‐sectional study of 98 healthy volunteers to investigate the connections between long‐term dietary patterns and gut microbiome composition (Wu et al., 2011), and we are interested in identifying a subset of important features associated with BMI, which is a widely used gauge of human body fat and associated with the risk of diseases. The soil data set contains 88 samples collected from a wide array of ecosystem types in North and South America (Lauber et al., 2009), and we are interested in discovering microbial features associated with the pH gradient, as pH was reported to be a strong driver behind fluctuations in the soil microbial communities (Morton et al., 2017). Prior to our feature selection analysis, the same filtering procedures were applied to the microbiome count data from these two data sets, where only the microbes with a taxonomy assignment at least to genus level or lower were retained for interpretation, and microbes present in fewer than 1% of the total samples were removed. Moreover, the count data were transformed into compositional data after replacing any zeroes by the maximum rounding error 0.5 (Lin et al., 2014). Specifically, the count data here refers to the number of raw sequencing reads in samples. After removing the microbes with the filtering procedures above and replacing zero counts with 0.5, we transform the count data into relative abundance for further analysis. Note that the log of relative abundances instead of the typically used log ratios is used for compositional lasso due to its clever formulation in Equation (2). Moreover, the same response variables are used as continuous or binary outcomes, with the binary classes obtained by the cut‐off value of medians.
Comparisons of feature selection methods in these two microbiome data sets are shown in Table 2, which are consistent with simulation results, where the best method chosen by prediction metric (MSE or AUC) or Stability in each data set can be drastically different. For the continuous outcome, based on MSE, random forests is the best in the BMI Gut data set, while being the worst based on Stability. Similarly, in the pH Soil data set, random forests is the second‐best method according to MSE, yet the worst in terms of Stability. If we use Stability as the evaluation criterion, then Elastic Net is the best in the BMI Gut and compositional lasso is the best in the pH Soil, yet both methods would be the worst if MSE was used as the evaluation criterion. Similarly, for the binary outcome, although random forest achieves a perfect AUC in both data sets, it is the least stable method with Stability <0.1. It is clearer in the binary case that compositional lasso is the best method for both data sets due to its highest Stability values and second highest AUCs. One important note is that the Stability values in these two experimental microbiome data sets are low: none of the feature selection method exceeds a stability of 0.5, indicating the challenging task of feature selection in real microbiome applications. However, this possibility of low Stability values was already reflected in our simulated scenarios of “extreme” correlation scenarios. Another important note, which might be counter‐intuitive, is that the data set with a high ratio (pH Soil) has higher stabilities than the data set with ratio close to 1 (i.e., similar p & n values) (BMI Gut). This might be explained by the clearer microbial signals in environmental samples than in human gut samples, but it also highlights the impact of the data set itself, whose characteristics cannot be easily summarized with the numbers of p and n, on feature selection results. Correlation structures between features as considered in our simulations could play an important role, and there may be many other unmeasured factors involved as well.
Apart from the comparisons based on point estimates, we can further compare prediction metrics and Stability with hypothesis testing using nested bootstrap (Wainer and Cawley, 2018). The outer bootstrap generates 100 bootstrapped replicates of the experimental microbiome data sets, and the inner bootstrap generates 100 bootstrapped data set for each bootstrapped replicate from the outer bootstrap. Feature selections are performed on each inner bootstrapped data set with 10‐fold cross‐validation after a 80:20 split of training and test sets. The variance of Stability is calculated based on the Stability values across the outer bootstrap replicates, and the variance of MSE or AUC is calculated across both inner and outer bootstrap replicates, as MSE or AUC is available for each bootstrap replicate while Stability has to be estimated based on feature selection results across multiple bootstrap replicates. Using the data sets of BMI Gut and pH Soil, Table 3 confirms with simulation results that raw value difference in MSE does not indicate statistical difference, yet difference in Stability does help to differentiate methods due to its higher precision. A comparison between the observed difference in Table 2 and the estimated mean difference from bootstrap in Table 3 further confirms this discovery. Compared to the estimated mean differences between compositional lasso and random forests based on stability (Table 3: 0.27 in the BMI Gut and 0.36 in the pH Soil), the observed differences (Table 2: 0.2 in the BMI Gut and 0.35 in the pH Soil) differ by 26% in the BMI Gut and 3% in the pH Soil. However, this difference is much more drastic based on MSE. Compared to the estimated mean differences between compositional lasso and random forests based on MSE (Table 3: 11.8 in the BMI Gut and 0.08 in the pH Soil), the observed differences (Table 2: 16.6 in the BMI Gut and 0.23 in the pH Soil) have huge differences of 41% and 160% in each data set, respectively. For binary outcome, confidence intervals of AUC are much tighter than MSE, probably due to the constrained range of AUC from 0 to 1. Although the two feature selection methods were able to be differentiated based on AUCs in BMI gut, they are similar to one another in the pH Soil data set. Hence, Stability is consistently shown to exhibit more optimal properties (i.e., lower false positive or negative rate, less variability) than prediction metrics such as MSE or AUC in experimental data applications as in simulations.
TABLE 2.
Method comparisons based on Stability Index and prediction metric (MSE/AUC) in experimental microbiome data sets with continuous or binary outcomes (methods ordered in terms of best MSE/Stability performance, followed with raw MSE/AUC/Stability values in parentheses)
| Dataset (Continuous) |
|
MSE (lower is better) | Stability (higher is better) | ||
|---|---|---|---|---|---|
| BMI Gut | 98 * 87 (0.9) | Random forests (4.99) Compositional lasso (21.59) Lasso (24.07) Elastic Net (25.33) | Elastic Net (0.23) Compositional lasso (0.22) Lasso (0.14) Random forests (0.02) | ||
| pH Soil | 89 * 2183 (24.5) | Elastic Net (0.23) Random forests (0.26) Lasso (0.34) Compositional lasso (0.46) | Compositional lasso (0.39) Lasso (0.31) Elastic Net (0.16) Random forests (0.04) |
| Dataset (Binary) |
|
AUC (higher is better) | Stability (higher is better) | ||
|---|---|---|---|---|---|
| BMI Gut | 98 * 87 (0.9) | Random forests (1.00) Compositional lasso (0.85) Elastic Net (0.78) Lasso (0.63) | Compositional lasso (0.29) Elastic Net (0.19) Lasso (0.14) Random forests (0.01) | ||
| pH Soil | 89 * 2183 (24.5) | Random forests (1.00) Compositional lasso (0.96) Elastic Net (0.94) Lasso (0.90) | Compositional lasso (0.46) Elastic Net (0.32) Lasso (0.28) Random forests (0.03) |
TABLE 3.
Hypothesis testing using Bootstrap to compare compositional lasso (CL) with random forests (RF) based on Stability or prediction metric (MSE/AUC) using two experimental microbiome data sets with continuous or binary outcomes (*indicate statistically significant)
| Dataset (Continuous) | Estimated mean difference (CL‐RF) in Stability index with 95% CI | Estimated mean difference (CL‐RF) in MSE with 95% CI |
|---|---|---|
| BMI Gut | 0.27 (0.17, 0.34)* | 11.8 (‐2.1, 41.2) |
| pH Soil | 0.36 (0.28, 0.44)* | 0.08 (‐0.28, 0.95) |
| Dataset (Binary) | Estimated mean difference (CL‐RF) in Stability index with 95% CI | Estimated mean difference (CL‐RF) in AUC with 95% CI |
|---|---|---|
| BMI Gut | 0.30 (0.11, 0.42)* | ‐0.09 (‐0.19, ‐0.02)* |
| pH Soil | 0.43 (0.37, 0.5)* | ‐0.02 (‐0.08, 0) |
5. DISCUSSION
In this article, we focus on discovering a reproducibility criterion for evaluating feature selection methods rather than developing a better feature selection method. We question the common practice of evaluating feature selection methods based on overall performance of model prediction (Knights et al., 2011), such as MSE or AUC, as we detect a stark contrast between prediction accuracy versus reproducible feature selection within a method. Instead, we propose to use a reproducibility criterion such as Nogueira's Stability measurement (Nogueira et al., 2017) for identifying the optimal feature selection method.
In both our simulations and experimental microbiome data applications, we have shown that Stability is a preferred evaluation criterion over MSE or AUC for feature selection, because of its closer reflection of the ground truth (false positive and false negative rates) in simulations, and its better capacity to differentiate methods due to its higher precision. Hence, if the goal is to identify the underlying true biological signal, we propose to use a reproducibility criterion like Stability instead of a prediction criterion like MSE or AUC to choose feature selection algorithms for microbiome data applications. MSE or AUC is better suited for problems where prediction accuracy alone is the focus. To reduce the possible risk of high stability yet low prediction accuracy, we recommend that researchers check the prediction performance when using Stability. We did not observe this occurrence in our simulations or applications, probably because our four chosen feature selection methods were known for their high prediction power in microbiome applications, but it might happen with methods that provide poor data fit. Moreover, if the researchers want to gain a holistic picture of both stability and prediction accuracy, they could consider coupling stability estimates with prediction error estimates in view of identifying feature selection algorithms that maximize both stability and prediction performance. In light of this, Kalousis et al. (2005) suggested using stratified 10‐fold cross‐validation, where at each iteration of the cross‐validated error estimation loop, there is a full internal cross‐validation loop aimed at measuring the stability of feature precedences returned by the feature selection algorithm.
The strength of our work lies in the comparisons of widely used microbiome feature selection methods using extensive simulations, and experimental microbiome data sets covering various sample types and data characteristics. The comparisons are further confirmed with nonparametric hypothesis testing using bootstrap. Although Nogueira et al. (2017) were able to derive the asymptotical normal distribution of Stability, their independent assumption for two‐sample test might not be realistic due to the fact that two feature selection methods are applied to the same data set. Hence our nonparametric hypothesis testing is an extension of their two‐sample test for Stability. However, our current usage of bootstrap, especially the nested bootstrap approach for experimental microbiome data applications, is computationally expensive; further theoretical development on hypothesis testing for reproducibility can be done to facilitate more efficient method comparisons based on Stability. Moreover, our current work relies on cross‐validation (CV) for choosing optimal parameters in feature selection methods. CV has been shown to be unstable in high‐dimensional data, and effective alternatives include estimation stability with cross‐validation (ESCV) (Lim and Yu, 2016) or stability selection (Meinshausen and Bühlmann, 2010), where the former aims at reducing the variance of estimation empirical loss, and the latter addresses the problem of proper regularization with a generic subsampling approach. Note that the definitions of stability in these two works are different from Nogueira's and they are designed to meet a different goal: stability in parameter tuning rather than in feature selection. Hence ESCV or stability selection can be used together with Nogueira's Stability Index to achieve the stability at both the levels of parameter tuning and feature selection, which has already been carried out in Nogueira's data application (Nogueira et al., 2017). Last but not least, although our paper is focused on microbiome data, we do expect the superiority of reproducibility criteria over prediction accuracy criteria in feature selection to apply in other types of data sets as well. We thus recommend that researchers consider incorporating stability into the evaluation criterion while performing feature selection in order to yield reproducible results.
OPEN RESEARCH BADGES
This article has earned Open Data and Open Materials badges. Data and materials are available at https://doi.org/10.5281/zenodo.4768073.
Supporting information
Supplementary Figures referenced in Sections 3, as well as the code for implementing the proposed methods, are available with this paper at the Biometrics website on Wiley Online Library. The code that implements the methodology, simulations, and experimental microbiome data applications is also available at the Github repository https://github.com/knightlab‐analyses/stability‐analyses.
ACKNOWLEDGMENTS
We gratefully acknowledge supports from IBM Research through the AI Horizons Network, and UC San Diego AI for Healthy Living program in partnership with the UC San Diego Center for Microbiome Innovation. This work was also supported in part by CRISP, one of six centers in JUMP, a Semiconductor Research Corporation (SRC) program sponsored by DARPA. LN was partially supported by NIDDK 1R01DK110541‐01A1.
Jiang L, Haiminen N, Carrieri A‐P et al. (2022) Utilizing stability criteria in choosing feature selection methods yields reproducible results in microbiome data. Biometrics, 78, 1155–1167. 10.1111/biom.13481
DATA AVAILABILITY STATEMENT
The data that support the findings of this study are openly available in the Github repository at https://doi.org/10.5281/zenodo.4768073.
REFERENCES
- Aitchison, J. (1982) The statistical analysis of compositional data. Journal of the Royal Statistical Society: Series B (Methodological), 44, 139–160. [Google Scholar]
- Altmann, A. , Toloşi, L. , Sander, O. & Lengauer, T. (2010) Permutation importance: A corrected feature importance measure. Bioinformatics, 26, 1340–1347. [DOI] [PubMed] [Google Scholar]
- Baker, M. (2016) 1,500 scientists lift the lid on reproducibility. Nature, 33, 452–454. [DOI] [PubMed] [Google Scholar]
- Belk, A. , Xu, Z.Z. , Carter, D.O. , Lynne, A. , Bucheli, S. , Knight, R. et al. (2018) Microbiome data accurately predicts the postmortem interval using random forest regression models. Genes, 9, 104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boulesteix, A.‐L. & Slawski, M. (2009) Stability and aggregation of ranked gene lists. Briefings in Bioinformatics, 10, 556–568. [DOI] [PubMed] [Google Scholar]
- Breiman, L. (2001) Random forests. Machine Learning, 45, 5–32. [Google Scholar]
- Duvallet, C. , Gibbons, S.M. , Gurry, T. , Irizarry, R.A. & Alm, E.J. (2017) Meta‐analysis of gut microbiome studies identifies disease‐specific and shared responses. Nature Communications, 8, 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Efron, B. & Tibshirani, R.J. (1994) An introduction to the bootstrap. Boca Raton, FL: CRC Press. [Google Scholar]
- Gevers, D. , Kugathasan, S. , Denson, L.A. , Vázquez‐Baeza, Y. , Van Treuren, W. , Ren, B. et al. (2014) The treatment‐naive microbiome in new‐onset crohn's disease. Cell Host & Microbe, 15, 382–392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goh, W.W.B. and Wong, L. (2016) Evaluating feature‐selection stability in next‐generation proteomics. Journal of Bioinformatics and Computational Biology, 14, 1650029. [DOI] [PubMed] [Google Scholar]
- Huang, S. , Haiminen, N. , Carrieri, A.‐P. , Hu, R. , Jiang, L. , Parida, L. et al. (2020) Human skin, oral, and gut microbiomes predict chronological age. Msystems, 5. 10.1128/mSystems.00630-19 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalousis, A. , Prados, J. & Hilario, M. (2005) Stability of feature selection algorithms. Fifth IEEE International Conference on Data Mining (ICDM'05). Piscataway, NJ: IEEE, 8 pp. [Google Scholar]
- Kalousis, A. , Prados, J. & Hilario, M. (2007) Stability of feature selection algorithms: A study on high‐dimensional spaces. Knowledge and Information Systems, 12, 95–116. [Google Scholar]
- Knights, D. , Costello, E.K. & Knight, R. (2011) Supervised classification of human microbiota. FEMS Microbiology Reviews, 35, 343–359. [DOI] [PubMed] [Google Scholar]
- Knights, D. , Parfrey, L.W. , Zaneveld, J. , Lozupone, C. & Knight, R. (2011) Human‐associated microbial signatures: examining their predictive value. Cell Host & Microbe, 10, 292–296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kurtz, Z.D. , Müller, C.L. , Miraldi, E.R. , Littman, D.R. , Blaser, M.J. & Bonneau, R.A. (2015) Sparse and compositionally robust inference of microbial ecological networks. PLoS Computional Biology, 11, e1004226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lauber, C.L. , Hamady, M. , Knight, R. & Fierer, N. (2009) Pyrosequencing‐based assessment of soil pH as a predictor of soil bacterial community structure at the continental scale. Applied and Environmental Microbiology, 75, 5111–5120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee, H.W. , Lawton, C. , Na, Y.J. & Yoon, S. (2013) Robustness of chemometrics‐based feature selection methods in early cancer detection and biomarker discovery. Statistical Applications in Genetics and Molecular Biology, 12, 207–223. [DOI] [PubMed] [Google Scholar]
- Li, H. (2015) Microbiome, metagenomics, and high‐dimensional compositional data analysis. Annual Review of Statistics and its Application, 2, 73–94. [Google Scholar]
- Lim, C. & Yu, B. (2016) Estimation stability with cross‐validation (ESCV). Journal of Computational and Graphical Statistics, 25, 464–492. [Google Scholar]
- Lin, W. , Shi, P. , Feng, R. & Li, H. (2014) Variable selection in regression with compositional covariates. Biometrika, 101, 785–797. [Google Scholar]
- Liu, Y. , Tang, S. , Fernandez‐Lozano, C. , Munteanu, C.R. , Pazos, A. , Yu, Y.‐z. et al. (2017) Experimental study and random forest prediction model of microbiome cell surface hydrophobicity. Expert Systems with Applications, 72, 306–316. [Google Scholar]
- Lu, J. , Shi, P. & Li, H. (2019) Generalized linear models with linear constraints for microbiome compositional data. Biometrics, 75, 235–244. [DOI] [PubMed] [Google Scholar]
- Meinshausen, N. & Bühlmann, P. (2010) Stability selection. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 72, 417–473. [Google Scholar]
- Morton, J.T. , Sanders, J. , Quinn, R.A. , McDonald, D. , Gonzalez, A. , Vázquez‐Baeza, Y. et al. (2017) Balance trees reveal microbial niche differentiation. MSystems, 2. 10.1128/mSystems.00162-16 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Namkung, J. (2020) Machine learning methods for microbiome studies. Journal of Microbiology, 58, 206–216. [DOI] [PubMed] [Google Scholar]
- Nogueira, S. (2018) Quantifying the stability of feature selection. Thesis, The University of Manchester.
- Nogueira, S. , Sechidis, K. & Brown, G. (2017) On the stability of feature selection algorithms. The Journal of Machine Learning Research, 18, 6345–6398. [Google Scholar]
- Poore, G.D. , Kopylova, E. , Zhu, Q. , Carpenter, C. , Fraraccio, S. , Wandro, S. et al. (2020) Microbiome analyses of blood and tissues suggest cancer diagnostic approach. Nature, 579, 567–574. [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- Santo, D. , Loncar‐Turukalo, T. , Stres, B. , Crnojevic, V. & Brdar, S. (2019) Clustering and classification of human microbiome data: Evaluating the impact of different settings in bioinformatics workflows. 2019 IEEE 19th International Conference on Bioinformatics and Bioengineering (BIBE). Piscataway, NJ: IEEE, pp. 838–845. [Google Scholar]
- Schloss, P.D. (2018) Identifying and overcoming threats to reproducibility, replicability, robustness, and generalizability in microbiome research. MBio, 9. 10.1128/mBio.00525-18 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi, P. , Zhang, A. & Li, H. (2016) Regression analysis for microbiome compositional data. Annals of Applied Statistics, 10, 1019–1040. [Google Scholar]
- Silverman, J.D. , Washburne, A.D. , Mukherjee, S. & David, L.A. (2017) A phylogenetic transform enhances analysis of compositional microbiota data. Elife, 6, e21887. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Statnikov, A. , Henaff, M. , Narendra, V. , Konganti, K. , Li, Z. , Yang, L. et al. (2013) A comprehensive evaluation of multicategory classification methods for microbiomic data. Microbiome, 1, 11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sze, M.A. & Schloss, P.D. (2016) Looking for a signal in the noise: revisiting obesity and the microbiome. MBio, 7, e01018–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomas, R.L. , Jiang, L. , Adams, J.S. , Xu, Z.Z. , Shen, J. , Janssen, S. et al. (2020) Vitamin D metabolites and the gut microbiome in older men. Nature Communications, 11, 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson, L.R. , Sanders, J.G. , McDonald, D. , Amir, A. , Ladau, J. , Locey, K. J. et al. (2017) A communal catalogue reveals earth's multiscale microbial diversity. Nature, 551, 457–463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tibshirani, R. (1996) Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society: Series B (Methodological), 58, 267–288. [Google Scholar]
- Wainer, J. & Cawley, G. (2018) Nested cross‐validation when selecting classifiers is overzealous for most practical applications. Preprint 2018, arXiv:1809.09446.
- Wu, G.D. , Chen, J. , Hoffmann, C. , Bittinger, K. , Chen, Y.‐Y. , Keilbaugh, S.A. et al. (2011) Linking long‐term dietary patterns with gut microbial enterotypes. Science, 334, 105–108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zou, H. & Hastie, T. (2005) Regularization and variable selection via the elastic net. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 67, 301–320. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Figures referenced in Sections 3, as well as the code for implementing the proposed methods, are available with this paper at the Biometrics website on Wiley Online Library. The code that implements the methodology, simulations, and experimental microbiome data applications is also available at the Github repository https://github.com/knightlab‐analyses/stability‐analyses.
Data Availability Statement
The data that support the findings of this study are openly available in the Github repository at https://doi.org/10.5281/zenodo.4768073.


