Task-selective place cells show behaviorally driven dynamics during learning and stability during memory recall

SUMMARY

Decades of work propose that hippocampal activity supports internal representation of learned experiences and contexts, allowing individuals to form long-term memories and quickly adapt behavior to changing environments. However, recent studies insinuate hippocampal representations can drift over time, raising the question: how could the hippocampus hold stable memories when activity of its neuronal maps fluctuates? We hypothesized that task-dependent hippocampal maps set by learning rules and structured attention stabilize as a function of behavioral performance. To test this, we imaged hippocampal CA1 pyramidal neurons during learning and memory recall phases of a new task where mice use odor cues to navigate between two reward zones. Across learning, both orthogonal and overlapping task-dependent place maps form rapidly, discriminating trial context with strong correlation to behavioral performance. Once formed, task-selective place maps show increased long-term stability during memory recall phases. We conclude that memory demand and attention stabilize hippocampal activity to maintain contextually rich spatial representations.

Graphical Abstract

In brief

Zemla et al. demonstrate that mice develop different neuronal spatial representations depending on task rules. With learning, place maps become more different. Initially unstable maps stabilize with experience during memory recall. These findings identify the importance of behavior and task demands on stability of neuronal activity patterns supporting long-term memory.

INTRODUCTION

The hippocampus is critical for formation and recall of episodic memories (Rolls, 2010; Scoville and Milner, 1957; Tulving, 1985, 2002; Tulving and Markowitsch, 1998) of people, places, objects, and events. Across mammals, hippocampal place cells show selective activity for spatial locations known as “place fields” (O’Keefe, 1978; O’Keefe and Dostrovsky, 1971). Originally perceived as a purely navigational mechanism (O’Keefe, 1978), subsequent studies suggest that place cell activity may support episodic memory functions by providing a spatial index (where) for behaviorally relevant events (what) such as environmental context (Leutgeb et al., 2005b; Markus et al., 1995; Muller and Kubie, 1987), object-stimulus association (Komorowski et al., 2009; Wood et al., 1999), goal trajectories (Ferbinteanu and Shapiro, 2003; Frank et al., 2000; Wood et al., 2000), and their sequence (when).

Accurate discrimination and adaptive behaviors to changing environments rely on context-specificity and flexibility of hippocampal place maps. Place cells achieve this by re-mapping, changing their firing fields and/or rates in response to changes in the spatial environment or salient cues within it (Danielson et al., 2016; Dupret et al., 2010; Ferbinteanu and Shapiro, 2003; Frank et al., 2000; Leutgeb et al., 2005a; Markus et al., 1995; Muller et al., 1991; Muller, 1996; Plitt and Giocomo, 2021; Wood et al., 2000). Interestingly, in dorsal CA1, learning a hippocampal-dependent task (Whitlock et al., 2006), or changes in task goals (Danielson et al., 2016; Dupret et al., 2010), causes place cell ensembles to remap, over-representing reward locations in an unchanging environment. This is associated with the storage of spatial information through plasticity (Pastalkova et al., 2006). It is unclear, however, how spatial maps evolve into orthogonal, contextual representations following learned behavior. Tracking the evolution of learned representations in the hippocampus is vital to understanding the mechanisms of memory storage and recall.

While flexibility accounts for environmental variables and adaptive changes, the stability of hippocampal representation is imperative to reliably support navigation, extract statistical regularities, and retain long-term memories. In fact, a major tenet of the cognitive map of space is that learned hippocampal place maps retain stable spatial activity in service of memory retrieval. However, recent long-term imaging studies show time-limited place cell reactivation (Hayashi, 2019; Ziv et al., 2013) and place field instability (Hainmueller and Bartos, 2018) in CA1. These studies showing representational drift over days raise the critical question: how are memories stable when their supposed neuronal substrates are not? A possibility is that these experiments did not account for behavioral influence on neuronal activity. In the absence of structured attention or memory demand, the neural representation did not require stability and drifted with time. We postulate that, under attentional control and memory-guided behavior, place maps stabilize to support reliable memory recall. Early evidence for this idea comes from in vivo electrophysiological recordings in CA1 where spatial map stability across hours increased as animals engaged in memory- and attention-dependent navigation (Kentros et al., 2004). Recent work in flying bats also reports stable hippocampal spatial code under tightly controlled navigational behavior (Liberti et al., 2022).

To directly test our hypothesis that hippocampal maps formed under structured attention with learning rules stabilize and maintain task-selectivity during memory recall, we used longitudinal two-photon imaging of hundreds of hippocampal CA1 pyramidal neurons while mice learned and performed a context-dependent spatial navigation task. This allowed us to examine mnemonic association of place maps with behaviorally relevant task features across learning and recall, and test whether activity of place cells stabilize as a function of memory experience and behavioral performance.

RESULTS

Mice learn to reliably perform odor-cued head-fixed spatial navigation

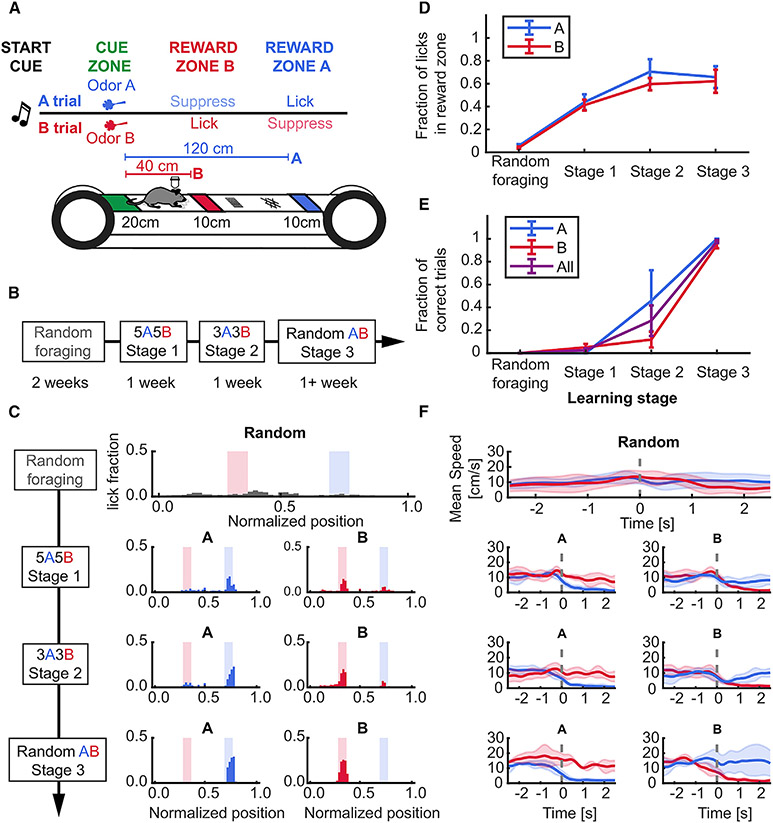
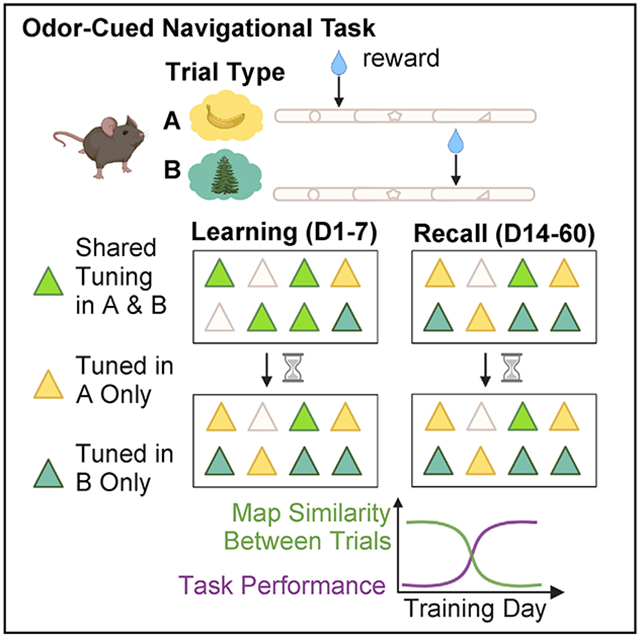
To study the time evolution and stability of place cells during episodic memory formation and recall, we developed a head-fixed spatial navigation task guided by odor cues. Mice were required to navigate to two discrete unmarked reward zones on an approximately 2 m linear treadmill, each associated with a distinct odor delivered at the start of the lap (Figures 1A-1D, Table S1). Successful performance required the animal to navigate a spatial trajectory contingent on odor cue memory while sustaining spatial attention to execute trial-appropriate active lick and lick-suppression behavior (Figure 1E, Table S1).

Figure 1. Stable learning of a head-fixed, odor-cued spatial navigation task.

(A) Schematic of task structure.

(B) Timeline for each stage of training: 2 weeks for randomly foraging (RF) and approximately 1 week on subsequent stages.

(C) Example lick distribution at each learning stage. Licking became progressively more specific to trial-selective reward zone with training (left, A trial laps; right, B trial laps).

(D) Lick fraction in associated reward zones increased in A and B trials during learning (RF vs. stage 3, paired t-test: A zone, 0.06 ± 0.01 vs. 0.66 ± 0.1, p = 0.031; B zone 0.04 ± 0.01 vs. 0.62 ± 0.1, p = 0.037; effect of training stage, One-way repeated measures (RM) ANOVA, A trials: p = 0.017; B trials: p = 0.008).

(E) Behavioral performance reached more than 85% in the last stage of training (RF vs. stage 3, paired t-test, A trials: 0 ± 0 vs. 1 ± 0, p = 0.04; B trials: 0 vs. 0.95 ± 0.03, p < 0.001; effect of training stage, one-way RM ANOVA, A trials: p < 0.001; B trials: p = 0.002).

(F) Example speed within ±2 seconds of entering the reward zones across training stages. At the final training stage (random AB), the animal stops upon entry into a trial-associated reward zone, running through non-rewarded zones. Dotted gray line shows onset time of reward zone entry. Data presented as mean ± standard error of the mean (error shades), n = 4 mice. See also Figure S1 and Table S1.

Following learning, consistent with the use of an odor-cue-dependent navigational strategy, the animals selectively decreased their speed immediately before entering (approximately 1 s) the correct reward zone (Figures 1D and S1A-S1D, Table S1), stopping almost completely within 2 s of entry. We did not observe significant speed differences between trial types in any animal, except for peri-reward bins (Figures S1E and S1F, Table S1). Thus, mice learned to use the contextual cues to perform the task.

Task-selective spatial activity emerges in CA1 following learning

If our task recruited episodic memory processes, we expected to observe trial-type-selective neural activity along the track segment before either reward zone, as observed in other memory-guided navigation studies (Ferbinteanu and Shapiro, 2003; Frank et al., 2000; Wood et al., 2000).

To verify this, we combined our behavior with two-photon imaging of Ca²⁺ activity in CA1 pyramidal neuron cell bodies expressing the fluorescent Ca²⁺ indicator GCaMP6f (Figure 2A). Alongside the majority of neurons that were spatially tuned as per either standard spatial information (S.I.) or tuning specificity (T.S.) criteria (see STAR Methods) in both trial types (A and B), we observed trial-selective neurons (A or B selective) that were place cells on A trials but not B trials, and vice-versa (Figures 2B-2D, Table S2). This distribution of trial selectivity was insensitive to the statistical criteria used to detect significantly tuned cells (either S.I. or T.S.) (Figure S2). Activity, as measured by activity rate (area under curve per min) or transient rate (transients per min), was not different between trial types when the animal did not run (Figure 2C, stop epochs, Table S2). During run epochs the activity and tuning of A- or B-selective neurons was primarily driven by trial type, rather than speed (Figures S1G-S1I). This suggests that neuronal activity was modulated primarily during navigation and incorporated information about the task contingency in an episodic-like manner.

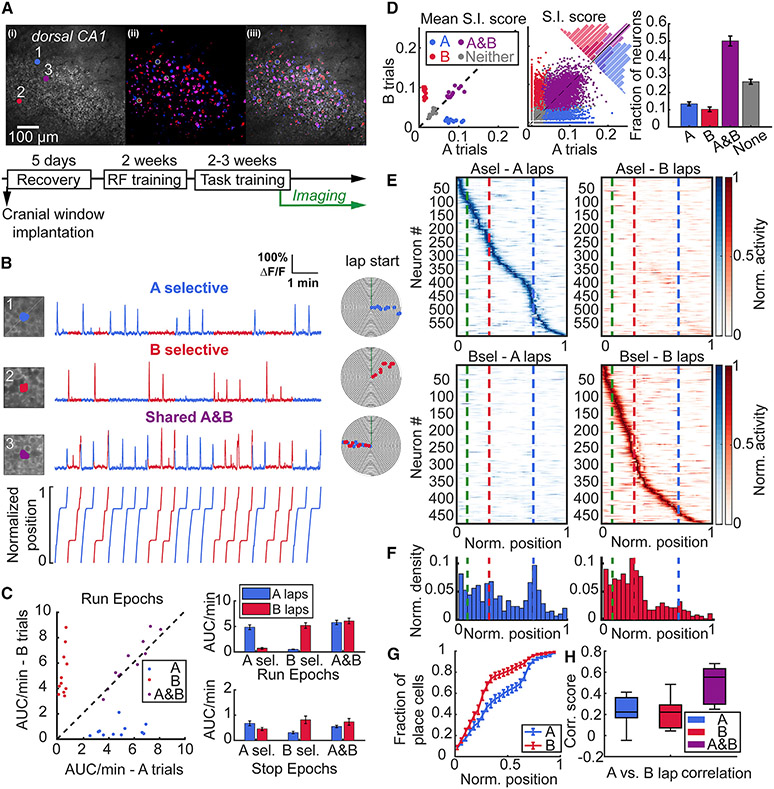
Figure 2. Task-selective place cells in dorsal CA1 during stable performance.

(A) (Top) Example field of view (FOV) of the CA1 pyramidal cell layer showing (1) the mean and (2) maximum intensity projection run-epoch imaging stacks and (3) overlay with neurons pseudocolored for trial selectivity in odor A (blue), and odor B (red) trials, while shared A and B are in magenta. (Bottom) Training timeline of mice, as in Figure 1B.

(B) Examples of A- (1) and B- (2) task selective and A and B shared (3) place cells. Numbers correspond with circled neurons in the FOV in A. Individual points on event spiral maps represent significant running-related Ca²⁺ events on A (blue) or B (red) trials.

(C) (Left) Calcium activity rate (area under curve per minute) of A-, B-, and A and B shared place cells plotted by each trial type during run epochs. Each point represents the mean from all neurons for 11 FOVs from 10 mice. (Right) Activity of task-selective neurons is greater on their respective task laps during run epochs (A-selective: 4.84 ± 0.47 vs. 0.7 ± 0.16, p = 0.003; B-selective: 0.51 ± 0.07 vs. 5.18 ± 0.55, **p = 0.003; shared: 5.77 ± 0.44 vs. 6.08 ± 0.56, p = 0.21), while no difference is observed during stop epochs (A-selective: 0.68 ± 0.1 vs. 0.46 ± 0.06, p = 0.082; B-selective 0.31 ± 0.05 vs. 0.82 ± 0.15, p = 0.009; shared: 0.55 ± 0.05 vs. 0.74 ± 0.13, p = 0.175). Similarly, the difference in transient rates is statistically significant between trials for A and B selective place cells during run epochs (A-selective: p = 0.003; B-selective, p = 0.003, data not shown). All comparisons were made by Wilcoxon signed-rank test and data reported as mean ± standard error of the mean.

(D) S.I. scores (bits/Ca²⁺ event) for each neuron type on A and B laps during each session plotted as (Left) mean of each animal, and (Center) pooled distribution of all 5158 imaged neurons. (Right) Fraction of place cells tuned according to S.I. (S.I. fraction: Friedman test, p < 0.001) showing highest number of A and B shared cells (A vs. A and B: 0.13 ± 0.01 vs. 0.5 ± 0.03, p = 0.003; B vs. A and B: 0.1 ± 0.01 vs. 0.5 ± 0.03, p = 0.003) and more A-than B-selective neurons (Fraction of A vs. B: 0.13 ± 0.01 vs. 0.1 ± 0.01, p = 0.014). Wilcoxon signed-rank test was used for comparisons.

(E) Rate maps from all mice for A- and B-task selective place cells on A and B laps. Each neuron’s rate is normalized to its maximum rate across both trial types and sorted according to the position of their maximum rate across 100 spatial bins on each lap type. Dashed lines indicate the end of odor zone in green, start of B reward zone in red, and start of A reward zone in blue.

(F) Distribution of place field centroids for A- and B-selective place cells across the track (25 spatial bins). Both categories of place cells are non-uniformly distributed across the track, with a skew toward the initial segment (zone I) of the track (place field distribution, A-selective: p = 0.009; B-selective: p < 0.001, Rayleigh test of uniformity). A-selective place cells also show aggregation at more distant locations on the track near the A reward zone.

(G) Distribution of place field centroids differs between A-selective and B-selective place cells (2-sample Kolmogorov-Smirnov test, p < 0.001).

(H) Pearson correlation of spatial TCs between A and B laps for A-, B-, and shared A and B place cells. Spatial correlation scores are low for task selective neurons with no difference between groups and significantly lower compared with task shared neurons consistent with effective discrimination between each category of place cells (A-selective: 0.24 ± 0.04; B-selective: 0.21 ± 0.04; A and B 0.49 ± 0.05; A- vs. A and B: p = 0.003; B- vs. A and B: p = 0.003, Wilcoxon signed-rank test). Central mark indicates median and top and bottom boxes indicate 25^th and 75^th percentiles, respectively. Whiskers denote the most extreme data points. Data shown from 11 FOV from n = 10 mice. See also Figure S2 and Table S2.

Place fields of A- and B-selective place cells spanned the entire track length (Figures 2E and S2D-S2F), and there was no difference in place field properties between trial types (Figures S2C and S2D). However, there was a significant difference in the distribution of place fields within A trials and B trials for trial-selective neurons (Figures 2F and 2G, Table S2). We observed an overabundance of place fields within the common track segment—from lap start until the B reward zone—on both trials, consistent with the greatest behavioral significance of this area in navigating a trial trajectory. There was a greater density of place fields in this segment on B trials, while the distribution of the longer trajectory A-selective place fields was more uniform across the track with increasing field density near the distant reward zone. Last, we compared the spatial tuning curve correlations between A and B trials for A- and B-selective place cells against shared A and B place cells. We observed low correlation scores for both A- and B-selective neurons (Figure 2H, Table S2), indicating that activity maps from A- and B-selective neurons discriminate between trial types. Significantly higher correlation scores were present among the A and B shared place cells (Figure 2H). Furthermore, we observed a broad range of correlation scores among the shared group—with some neurons approaching scores similar to those of the task selective neurons—suggesting that more complex trial-to-trial spatial dynamics exist among this subpopulation.

Place cells exhibit dynamic, behaviorally driven re-mapping properties between trial types

Changes in the sensory environment and behavioral demands can influence the activity of place cells by inducing re-mapping. Classically, re-mapping has been characterized by changes in place field firing rate, called rate re-mapping and/or place field location, referred to as global re-mapping (Leutgeb et al., 2005b). Given that the sensory environment in our task remained fixed (except for changes in odor identity at the lap start), any re-mapping activity between A and B trials would reflect behavioral modulation of spatial maps and suggest encoding of contextual or episodic structures of the task.

To examine the re-mapping features of A and B shared place cells, we classified each neuron into one of four categories according to their cross-trial spatial tuning curve similarity and place field-related calcium activity (Leutgeb et al., 2005b) (Figures 3A and S3, see STAR Methods): common, global re-mapping, activity re-mapping, and other. Common neurons had the same place field location in A and B trials with similar activity rates. Global re-mapping neurons had consistent shifts in place field location between trial types identified by the dissimilarity of their A and B tuning curves. Activity (akin to rate) re-mapping neurons were those with the same place field in A and B trials, but whose calcium activity was modulated by trial type. The greatest fraction of place cells was in the non-re-mapping common category, followed by global re-mapping neurons (Figure 3C, Table S3).

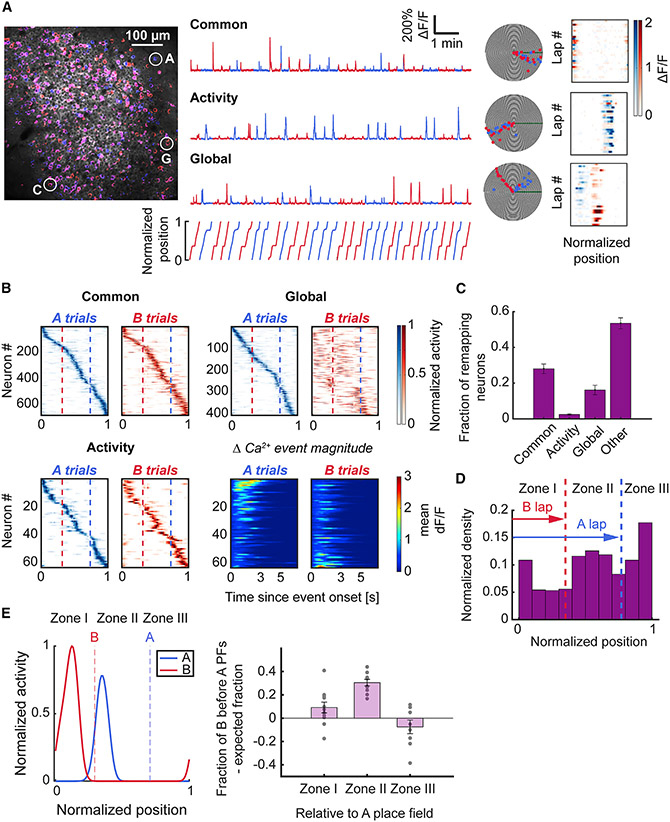
Figure 3. Place cells show distinct and task-oriented for ms of re-mapping between trial types.

(A) (Left) Imaging field overlaid with maximum intensity projection on A-laps (blue) and B-laps (red). (Right) Example ΔF/F traces and polar plots of different types of place cells. (Top) Common neuron that fires in its place field regardless of trial type. (Middle) Activity re-mapping neuron with place field calcium activity modulated by trial type. (Bottom) Global re-mapping neuron which has distinct place fields on each trial type. Colormaps (blue for A-trials, red for B-trials) on the right show the mean ΔF/F activity in each spatial bin on each trial. Note the difference in the ΔF/F signal intensity of the activity re-mapping neuron between A and B laps.

(B) Spatial tuning colormaps for each class of place cells. Cells are sorted according to the spatial bin of maximum rate on A laps. Note the predominant shift of global re-mapping neurons’ place fields toward earlier locations on the track on B laps. Bottom right panels depict the mean ΔF/F value relative to the onset of the Ca²⁺ event in the place field for activity re-mapping neurons. The activity map was sorted according to the difference between the peak mean ΔF/F value of Ca²⁺ transients in the place field on A vs. B trials.

(C) The difference in proportions was significant between the common class and activity and global re-mapping classes of place cells (Friedman test, p < 0.001; common vs. activity: 0.28 ± 0.03 vs. 0.02 ± 0, p = 0.002; common vs. global: 0.28 ± 0.03 vs. 0.16 ± 0.03, p = 0.032; Wilcoxon signed-rank test). The distribution of place cell categories was compared relative to normalized counts of all categories for each animal. Bars indicate mean ± standard error of the mean.

(D) Common place cells were distributed across the track according to spatial task demand. The place field density was lowest in zone I (before the B reward zone); the density increased across track length, in contrast with task-selective place maps, which show greater density at track start (Figure 2F) (Rayleigh test of uniformity, p < 0.001).

(E) Global re-mapping neurons exhibited task-oriented re-mapping of place fields. (Left) Example of a global re-mapping neuron with a place field centroid in zone II on A laps and a place field centroid in zone I on B laps. Right, quantification of the fraction of global re-mapping neurons with B fields before A fields in each zone, compared with the expected fraction (see STAR Methods). Place cells with place field centroids located in zone II (between the reward zones) on A laps exhibited a statistically significant shift of place fields on B trials to earlier positions on the track (zone II A vs. B lap field shift: 0.3 ± 0.03, one-sample Wilcoxon signed-rank test against 0, p < 0.001); 11 fields of view from n = 10 mice. See also Figure S3 and Table S3.

Our task design introduced an implicit behavioral gradient with progressively lower memory and attention demands once the animal had traversed the indicated goal location. To link place coding with this behavioral gradient in our analysis, we split the track into three spatial zones defined by the reward zones. Common place cells showed increasing density with track distance (Figure 3D, Table S3). Global re-mapping place cells tended to have their place fields in shorter trajectory B trials at earlier positions than on longer trajectory A trials (Figure 3E, Table S3). These results suggest that beyond task-centric encoding of information within CA1 subpopulations, information about trajectory length and/or scale are reflected within the maps.

Task-dependent spatial maps retain stable activity after learning during recall

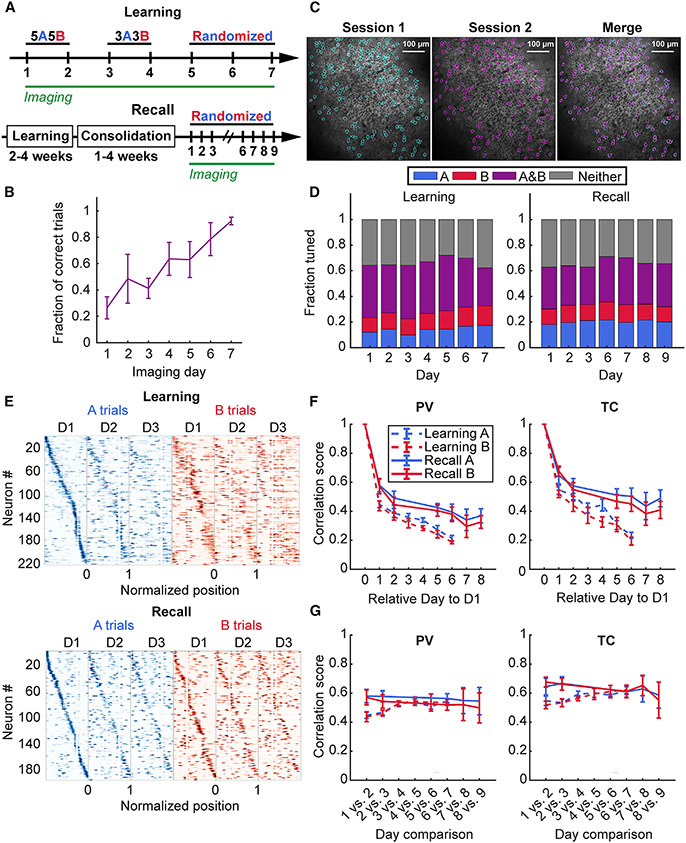
Next, we asked whether spatial maps emerging during the task remain stable as the memory is acquired and consolidated. Stable representations would imply the importance of place cell activity in facilitating long-term contextual memory recall in light of recent evidence for functional importance of place cells (Robinson et al., 2020). To determine whether place maps are more stable when learned within the structure of a memory task at longer timescales, we compared the place maps of the same CA1 pyramidal neurons imaged during an accelerated training regimen (learning) against place maps following consolidated learning (recall) (Figures 4A and 4B). Mice learned the task with 92 ± 2% accuracy (mean ± SEM; n = 6) by day 7 on the accelerated regimen (Figure 4B), with recall performance remaining consistently between approximately 80% and 100% (Figure 5D). We tracked neurons using an automated region of interest registration algorithm from the CaImAn analysis package (Giovannucci et al., 2019) (Figure 4C) (see STAR Methods).

Figure 4. Learning induces rapid re-mapping of place maps.

(A) Schematic of the accelerated training regimen and imaging schedule for odor-cued spatial navigation (see STAR Methods). (Bottom) Timeline for memory recall imaging experiments following learning.

(B) Learning performance during accelerated learning. Mice achieve high behavior performance by the last day of training (mean ± standard error of the mean 92 ± 2%, n = 6 mice).

(C) Example of matching spatial components (regions of interest) across two different sessions.

(D) Task-dependent tuning of place cells occurs as early as the first day of training and persists during learning with increase in fraction of A-trial tuned place cells during A, but not B trials (A trials: one-way repeated measures [RM] mixed effects analysis, effect of training day, p < 0.001; B trials: one-way RM mixed effects analysis, effect of training day, p = 0.27) with no change during recall (A trials: one-way RM mixed effects analysis, effect of training day, p = 0.92; B trials: one-way RM mixed effects analysis, effect of training day, p = 0.95). Data from n = 6 mice in learning and n = 5 mice in the recall cohort.

(E) Example spatial tuning maps that show rapid re-mapping of spatial activity during learning (top) in contrast to memory recall following learning (bottom).

(F) (Left) PV correlation of all matching cells relative to Day 1 of imaging shows rapid restructuring of run-related activity on the following training day that stabilizes on recall trials (A trials: two-way RM mixed effects analysis, effect of time, p < 0.001, effect of behavior, p = 0.015, interaction, p = 0.519; B trials: two-way RM mixed effects analysis, effect of time, p < 0.001, effect of behavior, p = 0.014, interaction, p = 0.18; day 2 vs. day 7, recall, A trials: 0.58 ± 0.05 vs. 0.39 ± 0.06, p = 0.003; B trials: 0.57 ± 0.05 vs. 0.38 ± 0.05, p = 0.002, n = 5 mice), but not during learning (day 2 vs. day 7, learning, A trials: 0.43± 0.03 vs. 0.19± 0.01; p = 0.028; B trials: 0.41 ± 0.04 vs. 0.19 ± 0.01, p = 0.053, n = 3 mice; day 7, learning vs. recall, A trials: 0.21 ± 0.02 vs. 0.39 ± 0.06, unpaired t-test, p = 0.027; B trials: 0.19 ± 0.01 vs. 0.38 ± 0.05, unpaired t-test, p = 0.014,n = 4 mice in learning and n = 5 mice in recall cohort). (Right) A similar trend was observed for the TC correlation scores between matching place cells selected using the T.S. criterion (A trials: two-way RM mixed effects analysis, effect of time, p < 0.001, effect of behavior, p = 0.017, interaction, p = 0.021; B trials: two-way RM mixed effects analysis, effect of time, p < 0.001, effect of behavior, p = 0.008, interaction, p = 0.189; day 2 vs. day 7, learning, A trials: 0.51 ± 0.03 vs. 0.22 ± 0.02, p = 0.028; B trials: 0.51 ± 0.03 vs. 0.19 ± 0.04, p = 0.045, n = 3 mice; day 2 vs. day 7 recall, A trials: 0.65 ± 0.06 vs. 0.5 ± 0.06, p = 0.014; B trials: 0.68 ± 0.03 vs. 0.45 ± 0.05, p = 0.006, n = 5 mice; day 7, learning vs. recall, A trials: 0.23 ± 0.02 vs. 0.5 ± 0.06, unpaired t-test, p = 0.009; B trials: 0.19 ± 0.03 vs. 0.45 ± 0.05, p = 0.01, n = 4 mice in learning and 5 mice in recall cohort). Paired t-test used for all statistics unless otherwise noted. Data from n = 6 mice in the learning and n = 5 mice in the recall cohort.

(G) Learning stabilizes neighboring session maps at the population level and between place cells. As learning progresses through each training stage, the population correlation scores approach those observed for the memory-consolidated recall cohort (A trials: two-way RM mixed effects analysis, effect of time, p = 0.042, effect of behavior, p = 0.044, interaction, p = 0.006; B trials: two-way RM mixed effects analysis, effect of time, p = 0.4; effect of behavior, p = 0.204, interaction, p = 0.012; day 1 vs. day 2 vs. day 6 vs. day 7, learning, A trials: 0.43 ± 0.03 vs. 0.54 ± 0.01, p = 0.034; B trials: 0.41 ± 0.04 vs. 0.52 ± 0.01, p = 0.136, n = 3 mice; day 1 vs. day 2 vs. day 6 vs. day 7, recall, A trials: 0.58 ± 0.05 vs. 0.56 ± 0.03, p = 0.611; B trials: 0.57 ± 0.05 vs. 0.52 ± 0.04, p = 0.20, n = 5 mice). For spatially tuned neurons, the stabilization occurred during learning on both A and B trials, but not during recall (A trials: two-way RM mixed effects analysis, effect of time, p = 0.492, effect of behavior, p = 0.16, interaction, p = 0.013; B trials: two-way RM mixed effects analysis, effect of time, p = 0.59, effect of behavior, p = 0.064, interaction, p = 0.003; day 1 vs. day 2 vs. day 6 vs. day 7, learning, A trials: 0.51 ± 0.03 vs. 0.61 ± 0.03, p = 0.028; B trials: 0.51 ± 0.03 vs. 0.6 ± 0.01, p = 0.036, n = 3 mice; day 1 vs. day 2 vs. day 6 vs. day 7, recall, A trials: 0.65 ± 0.06 vs. 0.61 ± 0.04, p = 0.47; B trials: 0.68 ± 0.03 vs. 0.61 ± 0.04, p = 0.162, n = 5 mice). Paired t-test used for all statistics unless otherwise noted. Data from n = 6 mice in the learning and n = 5 mice in the recall cohort. See also Figures S4 and S5 and Tables S4 and S5.

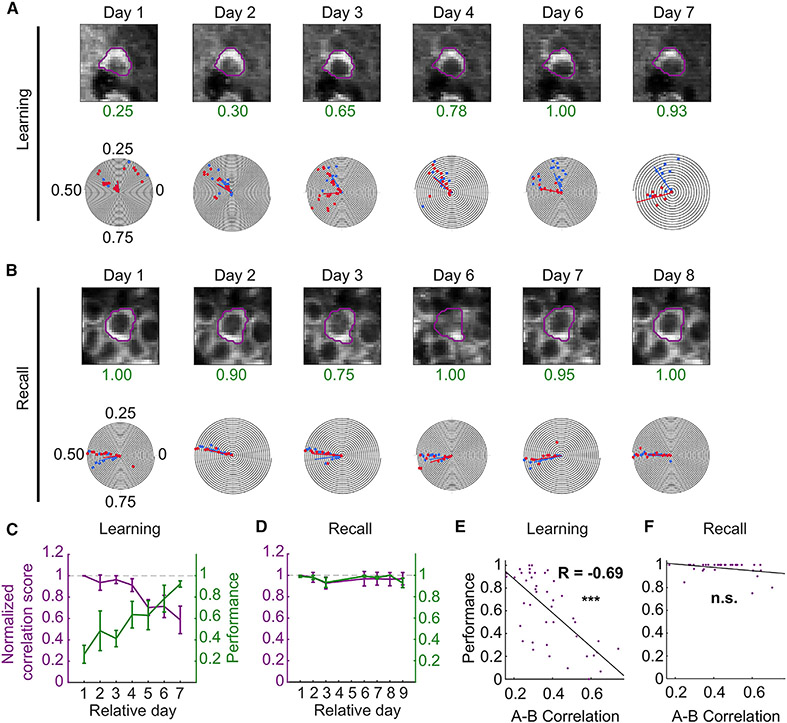
Figure 5. Dissimilarity between task spatial maps predicts animal performance.

(A) Image and polar plot of example neuron during learning. As the performance (green) of the animal increases with training, the task shared neuron splits its common place field into two task-dependent fields.

(B) During recall, the spatial fields of this neuron are stable.

(C and D) Overlay of plots of normalized TC correlation scores (left axis) and animal performance (right axis) of matched A and B spatially tuned neurons during learning (C) and recall (D). Normalized TC correlation scores were calculated as the A vs. B lap tuning correlation score on the relative session day divided by the A vs. B lap correlation score on the first day of imaging for each matched neuron. As the performance of animals improved during learning, place cell maps between task trials became progressively more decorrelated (p < 0.001; day 2: 0.94 ± 0.07, p = 0.011, n = 179 neurons from 6 mice; day 7: 0.59 ± 0.13, p < 0.001, n = 122 neurons from 6 mice). A similar effect was not observed during recall when animals performed with more than 90% accuracy on each day and the normalized correlation scores were near the expected value of 1 (p = 0.21; day 2: 0.99 ± 0.05, p = 0.996, n = 133 neurons from 5 mice; day 7: 0.95 ± 0.07, p = 0.073, n = 91 neurons from 5 mice), Kruskal-Wallis test. Tests for individual days were computed using a one-sample Wilcoxon signed-rank test against 1. Data from n = 6 mice in the learning and n = 5 mice in the recall cohort. Data presented as mean ± standard error of the mean (error bars).

(E and F) Scatterplots of A vs. B lap correlation against the performance from all sessions and animals during learning (E) and recall (F). There was a strong inverse relationship between the A-B correlation maps and performance for the learning (R = −0.69, p = 2.17 × 10⁻⁷, n = 44 sessions from 6 mice), but not recall (R = −0.32, p = 0.058, n = 35 sessions from 6 mice) cohort. See also Table S6.

To quantify spatial task selectivity across days, we selected all cells that were significantly tuned according to the T.S. criterion on a given session and compared their distribution across time. We chose the T.S. criterion to favor the selection of place cells with single place fields but achieved similar results using the S.I. criterion (Figure S4). As early as the first day of training, we observed trial-selective tuning on A and B trials and a subtle increase in the fraction of task-selective neurons across time (Figure 4D, Table S4). During the recall stage, the task-specific distribution of place cells remained stable across time (Figure 4D, Table S4). Importantly, we observed a significant difference in the stability of place maps between learning and recall phases, using correlation analyses at both the population (population vector [PV] correlation) and individual place cell (tuning curve [TC] score) level relative to the first imaging day. We found instability of the network during task learning, while the place map network showed remarkable stability during the recall sessions (Figures 4E, 4F, and S4G-S4I; PV, Table S5). The PV correlation decreased for both learning as well as recall in A and B trials, but the decorrelation was substantially greater for the learning cohort on day 6 and day 7 compared with recall (Figure 4F). When we specifically looked at place cells, we observed a rapid TC decorrelation beginning at day 2 for the learning and recall cohorts; however, the recall cohort maintained higher correlation at later days (Figure 4F, TC, Table S5). This suggests a stabilization of spatial representations following learning in the memory recall cohort.

To examine the rate at which the spatial network stabilized, we calculated the correlation between neighboring day sessions at the level of the population and individual place cells (Figure 4G, Table S5). We reasoned that as the animals learned the task rules, the activity maps would reach neighboring day scores similar to that of the recall cohort, which we expected to be fixed after learning. We observed that at the population level (PV score), the learning cohort experienced a time-dependent increase in neighboring day map similarity, gradually reaching the same level as the recall phase PV scores. The initial PV score was higher in the recall cohort compared with the learning cohort and did not show a time-dependent change (Figure 4G, left, Table S5). Similarly, spatial maps in the learning, but not recall, cohort increased their neighboring day correlation (TC score) across time (Figure 4G, right, Table S5).

Another way of examining representational drift is by comparing the degree of place field displacement across time. For this we calculated the mean change of the place field centroids relative to the first imaging session. Throughout learning and recall, centroids shifted across days in both A and B trials; however, the rate of place field centroid shift was consistently lower in the recall cohort compared with the learning cohort. The relative difference between place field re-mapping for learning vs. recall appeared earlier in B trials (from day 1) compared with A trials (from day 3) (Figures S4E and S4F) reflecting the episodic nature of the task.

Last, we imaged a subset of recall animals over a longer term to examine how long the activity of learned spatial maps can persist. We observed a surprisingly high level of map stability across 30 days of imaging, with a slow decay in correlation (Figures S4G-S4I). Overall, our imaging findings indicate that learning induces place re-mapping, which stabilizes in the long-term during recall phases following learning, when performance is stably high.

Dissimilarity between task-specific spatial maps predicts performance

While task-modulated place cells seem to be a feature of episodic spatial behavior, the link between learning and the activity of these maps remains unclear. To understand how strongly the rate of learning is coupled to the rate of task-dependent spatial map divergence, we compared the A and B spatial tuning correlation of place cells tuned in both trial laps (i.e., A and B tuned) during learning and recall relative to the first day of imaging across time. We noticed a greater tendency for place cells to split their place fields between tasks during learning (Figure 5A) than during recall (Figure 5B). TCs became more decorrelated as the performance of the animal increased during learning (Figures 5C and 5E and S4G-S4I, Table S6), but not during recall when performance reached a steady-state high (Figures 5D and 5F and S4G-S4I, Table S6). Thus, existing spatial maps are remapped to reflect the degree of task learning in CA1 and context selective divergence.

To further explore the stability of spatial maps and the relationship between task-specific maps and performance, we reversed the reward contingencies for a new cohort of three mice after learning the odor-reward associations (Figure S5). We observed a decline in performance on the first day of reversal which recovered with additional experience under the new reward rules. Accordingly, the A vs. B correlation of A and B tuned place cells initially increased under the new rules and decayed to lower levels with experience, suggesting the introduction of new reward contingencies induced a new phase of learning, as if it were a novel environment (Figure S5B). Analysis of the relative day and neighboring day correlation at both the population and neuron level showed stability patterns similar to the original learning paradigm: a decrease in stability during the reversal learning phase and then a trend toward increased stabilization during the recall phase (Figures S5C-S5G).

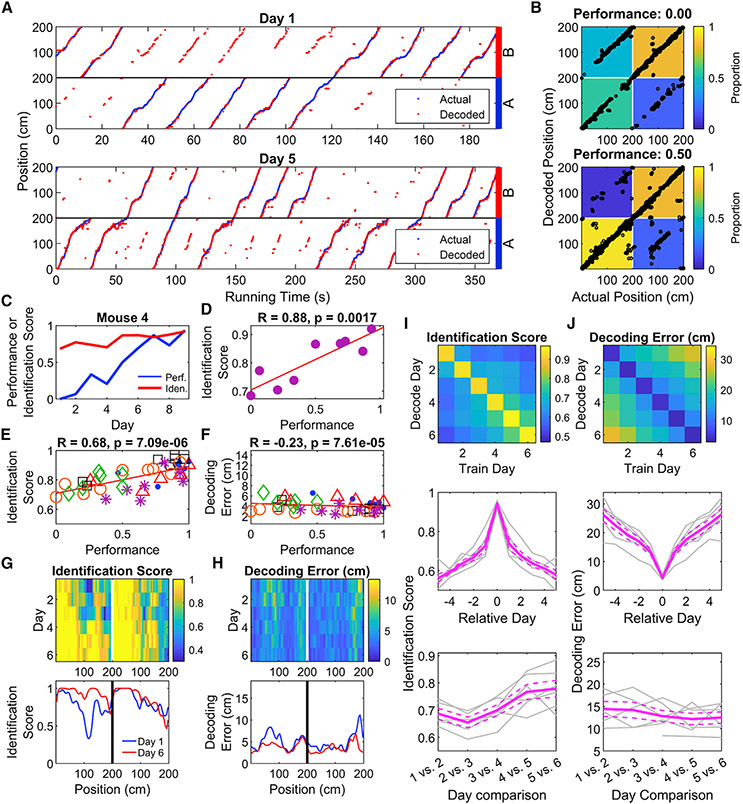
To link the differential activity of CA1 neurons to task performance, we used PV decoding to read out the position and context (A or B trial type) of the mice (Figures 6A and 6B). The decoder’s identification score (accuracy in predicting trial type) was positively correlated with behavioral performance across all mice (Figures 6C-6E, Table S7). Absolute error in decoding position was also negatively correlated with performance, but with a small effect size (Figure 6F, Table S7). The decoder improved the most around position 110 cm in context A, immediately before the reward zone for that context (Figure 6G, Table S7). Errors in absolute position also tended to be higher near the end of trials in both contexts, as well as immediately after reward zone B experienced in context A (Figure 6H), parts of trials with the most behavioral uncertainty. Additional analyses revealed that the neural population was most likely encoding position and trial type, as opposed to encoding speed (Figure S6). When applied to the reversal learning data, we found that the accuracy of the decoder decreased when the reward contingency rule was swapped, and this improved with additional training (Figures S7A-S7H), indicating the emergence of a new representation of space.

Figure 6. Place maps incorporate information about and predict location and trial type during task learning.

(A) A PV decoder accurately predicts the position of an animal during both the initial (top) and late (bottom) training sessions. Decoded mouse positions (red) are plotted against the actual positions (blue) as a function of time. On the late training session, the decoder for this animal identifies the trial the animal is on with high accuracy. Throughout the figure, positions 0–200 are represented twice, once each for A and B trials. Data from this mouse only are used in B–D.

(B) Confusion matrices quantifying decoding accuracy demonstrate improved accuracy in identifying trial type associated with improved performance. Black points represent the actual position and trial of the animal plotted against the decoder’s prediction. Each matrix cell represents the number of decoded points falling into each quadrant divided by the total data points in each trial type.

(C) Example plot showing that as the performance of a single mouse increases with subsequent training sessions, the identification score (proportion of data points correctly classified as trial type A or B) also increases.

(D) Same data as in (C) with performance plotted against decoding score, revealing a strong positive relationship between task performance and decoder score (two-sided one-sample t-test, p = 0.002).

(E) Cumulative analysis across all training sessions revealed a strong positive relationship between performance and identification score (two-way ANOVA, R = 0.68; effect of mouse, p = 0.34; effect of performance, p = 7.1 × 10⁻⁶; interaction, p = 0.55). Each point is a single training session and each mark type a different animal.

(F) Position decoding error and task performance shows only a weak relationship (two-way ANOVA, R = −0.23; effect of mouse, p = 1.5 × 10⁻⁵; effect of performance, p = 7.6 × 10⁻⁵; interaction, p = 0.03).

(G) Colormap showing improvement in the position-trial decoding accuracy as function of training session. Each row denotes the median decoding score (n = 6 animals). The decoding score increases progressively forward along the track during each training session, prominently observed on A trials. Bottom graph plots decoding score for sessions 1 and 6.

(H) Similar plot of the decoding position error averaged across all animals does not reveal such change during training.

(I) Top, Image depicting the identification score of classifiers trained on one day and tested on another (see STAR Methods). Middle, mean value of successive diagonals of the above image, showing the drop in identification score with experience. Bottom, identification score on adjacent days shows an increase with experience, indicating a stabilization of the neural representation of trial type (two-way ANOVA, effect of mouse, p = 0.14; effect of Day, p = 0.0001; interaction, p = 0.16).

(J) As in I, but for decoding error. Adjacent-day decoding error does not significantly change with experience (two-way ANOVA, effect of mouse, p = 0.02; effect of Day, p = 0.41; interaction, p = 0.07). See also Figures S6 and S7 and Table S7.

Data presented as mean ± standard error of the mean (gray lines), n = 6 mice.

We further tested the decoder by training and testing it on different days (Figures 6I and 6J, Table S7) (see STAR Methods). The identification score and decoding error showed a time-dependent degradation in line with the time course of TC and PV correlations (Figure 4F). When testing the decoder on consecutive days, the identification score, but not the decoding error, improved across days, indicating stabilized neural representations with experience. When we applied the decoder to the reversal learning data, we saw the next-day decoding dramatically decrease on the day the rule contingency was reversed (Figure S7I). This slowly increased with experience under the new rules. This effect was only seen for the identification score, not for decoding error of absolute position (Figure S7J).

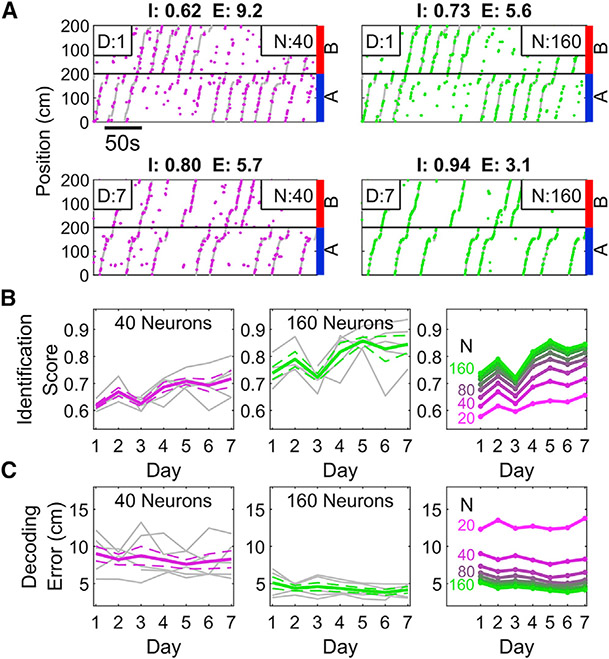
Since the performance of PV decoder increased across training days, we tested whether the neural representation became more efficient with experience. The identification score of the decoders constructed with small subsets of neurons were significantly worse across all training days (Figures 7A and 7B, see STAR Methods). With experience, all decoders improved, such that the number of neurons needed to achieve a given performance level shrank across days (Figure 7B). A similar relationship was observed for decoding error, but the magnitude of change with experience was relatively small. This is further evidence that the neural population adapts to efficiently and effectively represent task-relevant information during learning.

Figure 7. PV decoding becomes more efficient with experience.

(A) Top, sample performance of the PV decoder on training day 1 when trained with 40 (magenta, left) and 160 (green, right) neurons. Identification score (I) and decoding error (E) are indicated above the plots. As expected, the decoder performs better when more neurons are included. Bottom, same as above but on day 7 of training, demonstrating marked improvement over day 1. Note that the 40 neuron decoder on day 7 equals or exceeds the performance of the 160-neuron decoder on day 1.

(B) The Identification Score of the decoder increased as a function of experience. This was true for decoders trained on a small (left, 40) or large (middle, 160) number of neurons. (Right) Decoders trained on later sessions with few neurons could achieve similar accuracy as decoders trained on early sessions with many neurons, indicating an increased efficiency of encoding the space (two-way ANOVA, effect of number of neurons, p = 1.7 × 10⁻⁴; effect of day, p = 1.3 × 10⁻¹⁴; interaction, p = 0.98).

(C) As in B but for decoding error. Decoding Error only slightly improved with experience; the number of neurons was a stronger influence on Decoding Error (Two-way ANOVA, effect of number of neurons, p = 2.9 × 10⁻³¹; effect of Day, p = 1.7 × 10⁻⁹; interaction, p = 0.36, see STAR Methods).

Data presented as mean ± standard error of the mean (gray lines), n = 6 mice.

DISCUSSION

We developed a new task where mice navigate to reward locations in an odor-context dependent manner and imaged hippocampal pyramidal neuron activity over the course of learning and memory recall. This allowed us to assess how neuronal activity adopts episodic, spatial, and contextual features of memory-guided behavior and stabilizes as a function of attention and behavioral performance. We found that hippocampal cells were rapidly recruited and evolved into task-dependent maps with both orthogonal and overlapping representations of space. Context decodability was strongly correlated with task performance. Neural activity patterns were less stable during learning, changing day to day, but more stable during memory recall. The stability of learned place maps persisted during recall trials over 30 days as the animal’s performance maintained a high steady state. Both accuracy and efficiency of population decoding of context improved with experience, indicating a stabilization of maps as a function of behavioral performance. Taken together, our findings show that behaviorally defined activity of place maps is task selective and indeed stable under high contextual demand, help to resolve recent controversies about representational drift (Ziv et al., 2013; Hainmueller and Bartos, 2018; Kentros et al., 2004; Liberti et al., 2022), and strongly support the concept that the hippocampus can maintain long-term representations to reliably support memory recall.

Establishing the relationship between place cell activity and long-term memory representation with contextual dependencies requires longitudinal tracking of large populations of neurons during a behavioral task with sufficient context selectivity and mnemonic demand. Our behavioral paradigm achieved this, providing distinct advantages over previous freely moving behavioral tasks such as the continuous alternation T-maze (Wood et al., 2000). First, we trained animals to learn both odor-context task contingencies on the same belt (without changing environments). This way, we could ensure hippocampal representation of the task is due to operant learning of a behavior rather than the learning of other strategies, such as dead reckoning. Second, stable two-photon calcium imaging of transgenically expressed GCaMP+ neurons allowed us to longitudinally track the emergence and recall of task-selective place maps. Our results provide evidence for two key postulates of hippocampal dynamics: that existing place maps can reconfigure in response to an associational learning rule despite a constant physical environment (Dupret et al., 2010; Robinson et al., 2020) and that such task-selective place maps persist long after learning is achieved (Buzsáki and Moser, 2013; Kentros, 2006; Robinson et al., 2020).

Our data show that the hippocampus generated task-selective representations of space during learning that rapidly remapped between contexts. In well-trained mice, we captured a complex set of coding mechanisms for representation of both location and behavioral contexts. In cells with fields in both behavioral contexts, we observed the calcium analog of both rate and global re-mapping, whose activity is attributed to changes in context (Leutgeb et al., 2005b; Lu et al., 2013) and physical environment (Leutgeb et al., 2004, 2005b; Plitt and Giocomo, 2021), respectively. Given the structure of our task, where the physical environment remained constant while the odor-cued context changed, we were surprised to see a relatively smaller fraction of activity re-mapping place cells (analogous to rate re-mapping) as compared with global re-mapping cells. Perhaps the greater proportion of global re-mapping cells may be associated with animals using different trial-specific spatial reference frames to navigate toward reward zones. Overall, in line with other studies, our observations establish that hippocampal place cells can remap even within the same environment given changes in task demands, goal locations, or learning contingencies (Figure S5) (Danielson et al., 2016; Dupret et al., 2010; Ferbinteanu and Shapiro, 2003; Frank et al., 2000; Leutgeb et al., 2005a; Markus et al., 1995; Muller et al., 1991; Plitt and Giocomo, 2021; Wood et al., 2000).

We found an over-representation of place fields selectively around the trial-respective reward locations, in an episodically relevant manner. While place field density for B-selective place cells drops soon after crossing the near reward goal location B, A-selective place cell densities remain high throughout the track traversing both the near B and far A reward zones. Previous experiments document the dynamic recruitment of place cells with egocentric and allocentric reference frames during navigation (Gothard et al., 1996; Moore et al., 2021). It is thus plausible that the differential distribution of place fields between A and B trials may represent a shift between spatial reference frames which drives the recruitment of trial-specific place cell ensembles.

Recent studies show a high degree of representational drift across time in the hippocampus (Ziv et al., 2013; Hainmueller and Bartos, 2018) and other areas (Schoonover et al., 2021; Marks and Goard, 2021). Our results show representational drift was greatly reduced during memory retrieval sessions in task-engaged animals. This stabilization of place maps following learning resolves a debate in the field: how can the day-to-day instability of place cells reported in recent studies be reconciled with the hypothesis that they serve as the substrate for stable long-term episodic memories. Our findings support the idea that behaviorally driven place cell activity stabilizes with memory and attentional demands (Kentros et al., 2004). In contrast, rapid turnover of spatial map activity occurs during less structured behaviors such as random foraging (Ziv et al., 2013), and non-operantly rewarded spatial behaviors (Danielson et al., 2016; Hainmueller and Bartos, 2018). In short, our findings demonstrate that place fields are in fact stable over many days, provided that they encode a behavioral relevance to the animal, and learned place maps may indeed serve as a neural correlate for long-term memory. The reversal learning experiment reinforces the idea of divergence of place maps into task-selective ensembles with learning and subsequent stabilization of learned maps during memory recall, irrespective of the learning rule itself.

While decades of work in the hippocampus has examined how activity dynamics of place cells relate to episodic and contextual aspects of an environment (Aronov et al., 2017; Komorowski et al., 2009; MacDonald et al., 2011; Pastalkova et al., 2008; Rubin et al., 2019; Wood et al., 1999, 2000), the exact relationship of place maps with learning and executing learned behaviors during memory recall remains unclear. We used a neural decoder to predict both position and distinguish context (trial type) during learning (Brown et al., 1998; Rubin et al., 2015; Ziv et al., 2013). Here, we observed a strong correlation between task performance and the accuracy and efficiency with which the hippocampal map could predict position and context trial type. Very early in learning, the absolute location on the track could be decoded. Only later in learning could behavioral context be decoded. Although we found that the proportion of cells tuned to each behavioral context did not change significantly, we did observe that the decoder became more efficient with experience, such that fewer cells were necessary to accurately identify trial context. Our results bolster the importance of behavioral state on the stability of hippocampal representations, alongside a growing body of work binding spatial and non-spatial coding in the hippocampus with learning and attention (Wang et al., 2012; Muzzio et al., 2009;Taxidis et al., 2020). Beyond the hippocampus, the emergence of stable and sparse representations with learning has also observed in the motor cortex (Peters et al., 2014).

In terms of mechanisms, consistent with previous findings (Cohen et al., 2017; Sheffield et al., 2017), our trial-by-trial re-mapping occurs on very fast timescales, well below the temporal regime of typical plasticity mechanisms. Such a fast context-dependent switch could be supported by input-specific gating through inhibitory (Lovett-Barron et al., 2014; Sheffield et al., 2017; Turi et al., 2019) and disinhibitory circuits (Basu et al., 2016), and are worth further exploration. While intrinsic hippocampal synaptic mechanisms can lead to the progressive turnover of spatial representations (Dupret et al., 2010; Ziv et al., 2013), our results suggest that behavioral state and memory demand play important roles in modulating processes underlying drift and stability. Context discrimination behavior (Basu et al., 2016) and context-dependent place cell formation and re-mapping (Bittner et al., 2017) may rely on dendritic spikes mediated by coordinated activity between entorhinal cortex and CA3 inputs upon CA1 pyramidal neurons (Basu et al., 2016; Kamondi et al., 1998). Such non-linear dendritic integration may trigger non-Hebbian plasticity (Basu et al., 2013, 2016; Bittner et al., 2017; Dudman et al., 2007) during the learning phase of the task. In contrast, after encoding, long-term stabilization of ensembles may be mechanistically supported by Hebbian plasticity rules involving theta modulated burst firing (Epsztein et al., 2010, 2011; Lee et al., 2012), and experience-dependent strengthening of coincident tuned synaptic inputs (Cohen et al., 2017). Synchronized activity with higher order prefrontal cortical (Preston and Eichenbaum, 2013; Rajasethupathy et al., 2015; Spellman et al., 2015) and subcortical neuromodulatory inputs (Kaufman et al., 2020; Kentros et al., 2004; Solari and Hangya, 2018), as well as sharp-wave ripples (Roux et al., 2017; Fernán-dez-Ruiz et al., 2019), may be at play for the reactivation and stabilization of task-related place cell sequences (Dupret et al., 2010; Ito et al., 2015; Jadhav et al., 2012; Pastalkova et al., 2008).

In conclusion, our data show that the hippocampus rapidly generated orthogonal and overlapping task-selective place maps during learning. Shared place cells showed task selectivity by re-mapping their activity or place field location for alternating trial types. Interestingly, while behaviorally influenced representations of space emerged early on, these maps progressively diverged to more dissimilar cross-trial representations correlated to the animal’s increasing task performance. Once learned, place maps remained stable during memory recall signifying a memory-behavior imposed stability of hippocampal representations.

Limitations of the study

Our study tracked single neuron and population activity in CA1 of mice engaged in a well-controlled behavior task to show task selective place cell ensemble formation and subsequent stabilization during learning and recall, respectively. While it is clear that the hippocampus is engaged and shows task selective activity dynamics, our study does not address whether the hippocampus or its functional connectivity with entorhinal cortices are required for task performance. Calcium imaging allowed us to image 100 s of neurons simultaneously, but the slow kinetics of calcium and GCaMP limit the time resolution of our analyses. Furthermore, the calcium signals we record likely report bursts of activity and may miss single action potentials. Finally, our animals learned the task very effectively, so we had a limited number of error trials to decode and identify specific activity patterns or task selective cell types driving task performance. While much work remains to uncover the possible cellular and circuit mechanisms driving the experience dependent emergence and stabilization of place cell ensembles, this novel behavioral paradigm provides a rich substrate to study flexibility and stability of place maps in episodic and context-dependent manners.

STAR★METHODS

RESOURCE AVAILABILITY

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Jayeeta Basu (Jayeeta.Basu@nyulangone.org).

Materials availability

This study did not generate new unique reagents.

Data and code availability

• Data: All data reported in this paper will be shared by the lead contact upon request.

• Code: All original code has been deposited at zenodo (https://doi.org/10.5281/zenodo.7226595) https://github.com/rzemla/paper_analysis and is publicly available as of the date of publication.

• Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Mice

Experiments were performed with 4- to 12-month-old adult male mice on a C57BL/6J background transgenically expressing GCaMP6f from the Thy1 locus (GP5.5 JAX strain #024276) (Dana et al., 2014). All experiments were approved by the Institutional Animal Care and Use Committee at New York University Medical Center.

METHOD DETAILS

Hippocampal window and headpost implantation

Mice were implanted with a circular imaging window (3.0 mm × 1.5 mm [diameter × height]) centered at 2.3 mm AP and 1.5mm ML over the left dorsal-intermediate hippocampus surrounded by a modified 3-D printed headpost (Osborne and Dudman, 2014) for head fixation. Imaging cannulas were made by attaching a 3-mm diameter coverslip (64–0720 Warner) to a stainless steel cylindrical cannula using optical UV curing optical adhesive (NOA-61, Norland products) (Danielson et al., 2016).

In vivo two-photon imaging

Imaging was performed using a two-photon 8-kHz resonant scanner (Ultima, Bruker) with a 16×, 0.8 NA water-immersion objective (Nikon). Excitation was performed at 920 nm with an 80 MHz pulsed laser (Mai Tai DeepSee, Spectra Physics). GCaMP6f emission fluorescence was collected with a GaAsP photomultiplier tube (7422P-40, Hamamatsu) following red and green channel separation with a filter cube consisting of a dichroic mirror (T565lpxr, Chroma Technology) and filters (green, ET510/80m-2p; red, ET605/70m-2p, Chroma Technology). Images were acquired at a 30-Hz frame rate, 512 × 512 pixel resolution, and 1.5× digital zoom corresponding to a field size of 555 μm × 555 μm.

Behavior

Behavioral apparatus

Mice ran on a custom-built treadmill track where the belt consisted of 3 ~65 cm long distinct fabrics (macro-textures) enriched with 4 micro-textures (5 cm regions consisting of 5 ‘dice’ arranged flattened aluminum foil spheres, 4 crossed hook-and-loop strips, zig-zag glue pattern, and strip of woven material). The position of the mouse was measured using an optical rotary encoder (S5-720, US Digital). Lap onset and micro-texture crossings were detected by reading associated RFID tags with an RFID reader mounted below the animal (ID-20LA, SparkFun Electronics). Behavior tones of 4 kHz,10 kHz, and white noise were pre-recorded and played using an mp3 player (MP3 Player Shield, DEV-12660, SparkFun Electronics). The audio signal from each channel was then amplified (PAM8302, Adafruit) and played though a pair of speakers (25-1719S, Tang Band) located on the sides of the fixation platform. Licking of the animal was registered via a blunt-tipped steel cannula coupled to a capacitive touch sensor (SEN-12041, SparkFun Electronics). Behavioral programs were controlled with an Arduino Mega 2560 microcontroller. All behavioral data was acquired at a sampling rate of 10 kHz, with a data acquisition board (PCI-6052E, National Instruments) synchronized to the time of frame acquisition.

Olfactometer

A custom-built olfactometer was used for delivering fixed-concentration, spatially restricted odors to the mouse. Briefly, during non-odor zone navigation, animals were exposed to a constant background flow of air mixed with pure mineral oil (BP26291, Fisher Scientific) at a flow rate of 1 L/min. In the immediate 50 cm prior to odor zone entry, an odor charge program was initiated by closing the normally open (NO) inlet/outlet valves (225T021, NResearch Inc.) along the flow path through the mineral oil vial (M), while opening the flow path through either odor A or B vials by activating the respective normally closed (NC) inlet/outlet valves (225T011, NResearch Inc.). The odor-charged air was routed to an exhaust port during this period through a 3-way final valve (SH360T041, NResearch Inc.), while 1 L/min of air continued to be delivered. Charging was performed to ensure that a consistent steady-state concentration of odor was reached along the pre-delivery flow path (before the final valve) and to minimize latency of odor delivery to the animal. Upon entering the odor zone, the final valve was triggered via an RFID tag to switch routing of the odor-charged air from exhaust to the animal’s snout. Upon reaching the end of the odor zone, an RFID tag triggered the closure of either A or B path valves and opening of the background mineral oil air path. A constant vacuum of 1 L/min above the odor delivery port ensured scavenging of residual odors. 10% dilutions of pentyl acetate (Sigma-Aldrich, 109584) and (+)-α-Pinene (Sigma-Aldrich, P45680) in mineral oil were used as odor A and B, respectively. A photoionization detector (200B: miniPID Dispersion Sensor, Aurora Scientific) was used to verify steady-state odor concentration delivery prior to each imaging session. A steady-state odor onset latency (baseline to steady-state) of ~125 ms and off latency of ~75 ms (steady-state to baseline) was measured. Fresh dilutions of odors were prepared daily.

Random foraging

Following recovery from surgery (3–5 days), mice were water deprived and habituated to handling and head-fixation to behavioral apparatus. Water-deprived mice were then trained to operantly lick and receive 5% sucrose water rewards in regularly spaced reward zones along a ~2 m linear track consisting of fabrics and textures described above. Training began with 20 regularly distributed reward zones followed by a program of progressively fewer and more randomly distributed reward zones over 2 weeks. Access to ~1 μL sucrose droplets began immediately after entry into a reward zone and terminated following either an exit from the reward zone (20 cm initial length), a time-out period (7 s initial duration) that had elapsed since entry, or once a maximum number of collected rewards had been reached (10 reward initial limit). Sucrose rewards were delivered on alternate licks. Training was considered complete once mice ran at a rate of ~1 lap/min in search of 3 random reward zones per lap, each defined by a 10 cm length, 3 s time-out period, and 5 droplet collection limit. Animals were given a total of 1 mL of water daily.

Odor-cued spatial navigation task

Following successful training on random reward foraging, animals were introduced onto a structured training regimen that consisted of alternating blocks of A and B trial laps. During A trials, mice were presented with odor A (pentyl acetate) in a 20 cm cue zone at the onset of the track and ran 120 cm toward the A reward zone to collect 5% sucrose water, while suppressing licking immediately prior to (10 cm anticipatory zone) and inside of the B reward zone along the way. In contrast, during B trials, mice were presented with odor B (+-pinene) in the cue zone and ran 40 cm to collect reward within the B reward zone. Following reward collection in B zone, mice were required to suppress licking in the A anticipatory and reward zone for the trial to be registered as correct. On the first day of training, animals were placed on an alternating sequence of A and B laps for 10 trials to familiarize the animal with the two types of trials. Thereafter, a regimen of 5 sequential A and 5 sequential B laps (5A5B) was presented in an alternating block pattern which progressed to an alternating block of 3 A and 3 B laps (3A3B) and finally to randomized lap (random) presentation. Each rewarded lap was signaled by a 4 kHz tone for 0.5 s immediately prior to lap start. If the animal reached the start of the lap prior to the 0.5 s elapsing, the tone would stop playing. The odor was delivered across the initial 20 cm segment of the lap. Delivery of the trial-associated reward was restricted to the 10 cm reward zone, a 3 s collection time, and a maximum of 10 rewards. The successful behavior is measured based on the lick fraction as a function of normalized position along the track. Lick fraction was defined as the fraction of licks in the respective reward zone. We calculated this by quantifying the number of licks in each 2 cm wide spatial bin across all laps and normalized these counts across all the spatial bins for each set of A and B trials. Following >~80% task performance, incorrect behavior was punished by time-out laps. When the animal licked in either the anticipatory (10 cm prior to reward zone) or reward zone not associated with the current trial, a 0.5 s 10 kHz tone was played, signaling to the animal an incorrect choice. On the following time-out lap, a 0.5 s white noise was played prior to lap entry, neither odor A nor B was delivered, and no reward was available. We defined time-out trials as trials when the animal licked at least once within the incorrect reward zone location either within the 10 cm prior the reward zone or within the 10 cm wide reward zone itself. Time-out trials are only used to reinforce the animal’s learned behavior toward the end of training.

Accelerated training regimen

Animals were trained to randomly forage, similar to the previous protocol, over the course of 1–1.5 weeks rather than 2 weeks. After successful completion of random foraging mice underwent training for the odor-cued spatial navigation task. Animals were still trained in a block structure of 5A5B → 3A3B → Random until >80% accuracy was reached. However, rather than spending 1 week within each block type, animals were advanced quickly through the training schedule so that total task training was reduced to a single week. 2 days in 5A5B, 2 days in 3A3B, and 3 + days in Random.

Reversal learning spatial navigation task

For reversal experiments animals were trained as detailed above until >80% task performance. Recall stage was defined as the first day of training after two consecutive days of >80% task performance. Animals performed this task for three days of recall. The following day the odor-reward associations were reversed. Odor A was paired with the previous B trial reward zone and odor B was paired with the previous A trial reward zone. On this first day of reversal, random water rewards were manually delivered to the animal for two laps prior to imaging. For the remainder of the first training session, animals received alternating AB reversal trials. On all subsequent days A and B reversal trials were randomized. Reversal recall stage again was defined as the first day of training after two consecutive days of >80% task performance.

QUANTIFICATION AND STATISTICAL ANALYSIS

Image processing and signal extraction

Motion correction and ROI segmentation

Imaging time-series data was corrected for motion artifacts by using the NoRMCorre non-rigid motion correction algorithm implemented in MATLAB (Pnevmatikakis and Giovannucci, 2017). The first imaging session in each longitudinal imaging series was used as the template against which all future sessions were motion corrected. Segmentation of somatic regions of interest (ROIs) was performed using a constrained non-negative matrix factorization (CNMF) approach implemented in MATLAB as part of the CaImAn software package (Giovannucci et al., 2019; Pnevmatikakis et al., 2016). Non-somatic and low-quality components were manually discarded using a custom graphical interface.

Matching components across sessions

Individually identified somatic ROIs in each session were matched across sessions by using the register_multisession.py function as part of the CaImAn Python package. Matched components across all sessions were subsequently visualized and poorly matching or mismatching components were discarded. Discarding of component matches was blind to the calcium signal associated with a component on any given session.

Relative fluorescence change (ΔF/F)

The signal baseline (F_{0 baseline}) was calculated for each ROI by taking the fluorescence signal and calculating its 50^th percentile (median) value at each time point within a sliding 15 s time window using the prctfilt.m function as part of CaImAn. The same procedure was used to extract the background signal from the background component (F_{0 background}). The ΔF/F was then calculated as:

$$\frac{\Delta F}{F}=\frac{F-F_{0baseline}}{F_{0baseline}+F_{0background}}$$

The resultant ΔF/F signal was subsequently smoothed using an exponential filter with τ = 0.2s to reduce photon shot noise from signal acquisition (Jia et al., 2011).

Calcium event detection

Significant calcium events were identified using an algorithm previously used in the analysis of two-photon, CA1 hippocampal imaging data (Danielson et al., 2016; Dombeck et al., 2007; Zaremba et al., 2017). Briefly, for any given ΔF/F calcium trace, deflections from the baseline value due to acquisition noise and/or motion along the dorsoventral (z) axis should occur with equal frequency in both the positive and negative directions. Based on this assumption, the false-positive rate can be calculated for each putative event and an amplitude and duration threshold can be defined such that an event’s false-positive event rate does not exceed 5% (rate at which positive events occur with at least 20-fold higher probability than negative events). Using this approach, we identified initial putative events by detecting consecutive imaging frames whose onset occurred at 2 s.d. above the mean and whose offset occurred at 0.5 s.d. below the mean. All events within a session were classified according to their amplitude (in 0.5 sigma bins) and duration (in 250 ms bins). We calculated the false-positive rate for each amplitude-duration bin as the ratio of negative to positive events in that bin. Only positive events from bins with a false-positive ratio of less than 5% were included in the analysis.

To further improve the sensitivity of event detection, initially detected events were masked on the original fluorescence signal, the F_{0 baseline} was recalculated, and events were redetected on the updated ΔF/F signal. Two iterations of event-masked baseline recalculation were performed. Events that lasted less than 1 s were excluded from subsequent analysis.

Data analysis

Definition of run epochs

As described previously (Danielson et al., 2016; Zaremba et al., 2017), we defined running epochs as consecutive frames during which the mouse was moving forward with a minimum peak speed of 5 cm/s for at least 1 s in duration. Neighboring run epochs separated by less than 0.5 s were merged. All other epochs were defined as no run.

Selection of place cells

Spatial information

We identified spatially tuned cells (place cells) by computing their spatial information content relative to an empirically generated shuffle distribution as described previously (Danielson et al., 2016; Zaremba et al., 2017). Spatial information has greater sensitivity for the detection of place cells with single- and multiple-place fields, it has lower sensitivity for cells with broad, single fields. The spatial information content was defined as (Skaggs et al., 1993):

$$I_N=\sum _{i=1}^N{\lambda }_i\text{ln}\frac{{\lambda }_i}{\lambda }{p}_i$$

Where λ_i is the transient rate and p_i is fraction of running time spent in the i th spatial bin, λ is the overall transient rate, and N is the number of bins. The transient rate was defined as the ratio of the bin count of running-related transient onsets smoothed with a Gaussian kernel (σ = 3 bins) to the spatial bin occupancy time. We computed I_N for N = 2,4,5,10,20,25,50,100 bins. To create shuffle distributions for each of the N spatial bins, we randomly reassigned the transient onset times within the running-related epochs 1,000 times and recomputed the spatial information content for each reassignment $I_N^s$, where s is the index of the shuffle. To approximately account for the bias associated with spatial binning in the calculation of the spatial information content, we subtracted the mean of the shuffled null distribution from each N-binned estimate to obtain the adjusted I_N values:

$${\widehat{I}}_N=I_N-\frac{1}{1000}\sum _{s=1}^{1000}{I}_N^s$$

We then obtained a single estimate of the spatial information content for each neuron by taking the maximum of the adjusted information values $\widehat{I}=\underset{N}{\max }{\widehat{I}}_N$ for the true transient onset times and the shuffled onset times ${\widehat{I}}_s=\underset{N}{\max }{\widehat{I}}_N^{{}^s}$. The spatial tuning p-value was defined as the fraction of shuffle values s for which $\widehat{I}$ exceeded ${\widehat{I}}_s$. Neurons with a spatial tuning p-value < 0.05 were defined as place cells.

Tuning specificity

Tuning specificity is more sensitive for place cells with single fields regardless of field width at the expense of multi-field cell detection. We calculated the spatial tuning vector for each cell as described previously (Danielson et al., 2016) using the formula $\sum _j\frac{e^{i{\theta }_j}}{o({\theta }_j)}$, where θ_j is the binned position of the mouse (N = 200 bins, 1 bin ~ 1 cm) at the onset time of the j^th run-epoch transient, and o_j is the occupancy of the animal at position θ_j, i.e. the fraction of running frames that the animal spent at position θ_j. Calculation of the spatial tuning vector was restricted to only run epochs as defined above. The tuning specificity was defined as the magnitude of the spatial tuning vector. Statistical significance of the tuning specificity for each cell was determined by first generating a null tuning distribution by shuffling the transient onset times within the run-epoch frames and then computing the tuning specificity from each shuffle. The shuffle was performed 1,000 times for each cell and the p-value was defined as the fraction of the null distribution that exceeded the cell’s actual tuning specificity.

Activity rate

We calculated the activity rate as the cumulative area under the ΔF/F traces (AUC), from event onset to offset, of all significant calcium events in either run or no-run epochs and divided this sum by the amount of time the animal spent in respective epochs.

Place fields

To define the width of the place fields, we first calculated the rate map for each neuron by dividing the run-epoch event count in each spatial bin by the bin occupancy for N = 100 bins and then smoothed using a Gaussian kernel (σ = 3). To define spatially significant fields, we then fit each local maximum in the rate map with a Gaussian and defined the width as the distance between the locations where each fitted curve was at 20% of its peak value. Putative overlapping fields were merged into single fields. Only fields that had a minimum of 5 significant events on distinct laps were included in the analysis.

Spatial tuning curves (STC)

The tuning curves were defined as the ratio of a Gaussian-smoothed (σ = 3) count of significant run-epoch calcium events in each bin (N = 100) to the run-epoch occupancy. Each neuron’s tuning curve was normalized to its maximum activity across both trial types. For visualization purposes, tuning curves were smoothed again with a Gaussian kernel (σ = 3).

Task-selective and re-mapping place cell selection criteria

Task-selective neurons

Selective neurons were initially chosen as those which were spatially tuned by either the spatial information or tuning specificity criterion in one set of trials and by neither in the other set of trials. Only neurons that had at least 5 in-field, run-epoch calcium events on distinct laps and those in which the animal was in a run epoch 80% of the time of the equivalent spatial bin range of these calcium events on the other trial laps were included in analysis.

Common and global re-mapping neurons

To determine which neurons globally remapped, we performed a Pearson correlation of their rate maps (N = 100 bins) between correct A and B laps. Correlation was performed only between spatial bins with non-zero values in either trial. Neurons that had a positive, statistically significant (p-value < 0.05) correlation score were classified as common neurons (their spatial maps were similar), while neurons with non-significant scores (p >= 0.05) or significant negative scores (maps which are either dissimilar or anti-correlated) were classified as globally remapping. We verified that the distributions of correlation scores against their p-values for all common and global neurons separated into two distinct classes (Figure S3). Only neurons that were tuned according to tuning specificity were used in the analysis. All cells were required to have a single place field on each set of trials and at least 5 significant calcium events on distinct laps in their place fields. Additionally, for globally remapping neurons, animals must have been in a run epoch at least 80% of the time within the equivalent range of calcium onset bins of the other trials on at least 6 laps (to ensure that the animal was in a run epoch on both lap types).

Activity re-mapping neurons

Among the neurons that were selected as common, we examined the area under the curve (AUC) of in-field calcium events to determine whether there was a significant variation in activity associated with trial type. Given that animal speed contributes to CA1 place cell firing activity (Czurkó et al., 1999; Ekstrom et al., 2001; McNaughton et al., 1983), we performed a 2-way ANOVA test to determine the effect of task trial type and speed on the AUC of calcium events. Neurons that had a trial type effect p-value < 0.05 were classified as activity re-mapping. We further confirmed that this category was distinct from the common population by calculating the difference over sum ratio of the peak of the average of calcium transients between the in-field events of correct A trials and correct B trials (Figures S3G and S3H).

Global re-mapping field shifts

To test if place fields on the shorter B trials were significantly anticipatory of the place fields on the longer A trials, we compared the centroids of place fields for global remapping neurons (Figure 2E). Each neuron was sorted according to the zone of the A field centroid. We then computed the fraction of neurons with a B field earlier than the corresponding A field.

The probability of centroid B being earlier than centroid A is not constant across the track (Figure S3B); a uniform distribution of B fields would occur before A fields more often in Zone III and less often in Zone I. Therefore, we computed the expected fraction of B-before-A global remapping cells by using a resampling procedure to pair random fields together within each zone. These null values were then subtracted from the observed proportion of B-before-A global remapping cells to produce the values plotted in Figure 2E, right.

Population vector correlation

The normalized spatial tuning curves across 100 spatial bins were assembled for all neurons into a 2D matrix where the rows represented neuron indexes and columns the activity of all the neurons in each spatial bin. Thus, each column represented the population activity of all neurons at a particular bin. For similarity analysis, the population vector in each column was Pearson correlated against a different trial set or imaging session. The mean of the correlation scores from all bins was the population vector correlation score.

Tuning vector correlation

Between spatially tuned neurons on any two sessions, the spatial tuning vectors across 100 bins were Pearson correlated for each neuron and the mean of all correlated neurons was the tuning vector correlation score. Tuning correlation comparisons shown in the main text were shown for comparison against a single time point for illustration purposes. However, the results reflected the stated conclusions for other time points as well.

Population vector decoding

To demonstrate the relationship between behavioral performance and tuning fidelity of our recorded neurons, we performed population vector decoding (Figure 6). A separate decoder was constructed for each session for each mouse. For a given session, template tuning curves for each cell were constructed in a similar manner as described above, only using data when mice were running. Briefly, we divided the 200 cm track into 40 bins each for A and B trials (80 bins total), counted the number of calcium events in each bin, and smoothed with a Gaussian smoothing kernel with σ = 5 cm, then divided by the total time spent in each bin. Data from the first half of the session was used to define the template.

Time-varying rate vectors for each cell were constructed using data from the second half of the session using 250 ms bins, smoothed with a Gaussian smoothing kernel with sigma σ = 250 ms. For each time point in the second half of the session, the decoded position was the position corresponding to the highest correlation with the template matrix.

The performance of the decoder was quantified using two measures: “Identification Score” and “Decoding Error.” Identification score (Figures 6C-6E, 6G, and 6I) was defined as the proportion of data points that were correctly classified as belonging to A or B trials. Decoding Error (Figures 6F, 6H, and 6J) was defined as the mean absolute distance between the decoded and actual position when ignoring trial type. Distance was defined in a circular manner such that positions 0 and 200 were at the same point.

Effect of speed

In Figures S1G-S1I and S6, all activity was labeled as “Slow Speed” for running epochs with an instantaneous speed greater than 2 cm/s and less than 12.2 cm/s, or “Fast Speed” for running epochs with an instantaneous speed greater than 12.2 cm/s. To calculate the cutoff value of 12.2 cm/s, we calculated the 50^th percentile of speed during running across the 43 learning sessions from 6 mice, then took the mean across these values.

Speed-trial and position-speed decoders

To determine if the neural population was encoding position and trial type and not simply a speed modulation, we constructed two additional decoders in a manner similar to above.

For the “Speed-Trial” decoder (Figures S6A-S6D), we divided the running speed into 40 bins between −5 cm/s and 30 cm/s each for A and B trials (80 bins total), counted the number of calcium events in each bin, and smoothed with a Gaussian smoothing kernel with σ = 0.875 cm/s (1 bin), then divided by the total time spent in each bin. Data from the first half of the session was used to define the template.

The “Position-Speed” decoder (Figures S6E-S6H), was constructed the same way as the “Position-Trial” decoder (Figure 6), except the track was divided into 40 bins each for Slow and Fast Speed.

Normalized decoding error

To compare the accuracy of the various decoders in decoding position and speed, we computed the normalized decoding error (Figure S6J). We divided the raw decoding error by the maximum allowable error for each modality (100 cm maximum error for position, 35 cm/s maximum error for speed), and multiplied by 100 to get a % error for each decoder.

Subsampled decoder performance

To estimate the efficiency of the neural ensemble at representing position and trial type, we constructed additional decoders with subsets of available neurons (Figure 7). For each session, we randomly selected (without replacement) 20, 40, 60, 80, 100, 120, 140, 160, 180, 200, 220, 240, or 260 neurons to decode position and trial type and record identification score and decoding error. This process was repeated 10 times and the mean value across the 10 iterations was used as the performance of the subsampled classifier.

Population vector decoding across days

To further evaluate the stability of neural ensembles across time, we trained and tested the decoder on sessions separated by several days (Figures 6I,6J, S7I, and S7J). All data within a session was used to train and test the decoders across different days, as opposed to using only half of the data for same-day comparisons.

Spatial raster plots

Lap-by-lap raster plots were made by taking the mean run-epoch ΔF/F value from 100 spatial bins for each place cell.

Statistics

Statistical analysis of calcium data was done using Matlab R2020a (Mathworks) using custom-written scripts.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Chemicals, peptides, and recombinant proteins
(+)-α-Pinene 98%	Sigma-Aldrich	P45680-100ML
Pentyl acetate 99%	Sigma-Aldrich	109584-250ML
Pure mineral oil	Fisher Scientific	BP26291
Experimental models: Organisms/strains
Mouse: C57BL/6J-Tg(Thy1-GCaMP6f) - GP5.5	The Jackson Laboratory Dana et al., 2014	Strain #: 024276 RRID: IMSR_JAX:024276
Software and algorithms
Custom MATLAB analysis codes	This paper	https://doi.org/10.5281/zenodo.7226595
MATLAB 2022a	Mathworks	https://www.mathworks.com/products/matlab.html
Anaconda 2 Distribution 5.1.0/Python 2.7.0	Anaconda Inc.	https://www.anaconda.com/
Arduino IDE 1.6.12	Arduino	https://www.arduino.cc/en/software/OldSoftwareReleases
CaImAn-MATLAB	Flatiron Institute	https://github.com/flatironinstitute/CaImAn-MATLAB
CaImAn	Flatiron Institute	https://github.com/flatironinstitute/CaImAn
Fiji	Schindelin et al., 2012	https://imagej.net/software/fiji/
PrarieView Imaging Software 5.9	Bruker	https://www.bruker.com/en.html
Other
Arduino Mega 2560 Microcontroller	Arduino	https://store-usa.arduino.cc/products/arduino-mega-2560-rev3
Teensy 3.2 Development Board	PJRC	https://www.pjrc.com/store/teensy32.html
SparkFun Capacitive Touch Breakout	Sparkfun	SEN-12041
SparkFun MP3 Player Shield	Sparkfun	DEV-12660
Ultima Multiphoton Microscope	Bruker	https://www.bruker.com/en.html
GaAsP photomultiplier tube	Hamamatsu	7422P-40
Mai Tai DeepSee Laser	Spectra-Physics	https://www.spectra-physics.com/en/f/mai-tai-deepsee-ultrafast-laser
MakerBot Replicator 2X 3D Printer	MakerBot	MP04952
Cranial window Cannula Fabrication	New Jersey Precision Technologies, Inc.	54549-001
Cranial window Cannula stainless steel tubing 1.5 mm x1.8x12″	McMaster Carr	https://www.mcmaster.com/8988K17/
3 mm diameter coverslip	Warner Instruments	64-0720
RIVETS modified headpost	Osborne and Dudman, 2014	HHMI Janelia
UV curing optical adhesive	Norland products	NOA-61
3 mm Sterile Disposable Biopsy Punch	Integra LifeSciences	33-32
C&B Metabond® Quick Adhesive Cement System	Parkell	S380

Highlights.

• Odor-cued memory task engages mice to distinguish context and navigate to rewards

• Hippocampal cells evolve task-selective maps, increasing orthogonality with learning

• Place fields are unstable during learning but become stable during memory recall

• Context decodability improves with behavioral performance

INCLUSION AND DIVERSITY

One or more of the authors of this paper received support from a program designed to increase minority representation in their field of research. While citing references scientifically relevant for this work, we also actively worked to promote gender balance in our reference list. We avoided "helicopter science" practices by including the participating local contributors from the region where we conducted the research as authors on the paper.