The development of a mobile app‐focused deduplication strategy for the Apple Heart Study that informs recommendations for future digital trials

Abstract

An app‐based clinical trial enrolment process can contribute to duplicated records, carrying data management implications. Our objective was to identify duplicated records in real time in the Apple Heart Study (AHS). We leveraged personal identifiable information (PII) to develop a dissimilarity score (DS) using the Damerau–Levenshtein distance. For computational efficiency, we focused on four types of records at the highest risk of duplication. We used the receiver operating curve (ROC) and resampling methods to derive and validate a decision rule to classify duplicated records. We identified 16,398 (4%) duplicated participants, resulting in 419,297 unique participants out of a total of 438,435 possible. Our decision rule yielded a high positive predictive value (96%) with negligible impact on the trial's original findings. Our findings provide principled solutions for future digital trials. When establishing deduplication procedures for digital trials, we recommend collecting device identifiers in addition to participant identifiers; collecting and ensuring secure access to PII; conducting a pilot study to identify reasons for duplicated records; establishing an initial deduplication algorithm that can be refined; creating a data quality plan that informs refinement; and embedding the initial deduplication algorithm in the enrolment platform to ensure unique enrolment and linkage to previous records.

1. INTRODUCTION

Over the past few years, there has been increased interest in conducting pragmatic clinical trials (PCTs). PCTs are cost effective; they can reduce the burden on participants and the study team by providing greater flexibility on where, when and how the data are collected. The digital clinical trial (DCT) is a special case of the PCT that further allows investigators to incorporate mobile devices or digital tools to facilitate the conduct of a trial and/or to evaluate the use of digital platforms in an intervention in a real‐life setting (Inan et al., 2020). Mobile apps and wearable devices enable DCTs to provide opportunities to engage a larger number of participants with many more data elements collected per individual. Although it may be advantageous to have many more measurements of a given type and to have a diversity of types of measurements to address the study objectives, management of the data may become challenging and may pose threats to the integrity of the trial.

For example, studies that rely on apps for enrolment are at an increased risk of duplicated data, which can have serious implications on downstream analyses as well as issues for study conduct. In a systematic review conducted by Zhang et al. (2018), the authors state that ‘scholars have only started to employ apps in field experiments in the last 4 years’ and ‘most studies only used apps as an experimental treatment instead of an experimental platform’. Though many have studied this issue extensively by providing solutions in other contexts (Chaudhuri et al., 2003; Gravano et al., 2001), the challenges faced when conducting PCTs and mitigation solutions have yet to be fully characterized. Further, the specific issue of duplication has not been well described in the DCT literature. For example, the Clinical Trials Transformation Initiative (2022) provides an excellent set of guidelines to address various issues in the conduct, design and analysis of clinical trials that rely on digital tools. This particular issue, however, is not featured as one for investigators to consider in the design and analysis. Thus, currently, there is a gap in knowledge of how to plan for and mitigate deduplication issues when conducting DCTs.

The Apple Heart Study (AHS) was a prospective, single‐arm, site‐less, pragmatic study (Turakhia et al., 2019) conducted between 11/29/2017 and 02/21/2019, which faced and overcame some of these data management challenges. More specifically, the goal of the AHS was to evaluate the ability of an irregular pulse notification on the Apple Watch to identify signals consistent with atrial fibrillation. The study relied on an app on the participant's phone to enroll participants, collect data and monitor the heart rhythm for abnormalities using pulse data recorded on their Apple Watch. The AHS was a collaborative project between Apple Inc. and Stanford University. Our study team consisted of experts from both organizations that covered diverse disciplines including cardiovascular medicine, digital health, software engineering, biostatistics, epidemiology, clinical trials, data management, clinical informatics and clinical operations. Clinical operations were led by the Stanford Center for Clinical Research. Design, data management and data analysis were led by the Stanford Quantitative Sciences Unit. Data capture, security and housing were led by the Stanford Technology and Digital Solutions Team, and the Stanford Center for Digital Health provided expertise in the area of digital health. Key external collaborators included AmericanWell, a TeleHealth provider, and BioTelemetry, an ambulatory electrocardiogram provider. Governance of the AHS included an Executive Committee of strategic investigators that drove day‐to‐day decisions. The Executive Committee was advised by a larger Steering Committee of representatives from Stanford University, Apple Inc. and five external members including a patient advocate with atrial fibrillation. Additionally, a Data and Safety Monitoring Board was established to advise the team on trial integrity, conduct, safety and dissemination. Using team science principles, the study team met regularly (weekly meetings with the larger study team and biweekly meetings with smaller sub‐teams) to troubleshoot issues on study design, launch, enrolment, data management, analysis and interpretation of findings.

Through data monitoring procedures, the study team observed early in the recruitment phase that some participants were represented under multiple participant identifiers or IDs—an occurrence that we refer to as duplication of IDs—making it challenging to identify the unique number of participants enrolled and to link longitudinal data within an individual. Both tasks were critical to accomplish study goals. Behaviours of the participants and/or the devices may have contributed to duplication of records. Some examples include participants deleting, reinstalling and re‐enrolling through the app; app crashes or software updates that could cause loss of data; switching mobile devices; or sharing iCloud accounts with other individuals.

Entity resolution (ER) is the task of identifying and grouping various manifestations of the same real‐world object within one data source or between different sources (Benjelloun et al., 2009; Köpcke et al., 2010). This area of research is also referred to as deduplication, record linkage, object matching or linkage discovery. ER has several applications particularly in web searches, health data, financial transactions, law enforcement and more.

In this paper, we describe an issue with ER specifically as it arose in the AHS. We describe our approach to mitigating this problem so that we could achieve study goals. Lessons learned are translated into recommendations for future DCTs.

2. METHODS

2.1. Background

When designing the AHS (Turakhia et al., 2019), we established a system to verify unique identifiers that addressed anticipated scenarios that could lead to duplication issues. Our system involved having an ID for the participant (participant ID or PID) and an additional ID for the device (device ID or DID) so that data generated from a device would have both a corresponding PID and DID linked to a single participant. Data not generated from the device (e.g. study visit) would only have the PID. In the following, we describe in greater detail these two types of identifiers.

2.2. DID and PID

When a participant downloaded and opened the app, encrypted data were securely sent to Apple servers through an application program interface (API). The data included a system identifier referred to as the DID that allowed Apple servers and participant devices to exchange data. In addition, when a participant enrolled in the study through the app, they were assigned a PID generated by the app. Upon assignment of a PID to a participant, a mapping was established between the DID and PID.

We define duplication as the phenomenon of having multiple de‐linked records that appeared to belong to the same unique individual. This can occur in multiple ways. A new DID could be assigned to the same device throughout the study for a variety of reasons including software updates, device reboot and device updates. Like DIDs, new PIDs may be assigned to a participant with an existing assigned PID for a variety of reasons (Figure 1). Duplication (multiple PIDs corresponding to the same individual) occurs when either or both PID and DID are reassigned to the same person or device leading the data to become orphaned or no longer linked, where pieces of data from the same participant are mistakenly thought to belong to separate individuals. To solve these issues, we used ER techniques and developed an algorithm to establish which PIDs were associated with the same individual. The algorithm was designed to link data from multiple sources back together and create a true unique identifier per person enabling longitudinal views of data within a participant over time. The algorithm consists of multiple steps described in detail that follow and depicted in detail in Figure 2.

FIGURE 1.

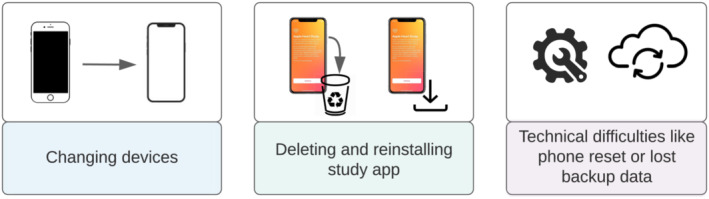
Common scenarios that potentially led to orphaned data

FIGURE 2.

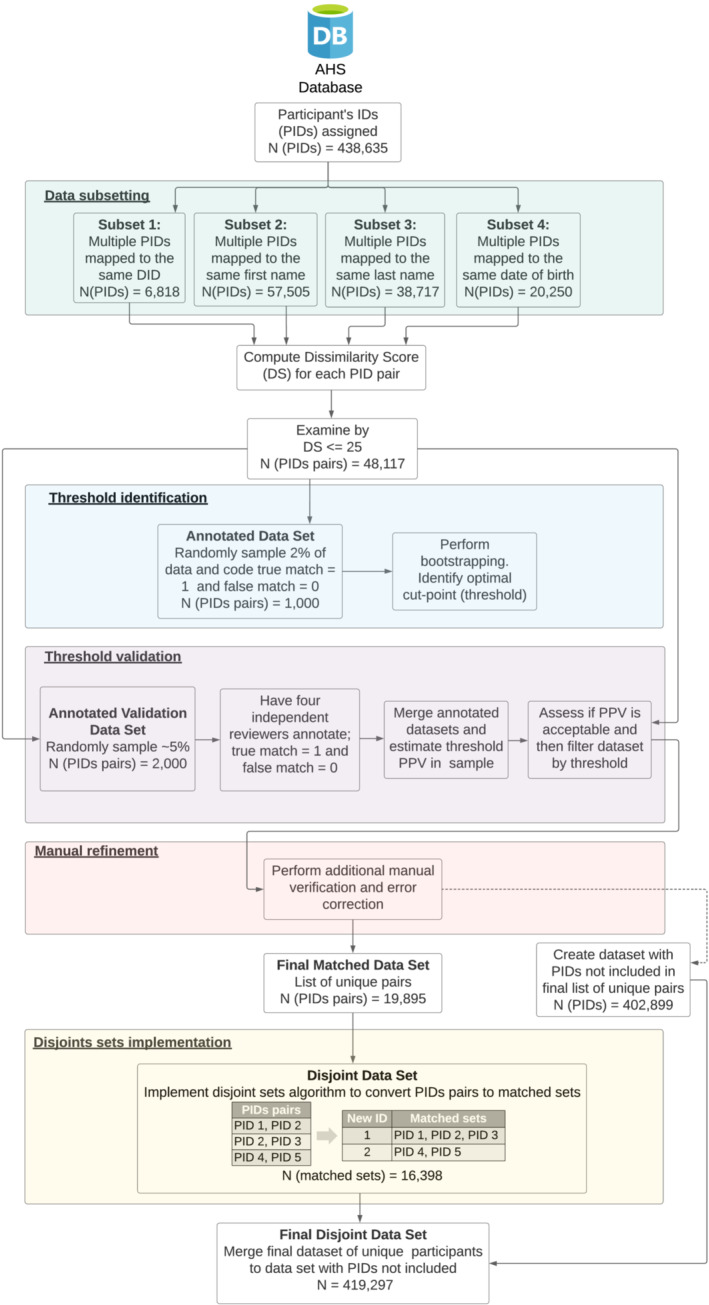
Step‐by‐step diagram of deduplication algorithm. DID, Device ID; DS, Dissimilarity score; PID, Participant's ID; PPV, positive predictive value

2.3. Key inputs to the algorithm

The algorithm leveraged data that contained participant identifiable information (PII), obtained by asking participants questions related to their identity and demographic information after providing consent. These data were encrypted, not accessible to the sponsor (Apple Inc.), and only available to an unblinded sub‐team of the larger AHS data science team at Stanford University.

The algorithm specifically used the combination of seven participant‐level identifiers: email, date of birth, first name, last name, phone number, state and consent date in order to assess the similarity of two records with different PIDs. All identifiers provided important information to our algorithm with varying levels of contribution; email, date of birth, first name, last name and phone allowed us to identify the individual and were referred to as strong identifiers, whereas the others were considered auxiliary to the strong identifiers. For example, the participant's state was useful in scenarios where individuals shared their first and last names and birthdays but differed by state, casting doubt on the records being linked. Consent date was also helpful. For example, suppose an individual enrolled and then subsequently updated the app and re‐enrolled. In this case two different PIDs would be attached to the respective data collected at the separate enrolments. Common PIIs with distinct consent dates close in time may reflect this sequence of events and increase the probability that the records belong to the same individual. Alternatively, common PIIs with the same consent date may indicate different family members joining the study simultaneously.

2.4. Dissimilarity score (DS)

There are numerous algorithms that have been developed to calculate the distance between two string values (Cohen et al., 2003). We used the optimal string‐alignment distance (osa) that relies on the Damerau–Levenshtein distance and returns the string distance taking into account deletion, insertion, substitution and transposition under the condition that no substring is edited more than once (Levenshtein, 1966). We implemented this using the stringdist R package (Van der Loo et al., 2014).

To calculate the dissimilarity score (DS) between two records, we first pre‐processed the data by standardizing strings, removing special characters including empty spaces and transforming all text to the lower case. We then calculated approximate string distance between each of the patient‐level identifiers and then summed the individual metrics to generate a single composite score that represented their dissimilarity. For example, email from one record was compared with email from a second record, and the string was quantified and recorded. The same process was repeated for each of the seven patient‐level identifiers. A DS of zero indicated the two strings being compared were identical, whereas nonzero DSs reflected the degree of dissimilarity, that is, higher scores indicated greater dissimilarity.

2.5. Algorithm execution and data sub‐setting

One downside of performing pairwise string comparison for a high volume of records is that it is computational expensive. Assessing distance among all pairs in the full data would have required over 96 billion pairwise comparisons. To mitigate this challenge, we identified four subsets of data where true matches were most likely to occur. The first subset was composed of record pairs with multiple PIDs associated with the same DID (Subset 1: multiple PIDs mapped to the same DID). The second and third subsets were record pairs with multiple PIDs associated with the same first and last name, respectively (Subset 2: multiple PIDs mapped to the same first name; Subset 3: multiple PIDs mapped to the same last name), and the fourth was formed by participants where multiple PIDs were associated with the same date of birth (Subset 4: multiple PIDs mapped to the same date of birth). The DS was calculated for each pairing in each of these four subsets.

2.6. Threshold identification

Empirical assessments of comparisons demonstrated that DSs > = 25 clearly corresponded to records from distinct participants, whereas comparisons with DSs < 25 more likely reflected a mixture of the same and different individuals. Thus, we restricted our focus on deriving a rule for records with DSs < 25.

For this purpose, we created an Annotated Data Set by randomly sampling 2% of pairwise comparisons with DSs < 25 and annotating each pair using a single reviewer to indicate whether the match was false (denoted as 0) or true (denoted as 1).

To identify the optimal threshold, we bootstrapped 10,000 samples from the Annotated Data Set, where within each bootstrap sample, a random 90% sample of the Annotated Data Set was allocated to a training data set in which the optimal cut‐point was calculated using the Youden index (Youden, 1950) that minimizes misclassification. This cut‐point was then applied to the remaining 10% of the bootstrap sample to estimate the accuracy for this specific cut‐point. These results were summarized by evaluating the mean, median, mode and spread and we chose the cut‐point as the mean of the 10,000 samples. The R package ‘OptimalCutpoints’, which defines the optimal cut as the point that maximizes the Youden function (the difference between true and false positive rates over all possible cut‐point values) using an empirical approach, was used to execute approaches (Lopez‐Raton & Rodriguez‐Alvarez, 2021).

2.7. Threshold validation

To assess the positive predictive value of the threshold in identifying true matches, we randomly resampled 5% of the original data set (excluding the 2% sample previously used) from records that had DSs under the identified threshold for annotation performed by four reviewers and called this new data set the Annotated Validation Data Set. There was no formal training for the reviewers or protocol for annotation, and subjective judgement was used. The final annotated value was taken to be the one defined by the majority of the four reviewers. In cases where majority could not be achieved, there was collaborative discussion to arrive at consensus. The positive predictive value was estimated as the proportion of the records in the Annotated Validation Data Set that was truly determined to be a duplicated record as defined by the final annotated value.

2.8. Manual refinement

Minimizing match errors was critical to our study, so after completing the algorithm execution, we performed a manual verification process where we manually examined pairs that were slightly above or below the threshold. Erroneous instances were corrected manually. Once we completed this manual verification and correction process, the pairs identified as true matches comprised our final matched data set.

2.9. Disjoint sets implementation

The last step was to find the intersections among all the matched pairs (referred to as the Final Matched Data Set). For example, suppose that PID 1 matched to PID 2 and PID 2 matched to PID 3. We then established that PID 1, PID 2 and PID 3 all corresponded to the same individual.

To understand the connection of all PIDs based on the pairwise matches, we first identified disjoints sets (pairs of matched PIDs with no PID in common). Those in the disjoint sets resulted in one unique ID per pair. PIDs that were not included in the disjoint data set were (1) those not included in one of the original four subsets with higher probability of being duplicates and (2) those PIDs excluded during the final matched data set creation (either by being above the threshold or by being deemed ‘not a match’ during the manual refinement step).

After executing the disjoint sets exercise described previously, we were able to create a data set of disjoint sets (Disjoint Data Set) where each row contained all PIDs that belonged together. Using the example above, suppose that the following matched pairs existed on the Final Matched Data Set: PID 1 matched to PID 2, PID 2 matched to PID 3, and PID 4 matched to PID 5. In this scenario, PID 1, PID 2 and PID 3 corresponded to the same individual, and PID 4 and PID 5 belonged to a separate individual because there were no PIDs in common. From this data set, we can arrive at unique IDs for those with multiple PIDs (Final Disjoint Data Set). A new unique ID was then added to each row allowing us to link PIDs that mapped to the same unique identifier and establish the longitudinal trajectory of each participant.

2.9.1. Assessing inter‐annotation reliability

To assess inter‐rater reliability among the four reviewers of the Annotated Validation Data Set used to describe the properties of the estimated cut‐point, each pair was recoded by the other reviewers, and Fleiss's kappa was calculated (Fleiss et al., 2003).

3. RESULTS

3.1. Algorithm execution and data sub‐setting

AHS had a total of 438,435 PIDs assigned in the study cohort by the end of the enrollment period (Figure 2). Recall from above that to make the algorithm computationally efficient, we created four subsets where two or more PIDs were associated with the same piece of data. Subset 1 (Multiple PIDs mapped to the same DID) was composed of 6818 unique PIDs where two or more PIDs were associated with the same DID. Subsets 2 and 3 (multiple PIDs mapped to the same first and last name, respectively)—the most common records at risk of duplication that included participants—were composed of 57,505 and 38,717 PIDs. The last subset, Subset 4 (multiple PIDs mapped to the same date of birth), was composed of 20,250 PIDs.

3.2. Threshold identification

DS was computed for each pair of PIDs, where DS was the sum of each of the seven individual identifiers. A description of the DS distribution and the number of pairs can be found in Table 1. The mean DS on the subsets where PIDs were associated with the same DID (mean = 8) and the date of birth (mean = 9) was lower than in the subsets where PIDs were associated with the same first name (mean = 16) or last name (mean = 14). This was expected as first and last names alone are weaker identifiers than DID or the date of birth.

TABLE 1.

Dissimilarity score (DS) characteristics by subset

Subset
Subset 1: Multiple PIDs mapped to same DID	N
N (PIDs)	6818
N (pairs with DS < = 25)	2715
DS distribution
Min	0
Median	7
Mean	8
Max	25
Subset 2: Multiple PIDs mapped to same first name
N (PIDs)	57,505
N (pairs with DS < = 25)	36,884
DS distribution
Min	0
Median	18
Mean	16
Max	25
Subset 3: Multiple PIDs mapped to same last name
N (PIDs)	38,717
N (pairs with DS < = 25)	30,395
DS distribution
Min	0
Median	9
Mean	14
Max	25
Subset 4: Multiple PIDs mapped to same date of birth
N (PIDs)	20,250
N (pairs with DS < = 25)	20,063
DS distribution
Min	0
Median	8
Mean	9
Max	25

PID pairs with DS < = 25 were then merged into a single data set, yielding a total of 48,117 unique PID pairs. A sample of approximately 2% was then extracted from this set of pairs (N = 1000, Min DS = 3, Max DS = 25) and manually coded to indicate true matches versus false matches.

We bootstrapped 10,000 times leaving 10% of the observations out each time in order to estimate and evaluate the optimal cut‐point. After summarizing resampling findings, we found the optimal cut‐point to be a DS of 22 (mean, median and mode of cut‐points across samples were all equivalent and equal to 22) with sensitivity = 0.986, 1 − specificity = 0.009 and AUC = 0.999 as shown in Figure 3. Note, however, that these properties are presented on the same data set used to identify the threshold and are therefore an overly optimistic view of the rule's properties.

FIGURE 3.

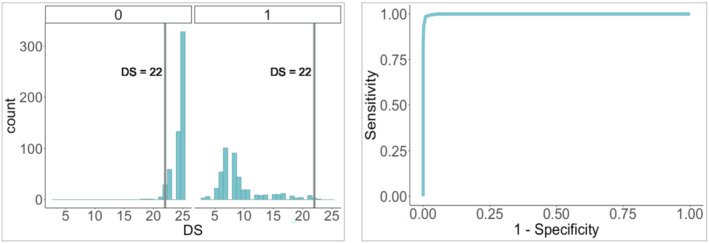
Left panel: Sample distribution by class (false match = 0 and true match = 1). Right panel: ROC for optimal cut‐point

3.3. Threshold validation

Using the Annotation Validation Data Set of 2000 observations, we found that a DS < = 22 provided a positive predictive value of 96% with the 95% confidence interval that spanned from 95% to 97%. All PID pairs were then filtered to include only pairs with DS < = 22. Based on the observed results we then restricted our Final Matched Data Set to those pairs with a DS < = 22.

3.4. Manual refinement

We performed additional manual validation of the data to ensure that those that had met the threshold were indeed a correct match and those that had been left out but were closer to the threshold were not actual matches that had been left out accidentally. If erroneous instances were identified, we then corrected that instance manually. Of the 1500 records that were manually evaluated, we encountered between 10 and 15 instances where manual correction was necessary (as this was an ad hoc procedure, we did not record the actual number of instances and are relying on memory). The resulting Final Matched Data Set included a total of 19,895 unique PID pairs.

3.5. Disjoint sets implementation

Application of the disjoint set algorithm resulted in 16,398 disjoint sets (or unique individuals). We found that on average, the Final Matched Data Set had two PIDs associated with the same individual and the number of PIDs associated with the same person ranged from 2 to 34.

All the PIDs that were not included in the Final Disjoint Data Set of 16,398 individuals were considered unique and not duplicated participants (N = 402,899). A new ID was assigned to each row of the merged data set, yielding our final cohort denominator of 419,297 participants.

3.6. Assessing inter‐annotation reliability

The interrater reliability of the four reviewers who independently coded the validation data set had a corresponding kappa statistic of 0.87, 95% CI (0.82, 0.91).

4. DISCUSSION

Despite having an initial system for identifying duplicated records, we still encountered duplicated participants in the AHS and were unexpectedly faced with having to refine a deduplication algorithm while the study was ongoing to ensure data quality and the integrity of study conduct and research findings. Our algorithm relied on the Damerau–Levenshtein distance to create a composite score to quantify the dissimilarity of two given records and employed resampling techniques to estimate and validate a decision rule. We found that of all PIDs generated, approximately 4% were duplicated. To increase computational efficiency, our algorithm focused on subsets of data where participants shared some information in common; this strategy along with parallelization allowed us to make our algorithm more computational efficient, reducing the number of comparisons from 96 billion to less than 3 billion. Our algorithm allowed us to map each PID with high accuracy to orphaned data with negligible impact to the original trial findings. Specifically, we found that our algorithm had a positive predictive value of 96% (with 95% confidence interval spanning from 95% to 97%). For the original goals of the AHS study, this means that even if the true positive predictive value were only 95% (the lower limit of the confidence interval), we would have falsely classified approximately 5% of the 16,398 cases or 819 records as being duplicates when they were not. The implications are that our estimated sample size of enrolled participants would go from 419,297 to 422,856. When calculating our main estimate—the irregular pulse notification rate—this would have changed the estimate from 0.52% to 0.51% (Perez et al., 2019). Thus, for the purposes of the AHS, the properties of the algorithm are such that potential changes to the interpretation of trial findings were minimal. For data sets of varying sizes, an understanding of the implications of an algorithm with a similar positive predictive value may vary depending on the sizes of the targeted enrollment and the Annotated Validation Data Set. For example, suppose application of the algorithm to a data set of 200 records similarly results in 4% of the records identified as duplicated. Suppose further that an Annotated Validation Data Set of 50 is established to characterize the positive predictive value. For an algorithm with similar performance (the positive predictive value of 96%), the lower bound of the confidence interval for the positive predictive value is 91%, meaning that one of the eight records may have been falsely flagged so that the estimated sample size of 192 may be actually as low as 191.

There are strengths to our approach. We included multiple reviewers in our validation step to minimize bias in our validation data set. We had access to PII data that allowed us to leverage ER techniques to deduplicate data and reduce the burden of looking at thousands of participants manually to identify duplicate participants. Adding manual validation and spot‐checking after execution of the algorithm was advantageous. The human brain can capture context in a way that algorithms may not. For example, in instances where we had two family members with nearly identical identifiers, differences in the records became immediately obvious to a reviewer who would notice that the two individuals were related but not the same. To illustrate this concept, Table 2 shows two participants with a DS of 18 (below the 22 threshold suggesting a match). At a closer look, we can conclude that these participants might be related because while they share the same phone number and last name, their first names are quite different (one is not a nickname of the other) and the pattern of their email naming system is similar although it results in distinct emails. Thus, the two IDs likely correspond to two different individuals from the same household. Another example is shown in Table 3, where common names accompanied by some similarities in identifiers (similar emails, year of birth and phone number) can suggest similarity by the algorithm but that are easily detected as distinct by the human brain. Finally, the principles behind our algorithm may be applied to data sets of varying sizes. For ease of adoption of the methods described here, we provide a simulated example data set of 10 records to illustrate how the code can be used (Appendix A).

TABLE 2.

Hypothetical example of family related match

PID1	PID2	e‐mail 1	e‐mail 2	Date of birth 1	Date of birth 2	First name 1	First name 2	Last name 1	Last name 2	Phone number 1	Phone number 2	State 1	State 2	Consent 1	Consent2
1	2	eeboy55@email.Com	eegirl55@email.Com	1/21/77	5/24/81	Mike	Barbara	Thomas	Thomas	1–111–111‐1111	1–111–111‐1111	IN	IN	6/22/18 7:30	6/22/18 7:13

TABLE 3.

Hypothetical example of common name match

PID1	PID2	e‐mail 1	e‐mail 2	Date of birth 1	Date of birth 2	First name 1	First name 2	Last name 1	Last name 2	Phone number 1	Phone number 2	State 1	State 2	Consent 1	Consent2
3	4	eemail.email59@mac.com	eemail.email1@mac.com	9/6/59	7/18/59	Tim	Tim	Thomas	Thomas	555–555‐5555	655–566‐6666	OK	CA	5/7/18 5:36	5/7/18 6:40

There were also limitations to our study. We did not explore or compare other string distance methods. Additionally, our string distance relied on the summation of dissimilarity on a number of string items, and we did not consider other ways of constructing the DS. We also did not compare the performance of an algorithm that employs fewer identifiers or uses a combination of identifiers. In addition, though our bootstrapping procedure captures the uncertainty of our algorithm in identifying an optimal cut‐point, we relied on the empirical approach for estimating Youden's index to identify an optimal cut‐point. It may be that other methods for estimating Youden's cut‐point are superior (Fluss et al., 2005). This is considered future work. Furthermore, we did not train reviewers when annotating in how to decide whether two given individuals were the same person (true match) or not (false match). Instead, we asked them to look at context and follow their intuition. Partly this was because we were unsure what to expect. This may have contributed to our agreement being less than ideal (kappa < 0.95). Finally, although our algorithm is designed to detect when multiple records come from the same individual, it does not address whether data classified under the same PID and DID may be arising from multiple individuals. Consider the scenario where multiple family members use the same device under one enrollment instance (one PID). Our algorithm will not detect such nuances.

There were important lessons that we gathered from our experience. Our study shows the importance of having deduplication algorithms in place prior to study launch. To that end, the collection of device IDs in addition to a participant ID on each piece of data is critical. Furthermore, the inclusion and secure access to PII data for deduplication algorithms are crucial to data scientists for ensuring data quality. Investigators should expect that the initially established deduplication algorithm will need to be further refined in an ongoing fashion. For this purpose, having a data quality plan in place that targets duplication is key. A pilot study can expose some of these challenges and should be conducted prior to launch. Finally, we highly recommend a plan embedded in the app to verify new enrollments at the time of enrollment via the initial deduplication algorithm. The potential participants can be prompted, for example, if their data ‘match’ a previous record while onboarding the study. Such preventive measures can go a long way to minimizing this issue from appearing downstream.

5. CONCLUSIONS

Our experience in the AHS with the creation and implementation of a deduplication algorithm developed and validated in real time provides the foundation for six principles that can be borrowed when conducting other studies with similar pragmatic features. They include the following: Collect device IDs in addition to participant IDs; collect and ensure secure access to PII; conduct a pilot study to identify reasons for duplicated records; establish an initial deduplication algorithm that can be refined; create a data quality plan that informs refinement; embed the initial deduplication algorithm in the enrolment platform to ensure unique enrolment and linkage to previous records.

ETHICS STATEMENT

The research protocol was approved by the Institutional Review Board at Stanford University and by a central Institutional Review Board (Advarra). The research protocol including consenting procedures was approved by the Institutional Review Board at Stanford University and by a central Institutional Review Board (Advarra). No material has been reproduced from other sources. The work presented here was developed as part of the Apple Heart Study, which has the following ClinicalTrials.gov number, NCT03335800.

APPENDIX A.

This appendix provides a simulated data set, code and detailed annotation to walk the user through application of the deduplication algorithm.

R packages

Simulated data

Data containing duplicate individuals

PID	DID	First_Name	Last_Name	DOB	Email	State	Phone	Consent_Date
1	1	Linda	Smith	10/29/1964	lsmith22@email.com	MA	453‐245‐0712	5/3/2017
2	2	Jennifer	Williams	8/18/1965	jenniferwilliams@email.com	PA	462‐946‐0095	5/10/2017
3	3	Susan	Brown	8/29/1972	susanbrowng@email.com	TN	630‐512‐5824	6/2/2017
4	4	Michael	Jones	10/24/1972	mjones@email.com	CA	258‐652‐4875	6/29/2017
5	5	James	Davis	7/20/1988	jamesdavis44@email.com	TX	880‐391‐9208	7/19/2017
6	6	Lidia	Smith	11/3/1993	lsmith12@email.com	FL	828‐304‐4350	9/4/2017
7	3	Sue	Brown	8/29/1972	susanbrowng@email.com	TN	630‐512‐5824	9/14/2017
8	4	Maria	Jones	11/22/1972	mjones@email.com	CA	258‐652‐4875	10/20/2017
9	2	Jennifer	William	8/18/1966	jenniferwilliams@email.com	PA	462‐946‐0095	12/5/2017
10	3	Sue	Brown	8/18/1966S	susanbrowng@email.com	TN	630‐512‐5825	10/24/17

Data cleaning

Remove all non‐alphanumeric characters (including spaces) and convert variables to the lower case. In our case we transformed: first name, last name, device ID (DID) and data of birth (DOB) but this can be extended to all the variables used in the matching function.

Data sub‐setting

Subset 1 (Multiple PIDs mapped to the same DID):

PID	DID	First_Name	Last_Name	DOB	Email	State	Phone	Consent_Date
2	2	jennifer	williams	8/18/1965	jenniferwilliams@email.com	PA	462‐946‐0095	5/10/2017
9	2	jennifer	william	8/18/1966	jenniferwilliams@email.com	PA	462‐946‐0095	12/5/2017
3	3	susan	brown	8/29/1972	susanbrowng@email.com	TN	630‐512‐5824	6/2/2017
7	3	sue	brown	8/29/1972	susanbrowng@email.com	TN	630‐512‐5824	9/14/2017
10	3	sue	brown	8/29/1972	susanbrowng@email.com	TN	630‐512‐5825	10/24/17
4	4	michael	jones	10/24/1972	mjones@email.com	CA	258‐652‐4875	6/29/2017
8	4	maria	jones	11/22/1972	mjones@email.com	CA	258‐652‐4875	10/20/2017

Subset 2 (Multiple PIDs mapped to the same first name):

PID	DID	First_Name	Last_Name	DOB	Email	State	Phone	Consent_Date
2	2	jennifer	williams	8/18/1965	jenniferwilliams@email.com	PA	462‐946‐0095	5/10/2017
9	2	jennifer	william	8/18/1966	jenniferwilliams@email.com	PA	462‐946‐0095	12/5/2017
7	3	sue	brown	8/29/1972	susanbrowng@email.com	TN	630‐512‐5824	9/14/2017
10	3	sue	brown	8/29/1972	susanbrowng@email.com	TN	630‐512‐5825	10/24/17

Subset 3 (Multiple PIDs mapped to the same last name):

PID	DID	First_Name	Last_Name	DOB	Email	State	Phone	Consent_Date
3	3	susan	brown	8/29/1972	susanbrowng@email.com	TN	630‐512‐5824	6/2/2017
7	3	sue	brown	8/29/1972	susanbrowng@email.com	TN	630‐512‐5824	9/14/2017
10	3	sue	brown	8/29/1972	susanbrowng@email.com	TN	630‐512‐5825	10/24/17
4	4	michael	jones	10/24/1972	mjones@email.com	CA	258‐652‐4875	6/29/2017
8	4	maria	jones	11/22/1972	mjones@email.com	CA	258‐652‐4875	10/20/2017
1	1	linda	smith	10/29/1964	lsmith22@email.com	MA	453‐245‐0712	5/3/2017
6	6	lidia	smith	11/3/1993	lsmith12@email.com	FL	828‐304‐4350	9/4/2017

Subset 4 (Multiple PIDs mapped to the same date of birth):

PID	DID	First_Name	Last_Name	DOB	Email	State	Phone	Consent_Date
3	3	susan	brown	8/29/1972	susanbrowng@email.com	TN	630‐512‐5824	6/2/2017
7	3	sue	brown	8/29/1972	susanbrowng@email.com	TN	630‐512‐5824	9/14/2017
10	3	sue	brown	8/29/1972	susanbrowng@email.com	TN	630‐512‐5825	10/24/17

Matching function

The following function takes four inputs:

1. data: This could be either the full data set or a subset (like the ones created above) depending on the size of the original data.

2. id: The name of the ID variable. In our example, this is the PID.

3. vars: The list of variables used to calculate the dissimilarity score (DS).

4. cutoff: This is an arbitrary and initial cut‐off determined by the user that may be refined. The idea is to have a cut‐off for which DSs below the cut‐off may be at risk of duplication. Initially, the user can apply the function to a small subset to refine where the focus should be (i.e. to filter out those highly divergent and dissimilar records).

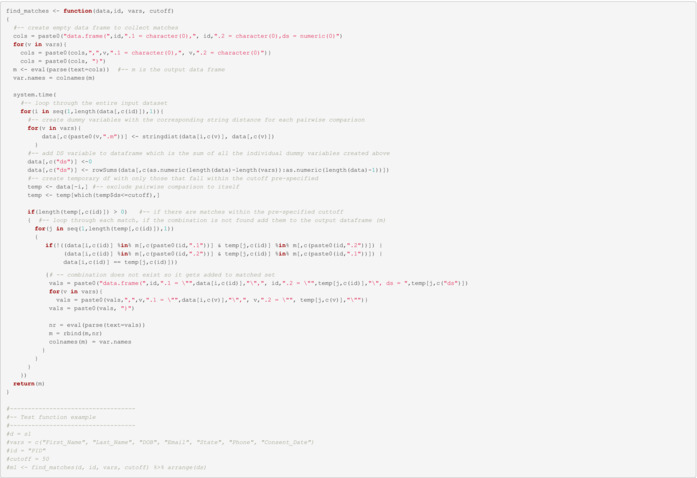
Execute matching function on each set

Pre‐specified cut‐off = 40

Note: Parallelization in this section is encouraged for large data sets.

Resulting matched sets

Matched Set 1

PID.1	PID.2	ds	First_Name.1	First_Name.2	Last_Name.1	Last_Name.2	DOB.1	DOB.2	Email.1	Email.2	State.1	State.2	Phone.1	Phone.2	Consent_Date.1	Consent_Date.2
2	9	6	jennifer	jennifer	williams	william	8/18/1965	8/18/1966	jenniferwilliams@email.com	jenniferwilliams@email.com	PA	PA	462‐946‐0095	462‐946‐0095	5/10/2017	12/5/2017
3	7	6	susan	sue	brown	brown	8/29/1972	8/29/1972	susanbrowng@email.com	susanbrowng@email.com	TN	TN	630‐512‐5824	630‐512‐5824	6/2/2017	9/14/2017
7	10	6	sue	sue	brown	brown	8/29/1972	8/29/1972	susanbrowng@email.com	susanbrowng@email.com	TN	TN	630‐512‐5824	630‐512‐5825	9/14/2017	10/24/17
3	10	9	susan	sue	brown	brown	8/29/1972	8/29/1972	susanbrowng@email.com	susanbrowng@email.com	TN	TN	630‐512‐5824	630‐512‐5825	6/2/2017	10/24/17
4	8	10	michael	maria	jones	jones	10/24/1972	11/22/1972	mjones@email.com	mjones@email.com	CA	CA	258‐652‐4875	258‐652‐4875	6/29/2017	10/20/2017
3	4	35	susan	michael	brown	jones	8/29/1972	10/24/1972	susanbrowng@email.com	mjones@email.com	TN	CA	630‐512‐5824	258‐652‐4875	6/2/2017	6/29/2017
3	8	36	susan	maria	brown	jones	8/29/1972	11/22/1972	susanbrowng@email.com	mjones@email.com	TN	CA	630‐512‐5824	258‐652‐4875	6/2/2017	10/20/2017
10	4	38	sue	michael	brown	jones	8/29/1972	10/24/1972	susanbrowng@email.com	mjones@email.com	TN	CA	630‐512‐5825	258‐652‐4875	10/24/17	6/29/2017

Matched Set 2

PID.1	PID.2	ds	First_Name.1	First_Name.2	Last_Name.1	Last_Name.2	DOB.1	DOB.2	Email.1	Email.2	State.1	State.2	Phone.1	Phone.2	Consent_Date.1	Consent_Date.2
2	9	6	jennifer	jennifer	williams	william	8/18/1965	8/18/1966	jenniferwilliams@email.com	jenniferwilliams@email.com	PA	PA	462‐946‐0095	462‐946‐0095	5/10/2017	12/5/2017
7	10	6	sue	sue	brown	brown	8/29/1972	8/29/1972	susanbrowng@email.com	susanbrowng@email.com	TN	TN	630‐512‐5824	630‐512‐5825	9/14/2017	10/24/17

Matched Set 3

PID.1	PID.2	ds	First_Name.1	First_Name.2	Last_Name.1	Last_Name.2	DOB.1	DOB.2	Email.1	Email.2	State.1	State.2	Phone.1	Phone.2	Consent_Date.1	Consent_Date.2
3	7	6	susan	sue	brown	brown	8/29/1972	8/29/1972	susanbrowng@email.com	susanbrowng@email.com	TN	TN	630‐512‐5824	630‐512‐5824	6/2/2017	9/14/2017
7	10	6	sue	sue	brown	brown	8/29/1972	8/29/1972	susanbrowng@email.com	susanbrowng@email.com	TN	TN	630‐512‐5824	630‐512‐5825	9/14/2017	10/24/17
3	10	9	susan	sue	brown	brown	8/29/1972	8/29/1972	susanbrowng@email.com	susanbrowng@email.com	TN	TN	630‐512‐5824	630‐512‐5825	6/2/2017	10/24/17
4	8	10	michael	maria	jones	jones	10/24/1972	11/22/1972	mjones@email.com	mjones@email.com	CA	CA	258‐652‐4875	258‐652‐4875	6/29/2017	10/20/2017
1	6	22	linda	lidia	smith	smith	10/29/1964	11/3/1993	lsmith22@email.com	lsmith12@email.com	MA	FL	453‐245‐0712	828‐304‐4350	5/3/2017	9/4/2017
8	1	34	maria	linda	jones	smith	11/22/1972	10/29/1964	mjones@email.com	lsmith22@email.com	CA	MA	258‐652‐4875	453‐245‐0712	10/20/2017	5/3/2017
3	4	35	susan	michael	brown	jones	8/29/1972	10/24/1972	susanbrowng@email.com	mjones@email.com	TN	CA	630‐512‐5824	258‐652‐4875	6/2/2017	6/29/2017
3	8	36	susan	maria	brown	jones	8/29/1972	11/22/1972	susanbrowng@email.com	mjones@email.com	TN	CA	630‐512‐5824	258‐652‐4875	6/2/2017	10/20/2017
3	1	38	susan	linda	brown	smith	8/29/1972	10/29/1964	susanbrowng@email.com	lsmith22@email.com	TN	MA	630‐512‐5824	453‐245‐0712	6/2/2017	5/3/2017
10	4	38	sue	michael	brown	jones	8/29/1972	10/24/1972	susanbrowng@email.com	mjones@email.com	TN	CA	630‐512‐5825	258‐652‐4875	10/24/17	6/29/2017
3	6	40	susan	lidia	brown	smith	8/29/1972	11/3/1993	susanbrowng@email.com	lsmith12@email.com	TN	FL	630‐512‐5824	828‐304‐4350	6/2/2017	9/4/2017

Matched Set 4

PID.1	PID.2	ds	First_Name.1	First_Name.2	Last_Name.1	Last_Name.2	DOB.1	DOB.2	Email.1	Email.2	State.1	State.2	Phone.1	Phone.2	Consent_Date.1	Consent_Date.2
3	7	6	susan	sue	brown	brown	8/29/1972	8/29/1972	susanbrowng@email.com	susanbrowng@email.com	TN	TN	630‐512‐5824	630‐512‐5824	6/2/2017	9/14/2017
7	10	6	sue	sue	brown	brown	8/29/1972	8/29/1972	susanbrowng@email.com	susanbrowng@email.com	TN	TN	630‐512‐5824	630‐512‐5825	9/14/2017	10/24/17
3	10	9	susan	sue	brown	brown	8/29/1972	8/29/1972	susanbrowng@email.com	susanbrowng@email.com	TN	TN	630‐512‐5824	630‐512‐5825	6/2/2017	10/24/17

Combine all matched sets into a single unique data frame

PID.1	PID.2	ds	First_Name.1	First_Name.2	Last_Name.1	Last_Name.2	DOB.1	DOB.2	Email.1	Email.2	State.1	State.2	Phone.1	Phone.2	Consent_Date.1	Consent_Date.2
2	9	6	jennifer	jennifer	williams	william	8/18/1965	8/18/1966	jenniferwilliams@email.com	jenniferwilliams@email.com	PA	PA	462‐946‐0095	462‐946‐0095	5/10/2017	12/5/2017
3	7	6	susan	sue	brown	brown	8/29/1972	8/29/1972	susanbrowng@email.com	susanbrowng@email.com	TN	TN	630‐512‐5824	630‐512‐5824	6/2/2017	9/14/2017
7	10	6	sue	sue	brown	brown	8/29/1972	8/29/1972	susanbrowng@email.com	susanbrowng@email.com	TN	TN	630‐512‐5824	630‐512‐5825	9/14/2017	10/24/17
3	10	9	susan	sue	brown	brown	8/29/1972	8/29/1972	susanbrowng@email.com	susanbrowng@email.com	TN	TN	630‐512‐5824	630‐512‐5825	6/2/2017	10/24/17
4	8	10	michael	maria	jones	jones	10/24/1972	11/22/1972	mjones@email.com	mjones@email.com	CA	CA	258‐652‐4875	258‐652‐4875	6/29/2017	10/20/2017
1	6	22	linda	lidia	smith	smith	10/29/1964	11/3/1993	lsmith22@email.com	lsmith12@email.com	MA	FL	453‐245‐0712	828‐304‐4350	5/3/2017	9/4/2017
8	1	34	maria	linda	jones	smith	11/22/1972	10/29/1964	mjones@email.com	lsmith22@email.com	CA	MA	258‐652‐4875	453‐245‐0712	10/20/2017	5/3/2017
3	4	35	susan	michael	brown	jones	8/29/1972	10/24/1972	susanbrowng@email.com	mjones@email.com	TN	CA	630‐512‐5824	258‐652‐4875	6/2/2017	6/29/2017
3	8	36	susan	maria	brown	jones	8/29/1972	11/22/1972	susanbrowng@email.com	mjones@email.com	TN	CA	630‐512‐5824	258‐652‐4875	6/2/2017	10/20/2017
10	4	38	sue	michael	brown	jones	8/29/1972	10/24/1972	susanbrowng@email.com	mjones@email.com	TN	CA	630‐512‐5825	258‐652‐4875	10/24/17	6/29/2017
3	1	38	susan	linda	brown	smith	8/29/1972	10/29/1964	susanbrowng@email.com	lsmith22@email.com	TN	MA	630‐512‐5824	453‐245‐0712	6/2/2017	5/3/2017
3	6	40	susan	lidia	brown	smith	8/29/1972	11/3/1993	susanbrowng@email.com	lsmith12@email.com	TN	FL	630‐512‐5824	828‐304‐4350	6/2/2017	9/4/2017

Find optimal cut‐point

Take random sample. In this example, we sample six observations.

PID.1	PID.2	ds	First_Name.1	First_Name.2	Last_Name.1	Last_Name.2	DOB.1	DOB.2	Email.1	Email.2	State.1	State.2	Phone.1	Phone.2	Consent_Date.1	Consent_Date.2
10	4	38	sue	michael	brown	jones	8/29/1972	10/24/1972	susanbrowng@email.com	mjones@email.com	TN	CA	630‐512‐5825	258‐652‐4875	10/24/17	6/29/2017
2	9	6	jennifer	jennifer	williams	william	8/18/1965	8/18/1966	jenniferwilliams@email.com	jenniferwilliams@email.com	PA	PA	462‐946‐0095	462‐946‐0095	5/10/2017	12/5/2017
3	4	35	susan	michael	brown	jones	8/29/1972	10/24/1972	susanbrowng@email.com	mjones@email.com	TN	CA	630‐512‐5824	258‐652‐4875	6/2/2017	6/29/2017
3	1	38	susan	linda	brown	smith	8/29/1972	10/29/1964	susanbrowng@email.com	lsmith22@email.com	TN	MA	630‐512‐5824	453‐245‐0712	6/2/2017	5/3/2017
4	8	10	michael	maria	jones	jones	10/24/1972	11/22/1972	mjones@email.com	mjones@email.com	CA	CA	258‐652‐4875	258‐652‐4875	6/29/2017	10/20/2017
3	10	9	susan	sue	brown	brown	8/29/1972	8/29/1972	susanbrowng@email.com	susanbrowng@email.com	TN	TN	630‐512‐5824	630‐512‐5825	6/2/2017	10/24/17

Manually annotate Data Set (truth)

PID.1	PID.2	ds	First_Name.1	First_Name.2	Last_Name.1	Last_Name.2	DOB.1	DOB.2	Email.1	Email.2	State.1	State.2	Phone.1	Phone.2	Consent_Date.1	Consent_Date.2	truth
10	4	38	sue	michael	brown	jones	8/29/1972	10/24/1972	susanbrowng@email.com	mjones@email.com	TN	CA	630‐512‐5825	258‐652‐4875	10/24/17	6/29/2017	0
2	9	6	jennifer	jennifer	williams	william	8/18/1965	8/18/1966	jenniferwilliams@email.com	jenniferwilliams@email.com	PA	PA	462‐946‐0095	462‐946‐0095	5/10/2017	12/5/2017	1
3	4	35	susan	michael	brown	jones	8/29/1972	10/24/1972	susanbrowng@email.com	mjones@email.com	TN	CA	630‐512‐5824	258‐652‐4875	6/2/2017	6/29/2017	0
3	1	38	susan	linda	brown	smith	8/29/1972	10/29/1964	susanbrowng@email.com	lsmith22@email.com	TN	MA	630‐512‐5824	453‐245‐0712	6/2/2017	5/3/2017	0
4	8	10	michael	maria	jones	jones	10/24/1972	11/22/1972	mjones@email.com	mjones@email.com	CA	CA	258‐652‐4875	258‐652‐4875	6/29/2017	10/20/2017	0
3	10	9	susan	sue	brown	brown	8/29/1972	8/29/1972	susanbrowng@email.com	susanbrowng@email.com	TN	TN	630‐512‐5824	630‐512‐5825	6/2/2017	10/24/17	1

Perform bootstrapping to find optimal cut‐point In this example, we do 50 bootstrapped.

Summary statistics of cut‐point identified during bootstrapping

Min.	1st Qu.	Median	Mean	3rd Qu.	Max.
10	10	10	15	10	35

Summary statistics of the accuracy of each bootstrapped sample

Note: In extremely small samples (such as this one), it is possible to have no observations in the test data set after applying the cut‐point identified in the training set. In those instances, it won't be possible to estimate accuracy.

Min.	1st Qu.	Median	Mean	3rd Qu.	Max.	NA's
0	0	1	0.6551724	1	1	21

Note: At this point additional validation/manual verification is encouraged, but we are skipping it on this example.

Filter matched set to matches that are equal or less than the cut‐point

PID.1	PID.2	ds	First_Name.1	First_Name.2	Last_Name.1	Last_Name.2	DOB.1	DOB.2	Email.1	Email.2	State.1	State.2	Phone.1	Phone.2	Consent_Date.1	Consent_Date.2
2	9	6	jennifer	jennifer	williams	william	8/18/1965	8/18/1966	jenniferwilliams@email.com	jenniferwilliams@email.com	PA	PA	462‐946‐0095	462‐946‐0095	5/10/2017	12/5/2017
3	7	6	susan	sue	brown	brown	8/29/1972	8/29/1972	susanbrowng@email.com	susanbrowng@email.com	TN	TN	630‐512‐5824	630‐512‐5824	6/2/2017	9/14/2017
7	10	6	sue	sue	brown	brown	8/29/1972	8/29/1972	susanbrowng@email.com	susanbrowng@email.com	TN	TN	630‐512‐5824	630‐512‐5825	9/14/2017	10/24/17
3	10	9	susan	sue	brown	brown	8/29/1972	8/29/1972	susanbrowng@email.com	susanbrowng@email.com	TN	TN	630‐512‐5824	630‐512‐5825	6/2/2017	10/24/17
4	8	10	michael	maria	jones	jones	10/24/1972	11/22/1972	mjones@email.com	mjones@email.com	CA	CA	258‐652‐4875	258‐652‐4875	6/29/2017	10/20/2017

Even though the last row (Michael and Maria) fall within the mean cut‐point of DS < = 15, just by looking at the data, we can tell that the PIDs belong to two different individuals. Instances like this should be manually excluded from the matched cohort.

Manual verification and correction

The last row of data is manually removed. Leaving the final matched data set

PID.1	PID.2	ds	First_Name.1	First_Name.2	Last_Name.1	Last_Name.2	DOB.1	DOB.2	Email.1	Email.2	State.1	State.2	Phone.1	Phone.2	Consent_Date.1	Consent_Date.2
2	9	6	jennifer	jennifer	williams	william	8/18/1965	8/18/1966	jenniferwilliams@email.com	jenniferwilliams@email.com	PA	PA	462‐946‐0095	62‐946‐0095	5/10/2017	12/5/2017
3	7	6	susan	sue	brown	brown	8/29/1972	8/29/1972	susanbrowng@email.com	susanbrowng@email.com	TN	TN	630‐512‐5824	630‐512‐5824	6/2/2017	9/14/2017
7	10	6	sue	su	brown	brown	8/29/1972	8/29/1972	susanbrowng@email.com	susanbrowng@email.com	TN	TN	630‐512‐5824	630‐512‐5825	9/14/2017	10/24/17
3	10	9	susan	sue	brown	brown	8/29/1972	8/29/1972	susanbrowng@email.com	susanbrowng@email.com	TN	TN	630‐512‐5824	630‐512‐5825	6/2/2017	10/24/17

Disjoint sets implementation

The following code is an implementation of the mathematical algorithm for disjoint sets and it was taken from: https://github.com/malllabiisc/cesi/blob/master/src/unionFind.py

Note: This section is written in Python and not R.

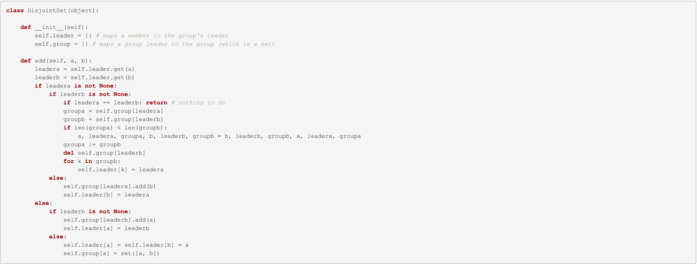
Disjoint sets execution on final matched set

Note: This section is written in Python and not R.

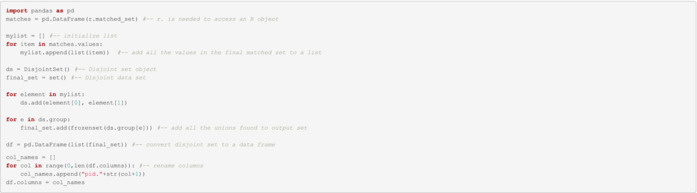
Disjoint Data Set

A truly unique ID can now be added to identify each individual, prevent duplication and link orphaned data together.

unique_id	pid.1	pid.2	pid.3
1	3	7	10
2	9	2	NULL

Final Disjoint Data Set

To create the final disjoint data set, we also need to take into account those PIDs not represented in the disjoint data set because these were found not to be duplicates. Unique PIDs and PIDs contained in the disjoint data set are then joined into a final disjoint data set where a truly unique identifier is assigned to each individual.

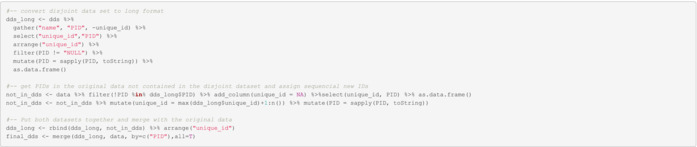
In this example, we found two duplicate individuals and established that we actually have seven unique individuals in the data.

unique_id	PID	DID	First_Name	Last_Name	DOB	Email	State	Phone	Consent_Date
1	10	3	sue	brown	8/29/1972	susanbrowng@email.com	TN	630‐512‐5825	10/24/17
1	3	3	susan	brown	8/29/1972	susanbrowng@email.com	TN	630‐512‐5824	6/2/2017
1	7	3	sue	brown	8/29/1972	susanbrowng@email.com	TN	630‐512‐5824	9/14/2017
2	2	2	jennifer	williams	8/18/1965	jenniferwilliams@email.com	PA	462‐946‐0095	5/10/2017
2	9	2	jennifer	william	8/18/1966	jenniferwilliams@email.com	PA	462‐946‐0095	12/5/2017
3	1	1	linda	smith	10/29/1964	lsmith22@email.com	MA	453‐245‐0712	5/3/2017
4	4	4	michael	jones	10/24/1972	mjones@email.com	CA	258‐652‐4875	6/29/2017
5	5	5	james	davis	7/20/1988	jamesdavis44@email.com	TX	880‐391‐9208	7/19/2017
6	6	6	lidia	smith	11/3/1993	lsmith12@email.com	FL	828‐304‐4350	9/4/2017
7	8	4	maria	jones	11/22/1972	mjones@email.com	CA	258‐652‐4875	10/20/2017

Garcia, A. , Lee, J. , Balasubramanian, V. , Gardner, R. , Gummidipundi, S. E. , Hung, G. , Ferris, T. , Cheung, L. , Desai, S. , Granger, C. B. , Hills, M. T. , Kowey, P. , Nag, D. , Rumsfeld, J. S. , Russo, A. M. , Stein, J. W. , Talati, N. , Tsay, D. , Mahaffey, K. W. , … on behalf of the Apple Heart Study Investigators (2022). The development of a mobile app‐focused deduplication strategy for the Apple Heart Study that informs recommendations for future digital trials. Stat, 11(1), e470. 10.1002/sta4.470

DATA AVAILABILITY STATEMENT

We are not able to provide data used to produce these results. We can, however, share code upon request.