A High‐End Estimate of Sea Level Rise for Practitioners

Abstract

Sea level rise (SLR) is a long‐lasting consequence of climate change because global anthropogenic warming takes centuries to millennia to equilibrate for the deep ocean and ice sheets. SLR projections based on climate models support policy analysis, risk assessment and adaptation planning today, despite their large uncertainties. The central range of the SLR distribution is estimated by process‐based models. However, risk‐averse practitioners often require information about plausible future conditions that lie in the tails of the SLR distribution, which are poorly defined by existing models. Here, a community effort combining scientists and practitioners builds on a framework of discussing physical evidence to quantify high‐end global SLR for practitioners. The approach is complementary to the IPCC AR6 report and provides further physically plausible high‐end scenarios. High‐end estimates for the different SLR components are developed for two climate scenarios at two timescales. For global warming of +2°C in 2100 (RCP2.6/SSP1‐2.6) relative to pre‐industrial values our high‐end global SLR estimates are up to 0.9 m in 2100 and 2.5 m in 2300. Similarly, for a (RCP8.5/SSP5‐8.5), we estimate up to 1.6 m in 2100 and up to 10.4 m in 2300. The large and growing differences between the scenarios beyond 2100 emphasize the long‐term benefits of mitigation. However, even a modest 2°C warming may cause multi‐meter SLR on centennial time scales with profound consequences for coastal areas. Earlier high‐end assessments focused on instability mechanisms in Antarctica, while here we emphasize the importance of the timing of ice shelf collapse around Antarctica. This is highly uncertain due to low understanding of the driving processes. Hence both process understanding and emission scenario control high‐end SLR.

Key Points

• A high‐end estimate of sea level rise in 2100 and 2300

• Decisionmaker/practitioner perspective on high‐end

• Timing of collapse of ice shelves critical

1. Introduction

Sea level rise (SLR) is a key aspect of climate change, with important consequences for coastal societies and low‐lying areas, especially small islands, deltas, and coastal cities (Oppenheimer et al., 2019). Human interference in the climate system leads to a continuing gradual warming and expansion of ocean water (i.e., the steric effect), mass loss from glaciers and polar ice sheets. Most of these effects continue long after emissions have slowed or stopped. Climate models simulating physical processes are used to reconstruct historical sea level change (excluding the ice sheet contribution), and consequently provide a method to project SLR given specific future anthropogenic CO₂ emissions and associated warming of the Earth system. Such a process‐based approach provides robust estimates of changes in the central part of the SLR distribution for projections and published studies using this method are in general agreement. However, estimating the tails of the distribution, which includes the ice sheet contribution remains contentious as not all the relevant processes are sufficiently understood or represented in the models, leading to variations between projections and multiple views of how the upper tail of the SLR distribution will evolve in future.

High‐end SLR projections provide information about the upper tail of the probability distribution of SLR, and are especially important for decisionmakers and practitioners (collectively referred to as practitioners) assessing long‐term risks and adaptation responses. High‐end projections, though by definition unlikely to occur, can provide information for adaptation planning, that is, defining a plausible “worst case” SLR to consider in an adaptation plan (Hinkel et al., 2015; Nicholls, Hanson, et al., 2021; Vogel et al., 2016). In addition, high‐end estimates provide insight on potential adaptation limits, tipping points and thresholds, and the level of climate mitigation required to keep SLR adaptation manageable in the future. In this context, it is also important to consider the long‐term commitment of SLR, requiring high‐end projections for time horizons well beyond 2100.

We emphasize that high‐end SLR information does not replace the quantification of the more likely central parts of the SLR distribution, but rather supplements these estimates. For example, a default adaptation plan may follow the median projection, with high‐end estimates used to inform the development of contingency options that can be applied in the case that high‐end SLR manifests. Such a planning approach is known as “adaptive planning” or “dynamic adaptive planning” in the literature (Haasnoot et al., 2013; Ranger et al., 2013). This is particularly the case when there are long lead times for action (i.e., the time to plan, design, finance, obtain support and implement the work) and long operational lives, such as for storm surge barriers or nuclear power stations, or where there is significant path‐dependency for decisions (e.g., when decisions have a long legacy that may preclude future options such as choosing between protection and retreat). Therefore, a “likely” range as used by Oppenheimer et al. (2019) as the central 66% of the probability distribution is not always sufficient (Hinkel et al., 2015).

Obtaining estimates of high‐end SLR can be approached in a statistical sense with probabilistic projections, as provided by Kopp et al. (2017, 2019) and Le Bars et al. (2017), but this approach may not capture possible contributions from processes not yet understood or included in climate models. To overcome this some studies define every percentile of conditional probability distributions based on an underlying assumption, such as including the Antarctic contribution from a single study (e.g., Goodwin et al., 2017). This suggests a higher confidence in the outcomes than is warranted by current physical understanding and is potentially misleading to practitioners since it does not reflect or communicate limits in our physical understanding of these processes. An alternative approach that provides estimates to address these difficulties are structured expert elicitation studies which have also been applied to provide estimates of high‐end SLR (Bamber et al., 2019). They attempt to capture the uncertainty due to the lack of knowledge (Lempert et al., 2003; Oppenheimer et al., 2019) that exists in model projections without relying on models, and which is impossible to constrain using a deterministic modeling approach. This approach combines the ad hoc judgment of a group of experts. However, the considerations regarding which processes are included, and which are not, is not made explicit and the interpretation of these estimates by experts is not necessarily the same as those of uninformed practitioners because they do not know the considerations of the experts. For this reason, in this paper, we prefer to use expert judgment based on physical reasoning to arrive at estimates which cannot be constrained by deterministic modeling. This is outlined in the Greenland and Antarctic sections and provides a transparent attribution of cause and effect.

The approach builds on Stammer et al. (2019), where they quantify high‐end SLR by synthesizing all the available physical evidence across observations, model sensitivity studies and modeled SLR scenario studies, and then assess and synthesize this information. Importantly, this approach aims to meet practitioner needs, which depend less on precise estimates of likelihood and more on evidence that is sufficiently credible, salient, and legitimate to support adaptation planning, including financing (Cash et al., 2003, 2002). “Salient” is used here in the context of relevance to practical needs. Within this framework, projections supported by multiple lines of evidence and eliciting broader confidence from the scientific community are of greater value as compared to projections further along the tail that feature fewer lines of evidence, and hence have lower confidence. This is an expansion of the approach based on building blocks (Stammer et al., 2019), in which the building blocks represent the amount of SLR beyond the likely range that practitioners will consider according to their risk‐averseness, emission scenarios, and how these evolve over time. It is key that the main processes are considered explicitly. The work is based on a WCRP grand challenge workshop on this topic where a wide variety of people were invited (∼25 scientists and ∼10 practitioners) including experts on all relevant sea level components and experts on the application of SLR information. The estimates for the specific components are made by a subset of authors as outlined in the acknowledgment statement.

Because the level of understanding of each sea level component differs, we employ different methods to assess each of them separately. For example, the understanding of the thermal expansion of the ocean and the glacier‐melt component is sufficient to use distributions derived from climate models directly. For those components, we assume that all necessary knowledge of the high‐end is captured in the distribution. However, for the Greenland and Antarctic ice sheet components the uncertainty is much larger, as understanding of physical processes is more limited, and hence a robust and reliable probability density function does not exist. We, therefore, choose to apply a process‐based expert judgment to the available lines of evidence to estimate a high‐end ice sheet contribution. By following this approach we deviate from (Fox‐Kemper et al., 2021), which provides a high‐end scenario with and without a specific Antarctic instability mechanism and includes structured expert elicitation. Hence, we take a complementary approach where we explicitly and transparently assess the physical processes leading to a high‐end estimate for Greenland and Antarctica.

The aim of this paper is to develop high‐end projections that are most strongly supported by physical evidence and yet are also salient for the decision and practitioner environment. We derive new high‐end estimates based on present physical understanding and demonstrate a methodological approach that may be regularly updated as the science evolves and improves, especially knowledge on ice sheets. Table S1 lists the author's contribution by section. Throughout this paper, we follow the definition of technical terms as defined in the glossary of the IPCC AR6 report (Matthews et al., 2021).

2. Practitioner Perspectives on High‐End Sea Level Projections

This paper explicitly considers practitioner perspectives in addition to SLR science to promote developing salient projections (e.g., Hinkel et al., 2019). Risk‐averse practitioners need to consider low likelihood, high consequence SLR futures that poses challenges to adaptation, in addition to median outcomes (Fox‐Kemper et al., 2021; Garner et al., 2018; Haasnoot et al., 2020; Hall et al., 2019; Hinkel et al., 2015; Nicholls, Hanson, et al., 2021). While median SLR projections have been relatively stable over time, several high‐end projections have emerged, especially in recent years (e.g., DeConto & Pollard, 2016). However, these high‐end projections have not been reviewed systematically from a user perspective, and most adaptation practitioners find them challenging to use, if they use them at all. Those practitioners that have applied them have had to develop their own understanding and guidance, including expertise on sea level science. This constitutes a high overhead to application when adaptation is often poorly funded.

An influential approach linking scientific exploration and decision requirements advises that scientific influence on decisions depends on the “salience, credibility, and legitimacy” of the information presented from the decision perspective (Cash et al., 2003, 2002). Of particular importance for high‐end SLR projections is salience, defined as “the relevance of information for an actor's decision choices, or for the choices that affect a given stakeholder.” In our view, salience for high‐end SLR projections derives from two factors.

First, scientific information used for decision‐making must consider all the major uncertainties and ambiguities across experts and models (Gold, 1993; Jones et al., 2014; Simpson et al., 2016). This requirement may be at odds with the physics‐based design of SLR projections. For example, the SLR scenarios provided by IPCC AR4 did not assign values outside the central likely range as information was absent (Meehl et al., 2007). In AR5, the possibility of several tenths of a meter above the likely range was considered as a high‐end possibility, reflecting rapid melting of the Antarctica and Greenland ice sheets: these processes, however were poorly understood and not captured directly in the physics‐based design (Church et al., 2013). While this exclusion is explicitly stated and makes sense from a physical science perspective, practitioners may misuse the results, as they will expect/assume that IPCC SLR scenarios cover all major uncertainties. AR6 moved to an emulator approach and covered a wider range of probabilities than earlier assessments reflecting the increased understanding of key physical processes that was unavailable for earlier assessments: the central range of estimates to 2100 is similar to earlier estimates, but also addresses high‐impact/low‐probability outcomes (Section 5), and provides a range of values from the literature. This evolution of the IPCC reports reflect increased understanding and provides improved treatment of the risk management context for adaptation planning, but alternative interpretations as presented here are possible, thereby increasing the understanding of high‐end estimates.

Second, salience requires a differentiation between scientific endeavors in general and what is sometimes called “actionable science,” which in the climate field is intended to support risk assessment and adaptation planning/investment (Bamzai et al., 2021; Beier et al., 2017; Moss et al., 2013; Vogel et al., 2016). New studies that challenge prior lines of evidence should be carefully reviewed, assessed, and debated before any application or incorporation into guidance (Nicholls, Hanson, et al., 2021). This avoids the “whiplash effect” wherein planners and all their efforts are undermined each time a new study questions their adopted projections. In this respect, we advocate this work to be used alongside (Fox‐Kemper et al., 2021) rather than replacing it.

Relevant examples of high‐end scenarios in planning exist in other fields. These support sound risk management, while adhering to a reasonable standard of practice to ensure appropriate resource allocation to the level of risk aversion. Accordingly, planners have found it advisable to frame high‐end risk with a standard that balances risk management objectives with finite resources, avoiding large opportunity costs where possible. For example, the UK National Risk Register defines a “reasonable worst‐case scenario” (RWCS) for use in planning. This is defined as “the worst plausible manifestation of that particular risk (once highly unlikely variations have been discounted) to enable relevant bodies to undertake proportionate planning” (HM Government, 2020). The RWCS “is designed to exclude theoretically possible scenarios which have so little probability of occurring that planning for them would be likely to lead to disproportionate use of resources” (Memorandum Submitted by the Government Office for Science and the Cabinet Office, 2011). The US Army Corps of Engineers selected a “maximum probable flood” for design purposes after the Great Mississippi River Flood of 1927. This is the “greatest flood having a reasonable probability of occurrence” and was preferred over a larger “maximum possible flood”, reflecting a meteorological sequence that, though reflective of historic events, was deemed highly implausible (Jadwin, 1928). This reasonableness standard has stood the test of time, including periodic review, and may be modified in the future to reflect changes to climate, land use, or other factors as appropriate.

For SLR, an example of a salient approach is The Thames Estuary Plan (TE2100), which addresses management of future coastal flood risk for London, UK. It was one of the first long‐term adaptation plans to address deep uncertainty (sometimes popularized as the unknown unknowns) with consideration of both more likely and high‐end SLR (Ranger et al., 2013). The term “H++” was created by TE2100 to describe a highly unlikely but possible high‐end range of SLR. While most attention is focused on the definite upper bound, the high‐end represents a range of values. H++ was designed to support a “dynamic robustness” planning approach that allows for consideration of a wide range of adaptation options as SLR observations and science develop over time (Ranger et al., 2013). This approach examines which extreme adaptation options should be kept open, whilst actively planning for smaller more likely SLR estimates and regularly reviewing the observed rates of SLR and the robustness of SLR projections. In TE2100, an upper‐end SLR exceeding 4.2 m in 2100 was initially adopted for planning. This includes a strom surge component which is not expected to change greatly in future. In 2009, after consideration of emerging science and observations, especially Greenland and West Antarctica, the 2100 upper‐end SLR projection was revised downwards to 2.7 m, of which 2 m is the time‐mean SLR (Lowe et al., 2009). This revised value is still used in practice today (Environmental Agency Guidance, 2021; Palmer et al., 2018). Hence, TE2100 demonstrates an adaptive process of science evaluation and revision of a salient high‐end scenario for adaptation planning. This inspires the estimates in this paper.

3. How We Develop a High‐End Estimate

To avoid overreliance on single studies, for example, as illustrated in the (Griggs, 2017) approach, we consider SLR‐related processes that are ideally supported by multiple lines of independent evidence. Our approach to construct high‐end SLR estimates uses information on SLR components that meet the following three requirements: (a) there is sufficient physical understanding of the relevant processes involved; (b) this understanding can be linked to a quantitative estimate of the associated SLR; (c) there is evidence to explain why the estimates we produce are expected to be in the upper tail of the range of responses. For SLR components where robust distributions are available, two times the standard deviation is warranted in view of the need to sample in the tail. For some components there is sufficient quantitative understanding to use the tail of a probability density function derived from physical models, but not for all components. In particular, the mean and variance of the ice sheet components are poorly constrained, and they cannot be derived directly from climate models. This continues to complicate development of a high‐end estimate.

Additionally, the covariance between sea level components is largely unknown because only the ocean component of SLR is directly derived from a large ensemble of climate models in which the relevant processes are coupled. The other sea level components are calculated off‐line from climate and land‐ice models, and hence require ad‐hoc assumptions about the co‐variance between components (Lambert et al., 2021), similar to what has been done in Fox‐Kemper et al. (2021) or via a covariance controlled by temperature changes (Palmer et al., 2020). To address this problem, we provide a range of high‐end values based on the assumption that the different components (glaciers, Greenland, Antarctica, steric expansion, land water storage change [LWSC]) are fully dependent (covariances all equal to 1, maximizing the uncertainty, and hence the upper end of the range) or fully independent (covariance all equal to 0, minimizing the uncertainty, providing a lower end of the range). At present, this is the only fully transparent way to consider the co‐variance between for instance the Greenland and Antarctic component. Additionally, it spans the full range of possible outcomes. However, it is unlikely that the complexity of processes involved, and the climate change patterns themselves are fully correlated or fully independent. To illustrate this one can think of the importance of atmospheric circulation changes and basal melt to high end. The first process is important in Greenland and the second in Antarctica. To what end both will change in a similar way is not known, hence full dependency is unlikely. At the same time global warming plays a role in both processes, hence fully independency is also unlikely.

For this reason, practitioners can decide whether to treat the uncertainties as fully independent, fully dependent, or in between depending on their level of risk‐averseness. For the independent case (all co‐variances zero), we take the median values of AR6 for the different components and define the high‐end to be characterized by two standard deviations above the median value. For the dependent case we can simply add the estimates of the different components.

The problem of estimating high‐end values for SLR is therefore not only about constraining the uncertainty in the component with the largest uncertainty, but also about understanding how the uncertainty in the SLR components are correlated with each other. The first problem is due to insufficient process understanding of the dynamics of the Antarctic ice sheet. The second problem is due to the surface mass balance (SMB) of the Greenland ice sheet, which requires Earth system models with fully coupled interactive ice sheets models to solve.

Here, we restrict ourselves to two time slices (2100 and 2300) and two climate scenarios (RCP2.6/SSP1‐2.6 and RCP8.5/SSP5‐8.5) which we call for simplicity the low and high scenario. The detailed physical reasoning behind the estimates of the individual cryospheric components is discussed in detail in Section 4 (Glaciers), Section 5 (Greenland), and Section 6 (Antarctica). Section 7 combines the storylines for the different SLR components in an estimate of the high‐end global mean SLR for the four scenarios being 2100 and 2300 low and high‐temperature change. We focus on the year 2100 because there is significantly more information available for this time horizon than for any other date in time. Moreover, the physical understanding decreases significantly after this time horizon. We focus on 2300 to highlight the long time‐scales involved for SLR, the necessity for adaptation and the benefits of mitigation. The scenarios rely strongly on the well‐known representative concentration pathways of RCP2.6/SSP1‐2.6, which has a median response at 2100 of just under 2°C, and RCP8.5/SSP5‐8.5 which has a median around 5°C in 2100 and 8°C–10°C in 2300. These correspond loosely to the core goal of the Paris Agreement and unmitigated emissions, respectively, and provide a significant range in future conditions. We limit our analyses to these scenarios because current understanding of the Antarctic response is not precise enough to distinguish intermediate scenarios between RCP2.6/SSP1‐2.6 and RCP8.5/SSP5‐8.5, as discussed in Section 7 in more detail. For each of the four scenarios, we provide a range in the high‐end estimate of SLR constraint by the dependent or independent addition of the different components.

The method provides estimates of the high‐end of projected global sea level change, and does not include the wide range of processes that contribute to regional sea level variations, nor does it consider regional and local vertical land motion, needed to determine the relative sea level changes at a particular coastal location, and that lead to changes in the frequency and magnitude of extreme sea level events at all time scales. Additionally, practitioners need to consider for example, bathymetric effects, possible changes in tides or surges and other near coastal processes. All these local effects and the possible changes therein need to be assessed separately, in particular human‐induced subsidence (Nicholls, Lincke, et al., 2021). We in effect assume that the global terms contribute significantly to the uncertainty in local SLR at most locations, but the local terms in the uncertainty budget vary in importance with location. Hence we focus on what is common to all locations. A simple additional step that practitioners could take is to realize that a large Antarctic contribution will influence regional sea level with higher values far from Antarctica due to gravitational effects. Operational tools to include this effect and all the other local to regional processes already exist and are applicable to any global scenario.

4. Glaciers

In this section, we detail the physical reasoning behind the estimates of the individual cryospheric components starting with glaciers (Section 4, Greenland Section 5 and Antarctica Section 6), as they do not immediately follow from the IPCC model ensemble results. Sections 4, 5, 6 have a similar structure starting with the processes which are relevant and ending with an evaluation of the high‐end contribution of the specific component. They each have a figure illustrating how the relevant processes contribute to high‐end SLR. The critical processes are eventually per cryospheric component summarized in Table 1 for each scenario.

Table 1.

Overview of Ciritical Processes for High‐End Estimate of the Cryospheric Components of Sea Level Rise Per Time Scale and Scenario

	2100‐low	2100‐high	2300‐low	2300‐high
Glaciers	Temperature increase	Temperature increase	Temperature increase, glacier mass equilibrium	Temperature increase, amount of glacier ice
Greenland	Temperature increase, outlet glacier acceleration	Temperature increase, albedo feedbacks, atmospheric circulation changes	Temperature increase	Temperature increase, albedo feedbacks, atmospheric circulation changes, tipping points
Antarctica	SMB, BMB, switch in flow below shelves	SMB, shelf collapse, BMB, calving, hydrofracturing	SMB, shelf collapse, BMB, calving, hydrofracturing	MISI, MICI, basal sliding

The Glacier Model Intercomparison Project Phase 2 (GlacierMIP2; Marzeion et al., 2020), is a community effort based on CMIP5 model runs estimating the mass loss of global glaciers. It includes 11 different glacier models, of which seven include all the glaciers outside of Greenland and Antarctica, and four are regional. The glacier models are forced by up to 10 General Circulation Models (GCMs) per RCP scenario, such that a total of 288 ensemble members form the basis of this most recent estimate of glacier mass change projections for the 21st century. Compared to this, projections that include the 23rd century are sparse and based on individual models (e.g., Goelzer et al., 2012; Marzeion et al., 2012). Some information about long‐term glacier mass change can be obtained from equilibrium experiments (e.g., Levermann et al., 2013; Marzeion et al., 2018).

4.1. Processes for Glaciers Relevant for High‐End SLR Scenarios

Temperature changes are critical to calculate glacier volume changes. Through the spatial distribution of glaciers on the land surface and a strong bias to Arctic latitudes, glaciers experience roughly twice the temperature anomalies of the global mean (Marzeion et al., 2020). Biases of projected spatial patterns of temperature increase, particularly concerning Arctic Amplification (stronger temperature change at high latitude), thus have the potential to impact projected glacier mass loss. However, we assume that the GCM ensemble size of GlacierMIP2 is large enough to adequately represent this uncertainty.

Other processes which may play a role are related to debris cover and ice‐ocean interaction. Only one of the glacier models taking part in GlacierMIP2 includes a parameterization of frontal ablation/calving (Huss & Hock, 2015), such that there is potential for underestimation of mass loss in the GlacierMIP2 ensemble as important ice‐ocean interaction processes are not represented. However, frontal ablation and calving will most strongly affect mass loss of ice currently below mean sea level (Farinotti et al., 2019), and hence they will contribute relatively little to SLR since that constitutes only 15% of the total glacier mass. Additionally, the mass loss projected in GlacierMIP2 for 2100 under RCP2.6/SSP1‐2.6 indicates that the number of tidewater glaciers will be greatly reduced even under low emissions and will retreat from contact with the ocean. Thus, ice‐ocean interaction may have strong effects on the timing of mass loss within the 21st century, but this is unlikely to play a large role at the end of the 21st century or later, and for greater temperature increases.

None of the global models and only one of the regional models in GlacierMIP2 (Kraaijenbrink et al., 2017) includes effects of debris cover on glacier mass balance. Strong surface mass loss has the potential to cause the surface accumulation of debris layers (e.g., Kirkbride & Deline, 2013) thick enough to insulate the ice below it, thus reducing melt rates (e.g., Nicholson & Benn, 2006). At the same time, a thin debris cover layer could enhance melt rates. The lack of representation of debris cover in GlacierMIP2 is estimated to be unlikely to have a significant impact on the considered high‐end range of projections.

4.2. Evaluation of the High‐End Contribution for Glaciers

Glaciers store less than 1% of the global ice mass (Farinotti et al., 2019), and contributed 0.7 mm/yr over the period 2010–2018 (Hugonnet et al., 2021). Their potential to contribute to SLR is thus limited by their total mass, and which is estimated to be 0.32 ± 0.08 m SLE (Farinotti et al., 2019). However, this limit does not affect their contribution within the 21st century: even under RCP8.5/SSP5‐8.5, GlacierMIP2 projects that 64% ± 20% of the glacier mass will remain by 2100. At the same time, the GlacierMIP2 projections show that the glacier contribution strongly depends on the temperature increase itself and less on precipitation changes, both affecting the SMB (Figure 1). This temperature increase is reasonably constrained by the large set of CMIP model ensemble and shows a Gaussian distribution.

Figure 1.

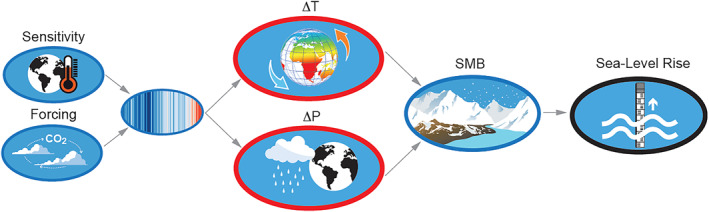
Causal relation between processes leading to a high‐end contribution of Glaciers to sea level rise (SLR). Climate forcing leads to patterns of temperature (ΔT) and precipitation (ΔP) change over the globe (colored stripes global mean change). These local climate variables control the surface mass balance (SMB) and thereby the volume change of glaciers which determines the SLR by the glacier component. Ice dynamics are usually highly simplified in glacier models and therefore omitted here.

Hence, both climate and appropriate physical processes are captured in the GlacierMIP2 projections and therefore a high‐end estimate for glaciers is based on the mean and twice the standard deviation of the GlacierMIP2 experiment as outlined in our definition of a high‐end estimate in Section 3. Table 1 and Figure 1 illustrate the critical processes required for a high‐end estimate of the glacier contribution. Similar tables and figures are presented in the later ice Sections to demonstrate and contrast the different processes for the different cryospheric components. Table 3 provides the references to the papers from which we derived the actual values to estimate the high‐end range. Our final high‐end values for the glaciers are based on the GlacierMIP2 result: 0.079 ± 0.056 m of ice volume change under RCP2.6/SSP1‐2.6 and 0.159 ± 0.086 m under RCP8.5/SSP5‐8.5 in 2100. We convert these to sea level equivalents by correcting for the fact that approximately 15% of the glacier volume is below sea level and arrive at a high‐end estimate of 0.15 m sea level equivalents under RCP2.6/SSP1‐2.6 and 0.27 m under RCP8.5/SSP5‐8.5 (being the mean plus twice the standard deviation). By 2300, glaciers might approach stabilization under RCP2.6/SSP1‐2.6 after having contributed 0.28 m to SLR (Cazenave et al., 2018). Their contribution would be limited by their current ice mass above flotation of 0.32 ± 0.08 m (Farinotti et al., 2019), for higher emission scenarios, which is then by definition the highest contribution possible.

Table 3.

A Comparison Between This Paper and the IPCC AR6 Values

	References a	Approach/processes	This paper	AR6 (Table 9.8 and Table 9.11)	Remarks
2100 +2°C
Thermal expansion	Fox‐Kemper et al. (2021)	AR6 assessment	0.18 b	0.18
Glaciers	Marzeion et al. (2020)	Temperature change, ensemble 10 climate models, 10 glacier models	0.15	0.11
Greenland	Fox‐Kemper et al. (2021)	AR6 assessment, medium confidence	0.10	0.30	<< c AR6
Antarctica	Levermann et al. (2020)	Basal melt for 16 ice sheet models	0.39	0.25	>>AR6
Land water storage change	Fox‐Kemper et al. (2021)	AR6 assessment	0.04	0.04
Total		Range depending on correlation (Section 3)	0.72–0.86	0.79
2100 +5°C
Thermal expansion	Fox‐Kemper et al. (2021)	AR6 assessment	0.36	0.36
Glaciers	Marzeion et al. (2020)	Temperature change, ensemble 10 climate models, 10 glacier models	0.27	0.20
Greenland	Delhasse et al. (2018, 2020) and Goelzer et al. (2020)	ISMIP6 assessment including circulation changes and missing feedbacks leading to deep uncertainty	0.29	0.59	<<AR6
Antarctica	Bulthuis et al. (2019), DeConto et al. (2021), and Golledge et al. (2015)	Mixture basal melt and ice dynamical studies	0.59	0.56
Land water storage change	Fox‐Kemper et al. (2021)	AR6 assessment	0.04	0.04
Total		Range depending on correlation (Section 3)	1.27–1.55	1.60
2300 +2°C
Thermal expansion	Fox‐Kemper et al. (2021)	AR6 assessment	0.35	0.35
Glaciers	Goelzer et al. (2012) and Marzeion et al. (2012)	Temperature change, single parameterized glacier models	0.28	0.29
Greenland	Fox‐Kemper et al. (2021)	AR6 assessment	0.39	1.28	<<AR6
Antarctica	Bulthuis et al. (2019), DeConto et al. (2021), and Golledge et al. (2015)	Four ice dynamical studies with a range of physical processes simulated	1.35	1.56
Land water storage change	Fox‐Kemper et al. (2021)	AR6 assessment	0.1	0.1
Total		Range depending on correlation (Section 3)	2.19–2.47	3.1
2300 +8°C–10°C
Thermal expansion	Fox‐Kemper et al. (2021)	AR6 assessment	1.51	1.51
Glaciers	Farinotti et al. (2019)	Temperature change, all glaciers melted	0.32	0.32
Greenland	Church et al. (2013), Delhasse et al. (2018, 2020)	SMB changes including deep uncertainty	2.5	2.23
Antarctica	Bulthuis et al. (2019), DeConto et al. (2021), and Golledge et al. (2015)	Four ice dynamical studies with a range of physical processes simulated	6	13.54	<<AR6
Land water storage change	Fox‐Kemper et al. (2021)	AR6 assessment	0.10	0.10
Total		Range depending on correlation (Section 3)	8.59–10.43	16.2

^a Reference used to compile the values in this study.

^b Values are in meters relative to a baseline period of 1995–2014.

^c >>/<< indicates more than 20% difference between this study and AR6. We used from AR6 the highest 83rd percentile projections across all probability distributions considered, including low confidence processes.

Table 3 summarizes all the references used for the different high‐end estimates of all the components and provides a comparison to the results of Fox‐Kemper et al. (2021).

5. Greenland

Currently, substantial ice mass loss is observed in Greenland (Bamber et al., 2018; Cazenave et al., 2018; A. Shepherd et al., 2020) with a rate over the period 2010–2019 equivalent to 0.7 mm/yr Global Mean Sea Level Rise (GMSLR; Fox‐Kemper et al., 2021). This is to a large extent driven by a change in the SMB, but also by increased dynamic loss of ice via marine‐terminating outlet glaciers (Csatho et al., 2014; Enderlin et al., 2014; King et al., 2020; Van Den Broeke, 2016).

5.1. Processes

For the 21st century outlet glaciers remain important (Choi et al., 2021; Wood et al., 2021), but for longer time scales changes in SMB are expected to dominate mass loss from the Greenland ice sheet, in particular for high‐emission forcing, as some marine‐terminating outlet glaciers begin to retreat onto land (e.g., Fürst et al., 2015). Since the IPCC AR5 report, several new studies with projections for Greenland up to 2100 have been published that were broadly consistent with the AR5 (e.g., Calov et al., 2018; Fürst et al., 2015; Golledge et al., 2019; Vizcaino et al., 2015). More recent studies, as also reported by Fox‐Kemper et al. (2021), however, have obtained significantly larger mass loss rates with values of up to 33 cm by 2100 (Aschwanden et al., 2019; Hofer et al., 2020; Payne et al., 2021). This can be explained by a larger sensitivity used for converting air temperature to melt, and averaging of the forcing over a large domain and applying a spatially constant scalar anomaly, an approach that has been disputed (Fürst et al., 2015; Gregory & Huybrechts, 2006; Van De Wal, 2001).

The Ice Sheet Model Intercomparison Project for CMIP6 (ISMIP6) ensemble mean results indicated a contribution of 0.096 ± 0.052 m for RCP8.5/SSP5‐8.5 in 2100 for a representative range of CMIP5 GCMs (Goelzer et al., 2020), where an unaccounted contribution for committed sea level of 6 ± 2 mm is additionally added (Goelzer et al., 2020; Price et al., 2011). However, recent results with CMIP6 forcing show a larger range with one model suggesting a contribution of 256 mm (Hofer et al., 2020; Payne et al., 2021). These results were obtained with a limited number of CMIP6 models, some of which are known to exhibit a large climate sensitivity and therefore may be biased high. The ISMIP6 results based on CMIP5 therefore provide a reasonable estimate of the uncertainty caused by GCMs, but they do not include an estimate of the uncertainty due to the more detailed and accurate Regional Climate Models (RCMs), which are forced by GCMs to arrive at detailed mass balance changes. ISMIP6 results are based on only one RCM used for downscaling the GCM results to SMB changes.

Uncertainties in modeling SMB have been further addressed using a common historical forcing (1980–2012) and comparing the output of 13 different SMB models for the Greenland ice sheet (Fettweis et al., 2020). They found that the ensemble mean produced the best estimate of SMB compared to observations, but the difference in surface melting between models was as much as a factor 3 (from 134 to 508 Gt/yr) and the trend in runoff also differed by a similar amount (from 4.0 to 13.4 Gt/yr/yr) for the common period 1980–2012. Combining the uncertainties in modeling SMB with those for the projected climate forcing indicates that the SMB component is poorly constrained and has large uncertainties, despite having dominated recent mass loss trends in Greenland (Van Den Broeke, 2016).

Further uncertainties in projections for the Greenland ice sheet related to specific processes include: (a) the importance of firn saturation which buffers meltwater prior to run off, (b) albedo lowering by darkening of the surface caused by dust or algal growth, (c) the strength of melt‐albedo and height‐SMB feedback mechanisms, both leading to additional mass loss, and (d) calving, all being processes that are poorly constrained and often not included in SMB models. Considering these processes has the potential to increase the contribution of Greenland and widen the uncertainty distribution. Furthermore, it is known that the current generation of GCMs do not capture recently observed atmospheric circulation changes (Delhasse et al., 2018, 2020; Fettweis et al., 2017; Hanna et al., 2018), and it is not yet clear whether these changes are forced by climate change or natural variability. Delhasse et al. (2018) estimated that Greenland atmospheric blocking, leading to persistence of enhanced warm air advection from the South and changes in cloudiness (Hofer et al., 2019), may lead to a doubling of mass loss due to SMB changes over the 21st century. This is an estimate for 2040–2050 which does not capture the positive albedo feedback arising from an expanding ablation zone, so we consider the doubling of the mass loss due to SMB changed caused on circulation changes as a lower bound of this effect. In all these studies, projections are made based by stand‐alone climate models, lacking many of the feedbacks discussed above (Fyke et al., 2018).

In contrast to the Antarctic ice sheet (discussed in the next Section), only a limited contribution of the dynamics of the outlet glaciers is to be expected (Fürst et al., 2015; Goelzer et al., 2020; Nick et al., 2013), This is because they occupy only a small fraction of the ice sheet perimeter, whereas in Antarctica the majority of the perimeter is in direct contact with the ocean.

Paleo‐simulations may be important for constraining near‐future mass loss from the Antarctic ice sheet, but provide few constraints for the Greenland ice sheet for the future transient nature of high‐end ice mass loss estimates on century time scales. They merely offer insight about sea level high stands during characteristic warm periods in the past.

5.2. Evaluation of the High‐End Contribution for Greenland

Critically important for generating a high‐end estimate for the Greenland ice sheet is the SMB as expressed in Figure 2. SMB and ocean changes are the driver for changes in outlet glaciers and ice sheet dynamics. While SMB and outlet glacier changes have contributed to observed SLR changes, SMB changes are expected to become more important on longer time scales and with stronger forcing. Changes in ice sheet dynamics are expected to be limited. For a high‐end estimate of the Greenland ice sheet there is most likely a strong divergence between the low warming and the high warming scenario, particularly beyond 2100. A recent study (Noël et al., 2021), based on a regional climate model forced with a GCM, indicates that the SMB over the ice sheet is negative for a global warming above 2.7 K for a constant topography, ignoring elevation‐change‐related feedbacks. If so, no processes adding mass to the ice sheet will exist and this has been argued to be a “tipping‐point” for the ice sheet. On the other hand, this is challenged by studies including dynamical changes of the topography (Gregory et al., 2020; Le clec'h et al., 2019) because the ice sheet may evolve to a smaller equilibrium state. The importance of the existence of a tipping‐point is merely on the millennial time scales, but a negative SMB at least suggests a strong nonlinear response to a large climate forcing. Table 1 illustrates the critical processes to consider when estimating a high‐end contribution for the Greenland ice sheet. For the 21st century, we estimate the high‐end estimate for the +5°C scenario to be around 0.30 m, being twice the ISMIP6 results (Goelzer et al., 2020) where the factor two arises from the possible atmospheric circulation changes (Church et al., 2013; Delhasse et al., 2018, 2020) that are not captured in the models. This factor of two should be interpreted as the deep uncertainty around the SMB changes in a changing climate caused by a poor understanding of modeling circulation changes and surface processes affecting the albedo. At this point, our approach deviates from Fox‐Kemper et al. (2021) who use expert judgment as part of their lines of evidence.

Figure 2.

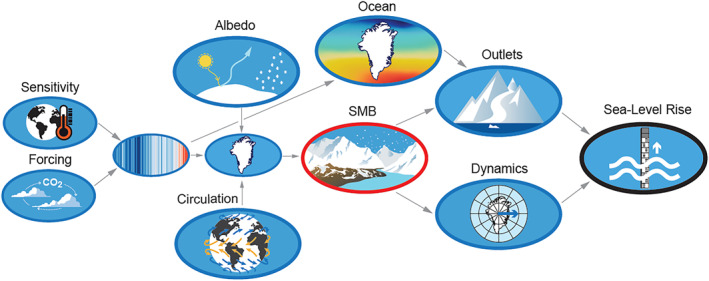
Causal relation between processes leading to a high‐end contribution of Greenland to sea level rise (SLR). Critical processes are albedo, ocean forcing and atmospheric circulation changes. These three processes impact the surface mass balance (SMB). Outlet glaciers change by changes in SMB and ocean forcing and SMB also influences the dynamics of the main ice sheet, where the ocean affects the outlet glaciers, together controlling the SLR.

For a +2°C scenario there seem to be few processes that can be large, hence we use the upper end of the very likely range assessed by AR6 being 0.10 m as the high‐end estimate (Fox‐Kemper et al., 2021). The omission of feedbacks and circulation changes are judged to only be important for large perturbations, justifying excluding them for a high‐end estimate. Consequently, high‐end projections in 2300 for a +2°C scenario are still constrained and estimated to be 0.3 m, as the SMB is the main driving process. The few studies, based on intermediate complexity climate models (Table 13.8, Church et al., 2013) suggest a high‐end contribution of 1.2 m in 2300 from the Greenland ice sheet under a high scenario. A more recent but similar result is obtained using an intermediate complexity model coupled to an ice sheet model (Van Breedam et al., 2020). Here, we suggest, following the projections in 2100, to include a factor 2 based on the possible atmospheric circulation changes above, as the deep uncertainty in the SMB, thereby arriving at a high‐end estimate of 2.5 m for Greenland under a +8°C–10°C scenario in 2300. This is close to the structured expert judgment by Bamber et al. (2019), but higher than the experiment by Aschwanden where the degree‐day factors are constrained by the observational period 2000–2015 (Fox‐Kemper et al., 2021).

6. Antarctica

Currently significant ice mass loss is observed in West‐Antarctica (Bamber et al., 2018; Cazenave et al., 2018; Rignot et al., 2019; A. Shepherd et al., 2018): over the period 2010–2019 Antarctica contributed 0.4 mm/yr to GMSL rise (Fox‐Kemper et al., 2021). Most studies indicate that ice loss in West Antarctica follows from increased rates of sub‐ice shelf melting caused by ocean circulation changes, in particular in the Amundsen Sea sector (Adusumilli et al., 2018; Paolo et al., 2015), but it is questioned whether this is the result of anthropogenic climate change or natural variability in the ocean as suggested by Jenkins et al. (2018) or by a combination of both processes (Holland et al., 2019). Against this background, it is important to consider which processes may lead to substantial continued or accelerated mass loss from Antarctica, and therefore its contribution to high‐end sea level scenarios. In addition, it needs to be considered whether there are instabilities in the system which influence high‐end estimates. We explore this in more detail than for the previous two components because of the large uncertainty and the large potential contribution to SLR from Antarctica.

6.1. Processes in Antarctica Relevant for High‐End Sea Level Scenarios

A major uncertainty in future Antarctic mass losses resulting in high‐end SLR is connected to the possibility of rapid and/or irreversible ice losses through instabilities in marine‐based parts of the ice sheet, as hypothesized for the Marine Ice Sheet Instability (MISI) and the Marine Ice Cliff Instability (MICI), see Pattyn et al. (2018) for further explanation. MISI is a self‐reinforcing mechanism within marine ice sheets that lie on a bed that slopes down towards the interior of the ice sheet. If these instabilities are activated it might be that they overshadow climate forcing scenarios. At present, floating ice shelves exert back stress on the inland ice, limiting the flow of ice off the continent and resulting in a stable ice sheet configuration. In the absence of ice‐shelf buttressing caused by loss of the shelf or substantial thinning, ice sheets on a bed sloping towards the interior are, under certain circumstances, inherently unstable (Schoof, 2007; Sergienko & Wingham, 2019, 2021), and stable grounding line positions can only be reached when the bed slopes in the opposite direction (sloping bed upwards to the interior; Pattyn et al., 2012). If ice shelf buttressing remains, however, stable grounding line positions can also be reached on downward sloping beds for specific geometric configurations (Cornford et al., 2020; Gudmundsson et al., 2012; Haseloff & Sergienko, 2018; Sergienko & Wingham, 2019). Weak buttressing may not prevent grounding‐line retreat, but may slow it.

Antarctic ice shelves modulate the grounded ice flow, and their thinning and weakening is crucial in the timing and magnitude of major ice mass loss or the onset of MISI. This onset of rapid MISI is controlled by the timing of ice shelf breakup or collapse, and the resulting loss of buttressing that otherwise would prevent MISI from occurring. Ice sheet models demonstrate that the permanent removal of all Antarctic ice shelves leads to MISI, West Antarctic ice sheet collapse, and 2–5 m SLR over several centuries (Sun et al., 2020).

The MICI hypothesis of rapid, unmitigated calving of thick ice margins triggered by ice shelf collapse has been included in an ice sheet model by DeConto and Pollard (2016); DeConto et al. (2021) and Pollard et al. (2015). Including the MICI processes was partly motivated by inconsistencies with reconstructed paleo sea level proxies (Bertram et al., 2018; DeConto & Pollard, 2016), but also has a sound physical process based support (Bassis et al., 2021; Crawford et al., 2021). Like MISI, the onset of MICI is triggered by the loss of buttressing ice shelves facilitating the creation of ice cliffs which subsequently destabilize. Its onset also depends on the magnitude of ocean and atmospheric warming. A major difference is the more rapid calving of the ice cliffs at the front of the ice sheet inducing a faster retreat.

Importantly, without the disintegration of buttressing ice shelves, neither MISI nor MICI can operate and the dynamic mass loss contribution from Antarctica to SLR is limited. The current atmospheric state is too cold for a large contribution from surface melt. Further, a few degrees of Antarctic warming leads to more snow accumulation, partly offsetting the increases in oceanic melt and the resulting loss of ice by changes in the ice flow (Seroussi et al., 2020). However, the possibility of larger changes induced by ocean processes cannot be excluded. It has been argued that, in particular, the waters below the Filchner‐Ronne ice‐shelf could warm by more than 2°C as a result of changes in ocean circulation (Hellmer et al., 2012). Both observations (Darelius et al., 2016; Ryan et al., 2020) and models (Hazel & Stewart, 2020; Naughten et al., 2017) support this as a possibility, although a recent study (Naughten et al., 2021) suggests that such a change in circulation may be unlikely under the climate scenarios considered here for the 21st century. The LARMIP experiments (Levermann et al., 2020) provide an indication that the impact of such a change could be on the order of 0.2 m global mean SLR by 2100.

Observations of basal melt are hampered by the inaccessibility of the sub‐ice‐shelf cavities, and modeling of basal melt is challenging both because of the lack of observational validation and the limited resolution of the cavities that is possible in models covering continental scales. To date, most ocean model components within coupled climate models do not include the regions beneath the ice shelves. Simplified parameterizations of sub‐shelf cavity circulation have been developed, such as the PICO‐model (Reese et al., 2018), or the cross‐sectional plume model (Lazeroms et al., 2018, 2019; Pelle et al., 2019). Alternatively (Jourdain et al., 2020), propose a parameterization of sub‐shelf melt based on the use of low‐resolution CMIP5 ocean models, calibrated to observed melt rates (see also Favier et al., 2019). Rather than attempting to explicitly resolve the sub‐shelf circulation (Levermann et al., 2020), estimated the Antarctic contribution based on low‐resolution ocean temperature change with a linear response function capturing all the uncertainties. This approach ignores dampening or self‐amplifying processes and concentrates on the forced response but includes a dynamical response of the ice sheet itself.

Ideally, sub‐shelf circulation and ocean melt should be represented in three dimensions, at the high spatial resolution, and interactively coupled with the ice sheet and the ocean models (Comeau et al., 2022; Smith et al., 2021). This represents a significant ongoing modeling challenge (e.g., Van Westen & Dijkstra, 2021), together with uncertainties in the bathymetry, limiting confidence in future projections of ice shelf loss.

It is also critical to consider other processes than basal melt or circulation changes that can lead to disintegration of the major ice shelves. In particular, one needs to consider calving and surface melt that can enhance ice shelf surface crevassing and hydrofracturing. While hydrofracturing is an important process to reduce or eliminate buttressing and facilitate ice sheet instability, fracturing without surface melt also weakens the ice shelves, particularly along their margins. This is observed in the Amundsen Sea region (Lhermitte et al., 2020), but is not yet fully implemented and validated in large‐scale ice sheet models, hindering an estimate of the timing of ice shelf collapse.

As the pace of future atmospheric warming and the capacity of firn to absorb melt water remain uncertain, predictions of ice shelf surface melting by 2100 and subsequent ice shelf disintegration under RCP8.5/SSP5‐8.5 vary widely. Based on a regional climate model (Trusel et al., 2015), compiled melt rates under warming scenarios. Under RCP8.5/SSP5‐8.5, several small ice shelves will be exposed by 2100 to melt rates exceeding the values observed at the time that the Larsen‐B ice‐shelf broke up in 2002. However, the major ice shelves (e.g., Filchner‐Ronne, Ross Amery) remain stable over this century, but likely not over longer time scales. These melt rates contrast with the results of independent simulations using simpler climate models and a different scheme to calculate surface melt (DeConto & Pollard, 2016) that suggest a much faster disintegration of the ice shelves. An updated assessment (DeConto et al., 2021) confirms the ice shelf stability for this century, but also shows a rapid disintegration soon after under RCP8.5/SSP5‐8.5. An intercomparison study showed that the increased melt is partly compensated by increased accumulation (Seroussi et al., 2020), regardless of the emissions scenario followed. It shows disintegration of some small ice shelves, but not the big shelves which constrain high‐end contributions to 2100. Soon after 2100, this is likely not the case any longer under RCP8.5/SSP5‐8.5. So this facilitates the construction of high‐end estimates for 2100 and 2300. For 2100, we can assume that the consequence in terms of SLR is not yet visible, but for 2300 we can be sure that the ice sheet has had sufficient time to start reacting to the break‐up of ice shelves under strong forcing scenarios.

6.2. What If the Major Ice Shelves Break Up?

Both MISI and MICI might be important for SLR if and when ice shelves collapse. Ice‐shelf collapse, therefore, can be considered the key prerequisite for these instabilities to commence. By “instability” we imply that, once initiated, the process of retreat continues irrespective of the applied climate forcing. MISI is a dynamic response of the ice sheet to a change in the buttressing conditions, whereas MICI might lead to direct mass loss via tall collapsing cliffs, which also may be a self‐sustaining process. Research on MICI has focused on the critical height at which vertical ice cliffs become unstable (Bassis & Walker, 2012; Clerc et al., 2019; Parizek et al., 2019) and plausible rates of calving and retreat (Schlemm & Levermann, 2019). Estimates of ice‐cliff calving have also used observations of calving ice‐fronts in Greenland as a constraint (e.g., DeConto & Pollard, 2016), although Greenland glaciers might not be representative of the behavior of wider and thicker outlet glaciers in Antarctica that have lost their ice shelves. The importance of the ice cliff calving mechanism, while likely relevant to high‐end sea level scenarios if ice shelves are lost, is currently disputed in the literature (Fox‐Kemper et al., 2021).

A second major uncertainty in the response of ice margins once shelves are lost is the uncertainty about the physics of the basal friction conditions near the grounding line, which could further enhance seaward ice flow (Pattyn et al., 2018; Tsai et al., 2015). As a result, the few existing ice model projections for 2300 vary considerably (Bulthuis et al., 2019; Golledge et al., 2015; Levermann et al., 2020), but should all be considered physically plausible and thereby provide independent lines of evidence for a high‐end SLR (see, Table 3 for values).

The Antarctic Buttressing Model Intercomparison project (ABUMIP; Sun et al., 2020) shows that instantaneous and sustained loss of all Antarctic ice shelves leads to multi‐meter SLR over several centuries (1–12 m in 500 yr from present). The participating models did not include MICI, and the variation in magnitude of ice loss was found to be related to subglacial processes, where plastic friction laws generally lead to enhanced ice loss. This experiment should be considered as an upper bound as artificially regrowth of ice shelves was prevented, and other dampening effects were ignored.

Paleo evidence of past ice loss might provide some constraints on the uncertainty in ice sheet models, but available data are mostly restricted to total ice loss and remain limited in their ability to constrain rates of ice loss (Dutton et al., 2015).

Regardless of the processes driving ice loss on the ice shelves, the retreat of ice also leads to an instantaneous and time‐delayed response of the underlying bedrock and an immediate reduction in gravitational attraction between the ice sheet and the nearby ocean. The resulting reduction of relative sea level at the grounding line may stabilize its retreat, providing a negative feedback (Barletta et al., 2018; DeConto et al., 2021; Gomez et al., 2010, 2015; Larour et al., 2019; Pollard et al., 2017) showed that these effects do little to slow the pace of retreat until after the mid‐twenty‐third century in the Amundsen Sea region. Coulon et al. (2021) also find that the West‐Antarctic ice sheet destabilizes for high‐forcing regardless of the mantle viscosity. At the same time, Kachuck et al. (2020) and Pan et al. (2022) indicate that the weak viscosity in West‐Antarctica might significantly reduce the West‐Antarctic contribution over the next 150 yr, because the rapid bedrock uplift compensates the grounding line retreat. Altogether, this suggests that for the shorter time scales over the next centuries, it cannot be excluded that this negative feedback plays a role, but improved 3D viscosity models are needed to quantify this effect.

6.3. Evaluation of the High‐End Contribution for Antarctica

A chain of processes illustrated in Figure 3 control the contribution from Antarctica to SLR. The stability of the ice shelves is central, and this is controlled by surface melt, bottom melt, calving and hydrofracturing. The relative importance of these factors changes because of regional climate change as estimated by global climate models. The uncertainty in the regional climate in the southern hemisphere is generally larger than in the northern hemisphere, increasing uncertainties in the Antarctic component (Heuzé et al., 2013; Russell et al., 2018). Once the ice shelves are broken up, the dynamics of the ice sheet, including the MISI and MICI mechanisms, control how much ice is lost. All studies for a 5°C warming at the end of the century indicate a multi‐meter contribution to GMSL from Antarctica on longer than a century time scale. Major ice shelves will disintegrate eventually under that magnitude of warming. The timing of the disintegration is uncertain, but unlikely to have a large effect on high‐end SLR already during the 21st century. For this reason, we consider the upper range of Bulthuis et al. (2019), Golledge et al. (2019, 2015), and Levermann et al. (2020), to estimate the high‐end contribution of the Antarctic Ice Sheet in 2100 to be 0.39 m for a +2°C scenario (Levermann et al., 2020) and 0.59 m for a +5°C scenario, which is close to the results by Edwards et al. (2021). We do this as no formal probability distributions are available for the likelihood of ice shelf collapse and cliff instability. The study by DeConto and Pollard (2016) is not included for our estimates for 2100, because of a potential overestimation of surface melt rates which initiates shelf disintegration too early. For 2300, only a limited number of ice dynamical studies exist, but they all agree that several meters of SLR from Antarctica is possible because of ice shelf collapse, and limited constraints on instability mechanisms and ice dynamics. Based on Bulthuis et al. (2019), DeConto et al. (2021), and Golledge et al. (2015), we estimate a high‐end contribution to be 1.35 m for a +2°C scenario and 6 m for a +8°C–10°C scenario in 2300. A more recent study by DeConto et al. (2021) including improved estimates for surface melt rates is included for the 2300 estimates. So, despite the different physics of all those studies, we believe that we can combine those studies for a high‐end estimate because they agree on the onset of shelf disintegration around 2100 and far ahead of 2300. For the +8°C–10°C scenario, we take the average of the three dynamical studies, while realizing that constraints on the rates of mass loss are highly uncertain and vary strongly among the models.

Figure 3.

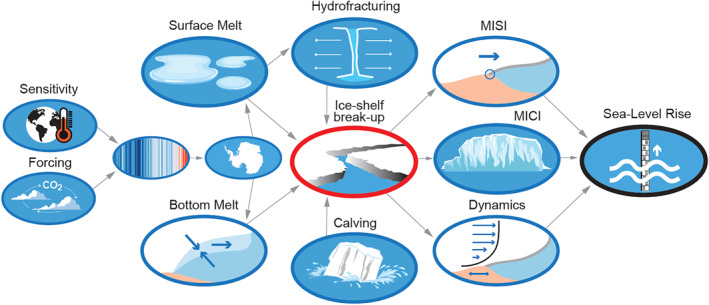
Causal relation between processes leading to a high‐end contribution of Antarctica to sea level rise (SLR). The Antarctic climate response affects Surface Melt and Bottom Melt, which together with Calving and Hydrofracturing determine the stability of the ice shelves. If the ice shelves break up, the dynamics encompassing instability mechanisms like Marine Ice Sheet Instability (MISI) and Marine Ice Cliff Instability (MICI) and basal sliding control the final contribution of the Antarctic ice sheet to high‐end SLR.

Table 1 illustrates the critical processes for a high‐end estimate for the Antarctic contribution.

In summary, it is not only the poor understanding of the dynamics of ice flow, but also the limited understanding of the processes controlling the break‐up of the major ice shelves that determines the uncertainty in the timing and magnitude of the Antarctic contribution to sea level. When combined, this leads to the Antarctic component having the largest uncertainties in the sea level projections.

7. Lines of Evidence for High‐End Scenarios

In Sections 4, 5, 6, we discussed the contribution of cryospheric components to SLR, which largely follow from CMIP climate model outputs applied as offline‐forcing for ice sheet model simulations. The critical processes for the different components are summarized in Table 1.

In this section, we integrate these components into a total high‐end SLR estimate focusing on the time slices 2100 and 2300 and the two temperature scenarios because there is a reasonable sample of studies available. The multiple lines of evidence enable us to go beyond single studies or even single multimodel experiments and provide a more complete synthesis of the plausible physical response, thereby creating estimates that are more salient to practitioners. Such an approach has been used for other seemingly intractable problems such as narrowing the range of Equilibrium Climate Sensitivity (Sherwood et al., 2020) as used in AR6.

For Greenland and Antarctica, the lines of evidence include an assessment of the physical processes. While we cannot define a precise percentile for the total high‐end SLR, our interpretation of the multiple lines of evidence as outlined in the Greenland and Antarctic Sections above, is that it lies in the tail and comprises an unlikely outcome. Circulation changes may be important for high‐end estimates but only under high forcing for Greenland, instability mechanisms and basal processes and uncertainty in timing of ice shelf collapse result in the high‐estimate for Antarctica under a high forcing. For low forcing the SMB changes control the high‐estimate for Greenland and the basal melt rate changes control the high‐estimate for Antarctica.

Since for longer time scales and higher temperature scenarios, the Antarctic ice sheet contribution dominates the uncertainty in SLR, we can essentially obtain an estimate of high‐end SLR by combining the cryospheric components and adding known contributions from thermal expansion and land water changes. Here, the thermal expansion component of SLR and its contribution to the high‐end follows directly from the thermal expansion of sea water assessed by Fox‐Kemper et al. (2021) as the resulting mean plus twice the standard deviation. The LWSC results mainly from groundwater changes and is partly induced by socio‐economic changes and partly due to climate change. In a review by Bierkens and Wada (2019), the upper end of the socio‐economic contribution is estimated to be 0.9 mm/yr, and the climate driven component is estimated to be 40 mm in 2100, independent of the scenario (Karabil et al., 2021). This is partly offset by the projections for more dams being built in the early 22nd century (Hawley et al., 2020; Zarfl et al., 2015). Recent papers argue for possible changes in precipitation (Wada et al., 2012), endorheic basin storage changes (Reager et al., 2016; Wang et al., 2018) and increased droughts (Pokhrel et al., 2021), all affecting SLR in a positive or a negative sense. As the LWSC components remains small in all cases and it is not critical for a high‐end estimate, here we simply follow (Fox‐Kemper et al., 2021).

A summary overview of the different components to SLR is shown in Table 2. Assuming perfect correlation between all contributions, the total global high‐end SLR estimate in 2100 amounts to 0.86 and 1.55 m for +2°C and +5°C, respectively. Focusing on 2300, these numbers increase considerably to 2.5 and 10.4 m, for +2°C and +8°C–10°C, respectively. Alternatively, assuming total independence of contributions, the high‐end rise is 0.72 and 1.27 m for 2100 and 2.2 and 8.6 m in 2300, for +2°C and +8°C–10°C, respectively. Hence, the assumption of independence significantly lowers the estimates; for a high scenario, the difference is around 0.3 m in 2100 and nearly 2 m in 2300.

Table 2.

The High‐End Estimates for the Different Sea Level Components, and Their Sum

		2100	2100	2300	2300
		+2°C	+5°C	+2°C	+8°C–10°C
Glaciers		0.15 a	0.27	0.28	0.32
Greenland		0.10	0.29	0.39	2.5
Antarctica		0.39	0.59	1.35	6
Thermal expansion		0.18	0.36	0.35	1.51
LWSC		0.04	0.04	0.10	0.10
Total high‐end estimate b	Upper end of the range	0.9	1.6	2.5	10
	Lower end of the range	0.7	1.3	2.2	9

^a Values are presented relative to 1995–2014 in meters. To compare to a baseline of 1986–2005 as used in AR5 and SROCC add 0.03 m for total sea level and 0.01 m for individual components.

^b The high‐end of the range follows from the assumption of perfect correlation (all covariances between the components equal to one), the low‐end of the range follows from the assumption of fully uncorrelated (all covariances between the components equal to zero).

Simply summing all high‐end components implies a perfect dependency between all the components which is unlikely, as explained above. It would for instance imply that enhanced basal melting in Antarctica is perfectly correlated to specific atmospheric conditions surrounding the Greenland ice sheet. Alternatively, less risk‐averse users could assume that all components are independent of each other, which is also not very likely. The high‐end estimates should be considered in the context of the mean and likely ranges reported by the IPCC assessments. This also implies that users who are less risk‐averse, or have the ability, to iteratively build resilience, can decide to consider the mean values for all components from an IPCC assessment and add the high‐end contribution from Antarctica and Greenland to develop a tailored, but still transparent high‐end estimate. In this way, the high‐end components and how best to sum them encourage discussion between sea level scientists and practitioners and co‐production of the most appropriate SLR scenarios for the respective needs, including the development of storylines (T. G. Shepherd & Lloyd, 2021). For a more easily accessible approach, and because both perfect correlation and full independence of all components seem unlikely based on today's understanding, practitioners might simply average the high end estimate projections in this paper between the two to derive a single, high end projection for use in planning, if that is more useful than a range.

Table 2 also indicates that the high‐end estimate for GMSL in 2100 for a significant warming of +5°C does differ from the conclusions drawn by Fox‐Kemper et al. (2021) and Oppenheimer et al. (2019), who argue that a GMSL of 2 m cannot be excluded, as supported by results from an expert elicitation process (Bamber et al., 2019). Table 3 shows the detailed differences between this study and (Fox‐Kemper et al., 2021) for Greenland and Antarctica showing lower values in this study for Greenland in 2100 for both scenarios and for Greenland and Antarctic for the 2°C scenario in 2300. A reason might be that the expert elicitation used by Fox‐Kemper et al. (2021) was influenced by DeConto and Pollard (2016) which is not used here. However, the closed nature of the expert elicitation method does not allow a firm conclusion.

In 2300, the contribution of the Antarctic ice sheet is poorly constrained, so the high‐end estimate is considerably higher than most previous estimates (Church et al., 2013; Oppenheimer et al., 2019), but not as high as (Fox‐Kemper et al., 2021). This points to the large uncertainties in projecting sea levels over multiple centuries which arises from: (a) the poorly constrained timing of the collapse of major ice shelves around Antarctica, and (b) the limited understanding of ice‐dynamical and subglacial processes. For 2100, the difference for Greenland seems to arise from the difference in structured expert judgment and our physical assessment of the literature.

All the high‐end scenarios imply a major adaptation challenge due to SLR, especially beyond 2100 (Haasnoot et al., 2020). What we present builds on a combination of model results and an assessment of different studies leading to lines of evidence per component, thereby providing practical and flexible guidance to practitioners. Further discussions between sea level scientists and practitioners facilitate the application of this knowledge most effectively. We recommend that these storylines should be updated at regular intervals (consistent to the IPCC process), reflecting the evolution of the body of knowledge. This provides a more robust update process than a whiplash response due to single new papers, which may contain high‐profile results but lack community consensus or understanding.

Table 2 indicates that the projected temperature has a large effect on the projected high‐end SLR during the 21st century and beyond. It also shows that the long timescales associated with slow processes in the ocean and ice sheets provide a strong incentive for mitigation. An SLR of 10 m by 2300 would be extremely challenging and costly, suggesting the need for a near‐universal retreat from the present coastline including the most developed and valuable areas, or alternatively, protection/advance on a scale that is hard to envisage, even where artificial protection is the norm today. For a 2°C temperature rise, a high‐end 2.5 m rise by 2300 would still present significant challenges, but with rates of SLR that are much slower, offering a wider range of adaptation options and choices. Current experience of rapidly subsiding cities (Nicholls & Tol, 2006) demonstrates that protection for such a magnitude of SLR is feasible if desired and it can be financed. Hence, both from an adaptation and mitigation perspective, smaller temperature increases are preferred.

Considering 2050, there is little difference between low and high‐temperature scenarios, as the tails of the distribution are more constrained on decadal time scales. This reflects that the major source of uncertainty—the break‐up of major ice shelves in Antarctica—is not foreseen over these time scales.

Addressing 2150 as a time horizon is desirable as many decisions extend over a century (i.e., beyond 2100), but difficult scientifically because of the uncertainty in the timing of a possible break‐up of the major Antarctica ice shelves. A first attempt is offered by Fox‐Kemper et al. (2021). We argue that there is no evidence for an early break‐up of major ice shelves combined with a major loss of grounded Antarctic ice mass influencing the high‐end estimate during the 21st century. At the same time, DeConto et al. (2021) indicate a break up of major ice shelves around 2100 or soon after for the high‐forcing scenario. The rate of mass loss which might then occur either by enhanced basal sliding or marine ice cliff and shelf instability is poorly constrained, making it extremely difficult to provide a high‐end SLR for 2150. It illustrates the high uncertainty in the acceleration of Antarctic ice mass loss. This uncertainty affects the high‐end estimate for 2300 much less than for 2150 under the high forcing scenario, as by then the major ice shelves are assumed to have broken up, and sufficient time has passed to allow for accelerated Antarctic ice mass loss. Hence, the precise timing is for this reason less critical at this time scale. For low +2°C forcing scenarios, the prevailing view (DeConto et al., 2021) is that ice shelf break up will occur in fewer regions and therefore the high‐end contribution of Antarctica will be considerably lower irrespective of the time scale.

These new high‐end estimates provide practitioners with a range of plausible, transparent, and salient high‐end sea level estimates that reflect our current physical understanding and reflect the author's views that it is not possible with the current level of understanding to match these to precise likelihoods. Further, it encourages practitioners to consider their vulnerability and adaptation options without misleading them about the level of understanding. In this way sea level scientists and practitioners can learn together about the application and co‐develop appropriate bespoke solutions. How practioners decide to use these numbers, including the low/high ranges should in our view depend on their risk‐averseness, among other factors, which they have to evaluate themselves.

We also purposely choose to define high‐end estimates for low/+2°C and high/+5°C in 2100 and +8°C–10°C in 2300 temperature increase, with respect to the pre‐industrial levels. We cannot provide a likelihood for either of these emissions‐driven warming scenarios, and moreover it is also not possible at present to define a high‐end for an intermediate emissions or temperature rise scenario (e.g., RCP4.5). While it is obvious that this will be intermediate to the values in Table 2, more detailed specification is not possible due to limited understanding of the time scales and strengths of the feedbacks of the ice components for an intermediate scenario. Essentially, we are convinced that the ice shelves will break‐up under high scenarios, but whether they will largely remain intact under lower scenarios is highly uncertain thereby making a distinction between RCP4.5 and RCP2.6/SSP1‐2.6 impossible with present levels of knowledge. In addition, there are fewer studies available for a robust high‐end estimate for RCP4.5. Irrespective of the scenario (Fox‐Kemper et al., 2021) estimate the sea level commitment associated with historical estimates to be 0.7–1.1 m up to 2300, which could probably be considered as the lower end of SLR to consider for practitioners.

8. Discussion

In this paper, we have attempted to provide physically based high‐end estimates of global SLR to 2100 and 2300 by providing specific high‐end numbers for SLR under the assumption of a +2°C and +5°C global mean temperature increase (in 2100). In particular, we aimed to provide practitioners with salient well‐supported information on low likelihood, high‐consequence cases that complement those provided by Fox‐Kemper et al. (2021). These high‐end estimates can be debated and tailored to individual risk‐averse decisions in adaptation planning and implementation, supporting more sound risk management, while adhering to a reasonable standard of practice to ensure appropriate resource allocation. In this way, planners have information available allowing them to frame high‐end risk using a standard that balances risk management objectives with finite resources, while avoiding large opportunity costs where possible.

This approach is different than that taken by Fox‐Kemper et al. (2021), in particular for projected sea level contributions from Greenland and Antarctica, and we highlight that our approach does not replace that of Fox‐Kemper et al. (2021), but instead complements it. Details of the difference are given in Table 3.

We present a range for the high‐end estimates, which is defined by the assumptions of how the different components are correlated. The choice of where in this range a user chooses to focus will depend on aspects such as their level of risk aversion and ideally will arise for any particular application through a detailed dialogue between the practitioners and sea level experts.

Hence, as an expert sea level community group we have attempted to quantify the processes controlling the sea level contribution from the different components based largely on the same evidence as used by Fox‐Kemper et al. (2021). The independent assessment of the literature presented here results in a different outcome. A key difference in the methods is that here we emphasize that the Antarctic contribution is likely to be controlled by the timing of the loss of major ice shelves around Antarctica. We attempted to follow lines of physical evidence which represent a snapshot of the current knowledge, and this will evolve as knowledge improves. As new physical insights emerge, so individual components of the analysis could be repeated by sub‐groups of experts (e.g., for Antarctica), resulting in an update of Table 3. In this way, the approach is modular and comparatively easy to update.

In this respect, the improved use of climate models including a dynamical ice sheet component will fill knowledge gaps with respect to the quantification of feedbacks which are not yet included in the modeling frameworks, and an improved understanding of correlations between different components of the climate system that contribute to global SLR. In addition, growing observational time series will also constrain the physics of the slow processes controlling ice shelf and ice sheet evolution. A strong focus on the timing of thinning and breakup of the Antarctic ice shelves is a critical aspect. At the same time, we also acknowledge that most studies fail to convincingly address the paleo sea level record and this requires further investigation, which may affect future high‐end sea level estimates.

This work was originally inspired by questions focusing on “what is a credible high‐end SLR for different timeframes?”, to aid climate risk assessment and adaptation planning. In addition, it demonstrates the large benefits of greenhouse gas mitigation for SLR over many centuries, which have only been explored in DeConto et al. (2021). Practitioners can use the high‐end estimates to “stress‐test” decisions for high‐end SLR and develop robust adaptive plans that acknowledge uncertainties about SLR and identify short‐term actions and long‐term options to adapt as necessary. While our results suggest a plausible high‐end, there are still aspects of sea level that are not well understood or which we cannot yet quantify and which might impact a future estimate of high‐end SLR, especially on timescales beyond 2100. These include processes associated with the Antarctic ice sheet that are not well understood but which have the potential to cause rapid SLR: better understanding might impact future estimates of the high‐end. Qualitatively this is consistent with the rapid expansion of high‐end SLR uncertainty identified by Fox‐Kemper et al. (2021) from 2100 to 2150, which is over a timescale of high interest to risk‐adverse practitioners. Future research on high‐end estimates in 2150 would be especially valuable, including under intermediate forcing scenarios (e.g., SSP3).

First, among these uncertainties is the rate of ice loss caused by MICI in Antarctica. The only continental‐scale model attempting to quantify the contribution of MICI to future SLR, uses constraints based on observations of calving at the termini of large marine‐terminating glaciers in Greenland. However, the geometry of some Antarctic outlet glaciers is very different to the relatively narrow, mélange‐filled fjordal settings in Greenland. For example, Thwaites Glacier in West Antarctica is about 10 times wider than Jakobshavn and drains a deep basin in the heart of West Antarctica >2 km deep in places. While MICI has not commenced at Thwaites, the ongoing loss of shelf ice and the retreat of the grounding line onto deeper bedrock could eventually produce a much taller and wider calving front than anything observed on Earth today. Hence models that include MICI in Antarctica, but limit calving rates to those observed on Greenland could be too conservative (e.g., DeConto et al., 2021) and should not be considered an upper bound on the possible SLR contribution from Antarctica. Similar uncertainties also exist for basal processes controlling the rate of mass loss once buttressing ice shelves are lost, with a large simulated range in SLR from Antarctica in response to strong imposed forcing (Sun et al., 2020).

Second, the timing when Antarctic ice shelves might be lost remains a key unknown. Shelf collapse may be caused by hydrofracturing, but this process is poorly understood. Some models assume hydrofracturing occurs if surface melt exceeds a threshold, but due to limited observations, the threshold is poorly constrained, as is the role of interannual variability in the melt, accumulation, and the detailed physics of the firn layer. For the break‐up of the Larsen B Ice Shelf in 2002, this variability was probably important, but there is insufficient data for a robust calibration. In addition, break‐up of ice shelves has been observed in response to processes triggered by ocean warming, processes which are not yet well quantified and that are omitted from all major existing models.

Third, most models are unable to capture the magnitude of SLR in previous warm periods in Earth history, suggesting that there are either processes missing or that the importance of the processes that are included are underestimated. Antarctica lost ice during these warm periods, but we do not know understand why, even not, if we use the lower estimates of Last Interglacial highstands as recently published (Dyer et al., 2021).

Because of these “Unknown Unknowns”, a flexible approach to risk and adaptation assessment is advisable recognizing the uncertainties of future SLR and realizing that major mitigation will prevent locking in a catastrophic commitment to SLR over multiple centuries. The fact that multiple lines of evidence are needed to build a salient and credible high‐end estimate also implies that the publication of a single new study should not change the approach—overreaction and a whiplash approach needs to be prevented. However, it also implies that the evidence leading to the high‐end values need to be periodically revisited at regular timescales to IPCC assessments.

Supporting information

Table S1

van de Wal, R. S. W. , Nicholls, R. J. , Behar, D. , McInnes, K. , Stammer, D. , Lowe, J. A. , et al. (2022). A high‐end estimate of sea level rise for practitioners. Earth's Future, 10, e2022EF002751. 10.1029/2022EF002751

Data Availability Statement

The data on which Table 2 is based are from Bulthuis et al. (2019), Church et al. (2013), DeConto et al. (2021), Delhasse et al. (2018, 2020), Farinotti et al. (2019), Fox‐Kemper et al. (2021), Goelzer et al. (2012, 2020), Golledge et al. (2015), Levermann et al. (2020), Marzeion et al. (2020, 2012).