Skip to main content
PMC home page
Science Advances logoLink to Science Advances
. 2022 Dec 23;8(51):eade4692. doi: 10.1126/sciadv.ade4692

Highly efficient charge transport across carbon nanobelts

Junfeng Lin 1,2,†, Shengda Wang 3,†, Fan Zhang 2, Bowen Yang 1, Pingwu Du 3, Chuanfeng Chen 2,4,*, Yaping Zang 1,2,*, Daoben Zhu 1
PMCID: PMC9788781  PMID: 36563157

Abstract

Carbon nanobelts (CNBs) are a new form of nanocarbon that has promising applications in optoelectronics due to their unique belt-shaped π-conjugated systems. Recent synthetic breakthrough has led to the access to various CNBs, but their optoelectronic properties have not been explored yet. In this work, we study the electronic transport performance of a series of CNBs by incorporating them into molecular devices using the scanning tunneling microscope break junction technique. We show that, by tuning the bridging groups between the adjacent benzenes in the CNBs, we can achieve remarkably high conductance close to 0.1 G0, nearly one order of magnitude higher than their nanoring counterpart cycloparaphenylene. Density functional theory–based calculations further elucidate the crucial role of the structural distortion played in facilitating the unique radial π-electron delocalization and charge transport across the belt-shaped carbon skeletons. These results develop a basic understanding of electronic transport properties of CNBs and lay the foundation for further exploration of CNB-based optoelectronic applications.

Carbon nanobelts can display outstanding electronic transport performance in molecular devices.

INTRODUCTION

Carbon nanobelts (CNBs), which can be broadly defined as double-stranded, belt-shaped conjugated carbon skeleton, have attracted great research interest for several decades because of their unique structures and potential applications as functional molecular materials (1–6). In particular, the unconventional radial π-conjugation along the highly strained loop of carbon makes CNBs appealing candidates toward optoelectronic applications such as single-molecule electronics, photovoltaics, and light-emitting diodes (7–9). The first armchair CNB consisting of solely fused benzene rings was first synthesized in 2017 and extended in 2018 (9, 10), and later, two types of all-benzene CNBs with chiral and zigzag structures have been reported (11–13). Recently, the family of CNBs is further expanded by the synthesis of new forms of CNBs containing nonhexagonal rings (14–18), heteroatom dopants (15, 17, 19–22), and complex topologies (23, 24). These breakthroughs inspire intensive experimental and theoretical explorations of fundamental physical properties associated with the unique belt-shaped structures of CNBs (25–28). Notably, the radial π-electron delocalization along the highly distorted carbon backbone of CNBs enhances their π-conjugation and leads to a small energy gap between their highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) , which demonstrates their potential applications in optoelectronics (1). Despite this progress, charge transport, a basic process governing the optoelectronic applications of CNBs, has not been explored yet, partly because of the limited availability of CNB compounds.

In this work, we explore the charge transport properties of a series of CNBs at the molecular level using the scanning tunneling microscope break junction (STM-BJ) technique (Fig. 1). By taking advantage of the unique radially oriented π-orbitals of CNBs, we can create well-defined single Au-CNB-Au junctions by directly connecting the belt-shaped π-surface to the Au electrodes (29). We find that the armchair (6,6)CNB consisting of fully fused benzenes has a high conductance similar to their ring-shaped skeleton cycloparaphenylene [6]CPP. In contrast, the pentagon-embedded nanobelts containing the same [6]CPP skeleton bridged by methylene ([6]CNB_M6) or nitrogen ([6]CNB_N3) show much improved charge transport efficiency, and their conductance is increased by nearly one order of magnitude and reaches ~10−1 G0 (G0 is conductance quantum). Density functional theory (DFT)–based calculations further elucidate the crucial role of the structural distortion played in facilitating the radial π-conjugation and charge transport in the CNB series. These intriguing electronic transport characteristics demonstrate the potential of CNBs as high-performance electronic materials and provide insights for designing belt-shaped molecular nanocarbons.

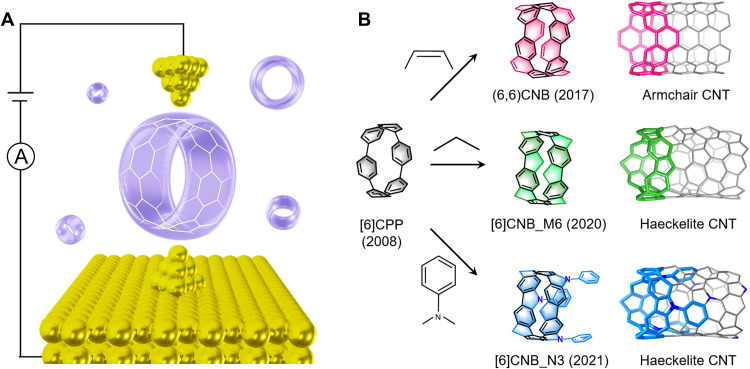
Fig. 1. Schematics of STM-BJ measurements of CNBs.

Fig. 1.

Open in a new tab

(A) Schematic of single-CNB junction. (B) Structures of [6]CPP, the three types of CNBs fused by different bridging groups and the corresponding CNTs.

RESULTS

We focus our study on three types of CNBs containing the same [6]CPP skeleton bridged by ethenylene [(6,6)CNB], methylene ([6]CNB_M6), or nitrogen ([6]CNB_N3) groups. The ethenylene-bridged (6,6)CNB is considered as the basic segment of armchair-type carbon nanotube (CNT) and is obtained from commercial resource (Tokyo Chemical Industry). The [6]CNB_M6 and [6]CNB_N3 containing the pentagon ring represent the segment structures of unconventional Haeckelite CNTs and are synthesized according to previously reported procedures (fig. S1) (14, 15). All molecules are dissolved into 1-chloronaphthalene solvent with a concentration of ~0.1 mM for the STM-BJ measurement in ambient conditions and room temperature. The STM-BJ technique is detailed in previous papers (30). Briefly, we push and pull an Au STM tip to form and break the contact with an Au substrate in the solution of target molecules under an applied tip bias. After breaking the atomic Au-Au contact, the molecule can bridge the STM tip and substrate and form single-molecule junctions. During this process, we record the conductance distributions against tip-substrate displacements and obtain individual conductance-displacement traces, where a plateau with a conductance lower than conductance quantum G0 (where G0 = 2e2/h) signifies the formation of single-molecule junctions (Fig. 2A).

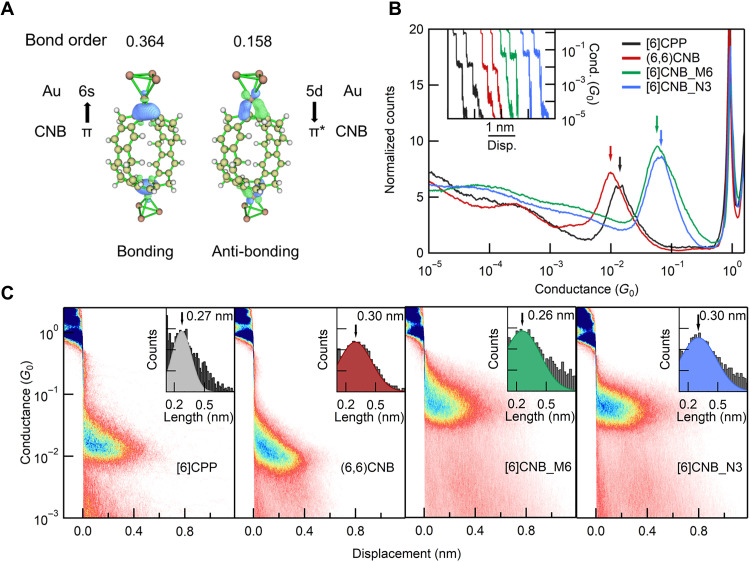
Fig. 2. STM-BJ measurement results of [6]CPP and CNBs.

Fig. 2.

Open in a new tab

(A) NAdO analysis (47) for the bond between CNBs and Au clusters calculated using the Multiwfn package (48). (B) One-dimensional (1D) conductance histograms of [6]CPP and three types of CNBs measured under an applied tip bias voltage of 0.1 V. Inset: Sample conductance traces of [6]CPP and CNBs. (C) 2D conductance histograms of [6]CPP and CNBs. Inset: The relative length distributions.

At a tip bias of 100 mV, we observe clear molecular conductance plateaus for all the three CNBs (Fig. 2), and this indicates the formation of stable single-CNB molecule junctions. Since there is no typical heteroatom anchor in the CNBs, we hypothesize that the junctions are formed through directly binding the distorted phenylene units to Au atoms via Au-π bonds. More specifically, the Au electrode binds to the C-C bond within the phenylene unit via electron donation from the filled molecular π-orbital to the 6s orbital of Au atom and back-donation from the filled 5d orbital of Au atom to the empty molecular π*-orbital. Natural adaptive orbital (NAdO) analysis further reveals the electron donation and back-donation channels contributing to the binding between CNBs and Au electrodes (Fig. 2A). Note that the formation of these Au-π bonding contacts is facilitated by the unique structural distortions presented in the belt-shaped carbon skeletons. Similar electrode-molecule bindings are also observed for other distorted π-conjugated systems such as CPPs (29), fullerene (C60) (31–33), and π-π stacked benzenes (34).

As can be seen from the one-dimensional (1D) conductance histograms compiled from thousands of the conductance traces, the armchair (6,6)CNB has a conductance of ~10−2 G0, which is slightly lower than their nanoring counterpart [6]CPP (29). In sharp contrast, the other two CNB molecules [6]CNB_M6 and [6]CNB_N3 with pentagon ring–embedded structures show a significantly higher conductance reaching close to ~10−1 G0, indicating their highly efficient charge transport characteristics. In the corresponding 2D histograms, we note that these CNB molecules have a similar conductance plateau length of ~0.3 nm (Fig. 2C), indicating a junction length of ~1.3 nm by accounting for the Au snapback length of ~1 nm in 1-chloronaphthalene solvent. These experimental junction lengths are in good agreement with theoretical predictions (see the Supplementary Materials for the detailed discussions), which demonstrates that we measure the conductance across the CNB backbone anchored to the Au electrodes through direct Au-π bonds. Notably, although every phenylene unit in these molecules can, in principle, provide multiple Au-π binding sites, we still can obtain well-defined junction configurations and observe narrow conductance peaks due to the relatively large Au snapback distance in 1-chloronaphthalene solvent (see fig. S2 for more detailed discussions). The larger Au snapback in 1-chloronaphthalene solvent than that in 1,2,4-trichlorobenzene (TCB) is also responsible for the observed narrower conductance peak of [6]CPP in 1-chloronaphthalene than in TCB.

DISCUSSION

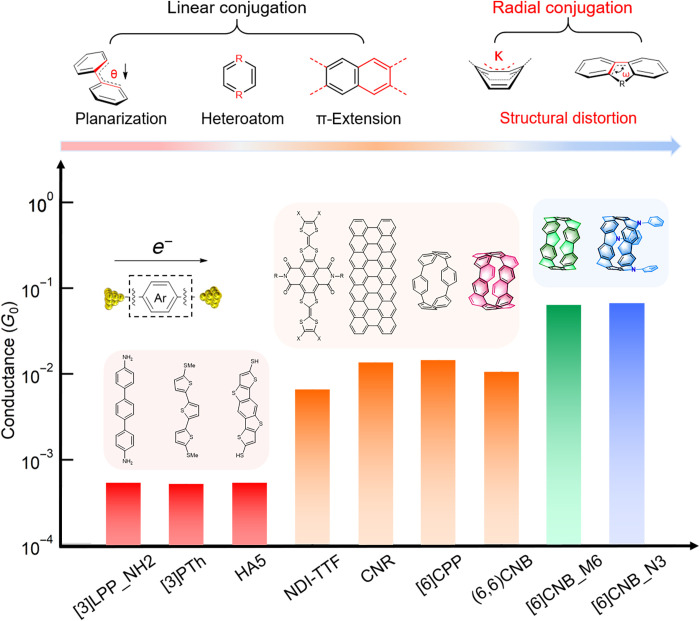
Note that the conductance of these CNBs is much higher than the typical linearly conjugated molecular wires. To understand this property, we first point out the basic structure-property relationships of single-molecule devices. It is well established that conjugated molecules with delocalized π-orbitals are favorable for conducting electrons (Fig. 3). This motivates constructing linearly conjugated molecular conducting wires such as linear oligo-phenylenes (LPPs) (35–37). Typically, planar molecular wires with extended aromatic structures or heteroatom substitutions exhibit enhanced π-conjugation and a small HOMO-LUMO gap, which generally leads to improved charge transport (38). On the basis of these principles, in recent years, various rigid fused conjugated wires have been designed to enhance molecular π-orbital delocalization and conductance. Notably, except the intrinsic electronic structure of molecular wires, the electrode-molecule coupling also largely influences the charge transport efficiency (39). Directly anchoring the molecular conducting π-channels to electrodes can promote electrode-molecule coupling and increase the conductance of single-molecule devices (38, 40).

Fig. 3. Conductance comparisons for the typical linearly conjugated molecular wires and CNBs.

Fig. 3.

Open in a new tab

(Top) Typical design strategy for enhancing charge transport of conjugated molecules.

Beyond the linearly conjugated molecular systems, radially conjugated carbon nanoring CPPs have been recently demonstrated as candidates for building highly conductive single-molecule devices (29). It has been shown that the small CPP rings exhibit a much higher conductance than their linear oligoparaphenylene counterparts due to the ring strain–induced distortions of π-orbitals. Here, we explore the charge transport properties of CNB, which is a member of the radially conjugated nanocarbon family and contains the CPP-building block with adjacent phenylene units fused by additional bridging groups. We show that compared with CPPs, the CNBs have a much improved charge transport efficiency, and their conductance reaches close to 10−1 G0, demonstrating their great potential as outstanding electronic components.

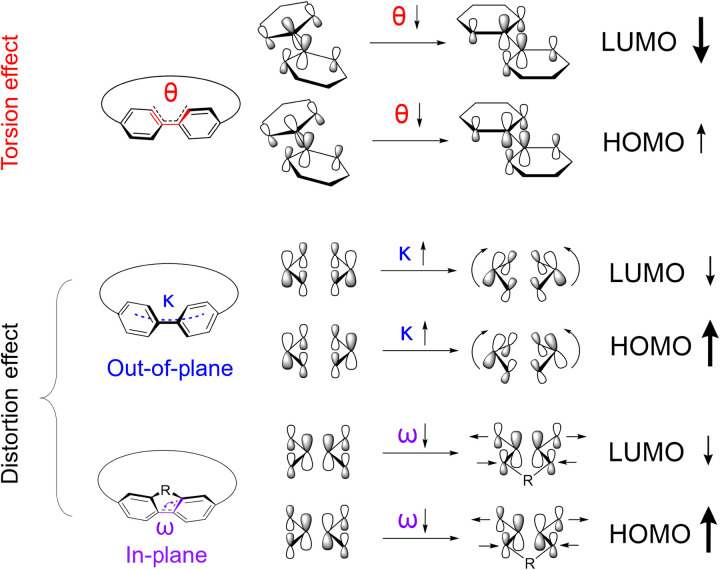
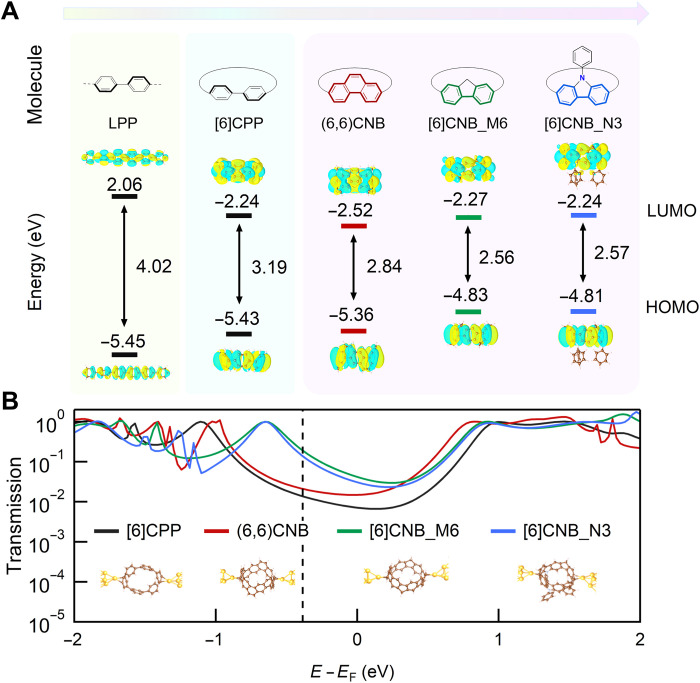
We hypothesize that the remarkably high conductance of the CNBs arises from their unique fused and highly strained radially conjugated structures. To better understand the structural effect, we first point out that converting a linear oligoparaphenylene wire into a cyclic system generates structural strain that reduces the torsion between neighboring phenylenes but increases the distortion of each phenylene unit (41). As illustrated in Fig. 4, the torsion effect generally decreases the LUMO energy by promoting the interring orbital overlapping, while the distortion effect increases the HOMO energy, which leads to the overall decrease of the HOMO-LUMO gap (42).

Fig. 4. Schematics of torsion and distortion effects on orbital interactions in CNBs.

Fig. 4.

Open in a new tab

To gain more quantitative understanding of these effects, we turn to DFT-based calculations to obtain the optimized molecular structures and orbitals (see the Supplementary Materials for detailed information). As shown in Table 1, the nanoring [6]CPP has a smaller torsion angle θ (27.4°) compared with that of the linear hexaparaphenylene wire [6]LPP (36.2°). Moreover, the [6]CPP shows increased out-of-plane bending with an average curvature κ of 0.248 Å−1. Because of these torsion and bending effects, [6]CPP displays a narrower HOMO-LUMO gap than its linear counterpart [6]LPP. Moreover, the bending effect leads to increased metal affinity of the outer π-surface of the phenylenes, thereby promoting the electrode-molecule binding through forming direct Au-π bonds. These bonding contacts are known for promoting orbital hybridization of electrodes and the molecular conducting π-channel, which are desired for achieving efficient charge transport properties (29).

Table 1. Averaged torsion angle [θ (°)], curvature [κ (Å−1)], and distortion angle [ω (°)] for [6]LPP, [6]CPP, and CNBs (optimized at B3LYP/6-31G* level).

Molecule [6]LPP [6]CPP (6,6)CNB [6]CNB_M6 [6]CNB_N3
θ (°) 41.6 27.4 0.005 0.03 0.8
κ (Å−1)* 0 0.248 0.248 0.258 0.259
ω (°) 121.1 120.0 117.9 107.8 107.1
Open in a new tab

*Diameters for calculation were taken from references (9, 14–15, 49).

Compared with [6]CPP, the CNBs with fused structures show almost eliminated interphenylene torsions and much larger strain-induced structural distortions. These structural features enable CNBs to have even smaller HOMO-LUMO gaps. Note that the structural distortion of CNBs can be further tuned by manipulating the bridging groups. For instance, the methyl- and nitrogen-fused nanobelt [6]CNB_M6 and [6]CNB_N3 feature more distorted conformations due to their higher structural strain induced by the embedding of pentagon units. These highly strained structures lead to the further increases of the HOMO energy. In contrast, the all-benzene (6,6)CNB has extended aromatic structure that stabilizes its frontier orbitals and decreases its HOMO and LUMO energy simultaneously, leading to a slightly larger HOMO-LUMO gap than the pentagon-embedded [6]CNB_M6 and [6]CNB_N3. It should be further noted that, in these CNBs, the electronic effect of the bridge atom itself, which has previously been widely used to tune the molecular electronic structure, does not exert obvious influence on the frontier electronic orbitals. These elucidate that structural distortion in these CNBs has a dominant impact on their electronic structures.

To better relate the electronic structures of CNBs to their transport properties, we model the CNB junctions and calculate their energy-dependent electron transmissions using Fritz Haber Institute ab initio molecular simulation (FHI-aims) with a Perdew-Burke-Ernzerhof (PBE) exchange-correlation functional (43–45). As shown in Fig. 5B and fig. S3, the optimized CNB junctions are formed through Au-π bonding in η2 fashion, which agrees with previous analysis based on orbital symmetry (29). Binding energy calculations further reveal that, compared with [6]CPP and pentagon-embedded CNBs, (6,6)CNB offers more possible electrode-molecule binding sites due to its extended π-conjugated structures (see figs. S4 to S5). Moreover, in contrast to conventional linear LPP junctions (fig. S6), the Au-π bonding in CPP and CNB junctions facilitates orbital hybridization of gold electrodes and the radially delocalized π-channels, thus yielding strong interfacial electronic coupling that is reflected by the significant peak spread of HOMO and LUMO resonances shown in the calculated transmission spectra. Moreover, the energy separation between HOMO and LUMO resonances of [6]CNB_M6 and [6]CNB_N3 is much smaller than that of (6,6)CNB and [6]CPP, which is due to the larger distortion effect in [6]CNB_M6 and [6]CNB_N3 as explained above. Since the HOMO and LUMO resonance positions are not accurately captured because of the errors inherent to DFT, we focus here on the qualitative trends at the shifted Fermi energy (dashed line). We see that the larger structural distortion of [6]CNB_M6 and [6]CNB_N3 leads to a smaller alignment of their HOMO resonances relative to the Fermi energy (EF), which gives rise to much higher transmission levels at EF and hence explains their higher conductance observed in experiments. For (6,6)CNB, the increased electrode-molecule binding sites yield more possible junction configurations with distinct conductance (see fig. S4). Statistical averaging of these junctions enables (6,6)CNB a slightly lower conductance than [6]CPP. Moreover, in contrast to [6]CPP (29), the shift in binding sites of the pentagon-embedded CNB leads to less obvious transmission changes (fig. S7), which is due to its fused, belt-shaped conjugated structures. Together, the structural distortion caused by the unique belt-shaped geometry of CNBs leads to a strong electrode-molecule electronic coupling and a small alignment of HOMO with respect to the EF, which are translated to the outstanding high conductance in the CNB junctions.

Fig. 5. Calculated frontier orbitals and transmission functions.

Fig. 5.

Open in a new tab

(A) Isosurface plots (contour value = 0.02) and energy of the frontier molecular orbitals of [6]LPP, [6]CPP, (6,6)CNB, [6]CNB_M6, and [6]CNB_N3. (B) Calculated transmission functions of [6]CPP, (6,6)CNB, [6]CNB_M6, and [6]CNB_N3. Inset: Junction geometries used for computing the transmissions.

In conclusion, we have studied the charge transport properties of CNBs using the STM-BJ technique. We find that, the single pentagon-embedded CNBs fused by methylene or nitrogen groups have remarkably high conductance close to 10−1 G0, nearly one order of magnitude higher than the standard armchair CNB composed of solely phenylenes and the nanoring analog CPP. Further structural analysis combined with DFT calculations elucidated the dominant role of structural distortion in CNBs played in tuning their electronic structures and promoting their charge transport. These results demonstrate that CNBs are appealing candidates for electronic applications and will motivate future design of optoelectronic materials capitalizing on structural distortion control of unconventional conjugated molecular systems.

MATERIALS AND METHODS

STM-BJ measurements

Single-molecule conductance measurements were carried out in ambient conditions and room temperature using a custom-built STM-BJ platform. Dilute solutions (~0.1 mM) of the molecules in 1-chloronaphthalene solvent were used for conductance measurements. The gold electrodes used in STM-BJ measurements were a gold tip created by mechanical cutting and a substrate coated with gold layer. During the process where the Au tip repeatedly pushed and pulled to contact with the substrate deposited with diluted solutions, single Au atom contact is broken to form and break Au-CNB-Au junctions under an applied bias of 100 mV. During each push-pull process, the current was recorded continuously to construct a conductance versus displacement trace. By compiling thousands of collected conductance traces (>3000 traces) without any data selection, 1D conductance histograms and 2D conductance-displacement histograms were constructed.

Theoretical methods

NAdO analysis

Gaussian 16 program (46) is used for the calculation. The optimization for CNB junction is carried out using a junction model consisting of a [6]CNB_M6 molecule attached to two Au clusters containing four Au atoms (the length of Au-Au bond is constrained to 2.88 Å) at the B3LYP/6-31G* level for carbon and hydrogen atoms and B3LYP/SDD level for Au atoms. After geometry optimization, the NAdO analysis is carried out using Multiwfn package.

Transmission calculation

The geometry optimization for single molecule is carried out at the B3LYP level implemented by the FHI-aims packages. For transmission calculation, we attach two Au clusters containing four Au atoms to the two sides for the all-optimized CNB structures and relax the junction geometries using the PBE exchange-correlation functional implemented by the FHI-aims packages at all-electron numeric atom-centered basis set level. After relaxation, the four-atom Au clusters are replaced by Au pyramids containing 60 Au atoms in six layers. In addition, the Landauer transmission across these junctions is calculated using the nonequilibrium Green’s function formalism.

Acknowledgments

Funding: We acknowledge financial support from the National Natural Science Foundation of China (22073109, 92161122, and 22225108) and Chinese Academy of Sciences (XDPB13).

Author contributions: Y.Z. conceived the idea and designed the project. J.L. and B.Y. carried out the STM-BJ measurements and data analysis. J.L. performed DFT calculations. S.W. and F.Z. synthesized the compounds under the guidance of P.D. and C.C. D.Z. commented on the data. The manuscript was written by Y.Z. and J.L. with contributions from all other authors.

Competing interests: The authors declare that they have no competing interests.

Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials.

Supplementary Materials

This PDF file includes:

Supplementary Text

Figs. S1 to S7

Table S1

Click here for additional data file. (694.7KB, pdf)

REFERENCES AND NOTES

  • 1.Y. Li, H. Kono, T. Maekawa, Y. Segawa, A. Yagi, K. Itami,Chemical synthesis of carbon nanorings and nanobelts. Acc. Mater. Res. 2,681–691 (2021). [Google Scholar]
  • 2.Y. Segawa, A. Yagi, H. Ito, K. Itami,A theoretical study on the strain energy of carbon nanobelts. Org. Lett. 18,1430–1433 (2016). [DOI] [PubMed] [Google Scholar]
  • 3.M. Hermann, D. Wassy, B. Esser,Conjugated nanohoops incorporating donor, acceptor, hetero- or polycyclic aromatics. Angew. Chem. Int. Ed. 60,15743–15766 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.B. Esser, F. Rominger, R. Gleiter,Synthesis of [6.8]3cyclacene: Conjugated belt and model for an unusual type of carbon nanotube. J. Am. Chem. Soc. 130,6716–6717 (2008). [DOI] [PubMed] [Google Scholar]
  • 5.H. Chen, Q. Miao,Recent advances and attempts in synthesis of conjugated nanobelts. J. Phys. Org. Chem. 33,e4145 (2020). [Google Scholar]
  • 6.Y. Segawa, D. R. Levine, K. Itami,Topologically unique molecular nanocarbons. Acc. Chem. Res. 52,2760–2767 (2019). [DOI] [PubMed] [Google Scholar]
  • 7.L. O. Jones, M. A. Mosquera, G. C. Schatz, M. A. Ratner,Charge transport and thermoelectric properties of carbon sulfide nanobelts in single-molecule sensors. Chem. Mater. 31,6506–6518 (2019). [Google Scholar]
  • 8.G. Aydın, O. Koçak, C. Güleryüz, I. Yavuz,Structural order and charge transfer in highly strained carbon nanobelts. New J. Chem. 44,15769–15775 (2020). [Google Scholar]
  • 9.G. Povie, Y. Segawa, T. Nishihara, Y. Miyauchi, K. Itami,Synthesis of a carbon nanobelt. Science 356,172–175 (2017). [DOI] [PubMed] [Google Scholar]
  • 10.G. Povie, Y. Segawa, T. Nishihara, Y. Miyauchi, K. Itami,Synthesis and size-dependent properties of [12], [16], and [24]carbon nanobelts. J. Am. Chem. Soc. 140,10054–10059 (2018). [DOI] [PubMed] [Google Scholar]
  • 11.K. Y. Cheung, S. Gui, C. Deng, H. Liang, Z. Xia, Z. Liu, L. Chi, Q. Miao,Synthesis of armchair and chiral carbon nanobelts. Chem 5,838–847 (2019). [Google Scholar]
  • 12.Y. Han, S. Dong, J. Shao, W. Fan, C. Chi,Synthesis of a sidewall fragment of a (12,0) carbon nanotube. Angew. Chem. Int. Ed. 60,2658–2662 (2021). [DOI] [PubMed] [Google Scholar]
  • 13.K. Y. Cheung, K. Watanabe, Y. Segawa, K. Itami,Synthesis of a zigzag carbon nanobelt. Nat. Chem. 13,255–259 (2021). [DOI] [PubMed] [Google Scholar]
  • 14.Y. Li, Y. Segawa, A. Yagi, K. A. Itami,A nonalternant aromatic belt: Methylene-bridged [6]cycloparaphenylene synthesized from pillar[6]arene. J. Am. Chem. Soc. 142,12850–12856 (2020). [DOI] [PubMed] [Google Scholar]
  • 15.F. Zhang, X. Du, D. Zhang, Y. Wang, H. Lu, C. Chen,A green fluorescent nitrogen-doped aromatic belt containing a [6]cycloparaphenylene skeleton. Angew. Chem. Int. Ed. 60,15291–15295 (2021). [DOI] [PubMed] [Google Scholar]
  • 16.X. Du, D. Zhang, Y. Guo, J. Li, Y. Han, C. Chen,Towards the highly efficient synthesis and selective methylation of C(sp3)-bridged [6]cycloparaphenylenes from fluoren[3]arenes. Angew. Chem. Int. Ed. 60,13021–13028 (2021). [DOI] [PubMed] [Google Scholar]
  • 17.J. Zhu, Y. Han, Y. Ni, G. Li, J. Wu,Facile synthesis of nitrogen-doped [(6.)m8]ncyclacene carbon nanobelts by a one-pot self-condensation reaction. J. Am. Chem. Soc. 143,2716–2721 (2021). [DOI] [PubMed] [Google Scholar]
  • 18.T. Shi, Q. Guo, S. Tong, M. Wang,Toward the synthesis of a highly strained hydrocarbon belt. J. Am. Chem. Soc. 142,4576–4580 (2020). [DOI] [PubMed] [Google Scholar]
  • 19.J. Nogami, Y. Nagashima, K. Miyamoto, A. Muranaka, M. Uchiyama, K. Tanaka,Asymmetric synthesis, structures, and chiroptical properties of helical cycloparaphenylenes. Chem. Sci. 12,7858–7865 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.S. Wang, J. Yuan, J. Xie, Z. Lu, L. Jiang, Y. Mu, Y. Huo, Y. Tsuchido, K. Zhu,Sulphur-embedded hydrocarbon belts: Synthesis, structure and redox chemistry of cyclothianthrenes. Angew. Chem. Int. Ed. 60,18443–18447 (2021). [DOI] [PubMed] [Google Scholar]
  • 21.S. Xue, D. Kuzuhara, N. Aratani, H. Yamada,Synthesis of a porphyrin(2.1.2.1) nanobelt and its ability to bind fullerene. Org. Lett. 21,2069–2072 (2019). [DOI] [PubMed] [Google Scholar]
  • 22.Y. Zhang, S. Tong, M. X. Wang,Synthesis and structure of functionalized zigzag hydrocarbon belts. Angew. Chem. Int. Ed. 59,18151–18155 (2020). [DOI] [PubMed] [Google Scholar]
  • 23.W. Fan, T. Matsuno, Y. Han, X. Wang, Q. Zhou, H. Isobe, J. Wu,Synthesis and chiral resolution of twisted carbon nanobelts. J. Am. Chem. Soc. 143,15924–15929 (2021). [DOI] [PubMed] [Google Scholar]
  • 24.Y. Segawa, T. Watanabe, K. Yamanoue, M. Kuwayama, K. Watanabe, J. Pirillo, Y. Hijikata, K. Itami,Synthesis of a Möbius carbon nanobelt. Nat. Synth. 1,535–541 (2022). [Google Scholar]
  • 25.V. Freixas, N. Oldani, R. Franklin-Mergarejo, S. Tretiak, S. Fernandez-Alberti,Electronic energy relaxation in a photoexcited fully fused edge-sharing carbon nanobelt. J. Phys. Chem. Lett. 11,4711–4719 (2020). [DOI] [PubMed] [Google Scholar]
  • 26.R. Kishi, M. Yamane, R. Sugiura, W. Yoshida, Y. Shimizu, M. Nakano,Theoretical study on aromatic and open-shell characteristics of carbon nanobelts composed of indeno[1,2-b]fluorene units: Dependence on the number of units and charge states. RSC Adv. 10,25736–25745 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.A. Pérez-Jiménez, J. Sancho-García,Theoretical insights for materials properties of cyclic organic nanorings. Adv. Theory Simul. 3,2000110 (2020). [Google Scholar]
  • 28.S. Seenithurai, J. Chai,Electronic properties of carbon nanobelts predicted by thermally-assisted-occupation DFT. Nanomater. 11,2224 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Y. Lv, J. Lin, K. Song, X. Song, H. Zang, Y. Zang, D. Zhu,Single cycloparaphenylene molecule devices: Achieving large conductance modulation via tuning radial π-conjugation. Sci. Adv. 7,eabk3095 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.L. Venkataraman, J. Klare, I. Tam, C. Nuckolls, M. Hybertsen, M. Steigerwald,Single-molecule circuits with well-defined molecular conductance. Nano Lett. 3,458–462 (2006). [DOI] [PubMed] [Google Scholar]
  • 31.C. Martin, D. Ding, J. Sørensen, T. Bjørnholm, J. Ruitenbeek, H. van der Zant,Fullerene-based anchoring groups for molecular electronics. J. Am. Chem. Soc. 130,13198–13199 (2008). [DOI] [PubMed] [Google Scholar]
  • 32.S. Fujii, H. Cho, Y. Hashikawa, T. Nishino, Y. Murata, M. Kiguchi,Tuneable single-molecule electronic conductance of C60 by encapsulation. Phys. Chem. Chem. Phys. 21,12606–12610 (2019). [DOI] [PubMed] [Google Scholar]
  • 33.C. Evangeli, K. Gillemot, E. Leary, M. T. Gonzalez, G. Rubio-Bollinger, C. J. Lambert, N. Agrait,Engineering the thermopower of C60 molecular junctions. Nano Lett. 13,2141–2145 (2013). [DOI] [PubMed] [Google Scholar]
  • 34.S. Schneebeli, M. Kamenetska, Z. Cheng, R. Skouta, R. Friesner, L. Venkataraman, R. Breslow,Single-molecule conductance through multiple π-π-stacked benzene rings determined with direct electrode-to-benzene ring connections. J. Am. Chem. Soc. 133,2136–2139 (2011). [DOI] [PubMed] [Google Scholar]
  • 35.Y. Zang, A. Pinkard, Z. Liu, J. Neaton, M. Steigerwald, X. Roy, L. Venkataraman,Electronically transparent Au−N bonds for molecular junctions. J. Am. Chem. Soc. 139,14845–14848 (2017). [DOI] [PubMed] [Google Scholar]
  • 36.B. Capozzi, E. Dell, T. Berkelbach, D. Reichman, L. Venkataraman, L. Campos,Length-dependent conductance of oligothiophenes. J. Am. Chem. Soc. 136,10486–10492 (2014). [DOI] [PubMed] [Google Scholar]
  • 37.Z. Cai, W. Lo, T. Zheng, L. Li, N. Zhang, Y. Hu, L. Yu,Exceptional single-molecule transport properties of ladder-type heteroacene molecular wires. J. Am. Chem. Soc. 138,10630–10635 (2016). [DOI] [PubMed] [Google Scholar]
  • 38.M. Koch, F. Ample, C. Joachim, L. Grill,Voltage-dependent conductance of a single graphene nanoribbon. Nat. Nanotechnol. 7,713–717 (2012). [DOI] [PubMed] [Google Scholar]
  • 39.T. Su, M. Neupane, M. Steigerwald, L. Venkataraman, C. Nuckolls,Chemical principles of single-molecule electronics. Nat. Rev. Mater. 1,1–15 (2016). [Google Scholar]
  • 40.Q. Zhou, K. Song, G. Zhang, X. Song, J. Lin, Y. Zang, D. Zhang, D. Zhu,Tetrathiafulvalenes as anchors for building highly conductive and mechanically tunable molecular junctions. Nat. Commun. 13,1803 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 41.Y. Segawa, A. Fukazawa, S. Matsuura, H. Omachi, S. Yamaguchi, S. Irle, K. Itami,Combined experimental and theoretical studies on the photophysical properties of cycloparaphenylenes. Org. Biomol. Chem. 10,5979–5984 (2012). [DOI] [PubMed] [Google Scholar]
  • 42.A. Narsaria, J. Poater, C. Fonseca Guerra, A. Ehlers, T. Hamlin, K. Lammertsma, F. Bickelhaupt,Distortion-controlled redshift of organic dye molecules. Chem 26,2080–2093 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 43.V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter, M. Scheffler,Ab initio molecular simulations with numeric atom-centered orbitals. Comput. Phys. Commun. 180,2175–2196 (2009). [Google Scholar]
  • 44.J. Perdew, K. Burke, M. Ernzerhof,Generalized gradient approximation made simple. Phys. Rev. Lett. 77,3865–3868 (1996). [DOI] [PubMed] [Google Scholar]
  • 45.V. Havu, V. Blum, P. Havu, M. Scheffler,Efficient O(N) integration for all-electron electronic structure calculation using numeric basis functions. J. Comput. Phys. 228,8367–8379 (2009). [Google Scholar]
  • 46.M. Frisch, G. Trucks, H. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, G. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. Janesko, R. Gomperts, B. Mennucci, H. Hratchian, J. Ortiz, A. Izmaylov, J. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. Montgomery Jr., J. Peralta, F. Ogliaro, M. Bearpark, J. Heyd, E. Brothers, K. Kudin, V. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. Burant, S. Iyengar, J. Tomasi, M. Cossi, J. Millam, M. Klene, C. Adamo, R. Cammi, J. Ochterski, R. Martin, K. Morokuma, O. Farkas, J. Foresman, D. Fox, Gaussian 16, Revision C.01 (Gaussian, 2016). [Google Scholar]
  • 47.J. Casals-Sainz, A. Fernandez-Alarcon, E. Francisco, A. Costales, A. Martin Pendas,Bond order densities in real space. J. Phys. Chem. A 124,339–352 (2020). [DOI] [PubMed] [Google Scholar]
  • 48.T. Lu, F. Chen,Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 33,580–592 (2012). [DOI] [PubMed] [Google Scholar]
  • 49.J. Xia, R. Jasti,Synthesis, characterization, and crystal structure of [6]cycloparaphenylene. Angew. Chem. Int. Ed. 51,2474–2476 (2012). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Text

Figs. S1 to S7

Table S1

Click here for additional data file. (694.7KB, pdf)

Articles from Science Advances are provided here courtesy of American Association for the Advancement of Science

RESOURCES