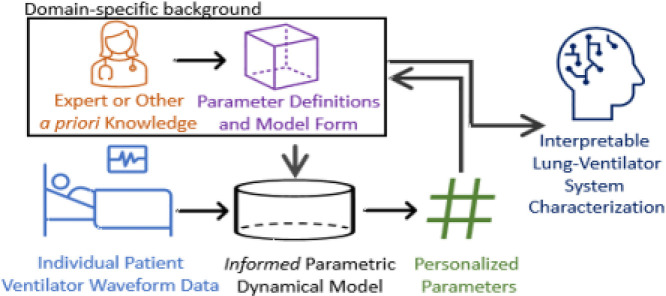
Abstract
Mechanical ventilation is an essential tool in the management of Acute Respiratory Distress Syndrome (ARDS), but it exposes patients to the risk of ventilator-induced lung injury (VILI). The human lung–ventilator system (LVS) involves the interaction of complex anatomy with a mechanical apparatus, which limits the ability of process-based models to provide individualized clinical support. This work proposes a hypothesis-driven strategy for LVS modeling in which robust personalization is achieved using a pre-defined parameter basis in a non-physiological model. Model inversion, here via windowed data assimilation, forges observed waveforms into interpretable parameter values that characterize the data rather than quantifying physiological processes. Accurate, model-based inference on human–ventilator data indicates model flexibility and utility over a variety of breath types, including those from dyssynchronous LVSs. Estimated parameters generate static characterizations of the data that are 50%–70% more accurate than breath-wise single-compartment model estimates. They also retain sufficient information to distinguish between the types of breath they represent. However, the fidelity and interpretability of model characterizations are tied to parameter definitions and model resolution. These additional factors must be considered in conjunction with the objectives of specific applications, such as identifying and tracking the development of human VILI.
Keywords: Biomedical informatics, Parameter estimation, Data assimilation, Health information management, Mathematical model, Kalman filters
Graphical abstract
1. Introduction
Hospitalized patients often undergo assisted ventilation, either due to the inability to breathe on their own or because care providers determine they should not do so. In such cases, respiration is supported by a programmable mechanical ventilator that actively supplies air to the lungs. Proper ventilator management is a particular concern in patients presenting acute respiratory distress syndrome (ARDS), a life-threatening condition associated with mortality in 3%–4% of intensive care unit (ICU) admissions [1], [2] and nearly 60% of ventilated COVID-19 patients under intensive care [3]. Mismatches in timing, breath-trigger threshold, or pressure/volume budget evince dyssynchronous interaction between patient and machine, which may contribute to problems such as edema and hypoxia [4]. Further, ventilator dyssynchrony may cause parenchymal damage termed ventilator-induced lung injury (VILI) and may exacerbate the effects of ARDS. Clinical management requires carefully specified thresholds and target quantities to provide necessary and sufficient respiration [5] while avoiding VILI, a major risk for assisted patients [6]. The prevalence of these cases strongly motivates additional lung-protective considerations [7], [8], [9], [10] to improve ventilated patient outcome.
Respiratory management would benefit from an improved understanding of the lung in the context of the clinical environment where VILI occurs, including interaction with the ventilator. Many investigations use controlled ventilation to probe lung properties ([11], [12], [13], [14], [15] as well as [16] and references therein). Compartment-based models, described in the following subsection, estimate the relationship between observed pressure () and volume () in terms of lung compliance and resistance. However, the signals primarily originate in the ventilator and are observed outside the patient to reflect the bulk effect of the lung system. Consequently, existing models try to infer lung-specific parameters governing lung dynamics from data that aggregate effects of respiratory, systemic, and healthcare processes.
A lung–ventilator system (LVS) comprises the interaction of the pulmonary system and breathing support. These produce a variety of dynamics observable in pressure and volume waveforms that are of primary focus in the study of VILI and ventilator dyssynchrony [17], [18], [19]. Simulating these behaviors in process-oriented models requires a high degree of either complexity or parameterization to account for dynamic heterogeneity in patients and respiratory therapies. Methods for identifying, classifying, and preventing dyssynchrony in timing and delivery of breath support are nascent applications in clinical informatics.
This work focuses on a hybrid model-based method for transforming LVS data into discrete parametric vectors that retain features of interest. The approach is intended for informatics applications that require description of the LVS rather than material lung properties, where further analysis demands the context of health care process information such as ventilator settings. Such a tool would benefit the scientific inquiry of VILI by facilitating data representation in algorithms capable of detangling the effects of ventilator settings from changes in the lung response. The following subsection revisits the existing method of LVS estimation to motivate the proposed approach which is oriented toward operational LVS representation and clinical translation.
1.1. The dynamic single-compartment model: framework and limitations
The single-compartment model [20] describes a stationary relationship in the respiratory tract by the equation
| (1) |
with parameters (possibly defined as nonlinear functions) for resistance () and elastance (). In practice, is the pressure with respect to a zero-volume reference; the system requires a baseline pressure parameter (viz. positive end-expiratory pressure, or PEEP) for the relationship to hold for arbitrary initial times.
This model is a fast and efficient means of estimating physiological lung properties from the relationship. However, it requires higher-fidelity process resolution to reproduce features of clinical interest even for the simplest cases [21]. Fig. 1 illustrates the failure of the linear model to capture waveform features such as the pressure plateau shape related to patient effort. Nonlinear extensions broaden resolution by adopting time- or state-dependent sub-models of tissue rheology to model specific components of lung injury from mechanistic understanding [16], [21], [22], [23], [24], [25], [26], while others increase complexity using multi-compartment frameworks [27], [28], [29], [30]. These enhancement strategies impose additional limitations, and no identified literature reports their application to mechanically ventilated human data.
Fig. 1.
Linear single-compartment state resolution: pressure observation () vs. optimal single compartment estimation () for human breaths of patient #1 with mild ventilator dyssynchrony [19]. Information about lung damage and disease may manifest itself in the shapes of waveform features not resolvable by the assumed relationship.
Limits of the compartmental framework create obstacles to personalization and clinical translation. The increased parametrization required to resolve specific dynamics may not capture signatures of ventilator dyssynchrony, such as those discussed in [31], [32], [33], in a way easy to estimate from data. Nonlinear compartmental models, such as those with state-dependent parametric effects, are more difficult to invert due to strongly correlated state and parameter effects. Inversion of multi-compartment models may not uniquely identify and ascribe parameter values without additional LVS knowledge even when compartments have unique parametric timescales. Likewise, time-varying formulations [24], [34], [35] may fully resolve dynamic elastance without the discrete structure needed to convey this information compactly. Caregivers versed in waveform descriptors and ventilation annotation schemes [36] may also have difficulty adopting complex parametric descriptions of lung deformation properties. Such ontological differences further limit the scope and effectiveness of translating patient-specific parameters into clinical and translational informatics (e.g., machine learning) domains for desirable applications such as LVS phenotyping and classifying dyssynchronous behaviors [19].
1.2. Purpose & outline
Understanding the severity and incidence of ventilator dyssynchrony and their relation to VILI, ARDS, and clinical outcomes requires quantifying the effects of the healthcare process. These effects must be inferred from data generated by non-stationary heterogeneous patient-treatment systems, a clinical informatics problem that may be investigated by learning algorithms. Developments in this context are precluded by the lack of compact representation of LVS waveform data, as current mechanistic models are too inflexible to produce them reliably. This work presents an inferential model-based approach that characterizes LVS waveform data into interpretable parametric descriptors where expert knowledge or other a priori definitions replace theory-driven mechanistic processes in the dynamical system. Discovery and hypothesis generation from LVS data regarding dyssynchrony, VILI, and ARDS may then be pursued, leveraging these parametric representations in correlational and distance-based informatics processes. The central hypothesis in this work is that parameter-expressed waveforms retain interpretable, distinguishing characteristics of data in digitized form. Such properties are essential to descriptor utility for categorizing waveform changes and deconvolving ventilator effects on the patient.
The remainder of this work is outlined as follows. Section 2 proposes a model approach to parametric estimation of LVS waveform data, outlines the employed inference scheme, and describes the data source. Section 3 presents experimental results of parameter estimation on human collected from ventilated patients diagnosed with ARDS. Section 4 discusses the gains and limitations of the proposed methodology in application to the clinical estimation environment.
2. Method
This section presents an LVS estimation approach comprising a simple linear dynamical system (Section 2.1) combined with a windowed ensemble-based estimation scheme (Section 2.2). The dynamical model generates waveforms from a simple, parametrically-defined forcing function that can be data-optimized to yield a parametric form of the ingested data. A windowed ensemble Kalman-type smoothing method is employed here to assimilate patient data and systematize data into a small set of patient-specific descriptors.
2.1. The data representation model
The presented model determines a parametric representation of LVS waveforms using a method conceptually recent related to work recent [37]. Rather than use physiological relationships to model data generation, the proposed method simulates parametric waveforms, including dyssynchronous breaths, within an inferential scheme. The approach circumvents direct resolution of the lung and ventilator which may require many parameters to model robustly, involve bulk process parametrizations at some scale, and must ultimately sacrifice mechanistic fidelity for functionality.
The proposed LVS waveform model simulates a signal (e.g., pressure or volume) according to the equation:
| (2) |
where is a smoothing parameter and is a time-dependent function of parameter vector . The value corresponds to a reference baseline, which is ventilator PEEP in LVS pressure applications. The user-defined periodic forcing function drives the system dynamics in time. The equation transforms parameters defining the function into the continuous state output . The forcing function and output states have equivalent parameter dependencies within this linear differential equation, with the input parameters generating localized features of the solution. In the following applications, the respiratory cycle length and baseline value are fixed values but may be estimated in other applications targeting patient-triggered ventilation.
The relationship of parameters to the solution is specified by forcing function , which may be customized per application. One may target specific waveform features or particular nuances of interest for a given application, leveraging domain-expert knowledge to maximize the relevance of parametric representation.
For simplicity, presented applications use a step function obtained by discretizing the breath cycle into equal epochs:
| (3) |
where is the breath cycle duration, is local breath time, indexes the epochs with common length , is a vector of amplitudes, and is the logical operator. The epochs-per-breath number defines the model resolution, and the simplified model is identified by the function in this discussion.
In the case where Eqn(3) defines the model, parameter interpretability is inherited through the forcing function, which localizes solution dependence on each parameter. Parameter values are therefore directly associated with the waveform amplitude and derivative over the time epochs that define them. In the LVS case, the first parameter is associated with initial inspiration and the last with the end of a breath; the other parameters have a resolution-dependent association with ordered epochs elapsing during the breath sequence.
For cases in which Eqn(3) has unequal epochs, estimation is improved by rescaling amplitudes to make parameter magnitudes independent of epoch lengths: .
2.2. Parameter inference via data assimilation
Personalizing the model proceeds by optimizing parameters so that simulated output fits the target data. Tracking the LVS evolution of a patient under mechanical ventilation requires estimating tens of thousands of breaths per day. The need to estimate many short features over this much longer scale constrains inference options based on speed, robustness, and comparability of estimates; such considerations discourage the use of Markov Chain Monte Carlo methods and windowed spectral decomposition.
In this work, parameter inference is accomplished by a windowed ensemble Kalman smoother (EnKS) [38], [39]. It approximates a Bayesian update scheme by minimizing the difference between a model forecast trajectory and associated external data using an ensemble forecast over times .
Identified parameters (viz. , of ) are minimizers of the cost function
| (4) |
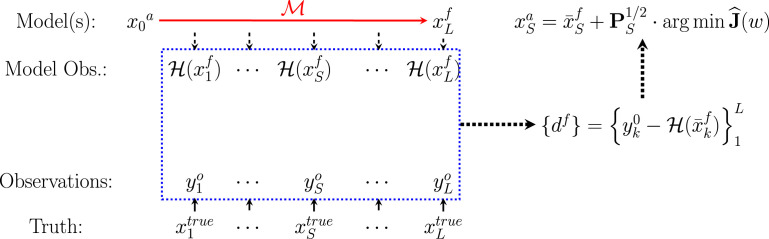
where is a covariance inflation factor to control the weight of data; initial data and parameters for the ensemble are characterized by mean and covariance ; and is the observation error covariance matrix. Symbols are simulated observations generated by using initial state and parameters , and is a sub-indexing of time to select data for assimilation. The ensemble of parameter variations about the optimal mean are retained to re-initialize model forecast at time for the next forecast-correction iteration. Fig. 2 illustrates the inference scheme, with additional details in SI Appendix A.
Fig. 2.
The schematic windowed assimilation process. The conceptual relationship between the true state, observational data, modeled data, and model states is shown. The model (, red) performs the forecast process over the window (blue), simulating equivalents of data as well as the error covariance structure. The optimal solution at any time within the window derives from error analysis of data-forecast mismatch. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
2.3. Experiments and data
Synthetic data inference experiments (SI Appendix C) verify the proposed method in cases with known, non-stationary parameters. The following section presents experiments performed on LVS data collected from mechanically ventilated patients with the approval of University of Colorado Multiple Institutional Review Board (COMIRB, protocol #18-1433). These prospective data comprise 50 patients admitted to University of Colorado critical care units during 2019–2021 with ARDS diagnoses [40] or ARDS risk factors such as COVID-19, sepsis, aspiration, and pneumonia. The cohort definition includes patients aged 18–89 years excluding pregnant women; the imprisoned; and those with facial fracture, esophageal fistula, recent (3 months) gastric or esophageal surgery, or recent variceal bleeding or banding. Hamilton G5 ventilator data were collected at 31.25 Hz using Hamilton DataLogger v5.0 software (www.hamilton-medical.com) beginning within 24 h of intubation or esophageal balloon placement for a maximum of 48 h. Additional details regarding patient demographics, ARDS etiology, and use of neuromuscular blockade (NMB) were gathered from electronic health records.
Numerical experiments use eleven 40-breath sequences (70–170 s) containing identifiable and consistent breath types without artifacts (e.g., discontinuities) caused by ventilator self-recalibration. Table 1 provides details for six source patients whose data are used in experiments. Sequences from the patients #1 and #2 are composed of either normal breaths or dyssynchronous breaths identified as flow-limited (FL), early ventilator-termination (eVT), or early reverse-trigger (eRT) types [32], [41]. Five additional sequences (SI Appendix D) from patients #3–#6 feature other types of LVS behavior. The eleven total sequences include six types of LVS dyssynchrony types; see [19] regarding the mechanics and clinical implications of these behaviors. The experiments do not exhaust all possible LVS dynamics, but they are representative of the various known dyssynchrony types that occur during a single ventilator cycle.
Table 1.
Description of patients whose LVS data are used in experiments. Age given in years. PF = PaO2/FiO2 ratio at admission, BMI = Body Mass Index in kg/m2, NMB = Neuromuscular Blockade usage, AA = African-American.
| Patient | Age | Sex | Race | PF ratio | BMI | NMB | ARDS risk |
|---|---|---|---|---|---|---|---|
| # 1a | 61 | F | White | 81 | 45.5 | F | Sepsis |
| # 2 | 43 | F | White | 80 | 72.1 | F | Pneumonia |
| # 3 | 62 | M | Black/AA | 136 | 33.5 | F | COVID-19 |
| # 4a | 41 | F | White | 365 | 17.8 | F | Other |
| # 5 | 70 | M | White | 271 | 21.3 | F | Sepsis |
| # 6 | 40 | M | Whiteb | 155 | 36.5 | T | COVID |
Patient death during encounter.
Hispanic or Latino ethnicity.
3. Results: Inferential data parametrization
This section explores experiments inferring parameter representations of data using the proposed inferential modeling method presented above. Data are estimated by optimizing model parameters, and these estimates are statistically summarized over each 40-breath sequence. Characterization of the data, a static waveform representative, is generated by applying the forward model to the summary mean (or another estimator). Synthetic data experiments (SI Appendix C) verify that model inversion quickly and accurately tracks parameter dynamics as needed for application to LVS data. The ensemble approximation also captures the parameter covariance structure (viz. the upstream dependence of on ) that may otherwise confound inversion.
The following sections estimate human LVS data in normal and more pathological cases, including parametric representation of pressure–volume loops. Supplemental Table B.4 contains experiment level hyper-parameters.
3.1. Normal breath estimates
In this and the following section, experiments explore 40-breath sequences of clinical LVS data from patients with ARDS. These 80–100 s intervals illustrate the fidelity of estimates for breaths of similar type, although practical applications may require shorter intervals for less regular data.
Table 2 presents breath-level mean errors for the pressure and volume estimated by parameters at various model resolutions for the cases presented. Experiments focus on pressure waveform estimation because the ventilator controls the volume delivery throughout each experiment. PEEP values () for pressure data are estimated as the mean minimum pressure across all breaths, while volume applications assume a zero-valued baseline. Period regularization within each window maintains a consistent parameter definition throughout the breath sequence and, in practice, may be applied to shorter sub-sequences when the breath cycle is irregular.
Table 2.
Breath-averaged RMS differences of continuous pressure estimation, with the lowest value for each sequence in bold.
| Model: | ||||
|---|---|---|---|---|
| Pressure (cm H2O) | ||||
| p#1 Normal 1 | 0.24 | 0.24 | 0.24 | 0.24 |
| p#1 Normal 2 | 0.25 | 0.25 | 0.25 | 0.25 |
| p#2 FL | 0.10 | 0.10 | 0.10 | 0.10 |
| p#2 eVT | 0.13 | 0.14 | 0.14 | 0.14 |
| p#2 Normal | 0.29 | 0.29 | 0.29 | 0.29 |
| p#2 eRT | 0.34 | 0.34 | 0.34 | 0.34 |
| Volume (ml) | ||||
| p#1 Normal 1 | 4.39 | 4.40 | 4.41 | 4.42 |
| p#1 Normal 2 | 4.09 | 4.11 | 4.13 | 4.06 |
| p#2 FL | 4.46 | 4.46 | 4.49 | 4.59 |
| p#2 eVT | 4.25 | 4.24 | 4.24 | 4.48 |
| p#2 Normal | 4.01 | 4.00 | 4.00 | 3.92 |
| p#2 eRT | 3.14 | 3.18 | 3.24 | 3.33 |
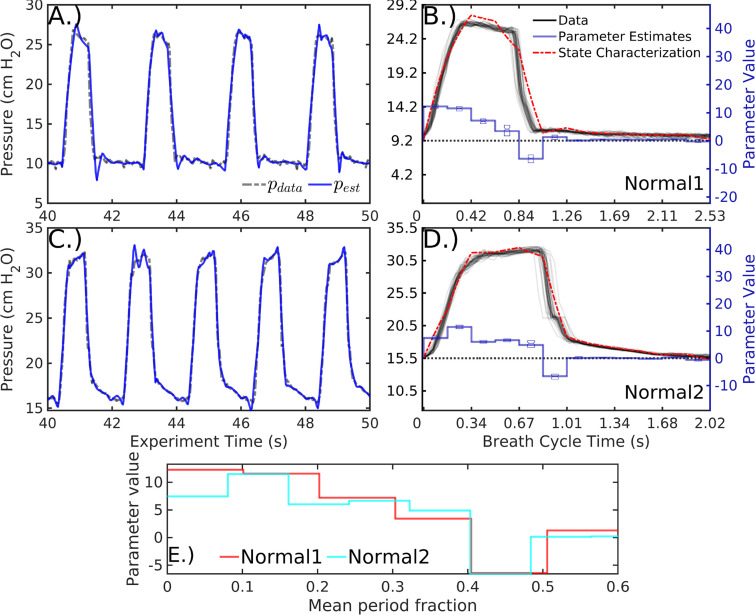
Fig. 3 shows the inference process using 12 epochs per breath () for sequences of normal, mildly dissimilar breath waveforms in patient#1 recorded 8.4 days apart. Individual breaths are well-resolved in continuous time with small relative errors that occur when the epoch-based parameter definitions span breath features. Inferred parameters give a low-dimensional representation of the data as both parameter vectors and state characterizations, together with quantified parameter uncertainties. The accuracy of these model summaries is affected by the parameter definitions, with characterized waveform including artifactual signatures of the parametric resolution.
Fig. 3.
Characterizing two patient#1 pressure data sequences with 12 parameters . Data (A and C, dashed black) are well-estimated by inference model estimates (blue) in continuous time on overlapping 1.2 s analysis windows. Tabulating data (B and D, black) and mean parameter estimates (blue, with inter-quartile range shown) in cyclic breath time compares the characterization (red) of each sequence with the data. Mean parameter vectors of the two sequences, which have significant distributional differences, are depicted over a normalized breath duration (E). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
Parameter estimate distributions of the two sequences of normal breaths distinct (, approximated via [42]), providing a direct way to categorize and distinguish breath sequence types. Differences in parameter mean likewise coarsely resemble differences in the breath shape. For example, the inspiration parameters of the first sequence during the first half of the breath show a monotone decrease whereas the second sequence’s parameters rise later into the breath, just as in the waveform pressure shapes (Fig. 3E).
3.2. More complex varieties of human breaths
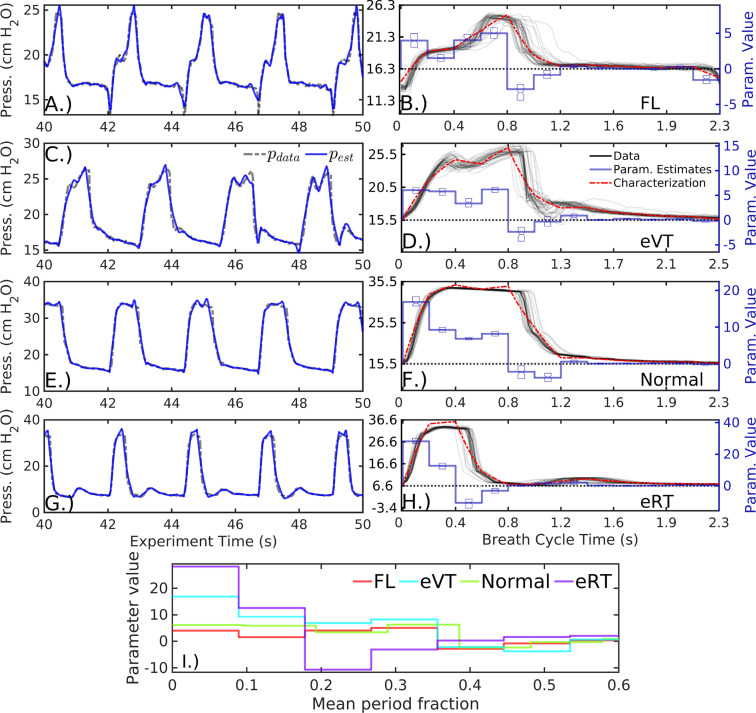
Patient#2 data comprise four sequences of breath types identified as flow-limited (FL), early ventilator-termination (eVT), normal, and early reverse-trigger (eRT). These sequences occur 4, 3, and 14 h apart, respectively, with roughly equal breath lengths for direct breath comparison. Parameter distributions for these sequences are again distinct (, pairwise), formalizing the illustrated differences in characterization and mean summaries (Fig. 4).
Fig. 4.
Characterizing four patient #2 pressure data sequences with , as in Fig. 3. Differences in the data waveforms have direct, interpretable relationships to differences between parameter descriptors, which could be used in resolution-dependent LVS breath classification. Summary parameter vectors (I.) are the means of statistically different and distinguishable distributions.
The characterizations and parameter average vectors encode the key differences observed in the data and may be interpreted similarly. For example, inspiration onset pressures () in normal and eRT sequences (third and fourth rows) are greater than those of FL and eVT sequences (first and second rows). Similarly, the eRT sequence requires a strong negative parameter () to complete its rapid exhalation. The eVT sequence pressure plateau notch is identified with a decrease in relative to its neighbors. Expiratory pressure rises observed in eVT and eRT breaths are likewise captured as positive transient values of breath parameter .
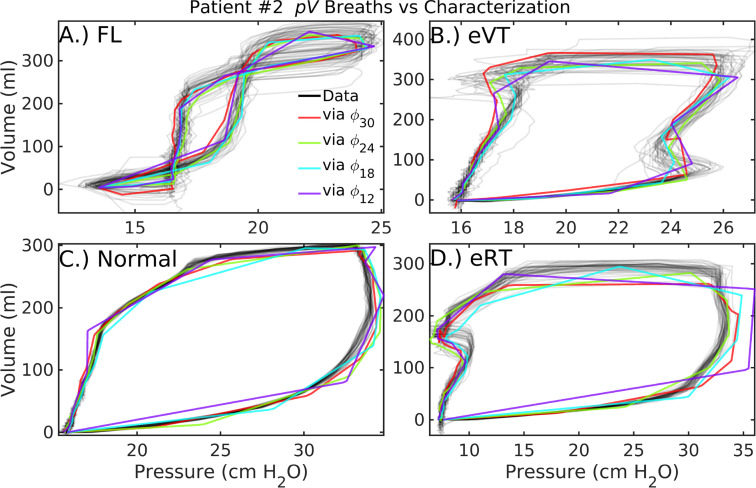
Estimated loop structures for patient#2 are presented in Fig. 5) at various parameter resolutions defined by . Among the model resolutions tested, the 24-parameter model () provides the best overall fit as measured by RMSE over all four sequences ( Table 2). However, -based characterization more accurately represents eVT (B) and normal (C) sequences. The static eRT trace (D) has inaccurate plateau pressure and expiratory volume at this same resolution. Notably, optimal resolutions differ for pressure and volume variables. Further, the 12-parameter model suffices to distinguish the eVT pressure sequence of patient#2 (Fig. 4, D) from the normal breath type (F). Meanwhile, the corresponding estimate at that resolution (Fig. 5, B in purple) misrepresents the net compliance, as approximated in terms of the slope over inspiration. It is likely advantageous to represent pressure and volume at different resolutions, as these waveforms differ in smoothness and timing of key features. This is easily pursued as representation of data does not require joint estimation.
Fig. 5.
Patient#2 loop characterizations at various parameter resolutions. In addition to normal breaths (C) similar to those of patient#1, these patient data feature flow-limited breaths (A), early ventilator-termination breaths (B), and early reverse-trigger breaths (D). Increasing model resolution generally improves parametric characterization of the data, although accuracy also depends on the summary window length and timing of features in the data. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
3.3. Characterization fidelity
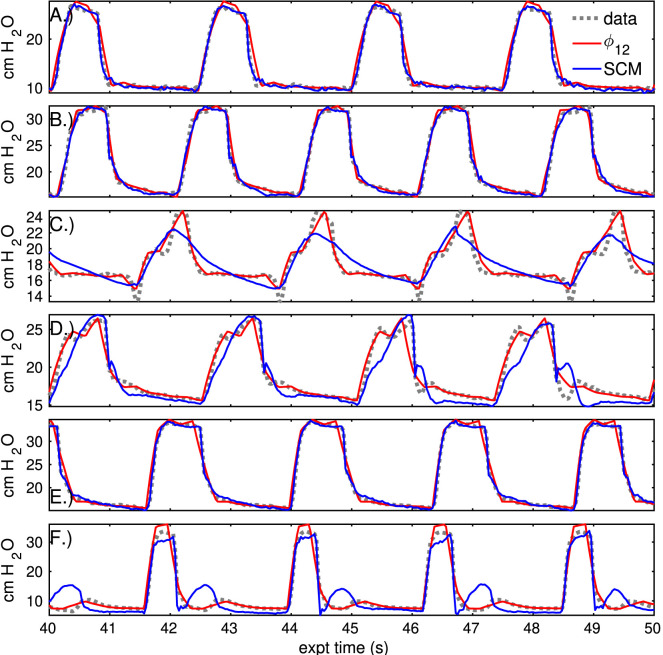
Waveform characterizations derived from parametric descriptors are more casually interpretable than parameters, and it is important to evaluate their fidelity. Fig. 6 compares stationary, low-resolution characterizations () to breath-by-breath estimates of the linear compartment model for the pressure sequences previously discussed. The differences are more pronounced in dyssynchronous breaths sequences (C,D,F) than in normal breaths (A,B,F), with higher accuracy achieved by the characterization. Table 3, Table D.5 presents the errors of these estimates to the continuous-time data at several resolutions.
Fig. 6.
Comparison of static sequence characterization to compartment model estimation. The previous set of pressure sequences (grey) are represented by static 12-parameter characterization (red) and by breath-to-breath application of the linear compartment model (blue). Estimation of normal breath pressures (A,B,E) is similar in both models. For breaths with marked dyssynchrony (C,D,F), static characterization outperforms the compartment model. Note that the compartment model estimate is dynamic while the red characterization is stationary, and time axes are regularized to a fixed breath cycle length to plot these signals together. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
Table 3.
Total estimate for various resolution characterizations and the single-compartment model (Eqn(1)), with the lowest value in each row in bold. The large compartment model error for the second sequence of patient#2 arises from a small, persistent difference in phase.
| MODEL | Eqn(1) | ||||
|---|---|---|---|---|---|
| Pressure (cm H2O) | |||||
| p#1 Normal 1 | 1.25 | 0.87 | 0.80 | 0.78 | 1.59 |
| p#1 Normal 2 | 0.98 | 0.84 | 0.89 | 0.78 | 1.91 |
| p#2 FL | 0.87 | 0.86 | 0.89 | 0.74 | 3.17 |
| p#2 eVT | 0.93 | 0.82 | 0.74 | 0.79 | 2.23 |
| p#2 Normal | 1.13 | 1.09 | 0.91 | 0.83 | 2.90 |
| p#2 eRT | 1.97 | 2.00 | 1.66 | 1.55 | 4.70 |
| Volume (ml) | |||||
| p#1 Normal 1 | 8.97 | 8.33 | 8.53 | 9.18 | 20.03 |
| p#1 Normal 2 | 7.75 | 7.31 | 7.62 | 11.56 | 23.23 |
| p#2 FL | 22.05 | 21.73 | 21.78 | 23.36 | 329.23 |
| p#2 eVT | 19.02 | 18.64 | 19.22 | 24.30 | 41.67 |
| p#2 Normal | 10.52 | 8.63 | 8.58 | 10.25 | 33.54 |
| p#2 eRT | 22.45 | 20.98 | 22.33 | 22.44 | 45.09 |
In normal pressure sequences, the low-dimensional characterization accuracy is comparable to the compartment model and estimates are qualitatively similar (Fig. 6). The relative difference in normal breath errors between the models is typically less than 20%, with several breaths contributing strongly to the compartment error. In contrast, compartmental pressure errors that are 60%–70% larger than those of the -characterization for breaths with dyssynchrony (panels C,D,F). Sequences of several other patients are estimated SI Appendix D with similar implications.
3.4. Summary
Numerical experiments results indicate successful parametric representations of LVS data using informed-model data assimilation. Several thousand time-dependent data points of each sequence are reduced to static -parameter descriptions (including PEEP and period) and may be estimated with higher accuracy by either increasing the number of parameters or shortening summary window lengths. In all cases, inferred parameters accurately represent breath data in continuous time with localized errors related to mis-timings between waveform features and parameter definitions. The patient breaths are distinguishable from the distribution of estimated parameters, even for the generic forcing function used here. These parameters are also interpretable through a priori definition of the forcing function, either as parameter descriptor vectors or as the waveforms characterizations generated by the forward model. Together, these points indicate that parameter distributions provide a meaningful way to estimate similarity of breaths or breath sequences.
The accuracy of parameter representation and fidelity of characterization are influenced by several factors. Parameter uncertainties are greatest where parameter epochs mis-align with waveform features or when waveform feature timings (including the cycle length) vary. The resolution-dependent relationship between discrete epochs and continuous data features influences uncertainty; these factors should be considered when choosing the number of parameters () and summary window length for an intended application. Increasing the number of parameters may achieve higher characterization fidelity, although this increases model sensitivity to noise in the data. Shorter statistical summary windows are needed for heterogeneous sequences to avoid multi-modal parameter distributions for which mean-based characterization may be inaccurate.
4. Discussion
This work presented a hypothesis-driven approach to modeling the lung–ventilator system (LVS) to infer interpretable parametric representations of human clinical data. Rather than resolving mechanistic processes, the proposed method emphasizes model inversion to overcome limitations of the compartment model framework (Section 1.1) by combining data- and model-driven methods. This method increases key inference attributes of resolution, inferability, and translatability by exchanging a physiology-based model framework for one able simulate heterogeneous LVS waveforms. The linear dynamical model employs a user-specified forcing function whose data-optimized parameters discretize the waveform properties. These model parameters are interpretable through their relationship to the forcing function they define and the waveform properties to which they are optimized. Simulations employed a simple non-specific forcing function whose parameters relate to waveform amplitude and derivative during various sub-phases of inspiration and expiration. Data-informed estimates could be distinguished and interpreted by parameter vectors as well as waveform characterization, the model image of the parameter distribution center. Parametric digitization of source waveform data may be analyzed in conjunction with other data streams (Section 4.3 below). Characterization presents parametrized data in a way familiar to domain experts, who may recognize physiological implications graphically and therefore directly aid in hypothesis generation.
The inferential model system successfully assimilated both synthetic data as well as sequences of human LVS data, comprising both normal and dyssynchronous breaths from patients with ARDS. Synthetic data experiments (SI Appendix C) showed dynamic parameter tracking through waveform shape changes, with small parameter errors related to insensitivity and sequential dependence. Experiments on patients #1 and #2 inferred parameters from normal breaths and several types of LVS dyssynchrony. These parameters showed statistically significant differences in distribution even between similar breath sequences. Additional experiments (SI Appendix D) apply the method to cases with remaining types of dyssynchrony observable during a single ventilator cycle [19]. Together, results support the hypothesis of this work by indicating that the parametrization technique applies across the breath types of particular interest in ARDS research while encoding enough detail to discriminate between them at a granular level.
The model generates waveform characterizations from estimated parameter distributions, which are easily extended to loops by independent application to pressure and volume sources. Parametric summaries, or the forward-model characterizations they induce via , provide an effective basis for discretely organizing, comparing, and analyzing waveform data. Coarse estimation with a 12-parameter model showed error reductions of more than 50% compared with the linear compartment model in dyssynchronous sequences. Accuracy may be improved by increasing a more highly parameterized model, although this should be considered in relation to the structure of the forcing function and objective use of the estimates (Section 4.2 below).
4.1. Hypothesis-driven inference
In broad view, this model strategy is an example of hypothesis-driven inferential modeling in which prior knowledge informs the parameter design of the model, and those parameter values are informed by patient data. This hybrid approach is neither purely empirical like machine learning, nor representative of physical or mechanistic processes as in data assimilation. Parameter estimates, therefore, occupy a grey area between those of more familiar methods. Interpretation – of parameter values or waveform characterization – is based on a priori definitions, while the model itself bears no link to the physical data-generating process. Unlike machine learning, however, parameter values and their patient-level differences may be interpreted in relation to the source data and these definitions. Background knowledge may be incorporated to define the forcing function, which structures parameter definitions without influencing their values like an uninformative Bayesian prior distribution. A large covariance factor () in the inference process ensures that parameter values are strongly informed by the data while parameter definitions control the model output space. From this perspective, the prior knowledge defining the parameters acts as a constraint framework for posing testable hypotheses of the model. The method is also generalizable, although this work focused on ventilator-supported respiration. Namely, the parametrization of clinical waveforms is translatable to other domains (e.g., capnography [43] or intracranial hemodynamics [44], [45]) where underlying processes evade efficient or flexible models needed for analysis at longer timescales.
4.2. Pragmatic limitations and trade-offs
While parameter and characterization fidelities are higher than the compartment model for breaths with dyssynchrony, important limitations exist on interpretability and representation errors. Interpretation depends on the definition of the forcing function, which may be tailored to incorporate domain-specific considerations or knowledge. The generic forcing function used in experiments is highly flexible but generic. Therefore, its parameters could only be interpreted in relation to breath behavior during a certain interval of the breath. More sophisticated parameters can provide more granular interpretation but may be difficult to estimate quickly and accurately. For example, if feature timings – such as the durations of flow phases – are estimable parameters, sequential dependence strongly correlates their values. Here, efficient inference is confounded by parameters being defined in relation to one another within the breath cycle: a change in one parameter requires compensatory changes in others. The trade-off between flexibility and interpretability results from the generic forcing function adopted in experiments. However, interpretability can be refined by incorporating additional knowledge of the target waveforms into the model forcing function without sacrifice. For example, the inspiration phase can be targeted at higher resolution than expiration by scaling parameter epochs based on the inspiration-to-expiration (I:E) ratio.
The statistical summary process over a temporal window imposes stationarity assumptions with consequences for interpretability, generalizability, and use of estimates to differentiate breaths. The minimum resolution needed to capture breath-level features is identified by the Nyquist sampling theorem [46]: a number of parameters is needed to resolve features with timescale . Increasing parameter resolution improves the overall fidelity of waveform characterization, up to the threshold of fitting observation noise. However, well-estimated parameter distributions may be non-gaussian, generating characterizations with inaccurate features due to variability of breath length or feature timing. In particular, the averaging process may eliminate features of interest (e.g., patients #5 and #6 in SI Appendix D) that are captured in the sampled parameter estimates. Characterization fidelity increases by shortening the summary window length from 40 breaths (70–170 secs in the experiments) to a few (10–15 s), although this depends on the data. Shorter summary windows (1–3 breaths or 10 secs) assume little stationarity – and are therefore generalizable – and should be assumed for arbitrary sequences of LVS data. The ideal number of parameters and the summary length thus present bias–variance trade-offs, with application-specific resolution requirements considered in tandem with the desired summary precision, stability of parameter estimates, and temporal granularity.
Tuning the quantity of generic-model parameters () and stationarity assumptions may not be suitable for some forms of LVS dyssynchrony. For example, double-triggered breaths result from multiple ventilator cycles occurring within a patient breath cycle. This dyssynchrony was not included in experiments precisely because it is not indexed by the ventilator the same way as other types and must therefore be treated differently in the model and data processing. Multi-modality in estimated parameters may identify specific forms such as reverse-triggered breaths, which may have a particular repeating sequence of different breath types (e.g., a (normal, normal, reverse trigger) breath cycle). In this case, time-ordered parameter estimates are required to discern the sequence from one with a complete transition from normal breaths to reverse-triggered ones. Robust statistical description, such as non-parametric discrimination analysis [47], may be necessary to accurately summarize non-stationary breath sequences from multivariate parameter estimates with correlated components.
4.3. Informatics-minded applications
The purpose of encoding LVS waveforms into discrete parameters is for use in research informatics applications involving machine learning and other automated methods. The inference system presented defines vectors to serve in learning tasks such as identification and classification in conjunction with domain-specific information. For studies focusing on individuals, it permits the algorithmic analysis of breath progression in relation to adjunct patient record information not encoded by parameters. Patient status, intervention, and lung response compose a more complete description of respiration within the health care processes, a representation needed to separate lung changes from commingled signals.
The method proposed in this work facilitates the formulation and testing of hypotheses about the role of LVS dyssynchrony in relation VILI, ARDS, and patient outcome. Changes in breath behavior and injuries may arise from isolated events as well as accumulated effects over time. The dynamics are influenced by ventilator settings changes, sedation, and manipulations performed in response to patient–ventilator interaction and these should be detangled from changes in the patient lung state. Limited to intervals of static ventilator settings and documented sedation, parameter trend analysis over hour timescales may differentiate VILI associated with the duration of ventilation from injuries arising from patient efforts such as coughing or voluntary breaths. Breath characterization also provides a framework for quantifying the severity of several types of ventilator dyssynchrony, allowing one to measure distance from a normal breath or to penalize the loss of breath smoothness.
Such studies targeting the sources of VILI and quantifying their contributions may improve the understanding of lung–ventilator interaction and its consequences on ARDS patient outcomes. Wider, cohort-oriented works in this vein may create new pathways to improved lung-protective ventilator management and patient care strategies. However, applications involving inter-patient comparison require normalization of LVS parameter vectors augmented by patient record information. Additional work is needed to identify suitable normalizations and distance functions required for algorithmic comparisons of data summaries comprising parameterized waveforms and peripheral information.
4.4. Concluding remarks
Changes in lung compliance, capacity, and alveolar recruitment affect the time distribution of lung volume and pressure in response to ventilator forcing. Model parameters quantify observed properties of this distribution with definitions detached from process resolution. This fact limits identifying the source of LVS changes, which may originate from material changes in and of the lungs as well as changes in ventilator settings and patient state. Practical applications, therefore, require analyzing characterization within the full patient-data environment, including knowledge of ventilator settings which the experiments here did not consider. Investigation of the relationship between lung physiology and estimated parameters can proceed in tandem with LVS waveform research, such as those of ventilator control mechanisms e.g., [48], as well as models with explicit process mechanisms [26] and injury-specific waveform representation [37]. Although such considerations are beyond the scope of this discussion, the hypothesis-informed parameter descriptions can augment those analyses as low-dimensional representations of waveform data by providing both flexibility and interpretability in a discrete form.
CRediT authorship contribution statement
J.N. Stroh: Conceptualization, Methodology, Software, Investigation, Validation, Analysis, Resources, Visualization. Bradford J. Smith: Investigation, Conceptualization, Writing – review & editing, Resources, Project administration, Funding acquisition. Peter D. Sottile: Data curation, Investigation, Conceptualization, Resources, Writing – review & editing, Funding acquisition. George Hripcsak: Writing – review & editing, Conceptualization. David J. Albers: Funding acquisition, Project administration, Supervision, Conceptualization, Methodology, Resources.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
JNS thanks CU Anschutz colleagues Y.Wang and M.Şirlanci for thoughtful discussions and helpful clarifications. This work was supported by R01HL151630 (BJS, USA, PDS, USA, DJA, USA ).
Appendix A. Windowed smoothing via ensemble Kalman transform
In linear ensemble Kalman filtering, the correction of the forecast state is defined as a linear combination of ensemble perturbations about the forecast state. In particular, the Kalman update is , with superscripts denoting the analysis and forecast, respectively. The gain matrix may be computed in several different ways, but the full-rank ensemble case always reduces to manufacturing a matrix of the form , where is a matrix of scaled ensemble state anomalies about the ensemble mean. Importantly, the column space of is determined by the column space of . Therefore, the analysis has the form where is an optimal weight vector for columns of determined by applying the remaining Kalman gain factors to the data. This implementation is referred to as the ensemble transform as each state in the ensemble span (i.e., the possible EnKF analyses) is uniquely identified with an ensemble expansion coefficient where is the ensemble size. The ensemble of forecast states is used in the ensemble Kalman filter to approximate dynamical uncertainties. Namely, the ensemble state anomaly matrix is formed column-wise by deviations about their mean and scaled by ; it is a Cholesky factor of an empirical rank- approximation to the true model error covariance . Because error distributions of the model and data are assumed to be gaussian, the analysis may equivalently be identified by minimizing the common cost function
| (A.1) |
over the -dimensional subspace . Here, is the error covariance matrix associated with the observation process, which includes error and uncertainties involved in translating model states to equivalents of observational data as well as instrument errors when generating observational data from the real world. The inverse of the hessian matrix associated with identifies the posterior error covariance matrix [49]. From a Bayes’ Rule perspective, this optimum is the mode of the posterior probability distribution produced when the forecast model is updated based on new data [50].
A.1. Asynchronous smoothing
Extensions of the EnKF method described above to assimilate observations occurring at various times within a moving window are developed in e.g. [51], [52]. The passage below follows the variational perspective of [53], [54] for conciseness.
The equivalent of Eq. (A.1) conditioning the optima transform variable on multiple observations in the window is given by the quadratic function:
| (A.2) |
| (A.3) |
Here, indexes the times associated with observations being assimilated, at which times one requires observed model forecast anomalies and scaled misfits to the data . In Eq. (A.3), the object is the hessian matrix for the system linearized about the initial trajectory , the vector is the linear coefficient, and is initial trajectory error. In applications with overlapping-windowed analysis, regulates whether data assimilated in a previous window are re-assimilated in the present one.
A linear approximation to the variational optimum is found algebraically by targeting the mode of the posterior distribution. Specifically, solving yields the (approximately) optimal coefficient
| (A.4) |
where is an optional covariance inflation factor with increasing relative weight on errors to the data. The true minimum of the nonlinear problem may be obtained by minimizing Eq. (A.2) by iterating over re-forecasts; Ref. [54] includes a more comprehensive analysis of different schemes for computing the full optimum. Such approaches are important in strongly nonlinear systems whose ensemble of solutions diverges strongly within the assimilation window, which is not the case with the simple model considered in this work.
Once the optimal analysis state is calculated, the ensemble variations about this new distributional center are found by re-weighting the forecast covariance Cholesky factors by those of the quadratic program inverse Hessian matrix: .
Appendix B. Algorithm parameters for experiments
See Table B.4.
Table B.4.
Non-forcing parameters and experiment details are given, where ‘data’ indicates values extracted from the data.
| Symbol | Synthetic expt. | Human expt. | |
|---|---|---|---|
| Ensemble size | 32 | 60 | |
| Sample rate (Hz) | – | 25 | 31.25 |
| Window length | 75 | 50 | |
| Update step | 25 | 20 | |
| ODE parameter | |||
| Reference state | 20 | data | |
| Breath cycle | 5 s | data | |
| Initial parameters | – | 0.5 | 0.5 |
| Data RMSE | 5% | 5% | |
| Parameter RMSE | 0.025 | 0.025 | |
| Covariance inflation | 100 | 100 |
Appendix C. Parameter accuracy via synthetic data experiments
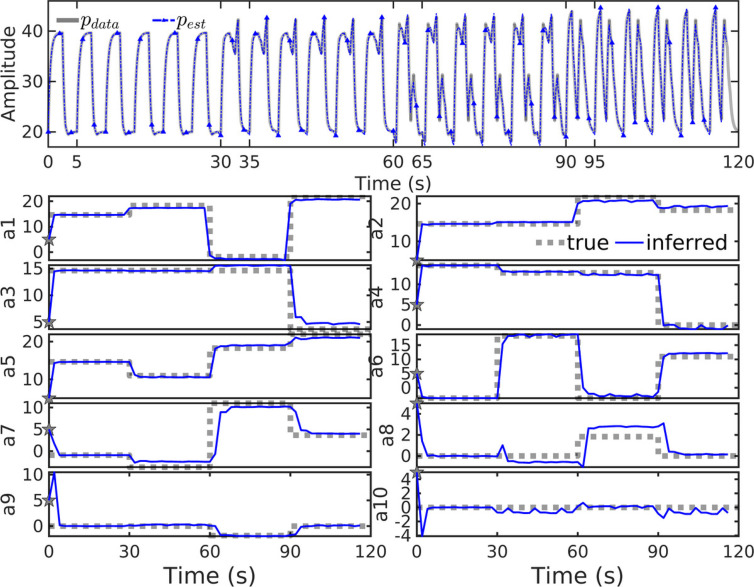
Parameters were changed every 8 breaths in the 10-parameter model () with a fixed 5-second cycle length to generate two minutes of 25 Hz synthetic data (Fig. C.7, top panel in grey). Inference experiment results (blue, throughout figure) use a high covariance inflation factor () to sharply focus the solution on a noise-contaminated version of these data. Simulated waveforms accurately reconstruct window-wise trajectories (top, blue) from local parameter estimates inferred from noisy data. Estimated parameter values (lower, blue) accurately and quickly track changes of the true parameters defining the data (lower, grey), with transitions to new parameter values occurring within two update windows (twice the length of , or about 2 s).
Fig. C.7.
Inversion of with synthetic data (upper panel, grey) generated by known parameters (lower panels, dashed grey) correctly identifies the correct parameter values and their changes in time. Reconstructed waveforms (upper, blue) accurately track the correct solutions. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
Early breath parameters change sooner than parameters later in the breath, seen by comparing transitions of and to those of and (around 60 s). This is a result of early-breath data begin assimilated sooner, with upstream parameter dependence also evident in the estimates. For example, the value of is slightly underestimated for and the value of is correspondingly slightly overestimated to compensate. Relative errors are smallest for large magnitude parameters and largest for those with values near zero (such as ). The large error in estimated for , where the true value of 1.8 is estimated near 2.8, is a consequence of diminished model sensitivity to smaller-magnitude parameters. The inversion process accurately infers the parameters dominant in determining the solution shape, aptly tracks parameter set changes in time, and thereby gives dynamic representations of the data via model parameters.
Appendix D. Estimation of additional patients
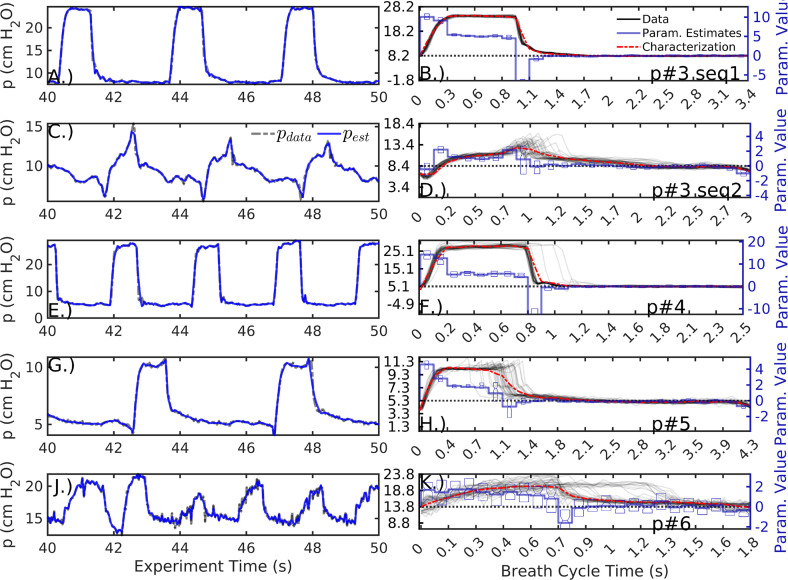
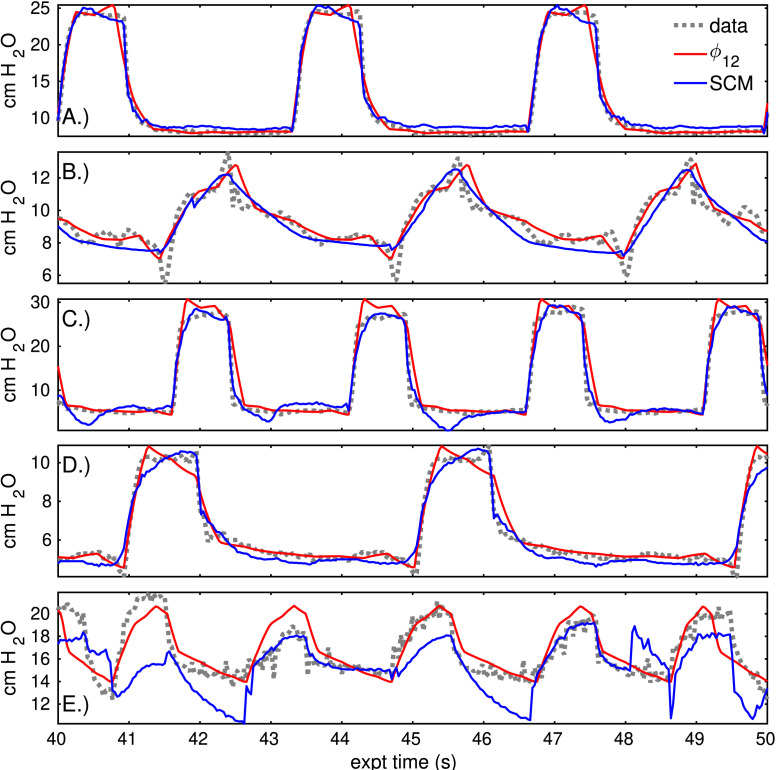
This addenda estimates several breath sequences in addition to those of Section 3. The estimated sequences from three patients (#3–#6) were selected for a minimum of data artifacts and consistency of waveform behavior. In these sequences, the windowed model inversion tightly fits the parametric model to data (Fig. D.8, left column) regardless of the waveform shape. Characterizations (right, red) give low-dimensional representations including resolution-dependent inaccuracies. For example, the pressure peak of patient#3 sequence 2 (second row) is highly variable in both amplitude and timing; the associated characterization based on the mean is inaccurate, but the variability is captured and encoded into the parameter uncertainty (left, blue). Similar inaccuracy is evident in the late pressure plateau pressure peak of patient #5’s sequence (fourth row). Rather than increasing the number of parameters, resolving it requires decreasing the summary window to 4–5 breath windows. The pressure waveforms of patient #6’s sequence (bottom row) have an irregular cycle, leading to a bimodal parameter estimate when assuming a common period for the 40 breaths. This generates large uncertainties in all estimated parameters, and the sequence is best characterized by the coarse resolution model. Nevertheless, static characterizations based on the mean parameter vector generally have lower RMSE over the 40-breath sequence than corresponding estimates made by the linear compartment model ( Table D.5). The first sequence of patients is better estimated by the compartment model than the low-resolution characterization (); for all other sequences, errors decrease by over 40% using the 12 parameter model (Fig. D.9).
Table D.5.
RMS errors (RMSE) of estimates to data for various resolutions and the single compartment model (Eqn(1)), with lowest error among proposed static model characterizations is indicated in bold. Large errors in volume of compartment model estimation result from persistent differences in phase.
| MODEL | Eqn(1) | ||||
|---|---|---|---|---|---|
| Pressure (cm H2O) | |||||
| p#3 seq1 | 1.03 | 0.80 | 0.60 | 1.11 | 0.65 |
| p#3 seq2 | 0.70 | 0.66 | 0.63 | 0.62 | 1.43 |
| p#4 | 2.61 | 2.27 | 2.06 | 1.87 | 4.71 |
| p#5 | 0.63 | 0.62 | 0.63 | 0.63 | 3.32 |
| p#6 | 1.50 | 1.51 | 1.57 | 1.97 | 3.46 |
| Volume (ml) | |||||
| p#3 seq1 | 16.92 | 12.11 | 10.07 | 9.70 | 23.81 |
| p#3 seq2 | 56.55 | 55.83 | 55.80 | 55.60 | 349.77 |
| p#4 | 29.31 | 29.09 | 29.59 | 31.37 | 58.43 |
| p#5 | 44.02 | 43.76 | 43.71 | 43.70 | 230.45 |
| p#6 | 148.32 | 148.73 | 155.00 | 166.66 | 262.49 |
Fig. D.8.
Parameter estimation and characterization () of additional pressure sequences, as in Figs. 3, 4. Specific dyssynchrony types are not identified but breaths in the first and third row are relatively normal. Rows two and four are suspected to feature delayed cycling and early cycling, respectively; both include ineffective triggering but the dyssynchrony type cannot be confirmed without esophageal pressure data, which is unavailable during these sequences. The last row features breaths with an irregular cycle; the data plotted in panel K indicate a bimodal breath cycle.
Fig. D.9.
Compartment model estimate and static characterization () compared to pressure data, as in Fig. 6. The rows correspond to the rows of the previous figure and of the following table. The time axis of each sequence is regularized to a fixed breath cycle length to depict these signals together.
References
- 1.Bellani G., Laffey J.G., Pham T., Fan E., Brochard L., Esteban A., Gattinoni L., Van Haren F., Larsson A., McAuley D.F., et al. Epidemiology, patterns of care, and mortality for patients with acute respiratory distress syndrome in intensive care units in 50 countries. JAMA. 2016;315(8):788–800. doi: 10.1001/jama.2016.0291. [DOI] [PubMed] [Google Scholar]
- 2.Matthay M.A., Zemans R.L., Zimmerman G.A., Arabi Y.M., Beitler J.R., Mercat A., Herridge M., Randolph A.G., Calfee C.S. Acute respiratory distress syndrome. Nat. Rev. Dis. Primers. 2019;5(1):1–22. doi: 10.1038/s41572-019-0069-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Tzotzos S.J., Fischer B., Fischer H., Zeitlinger M. Incidence of ARDS and outcomes in hospitalized patients with COVID-19: A global literature survey. Crit. Care. 2020;24(1):1–4. doi: 10.1186/s13054-020-03240-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Unroe M., MacIntyre N. Evolving approaches to assessing and monitoring patient–ventilator interactions. Curr. Opin. Crit. Care. 2010;16(3):261–268. doi: 10.1097/MCC.0b013e328338661e. [DOI] [PubMed] [Google Scholar]
- 5.Pelosi P., Ball L., Barbas C.S., Bellomo R., Burns K.E., Einav S., Gattinoni L., Laffey J.G., Marini J.J., Myatra S.N., et al. Personalized mechanical ventilation in acute respiratory distress syndrome. Crit. Care. 2021;25(1):1–10. doi: 10.1186/s13054-021-03686-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Beitler J.R., Malhotra A., Thompson B.T. Ventilator-induced lung injury. Clin. Chest Med. 2016;37(4):633–646. doi: 10.1016/j.ccm.2016.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.East T.D., Böhm S.H., Wallace C.J., Clemmer T.P., Weaver L.K., Orme Jr. J.F., Morris A.H. A successful computerized protocol for clinical management of pressure control inverse ratio ventilation in ARDS patients. Chest. 1992;101(3):697–710. doi: 10.1378/chest.101.3.697. [DOI] [PubMed] [Google Scholar]
- 8.Amato M.B.P., Barbas C.S.V., Medeiros D.M., Magaldi R.B., Schettino G.P., Lorenzi-Filho G., Kairalla R.A., Deheinzelin D., Munoz C., Oliveira R., et al. Effect of a protective-ventilation strategy on mortality in the acute respiratory distress syndrome. N. Engl. J. Med. 1998;338(6):347–354. doi: 10.1056/NEJM199802053380602. [DOI] [PubMed] [Google Scholar]
- 9.Gattinoni L., Caironi P., Cressoni M., Chiumello D., Ranieri V.M., Quintel M., Russo S., Patroniti N., Cornejo R., Bugedo G. Lung recruitment in patients with the acute respiratory distress syndrome. N. Engl. J. Med. 2006;354(17):1775–1786. doi: 10.1056/NEJMoa052052. [DOI] [PubMed] [Google Scholar]
- 10.Chiumello D., Carlesso E., Cadringher P., Caironi P., Valenza F., Polli F., Tallarini F., Cozzi P., Cressoni M., Colombo A., et al. Lung stress and strain during mechanical ventilation for acute respiratory distress syndrome. Am. J. Respir. Crit. Care Med. 2008;178(4):346–355. doi: 10.1164/rccm.200710-1589OC. [DOI] [PubMed] [Google Scholar]
- 11.Stamenovic D., Yager D. Elastic properties of air-and liquid-filled lung parenchyma. J. Appl. Physiol. 1988;65(6):2565–2570. doi: 10.1152/jappl.1988.65.6.2565. [DOI] [PubMed] [Google Scholar]
- 12.Stamenovic D. Micromechanical foundations of pulmonary elasticity. Physiol. Rev. 1990;70(4):1117–1134. doi: 10.1152/physrev.1990.70.4.1117. [DOI] [PubMed] [Google Scholar]
- 13.Suki B., Bates J.H. Lung tissue mechanics as an emergent phenomenon. J. Appl. Physiol. 2011;110(4):1111–1118. doi: 10.1152/japplphysiol.01244.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Bates J.H., Smith B.J. Ventilator-induced lung injury and lung mechanics. Ann. Transl. Med. 2018;6(19) doi: 10.21037/atm.2018.06.29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Knudsen L., Ochs M. The micromechanics of lung alveoli: Structure and function of surfactant and tissue components. Histochem. Cell Biol. 2018;150(6):661–676. doi: 10.1007/s00418-018-1747-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Bates J.H., Gaver D.P., Habashi N.M., Nieman G.F. Atelectrauma versus volutrauma: A tale of two time-constants. Crit. Care Explor. 2020;2(12) doi: 10.1097/CCE.0000000000000299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Gustafsson P.M., Robinson P.D., Gilljam M., Lindblad A., Houltz B.K. Slow and fast lung compartments in cystic fibrosis measured by nitrogen multiple-breath washout. J. Appl. Physiol. 2014;117(7):720–729. doi: 10.1152/japplphysiol.01274.2013. [DOI] [PubMed] [Google Scholar]
- 18.Skov L., Green K., Stanojevic S., Jensen R., Buchvald F., Ratjen F., Nielsen K.G. Lung compartment analysis assessed from N2 multiple-breath washout in children with cystic fibrosis. Pediatr. Pulmonol. 2020;55(7):1671–1680. doi: 10.1002/ppul.24773. [DOI] [PubMed] [Google Scholar]
- 19.Sottile P.D., Albers D., Smith B.J., Moss M.M., et al. Ventilator dyssynchrony–detection, pathophysiology, and clinical relevance: A narrative review. Ann. Thorac. Med. 2020;15(4):190. doi: 10.4103/atm.ATM_63_20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Otis A.B., McKerrow C.B., Bartlett R.A., Mead J., McIlroy M., Selverstone N., Radford E., Jr. Mechanical factors in distribution of pulmonary ventilation. J. Appl. Physiol. 1956;8(4):427–443. doi: 10.1152/jappl.1956.8.4.427. [DOI] [PubMed] [Google Scholar]
- 21.Chelucci G., Brunet F., Dall’Ava-Santucci J., Dhainaut J., Paccaly D., Armaganidis A., Milic-Emili J., Lockhart A. A single-compartment model cannot describe passive expiration in intubated, paralysed humans. Eur. Respir. J. 1991;4(4):458–464. [PubMed] [Google Scholar]
- 22.Maksym G.N., Bates J.H. A distributed nonlinear model of lung tissue elasticity. J. Appl. Physiol. 1997;82(1):32–41. doi: 10.1152/jappl.1997.82.1.32. [DOI] [PubMed] [Google Scholar]
- 23.Massa C.B., Allen G.B., Bates J.H. Modeling the dynamics of recruitment and derecruitment in mice with acute lung injury. J. Appl. Physiol. 2008;105(6):1813–1821. doi: 10.1152/japplphysiol.90806.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Chiew Y.S., Pretty C., Docherty P.D., Lambermont B., Shaw G.M., Desaive T., Chase J.G. Time-varying respiratory system elastance: A physiological model for patients who are spontaneously breathing. PLoS One. 2015;10(1) doi: 10.1371/journal.pone.0114847. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hamlington K.L., Smith B.J., Allen G.B., Bates J.H. Predicting ventilator-induced lung injury using a lung injury cost function. J. Appl. Physiol. 2016;121(1):106–114. doi: 10.1152/japplphysiol.00096.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Mellenthin M.M., Seong S.A., Roy G.S., Bartolák-Suki E., Hamlington K.L., Bates J.H., Smith B.J. Using injury cost functions from a predictive single-compartment model to assess the severity of mechanical ventilator-induced lung injuries. J. Appl. Physiol. 2019;127(1):58–70. doi: 10.1152/japplphysiol.00770.2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Crooke P., Head J., Marini J., Hotchkiss J. Patient–ventilator interaction: A general model for nonpassive mechanical ventilation. Math. Med. Biol.: J. IMA. 1998;15(4):321–337. [PubMed] [Google Scholar]
- 28.Bates J.H., Allen G.B. The estimation of lung mechanics parameters in the presence of pathology: A theoretical analysis. Ann. Biomed. Eng. 2006;34(3):384–392. doi: 10.1007/s10439-005-9056-6. [DOI] [PubMed] [Google Scholar]
- 29.Li H., Haddad W.M. Optimal determination of respiratory airflow patterns using a nonlinear multicompartment model for a lung mechanics system. Comput. Math. Methods Med. 2012;2012 doi: 10.1155/2012/165946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Hou S.P., Meskin N., Haddad W.M. 2014 American Control Conference. IEEE; 2014. A general multicompartment lung mechanics model with nonlinear resistance and compliance respiratory parameters; pp. 566–571. [Google Scholar]
- 31.Mellott K.G., Grap M.J., Munro C.L., Sessler C.N., Wetzel P.A. Patient-ventilator dyssynchrony: Clinical significance and implications for practice. Crit. Care Nurse. 2009;29(6):41. doi: 10.4037/ccn2009612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Sottile P.D., Albers D., Higgins C., Mckeehan J., Moss M.M. The association between ventilator dyssynchrony, delivered tidal volume, and sedation using a novel automated ventilator dyssynchrony detection algorithm. Crit. Care Med. 2018;46(2) doi: 10.1097/CCM.0000000000002849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Oto B., Annesi J., Foley R.J. Patient–ventilator dyssynchrony in the intensive care unit: A practical approach to diagnosis and management. Anaesth. Intensive Care. 2021;49(2):86–97. doi: 10.1177/0310057X20978981. [DOI] [PubMed] [Google Scholar]
- 34.Avanzolini G., Barbini P., Cappello A., Cevenini G., Chiari L. A new approach for tracking respiratory mechanical parameters in real-time. Ann. Biomed. Eng. 1997;25(1):154–163. doi: 10.1007/BF02738546. [DOI] [PubMed] [Google Scholar]
- 35.van Drunen E.J., Chiew Y.S., Pretty C., Shaw G.M., Lambermont B., Janssen N., Chase J.G., Desaive T. Visualisation of time-varying respiratory system elastance in experimental ARDS animal models. BMC Pulm. Med. 2014;14(1):1–9. doi: 10.1186/1471-2466-14-33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Chatburn R.L., Volsko T.A. Documentation issues for mechanical ventilation in pressure-control modes. Respir. Care. 2010;55(12):1705–1716. [PubMed] [Google Scholar]
- 37.Agrawal D.K., Smith B.J., Sottile P.D., Albers D.J. A damaged-informed lung ventilator model for ventilator waveforms. Front. Physiol. 2021;12 doi: 10.3389/fphys.2021.724046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Sakov P., Evensen G., Bertino L. Asynchronous data assimilation with the EnKF. Tellus Ser. A: Dynam. Meteorol. Oceanogr. 2010;62(1):24–29. doi: 10.1111/j.1600-0870.2009.00417.x. [DOI] [Google Scholar]
- 39.Bocquet M., Sakov P. Joint state and parameter estimation with an iterative ensemble Kalman smoother. Nonlinear Processes Geophys. 2013;20(5) doi: 10.5194/npg-20-803-2013. [DOI] [Google Scholar]
- 40.Force A.D.T., Ranieri V., Rubenfeld G., Thompson B., Ferguson N., Caldwell E., Fan E., Camporota L., Slutsky A. Acute respiratory distress syndrome. JAMA. 2012;307(23):2526–2533. doi: 10.1001/jama.2012.5669. [DOI] [PubMed] [Google Scholar]
- 41.Baedorf Kassis E., Su H.K., Graham A.R., Novack V., Loring S.H., Talmor D.S. Reverse trigger phenotypes in acute respiratory distress syndrome. Am. J. Respir. Crit. Care Med. 2021;203(1):67–77. doi: 10.1164/rccm.201907-1427OC. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Alexander R.A., Govern D.M. A new and simpler approximation for ANOVA under variance heterogeneity. J. Educational Stat. 1994;19(2):91–101. [Google Scholar]
- 43.Thompson J.E., Jaffe M.B. Capnographic waveforms in the mechanically ventilated patient. Respir. Care. 2005;50(1):100–109. [PubMed] [Google Scholar]
- 44.Czosnyka M., Pickard J.D. Monitoring and interpretation of intracranial pressure. J. Neurol. Neurosurg. Psychiatry. 2004;75(6):813–821. doi: 10.1136/jnnp.2003.033126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Fan J.-Y., Kirkness C., Vicini P., Burr R., Mitchell P. Intracranial pressure waveform morphology and intracranial adaptive capacity. Am. J. Crit. Care. 2008;17(6):545–554. [PubMed] [Google Scholar]
- 46.Widrow B. A study of rough amplitude quantization by means of Nyquist sampling theory. IRE Trans. Circuit Theory. 1956;3(4):266–276. [Google Scholar]
- 47.Silverman B.W., Jones M.C. E. Fix and JL hodges (1951): An important contribution to nonparametric discriminant analysis and density estimation: Commentary on Fix and Hodges (1951) Int. Stat. Rev./Rev. Int. Stat. 1989:233–238. [Google Scholar]
- 48.Chiumello D., Cressoni M., Colombo A., Babini G., Brioni M., Crimella F., Lundin S., Stenqvist O., Gattinoni L. The assessment of transpulmonary pressure in mechanically ventilated ARDS patients. Intensive Care Med. 2014;40(11):1670–1678. doi: 10.1007/s00134-014-3415-4. [DOI] [PubMed] [Google Scholar]
- 49.Thacker W.C. The role of the Hessian matrix in fitting models to measurements. J. Geophys. Res.: Oceans. 1989;94(C5):6177–6196. [Google Scholar]
- 50.Wikle C.K., Berliner L.M. A Bayesian tutorial for data assimilation. Physica D. 2007;230(1–2):1–16. doi: 10.1016/j.physd.2006.09.017. [DOI] [Google Scholar]
- 51.Hunt B., Kalnay E., Kostelich E., Ott E., Patil D., Sauer T., Szunyogh I., Yorke J., Zimin A. Four-dimensional ensemble Kalman filtering. Tellus A. 2004;56(4):273–277. [Google Scholar]
- 52.Harlim J., Hunt B.R. Four-dimensional local ensemble transform Kalman filter: Numerical experiments with a global circulation model. Tellus A. 2007;59(5):731–748. [Google Scholar]
- 53.Sakov P., Oke P.R. Implications of the form of the ensemble transformation in the ensemble square root filters. Mon. Weather Rev. 2008;136(3):1042–1053. doi: 10.1175/2007MWR2021.1. [DOI] [Google Scholar]
- 54.Bocquet M., Sakov P. An iterative ensemble Kalman smoother. Q. J. R. Meteorol. Soc. 2014;140(682):1521–1535. [Google Scholar]