Contextual inference in learning and memory

Abstract

Context is widely regarded as a major determinant of learning and memory across numerous domains, including classical and instrumental conditioning, episodic memory, economic decision making, and motor learning. However, studies across these domains remain disconnected due to the lack of a unifying framework formalizing the concept of context and its role in learning. Here, we develop a unified vernacular allowing direct comparisons between different domains of contextual learning. This leads to a Bayesian model positing that context is unobserved and needs to be inferred. Contextual inference then controls the creation, expression and updating of memories. This theoretical approach reveals two distinct components that underlie adaptation, proper learning and apparent learning, respectively referring to the creation and updating of memories versus time-varying adjustments in their expression. We review a number of extensions of the basic Bayesian model that allow it to account for increasingly complex forms of contextual learning.

Placing context in context

Central to the operation of the brain is the ability to store and maintain multiple memories of the environment, and retrieve them as the need arises. The notion of context (see Glossary) has emerged as being a key component of how the brain manages this complex task: it controls whether and how much conditioned fear memories are expressed [1–3], episodic memories are recalled [4–6], spatial locations remembered [7–10] and motor skills activated [11–13]. Thus, classical work on contextual memories suggests that, by knowing the current context, the challenging problem of managing multiple memories can be reduced to the simpler problem of dealing with one memory at a time.

But what is context, and how does the brain determine the current context? To borrow from James [14], “Everybody knows what context is.” Indeed, from the experimenter’s point of view, context is usually clearly defined, e.g. by the room in which the experiment is taking place, or salient landmarks unique to an environment. However, in the real world, contexts are neither clearly defined nor labeled, and in general they cannot be unequivocally defined by the features of the environment. For example, contexts for fear conditioning in laboratory experiments are commonly operationalized by the identity of specific sensory cues or experimental chambers. But how does contextual fear conditioning happen in the wild? When a mouse escapes a ferret in a clearing of a forest, what constitutes the ‘context’ for this fearful memory? Is it the particular forest, any forest in general, the clearing, the time of the day, or the chirping of the birds in the background, or the sequence of actions that led to this traumatic encounter? Similarly, when a chef has learned to generate different knife movements under a range of contexts such as when dealing with oranges or tomatoes, what movement should she use when slicing a persimmon for the first time, and how should any motor errors update the memories for existing contexts [15]?

Here we review empirical evidence and computational models of how the brain breaks down our continuous stream of sensorimotor experience into distinct contexts such that the consequent creation, expression and updating of memories supports flexible and adaptive behavior. We emphasize the commonalities that exist across sensory, motor and cognitive domains. A common theme that emerges is that the computational task of inferring the current context is non-trivial, and the way the brain solves this task has profound consequences on the processing of memories.

Context-dependent effects on long-term memory

The role of context in learning and memory is ubiquitous. All forms of long-term memory, from declarative (semantic [16] and episodic [17]) to nondeclarative (associative [18], nonassociative [19, 20], procedural [21] and priming [22, 23]), exhibit context-dependence, whereby the expression of remembered information or learned behaviors depends on contextual factors, such as sensory cues in the environment, location and time. Here we provide some examples of paradigms that suggest context is important in the four broad areas of classical conditioning, episodic memory, economic decision making and motor learning – and a unified terminology to describe these results (see Box 1).

Box 1 - Contextual learning: a unifying view.

Although the different experimental domains in which contextual learning has been studied each have developed historically their own idiosyncratic terminologies, their paradigms can be broadly described using a common set of key concepts (Fig. 1). By definition, in contextual learning experiments, context (Fig. 1, red and blue) changes over time (typically progressing in trials). Each context is associated with a specific set of contingencies (gray boxes) defining the kind of sensory stimuli that can occur in the context, and how feedback depends on these and the subject’s actions. In general, it is useful to distinguish between two kinds of sensory stimuli that subjects can receive in a context: sensory cues and feedback. There may be sensory cues (pink; e.g. the appearance of the environment) that are informative about the context but have no further direct task-relevance. When subjects also have the opportunity to choose an action in a trial (green; e.g. a button press, or joint torques to move the arm), and in turn receive feedback (purple; e.g. reward or movement kinematics), this feedback can directly depend not only on their action but also on some specific stimuli they receive, that define (albeit, in general, only probabilistically) the current state (orange). Therefore, the critical difference between sensory cues and states is that once the context is known, only state affects feedback (i.e. is task relevant).

Collectively, the findings in different domains reveal a number of domain-general features of contextual learning. First, the internal representation of context is determined by a complex interaction between three main factors: 1) feedback signals that are performance related (e.g. rewards, punishments, movement accuracy), 2) sensory cues that have neutral valence and are not performance related (e.g. the appearance of the environment) and 3) spontaneous factors that are independent of experimentally controlled stimuli (e.g. the passage of time, or uncontrolled stimuli). Second, the effects of each of these factors are experience-dependent. This means that not only the way rewards and sensory cues are associated with different contexts is subject to learning (the first two factors) but also the propensity with which different contexts appear and transition over time (the third factor). For example, experience with more volatile environments can lead to the mere passage of time mediating more abrupt shifts in context (see also Box 5). Third, once an internal representation of context is determined, it has widespread effects on the creation, expression, and updating of memories. In general, memories related to the currently active context are predominantly expressed and/or updated, whereas new memories are laid down in contexts that are believed to be novel.

Classical conditioning

In classical conditioning [24, 25] (Fig. 1a), an unconditioned stimulus (US, e.g. a foot shock for a rat; Fig. 1a, feedback, purple) is presented with a conditioned stimulus (CS, e.g. a tone; state, orange) in an acquisition phase. Over numerous trials, the conditioned stimulus comes to elicit a conditioned response (e.g. freezing) that grows in strength and/or frequency. If the unconditioned stimulus is then withheld (change in contingency, in the gray box) in an extinction phase, the conditioned response becomes progressively weaker over trials. If acquisition and extinction are performed in distinct environments (environments A and B, respectively; sensory cues, pink), returning the animal to the acquisition environment (A) leads to re-expression of the conditioned response (ABA renewal) [26, 27]. Thus, the information learned in the acquisition and extinction phases of the experiment (that the CS does and does not predict the US, respectively) has been linked to the specific contexts defined by different sensory cues (environments A and B) and contingencies.

Fig. 1 |. Elements of contextual learning in different domains.

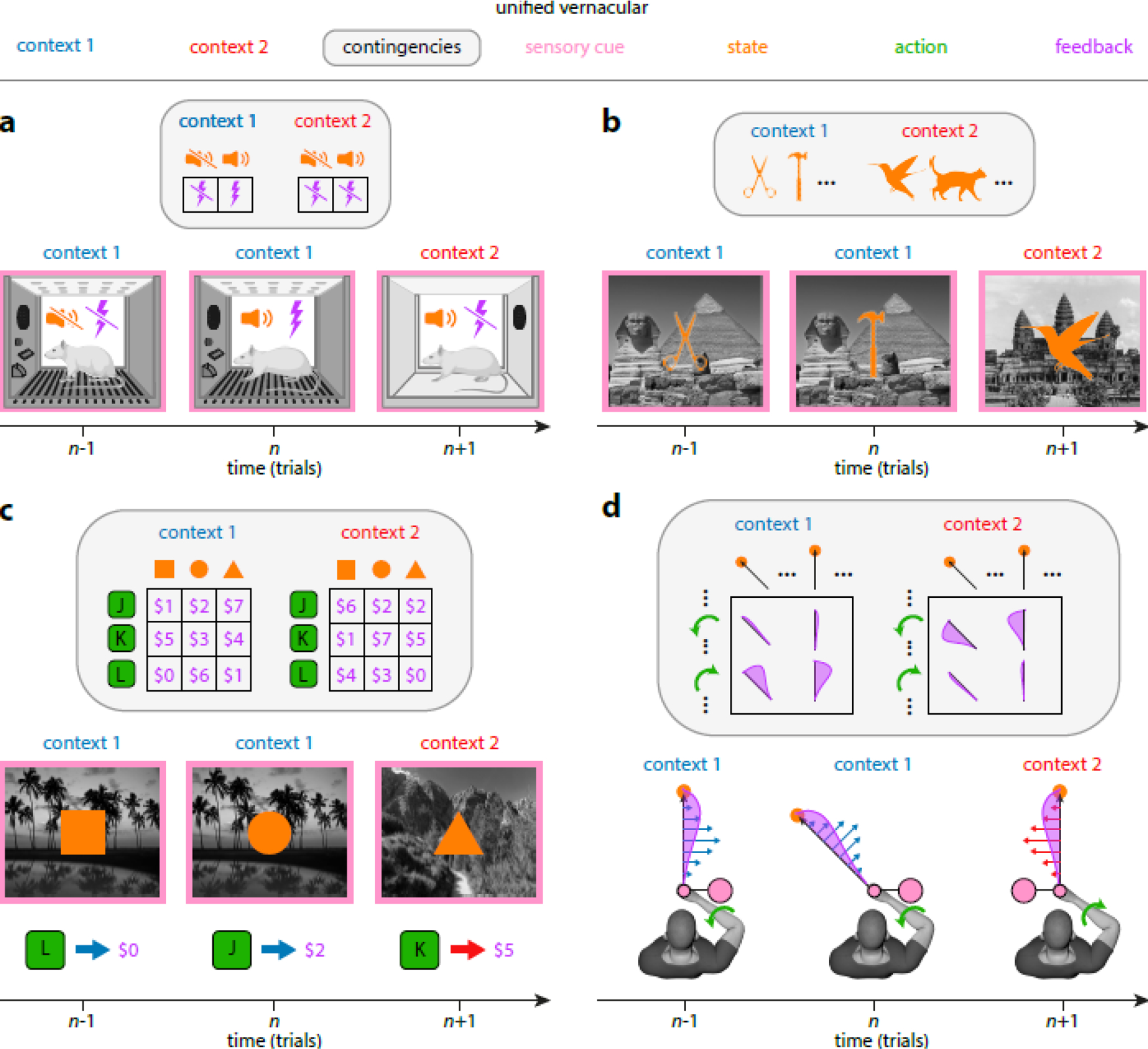
Top row shows key elements of contextual learning (color coded; see also Box 1), panels show how they apply to specific domains. Three consecutive trials in a typical classical conditioning (a), episodic memory (b), instrumental learning (c) and motor adaptation (d) task. For each task, the first two trials (trials n−1 and n) are in context 1 (blue), and the last trial (trial n+1) is in context 2 (red). Each context can be associated with an observed sensory cue (pink, conditioning chamber in a, background image in b and c, and orientation of virtual tool in d). The sensory cue is informative of the context but is not directly related to task performance. On each trial, the participant observes a state (orange, presence or absence of auditory tone in a, foreground image in b and c, and target location in d). The participant selects an action (green, no action is taken in a and b, discrete button press in c, and continuous elbow joint torque in d). Given the state and action (if applicable), the participant receives feedback (purple, presence or absence of foot shock in a, no feedback in b, monetary reward in c, and observed hand trajectory in d). The relationship between state, action and feedback is determined by the context-specific contingencies (gray box). The straight arrows in d show velocity-dependent forces produced by the handle of the robot (not shown) grasped by the participant. Note that some of the specific experimental paradigms only use a subset of these ingredients. For example, actions are usually not considered in classical conditioning (a) or (the study phase of) episodic memory experiments (b; in this case, typically there is not even feedback, but see [142]), motor learning experiments (d) often have only one state (i.e. the same target across all trials) for each context, and many paradigms do not use any context-specific sensory cues. In addition, historically, the same term has come to refer to different concepts in different domains: for example, the term “state” as used in state-space models of motor learning [72, 114, 128] refers to the concept that we here call “contingency”, while we reserve the use of the term “state” in a sense that is closest to that used in reinforcement learning [120]. Finally, sometimes terms other than “context” are used to express the same concept (e.g. “task set” or “abstract rule” in economic decision making).

While in the experiments described above, context can be unambiguously identified by the physical location or environment of the subject (indeed, the sensory cue, such as the experimental chamber, is often referred to as the “context” in these experiments), there are other phenomena which have been explained by other, more subtle notions of context. For example, reaquisition of the conditioned response a second time, after having extinguished it once, is faster than initial acquisition (rapid reaquisition, also known as savings) [28, 29]. In fact, even the (repeated) presentation of the US alone can lead to the re-expression of the conditioned response on the first presentation of the CS (reinstatement) [30, 31]. In both cases, it has been suggested that different (and opposite) memories have been laid down in the original acquisition and extinction phases, which have been linked to different contexts (rather than extinction simply erasing the originally acquired memory, as the term “extinction” may suggest) [32]. According to these theories, the presence of the US (in reinstatement) or the CS and the US (in savings) in the second phase of the experiment act as contextual cues, recalling the acquisition context and thus giving rise to the conditioned response.

The phenomenon of spontaneous recovery represents an even more intriguing case of context being implicitly defined [24, 33]. Here, after extinction, the passage of time alone can lead to the reappearance of the conditioned response. This has been suggested to be caused by a temporally evolving internal representation of context that, in the absence of salient stimuli, changes over time as fundamentally determined by its intrinsic dynamics and can eventually return to the original acquisition context [18, 34]. Moreover, the partial reinforcement extinction effect [35] suggests that even the temporal dynamics of the context representation are experience-dependent. In this paradigm, the rate of extinction of the conditioned response (assumed to be due to the emergence of the memory for the “extinction” context) is slower if the CS and US are paired inconsistently during the acquisition phase (so that the omission of the US on one trial does not necessarily imply that “extinction” will persist on the next trial) [32].

Episodic memory

The notion of context has been central to theories of episodic memory. In a typical episodic memory experiment (Fig. 1b), participants observe a state that varies from trial to trial (e.g. a visual shape in the foreground). The set of possible states depends on the current context (indexed by a sensory cue, background image), which changes on a slower timescale than the state. Recall of a memory for a state is facilitated by reinstating the conditions (i.e. context) in which that memory was originally encoded [36]. For example, spontaneous changes in context over time (similar to those thought to account for spontaneous recovery of classical conditioning or motor learning), have been suggested to underlie some of the most common effects in episodic memory recall [4, 6]. These include the recency effect, whereby the ability to recall an item (the state) declines with the passage of time since encoding or the presence of intervening items, and the contiguity effect, in which recall of an item is facilitated by the presentation or recall of an item that was presented nearby in time to the target item. Both of these effects have been accounted for by assuming a notion of context that gradually drifts over time and is in turn used to index the memory of a past item at recall. This results in recent items sharing a similar context to the current context and, more generally, temporally contiguous items sharing a similar context to one another [4] (see Ref. [37] for a review of whether context gradually drifts or abruptly shifts).

Contexts relevant for episodic memory do not seem to just simply drift at random. They have also been shown to be controlled by specific, potent sensory cues. For example, in a number of studies, participants read, watched or listened to narratives consisting of a stream of items, punctuated by event boundaries (also known as context shifts) that in turn were marked by rapid changes in perceptual, temporal or semantic information. In text narratives, time shift signals at the beginning of a sentence such as “A while later...” can act as sensory cues that are indicative of a new event [38]. A common finding is that within-event items are recalled and recognized more easily than across-event items. For example, serial recall (recall of items in the order in which they were experienced) is poorer across event boundaries compared to within the same event [38–40]. Consistent with a reduction in memory for the temporal order of items across event boundaries, recency discrimination (memory for which of two items was presented most recently) is less accurate when items are separated by event boundaries [36, 39, 41–43]. Similarly, items separated by event boundaries are remembered as being further apart in time compared to those presented within the same event [17, 42, 44]. Recognition of a previous item is also less accurate when an event boundary separates the encoding of the item and the subsequent recognition test [45, 46]. The effects of event boundaries can also be observed in more naturalistic settings. For example, walking through a doorway leads to impaired recognition of items encountered in the previous room [47, 48]. In addition, when a person returns to the same room (ABA structure), their memory for the items of that room (room A) is better compared to when they go to another room (room C, ABC structure) [47], echoing ABA renewal in classical conditioning.

While the identity of context is usually assumed to be objectively defined by the experimenter in classical conditioning paradigms, the experiments on episodic memory described above highlight how context is very much a subjectively constructed concept that is in the eye of the individual. In particular, for high-dimensional, multi-sensory naturalistic stimuli, such as movies, there is no clear and unambiguous ground-truth segmentation of the stimulus stream into discrete events, and hence event boundaries can only be determined in the first place by asking participants to explicitly report perceived event boundaries [49, 50], or by observing abrupt shifts in brain activity [51] or bursts of autonomic arousal [52] indicative of perceived event boundaries. Despite this, participants often agree on the location of event boundaries [53], and individuals who have a higher segmentation agreement score (a measure of the degree to which the event boundaries identified by an individual agree with those identified by the group) exhibit better recall, recognition and order memory performance [54–56], suggesting that normative event boundaries exist.

Economic decision making and instrumental learning

In a typical economic decision making or instrumental learning experiment (Fig. 1c), participants observe a state that varies from trial to trial (e.g. a shape), choose from a set of n actions and receive a reward (feedback) that depends on both the state and the chosen action (the contingencies). This task can be generalized to a contextual variant, in which, unbeknownst to participants, the contingencies can change depending on the context, which remains constant over a number of trials (as opposed to stimuli which can change on every trial) [57]. At the beginning of an experiment, participants do not know the contingencies, and hence they obtain relatively little reward. Then, through trial-and-error learning, they come to select better actions, as indicated by an increase in performance, and in turn obtain more reward. Following a context switch, performance drops abruptly before increasing steadily to a plateau [58–60]. This increase in performance is faster if the current context has been experienced before [59, 60] (analogous to rapid reacquisition in classical conditioning), suggesting that participants use feedback to retrieve a previously learned context-specific policy (mapping from states to actions), rather than learn a new policy from scratch. Importantly, performance increases even for those states of a context that have not been yet encountered since the reinstatement of the context, suggesting that participants retrieve entire context-specific policies rather than just the actions specific to individual states [61, 62].

By presenting context-specific sensory cues (e.g. a color), which provide a second source of information about the context in addition to the feedback, the increase in performance following a context switch can be accelerated further, suggesting that participants can use sensory cues to aid retrieval of the appropriate policy [59]. Moreover, in experiments where a single context can be associated with multiple sensory cues, contexts associated with more cues are inferred to be more probable when a new sensory cue is presented, as revealed by a preferential retrieval of the policy for the context associated with most sensory cues [63]. This suggests that the information about sensory cues associated with a context includes information at a higher level of abstraction (e.g. the diversity of cues) than just the identity of the specific cues that have already been encountered in that context. Similarly, information about state-action-feedback contingencies can also be learned at a higher level of abstraction than just a simple lookup-table. For example, in an experiment in which contexts were associated with abstract relationships between actions and feedback (defining the parametric form of the dependence of feedback on actions, e.g. linearly increasing or decreasing with key position on a keyboard, but with the exact parameters of the linear relation changing across blocks of trials of the same context), participants were able to exploit this abstract knowledge (linearity) about the contingencies to efficiently guide their exploration in novel blocks [64].

Finally, in a two-step sequential decision-making paradigm using four different contexts with a rich transition structure, participants showed learning and transfer effects indicative of having also learned this context transition structure, rather than just the contingencies corresponding to individual contexts, and their overall frequencies [65].

Motor adaptation

In motor adaptation (Fig. 1d), participants make movements (action) in the presence of a perturbation such as a viscous force field [66] or visuomotor rotation [67]. Each perturbation represents a contingency between action and the feedback (kinematic error). These perturbations are meant to be analogous to the experience of interacting with objects in the real world that have different physical properties. The abrupt introduction of a perturbation leads to large kinematics errors, which gradually decrease over trials as participants adapt their motor output to compensate for the perturbation. When two opposite perturbations (e.g. force fields with opposite directions) are presented in a random order, the memories of the two contingencies interfere such that minimal adaptation occurs. However, if each perturbation is paired with a unique sensory cue, robust adaptation to both perturbations is possible (e.g. Refs. [12, 21]). Interestingly, however, not all sensory cues are effective at reducing interference, and among those that are effective, some are more effective than others [68], and different cues engage implicit and explicit learning processes to different degrees [69]. Moreover, the effectiveness of sensory cues may change with experience as novel cue-context associations are learned [12, 13].

On a single-trial basis, sensory cues interact with perturbations to determine how much adaptation occurs: single-trial learning (the change in adaptation following a single trial with a perturbation) is greater when the sensory cue and the perturbation in that trial are indicative of the same context vs. different contexts [13]. Single-trial learning is also greater when a perturbation is likely to persist from one trial to the next compared with when it is likely to revert to the opposite perturbation [70, 71]. Thus, the dynamics of adaptation are sensitive to the environmental consistency (or its inverse, volatility). Importantly, many of the phenomena observed in classical conditioning have direct analogues in the motor domain, including spontaneous recovery [72], reinstatement (known as evoked recovery [13]) and savings [73]. Moreover, these phenomena have been shown to depend on a variety of experimental manipulations in subtle ways. For example, spontaneous recovery increases if the acquisition phase is extended [74] and decreases if the acquisition phase is preceded by a counter-acquisition phase in which the opposite perturbation is presented [75]. In addition, savings is more pronounced when a perturbation is large or abruptly introduced compared to when it is small or gradually introduced [76]. A recent study has shown that a model of motor learning that includes, at its core, contextual inference can provide a unified explanation for all these findings [13].

Bayesian theories of context-dependent learning

In Box 1, we summarize the main domain-general features of contextual learning that can be distilled from the findings presented in the previous section. These general features motivate a unifying theoretical framework for contextual learning. At the same time, they also represent the desiderata for such a theory, specifying the space of empirical phenomena that needs to be captured. We now turn to developing such a theoretical framework.

Given that, as we argued above, there is no objective ground truth for context, it is the subjective beliefs of the learner about the context that controls learning and memory. Bayesian models of cognition provide a mathematical formalism for rigorously defining such beliefs and how they should be updated in light of past and current sensory experience [77]. Under this view, context is a prominent example of a so-called latent variable that cannot be observed directly, only indirectly via its potentially stochastic effects on the observable features of the environment [78]. In particular, as we saw above (Box 1), context controls the appearance of the environment (e.g. the distribution of states or sensory cues) and other task-relevant associations, such as state-action-feedback contingencies [3, 79, 80]. Beliefs about context are then expressed as a posterior probability distribution, defining the probabilities with which the learner believes it is currently in any particular context.

In order to define the posterior distribution of a latent variable, such as the current context, Bayesian models start from a generative process that specifies the learner’s assumptions about the environment, its latent and observed variables, and their statistical relationships (i.e. how the distribution of each variable may depend on some of the other variables). This can be visualized as a graphical model consisting of nodes (representing random variables) and edges between the nodes (representing probabilistic relationships between the random variables). Fig. 2a show graphical models for a multiple-context environment (cf. the model for a single-context environment in Fig. 2b). This model captures the essence of many of the contextual learning experiments described above (Fig. 1), and uses the variables defined in our unified vernacular (Box 1). Specifically, there exists a set of contexts (indexed by c), each described by its set of (potentially temporally evolving) contingencies, $x_t^{(c)}$ (empty circles with differently colored contours), which define the probability with which different observations may be made about sensory cues (q_t, pink), states (s_t, orange), and feedback (r_t, purple), the latter also being conditioned on the subject’s actions (a_t, green). Critically, the current context c_t (blue and red filled circles) acts as a top-level “gating” variable that determines (connections with filled or empty circular heads) which contingency is currently at play, i.e. it determines the observations (black vs. gray vertical arrows, for contingencies that are gated in vs. out in a given time step, respectively). Moreover, this context variable also evolves over time according to its own dynamics (horizontal arrows in the top row), as determined by context-dependent transition probabilities (Fig. 2c, see also Box 6; transition probabilities are included in the contingencies of the current context, but to avoid clutter, the corresponding arrow from contingency to next context is not shown in Fig. 2a).

Fig. 2 |. Internal model of the environment commonly imputed to learners.

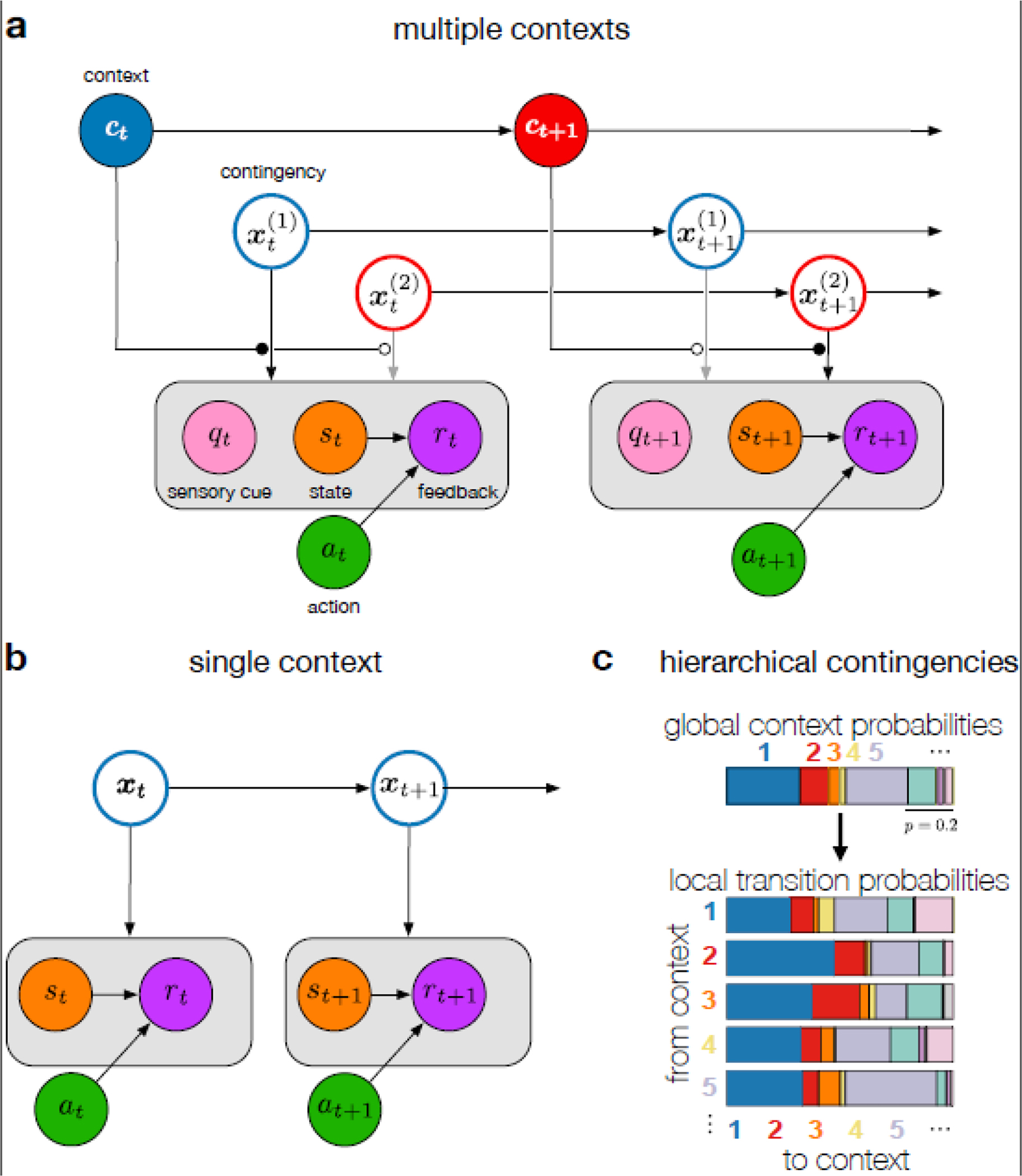
a-b. Graphical models underlying multiple context (a) and single context models (b). Temporal changes in variables (circles) are formalized by introducing multiple nodes for them, each corresponding to the value of the variable in a different time step (subscript), and then introducing directed edges (horizontal arrows) between them to describe how their future values depend on their past values (i.e. internal dynamics). The value of a variable in a given time step can also depend on other variables in the same time step (vertical arrows). a. Multiple-context model [12, 13, 58, 59, 95]. Contexts (top nodes, color represents the identity of the active context) evolve according to Markovian transition probabilities. Each context has its own contingency (only two shown for simplicity; in general, the number of contexts and contingencies can be unbounded). Contexts can also be associated with sensory cues (pink) of which the appearance probabilities are also dictated by the context-specific contingencies. Only the contingency associated with the active context influences the observed sensory cue, state (orange) and feedback (purple) variables (gating by context, black vs. gray arrows). Feedback can depend on both an observed state and an action (green). In general, the active contingency can also affect the next context transition (for clarity, arrows not shown). In addition, states may not be directly observable and may have their own (action-dependent) dynamics [120] (also not shown for clarity). Gray box indicates that the contingency, x_t, determines the joint distribution of the variables inside the box (here: q_t, s_t and r_t) b. Single-context model [57, 119, 116] in which only a single contingency exists. c. Hierarchical contingencies: an example of transition probabilities (as generated by a hierarchical Dirichlet process). The set of probabilities for transitioning ‘from’ each context (bottom, horizontal multicolored bars, with the width of each stripe showing the probability of transitioning to each ‘to’ context) is a variation on a global set of probabilities (top). This way, learning about the local transition probabilities in a particular context informs inferences about global transition probabilities, in turn informing inferences about other local transition probabilities, even for context transitions that have not yet been observed.

Box 6 - Hierarchical Bayesian models.

In hierarchical Bayesian models, the prior distributions of the “local” parameters, determining the context-specific contingencies, depend on a shared “global” hyperparameter, which in turn has a hyperprior distribution of its own. During inference, both the local parameters and the global hyperparameters of the prior distributions are learned, with the latter supporting learning-to-learn or meta-learning. Thus, this hierarchical organization induces dependencies between the contingencies of each context during learning. That is, experience in one context will lead to the global hyperparameters being updated, and this in turn will cause the contingencies of all contexts to be updated. Consequently, in the small-data regime, hierarchical models support well-informed inferences about the contingencies of previously experienced contexts (backward transfer) as well as future contexts that have yet-to-be experienced (forward transfer). In particular, rather than having to learn the contingencies of each new context from scratch, which would be inefficient, the learned prior distributions of the contingencies can be exploited to initialize the contingencies of a new context in a sensible way such that they only require fine tuning, thus allowing rapid improvement in performance [169, 170].

In cognitive science, hierarchical Bayesian models have been used to explain how humans learn concepts [171], abstract knowledge [172] and inductive biases [173]. In the context of contextual learning, the hierarchical Dirichlet process (HDP) is a Bayesian nonparametric model [174] that has been proposed as a model of how humans balance the trade-off between specialization and generalization in multiple-context environments [13]. Specifically, the HDP was used to define a distribution on a context transition matrix in a hierarchical manner, such that each local transition distribution (row of the transition matrix), corresponding to the transition probabilities when starting from each specific context, depended on a global transition distribution that was shared across contexts, determining the expected overall frequency of each context (Fig. 2c).

While building on the same theoretical concepts, this hierarchy in the contents of contexts (the contingencies) is different from the hierarchical representation of the contexts themselves we discuss in Box 4. For example, even with a simple “flat” representation of contexts, contingencies can still be organized hierarchically. Indeed, a hierarchical representation of the transition probabilities between contexts (one component of their contingencies) has been shown to underlie spontaneous recovery and anterograde interference in motor learning – without invoking a hierarchical representation of contexts per se [13].

For example, for the mouse in the forest, relevant sensory cues may be the density of trees, and the lighting conditions, states may be associated with the appearance or absence of a ferret, actions may include searching for food or trying to escape, and feedback may be related to consuming food vs. being consumed. This mouse may distinguish two contexts, associated with a safe and unsafe environment depending on whether there are nearby predators, with the probabilities of observing different sensory cues and states, and receiving different feedback for different action (the contingencies), under each context likely being different. The longer the mouse waits near a watering hole, the higher the probability of being in the unsafe context may become (context transitions).

According to the generative process underlying contextual learning (Fig. 2a), both the current context, c_t, and the contingencies corresponding to each possible context, $x_t^{(c)}$, are latent variables. Thus, the Bayesian contextual learner needs to simultaneously infer both of these quantities. Note that, in Bayesian models, inference is uniquely determined in principle (at the computational level of analysis) as the probabilistic inversion of the generative model, without any free parameters or process-level assumptions (although in practice, algorithmic-level choices may still need to be made; Box 2). Specifically, inferences about $x_t^{(c)}$ constitute a (long-term) memory of context c. As we discuss below, this is compatible with how classical single-context theories of learning formalized the contents of memory (Fig. 2b) and accounted for a broad range of empirical findings in simple (single-context) learning paradigms. However, the Bayesian contextual learning model also requires inferences to be performed and continually updated about c_t. Therefore, the learner needs to infer the probability that each context is currently active. In some situations, such as when our mouse is in the jaws of a ferret, the sensory evidence may be overwhelmingly in favor of the unsafe context, such that the probability of this context is effectively 1, whereas when our mouse moves from a shrub into a clearing it may infer an intermediate probability for the unsafe context. In the next section, we describe the functional consequences of these inferences, and how they should ultimately be reflected in behavior.

Box 2 - Curbing the complexity of contextual inference.

The task of the Bayesian contextual learner is to infer (by applying Bayes’ rule) the joint posterior distribution over all latent variables ${ℒ}_t$ (i.e. the set of contingencies, $x_t^{(c)}$, and contexts, c_t, see Fig. 2a) given the history of all observed variables ${𝒪}_{0:t}$ (i.e. the sequence of sensory cues, q_0:t, states, s_0:t, actions, a_0:t, and instances of feedback, r_0:t). This inference process performs a probabilistically appropriate inversion of the generative process we described in the text (and Fig. 2a). In general, this inversion would require computing a posterior, $\text{P}\left({ℒ}_{0:t}\mid {𝒪}_{0:t}\right)$, over the whole history of latent variables up to the current time point, t, as a function of the whole history of observations. However, in reality, it is often only the posterior over the latent variables for the last (or a couple of most recent) time step(s), $\text{P}\left({ℒ}_t\mid {𝒪}_{0:t}\right)$, that is required by downstream computations. Moreover, this posterior can typically be computed online, in a recursive manner, such that the posterior computed in the previous time step can be combined with observations in just the last time step, so that no memory for all previous observations is required:

$$\stackrel{\text{new}\text{posterior}}{\overbrace{\text{P}\left({ℒ}_t\mid {𝒪}_{0:t}\right)}}\propto \underset{\begin{array}{c}\text{information}\text{from}\\ \text{current}\\ \text{observations}\end{array}}{\underbrace{\text{P}\left({𝒪}_t\mid {ℒ}_t\right)}}\int \underset{\begin{array}{c}\text{internal}\text{model}\text{of}\\ \text{latent}\text{dynamics}\end{array}}{\underbrace{\text{P}\left({ℒ}_t\mid {ℒ}_{t-1}\right)}}\stackrel{\text{previous}\text{posterior}}{\overbrace{\text{P}\left({ℒ}_{t-1}\mid {𝒪}_{0:t-1}\right)}}\text{d}{ℒ}_{t-1}$$ (1)

Note that Eq. 1 also exposes how inference is fully determined by the generative process: the first and second term on the right hand side respectively correspond to the vertical and horizontal arrows in Fig. 2a.

Nevertheless, even in the simplest case (such as that shown in Eq. 1), computing the posterior may still be radically intractable, and so only an approximate version will be computed. The precise nature of the approximations the brain might be using for this is unknown (see Outstanding Questions). Here we simply assume that they are sufficiently accurate to yield the basic effects of contextual inference we describe below that would follow from (near)-exact computations. In fact, sometimes even simple-looking heuristics can efficiently approximate such complex-looking computations [11, 58, 85, 143–145]. For example, it may be possible to show that successful process-level models of contextual effects on episodic memory [4, 146] correspond to approximate forms of inference under a model such as the one we present here.

Approximate forms of inference may even provide a better account of data than exact inference. For example, it has been suggested that the classical, smoothly increasing (and eventually asymptoting) learning curve in classical and operant conditioning (such as those simulated in Fig. 4) is an artifact of group averaging. Instead, individual subjects show abrupt steps in behavioral responses that fluctuate bidirectionally, with decreases as well as increases in performance after an initial rise to an unstable asymptote [147]. Behaviors such as these cannot easily be accounted for by exact contextual inference, where both the estimated contingencies and context probabilities change gradually over time. However, they may arise from a particularly powerful approximation that is based on using Monte Carlo samples to represent complex posterior distributions [78]. Indeed, sampling-based approximations have been suggested to underlie a number of cognitive [148] as well as neural phenomena [100]. Specifically, in the context of learning, they have also been suggested to underlie contextual inference [13, 58, 149] and account for the kind of abrupt and bidirectional fluctuations in performance that had been described empirically [149].

Note that here we have assumed a graphical model with a fixed structure underlies inference in contextual learning. However, classical conditioning experiments suggest that context may play diverse roles in associative learning, such that animals can treat it as having a purely modulatory or additive effect on contingencies, or deem it altogether irrelevant [81, 82]. This diversity has been accounted for by Bayesian theories assuming that animals consider alternative structures for the generative model, each being a special case of the one we present here, and perform hierarchical inference over these structures, treating the correct model structure as “just another” high-level latent variable to be inferred [83]. Whether such hierarchical learning of multiple simpler structures is a better account of these phenomena than learning the contingencies within a single more complex structure remains to be tested.

Consequences of contextual inference

The posterior distribution over contexts expresses the probability that each known context or a yet-unknown novel context is currently active. In turn, this posterior controls the expression, updating and creation of memories as we detail below.

Contextual mixing for memory expression

If the current context, and its corresponding contingency, were known to the learner, then choosing the best action at a given time would be straightforward (even if tedious): the learner would need to select the action that is associated with the most desirable (highest utility) feedback according to this contingency. Thus, behavior would be driven only by a single memory – that corresponding to the current context. However, given that, in general, there is uncertainty about the current context, as expressed by the posterior over c_t, in principle the memories for all contexts need to be consulted [13, 58, 84–87]. Specifically, according to the rules of Bayesian decision theory [88], the expected utility of each action can be computed by averaging its utility across contexts, weighted by the posterior context probabilities, and the action with the highest expected utility can be chosen. When the utility of an action is defined as the squared error from some context-dependent target action (for every context), such as in motor control [89] (but see Refs. [90–92]), the action with the highest expected utility is simply the weighted average of the target actions in each context, with the weights given by the posterior context probabilities.

The critical insight in all these cases is that the contents of several memories (those associated with contexts that have a non-zero probability) need to be mixed for optimal behavior. This is notably different from classical accounts of memory recall that focus on how a single memory is retrieved at a time [93, 94]. Similar to these classical theories, several recent models of context-dependent learning also express a single memory on each trial – the memory associated with the single most probable context – rather than mix memories [59, 76, 95]. In doing so, they ignore uncertainty about the context, which, in general, will lead to suboptimal action selection. Interestingly, in the domain of motor control, the idea that the output of different modules mix linearly “on demand” has been quite well accepted [11, 96–98], but its relationship to contextual inference, and more generally the factors governing the mixing proportions have not been explored until recently [13]. In contrast, there have only been sporadic suggestions for such mixing of memories in the domains of episodic [86], spatial memory [10] and human instrumental learning [58], and these have not been supported experimentally by a systematic analysis of behavior.

Contextual de-mixing for memory updating and creation

Once feedback is received, after having executed an action, the contextual learner is faced with a difficult credit assignment problem [11, 85]. As it is uncertain which context is currently “active”, it is not obvious which context was responsible for the feedback and hence which memory should be updated by it. Once again, the posterior distribution over contexts holds the normative solution to this problem [13, 58, 87, 99–101]. In particular, the same feedback now needs to be de-mixed, such that all memories are updated in proportion to the posterior probabilities of their corresponding contexts. In other words, the same memory needs to be updated with an effective learning rate that is dynamically modulated depending on the posterior probability assigned to its corresponding context at any given time.

Given that exact inference in multiple-context models is often intractable (see Box 2), a computationally cheap alternative that is commonly used in models of human learning [59, 76, 86, 95] is to definitively assign each trial to the context with the highest probability. However, this approximation ignores uncertainty about the context and leads to only a single memory being updated on each trial. This non-Bayesian heuristic has been justified on the basis that it does not qualitatively affect model behavior [86, 95] compared to more properly Bayesian methods [13, 58]. However, this is likely to only be true for paradigms that do not directly test how memories are updated on a single-trial basis, as we discuss below.

Just as memory recall should not be confined to retrieving a single memory, in general, memory updating also needs to occur in parallel for multiple contexts. Although this may sound somewhat unorthodox, compared to conventional concepts of memory processing (e.g. the updating of episodic memories by consolidation or reconsolidation [102]), there is experimental evidence for such de-mixed memory updating. In motor learning, a recent experiment specifically introduced a cue-conflict situation to increase contextual uncertainty at the time of memory updating [13]. This allowed the demonstration of the graded (de-mixed) updating of two different motor memories as predicted by contextual de-mixing. While this graded updating was evident at the level of individual subjects, whether it was also graded at the level of individual trials, or might have been approximated by probabilistic all-or-none updating, has not been resolved (see Outstanding Questions).

Outstanding Questions Box.

• Current models of context-dependent learning only ever update existing memories or add new ones. Does the brain also reorganize existing memories, such as by pruning or merging existing memories? Does sleep play a role in the reorganization of memories? How are these operations related to classically described memory processes such as consolidation and reconsolidation?

• How can proper and apparent learning be measured and distinguished at the behavioral and neural levels? Beside recently described effects on overt behavior, are there covert behavioral signatures of proper and apparent learning? For example, does contextual uncertainty – a hallmark of apparent learning – manifest in reactions times, reflex gains or pupil size?

• How does the brain represent contexts in a compositional manner? By composing novel contexts from other known contexts, compositional representations can support combinatorial generalization.

• Does the brain represent contexts and their contents hierarchically, and if so, what kind of hierarchy is it (which aspects of the contingencies does it involve, beside transition probabilities) and how deep is the hierarchy?

• How domain-general is the simultaneous and graded expression and updating of multiple memories that has so far only been demonstrated empirically in motor adaptation? When expressing multiple memories, are there ways of combining them other than just a simple average? Can multiple memories be updated simultaneously on a single trial, or is only one memory updated at a time, with graded updating emerging only due to averaging across trials?

• Does the brain use a fixed number of memories at all times, simply discounting those that have not been linked to a previously encountered context, or does it dynamically add new memories on the go as the need arises?

• Is there a specialized brain area for computing timescales general-purpose contextual inferences, or are there distinct areas performing domain-specific forms of contextual inference, perhaps at different time scales?

• How are the effects of contextual inference on memory creation, updating, and expression implemented mechanistically in neural circuits? Given that exact contextual inference is intractable, what approximate algorithms does the brain use for it? What neural code is used to encode graded uncertainty about context? How do these processes play into continual learning in biological circuits?

Sometimes, all existing memories seem inappropriate in a situation, and so updating them, even if with the appropriate de-mixing, would be inappropriate and instead an altogether new memory needs to be created. Indeed, classical accounts of memory creation often highlight the importance of novelty or prediction errors in mediating this process [3, 5]. In line with this, if contextual inference is performed over an open-ended set of contexts, also allowing for yet-unseen novel contexts, contextual de-mixing automatically gives rise to memory creation when the posterior probability of a novel context (the formal definition of ‘novelty’ in this framework) is sufficiently high. A fundamental prediction of memory creation being driven by contextual inference is the widely observed hysteretic “boiling frog effect”: a single abrupt change in the environment often triggers the creation of a new memory, but many small changes adding up to the same total effect typically do not. This is because after each small change, the memory of the current context may still seem appropriate, albeit a little off, and so updating it is justified by contextual inference, that is its probability under the posterior is high (Fig. 3a, top). An abrupt transition to a novel situation leads to the probabilities of all known contexts being low, and thus (because probabilities need to sum to one), the probability of a novel context must necessarily be high (Fig. 3a, bottom). This effect has been described in a number of different domains. In episodic memory, small changes to sensory stimuli have been suggested to lead to a gradual updating of their memories, whereas abrupt changes lead to the laying down of new memories [86]. This principle was shown to also account for event segmentation in naturalistic videos [103]. Analogous effects are seen in place cell remapping, a putative neural correlate of the inference of a new context [104], and the concomitant creation of new spatial memories [105] (but see Ref. [106]): remapping depends non-linearly on the similarity of environments [107], and is diminished by the gradual introduction of environmental changes [108]. In motor control, savings is greater for an abruptly (versus gradually) introduced perturbation [109] and de-adaptation is faster after the removal of an abruptly (versus gradually) introduced perturbation [110], as in these cases multiple memories are thought to have been created, allowing flexible switching between them. Similarly, in classical conditioning, the gradual extinction of a CS-US pairing prevents fear recovery (spontaneous recovery and reinstatement), as the memory learned in the acquisition phase is unlearned, in contrast to when extinction is abrupt and a new memory is created, thus preserving the original memory [111, 112].

Fig. 3 |. Classical paradigms explained by contextual inference.

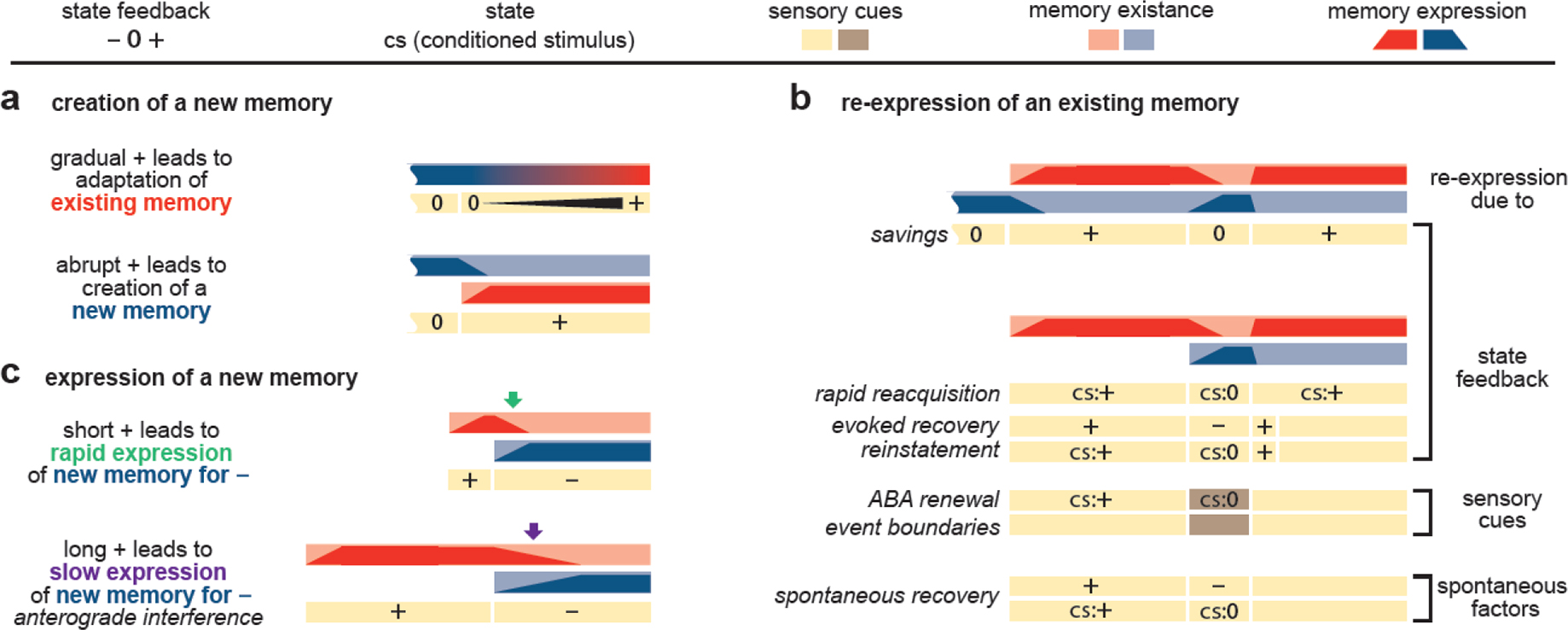
Each paradigm is schematically represented by three rows (two rows in panel a, top). The bottom row (rows in panel b) with yellow/brown colored bars shows the time course of the experiment in terms of state feedback (positive, +, negative, −, null, 0, or absent, blank), sensory cues (yellow and brown), and state (CS). For motor control, +, 0, and − reflect the strength and direction of a perturbation applied to the hand during reaching. For conditioning +, and 0 reflect the presence/absence of a US. The top two rows (top row in panel a, top) with red/blue colored bars show the memories that are relevant to the experiment (red for +, blue for 0 or −); for each memory, the bar with pale background extends from the time the memory was created until the end of the experiment (scalloped edge reflects a pre-existing memory). Dark shading within each bar shows the expression of the corresponding memory at each point in time (the height of the dark shading represents the level of expression, between 0 and 1, with the expression across existing contexts summing to 1). Below we highlight the paradigms (see main text and Box 3 for details of the paradigms and explanation of the mechanisms). a. Top: for a gradually introduced perturbation (black expanding triangle in second row) the existing memory is updated (blue changing to red in first row). Bottom: memory creation occurs for an abruptly introduced perturbation. b. Paradigms in which an initially learned memory (red) is re-expressed later in the paradigm after another memory has been expressed. Re-expression can rely on the state feedback, sensory cue or spontaneous factors. c. New memory expression. Anterograde interference, in which learning a second contingency (here, − perturbation) is slower if another contingency (here, + perturbation) has initially been learned, with the amount of interference increasing with the length of initial learning (long + vs. short +), that is when the environment is less volatile. Green and purple arrows to point to rapidly vs. slowly changing levels of memory expression, respectively.

Proper and apparent learning

Contextual mixing and demixing also provide a new lens onto one of the most classical phenomena in experimental psychology: the learning curve. A learning curve shows a gradual improvement in performance (or “adaptation”) on a task over time (typically, consecutive trials) as training, or learning proceeds. As such, the traditional interpretation of a learning curve has been that a memory (or a collection of memories) is being incrementally updated, and the behaviorally observable gradual changes in performance are due to these memory updates. Indeed, classical [25, 113, 114] and more modern [72] models of learning directly postulate this mechanism. Fig. 4a shows a simple simulated example of such proper learning. However, the dependence of memory expression on context probabilities means that adaptation can also arise from a distinctly different mechanism: apparent learning [13]. Apparent learning refers to a change in contextual mixing in memory expression due to an update in the estimated context probabilities (Fig. 4b). Indeed, apparent, rather than proper, learning may underlie a host of phenomena that had traditionally been attributed to proper learning (Box 3). Of course, adaptation can also arise from a mixture of proper and apparent learning (Fig. 4c).

Fig. 4 |. Identical learning curves can arise due to proper or apparent learning, or their combination.

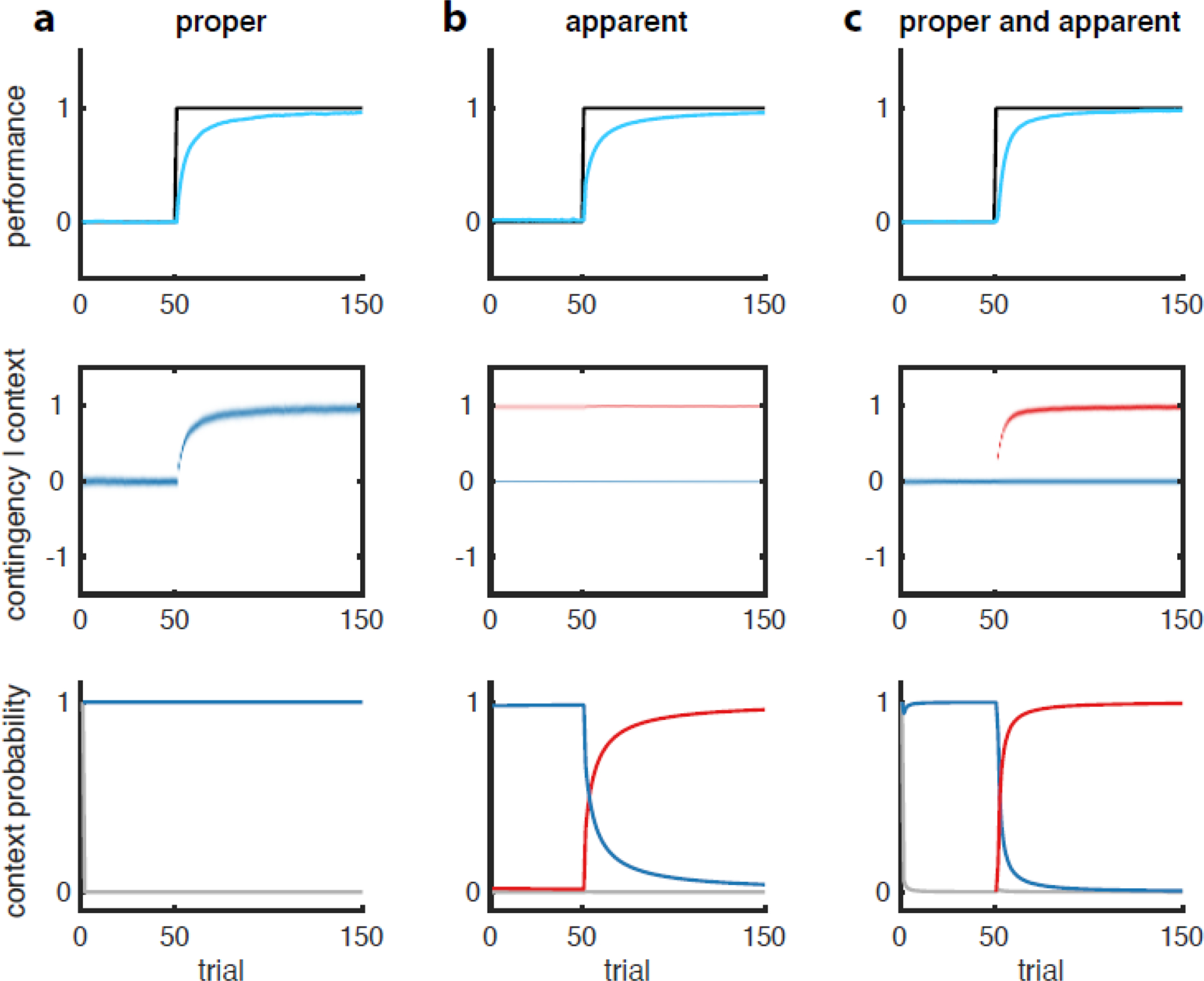
Simulations of a model of contextual learning [13] in response to a step change in a (deterministic) contingency (black line, top row) under three different scenarios (a-c). The three scenarios unfold under different parameter settings and initial conditions (e.g. 1 vs. 2 memories). Task performance (top row, cyan) is a mixture of the inferred contingency distributions for each context (middle row, blue and red). For simplicity, each inferred contingency directly determines a response magnitude appropriate for the corresponding context. The mixture is weighted by the associated context probabilities (bottom row, blue and red – gray shows the probability a potential novel context). a. Pure proper learning: the “contingency” corresponding to the relevant state (e.g. defined by the presentation of the CS, or a movement target) is simply a scalar, such as the probability of receiving the US as feedback in that state, or the magnitude of force perturbation when reaching to that target. In naive subjects, the estimate of this contingency is initially 0, and over training it is increased as the CS is consistently paired with US, or the force perturbation with the target (middle row). This gives rise to a classical learning curve. Note that in this example, contextual inference plays no role whatsoever, as (the simulated subject assumes) there is only a single context at play at all times of which the probability can thus only be constant one at all times (bottom row). b. Pure apparent learning: an existing (red) memory whose contingency has previously been updated to some non-zero level (here taken to be 1, for simplicity) is expressed more over time, relative to a baseline memory (blue, taken to be at zero), as its associated context is inferred to be active with increasing probability (bottom row, probability of red context increases). Thus, memory updating plays no role here, as the estimated contingencies for both contexts are constant through time (middle row). c. Mixture of proper and apparent learning: a new (red) memory is created and updated but also expressed more over time. Critically, these distinct forms of learning can produce identical adaptation curves (a-c, top panels), despite having radically different internal representations (middle and bottom panels).

Box 3 - Apparent learning phenomena.

Fundamental to apparent learning is the idea that stored memories can lie dormant without being fully expressed. This is analogous to the phenomenon of retrieval failure, whereby information stored in memory is temporally inaccessible, such as when a word is on the tip of the tongue [150]. It has been suggested that retrieval failure, like apparent learning, occurs when the context in which a memory was encoded (the learning context) differs from the current context (the test context) [18]. Consistent with this interpretation, retrieval failure can be overcome if sensory cues associated with the learning context are presented at test time [16], reminiscent of reinstatement and evoked recovery. However, whereas the term retrieval failure has negative connotations, apparent learning is a consequence of optimal Bayesian contextual inference, and hence memory suppression (retrieval failure) can be viewed as a normative phenomenon.

Apparent learning has recently also been suggested to underlie several classical learning phenomena [13]. According to this account, rapid reacquisition (savings) occurs because the acquisition context is inferred to be more probable the second time it is experienced, and hence its associated memory is expressed more (Fig. 3b). Spontaneous recovery occurs because the acquisition context is inferred to be more probable following the passage of time based on the dynamics of context transitions, and hence its associated memory is re-expressed (Fig. 3b). Evoked recovery/reinstatement and ABA renewal occur because the re-presentation of sensory feedback (evoked recovery/reinstatement) or sensory cues (ABA renewal) associated with the acquisition phase provides strong evidence that the acquisition context is active again, and hence its associated memory is re-expressed (Fig. 3b). Anterograde (or pro-active) interference means that adaptation to a given contingency, or the study of some information (acquisition phase), can slow down subsequent adaptation to a new contingency, or impair the memory of more recently studied information, with this effect becoming stronger when the acquisition phase lasts for longer [18, 151, 152]. This happens because extensive experience with the first contingency makes the learner believe it is less probable that they will transition to any other contingency, and hence the memory associated with the second contingency is expressed less (Fig. 3c). Environmental consistency (the inverse of between-context volatility, Box 5) can affect single-trial learning simply through apparent learning. That is, in a more (less) consistent environment there is a higher (lower) probability with which the current context is expected to persist to the next trial, leading to more (less) expression of an updated memory (even though the same amount of proper learning takes place across those environments).

Varieties of context-dependent learning models

The theoretical framework developed above can be modified or generalized in a variety of ways to capture distinct features of the environment and the corresponding features that characterize learning about the environment. This can be achieved by incorporating alternative modeling assumptions into the generative process, which in turn alters the inference process and the organization of experience into context-specific memories.

Single- vs. multiple-context models

Most models of learning do not have a notion of context. Some of these have been explicitly cast in similar Bayesian terms as the contextual learning model we describe above, such as Kalman filter-based models of motor learning [115], or classical conditioning [116], or models of economic decision-making with Bayesian priors on reward contingencies [57, 117]. As such, the generative model underlying these models is a special case of that shown in Fig. 2a, in which there is only one set of contingencies that is always active (Fig. 2b, Fig. 4a).

Importantly, even classical models that have not been formalized as Bayesian models originally can often be re-derived as being equivalent to such models (for example, see Refs. [118] and [119] for Bayesian treatments of the Rescorla-Wagner model [25] of classical conditioning, and of state-space models [72, 114] in motor learning, respectively). Once formalized in this way, a comparison to the general multiple-context case of Fig. 2a immediately exposes the fundamentally single-context nature of these models. This may be puzzling at first, as some of these models also suggest the presence of several memory traces (represented as prediction weights associated with different stimuli [25], or processes associated with different underlying learning and/or retention rates [72]), which may appear to be similar to the multiple memories that correspond to distinct contexts in the model of contextual learning we describe above (i.e. inferences about $x_t^{(c)}$ for each c). However, there is a critical difference between these notions of multiple memories. In the contextual learning model, the observations in each time step are assumed to be generated by a single context at a time. As a consequence, when a context is inferred not to have been responsible for the observations through some period of time, its memory is preserved (modulo assumptions about the intrinsic ongoing dynamics of its contingencies), and – by the virtue of apparent learning – it can be easily reinstated once the context is inferred to be active again. Single context models with multiple memory traces assume, even if implicitly, that all contingencies represented in these traces contribute (with fixed relative weights) at all times, and thus also express and update all these traces at all times. As a consequence, there is no “going back” to a previously represented mental state, unless by re-learning. In other words, single-context models are unable to show apparent learning by construction, and it is this inability that prevents them from going back. Multiple-context models can further differ in the representation that indexes the current context in them. This can be as simple as a pointer to one of a discrete number of different contexts, as we assumed above, or more complex, using compositional or continuous representations (Box 4).

Box 4 - Simple vs. complex context representations.

In the main text, we have formalized the notion of context simply as a discrete latent cause. Such simple latent-cause models [3, 13] assume that exactly one latent cause is active at each point in time, and hence there is a one-to-one mapping between latent causes and contexts. In contrast, compositional latent-cause models [1, 79, 80] assume that multiple latent causes can be active at each point in time, and hence a context is formalized as a unique combination of latent causes. Importantly, such compositional representations allow powerful forms of generalization, as previously experienced latent causes can be combined in new ways to represent novel contexts [153]. For example, in grid-world navigation tasks, humans represent the context compositionally (when beneficial to do so) by inferring separate latent causes for the reward function (goal location) and the state transition function (mapping from states and actions to next states), allowing new tasks to be learned quickly by representing them as novel combinations of previously experienced reward and state transition functions [154, 155]. Likewise, in motor control, we may be able to draw upon our prior experience with different objects so as to combine them to control a novel object [156, 157].

Contexts may also vary on a continuum, rather than each being an island entire of itself, equidistant from all other contexts. In this case, the contingencies for different contexts need (and should) not be assumed to be independent a priori, and instead their similarities and dissimilarities can be assumed to reflect the metric relationships between the contexts themselves. Once again this can result in greatly improved generalization. For example, having learned to control objects that all lie on the same object manifold (e.g. bicycles of different wheel diameter, weight, and height), we can quickly adapt to novel objects on the same manifold [158, 159].

Whether discrete, compositional, or continuous – all the aforementioned representations are “flat”. Instead, contexts may be hierarchically organized, as in the example given in the introduction: the mouse’s encounter with the ferret may be associated with multiple contexts at different levels of a hierarchy, identifying the forest in which the encounter happened, the specific clearing within the forest, and the scrub in the clearing. Moreover, these contexts may evolve on different timescales [51, 160]. For example, the mouse moves between forests relatively slowly but, within a forest, darts from shrub to shrub. Indeed, there is evidence that even random material is organized hierarchically in memory [161], suggesting a strong inductive bias for hierarchical context representations. To accommodate these inductive biases, the generative model underlying contextual learning that we proposed above (Fig. 2a) can be extended with a hierarchical representation of contexts [162, 163].

A critical difference between single and multiple-context models is the way they interpret environmental variability, that is volatility. While single context models have to assign volatility to changes in the contingency, multi-context models can assign the same volatility to either changes in contingencies or to changes in the context (see Box 5).

Box 5 - Volatility.

In classical single-context models of learning, the volatility of the environment is defined as the trial-to-trial variability of the contingencies. In the Kalman filter [116, 164] (Fig. 2b), this variability is determined by the variance of the “process noise”, the noise in the temporal evolution of contingencies (x). Greater process noise in the generative model produces greater uncertainty during inference and hence a larger Bayes-optimal learning rate [119, 165, 166]. However, in multiple-context models, the term volatility has been used to describe an alternative property of the environment [58], namely how likely the context is to switch from one trial to the next, as determined by the context transition probabilities.

Unfortunately, these distinct types of volatility, which we refer to as within- and between-context volatility, have sometimes been conflated. For example, single-context models that estimate within-context volatility have been used to draw inferences about how humans learn in multiple-context economic decision-making tasks, where the reward rate stays fixed for a number of trials but occasionally switches (e.g. between 0.2 and 0.8) from one trial to the next in a covert manner (i.e. without explicit cues) [57, 165]. When rewards are generated by such a switching multi-context process, a single-context model learns that the within-context volatility has increased (as a single, context-invariant reward rate is assumed to have jumped from 0.2 to 0.8, or vice versa), despite the fact that the true within-context volatility of the generative process is actually zero (the reward rate in each context never changes). Indeed, the learning rate of subjects exposed to such a process has been shown to increase with more switching – as revealed by fitting the learning rate of a Rescorla-Wagner model (a paradigmatic single-context model, as discussed above) to their binary choices [57, 167]. This is as it would be expected from a single-context learner that adjusts its learning rate to the volatility of the environment. However, more recently, it has been shown that changes in memory expression due to contextual inference in a multiple-context model can mimic changes in the learning rate of a single-context model [13]. Specifically, in an analogous setting in motor adaptation, environmental consistency (the inverse of between-context volatility) has been shown to underlie apparent changes in learning rate (Box 3). This leaves open the possibility that earlier results on the effects of reward rate switching on (apparent) learning rates [57, 167] reveal signatures of contextual inference, rather than providing evidence for the adjustment of (proper) learning rates per se (see also [168]). Using the appropriate (multiple-context) model class for a model-based (re)analysis of the data will be necessary to properly adjudicate between these hypotheses.

Static vs. dynamic contingencies

A critical design choice is whether the context-specific contingencies are assumed to be static over time or time varying. (Note that even inferences about static contingencies will vary over time as more experience is accrued.) This choice remains relevant even for non-Bayesian models of learning. For example, models in which memories are biased towards recent observations (e.g. by using a constant learning rate) and/or change even in the absence of experience (e.g. due to adaptive forgetting) implicitly assume that contingencies are time varying [25, 59, 72]. In contrast, models in which memories depend equally on all past observations (at least within the same context, e.g. by using a learning rate that scales inversely with the number of observations) and do not change in the absence of experience implicitly assume that contingencies are static [120].

All current models of motor learning (regardless of whether they assume the environment consists of a single context or multiple contexts) agree that time-varying contingencies are critical for capturing the dynamics of motor memories [12, 13, 70, 72, 76, 99, 114, 119, 121–128]. Similarly, the most widely used models of conditioning and simple economic decision making tasks use a constant learning rate, thus implicitly assuming time-varying contingencies [25, 129]. In contrast, models of context-dependent economic decision making tasks have typically not considered the notion of time-varying contingencies [58, 59, 85, 95]. Bayesian models of these tasks assume that contingencies (reward functions) are static and thus weight all observations within the same context equally [58, 95].

Context transition dynamics

Once the notion of multiple contexts is introduced, inferring the current context becomes critical, as memory creation, expression and updating all depend on this inference. In turn, this inference depends on the context dynamics, that is the transition probabilities between contexts. The simplest class of models assumes uniform transition probabilities (with the potential exception of a self-transition bias that makes the “from” context the most probable), thus implying some fixed level of between-context volatility [59] (Box 5). A somewhat richer class of models breaks this (near) uniformity by having transition probabilities depend on the “to” context (thus differentiating the overall frequency of contexts) but constraining them to be the same for each “from” context [95, 104]. Again, a self-transition bias can be added [86], which might itself change over time in varying-volatility models (i.e. models with time-varying between-context volatility) [58]. Such models are not able to account for differences in learning that arise in environments that differ only in the transitions between contexts, such as the effect of environmental consistency on single-trial learning [70, 71] (Box 3), spontaneous recovery and the recently demonstrated learning of rich context transition structures in a two-step sequential decision making paradigm [65].

At the other extreme are models in which transition probabilities depend on both the “from’ and “to” contexts, without any additional constraints [84]. While these models are very flexible (i.e. they can learn any context transition matrix), they afford no generalization across contexts, such that the transition probabilities from each newly encountered context need to be learned from scratch (see also “Hierarchy” below). A compromise between complete uniformity and extreme flexibility is provided by hierarchical models, in which transition probabilities also depend on both the “from” and “to” contexts but are expected, a priori, to exhibit some degree of similarity between each “from” context, thereby supporting generalization and meta-learning. Such a model has recently accounted for empirical data from a large set of different paradigms using a diverse array of context transition structures [13].

Known vs. unknown number of contexts

Some models assume that the learner knows the true number of contexts in the environment (e.g. by fixing the number of contexts/modules in the model) [11, 12, 58, 85, 99, 130]. These models have no notion of memory creation as the number of memories is fixed from the start. However, in most real-world scenarios, it is unrealistic to assume that the learner knows the true number of contexts, as this number is in general only knowable through experience. Therefore, another class of models learns the number of contexts in the environment from experience. These models either assume that there is a finite number of contexts that really exist, we just don’t know a priori what this number is [1, 79, 80, 131], while others (so called Bayesian nonparametric models, e.g. the the hierarchical Dirichlet process, see also below under “Hierarchy”) assume that there really is an infinite number of contexts and it is only the number of contexts we experience over any limited time that remains necessarily finite [3, 13, 59, 86, 87, 95, 104]. Either way, these models create a new memory whenever a novel context is inferred. It is currently an open question (see Outstanding Questions) whether the brain uses a fixed number of memories at all times, and just discounts those that have not been linked to a previously encountered context (by setting the corresponding context probabilities to zero for expression and updating), or it dynamically adds new memories on the go as the need arises (whenever a new context is encountered).

Reorganization of context-specific memories

In addition to creating new memories when novel contexts are encountered, in a resource-rational framework [132], it may also be beneficial to reorganize existing memories. For example, if a context has not been encountered for a long time, it may be useful to prune the memory of this context to free up computational resources. Similarly, if multiple memories become sufficiently similar, it may justify the merging of these memories. Although heuristics for deciding when to prune or merge memories have been proposed [133, 134], a principled Bayesian account of memory pruning and merging would require that these pruning and merging operations emerge naturally as a consequence of inference in an appropriately defined generative model (e.g. a model in which novel contexts can appear and previously encountered contexts can disappear or merge). One example of such a generative model is the multiple target tracking model in the signal processing literature, where novel targets (akin to contingencies) can be “born” at different points in time and existing targets can split, merge and “die” [135–137]. Making an optimal decision about whether to prune an existing memory may involve weighing the benefits of freeing up memory and computational resources against the costs of removing a memory that is needed later. It is again an open question whether such reorganization actually takes place and, if so, whether sleep has a special role in such reorganization, as is suggested by a diverse array of beneficial effects of sleep on motor and perceptual skills [138–140].

Hierarchical contingencies and learning-to-learn

Although the creation of separate memories for different contexts prevents interference, it also prevents the beneficial transfer of context-general knowledge when contexts share common properties and features. The ability to share knowledge across contexts is crucial for transfer learning and learning-to-learn. Therefore, in multiple-context environments, it is desirable not only to create separate memories for each context but to also allow those memories to share common elements. Hierarchical Bayesian models naturally achieve this trade-off between specialization and generalization (see Box 6) by exploiting an inductive bias that states that the contingencies of different contexts share some common structure [141].

Concluding remarks and future directions

A growing body of experimental and modeling work suggests that humans and other animals segment their continuous stream of sensorimotor experience into distinct contexts. This is true in multiple domains of cognition, including classical conditioning, episodic memory, reinforcement learning, spatial cognition and motor learning [3, 7, 13, 38, 95]. At the heart of segmentation lies contextual inference, which controls how memories are created, updated and expressed. Importantly, the dependence of memory expression on contextual inference gives rise to a form of learning that until recently has been unappreciated: apparent learning.

Apparent learning has important implications for the future of studying learning and memory (see Outstanding Questions), as it implies that observed behavior does not provide a direct window into proper learning. Thus, to appropriately interpret behavioral data, and to study the neural mechanisms of learning, a more nuanced approach will be necessary. Given that adaptive changes in behavior can arise from a combination of proper and apparent learning, contextual inference must be considered so as to identify reliably the individual contributions of these processes. In general, contextual inferences could either be measured (e.g. using neural measurements) or inferred from behavior (e.g. using a computational model). In lieu of reliable methods for measuring contextual inferences directly, a model capable of exhibiting both proper and apparent learning could be fit to the data of a participant to discern the contributions of these two forms of learning [13]. Dissecting the contributions of proper and apparent learning to behavior will be instrumental for identifying their respective neural underpinnings.

Highlights.

• Context has widespread effects on memory and learning across multiple domains.

• Context is rarely directly observed by the learner and needs to be inferred.

• Contextual inference is determined by three main factors: performance-related feedback signals, performance-unrelated sensory cues, and spontaneous factors, such as the passage of time.

• Contextual inference controls memory creation, updating and expression across a variety of domains. In general, this requires multiple memories to be recalled and modified at any time.

• Adaptation is not a monolithic process but arises from a combination of two distinct processes: proper learning, involving the creation and updating of memories, and apparent learning, involving changes in how existing memories are expressed.

• Many classical learning phenomena, typically attributed to proper learning, have been shown to arise primarily from apparent learning.

Glossary

ABA renewal

a conditioned response can be reinstated by re-exposure to the conditioning context (A) following extinction in a different context (B) (cf. ABA structure)

ABA structure

a task with two contexts, A and B, which are experienced in the order A then B and then A again (cf. ABA renewal)

ABC structure

a task with three contexts, A, B and C, experienced in that order

Action

a choice made by a participant such as a button press or arm movement

Anterograde interference

learning a contingency is slower if a different contingency has been learned previously, with the amount of interference increasing with the length of experience of the first contingency

Apparent learning

a change in how context-specific memories are differentially expressed due to a change in belief about the current context. Based on behavior alone, it may appear as though proper learning has taken place, hence the name

Consolidation

a time-dependent process by which recent learned experiences are transformed and stabilized into long-term memory

Context shifts

see Event boundaries

Context

a discrete variable that controls which one of potentially many contingencies is currently active, i.e. determines the statistics of sensory cues, states, actions, and feedback

Contextual inference

the process of inferring the current context from a sequence of observations of sensory cues, states, actions and feedback

Contiguity effect

the finding that stimuli that occur close together in time become associated to each other so that recall of an item is facilitated by the presentation or recall of a different item that was presented in close temporal proximity

Contingency

the context-specific statistical relationship between sensory cues, states, actions, and feedback

Environmental consistency

the tendency of the environment to stay the same over time, typically in reference to the context (i.e. the inverse of between-context volatility)

Event boundaries

the transition points that segment a continuous stream of sensory observations (such as a movie) into a series of discrete events, such as at scene changes in a movie

Evoked recovery

the re-expression of a previously extinguished motor memory following re-exposure to the perturbation associated with that memory (cf. Reinstatement)

Extinction

the disappearance of a conditioned response when no longer reinforced

Feedback

sensory input that either has intrinsic valence or is related to task performance (e.g. rewards, punishments, movement accuracy) and that can depend on state, action, as determined by the currently active contingency

Force field

typically two-dimensional planar forces exerted at the handle of a robot grasped by a participant that depend on the state of the hand (e.g. the velocity of the hand in a viscous force field)

Hierarchical Dirichlet process

a nonparametric Bayesian model that supports the hierarchical generation of context transition probability matrices between infinitely many contexts

Kinematic error

the spatial error, for example, of a reaching movement

Object manifold

the properties of objects (such as a bike or hammer) can be characterized by a set of parameters (e.g. inertia, damping). However the parameters for bikes do not span the entire range of possibilities but live on a lower dimension than the full space of object parameters (i.e. a manifold)

Partial reinforcement extinction effect

the rate of extinction of a learned behavior is slower if the behavior was only reinforced on a fraction of acquisition trials, rather than on all trials

Place cell remapping

The phenomenon by which place cells change their firing patterns (place fields) when the environment changes (e.g. by changing salient landmarks)

Policy

a strategy that a participant uses in pursuit of goals. The policy determines (sometimes stochastically) the action that will be taken as a function of the state and the current contingency

Proper learning

an update to the estimates of context-specific contingencies

Rapid reaquisition

faster relearning of a contingency (following its extinction) compared to initial learning of the same contingency

Recency discrimination

after being presented with a series of items, participants are asked to determine which of a set of items was presented more recently

Recency effect

stimuli that are presented more recently are remembered better than those that came earlier

Reconsolidation

the process by which, upon its recall, a previously consolidated memory is potentially modified, and then consolidated

Reinstatement

the return of a previously extinguished conditioned response after the presentation of the unconditioned stimulus alone (cf. Evoked recovery)

Retrieval failure

the temporary inability to access information that is stored in memory

Savings

see Rapid reaquisition

Segmentation agreement score

a measure of how well the event boundaries perceived by an individual agree with the typical event boundaries of a group

Sensory cue

sensory input that has neutral valence and is not performance related (e.g. the appearance of the environment). Sensory cues may be informative of the context, but given the context, the sensory cue (unlike state) does not affect feedback

Serial recall

after being presented with a series of items, participants are asked to recall the items in the order in which they were presented

Single-trial learning

the change in behavior induced by a single trial. Although called “learning”, this change in behavior can arise through apparent, rather than proper, learning

Spontaneous recovery

the re-emergence of a previously extinguished response after a delay

State

a latent or observed variable that determines the feedback (often depending on the action taken). The same state can be associated with different feedback under different contexts

Utility

the scalar measure of the goodness of an action which can be a function of quantities that have intrinsic valence or are related to task performance, such as, rewards, punishments, movement accuracy

Visuomotor rotation

a rotation of the visual representation of the hand (e.g. a cursor) about the start location of a reaching movement

Volatility

the rate of change of the environment. Within-context volatility refers to the trial-to-trial variability of context-specific contingencies, whereas between-context volatility (the inverse of environmental consistency) refers to the trial-to-trial variability of the context itself, as determined by the context transition probabilities