Abstract.
Purpose
U-Net is a deep learning technique that has made significant contributions to medical image segmentation. Although the accomplishments of deep learning algorithms in terms of image processing are evident, many challenges still need to be overcome to achieve human-like performance. One of the main challenges in building deeper U-Nets is black-box problems, such as vanishing gradients. Overcoming this problem allows us to develop neural networks with advanced network designs.
Approach
We propose three U-Net variants, namely efficient R2U-Net, efficient dense U-Net, and efficient fractal U-Net, that can create highly accurate segmentation maps. The first part of our contribution makes use of EfficientNet to distribute resources in the network efficiently. The second part of our work applies the following layer connections to design the U-Net decoders: residual connections, dense connections, and fractal expansion. We apply EfficientNet as the encoder to our three decoders to design three conceivable models.
Results
The aforementioned three proposed deep learning models were tested on four benchmark datasets, including the CHASE DB1 and digital retinal images for vessel extraction (DRIVE) retinal image databases and the ISIC 2018 and HAM10000 dermoscopy image databases. We obtained the highest Dice coefficient of 0.8013, 0.8808, 0.8019, and 0.9295 for CHASE DB1, ISIC 2018, DRIVE, and HAM10000, respectively, and a Jaccard (JAC) score of 0.6686, 0.7870, 0.6694, and 0.8683 for CHASE DB1, ISIC 2018, DRIVE, and HAM10000, respectively. Statistical analysis revealed that the proposed deep learning models achieved better segmentation results compared with the state-of-the-art models.
Conclusions
U-Net is quite an adaptable deep learning framework and can be integrated with other deep learning techniques. The use of recurrent feedback connections, dense convolution, residual skip connections, and fractal convolutional expansions allow for the design of improved deeper U-Net models. With the addition of EfficientNet, we can now leverage the performance of an optimally scaled classifier for U-Net encoders.
Keywords: biomedical imaging, deep learning, image segmentation, U-Net, encoder
1. Introduction
The inception of deep learning has led to a boom in large-scale automated data analysis. In recent years, many advancements have been made in deep learning applications. In computer vision applications, convolutional neural networks (CNN)1 have played a significant role. Various breakthroughs have been made in the field of CNN-based computer vision and image processing in the form of different architectures,2 such as inception,3 ResNet,4 DenseNet,5 attention gates,6 and many others. These developments have contributed to many problems in the areas of classification and detection. Deep learning has become more prevalent in the field of automated data analysis. Its potential has been explored in areas such as biomedical imaging and radiation therapy.7,8 CNNs have also shown tremendous potential in biomedical imaging.9,10 In biomedical image analysis, image segmentation is one of the most commonly pursued problems,9,11 and it is a key component of biomedical image analysis. This is due to the failure of classification-based networks to provide adequate pixel-level contextual information for medical image processing. Segmentation methods classify each pixel based on the given problem, thereby providing more detailed results to physicians who are then able to make a more informed diagnosis. Segmentation maps produce boundary regions for cells, tumors, nerves, blood vessels, etc. This creates the problem for segmentation models to be able to work well on objects of different shapes and sizes. The problem is further compounded by the myriad of different image modalities in biomedical imaging.
U-Net is a deep neural network specifically designed to handle the biomedical segmentation issue.12 The U-Net model has two paths, namely a contracting path and an expansive path. The two paths allow the system to learn better contextual and localization information. The vanilla U-Net model has been modified extensively since its development in 2015. This is possible due to the modular design of U-Net that makes it highly adjustable with modules from other neural network models. It is also well known that the performance of neural networks is improved by scaling up the network at the cost of resources.
To improve the performance of U-Net-based semantic segmentation, our previous work13 introduced EfficientNet14 with recurrent residual U-Net (R2U-Net)15 as well as DenseNet5 into the U-Net encoder. This study extends the aforementioned work, in which a fractal network architecture is also introduced into U-Net. The proposed approach differs from existing techniques in the following aspects: we modified the vanilla U-Net architecture with more robust deep network connections schemes, including (1) EfficientNet,14 a pretrained encoder that uses compound scaling for optimal parameter distribution; (2) recurrent residual U-Net (R2U-Net),15 which uses residual learning and recurrent layers to promote deeper learning; (3) DenseNet,5 which uses dense skip connections to allow more layers; and finally, (4) FractalNet,16 which employs fractal expansions to improve network gradient propagation. The detailed design of our proposed segmentation methods is described in the following section.
2. Model Architecture
2.1. U-Net
The overall design of a U-Net model can be divided into two paths. The first is the contracting path, also known as the analysis path or the encoder. The second is an expansion path that consists of concatenations and up-convolutions. It is usually referred to as the synthesis path or the decoder. The U-Net architecture consists of blocks that are composed of a sequence of convolutions followed by a rectified linear unit (ReLU). The skip connections between the contracting layer and the expansive layer transfer contextual information about an image to the corresponding layer. The configuration allows the network to learn about the pixel-level classification of the contracting path and then use it to create an image with a fully segmented structure.12 The basic U-Net architecture is illustrated in Fig. 1. The U-Net’s high modularity and adaptable nature make it a great choice for various segmentation tasks. Its low-level design can be easily augmented by other modules and architectures. This allows U-Net to be tuned to fit specific applications. It also means that U-Net can be continuously improved with new features and methods. In this paper, we propose three new U-Net-based image segmentation models that encapsulate three existing methods—R2U-Net, DenseNet, and FractalNet—as a decoder and then respectively incorporate them into an EfficientNet-based encoder. These combinations result in three proposed deep models: efficient R2U-Net, efficient dense U-Net, and efficient fractal U-Net.
Fig. 1.
U-Net architecture. The arrows represent the different operations, the blue boxes represent the feature map at each layer, and the gray boxes represent the cropped feature maps from the contracting path.
2.2. Efficient R2U-Net
R2U-Net combines deep residual learning4 and recurrent convolutional neural network17 (RCNN) onto U-Net. The goal here is to combine the two major neural network architectures into one architecture. First, residual learning allows for the development of deeper neural networks. Standard CNNs can suffer from the vanishing gradient problem if too many hidden layers are introduced.4 Residual skip connections can transfer feature maps from a previous layer to a deeper one. Repeated use of these connections can help improve gradient propagation and allow deeper neural networks to be created.
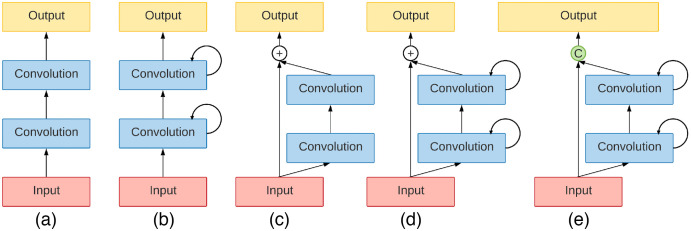
The second integral part of R2U-Net is the RCNN, which combines the feedback loops with the residual skip connections. These recurrent connections provide RCNNs with a feature map that can be input to the preceding layer at discrete time steps. This feature allows RCNNs to extract useful information from the data.17 The design of such modules is displayed in Fig. 2.
Fig. 2.
Different variants of residual and recurrent convolutional blocks: (a) forward only block, (b) recurrent block, (c) residual block, (d) recurrent residual block (R2), and (e) proposed R2 block with channel-wise concatenation. This figure is modified from the work by Alom et al.15
Considering the ’th input as and as the pixel locations of the ’th feature map, the output of the residual RCNN block is expressed as
| (1) |
Here and correspond to the activation of the forward and recurrent output, respectively, and and denote the weights of the forward layer and recurrent layer of the ’th feature map. The term is a bias term. The output of a recurrent convolution layer is passed into an ReLU activation function, formulated as
| (2) |
The overall output of the residual RCNN block is simplified as
| (3) |
Here is the output of the residual RCNN block. This paper proposes a novel modification [Fig. 2(e)] to the existing RCNN block, which replaces channel-wise addition with channel-wise concatenation. This is because channel-wise addition can cause the information to be altered between layers.5 Also the ’th feature map is not necessarily correlated across different layers.5 Concatenation better preserves the feature maps when combined from multiple layers. Accordingly, Eq. (3) is reformulated as
| (4) |
Here represents channel-wise concatenation. Our proposed model replaces all standard convolutional blocks in the expansive path with the modified residual RCNN block and incorporates the EfficientNet-based encoder in the contracting path. We designate this model as efficient R2U-Net.
Although it is very important to improve the efficiency of deep neural networks, it is also very challenging to do so efficiently. The common ways of scaling up a network are usually done by adding more layers or more filters. EfficientNet14 is a family of pretrained encoders that uses compound scaling to determine the network scaling parameters. Compound scaling uses fixed ratios to automatically select the appropriate depth, width, and resolutions for the model.14 Figure 3 illustrates the common scaling methods as well as compound scaling. Compound scaling is an efficient method for minimizing network complexity. It can scale up a network more effectively than other methods. An EfficientNet encoder consumes up to eight times fewer parameters when compared with similar networks.14 This is ideal when building networks with a limited resource budget. In our proposed model, we introduce the EfficientNet encoder into the U-Net architecture. It allows us to achieve a deeper contracting path that can provide higher image segmentation performance. With the flexibility of a fixed budget network, such as EfficientNet, we can focus on improving our decoder. Our proposed EfficientNet R2U-Net architecture is pictured in Fig. 4.
Fig. 3.
(a) Baseline model. (b)–(d) Conventional scaling methods that only increase one dimension of the network: width, depth, or resolution. (e) Compound scaling method that uniformly scales all three dimensions with a fixed ratio.14
Fig. 4.
Our proposed efficient R2U-Net model consists of the residual recurrent U-Net with the EfficientNet encoder.
2.3. Efficient Dense U-Net
We also introduce a second convolution block based on densely connected convolutional networks (DenseNet).5 DenseNet is a deep learning architecture inspired by ResNet. The ResNet model does not solve the issue of vanishing gradients completely, it only slows down its effects. DenseNet has two major modifications over ResNet. First, every layer in a block receives the feature or identity map from all of its preceding layers.5 The feature maps are then passed onto the next layer. This design ensures that any given layer has the same information as the previous ones. The second major change is that identity maps are combined into tensors, which is in contrast to ResNet, in which element-wise addition is used. This allows DenseNet to preserve identity maps from prior layers.5 This configuration is presented in Fig. 5. As information is more easily preserved between layers, DenseNet blocks can have fewer channels and save on computational resources. The output for each layer in a dense block is described as
| (5) |
where represents the dense mapping function. Our second U-Net model replaces all standard convolutional blocks in the expansive path with the DenseNet blocks. We designate this model as efficient dense U-Net.
Fig. 5.
Five-layer DenseNet block.
2.4. Efficient Fractal U-Net
FractalNet is a neural network architecture design based on the principle of fractal geometry expansion and similarity. This network uses repeated fractal expansions to generate unit blocks with multiple paths with each path having a geometrically increasing number of hidden layers.16 Widening the network by adding multiple paths is an idea partially inspired by the inception module.3 Intermediary join layers merge outputs from different paths at regular geometric intervals. The final result is a network architecture that promotes gradient propagation without the typical residual skip connections. This behavior is achieved due to the different paths outputting different levels of gradient information. The fractal neural network designed by Larsson et al.16 outperformed the ResNet architecture by a significant margin. Figure 6 showcases the basic representation of fractal architecture. Let denote the output of the Cth fractal truncation. is defined as the unit base case and is customized according to the needs of the algorithms:
| (6) |
Fig. 6.
(a) Expansion rule to generate the fractal architecture. The base case has a single set of chosen layers; (b) fractal block with ; and (c) fractal block with .
With defined, successive fractals are generated by the following relationship:
| (7) |
where denotes the join operation and ° represents composition. The join operation aggregates the output of two or more hidden layers by computing the element-wise mean. A consequence of this expansion rule is that the number of operations increases exponentially as increases. It is also possible to generate networks with different expansion rules to produce the desired result, though this requires further experimentation.
The fractal architecture has seen some adoption in U-Net applications. Bai et al.18 implemented a U-Net model in which the fractal block employs variable filter sizes and a residual skip connection. Kumar et al.19 designed a U-Net model in which the fractal expansion resembles the original FractalNet architecture. The unit block consists of a convolution layer, batch normalization, leaky ReLU, and dropout in our implementation. For the join operation, there are several choices of layers. The original execution of FractalNet employed element-wise mean. However, in our application, we replace element-wise mean with channel-wise concatenation. This is due to the same reasons outlined in Sec. 2.2; concatenation preserves the features maps as they were and improves information flow in the network. The expansion rule of our implementation is simplified in the following equation:
| (8) |
We perform two tests with two different fractal U-Net models. The first model is an entirely fractal-based network. This is used for a baseline comparison against R2U-Net; it narrowly outperforms R2U-Net. The second implementation is a combination of EfficientNet with the fractal architectures, dubbed efficient fractal U-Net. Both models have .
3. Experimental Setup
3.1. Datasets
Our proposed network model is tested on four popular medical image datasets: CHASE DB1,20 DRIVEDB,21 ISIC 2018,22,23 and HAM10000.23 Examples of all datasets are shown in Fig. 7.
Fig. 7.
Samples from the (a) CHASE DB1, (b) ISIC 2018, (c) DRIVE, and (d) HAM10000 datasets, including both images and segmentation maps.
3.1.1. CHASE DB1 dataset
CHASE DB1 is a retinal fundus dataset consisting of 28 colored images of dimensions as well as their corresponding blood vessel segmentation maps. We selected 23 of the images for training, and the remaining 5 were left for testing the model for an approximate 82:18 split. Due to the limited data samples, we opt for a patch-based approach. Each sample in the training and testing sets is randomly sampled to produce 160 patches of size . This results in a total of 3680 patches for training and 800 patches for testing.
3.1.2. DRIVE DB dataset
The digital retinal images for vessel extraction (DRIVE) dataset is a publicly available set of images for comparative studies in the segmentation of blood retina vessels. The DRIVE dataset contains a total of 40 images compressed as JPEG with a resolution of . Due to the limited number of samples, we implemented the same patch-based approach as with the CHASE DB1 dataset. After the patching process, the dataset ended up with a total of 4000 patches for training and 1000 patches for testing ( for each patch).
3.1.3. ISIC 2018 dataset
ISIC 2018 is a skin lesion dataset comprising 2594 dermoscopy-colored images of different resolutions. Due to resource constraints and to standardizing the data, all images and ground truths were resized to . The resized dataset is randomly split in an 80:20 ratio, resulting in 2075 training samples and 519 testing samples.
3.1.4. HAM10000 dataset
The human against machine with 10,000 training images (HAM10000) dataset is a collection of dermatoscopic images from different modalities, such as diagnosis of basal cell carcinoma, melanocytic nevi, vascular lesions, and melanoma. The images and segmentation mask have a size of , resized to for computational resource restrictions. A total of 5000 images was used for training, and another 5000 samples were used for testing.
3.2. Evaluation Metrics
We consider several quantitative metrics to evaluate the performance of our models, including accuracy (Acc), Sørensen–Dice coefficient (Dice), and Jaccard (JAC) index. The accuracy score is described in Eq. (9). To calculate these, we also need the variables from the resulting confusion matrix: true positive (TP), true negative (TN), false positive (FP), and false negative (FN):
| (9) |
The Sørensen–Dice coefficient is expressed in Eq. (10). It is a measure of the similarity between two samples.24 Here GT refers to the ground truth, and SR refers to the segmentation result:
| (10) |
The JAC index, also known as intersection over union (IoU), is a measure of the overlap between two samples.25 It is defined in the following equation:
| (11) |
Finally, to compute the aforementioned evaluation metrics, the ground truth from testing data and the corresponding predicted outputs of the DL models are used to produce scores of evaluation metrics. For our proposed architectures, to measure the uncertainty of the prediction provided by the DL models, each model is evaluated by three different trials. Then the average values from those three different trials are reported in the results section along with the respective standard deviation as a measure of uncertainty of the estimation.
3.3. Parameter Settings
In our implementation of U-Net, we use EfficientNet-B714 as the encoder, which is the deepest pretrained encoder in the EfficientNet family, with the filter’s set size as follows: 32 filters for the first and second levels on the encoder side, 48 filters in the third level, 80 filters in the fourth level, and 224 in the bridge between the encoder and decoder paths. All other convolutional blocks are replaced with either DenseNet blocks or our modified residual RCNN blocks.
We apply batch normalization after each convolution, in which the output from each layer is normalized to have a zero mean and a variance of one. This helps deal with training problems that arise due to poor initialization and helps gradient flow in deeper models.26 The activation function used in our models is leaky ReLU. Leaky ReLU allows a small, positive gradient when a unit is not active, improving the overall performance of the network.27 Finally, dropout is also applied to prevent the overfitting issue.28
The models are trained using an adaptive learning rate for up to 200 epochs with the early stopping criteria. The batch size for training the CHASE DB1 and DRIVEDB datasets is 16, and for ISIC 2018 and HAM10000, it is 8. The validation accuracy and validation loss are shown in Fig. 8.
Fig. 8.
Validation history performances for CHASE DB1: (a) accuracy and (b) loss; ISIC2018: (c) accuracy and (d) loss; HAM10000: (e) accuracy and (f) loss; and DRIVE: (g) accuracy and (h) loss of R2U-Net, dense U-Net, fractal U-Net, efficient fractal U-Net, efficient dense U-Net, and efficient R2U-Net.
4. Results
We first evaluate the performance of our models on the CHASE DB1 dataset. Figure 9 plots the training accuracy and loss between the proposed efficient U-Net models and their regular counterparts. The segmentation results for CHASE DB1 are presented in Fig. 10, alongside the fundus images and the ground truths. It is clear that many of the structures in the field of information are properly categorized and identified. The results of our experiments are presented in Table 1. Our proposed models achieve a better accuracy, Dice coefficient, and JAC score against other segmentation models, including Attention U-Net29 and TransUNet.30
Fig. 9.
Training (a) accuracy and (b) loss of R2U-Net, dense U-Net, fractal U-Net, efficient fractal U-Net, efficient dense U-Net, and efficient R2U-Net on the CHASE DB1.
Fig. 10.
Sample segmentation results on the CHASE DB1 dataset: (a) input patches, (b) ground truths, (c) efficient dense U-Net result, (d) efficient R2U-Net result, and (e) efficient fractal U-Net result.
Table 1.
Evaluation metrics between state-of-the-art models and the proposed models on the CHASE DB1 dataset. The best performance is denoted in bold font for each of the performance metrics.
| Model | Year | Acc ± St. dev. | Dice ± St. dev. | JAC ± St. dev. |
|---|---|---|---|---|
| U-Net | 2015 | 0.9652 | 0.7938 | 0.6581 |
| Attention U-Net | 2018 | 0.9646 | 0.7868 | 0.6485 |
| TransUNet | 2021 | 0.9646 | 0.7910 | 0.6543 |
| Residual U-Net | 2017 | 0.9652 | 0.7932 | 0.6573 |
| Recurrent U-Net | 2018 | 0.9658 | 0.7933 | 0.6574 |
| R2U-Net | 2018 | 0.9655 | 0.7917 | 0.6552 |
| Fractal U-Net | 2021 | 0.9660 | 0.7955 | 0.6604 |
| Efficient fractal U-Net | 2021 | 0.9657 ± 0.0006 | 0.7949 ± 0.0049 | 0.6595 ± 0.0068 |
| Efficient dense U-Net | 2021 | 0.9657 ± 0.0004 | 0.7986 ± 0.0060 | 0.6647 ± 0.0083 |
| Efficient R2U-Net | 2021 | 0.9663 ± 0.0005 | 0.8013 ± 0.0051 | 0.6686 ± 0.0071 |
Our second evaluation is on the ISIC 2018 dataset. Figure 11 plots the training accuracy and loss between the proposed efficient U-Net models and their counterparts for the ISIC 2018 dataset. The segmentation results are shown in Fig. 12. The quantitative metrics for the dataset are presented in Table 2 against other comparable models. Once again, the proposed models achieve better results on the Dice coefficient and JAC score. We choose these metrics for comparison because these two are commonly used to evaluate dermoscopy datasets.7
Fig. 11.
Training (a) accuracy and (b) loss of R2U-Net, dense U-Net, fractal U-Net, efficient fractal U-Net, efficient dense U-Net, and efficient R2U-Net on the ISIC 2018 dataset.
Fig. 12.
Sample segmentation results on the ISIC 2018 dataset: (a) input images; (b) ground truths; (c) efficient dense U-Net result; (d) efficient R2U-Net result; (e) efficient fractal U-Net result; and (f) images with contours for ground truth (red), efficient dense U-Net result (green), efficient R2U-Net result (blue), and efficient fractal U-Net result (magenta).
Table 2.
Evaluation metrics between state-of-the-art models and the proposed models on the ISIC 2018 dataset. The best performance is denoted in bold font for each of the performance metrics.
| Model | Year | Acc ± St. Dev. | Dice ± St. Dev. | JAC ± St. Dev. |
|---|---|---|---|---|
| U-Net | 2015 | 0.9437 | 0.8585 | 0.7521 |
| Attention U-Net | 2018 | 0.9438 | 0.8553 | 0.7472 |
| TransUNet | 2021 | 0.9026 | 0.7283 | 0.5727 |
| Residual U-Net | 2017 | 0.9408 | 0.8586 | 0.7522 |
| Recurrent U-Net | 2018 | 0.9471 | 0.8686 | 0.7677 |
| R2U-Net | 2018 | 0.9453 | 0.8661 | 0.7638 |
| Fractal U-Net | 2021 | 0.9424 | 0.8531 | 0.7438 |
| Efficient fractal U-Net | 2021 | 0.9499 ± 0.0008 | 0.8749 ± 0.0012 | 0.7776 ± 0.0018 |
| Efficient dense U-Net | 2021 | 0.9507 ± 0.0034 | 0.8808 ± 0.0064 | 0.7870 ± 0.0103 |
| Efficient R2U-Net | 2021 | 0.9474 ± 0.0013 | 0.8743 ± 0.0018 | 0.7767 ± 0.0029 |
As the final part of the evaluation, we tested the proposed architectures with two additional datasets: DRIVE DB and HAM10000. Figures 13 and 14 depict the training accuracy and loss between the proposed models and their counterparts for the DRIVE DB and HAM10000 datasets, respectively. This evaluation is meant to provide a better idea of how well the proposed models are generalized with datasets from different sources, in addition to having supporting results to conclude which model performs better among the three architectures. The quantitative metrics for these datasets are provided in Tables 3 and 4; meanwhile, the segmentation results are illustrated in Fig. 15. As is observed in both datasets, the proposed EfficientNet-based models achieve better results compared with their counterpart model.
Fig. 13.
Training (a) accuracy and (b) loss of R2U-Net, dense U-Net, fractal U-Net, efficient fractal U-Net, efficient dense U-Net, and efficient R2U-Net on the DRIVEDB dataset.
Fig. 14.
Training (a) accuracy and (b) loss of R2U-Net, dense U-Net, fractal U-Net, efficient fractal U-Net, efficient dense U-Net, and efficient R2U-Net on the HAM10000 dataset.
Table 3.
Segmentation results evaluation and comparison using the DRIVE dataset. The best performance is denoted in bold font for each of the performance metrics.
| Model | Year | Acc ± St. Dev. | Dice ± St. Dev. | JAC ± St. Dev. |
|---|---|---|---|---|
| U-Net | 2015 | 0.9521 | 0.7967 | 0.6621 |
| Attention U-Net | 2018 | 0.9543 | 0.7963 | 0.6615 |
| TransUNet | 2021 | 0.9549 | 0.7980 | 0.6639 |
| Residual U-Net | 2017 | 0.9540 | 0.7998 | 0.6664 |
| Recurrent U-Net | 2018 | 0.9539 | 0.8013 | 0.6685 |
| R2U-Net | 2018 | 0.9522 | 0.7954 | 0.6603 |
| Fractal U-Net | 2021 | 0.9529 | 0.7954 | 0.6603 |
| Efficient fractal U-Net | 2021 | 0.9549 ± 0.0008 | 0.7975 ± 0.0012 | 0.6631 ± 0.0016 |
| Efficient dense U-Net | 2021 | 0.9528 ± 0.0010 | 0.7967 ± 0.0033 | 0.6620 ± 0.0045 |
| Efficient R2U-Net | 2021 | 0.9535 ± 0.0027 | 0.8019 ± 0.0043 | 0.6694 ± 0.0059 |
Table 4.
Segmentation results evaluation and comparison using the HAM10000 dataset. The best performance is denoted in bold font for each of the performance metrics.
| Model | Year | Acc ± St. Dev. | Dice ± St. Dev. | JAC ± St. Dev. |
|---|---|---|---|---|
| U-Net | 2015 | 0.9569 | 0.9159 | 0.8448 |
| Attention U-Net | 2018 | 0.9548 | 0.9120 | 0.8382 |
| TransUNet | 2021 | 0.9182 | 0.8273 | 0.7055 |
| Residual U-Net | 2017 | 0.9588 | 0.9205 | 0.8527 |
| Recurrent U-Net | 2018 | 0.9583 | 0.9205 | 0.8527 |
| R2U-Net | 2018 | 0.9549 | 0.9132 | 0.8403 |
| Fractal U-Net | 2021 | 0.9573 | 0.9179 | 0.8483 |
| Efficient fractal U-Net | 2021 | 0.9625 ± 0.0010 | 0.9275 ± 0.0023 | 0.8648 ± 0.0039 |
| Efficient dense U-Net | 2021 | 0.9640 ± 0.0014 | 0.9295 ± 0.0014 | 0.8683 ± 0.0024 |
| Efficient R2U-Net | 2021 | 0.9627 ± 0.0011 | 0.9281 ± 0.0018 | 0.8659 ± 0.0032 |
Fig. 15.
Sample segmentation results on the (rows 1 to 4) the DRIVE DB dataset and (rows 5 to 8) HAM10000 dataset: (a) input images; (b) ground truths; (c) efficient fractal U-Net result; (d) efficient dense U-Net result; and (e) efficient R2U-Net U-Net result.
5. Ablation Study
We perform ablation studies on our results to compare the metrics of the different network architectures and note which structure resulted in an improved performance.
5.1. Comparison Between EfficientNet and Non-EfficientNet Models
The first comparison is between models with and without the EfficientNet encoder. For the ISIC 2018 and HAM10000 datasets, all of the EfficientNet models outperformed the non-EfficientNet models. In the case of the CHASE DB1 dataset, the EfficientNet models outperformed the other models in accuracy, Dice coefficient, and JAC score. For the DRIVE DB dataset, the models with EfficientNet encoders outperformed all other models in all of the evaluation metrics except the accuracy (similar performance to TransUNet). The improved performance scores can be attributed to the increased number of layers in the efficient encoder and the compound scaling, which distributes them for optimal performance.
Because EfficientNet compound scaling is not available as a decoder, we had to implement different architectures for the decoder. In particular, the decoder has significantly fewer parameters than the encoder. As such, some of the performance gains in the encoder could be lost in the decoder. This loss has two consequences; first, it is plausible that the decoder bottlenecks all U-Net models that use the EfficientNet encoder. Second, this implies that there is further room for improvement in such models by adjusting the decoder. Overall, the expansion of networks with the EfficientNet encoder increases the networks’ segmentation capabilities.
5.2. Comparison within EfficientNet Models
The final evaluation comparison is within the Efficient U-Net-based models. For the CHASE DB1 dataset, we first compare Efficient R2U-Net and Efficient dense U-Net. In this dataset, the Efficient R2U-Net was better in all metrics versus the efficient dense U-Net. This phenomenon could be attributed to the recurrent connection in R2U-Net. Furthermore, this might be explained due to the dense block having more frequent concatenations, which results in a higher number of parameters. A higher number of parameters can lead to slight overfitting problems.31 Compared with efficient fractal U-Net, both techniques yield a slightly higher segmentation accuracy, dice coefficient, and JAC score. The advantage of introducing fractal blocks into efficient U-Net is that it constructs deep networks without residual connections and typically performs better than standard residual networks.16 This statement echoes with the results obtained in a few of our experiments, in which efficient fractal U-Net outperforms the other EfficientNet-based models.
In the case of DRIVE DB, the performance of EfficientNet-based models varies in comparison with the performance obtained with CHASE DB. It is observed that efficient R2U-Net and efficient fractal U-Net outperform the dense block-based U-Net. However, among these two, the R2 block-based U-Net performs better in all of the evaluation metrics.
For the ISIC 2018 and HAM10000 datasets, we compare efficient R2U-Net, efficient dense U-Net, and efficient fractal U-Net, focusing on the Dice coefficient and JAC score. In this dataset, the dense block does indeed contribute better than the R2 block. This is assuming that training on this dataset does not cause overfitting for the dense block. We also have the efficient fractal U-Net for comparison, which performs similar to the efficient R2U-Net model. This could be explained by the addition of the EfficientNet encoder itself. The fractal block has a higher number of parameters than the R2 block. The addition of the EfficientNet encoder could result in the fractal U-Net architecture being overfitted. Overfitting does not happen in the vanilla variants because the number of parameters is sufficiently low, but the efficient encoder adds a large number of layers and operations. Finally, efficient dense U-Net shows a better score than the Efficient R2U-Net. The dense block has greater interconnectivity between its convolution layers than the fractal block because every layer is connected to all preceding layers in a dense block. The fractal block ends up with a similar number of parameters as the dense block because the fractal block in our models had seven convolution layers across all its paths versus the four layers in the dense block. As such, it can be concluded that the higher interconnectivity makes up for the reduced number of layers in the dense block, which makes it superior to the fractal and R2 blocks.
5.3. Statistical Analysis
In this work, we compare the performance of several non-EfficientNet-based models with the EfficientNet-based models. To analyze whether there is a significant difference between their performance, nonparametric statistical tests, such as Friedman test,32 Iman and Davenport’s test,33 and the Nemenyi test,34 are performed.
5.3.1. Friedman test
The Friedman test32 is used when several performances are compared, and it is needed to determine if the performance differences are statistically significant or not. In this analysis, we test the hypothesis to compare the performance metrics of the deep learning models. The hypothesis is set as follows.
: The performance of the deep learning models is equal.
: The performance of the deep learning models is different.
For the Friedman test, the evaluation metrics used here include ACC, Dice, and JAC. Table 5 shows the average ranking of performance based on the evaluation metrics for each model, averaging for the four datasets.
Table 5.
Ranking of evaluation metric scores from deep learning models (smaller value, better performance).
| U-Net | Attention U-Net | TransUNet | Residual U-Net | Recurrent U-Net | R2U-Net | Fractal U-Net | Efficient fractal U-Net | Efficient dense U-Net | Efficient R2U-Net | |
|---|---|---|---|---|---|---|---|---|---|---|
| ACC | 8 | 7 | 7.75 | 6 | 4.25 | 7 | 5.75 | 2.75 | 3.5 | 3 |
| Dice | 6.5 | 8.75 | 8.25 | 5 | 4.25 | 7.75 | 6.75 | 3.5 | 2.5 | 1.75 |
| JAC | 6.5 | 8.75 | 8.25 | 5 | 4.25 | 7.75 | 6.75 | 3.5 | 2.5 | 1.75 |
| Average () | 7 | 8.16 | 8.08 | 5.33 | 4.25 | 7.5 | 6.42 | 3.25 | 2.83 | 2.16 |
The chi-square value is calculated based on the squared average of the ranking performance () of each deep learning model. The chi-square for the Friedman test is computed as
| (13) |
where (the number of evaluation metrics) and (the deep learning models). is the average ranking of each deep learning model. The chi-square for the Friedman test is 14.97. The critical value obtained from the chi-square critical value table 33 is 3.325, with a level of significance and (i.e., 9) degrees of freedom. The chi-square observed statistic is greater than the critical value; therefore, this test supports the rejection of the null hypothesis.
5.3.2. Iman and Davenport’s test
Once the chi-square is computed, we perform Iman and Davenport’s test (),35 which is a less conservative statistical test derived from the Friedman test. The value is computed as follows:
| (14) |
The obtained is 2.489 using Eq. (14). We compare with the critical value obtained from the distribution table 36 with and degrees of freedom (9 and 18) and a confidence level of 95% (). The critical value obtained is 2.456, which is lower than the value, meaning that there is a significant difference among the recorded performances with a probability ; therefore, we must reject the , and we can state that there is sufficient evidence to conclude that the deep learning model used leads to statistically significant differences in performance.
5.3.3. Nemenyi test
To identify which model performs the best, we employ the Nemenyi test. The Nemenyi test34 identifies the group of data that stands out from the rest, given that the prior global statistical test, a Friedman test for our case, has rejected the hypothesis that the groups of data are similar.
The Nemenyi test is performed to identify which deep learning model has a significant difference in terms of performance compared with the others. To this end, it is needed to get the different average rankings among the deep learning models (paired comparison). The quality of the models is significantly different if the corresponding average ranking is at least as high as its critical difference (CD). The CD is computed as follows:
| (15) |
where is a critical value for multiple nonparametric comparisons, in which and was equal to 3.16 (Table B.16 of Ref. 37 for ). The obtained CD is 7.81.
In Table 6, the values indicate the average ranking differences between performances of the models. There is no average ranking higher than the CD; therefore, we cannot conclude the existence of a significant difference between the proposed EfficientNet-based models and the state-of-the-art models. However, these differences are generally consistent as compared with the non-EfficientNet-based models, which is congruent with the quantitative results reported in the performance of the compared architectures. Among the three proposed models, Efficient R2U-Net shows the higher difference values in general compared with the non-EfficientNet-based architectures.
Table 6.
Difference between the average ranking on each pair of deep learning models. The highest difference in average ranking for each model compared with the others is denoted in bold font.
| MODEL | U-Net | Attention U-Net | TransUNet | Residual U-Net | Recurrent U-Net | R2 U-Net | Fractal U-Net | Efficient fractal U-Net | Efficient dense U-Net | Efficient R2U-Net |
|---|---|---|---|---|---|---|---|---|---|---|
| U-Net | 0.00 | 1.17 | 1.08 | 1.67 | 2.75 | 0.50 | 0.58 | 3.75 | 4.17 | 4.83 |
| Attention U-Net | 1.17 | 0.00 | 0.08 | 2.83 | 3.92 | 0.67 | 1.75 | 4.92 | 5.33 | 6.00 |
| TransUNet | 1.08 | 0.08 | 0.00 | 2.75 | 3.83 | 0.58 | 1.67 | 4.83 | 5.25 | 5.92 |
| Residual U-Net | 1.67 | 2.83 | 2.75 | 0.00 | 1.08 | 2.17 | 1.08 | 2.08 | 2.50 | 3.17 |
| Recurrent U-Net | 2.75 | 3.92 | 3.83 | 1.08 | 0.00 | 3.25 | 2.17 | 1.00 | 1.42 | 2.08 |
| R2 U-Net | 0.50 | 0.67 | 0.58 | 2.17 | 3.25 | 0.00 | 1.08 | 4.25 | 4.67 | 5.33 |
| Fractal U-Net | 0.58 | 1.75 | 1.67 | 1.08 | 2.17 | 1.08 | 0.00 | 3.17 | 3.58 | 4.25 |
| Efficient fractal U-Net | 3.75 | 4.92 | 4.83 | 2.08 | 1.00 | 4.25 | 3.17 | 0.00 | 0.42 | 1.08 |
| Efficient dense U-Net | 4.17 | 5.33 | 5.25 | 2.50 | 1.42 | 4.67 | 3.58 | 0.42 | 0.00 | 0.67 |
| Efficient R2U-Net | 4.83 | 6.00 | 5.92 | 3.17 | 2.08 | 5.33 | 4.25 | 1.08 | 0.67 | 0.00 |
5.4. Limitations
In this paper, we present three U-Net architectures that incorporate popular deep learning models for medical image segmentation applications. The proposed models achieved anticipated results on four popular datasets. However, there are some limitations of this study. First, due to hardware resource constraints, we had to reduce the resolution of images in the ISIC 2018 and the HAM10000 datasets. Second, we limited the number of feature maps in some hidden layers to reduce the trainable parameters for the same reason. This can have a possible impact on the performance of the models. Our models also have a commonality limitation when it comes to the performance for inputs when the global context is important, the skip connections allow the models to reduce the vanishing gradients and leverage the feature representation in a local context; however, the global attention is still a pending task within the proposed architectures.
It is also noted that both efficient dense U-Net and efficient R2U-Net had a similarly strong performance. In the current setup, each had a top performance in at least one of the four datasets tested, which leads to the inconclusiveness of which is the superior architecture. Further experimentation will be required to understand the pros and cons of the models against each other and to comprehensively investigate which model is ideal in which situations.
For a better understanding of the limitations of the proposed architectures, Fig. 16 illustrates the outcomes from each of the EfficientNet-based models over the four datasets with unsuccessful segmentation. The lack of accurate segmentation for local context is noticeable, mostly for the retinal imaginary datasets, as the predicted segmentation mask shows several regions (represented with red bounding boxes) with false positive predictions.
Fig. 16.
Examples of unsuccessful segmentations over the four datasets: (1) ISIC2018, (2) HAM10000, (3) CHASEDB1, and (4) DRIVE, using the three EfficientNet-based models proposed: (a) efficient dense U-Net, (b) efficient fractal U-Net, and (c) efficient R2U-Net.
6. Conclusion
The U-Net deep learning framework is a powerful tool that has been successfully used in various biomedical image segmentation tasks. Precise segmentation of biomedical images is very important for the proper diagnosis of diseases. U-Net is a deep learning framework that can efficiently identify and classify structures of interest in biomedical images. Additionally, U-Net itself is quite adaptable and can be integrated with more deep learning techniques. With the addition of EfficientNet, we can now leverage the performance of an optimally scaled classifier for U-Net encoders. Statistical analysis provided sufficient evidence to state a significant difference in the performance of the EfficientNet-based models compared with the non-EfficientNet-based models from the calculations of the Friedman test and Iman and Davenport’s test. The use of recurrent feedback connections and residual skip connections allows for the design of a deeper U-Net with a higher number of convolutions. A similar performance is achieved using densely connected convolutional networks and fractal-based encoder architecture. Efficient dense U-Net and efficient R2U-Net both had a similarly better performance when compared with other models including efficient fractal U-Net. Future research will investigate more accurate algorithms for compound scaling in EfficientNet for biomedical image segmentation.
Biographies
Nahian Siddique received his BS degree in electrical and electronic engineering from Islamic University of Technology, Gazipur, Bangladesh, in 2017. He is currently pursuing his MS degree in electrical and computer engineering at Purdue University Northwest. His current research interests include deep learning, computer vision, biomedical image processing, and remote sensing.
Sidike Paheding received his PhD in electrical engineering from the University of Dayton. He is currently an assistant professor in the Department of Applied Computing of Michigan Technological University. Prior to joining Michigan Tech, in 2020, he was a visiting assistant professor at Purdue University Northwest. His research interests include image/video processing, machine learning, deep learning, computer vision, and remote sensing. He is an associate editor of Signal, Image and Video Processing (Springer) and Photogrammetric Engineering and Remote Sensing.
Abel A. Reyes Angulo received his MS degree in electrical and computer engineering from Purdue University Northwest in 2021. He is currently a PhD student in computational science and engineering at Michigan Technological University. His research interests include, but are not limited to, machine learning, deep learning, artificial intelligence, computer vision, software development, cyber-security, and virtual reality.
Md. Zahangir Alom received his BS and MS degrees in computer engineering from the University of Rajshahi, Bangladesh, and Chonbuk National University, South Korea, in 2008 and 2012, respectively, and his PhD in electrical and computer engineering from the University of Dayton in 2018. He is a research engineer at the University of Dayton, Ohio, USA. His research interests include machine learning, deep learning, medical imaging, and computational pathology. He is a student member of IEEE, a member of the International Neural Network Society, and a member of the Digital Pathology Association, USA.
Vijay K. Devabhaktuni received his BEng degree in electronics and electrical engineering and his MSc degree in physics from the Birla Institute of Technology and Science, Pilani, India, in 1996 and his PhD in electronics from Carleton University, Ottawa, ON, Canada, in 2003. He held the Natural Sciences and Engineering Research Council of Canada (NSERC) postdoctoral fellowship and researched with Dr. J. W. Haslett at the University of Calgary, Calgary, AB, Canada, from 2003 to 2004. In 2005, he taught at Penn State Behrend, Erie, PA, USA. From 2005 to 2008, he held the prestigious Canada research chair in computer-aided high-frequency modeling and design at Concordia University, Montréal, QC, Canada. In 2008, he joined the Department of Electrical Engineering and Computer Science, the University of Toledo, Toledo, OH, USA, as an associate professor, where he was promoted to a professor in 2013. In 2018, he became the chair of the Department of Electrical and Computer Engineering, Purdue University Northwest, Hammond, IN, USA.
Disclosures
The authors do not have any conflicts of interest.
Contributor Information
Nahian Siddique, Email: nahiansiddique10@gmail.com.
Sidike Paheding, Email: spahedin@mtu.edu.
Abel A. Reyes Angulo, Email: areyesan@mtu.edu.
Md. Zahangir Alom, Email: Zahangir.Alom@stjude.org.
Vijay K. Devabhaktuni, Email: vijay.devabhaktuni@maine.edu.
References
- 1.LeCun Y., et al. , “Gradient-based learning applied to document recognition,” Proc. IEEE 86(11), 2278–2324 (1998). 10.1109/5.726791 [DOI] [Google Scholar]
- 2.Alom M. Z., et al. , “A state-of-the-art survey on deep learning theory and architectures,” Electronics 8(3), 292 (2019). 10.3390/electronics8030292 [DOI] [Google Scholar]
- 3.Szegedy C., et al. , “Going deeper with convolutions,” in Proc. IEEE Conf. Comput. Vision and Pattern Recognit., pp. 1–9 (2015). [Google Scholar]
- 4.He K., et al. , “Deep residual learning for image recognition,” in Proc. IEEE Conf. Comput. Vision and Pattern Recognit., pp. 770–778 (2016). [Google Scholar]
- 5.Huang G., et al. , “Densely connected convolutional networks,” in Proc. IEEE Conf. Comput. Vision and Pattern Recognit., pp. 4700–4708 (2017). [Google Scholar]
- 6.Vaswani A., et al. , “Attention is all you need,” in Adv. Neural Inf. Process. Syst., pp. 5998–6008 (2017). [Google Scholar]
- 7.Al-Masni M. A., et al. , “Skin lesion segmentation in dermoscopy images via deep full resolution convolutional networks,” Comput. Methods Prog. Biomed. 162, 221–231 (2018). 10.1016/j.cmpb.2018.05.027 [DOI] [PubMed] [Google Scholar]
- 8.Sahiner B, et al. , “Deep learning in medical imaging and radiation therapy,” Med. Phys. 46(1), e1–e36 (2019) 10.1002/mp.13264 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Litjens G., et al. , “A survey on deep learning in medical image analysis,” Med. Image Anal. 42, 60–88 (2017). 10.1016/j.media.2017.07.005 [DOI] [PubMed] [Google Scholar]
- 10.Shen D., Wu G., Suk H.-I., “Deep learning in medical image analysis,” Annu. Rev. Biomed. Eng. 19, 221–248 (2017). 10.1146/annurev-bioeng-071516-044442 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bakator M., Radosav D., “Deep learning and medical diagnosis: a review of literature,” Multimodal Technol. Interact. 2(3), 47 (2018). 10.3390/mti2030047 [DOI] [Google Scholar]
- 12.Ronneberger O., Fischer P., Brox T., “U-Net: convolutional networks for biomedical image segmentation,” Lect. Notes Comput. Sci. 9351, 234–241 (2015). 10.1007/978-3-319-24574-4_28 [DOI] [Google Scholar]
- 13.Siddique N., et al. , “Recurrent residual U-Net with EfficientNet encoder for medical image segmentation,” Proc. SPIE 11735, 117350L (2021). 10.1117/12.2591343 [DOI] [Google Scholar]
- 14.Tan M., Le Q. V., “EfficientNet: rethinking model scaling for convolutional neural networks,” in Int. Conf. Mach. Learn., pp. 6105–6114 (2019). [Google Scholar]
- 15.Alom M. Z., et al. , “Recurrent residual U-Net for medical image segmentation,” J. Med. Imaging 6(1), 014006 (2019). 10.1117/1.JMI.6.1.014006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Larsson G., Maire M., Shakhnarovich G., “FractalNet: ultra-deep neural networks without residuals,” in 5th Int. Conf. Learn. Represent., ICLR 2017, Conf. Track Proc., Toulon, 24-26 April (2017). [Google Scholar]
- 17.Liang M., Hu X., “Recurrent convolutional neural network for object recognition,” in Proc. IEEE Conf. Comput. Vision and Pattern Recognit., pp. 3367–3375 (2015). 10.1109/CVPR.2015.7298958 [DOI] [Google Scholar]
- 18.Bai Z., et al. , “Liver tumor segmentation based on multi-scale candidate generation and fractal residual network,” IEEE Access 7, 82122–82133 (2019). 10.1109/ACCESS.2019.2923218 [DOI] [Google Scholar]
- 19.Kumar A., et al. , “CSNet: a new DeepNet framework for ischemic stroke lesion segmentation,” Comput. Methods Programs Biomed. 193, 105524 (2020). 10.1016/j.cmpb.2020.105524 [DOI] [PubMed] [Google Scholar]
- 20.Fraz M. M., et al. , “An ensemble classification-based approach applied to retinal blood vessel segmentation,” IEEE Trans. Biomed. Eng. 59(9), 2538–2548 (2012). 10.1109/TBME.2012.2205687 [DOI] [PubMed] [Google Scholar]
- 21.“DRIVE DB digital retinal images for vessel extraction,” https://drive.grand-challenge.org/ (accessed 2022-03-14).
- 22.Codella N., et al. , “Skin lesion analysis toward melanoma detection: A challenge at the 2017 international symposium on biomedical imaging (ISBI), hosted by the international skin imaging collaboration (ISIC),” in 2018 IEEE 15th Int. Symp. Biomed. Imaging (ISBI 2018), pp. 168–172, IEEE; (2018). [Google Scholar]
- 23.Tschandl P., Rosendahl C., Kittler H., “The HAM10000 dataset, a large collection of multi-source dermatoscopic images of common pigmented skin lesions,” Sci. Data 5, 180161 (2018). 10.1038/sdata.2018.161 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Dice L. R., “Measures of the amount of ecologic association between species,” Ecology 26(3), 297–302 (1945). 10.2307/1932409 [DOI] [Google Scholar]
- 25.Jaccard P., “The distribution of the flora in the alpine zone,” New Phytol. 11(2), 37–50 (1912). 10.1111/j.1469-8137.1912.tb05611.x [DOI] [Google Scholar]
- 26.Ioffe S., Szegedy C., “Batch normalization: accelerating deep network training by reducing internal covariate shift,” in Int. Conf. Mach. Learn., pp. 448–456, PMLR: (2015). [Google Scholar]
- 27.Maas A. L., Hannun A. Y., Ng A. Y., “Rectifier nonlinearities improve neural network acoustic models,” in Proc. ICML, p. 3 (2013). [Google Scholar]
- 28.Srivastava N., et al. , “Dropout: a simple way to prevent neural networks from overfitting,” J. Mach. Learn. Res. 15(1), 1929–1958 (2014). [Google Scholar]
- 29.Oktay O., et al. , “Attention U-Net: learning where to look for the pancreas,” arXiv preprint arXiv:1804.03999 (2018).
- 30.Chen J., et al. , “TransUNet: transformers make strong encoders for medical image segmentation,” arXiv preprint arXiv:2102.04306 (2021).
- 31.Minaee S., et al. , “Image segmentation using deep learning: a survey,” IEEE Trans. Pattern Anal. Mach. Intell. (2021). [DOI] [PubMed] [Google Scholar]
- 32.Friedman M., “The use of ranks to avoid the assumption of normality implicit in the analysis of variance,” J. Am. Stat. Assoc. 32(200), 675–701 (1937). 10.1080/01621459.1937.10503522 [DOI] [Google Scholar]
- 33.Piegorsch W. W., “Tables of P-values for t-and chi-square reference distributions,” University of South Carolina Statistics Technical Report (2002).
- 34.Nemenyi P. B., “Distribution-free multiple comparisons,” PhD thesis, Princeton University (1963). [Google Scholar]
- 35.Iman R. L., Davenport J. M., “Approximations of the critical region of the Friedman statistic,” Commun. Stat. 9, 571–595 (1980). 10.1080/03610928008827904 [DOI] [Google Scholar]
- 36.Sheskin D. J., Handbook of Parametric and Nonparametric Statistical Procedures, CRC Press; (2003). [Google Scholar]
- 37.Zar J. H., Biostatistical Analysis, Prentice Hall; (1999). [Google Scholar]