Abstract
Contamination events in water distribution networks (WDNs) can have a huge impact on water supply and public health; increasingly, online water quality sensors are deployed for real-time detection of contamination events. Machine learning has been used to integrate multivariate time series water quality data at multiple stations for contamination detection; however, accurate extraction of spatial features in water quality signals remains challenging. This study proposed a contamination detection method based on generative adversarial networks (GANs). The GAN model was constructed to simultaneously consider the spatial correlation between sensor locations and temporal information of water quality indicators. The model consists of two networks—a generator and a discriminator—the outputs of which are used to measure the degree of abnormality of water quality data at each time step, referred to as the anomaly score. Bayesian sequential analysis is used to update the likelihood of event occurrence based on the anomaly scores. Alarms are then generated from the fusion of single-site and multi-site models. The proposed method was tested on a WDN for various contamination events with different characteristics. Results showed high detection performance by the proposed GAN method compared with the minimum volume ellipsoid benchmark method for various contamination amplitudes. Additionally, the GAN method achieved high accuracy for various contamination events with different amplitudes and numbers of anomalous water quality parameters, and water quality data from different sensor stations, highlighting its robustness and potential for practical application to real-time contamination events.
Keywords: Contamination detection, Generative adversarial network, Multi-site time series data, Water distribution system, Water quality
Graphical abstract
Highlights
-
•
Generative adversarial networks (GANs) are developed to detect contamination events.
-
•
The contamination detection model is built using only water quality data.
-
•
Fusing alarms fully exploits the strength of single-site and multi-site models.
-
•
The GAN model is robust for diverse contamination events.
1. Introduction
Water distribution networks (WDNs) represent critical infrastructure for the safe and reliable delivery of freshwater to residential and business customers [1,2]. However, especially in developing countries, one challenge inherent in WDN management is the occurrence of contamination events due to ageing pipelines, lack of operational and maintenance management, and poor construction quality [3,4]. When a pollution accident occurs in a WDN, polluted water can spread quickly throughout the network unless detected and a timely response initiated. Such incidents not only interrupt the water supply and potentially cause huge economic losses but also lead to environmental damage and public health issues [5]. Examples include an incident that occurred in Hubei (China) in March 2010, where water containing sodium nitrite was accidently sucked back into the WDN and affected more than 400 people and contamination events reported in Zhejiang (China) in May and December 2012, where chemical emissions from upstream industry caused a persistent odour within the WDN that affected more than two million residents [5]. Therefore, rapid and accurate detection of WDN contamination could promote the instigation of remedial measures that might reduce the economic losses associated with contamination events [6,7].
Signals of water quality received from sensors can be analysed to detect contamination events [8,9]. Following the recent development of wireless networks and online sensors, multi-parameter water quality data can be obtained at low cost and in near real-time [10]. However, single parameters are normally used as surrogate indicators of contamination events [11,12]. Moreover, accurate detection of anomalies can often be hampered by sensor faults, signal transmission anomalies, and many other factors leading to overall low detection accuracy. Several earlier experimental studies [[13], [14], [15], [16]] investigated the response to various contamination intrusions (e.g., pesticides, herbicides, bacteria, and inorganic chemicals) of multiple water quality parameters that included conductivity, total organic carbon (TOC), free chlorine, chloride, oxidation-reduction potential, ammonia, and nitrate. Their published results showed that the intrusion of different contaminants can cause different responses in water quality indicators and lead to synchronous changes in multiple parameters. To improve the performance of methods for detecting contamination events, recent work has focused on using multi-parameter fusion algorithms to detect anomalous water quality [17,18]. In more recent studies, time series water quality data represented by six water quality parameters (i.e., total chlorine, pH, electrical conductivity (EC), temperature, TOC, and turbidity) were analysed to provide fused anomaly alarms for contamination events [[19], [20], [21], [22], [23]]. Such multi-parameter fusion algorithms usually represent a simple fusion of anomalous results from individual parameters that fail to fully explore the correlations between multiple parameters. Moreover, the spatiotemporal scope of a WDN is large, and existing anomaly detection methods are mostly performed only for a limited number of monitoring stations, and they exclude certain factors such as the water source, operational hydraulic changes, tank levels, and longitudinal and radial mixing, which can result in very high variability of water quality parameters [24]. [25] found that anomaly detection models using sensor data from multiple sites could reduce false positive/negative rates and overcome some of the drawbacks of single-site event detection models, such as a lack of consideration of hydraulic conditions and sensor data correlations among multiple sites. Therefore, using multivariate water quality data from multiple sites is paramount for accurately detecting contamination events.
Contamination event detection methods can be divided broadly into statistical, hydraulic-model-based, and machine-learning-based approaches. In a statistical approach, the determination of contamination event detection is often based on the distribution of water quality parameter data [7,13,26]. However, owing to the nonlinear and nonstationary characteristics of water quality, statistical methods are usually unsuitable for detecting small abnormal changes in WDNs [21]. Hydraulic-model-based approaches detect contamination events by comparing observed real-time data with predicted values using a water quality and hydraulic network model [[27], [28], [29]]. Hydraulic models require calibration to properly simulate the behaviour of a WDN. However, appropriate calibration is difficult to implement in practice, especially for large WDNs, because of the complexity of network topology and data limitations. The machine learning approach is considered an alternative for predicting real-time data of water quality parameters and identifying anomalous contamination events. Various machine learning algorithms have been applied for contamination event detection in WDNs, such as artificial neural networks [10,27,30], support vector machine [31,32], ensemble stacking models [21], and long short-term memory [33]. These models can capture the features of water quality time series data based on tests using a database compiled from the output of a single-site sensor. However, these models do not take advantage of the spatial relationship of multi-site sensor data, and they can increase the false alarm rate when the monitoring station experiences high hydraulic variation during normal operation. When a contamination event occurs, it often causes fluctuation in the water quality monitored by sensors at multiple sites, and the response time of the sensors at the different sites varies. Therefore, exploring the spatiotemporal distribution pattern of information from multiple sensors at multiple sites is important to improve prediction accuracy and enhance the performance of contamination event identification.
Currently, most multi-site detection approaches use some semi-supervised [19] or unsupervised [34] single-site methods to independently analyse the time series data from each site, and then assess the spatial similarity of upstream and downstream water quality data to detect contamination events. Hydraulic and water quality simulations are used for multi-site sensor data generation [35,36] or incorporated into the overall event detection process of spatially distributed sensors [27]. The time interval during which contaminated water is received must be known in advance for spatial analysis measurements taken from multiple sensor stations. Although multi-site anomaly detection is a promising approach for improving detection performance, practical application is limited by the requirement for an accurate hydraulic and water quality model.
Recently, generative adversarial networks (GANs) have been proposed as a new framework for estimating generative models to learn the latent space distribution of given data [37], which allows further exploration of the spatiotemporal distribution pattern of information from multiple sensors at multiple sites for anomaly detection. Anomaly detection methods based on GANs have become dominant in image recognition owing to their ability to simulate the complex high-dimensional distribution of images [[38], [39], [40], [41]]. Moreover, in recent years, GANs have also been adopted for time series anomaly detection [[42], [43], [44], [45]]. Deep learning neural networks, such as convolutional neural networks, can be inserted into the GAN framework for feature extraction of input data. Previous research has shown that changes in multiple sets of time series data tend to be synchronous, while in a WDN, there is a lag in the time of change in water quality data at multiple stations. Therefore, a GAN model that can learn the spatiotemporal distribution patterns of data from multi-site sensors should be built to identify contamination events.
Here, we propose a novel GAN-based multivariate multi-site contamination event detection method that can effectively capture spatiotemporal patterns in water quality data. The primary contributions can be summarised as follows.
A summation image transformation method is proposed to transform the multiple data streams from the different sites at a certain time step, which helps incorporate the multivariate water quality data from the multiple sites for convolution calculation.
A new GAN-based model consisting of a generator and a discriminator is proposed to analyse the temporal correlation of the time series data and the correlation between multiple variables using convolution filters and to calculate the anomaly score at each time step.
Bayesian sequential analysis is introduced to update the event probabilities for single and multiple sites separately after classifying anomalies based on anomaly scores, which are fused to generate alarms for anomaly events.
The performance of the proposed GAN-based contamination event detection method is evaluated using real WDN data and compared with that of a multivariate unsupervised method; that is, a minimum volume ellipsoid (MVE)-based event detection model [34].
2. Methodology
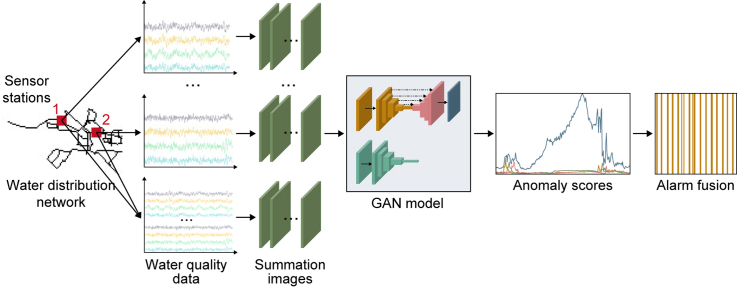
Based on the assumption that the occurrence of a contamination event causes water quality to change at multiple sensing sites across a WDN, an unsupervised method for detecting contamination events is developed based on the GAN. The GAN-based contamination event detection method consists of three steps: (1) data transformation: the time series data of water quality parameters from a single site and multiple sites are transformed into images; (2) outlier identification: normal and abnormal conditions are identified based on the anomaly score calculated by the GAN; and (3) event classification: the probability of event occurrence is updated using Bayesian sequential analysis, and events are classified by fusing alarms from single-site and multi-site event classifications. These steps are described in more detail in Fig. 1.
Fig. 1.
Schematic of the proposed GAN-based method for spatial contamination event detection.
2.1. Data transformation
Spatial event classification requires collecting water quality data from multiple sensor stations. The placement of water quality sensor stations is assumed to have been previously determined; otherwise, an optimal sensor placement method could be used to address this problem [46,47]. A contaminant might spread within a network through multiple flow paths, meaning that the time taken to reach different stations will be different. Therefore, neighbouring stations within the network are grouped together for event detection.
The proposed GAN-based method combines the results of local event classification and spatial event classification. The difference between local and spatial event classification lies in using data sets. Local event classification is applied to the data set of each sensor station, while spatial event classification is applied to the data sets of all sensors. Therefore, the selected N sensor stations are divided into N+1 groups; that is, N groups each containing data from an individual sensor station and an additional group containing all sensor data. The data transformation processes for both local and spatial event classification are consistent.
The data of water quality parameters are measured in different units. For mapping different water quality parameters on the same scale, the normalization of input parameters is conducted using the z-score approach:
| (1) |
where and are the normalized and raw data of water quality parameter i at sensor station j at time step t, respectively, and and are the mean and standard deviation of water quality parameter i at sensor station j, respectively, obtained from the training data set.
Summation image transformation is proposed to transform multivariate time series data into images by superimposing the signals between variables for each time step. Suppose Nr water quality parameters are measured for each sensor station. Then, for each time step, V normalized data () of the water quality parameters can be obtained from the analysed N sensor stations and transformed into a summation image. When N = 1, the summation image transformation is used in local event classification. If X is a column vector of length V that represents the water quality data, then can be the summation image at time step t for event classification, which can be defined as follows:
| (2) |
where is the transpose and I represents a column vector of size V with every element equal to 1. To reduce the effect of noise, the summation image of each moment is averaged over the previous d time steps.
The transformation encodes the relationship between water quality parameters and sensor stations into spatial information by superimposing the signals of each variable. Abnormal trends can be amplified during contamination using the superposition of water quality signals between different sensor stations. Moreover, noise is washed out by the averaging process on the temporal axis, making the method robust to impulse noise at some points.
2.2. Anomaly identification
2.2.1. GAN model
The GAN model is constructed for generative modelling using deep learning methods, such as convolutional neural networks, which are used widely in image processing tasks. The standard GAN model consists of two networks: the generator and the discriminator. The generator (G) is trained to learn a mapping from several historical summation images to the current expected summation image, , where represents the number of previous images considered before the current time step t. Only normal data are used in the training process to learn the latent vector space of the normal distribution. The purpose of the discriminator (D) is to distinguish the generated image from an actual normal image. Considering the nonstationary water quality characteristics, the current water quality situation is determined through comparison with historical summation images, , which are considered to represent the background water quality. Therefore, the historical series of summation images are used as reference information against which D can identify the generated and actual normal images.
The architecture of the proposed GAN model shown in Fig. 2 is a modification of CycleGAN architecture [39,48], which achieves compelling results in image-to-image translation. G consists of a contracting encoder and an expansive decoder, and it uses symmetrical long skip connections as a means of feature concatenation to recover fine-grained details in the prediction process. G uses the historical summation images and outputs the current reconstructed summation image . D consists of a regular downsampling convolutional network and outputs a vector scoring the realness of a given image sequence. The historical summation images, , are combined with the current measured (real) or reconstructed (estimated) summation images as the input for D. For both G and D, a pointwise convolutional layer is employed on the top of the networks to capture the temporal information from the sequence of summation images without changing the size of the images, and then a regular convolutional layer is used to extract the spatial information of multivariate water quality parameters. An attention mechanism—the Convolutional Block Attention Module (CBAM) [49]—is used in the discriminator network to boost the representation power of the convolutional neural network by focusing on important features and suppressing unnecessary information. After each convolution operation, the convolution features are fed into CBAM to highlight the important features using channel and spatial attention modules and the refined convolution features are output. CBAM is not used in the generator network because the auto-encoder and skip connection structures in G assist the generator in feature learning, and adding CBAM would only complicate the network.
Fig. 2.
The architecture of the proposed GAN model.
The improved Wasserstein GAN loss [50,51] is adopted as the adversarial loss to stabilize the training process:
| (3) |
| (4) |
where represents the probability distribution of the summation images generated by G; represents the probability distribution of the real summation images; represents the probability distribution of the interpolated summation images in equation (4); is a feature vector output by D; is the mathematical expectation when the summation image generated by G is used as the input for D; is the mathematical expectation when the real summation image is used as the input for D; is the mathematical expectation when the random interpolation sampling is used as the input for D; is the gradient for the interpolated summation images in equation (4); is randomly generated uniformly in the interval [0,1]; and is the coefficient of the gradient penalty item, which is set to 10 following [51].
G is trained to produce images to deceive D by minimizing the adversarial loss. Additionally, is employed as the reconstruction loss between the generated and real images to help G learn the normal distribution of the training data. The reconstruction loss is defined as follows:
| (5) |
In the GAN model, G and D networks are trained and updated simultaneously. The ultimate goal of model training is not to minimize the loss of any single network, but to find a stable state where the losses of both G and D converge.
2.2.2. GAN-based anomaly score
Only training data collected during normal conditions are used to train the GAN model. Therefore, a well-trained generator should ideally generate images that the discriminator can barely distinguish from real images when the test data are similar to the normal data in the training data set. When the test data set deviates from normal data distribution, the reconstruction loss of the generated and the real images will increase, and the discriminator will be able to more easily distinguish generated images from real images. Therefore, the trained G and D are both employed to detect anomalies in the test data set using an anomaly score based on reconstruction loss in G and feature loss in D. The GAN-based anomaly score at t is defined as follows:
| (6) |
where is the weighting parameter regulating the relative importance of the reconstruction loss and the feature loss to the anomaly score. Here, the generator and the discriminator are considered equally important and thus is set to 0.5.
2.2.3. Anomaly detection
The GAN-based anomaly score can measure the degree of abnormality of water quality data at each time step. The anomaly scores are close to 0 during the normal state. Ideally, all the calculated anomaly scores during the training process should be bounded to a small interval because the training data set is obtained under normal operation conditions. However, because the original data are not cleaned and the models might not be well trained, there will be some moments when the calculated anomaly scores are relatively large. Therefore, setting a threshold to classify normal conditions and outliers based on the calculated anomaly scores is important.
Most previous related studies [22,34,36] adopted empirical predefined values as classification thresholds that included the majority (e.g., 95% or 99%) of the calculated anomaly scores during the training process. Additionally, a value of three times the standard deviation is normally used as the threshold value [13]. However, these methods are difficult to apply because the number of outliers in a normal operating data set is random and the anomaly scores do not present a normal distribution. Considering that the calculated anomaly scores at the time of abnormality have a substantial jump compared to the normal time, a sequential incremental comparison method is proposed to select the threshold for anomaly identification. Let be a collection of anomaly scores for the training data set. We arrange the anomaly scores in this set from smallest to largest to derive a new collection: (). There is a large increase in the relative increment at the cut-off point between normal and abnormal times. Therefore, a threshold is set based on the sequential increment:
| (7) |
where is the relative increment. An incremental threshold is first delineated instead of directly delineating the outlier threshold. The increments calculated from the anomaly scores in are compared with . Assuming that is the first increment greater than , then is set as the anomaly score classification threshold . Outliers are identified when the calculated anomaly scores exceed the preset threshold . Because a small anomaly score indicates that the time point corresponds to a normal state, incremental comparisons do not need to be performed from the beginning. In this study, incremental comparisons were performed starting from the 80th percentile anomaly score in (80% of the anomaly scores in the training data set were lower than ).
2.3. Event detection
2.3.1. Event occurrence likelihood calculation
Contamination event detection should be distinguished from outlier identification. In the normal operation process, temporary outliers can be generated from the water quality monitoring data time series owing to technical faults such as external electromagnetic signal infection and data transmission failure. The likelihood of event occurrence is reinforced successively with a succession of outliers. The Bayesian sequential rule [19] is applied to update the probability of an event P(t) based on the results of outlier classification:
| (8) |
where TPR is the true positive rate, calculated as the ratio of the number of time steps correctly classified as anomalies to the total number of time steps during which the WDN is under contamination. Here, TPR is set to 0.5, assuming no prior information about contamination events is available. FPR is the false positive rate, which is calculated as the ratio of the number of time steps incorrectly classified as anomalies to the total number of time steps during which the WDN is under normal conditions; thus, it is equivalent to the ratio of anomaly scores exceeding the threshold to the size of the training data set. is the event probability at time t. Initially, the prior probability of a contamination event is set to a small value (e.g., ) because contamination events are rare. An event alarm is launched when the calculated probability exceeds a specific threshold . A high threshold can improve the reliability of the event alarm and reduce the number of false positives. Here, the threshold probability is set to .
The routine operational hydraulic changes of a WDN can result in short-term high variability in water quality parameters [23,27]. To distinguish normal background variability from contamination events, the calculated probability is smoothed using a simple exponential smoothing model [52] that considers the effect from the previous time step:
| (9) |
where the smoothing parameter determines the importance given to the most recently updated event probability. The robustness of the event detection model will be improved because impulse noise, such as fluctuation in water quality parameters associated with routine operations or sensor faults, is washed away via the smoothing process. A low value of means that more time will be needed to react to a change in event probability and that more anomalies will be needed to update the event probability to the alarm threshold. Here, the smoothing parameter is set to following [21].
2.3.2. Multi-alarm fusion
The GAN-based contamination event detection model is applied separately to a set of single-site and multi-site measurements. The single-site model can focus more on the patterns of multi-parameter variation over time at each station, while the multi-site model can extract the spatiotemporal patterns of water quality parameters from multiple sites. At each time step, both the single-site and the multi-site contamination event detection models can provide univariate event probabilities. To fully exploit the water quality relationship between and within sensor stations, the event probabilities calculated by both the single-site and the multi-site models are fused to provide a combined event probability that reflects the likelihood of a contamination event based on multivariate water quality parameters from all analysed sites. Usually, different weights must be allocated to the single-site and multi-site models to reflect their relative influence on the synchronized decision. Here, the single-site and multi-site models are unsupervised models that do not have contamination information in advance; therefore, uniform weights are used to reflect the lack of prior information. The final alarm is launched when any of the calculated event probabilities from the single-site and multi-site models exceed the preset threshold.
2.4. Baseline method for comparison
The MVE classification model proposed by Ref. [34] is used as a baseline model for comparison purposes. It is a multivariate unsupervised method that incorporates the MVE classifier for outlier identification and subsequently performs sequence analysis utilizing the MVE binary output for event classification. The MVE-based detection model has been applied to both single-site [34,53] and multi-site models [35,36] because it has high accuracy and detection capability, and because model construction and training do not require information on contamination events.
For each sensor station, the MVE classifier enables simultaneous analysis of water quality parameters. It is constructed by finding the minimal ellipsoid that includes 99% of the time series data in the training data set of water quality parameters. The ellipsoid dimension corresponds to the number of monitored water quality parameters. The classier only exploits data obtained under normal operating conditions for constructing the ellipsoid. The ellipsoid is found using the Khachiyan algorithm [54] by iteratively constructing a sequence of decreasing ellipsoids until a minimum bound is satisfied. After the ellipsoid parameters are found, new measurements can be classified as normal (abnormal) if situated inside (outside) the ellipsoid.
Event classification is based on sequence analysis because a succession of outliers represents stronger evidence of event occurrence. The sequence analysis calculates the occurrence probability of a contamination event using the proportion and continuity of outliers in a sliding window. The analysis sequence length is 25 min of measurements, and the calculation formula and the parameters are described comprehensively in Ref. [34]. When the calculated probability exceeds a predetermined event threshold, an alarm will be triggered. Here, the event threshold is set to 0.8, which is higher than the value (0.6) in Ref. [34] because a higher event threshold can reduce the number of false alarms.
The MVE-based contamination event detection method is applied independently to the measured data set of each sensor station. The final alarm is triggered when the calculated probability for any sensor station exceeds the predetermined threshold.
2.5. Performance evaluation
Four indicators are employed to evaluate the performance of the detection methods: (1) number of false alarms, (2) event detection rate, (3) F1 score, and (4) average detection time.
The number of false alarms represents the number of alarms triggered during normal conditions; fewer false alarms mean the model is more reliable.
The event detection rate is calculated as follows:
| (10) |
where p is the number of contamination events and represents detection (denoted by 1) or lack of detection (denoted by 0) of the ith contamination event. The event detection rate is calculated based on the event level instead of the time step level (for one detected contamination event, alerts are only counted once even though multiple time steps are alarmed).
The F1 score can be interpreted as the harmonic mean of precision and recall, which can be calculated as follows:
| (11) |
| (12) |
| (13) |
where TP represents true positives (the number of observations classified as anomalies that are actual contamination events), FN represents false negatives (the number of observations classified as normal events that are contamination events), FP represents false positives (the number of observations classified as anomalies that are normal events), precision is the ratio of the number of time steps correctly classified as under contamination to the total number of time steps classified under contamination, and recall is the ratio of the number of time steps correctly classified as under contamination to the total number of time steps during which the WDN is under contamination. This score ranges from 0 to 1, with 1 being the best achievable score.
The average detection time is the average time taken by the detection model to successfully detect contamination events, and contamination events that are not detected are not considered. For each detected contamination event, the detection time is defined as the elapsed time from the start of the contamination event to the time when the contamination is first identified.
3. Case study
The presented GAN-based contamination event detection method was applied to a skeletonized real-world WDN case study in China: the Yantian network (YTN) (Fig. 3). The YTN has two water sources (S1 and S2): 952 demand nodes and 1175 pipes. Overall, 33 water quality sensor stations were deployed in the YTN. The average demand for the gravity-fed S1 water supply is 36,000 m3 d−1. The total head of S1 ranges from 59.02 to 61.62 m, and the net outflow ranges from 238 to 660 L s−1. S2 has two outlets, and it supplies water under the action of both gravity and pressure. The total average demand is 42,000 m3 d−1. The total head of the pressure-based outlet of S2 ranges from 76.99 to 89.03 m, and the net outflow ranges from 27 to 245 L s−1. The total head of the gravity-based outlet of S2 ranges from 54.03 to 55.44 m, and the net outflow ranges from 104 to 539 L s−1. The YTN has a 24-h demand pattern, with a demand interval of 5-min.
Fig. 3.
Real-world WDN case study (the Yantian Network).
3.1. Water quality simulation
The performance of a contamination event detection method should ideally be evaluated based on real contamination events. However, owing to the lack of records of contamination events in WDNs, simulated data are normally used for model training and performance assessment. In this case study, the water quality data set of the two water sources (S1 and S2) included six water quality parameters with a 5-min time step. The monitored water quality parameters were total chlorine, pH, EC, TOC, temperature, and turbidity. The EPANET model [55] was used for hydraulic simulation, and a multi-species extension [56] was applied to simulate the complex water quality reaction and to generate a spatial water quality database for all the nodes of the network. The EPANET input file contained network topology, initial heads, demand patterns, pump and valve curves, and operational rules. The main inputs of the multi-species extension comprised a set of equilibrium and ordinary differential equations for the mass parameters and the effects of the carbonate system and free chlorine on pH. Chlorine was represented by first-order decay with a rate constant K of 1 (d−1), while pH was represented by a series of equilibrium equations related to chlorine and carbonate [27,57]. Other water quality parameters (except chlorine and pH) were considered conservative constituents. The principal equations of the water quality model describing the reaction kinetics can be expressed as follows:
| (14) |
| (15) |
| (16) |
where alkalinity (mg L−1 as CaCO3) was set to a constant value (e.g., 260 mg L−1 as CaCO3) at S1 and S2.
The contamination events were generated artificially by adding random disturbances to the normal data set, as performed in most other related studies [19,21,22]. The disturbances were generated randomly by considering amplitude, duration, direction (e.g., increase or decrease in value of water quality parameters), and the number of influenced water quality parameters. The peak value of the disturbance was calculated by multiplying the amplitude and the standard deviations of the water quality parameters during routine operation (in this case study, TOC: 0.93 ppb, pH: 0.20, EC: 49.52 mS cm−1, temperature: 1.15 °C, total chlorine: 0.15 mg L−1, and turbidity: 0.84 NTU). The influenced water quality parameters were randomly selected from six water quality parameters for each contamination event. The random event generation process was performed near S1 to ensure that most sensor stations could receive contaminated water. Each generated contamination event lasted 10 h with at least one water quality parameter affected and with a random sample of deviations from normal patterns for each water quality parameter ranging between 1.0 and 3.0 as the event amplitude. The direction of deviation for each affected water quality parameter was selected randomly for each event. The generation of contamination events is described by Ref. [21]. The interval between each contamination event was 3–4 d to eliminate the effects of previous contamination events. Owing to dilution processes, the amplitude of contamination events near the source might be depressed when passed to the downstream nodes. To test the performance of the GAN-based contamination event detection model under different combinations of sensor stations, two different groups of sensor stations at different distances from the contamination source were selected as event detection system (EDS) stations. The first group of EDS stations close to the contamination source included sensors 1, 2, and 3 (Sensor Group 1), while the second group of EDS stations far from the contamination source included sensors 7, 10, and 14 (Sensor Group 2).
The network is simulated (both hydraulics and water quality) for 80 d, with 5-min time steps. The first 14 d are simulated to obtain the stable initial values of the constituents throughout the network. The remaining 66 d of data are divided into a training data set (67%) and a test data set (33%).
3.2. GAN model application
The multivariate time series water quality data were transformed into summation images using the superposition of water quality signals with time duration d = 5, and a historical time window with a size of was adopted by the GAN model to predict and identify the current water quality situation. Image padding (padding value was set to 0) was adopted to maintain images of the same size (32 × 32 parameters) for training the GAN model. Both single-site and multi-site measurements were fed into the same GAN architecture. The hyper-parameters of the GAN models used in the case study comprised optimal parameters identified from a series of trials (Table 1). The running time for training the GAN model was approximately 25 min. Evaluating a new observation and triggering event alarms was instantaneous, and the process was completely automatic. All experiments were performed using Google Colab Pro (Google), which is a cloud service available for deep learning research.
Table 1.
Hyper-parameters of the GAN models used in the case study.
| Hyper-parameter | Value |
|---|---|
| Activation function | ReLU (rectified linear unit) |
| Learning rate | 0.0001 |
| The size of minibatches | 128 |
| Epochs | 150 |
| Optimizer | Adam |
| Filter size | 3 × 3 |
| Channels in G | 32, 32, 64, 128, 256, 256, 256, 128, 64, 32, 1 |
| Channels in D | 10, 10, 20, 40, 80, 80 |
| Normalization | Instance normalization |
| Stride | 2 |
| Momentum | 0.5 |
| Attention module in D | CBAM |
4. Results and discussion
4.1. GAN-based contamination event detection model
Contamination events are detected by performing an event probability update after identifying a series of anomalies. Anomalies can be identified from GAN-based anomaly scores by thresholding the score level. Fig. 4 shows the distribution and sequential increment of GAN-based anomaly scores using single-site and multi-site measurements of the normal training data set. In Fig. 4a and b, the distribution patterns of both single-site and multi-site distributions can be seen to be similar, with most of the anomaly scores concentrated in few areas. However, because the ranges of the calculated anomaly scores are substantially different, setting threshold values directly for both single-site and multi-site GAN models is difficult. A sequential incremental comparison was applied to obtain the anomaly score thresholds for both single-site and multi-site GAN models. As shown in Fig. 4c and d, most of the increments in the middle of the sorted anomaly scores are small. A large increase in the relative increment can be seen at both ends of the percentage of the anomaly scores. The closer the anomaly score is to 0, the more likely the test time point corresponds to a normal state. Therefore, only the larger part of the anomaly scores is considered when determining the incremental threshold. Owing to the different distributions of the anomaly score increments, different incremental thresholds were set for the single-site () and multi-site () GAN models. The thresholds of the anomaly scores can be determined based on the incremental thresholds for the single-site and multi-site GAN models. The original water quality data contain some anomalies due to sensor failure and other factors. Therefore, very few exceptionally high abnormal values are in the calculated anomaly scores. High incremental thresholds that increase the threshold for obtaining anomalies would reduce the chances of false negative alarms but cause the models not to report minor contamination events. Low incremental thresholds enable the detection of smaller contamination events but increase the chances of false negative alarms. Thus, when the monitoring stations do not experience high hydraulic variability during operation and when the accuracy of the water quality sensors is high, smaller incremental thresholds can improve model performance by increasing the chances of minor anomaly detection. When the monitoring stations experience high hydraulic variability during operation or when errors associated with the water quality sensors are large, setting higher thresholds is better to avoid reporting more false negatives.
Fig. 4.
Distribution and sequential increment of the GAN-based anomaly scores using single-site (a, c) and multi-site measurements (b, d).
The single-site model trains an individual GAN model for each sensor station, and an alert is issued when an alert is triggered at any of the stations, whereas the multi-site model trains a GAN model for multiple sensor stations. The proposed GAN-based model for event detection integrates the results of both single-site and multi-site models. Fig. 5 shows event alarms of the single-site, multi-site, and combined models for the training and testing data sets with contamination events. The models were first trained using the training data set with normal conditions, and then tested with the training and testing data sets containing the generated contamination events. Note that the random contamination events were added to both the training and the testing data sets with amplitude of between 1.0 and 1.5, with each event randomly affecting 3–6 water quality parameters. The monitored data of Sensor Group 1 were used to train and test the GAN-based model. The combined model can be seen to detect more contamination events than any of the single-site and multi-site models for both the training and the testing data sets. For the same contamination event, the alarm duration of the multi-site model is usually longer than that of the single-site model. The single-site model is more concerned with temporal changes in multiple water quality parameters at a single site, whereas the multi-site model detects spatial and temporal changes in water quality parameters at multiple sites. Nevertheless, the multi-site model cannot fully replace the single-site model because there are instances when the multi-site model missed an event or triggered a false alarm when the single-site model provided an alarm correctly (highlighted in the red box in Fig. 5). However, the combined model could exploit the strengths of both single-site and multi-site models.
Fig. 5.
Event alarms of single-site, multi-site, and combined models for training (a) and testing (b) data sets with contamination events.
The characteristics of the single-site and multi-site models can be further elucidated by comparing the variation in anomaly scores during a contamination event. Fig. 6 shows the time series of the normalized water quality parameters monitored by Sensor Group 1, together with the GAN-based anomaly scores of both the single-site and the multi-site models for the event highlighted in Fig. 5. An increased anomaly score of similar size is generated by both the single-site and the multi-site models toward the end of the contamination event; however, only the single-site model triggers a true alert owing to the different thresholds. Substantial change is evident in the water quality parameters after approximately 1000 time steps, even without a contamination event. This reflects that some operational hydraulic changes during normal conditions can result in high variability in water quality parameters similar to contamination events. The single-site model generates small increased anomaly scores at the beginning and end of the process, but no alarm is triggered, whereas the multi-site model triggers a false alarm. The single-site model is more likely to detect abrupt changes in water quality, whereas the multi-site model can continuously amplify an abnormal signal during the ongoing process of water quality changes by superimposing the water quality change characteristics of multiple sites at different moments. To reduce false alarms, relevant routine operations could be checked before an alarm is triggered.
Fig. 6.
The time series of the normalized water quality parameters monitored by Sensor Group 1 and the GAN-based anomaly scores of both single-site and multi-site models for the event are highlighted in Fig. 5.
Four experiments with different amplitudes of contamination events ranging from 1.0 to 3.0 (i.e., 1.0–1.5, 1.5–2.0, 2.0–2.5, and 2.5–3.0) were conducted to compare event detection performance between the single-site, multi-site, and combined models. The random events were added to both the training and the testing data sets, with each event randomly affecting 3–6 water quality parameters. Details of the detection performance of the single-site, multi-site, and combined models for events of different amplitude based on the data of Sensor Group 1 are listed in Table 2. For contamination events with small amplitude (<2.0), the single-site model has poor detection performance, and the multi-site model can detect more contamination events. As the contamination event amplitude increases, the single-site model's performance improves markedly. The single-site model detects most contamination events and generates fewer false alarms for contamination events with high amplitude (>2.5). The detection performance of the multi-site model changes little with increasing amplitude of the contamination events, but the multi-site has a higher F1 score and a shorter detection time than the single-site model. The combined model has a higher event detection rate, higher F1 score, and shorter average detection time than those of either the single-site or the multi-site models for all contamination event amplitudes using both the training and the testing data sets; that is, the combined model improves detection accuracy, increases the number of detected events, and shortens the detection time. However, the combined model generates more false alarms than either the single-site model or the multi-site model in most situations because all the false alarms of the single-site and multi-site models are combined. The combined model has improved event detection performance when both single and multi-site models have fewer false alarms. When these models generate varying levels of false alarms, different weights could be allocated to reflect their relative influence on the synchronized decision based on detection accuracy. Moreover, as shown in Fig. 5, some false alarms could be reduced by verifying whether there are any normal operational hydraulic changes.
Table 2.
Detection performance of single-site, multi-site, and combined models for events of different amplitude based on the data of Sensor Group 1.
| Data | Amplitude | Models | False alarm | Event detection rate | F1 score | Average detection time (min) |
|---|---|---|---|---|---|---|
| Training | 1.0–1.5 | Single-site | 6 | 0.36 | 0.13 | 57.4 |
| Multi-site | 6 | 0.71 | 0.50 | 52.3 | ||
| Combined | 10 | 0.79 | 0.50 | 51.6 | ||
| 1.5–2.0 | Single-site | 4 | 0.57 | 0.21 | 46.5 | |
| Multi-site | 5 | 0.86 | 0.59 | 47.2 | ||
| Combined | 7 | 0.93 | 0.61 | 45.5 | ||
| 2.0–2.5 | Single-site | 3 | 0.86 | 0.30 | 46.8 | |
| Multi-site | 5 | 1.00 | 0.68 | 43.3 | ||
| Combined | 6 | 1.00 | 0.69 | 40.5 | ||
| 2.5–3.0 | Single-site | 3 | 0.93 | 0.44 | 43.2 | |
| Multi-site | 4 | 1.00 | 0.73 | 39.0 | ||
| Combined | 5 | 1.00 | 0.74 | 36.1 | ||
| Testing | 1.0–1.5 | Single-site | 1 | 0.29 | 0.02 | 63 |
| Multi-site | 2 | 0.71 | 0.42 | 55.6 | ||
| Combined | 2 | 0.86 | 0.42 | 53.8 | ||
| 1.5–2.0 | Single-site | 1 | 0.57 | 0.11 | 65.3 | |
| Multi-site | 3 | 0.86 | 0.53 | 47.3 | ||
| Combined | 3 | 0.86 | 0.53 | 47.3 | ||
| 2.0–2.5 | Single-site | 1 | 0.71 | 0.19 | 51.4 | |
| Multi-site | 3 | 0.86 | 0.56 | 41.7 | ||
| Combined | 3 | 0.86 | 0.56 | 40 | ||
| 2.5–3.0 | Single-site | 1 | 0.86 | 0.39 | 47.3 | |
| Multi-site | 3 | 0.71 | 0.59 | 38 | ||
| Combined | 3 | 0.86 | 0.59 | 40 |
4.2. Comparison of the GAN-based model with the MVE-based model
The performance of the combined GAN-based contamination event detection model was compared with that of the MVE-based model in identical multiple experiments. Fig. 7 depicts the receiver operating characteristic (ROC) curve of both the combined GAN-based and the MVE-based models using Sensor Groups 1 and 2 during the testing experiments for contamination events with four different amplitudes (1.0–1.5, 1.5–2.0, 2.0–2.5, and 2.5–3.0). The ROC curve depicts the performance trade-off between the true positive rate and the false positive rate for different event probability thresholds. The ROC curve is constructed at the time step level instead of at the event level (i.e., the alarm is compared with the real situation and classified as a true positive or a false positive for every time step). The results demonstrate that the GAN-based model outperforms the MVE-based model for all contamination event experiments with different amplitudes. The ROC curve area calculated using Sensor Group 1 (near the contamination source) is larger than that calculated using Sensor Group 2 (far from the contamination source) for both the GAN-based and the MVE-based models for contamination events with the same amplitudes. The performance of both the GAN-based and the MVE-based models is improved with an increase in the contamination amplitude. Event amplitude might be depressed owing to dilution processes, thereby affecting the performance of the event detection models.
Fig. 7.
Receiver operating characteristic (ROC) curves of both the combined GAN-based and the MVE-based models using data from different groups of sensors during the testing experiments for contamination events with different amplitudes: a–d, ROC curves using Sensor Group 1 for events with amplitudes of 1.0–1.5 (a), 1.5–2.0 (b), 2.0–2.5 (c), and 2.5–3.0 (d); e–h, ROC curves using Sensor Group 2 for events with amplitudes of 1.0–1.5 (e), 1.5–2.0 (f), 2.0–2.5 (g), and 2.5–3.0 (h).
Comparative results of the GAN-based and MVE-based models using Sensor Groups 1 and 2 are listed in Table 3. When the sensors (Sensor Group 1) are closer to the contamination source, the detection performance of the GAN-based model is better than that of the MVE-based model for events with lower amplitude (<2.0). As the amplitude of contamination increases, the detection performance of the MVE-based model markedly improves. When the contamination amplitude exceeds a certain value (>2.5), the detection performance of the MVE-based model exceeds that of the GAN-based model. When the sensors (Sensor Group 2) are far from the contamination source, the detection performance of the GAN-based model is better than that of the MVE-based model for all event experiments, and the MVE-based model generates more false alarms. Although the distance from the contamination source reduces the accuracy of the model, the GAN-based model yields better performance in all conditions, indicating that the GAN-based model is more robust than the MVE-based model. Notably, owing to dilution processes and hydraulic variability during routine operation, not only will the amplitude of contamination events generated at upstream nodes be reduced, but also the trend of water quality change might also be altered, which might cause the MVE-based model to exhibit poorer performance when the sensors are far from the contamination source. Despite the advantages of the GAN-based model demonstrated in this case study, the MVE-based model still shows reasonable performance in some cases, such as when the sensor stations do not encounter high hydraulic variability during operation and when only contamination events with high amplitude need to be identified because low-amplitude events might not have much impact in some circumstances.
Table 3.
Comparative results of GAN-based and MVE-based models using Sensor Groups 1 and 2. Higher performance indicator values are marked in with ∗.
| Sensors | Amplitude | Models | False alarm | Event detection rate | F1 score | Average detection time (min) |
|---|---|---|---|---|---|---|
| Group 1 | 1.0–1.5 | GAN | 2∗ | 0.86∗ | 0.42∗ | 53.8∗ |
| MVE | 2∗ | 0.57 | 0.36 | 54.5 | ||
| 1.5–2.0 | GAN | 3 | 0.86∗ | 0.53∗ | 47.3 | |
| MVE | 2∗ | 0.71 | 0.41 | 47.0∗ | ||
| 2.0–2.5 | GAN | 3 | 0.86∗ | 0.56∗ | 40.0∗ | |
| MVE | 2∗ | 0.86∗ | 0.54 | 44.2 | ||
| 2.5–3.0 | GAN | 3 | 0.86 | 0.59 | 40.0 | |
| MVE | 2∗ | 1.00∗ | 0.66∗ | 37.3∗ | ||
| Group 2 | 1.0–1.5 | GAN | 1∗ | 1.00∗ | 0.34∗ | 84.9 |
| MVE | 15 | 0.43 | 0.22 | 74.0∗ | ||
| 1.5–2.0 | GAN | 2∗ | 0.86∗ | 0.41∗ | 71.7∗ | |
| MVE | 16 | 0.71 | 0.31 | 78.8 | ||
| 2.0–2.5 | GAN | 3∗ | 1.00∗ | 0.44∗ | 69.0∗ | |
| MVE | 15 | 0.86 | 0.38 | 73.7 | ||
| 2.5–3.0 | GAN | 2∗ | 1.00∗ | 0.45∗ | 67.6∗ | |
| MVE | 16 | 0.86 | 0.42 | 67.8 |
4.3. Effects of contamination characteristics on detection performance
Whether the detection performance of the GAN-based model is affected by contamination events with different characteristics is important to determine. The box plots presented in Fig. 8 show the distribution of four evaluation indicators for different amplitudes, together with the number of influenced water quality parameters using Sensor Groups 1 and 2 during the testing experiments (ten experiments were conducted for each set of event amplitude and number of influenced water quality parameters).
Fig. 8.
Distribution of four evaluation indicators for different amplitudes and the number of influenced water quality parameters during the testing experiments: a, c, e, g, Group 1; b, d, f, h, Group 2.
Results show that the detection performance of the GAN-based model is improved for contamination events with increasing amplitude. Greater distance between the sensor stations and the contamination source increases the false alarms and detection time and reduces the F1 score; however, the event detection rate does not change substantially. This is because the labelling of contamination events in this study only considers the time to add contamination from the source, and it takes more time for contaminants to be transmitted to more distant sensors. In the time between contamination addition and transmission to the sensors, the sensors do not receive contaminated water, but they are marked as real events. Additionally, the sensors still receive contaminated water for a certain time after the injection of the contamination has stopped, but these time points are marked as normal. These factors also result in a lower F1 score and a longer detection time. The GAN-based model generates more false alarms using Sensor Group 2 for contamination events with higher amplitude. Fig. 9 shows the event alarms of the proposed GAN-based model using Sensor Group 2 during one testing process. There are a few cases where multiple interval alarms are triggered after a contamination event. Owing to complex hydraulic variations, the sensors might receive contaminated water at multiple intervals for the same contamination event. The alarms for intervals of contaminated water caused by the cessation of contamination injection are considered false alarms, and the GAN-based model is more likely to generate such false alarms for contamination events with higher amplitude. Considering the time of contaminant transport in the WDN, the alarms within 24 h of the start of contamination injection are considered true alarms. Fig. 10 shows the distribution of false alarms for events of different amplitude and numbers of influenced water quality parameters using Sensor Group 2 during the testing experiments, considering different event duration flags. The number of false alarms can be seen to be substantially reduced after the transportation time is considered in triggering event alarms, which means that contaminants could affect the network for a long time after injection. In practice, despite the identification of contaminants, water must be discharged in the affected area for a long time to ensure water security.
Fig. 9.
Event alarms of the proposed GAN-based model using Sensor Group 2 during one testing process (contamination characteristics: amplitude is 2.0–2.5 and the number of influenced water quality parameters is 5).
Fig. 10.
Distribution of false alarms for events with different amplitude and different numbers of influenced water quality parameters using Sensor Group 2 during the testing experiments, with consideration of different event duration flags: a, alarms during the time of contamination injection (in this study, each contamination event lasted 10 h) are regarded as true alarms; b, alarms within 24 h of the start of contamination injection are regarded as true alarms.
As shown in Fig. 8, the number of influenced water quality parameters has little effect on the detection performance of the model. Contamination events with a higher number of influenced water quality parameters do not necessarily lead to an increase in detection performance. The detection performance of the GAN-based model is better for contamination events with 2–3 water quality parameters affected than contamination events with six water quality parameters affected. This is because, in the training data set, some operational hydraulic changes might cause simultaneous changes in most water quality parameters. Some contamination events (with most water quality parameters affected) that have similar change patterns as the normal state under routine operation are classified as normal by the GAN-based model.
5. Conclusions
A GAN-based contamination event detection method was developed in this study for the detection of contamination events in a WDN. The proposed GAN-based model detects contamination events by simultaneously analysing multiple water quality parameter data from multiple sensor stations. First, the measured water quality data are transformed into superimposed images fusing different water quality parameters from multiple stations. Then, the GAN-based model is constructed to measure the degree of abnormality at each time step by calculating anomaly scores based on two networks, G and D. Bayesian sequential analysis is used to update the contamination event probability after identifying the anomalies using the anomaly score threshold. Finally, the final alarm is generated by combining the early warning results of single-site and multi-site models.
The effectiveness of the GAN-based model was tested in a case study of a real WDN, and contamination data generated by water quality simulations based on the chemical reaction kinetics and network hydraulics were used to evaluate detection performance. The main conclusions derived are summarised below.
-
(1)
The proposed GAN-based model, which is trained using only data obtained under normal conditions, improves the detection rate and time compared with those of the individual single-site and multi-site models and the MVE-based benchmark model.
-
(2)
The proposed GAN-based model is robust to contamination events with different amplitude and monitored at different sensor stations. For two sensor groups located at different distances from the contamination source, the GAN-based model can achieve a high event detection rate and reduce the number of false alarms, whereas the MVE-based model has lower detection performance for the sensor group located furthest from the contamination source. Additionally, the detection rate of the GAN-based model is high for various contamination events with different amplitude and different numbers of water quality parameters affected during the events, highlighting its robustness for contamination event detection.
-
(3)
The event detection rate is improved by fusing the alarms of the individual single-site and multi-site models. This is probably because the GAN-based model combines the advantages of both single-site and multi-site models and can detect both abrupt changes and ongoing changes in water quality.
Although the detection performance of the proposed GAN-based model was tested with contamination events of different amplitude and different sensor data sources, more experiments should be conducted to test and generalize the GAN-based model. This study was based on the assumption that contamination occurs upstream of the sensor combination to ensure that all sensors in a sensor group received contaminated water. The performance of the GAN-based model in detecting contamination events should be tested for different combinations of sensor stations in the future, and the effect of the anomaly detection model could be considered in the optimal arrangement of sensors. Theoretically, for a contamination source close to a sensor station, the anomaly score calculated by the GAN model will be high. In future research, the anomaly scores calculated by the GAN model could be used to further analyse the possibility of locating contamination sources. In practical application, if there are few sensor stations within a WDN and the distance between adjacent stations is large, the similarity between water quality data of different stations will be small and unsuitable for application in a multi-site model. In this situation, only a single-site model should be considered. In this study, multiple sets of contamination events affecting different water quality parameters were considered for performance testing, and future work could investigate the impact of the model on each water quality parameter metric. The current study used data from the previous 2.5 h to identify the normal mode. In future studies, the effects of input water quality data over different lengths of time are recommended to be examined.
Declaration of interests
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
This research was supported by the National Natural Science Foundation of China (52122901, 52079016), Fundamental Research Funds for the Central Universities (DUT21GJ203), and the UK Royal Society (Ref: IF160108 and IEC∖NSFC∖170249). The visit of Zilin Li to the University of Exeter (UK) was sponsored by the China Scholarship Council (202106060094).
References
- 1.Beker B.A., Kansal M.L. Fuzzy logic-based integrated performance evaluation of a water distribution network. J. Water Supply Res. Technol. 2022;71:490–506. doi: 10.2166/aqua.2022.004. [DOI] [Google Scholar]
- 2.Bui X.K., Marlim M.S., Kang D. Water network partitioning into district metered areas: a state-of-the-art review. Water (Switzerland) 2020;12 doi: 10.3390/W12041002. [DOI] [Google Scholar]
- 3.Che T.C., Duan H.F., Lee P.J., Pan B., Ghidaoui M.S. Transient frequency responses for pressurized water pipelines containing blockages with linearly varying diameters. J. Hydraul. Eng. 2018;144 doi: 10.1061/(asce)hy.1943-7900.0001499. [DOI] [Google Scholar]
- 4.Liu G., Zhang Y., Knibbe W.J., Feng C., Liu W., Medema G., van der Meer W. Potential impacts of changing supply-water quality on drinking water distribution: A review. Water Res. 2017 doi: 10.1016/j.watres.2017.03.031. [DOI] [PubMed] [Google Scholar]
- 5.Xin K.L., Tao T., Li S., Yan H. Contamination accidents in China's drinking water distribution networks: status and countermeasures. Water Pol. 2017;19:13–27. doi: 10.2166/wp.2016.157. [DOI] [Google Scholar]
- 6.Liu S., Che H., Smith K., Chang T. A real time method of contaminant classification using conventional water quality sensors. J. Environ. Manag. 2015;154:13–21. doi: 10.1016/j.jenvman.2015.02.023. [DOI] [PubMed] [Google Scholar]
- 7.McKenna S.A., Wilson M., Klise K.A. Detecting changes in water quality data. J. Am. Water Works Assoc. 2008;100:74–85. doi: 10.1002/j.1551-8833.2008.tb08131.x. [DOI] [Google Scholar]
- 8.Liu S., Che H., Smith K., Lei M., Li R. Performance evaluation for three pollution detection methods using data from a real contamination accident. J. Environ. Manag. 2015;161:385–391. doi: 10.1016/j.jenvman.2015.07.026. [DOI] [PubMed] [Google Scholar]
- 9.Yang Y.J., Haught R.C., Goodrich J.A. Real-time contaminant detection and classification in a drinking water pipe using conventional water quality sensors: techniques and experimental results. J. Environ. Manag. 2009;90:2494–2506. doi: 10.1016/j.jenvman.2009.01.021. [DOI] [PubMed] [Google Scholar]
- 10.Rodriguez-Perez J., Leigh C., Liquet B., Kermorvant C., Peterson E., Sous D., Mengersen K. Detecting technical anomalies in high-frequency water-quality data using artificial neural networks. Environ. Sci. Technol. 2020;54:13719–13730. doi: 10.1021/acs.est.0c04069. [DOI] [PubMed] [Google Scholar]
- 11.Guepie B.K., Fillatre L., Nikiforov I. Sequential monitoring of water distribution network. IFAC Proc. Vol. 2012 doi: 10.3182/20120711-3-BE-2027.00114. (IFAC-PapersOnline). IFAC. [DOI] [Google Scholar]
- 12.Hou D., Chen Y., Zhao H., Huang P., Zhang G. Transducer and Microsystem Technologies. 2013. Water quality anomaly detection method based on RBF neural network and wavelet analysis; pp. 3–6. [DOI] [Google Scholar]
- 13.Byer D., Carlson K.H. Real-time detection of intentional chemical contamination in the distribution system. J. Am. Water Works Assoc. 2005;97:130–133. doi: 10.1002/j.1551-8833.2005.tb10938.x. [DOI] [Google Scholar]
- 14.Hall J., Zaffiro A.D., Marx R.B., Kefauver P.C., Radha Krishnan E., Haught R.C., Herrmann J.G. On-line water quality parameters as indicators of distribution system contamination. J. Am. Water Works Assoc. 2007;99:66–77. doi: 10.1002/j.1551-8833.2007.tb07847.x. [DOI] [Google Scholar]
- 15.King K.L., Kroll D. Trigger and detection method for threat agents in drinking water. Opt. Photonics Glob. Homel. Secur. 2005;5781:63–74. doi: 10.1117/12.606961. [DOI] [Google Scholar]
- 16.Kroll D., King K. Laboratory and flow loop validation and testing of the operational effectiveness of an on-line security platform for the water distribution system. 8th Annu. Water Distrib. Syst. Anal. Symp. 2006. 2008;173 doi: 10.1061/40941(247)173. [DOI] [Google Scholar]
- 17.Liu S., Smith K., Che H. A multivariate based event detection method and performance comparison with two baseline methods. Water Res. 2015;80:109–118. doi: 10.1016/j.watres.2015.05.013. [DOI] [PubMed] [Google Scholar]
- 18.Liu S., Che H., Smith K., Chen L. Contamination event detection using multiple types of conventional water quality sensors in source water. Environ. Sci. Process. Impacts. 2014;16:2028–2038. doi: 10.1039/c4em00188e. [DOI] [PubMed] [Google Scholar]
- 19.Arad J., Housh M., Perelman L., Ostfeld A. A dynamic thresholds scheme for contaminant event detection in water distribution systems. Water Res. 2013;47:1899–1908. doi: 10.1016/j.watres.2013.01.017. [DOI] [PubMed] [Google Scholar]
- 20.Housh M., Ostfeld A. An integrated logit model for contamination event detection in water distribution systems. Water Res. 2015;75:210–223. doi: 10.1016/j.watres.2015.02.016. [DOI] [PubMed] [Google Scholar]
- 21.Li Z., Zhang Chi, Liu H., Zhang Chao, Zhao M., Gong Q., Fu G. Developing stacking ensemble models for multivariate contamination detection in water distribution systems. Sci. Total Environ. 2022;828 doi: 10.1016/j.scitotenv.2022.154284. [DOI] [PubMed] [Google Scholar]
- 22.Perelman L., Arad J., Housh M., Ostfeld A. Event detection in water distribution systems from multivariate water quality time series. Environ. Sci. Technol. 2012;46:8212–8219. doi: 10.1021/es3014024. [DOI] [PubMed] [Google Scholar]
- 23.Zou X.Y., Lin Y.L., Xu B., Guo Z.B., Xia S.J., Zhang T.Y., Wang A.Q., Gao N.Y. A novel event detection model for water distribution systems based on data-driven estimation and support vector machine classification. Water Resour. Manag. 2019 doi: 10.1007/s11269-019-02317-5. [DOI] [Google Scholar]
- 24.Zhao H. 2015. Research on Water Quality Anomaly Detection and Anomaly Characteristic Analysis for Urban Water Supply. [Google Scholar]
- 25.Roehl E.A., Jr., Cook J.B., Daamen R.C., Mundry U.H. Interpreting real-time online monitoring data for water quality event detection. Water Res. Found. 2014 [Google Scholar]
- 26.Klise K.A., McKenna S.A. Multivariate applications for detecting anomalous water quality. 8th Annu. Water Distrib. Syst. Anal. Symp. 2006. 2007;130 doi: 10.1061/40941(247)130. [DOI] [Google Scholar]
- 27.Housh M., Ohar Z. Integrating physically based simulators with Event Detection Systems: multi-site detection approach. Water Res. 2017;110 doi: 10.1016/j.watres.2016.12.003. [DOI] [PubMed] [Google Scholar]
- 28.Sun Q., Zhang Y., Lu B., Liu H. Flow measurement-based self-adaptive line segment clustering model for leakage detection in water distribution networks. IEEE Trans. Instrum. Meas. 2022;71:1–13. doi: 10.1109/TIM.2022.3165258. [DOI] [Google Scholar]
- 29.Yang X., Boccelli D.L. Model-based event detection for contaminant warning systems. J. Water Resour. Plann. Manag. 2016;142 doi: 10.1061/(ASCE)WR.1943-5452.0000689. [DOI] [Google Scholar]
- 30.Fu G., Makropoulos C., Butler D. Simulation of urban wastewater systems using artificial neural networks: embedding urban areas in integrated catchment modelling. J. Hydroinf. 2010;12:140–149. doi: 10.2166/hydro.2009.151. [DOI] [Google Scholar]
- 31.Fan J., Wang S., Li H., Yan Z., Zhang Y., Zheng X., Wang P. Modeling the ecological status response of rivers to multiple stressors using machine learning: a comparison of environmental DNA metabarcoding and morphological data. Water Res. 2020;183 doi: 10.1016/j.watres.2020.116004. [DOI] [PubMed] [Google Scholar]
- 32.Huang P., Jin Y., Hou D., Yu J., Tu D., Cao Y., Zhang G. Online classification of contaminants based on multi-classification support vector machine using conventional water quality sensors. Sensors. 2017;17 doi: 10.3390/s17030581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Qian K., Jiang J., Ding Y., Yang S. Deep learning based anomaly detection in water distribution systems. 2020 IEEE Int. Conf. Networking, Sens. Control. 2020 doi: 10.1109/ICNSC48988.2020.9238099. ICNSC 2020. [DOI] [Google Scholar]
- 34.Oliker N., Ostfeld A. Minimum volume ellipsoid classification model for contamination event detection in water distribution systems. Environ. Model. Software. 2014;57:1–12. doi: 10.1016/j.envsoft.2014.03.011. [DOI] [PubMed] [Google Scholar]
- 35.Oliker N., Ohar Z., Ostfeld A. Spatial event classification using simulated water quality data. Environ. Model. Software. 2016;77:71–80. doi: 10.1016/j.envsoft.2015.11.013. [DOI] [Google Scholar]
- 36.Oliker N., Ostfeld A. Network hydraulics inclusion in water quality event detection using multiple sensor stations data. Water Res. 2015;80:47–58. doi: 10.1016/j.watres.2015.04.036. [DOI] [PubMed] [Google Scholar]
- 37.Goodfellow I., Pouget-Abadie J., Mirza M., Xu B., Warde-Farley D., Ozair S., Courville A., Bengio Y. Generative adversarial networks. Commun. ACM. 2020;63:139–144. doi: 10.1145/3422622. [DOI] [Google Scholar]
- 38.Chen D., Yue L., Chang X., Xu M., Jia T. NM-GAN: noise-modulated generative adversarial network for video anomaly detection. Pattern Recogn. 2021;116 doi: 10.1016/j.patcog.2021.107969. [DOI] [Google Scholar]
- 39.Choi Y., Lim H., Choi H., Kim I.J. GAN-based anomaly detection and localization of multivariate time series data for power plant. Proc. - 2020 IEEE Int. Conf. Big Data Smart Comput. BigComp. 2020:71–74. doi: 10.1109/BigComp48618.2020.00-97. 2020. [DOI] [Google Scholar]
- 40.Goodfellow I., Pouget-Abadie J., Mirza M., Xu B., Warde-Farley D., Ozair S., Courville A., Bengio Y. Generative adversarial nets. Adv. Neural Inf. Process. Syst. 2014;27 [Google Scholar]
- 41.B. Mohammadi, M. Fathy, M. Sabokrou, Image/Video Deep Anomaly Detection: A Survey. arXiv 2021. arXiv preprint arXiv:2103.01739.
- 42.Bashar M.A., Nayak R. TAnoGAN: time series anomaly detection with generative adversarial networks. 2020 IEEE Symp. Ser. Comput. Intell. SSCI 2020. 2020:1778–1785. doi: 10.1109/SSCI47803.2020.9308512. [DOI] [Google Scholar]
- 43.Ducoffe M., Haloui I., Gupta J. Sen. Anomaly detection on time series with wasserstein GAN applied to PHM. Int. J. Prognostics Health Manag. 2019;10 [Google Scholar]
- 44.Li D., Chen D., Jin B., Shi L., Goh J., Ng S.K. MAD-GAN: multivariate anomaly detection for time series data with generative adversarial networks. Lect. Notes Comput. Sci. 2019:703–716. doi: 10.1007/978-3-030-30490-4_56. (including Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinformatics) 11730 LNCS. [DOI] [Google Scholar]
- 45.Yoon J., Jarrett D., van der Schaar M. Time-series generative adversarial networks. Adv. Neural Inf. Process. Syst. 2019;32:1–11. [Google Scholar]
- 46.Giudicianni C., Herrera M., Di Nardo A., Creaco E., Greco R. Multi-criteria method for the realistic placement of water quality sensors on pipes of water distribution systems. Environ. Model. Software. 2022;152 doi: 10.1016/j.envsoft.2022.105405. [DOI] [Google Scholar]
- 47.Ostfeld A., Uber J.G., Salomons E., Berry J.W., Hart W.E., Phillips C.A., Watson J.-P., Dorini G., Jonkergouw P., Kapelan Z., di Pierro F., Khu S.-T., Savic D., Eliades D., Polycarpou M., Ghimire S.R., Barkdoll B.D., Gueli R., Huang J.J., McBean E.A., James W., Krause A., Leskovec J., Isovitsch S., Xu J., Guestrin C., VanBriesen J., Small M., Fischbeck P., Preis A., Propato M., Piller O., Trachtman G.B., Wu Z.Y., Walski T. The battle of the water sensor networks (BWSN): a design challenge for engineers and algorithms. J. Water Resour. Plann. Manag. 2008;134:556–568. doi: 10.1061/(asce)0733-9496. 2008)134:6(556. [DOI] [Google Scholar]
- 48.Zhu J.Y., Park T., Isola P., Efros A.A. Unpaired image-to-image translation using cycle-consistent adversarial networks. Proc. IEEE Int. Conf. Comput. Vis. 2017:2242–2251. doi: 10.1109/ICCV.2017.244. 2017-Octob. [DOI] [Google Scholar]
- 49.Woo S., Park J., Lee J.Y., Kweon I.S. CBAM: convolutional block attention module. Lect. Notes Comput. Sci. 2018:3–19. doi: 10.1007/978-3-030-01234-2_1. (including Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinformatics) 11211 LNCS. [DOI] [Google Scholar]
- 50.Arjovsky M., Chintala S., Bottou L. 2017. Wasserstein GaN. arXiv. [Google Scholar]
- 51.Gulrajani I., Ahmed F., Arjovsky M., Dumoulin V., Courville A.C. Improved training of wasserstein gans. Adv. Neural Inf. Process. Syst. 2017;30 [Google Scholar]
- 52.Rubinstein R.Y., Kroese D.P. Springer; 2004. The Cross-Entropy Method: A Unified Approach To Combinatorial Optimization, Monte-Carlo Simulation, And Machine Learning. [Google Scholar]
- 53.Oliker N., Ostfeld A. Comparison of two multivariate classification models for contamination event detection in water quality time series. J. Water Supply Res. Technol. - AQUA. 2015;64:558–566. doi: 10.2166/aqua.2014.033. [DOI] [Google Scholar]
- 54.Khachiyan L.G. Rounding of polytopes in the real number model of computation. Math. Oper. Res. 1996;21:307–320. doi: 10.1287/moor.21.2.307. [DOI] [Google Scholar]
- 55.Rossman L.a. 2000. Epanet 2: Users Manual 1-200. [Google Scholar]
- 56.Shang F., Uber J.G., Rossman L.A. EPANET multi-species extension software and user's manual. Environ. Prot. Agency USA. 2008;7:113. [Google Scholar]
- 57.Ohar Z., Ostfeld A. Optimal design and operation of booster chlorination stations layout in water distribution systems. Water Res. 2014;58:209–220. doi: 10.1016/j.watres.2014.03.070. [DOI] [PubMed] [Google Scholar]