Abstract
The main goal of this study is to evaluate the impact of population mobility on electricity generation in Russian cities in the conditions of the spread of COVID-19, and identify hotspots. Furthermore, the evaluation is also conducted using hybrid fuzzy decision-making modelling. In this context, q-ROF DEMATEL and TOPSIS methods are taken into consideration. Additionally, a comparative evaluation is also performed with the help of Intuitionistic and Pythagorean fuzzy sets. The results are quite similar that allows to conclude that the findings are reliable and coherent. The study proves the hypothesis that human behavior changed during the COVID-19 pandemic, and electricity consumption is declining in major cities around the world. The biggest fall in energy generation was in Moscow and Yekaterinburg. In St. Petersburg and Nizhny Novgorod, the fall in energy generation is no so crucial because these cities have low building density. The study uses Long Short-Term Memory models with many different parameters. The Q-Rung Orthopair Fuzzy Sets model forecasts new COVID-19 using ten parameters. This study identifies factors influencing the spread of COVID-19 based on the theory of "broken windows" and outlines directions in limiting population mobility, which can form the basis of state policy. According to the analysis the air temperature is the variable that most affects this process.
Keywords: Energy economics, Power resources, Energy sustainability, Energy optimization, Energy saving strategies
Energy economics; Power resources; Energy sustainability; Energy optimization; Energy saving strategies.
1. Introduction
The coronavirus pandemic has been actively spreading throughout the world since December 2019, forcing the World Health Organization to declare a global pandemic (Hosseini, 2020; Bhuiyan et al., 2021). As of November 2021, Russia is among the leaders in countries with the most deaths and new identified cases per day. In order to reduce the rate of new infections, the Ministry of Health employed strategies, which consisted of restricting mass gatherings, quarantining, wearing masks, gloves and other protective equipment. The immediate decrease in mobility led to an increase in the number of people staying in their living quarters for longer than usual, leading to changing behavior habits. This, in turn, affects the dynamics and volumes of electricity consumption in Russian cities (Statdata, 2020; Russian Ministry of Health, 2020).
The novelty of this study is the evaluation of the impact of COVID-19 on electricity energy generation and production. This paper proves the idea that electricity energy consumption is more dependent on economic sustainable growth and efficient resources policy (Huang et al., 2020). It identifies factors influencing the spread of COVID-19 based on the theory of "broken windows" and outlines directions in limiting population mobility, which can form the basis of state policy. Amongst cities most affected by the pandemic are Moscow, St. Petersburg, Yekaterinburg, and Nizhny Novgorod.
These cities have a population of over 0.5 million, along with high housing density, which may explain the prevalence of COVID-19. However, some outbreaks do not correlate with these factors and may be associated with the population's seasonal travel. Uncertainty over Russia's economic state remains, despite the fact that general restrictive measures began to be lifted in early June of 2021. The estimate of the International Monetary Fund shows a decline in Russia's GDP of 5.5% in 2020 and subsequent growth of 3.5% in 2021. Estimates of the spread of COVID-19, based on official statistics, indicate a large number of infections with a strong downward trend even after the peak. Italian researchers also suggest maintaining partial restrictive and supervisory measures at a level that prevents a possible resumption of the infection's spread for many years (Bertuzzo et al., 2020).
The short-term state policy in the field of energy has changed in connection with the measures taken in the country and its partners. Existing studies reflect changes in the generation and consumption of electricity in territories subject to COVID-19-related restrictions. This research paper aims to develop tools for forecasting the impact of urban mobility in large cities prone to high rates of COVID-19 infections on electricity generation and consumption in Russia. The model uses open data to successfully forecast future changes in energy consumption and production (Yandex, 2021; Statdata, 2020; Russian Ministry of Health, 2020; Shea and Poast, 2018; Sun and Hong, 2017; Tintelnot et al., 2017; Tomar and Gupta, 2020; Valta, 2012; Wei and Yermack, 2011).
Furthermore, another evaluation is conducted using hybrid fuzzy decision-making modelling. Within this framework, q-ROF DEMATEL and TOPSIS methods are taken into consideration. Additionally, a comparative evaluation is also performed with the help of Intuitionistic and Pythagorean fuzzy sets. The data, related to the buyer and seller, allow to conduct a detailed analysis of energy companies and macroeconomic effects associated with them and their industry.
The paper has some novelties. SWARA method has two new applications have an influence on the originality of the proposed model. On the other side, considering q-ROFSs in the analysis process brings some advantages. Because a wider space is used with q-ROFSs by comparing with IFSs and PFSs, more precise results can be reached. The paper is organized as follows: there are six different parts in this study. In the following part, the review of literature is shared. The third part is related to the methods of research. The results are given in the fourth part. The fifth part includes the discussion. The final section presents the conclusions of the study.
2. Literature review
The world is experiencing the effects of the coronavirus infection. As a result, various international, state, and private organizations are developing solutions to assess the damage to the population's health and the economy of the world and in Russia. According to the WHO, the number of confirmed cases of COVID-19 infections in Russia is 8,5 million as of November 2021 (WHO, 2021). On January 23, 2020, Russia began to introduce the first restrictive measures, which initially concerned only border crossing. From March 25 to May 11, 2020 quarantine measures were introduced in regions of Russia, which implied restrictions on mass gatherings, including those in specific workplaces. The efficiency of the adopted measures is confirmed by studies of monitoring hospitalization, as well as the impact of quarantine measures based on empirical evidence from the United States (Fowler et al., 2021). The article also takes into account existing methods for forecasting COVID-19-related statistics to increase the accuracy of the models by Fowler. Many researchers found the impact of COVID-19 pandemic on oil consumption in the United States, China and developing countries (Sánchez-Úbeda et al., 2022; Ashkanani et al., 2022; Lazo et al., 2022; Ku et al., 2022).
Factors determining the diffusion of COVID-19 and suggested strategies to prevent future accelerated viral infectivity similar to the ongoing pandemic are discussed in many studies (Askitas et al., 2021; Liu et al., 2022; Sánchez-López et al., 2022).
Influence of population density, temperature, and absolute humidity on the spread and decay durations of COVID-19 are discussed in comparative studies of scenarios in Europe, Malaysia, China, England, Germany and Japan (Flaxman et al., 2020; Diao et al., 2021; Toosty et al., 2022; Wen et al., 2022; Ueno, 2022).
The general situation could undoubtedly affect consumption and, accordingly, electricity generation in Russia. According to one of the latest reports from the Russian Ministry of Energy, the volume of demand for electricity in Russia has not decreased as much as in other European countries (Eroğlu, 2020). In the period from March 30 to May 25, the demand for electricity in the Unified Energy System (UES) of Russia decreased by 3.9% relative to the same period in 2019, and by 3.5% relative to the average value in 2017–2019. According to the report, the largest decline was recorded in the first week of self-isolation, which partially coincides with a high level in the "self-isolation index" in Russia (Yandex, 2021). Furthermore, following a decrease in consumption, the production of electricity subsequently declined. This fact had the greatest impact on electricity generation at thermal power stations. Their capacities fell on average by 15%, while the capacities of some other types of power plants increased, specifically in hydroelectric power plants due to the high-water hydrological situation (Happle et al., 2020).
Research on the impact of COVID-19 on the energy markets and FX market has mainly focused on changes in the amount of direct and indirect carbon dioxide production, as well as developing new strategies to begin the active adoption of renewable energy sources (RES) policies and prospects of their further expansion in the face of declining demand (Eroğlu, 2020; Rugani and Caro, 2020). In 2020 particularly, a reduction in the implementation of new renewable energy sources in the world is already noticeable and to be expected, due to an overall decrease in demand for electricity, which is confirmed by different studies (Eroğlu, 2020; Rugani and Caro, 2020). They also describe a reduction of carbon dioxide emissions in France and Italy due to reduced mobility and temporary suspension of the activities of certain sectors of the economy (Schwert, 1981; Ahn et al., 2017).
Moreover, the mobility of people during and after the easing of quarantine measures will still be lower than it was before the coronavirus outbreak. Lee et al. (2015) cites the increasing share of teleworking in various sectors of employment and the decrease in international travel, especially for recreational purposes, as the main reasons for this phenomenon (Hong and Lin, 2013).
Population mobility figures are prominent in the context of the broken window theory. The negative impact on public health under this concept is confirmed by recent work (Chen and Ban, 2018). It has also been observed that government policies have a large impact on reducing the perception of risk among the population. In this case, the population mobility index may reflect the perception of risk in relation to COVID-19. This results in the aggravation of the overall epidemiological situation and, subsequently, energy consumption (Chen et al., 2017; Das and Kjærgaard, 2019).
Forecasting electricity demand using regression models and neural networks has been a fairly popular topic for researchers lately. Long Short-Term Memory (LSTM) models are exceptionally accurate in this regard, but more complex structures and approaches to solving multivariate time series sets also show promising results (Chen et al., 2019). Models like these have also been used with great success in forecasting the future spread of COVID-19. For example, researchers have already presented a neural network based on Keras LSTMs to accurately forecast new cases of the coronavirus infection in India (Beltran and Cerpa, 2014; Bollinger and Evins, 2019).
This article aims to study the factor of urban population mobility in the context of measures introduced in Russia due to the threat of the virus’ spread. Reduced human mobility is assumed to lead to a decrease in electricity consumption, and this effect is also supported by enterprises through compliance with regulatory measures and reduced demand in some sectors of the economy. As more precautions to ease restrictive measures or decrease the number of people infected in a city are taken, more people tend to increase their mobility and, as a consequence, increase the overall urban electricity consumption.
This concept reflects the provisions of the broken windows theory, according to which, if someone broke a glass window in a house and no one fixed it, then soon all of the windows in the house will be broken as well (Engel et al., 2014).
3. Methods
In this study, a comparative evaluation is performed by using long short-term memory and hybrid fuzzy decision-making models (Lin et al., 2020; Liu et al., 2022; Mao et al., 2020; Meshram et al., 2020). In this section, the theoretical background of these models is defined.
3.1. Sample and data
The main goal of this study is to determine the degree of influence of the restrictive measures introduced in connection with COVID-19 on energy consumption and production. Moreover, during the analysis, additional results may arise, and new hypotheses may appear, which will be confirmed or refuted (Akhavan et al., 2018). Two different models are generated by considering the Keras LSTM. The first model forecasts power generation and uses 76 parameters. The second LSTM model estimates new COVID-19 cases across countries. It involves 10 parameters, the data for which are publicly available (Keras model, 2020). This model is already actively used for forecasting energy consumption (Bouktif et al., 2018).
3.2. Measures of variables
For the LSTM expansion function, SELU is used on the first layer. The SELU activation function multiplies the scale (>1) by the output of the tf.keras.activations.elu function to provide a slope greater than one for positive inputs. ELU is utilized on the second layer. ELUs have negative values that bring the average activations closer to zero. Average activation values close to zero allow faster learning as they bring the gradient closer to a natural gradient. ELUs saturate to a negative value when the argument gets smaller. Saturation refers to a small derivative that reduces variation and information that extends to the next level (Bedi and Toshniwal, 2019).
Furthermore, to solve the problem of training on a set of time series with multivariate values, weights are applied from previous trainings to all subsequent values in a cumulative effect. Some parameters that show little importance for the model are eliminated. The importance in this case is calculated as the difference in Root Mean Square. To measure the importance of the variable, a large sample (150 time series) of xˆdata is taken and the forecast of the ŷ model is calculated. Then, each variable xi is measured (and only this variable) by a random normal distribution centered at 0 on a scale of 1000 and the forecast yî is calculated. The final effect of this disturbance is measured in terms of the RMS difference between the original ŷ and the modified ŷ. The greater the difference in RMS, the greater the importance of the variable. This improves the accuracy of earlier models (Shea and Poast, 2018; Sun and Hong, 2017; Tintelnot et al., 2017; Tomar and Gupta, 2020; Valta, 2012; Wei and Yermack, 2011).
Electricity consumption in the UES of Russia in April 2020 decreased by 2.9% (relative to April 2019). The article uses open statistics on COVID-19 infections, data on the generation and consumption of electricity, as well as other related parameters to estimate future consumption and production of electricity in Russia and its regions (Mosteiro-Romero et al., 2017; Ni, 2019; Norouzi et al., 2020; O'Brien et al., 2019; Oberfield, 2018).
The model is in two parts. The first model forecasts future quarantine measures, which are tentatively expected to have the greatest impact on electricity generation data. It is worth noting that in the case of a low RMS difference for the quarantine measures index; this parameter can be supplemented or replaced by another more significant one to improve the forecasting accuracy. The second model combines the data obtained from the first and historical data on the energy industry in Russia and estimates with some certainty the further actual and planned production of electricity (Miller, 2007; Mohammadi and Taylor, 2017). It is proposed to use open data and developments from Yandex as additional indexes of mobility.
3.3. Models and data analysis procedure
Intuitionistic fuzzy sets (I) identify the membership ( and non-membership ( degrees. Hence, more effective solutions can be provided. These sets are shown in Eq. (1) (Alcantud et al., 2020).
| (1) |
In this context, the condition that should be satisfied is .
Pythagorean fuzzy sets (P) demonstrate an extended fuzzy membership grade as stated in Eq. (2) (Gao and Deng, 2021).
| (2) |
For this purpose, the condition in Eq. (3) should be met.
| (3) |
Q-rung orthopair fuzzy sets (q-ROFSs) is an extension of P and I. They are often used in the case of an uncertainty problem in the complex decision-making process. Eq. (4) explains these sets and Eq. (5) gives information about the condition (Ali and Mahmood, 2020).
| (4) |
| (5) |
Figure 1 compares these fuzzy sets.
Figure 1.
Membership and non-membership degrees of IFS, PFS, and q-ROFSs.
Eq. (6) indicates the degree of indeterminacy.
| (6) |
The mathematical details of these fuzzy sets are shown in Eqs. (7), (8), (9), (10), and (11) (Lin et al., 2020).
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
Eq. (12) is also considered for defuzzification.
| (12) |
The DEMATEL methodology calculates the items’ weights. Therefore, more essential factors can be identified. Firstly, the direct-relation matrix is constructed by comparing the items with each other. Eq. (13) identifies this matrix (Braga et al., 2021).
| (13) |
Secondly, this matrix is normalized by Eqs. (14) and (15) (Mao et al., 2020).
| (14) |
| (15) |
The total relation matrix is generated in the next step with the following Eq. (16).
| (16) |
The sums of rows and columns that are and are computed by Eqs. (17) and (18).
| (17) |
| (18) |
The sum of these values is used to define the significance of the items. However, the causal relations are determined by considering the difference of these values and Eq. (19).
| (19) |
TOPSIS makes an evaluation regarding the ranking of different alternatives. Firstly, normalized values are calculated by Eq. (20) (Sałabun et al., 2020).
| (20) |
Secondly, the weighted values are computed with Eq. (21).
| (21) |
Then, the positive () and negative () ideal solutions are defined with Eqs. (22) and (23).
| (22) |
| (23) |
Eqs. (24) and (25) are used to compute the distances to the best () and worst alternatives.
| (24) |
| (25) |
In the final stage, the relative closeness to the ideal solutions () is defined with Eq. (26) (Meshram et al., 2020).
| (26) |
The proposed model has some novelties. In this model, SWARA method is improved with the name of M-SWARA. With the help of this improvement, impact relation map can be created. In addition to this issue, in this proposed model, golden ratio is taken into consideration to calculate the weights in bipolar q-ROFSs. Hence, these two new applications have an influence on the originality of the proposed model. On the other side, considering q-ROFSs in the analysis process brings some advantages. Because a wider space is used with q-ROFSs by comparing with IFSs and PFSs, more precise results can be reached. Moreover, a comparative evaluation has been performed by considering both IFSs, PFSs and q-ROFSs.
4. Results
4.1. Analysis results for forecasting the energy generation
The model for forecasting electricity generation uses the time series of each individual powerplant, consisting of 36 parameters, including: installed capacity at the end of the reporting period, Gcal/hour; Fuel consumption for production, thousand cubic meters; Natural gas; Cost of fuel burned, thousand rubles; Coal, etc. Each of these parameters is duplicated by its own data from the beginning of the year. As a result, the model processes 76 parameters.
This model forecasts new cases of infections using 10 parameters, including: new cases of infections (together with data for the last 1, 7 and 14 days), the index of quarantine measures (together with data for the last 1, 7 and 14 days), the population of the country and its annual growth.
The Quarantine Measures Index consists of the following data set, collected from open sources, regarding the quarantine measures introduced in each individual country, where:
-
0
– No restrictions on movement;
-
1
– Full or partial closure of borders with other countries;
-
2
– Restriction on mass gatherings and/or introduction of wearing protective equipment;
-
3
– Restriction of being in living quarters.
The model for forecasting the impact of quarantine measures on the number of new COVID-19 infections showed that there was no serious slowdown in the spread of the pandemic in Russian cities in 2020 (Appendix A2-D2). Table 1 gives information about the t-statistics.
Table 1.
T-statistics for Long Short-Term Memory model.
| City | T-Statistics (99% confidence level) | T-statistics (95% confidence level) |
Probability |
|---|---|---|---|
| Moscow | –3.60 | –2.22 | .46 |
| St. Petersburg |
–1.16 | –3.67 | .89 |
| Ekaterinburg | –3.61 | –3.67 | .89 |
| Nizhniy Novgorod | –3.62 | –2.00 | .57 |
Source: Author calculation.
The model performance can be varied in short time (1–6 months) periods. The random sample was selected from various term horizons from one month to four months as in Table 2. The results show that error values (1 month forecast) are consistent with low standard deviation. The accuracy for 1 month forecast in the RMSE is 81% and MAPE is at its lowest level. It is clear that the LSTM model is accurate and stable in this term.
Table 2.
Model performance for Long Short-Term Memory model.
| RMSE | MAPE | PCC | Accuracy (%) | Horizon, days |
|---|---|---|---|---|
| 1985 | 17.05 | .01 | 82 | 30 |
| 2461 | 20.80 | .24 | 79 | 60 |
| 2386 | 18.87 | -.41 | 81 | 90 |
| 2584 | 40.70 | -.21 | 59 | 120 |
| 2848 | 63.47 | -.32 | 36 | 150 |
Source: Author calculation.
The Random Forest regression model is supposedly effective in forecasting the time series of electricity generation. Its estimation capabilities are at least comparable with the ones achieved in other studies. But its main advantage for this paper is the ability to indicate low-impact datasets, which might be as important for forecasting electricity generation on the base of mobility impact as a complex multi-layer structure of the tree-based ensemble. The most influential feature of urban mobility in this study are COVID-19 measures.
Since the paper uses LTSM as the base classifier, it would be necessary to pay attention to the selection and optimal final tuning hyperparameters (Table 2), such as:
-
1.
number of trees,
-
2.
levels,
-
3.
cases in the leaves,
-
4.
number of features in random subsample.
Various combinations of L1-L4, L12, L24, L36 time lags were improved for the Trees Regressor model by training the LSTM models (Table 3). Results suggest using only 7 lagged variables as features or a combination of lagged features with similar performance for the LSTM model.
Table 3.
Performance metrics of the LSTM model.
| Parameter | Coefficient | SE | z | P>|z| |
|---|---|---|---|---|
| L1 | ,3722 | ,631 | ,59 | ,555 |
| L2 | -,1261 | ,228 | -,554 | ,58 |
| L3 | -,8193 | ,217 | -3,776 | 0 |
| L4 | -,2614 | ,39 | -,671 | ,502 |
| L12 | ,3132 | ,167 | 1,878 | ,06 |
| L24 | ,2908 | ,219 | 1,325 | ,185 |
| L36 | ,2798 | ,233 | 1,201 | ,23 |
Source: Author calculation.
To investigate the parameters of the model, a set of statistical tests and additional parameters can be used (Table 4): the Ljung-Box, Jarque-Bera, Probability, Heteroskedasticity, Skew and Kurtosis.
Table 4.
Model testing.
| Ljung-Box (L1) (Q) | ,12 | Jarque-Bera (JB) | ,09 |
|---|---|---|---|
| Probability (Q) | ,73 | Probability (JB) | ,96 |
| Heteroskedasticity (H) | 1,83 | Skew | -,06 |
| Probability (H) (two-sided) | ,1 | Kurtosis | 3,09 |
Source: Author calculation.
The Ljung-Box, Jarque-Bera, Skew and Kurtosis tests can characterize a significant level of model accuracy during instability. Table 2 shows the average values of the tests. In addition, the indicators of Probability and Heteroskedasticity prove the stability of modeling, confirming the results [31, 32].
The selection approach may not have the biggest advantage in terms of error, accuracy, and overall specification. However, it provides a good measure of the mobility data influence on energy generation and helps to improve the efficiency of forecasting models, which may be used in the future to estimate the urban mobility impact on energy generation.
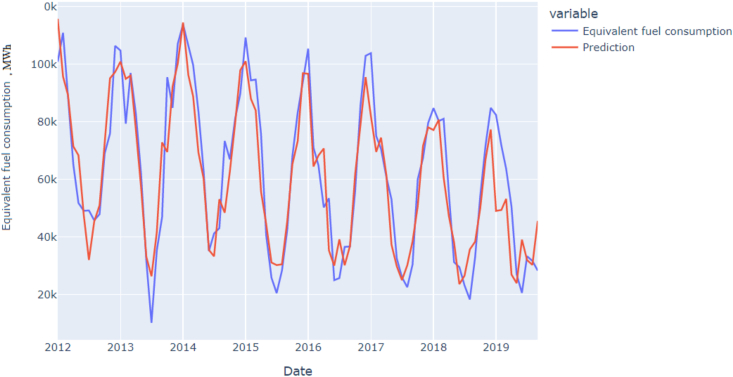
The comparison of actual energy data against the predicted energy value by the LSTM model for the period from 2012 to 2019 for a 1-month prediction can prove high quality of validation. Figure 2 shows good accuracy and good fine tuning for the 1-month term horizon.
Figure 2.
Actual vs. predicted forecast by the LSTM model, MWh. Source: calculated by the authors.
If a country does not have its own energy resources, it is forced to import it from abroad. This situation creates other problems for the country's economy. A country forced to import energy from abroad faces political risks. In addition to the aforementioned issue, payment for energy purchased from abroad is made in foreign currency.
This situation leads to the country accepting currency risks. Finally, the increase in energy imports negatively affects the country's trade balance. Subsequently, the country's economic fragility is increased. Therefore, solving this problem is vital for the country's sustainable economic development against the backdrop of COVID-19. Given this information, it is clear that the subject of the project is of high scientific quality (Oksuz and Ugurlu, 2019; Ortigueira-Sánchez, 2016; Pappalardo et al., 2015; Pierce and Schott, 2016; Reinhart et al., 2013).
4.2. Q-ROF hybrid decision making approach for the validation
Firstly, the criteria of pandemics and electricity generation are weighted with Q-ROF DEMATEL. For this purpose, the criteria of COVID-19 and electricity generation are defined as in Table 5.
Table 5.
The criteria of COVID-19 and electricity generation.
| Criteria of Energy Generation | Definition |
|---|---|
| C1 | Population |
| C2 | Air Temperature |
| C3 | Capacity of energy production |
| C4 | Capacity of manufacturing industry |
| Criteria of COVID-19 | Definition |
| C5 | New Cases |
| C6 | Total Infected People |
| C7 | Death Rate |
| C8 | Variants |
Source: Author calculation.
The population has an increasing impact on energy generation. Moreover, the capacity of energy production and manufacturing industry is quite significant with respect to the energy generation. Table 5 also indicates that the COVID-19 process affects this situation. Within this framework, new cases, total infected people, death rate and variants are taken into consideration. Linguistic scales are defined in Table 6 and evaluations for the criteria are given in Table 7.
Table 6.
Linguistic scales, membership and non-membership degrees for criteria and alternatives.
| Linguistic Scales for Criteria | Linguistic Scales for Alternatives | Membership Degrees | Non-membership Degrees |
|---|---|---|---|
| no (n) | worst (w) | .10 | .90 |
| some (s) | bad (p) | .30 | .70 |
| normal (m) | normal (f) | .60 | .40 |
| high (h) | well (g) | .80 | .20 |
| very high (vh) | perfect (b) | .90 | .10 |
Source: Author calculation.
Table 7.
Linguistic evaluations by decision makers for the criteria.
| - | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| - | DM1 | DM2 | DM3 | DM1 | DM2 | DM3 | DM1 | DM2 | DM3 | DM1 | DM2 | DM3 | DM1 | DM2 | DM3 | DM1 | DM2 | DM3 | DM1 | DM2 | DM3 | DM1 | DM2 | DM3 |
| C1 | H | H | H | H | H | H | H | H | H | M | H | M | H | H | H | H | H | H | M | M | M | |||
| C2 | H | H | H | M | M | M | H | H | H | M | M | M | H | H | H | H | H | H | H | H | H | |||
| C3 | M | M | M | VH | VH | H | H | H | H | M | VH | VH | M | M | M | M | M | M | H | H | H | |||
| C4 | H | H | H | H | H | H | H | H | H | M | M | M | M | M | M | H | H | H | H | H | H | |||
| C5 | M | M | M | H | H | H | H | H | H | M | M | M | H | H | H | H | H | H | H | H | H | |||
| C6 | H | H | M | H | H | H | M | VH | VH | M | M | M | H | H | H | M | H | H | M | H | H | |||
| C7 | M | H | H | M | H | H | M | M | M | H | H | M | M | VH | H | H | H | H | M | M | M | |||
| C8 | H | M | M | H | H | H | H | H | H | H | M | M | H | H | H | H | M | M | H | H | H | |||
C: criterion.
Source: Author calculation.
There are four classification parameters for proposed modelling: linguistic scales degrees for criteria and alternatives, membership and non-membership degrees. In Table 7, the linguistic evaluations are obtained with the values stated in Table 6.
Average fuzzy preferences for direct relation matrix are stated in Table 8.
Table 8.
Average fuzzy preferences for direct relation matrix.
| - | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 |
|---|---|---|---|---|---|---|---|---|
| C1 | .80 | .80 | .80 | .67 | .80 | .80 | .60 | |
| C2 | .80 | .60 | .80 | .60 | .80 | .80 | .80 | |
| C3 | .60 | .87 | .80 | .80 | .60 | .60 | .80 | |
| C4 | .80 | .80 | .80 | .60 | .60 | .80 | .80 | |
| C5 | .60 | .80 | .80 | .60 | .80 | .80 | .80 | |
| C6 | .73 | .80 | .80 | .60 | .80 | .73 | .73 | |
| C7 | .73 | .73 | .60 | .73 | .77 | .80 | .60 | |
| C8 | .67 | .80 | .80 | .67 | .80 | .67 | .80 |
C: criterion.
Source: Author calculation.
Average fuzzy preferences for direct relation matrix show that Population, Air Temperature, Capacity of energy production, Capacity of manufacturing industry, New Cases, Total Infected People, Death Rate, Variants are in corridor from 0.60 to 0.80. Membership and non-membership degrees are shown in Table 9 for the criteria.
Table 9.
Membership and non-membership degrees for the criteria.
| - | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| - | μ | v | μ | V | μ | V | μ | v | μ | v | μ | v | μ | v | μ | v |
| C1 | .80 | .20 | .80 | .20 | .80 | .20 | .67 | .33 | .80 | .20 | .80 | .20 | .60 | .40 | ||
| C2 | .80 | .20 | .60 | .40 | .80 | .20 | .60 | .40 | .80 | .20 | .80 | .20 | .80 | .20 | ||
| C3 | .60 | .40 | .87 | .13 | .80 | .20 | .80 | .20 | .60 | .40 | .60 | .40 | .80 | .20 | ||
| C4 | .80 | .20 | .80 | .20 | .80 | .20 | .60 | .40 | .60 | .40 | .80 | .20 | .80 | .20 | ||
| C5 | .60 | .40 | .80 | .20 | .80 | .20 | .60 | .40 | .80 | .20 | .80 | .20 | .80 | .20 | ||
| C6 | .73 | .27 | .80 | .20 | .80 | .20 | .60 | .40 | .80 | .20 | .73 | .27 | .73 | .27 | ||
| C7 | .73 | .27 | .73 | .27 | .60 | .40 | .73 | .27 | .77 | .23 | .80 | .20 | .60 | .40 | ||
| C8 | .67 | .33 | .80 | .20 | .80 | .20 | .67 | .33 | .80 | .20 | .67 | .33 | .80 | .20 | ||
C: criterion.
Source: Author calculation.
Membership and non-membership degrees for Population, Air Temperature, Capacity of energy production, Capacity of manufacturing industry, New Cases, Total Infected People, Death Rate, Variants show that are in corridor from 0.20 to 0.80. The score function values of q-rung orthopair fuzzy sets are demonstrated in Table 10.
Table 10.
Score function values of q-rung orthopair fuzzy sets for the criteria.
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | |
|---|---|---|---|---|---|---|---|---|
| C1 | .000 | .504 | .504 | .504 | .259 | .504 | .504 | .152 |
| C2 | .504 | .000 | .152 | .504 | .152 | .504 | .504 | .504 |
| C3 | .152 | .649 | .000 | .504 | .504 | .152 | .152 | .504 |
| C4 | .504 | .504 | .504 | .000 | .152 | .152 | .504 | .504 |
| C5 | .152 | .504 | .504 | .152 | .000 | .504 | .504 | .504 |
| C6 | .375 | .504 | .504 | .152 | .504 | .000 | .375 | .375 |
| C7 | .375 | .375 | .152 | .375 | .438 | .504 | .000 | .152 |
| C8 | .259 | .504 | .504 | .259 | .504 | .259 | .504 | .000 |
C: criterion.
Source: Author calculation.
Score function values of q-rung orthopair fuzzy sets for Population, Air Temperature, Capacity of energy production, Capacity of manufacturing industry, New Cases, Total Infected People, Death Rate, Variants are in corridor from 0.152 to 0.649. Normalized matrix is computed as in Table 11.
Table 11.
Normalized relation matrix.
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | |
|---|---|---|---|---|---|---|---|---|
| C1 | .000 | .172 | .172 | .172 | .088 | .172 | .172 | .052 |
| C2 | .172 | .000 | .052 | .172 | .052 | .172 | .172 | .172 |
| C3 | .052 | .221 | .000 | .172 | .172 | .052 | .052 | .172 |
| C4 | .172 | .172 | .172 | .000 | .052 | .052 | .172 | .172 |
| C5 | .052 | .172 | .172 | .052 | .000 | .172 | .172 | .172 |
| C6 | .128 | .172 | .172 | .052 | .172 | .000 | .128 | .128 |
| C7 | .128 | .128 | .052 | .128 | .149 | .172 | .000 | .052 |
| C8 | .088 | .172 | .172 | .088 | .172 | .088 | .172 | .000 |
C: criterion.
Source: Author calculation.
Normalized relation matrix shows the power of connection between Population, Air Temperature, Capacity of energy production, Capacity of manufacturing industry, New Cases, Total Infected People, Death Rate, Variants. Total relation matrix is constructed as in Table 12.
Table 12.
Total relation matrix.
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | |
|---|---|---|---|---|---|---|---|---|
| C1 | 1.578 | 2.379 | 1.917 | 1.800 | 1.725 | 1.866 | 2.111 | 1.827 |
| C2 | 1.685 | 2.166 | 1.779 | 1.749 | 1.652 | 1.821 | 2.064 | 1.863 |
| C3 | 1.493 | 2.228 | 1.622 | 1.656 | 1.647 | 1.622 | 1.858 | 1.783 |
| C4 | 1.672 | 2.306 | 1.858 | 1.605 | 1.643 | 1.715 | 2.050 | 1.859 |
| C5 | 1.563 | 2.296 | 1.850 | 1.635 | 1.594 | 1.805 | 2.037 | 1.858 |
| C6 | 1.618 | 2.292 | 1.849 | 1.635 | 1.733 | 1.655 | 2.000 | 1.818 |
| C7 | 1.431 | 1.976 | 1.537 | 1.485 | 1.503 | 1.592 | 1.647 | 1.533 |
| C8 | 1.580 | 2.279 | 1.837 | 1.656 | 1.723 | 1.728 | 2.025 | 1.697 |
C: criterion.
Source: Author calculation.
Criteria weights are computed in the final stage, and they are given in Table 13.
Table 13.
Criteria weights.
| Criteria | q-ROF DEMATEL |
DEMATEL |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| D | E | D + E | D-E | Weighting Results |
D | E | D + E | D-E | Weighting Results |
|
| C1 | 15.204 | 12.621 | 27.825 | 2.583 | .121 | 50.411 | 46.663 | 97.075 | 3.748 | .122 |
| C2 | 14.779 | 17.922 | 32.701 | -3.144 | .142 | 49.652 | 54.935 | 104.587 | -5.282 | .132 |
| C3 | 13.910 | 14.249 | 28.159 | -.339 | .122 | 49.685 | 50.083 | 99.768 | -.398 | .126 |
| C4 | 14.708 | 13.221 | 27.929 | 1.487 | .121 | 49.619 | 47.481 | 97.100 | 2.138 | .122 |
| C5 | 14.639 | 13.219 | 27.858 | 1.420 | .121 | 49.620 | 48.853 | 98.473 | .767 | .124 |
| C6 | 14.599 | 13.804 | 28.402 | .795 | .123 | 50.434 | 48.238 | 98.672 | 2.195 | .124 |
| C7 | 12.704 | 15.792 | 28.497 | -3.088 | .124 | 47.374 | 51.166 | 98.540 | -3.792 | .124 |
| C8 | 14.524 | 14.238 | 28.762 | .286 | .125 | 49.607 | 48.984 | 98.591 | .624 | .124 |
| Criteria | IF DEMATEL | PF DEMATEL | ||||||||
| D | E | D + E | D-E |
Weighting Results |
D | E | D + E | D-E |
Weighting Results |
|
| C1 | 16.269 | 13.761 | 30.031 | 2.508 | .121 | 16.269 | 13.761 | 30.031 | 2.508 | .121 |
| C2 | 15.820 | 18.909 | 34.729 | -3.088 | .140 | 15.820 | 18.909 | 34.729 | -3.088 | .140 |
| C3 | 14.765 | 15.303 | 30.069 | -.538 | .122 | 14.765 | 15.303 | 30.069 | -.538 | .122 |
| C4 | 15.724 | 14.317 | 30.040 | 1.407 | .122 | 15.724 | 14.317 | 30.040 | 1.407 | .122 |
| C5 | 15.670 | 14.310 | 29.980 | 1.360 | .121 | 15.670 | 14.310 | 29.980 | 1.360 | .121 |
| C6 | 15.765 | 14.848 | 30.613 | .916 | .124 | 15.765 | 14.848 | 30.613 | .916 | .124 |
| C7 | 13.911 | 16.870 | 30.781 | -2.959 | .125 | 13.911 | 16.870 | 30.781 | -2.959 | .125 |
| C8 | 15.685 | 15.290 | 30.975 | .394 | .125 | 15.685 | 15.290 | 30.975 | .394 | .125 |
C: criterion.
Source: Author calculation.
DEMATEL matrix shows the criteria weights between Population, Air Temperature, Capacity of energy production, Capacity of manufacturing industry, New Cases, Total Infected People, Death Rate, Variants. Table 13 indicates that air temperature has the highest weight regarding energy generation. This result is the same for all different analyses. Therefore, it is concluded that the analysis results are coherent and reliable. It is very important to determine the amount of energy to be produced. Otherwise, the energy that meets the demand will not be produced and this will lead to a decrease in energy efficiency. According to the analysis results obtained in this study, the air temperature is the variable that most affects this process. In this context, future forecasts for air temperature should be taken into consideration. This will contribute to a more accurate determination of the amount of energy production. In the second stage, alternative cities are ranked with respect to the COVID-19 and electricity generation criteria using QROF-TOPSIS. In the first stage, alternative cities are defined in Table 14.
Table 14.
Alternative cities for evaluating the COVID-19 and electricity generation criteria.
| Alternative Set | Cities |
|---|---|
| Alternative 1 (A1) | Moscow |
| Alternative 2 (A2) | St. Petersburg |
| Alternative 3 (A3) | Nizhny Novgorod |
| Alternative 4 (A4) | Yekaterinburg |
Source: Author calculation.
Linguistic evaluations for the alternative cities are given in Table 15.
Table 15.
Linguistic evaluations of decision makers for the alternative cities.
| C1 |
C2 |
C3 |
C4 |
C5 |
C6 |
C7 |
C8 |
|||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DM1 | DM2 | DM3 | DM1 | DM2 | DM3 | DM1 | DM2 | DM3 | DM1 | DM2 | DM3 | DM1 | DM2 | DM3 | DM1 | DM2 | DM3 | DM1 | DM2 | DM3 | DM1 | DM2 | DM3 | |
| A1 | F | G | F | G | F | G | F | F | F | G | G | G | F | F | F | F | F | F | G | G | B | F | F | G |
| A2 | F | G | B | G | F | G | F | F | F | P | G | B | G | F | G | F | G | F | P | F | B | G | G | G |
| A3 | G | G | G | G | G | G | F | F | F | F | F | F | F | F | F | G | G | G | F | G | F | P | F | B |
| A4 | G | G | B | F | F | G | P | P | B | G | G | B | F | F | G | B | B | B | G | G | G | F | F | F |
C: criterion; A: alternative.
Source: Author calculation.
Thirdly, the membership and non-membership degrees for the decision matrix are indicated in Table 16.
Table 16.
Membership and non-membership degrees for the decision matrix.
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| μ | v | Μ | v | μ | v | μ | v | μ | V | μ | V | μ | v | Μ | v | |
| A1 | .67 | .33 | .73 | .27 | .60 | .40 | .80 | .20 | .60 | .40 | .60 | .40 | .83 | .17 | .67 | .33 |
| A2 | .77 | .23 | .73 | .27 | .60 | .40 | .67 | .33 | .73 | .27 | .67 | .33 | .60 | .40 | .80 | .20 |
| A3 | .80 | .20 | .80 | .20 | .60 | .40 | .60 | .40 | .60 | .40 | .80 | .20 | .67 | .33 | .60 | .40 |
| A4 | .83 | .17 | .67 | .33 | .50 | .50 | .83 | .17 | .67 | .33 | .90 | .10 | .80 | .20 | .60 | .40 |
C: criterion; A: alternative.
Source: Author calculation.
Table 17 explains the details of the score functions.
Table 17.
Score function values with q-rung orthopair fuzzy sets for the alternatives.
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | |
|---|---|---|---|---|---|---|---|---|
| A1 | .259 | .375 | .152 | .504 | .152 | .152 | .574 | .259 |
| A2 | .438 | .375 | .152 | .259 | .375 | .259 | .152 | .504 |
| A3 | .504 | .504 | .152 | .152 | .152 | .504 | .259 | .152 |
| A4 | .574 | .259 | .000 | .574 | .259 | .728 | .504 | .152 |
C: criterion; A: alternative.
Source: Author calculation.
Normalized decision matrix is constructed as in Table 18.
Table 18.
Normalized decision matrix.
| Criteria/Alternatives | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 |
|---|---|---|---|---|---|---|---|---|
| A1 | .282 | .483 | .577 | .614 | .301 | .163 | .699 | .428 |
| A2 | .477 | .483 | .577 | .316 | .744 | .277 | .185 | .831 |
| A3 | .549 | .649 | .577 | .185 | .301 | .539 | .316 | .251 |
| A4 | .625 | .334 | .000 | .699 | .514 | .779 | .614 | .251 |
C: criterion; A: alternative.
Source: Author calculation.
Weighted decision matrix is constructed as in Table 19.
Table 19.
Weighted decision matrix.
| Criteria/Alternatives | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 |
|---|---|---|---|---|---|---|---|---|
| A1 | .034 | .069 | .071 | .075 | .036 | .020 | .087 | .053 |
| A2 | .058 | .069 | .071 | .038 | .090 | .034 | .023 | .104 |
| A3 | .066 | .092 | .071 | .022 | .036 | .067 | .039 | .031 |
| A4 | .076 | .047 | .000 | .085 | .062 | .096 | .076 | .031 |
| C: criterion; A: alternative | ||||||||
Source: Author calculation.
Table 20 indicates the important values of Q-ROFSs.
Table 20.
The values of D+, D-, RCi with Q-ROFSs.
| Alternatives | D+ | D- | RCi |
|---|---|---|---|
| A1 | .117 | .113 | .492 |
| A2 | .105 | .121 | .536 |
| A3 | .123 | .102 | .453 |
| A4 | .115 | .122 | .515 |
A: alternative.
Source: Author calculation.
Comparative ranking results of the alternative cities are identified in Table 21.
Table 21.
Comparative ranking results of the alternative cities.
| Alternatives | q-ROF DEMATEL-TOPSIS | PF DEMATEL-TOPSIS | IF DEMATEL-TOPSIS |
|---|---|---|---|
| A1 | 3 | 3 | 3 |
| A2 | 1 | 1 | 1 |
| A3 | 4 | 4 | 4 |
| A4 | 2 | 2 | 2 |
A: alternative.
Source: Author calculation.
St. Petersburg is ranked first whereas Yekaterinburg takes the second place. The findings are the same for all different evaluations. This situation demonstrates that the analysis results are quite reliable.
5. Discussion
This paper proves that automated mobility forecasting via machine learning algorithms is very effective for sustainable energy production in Russia (O'Brien et al., 2019; Oberfield, 2018). Thus, the article determines the impact of the population's mobility within each individual city on the local spread of COVID-19. After the validation of this model, it becomes possible to add several new parameters, such as movement between settlements and the associated forecast of new outbreaks of the coronavirus infection.
Firstly, this paper fills the gap of the problem of determining the most important factors consequential to human mobility and energy consumption in Russian cities. To achieve this goal, machine learning techniques are considered. As a result, the analysis identifies the key problems that affect people's mobility during a pandemic. Thus, this paper proves the present proposals for solving the problems of this research (Remmen et al., 2018).
Secondly, the indicators of energy consumption of the countries are determined. The future energy consumption of countries is estimated using econometric methods. These estimates are compared with energy consumption in Russian cities. As a result, this study helps future researchers to determine the amount of additional energy necessary for recovery. In turn, it becomes possible to develop solutions to meet this additional energy demand of Russian cities (Remmen et al., 2018).
Furthermore, a high accuracy model for new cases of COVID-19 will provide insight into the impact on energy efficiency (Huang et al., 2020; Mikhaylov, 2018, 2021).
As shown in Appendix 3-4, the mobility in Russian cities (Moscow, St. Petersburg, Nizhny Novgorod, Yekaterinburg) is quantified. The largest contribution to forecasting dynamic mobility is made by data related to daily confirmed cases of the disease in Russian cities and the restrictive policies of the Russian government.
It is possible that people are sensitive to news of confirmed cases of COVID-19. They themselves actively restrict travel and maintain social distancing. Among various public policy measures, orders to restrict restaurant operations and to stay at home make the largest contribution to forecasting dynamic mobility indicators. It is worth noting that the model achieves maximum efficiency when applied in forecasting regarding a 1-month time period, which imposes difficulty on practical application (Mosteiro-Romero et al., 2017). Nevertheless, the model does not find price shocks. It is not able to forecast quick market crashes (e.g., the decline in prices related to COVID-19) (Ni, 2019; Norouzi et al., 2020).
These results contribute to tree-based machine learning forecasting approaches for energy production.
Furthermore, another evaluation is also conducted by using the hybrid fuzzy decision-making model. In this regard, q-ROF DEMATEL and TOPSIS methods are taken into consideration. Additionally, a comparative evaluation is performed with the help of Intuitionistic and Pythagorean fuzzy sets. The results are quite similar. This situation gives information that the findings are reliable and coherent. It is identified that air temperature has the highest weight regarding the energy generation. Furthermore, St. Petersburg is ranked first, whereas Yekaterinburg takes the second place.
The important issue in energy production is that the amount of production is proportional to the demand. If less energy is produced than is in demand, customer dissatisfaction will occur. However, energy produced far above the demand will not be purchased by customers. This situation will cause significant losses and damage to energy companies. Therefore, it is necessary to determine the energy demand in this process. For this purpose, it is necessary to predict the energy demand by making a comprehensive analysis. According to the analysis results of this study, the amount of COVID-19 cases should be taken into consideration in this process. In other words, the factor that should be considered the most when projecting energy demand is the COVID-19 cases expectations for the future.
These contributions close the gap in creation of effective forecasting model (during the COVID-19 pandemic) for electricity consumption in major cities around the world. The models (Askitas et al., 2021; Liu et al., 2022; Sánchez-López et al., 2022) based on the factors determining the diffusion of COVID-19 and suggested strategy to prevent future accelerated viral infectivity. But this model can be used for created energy consumption scenarios in Europe, Malaysia, China, England, Germany and Japan like in previous papers (Flaxman et al., 2020; Diao et al., 2021; Toosty et al., 2022; Wen et al., 2022; Ueno, 2022).
6. Conclusions
As a result of the increased mobility of the population in large cities, energy consumption is also growing. This situation creates negative consequences for the country's economy. If the growth in energy consumption exceeds the country's energy supply, then certain problems may arise. Electricity is an urgent need for any country.
The SWARA method has new applications have an influence on the originality of the proposed model: (1) considering q-ROFSs in the analysis process brings some advantages, (2) wider space is used with q-ROFSs by comparing with IFSs and PFSs, more precise results can be reached.
This study identifies factors influencing the spread of COVID-19 based on the theory of "broken windows" and outlines directions in limiting population mobility, which can form the basis of state policy. This study contributes to scientific literature by examining the negative impact of the spread of the COVID-19 pandemic on energy markets. The theoretical basis for this question is as follows: with no restrictions, the citizens who panicked during the COVID-19 outbreak are increasing mobility in big cities. This situation causes problems in many aspects. One such problem concerns the energy sector.
Therefore, the country must meet this excessive energy demand. This situation causes additional costs. By analyzing the impact on electricity generation and consumption, this study complements the analysis of the implications for government authorities. The main contribution of this study is to conduct an evaluation by using both quantitative methods and fuzzy decision-making methodology. Hence, it is possible to test the validity of the analysis results. Nevertheless, the main limitation of this study is examining only Russia. Hence, in the future studies, different countries can be taken into consideration. The area for future research is in the evaluation of the COVID-19 macro effect for developed and emerging markets and micro effect on energy companies.
Declarations
Author contribution statement
Jaehyung An: Conceived and designed the experiments.
Alexey Mikhaylov: Contributed reagents, materials, analysis tools or data; Wrote the paper.
Hasan Dinçer: Performed the experiments.
Serhat Yüksel: Analyzed and interpreted the data.
Funding statement
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Data availability statement
Data associated with this study has been deposited at 10.17632/jksdccs4dn.1.
Declaration of interests statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
Appendix A. Supplementary data
The following is the supplementary data related to this article:
Appendix 1(A-D).
Forecasting electricity generation at a power station in Russian cities, MWh.
Source: compiled by the authors.
Appendix 2(A-D).
Forecasted values of new COVID-19 cases in Russian cities, persons per day.
Source: Russian Ministry of Health (2020), compiled by the authors.
Appendix 3(A-D).
Model accuracy for new cases of COVID-19: a) Moscow, b) St. Petersburg, c) Nizhny Novgorod, d) Yekaterinburg.
Source: Russian Ministry of Health (2020), compiled by the authors.
Appendix 4(A-D).
Mobility index in Russian cities by Yandex: a) Moscow, b) St. Petersburg, c) Nizhny Novgorod, d) Yekaterinburg.
Source: Russian Ministry of Health (2020), Yandex (2020), compiled by the authors.
References
- Ahn K.U., Kim D.W., Park C.S., de Wilde P. Predictability of occupant presence and performance gap in building energy simulation. Appl. Energy. 2017;208:1639–1652. [Google Scholar]
- Akhavan A., Phillips N.E., Du J., Chen J., Sadeghinasr B., Wang Q. Accessibility inequality in houston. IEEE Sens Lett. 2018;3:1–4. [Google Scholar]
- Alcantud J.C.R., Khameneh A.Z., Kilicman A. Aggregation of infinite chains of intuitionistic fuzzy sets and their application to choices with temporal intuitionistic fuzzy information. Inf. Sci. 2020;514:106–117. [Google Scholar]
- Ali Z., Mahmood T. Maclaurin symmetric mean operators and their applications in the environment of complex q-rung orthopair fuzzy sets. Comput. Appl. Math. 2020;39:1–27. [Google Scholar]
- Ashkanani A.M., Bahman A.M., Aljuwayhel N.F. Electric Power Systems Research205; 2022. Impact of COVID-19 Interventions on Electricity Power Production: an Empirical Investigation in Kuwait. [Google Scholar]
- Askitas N., Tatsiramos K., Verheyden B. Estimating worldwide effects of non-pharmaceutical interventions on COVID-19 incidence and population mobility patterns using a multiple-event study. Sci. Rep. 2021;11(1):1972. doi: 10.1038/s41598-021-81442-x. 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bedi J., Toshniwal D. Deep learning framework to forecast electricity demand. Appl. Energy. 2019;238:1312–1326. https://www.mendeley.com/catalogue/0ea0f872-58e8-3d81-b3ed-f7634501fa13/ [Google Scholar]
- Beltran A., Cerpa A.E. BuildSys 2014 - Proc. 1st ACM Conf. Embed. Syst. Energy-Efficient Build. Association for Computing Machinery, Inc; New York, New York, USA: 2014. Optimal HVAC building control with occupancy prediction; pp. 168–171. [Google Scholar]
- Bertuzzo E., Mari L., Pasetto D., Miccoli S., Casagrandi R., Gatto M., Rinaldo A. The geography of COVID-19 spread in Italy and implications for the relaxation of confinement measures. Nat. Commun. 2020;11:4264. doi: 10.1038/s41467-020-18050-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhuiyan M.A., An J., Mikhaylov A., Moiseev N., Danish M.S.S. Renewable energy deployment and COVID-19 measures for sustainable development. Sustainability. 2021;13(8):4418. [Google Scholar]
- Bollinger L.A., Evins R. HUES: a holistic urban energy simulation platform for effective model integration. Proc Int Conf CISBAT 2015 Futur Build Dist Sustain Build Environ. 2019;160 [Google Scholar]
- Bouktif S., Fiaz A., Ouni A., Serhani M.A. Optimal deep learning LSTM model for electric load forecasting using feature selection and genetic algorithm: comparison with machine learning approaches. Energies. 2018;11:1636. [Google Scholar]
- Braga I.F., Ferreira F.A., Ferreira J.J., Correia R.J., Pereira L.F., Falcão P.F. A DEMATEL analysis of smart city determinants. Technol. Soc. 2021;66 [Google Scholar]
- Chen C., Ban X. 97th Annu Meet Transp Res Board; Washington DC, United States: 2018. Transportation Big Data: Promises, Issues, and Implications. [Google Scholar]
- Chen Y., Hong T., Luo X., Hooper B. Development of city buildings dataset for urban building energy modeling. Energy Build. 2019;183:252–265. [Google Scholar]
- Chen Y., Hong T., Piette M.A. Automatic generation and simulation of urban building energy models based on city datasets for city-scale building retrofit analysis. Appl. Energy. 2017;205:323–335. 2017. [Google Scholar]
- Das A., Kjærgaard M.B. UbiComp/ISWC 2019- - Adjun. Proc. 2019 ACM Int. Jt. Conf.Pervasive Ubiquitous Comput. Proc. 2019 ACM Int. Symp. Wearable Comput. Association for Computing Machinery, Inc; New York, New York, USA: 2019. Precept: occupancy presence prediction inside a commercial building; pp. 486–491. [Google Scholar]
- Diao Y., Kodera S., Anzai D., et al. Influence of population density, temperature, and absolute humidity on spread and decay durations of COVID-19: a comparative study of scenarios in China, England, Germany, and Japan. One Health. 2021;12 doi: 10.1016/j.onehlt.2020.100203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engel C., Beckenkamp M., Glöckner A., Irlenbusch B., Hennig-Schmidt H., Kube S., Kurschilgen M., Morell A., Nicklisch A., Normann H.-T., Towfigh E. First impressions are more important than early intervention: qualifying broken windows theory in the lab. Int. Rev. Law Econ. 2014;37:126–136. [Google Scholar]
- Eroğlu H. Environment, Development and Sustainability; 2020. Effects of Covid-19 Outbreak on Environment and Electricity Energy Sector. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flaxman S., Mishra S., Gandy A., Unwin H.J.T., Mellan T.A., Coupland H., Whittaker C., et al. Estimating the effects of non-pharmaceutical interventions on COVID-19 in Europe ( ) Nature. 2020;584(7820):257–261. doi: 10.1038/s41586-020-2405-7. 2020. [DOI] [PubMed] [Google Scholar]
- Fowler J.H., Hill S.J., Obradovich N., Levin R., Gao X., Deng Y. Generating method of Pythagorean fuzzy sets from the negation of probability. Eng. Appl. Artif. Intell. 2021;105 [Google Scholar]
- Gao X., Deng Y. Generating method of Pythagorean fuzzy sets from the negation of probability. Engineering Applications of Artificial Intelligence. 2021;105:104403. [Google Scholar]
- Happle G., Fonseca J.A., Schlueter A. Contextspecific urban occupancy modeling using location-based services data. Build. Environ. 2020;175 [Google Scholar]
- Hong T., Lin H.W. Occupant behavior: impact on energy use of private offices Energy Technologies Area, Berkeley, CA (United States) 2013. https://eta.lbl.gov
- Hosseini S.E. An outlook on the global development of electricity and sustainable energy at the time of COVID-19. Energy Res. Social Sci. 2020;68 doi: 10.1016/j.erss.2020.101633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang C.-J., Chen Y.-H., Ma Y., Kuo P.-H. Multiple-input deep convolutional neural network model for COVID-19 forecasting in China. 2020. https://www.medrxiv.org/content/10.1101/2020.03.23.20041608v1.full.pdf+html
- Keras model . Layer activation functions. 2020. https://keras.io/api/layers/activations/ [Google Scholar]
- Ku A.L., Qiu Y.L., Lou J., Nock D., Xing B. Applied Energy310; 2022. Changes in Hourly Electricity Consumption under COVID Mandates: A Glance to Future Hourly Residential Power Consumption Pattern with Remote Work in Arizona. [Google Scholar]
- Lazo J., Aguirre G., Watts D. An impact study of COVID-19 on the electricity sector: a comprehensive literature review and Ibero-American survey. Renew. Sustain. Energy Rev. 2022;158 doi: 10.1016/j.rser.2022.112135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee S.H., Hong T., Piette M.A., Sawaya G., Chen Y., Taylor-Lange S.C. Accelerating the energy retrofit of commercial buildings using a database of energy efficiency performance. Energy. 2015;90:738–747. [Google Scholar]
- Lin M., Li X., Chen L. Linguistic q-rung orthopair fuzzy sets and their interactional partitioned Heronian mean aggregation operators. Int. J. Intell. Syst. 2020;35(2):217–249. [Google Scholar]
- Liu J., Zhang Z., Fan X., et al. Applied Energy310; 2022. Power System Load Forecasting Using Mobility Optimization and Multi-Task Learning in COVID-19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mao S., Han Y., Deng Y., Pelusi D. A hybrid DEMATEL-FRACTAL method of handling dependent evidences. Eng. Appl. Artif. Intell. 2020;91 [Google Scholar]
- Meshram S.G., Alvandi E., Meshram C., Kahya E., Al-Quraishi A.M.F. Application of SAW and TOPSIS in prioritizing watersheds. Water Resour. Manag. 2020;34(2):715–732. [Google Scholar]
- Mikhaylov A. Volatility spillover effect between stock and exchange rate in oil exporting countries. Int. J. Energy Econ. Pol. 2018;8(3):321–326. [Google Scholar]
- Mikhaylov A. Mendeley Data; 2021. Energy in Russia; p. V1. [Google Scholar]
- Miller H. Place-based versus people-based geographic information science. Geogr Compass. 2007;1:503–535. [Google Scholar]
- Mohammadi N., Taylor J.E. Urban energy flux: spatiotemporal fluctuations of building energy consumption and human mobility-driven prediction. Appl. Energy. 2017;195:810–818. [Google Scholar]
- Mosteiro-Romero M., Fonseca J.A., Schlueter A. Energy Proc, Elsevier Ltd; 2017. Seasonal Effects of Input Parameters in Urban-Scale Building Energy Simulation. [Google Scholar]
- Ni Y. Research on the ownership structure and market value of Chinese listed commercial banks. Am. J. Ind. Bus. Manag. 2019;9:1995–2007. [Google Scholar]
- Norouzi N., Zarazua de Rubens G., Choupanpiesheh S., Enevoldsen P. When pandemics impact economies and climate change: exploring the impacts of COVID-19 on oil and electricity demand in China. Energy Res. Social Sci. 2020;68 doi: 10.1016/j.erss.2020.101654. https://www.mendeley.com/catalogue/7b63eef6-805d39d9-9315-0e0da8fb8a82/ [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Brien D.T., Farrell C., Welsh B.C. Broken (windows) theory: a meta-analysis of the evidence for the pathways from neighborhood disorder to resident health outcomes and behaviors. Soc. Sci. Med. 2019;228:272–292. doi: 10.1016/j.socscimed.2018.11.015. [DOI] [PubMed] [Google Scholar]
- Oberfield E. A theory of input-output architecture. Econometrica. 2018;86(2):559–589. [Google Scholar]
- Oksuz I., Ugurlu U. Neural network based model comparison for intraday electricity price forecasting. Energies. 2019;12(23):4557. [Google Scholar]
- Ortigueira-Sánchez L.C. Influencing factors on citizen safety perception: systems and broken windows theories. International Review on Public and Nonprofit Marketing. 2016. https://www.mendeley.com/catalogue/f2a18794-ecb1-3ab3-b054-f9df0926458b/ 14(1), pp.95–111.
- Pappalardo L., Simini F., Rinzivillo S., Pedreschi D., Giannotti F., Barab´asi A.L. Returners and explorers dichotomy in human mobility. Nat. Commun. 2015;6:1–8. doi: 10.1038/ncomms9166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pierce J.R., Schott P.K. The surprisingly swift decline of US manufacturing employment. Am. Econ. Rev. 2016;106(7):1632–1662. [Google Scholar]
- Reinhart C.F., Dogan T., Jakubiec J.A., Rakha T. Proc Build Simul 2013. Chambery; 2013. UMI – an urban simulation environment for building energy use, daylighting and walkability. [Google Scholar]
- Remmen P., Lauster M., Mans M., Fuchs M., Osterhage T., Müller D. TEASER: an open tool for urban energy modelling of building stocks. J Build Perform Simul. 2018;11:84–98. [Google Scholar]
- Rugani B., Caro D. Science of The Total Environment; 2020. Impact of COVID-19 Outbreak Measures of Lockdown on the Italian Carbon Footprint. [online] 737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Russian Ministry of Health . Map of the spread of coronavirus in our country. 2020. https://covid19.rosminzdrav.ru/?gclid=CjwKCAjwx9_ [Google Scholar]
- Sałabun W., Wątróbski J., Shekhovtsov A. Are mcda methods benchmarkable? a comparative study of topsis, vikor, copras, and promethee ii methods. Symmetry. 2020;12(9):1549. [Google Scholar]
- Sánchez-López M., Moreno R., Alvarado D., et al. The diverse impacts of COVID-19 on electricity demand: the case of Chile. Int. J. Electr. Power Energy Syst. 2022;138 [Google Scholar]
- Sánchez-Úbeda E.F., Portela J., Muñoz A., Chueca Montuenga E., Hallack M. Impact of COVID-19 on electricity demand of Latin America and the Caribbean countries. Sustainable Energy, Grids and Networks30. 2022 [Google Scholar]
- Schwert G.W. Using financial data to measure effects of regulation. J. Law Econ. 1981;24(1):121–158. [Google Scholar]
- Shea P.E., Poast P. War and default. J. Conflict Resolut. 2018;62(9):1876–1904. [Google Scholar]
- Statdata . The largest cities of Russia by population. 2020. http://www.statdata.ru/largest_cities_russia [Google Scholar]
- Sun K., Hong T. A framework for quantifying the impact of occupant behavior on energy savings of energy conservation measures. Energy Build. 2017;146:383–396. 2017. [Google Scholar]
- Tintelnot F., Kikkawa A., Mogstad M., Dhyne E. University of Chicago Working Paper; 2017. Trade and Domestic Production Networks. [Google Scholar]
- Tomar A., Gupta N. Science of The Total Environment; 2020. Prediction for the Spread of COVID-19 in India and Effectiveness of Preventive Measures. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Toosty N.T., Hagishima A., Bari W., Zaki S.A. Behavioural changes in air-conditioner use owing to the COVID-19 movement control order in Malaysia. Sustain. Prod. Consum. 2022;30:608–622. doi: 10.1016/j.spc.2022.01.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ueno T. Capturing changes in residential occupant behavior due to work from home in Japan as a consequence of the COVID-19 pandemic. Sustainability. 2022;14(4):2180. [Google Scholar]
- Valta P. Competition and the Cost of debt. J. Financ. Econ. 2012;105(3):661–682. [Google Scholar]
- Wei C., Yermack D. Investor reactions to CEOs' inside debt incentives. Rev. Financ. Stud. 2011;24(11):3813–3840. [Google Scholar]
- Wen L., Sharp B., Suomalainen K., Sheng M.S., Guang F. The impact of COVID-19 containment measures on changes in electricity demand. Sustainable Energy, Grids and Networks. 2022;29 [Google Scholar]
- WHO WHO announces COVID-19 outbreak a pandemic. WHO. 2021. http://www.euro.who.int/en/healthhttp://www.euro.who.int/en/health-topics/health-emergencies/coronavirus-covid-19/news/newstopics/health-emergencies/coronavirus-covid-
- Yandex . Map of the spread of coronavirus in Russia and the world. 2021. https://yandex.ru/maps/covid19/isolation?ll=41.775580%2C54.894027&z=3 [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data associated with this study has been deposited at 10.17632/jksdccs4dn.1.