Assessing the Effects of Delay to NMP via Audio Analysis

Abstract

For network music performance (NMP), end-to-end delay is the most critical factor affecting the quality of experience (QoE) of the musicians, as longer delays prevent the musicians from synchronizing. To analyze the sensitivity of QoE to delay, we performed a controlled NMP experiment, where 11 pairs of musicians performed under a wide range of delays. The analysis of the QoE questionnaires answered by the participants produced results with wide variances, making the extraction of solid conclusions quite difficult. In this paper, we complement the subjective study with an analysis of the performance tempo of the NMP sessions. Specifically, we used signal processing techniques to analyze the audio recordings of the experiments, to recover the performance tempo of the musicians, assess its evolution during each session, and correlate it with the underlying delay. The results of the analysis indicate that musicians in real NMP settings are more tolerant to delay than previously thought, managing to reach and maintain a steady tempo even with one-way delays of 40 ms. We also study how the performance tempo is related to delay, finding that the exact relationship between the two depends on the musicians.

Introduction

During the COVID-19 pandemic, a wide range of real-time remote collaboration methods were employed to continue everyday life and work in physical isolation conditions. Network Music Performance (NMP), the performance of music when musicians are connected over a network is a special case of remote collaboration. NMP is useful for music teaching, rehearsing, and even recording. Human-to-human communication, however, has strict delay restrictions: voice communication requires delays of no more than 100 ms to prevent participants from talking over each other. NMP is far stricter: in studies where the remote participants attempted to maintain synchronization while clapping their hands to a beat, delays of more than 25–30 ms were problematic [1].

Although this would seem to make NMP an academic curiosity, many musicians have found that when using specialized NMP tools, they can perform satisfactorily over moderate distances, indicating that the human tolerance to delay may be higher that what the hand clap studies indicate. These tools usually transmit uncompressed audio, since even the lowest delay audio codecs, like Opus, introduce delays of at least 5 ms [2]. Indeed, our own pilot study with four pairs of musicians found that higher levels of delay can be tolerated in real NMP scenarios [3]. For this reason, we believe that it is important to revisit the issue of how much delay is acceptable for NMP under realistic circumstances.

To this end, we designed a controlled experiment with 11 pairs of musicians performing actual musical pieces over carefully controlled delays, using questionnaires to assess the Quality of Experience (QoE) in a subjective manner [4]. The analysis of these questionnaires revealed that not only different musicians perceive the same conditions in quite different ways, even the responses from the same musicians are not consistent with the underlying parameters; for example, their perception of delay does not follow the actual experimental delay. Therefore, although the subjective evaluation indicated that performances with delays of up to 40 ms can be satisfactory to the participants, the high variance of the results makes drawing concrete conclusions harder.

Having recorded audio from all the NMP sessions, we decided to employ audio analysis techniques to examine whether musicians are able to synchronize as delay is increased, that is, whether they manage to reach and maintain a steady tempo during their performance. Our preliminary analysis indicated that NMP is actually feasible at higher delays than 25–30 ms, albeit with a reduced tempo [5]. In addition to a more detailed tempo analysis which confirms that NMP is feasible at delays of up to 40 ms, in this paper, we examine the relationship between delay and tempo, which was reported to be linear in hand clapping experiments [6]. Our results confirm that it is also linear with real music performances, but with a slope that depends on the musicians.

The outline of the rest of the paper is as follows. We present related work on assessing the QoE of NMP in “Related Work”. “Experimental Setup” describes the setup of our experimental scenarios. “Tempo Detection” presents the procedure used to recover the tempo and “Tempo Analysis Results” presents the results from the tempo analysis of the sessions, while “Tempo Analysis Discussion” discusses the results. “Relation of Tempo to Delay” then examines the relationship between delay and tempo. We summarize our findings and discuss future work in “Conclusions and Future Work”.

Related Work

Studies on synchronization during human interaction have long concluded that delay is a critical factor for synchronization; for NMP, in particular, many studies have indicated that human tolerance to delay is far lower than that for teleconferencing, with participants reducing their tempo to compensate for higher delays.

To examine these effects, many studies used performers trying to synchronize hand claps. Hand claps have a very simple audio envelope, making it easy to detect tempo variations, even by visual observation of the recorded waveforms. Other studies have used musical instruments, but their small size made drawing conclusions from them harder. In this section, we review both types of study. A comprehensive review of the state of the art in NMP circa 2016, which also covers synchronization issues, can be found in [7].

Studies Using Hand Claps

Schuett et al. [1] investigated the effect of delay in tempo, proposing and evaluating the Ensemble Performance Threshold (EPT), which is the amount of one-way delay above which clapping performers cannot synchronize. Two performers participated in that experiment, with different starting tempos and delays. They were informed of the amount of delay as it was increased, until the experiment was stopped at 100 ms. The main findings were as follows:

1. If the delay was greater than 30 ms, the tempo would begin to slow down. This threshold was considered as the EPT for impulsive music.

2. A strategy of leader–follower was used by the performers to maintain a steady tempo when the one-way delay was 50–70 ms.

3. EPT varies depending on the type of music (speed, style, attack times of instruments, etc).

4. When delay is 10–20 ms, it may be providing a stabilizing effect on the tempo. A delay of 10–20 ms may be better for ensemble performance than 0 ms of delay.

It is important to point out here that, considering that the speed of sound is 343 m/s, there is a non-negligible audio delay between musicians located in the same space (about 3 ms per meter). This means that 5–10 ms of delay are typical for musicians playing in the same room, while a delay of 0 ms is unnaturally low. In a large orchestra, where the distances (and delays) are much larger, musicians rely on a conductor’s gestures to achieve synchronization, as light travels faster than sound.

Gurevich et al. [8, 9] used seventeen pairs (34 performers) in clapping sessions with variable delays. Each duo performed twelve trials. The subjects were located in two acoustically isolated rooms. The authors reported that for delays shorter than 11.5 ms, 74% of the performances sped up. At delays of 14 ms and above, 85% slowed down. No correlation with the starting tempo was found in the range sampled.

Driessen et al. [6] experimented with two musicians who performed a clapping session with varying delays. The musicians were asked to follow a metronome that was set at 90 Beats per Minute (BPM) and clap for at least 60 s; they answered a subjective questionnaire about their experience after each session. Each session consisted of seven trials with total delays between 30 ms and 90 ms, in 10 ms increments, but in a random order. The authors reported that the tempo of the musicians slowed down as delay was increased. They calculated that the amount by which the tempo decreased was approximated by just over half (0.58) of the initial tempo times the delay in seconds; note that they only used a single starting tempo, though.

Farner et al. [10] asked 11 pairs (22 subjects) to clap together for at least seven measures of a simple rhythmic pattern. The underlying delays were from 6 to 68 ms. The tempo was found to decrease more rapidly with time for higher delays, and the relation was approximately linear. In addition, the tempo tended to increase at the shortest delay. The subjective evaluation showed that participants evaluated the trials as good when delay was short. Above 25 ms, the tempo variations increased, so this value was considered to be the delay tolerance threshold (similar to the EPT of Schuett et al. [1]).

Chafe et al. [11] examined performances by 24 pairs (48 performers) of clappers under different delays. The subjects performed a clapping rhythm from separate sound-isolated rooms, via headphones and without visual contact. One-way delays between pairs were set electronically in the range 3–78 ms. The goal was to quantify the envelope of time delay within which two individuals produce synchronous performances. The authors reported that for delays between 10 and 25 ms, performance was natural. For delays lower than 10 ms, tempo accelerated, while for delays over 25 ms, the tempo decelerated.

To summarize, the delay threshold for rhythmic hand clapping was found to be 25–30 ms. Multiple strategies were employed by the subjects to cope with delay, such as slowing down the tempo. Musical instruments, however, are not as simple to analyze as hand claps and musical performances are more complex than clapping sessions. We discuss NMP studies using actual musical performances in the next subsection.

Studies Using Musical Instruments

Barbosa et al. [12] investigated the self-delay feedback effect, where a musician listens to her/his sound delayed. In their experiments, four musicians played bass, percussion, piano, and guitar. Musicians listened to the feedback from their own instruments through headphones with delay. Their performance was synchronized with a metronome over several takes with different tempos. For each take, the feedback delay was increased, until the musician was not able to keep up a synchronous performance. The authors reported that regardless of the instrumental skills or the instrument, all musicians were able to tolerate more delay at slower tempos, concluding that tempo and latency have a reverse relationship.

Barbosa et al. [13] investigated how the attack time of notes affects the tempo, depending on delay. Two musicians performed cello and violin and the recordings were analyzed. The delay introduced was 0–180 ms. A starting metronome was used, set to 80 BPM. Two experiments were conducted, one with slow attack from the musicians and another with sharp attack. The analysis of the audio files showed that tempo was generally higher in the sharp attack experiment than in the slow attack one. In both cases, tempo decreased with delay and started at about 75 BPM (lower than the 80 BPM of the starting metronome).

Bartlette et al. [14] asked two pairs of musicians (four participants) to perform two Mozart duets, while isolated visually and connected through microphones and headphones. Two clarinets were in one pair, and two stringed instruments (violin and viola) were in the other pair. Different levels of one-way latency (0, 20, 40, 50, 80, 100, 120, 150, and 200 ms) were introduced. After each performance, the musicians rated its musicality and level of interactivity. The authors measured four aspects of expression, pacing, regularity, coordination, and musicality. Pacing denotes the tempo of a musical performance, regularity denotes timing within parts, which may be characterized by quasi-isochrony, or nearly metronomic note timing, and coordination denotes timing between parts, thus mean asynchrony; these were measured objectively. Finally, musicality was assessed subjectively by the participants, with higher ratings given for more musical and interactive performances. Although the musicians chose different strategies to handle latency, both duets were strongly affected by delays of 100 ms or more, where the musicians rated the performances as neither musical nor interactive, and they reported that they played as individuals and listened less and less to one another.

Chew et al. [15, 16] asked two pianists to perform Pulenc’s sonata for two pianos. This sonata has three movements (parts) which should be played at different tempos (46, 132, and 160 BPM). The experimenters introduced 0–150 ms of audio delay. The musicians were placed in the same room with visual contact, but they heard each other’s sound delayed. After each repetition, they answered three questions regarding the ease of playing, the ease of creating musical interpretation, and the ease to adapt in the condition. The authors reported that in the first part (Prelude, at 132 BPM), the participants had trouble synchronizing when the delay was over 150 ms. Both musicians agreed that adaptation was possible below 50 ms. In the second part (Rustique, at 46 BPM), both musicians agreed that synchronization was possible with up to 75 ms of delay. In the third part (final, at 160 BPM), difficulties appeared even with 10 ms of delay. The musicians mentioned that they could overcome delay issues under 50 ms by practicing.

Cârot et al. [17] asked five professional drummers to perform (one at a time) with one professional bass player. This way, a direct comparison of each rhythm section constellation was possible. The audio delay was 0–70 ms. The experiments were performed at tempos of 60, 100, 120, and 160 BPM and the delay was increased from 0 ms in steps of 5 ms, until one of the musicians felt uncomfortable or when they started to slow down. The musicians had to evaluate the actual delay situation as “excellent”, “tolerable”, or “not tolerable”. The authors reported that the overall delay thresholds ranged between 0 and 65 ms and that the musicians did not exhibit a common latency acceptance value.

Olmos et al. [18] worked with six singers, one conductor and one pianist to simulate an orchestra placement. The singers were divided into three groups, each of which performed one of the following pieces: “Il core vi dono...”, from Mozart’s Cosi fan tutte (mezzosoprano and baritone voices); “Ah! – Voi signor” from Verdi’s La Traviata (soprano, tenor, and bass-baritone voices); and “Bess you are my woman” from Gershwin’s Porgy and Bess (soprano and bass-baritone voices). The music pieces were selected for their varying rhythmic complexity. Six different combinations of audio and video delays were selected to simulate the latency conditions between Montreal, New York, San Francisco, and Tromsø. Each isolated room contained two speakers, two cameras and two monitors, with each monitor/camera/speaker set representing the audio and video from a different location. The singers were able to see and hear each other through the video monitors and speakers at all times. After each performance, the singers were asked to complete a questionnaire, rating their experience on a Likert scale of 1–7. The questions were How satisfied were you with the performance, How would you rate your emotional connection with the remote singer, How would you rate your emotional connection with the conductor, How important was the audio, and How important was the video. The authors reported that the singers managed to cope with delay under all conditions. They also reported that the singers had a feeling of “disconnect” between what they heard and the events to which they reacted. An important observation was that the conductor turned out to be very important for synchronization. The authors also reported that as delay increased, the tempo increased; a possible explanation for this was the role of the conductor.

Delle Monache et al. [19] asked ten musicians to perform in duos, with each duo repeating their performance under six different delays (28, 33, 50, 67, 80, and 134 ms). The sequence of delays was randomized for each duo. The musicians performed mandolin, accordion, guitar, percussion, harp, flute, and alto sax. The setup included audio contact via microphones and loudspeakers and visual contact via cameras and video monitors. The participants were asked to fill in a 5-item questionnaire after each repetition, and a general 27-item questionnaire at the end of each session. Further comments were collected at the end of the test. The answers to The sense of playing in the remote environment was compelling and The delay affected the sense of involvement revealed that delay had a negative effect to musicians’ involvement in the environment. Another observation was that for higher delays, musicians could not understand who was responsible for playing out of time. Finally, the authors found that the musicians did not focus on the video monitors, focusing instead on the audio signal.

Rottondi et al. [20] asked eight musicians to participate in NMP experiments. The musicians had at least 8 years of musical experience and were grouped in seven pairs; some performed in more than one pair. The instruments the participants played were acoustic, classical and electric guitar, electric piano, keyboards (strings), clarinet, and drums. Each repetition was characterized by different tempo and network settings in terms of reference BPM, network latency, and jitter. After each session, the participants evaluated two subjective parameters: the quality of their interactive performance and the perceived delay. If the musicians spontaneously aborted their performance within the first 50 s, the quality and delay ratings were set to the worst values. The authors applied audio recording analysis to evaluate six audio features: spectral entropy, spectral flatness, spectral spread, spectral centroid, spectral skewness, and spectral kurtosis. The authors reported that the noisiness of the instrument, which is captured by spectral entropy, flatness, and spread, has an impact on the perceived delay. They also reported that perceived delay is strongly affected by the timbral and rhythmic characteristics of the combination of instruments and parts. Finally, they reported that the musicians’ capability of estimating the network delay is biased by the perceived interaction quality of the performance. This means that large network delays (i.e., larger than 75 ms) do not prevent networked musical interaction, but they limit the selection of the instrument/part combinations. The authors concluded that the quality of the musical experience is not only a function of the delay, but it also depends on factors such as the audio characteristics of the instruments, the role of the musician, the music genre, etc.

We used the same methodology as above to analyze the results of our own NMP experiments [21], employing a larger number of participants and examining how delay influences a large number of QoE metrics and the performance tempo; in addition to grouping the performances based on their audio features, we also used the music genre and the musician’s role for grouping. We found that all the QoE variables were more affected by delay with brighter and noisier instruments, performers that had a rhythm role, and musical pieces with a more rhythmic structure. On the other hand, the effects of the audio and musical features on the performance tempo were not that clear. Compared to the above study, we found that delay is more detrimental to rhythmic performances in general, not just on performances with faster initial tempos.

Experimental Setup

For our experiments, we used two visually and aurally isolated rooms on the same floor of our building. Musicians performed with their counterparts in separate rooms, while listening to them through headphones and seeing them through a 32” monitor. As shown in Fig. 1, an eight-channel analog mixing console was used in each room for audio routing, monitoring, and recording. Audio was captured by condenser microphones and closed type headphones were used by the musicians to listen to each other. A video camera captured and sent a composite video signal through the existing network cabling to the 32” monitor of the other room (red lines in the figure). The network cables were patched directly to each other, without passing through any network equipment; we simply used one pair of the UTP cables to transmit the composite video signal.

Fig. 1.

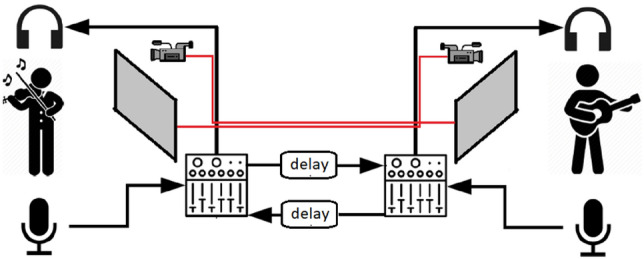
Experimental setup

We used composite video to achieve the lowest possible visual delay between musicians; with the analog signal, we did not have to wait for entire frames to be captured before transmission and received before display. We experimentally measured the round trip video delay by placing a smartphone with a running chronometer in front of the camera in one room, and turning the video camera to the video monitor in the other room, thus reflecting the transmitted image back to the first room. We then recorded with another smartphone’s camera both the chronometer and its reflected image, and analyzed the video in a video editor, finding out that the round trip delay was 30 ms; therefore, the one-way delay was 15 ms.

The two mixing consoles were also connected through the existing network cabling, using direct cable patching; hence, the audio signal was also transmitted in analog form from one room to the other. The reason for connecting them directly was to be able to achieve perfectly fixed audio delays, even below 10 ms, which is impossible when computers and network devices intervene in the signal path. We used AD-340 audio delay boxes by Audio Research, via which we were able to set the audio delay in each direction to the desired value. Apart from the delay boxes, the other delays in the audio path were negligible: the microphones and headphones were next to the musicians, minimizing the distance traveled by the audio waves, while the electrical signals traveled at 2/3 the speed of light.

Most NMP studies use Mouth to Ear (M2E) delay, which is the end-to-end delay between the microphone at one end and the speaker at the other end. In our work, we use the My Mouth to My Ear (MM2ME) delay, as shown in Fig. 2. MM2ME is the two-way counterpart to M2E, over which it has three advantages. First, when musicians play together, each musician plays one note and expects to listen to the other musicians’ note to play the next one. Second, measuring MM2ME delay accurately is much easier than measuring M2E delay, as it can be done at one endpoint, by simply reflecting the transmitted sound at the other endpoint; in contrast, M2E needs to be measured at both endpoints, thus requiring perfectly synchronized clocks [22]. Third, MM2ME takes into account any asymmetry between the two directions of a connection.

Fig. 2.

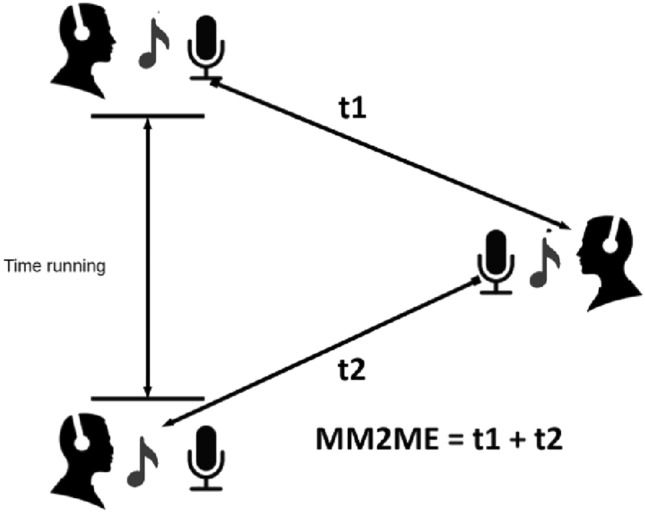
My mouth to my ear delay

The 22 musicians participating in the study performed in pairs (11 pairs in total), with each pair playing different musical instruments: piano, organ, acoustic guitar, electric guitar, bass, violin, and flute, as well as traditional instruments, including the lute, oud, bouzouki, toumberleki, and santouri. Each pair of musicians played a 1 min musical part of their choice, following their own tempo. In Table 1, we first show the music genre of the piece performed by each duet and then the instrument played and the role of each musician, that is, whether they played a rhythm (R) or a solo (S) part.

Table 1.

Performance details for each duet

Duet	1	2	3	4	5	6	7	8	9	10	11
Genre	Folk	Folk	Rock	Rock	Funk	Funk	Rock	Rock	Classic	Folk	Folk
Instr	Piano	Piano	El Gtr	Bass	Organ	Bass	Bass	El Gtr	Flute	Ac Gtr	Lute
Role	R	R	R	R	R	R	R	R	S	R	R
Instr	Sant	Oud	El Gtr	El Gtr	El Gtr	Toum	Ac Gtr	Violin	Violin	Bouz	Violin
Role	S	S	R	R	R	R	R	S	S	S	S

Each pair repeated their chosen musical piece ten (10) times, using a different MM2ME delay setting for each repetition. Musicians were not informed about the delay variations, or about the purpose of the experiment, and we randomly set the order in which the audio delay values and sampling rates were set for each repetition; the delays and their order are shown in Table 2. The main goal was to conduct an experiment that would allow us to evaluate multiple variables without bias in the answers. The MM2ME delay values used range from 0 ms to 120 ms (equivalent to 0 ms to 60 ms in one direction). Since sound travels 3.43 m in 10 ms, two musicians located in the same room would experience an MM2ME delay of 20–40 ms (10–20 ms one way). We tested a range of higher delays to see until which point the QoE was still acceptable, but also lower delays to see how delay is perceived by the musicians.

Table 2.

MM2ME delays used in each repetition

Repetition	1	2	3	4	5	6	7	8	9	10
MM2ME delay (ms)	10	25	35	30	20	0	40	60	80	120

Tempo Detection

The analysis of the questionnaires gathered during our study [4] indicated that the QoE of the musicians did not drop significantly when the MM2ME delay grew from 60 to 80 ms (or, from 30 to 40 ms one way), which means that the EPT for actual music performances may be higher than previously considered. However, the results from the subjective evaluation exhibit a high variance, which makes drawing concrete conclusions harder. The question arises, then, whether musicians can actually synchronize at this delay setting.

Having recorded audio from all the experiments, we decided to examine whether the performers could reach and maintain a steady tempo during their performances, by looking at the evolution of the tempo during each performance. Previous studies of tempo in NMP relied on hand claps, which have a simple audio signature, making it easy to note how the tempo evolves by simply looking at the waveform of the recordings. With real musicians, however, this is not possible. Even worse, since each duet selected their own musical piece and tempo, we did not even know what the intended tempo of each performance was. For this reason, we used a signal analysis toolkit to recover, as far as possible, the tempo of the performances using only the recorded audio.

We analyzed the audio recordings using the MIRToolbox [23]. To determine the tempo at a period of time, we start with the event density, which estimates the average number of note onsets per second as follows:

$$\begin{array}{c}\hfill E=\frac{O}{T},\end{array}$$ 1

where E is event density, O is the number of note onsets, and T is the duration of the musical piece. The MIRToolbox estimates how the music tempo, measured in BPM, varies over time, by detecting the note onsets via signal processing of the audio. The analysis is not perfect, as it depends on each instrument’s sonic signature and manner of playing, but it is revealing, especially for instruments with very clear sonic signatures, for example percussive ones, or with performances where the instrument plays a rhythmic pattern. We performed this analysis for each side of every NMP performance.

These results are not easily amenable to numerical summarization, since musicians adapt their playing over time as they listen to each other; as a result, each performance leaves a unique time-varying imprint, and we have 220 of them (each of the 22 musicians performed their piece ten times, while we varied the audio delay). However, when presented visually, they show interesting trends. The figures in the following section show how the tempo (in BPM) varies over time (in seconds) for each musician; each figure shows one such curve for each delay value, corresponding to one performance by a single musician.

Tempo Analysis Results

In this section, we present a representative set of tempo evolution figures from our NMP experiments, trying to point out different cases where synchronization succeeds or fails. To reduce visual clutter, we only show results at 40 ms intervals, that is, with 0, 40, 80, and 120 ms MM2ME delays, with progressively lighter curves corresponding to increasing MM2ME delays. The rationale behind using only 4 out of the 10 delay values is that they represent very low delay (lower than what is natural in a music performance), reasonable delay (the delay of a moderately large room or studio space), high delay (specifically, the delay level that seemed acceptable in the subjective study), and very high delay (the delay level that seemed unacceptable in the subjective study).

Figures 3 and 4 show the delay variation for each instrument of duet 1, which played a folk song using piano for the rhythm part and santouri (a hammered stringed folk instrument) for the solo part. We can see that with a delay of 0 ms (the darkest curve), which is unnaturally low, both musicians actually speed up their tempo in the beginning of the performance, as reported in the previous studies. As the delay grows (progressively lighter curves), the tempo slows down. Both musicians have a hard time keeping a steady tempo at the two highest delay values, as evidenced from the ups and downs in the curves.

Fig. 3.

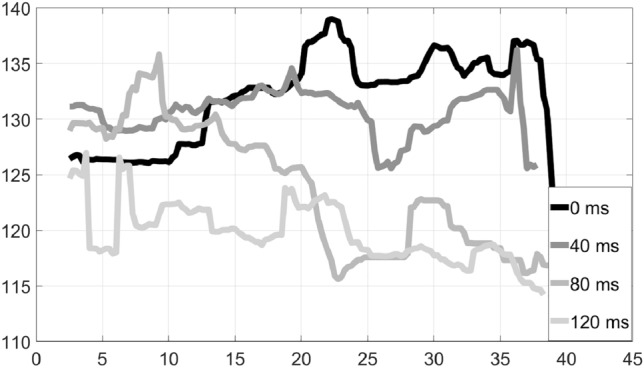
Tempo variation over time: Duet 1, Piano–Rhythm–Folk

Fig. 4.

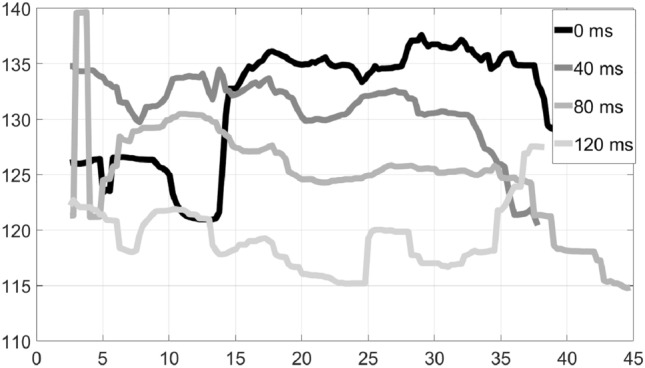
Tempo variation over time: Duet 1, Santouri–Solo–Folk

On the other hand, in duet 2, which played another folk song using piano for the rhythm part and oud (a short-neck lute-like folk instrument) for the solo part, Figs. 5 and 6 show a different situation: the instrument playing the rhythm part is visibly affected by delay, since as the delay grows, the tempo drops; however, the tempo is steady in all but the highest delay value. The instrument playing the solo part shows larger tempo variations, even though the tempo does generally drop with growing delay. An exception is the highest delay setting, where the tempo varies widely. Of course, due to the method we are using to detect the tempo (note onsets), solo parts where musicians play more freely and improvise are harder to characterize precisely in terms of tempo, so it is possible that tempo recovery may not be perfectly accurate.

Fig. 5.

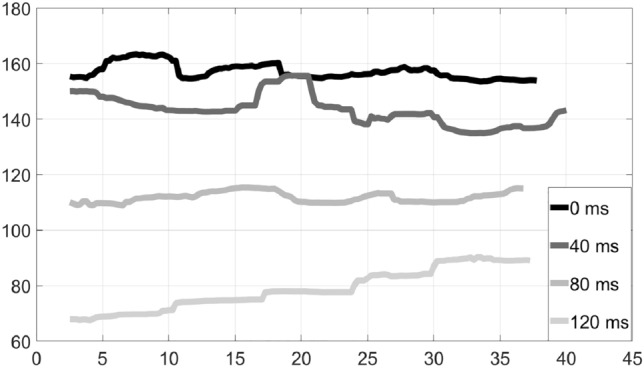
Tempo variation over time: Duet 2, Piano–Rhythm–Folk

Fig. 6.

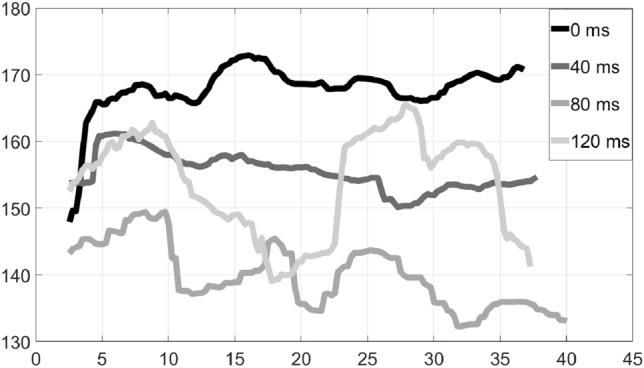
Tempo variation over time: Duet 2, Oud–Solo–Folk

In duet 3, where the musicians played a rock part with two electric guitars both having a rhythm role, we can see in Figs. 7 and 8 that both sides exhibit tempo variations; however, the musicians do manage to keep a relatively steady tempo, except for the highest delay value of 120 ms. Again, the tempo tends to drop with higher delays. Note that the performance ends at different times for each delay value; however, both musicians finish at the same time in each case.

Fig. 7.

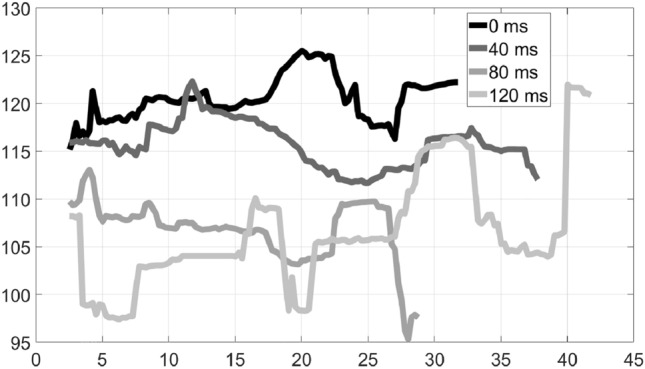
Tempo variation over time: Duet 3, Electric Guitar–Rhythm–Rock

Fig. 8.

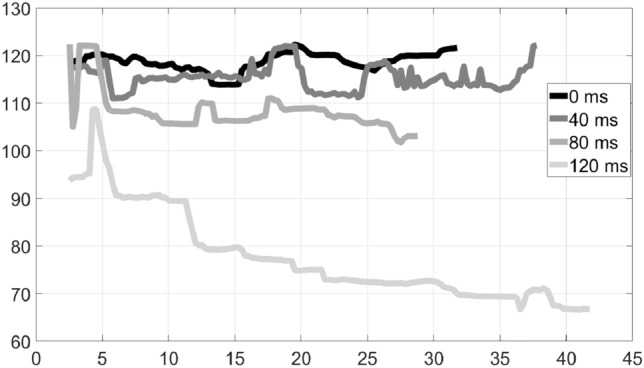
Tempo variation over time: Duet 3, Electric Guitar–Rhythm–Rock

The difficulty of keeping a steady tempo at higher delays is also apparent in Fig. 9 which shows one side of duet 5, the organ (the other side played electric guitar). This duet played a funk piece with both instruments having a rhythm role. Again, tempo drops with higher delays, and has wild variations at a delay of 120 ms. Duet 6 also performed a funk piece, with a bass and a toumberleki (a small drum-like folk instrument played with the hands) both having rhythm roles. As shown in Fig. 10, for the toumberleki, the beat is noticeably slower for higher delays, and hard to keep steady when delay reaches 120 ms; note that as a percussive instrument, the toumberleki is the easiest case for automated tempo detection.

Fig. 9.

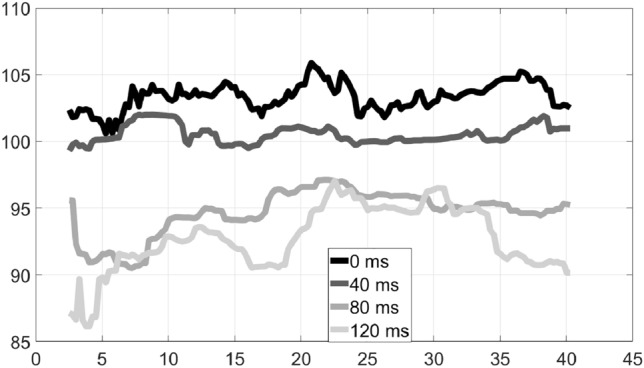
Tempo variation over time: Duet 5, Organ–Rhythm–Funk

Fig. 10.

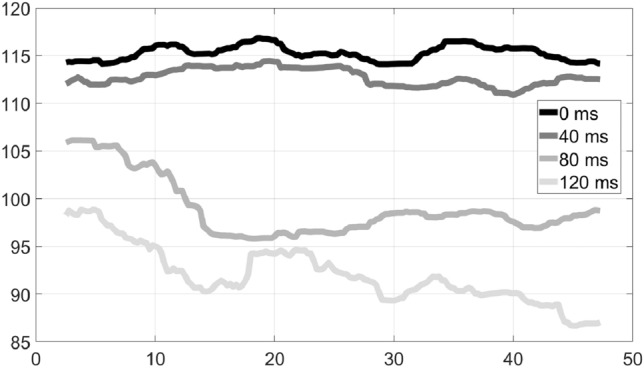
Tempo variation over time: Duet 6, Toumberleki–Rhythm–Funk

There are also cases where both sides of a duet managed to maintain the same rhythm, as with duet 7, where a rock piece was performed with bass and acoustic guitar, both having rhythm roles. As shown in Figs. 11 and 12, the rhythm is steady with delays of up to 80 ms; there is a very slight reduction in tempo from 40 to 80 ms, but at 120 ms, the tempo either slows down continuously or varies wildly.

Fig. 11.

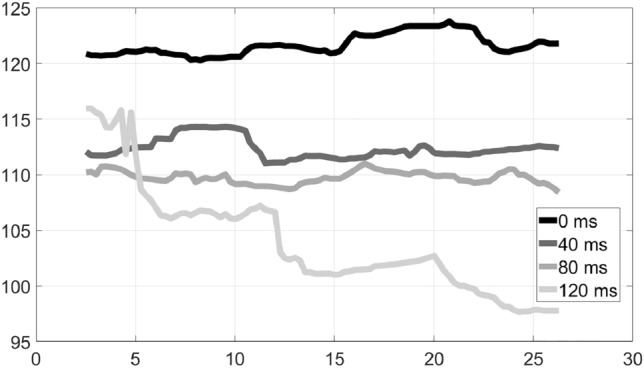
Tempo variation over time: Duet 7, Bass–Rhythm–Rock

Fig. 12.

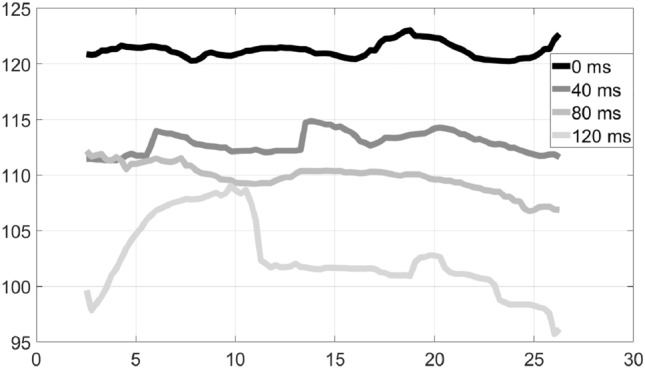
Tempo variation over time: Duet 7, Acoustic Guitar–Rhythm–Rock

Duet 8, where a rock piece was performed, is unusual, in that the rhythm instrument (guitar), shown in Fig. 13, has an unsteady tempo, while the solo instrument (violin), shown in Fig. 14, has a very steady tempo, despite the visible slowdown at delays of 80 and 120 ms. The reason for this is the very different expertise levels of the musicians: the violinist was a 45-year-old professional musician, while the guitarist was a 23-year-old amateur one. Hence, the violinist’s solo tempo was found to be more stable than the guitarist’s, even though it was the guitarist who was supposed to keep a stable rhythm with the guitar. This is an indication that more experienced musicians may manage to partially compensate for delay by adapting their performance.

Fig. 13.

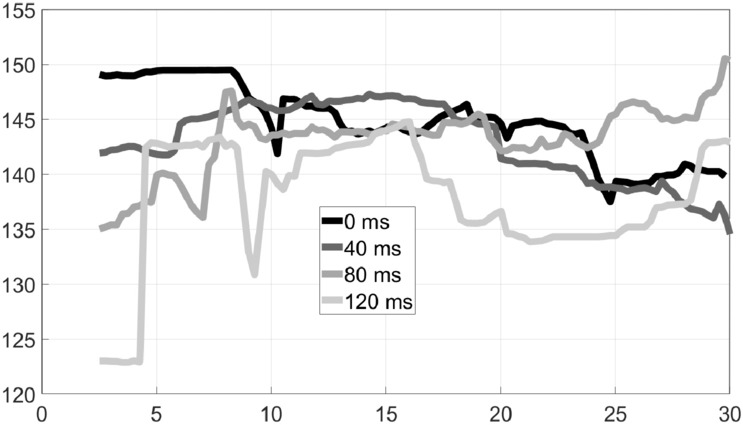
Tempo variation over time: Duet 8, Electric Guitar–Rhythm–Rock

Fig. 14.

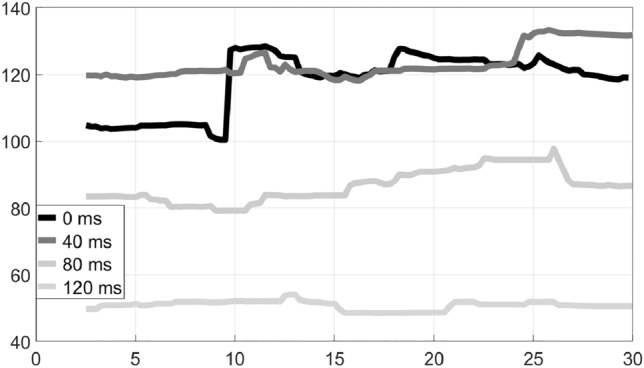
Tempo variation over time: Duet 8, Violin–Solo–Rock

In duet 10, a folk piece was performed with acoustic guitar for the rhythm part and bouzouki (a small lute-like folk instrument) for the solo part. As shown in Fig. 15, the tempo of the guitar speeded up at 0 ms, progressively slowing down as delay grew, but it was relatively stable even at the highest delay setting. Similarly, in duet 11, where another folk piece was performed with a lute for the rhythm part and a violin for the solo part, Fig. 16 shows that the lute had very good tempo stability at all delay values, except for the speedup at the lowest delay setting of 0 ms.

Fig. 15.

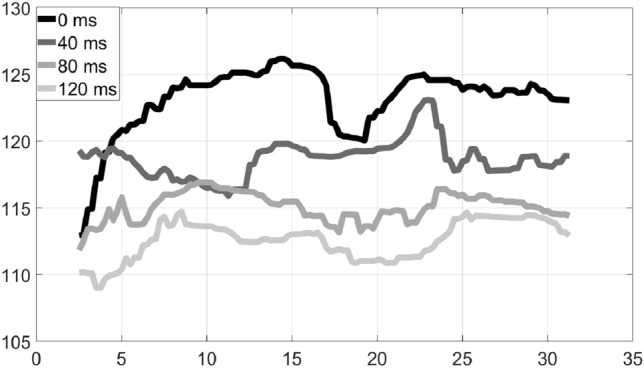
Tempo variation over time: Duet 10, Acoustic Guitar–Rhythm–Folk

Fig. 16.

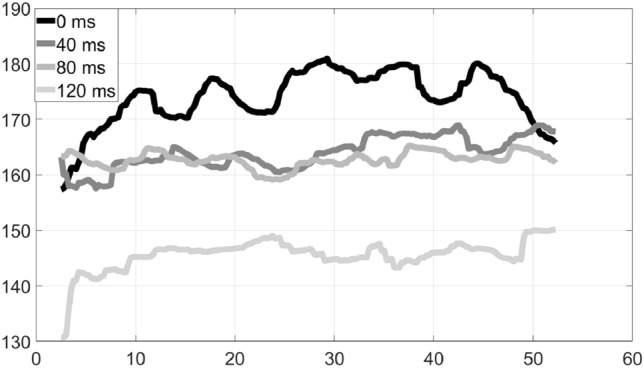
Tempo variation over time: Duet 11, Lute–Rhythm–Folk

Tempo Analysis Discussion

From the results presented in the previous section, we can make the following general observations:

1. At the (unnaturally) low delay of 0 ms, musicians tend to speed up their tempo in the beginning of the session.

2. As delays rise beyond 40 ms (the natural delay), musicians adapt by slowing down the tempo of their performance.

3. In most cases, musicians manage to keep a steady tempo at delays of up to 80 ms.

4. At a delay of 120 ms, most performances break down, exhibiting either continuously slowing or wildly varying tempos.

5. Instruments performing rhythm parts are more clearly affected by delay, as shown by their more visibly delineated curves.

Past work has found that musicians who perform percussive instruments tend to suffer more from delay than others. Indeed, the hand clap synchronization experiments fall exactly into this category, as a very clear pattern is used, which is easy to detect by simply looking at the signal waveforms. Our study indicates that this is true in general for the instruments having the rhythmic role of a duet. We should also point out that even though solo instruments seem to follow more irregular tempos, this may be an artifact of our audio analysis which relies on a steady production of note onsets; with improvisational parts, performers are expected to more often deviate from the base rhythmic pattern; therefore, the analysis may show an irregularity that does not exist in the actual performance.

The most interesting observation of course is that the limits to tolerance can vary considerably; most musicians could achieve a stable tempo at MM2ME delays of 80 ms, corresponding to a one-way delay of 40 rather than 20–30 ms, higher than what was previously considered the limit to synchronization, even though this may come at the cost of a minor slow down in the performing tempo. This verifies the results from our subjective QoE study [4], which indicated that musicians in most cases considered their NMP sessions to be satisfying even with MM2ME delays of 80 ms.

Relation of Tempo to Delay

Our analysis shows that the tempo in NMP sessions with actual musical performances drops with increasing delay, extending previous studies which documented this phenomenon with hand claps. In addition to the visual inspection of the tempo evolution figures in “Tempo Analysis Results”, we performed an ANOVA analysis for repeated measures of the average tempo scores for each session and for delays of 0, 40, 80, and 120 ms (MM2ME). The p value was computed equal to 0.007 ($p<0.05$). This indicates a strong statistical significance in the delay/tempo relationship, that is, the calculated tempos were statistically correlated with the delay values, in the sense that higher delays did lead to slower tempos.

The question then arises if there is a specific relationship between delay and tempo, that is, if we can predict how much the tempo will slow down, depending on the audio delay. As mentioned in “Related Work”, Driessen et al. [6] based on their experiments with hand claps concluded that tempo and delay are related as follows:

$$\begin{array}{c}\hfill BPM(d)=BPM-0.58\times BPM\times d,\end{array}$$

where d is the M2E delay in seconds, BPM is the intended tempo, and BPM(d) is the resulting tempo with this delay. There are, however, two issues with this model. First, it implies that at a delay of 0, the tempo is unchanged ($BMP(d)=BPM$), which is unlikely, as most studies indicate that the tempo actually speeds up at this delay level. Second, since all the experiments were made with the same starting tempo (90 BPM), it is possible that the BPM factor in the multiplicative term is actually a constant, which would simplify the model to a linear one

$$\begin{array}{c}\hfill BPM(d)=BPM-52.2\times d.\end{array}$$

Since in our NMP experiments, we used actual musicians, which seem to have a higher tolerance to delay, musical pieces with different tempos, and a large number of performances, we have enough data points to perform a regression analysis. The easiest way to do this would be to perform linear regression between the delay values tested and the average performance tempos detected for each performance. Unfortunately, we have two problems. First, not all performances are successful, in the sense that the musicians cannot always find a common tempo. This is clear from the figures in “Tempo Analysis Results”, where some curves have wild variations. Using an average tempo value for such performances adds noise to the data set.

Second, the signal processing method we used cannot always accurately estimate the tempo. This is evident in Table 3, where we show the average BPM detected for each musician (musicians 1 and 2 are duet 1, musicians 3 and 4 and duet 2, and so on) and each delay value. Note that we rounded the values returned by the MIRToolbox to integers, and used these values for all further processing. A quick glance at the table shows some very odd values. For example, for musician 11, the tempo at delays of 20–40 ms alternates between values of 58–59 BPM and 115–122 BPM; looking at musician 12, the other side of the duet, the tempo seems to be slightly more than 100 BPM, indicating that the MIRToolbox must have missed half of the note onsets for musician 11. This also happens in the reverse direction: musician 12 at a delay of 60 ms seems to suddenly double the tempo from 101 to 197 BPM.

Table 3.

Detected tempo for all performances

Delay	0	10	20	25	30	35	40	60	80	120
1	133	130	134	134	130	133	130	131	129	119
2	137	136	135	131	132	134	131	130	127	119
3	100	172	157	167	112	107	143	79	108	158
4	151	173	155	157	168	161	140	154	163	161
5	120	122	117	115	119	119	116	109	108	103
6	119	121	115	113	119	117	119	105	108	87
7	72	92	55	112	103	134	159	151	174	158
8	60	57	56	89	56	97	58	89	78	57
9	103	103	101	102	99	101	100	98	94	92
10	104	104	101	103	100	101	101	197	78	57
11	71	106	58	122	59	115	58	94	105	143
12	104	104	101	103	100	101	101	197	78	57
13	123	121	117	119	112	115	113	108	108	103
14	122	121	117	59	113	115	113	109	108	102
15	145	113	112	96	61	83	142	141	144	138
16	118	149	109	132	116	104	125	87	51	86
17	104	138	155	91	119	101	93	117	87	126
18	126	91	121	102	108	109	106	123	117	122
19	123	124	120	118	121	120	119	118	115	113
20	123	126	112	89	121	64	125	117	116	111
21	169	97	170	163	87	150	178	161	153	153
22	172	175	170	163	168	165	164	164	162	145

Apparently, we have a number of problematic BPM values, either due to failed performances, or due to inaccurate BPM estimation, which need to be removed before applying any statistical processing. To clean up our data, we will first remove any values that are outliers. To determine which values are outliers, we use the same procedure as in Rottondi et al. [20], that is, we calculate the 1st and 3rd quartile of the tempo distribution for each musician, and then calculate the Inter Quartile Range (IQR), which is the difference between these two quartiles (the range of the middle 50% of the values) and then classify as an outlier any value that is lower than the 1st quartile minus 1.5 times the IQR or more than the 3rd quartile plus 1.5 times the IQR. By removing these values from the table, we end up with Table 4, with gaps at the positions where the outliers were.

Table 4.

Detected tempo and statistics for all performances, excluding outliers

Delay	0	10	20	25	30	35	40	60	80	120	Slope	Intercept
1	133	130	134	134	130	133	130	131	129		$-$0.0416	132,9416
2	137	136	135	131	132	134	131	130	127		$-$0.1199	136,5533
3	100	172	157	167	112	107	143	79	108	158	$-$0.0453	132,2028
4	151	173	155	157	168	161		154	163	161	0.0089	159,9574
5	120	122	117	115	119	119	116	109	108	103	$-$0.1607	121,5504
6	119	121	115	113	119	117	119	105	108		$-$0.1718	120,8385
7	72	92	55	112	103	134	159	151	174	158	0.8682	84,5349
8	60	57	56	89	56	97	58	89	78	57	0.0393	68,0504
9	103	103	101	102	99	101	100	98	94		$-$0.1089	103,7423
10	104	104	101	103	100	101	101				$-$0.0922	104,1078
11	71	106	58	122	59	115	58	94	105	143	0.4723	73,2649
12	104	104	101	103	100	101	101				$-$0.0922	104,1078
13	123	121	117	119	112	115	113	108	108	103	$-$0.1661	120,8747
14	122	121	117		113	115	113	109	108	102	$-$0.1649	120,5711
15	145	113	112	96	61	83	142	141	144	138	0.2907	105,2907
16	118	149	109	132	116	104	125	87	51	86	$-$0.5619	131,3010
17	104	138	155	91	119	101	93	117	87	126	$-$0.0708	116,0736
18	126	91	121	102	108	109	106	123	117	122	0.1124	107,7791
19	123	124	120	118	121	120	119	118	115		$-$0.0976	123,0309
20	123	126	112		121		125	117	116	111	$-$0.0933	123,0737
21	169		170	163		150	178	161	153	153	$-$0.1473	169,1219
22	172	175	170	163	168	165	164	164	162		$-$0.1443	171,8110

Using the remaining values for each musician, we can perform linear regression between the delay values and the tempos. The slopes and intercepts for the regression lines are shown in the final columns of Table 4. Since the first delay value is 0 ms, the intercept of the regression line, that is, the point where the regression line meets the y axis, is the predicted tempo at that delay. We see that there is a wide variance of slopes: there are some positive ones, for musicians 4, 7, 8, 11, 15, and 18, indicating that tempo speeds up with delay, which is contrary to what we saw in the graphs. The problem is that some lines have so much variation, that even the outlier test did not manage to clean them up; see, for example, the lines for musicians 7 and 8 (duet 4). But even the lines with negative slopes are so widely divergent, that using even the cleaned up data to perform regression and come up with an average slope for all musicians is a futile exercise.

On the other hand, we can see that there are some duets which have very closely matching slopes and intercepts: duets 3, 5, 7, 10, and 11. This indicates that the musicians of these duets behaved in the same way with increasing delay. A visual inspection of the figures showing the tempo evolution for these duets verifies that they represent mostly successful performances. In addition, the slopes of all these duets are close to each other, ranging from $-0.0922$ to $-0.1718$. The average of these slopes is $-0.1347$, which leads to the following linear formula:

$$\begin{array}{c}\hfill BPM(d)=BPM-0.1347\times d^{\prime },\end{array}$$

where $d^{\prime }$ is the MM2ME (two-way) delay in milliseconds used in our experiments. To make the formula comparable to that of Driessen et al., which uses d, the M2E (one-way) delay in seconds, we note that $d^{\prime }=1000\times 2\times d$. Therefore, by substitution, we have

$$\begin{array}{c}\hfill BPM(d)=BPM-269.4\times d.\end{array}$$

Using as a reference value the 90 BPM used by Driessen et al. in their experiments, their formula predicts that at a one-way (M2E) delay of 30 ms (60 ms MM2ME), the tempo will be around 88.4 BPM, while our formula predicts that it will be around 82 BPM, a much steeper reduction. Any such formula, however, is only applicable for the delay range within which the musicians manage to reach and maintain a steady tempo. In addition, given the differences in the slopes even between the duets that behaved similarly, it is safer to say that the exact slope depends on the musicians. For example, using the average slopes of each of the successful duets mentioned above, the predicted tempo at that delay level would range from 80 to 84.3 BPM.

Conclusions and Future Work

We performed a set of NMP experiments, where the audio delay between a pair of musicians was varied in a controlled manner for each session. In the experiments reported in this paper, 22 musicians participated as pairs, playing a diverse set of musical instruments in a variety of musical styles, constituting the largest NMP study with actual musical performances that we are aware of. The analysis of the questionnaires reported in our previous work indicated that in actual NMP performances, the tolerance of the musicians to delay is higher than previously thought.

This paper presents an analysis of the recorded audio from these NMP sessions, using signal processing techniques to recover the performance tempo of each musician. Our analysis shows that even though musicians tend to slow down their tempo as delays grow, most of them can synchronize and maintain a stable tempo with one-way delays of up to 40 ms, but not with delays of 60 ms. This confirms the results of the subjective QoE analysis which indicated that the acceptable delay threshold for NMP is closer to 40 ms over a wide range of instruments and musical pieces, rather than the 25–30 ms widely cited in the literature.

On the other hand, we found that although it is clear that there is a relationship between the delay and the resulting tempo in NMP, it is hard to characterize this relationship with a single linear equation covering all sessions. After discounting the outlier values which are due to the inaccuracies of our tempo recovery method, we saw a wide variation between the performances. Our best guess at an exact relationship between the delay and tempo comes from a cluster of performances with very similar slopes between the musicians in each duet, but a safer conclusion is that the exact relationship depends on the participating musicians.

We are currently working on an analysis of the videos recorded during our experiments, using emotion recognition tools based on machine learning algorithms for facial feature extraction; early results from this direction of research are reported in [24], constituting another mode of analysis of the musicians’ experience in NMP.

Funding

This research was supported by the Research Center of the Athens University of Economics and Business.

Data availability

The data that support the findings of this study are not openly available due to the need to protect the privacy of the performers, which are seen and heard in the video and audio recordings, respectively. These data are available from the corresponding author upon reasonable request, provided that the requesting party respects the EU General Data Protection Regulation rules.

Declarations

Conflict of Interest

On behalf of all authors, the corresponding author states that there is no conflict of interest.