Abstract
Uncovering the non-trivial brain structure–function relationship is fundamentally important for revealing organizational principles of human brain. However, it is challenging to infer a reliable relationship between individual brain structure and function, e.g., the relations between individual brain structural connectivity (SC) and functional connectivity (FC). Brain structure–function displays a distributed and heterogeneous pattern, that is, many functional relationships arise from non-overlapping sets of anatomical connections. This complex relation can be interwoven with widely existed individual structural and functional variations. Motivated by the advances of generative adversarial network (GAN) and graph convolutional network (GCN) in the deep learning field, in this work, we proposed a multi-GCN based GAN (MGCN-GAN) to infer individual SC based on corresponding FC by automatically learning the complex associations between individual brain structural and functional networks. The generator of MGCN-GAN is composed of multiple multi-layer GCNs which are designed to model complex indirect connections in brain network. The discriminator of MGCN-GAN is a single multi-layer GCN which aims to distinguish the predicted SC from real SC. To overcome the inherent unstable behavior of GAN, we designed a new structure-preserving (SP) loss function to guide the generator to learn the intrinsic SC patterns more effectively. Using Human Connectome Project (HCP) dataset and Alzheimer’s Disease Neuroimaging Initiative (ADNI) dataset as test beds, our MGCN-GAN model can generate reliable individual SC from FC. This result implies that there may exist a common regulation between specific brain structural and functional architectures across different individuals.
Keywords: Brain connectivity, Structure-function relationship, Graph convolution networks, Generative adversarial network
1. Introduction
A fundamental question in neuroscience is how to understand structure-function relationship of human brain. It is widely believed that brain structural architecture provides the substrate where rich functionality arises from, and therefore, the dynamics of brain function are closely related to the relatively fixed structure organization. Numerous studies confirmed that brain structure can determine, at least partially, brain functional patterns. For example, the concept of “connectional fingerprint” (Passingham et al., 2002) suggests that each brain’s cytoarchitectonic area has a unique set of extrinsic inputs and outputs, which largely determine the function that each brain area performs. This close relationship between structural connection pattern and brain function has been confirmed and replicated in many literatures. For example, our previous work (Zhu et al. 2011, 2012, 2013) proved that the same functional regions tend to possess consistent structural connectivity patterns across different individuals and populations. Koch et al. (2002) directly compared brain structural connectivity (SC) and functional connectivity (FC) and found that regions which directly linked by structural connectivity show high functional connectivity. Skudlarski et al. (2008) reported a significant overall agreement between SC and FC by calculating the partial correlation between the two global matrices. Some other studies implemented computational models to study the brain structure-function relationship at macroscale (Honey et al., 2009; Gong et al., 2009), mesoscale (Wang et al., 2013), and microscale (Pernice et al., 2011). A consistent result achieved by these studies is that strong functional interactions tend to be accompanied with strong structural connections. On the other hand, some studies also found that parts of the FC may be not supported by the underlying SC. Greicius et al. (2009) studied the relations between SC and four default mode network (DMN) related brain regions and found that strong FC can still exist without direct SC. This may be due to several factors. Firstly, the complex indirect interactions may widely exist among different brain regions. The functional connections observed between regions with little or no direct structural connections may be mediated by indirect structural connections. Secondly, brain’s structure-function behaves under a distributed and heterogeneous pattern: at network level, many functional relationships arise from non-overlapping sets of anatomical connections (Misic et al., 2016), which means functional networks do not necessarily correspond to the underlying structural substrate with a simple node-to-node mapping. Therefore, how to represent and analyze the relationship between brain structural and functional network, especially at individual level, is still challenging.
The existing approaches that have been used to explore brain structure-function relationship can be broadly divided into two categories: the first approach is to conduct association analysis using correlation coefficient, which mainly focuses on simple and linear relationship between SC and FC (Koch et al., 2002; Skudlarski et al., 2008). The second is to apply graph theory to both brain structural and functional network for quantitative analysis, such as small world property (Achard et al., 2006; IturriaMedina et al., 2008; Sporns and Zwi, 2004), modular structure property (Zamora-Lpez et al., 2016; Diez et al., 2015), and rich-club organization Van Den Heuvel and Sporns, 2011; Van Den Heuvel et al., 2012). All these approaches have fundamentally advanced our understanding of the relationship between brain structure and function at population level, but they are limited in charactering individual variability in subject-specific brain network. In addition to the above two widely used strategies, some other computational models have also been developed to bridge the gap between structural network topology and the related function by examining their relations at multiple scale and resolution (Honey et al., 2009), modeling dynamics (Pernice et al., 2011) and constructing local mm-scale networks using animal model (Wang et al., 2013). However, because of brain’s distributed and heterogeneous structure-function pattern, traditional methods are limited to represent the complex relationship between individual SC and FC.
Recent advances in deep learning have revolutionized the fields of machine learning (Hinton and Salakhutdinov, 2006; LeCun et al., 2015) and brought breakthroughs for computational neuroimaging field including reconstruction (Sun et al., 2019), segmentation (Wang et al., 2015), detection (Sirinukunwattana et al., 2016), and computer-aided diagnosis (Roth et al., 2015). Among numerous deep learning models, graph convolutional network (GCN) (Kipf and Welling, 2016; Wu et al., 2020; Zhang et al., 2020c) generalizes the convolutional operations from grid data to graph data and witnesses great success in brain network domain recently (Ktena et al., 2018; Kazi et al., 2019; Parisot et al., 2018; Zhang et al., 2019b, 2020b, 2021). More importantly, the generative adversarial network (GAN) (Goodfellow et al., 2014; Hong et al., 2019) provides an efficient way to revisit the complex relationship between brain structure and function: as a generative model, GAN can powerfully handle the brain’s distributed and heterogeneous structure-function pattern. Moreover, compared to other generative models, GAN effectively converts the regression problem to a classification problem through the adversarial training scheme. In this way, an explicit regression loss function is unnecessary, and the criterion used to evaluate the performance of the predictions is implicitly learned from the data. This can be especially suitable for areas with insufficient prior knowledge, such as brain network.
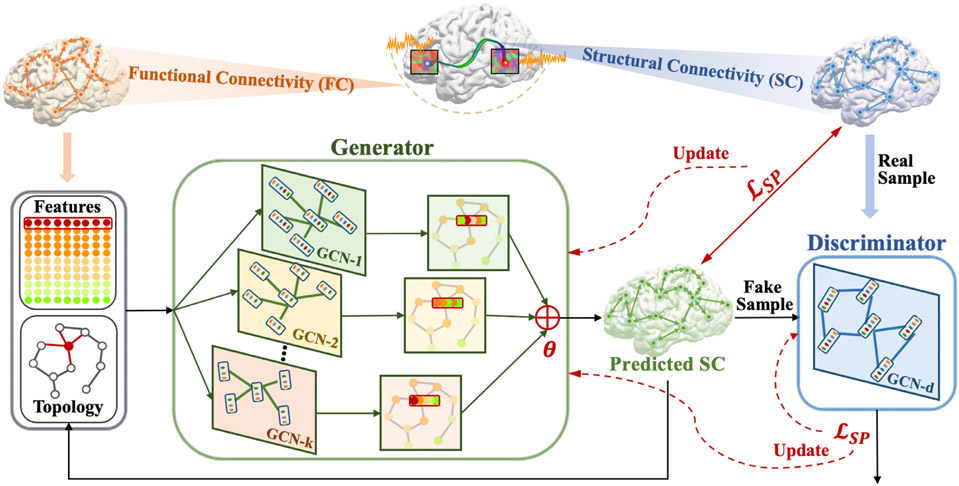
In this work, we proposed a multi-GCN based generative adversarial network (MGCN-GAN) (Fig. 1) to learn individual SC from the corresponding individual FC. We adopted GAN to handle brain’s distributed and heterogeneous pattern. To overcome the inherent unstable behavior of GAN (Goodfellow et al., 2014; Hong et al., 2019) caused by the adversarial training scheme, we proposed a novel structure-preserving (SP) loss function to guide the generator to learn the intrinsic SC patterns more effectively. In order to capture the complex relationship buried in both direct and indirect brain connections, we constructed the generator and discriminator using GCN. However, traditional GCN has two limitations: First, comparing to widely used convolutional neural network (CNN) that has multiple filters to capture multiple feature spaces, conventional GCN only has one filter (weight matrix) in each GCN layer and therefore can only learn a single feature map. Second, the performance of GCN may gradually decrease with increasing number of layers (Zhao and Akoglu, 2019) and which limits the power of learning by deepening the network as CNN does. To address these limitations, we designed a multi-GCN based generator that used multiple GCNs instead of one deep GCN to simultaneously capture underlying complex interactions in brain network and avoid the performance decay by stacking more layers in a single GCN. We tested our methods on two datasets: Human Connectome Project (HCP) dataset (Van Essen et al., 2012) and Alzheimer’s Disease Neuroimaging Initiative (ADNI) dataset (Petersen et al., 2010). Our results show that the proposed MGCN-GAN can generate reliable individual SC based on corresponding individual FC. More importantly, our results imply that there may exist a common regulation between specific brain structural and functional architectures across individuals.
Fig. 1.
An illustration of the proposed multi-GCN based generative adversarial network (MGCN-GAN). Firstly, by using brain atlas (Destrieux Atlas (Destrieux et al., (2010)) and Desikan-Killiany Atlas (Desikan et al., (2006)) along with diffusion MRI and rs-fMRI data, we extracted the averaged BOLD signal of each brain region. Then we constructed functional connectivity (FC) by different methods (correlation, partial correlation, threshold FC, and binarized FC) and structural connectivity (SC) by diffusion MRI derived fiber counts. SC was used as 1) ground truth to guide the generator at the beginning of the training process; 2) real samples of discriminator. FC was used as: (1) features associated with the nodes; (2) initialization of the GCN topology. The features and topology were fed into generator to predict SC. The predicted SC were used to (1) iteratively update the GCN topology and (2) train discriminator as fake samples. The whole model is trained based on the proposed structure preserving (SP) loss function.
Our proposed MGCN-GAN advances the state of the art in two ways: firstly, our model is designed to capture individual-specific structure-function relationship. Previous publication (Batista-Garcia-Ramo and Fernandez-Verdecia, 2018) found that similar structural damage of patients with the same pathology show different dysfunctions, which indicates the variability of individual structure–function relationship. Unveiling individual structure–function relationship is fundamentally important to the comprehensive understanding of individual variation in brain structure and function and is the premise and key step for personalized medicine. Secondly, we introduced multi-GCN architecture into GAN framework and designed a structure preserving (SP) loss function to help the model to generate high-quality SC. The MGCN-GAN is a flexible architecture with adjustable GCN components to fit different tasks with varying complexity.
2. Related work
Graph convolutional network (GCN) (Kipf and Welling, 2016; Wu et al., 2020) was developed to manipulate graph topological properties in a deep manner. Recently, it has been used to define and represent brain network for deep modeling of brain structural and/or functional connectivity under a given task, i.e., classification (Zhang et al., 2019a, 2020a, 2021; Huang et al., 2020). In this section, we reviewed the most recent GCN-related studies on brain network from two views: (1) the definition of the input graph – group-level GCN model vs individual-level GCN model (Section 2.1), and (2) the architecture of the GCN framework – single-GCN architecture vs multi-GCN architecture (Section 2.2).
2.1. Group-level GCN model vs individual-level GCN model
Based on different definitions of input graph, existing GCN-based studies on brain network can be grouped into two categories – group-level GCN model and individual-level GCN model. In group-level GCN model, the input graph represents the whole populations. For example, Parisot et al. (2018) used imaging features of individuals as nodes and encoded pairwise similarities between non-imaging features as edge weights. By this way, the whole populations were represented as a sparse graph, upon which a GCN was built in a semi-supervised learning task to predict conversion to Alzheimer’s disease. Kazi et al. (2019) constructed a similar graph structure, where each node was a feature vector generated from imaging data to represent an individual and the non-imaging data was used to measure the similarities between the connecting nodes. To break the limitation of applying the same filter size to all layers, Kazi et al. proposed an InceptionGCN model, in which the filter size of different GCN layers can be different, and thus make the model more efficient in capturing useful features. To better measure the similarity between two connecting nodes, Song et al. (2021) designed a similarity-aware adaptive calibrated GCN (SAC-GCN). In this work, a calibration mechanism was proposed to fuse fMRI and DTI information into edges and a pre-trained GCN was used to calculate the similarity between each pair of subjects. However, group-level GCN model can be limited in the flexibility when handling the large sample size and in capability when representing rich individual information. Individual-level GCN model takes individual graph as input. Each node in the individual graph represents an anatomical brain region, and the edge denotes the relationships between the two connecting brain regions, such as the morphological, functional or structural connectivity. Ktena et al. (2018) used functional connectivity to create individual graph and leveraged siamese graph convolutional network (s-GCN) to learn a graph similarity metric which was incorporated into a classification task at later steps. Zhang et al. (2019a, 2020a) combined individual-level GCN model with recurrent neural network (RNN) models to deal with both brain structural and functional connectivity when identifying the mild cognitive impairment patients. Zhang et al. (2021) also proposed a topology learnable GCN model: the topology of the GCN was initialized by individual structural connectivity and iteratively updated by functional information to maximize its classification power for MCI patients. In general, most GCN studies focused on extracting useful features from brain connectivity data to do classification or to conduct associative analysis. Inferring the relationship between structural and functional networks at individual level has not yet been studied.
2.2. Single-GCN architecture vs multi-GCN architecture
Several GCN studies summarized in Section 2.1 adopt single-GCN architecture. To further take advantages of complementary information provided by different scales and modalities, some studies tried to build multiple GCNs for different brain graphs. Zhang et al. (2018) proposed a multi-view GCN to handle different brain connectivity graphs (BCGs) derived from DTI imaging data using different tractography algorithms. A pair-wise matching strategy was adopted to fuse the output of each GCN to conduct classification of Parkinson’s disease patients. Huang et al. (2020) designed an attention-diffusion-bilinear neural network to integrate structural connectivity and functional connectivity for predicting frontal lobe epilepsy, temporal lobe epilepsy, and healthy subjects. This framework consists of two GCNs for two scales – direct connections and indirect connections. Zhang et al. (2019b) trained different GCNs for multiple graphs with respect to multi-modal brain networks. The features generated by each GCN were concatenated to conduct classification of patients with Parkinson’s disease. In general, by building independent GCNs for each type of brain connectivity, multi-GCN architecture is able to capture more comprehensive information from multi-modal data and therefore, improve the model performance.
3. Materials and methods
3.1. Participants and data description
HCP dataset.
In this work, we selected all the 1064 subjects which have structure MRI (T1-weighted), resting state fMRI (rs-fMRI) and diffusion MRI data from HCP S1200 release. For the T1-weighted MRI data, the Field of View (FOV) is 224 mm×224 mm, voxel size is 0.7 mm isotropic, TR = 2.4 s, TE = 2.14 ms and flip angle = 8° For the rs-fMRI data, the FOV is 208 mm×180 mm, 72 slices, voxel size is 2.0 mm isotropic, TR=0.72 s, TE=33.1 ms, flip angle = 52° and there are 1200 vol for each subject. For the diffusion MRI data, the gradient direction is 288, the FOV is 210 mm×180 mm, 111 slices, voxel size is 1.25 mm isotropic, TR=5.52 s, TE=89.5 ms and flip angle = 78°.
ADNI dataset.
We used 132 normal control (CN) subjects (68 females, 64 males; 76.45 ± 7.68 years.) from ADNI dataset. Each subject has structure MRI (T1-weighted), rs-fMRI and diffusion MRI data. The FOV of T1-weighted MRI is 240 mm×256 mm×208 mm and the voxel size is 1.0 mm isotropic, TR = 2.3 s. The diffusion MRI data has 54 gradient directions, the FOV is 232 mm×232 mm×160 mm and the voxel size is 2.0 mm isotropic, TR = 7.2 s and TE = 56 ms. The rs-fMRI data has 197 vol, the FOV is 220 mm×220 mm×163 mm, voxel size is 3.3 mm isotropic, TR = 3 s, TE = 30 ms and flip angle = 90°.
3.2. Data preprocessing
We applied the same standard preprocessing procedures as in Zhu et al. (2014a) and Wang et al. (2019) to both HCP and ADNI datasets. In brief, we applied skull removal for all three modalities and registered T1 and fMRI to DTI space by FLIRT in FM-RIB Software Library (FSL) (Jenkinson et al., 2012). For rs-fMRI images, we applied spatial smoothing, slice time correction, temporal pre-whitening, global drift removal and band pass filtering (0.01–0.1 Hz) via FEAT command in FSL. For DTI images, we applied eddy current correction using FSL and fiber tracking via MedINRIA (Toussaint et al., 2007)). For T1 images, we conducted segmentation using FreeSurfer package (Fischl, 2012) and then adopted the Destrieux Atlas (Destrieux et al., 2010) and Desikan-Killiany Atlas (Desikan et al., 2006) for ROI labeling.
3.3. Generation of functional connectivity and structural connectivity
For each subject, the whole brain is divided into 148/68 (148 for Destrieux Atlas and 68 for Desikan-Killiany Atlas) ROIs and represented as a network with 148/68 nodes. Averaged fMRI signal was calculated for each brain region and normalized by the standard Z-score normalization (Jain et al., 2005) formulated as:
| (1) |
where fi is the averaged fMRI signal of brain region i, fμ and fσ are the mean and the standard deviation of all 148/68 averaged fMRI signals. There exist several measurements to represent pair-wise relationship between two fMRI derived BOLD signals, such as correlation (Zhu et al., 2014b), partial correlation (Marrelec et al., 2006) and covariance (Challis et al., 2015). Since how to effectively represent the functional relationships among brain regions is still an open research area, in this work, we adopted four different measures that have been used in the field (Table 1) to construct functional connectivity (FC, denoted as F = [Fi, j] ∈ RN×N) including: (1) Pearson correlation coefficient (PCC), (2) Sparse inverse covariance estimation with the graphical lasso (Sparse ICOV), (3) binarized FC and (4) threshold FC. Pearson correlation coefficient (PCC) between the BOLD time series of two regions of interest derived from resting state fMRI data is the most used functional measurement to estimate functional connectivity (Batista-Garciá-Ramo and Fernañez-Verdecia, 2018). Partial correlation provides a convenient graphical representation for functional interactions. In this work, we used sparse inverse covariance estimation with the graphical lasso (Sparse ICOV) (Friedman et al., 2008) to capture the partial correlations. In Friedman et al. (2008), the sparse inverse covariance matrix is estimated by maximizing the L1 penalized log-likelihood of the observed data with assumption of Gaussian distribution. In this paper, for each subject, we apply the graphical lasso method for learning individual sparse functional connectivity F. Let gt,i be the fMRI signal of brain region i at time t for one subject. Denote by G = [gt,i] ∈ RT×N the fMRI signals over N regions spanning time T. Assume that the tth sample gt = [gt,1 , … , gt,N]T ∈ RN is drawn i.i.d. from some Gaussian distribution with the precision matrix F for encoding the conditional independencies between any two ROIs. The empirical sample covariance is:
| (2) |
where is the mean of T samples. The optimization problem of the graphical Lasso is
| (3) |
Table 1.
Multiple types of FC measures.
| Methods | Formula |
|---|---|
| PCC | |
| Sparse ICOV | |
| Binary FC | 1. 2. |
| Threshold FC | 1. 2. |
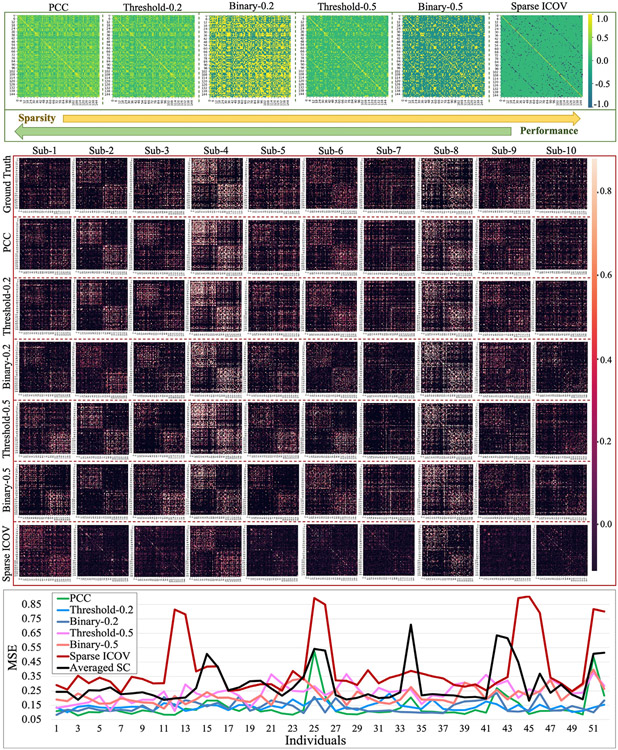
Where ρ is the regularization parameter of the L1 regularization to control the sparsity of F. Binary FC and Threshold FC are another two widely used strategies to control the susceptibility to noise (van den Heuvel et al., 2017). We applied our proposed method on these multiple types of FC measures, and the prediction results of structure connectivity are summarized in Section 4.4 (Fig. 8).
Fig. 8.
We adopted multiple types of FC measures for SC prediction. These measures are: (1) Pearson correlation coefficient (PCC), (2) Sparse inverse covariance estimation with the graphical lasso (Sparse ICOV), (3) binarized FC, and (4) threshold FC to generate FC (Section 3.3). For binarized FC and threshold FC, we set two different thresholds – 0.2 and 0.5. The first block shows the 6 FCs of one randomly selected subject. The second block shows the predicted SCs of the same 10 subjects used in Fig. 3(a2). For each subject in the testing dataset, we calculated MSE of all the 6 predicted SCs and showed the results by line chart in the third block.
The structural connectivity (SC) was created in terms of fiber counts, denoted as S ∈ RN×N. Si,j ∈ R is the number of fibers connecting brain regions i and j. Then, we conducted normalization of S using (4) and (5).
| (4) |
| (5) |
Sμ and Sσ are the mean and the standard deviation of S. Because the fiber count can be a value from zero to a few thousands, which often follows a skewed distribution. Log transformation can equalize the standard deviations and make the distribution of the sample mean more consistent with a normal distribution (Curran-Everett, 2018). Therefore, we first used log transformation to shrink the range of the fiber counts by (4) and then used (5) for normalization.
3.4. Method overview
We proposed a Multi-GCN based GAN (MGCN-GAN) model to generate individual SC from the corresponding FC. Similar to vanilla GAN (Goodfellow et al., 2014; Hong et al., 2019), MGCN-GAN is built on two components, i.e., generator and discriminator. To capture the highly complex relationship between SC and FC at the connectome level, we used multi-layer GCN architecture (Section 3.5) to design the generator and discriminator, namely Multi-GCN based generator and single-GCN based discriminator, respectively (Section 3.6). Given an individual SC and the associated FC, the generator is trained to create real-like individual SC by competing with the discriminator based on an adversarial training scheme. The specific training steps are shown as follows: (i) FC is used as initial topology of brain network as well as features associated with the nodes; (ii) based on current topology, different GCN components of generator map the FC to different feature spaces to explore the latent relationship between SC and FC, and each GCN component outputs one feature matrix; (iii) all the output feature matrices are combined by learnable coefficients to generate the predicted SC in current iteration; (iv) discriminator acts as a classifier to differentiate the input SC as real SC (real samples) from the predicted SC (fake samples) generated by the generator; (v) the topology of the generator is updated by the predicted SC in the next iteration. Given the training data consisting of FC samples and their corresponding real SC samples, the whole model is trained based on the proposed SP loss function (Section 3.7).
3.5. Graph convolutional network (GCN)
In many applications, data are generated from non-Euclidean domains and represented as graphs with complex interdependency and relationships between graph nodes. The complexity of graph data has imposed significant challenges on the existing deep learning algorithms, such as CNN model. Graph convolutional network (GCN) (Kipf and Welling, 2016; Wu et al., 2020; Zhang et al., 2020c) extends traditional CNN by applying convolutional operations on graph-based instead of Euclidean-based neighbors and is essential to various applications. In this work, to represent the latent interactions between brain SC and FC, we adopt a multi-layer GCN architecture to build the proposed MGCN-GAN model. For the ease of better understanding GCN architecture, we first introduce the notations of a graph and the graph convolution operation used in this work.
Graph.
Let 𝓖 = (𝓥, 𝓔) to be an undirected graph, where 𝓥 = {v1, v2, ⋯ , vn} is a set of vertices and 𝓔 = {ei,j∣i, j = 1, 2, ⋯ , n} is a set of edges. If there exists an edge connecting two vertexes vi and vj, then ei,j > 0, otherwise, ei,j = 0. Each vertex vi can have its own attributes (features) which can be represented by a vector xi ∈ R1×d, d is the dimension of the attributes (features). 𝓧 = [x1; x2 ; ⋯ ; xn] ∈ Rn×d is the feature matrix of graph 𝓖. The topology of 𝓖 can be represented by a weighted adjacency matrix 𝓐 = [ai,j] ∈ Rn×n, for all i, j, ai,j = ei,j. Thus, 𝓖 also can be represented by 𝓖 = (𝓐, 𝓧).
Graph Convolution Operation.
As shown in Shuman et al. (2013), the traditional convolution operators can be generalized to the graph setting by defining filters in the graph spectral domain. For a graph 𝓖 = (𝓐, 𝓧) with the adjacency matrix 𝓐 = [ai,j] ∈ Rn×n and node-wise feature matrix = [x1; x2; ⋯ ; xn] ∈ Rn×d, its normalized graph Laplacian is defined as = , where IN is the identity matrix and 𝓓 = ∑ai,j is the diagonal degree matrix. In general, the graph spectral convolution can be carried out by a convolutional network with convolutional layers of the polynomial form. For example, a two-layer GCN was formulated as in Kipf and Welling (2016), where is the Laplacian transformation of 𝓐. In our previous work Zhang et al., 2019a), we compared with other three different Laplacian transformations of 𝓐: 1) , 2) , and 3) and found that and give similar performance. Therefore, in this work we directly used the functional connectivity to initialize the adjacency matrix without using Laplacian transformation, the reasons are as follows: (1) compared to , needs less computational cost; 2) to infer the reliable relationship between structural and functional connectivity, using the original FC matrix may be more appropriate than applying extra transformation on FC.
Based on above discussion, the convolutional process of multi-layer graph convolutional network can be formulated as (6) and (7):
| (6) |
| (7) |
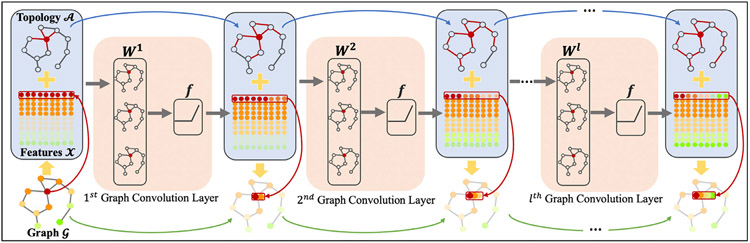
where σ is the nonlinear activation function, Hl is the output of the lth convolution layer, Wl ∈ RFi×F0 is the weight matrix, Fi is the input feature size and F0 is the output feature size. As shown in Fig. 2, Wl acts like a filter which selects related features from neighbors and defines how to combine these features. By stacking multiple graph convolutional layers, information from high-order neighbors (indirectly connected via other nodes) can be propagated along graph topology defined by the adjacency matrix 𝓐. In this work, we represented brain as a graph, and took the individual FC as the feature matrix i.e., 𝓧 = F and the initialized topology 𝓐0 = F. By conducting graph-based convolution via the proposed MGCN-GAN model, we iteratively updated the graph topology and learned the individual SC (Section 3.6).
Fig. 2.
Illustration of the graph convolution process. A graph 𝓖 can be represented by an adjacency matrix 𝓐 and a feature matrix 𝓧. The GCN takes the two matrices as input to conduct graph convolution. We used the red node as an example to show the convolution process. The neighbors with the same order have the same color in graph 𝓖. The colors of features are the same as the corresponding nodes. For the lth layer, the red edges of the input adjacency matrix 𝓐 indicate the neighbors that participate in the convolution process and the features of these activate neighbors are non-transparent.
3.6. Multi-GCN based GAN (MGCN-GAN)
Multi-GCN based Generator.
Inspired by the great success of CNN that uses multiple filters to identify different features, the proposed generator consists of multiple multi-layer GCNs. Different GCN components are designed for different feature spaces and each of them will learn a latent mapping from individual FC to its corresponding SC. Through paralleling multiple GCNs, the generator has the capacity to model complex relationship between FC and SC, which will be demonstrated by our experimental results in Section 4. Specifically, a generator that is composed by k multi-layer GCNs can be formulated by (8), (9) and (10),
| (8) |
| (9) |
| (10) |
where Gi, i = 1, 2, 3, ⋯ , k represents the ith GCN and ∥ denotes parallel operation. Each GCN takes the individual FC (F) as input and outputs the predicted individual SC. Then, we used the learnable coefficients θ = (θ1, θ2, …, θk) to fuse (⊕) these k predictions and obtained the final prediction Sp = g({Gi}, θ ). During the training process, topology T is initialized by F and iteratively updated by T = g({Gi}, θ ). After training, each multi-layer GCN learns an independent mapping that represents a potential relationship between the input FC and SC. In order to enhance the capability of generator, we paralleled multiple GCNs to capture the complex relationships between individual SC and FC.
Single-GCN based Discriminator.
In order to distinguish the two sets of graph data – real SCs and the predicted ones generated by the generator, the discriminator is composed by a multi-layer GCN, Gd = G(SC, I, Wd), and followed by two fully-connected layers. The input SC can be the real SC matrix – S, derived from diffusion MRI and predicted SC matrix – Sp, created by generator. They are treated as real and fake samples during the training process. Different from generator, we used identity matrix as input feature matrix for discriminator. This is because discriminator aims to learn the rules that can be used to decide whether the input connectivity matrix is a valid SC matrix, any external knowledge should be excluded.
3.7. Structure-preserving (SP) loss function
In the adversarial training scheme, the generator is optimized according to the feedback of discriminator. However, in this SC prediction task, the generator is trained to generate real-like individual SCs while the discriminator is trained to identify the real SCs from the predicted ones. The classification task of discriminator is much easier than the regression task of generator. Thus, the discriminator may easily differentiate real SCs from predicted SCs after a few training iterations and the generative adversarial loss would be close to 0, resulting in zero back-propagated gradients in generator. In such case, the generator cannot be optimized and will keep generating invalid SCs. To break this dilemma, maintaining the balance between generator and discriminator regarding the optimization capability during the entire training process is important. We designed a new structure-preserving (SP) loss function to train our discriminator and generator. The SP loss function is combined by three parts: mean squared error (MSE) loss, Pearson’s correlation coefficient (PCC) loss and GAN loss. It is formulated by (11), (12) and (13).
| (11) |
| (12) |
| (13) |
where the regularization parameters α and β are initialized by 1 and will gradually reduce to 0 later in the training process to let the model learn completely from the data. The three components of SP loss aim to guide the learning process from different perspectives. MSE loss (𝓛MSE) forces the predicted SC to be the same scale as real SC at element-wise level. It is designed to control the magnitude of the predicted SC. PCC loss (𝓛PCC) maximizes the similarity of overall pattern between predicted SC and real SC. It attempts to constrain the structure of the predicted SC. PCC loss is formulated by (13), which consists of two components: 1) brain-level PCC loss (𝓛PCC−b) and 2) region-level PCC loss (𝓛PCC−r). Brain-level PCC loss calculates the PCC between predicted SC matrix and real SC matrix, which measures the overall correlation between the predicted and real SCs. Region-level PCC loss calculates the correlation for each brain region (each row/column of the connectivity matrix), which measures the correlation of each brain region pairs of the predicted and real SCs. GAN loss (𝓛GAN ) effectively converts the regression problem to a classification problem and endows our model the power to implicitly learn the criterion, which is used to evaluate the quality of the predictions, from the data. It is formulated by (12), where 𝓓(S) and 𝓓(Sp) are the classification results predicted by discriminator. The adversarial GAN loss guides the generator to create real-like SC to fool the discriminator by assigning a “true” label to the predicted SC as well as guides the discriminator to differentiate the two kinds of inputs correctly.
4. Results
We applied our proposed MGCN-GAN to infer individual SC from the associated FC. For each sample (subject) in training dataset, the real SC is used as the real sample for discriminator ((11) and (12)) and as the ground truth for the generator at the beginning of the training process ((11) and (13)). The individual FC is used to initialize the adjacency matrix as well as to be the feature matrix ((8), (9) and (10)). During the adversarial training process, the topology of the graph is iteratively updated. The results of this work will be organized as follows: 4.1) introducing the experimental settings; 4.2) measuring the predicted SCs from three perspectives using two independent datasets; 4.3) evaluating the prediction performance with different atlases; 4.4) comparing the prediction performance of different types of FC measures; 4.5) evaluating different model settings including different GCN architectures, the learnable combination coefficients – θ, different loss functions; and 4.6) comparison with other widely used methods.
4.1. Experimental setting
Data Setting.
We conducted our experiments using two datasets: HCP and ADNI. For HCP dataset, we used 600 subjects for training and 464 subjects for testing. For ADNI dataset, we used 80 CN subjects for training and 52 CN subjects for testing. The details of the two datasets and the data preprocessing pipeline are introduced in Sections 3.1 and 3.2. For each subject, following the process in Section 3.3, we created the individual SC and FC.
Model Setting.
In this work, three two-layer GCNs are paralleled in generator. The model size of GCN components in generator is: G1 = (74, 148), G2 = (148, 148) and G3 = (296, 148), Gi = (F1, F2, ⋯ , Fl) represents an l-layer GCN and output feature dimension of the lth layer is Fl. The three GCNs are combined by the learnable coefficient θ which is initialized by θi = (0, 0, 0). We also tested different model architectures and different initializations of θ in Section 4.5. The discriminator is composed of one three-layer GCN followed by two fully connected layers. The model size of the GCN component is: Gd = (148, 296, 148), and the output feature dimensions of the two fully connected layers are 1024 and 2, respectively. For both generator and discriminator, activation function Relu and layernorm are used at each layer. The entire model was trained in an end-to-end manner. During the training process, the Adam optimizer was used to train the whole model with standard learning rate 0.001, weight decay 0.01, and momentum rates (0.9, 0.999).
4.2. Predicted structural connectivity
In this section, we used three strategies to evaluate the quality of the predicted SCs. Firstly, we plotted the predicted SC and real SC pairs to illustrate the overall similarity patterns via visual inspection. Secondly, we quantitatively measured the similarity between the predicted SCs with real ones using six measures (MSE, cosine similarity, PCC, mean degree, mean strength and mean clustering coefficient) that can comprehensively depict the similarity between our predicted SC and the real SC from three perspectives: magnitude, overall pattern and graph property. Thirdly, we examined the prediction performance of predicted SC by focusing on the overlaps of top connectivity between predicted SCs and the real SCs. The individual SCs and FCs used in this section were generated via Destrieux atlas.
4.2.1. Visualization of predicted SCs and real SCs
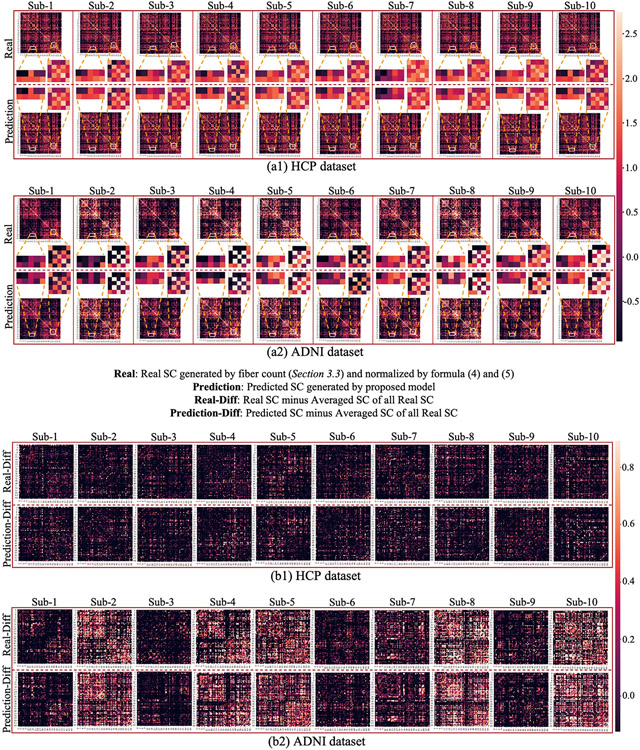
To visually evaluate the similarity between the predicted SCs and the real SCs, we randomly selected 20 subjects from HCP and ADNI datasets and showed the prediction results in Fig. 3. We used two ways to visualize the results: first, we directly displayed the predicted SC and the real SC of each subject in Fig. 3(a1, a2). To demonstrate the details of the prediction, we extracted two patches at the same location of the predicted SCs and real SCs and showed them in the middle. From the enlarged patches, we can see that our proposed model can predict not only the overall patterns, but also the subtle differences across individuals. Secondly, to better visualize the prediction result at individual level, we remove the consistent pattern across individuals by subtracting the population-averaged SC based on the matrices in Fig. 3(a1, a2) and showed the residual matrices in Fig. 3(b1, b2). We can see that our method effectively characterized and preserved the corresponding individual SC patterns during the prediction. Of note, all these predictions are based on individual FC, which suggests the existence of a common regulation between individual brain structural and functional architectures.
Fig. 3.
(a1, a2): Comparison of the predicted SCs and real SCs of 20 randomly selected subjects in HCP (a1) and ADNI (a2) datasets. For both datasets, we showed 10 real SC matrices (the first row) and the corresponding 10 predicted SC matrices (the second row). Each column belongs to the same subject. Two patches of the matrices are extracted from the same location and their enlarged patches are showed in the middle. (b1, b2): Comparison of the predicted SCs and real individual SCs after subtracting the population-averaged SC. To better visualize the individual variability, the population-averaged SC was subtracted from each of the forty matrices in (a1) and (a2). The brain connectivity was generated via Destrieux atlas.
4.2.2. Quantitatively measuring the similarity between predicted SCs and real SCs
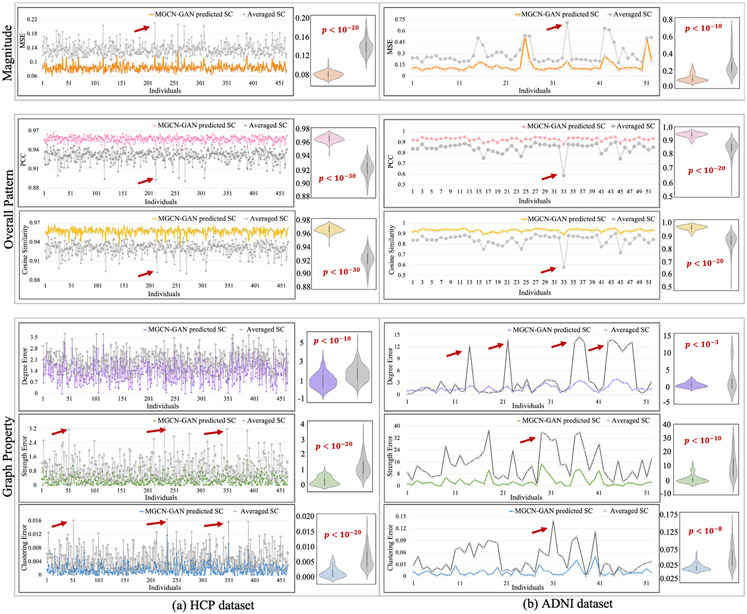
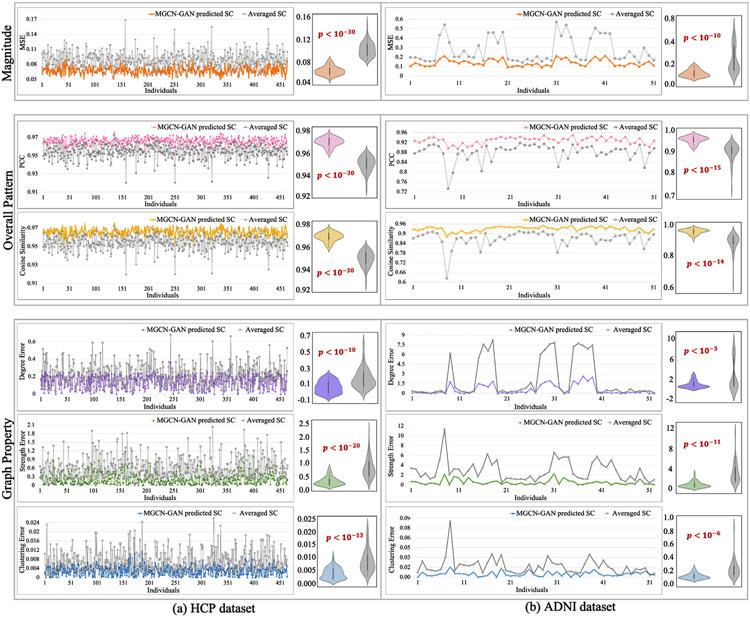
We quantitatively measured the similarity between the predicted SCs and real SCs from three perspectives: magnitude, overall pattern and graph property. Specifically, we adopted six measures in total, including MSE for magnitude, cosine similarity and PCC for overall pattern, and mean degree, mean strength and mean clustering coefficient for graph property. In graph theory, the mean degree is the average of the degrees (the number of edges connected to a node) of all the nodes, which is a widely used measure for network density (Rubinov and Sporns, 2010). The strength of a node in a graph is defined as the increase in the number of connected components in the graph upon removal of the node, which measures the vulnerability of the graph (Gusfield, 1991). The mean clustering coefficient for the graph reflects, on average, the prevalence of clustered connectivity around individual nodes (Rubinov and Sporns, 2010). All the three graph measures are used to describe the overall characteristics of a network, such as segregation and integration (Rubinov and Sporns, 2010). In this work, we calculated two differences for each measure at individual level: one is the difference between our predicted SC and real SC, and the other is the difference between the population-averaged SC and the real SC. If our predicted SC is more similar to real SC than the averaged one, this represents our model is effective in characterizing individual-specific relationship between brain structural and functional connectivity. We showed the two differences by line chart and displayed the distributions by violin plot. We also performed significance analysis with p-value calculated via one tail two sample T-test. The results are shown in Fig. 4 for both HCP (Fig. 4(a)) and ADNI datasets (Fig. 4(b)). We can see that the predicted SCs have significantly lower MSE, higher cosine similarity and PCC and smaller deviation of all the three global metrics compared to the averaged SC. We used red arrows to highlight some peaks in the line chart and these peaks represent some subjects that have large deviation from other subjects in terms of the related measures. Since all the samples are normal brains, the highlighted subjects are likely the outliers when constructing real SC. We have discussed these samples and the resulting correlation patterns between the two curves in the section of discussion.
Fig. 4.
We quantitatively measured the similarity between predicted SCs and real SCs from three perspectives (magnitude, overall pattern and network property) by using six measures (MSE, cosine similarity, PCC, mean degree, mean strength and mean clustering coefficient). We calculated two differences for each measure at individual level: one is the difference between our predicted SC and real SC, and the other is the difference between the population-averaged SC and the real SC. We showed the two sets of differences by line chart and displayed the distributions by violin plot. The significance analysis was also conducted with p-value calculated by one tail two sample T-test.
4.2.3. Connectivity level similarity between predicted SCs and real SCs
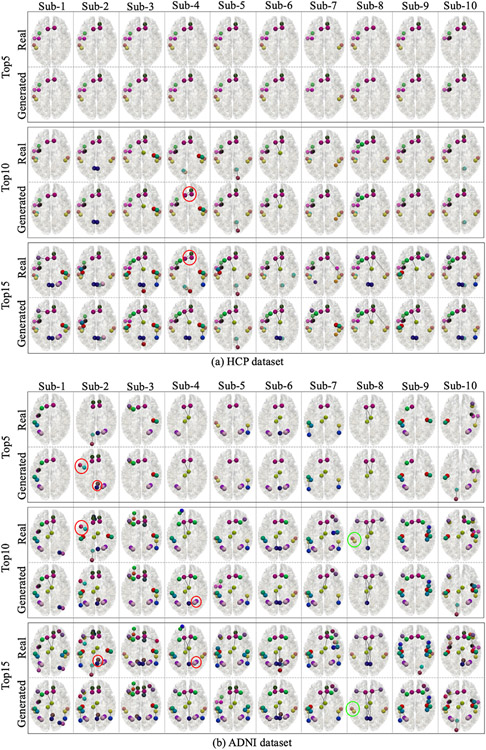
To further examine the prediction performance at connectivity level, we showed the top 5, top 10 and top 15 strongest connectivity in both real SCs and predicted SCs for the same 20 subjects in Fig. 5. We can see that due to the widely existing individual variations, the top connectivity of different subjects are different. However, for both datasets, the predicted SCs can capture most top 5 connectivity (missed 3 connections in two ADNI subjects). For top 10 connectivity, the predicted SCs in both datasets can also capture most of them. For top 15 connectivity, both datasets can capture at least 12 of them. Among these miss-predictions, there are two types of mistakes: the first type is the missing top connectivity. However, most of the missed connectivity can be found in the following top connectivity in the predicted SCs. For instance, we highlighted one example in Fig. 5 by green circle. The second type of mistakes is the redundant top connectivity. It means the predicted SCs contain some connectivity that are not among the real SCs. Similar to the missing cases, the redundant connectivity can also be found in the following top connectivity in real SCs. We also highlighted some examples in Fig. 5 by red circles. In addition, we found that all the missing or redundant SCs in our prediction results can be found in the top 25 connectivity in predicted SCs and the real SCs. In general, our model can robustly recover the strongest individual connectivity from the individual FC.
Fig. 5.
Comparison of the top connectivity in the predicted SC and real SC for the same 20 subjects showed in Fig. 3. For both datasets, we showed the top 5 (the first block), top 10 (the second block) and top 15 (the third block) strongest connectivity in real SC and predicted SC. The colorful bubbles and links represent different brain regions and structural connections. The colors used in this figure are the same with Destrieux atlas in FreeSurfer.
4.3. Evaluation of the predicted SC using different atlases
The generation of brain connectivity relies on the adopted brain atlas. To test the performance of the proposed model on different brain atlases, we used another widely used brain atlas – Desikan-Killiany atlas, to generate individual SCs and FCs and conducted experiments. The predicted SC and the real SC based on Desikan-Killiany atlas of the same 20 subjects used in Fig. 3 were shown in Fig. 6. We can see that the results using different brain atlases are consistent: our method can reliably characterize both the overall pattern and the subtle differences of individual SCs for both atlases with different number of brain regions.
Fig. 6.
(a1, a2): Comparison of the predicted SCs and real SCs of the same 20 subjects as used in Fig. 3. The brain connectivity was generated via Desikan-Killiany atlas. Each column belongs to the same subject. For each subject, we showed the real SC matrix in the first row and the predicted SC matrix in the second row. Two patches of the matrices are extracted from the same location and their enlarged patches are showed in the middle. (b1, b2): Comparison of the predicted SCs and real individual SCs after subtracting the population-averaged SC. To better visualize the individual variability, the population-averaged SC was subtracted from each of the forty matrices in (a1) and (a2).
To quantitatively measure the similarity between predicted SCs with real SCs based on Desikan-Killiany atlas, we calculated the MSE, cosine similarity, PCC, mean degree, mean strength and mean clustering coefficient for each subject in the testing dataset and showed the results in Fig. 7. Similar to the result using the other brain atlas in Fig. 4, the predicted SCs have significantly lower MSE, higher cosine similarity and PCC and smaller deviation of all the three global metrics compared to the averaged SC.
Fig. 7.
We quantitatively measured the similarity between the predicted SCs with real SCs (based on Desikan-Killiany atlas) from three perspectives (magnitude, overall pattern and network property) by using six measures (MSE, cosine similarity, PCC, mean degree, mean strength and mean clustering coefficient). We calculated two differences for each measure at individual level: one is the difference between our predicted SC and real SC, and the other is the difference between the population-averaged SC and the real SC. We showed the two sets of differences by line chart and displayed the distributions by violin plot. The significance analysis was also conducted with p-value calculated by one tail two sample T-test.
4.4. Evaluation of the predicted SC using different types of FC measures
In this work, we adopted the most widely used Pearson correlation coefficient (PCC) to generate FC. Yet, how to effectively represent FC is still an open research area and there exist different ways to define FC in the field. To examine the potential influence of different types of FC measures to our SC prediction, we applied our proposed model to four types of FC measurements (defined in Section 3.3): (1) Pearson correlation coefficient (PCC), (2) Sparse inverse covariance estimation with the graphical lasso (Sparse ICOV), (3) binarized FC and (4) threshold FC. For binarized FC and threshold FC, we set different thresholds – 0.2 and 0.5. Thus, there are 6 different FCs that need to be compared in this section. For each subject, we used Destrieux atlas along with the 6 different measures to generate SC and FCs. We randomly selected one subject to display its 6 FCs in the first block of Fig. 8 and showed the predicted SCs of the same 10 subjects used in Fig. 3(a2) in the second block. For each subject in the testing dataset, we calculated MSE of all the 6 predicted SCs and showed the results by line chart in the third block of Fig. 8. We found that different FC measures have slight influence on the prediction performance: as the sparsity of FC increases, the prediction accuracy will decrease. One possible explanation, as suggested by previous studies (Santarnecchi et al., 2014; Goulas et al., 2015), is that the performance degradation may be due to the overlook of potentially useful information when enforcing sparsity or thresholding.
4.5. Model evaluation
An effective model should have the capability to capture individual characteristics and avoid to being “trapped” in common SC patterns. To measure the effectiveness of a model, we proposed three measures:
MSE (Real, Prediction of same subject), which is the MSE between the real SC and predicted SC of the same subject. This measure directly evaluates the similarity between the real SC and the corresponding prediction. A smaller value indicates higher similarity. Thus, to generate reliable SC, this measure should keep decreasing before converged.
MSE (Real, Prediction of different subjects), which is the MSE between the prediction and the real SC of different subjects. A reliable prediction should avoid being “trapped” in common SC patterns at population level. Therefore, this measure is expected to keep increasing during the training process.
MSE (Real, Prediction of different subjects) – MSE (Real, Prediction of same subject), which is the difference of the above two measures and an increasing value is expected.
In this section, using the three measures we evaluated different model settings including different GCN architectures, the learnable combination coefficients – θ, and different loss functions.
4.5.1. Evaluation of different GCN architectures
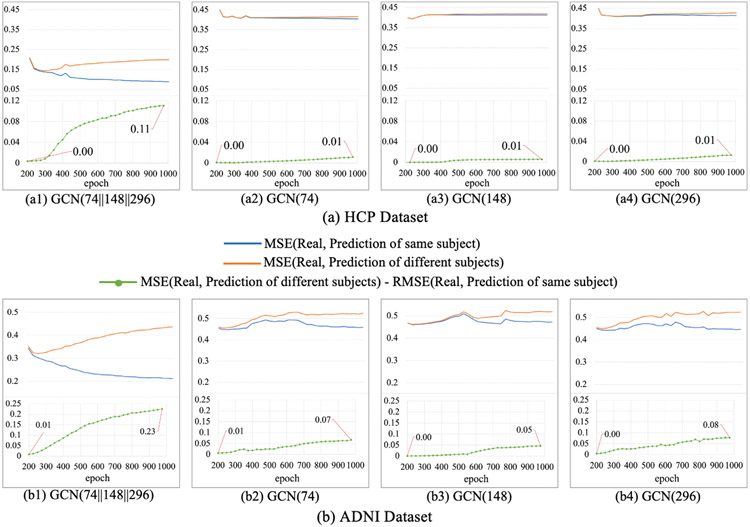
The generator was built on multiple GCNs, in order to verify the necessity of multi-GCN architecture, we conducted experiments to compare the performance of different generator architectures and showed the results in Fig. 9. We can see that, for predicted SCs generated from multi-GCN generator in both datasets (a1 and b1), the MSE (Real, Prediction of same subject) keeps decreasing and the MSE (Real, Prediction of different subjects) keeps increasing. For predicted SCs generated from single-GCN generator in both datasets (a2-a4, b2-b4), the difference between trajectories of MSE (Real, Prediction of same subject) and MSE (Real, Prediction of different subjects) is much smaller and the MSE (Real, Prediction of different subjects) – MSE (Real, Prediction of same subject) only has slight increase. This result indicates that the predicted SCs generated from multi-GCN generator can efficiently learn the individual differences in SCs, while single-GCN generator only captures a common pattern at population level.
Fig. 9.
Results of different generator architectures for HCP dataset (a) and ADNI dataset (b). GCN(G1∥G2∥…Gk) represents the architecture of generator. The generator is composed of k two-layer GCNs, and the output feature dimension of the first layer of ith GCN is Gi.
4.5.2. Evaluation of the learnable combination coefficients
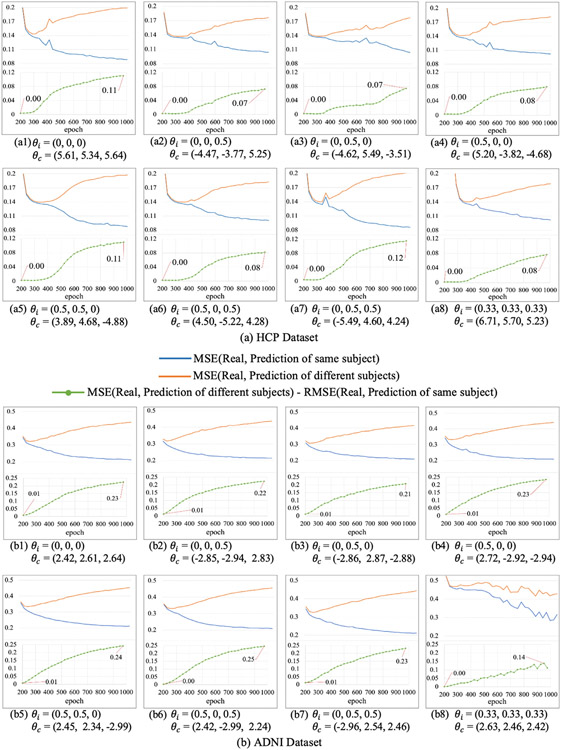
In our model, the multiple GCNs in generator are combined by learnable coefficients – θ. In order to test the influence of the coefficients to the proposed MGCN-GAN model, we initialized the coefficients with different values and compared the prediction performance. The results are shown in Fig. 10. In general, the initialization of the learnable coefficients has very slight influence on the prediction results. Moreover, the coefficient with different initialization θi always converge to stable coefficient θc which is approximately equal for different GCNs in generator. It suggests all the GCNs have similar contributions to the results. Like the filters in CNN, multiple GCNs with different size of output features can be flexible and efficient for characterizing the complex FC-SC mapping.
Fig. 10.
Results of different initializations of the learnable combination coefficients of HCP dataset (a) and ADNI dataset (b). θi is the initialization of the learnable coefficients and θc is the corresponding converged value.
4.5.3. Evaluation of SP loss function
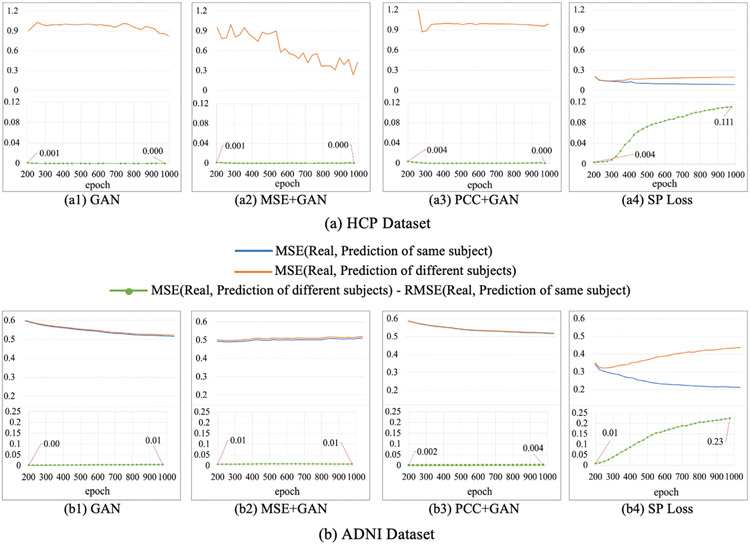
To demonstrate the superiority of the proposed SP loss function, we compared our SP loss with GAN loss, combination of GAN loss and MSE loss, and combination of GAN loss and PCC loss and showed the results in Fig. 11. From the results we can see that the gap between trajectories of MSE (Real, Prediction of same subject) and MSE (Real, Prediction of different subjects) using SP loss function (a4 and b4) is increasing as the training progresses, which means individual characteristics are gradually learned. While the trajectories of MSE (Real, Prediction of same subject) and MSE (Real, Prediction of different subjects) using other three loss functions (a1-a3, b1-b3) almost coincide during the training process and this implies that the other three loss functions may be limited in capturing potential subtle differences across individuals in the proposed model. The reason is that MSE only focuses on the element-wise similarity within the connectivity and overlooks the overall patterns. PCC has better performance in describing the overall connectivity patterns, but it may also overlook the connection magnitude across different connectivity and different individuals. However, both of MSE and PCC are important components in our designed SP loss to capture the subtle differences between real and predicted SCs
Fig. 11.
Results of MGCN-GAN with different loss functions on HCP dataset (a) and ADNI dataset (b).
4.6. Comparison with other widely used methods
To further demonstrate the effectiveness of the proposed MGCN-GAN, we compared the proposed model with three state-of-the-art models – CNN, multi-GCN, and CNN based GAN. In addition, for the comparison purpose we also included the linear regression as a baseline. For fair comparison, we used the same dataset to train and evaluate the four methods (HCP dataset, 600 training/464 testing). Since Section 4.5 showed that both MSE and PCC have contributions in capturing the subtle differences between real and predicted SCs, here we combined these two measures (MSE + PCC) as loss function in linear regression, CNN, and Multi-GCN, and used the proposed SP loss in CNN based GAN and the proposed MGCN-GAN. We adopted six types of measures (Section 4.2) to evaluate the performance of different models and summarized the results in Table 2. As shown in Table 2, we found: (1) compared to deep models, linear regression has worse performance for all the evaluation measures; (2) among different deep neural network architectures, GCN based approaches outperform CNN based methods when modeling brain networks in this application and (3) our proposed MGCN-GAN has the best prediction performance comparing to Multi-GCN (without GAN) and CNN based GAN. In general, this result demonstrates the superiority of graph-topology-based over the Euclidean-based convolution in brain connectivity analysis and the potential of using multiple GCNs to characterize complex feature space in GAN.
Table 2.
Comparison with other widely used methods.
| Model Setting |
Magnitude | Overall Pattern |
Graph Property |
||||
|---|---|---|---|---|---|---|---|
| Methods | Loss Function | MSE | PCC | Cosine Similarity | Degree error | Strength error | Clustering Coefficient error |
| Linear regression | MSE+PCC | 0.230±0.05 | 0.86±0.020 | 0.86±0.020 | 2.3±0.6 | 1.39±0.85 | 0.012±0.007 |
| CNN | MSE+PCC | 0.132±0.02 | 0.91±0.010 | 0.91±0.010 | 1.6±0.7 | 0.92±0.64 | 0.006±0.004 |
| Multi-GCN | MSE+PCC | 0.094±0.03 | 0.94±0.004 | 0.94±0.004 | 1.5±0.5 | 0.35±0.26 | 0.004±0.002 |
| CNN based GAN | SP Loss | 0.106±0.02 | 0.94±0.010 | 0.94±0.010 | 1.5±0.7 | 0.82±0.62 | 0.004±0.003 |
| MGCN-GAN | SP Loss | 0.084±0.01 | 0.96±0.005 | 0.96±0.005 | 1.3±0.6 | 0.29±0.25 | 0.002±0.001 |
5. Discussion
5.1. Outliers in normal brains
In this work, we used six measures to quantitatively evaluate the similarity between predicted SCs and real SCs, including MSE for magnitude, cosine similarity and PCC for overall pattern, and global metrics including mean degree, mean strength and mean clustering coefficient for graph property. The results are shown in Fig. 4. We can see that there is a correlated pattern between the two groups of MSE values. That is, for some samples that have large MSE between the population averaged SC and the real individual SC, the MSE between the predicted SC and real individual SC is also slightly larger. Because all the samples we used in this work are normal brains, if a subject has significantly large MSE between individual SC and averaged SC comparing to other subjects, it is likely that this sample is an outlier. In such case, the MSE between the predicted SC and the real individual SC will be large, too. Therefore, the plot of the two groups of MSE values shows a correlated pattern. Even so, the difference between predicted SC and individual SC is much smaller than the difference between averaged SC and individual SC. This result implies our method is effective in characterizing the true relationship between SC and FC at individual level.
5.2. Extending the learned mapping to MCI patients
In this work, our model is designed to infer the relationship between SC and FC on normal brains. To examine the potential influence when applying our method to disease populations, we used another 118 mild cognitive impairment (MCI) subjects (63 females, 55 males; 74.05 ± 8.29 years.) from ADNI dataset and conducted three experiments that used different clinical groups for model training: (A) 60 CN, (B) 60 MCI, and (C) the mix of 60 CN and 60 MCI. For each experiment the same testing dataset including 72 CN and 58MCI was applied. To compare the connectivity-level patterns of different groups, we calculated group-level MSE in Fig. 12. The mean value of each MSE matrix was reported in Fig. 12(D). From the results we can see that 1) if the training and testing process used the samples from the same clinical group, the prediction result tend to achieve better performance. For example, the experiment (A) used CN group for training, the MSE of CN group (0.073±0.0079) in testing is much smaller than MCI group (0.096±0.0068). Similarly, in the experiment (B) the MCI group obtained better testing performance than CN group. (2) when using a mixture of CN and MCI to train the model, the testing performance of both groups decrease compared to using single group for training. This result suggests that the FC-SC relationship of different groups might be different, and the proposed model is more effective in capturing the relationship of homogeneous samples.
Fig. 12.
We trained the model using (A) 60 CN, (B) 60 MCI, and (C) the mix of 60 CN and 60 MCI. For each model the same testing dataset (72 CN and 58MCI) was used. Each matrix in (A–C) represents the group-level MSE. The mean value of each MSE matrix was listed in (D).
5.3. Limitations and future work
In this work, we adopted PCC as the FC measurement to represent pair-wise relations between two brain regions. Therefore, the proposed MGCN-GAN model does not consider directional information in brain network mapping. However, our method can be flexibly extended to directed graphs by adopting an asymmetry adjacency matrix to define the convolution operations. In our future work, we plan to examine if introducing directional information can improve the SC prediction compared to using undirected brain connectivity. Another limitation of this work, which is also a general challenge suffered by deep neural networks, is the interpretability (Ghorbani et al., 2019) of the deep model. Indeed, several strategies have been proposed to interpret neural network predictions. For example, feature importance interpretation (Simonyan et al., 2013; Shrikumar et al., 2017; Sundararajan et al., 2017) tries to assign importance scores to each feature, and sample importance interpretation (Koh and Liang, 2017) will assign importance scores to each training example. However, these methods cannot be directly applied to this work due to the following reasons: (1) this work aims to infer the brain structure-function relationship at individual level. Each input sample provides unique individual information, and all the samples are therefore equally important. (2) for feature importance interpretation, a commonly used approach is to generate saliency maps to highlight unique features which can depict the visually alluring locations in the input image. However, for non-Euclidean graph data, the important features can be isolated nodes or a sub-network that are not continuous in spatial domain, which makes it difficult to distinguish them from noise. In general, further efforts are highly needed to explore appropriate strategies for interpretation of graph-based deep models, especially in brain network studies.
6. Conclusions
In this paper, we proposed a Multi-GCN based GAN (MGCN-GAN) model to generate individual SC from the corresponding individual FC. By adopting generative adversarial network (GAN), our proposed MGCN-GAN model can: (1) effectively handle brain’s distributed and heterogeneous pattern; (2) learn the complex relationship between brain structure and function by leveraging adversarial training scheme to avoid designing an explicit regression loss function. By embedding multiple GCNs into GAN framework, our MGCN-GAN model can be used to represent the complex direct and/or indirect interactions in brain network. To overcome the inherent unstable behavior of vanilla GAN, we proposed a novel structure-preserving (SP) loss function to simultaneously capture the overall SC patterns and subtle differences across individuals during the training process. We tested our model and SP loss on two independent datasets (HCP and ADNI), two different brain atlas (Destrieux Atlas and Desikan-Killiany Atlas, Section 4.3), and six different FC generation measures (Section 4.4). The results demonstrate that our proposed model can effectively predict individual SC from the corresponding individual FC, and thus imply that there may exist a common regulation between specific brain structural and functional architectures across individuals. All the codes of this paper have been released via GitHub (https://github.com/qidianzl/Recovering-Brain-Structure-Network-Using-Functional-Connectivity).
Acknowledgements
D Zhu was partially supported by National Institutes of Health (R01AG075582). L Wang was partially supported by National Science Foundation (DMS-2009689). We thank the ADNI and HCP projects for sharing their valuable MRI datasets.
Footnotes
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
CRediT authorship contribution statement
Lu Zhang: Methodology, Conceptualization, Writing – original draft. Li Wang: Formal analysis, Methodology. Dajiang Zhu: Writing – review & editing, Conceptualization, Funding acquisition.
References
- Achard S, Salvador R, Whitcher B, Suckling J, Bullmore E, 2006. A resilient, low-frequency, small-world human brain functional network with highly connected association cortical hubs. J. Neurosci 26, 63–72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Batista-Garciá-Ramo K, Fernañdez-Verdecia CI, 2018. What we know about the brain structure–function relationship. Behav. Sci 8, 39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Challis E, Hurley P, Serra L, Bozzali M, Oliver S, Cercignani M, 2015. Gaussian process classification of alzheimer’s disease and mild cognitive impairment from resting-state fmri. Neuroimage 112, 232–243. [DOI] [PubMed] [Google Scholar]
- Curran-Everett D, 2018. Explorations in statistics: the log transformation. Adv. Physiol. Educ 42, 343–347. [DOI] [PubMed] [Google Scholar]
- Desikan RS, Seģonne F, Fischl B, Quinn BT, Dickerson BC, Blacker D, Buckner RL, Dale AM, Maguire RP, Hyman BT, et al. , 2006. An automated labeling system for subdividing the human cerebral cortex on mri scans into gyral based regions of interest. Neuroimage 31, 968–980. [DOI] [PubMed] [Google Scholar]
- Destrieux C, Fischl B, Dale A, Halgren E, 2010. Automatic parcellation of human cortical gyri and sulci using standard anatomical nomenclature. Neuroimage 53, 1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diez I, Bonifazi P, Escudero I, Mateos B, Munõz MA, Stramaglia S, Cortes JM, 2015. A novel brain partition highlights the modular skeleton shared by structure and function. Sci. Rep 5, 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B, 2012. Freesurfer. Neuroimage 62, 774–781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedman J, Hastie T, Tibshirani R, 2008. Sparse inverse covariance estimation with the graphical lasso. Biostatistics 9, 432–441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghorbani A, Abid A, Zou J, 2019. Interpretation of neural networks is fragile. In: Proceedings of the AAAI Conference on Artificial Intelligence (pp. 3681–3688). volume 33. [Google Scholar]
- Gong G, He Y, Concha L, Lebel C, Gross DW, Evans AC, Beaulieu C, 2009. Mapping anatomical connectivity patterns of human cerebral cortex using in vivo diffusion tensor imaging tractography. Cereb. Cortex 19, 524–536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodfellow I, Pouget-Abadie J, Mirza M, Xu B, Warde-Farley D, Ozair S, Courville A, Bengio Y, 2014. Generative adversarial nets. Adv. Neural Inf. Process. Syst 2, 2672–2680. [Google Scholar]
- Goulas A, Schaefer A, Margulies DS, 2015. The strength of weak connections in the macaque cortico-cortical network. Brain Struct. Funct 220, 2939–2951 [DOI] [PubMed] [Google Scholar]
- Greicius MD, Supekar K, Menon V, Dougherty RF, 2009. Resting-state functional connectivity reflects structural connectivity in the default mode network. Cereb. Cortex 19, 72–78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gusfield D, 1991. Computing the strength of a graph. SIAM J. Comput 20, 639–654. [Google Scholar]
- Van den Heuvel MP, de Lange SC, Zalesky A, Seguin C, Yeo BT, Schmidt R, 2017. Proportional thresholding in resting-state fmri functional connectivity networks and consequences for patient-control connectome studies: issues and recommendations. Neuroimage 152, 437–449. [DOI] [PubMed] [Google Scholar]
- Hinton GE, Salakhutdinov RR, 2006. Reducing the dimensionality of data with neural networks. Science 313, 504–507. [DOI] [PubMed] [Google Scholar]
- Honey CJ, Sporns O, Cammoun L, Gigandet X, Thiran J-P, Meuli R, Hagmann P, 2009. Predicting human resting-state functional connectivity from structural connectivity. Proc. Natl. Acad. Sci 106, 2035–2040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hong Y, Hwang U, Yoo J, Yoon S, 2019. How generative adversarial networks and their variants work: an overview. ACM Comput. Surv. (CSUR) 52, 1–43. [Google Scholar]
- Huang J, Zhou L, Wang L, Zhang D, 2020. Attention-diffusion-bilinear neural network for brain network analysis. IEEE Trans. Med. Imaging 39, 2541–2552. [DOI] [PubMed] [Google Scholar]
- Iturria-Medina Y, Sotero RC, Canales-Rodríuez EJ, Alemá-Gómez Y, Melie–Garciá L, 2008. Studying the human brain anatomical network via diffusion-weighted mri and graph theory. Neuroimage 40, 1064–1076. [DOI] [PubMed] [Google Scholar]
- Jain A, Nandakumar K, Ross A, 2005. Score normalization in multi-modal biometric systems. Pattern Recognit. 38, 2270–2285. [Google Scholar]
- Jenkinson M, Beckmann CF, Behrens TE, Woolrich MW, Smith SM, 2012. FSL. Neuroimage 62, 782–790. [DOI] [PubMed] [Google Scholar]
- Kazi A, Shekarforoush S, Krishna SA, Burwinkel H, Vivar G, Kortuem K, Ahmadi SA, Albarqouni S, Navab N, 2019. Inceptiongcn: receptive field aware graph convolutional network for disease prediction. In: Proceedings of the International Conference on Information Processing in Medical Imaging. Springer; pp. 73–85. [Google Scholar]
- Kipf TN, & Welling M (2016). Semi-supervised classification with graph convolutional networks. arXiv preprint arXiv:1609.02907. [Google Scholar]
- Koch MA, Norris DG, Hund-Georgiadis M, 2002. An investigation of functional and anatomical connectivity using magnetic resonance imaging. Neuroimage 16, 241–250. [DOI] [PubMed] [Google Scholar]
- Koh PW, Liang P, 2017. Understanding black-box predictions via influence functions. In: Proceedings of the International Conference on Machine Learning (pp. 1885–1894). PMLR. [Google Scholar]
- Ktena SI, Parisot S, Ferrante E, Rajchl M, Lee M, Glocker B, Rueckert D, 2018. Metric learning with spectral graph convolutions on brain connectivity networks. Neuroimage 169, 431–442. [DOI] [PubMed] [Google Scholar]
- LeCun Y, Bengio Y, Hinton G, 2015. Deep learning. Nature 521, 436–444. [DOI] [PubMed] [Google Scholar]
- Marrelec G, Krainik A, Duffau H, Peĺe ģrini-Issac M, Leheŕicy S, Doyon J, Benali H, 2006. Partial correlation for functional brain interactivity investigation in functional mri. Neuroimage 32, 228–237. [DOI] [PubMed] [Google Scholar]
- Mišic B, Betzel RF, De Reus MA, Van Den Heuvel MP, Berman MG, McIntosh AR, Sporns O, 2016. Network-level structure-function relationships in human neocortex. Cereb. Cortex 26, 3285–3296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parisot S, Ktena SI, Ferrante E, Lee M, Guerrero R, Glocker B, Rueckert D, 2018. Disease prediction using graph convolutional networks: application to autism spectrum disorder and alzheimer’s disease. Med. Image Anal 48, 117–130. [DOI] [PubMed] [Google Scholar]
- Passingham RE, Stephan KE, Kötter R, 2002. The anatomical basis of functional localization in the cortex. Nat. Rev. Neurosci 3, 606–616. [DOI] [PubMed] [Google Scholar]
- Pernice V, Staude B, Cardanobile S, Rotter S, 2011. How structure determines correlations in neuronal networks. PLoS Comput. Biol 7, e1002059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petersen RC, Aisen P, Beckett LA, Donohue M, Gamst A, Harvey DJ, Jack C, Jagust W, Shaw L, Toga A, et al. , 2010. Alzheimer’s disease neuroimaging initiative (adni): clinical characterization. Neurology 74, 201–209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roth HR, Lu L, Liu J, Yao J, Seff A, Cherry K, Kim L, Summers RM, 2015. Improving computer-aided detection using convolutional neural networks and random view aggregation. IEEE Trans. Med. Imaging 35, 1170–1181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubinov M, Sporns O, 2010. Complex network measures of brain connectivity: uses and interpretations. Neuroimage 52, 1059–1069. [DOI] [PubMed] [Google Scholar]
- Santarnecchi E, Galli G, Polizzotto NR, Rossi A, Rossi S, 2014. Efficiency of weak brain connections support general cognitive functioning. Hum. Brain Mapp 35, 4566–4582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shrikumar A, Greenside P, Kundaje A, 2017. Learning important features through propagating activation differences. In: Proceedings of the International Conference on Machine Learning (pp. 3145–3153). PMLR. [Google Scholar]
- Shuman DI, Narang SK, Frossard P, Ortega A, Vandergheynst P, 2013. The emerging field of signal processing on graphs: extending high-dimensional data analysis to networks and other irregular domains. IEEE Signal Process. Mag 30, 83–98. [Google Scholar]
- Simonyan K, Vedaldi A, & Zisserman A (2013). Deep inside convolutional networks: visualising image classification models and saliency maps. arXiv preprint arXiv:1312.6034. [Google Scholar]
- Sirinukunwattana K, Raza SEA, Tsang Y-W, Snead DR, Cree IA, Rajpoot NM, 2016. Locality sensitive deep learning for detection and classification of nuclei in routine colon cancer histology images. IEEE Trans. Med. Imaging 35, 1196–1206. [DOI] [PubMed] [Google Scholar]
- Skudlarski P, Jagannathan K, Calhoun VD, Hampson M, Skudlarska BA, Pearlson G, 2008. Measuring brain connectivity: diffusion tensor imaging validates resting state temporal correlations. Neuroimage 43, 554–561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song X, Zhou F, Frangi AF, Cao J, Xiao X, Lei Y, Wang T, Lei B, 2021. Graph convolution network with similarity awareness and adaptive calibration for disease-induced deterioration prediction. Med. Image Anal 69, 101947. [DOI] [PubMed] [Google Scholar]
- Sporns O, Zwi JD, 2004. The small world of the cerebral cortex. Neuroinformatics 2, 145–162. [DOI] [PubMed] [Google Scholar]
- Sun L, Fan Z, Ding X, Huang Y, Paisley J, 2019. Region-of-interest undersampled mri reconstruction: a deep convolutional neural network approach. Magn. Reson. Imaging 63, 185–192. [DOI] [PubMed] [Google Scholar]
- Sundararajan M, Taly A, Yan Q, 2017. Axiomatic attribution for deep networks. In: Proceedings of the International Conference on Machine Learning (pp. 3319–3328). PMLR. [Google Scholar]
- Toussaint N, Souplet J-C, Fillard P, 2007. Medinria: medical image navigation and research tool by inria. In: Proceedings of the MICCAI’07 Workshop on Interaction in Medical Image Analysis and Visualization. [Google Scholar]
- Van Den Heuvel MP, Kahn RS, Goñi J, Sporns O, 2012. High-cost, high–capacity backbone for global brain communication. Proc. Natl. Acad. Sci 109, 11372–11377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Den Heuvel MP, Sporns O, 2011. Rich-club organization of the human connectome. J. Neurosci 31, 15775–15786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Essen DC, Ugurbil K, Auerbach E, Barch D, Behrens TE, Bucholz R, Chang A, Chen L, Corbetta M, Curtiss SW, et al. , 2012. The human connectome project: a data acquisition perspective. Neuroimage 62, 2222–2231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L, Gao Y, Shi F, Li G, Gilmore JH, Lin W, Shen D, 2015. Links: learning-based multi-source integration framework for segmentation of infant brain images. Neuroimage 108, 160–172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L, Thompson PM, Zhu D, 2019. Analyzing mild cognitive impairment progression via multi-view structural learning. In: Proceedings of the International Conference on Information Processing in Medical Imaging (pp. 656–668). Springer. [Google Scholar]
- Wang Z, Chen LM, Ne ģyessy L, Friedman RM, Mishra A, Gore JC, Roe AW, 2013. The relationship of anatomical and functional connectivity to resting-state connectivity in primate somatosensory cortex. Neuron 78, 1116–1126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu Z, Pan S, Chen F, Long G, Zhang C, Philip SY, 2020. A comprehensive survey on graph neural networks. IEEE Trans. Neural Netw. Learn. Syst 32 (1), 4–24. [DOI] [PubMed] [Google Scholar]
- Zamora-López G, Chen Y, Deco G, Kringelbach ML, Zhou C, 2016. Functional complexity emerging from anatomical constraints in the brain: the significance of network modularity and rich-clubs. Sci. Rep 6, 1–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang L, Wang L, Gao J, Risacher SL, Yan J, Li G, Liu T, Zhu D, Initiative ADN, et al. , 2021. Deep fusion of brain structure-function in mild cognitive impairment. Med. Image Anal 72, 102082. [DOI] [PubMed] [Google Scholar]
- Zhang L, Wang L, Zhu D, 2020a. Jointly analyzing alzheimer’s disease related structure-function using deep cross-model attention network. In: Proceedings of the IEEE 17th International Symposium on Biomedical Imaging (ISBI). IEEE; pp. 563–567. [Google Scholar]
- Zhang L, Wang L, Zhu D, 2020b. Recovering brain structural connectivity from functional connectivity via multi-gcn based generative adversarial network. In: Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer; pp. 53–61. [Google Scholar]
- Zhang L, Zaman A, Wang L, Yan J, Zhu D, 2019a. A cascaded multimodality analysis in mild cognitive impairment. In: Proceedings of the International Workshop on Machine Learning in Medical Imaging. Springer; pp. 557–565. [Google Scholar]
- Zhang X, He L, Chen K, Luo Y, Zhou J, Wang F, 2018. Multi-view graph convolutional network and its applications on neuroimage analysis for parkinson’s disease. In: In Proceedings of the AMIA Annual Symposium, 2018. American Medical Informatics Association Proceedings; (p. 1147)volume. [PMC free article] [PubMed] [Google Scholar]
- Zhang Y, Zhan L, Cai W, Thompson P, Huang H, 2019b. Integrating heterogeneous brain networks for predicting brain disease conditions. International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer; pp. 214–222. [Google Scholar]
- Zhang Z, Cui P, Zhu W, 2020c. Deep Learning On graphs: A survey. [Google Scholar]
- Zhao L, & Akoglu L (2019). Pairnorm: tackling oversmoothing in gnns. arXiv preprint arXiv:1909.12223. [Google Scholar]
- Zhu D, Li K, Faraco CC, Deng F, Zhang D, Guo L, Miller LS, Liu T, 2012. Optimization of functional brain rois via maximization of consistency of structural connectivity profiles. Neuroimage 59, 1382–1393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu D, Li K, Guo L, Jiang X, Zhang T, Zhang D, Chen H, Deng F, Faraco C, Jin C, et al. , 2013. Dicccol: dense individualized and common connectivity-based cortical landmarks. Cereb. Cortex 23, 786–800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu D, Li K, Terry DP, Puente AN, Wang L, Shen D, Miller LS, Liu T, 2014a. Connectome-scale assessments of structural and functional connectivity in mci. Hum. Brain Mapp 35, 2911–2923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu D, Li K, Terry DP, Puente AN, Wang L, Shen D, Miller LS, Liu T, 2014b. Connectome-scale assessments of structural and functional connectivity in mci. Hum. Brain Mapp 35, 2911–2923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu D, Zhang D, Faraco C, Li K, Deng F, Chen H, Jiang X, Guo L, Miller LS, Liu T, 2011. Discovering dense and consistent in the brain. In: Proceedings of the Biennial International Conference on Information Processing in Medical Imaging. Springer; pp. 97–110. [DOI] [PubMed] [Google Scholar]