Abstract
The HIV reservoir is a population of 1–10 million anatomically dispersed, latently infected memory CD4+ T cells in which HIV DNA is quiescently integrated into human chromosomal DNA. When antiretroviral therapy (ART) is stopped and HIV replication initiates in one of these cells, systemic viral spread resumes, rekindling progression to AIDS. Therefore, HIV latency prevents cure. The detection of many populations of identical HIV sequences at unique integration sites implicates CD4+ T cell proliferation as the critical driver of reservoir sustainment after a prolonged period of effective ART. Initial reservoir formation occurs during the first week of primary infection usually before ART is started. While empirical data indicates that both de novo infection and cellular proliferation generate latently infected cells during early untreated infection, it is not known which of these mechanisms is predominant. We developed a mathematical model that recapitulates the profound depletion and brisk recovery of CD4+ T cells, reservoir creation, and viral load trajectory during primary HIV infection. We extended the model to stochastically simulate individual HIV reservoir clones. This model predicts the first detection of HIV infected clones approximately 5 weeks after infection as has recently been shown in vivo and suggests that substantial, uneven proliferation among clones during the recovery from CD4+ lymphopenia is the most plausible explanation for the observed clonal reservoir distribution during the first year of infection.
1. Introduction
The HIV latent reservoir is a population of resting memory CD4+ T cells that contain HIV-1 DNA integrated within their human chromosomal DNA.1, 2, 3, 4 Resumption of HIV replication within one latently infected cell can spark systemic spread of virus, usually within days to weeks of antiretroviral therapy (ART) analytical treatment interruption (ATI).5, 6, 7, 8 The HIV reservoir size is stable over decades of ART9,10 and imperturbable, even if pharmacologically powerful agents are given that reactivate the virus in cell culture.11,12 Persistence of HIV latency therefore precludes cure and necessitates lifelong ART.
The latent reservoir is first seeded by de novo infection, which generates CD4+ T cells carrying distinct HIV DNA proviruses inserted into unique human chromosomal integration sites. Long-term studies of individuals on prolonged ART show that the reservoir often contains multiple cells carrying genetically identical HIV DNA provirus sequences,13, 14, 15, 16, 17, 18, 19 within the exact same human chromosomal integration site.18,20, 21, 22 The high abundance of these clones demonstrates that proliferation of infected memory CD4+ T cells plays a vital role in sustaining the HIV reservoir during ART.23 Most observed clones in the HIV reservoir are closely related to the HIV RNA sequences observed during the last year of untreated infection prior to ART,24 and sequence clones wax and wane in size during ART.25 Therefore, the process of individual clone establishment, expansion, and contraction, appears to be highly dynamic before and during ART. Yet, the contribution of de novo infection to the reservoir is likely inconsequential during effective ART.23,26
Less is known about the relative importance of de novo infection versus proliferation during the initial formation of the HIV reservoir. HIV latency is established very early during primary infection. In non-human primate models, reservoir seeding occurs within three days of viral challenge.27,28 In humans, initiation of ART within 10 days after estimated HIV infection leads to a reduced latent reservoir size29 and substantial delays in viral rebound after ATI30, 31, 32, 33 suggesting that the reservoir formation begins in the first week after HIV acquisition.32,34 Clones of infected cells have been detected in vivo in a cohort of untreated individuals approximately 5 weeks into primary HIV infection,35 which indicates that de novo infection and cellular proliferation are both involved in reservoir formation during early untreated infection, although the relative contributions of these two mechanisms over time is less clear.
During chronic ART, the clonal structure of the HIV reservoir appears to be highly organized. The reservoir is composed of a small number of high-rank, large clones and a far larger number of low-rank, small clones.23 This trend is evident when all HIV DNA is measured or when replication competent viruses are assessed alone.36 A similar structure is observed for clones within the entire T cell repertoire as defined by T cell receptor (TCR) sequencing,37, 38, 39 which suggests that HIV reservoir clone dynamics may be partially or fully governed by more general rules of CD4+ T cell immunity.40 The HIV reservoir's clonal structure is clearly evident after a year or less of ART initiation and has been observed in individuals who started ART soon after primary infection,18,22,33,38 further suggesting that viral and cellular dynamics during primary infection both contribute to its establishment.
Aside from viral infection and latent cell proliferation, early formation of the HIV reservoir may be impacted by several coupled, non-linear processes including a mounting immune response,41 CD4+ T cell activation,42 and target cell limitation,43 necessitating the use of mathematical models to decipher the sparse pre-treatment data available. In previous modelling studies, generation of latently infected cells during untreated primary infection was ascribed entirely to de novo viral infection of memory CD4+ T cells with subsequent conversion to a resting state.6,9,41,42 However, cellular proliferation is likely to contribute to reservoir formation in this time as well. Primary HIV infection is characterized by profound CD4+ T cell lymphopenia and peak viremia two weeks post-infection, followed by an incomplete, but brisk recovery in CD4+ T cell levels over the next four weeks. CD4+ T cell reconstitution is likely to be driven at least partially by homeostatic proliferation. Mouse and primate models of CD4+ T cell recovery following depletion conclude that homeostatic proliferation is “blind” at the cell subset level with overall competition between CD4+ and CD8+ T cells for limited resources and space during homeostatic proliferation44, 45, 46, 47, 48, 49, 50 but highly “uneven” at the single clone level with some TCR-defined clones outcompeting others due to variable binding affinity to self-antigens.33,45,51 If latent reservoir cells mimic overall CD4+ T cell behavior, it is possible that they are affected by these phenomena during recovery from lymphopenia as well.
To understand the relative contributions of de novo infection and cellular proliferation in early latent reservoir formation during primary infection, we developed models of HIV primary infection that selectively include and exclude blind and uneven proliferation of latently infected cells during recovery from CD4+ lymphopenia. Our method is comprised of three interconnected steps. First, we developed a group of 12 competing deterministic models to ascertain the role of blind T cell proliferation during primary infection. Underpinning all these models is the assumption that latently infected cells mirror the general behavior of CD4+ T cells. These models were fit to empirical viral load and CD4+ T cell data from 12 untreated individuals during primary infection,52,53 with the best model being selected via Akaike Information Criterion. Next, the best fitting model was simulated stochastically to investigate the role of uneven proliferation during the formation of the latent reservoir. Finally, the competing regimes of the stochastic simulations were evaluated using a resampling procedure of modelled data mimicking limited empirical data. The best fitting model output suggests that extensive proliferation of CD4+ T cells may drive the observed size and clonal structure of the HIV reservoir during the first several weeks of infection and up to one year post ART. Our model makes the empirically confirmed prediction that HIV sequence clones should be discoverable within a month of HIV infection despite the fact that most circulating HIV DNA sequences are in actively infected cells with unique non-clonal sequences.35
2. Methods and materials
2.1. Deterministic mathematical model
We developed several competing mathematical models to study the potential role of blind proliferation in the formation of the latent reservoir during primary HIV infection. All candidate models are derived from the following master system:
| [1] |
The infection is assumed to occur at some time point t0. The variable represents the concentration [cells/ L] of CD8+ T cells at time . The CD4+ T cells are divided into four compartments: non-susceptible, susceptible, latently infected and actively infected. We denote the concentration [cells/ L] of these at time by and respectively. For data fitting purposes, the reservoir of latently infected cells represents the total HIV DNA rather than the much smaller subset of genomically intact or replication competent sequences.54 Finally, represents the plasma viral load over time [copies/ L]. We use the term all infected cells to refer to the sum of actively and latently infected cells.
The viral component of the model builds upon the canonical model of viral dynamics by differentiating activated and non-activated CD4+ T cells.55, 56, 57 The virus is cleared at a rate . Actively infected cells produce virus at a rate , which describes the aggregate rate of constant viral leakage and burst upon cell death and die at a rate . The susceptible cells, , are infected by the virus at a rate [ L/virus -day]. We assume that a fraction, , of infection events generate latently infected cells and the remaining fraction, , leads to productively infected cells. Latently infected cells reactivate and become productively infected at a rate [cell/ L - day].
In contrast to previous infection models, we incorporated the blind proliferation hypothesis to explain cellular dynamics. We assumed that there is an inherent competition for resources between CD8+ and CD4+ T cells that impacts expansion and cell survival. We modelled this by logistically limiting the growth of the CD8+ T cells and the non-actively infected CD4+ T cell subsets by their sum. A similar mathematical formulation of blind homeostasis was considered in Ref. 47 to explain experiments of T cell reconstitution following CD4+ depletion in mice.45 The assumption of blind proliferation is justified by the observed CD8+ T cell expansion after CD4+ depletion in macaques,50 profound CD4+ T cell expansion after CD8+ T cell depletion58 and CD4+ T cell homeostatic proliferation after CD4+ T cell depletion.59 The turnover rates [cells/ L - day] are denoted by . The functional carrying capacity of the system is denoted by [cells/ L]. We considered a set of competing models that did not include this assumption by excluding the CD8+ T cell compartment entirely.
We evaluated the possible importance of several additional mechanisms. First, the killing of actively infected cells by CD8+ T cells at a rate , with or without the HIV antigen stimulation of CD8+ T cells at a rate as described by function . We considered two forms for , either linear or concentration dependent as given by equation.2
| [2] |
Second, we considered the possibility that the virus removes non-susceptible cells from their compartment at a rate [ L/virus -day]. A proportion undergoes bystander killing60 and the remaining fraction becomes susceptible, i.e. upregulates CCR5, as part of the mounting cellular immune response to the virus. Finally, we investigated the possible role of generation of non-susceptible cells by the thymus at a constant rate .
We assessed the above assumptions individually and in combination. Overall, we constructed 12 competing models. A detailed account of the model selection can be found in Supporting Information S1.
2.2. Model fitting and parameter estimation
We fitted our deterministic primary infection model (instances of equation1) to digitally extracted viral loads and matching CD4+ T cell counts from 12 participants from the Females Rising through Education, Support and Health cohort (FRESH).52,53 Our goal was to capture generalized trends in viral expansion, peak, contraction and setpoint, and CD4+ T cell contraction, re-expansion and re-establishment of a setpoint. We employed a nonlinear, mixed-effects modelling approach implemented in Monolix.61 Full details of model fitting can be found. We fixed 9 of 17 parameters from reported values in the literature and estimated the remaining 8. For fitting the deterministic model, we made a simplifying assumption that .
We also fixed the initial conditions of the different variables in our model. We set and . As we have no CD8+ T cell data, we have set , the mean pre-infection values reported in the RV217 study,62 for models requiring it. We have assumed that susceptible cells are represented primarily by CCR5+ T cells, which in this cohort are found to be between 1 and 12% of total CD4+ T cells in the plasma pre-infection.53 We therefore set to be 10% and to be 90% of total CD4+ T cells for all participants. The resulting carrying capacity was found by assuming steady state pre-infection such that .
The parameters and governing clone proliferation rates and the latency fraction are unknown. Therefore, we performed sensitivity analyses to examine the effects of these three parameters on the size of the latent reservoir throughout infection and its clonal structure at 50 days post-infection.
2.2.1. Model selection
For the best fit of each model, we computed the log-likelihood ()and the Akaike Information Criteria (AIC). AIC takes into account the number of independent parameters being estimated in a model and how well that model predicts the observed data. We assumed that models were equivalently supported by the data if the difference between their AIC values was less than two. The corresponding AIC scores for the 12 models considered is shown in Table 1.
Table 1.
Summary of deterministic model parameters and initial conditions. When estimated, the value shown is from the population level fits.
| Parameter | Value | Dimension | Source |
|---|---|---|---|
| −3.76 | days | estimated | |
| 500 | cells/ L | 62 | |
| cells/ L | fixed | ||
| cells/ L | fixed | ||
| cells/ L | fixed | ||
| 0.085 | cells/( L-day) | estimated | |
| 0.251 | cells/( L-day) | estimated | |
| 0.311 | cells/( L-day) | estimated | |
| 0.251 | cells/( L-day) | assumed equal to | |
| L/(virus-day) | estimated | ||
| 0.26 | NA | estimated | |
| NA | 63 | ||
| L/(virus-day) | estimated | ||
| 1 | day | 64 | |
| virus/(cell-day) | 65,66 | ||
| 23 | 67 | ||
| 6 |
2.3. Stochastic mathematical model of individual clones within the latent reservoir
We were principally concerned with whether and how the proliferation, specifically uneven proliferation, of latently infected cells affects formation and sustainment of the clonal structure of the HIV reservoir during primary infection. To study the clonal distribution of the latent reservoir, we used a stochastic model in-place of the latent compartment in equation.1 We let , where denotes the number of cell members in clone at time and denotes the number of distinct clones. In any short time-interval, four events can occur: a new distinct sequence can be introduced into the latent reservoir, an existing member of a clone can proliferate, a clone can contract in size or extinguish, or an existing member of a clone can convert to an actively infected cell and reactivate HIV.
Each new viral infection of a cell is associated with a unique combination of HIV DNA sequence, generated due to the error prone HIV reverse transcriptase, and unique human chromosomal integration site.19,22,68,69 Therefore, we assumed that each infection event that generates a latently infected cell introduces a new viral sequence. We also assumed that each new sequence population to have an initial size of , such that
| [3] |
with probability .
Each clone in the reservoir may die out stochastically or expand due to cellular proliferation. We referred to a clone with a single member, , as a singleton. Upon proliferation, a single copy of HIV DNA is created with the human DNA polymerase, generating equivalent HIV DNA sequences and human chromosomal integration sites in the two daughter cells. Therefore, we allowed each clone in the reservoir to grow () with probability and decline () with probability . When its HIV DNA sequence is considered to be part of a true clone in our model output.
The parameter represents the proliferation rate of the clone . Based on the observations that distinct T cell clones proliferate at vastly different rates in response to lymphopenia,45 and that the HIV reservoir is characterized by variability in clone size over 5-6 orders of magnitude,23 we allowed each clone to take on a different proliferation rate. Specifically, we defined uneven proliferation by assuming that the turnover rates are lognormally distributed, with corresponding mean and variance .
Our simulations were run in Matlab. We simulated the deterministic compartments using ode4570 and used a Gillespie tau-leap of the same time-step for the stochastic compartment.71 Each was updated simultaneously. Simulations were run in a liter of blood to simulate observed clinical values and to avoid numerical intractability of whole-body simulations.
3. Results
3.1. Blind proliferation between T cells explain the CD4+ reconstitution during primary infection
The most parsimonious model by Akaike Information Criterion (AIC) score is shown in Fig. 1 and mathematically here:
| [4] |
| [5] |
| [6] |
| [7] |
| [8] |
| [9] |
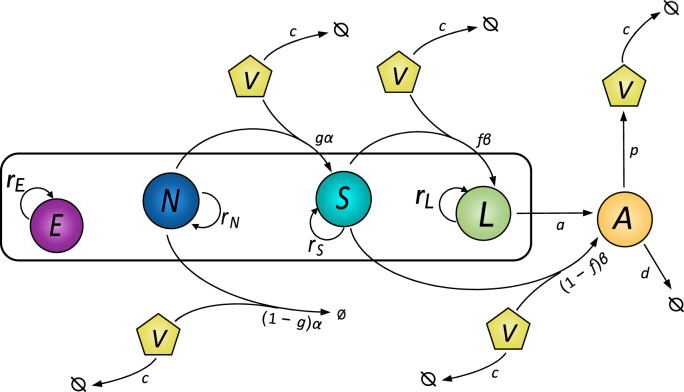
Fig. 1.
Most parsimonious mathematical model of primary HIV infection. represents CD8+ T cells. The CD4+ T cells are divided into four compartments: non-susceptible (), susceptible (), latently infected () and actively infected (). The virus is represented by .
Key assumptions required for model fit to data include blind proliferation of both CD4+ and CD8+ T cells, density-dependent virus induced bystander killing of non-susceptible CD4+ T cells, and density-dependent virus-induced activation of non-susceptible CD4+ T cells to susceptible CD4+ T cells via upregulation of CCR5+. CD8+ T cell expansion is driven solely by blind proliferation. Notably, models that did not include blind proliferation of both CD8+ and CD4+ T cells, model 1–3 and model 12, scored most poorly. Therefore, blind homeostasis was essential for replicating the partial CD4+ T cell recovery following lymphopenia. The non-susceptible compartment and activation parameter , was required to explain the initial rapid decline of the CD4+ T cells, as susceptible cells make a small proportion of the CD4+ T cell repertoire. As studies in humans with hyperacute infection have shown that 5–20% of activated CD8+ T cells during primary infection are responding to the virus53, we also simulated an alternative model that incorporates HIV-induced CD8+ T cell activation. This model also fitted data well but had a limited impact on latent reservoir dynamics as shown.
The population level parameters found under these assumptions are in Table 1. Certain solved model parameters correlated. Hence, we do not claim to have identified their absolute values. The individual parameter values used for each participant can be found.
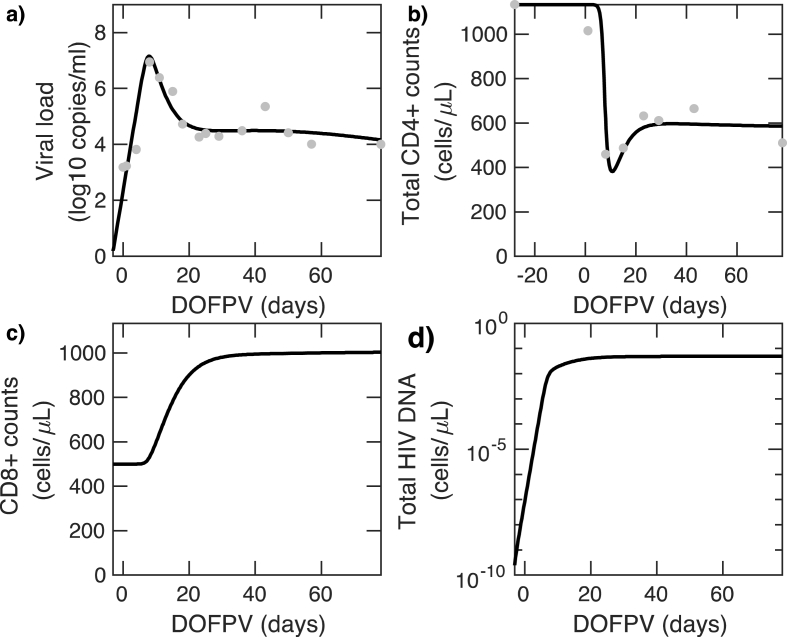
In Fig. 2, we show the model fit to data from a single study participant. For measurements of cellular concentrations, we scaled simulation results, which are run in 1 L of blood, to one and stated viral load results in . Simulation results from our model closely recapitulated longitudinal measures of viral load (Fig. 2a) and total CD4+ counts, which is the sum of , (Fig. 2b). The expansion behavior of the CD8+ T cell trajectories (Fig. 2c) while not available to us from this study, fell within the range observed during primary infection in other studies.62 The reservoir volume (measured as total reservoir HIV DNA in Fig. 2d) expands to levels observed during chronic ART treatment72 with an HIV DNA setpoint within 2 weeks of infection. Model fits for the other study participants are shown. Predicted trajectories for suggested that each of these cell populations equilibrates to a quasi-steady state 20–40 days after infection.
Fig. 2.
Longitudinal results of deterministic mathematical model fits (black line) to data from participant 11 (dots). a) viral load b) CD4+ T cells , c) CD8+ T cells d) Latent reservoir size. X-axis shown in days following onset of plasma viremia (DOFPV). Model fits for all study participants are shown.
3.2. Cellular proliferation is required to recapitulate the inverse correlation observed between the CD4+ T cell nadir and the HIV reservoir volume
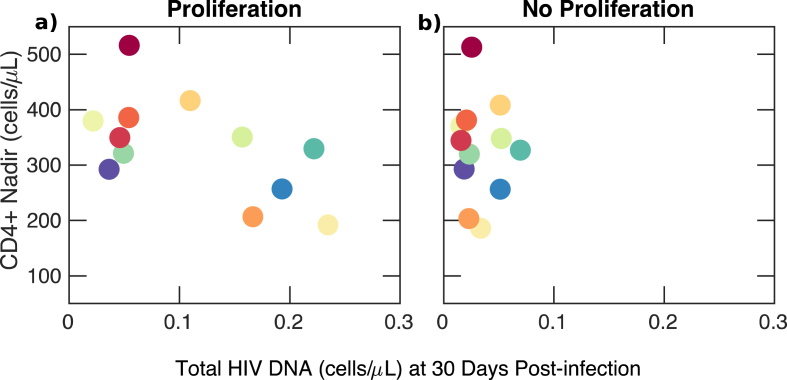
Previous studies have identified that levels of HIV-1 proviral DNA during chronic ART are negatively correlated with the CD4+ T cell nadir during primary infection73,particularly if ART is started during acute infection.74 In order to establish whether this correlation occurs during untreated primary infection in our simulations, we compared the CD4+ T cell nadir and size of the latent reservoir at 30 days post-infection under our deterministic model as shown in Fig. 3. Simulating all participants using parameter values derived from our individual fits, we identified that the CD4+ T-cell nadir as estimated from the model had a significant, negative correlation with the size of the latent reservoir 30 days post-infection (, p < 0.05). At later times during infection, the correlation weakened in agreement with.74 However, no correlation existed if reservoir proliferation was excluded from simulations (i.e. set ), which suggests that the observed correlation is mechanistically related to latent cell proliferation during primary infection.
Fig. 3.
Inverse correlation between CD4+nadir and latent reservoir volume at 30 days after primary infection in model simulations. a) An inverse correlation between the latent reservoir and CD4 + T cell nadir exists if the latent reservoir proliferates () (p < 0.05). Each color corresponds to model fitting to one of twelve participants in the FRESH cohort. b) Correlation between the latent reservoir and CD4 + T cell nadir disappears if the latent reservoir does not proliferate (). (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)
3.2.1. Individual clone expansion is predicted to occur immediately after reservoir formation
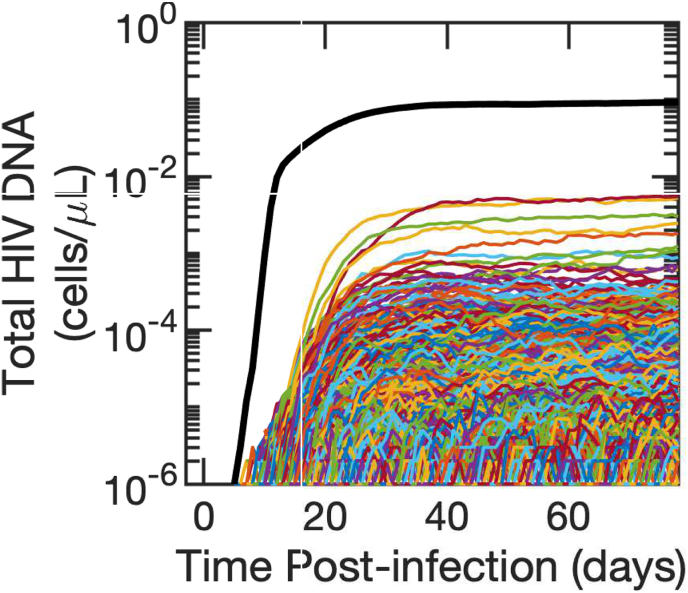
We next simulated our stochastic model with individual clones. A single realization of the latent reservoir is shown in Fig. 4. Expanding clones are observed in the latent reservoir less than a day after it is seeded, and new HIV DNA sequences are added to the reservoir continuously throughout untreated infection due to new infection events. The individual clones sum to a reasonable approximation of reservoir size, comparable to the deterministic model simulations in Fig. 2d.
Fig. 4.
Simulated single clone dynamics during primary HIV infection. Each clone is represented by a single-colored line. The sum of all clones is shown in black. The mean of , and the variance . Corresponding sensitivity analysis are depicted.
Assuming otherwise unchanged infection dynamics, HIV reservoir size could potentially be determined by three parameters in our stochastic model: the latency fraction, (fraction of newly infected cell entering latency), mean clone proliferation rate, , and variance of proliferation rates across clones, . We find that altering the latency fraction by several orders of magnitude had a negligible impact on the projected size of the reservoir. Increasing latent cell proliferation rates to twice those in other non-susceptible CD4 T cells resulted in several-fold larger reservoir volumes. Increasing the variance in proliferation rate across reservoir clones also generated larger reservoir volumes and increased the sensitivity of the model to latency fraction in a non-linear fashion. While moderate mean proliferation rates and variances lead to plausible latent reservoir sizes in stochastic model simulations, very large mean rates and/or variances may result in unrealistically large latent reservoirs comprising more than 50% of an individual's CD4+ T cell repertoire. Therefore, we were able to establish upper bounds on values for the mean and variance of latent cell proliferation rate.
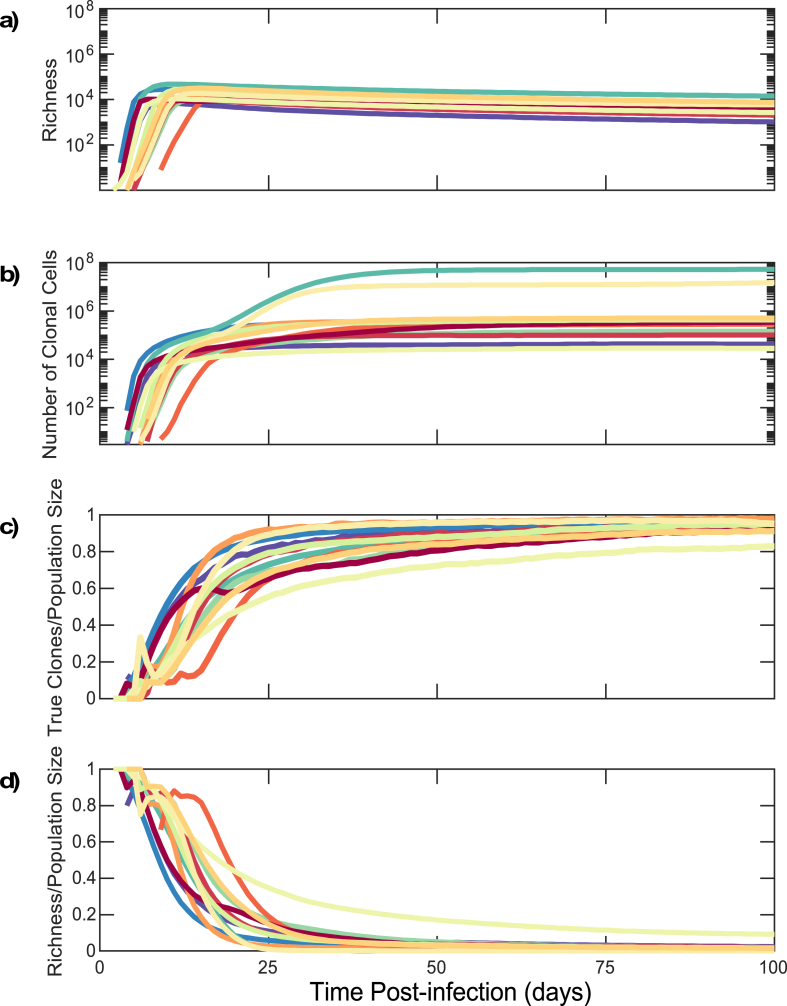
3.3. The latent reservoir reaches its highest sequence richness during the first 10 days of HIV infection
We next considered the dynamics of sequence richness of the latent reservoir. Sequence richness is the number of unique total HIV DNA sequences or chromosomal integration sites in the body and a marker of the number of latent cells generated by de novo HIV infection. Mathematically, we defined sequence richness at time , , as
| [10] |
As shown in Fig. 5a, in model realizations of all study participants, the reservoir rapidly accumulates richness during the first 10 days of infection due to unchecked viral replication leading to widespread infection of new cells with unique sequence and chromosomal integration sites. Following peak viremia, the richness declines gradually towards a steady state, as stochastic burnout of some clones, balances formation of new sequences due to new ongoing infection events.
Fig. 5.
Establishment of clonal predominance in the HIV reservoir within the first month of infection due to rapid proliferation of CD4+T cells from stochastic model simulations. (a) Richness of HIV DNA sequences within latently infected reservoir cells. (b) Number of HIV DNA reservoir sequences within proliferative CD4+ T cell clones. (c) Clonal sequence: total sequence population size ratio for latently infected cells. (d) Richness: total sequence population size ratio for latently infected cells. Each color corresponds to an individual as in Fig. 3. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)
3.4. Proliferative clones predominate in the latent reservoir within two weeks of primary HIV infection
In model simulations, expansion of sequence richness among reservoir cells terminates at the CD4+ T cell nadir 10 days post infection (Fig. 2b, d). This is followed by 2–4 weeks of rapid blind proliferation of CD4+ and CD8+ T cells to allow recovery from CD4+ lymphopenia. As part of this process, proliferation occurs among individual CD4+ T cell clones within the latent reservoir (Fig. 5b). Within two weeks of infection 12%–71% of the latent reservoir is predicted to consist of clones derived from proliferation; within 100 days of infection 82%–98% of the latent reservoir is predicted to consist of clones derived from proliferation (Fig. 5c).
We normalized sequence richness according to the total number of latently infected cells (Fig. 5d). The maximum value of this ratio approached 0.88–1.0 within the latent reservoir 10 days after infection as nearly all reservoir HIV DNA sequences are unique prior to clonal expansion. However, this ratio rapidly declined over the next 2 weeks to 0.5 by day 9–20 and 0.1 by day 18–88. This result implies that while viral infection establishes the reservoir extremely early after HIV transmission, the reservoir is maintained thereafter primarily by clonal cellular proliferation in response to CD4+ lymphopenia following peak viremia.
3.5. Proliferative reservoir clones are obscured by a larger population of non-clonal sequences within actively infected cells during untreated infection
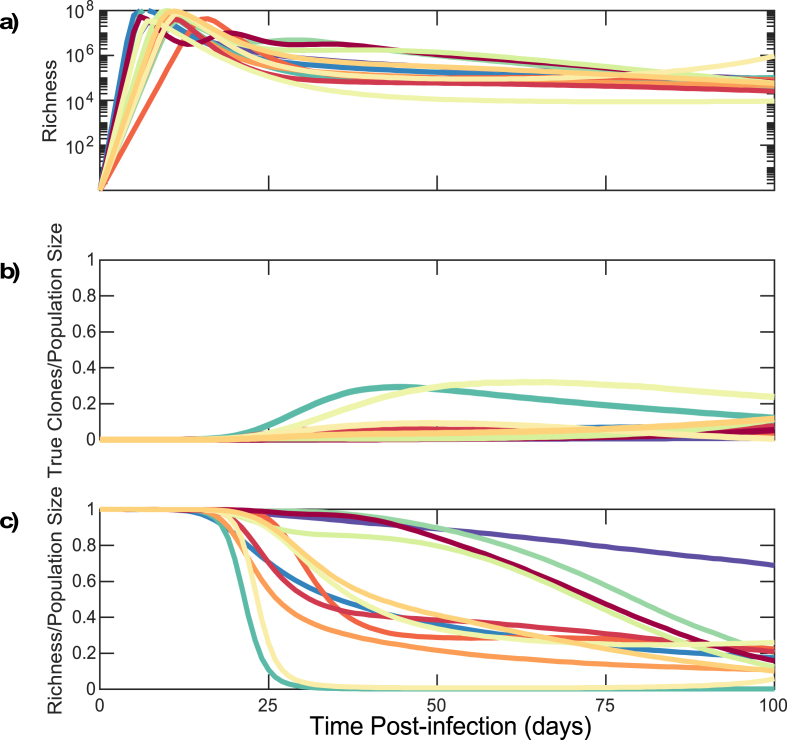
There are currently no experimental methods available to isolate latent reservoir HIV DNA sequences from sequences within cells harboring active HIV replication during untreated infection. Instead, the latent reservoir is obscured by a population of rapidly mutating sequences from actively infected shorter-lived cells, each with a unique genetic signature and chromosomal integration site.
However, we can distinguish latently infected cells from actively infected cells in our model. Therefore, we performed the above analysis inclusive of actively infected cells, each of which contributes a unique sequence singlet to the overall population of infected cells. Early during untreated infection, the number of actively infected cells outnumbers the number of latently infected cells by 1-3 orders of magnitude, such that observed richness is driven mostly by actively infected cells (Fig. 6a compared to Fig. 5a). During the first 10 days of infection, the proportion of clones among all sequences is extremely low (range: - ) (Fig. 6b).
Fig. 6.
HIV DNA reservoir sequences are obscured by a cloud of non-clonal sequences from actively infected cells during early untreated infection in stochastic model simulations. (a) Richness of HIV DNA sequences within all infected cells. (b) Clonal sequence: total sequence population size ratio in all infected cells. (c) Richness: total sequence population size ratio within all infected cells. Each color corresponds to an individual as in Fig. 3. Sensitivity analysis of the mean and variance of the turnover rate are shown. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)
Upon establishment of a viral load and reservoir steady state at 25–50 days, most HIV DNA sequences obtained from a clinical sample are truly unique and the ratio of clones to population size is still predicted to be relatively low (range: - , Fig. 6b), as actively infected cells still outnumber clonally expanding latently infected cells. Accordingly, the ratio of richness to the total population remains high Fig. 6c. Within 100 days of infection to of all infected cells are predicted to consist of clones Fig. 6b.
We examined whether these predictions were robust to uncertainty regarding key reservoir model parameters. Lower mean proliferation and higher variance in proliferation rate result in slight delays in the timing of clonal predominance within the HIV reservoir as does higher variance in turnover rates. While these parameters may indeed vary across infected persons, it is a generalizable property of our model output that a majority of the latent reservoir, but a minority of all infected cells, are composed of sequence clones within a month of infection.
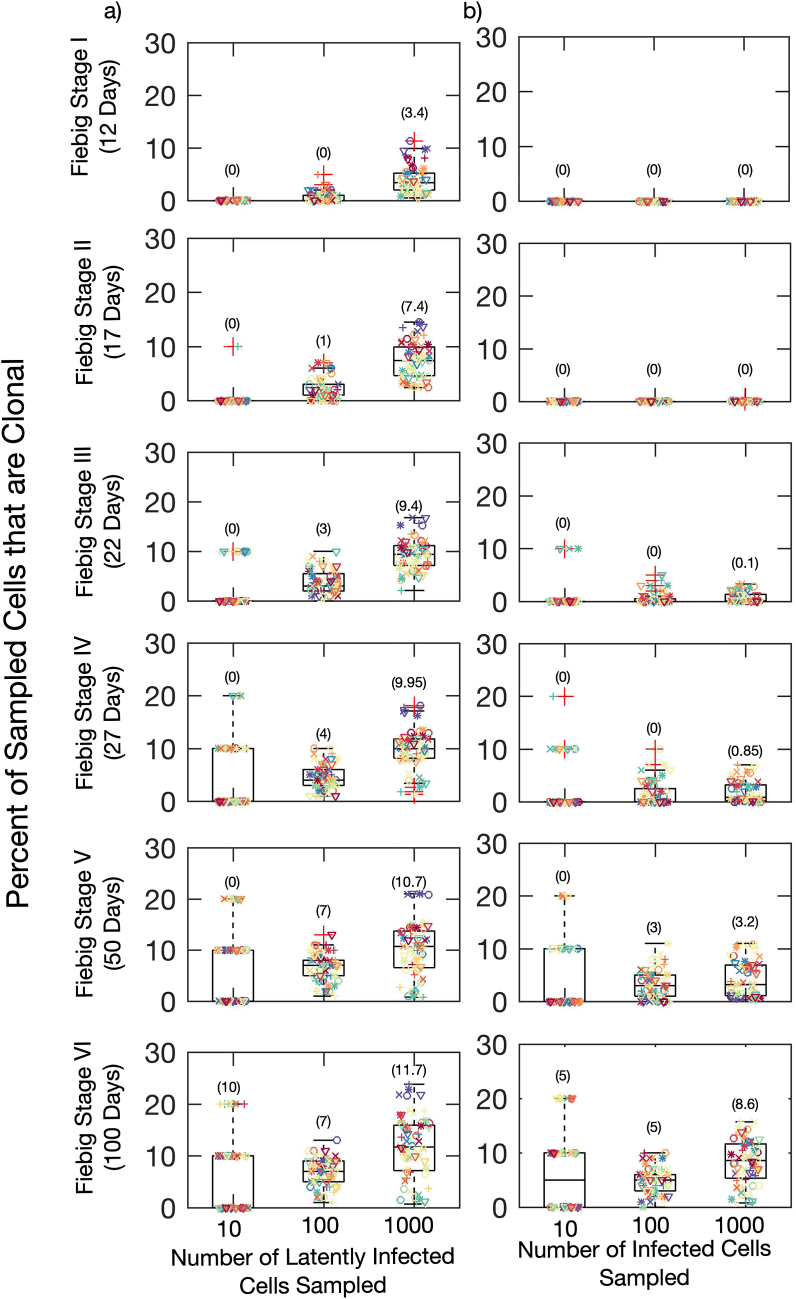
3.6. Adequate sequence sample size would ensure the detection of HIV DNA clones within 2–3 weeks of primary infection
Our model projected that by Fiebig stage IV (day 27), 70–95% of HIV DNA sequences within the reservoir were clonal (Fig. 5c). However, only 2–20% of total HIV DNA sequences were clonal (Fig. 6b) making the detection of clones in the reservoir challenging. Another barrier to detecting clonal HIV DNA from the reservoir is that the sequence sample size in most reservoir studies are low, varying between 10 in studies studying intact, replication-competent viruses and 100-1000 in studies of total HIV DNA.18,22,36,54 Therefore, in studies of ART-treated study participants, many observed singleton sequences may actually be members of large proliferative clones.23
3.7. Experimental data supporting the model predictions
In a recent study of untreated individuals, clones were not observed in 3 participants sampled during Fiebig III-IV stages of infection (days 22–27), but 4 participants sampled during Fiebig stage IV-V ( day 30–70 post infection) had at least one detectable HIV DNA clone based on chromosomal integration site analysis.35 The number of HIV DNA integration sites sampled in the Fiebig IV-V participants varied from 48 to 709. The mean percentage of clones among all sequences in the Fiebig stage V participants was extremely low (0.72%).
Results from this study are in keeping with our model's predictions (7). We performed sampling of HIV DNA sequences from model-generated data to identify sequence sample size required for the detection of clones at different times post-infection (corresponding to distinct Fiebig stages). The fraction of the sample identified as clonal is shown in Fig. 7.
Fig. 7.
Increased likelihood of detection of proliferative clones within the reservoir at later sampling times and greater HIV DNA sequence sample size from stochastic model simulations. Sampling from: a) Latently Infected Cells only, b) All Infected Cells. Each color represents simulation results for an individual as in Fig. 3 and each symbol represents one of five simulation results. The number in brackets represents the mean number of clones found across all simulations. The sensitivity on probability of clone detection on mean and variance of turnover rate is shown. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)
If technology existed to sample only HIV DNA sequences from the latently infected reservoir, then sampling of 1000 sequences would reliably detect clones by Fiebig I while sampling of 100 sequences would usually detect clones by Fiebig III (Fig. 7, left column). However, with sampling of all HIV DNA sequences (Fig. 7, right column), clones would almost never be evident during Fiebig stages I-III. A sequence sample size of 1000 would sometimes allow the detection of a low percentage of clones during Fiebig IV as in Ref. 35 and usually allows their detection by Fiebig stage V. A sequence sample size of 100 would reliably detect clones only after 2 months of untreated infection (Fiebig V) (Fig. 7).
These results are dependent on the mean and variance of turnover rates. Lower mean and variance of latent cell proliferation rates results in a lower probability of detection of clones 50 days after infection. Nevertheless, if any latent reservoir proliferation occurs our model predicted that proliferative clones should be possible from Fiebig Stage III of active infection given a sequence sample size of 100 HIV DNA sequences.
3.8. Uneven proliferation establishes the clonal distribution of the latent reservoir within 2–3 weeks of primary infection
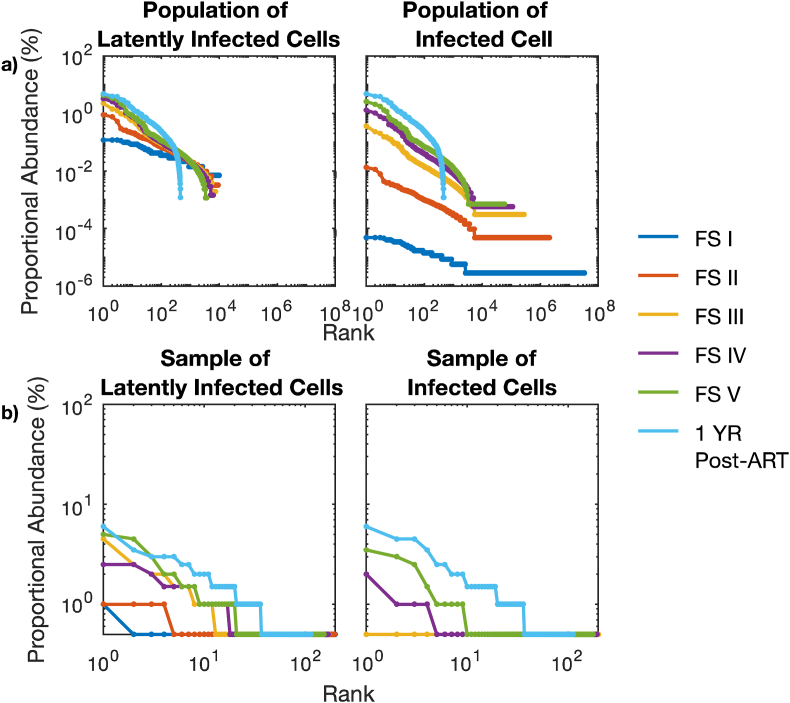
We demonstrated previously that the HIV reservoir has a fixed clonal structure consisting of a small number of large clones and a large number of smaller clones. The rank of each clone according to its size can be used to roughly estimate its size based on a power law relationship with a slope that approximates one.23
In Fig. 8 we compared the clonal distribution of the latent reservoir within a single individual at different Fiebig stages. Clonal structure within the simulated reservoir was evident by Fiebig stage II ( day 17), immediately after recovery from CD4+ T cell nadir (Fig. 8, orange). The uneven proliferation of individual HIV DNA clones in the reservoir was sufficient to explain the HIV reservoir structure. As infection progresses, the largest clones comprised a greater proportion of the reservoir (Fig. 8a, left). This remained true even if we considered the indistinguishable HIV sequences arising from actively infected cells. A long tail of singleton sequences, clones containing only one member , was observed at all Fiebig stages during untreated infection (Fig. 8a, right). The rank-order distributions were also somewhat steeper at later Fiebig stages as the richness of the reservoir decreased (Fig. 8a).
Fig. 8.
Rank abundance curves from stochastic model simulations for a single participant during sequential stages of early HIV infection. a) Rank abundance curves of all HIV DNA sequences in latently infected cells only (left) and all infected cells (right). b) Rank abundance curves of 200 randomly sampled HIV DNA sequences in latently infected cells only (left) and all infected cells (right). The impact of mean and variance of lymphocyte proliferation rates on reservoir clonal structure are shown.
When we simulated the reservoir after one year of ART started at Fiebig Stage V (100 days post-infection), the clonal distribution of the simulated reservoir after 1 year of effective ART treatment was similar to that of the point at which ART was initiated, though the singleton tail was effectively eliminated. Notably, the rank-order distribution was equivalent between all infected cells and latently infected cells after a year of ART due to the elimination of actively infected cells (Fig. 8a light-blue).
We next carried out an equivalent analysis assuming clinical sampling of 200 HIV DNA sequences (Fig. 8b). Only at Fiebig stages IV and V were multiple clones detected with sampling of sequences from all infected cells, despite our prediction that the clonal structure was established 2 weeks earlier. The distributions we observed after one-year of ART resembled clonal distributions observed during ART in study participants,23 exhibiting a tail of observed singletons which are in fact likely to be members of larger clones.
Varying the mean proliferation rate of clones did not impact the rank-order slope or the observed distribution of clone frequency assuming known sampling limitations. With no proliferation, our model projected that the reservoir would be composed entirely of singletons and the clonal distribution would not be distinct from a uniform distribution (Kolmogorov-Smirnoff test, p > 0.05). The clonal distribution contained a slightly greater proportion of large clones at a higher proliferation rate relative to a lower proliferation rate (Kolmogorov-Smirnoff test, p < 0.05). This distinction was lost with a sequence sample size of 200.
The clonal distribution became steeper with increasing variance of the proliferation rates due to the steeper rank abundance curves at higher variances (Kolmogorov-Smirnoff test, p = 0.05). This distinction was maintained even with a sequence sample size of 200.
4. Discussion
The primary obstacle to the eradication of HIV is a reservoir of latently infected resting memory CD4+ T cells.9,75 Our work developed the hypothesis that a steady HIV reservoir population is established during primary infection due to a rapid, blind and uneven CD4+ T cell proliferation. At the core of our assumptions is that the HIV infected reservoir cells behave according to rules governing overall T cell dynamics during recovery from lymphopenia.24
Our model generated realistic trajectories for HIV viral load, CD4+ T cell contraction and partial recovery, and CD8+ T cell count expansion during primary infection. The model also recapitulated the reservoir's early formation, its ultimate size and its clonal distribution. Model fits could be improved with complimentary CD8+ T cell data. Importantly, though further experimental verification is required to confirm our hypothesis, our model's results are consistent with recent data showing that HIV DNA clones become detectable in approximately 50% HIV infected individuals 1–2 months after primary infection.35
Sampling the reservoir during early infection is difficult for two reasons. First, most observed HIV DNA sequences are from actively infected cells that have a much shorter lifespan than reservoir cells, harbor truly unique HIV DNA sequences and cannot be discriminated experimentally from the reservoir-derived sequences.76 Second, current studies dramatically under sample the reservoir: during prolonged ART, sequences which are only observed once are likely to be members of large clones rather than truly unique.23 Despite these issues, our model predicted that repeated HIV DNA integration sites can sometimes be detected within the first 1–2 months of HIV infection, consistent with the results in Ref. 35. While doublets and triplets, clones with two or three members respectively, are only sporadically observed at these timepoints, even with large sample sizes, we predicted that by this timepoint, there was already a fully formed, mature HIV DNA reservoir with an organized clonal structure. In fact, the doublets and triplets are likely to represent extremely large clones whose size is obscured by under sampling, consisting of more than a million cells each. This signifies that certain clones may undergo roughly twenty divisions during the 2–3 weeks recovery period from CD4+ lymphopenia.
While observed heterogeneity in clone size are predicted by our model and may be linked mechanistically with known properties of homeostatic proliferation, it is also quite possible that some of the largest clones may be generated due to the recognition of a cognate antigen presented by HIV-infected cells or by cells infected with other ubiquitous chronic viruses such as cytomegalovirus or Epstein-Barr Virus. Recent data demonstrating antigen specific clones in the HIV reservoir indeed suggests that both mechanisms may be at play.77, 78, 79 It will be a critical though challenging goal for the field to distinguish the percentage of clones which emerge due to homeostatic versus antigen driven proliferation during different stages of reservoir establishment and sustainment. Notably, current technologies lack the ability to track viral antigen specificity for all infected CD4+ T cells. On the other hand, a T cell may have a TCR specific for a given antigen due to distant viral exposure and still undergo recent homeostatic proliferation.
Our conclusions demonstrate that cure interventions, even those given during primary infection, might face an enormous challenge. Even limited seeding of the reservoir will be followed by a period of cellular proliferation during recovery from the CD4+ T cell nadir that will expand the size of the reservoir 10-fold. Lymphocyte anti-proliferative agents have been proposed as a means to reduce reservoir size during chronic ART.80 While this approach might be considered in an adjunctive fashion during primary infection, the immunosuppressive features of these drugs raise concerns that they may hamper the long-term cytolytic immune response to HIV. Based on comparable experience following stem cell transplantation,80 it is also questionable whether these agents could sufficiently suppress the potentially powerful homeostatic forces underlying recovery from lymphopenia.
Our model does reinforce the utility of ART during the first week of acute HIV in limiting reservoir volume.34 Presumably, this intervention would limit the extent of reservoir seeding, and also limit the extent of CD4+ T cell nadir decline, thereby decreasing the extent of homeostatic proliferation required to reconstitute the overall CD4+ T cell population.
Several important limitations of our study are worth noting. First, while we establish that recovery from CD4+ lymphopenia and uneven proliferation are sufficient to generate the observed clonal structure of the HIV reservoir and argue that the reservoir may be formed rapidly during primary infection, key reservoir-sustaining events continue to occur through all subsequent stages of infection. While there is evidence to suggest that HIV infected cells proliferate and do so during untreated primary infection, further evidence is required to ascertain whether they undergo homeostatic and antigenic proliferation in the same way non-infected CD4+ T cells do. Our model is not intended to explain sustainment of a stable reservoir during chronic treated infection. HIV DNA clones wax and wane in size during chronic ART, which suggests that substantial dynamics exists within the reservoir years after recovery from lymphopenia.24 These clonal expansions and contraction may again relate to recognition of cognate antigen by certain clones rather than a homeostatic process24 though their survival does not seem dependent on cytotoxic T lymphocyte selection.81
Moreover, a majority of reservoir sequences observed during prolonged ART arise from timepoints immediately before ART initiation, suggesting that the biologic events which generate reservoir cells and large clones are highly dynamic and continue after primary infection.82,83 ART initiation is also followed by a surge in levels of activated, proliferating CD4+ T cells.84 This process could also further expand a pre-existing reservoir. Neither of these processes is mutually exclusive of extensive cellular proliferation as a driver of reservoir formation during primary HIV infection, and the latter has substantial parallels.
Second, in this study, we have focussed on the total HIV DNA, but only a small fraction of these sequences is replication-competent.85 As a result, the clones that have been discovered during early HIV infection are probably not replication competent. Nevertheless, viral rebound in patients who initiate ART after only days of infection proves that the replication-competent reservoir is created extremely early during primary HIV infection.30,31,86 Because replication-competent HIV periodically reactivates and is targeted by the immune system, and CD4 T cell proliferation is often not associated with viral reactivation,36,54,87,88 it remains unclear whether all conclusions drawn from modelling total HIV DNA during primary infection can be extrapolated to the replication-competent reservoir.
Finally, our most parsimonious model does not include an immune response to the virus during primary infection. Our objective was not to identify different drivers of viral load set-point or CD4+ T cell nadir, and thus we opted for a simpler model. In our model, the CD4+ and CD8+ T cell equation does not incorporate the possibility that as many as 5–20% of these cells may be reacting to HIV-infected cells and therefore have their proliferation governed by the HIV antigen abundance rather than the homeostasis or expansion due to exposure to other non-HIV antigens.53 However, we have performed deterministic simulations including CD8+ T cell activation which suggest that this effect is unlikely to negate the critical role of extensive restorative proliferation in rapidly restoring lymphocyte count following depletion.
In summary, we have explored the hypothesis that blind, uneven T cell recovery from CD4+ lymphopenia drives the bulk of early HIV reservoir generation. Future curative therapies will need to address the mechanisms that drive the expansion behaviors of individual T cell clones.
Author contribution
FATB, DB, JTS, MP conceived and presented the idea regarding the role of proliferation in structuring the clonal distribution of the latent reservoir. FATB, ERD and EFCO developed the model with feedback from DAS, DB and JTS. FATB tested the models and wrote all the code. FATB performed subsequent analysis. JTS and FATB wrote the manuscript. All authors discussed the results and approved the final manuscript.
Funding
JTS received funding from the NIH/NIAID grant UM1 AI126623.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
JTS, EDCO thank NIH (UM1 AI126623 & R01AI150500). DBR thanks the Washington Research Foundation, the UW/Fred Hutch Center for AIDS Research (AI027757), and the NIH (K25 AI155224). ERD thanks NCATS (KL2 TR002317).
Contributor Information
Florencia A. Tettamanti Boshier, Email: f.boshier@ucl.ac.uk.
Joshua T. Schiffer, Email: jschiffe@fredhutch.org.
Data availability
Empirical data was digitally extracted from publicly available paper. Code for simulations and plotting are available on github https://github.com/ftettamanti/HIV_LR_proliferation.
References
- 1.Josefsson L., von Stockenstrom S., Faria N.R., et al. The HIV-1 reservoir in eight patients on long-term suppressive antiretroviral therapy is stable with few genetic changes over time. Proc Natl Acad Sci USA. 2013;110:E4987–E4996. doi: 10.1073/pnas.1308313110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Finzi D., Hermankova M., Pierson T., et al. Identification of a reservoir for HIV-1 in patients on highly active antiretroviral therapy. Science. 1997;278:1295–1300. doi: 10.1126/science.278.5341.1295. [DOI] [PubMed] [Google Scholar]
- 3.Finzi D., Blankson J., Siliciano J.D., et al. Latent infection of CD4+ T cells provides a mechanism for lifelong persistence of HIV-1, even in patients on effective combination therapy. Nat Med. 1999;5:512–517. doi: 10.1038/8394. [DOI] [PubMed] [Google Scholar]
- 4.Chun T.W., Carruth L., Finzi D., et al. Quantification of latent tissue reservoirs and total body viral load in HIV-1 infection. Nature. 1997;387:183–188. doi: 10.1038/387183a0. [DOI] [PubMed] [Google Scholar]
- 5.Colby D.J., Trautmann L., Pinyakorn S., et al. Rapid HIV RNA rebound after antiretroviral treatment interruption in persons durably suppressed in Fiebig I acute HIV infection. Nat Med. 2018;24:923–926. doi: 10.1038/s41591-018-0026-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hill A.L., Rosenbloom D.I.S., Fu F., Nowak M.A., Siliciano R.F. Predicting the outcomes of treatment to eradicate the latent reservoir for HIV-1. Proc Natl Acad Sci USA. 2014;111:13475–13480. doi: 10.1073/pnas.1406663111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hurst J., Hoffmann M., Pace M., et al. Immunological biomarkers predict HIV-1 viral rebound after treatment interruption. Nat Commun. 2015;6 doi: 10.1038/ncomms9495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Williams J.P., Hurst J., Stöhr W., et al. HIV-1 DNA predicts disease progression and post-treatment virological control. Elife. 2014;3 doi: 10.7554/eLife.03821. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Siliciano J.D., Kajdas J., Finzi D., et al. Long-term follow-up studies confirm the stability of the latent reservoir for HIV-1 in resting CD4 + T cells. Nat Med. 2003;9:727–728. doi: 10.1038/nm880. [DOI] [PubMed] [Google Scholar]
- 10.Crooks A.M., Bateson R., Cope A.B., et al. Precise quantitation of the latent HIV-1 reservoir: implications for eradication strategies. JID (J Infect Dis) 2015;212:1361–1365. doi: 10.1093/infdis/jiv218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Archin N.M., Kirchherr J.L., Sung J.A.M., et al. Interval dosing with the HDAC inhibitor vorinostat effectively reverses HIV latency. J Clin Invest. 2017;127:3126–3135. doi: 10.1172/JCI92684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Shapiro M.B., Cheever T., Malherbe D.C., et al. Single-dose bNAb cocktail or abbreviated ART post-exposure regimens achieve tight SHIV control without adaptive immunity. Nat Commun. 2020;11:70. doi: 10.1038/s41467-019-13972-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Chomont N., El-Far M., Ancuta P., et al. HIV reservoir size and persistence are driven by T cell survival and homeostatic proliferation. Nat Med. 2009;15:893–900. doi: 10.1038/nm.1972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Cohn L.B., da Silva I.T., Valieris R., et al. Clonal CD4+ T cells in the HIV-1 latent reservoir display a distinct gene profile upon reactivation. Nat Med. 2018;24:604–609. doi: 10.1038/s41591-018-0017-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Horsburgh B.A., Lee E., Hiener B., et al. AIDS; London, England): 2020. High Levels of Genetically-Intact HIV in HLA-DR+ Memory T-Cells Indicates Their Value for Reservoir Studies. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.McManus W.R., Bale M.J., Spindler J., et al. HIV-1 in lymph nodes is maintained by cellular proliferation during antiretroviral therapy. J Clin Invest. 2019;130:4629–4642. doi: 10.1172/JCI126714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Von Stockenstrom S., Odevall L., Lee E., et al. Longitudinal genetic characterization reveals that cell proliferation maintains a persistent HIV type 1 DNA pool during effective HIV therapy. JID (J Infect Dis) 2015;212:596–607. doi: 10.1093/infdis/jiv092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Wagner T.A., McKernan J.L., Tobin N.H., Tapia K.A., Mullins J.I., Frenkel L.M. An increasing proportion of monotypic HIV-1 DNA sequences during antiretroviral treatment suggests proliferation of HIV-infected cells. J Virol. 2013;87:1770–1778. doi: 10.1128/jvi.01985-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Nickle D.C. Evolutionary indicators of human immunodeficiency virus type 1 reservoirs and compartments. J Virol. 2003;77 doi: 10.1128/JVI.77.9.5540-5546.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Cohn L.B., Silva I.T., Oliveira T.Y., et al. HIV-1 integration landscape during latent and active infection. Cell. 2015;160:420–432. doi: 10.1016/j.cell.2015.01.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Einkauf K.B., Lee G.Q., Gao C., et al. Accumulation of intact proviruses at distinct chromosomal positions during long-term antiretroviral therapy. J Clin Invest. 2019 doi: 10.1172/JCI124291. in-press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Maldarelli F., Wu X., Su L., et al. Specific HIV integration sites are linked to clonal expansion and persistence of infected cells. Science. 2014;345:179–183. doi: 10.1126/science.1254194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Reeves D.B., Duke E.R., Wagner T.A., Palmer S.E., Spivak A.M., Schiffer J.T. A majority of HIV persistence during antiretroviral therapy is due to infected cell proliferation. Nat Commun. 2018;9:4811. doi: 10.1038/s41467-018-06843-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wang Z., Gurule E.E., Brennan T.P., et al. Expanded cellular clones carrying replication-competent HIV-1 persist, wax, and wane. Proc Natl Acad Sci USA. 2018;115:E2575–E2584. doi: 10.1073/pnas.1720665115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Pankau M.D., Reeves D.B., Harkins E., et al. Dynamics of HIV DNA reservoir seeding in a cohort of superinfected Kenyan women. PLoS Pathog. 2020;16 doi: 10.1371/journal.ppat.1008286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Kearney M.F., Wiegand A., Shao W., et al. Ongoing HIV replication during ART reconsidered. Open Forum Infect Dis. 2017;4 doi: 10.1093/ofid/ofx173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Whitney J.B., Hill A.L., Sanisetty S., et al. Rapid seeding of the viral reservoir prior to SIV viraemia in rhesus monkeys. Nature. 2014;512:74–77. doi: 10.1038/nature13594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Whitney J.B., Lim S.Y., Osuna C.E., et al. Prevention of SIVmac251 reservoir seeding in rhesus monkeys by early antiretroviral therapy. Nat Commun. 2018 doi: 10.1038/s41467-018-07881-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Ananworanich J., Robb M.L. The transient HIV remission in the Mississippi baby: why is this good news? J Int AIDS Soc. 2014;17 doi: 10.7448/ias.17.1.19859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Conway J.M., Perelson A.S., Li J.Z. Predictions of time to HIV viral rebound following ART suspension that incorporate personal biomarkers. PLoS Comput Biol. 2019;15 doi: 10.1371/journal.pcbi.1007229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Garcia-Broncano P., Maddali S., Einkauf K.B., et al. Early antiretroviral therapy in neonates with HIV-1 infection restricts viral reservoir size and induces a distinct innate immune profile. Sci Transl Med. 2019;11 doi: 10.1126/scitranslmed.aax7350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Henrich T.J., Hatano H., Bacon O., et al. HIV-1 persistence following extremely early initiation of antiretroviral therapy (ART) during acute HIV-1 infection: an observational study. PLoS Med. 2017;14 doi: 10.1371/journal.pmed.1002417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Jameson S.C. T cell homeostasis: keeping useful T cells alive and live T cells useful. Semin Immunol. 2005;17:231–237. doi: 10.1016/j.smim.2005.02.003. [DOI] [PubMed] [Google Scholar]
- 34.Ananworanich J., Chomont N., Eller L.A., et al. HIV DNA set point is rapidly established in acute HIV infection and dramatically reduced by early ART. EBioMedicine. 2016;11:68–72. doi: 10.1016/j.ebiom.2016.07.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Coffin J.M., Wells D.W., Zerbato J.M., et al. Clones of infected cells arise early in HIV-infected individuals. JCI Insight. 2019;4 doi: 10.1172/jci.insight.128432. 0–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Hosmane N.N., Kwon K.J., Bruner K.M., et al. Proliferation of latently infected CD4 \textlesssup\textgreater+\textless/sup\textgreater T cells carrying replication-competent HIV-1: potential role in latent reservoir dynamics. J Exp Med. 2017;214:959–972. doi: 10.1084/jem.20170193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Desponds J., Mora T., Walczak A.M. Fluctuating fitness shapes the clone-size distribution of immune repertoires. Proc Natl Acad Sci USA. 2016;113:274–279. doi: 10.1073/pnas.1512977112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Lindau P., Mukherjee R., Gutschow M.V., et al. Cytomegalovirus exposure in the elderly does not reduce CD8 T cell repertoire diversity. J Immunol. 2019;202:476–483. doi: 10.4049/jimmunol.1800217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Oakes T., Heather J.M., Best K., et al. Quantitative characterization of the T cell receptor repertoire of naïve and memory subsets using an integrated experimental and computational pipeline which is robust, economical, and versatile. Front Immunol. 2017;8 doi: 10.3389/fimmu.2017.01267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Sengupta S., Siliciano R.F. Cell Press; 2018. Targeting the Latent Reservoir for HIV-1. Immunity. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Ndhlovu Z.M., Kazer S.W., Nkosi T., et al. Augmentation of HIV-specific T cell function by immediate treatment of hyperacute HIV-1 infection. Sci Transl Med. 2019;11 doi: 10.1126/scitranslmed.aau0528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Mohri H., Perelson A.S., Tung K., et al. Increased turnover of T lymphocytes in HIV-1 infection and its reduction by antiretroviral therapy. J Exp Med. 2001;194:1277–1287. doi: 10.1084/jem.194.9.1277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Regoes R.R., Wodarz D., Nowak M.A. Virus dynamics: the effect of target cell limitation and immune responses on virus evolution. J Theor Biol. 1998;191:451–462. doi: 10.1006/jtbi.1997.0617. [DOI] [PubMed] [Google Scholar]
- 44.Adleman L.M., Wofsy D. T-cell homeostasis: implications in HIV infection. J Acquir Immune Defic Syndr Hum Retrovirol. 1993;6:144–152. [PubMed] [Google Scholar]
- 45.Adleman L.M., Wofsy D. Blind T-cell homeostasis in CD4-deficient mice. J Acquir Immune Defic Syndr Hum Retrovirol. 1996;11:334–340. doi: 10.1097/00042560-199604010-00003. [DOI] [PubMed] [Google Scholar]
- 46.Mackall C.L., Fleisher T.A., Brown M.R., et al. Distinctions between CD8+ and CD4+ T-cell regenerative pathways result in prolonged T-cell subset imbalance after intensive chemotherapy. Blood. 1997;89:3700–3707. [PubMed] [Google Scholar]
- 47.Mehr R., Perelson A.S. Blind T-cell homeostasis and the CD4/CD8 ratio in the thymus and peripheral blood. J Acquir Immune Defic Syndr Hum Retrovirol. 1997;14:387–398. doi: 10.1097/00042560-199704150-00001. [DOI] [PubMed] [Google Scholar]
- 48.Roch B., Dautigny N., Pereira P. Peripheral T lymphocytes: expansion and potential homeostatic regulation of pool sizes and CD4/CD8 ratios in vivo. Eur J Immunol. 1989;19:905–911. doi: 10.1002/eji.1830190518. [DOI] [PubMed] [Google Scholar]
- 49.Takada K., Jameson S.C. Naive T cell homeostasis: from awareness of space to a sense of place. Nat Rev Immunol. 2009;9:823–832. doi: 10.1038/nri2657. [DOI] [PubMed] [Google Scholar]
- 50.Engram J.C., Cervasi B., Borghans J.A.M., et al. Lineage-specific T-cell reconstitution following in vivo CD4+ and CD8+ lymphocyte depletion in nonhuman primates. Blood. 2010;116:748–758. doi: 10.1182/blood-2010-01-263814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Moon J.J., Chu H.H., Pepper M., et al. Naive CD4+ T cell frequency varies for different epitopes and predicts repertoire diversity and response magnitude. Immunity. 2007;27:203–213. doi: 10.1016/j.immuni.2007.07.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Mabuka J.M., Dugast A.S., Muema D.M., et al. Plasma CXCL13 but not B cell frequencies in acute HIV infection predicts emergence of cross-neutralizing antibodies. Front Immunol. 2017;8 doi: 10.3389/fimmu.2017.01104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Ndhlovu Z.M., Kamya P., Mewalal N., et al. Magnitude and kinetics of CD8+ T cell activation during hyperacute HIV infection impact. Viral Set Point. Immun. 2015 doi: 10.1016/j.immuni.2015.08.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Ho Y.C., Shan L., Hosmane N.N., et al. XReplication-competent noninduced proviruses in the latent reservoir increase barrier to HIV-1 cure. Cell. 2013;155:540–551. doi: 10.1016/j.cell.2013.09.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Ho D.D., Neumann A.U., Perelson A.S., Chen W., Leonard J.M., Markowitz M. Rapid turnover of plasma virions and CD4 lymphocytes in HIV-1 infection. Nature. 1995 doi: 10.1038/373123a0. [DOI] [PubMed] [Google Scholar]
- 56.Ribeiro R.M., Perelson A.S. The analysis of HIV dynamics using mathematical models. AIDS and Other Manifestations of HIV Infect. 2004 doi: 10.1016/B978-012764051-8/50037-8. [DOI] [Google Scholar]
- 57.Wei X., Ghosh S.K., Taylor M.E., et al. Viral dynamics in human immunodeficiency virus type 1 infection. Nature. 1995 doi: 10.1038/373117a0. [DOI] [PubMed] [Google Scholar]
- 58.Okoye A., Park H., Rohankhedkar M., et al. Profound CD4+/CCR5+ T cell expansion is induced by CD8+ lymphocyte depletion but does not account for accelerated SIV pathogenesis. J Exp Med. 2009;206:1575–1588. doi: 10.1084/jem.20090356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Kumar N.A., McBrien J.B., Carnathan D.G., et al. Antibody-mediated CD4 depletion induces homeostatic CD4+ T cell proliferation without detectable virus reactivation in antiretroviral therapy-treated simian immunodeficiency virus-infected macaques. J Virol. 2018;92 doi: 10.1128/JVI.01235-18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Matrajt L., Younan P.M., Kiem H.-P., Schiffer J.T. The majority of CD4+ T-cell depletion during acute Simian-human immunodeficiency virus SHIV89.6P infection occurs in uninfected cells. J Virol. 2014 doi: 10.1128/jvi.03428-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Antony 2019 France: lixsoft SAS. 2018. http://lixoft.com/products/monolix/ Monolix version 2018R1.
- 62.Robb M.L., Eller L.A., Kibuuka H., et al. Prospective study of acute HIV-1 infection in adults in East Africa and Thailand. N Engl J Med. 2016;374:2120–2130. doi: 10.1056/NEJMoa1508952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Conway J.M., Perelson A.S. Residual viremia in treated HIV+Individuals. PLoS Comput Biol. 2016 doi: 10.1371/journal.pcbi.1004677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Markowitz M., Louie M., Hurley A., et al. A novel antiviral intervention results in more accurate assessment of human immunodeficiency virus type 1 replication dynamics and T-cell decay in vivo. J Virol. 2003;77:5037–5038. doi: 10.1128/JVI.77.8.5037-5038.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Hockett R.D., Michael Kilby J., Derdeyn C.A., et al. Constant mean viral copy number per infected cell in tissues regardless of high, low, or undetectable plasma HIV RNA. J Exp Med. 2002 doi: 10.1084/jem.189.10.1545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Perelson A.S., Kirschner D.E., De Boer R. Dynamics of HIV infection of CD4 + T cells. Math Biosci. 1993 doi: 10.1016/0025-5564(93)90043-A. [DOI] [PubMed] [Google Scholar]
- 67.Ramratnam B., Bonhoeffer S., Binley J., et al. Rapid production and clearance of HIV-1 and hepatitis C virus assessed by large volume plasma apheresis. Lancet. 1999 doi: 10.1016/S0140-6736(99)02035-8. [DOI] [PubMed] [Google Scholar]
- 68.Sanjuan R., Domingo-Calap P. Mechanisms of viral mutation. Cell Mol Life Sci. 2016;73:4433–4448. doi: 10.1007/s00018-016-2299-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Schröder A.R.W., Shinn P., Chen H., Berry C., Ecker J.R., Bushman F. HIV-1 integration in the human genome favors active genes and local hotspots. Cell. 2002;110:521–529. doi: 10.1016/S0092-8674(02)00864-4. [DOI] [PubMed] [Google Scholar]
- 70.Shampine L.F., Reichelt M.W. The MATLAB ODE suite. SIAM J Sci Comput. 1997;18:1–22. doi: 10.1137/S1064827594276424. [DOI] [Google Scholar]
- 71.Gillespie D.T. Approximate accelerated stochastic simulation of chemically reacting systems. J Chem Phys. 2001;115:1716–1733. doi: 10.1063/1.1378322. [DOI] [Google Scholar]
- 72.Cheret A., Bacchus-Souffan C., Avettand-Fenoel V., et al. Combined ART started during acute HIV infection protects central memory CD4+ T cells and can induce remission. J Antimicrob Chemother. 2015;70 doi: 10.1093/jac/dkv084. [DOI] [PubMed] [Google Scholar]
- 73.Boulassel M.R., Chomont N., Pai N.P., Gilmore N., Sékaly R.P., Routy J.P. CD4 T cell nadir independently predicts the magnitude of the HIV reservoir after prolonged suppressive antiretroviral therapy. J Clin Virol. 2012;53:29–32. doi: 10.1016/j.jcv.2011.09.018. [DOI] [PubMed] [Google Scholar]
- 74.Soriano-Sarabia N., Bateson R.E., Dahl N.P., et al. Quantitation of replication-competent HIV-1 in populations of resting CD4+ T cells. J Virol. 2014;88:14070–14077. doi: 10.1128/JVI.01900-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Persaud D., Pierson T., Ruff C., et al. A stable latent reservoir for HIV-1 in resting CD4(+) T lymphocytes in infected children. J Clin Invest. 2000;105:995–1003. doi: 10.1172/JCI9006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Blankson J.N., Finzi D., Pierson T.C., et al. Biphasic decay of latently infected CD4 + T cells in acute human immunodeficiency virus type 1 infection. J Infect Dis. 2000;182:1636–1642. doi: 10.1086/317615. [DOI] [PubMed] [Google Scholar]
- 77.Mendoza P., Jackson J.R., Oliveira T.Y., et al. Antigen-responsive CD4+ T cell clones contribute to the HIV-1 latent reservoir. J Exp Med. 2020:217. doi: 10.1084/jem.20200051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Simonetti F.R., Zhang H., Soroosh G.P., et al. Antigen-driven clonal selection shapes the persistence of HIV-1–infected CD4+ T cells in vivo. J Clin Invest. 2021;131 doi: 10.1172/JCI145254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Gantner P., Pagliuzza A., Pardons M., et al. Single-cell TCR sequencing reveals phenotypically diverse clonally expanded cells harboring inducible HIV proviruses during ART. Nat Commun. 2020;11 doi: 10.1038/s41467-020-17898-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Reeves D.B., Peterson C.W., Kiem H.-P., Schiffer J.T. Autologous stem cell transplantation disrupts adaptive immune responses during rebound Simian/human immunodeficiency virus viremia. J Virol. 2017;91 doi: 10.1128/jvi.00095-17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Antar A.A.R., Jenike K.M., Jang S., et al. Longitudinal study reveals HIV-1–infected CD4+ T cell dynamics during long-term antiretroviral therapy. J Clin Invest. 2020;130:3543–3559. doi: 10.1172/JCI135953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Abrahams M.R., Joseph S.B., Garrett N., et al. The replication-competent HIV-1 latent reservoir is primarily established near the time of therapy initiation. Sci Transl Med. 2019;11 doi: 10.1126/scitranslmed.aaw5589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Brodin J., Zanini F., Thebo L., et al. Establishment and stability of the latent HIV-1 DNA reservoir. Elife. 2016;5 doi: 10.7554/eLife.18889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Hunt P.W., Cao H.L., Muzoora C., et al. Impact of CD8+ T-cell activation on CD4+ T-cell recovery and mortality in HIV-infected Ugandans initiating antiretroviral therapy. AIDS. 2011;25:2123–2131. doi: 10.1097/QAD.0b013e32834c4ac1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Bruner K.M., Wang Z., Simonetti F.R., et al. A quantitative approach for measuring the reservoir of latent HIV-1 proviruses. Nature. 2019 doi: 10.1038/s41586-019-0898-8. Nature Publishing Group. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Li J.Z., Etemad B., Ahmed H., et al. The size of the expressed HIV reservoir predicts timing of viral rebound after treatment interruption. AIDS. 2016;30:343–353. doi: 10.1097/QAD.0000000000000953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Musick A., Spindler J., Boritz E., et al. HIV infected T cells can proliferate in vivo without inducing expression of the integrated provirus. Front Microbiol. 2019;10:2204. doi: 10.3389/fmicb.2019.02204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Kwon K.J., Timmons A.E., Sengupta S., et al. Different human resting memory CD4+ T cell subsets show similar low inducibility of latent HIV-1 proviruses. Sci Transl Med. 2020;12 doi: 10.1126/scitranslmed.aax6795. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Empirical data was digitally extracted from publicly available paper. Code for simulations and plotting are available on github https://github.com/ftettamanti/HIV_LR_proliferation.