Deformable CT Image Registration via a Dual Feasible Neural Network

Abstract

Purpose:

A quality assurance (QA) CT scans is usually acquired during cancer radiotherapy to assess for any anatomical changes which may cause an unacceptable dose deviation and therefore warrant a replan. Accurate and rapid deformable image registration (DIR) is needed to support contour propagation from the planning CT (pCT) to the QA CT to facilitate dose volume histogram (DVH) review. Further, the generated deformation maps are used to track the anatomical variations throughout the treatment course and calculate the corresponding accumulated dose from one or more treatment plans.

Methods:

In this study, we aim to develop a deep learning-based method for automatic deformable registration to align the pCT and the QA CT. Our proposed method, named dual-feasible framework, was implemented by a mutual network that functions as both a forward module and a backward module. The mutual network was trained to predict two deformation vector fields (DVFs) simultaneously, which were then used to register the pCT and QA CT in both directions. A novel dual feasible loss was proposed to train the mutual network. The dual-feasible framework was able to provide additional DVF regularization during network training, which preserves the topology and reduces folding problems. We conducted experiments on 65 head-and-neck cancer patients (228 CTs in total), each with 1 pCT and 2-6 QA CTs. For evaluations, we calculated the mean absolute error (MAE), peak-signal-to-noise ratio (PSNR), structural similarity index (SSIM), target registration error (TRE) between the deformed and target images and the Jacobian determinant of the predicted DVFs.

Results:

Within the body contour, the mean MAE, PSNR, SSIM, and TRE are 122.7 HU, 21.8 dB, 0.62 and 4.1 mm before registration and are 40.6 HU, 30.8 dB, 0.94 and 2.0 mm after registration using the proposed method. These results demonstrate the feasibility and efficacy of our proposed method for pCT and QA CT deformable image registration.

Conclusion:

In summary, we proposed a deep learning-based method for automatic DIR to match the pCT to the QA CT. Such DIR method would not only benefit current workflow of evaluating dose volume histograms (DVHs) on QA CTs but may also facilitate studies of treatment response assessment and radiomics that depend heavily on the accurate localization of tissues across longitudinal images.

1. Introduction

Compared with photon radiation therapy, proton radiation therapy features advantageous dosimetric properties attributed to the Bragg Peak and virtually no exit dose, which may have better clinical outcomes.^1-5 However, a small shift of the high dose gradient at the distal end of the Bragg peak can lead to substantial under-dose on target tumor or over-dose on critical organs.⁶ Throughout the course of treatment, such shifts can be caused by patient setup uncertainty, tumor shrinkage or patient weight loss, which results in delivered dose that deviates from the planned dose.

Quality assurance (QA) CT scans can be regularly acquired in order to track the anatomical changes and assess the necessity of a replan to mitigate the aforementioned problems.^7,8 In our clinic, we acquire a weekly QA CT for each head-and-neck (HN) cancer patient because tumor shrinkage is commonly observed.⁹ The current practice is for the physicians to fuse the QA CT and the planning CT (pCT) using rigid/non-rigid registration to visualize any anatomical changes and then re-contour on the QA CT when large anatomical changes are observed. In these instances, new dose volume histograms (DVHs) are generated from the contoured CT QA images to quantify important dosimetric endpoints that guide the decision to continue with the current plan or replan. While this process is important for ensuring high quality treatments, there are challenges. Re-contouring is very tedious and time-consuming for clinicians, especially for tumor sites with many critical organs such as HN. Current registration-based contour propagation always introduces errors, especially for flexible structures such as cervical spine and deformable soft tissue organs.¹⁰ Thus, it is desirable to have an efficient deformable image registration (DIR) method that provides accurate and fast contour propagation from the pCT to a QA CT.¹¹ Such a DIR method that accurately maps tissue locations across longitudinal imaging studies is certainly needed in proton radiation therapy for DVH evaluation and replanning, yet there may be broader applications for assessing treatment response assessment and radiomics beyond radiation therapy.

Recently, deep learning (DL)-based deformable image registration methods have been developed due to its superior performance, such as faster runtime and improved robustness over conventional methods. Recent review papers^12,13 summarized the latest development of DL-based DIR. Three major categories of the DL-based DIR are deep iterative registration, supervised transformation prediction and unsupervised transformation prediction. Deep iterative registration inherits the iterative nature of conventional DIR methods,¹⁴ which can be time consuming to compute. For the network training, supervised transformation prediction requires a known ‘ground truth’ deformation vector field (DVF), which is usually artificially generated and therefore may differ from the actual physiological deformation.¹⁵ Given both source and target images, deep neural networks are trained to generate DVF corresponding to the input image pair (including moving and target images), thereby enabling significantly faster registration. However, without the ground truth transformations, it is difficult to define the proper loss functions of the networks. To solve this problem, a spatial transformer network (STN)¹⁶ was proposed to generate the deformed image which enables image similarity loss calculation during the training process. As a result of STN, unsupervised transformation prediction was proposed which eliminates the need for ‘ground truth DVF’ by directly maximizing the image similarity between the deformed and target images. VoxelMorph,¹⁷ a fast DL-based DIR, was proposed to build a convolutional neural network (CNN) to rapidly compute a DVF to match the moving image to target image. To overcome the potential degeneracy problem of registration fields, a recent DIR method, called CycleMorph, was proposed.¹⁸ CycleMorph utilized cycle consistency to force the deformed image to return to the original image. This cycle consistency in the image domain may avoid discretization errors from the real-world implementation of inverse deformation fields.

Inspired by CycleMorph, we proposed an unsupervised, dual-feasible DIR method for the registration of HN pCT and QA CT in this study. This approach has 3 distinctive strengths: 1) The dual-feasible framework was able to preserve the topology of the images, reduce folding problems and generate more plausible DVF. 2) The mutual network enables the transfer of knowledge between the forward and backward registration via parameter sharing. 3) Our model was optimized under an unsupervised manner, which means ground truth DVF was not needed.

2. Methods and materials

2.A. Overview

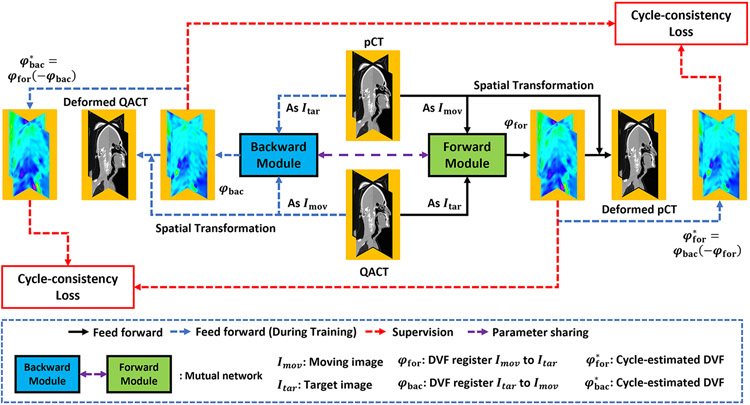
Figure 1 shows the flow chart of the proposed framework. The optimization of the mutual network model and the inference of a new patient’s pCT and QA CTs follow the similar feed forward path of the dual-feasible framework. During optimization, the network takes a set of pCT and QA CTs from one patient as input at each iteration, and then outputs the deformable vector fields (DVFs) that deformably register this patient’s pCT to match the QA CTs. The deformable registration is achieved by predicting the DVF from the moving (e.g., pCT) and target image (e.g., QA CT) and then applying the DVF to the moving image via spatial transformer to obtain the deformed image.¹² The network was trained in an unsupervised manner, as ground truth DVFs are not needed during optimization.¹⁹ Thus, the loss function was designed as a combination of several image difference losses calculated between the deformed image and target image and regularization loss calculated from the DVFs and deformed images.

Figure 1.

The workflow of the proposed dual-feasible deep learning-based deformable registration method. The black arrow denotes the feedforward path in both the training and inference procedure. The blue dashed arrow denotes the feedforward path for the training procedure only. The red dashed arrow denotes the supervision.

The deep learning-based unsupervised deformable registration method may face the challenge that the generated DVF does not explicitly enforce the criterion to guarantee topology preservation, which often results in inaccurate image registration with the loss of structural information.²⁰ To overcome this challenge, we integrated a backward path that deformably registered the QA CT to match the pCT. Therefore, the network was implemented by two subnetworks, namely, a forward module and a backward module. Given a patient’s pCT and QA CT, the forward module aims to deformably register the pCT to match the QA CT. Meanwhile, the backward module aims to deformably register the QA CT to match the pCT. The two modules have the same architecture and share their learnable parameters so that they can iteratively provide mutual regularization during the training process. By integrating both the forward and backward modules into the dual feasible optimization framework, the mutual network can improve the registration performance.

2.B. Mutual network

The mutual network is used in both forward and backward paths and is alternatively optimized during forward and backward paths. Therefore, we introduce the network architecture design of only the forward module. Suppose one patient’s pCT I_pCT ∈ R^w×h×d and QA CTs $\{I_{\text{QACT}}^i\}\in R^{w\times h\times d}$ (i ∈ {1,2, …, k}) are fed into a forward module to derive the DVFs {φⁱ} ∈ R^w×h×d×3 that can deformably register the I_pCT to match the $\{I_{\text{QACT}}^i\}$ via spatial transformer,²¹ i.e., {φⁱ ∘ I_pCT} ∈ R^w×h×d. The network used in forward path is shown in Fig. 2. Accordingly, the network used in backward path is shown in Fig. 1* in supplement. The generator is used to derive the DVFs {φⁱ}, and is composed of several convolutional layers, each of which has stride size of 2×2×2 to downscale the output size. A residual network block was used to enable the network to learn the residual between I_pCT and $\{I_{\text{QACT}}^i\}$, namely the difference image which encoded the underlying tissue deformation. After the last layer of the residual block, a deconvolutional layer with trilinear interpolation was used to up-sample the output to achieve end-to-end consistency in image size. This output is the derived DVF {φⁱ}. The aim of trilinear interpolation is to generate smooth for deformable registration.²² Then, by using spatial transformer, we can apply the DVF {φⁱ} on the moving image I_pCT to obtain the deformed image {φⁱ ∘ I_pCT}. The discriminator, designed as a fully convolutional network (FCN), was used to output the reliability score of the input images. The input images can be either a batch of target image ($\{I_{\text{QACT}}^i\}$) or deformed image {φⁱ ∘ I_pCT}. The network architectures details are shown in Table 1* and Table 2* of supplement.

Figure 2.

Network architecture/framework used in forward module.

2.C. Dual feasible

Although recent deep learning-based deformable registration methods have been developed to perform CT registration with voxel wise one-to-one correspondence,¹² deformations are generally represented discretely with a finite number of parameters, so there may be some small violations. Namely, the estimated DVF {φⁱ} from I_pCT to $\{I_{\text{QACT}}^i\}$ is not equal to the inverse of the estimated DVF from QA CT to pCT. To mitigate this problem, the proposed dual-feasible framework improves the reasonability of the optimized module through bilateral deformable registration. The module is able to register the pCT to match the QA CT (forward module in Fig. 1) and register the QA CT to match the pCT (backward module in Fig. 1) at the same time. Suppose we have a set of pCT I_pCT and QA CT I_QACT, and the forward and backward modules generate two DVFs {φ_for} and {φ_bac}. The dual-feasible loss is represented by:

$$L_{\text{dual}-\text{feasible}}=L_{\text{for}}\left({\phi }_{\text{for}},I_{\text{pCT}},I_{\text{QACT}}\right)+L_{\text{bac}}\left({\phi }_{\text{bac}},I_{\text{QACT}},I_{\text{pCT}}\right),$$ (1)

where, L_for and L_bac represents the loss of the forward module and the backward module, respectively. The loss includes the image difference loss, the adversarial loss, and the DVF smoothness loss.

The image difference loss in this work was implemented via a combination of normalized cross-correlation (NCC) loss²² calculated between deformed pCT and QA CTs and Huber loss²³ calculated between the gradient of deformed pCT and the gradient of QA CTs. NCC loss is used to measure the structural similarity between the deformed image and the target image globally. To further increase the local structure similarity between deformed pCT and QA CTs, we introduced another Huber loss that is calculated between the gradient of deformed pCT and the gradient of QA CTs. The Huber loss is a loss function used in robust regression, that is less sensitive to outliers in data than the squared error loss.²⁴ Given moving image I_pCT, target images $\{I_{\text{QACT}}^i\}$, derived DVFs {φⁱ}, and deformed images {φⁱ ∘ I_pCT}, The image difference loss was represented as follows:

$$L_{\text{for}}^{\text{diff}}=\sum \begin{array}{c}\hfill \\ i\hfill \end{array}\left(1-\text{NCC}\left({\phi }^i\circ I_{\text{pCT}},I_{\text{QACT}}^i\right)+\text{Huber}\left(\nabla \left({\phi }^i\circ I_{\text{pCT}}\right),\nabla \left(I_{\text{QACT}}^i\right)\right)\right),$$ (2)

where, NCC(·) denotes the NCC loss, Huber(·) denotes the Huber loss, ∇(·) denotes the gradient of a 3D image along height, width, and depth directions.

Since the network was designed to be trained in a completely unsupervised manner, DVF regularization is necessary to generate realistic DVF. Smoothness constraint was commonly used in the literature for DVF regularization. In this work, the l₁-norm ²⁵ of first order gradient of DVF is used as the regularization term. We add the minimization of this regularization term with $L_{\text{for}}^{\text{diff}}$ together for the optimization of mutual network.

In addition, adversarial loss is used to guide the realism of the deformed image. In this work, sigmoid cross entropy (SCE) is used as adversarial loss. During optimization, the generator of forward module generates DVFs that move I_pCT to match the $\{I_{\text{QACT}}^i\}$ under the minimization of $L_{\text{for}}^{\text{diff}}$, regularization term of {φⁱ} and SCE of {φⁱ ∘ I_pCT}, namely mislead the discriminator of forward module to treat {φⁱ ∘ I_pCT} as real images. Thus, the generator g_for can be optimized by the following:

$$g_{\text{for}}=\text{arg}{\text{min}}_{g_{\text{for}}}{L}_{\text{for}}^{\text{diff}}+\sum \begin{array}{c}\hfill \\ i\hfill \end{array}{\Vert \nabla \left({\phi }^i\right)\Vert }_1+\sum \begin{array}{c}\hfill \\ i\hfill \end{array}\text{SCE}\left({\phi }^i\circ I_{\text{pCT}},1\right).$$ (3)

The discriminator learned to differentiate the deformed image from target image, so that the realism of the deformed image can be improved to a similar level of that of target image. Namely, the discriminator d_for can be optimized by the following:

$$d_{\text{for}}=\text{arg}{\text{min}}_{d_{\text{for}}}\sum \begin{array}{c}\hfill \\ i\hfill \end{array}\left(\text{SCE}\left({\phi }^i\circ I_{\text{pCT}},0\right)+\text{SCE}\left(I_{\text{QACT}}^i,1\right)\right).$$ (4)

In addition, topological preservation is not explicitly enforced by the DVF generated using the unsupervised deformable registration method, which causes a loss of structural information and may result in inaccurate image registration.²⁰ To overcome this challenge, we integrated the strategy of DVFs’ cycle-consistency (which is introduced in ²⁶) into the training procedure of the label-driven cycle-network. To achieve this strategy, as introduced by Zhang²⁶, we apply the DVF φ_bac to DVF −φ_for to derive the estimated DVF of φ_for, denoted as ${\phi }_{\text{for}}^{\ast }$ and vice versa.

$$\{\begin{array}{c}{\phi }_{\text{for}}^{\ast }={\phi }_{\text{bac}}(-{\phi }_{\text{for}})\hfill \\ {\phi }_{\text{bac}}^{\ast }={\phi }_{\text{for}}(-{\phi }_{\text{bac}})\hfill \end{array}\phantom{\}}$$ (5)

Then, we minimize the distances between φ_for and ${\phi }_{\text{for}}^{\ast }$, and between φ_bac and ${\phi }_{\text{bac}}^{\ast }$.

Thus, the total loss for updating generator g_for can be optimized by the following:

$$g_{\text{for}}=\text{arg}{\text{min}}_{g_{\text{for}}}{L}_{\text{for}}^{\text{diff}}+\sum \begin{array}{c}\hfill \\ i\hfill \end{array}{\Vert \nabla \left({\phi }^i\right)\Vert }_1+\sum \begin{array}{c}\hfill \\ i\hfill \end{array}{\Vert {\phi }_{\text{for}}^{i,\ast }-{\phi }_{\text{for}}^i\Vert }_1+\sum \begin{array}{c}\hfill \\ i\hfill \end{array}\text{SCE}\left({\phi }^i\circ I_{\text{pCT}},1\right).$$ (6)

where ${\phi }_{\text{for}}^{i,\ast }$ is the cycle estimation of ${\phi }_{\text{for}}^i$, and calculated via Eq (5).

2.D. Dataset

Sixty-five HN cancer patients who underwent radiotherapy were retrospectively investigated. Each patient has one pCT and 2-6 QA CTs (228 CTs in total). The pCT and QA CTs were first rigidly registered on a grid of 1.0×1.0×1.0 mm³ voxels. The axial grid width of pCT and QA CT was 512 × 512 pixels while the number of axial slices ranged from 428 to 471 for different patients. The quality assurance CT were acquired using the same CT imaging protocols with the same patient setup as the original planning CT. Therefore, they have the same image quality.

The overall performance of the proposed method was evaluated via a five-fold cross-validation study. Specifically, the 65 patient datasets were first randomly and equally separated into five groups, out of which four groups were used for training; and the remaining set was used for testing. The training and testing experiments were repeated five times by rotating each group as the testing group.

2.E. Implementation and evaluation

Our proposed algorithm and the competing algorithm (VoxelMorph) were implemented in Python 3.6 and TensorFlow on a NVIDIA Tesla V100 GPU with 32GB of memory. The Adam gradient optimizer with a learning rate of 2e-4 was used for optimization.

Mean absolute error (MAE), peak-signal-to-noise ratio (PSNR), structural similarity index (SSIM) and target registration error (TRE) between the deformed pCT and the QA CTs were calculated to quantitatively evaluate the performance of the proposed method. The TRE was calculated as Euclidean distance between the landmark positions in the QA CT and deformed CT. For TRE calculation, landmarks such as the tip of the spinous process and unique locations on bony and soft tissue structures were carefully identified by an experienced medical physicist. For each patient, we selected 10-20 landmarks to evaluate the TRE. With the location of the i-th landmark being denoted as L_i ∈ R³ in the QA CT and the location of its corresponding landmark in the same patient’s pCT or deformed CT (denoted as ${\widehat{L}}_j^i\in R^3$), the TRE was calculated as:

$$TRE(i,j)=\Vert L_i-{\widehat{L}}_j^i{\Vert }_{{}_2},$$ (7)

where, ∥·∥₂ denotes the l₂-norm.

The Jacobian determinant was calculated to assess the fidelity of the predicted DVF, such as topology preservation and mitigation of the problem of unrealistic folding. Visual assessment was performed by comparing the original images, deformed images and their respective difference images. Visual analysis was supplemented with quantitative intensity profiles along lines in the anterior-posterior direction. Line profiles are also plotted to cross key anatomical structures to assess the image alignment.

3. Results

To evaluate the performance of the proposed dual-feasible method, registration results between pCT and QA CT in both directions were compared to VoxelMorph¹⁷. In the forward registration, the pCT was deformed to match the QA CT (shown in Fig. 3, a3 and b3 shows the deformed pCT via VoxelMorph, and a4 and b4 shows the deformed pCT via proposed method without using DVF’s cycle-consistency regularization, a5 and b5 shows the deformed pCT via proposed method using DVF’s cycle-consistency regularization). In the backward registration, the QA CTs were deformed to match the pCT (shown in supplement Fig. 2*, where a3 and b3 shows the deformed QA CT via VoxelMorph, and a4 and b4 shows the deformed QA CT via proposed method without using DVF’s cycle-consistency regularization, a5 and b5 shows the deformed QA CT via proposed method using DVF’s cycle-consistency regularization).

Figure 3.

Forward deformation results shown in sagittal views. (a1) shows the pCT (moving). (a2) shows the QA CT (target). (a3) shows the deformed CT via VoxelMorph. (a4) shows the deformed CT via proposed method without using DVF’s cycle-consistency regularization. (a5) shows the deformed CT via proposed method using DVF’s cycle-consistency regularization. (b1-b5) show the corresponding zoomed-in image of (a1-a5). (c2-c5) show the difference images before registration, after VoxelMorph registration, after the proposed registration without using DVF’s cycle-consistency regularization and after the proposed registration using DVF’s cycle-consistency regularization respectively. (d2-d5) show the corresponding zoomed-in image of (c2-c5). The window level of CTs is set to [−1000, 1000] HU. The difference image window level is [−300 300] HU.

For further evaluations, difference images before registration (shown in c2 and d2), after VoxelMorph registration (shown in c3 and d3) and after the proposed registration without and with the DVF cycle-consistency regularization (shown in c4 and d4, and c5 and d5, respectively) were plotted in Fig. 3 and supplement Fig. 2* for the forward and backward registration, respectively. As can be seen from the difference image comparison within selected region-of-interest (ROI) (shown in d5 vs. d4, d3 and d2) in Fig. 3 and supplement Fig. 2* especially near the spinous process, the alignment between the pCT and the QA CT was improved by the proposed DIR method for both the forward and backward registration as compared to VoxelMorph and the proposed method without using DVF’s cycle-consistency regularization.

To further evaluate the structural alignment, we plotted the intensity profile of the pCT, QA CT and deformed CT along the red dashed lines that are shown in Fig. 3 (a2) and supplement Fig. 2* (a2). The intensity profiles are shown in Fig. 4 and supplement Fig. 3* (subfigure c). As compared to VoxelMorph’s results and the proposed method without using DVF’s cycle-consistency regularization, our registration results resemble the intensity profiles of the target images more closely for both the forward and backward registration.

Figure 4.

(a1) shows the fusion images between moving image (a1 in Fig. 3) and target image (a2 in Fig. 3), (a2-a4) show the fusion image between moving image (a1 in Fig. 3) and deformed images (a3-a5 in Fig. 3), which are deformed image via VoxelMorph, the proposed method without using DVF’s cycle-consistency regularization, and the proposed method using DVF’s cycle-consistency regularization. (b1-b4) show the corresponding zoomed-in image of (a1-a4). (c) shows the intensity profiles of pCT, QA CT, deformed CT via VoxelMorph, via proposed method without using DVF’s cycle-consistency regularization and via proposed method using cycle-consistency regularization. The intensity profile was along the red dashed line in (a2) of Fig. 3.

For better visualization, the fusion images between the moving image and the target image (a1 and b1), and the fusion images between the deformed image and the target image of this HN patient (a2 and b2 generated by VoxelMorph, a3 and b3 via proposed method without using DVF’s cycle-consistency regularization and a4 and b4 via proposed method using DVF’s cycle-consistency regularization) are shown in Fig. 4 and supplement Fig. 3*. In the fusion images, the deformed images and the target image are shown in the red and green channels, respectively. As shown in zoomed-in images comparison of b4 vs. b1, b2 and b3 in both Fig. 4 and supplement Fig. 3*, the spinous process alignment between the pCT and the QA CT was significantly improved by the proposed DIR method for both the forward path and backward path.

Table 1 and 2 show the average TRE, MAE, PSNR, SSIM and Jacobian determinant of the predicted DVFs for all the 65 patients for the forward and the backward registration. For the forward registration, the average TRE for the proposed DIR method was 2 mm which was improved by 50% as compared to the TRE before registration. The smaller TRE standard deviations of the proposed method also demonstrate better registration robustness. Within the HN body contour, the average MAE is less than 50 HU between the QA CT and the CT deformed by the proposed method. As compared to the performance of VoxelMorph, the MAE improved by 14 HU. Higher PSNR (30.8 dB of proposed method vs. 21.8 dB of before DIR and 28.2 dB obtained by VoxelMorph) and SSIM (0.94 of proposed method vs. 0.62 of before DIR and 0.91 obtained by VoxelMorph) also demonstrate the performance of the proposed dual-feasible DIR. The superior performance of the proposed method over VoxelMorph was also demonstrated by the relatively smaller percentage of voxels that have a negative Jacobian determinant value, indicating improved topology preservation and DVF regularization.

Table 1.

Numerical results calculated between pCT and QA CT (before DIR) and between deformed CT and QA CT obtained by VoxelMorph and the proposed method w/o and with using DVF’s cycle-consistency regularization within HN body contour during the forward registration.

Metrics	Before DIR	VoxelMorph	Proposed (w/o)	Proposed (w)
TRE (mm)	4.01±1.98	2.32±1.64	2.00±1.21	2.02±1.36
MAE (HU)	122.7±47.0	54.5±12.7	40.7±8.9	40.6±8.7
PSNR (dB)	21.8±2.1	28.2±1.9	30.8±1.9	30.8±2.0
SSIM	0.62±0.24	0.91±0.06	0.94±0.04	0.94±0.04
Jacobian	N/A	0.9%±1.2%	0.5%±0.7%	0.4%±0.5%

Table 2.

Numerical results calculated between pCT and QA CT (before DIR) and between deformed CT and QA CT obtained by VoxelMorph and the proposed method w/o and with using DVF’s cycle-consistency regularization within HN body contour during the backward registration.

Metrics	Before DIR	VoxelMorph	Proposed (w/o)	Proposed (w)
TRE (mm)	4.01±1.98	2.85±2.07	2.13±1.34	2.07±1.39
MAE (HU)	122.9±46.9	59.9±14.5	46.1±8.5	46.1±8.6
PSNR (dB)	21.7±2.1	27.5±1.9	29.9±1.7	29.8±1.7
SSIM	0.62±0.25	0.91±0.05	0.94±0.04	0.94±0.04
Jacobian	N/A	1.1%±1.6%	0.4%±0.8%	0.3%±0.6%

4. Discussion

DIR is an important tool in clinical radiotherapy and can be used in a wide range of applications, from image fusion, motion tracking,²⁷ contour propagation,²⁸ and accumulative dose calculation. However, one challenge of DIR is the regularization of the DVF since the DIR is intrinsically an ill-posed problem. Proper DVF regularization could preserve the organ topology and reduce the implausible folding of voxels, which could in turn increase the accuracy of DIR-based applications, such as contour propagation and dose accumulation. In this study, we have proposed a dual-feasible network which implicitly imposes bilateral DVF regularization by registering the images in both the forward and backward directions via a shared mutual network. This adversarial network could provide additional DVF regularization that improves deformations by preserving topology and reducing folds. The proposed network took less than 1 minute to perform the bi-directional image registration. The performance of the proposed method was investigated through qualitative and quantitative evaluations.

Some other important features of the network include the use of residual blocks and the cycle consistency loss. The residual blocks help to learn the differences between deformable soft tissue regions and avoid deforming the bony structures. In this work, the residual block was implemented by a stack of two convolutional layers, such that the output was taken by summing the input feature map and feature map that is extracted via two additional, deeper convolutional layers. The non-linearity is then applied via this addition in the generator’s layer path. By using several residual blocks in the generator, the generator updates the model parameters in the shallow layers based on the spatial regions that are most relevant to a given task, i.e., structural matching. The generator network has the ability to highlight the features from previous layers to align the images. Thus, the integration of residual blocks in the generator network can better capture the structural differences between the moving and target images. Different from lung deformation which shows motion invertibility due to cyclic respiratory motion, the deformation of HN image registration for patient undergoing radiation therapy may not be fully invertible due to anatomical changes such as tumor shrinkage and progression. Additionally, the pCT and QA CT are separately reconstructed from different CT imaging sessions which also impairs the invertibility of the registration. Therefore, we introduce the cycle consistency loss term to preserve the image topology and improve the mutual registration performance.

As compared to CycleMorph, the differences in network architecture are that first the networks of generating DVF in CycleMorph are implemented via several deconvolutional layers to make them as an end-to-end network. In our network of generating DVF, as can be seen from Table 1*, a down-sampling rate of 4 was implemented by using three convolution layers (with stride size of 2) and a deconvolutional layer. Then, to match the final output resolution with input resolution, rather than using another two deconvolutional layers, we used bilinear interpolation to change the output DVF’s resolution. This is because that bilinear interpolation could generate smooth DVFs that model the actual head and neck motion more accurately than deconvolutional layers. The second difference is that we used additional discriminator network to judge the realism of the generated DVF. Given that our method and CycleMorph are unsupervised deep learning-based methods. These methods may face the challenge of lack of DVF regularization. To overcome this challenge, we proposed to use both discriminator and smoothness constraints for DVF regularization. The discriminator was trained to differentiate the deformed images from the fixed images, generating a loss term by penalizing unrealistic deformed images. Therefore, generator of the proposed network was encouraged to predict realistic DVFs.

Another potential application of the proposed method is to perform longitudinal image registration to register multiple QA CTs to the planning CT to analyze the anatomical variation throughout the course of treatment. Since the dual-feasible network can facilitate bi-directional registration, it is capable of co-registering all of the available QA CTs to a common planning CT image coordinate system. By doing so, we can analyze the longitudinal anatomical variations, which in turn could guide the physician about the margins needed to safely administer the prescribed dose without violating OAR constraints considering both the patient setup uncertainty and patient response to treatment.

No prepossessing was applied to the QA CT images to improve the image quality before deformable image registration using the proposed method. Therefore, the CT image artifacts seen clinically are present in this study. Suboptimal image quality of the QA CT images, such as inter-fraction variations in the altered HU values and streak artifacts, could impact the accuracy of image registration. Deep learning-based image synthetic approaches have been investigated and shown promising result in improving the image quality.²⁹ Therefore, combination of these approaches with the proposed method may further improve the image registration results.

Images were evaluated using qualitative and quantitative methods. The qualitative evaluations included the visual inspections of the deformed, fusion, difference images and intensity profiles. The quantitative metrics used for analysis were TRE, MAE, PSNR and SSIM. Across the various evaluation metrics, our dual-feasible network has shown superior performance as compared to VoxelMorph. However, further analysis beyond the scope of this paper is still warranted for task-specific applications to evaluate the clinical relevance, such as the accuracy of contour propagation, dose volume histogram analysis, informative optimal margin selection in optimization structure creation and dose accumulation.

5. Conclusion

We proposed a deep learning-based dual-feasible network for automatic deformable image registration of planning CT and QA CTs. The efficacy and accuracy of our method have been tested on a dataset of head and neck cancer patients and benchmarked against the results from VoxelMorph. Our method can perform accurate and fast deformable registration between planning CT and QA CTs, which could support multiple clinical applications.