Abstract
COVID-19 is the most serious public health event of the 21st century and has had a huge impact across the world. The spatio-temporal pattern analysis and simulation of epidemic spread have become the focus of current research. LSTM model has made a lot of achievements in the prediction of infectious diseases by virtue of its advantages in time prediction, but lacks the spatial expression. CA model plays an important role in epidemic spatial propagation modeling due to its unique evolution characteristics from local to global. However, no existing studies of CA have considered long-term dependence due to the impact of time changes on the evolution of the epidemic, and few have modeled using location data from actual diagnosed patients. Therefore, we proposed a LSTM-CA model to solve above mentioned problems. Base on the advantages of LSTM in temporal level and CA in spatial level, LSTM and CA are integrated from the spatio-temporal perspective of geography based on the fine-grained characteristics of epidemic data. The method divides the study area into regular grids, simulates the spatial interactions between neighborhood cells with the help of CA model, and extracts the parameters affecting the transition probability in CA with the help of LSTM model to assist evolution. Simulations are conducted in Python 3.4 to model the propagation of COVID-19 between Feb, 6 to Mar 20, 2020 in China. Experimental results show that, LSTM-CA performs a higher statistical accuracy than LSTM and spatial accuracy than CA, which could demonstrate the effectiveness of the proposed model. This method could be universal for the temporal and spatial transmission of major public health events. Especially in the early stage of the epidemic, we can quickly understand its development trend and cycle, so as to provide an important reference for epidemic prevention and control and public sentiment counseling.
Keywords: COVID-19, LSTM, CA, Spatio-temporal, Modeling
1. Introduction
The outbreak of the Corona Virus Disease 2019 (COVID-19) has had a serious impact on people's lives and health, social security and economic growth trends in China as well as the world [1], [2], [3], [4]. In March 2020, the World Health Organization declared COVID-19 a pandemic [5]. Modeling the spatio-temporal transmission trend of infectious diseases is the primary task of establishing and improving epidemic prevention and control system, especially for highly pathogenic infectious diseases with fast transmission speed [6], [7], [8], [9], which makes the prediction of infectious diseases an important research topic.
Time series statistics of epidemic cases record information such as daily new cases, recovered cases, death cases. To simulate the time series spread of the epidemic, classical analytical and numerical models in epidemiology were employed based on statistical data [10], [11]. Among prediction methods for modeling based on nonlinear relations in time series, Long Short-Term Memory (LSTM) networks is considered as the most representative one [12]. LSTM solves the problem of limited long-term dependence of Recurrent Neural Network (RNN) by adding internal gating mechanism [13], has been quite successful and widely used on a number of issues, such as high-speed traffic forecast, stock price forecasts and air pollution forecasts [14], [15], [16], [17]. Nanshan Zhong's team demonstrated the effectiveness of SEIR and LSTM in predicting the epidemic situation of infectious diseases at the very beginning of the COVID-19 outbreak [18]. Li et al. built a prediction model using a fusion neural network combined Convolutional Neural Networks (CNN) with LSTM to estimate the future infection risk by considering the spatial pattern and temporal trend of population movement [19]. ArunKumar proposed state-of-art deep learning Recurrent Neural Networks (RNN) models to predict the country-wise cumulative confirmed cases, cumulative recovered cases and the cumulative fatalities [20]. However, at the early stage of the spread of infectious diseases, the time series data of cumulative infections is as high as a rising trend, is a non-stationary series. Therefore, LSTM can only successfully make short-term prediction according to the time sequence, while long-term forecast results show that the existing number of confirmed cases will continue to grow, unable to estimate the development of the ceiling, this is clearly contrary to fact.
To control the propagation of the disease, the government took a series of Non-Pharmaceutical Interventions (NPI), such as home quarantine and travel ban [21], [22]. Although these measures can slow down the spread of the epidemic to a certain extent [23], [24], each time the prevention and control of the epidemic will cause significant losses to the economic and social development of the affected areas [25], [26]. Therefore, in addition to a reasonable anticipation of the temporal level of the development of epidemic, effective judgment and prediction of the spatial spread of epidemic diseases should also be made, which helps the decision-making departments in different areas for different levels of precision differential control, in order to minimize its epidemic control costs as well as to effectively control the spread of the epidemic [27].
As of Cellular Automaton (CA) has the characteristics of discrete time, space and state, and can reflect the complex changes of the whole system by synchronous evolution of local rules, which provides a promising direction for the spatial simulation of infectious diseases. A few years ago, A lot of research in this field has emerged. For example, Li et al. simulated the transmission process of HIV/AIDS with the classical two-dimensional cellular automata, and considered the influence of population size, initial infection rate and other factors on the transmission of the disease [28]. Guan Chao et al. proposed a cellular automaton model with extended neighborhood to simulate an infectious disease outbreak, and facilitated the study of the dynamics of epidemics of different infectious diseases [29]. Peter M.A. Sloot et al. constructed a 4-state cellular automata model to study the transmission characteristics of AIDS using European AIDS distribution data [30]. Since the outbreak of COVID-19, scholars have also modeled and predicted it based on CA [31]. Some researchers used sequential evolutionary genetic algorithm to optimize the parameters of the CA model to simulate the COVID-19 epidemic development curve [32], [33]. The spread of COVID-19 is also simulated by using a probabilistic cellular automaton and effects of distinct quarantine regimes on disease propagation are investigated [34], [35]. However, those methods have two limitations. Firstly, existing models does not take the influence of temporal dependence into account, so the model is not satisfactory for the prediction of continuous time series data in its present form. All the models mentioned above fail to consider the complex behavior of cells in the process of disease transmission, and fail to discuss the influence of various factors such as population flow on disease transmission, thus failing to achieve the purpose of effective prediction. On the other hand, most of the existing CA-based simulations of infectious diseases are based on virtual geographic grids (simulated data), each small box or cell in this lattice can be occupied by a person [36], instead of a real house or residential area. Although they can simulate the impact of policy changes on the spread of epidemics, they cannot simulate, let alone predict, the spread of epidemics in real areas.
In this paper, based on the advantages of CA and LSTM in space and time, the integration and coupling of LSTM-CA were carried out from the mechanism, and the spatio-temporal prediction method of epidemic spread of infectious diseases was constructed to model the spatio-temporal propagation of COVID-19 in China. In LSTM-CA, LSTM makes use of its gating advantages to automatically extract the time information generated by long-term dependence in historical data, make a long-term series prediction of epidemic development in each cell, and thereby affect the transition probability of CA. CA makes use of the advantage of spatial dimension and finally determines the state of the microscopic cellular unit by defining the transformation rules of the cell. Through the evolution of CA in the micro state, the statistical data in the macro state is obtained, and the statistical data is fed to LSTM for a new round of update of the transition probability until the prediction step size or convergence is reached. A lattice in CA can be generalized as a real area of China, and GIS was employed to enable people to understand the epidemic propagation more intuitively. Summarily, our core contributions of our proposed LSTM-CA method could be listed as below:
-
•
In terms of time series, the LSTM-CA method proposed in this paper can get a good simulation effect of epidemic situation, and the average prediction statistical accuracy of epidemic situation reaches as high as 94 %.
-
•
The proposed LSTM-CA model mines its changing trend from time series, simulates its diffusion result from spatial level, and achieves spatio-temporal prediction.
-
•
The proposed LSTM-CA method can significantly reduce the modeling complexity of epidemic simulation and improve the computational efficiency of spatio-temporal data. It provides a novel way for spatio-temporal simulation of infectious diseases in complex environment.
-
•
This study demonstrates the effectiveness of location-based modeling for epidemic modeling and prediction.
In the subsequent sections, we present details about the LSTM-CA models. Firstly, detailed theory of proposed LSTM-CA method and experimental data used in our study are given in Section 2. Afterwards, analysis and discussion of the simulated results are reported in Section 3. Finally, in Section 4, the main contributions of this paper are summarized as well as future work items are enumerated.
2. Methodology
2.1. Model description
In this section, we define a spatially explicit epidemiological model through combining CA with the transition probability parameters estimated by LSTM. We suppose that, each cell in the CA represents a real geographical unit of 10 km*10 km on the map of China, and the grid has attributes such as geographical location, population density, migration index, and confirmed number of COVID-19 cases. By defining transformation rules, the simulation evolution of epidemic situation based on CA is realized. The main features of LSTM-CA model are as mentioned below: 1) Since we defined a real spatial unit as cellular unit in CA, the transformation of disease status of a single patient is not considered in this model, and we mainly consider the change of the total number of diagnosed patients with cellular unit as the principal part. 2) Interaction between CA model and LSTM model mainly depends on three indicators, namely relative growth infectious rate (IR), recovered rate (RR) and death rate (DR), which jointly determine the number of confirmed cases in each cell. The relative growth infectious rate is responsible for increasing the number of confirmed cases, while cure rate and death rate are responsible for removing the number of confirmed cases. 3) No birth or immigration is considered, keeping the total number of people in the population constant. 4) Since Wuhan was the main outbreak area in China at the beginning of 2020, in order to reflect the impact of the number of people migrating from Wuhan on the development of the local epidemic, we took the migration index as one of the attributes of the grid to control the evolution of the cumulative number of confirmed cases in the grid. With these features considered, the framework of LSTM-CA can be established as a combination of LSTM and CA model as is described in following subsections.
2.2. Model building and implementation
2.2.1. Extension of LSTM
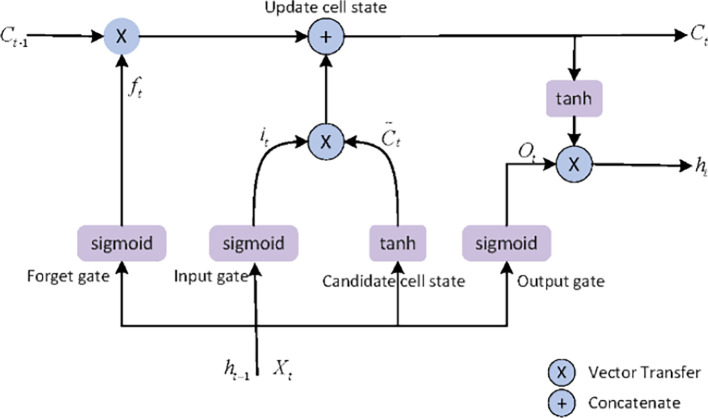
LSTM, a typical variant of RNN, adds memory units between neurons in the hidden layer so that can control the information of time series. The memory and forgetting degree of the previous data information and the current data information can be controlled through several controllable gates when each unit of the hidden layer of LSTM is transferred each time, such as forgetting gate, input gate and output gate, so as to make the recurrent neural network memory information for a longer time, for the practical application of recurrent neural network also has a greater role. Compared with ordinary RNN, LSTM increases the controllability of memory function. The traditional LSTM infrastructure network structure for time series prediction is shown in Fig. 1 , and Hochreiter et al. introduced the formula principle of LSTM in detail [12].
Fig. 1.
The structure of LSTM. LSTM consists of forgetting gate, input gate and output gate. The forgetting gate is responsible for selectively forgetting information in the cell state, the input gate determines what new information to store in the cell state, and the output gate determines what values to output.
In this study, we apply LSTM model with rolling update mechanism for relatively long forecast period, as what we did in our previous work [37]. Therefore, the confirmed cases, recovered cases and death cases can be projected by LSTM model, and based on the predicting result, the IR, RR and DR, which would be employed in CA modeling are calculated according to these formulas:
| (1) |
| (2) |
| (3) |
where the , , represents the number of daily confirmed, daily recovered and daily death cases on day , and , , and describe the accumulated number of confirmed, recovered and death cases on day , respectively.
2.2.2. CA model algorithm
In the early 1940s, Von Neumann proposed the concept of CA, which has been widely used as a bottom-up dynamic modeling method to simulate the evolution of complex linear systems [38]. In the 1980s, S.Wolfram [39] made a comprehensive study of CA. CA represent entities in discrete space and they have certain behavior rules. These cells are contained in a grid with a set of rules of behavior that they can interact with and influence their state over time. This numerical approach is consistent with understanding the precise nature of disease contamination in controlled environments. CA is used to simulate the interaction mechanism of space system from top to bottom by reflecting the changes of micro scale through four elements: cell, cell state, neighborhood and transformation rules.
For the CA model, defining five basic components, including cell space, cell state, neighborhood, time step, and transition rules is needed. Space can be represented as a grid of discrete cells. Each cell saves an initial state from a predefined finite set of states and evolves along discrete time steps, with the neighbors of a given cell defined as a set of cells based on proximity. CA captures the spatial dependence of local interactions between cells by establishing transition rules that are applied to each cell in regular discrete time steps, and calculates the new state of a given cell by considering the previous state of the given cell and the cells surrounding the defined neighborhood. For the prediction model of infectious disease transmission, the precise transformation rule is the key factor to determine the prediction ability of the model. The automaton rules in our study can be listed below:
-
-
Rule 1, the cell is the most basic and smallest unit in the CA model and is the object of model research.
-
-
Rule 2, cell space represents as a grid of discrete cells where the cell located.
-
-
Rule 3, cell state is the state of each cell, in our study, the state is depended on a series of attributes of this cell, such as population density, migration index and geographic location.
-
-
Rule 4, neighborhood can influence the state of each cell. It usually includes the Von Neumann neighborhood and the Moorish neighborhood. The von Neumann neighborhood has eight neighbors while the Moorish neighborhood has four basic adjacent neighbors. Considering the geographical proximity of infectious disease transmission, we choose the Von Neumann neighborhood in our research.
-
-
Rule 5, time step controls the evolution of our model, each cell can evolute to a new state at each time step.
-
-
Rule 6, transition rules are the core compartment of CA model. CA model has three characteristics in simulation: synchronous change, local influence (by adjacent cells), global consistency (all cells are bound by the same rules), and the state of each cell changes with the change of time. The state of the cell at the next moment is determined by the current state of the cell and the state of its neighborhood, that is, the transformation process of traditional CA can be expressed by the following formula:
| (4) |
where represents the cellular state of cell at time , represents the cellular state of cell at time , represents the neighborhood cellular state of cell at time , and represents the transformation function of cell from the state at time to the state at time .
Population movement during the Spring Festival travel rush is an important reason for the rapid spread of COVID-19 in China in early 2020, so we took the migration index into consideration in the modeling. In addition, the spread of the disease is population-based, so we also considered the impact of the local population density on the spread of the disease. Based on the transmission characteristics of COVID-19, the transformation rules of cellular automata in this paper can be defined as follows:
| (5) |
where represents the relative growth infectious rate, recovered rate and death rate at time , respectively. indicates the population migration from Wuhan to the cell , while signifies the population density at time . Moreover, denotes random events at time , is the transition rule function, which signifies a set of transition rules [40], [41].
2.2.3. LSTM-CA
By combining LSTM and CA, LSTM makes use of its gating advantages to automatically extract the time information generated by long-term dependence in historical data, make a long-term series prediction of epidemic development, and affect the transition probability of each cell in CA with migration index, population density and random factors. CA makes use of the advantage of spatial dimension and finally determines the state of the microscopic cellular unit by defining the transformation rules of the cell.
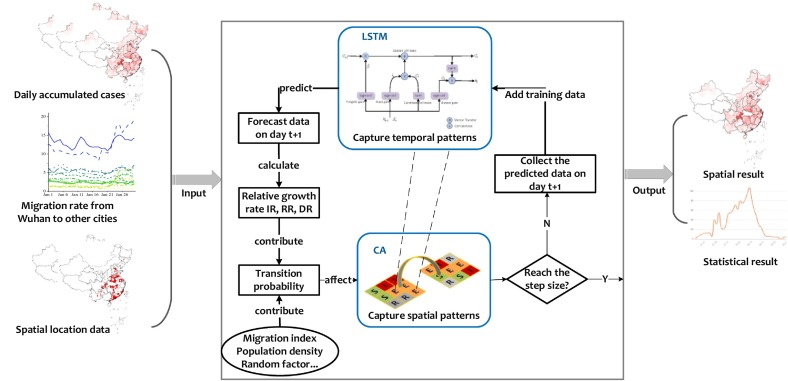
The main procedure of LSTM-CA model is illustrated in Fig. 2 . Estimating a LSTM-CA model typically involves the following steps:
-
(1)
Construct the LSTM model with statistical data of COVID-19. At first, an improved model is built based on LSTM with daily confirmed cases training set. Then, to improve the accuracy of the prediction, the rolling update mechanism is embedded with LSTM for long-term projections. Finally, calculating the relative growth rate IR, RR and DR. We implemented time series forecasting for each cell.
-
(2)
Initialize CA model with two time period confirmed location files, and assign factors influencing model evolution, such as IR, RR, DR, migration index and population density to the model. Then, set threshold values for evolution.
-
(3)
LSTM and CA models are connected by relative growth rates and statistical data of predict, the model then begins to iterate until the predicted step size is reached.
-
(4)
When evolution stops, predicted results are exported as raster file, while spatial and statistical data are collected, and spatial and statistical accuracy are calculated to evaluate the model.
Fig. 2.
The procedure of LSTM-CA proposed in this study. The input of LSTM-CA consists of daily confirmed cases data, migration rate data and spatial location data. After the processing of LSTM-CA combined with two model, the output data including spatial and statistical result are given when reaching the predictive step size.
Eq. (5) defines the transition rule function of CA. It can be seen that based on the traditional CA conversion function, this paper adds the characteristics of the cell itself, its environmental conditions and random infection factors to expand the CA conversion rule. The extended transition probability can be calculated by a series of formulas, as follows.
At time, the probability of cell converting from the state at time t to the state at time is , which is determined jointly by the transition probability of the cell itself , the influence probability of the cell neighborhood , the cell's own environmental factors affecting the probability and the random disturbance term , can be expressed as:
| (6) |
in which , can be calculated according to the traditional CA transition probability calculation method[40], through the two-stage infected data. represents the influence probability of migration index and population density on the central cell, which can be expressed as:
| (7) |
The above formulas can be synthesized as:
| (8) |
where , and represents the relative growth rate of the number of patients infected, recovered and death in the cell itself, and is the improved self-transition probability at time t. shows the effect of neighborhood probability, is the influence probability of the neighborhood cell value on the change of the central cell value. represent the influence probability of migration index and population density, respectively. represents some disturbances with uncertainty and contingency (such as accidental factors include natural disasters, wars, political events, etc.), and its calculation formula can be expressed as follows:
| (9) |
where is a random number between 0 and 1, is used to control the interference strength of the random disturbance term, and is an integer between 1 and 10.
The raster files used in our study were prepared in ArcGIS ver. 10.5, whereas modeling procedure were conducted in Python 3.4, using GDAL 3.3.0, Numpy 1.21, Matplotlib 3.3.2, and Scikit-Learn 0.23.2 libraries.
2.3. Evaluation criterion
In this study, we measure the effectiveness of the model in two dimensions: Statistical Accuracy (StAcc) and Spatial Accuracy (SpAcc). StAcc, as its name suggests, indicates the forecast accuracy of the model. , where is the predicted number of confirmed cases in China, and is the actual confirmed cases count. SpAcc is computed by the accuracy of cellular prediction with confirmed cases. , where represents the number of cells which have predicted confirmed cases and is the number of cells with confirmed cases in fact.
2.4. Datasets
For this study, we employed four publicly available datasets for China (excluding Hong Kong, Macao and Taiwan), including COVID-19 statistical data, migration index data, population census data and spatial location data of confirmed cases. Considering the fine-grained location data of patients were obtained between February 6, 2020 and March 20, 2020, we selected this period as the main time range for this study. All spatial data were unified to the Lambert Conformal Conic (LCC) coordinate system. Details of those datasets are listed in Table 1 . Moreover, to eliminate the influence of different dimensions, the migration rate, population census data were normalized to (0,1).
Table 1.
Details of experimental datasets.
2.4.1. COVID-19 statistical data
Statistical data on COVID-19 in country level of China from February 6, to March 20, 2020 is derived from real-time statistics from John Hopkins University. The most updated epidemical data of COVID-19 are provided by an ArcGIS platform repository published by Dong et al. [42], the Johns Hopkins University Center for Systems Science and Engineering (CSSE) compiles from state health department reports and makes available through a public repository. The data we used included the daily accumulated confirmed cases, deaths cases, cured cases and daily new confirmed cases in this paper (Fig. 3).
Fig. 3.
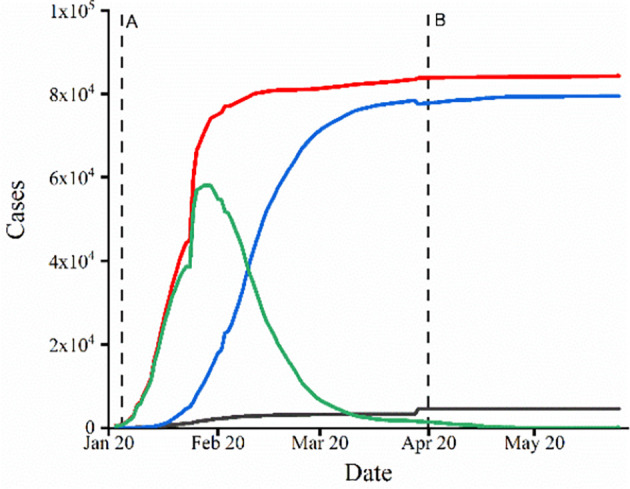
Number of accumulated confirmed cases (red), recovered cases (blue), death cases (gray), and active confirmed cases (green) in China from Jan. 22 to Jun. 14. A and B represents the day when Wuhan was locked and unlocked, respectively (For interpretation of the references to colour in all figure legend in this paper, the reader is referred to the web version of this article.) (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
2.4.2. Migration index data
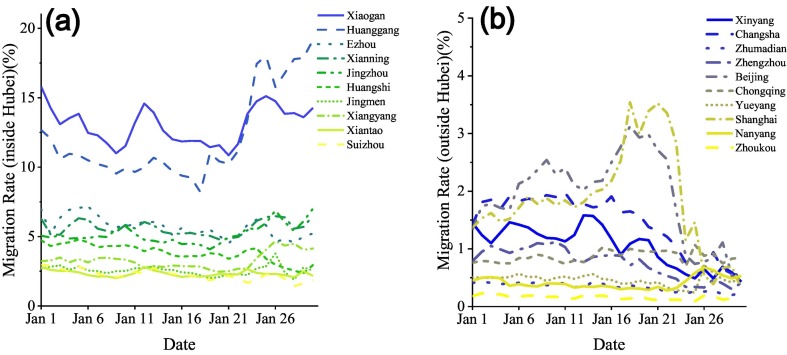
Baidu's migration index reflects the rate of people moving in or out of a city. In our study, we collected migration index data from Wuhan to other prefecture-level cities (Fig. 4). These data are available through at Harvard University. We plotted the migration rate from Wuhan to other prefecture-level cities inside Hubei and outside Hubei, respectively. Considering China announced a lockdown of Wuhan in Jan 23, 2020, we collected the migration rate data from Jan 1, to Jan 31, 2020 to model LSTM-CA.
Fig. 4.
Migration rate from Wuhan to other top 10 prefecture-level cities inside Hubei (a) and outside Hubei (b).
2.4.3. Population census data
Population census data is contained from the Resource and Environmental Data Cloud Platform. The dataset is a 1 km*1 km grid of population spatial distribution data, reflecting the detailed spatial distribution of population data in the whole country, contains 2015 population size, area, demographic characteristics, and other provincial attributes. The data is a grid data type, and each grid represents the number of people in the grid range. In order to ensure the consistency of the research scale, we resampled it and obtained the population density data of 10 km*10 km.
2.4.4. Patient location data
The daily spatial location of infected cases of COVID-19 are derived from a publicly repository provided by GeoHey. GeoHey compromised the spatial location of confirmed cases from Tencent Kandian and Nandu Media, which is accurate to the neighborhood or building where the confirmed patient lives. The time period of this dataset is from February 6, 2020 to March 20, 2020. In order to unify the scale with migration index, population density and other data, we dropped the case points onto a grid of 10 km*10 km by ArcMap 10.5, and calculated the sum of the number of cases in this grid, which was used to obtain the raster data map of the confirmed location, so as to facilitate the calculation of each grid.
3. Simulation and discussion
In this section, two group of experiments are performed to analyze the effectiveness of our proposed LSTM-CA model for predicting the spread of COVID-19 in China. That is to simulate the spatial propagation of COVID-19 by CA and LSTM-CA. Then the comparison of StAcc between LSTM and LSTM-CA and SpAcc between CA and LSTM-CA are analyzed to validate the performance of our proposed model.
3.1. Simulation of COVID-19 propagation based on CA model
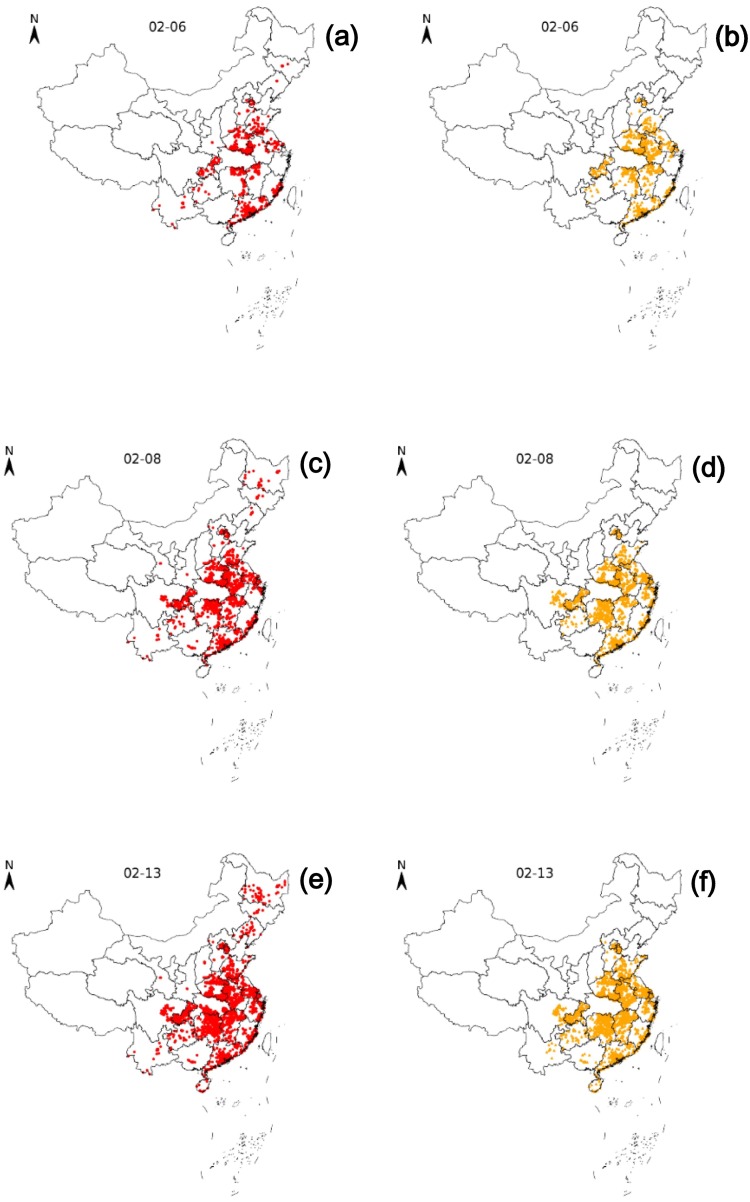
Based on the CA model, we simulated the nationwide spread trend of COVID-19 with the geographical location data of confirmed patients on February 6, and February 7, 2020 (except Hubei province, Hong Kong, Macao and Taiwan) as input. The modeling results are shown in Fig. 5 . As can be seen from the graph, the spread of the epidemic is mainly centered in Hubei and spreading to neighboring cities. In addition, the epidemic is also spreading faster in the Yangtze River Delta, Pearl River Delta, Beijing and other regions with large population bases and large floating populations. According to the comparison between the real transmission situation and the simulation situation, the CA model can simulate the spatial transmission trend of the epidemic basically. However, sporadic outbreaks in the process could not be captured in time, which led to inaccurate prediction of epidemic changes in Gansu, Shaanxi, Yunnan, Guangxi, Shanxi and Hebei province by CA model.
Fig. 5.
Comparison of the spread of COVID-19 based on CA in actual results (the map with red point) and simulated results (the map with orange point) in Feb. 6 (a and b), Feb. 8 (c and d), Feb. 13. (e and f), 2020, respectively. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
3.2. Simulation of COVID-19 propagation based on LSTM-CA model
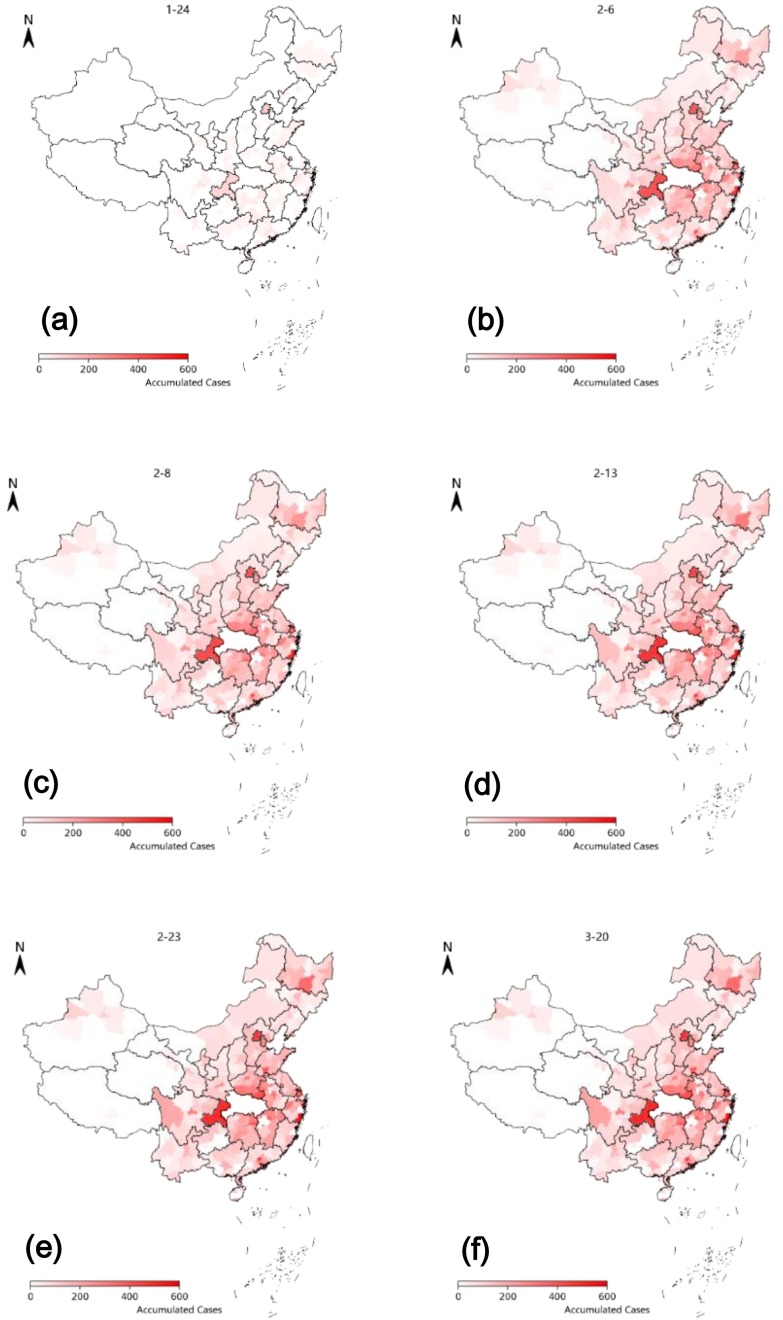
Based on the geographical location data of confirmed patients, CA model alone cannot simulate the outbreak time and scale in places without epidemic disease in initial training data, since CA only considers spatial dependence and ignores the influence of time dependence caused by time changes on evolution rules. After adding LSTM model, according to LSTM's advantage in time series prediction, the transformation probability of CA at the time of evolution was gradually adjusted, so that the epidemic changes in Gansu, Shaanxi, Yunnan, Guangxi, Shanxi and Hebei province could be appropriately simulated. The modeling results of LSTM-CA are shown in Fig. 6 . The modeling results can capture sporadic outbreaks of epidemics in provinces far away from Hubei province, such as Xinjiang, Northeast China, Yunnan and Guangxi province, so as to dynamically adjust the modeling results. According to Fig. 6, from the perspective of visual effects, LSTM-CA is basically consistent with the simulation of real epidemic transmission. Meanwhile, similar to the conclusion in Section 3.1, the epidemic spread faster in the Pearl River Delta and Yangtze River Delta. According to our analysis, the more developed the economy is, the faster the epidemic spread, which is consistent with the conclusions of previous studies [43].
Fig. 6.
Accumulated confirmed cases predicted with LSTM-CA model in China. (a) Feb. 6, 2020 (actual number), (b) Feb.6, 2020 (predicted number), (c) Feb.8, 2020 (predicted number), (d) Feb.13, 2020 (predicted number), (e) Feb.23, 2020 (predicted number), (e) Mar. 20, 2020 (actual number).
3.3. Validation of simulated LSTM-CA
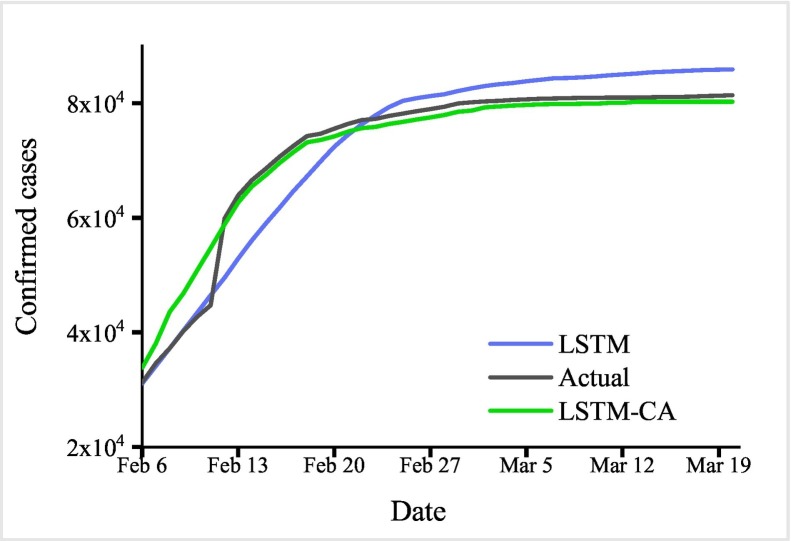
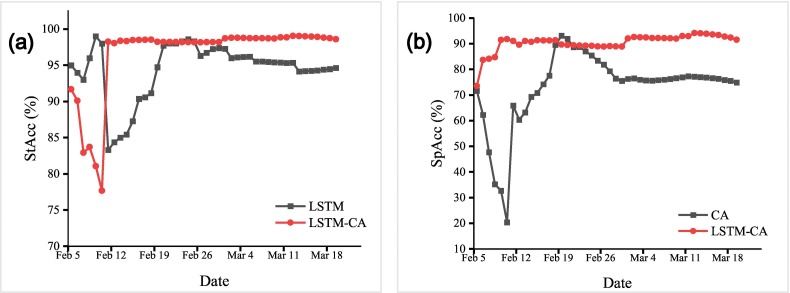
In this section, we compared the predictive result between LSTM, LSTM-CA and the actual number of confirmed cases. As is shown in Fig. 7 , we can see that the epidemic curve simulated by LSTM-CA is more consistent with the real situation. We also compared StAcc of LSTM and LSTM-CA, and SpAcc of LSTM-CA and CA. The experimental results are shown in the Fig. 8 below, from which it can be drawn that LSTM-CA has higher accuracy than LSTM in terms of statistical number prediction. In terms of spatial prediction, LSTM-CA has higher spatial accuracy than CA.
Fig. 7.
The number of accumulated confirmed cases predicted by LSTM (blue), LSTM-CA (green) between Feb. 6 and Mar. 20, 2020. The gray line represents the actual data of COVID-19 in China. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
Fig. 8.
(a) Comparison of the statistical predict accuracy of LSTM and LSTM-CA. (b) Comparison of the spatial predict accuracy of CA and LSTM-CA.
An accuracy assessment revealed a very high statistical average accuracy (>94 %) between simulated results and actual confirmed cases in China from February 6, 2020 to Mar. 20, 2020, as is illustrated in Fig. 8 (a). Meanwhile, the spatial accuracy of LSTM-CA is always approximately 90 %, as is shown in Fig. 8 (b).
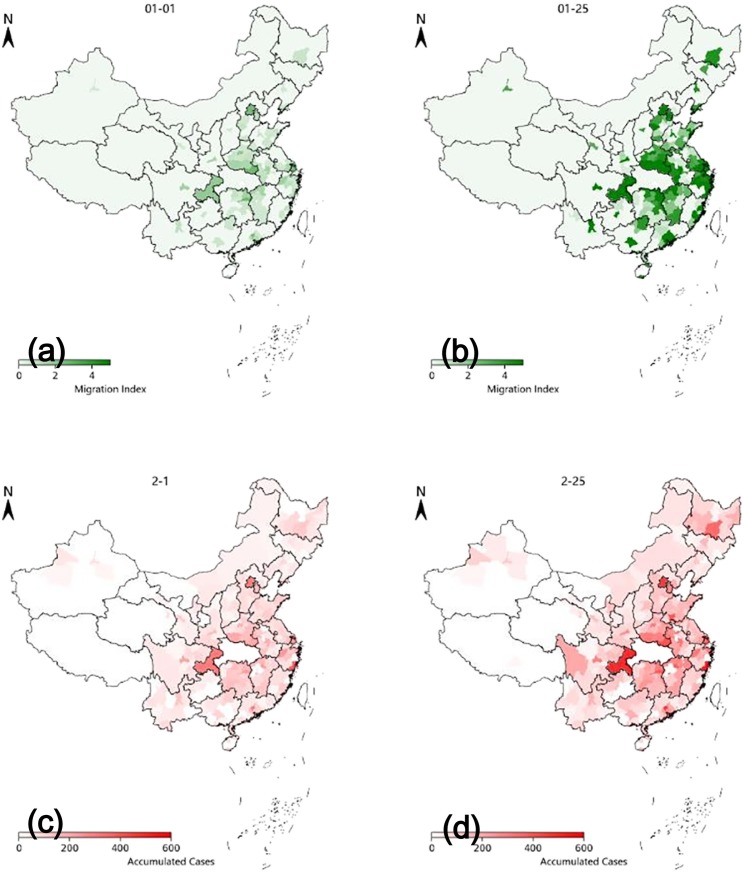
In the modeling of LSTM-CA, we not only considered the impact of local population density on the spread of the epidemic, but also included the impact of Wuhan's population migration before the Spring Festival on the development and changes of the local epidemic. Therefore, we also analyzed the impact of population size flowing from Wuhan to prefecture-level cities in all provinces (except Hubei province) on the development of the epidemic there one month later. As shown in Fig. 9 , the distribution of migration index on January 1 (Gregorian New Year) and January 25 (Lunar New Year) was highly correlated with the distribution of cumulative confirmed cases in prefecture-level cities across the country on February 1 and February 25. This indicates that the proposed LSTM-CA model can reflect the main conclusion that population mobility drives the spread of the epidemic, and is consistent with the conclusion of existing studies [44].
Fig. 9.
The impact of population flow from Wuhan to prefecture-level cities in all provinces (except Hubei province) and the distribution of confirmed cases simulated by LSTM-CA. (a) Migration rate on New year, 2020. (b) Migration rate on Lunar New year, 2020. (c) Confirmed cases on Feb. 1, 2020. (d) Confirmed cases on Feb. 25, 2020.
4. Conclusion
In this paper, the coupling of LSTM and CA is realized. Based on the advantages of LSTM in time dimension and CA in space dimension, LSTM and CA are integrated based on machine learning model from the spatio-temporal perspective of geography based on the fine-grained characteristics of epidemic data. The method divides the study area into regular grids, simulates the spatial interactions between neighborhood cells with the help of CA model, and extracts the time series dependencies with the help of LSTM model. The innovation lies in the integration of time and space information, which provides a new way to solve the short-term epidemic trend prediction. The hybrid model not only has the ability of spatially fine and near real-time prediction of epidemic trend, but also has the attribute of geographical information in the prediction results of epidemic statistics, which can be directly used to achieve visual expression on the map.
Of course, the results of our proposed method also have a lot to do with the willingness of the public to cooperate, so changes in individual behavior should be considered further. Our future research will focus on the following aspects: First, we will combine prediction and decision-making, establish a complete epidemic prediction and decision-making linkage system, and use GIS technology to display the development and changes of the epidemic more vividly. Second, due to limited data acquisition, the model in this paper cannot be verified in a larger scope. In the future, new data should be generated based on simulation environment to assist modeling. In addition, we reiterate our call for public health authorities around the world to provide more anonymous, location-based patient data so that researchers can further study the spatial-temporal patterns and characteristics of COVID-19 transmission.
Notes
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
Acknowledgement
This research was supported by the Fundamental Research Funds for the Central Universities under Grant Nos. 2652020002, 2652020001 and 2652020004 and 2021 Graduate Innovation Fund Project of China University of Geosciences, Beijing, grant number ZY2021YC010.
CRediT authorship contribution statement
H. L. and X. Z. conceptualized the initial idea. X. Z. and H. L. provided funding support. P. W. collected receipts, conducted the model analysis, calculated the result and wrote the first draft of the manuscript. R. M. contributed to the data processing. All authors participated in the analysis and discussion of the results, and participated in the revision of the manuscript.
Data availability
All tha data source used in our research is listed in our mauscript
References
- 1.Hsiang S., Allen D., Annan-Phan S., Bell K., Bolliger I., Chong T., Druckenmiller H., Huang L.Y., Hultgren A., Krasovich E. The effect of large-scale anti-contagion policies on the COVID-19 pandemic. Nature. 2020;584(7820):262–267. doi: 10.1038/s41586-020-2404-8. [DOI] [PubMed] [Google Scholar]
- 2.Li R., Pei S., Chen B., Song Y., Zhang T., Yang W., Shaman J. Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV-2) Science. 2020;368(6490):489–493. doi: 10.1126/science.abb3221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Su F., Fu D., Yan F., Xiao H., Pan T., Xiao Y., Kang L., Zhou C., Meadows M., Lyne V. Rapid greening response of China's 2020 spring vegetation to COVID-19 restrictions: implications for climate change. Sci Adv. 2021;7(35) doi: 10.1126/sciadv.abe8044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Wang C., Horby P.W., Hayden F.G., Gao G.F. A novel coronavirus outbreak of global health concern. Lancet. 2020;395(10223):470–473. doi: 10.1016/S0140-6736(20)30185-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Organization W.H. 2020. 2020-World Health Organization-Coronavirus Disease 2019 (COVID-19) Situation Report 51.pdf. [Google Scholar]
- 6.Azimi P., Keshavarz Z., Laurent J.G.C., Stephens B., Allen J.G. Mechanistic transmission modeling of COVID-19 on the Diamond Princess cruise ship demonstrates the importance of aerosol transmission. Proc Natl Acad Sci. 2021;118(8) doi: 10.1073/pnas.2015482118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kissler S.M., Tedijanto C., Goldstein E., Grad Y.H., Lipsitch M. Projecting the transmission dynamics of SARS-CoV-2 through the postpandemic period. Science. 2020;368(6493):860–868. doi: 10.1126/science.abb5793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Oliveira J.F., Jorge D.C., Veiga R.V., Rodrigues M.S., Torquato M.F., da Silva N.B., Fiaccone R.L., Cardim L.L., Pereira F.A., de Castro C.P. Mathematical modeling of COVID-19 in 14.8 million individuals in Bahia, Brazil. Nat Commun. 2021;12(1):1–13. doi: 10.1038/s41467-020-19798-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Rockett R.J., Arnott A., Lam C., Sadsad R., Timms V., Gray K.-A., Eden J.-S., Chang S., Gall M., Draper J. Revealing COVID-19 transmission in Australia by SARS-CoV-2 genome sequencing and agent-based modeling. Nat Med. 2020;26(9):1398–1404. doi: 10.1038/s41591-020-1000-7. [DOI] [PubMed] [Google Scholar]
- 10.Giuliani D., Dickson M.M., Espa G., Santi F. Modelling and predicting the spatio-temporal spread of COVID-19 in Italy. BMC Infect Dis. 2020;20(1):10. doi: 10.1186/s12879-020-05415-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Koo J.R., Cook A.R., Park M., Sun Y., Sun H., Lim J.T., Tam C., Dickens B.L. Interventions to mitigate early spread of SARS-CoV-2 in Singapore: a modelling study. Lancet Infect Dis. 2020;20(6):678–688. doi: 10.1016/S1473-3099(20)30162-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hochreiter S., Schmidhuber J. Long short-term memory. Neural Comput. 1997;9(8):1735–1780. doi: 10.1162/neco.1997.9.8.1735. [DOI] [PubMed] [Google Scholar]
- 13.Graves A., Mohamed A.-r., Hinton G. 2013 IEEE international conference on acoustics, speech and signal processing. IEEE; 2013. Speech recognition with deep recurrent neural networks. [Google Scholar]
- 14.Cortez B., Carrera B., Kim Y.-J., Jung J.-Y. An architecture for emergency event prediction using LSTM recurrent neural networks. Expert Syst Applic. 2018;97:315–324. [Google Scholar]
- 15.Nelson D.M.Q., Pereira A.C.M., de Oliveira R.A. 2017 International Joint Conference on Neural Networks. 2017. Stock market's price movement prediction with LSTM neural networks; pp. 1419–1426. [Google Scholar]
- 16.Zhang Q., Lam J.C., Li V.O., Han Y. 2020. Deep-AIR: a hybrid CNN-LSTM framework for Fine-grained air pollution forecast. arXiv preprint arXiv:2001.11957. [Google Scholar]
- 17.Zhang T., Guo G. Graph attention LSTM: a spatiotemporal approach for traffic flow forecasting. IEEE IntellTranspSystMag. 2022;14(2) [Google Scholar]
- 18.Yang Z., Zeng Z., Wang K., Wong S.-S., Liang W., Zanin M., Liu P., Cao X., Gao Z., Mai Z., Liang J., Liu X., Li S., Li Y., Ye F., Guan W., Yang Y., Li F., Luo S., Xie Y., Liu B., Wang Z., Zhang S., Wang Y., Zhong N., He J. Modified SEIR and AI prediction of the epidemics trend of COVID-19 in China under public health interventions. J Thorac Dis. 2020;12(3):165–174. doi: 10.21037/jtd.2020.02.64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Li Z., Li X., Porter D., Zhang J., Weissman S. Monitoring the spatial spread of COVID-19 and effectiveness of control measures through human movement data: proposal for a predictive model using big data analytics. JMIR ResProtoc. 2020;9(12):1–10. doi: 10.2196/24432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.ArunKumar K., Kalaga D.V., Kumar C.M.S., Kawaji M., Brenza T.M. Forecasting of COVID-19 using deep layer recurrent neural networks (RNNs) with gated recurrent units (GRUs) and long short-term memory (LSTM) cells. Chaos, SolitonsFractals. 2021;146 doi: 10.1016/j.chaos.2021.110861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Flaxman S., Mishra S., Gandy A., Unwin H.J.T., Mellan T.A., Coupland H., Whittaker C., Zhu H., Berah T., Eaton J.W. Estimating the effects of non-pharmaceutical interventions on COVID-19 in Europe. Nature. 2020;584(7820):257–261. doi: 10.1038/s41586-020-2405-7. [DOI] [PubMed] [Google Scholar]
- 22.Lai S., Ruktanonchai N.W., Zhou L., Prosper O., Luo W., Floyd J.R., Wesolowski A., Santillana M., Zhang C., Du X. Effect of non-pharmaceutical interventions to contain COVID-19 in China. Nature. 2020;585(7825):410–413. doi: 10.1038/s41586-020-2293-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Diarra M., Kebir A., Talla C., Barry A., Faye J., Louati D., Opatowski L., Diop M., White L.J., Loucoubar C. Non-pharmaceutical interventions and COVID-19 vaccination strategies in Senegal: a modelling study. BMJ Glob Health. 2022;7(2) doi: 10.1136/bmjgh-2021-007236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Soltesz K., Gustafsson F., Timpka T., Jaldén J., Jidling C., Heimerson A., Schön T.B., Spreco A., Ekberg J., Dahlström Ö.J.N. The effect of interventions on COVID-19. Nature. 2020;588(7839):E26–E28. doi: 10.1038/s41586-020-3025-y. [DOI] [PubMed] [Google Scholar]
- 25.Yoosefi Lebni J., Abbas J., Moradi F., Salahshoor M.R., Chaboksavar F., Irandoost S.F., Nezhaddadgar N., Ziapour A. How the COVID-19 pandemic effected economic, social, political, and cultural factors: a lesson from Iran. Int J Soc Psychiatry. 2021;67(3):298–300. doi: 10.1177/0020764020939984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.You S., Wang H., Zhang M., Song H., Xu X., Lai Y. Assessment of monthly economic losses in Wuhan under the lockdown against COVID-19. Humanit Soc Sci Commun. 2020;7(1):1–12. [Google Scholar]
- 27.Gong B., Zhang S., Yuan L., Chen K.Z. A balance act: minimizing economic loss while controlling novel coronavirus pneumonia. J Chin Gov. 2020;5(2):249–268. [Google Scholar]
- 28.Xuan H., Xu L., Li L. A CA-based epidemic model for HIV/AIDS transmission with heterogeneity. Ann Oper Res. 2009;168(1):81. doi: 10.1007/s10479-008-0369-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Guan C., Yuan W., Peng Y. 2011 Fourth International Joint Conference on Computational Sciences and Optimization. IEEE; 2011. A cellular automaton model with extended neighborhood for epidemic propagation. [Google Scholar]
- 30.Sloot P.M., Boukhanovsky A.V., Keulen W., Tirado-Ramos A., Boucher C.A. A grid-based HIV expert system. J Clin Monit Comput. 2005;19(4):263–278. doi: 10.1007/s10877-005-0673-2. [DOI] [PubMed] [Google Scholar]
- 31.Moghari S., Ghorani M. A symbiosis between cellular automata and dynamic weighted multigraph with application on virus spread modeling. Chaos, SolitonsFractals. 2022;155 doi: 10.1016/j.chaos.2021.111660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Ghosh S., Bhattacharya S. A data-driven understanding of COVID-19 dynamics using sequential genetic algorithm based probabilistic cellular automata. Appl Soft Comput. 2020;96 doi: 10.1016/j.asoc.2020.106692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Monteiro L.H.A., Gandini D., Schimit P.H.J. The influence of immune individuals in disease spread evaluated by cellular automaton and genetic algorithm. Comput Methods Programs Biomed. 2020;196 doi: 10.1016/j.cmpb.2020.105707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Medrek M., Pastuszak Z. Numerical simulation of the novel coronavirus spreading. Expert SystApplic. 2021;166 doi: 10.1016/j.eswa.2020.114109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Monteiro L., Fanti V., Tessaro A.J.E.C. On the spread of SARS-CoV-2 under quarantine: a study based on probabilistic cellular automaton. EcolComplex. 2020;44 [Google Scholar]
- 36.Ghosh S., Bhattacharya S.J.S.C.S. Computational model on COVID-19 pandemic using probabilistic cellular automata. SN ComputSci. 2021;2(3):1–10. doi: 10.1007/s42979-021-00619-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Wang P., Zheng X., Ai G., Liu D., Zhu B. Time series prediction for the epidemic trends of COVID-19 using the improved LSTM deep learning method: case studies in Russia, Peru and Iran. Chaos, SolitonsFractals. 2020;140 doi: 10.1016/j.chaos.2020.110214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Neumann J., Burks A.W. University of Illinois press Urbana; 1966. Theory of self-reproducing automata. [Google Scholar]
- 39.Wolfram S. Cellular automata as models of complexity. Nature. 1984;311(5985):419–424. [Google Scholar]
- 40.Chenghu Z., Zhanli S., Yichun X. Science Press; Beijing: 1999. Geo-cellular automata research. [Google Scholar]
- 41.Liu X., Li X., Yeh A.G.-O., He J., Tao J. Discovery of transition rules for geographical cellular automata by using ant colony optimization. SciChina SerDEarth Sci. 2007;50(10):1578–1588. [Google Scholar]
- 42.Dong E., Du H., Gardner L. An interactive web-based dashboard to track COVID-19 in real time. Lancet Infect Dis. 2020;20(5):533–534. doi: 10.1016/S1473-3099(20)30120-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Liu D., Zheng X., Zhang L.J.L. Simulation of spatiotemporal relationship between COVID-19 propagation and regional economic development in China. 10(6) 2021. p. 599. [Google Scholar]
- 44.Jia J.S., Lu X., Yuan Y., Xu G., Jia J., Christakis N.A. Population flow drives spatio-temporal distribution of COVID-19 in China. Nature. 2020;582(7812):389–394. doi: 10.1038/s41586-020-2284-y. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All tha data source used in our research is listed in our mauscript