IRAA: A statistical tool for investigating a protein–protein interaction interface from multiple structures

Abstract

Understanding protein–protein interactions (PPIs) is fundamental to infer how different molecular systems work. A major component to model molecular recognition is the buried surface area (BSA), that is, the area that becomes inaccessible to solvent upon complex formation. To date, many attempts tried to connect BSA to molecular recognition principles, and in particular, to the underlying binding affinity. However, the most popular approach to calculate BSA is to use a single (or in some cases few) bound structures, consequently neglecting a wealth of structural information of the interacting proteins derived from ensembles corresponding to their unbound and bound states. Moreover, the most popular method inherently assumes the component proteins to bind as rigid entities. To address the above shortcomings, we developed a Monte Carlo method‐based Interface Residue Assessment Algorithm (IRAA), to calculate a combined distribution of BSA for a given complex. Further, we apply our algorithm to human ACE2 and SARS‐CoV‐2 Spike protein complex, a system of prime importance. Results show a much broader distribution of BSA compared to that obtained from only the bound structure or structures and extended residue members of the interface with implications to the underlying biomolecular recognition. We derive that specific interface residues of ACE2 and of S‐protein are consistently highly flexible, whereas other residues systematically show minor conformational variations. In effect, IRAA facilitates the use of all available structural data for any biomolecular complex of interest, extracting quantitative parameters with statistical significance, thereby providing a deeper biophysical understanding of the molecular system under investigation.

1. INTRODUCTION

Understanding protein–protein interactions (PPIs) is fundamental to infer how different molecular systems work, for example, organism‐based immunity, cell‐based signaling, and structure‐based enzyme inhibition. Any loss‐ or excess‐ of interaction between proteins may significantly affect the outcome of that interaction and likely cause an altered phenotype, possibly leading to a disease state. Moreover, any mutations in any of the interacting proteins may swing the balance in either direction. Functional characterization of PPIs is therefore of prime importance for effective drug discovery. Functional properties of interacting proteins may directly be predicted from their 3D structures. Therefore, 3D structures of the proteins before and after they form a complex may point towards their binding affinity, defined as the strength of their interaction. Predicting binding affinities from structural models has been an active field of research for almost five decades (Janin, 1995; Kastritis & Bonvin, ²⁰¹³; Richards, ¹⁹⁵⁸). Approaches span all the way from classical force‐field calculations, first principle binding free energy simulations (Lopez et al., 2020), to machine learning‐based methods (Wang et al., 2019). A dedicated section describing in details the modern machine learning‐based approaches for PPI prediction can be found in our previous work (Kyrilis et al., 2021).

Buried surface area (BSA) is one of the major predictors of binding affinity and it significantly correlates to the experimentally measured dissociation constant (K_d) (Kastritis et al., 2011; Kastritis et al., ²⁰¹⁴; Kastritis & Bonvin, ²⁰¹³). When a protein forms a complex with another protein, some fraction of its initial solvent accessible surface area (SASA) gets buried inside the interface between the proteins, referred as BSA (Lee & Richards, 1971). BSA is also shown to be related to the interaction energy defined according to Chothia–Janin model (Chothia & Janin, 1975; Miller et al., ¹⁹⁸⁷). The residues that are highly buried upon complex formation are most likely to be the interface residues (IRs) if no allosteric changes occur. Identification of residues forming the interface and their properties play a crucial role in determining the binding specificity of the complex (Jones & Thornton, 1997), and subsequently in PPI prediction.

In practice, BSA is calculated from a 3D structure of a bound complex of the two proteins of interest. The difference between the SASA calculated first by treating the component proteins together and then by treating them as separate entities, gives the value of BSA. The drawback of this approach is that it uses (a) only the bound structures, and (b) only one bound structure out of a pool of bound structures, based on subjective criteria. Developments in the protein–protein docking benchmark over the last 20 years (Chen et al., 2003; Mintseris et al., ²⁰⁰⁵; Vreven et al., ²⁰¹⁵) have incorporated BSA calculations considering the unbound states, even for specific complexes (e.g., antibody–antigen interactions; Guest et al., ²⁰²¹). However, even though there exist multiple structural data of the same protein complex derived by modern structural biology methods (Guest et al., 2021; Richardson et al., ²⁰²¹), still, a single best complex is considered for subsequent analysis. That means, this approach assumes the component proteins to be rigid bodies, making the calculated BSA only an approximate single value. Furthermore, the structural data of the proteins in their unbound states are seldom used in calculation of BSA. Currently, there is no systematic algorithm that could combine the structural information from multiple bound as well as unbound structures to identify and investigate the most probable IRs; such algorithm will be critical for understanding protein–protein recognition, also in the context of the current COVID‐19 pandemic.

In this paper, we propose an algorithm, dubbed as “Interface Residue Assessment Algorithm” (IRAA), to overcome this problem. Our method combines all the available 3D structural data of the protein complex, in their complexed form as well as in their individual unbound states, and derives a distribution of BSA (in total as well as a distribution per residue). Multiple structures (bound and unbound) of the same protein complex system may contain snapshots of the system in different conformations. By analyzing all these scattered single, static 3D structures together, our method sees it, equivalently, as an ensemble 3D system. Creating a representative dynamic system out of single static structures is a fresh approach, and that facilitates our method to identify the most probable IRs and provides insights into the behavior of each of the IRs.

The structure of the article is as follows. In Section 4, we first describe the general definitions and procedure of calculating SASA and BSA. We then describe the novel algorithm, IRAA, to derive combined BSA‐based statistical distributions, its implementation and limitations. In Sections 5 and 6, we demonstrate the algorithm using a complex, currently of prime importance, that of host (human) Angiotensin Converting Enzyme‐Related Carboxypeptidase 2 (ACE2) and SARS‐CoV‐2 Spike protein, short ACE2‐S‐protein. Finally, the results and key observations stemming from this work are described in Sections 2 and 3.

2. METHODS

2.1. Solvent accessible surface area

SASA is defined as the surface area of the protein that is accessible to water molecule. It is calculated by using the algorithm developed by (Lee & Richards, 1971). The algorithm essentially treats a water molecule as a sphere of radius 1.4 Å which is rolled over the 3D structure of the protein. The surface traced by the center of the sphere is called as SASA, in Ų. A package called FreeSASA (Mitternacht, 2016) is used to calculate the SASA with Lee and Richards algorithm. Note, the package can return the values of SASA per residue. Total SASA can be then calculated by summation over all the residues.

The calculated SASA values may differ depending on the algorithm used as well as other parameters, especially, the probe radius, that is, van der Waal radius of water molecule as a probe. To investigate the effect of algorithm of choice and probe radius. We performed a comparative analysis by calculating BSA using two algorithms, Lee and Richards (1971) and Shrake and Rupley (1973). For each method, we used the probe radius of default value of 1.4 Å and slightly higher value of 1.6 Å. As shown in Figure S1, it is noticed that the effect of probe radius is higher than the actual algorithm used.

2.2. Buried surface area

BSA is defined as the fraction of the SASA of the residues of a protein, that is buried away after the protein forms a complex. Using “n” structures of [AB] complex the average BSA is calculated as

$$\mathit{BS}{A}_{\mathit{\text{Bound}}}=\begin{array}{l}\frac{{\sum }_{i=1}^n{\left[A\right]}_{\mathit{Bo}\mathrm{u}\mathit{nd},\mathit{\text{isol}}}}{n}+\frac{{\sum }_{i=1}^n{\left[B\right]}_{\mathit{\text{Bound, isol}}}}{n}\\ -\frac{{\sum }_{i=1}^n{\left[\mathit{AB}\right]}_{\mathit{\text{Bound, complexed}}}}{n}\end{array}$$ (1)

where [A] and [B] are SASA values summed over all residues of components A and B, respectively. [A] and [B] are calculated by isolating the structures of A and B respectively (denoted with suffix “isol”), while [AB] is the SASA with components A and B building a complex (denoted with subscript “complexed”).

2.3. Most probable interface residues

Residues at the interface tend to be highly buried after binding, thereby having high BSA values. Considering only the structures of bound complexes, all the residues that show absolute BSA value higher than a threshold set at 1.5 Å² are classified as most probable IRs or in short called as IRs. The threshold value is set as a tunable parameter (default to 1.5 Å²). Furthermore, we performed a scan of threshold value between 0 and 2 Å² in steps of 0.5 Å². The corresponding lists of identified IRs are shown in Table S1.

Structures may have missing residues/regions. A residue identified in one structure might be missing in another structure. Since, identification of the IRs is done based on multiple structures, missing residues/regions have less impact on the identification of IRs.

2.4. Solvent accessible and buried surface areas of IRs (iSASA and iBSA) from bound structures and unbound structures

Suppose, there are “n” structures of bound complexes [AB], and “l” and “m” unbound structures of components A and B, respectively. From the above IR identification process, we identify p and q number of IRs of components A and B, respectively. Below are simple matrix representations of (a) the SASA values of the IRs from bound structures, with components A and B in complexed state

$$\begin{array}{l}{A}_{A,\mathit{\text{Bound, complexed}}}={\left[\begin{array}{ccc}\mathit{sasa}\left(A_{1,1}\right)& \cdots & \mathit{sasa}\left(A_{1,n}\right)\\ ⋮& \ddots & ⋮\\ \mathit{sasa}\left(A_{p,1}\right)& \cdots & \mathit{sasa}\left(A_{p,n}\right)\end{array}\right]}_{\mathit{pxn}},\&\\ \mathit{\text{iSAS}}{A}_{B,\mathit{\text{Bound, complexed}}}={\left[\begin{array}{ccc}\mathit{sasa}\left(B_{1,1}\right)& \cdots & \mathit{sasa}\left(B_{1,n}\right)\\ ⋮& \ddots & ⋮\\ \mathit{sasa}\left(B_{q,1}\right)& \cdots & \mathit{sasa}\left(B_{q,n}\right)\end{array}\right]}_{\mathit{qxn}}\end{array}$$ (2)

$$\mathit{\text{iSAS}}{A}_{A,\mathit{\text{Bound}},\mathit{\text{isol}}}={\left[\begin{array}{ccc}\mathit{sasa}\left(A_{1,1}\right)& \cdots & \mathit{sasa}\left(A_{1,n}\right)\\ ⋮& \ddots & ⋮\\ \mathit{sasa}\left(A_{p,1}\right)& \cdots & \mathit{sasa}\left(A_{p,n}\right)\end{array}\right]}_{\mathit{pxn}},\&$$

$$\mathit{\text{iSAS}}{A}_{B,\mathit{\text{Bound}},\mathit{\text{isol}}}={\left[\begin{array}{ccc}\mathit{sasa}\left(B_{1,1}\right)& \cdots & \mathit{sasa}\left(B_{1,n}\right)\\ ⋮& \ddots & ⋮\\ \mathit{sasa}\left(B_{q,1}\right)& \cdots & \mathit{sasa}\left(B_{q,n}\right)\end{array}\right]}_{\mathit{qxn}}$$ (3)

(b) the SASA values of the IRs from bound structures with components A and B in isolated states

$$\mathit{iBS}{A}_{A,\mathit{\text{Bound}}}={\left[\begin{array}{ccc}\mathit{bsa}\left(A_{1,1}\right)& \cdots & \mathit{bsa}\left(A_{1,n}\right)\\ ⋮& \ddots & ⋮\\ \mathit{bsa}\left(A_{p,1}\right)& \cdots & \mathit{bsa}\left(A_{p,n}\right)\end{array}\right]}_{\mathit{pxn}},\&$$

$$\mathit{iBS}{A}_{B,\mathit{\text{Bound}}}={\left[\begin{array}{ccc}\mathit{bsa}\left(B_{1,1}\right)& \cdots & \mathit{bsa}\left(B_{1,n}\right)\\ ⋮& \ddots & ⋮\\ \mathit{bsa}\left(B_{q,1}\right)& \cdots & \mathit{bsa}\left(B_{q,n}\right)\end{array}\right]}_{\mathit{qxn}}$$ (4)

(c) the BSA values of the IRs, obtained by subtracting matrices in Richards (1958) from that in Lopez et al. (2020).

$$\mathit{\text{iSAS}}{A}_{A,\mathit{\text{Unbound}}}={\left[\begin{array}{ccc}\mathit{sasa}\left(A_{1,1}\right)& \cdots & \mathit{sasa}\left(A_{1,l}\right)\\ ⋮& \ddots & ⋮\\ \mathit{sasa}\left(A_{p,1}\right)& \cdots & \mathit{sasa}\left(A_{p,l}\right)\end{array}\right]}_{\mathit{pxl}},\&$$

$$\mathit{\text{iSAS}}{A}_{B,\mathit{\text{Unbound}}}={\left[\begin{array}{ccc}\mathit{sasa}\left(B_{1,1}\right)& \cdots & \mathit{sasa}\left(B_{1,m}\right)\\ ⋮& \ddots & ⋮\\ \mathit{sasa}\left(B_{q,1}\right)& \cdots & \mathit{sasa}\left(B_{q,m}\right)\end{array}\right]}_{\mathit{qxm}}$$ (5)

and finally (d) the SASA values of the IRs from unbound structures of components A and B.

Where the dimension of each resultant matrix is shown at the bottom‐left, in a format, for example, pxq. All above matrices are similar in structure. One row consists of values (of either BSA or SASA) corresponding to one IR. One column consists of values (of either BSA or SASA) corresponding to all IRs in one structure.

2.5. Interface residues assessment algorithm

IRAA is developed to combine multiple 3D structural data of both bound and unbound states to identify IRs and calculate distribution of BSA.

The underlying principle involves random sampling of the distribution/s, followed by a step of combining sample values as per the given mathematical function/s. The process of random sampling followed by subsequent arithmetic is nothing but Monte Carlo method.

Monte Carlo method is a computational statistical method of picking samples randomly (Henry, 2019). The earliest attempt of Monte Carlo application dates back to 1930s, a variant developed by Enrico Fermi, while studying neutron diffusion (Metropolis, 1987). Monte Carlo method is used in diverse fields and multitude of problems ranging from Bioinformatics, Physics to Artificial Intelligence. Problems that are probabilistic in nature and that involve processes following one or more complex probability distributions, are well suited for solving with Monte Carlo method. Here, all the bound and unbound structures are independent static structures, each representing a snapshot of different conformational states. The calculation of BSA (i.e., difference in ASA values) from any pair of unbound‐bound structures, where the formation of a pair (and thereby calculating the corresponding BSA) is completely probabilistic in nature, is a perfectly suitable problem for Monte Carlo method.

Suppose we want to calculate BSA using Equation (1) by using only one of each unbound and bound structures of [A], [B], and [AB]. We could either pick the best structures among [A], [B], and [AB] or we could randomly pick a structure from list of [A], [B], and [AB].

However, if there are n, l, and m structures of [A], [B], and [AB], respectively, then there are $\left(n\bullet l\bullet m\right)$ different possible combinations, each with an equal probability. Instead of spanning the pool of all possible structure combinations, we create per IR, distributions of SASA values derived from different bound and unbound structures. We can then sample these distributions via Monte Carlo method and estimate the distribution of BSA. Below we describe the process of creating distributions of SASA per IR.

For this purpose, we use matrices in Equations (2) and (5), basically representing SASA values from unbound states and bound/complexed states. The values in ith row in a matrix corresponding to ith IR, are used to estimate the corresponding probability density function (PDF_i) using Gaussian kernel (bandwidth equal to 0.15), using Scipy (Virtanen et al., 2020) computing package in Python. As a result, for each matrix, we create a set of p or q distributions corresponding to p or q IRs in that matrix. These distributions are graphically represented by columns with multiple curves in Figure 1, and are represented as four sets:

FIGURE 1.

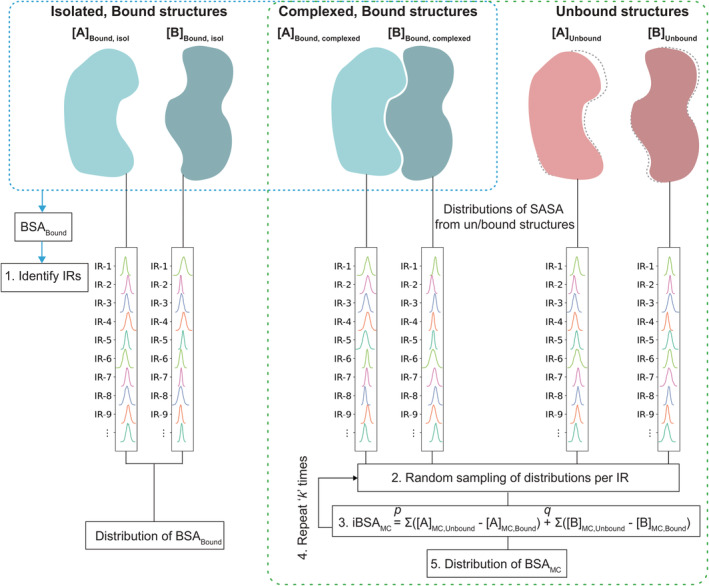
Graphical representation of the method. Bound structures of a complex [AB] are represented as blue blobs and its individual components [A] and [B] in unbound states are represented as pink blobs. Bound structures are used to identify the most probable IRs (i.e., as described in Step 1 in Section 4) and distribution of BSA bound from bound structures only (blue dotted box). All bound structures in complexed state and all unbound structures are used to create prob. density functions (represented as columns with multiple curves) of SASA values per IR. These are used for random sampling by Monte Carlo method and finally to estimate distribution of BSA_MC from Monte Carlo method. BSA, buried surface area; IR, interface residue; SASA, solvent accessible surface area.

${\left\{{\mathit{PDF}}_{A,\mathit{\text{bound}},\mathit{\text{complexed}}}\right\}}_1^q,{\left\{{\mathit{PDF}}_{B,\mathit{\text{bound}},\mathit{\text{complex}}}\right\}}_1^q,{\left\{{\mathit{PDF}}_{A,\mathit{\text{unbound}}}\right\}}_1^p,\mathit{\text{and}}{\left\{{\mathit{PDF}}_{B,\mathit{\text{unbound}}}\right\}}_1^q$. In the following section, we describe our algorithm to randomly sample these distributions and combine the values to calculate BSA.

IRAA has essentially two core components, (a) generating distributions of SASAs, and (b) the Monte Carlo method to sample the distributions and combine the values. The workflow of IRAA consists of the steps described below. The graphical representation of the procedure is shown in Figure 1.

Step 1. Identify IRs of the components using all the bound structures, as described in Section 4.3.

Step 2. Using all the bound and unbound structures, create the matrices as shown in Equations (2), (3), (4), (5). And using only Equations (2) and (5), generate the sets of probability distributions per IR:

$${\left\{{\mathit{PDF}}_{A,\mathit{\text{bound}},\mathit{\text{complexed}}}\right\}}_1^q,{\left\{{\mathit{PDF}}_{B,\mathit{\text{bound}},\mathit{\text{complex}}}\right\}}_1^q,{\left\{{\mathit{PDF}}_{A,\mathit{\text{unbound}}}\right\}}_1^p,\mathit{\text{and}}{\left\{{\mathit{PDF}}_{B,\mathit{\text{unbound}}}\right\}}_1^q.$$

Step 3. Draw p samples from p distributions ${\left\{{\mathit{PDF}}_{A,\mathit{\text{unbound}}}\right\}}_1^p$, and another p samples from ${\left\{{\mathit{PDF}}_{A,\mathit{\text{bound}},\mathit{\text{complexed}}}\right\}}_1^q$. Similarly, draw q samples from q distributions ${\left\{{\mathit{PDF}}_{B,\mathit{\text{unbound}}}\right\}}_1^q$ and another q samples from ${\left\{{\mathit{PDF}}_{B,\mathit{\text{bound}},\mathit{\text{complex}}}\right\}}_1^q$, all represented as column matrices

$$A_{\mathit{MC},\mathit{\text{unbound}}}={\left[\begin{array}{c}\mathit{sas}{a}_1\\ \mathit{sas}{a}_2\\ ⋮\\ \mathit{sas}{a}_p\end{array}\right]}_{1\mathit{xp}},A_{\mathit{MC},\mathit{\text{Bound}}}={\left[\begin{array}{c}\mathit{sas}{a}_1\\ \mathit{sas}{a}_2\\ ⋮\\ \mathit{sas}{a}_p\end{array}\right]}_{1\mathit{xp}}\&B_{\mathit{MC},\mathit{\text{unbound}}}={\left[\begin{array}{c}\mathit{sas}{a}_1\\ \mathit{sas}{a}_2\\ ⋮\\ \mathit{sas}{a}_q\end{array}\right]}_{1\mathit{xq}},B_{\mathit{MC},\mathit{\text{Bound}}}={\left[\begin{array}{c}\mathit{sas}{a}_1\\ \mathit{sas}{a}_2\\ ⋮\\ \mathit{sas}{a}_q\end{array}\right]}_{1\mathit{xq}}.$$

Step 4. BSA is calculated by subtracting the pairs of matrices generated in Step 3, resulting in two column vectors of size p and q, respectively:

$${\left[\mathit{\text{iBSA}}\_A_{\mathit{MC}}\right]}_{\mathit{px}1}=A_{\mathit{MC},\mathit{\text{Unbound}}}-A_{\mathit{MC},\mathit{\text{Bound}}}\&{\left[\mathit{iBSA}\_B_{\mathit{MC}}\right]}_{\mathit{qx}1}=B_{\mathit{MC},\mathit{\text{Unbound}}}-B_{\mathit{MC},\mathit{\text{Bound}}}.$$

Step 5. Total BSA is calculated by summation over all IRs of A and B.

Repeat Steps 3–5 over “k” iterations to generate a distribution of “k” iBSA_MC values

$${\left[\mathit{iBS}{A}_{\mathit{MC}}\right]}_{\mathit{kx}1}=\sum _1^p{\left[\mathit{\text{iBSA}}\_A_{\mathit{MC}}\right]}_{\mathit{px}1}+\sum _1^q{\left[\mathit{\text{iBSA}}\_B_{\mathit{MC}}\right]}_{\mathit{qx}1}.$$

At the end of k iterations, we generate a distribution of iBSA_MC, that has essentially combined all the structural data together.

Since, in all our calculations, we only consider the IRs, we may drop the suffix “i” from iBSA_MC terms, and simply call it BSA_MC.

2.6. Implementation

IRAA is a Python‐based algorithm. The structure of the scripts of IRAA consists of three parts, the Jupyter notebook – Run_IRAA.ipynb. The notebook provides a step‐by‐step workflow, allowing the user to interactively execute/manipulate the steps.

Some helper scripts can be found under iraa_utils. In addition, the data folder is present consisting of all the Protein Data Bank (PDB) structure files.

Paths of all the subfolders are set relative to the notebook (.jpnb) file. To avail ease‐of‐use to the user, an ipython‐widgets based GUI is developed within the Jupyter notebook. The notebook reads the relevant PDB file IDs and expects the corresponding mmCIF files to be present under data folder. The processed subfiles and SASA files are then created and saved under the data folder. The notebook then reads the SASA values for the subsequent analysis as detailed in Section 4.5. We caution the users not to utilize structurally redundant, identical protein complexes to derive distributions of interface properties.

For demonstration, the IRAA is applied to a critical system of current times, i.e., the complex of human ACE2 and SARS‐CoV‐2 Spike protein, short ACE2‐S‐protein, as discussed in details in Section 4.3. The Jupyter Notebook Run_IRAA.ipynb not only provides a transparent view on what is under the hood, but also gives a full control of the parameters and the steps within the workflow. IRAA is developed as an application to investigate ACE2‐S‐protein complexes but can be easily adapted (both IRAA procedure and its code) to any protein complex that has multiple bound/unbound structures.

2.7. Bayesian parameter estimation

We use PyMC3 (Kruschke, 2013), a probabilistic programming package in Python, that fits Bayesian models using notably MCMC methods. To quantitatively assess how different any two groups of data are from the other, we perform a rigorous Bayesian parameter estimation, using the module—Bayesian Estimation Supersedes the T‐test (BEST) under PyMC3 based on Kruschke (2013). Driven by Bayesian probability, this is a comprehensive and more solid approach than the testing approaches that involve expressing a null hypothesis. Moreover, we estimate the uncertainty associated with the estimated parameter that accounts for our lack of knowledge of the model parameters. For a given (groups 1 and 2) data, we calculate two parameters, namely, (a) the effect size, and (b) a high‐density probability interval around the effect size. Farther the value of effect size from 0 (and the 95% HDI), the better it is.

The posterior distributions of all model parameters are estimated by the process of MCMC sampling within PyMC3. The MCMC process generates a large (up to 100,000) representative sample of credible parameter values that better represents the underlying posterior distribution. Note the MCMC process generates sample of parameter values and not that of the actual data. For each credible parameter estimate (μ1, μ2, σ1, and σ2), the effect size if computed as (μ1 − μ2)/√((σ1² + σ2²)/2). A distribution of effect size (also of 100,000 samples) is computed along with a 95% credible interval, a high‐density probability Interval (HDI). If the means of two groups are not significantly different, then the effect size would tend toward 0. Therefore, a higher effect size indicates a significant difference between the two groups. Unlike a single‐point value of p ≤ 0.05 in standard t‐test, the interpretation of Bayesian estimation is not black‐and‐white, it uses an entire distribution of parameters for calculating the effect size. The conclusions are probabilistic in nature, and therefore, we observe if the estimated 95% HDI of the distribution of effect size does or does not include 0. Moreover, a Region of Practical Equivalence (ROPE) of −0.1 to 0.1 around the null value (0) is considered as 0, such that, the effect size indicates a significant difference in the two groups only if the ROPE is completely outside the 95% HDI.

2.8. Molecular dynamics simulation data set assessment

IRAA allows to use molecular dynamics (MD) simulation data set to identify IRs as well as to calculation BSA distribution. To demonstrate, we used an MD data set by D. E. Shaw of the human ACE2 ectodomain in a complex with the RBD of a SARS‐CoV‐2‐Spike protein (DESRES‐ANTON‐10905033; release date April 6th, 2020). The system was produced using PDB entry 6M17 and the MD was performed on Anton supercomputer for 10 μs with frames saved every 1.2 ns. For details ref to Molecular Dynamics Simulations Related to SARS‐CoV‐2″, D. E. Shaw Research Technical Data, 2020, https://www.deshawresearch.com/downloads/download_trajectory_sarscov2.cgi/.

For our analysis, we extracted every 100th frame (every 120 ns), and used in total 84 frames. To adapt to the FreeSASA calculations requirements, we removed zinc atom at the ACE2 enzymatic cleft as well as glucosylation sites at Spike protein and ACE2. Moreover, the residues in different protonation states were renamed to their original names.

2.9. PDB data diversity assessment

To assess how diverse (or similar) the structures are to each other, we performed a pair‐wise alignment root mean squared distance (RMSD) calculation of Cα‐atom using PyMol v. 2.4.0a0 using align multi‐step superposition algorithm, with five cycles of refinement. Every chain of unbound S‐protein was paired up with every other S‐protein chain (including two other chains of the same structure) to calculate Cα‐atom RMSD. Altogether 65,703 alignments were performed for S‐protein unbound structure. Similar calculation is performed on ACE2‐S‐protein bound structures. Here the Cα‐atom RMSDs were calculated between all ACE2‐S‐protein complexes, considering only the bound chain of S‐protein and the ACE2 chain and not the whole structure. Altogether, 4753 alignments were performed for ACE2‐S‐protein complex. Distribution of RSMD values (A) and the RMSD dissimilarity matrix (B) is shown for unbound S‐protein (Figure S2a,b) and the ACE2‐S‐protein complex (Figure S3a,b).

PyMol uses a per‐residue level sequence alignment using BLOSUM62 scoring matrix, followed by structural superposition in cyclic refinement steps; for details, refer to PyMol v. 2.4.0a0 documentation (https://pymol.org/dokuwiki/).

3. APPLICATION TO ACE2‐SARS‐COV‐2 S‐PROTEIN COMPLEX

SARS‐CoV‐2 has caused the worldwide pandemic COVID‐19, with 180 million infections and more than 570 million deaths as of July 2022 (WHO). SARS viruses are regarded as one of the most dangerous viruses by World Health Organization (WHO). The patients are seen to have diverse responses to the infection for reasons not yet fully understood. There is an insurgence in vaccine development programs throughout many countries; however, any mutation that significantly affects the structural and consequently functional properties of the virus, may impair the immune response by the host as well as antivirals. Therefore, structural characterization of the host (human) Angiotensin Converting Enzyme‐Related Carboxypeptidase 2 (ACE2) protein and the viral Spike protein (S‐protein) complex is not only crucial for efficient drug discovery (Mercurio et al., 2021) but also for understanding virus protein structure, function and interactions (Wang et al., 2020). To serve the same purpose, attempts have been made to determine the structure of the ACE2 and S‐protein, both in their bound and unbound states. As of May 2022, there have been 390 structures submitted on Protein Data Bank (PDB) (Berman et al., 2000), that have either ACE2, S‐protein or both proteins present.

We apply IRAA to the bound and unbound structures of ACE2 and S‐protein, and derive the combined distribution of BSA. A local repository of relevant structural data is maintained and updated automatically, as described in Section 6. Based on the filtering and curation criteria as outlined in Section 6, a subset of structures is further analyzed. Some key observations made are based on the statistical properties of the complex and are discussed in Section 2.

4. DATA

All relevant structures are downloaded from PDB by matching the PDB IDs and Uniprot codes for human ACE2 (Q9BYF1, ACE2_HUMAN) and SARS‐CoV‐2 S‐protein (P0DTC2, SPIKE_SARS2), respectively. As of May 2022, we have extracted 390 PDB entries in mmCIF format.

The notebook reads every structure, and compares the protein sequence with reference sequences to cross‐check the identity and alignment of the individual chains. The Uniprot sequences of codes Q9BYF1 and P0DTC2 are used as reference sequence (and for numbering) of ACE2 and SARS‐CoV‐2 S‐protein, respectively. The structures are grouped into three groups according to their structure type, ACE2‐S‐protein complex, only ACE2, only SARS‐CoV‐2 S‐protein.

Structures are excluded if encountered the following criteria, (a) any non‐human host ACE2, (b) SARS‐CoV (previous to 2019) S‐protein structures, (c) structures in complex with other biomolecules (e.g., antibodies) that may inhibit the receptor binding domain. PDB IDs of all the structures that are included in the analysis are listed in Table S2.

In this work, we analyzed 98 ACE2‐S‐protein complex structures, 363 unbound S‐protein chains, and 6 unbound ACE2 protein structures derived from total number of 76, 121, and 4 PDB files, respectively, as summarized in Table S2, after filtering over 600 relevant PDB files. To inspect the diversity of in the PDB structures, Root‐mean‐square‐deviations of main chain atoms (RMSDs) were calculated using PyMOL (Schrodinger, 2010). The RMSD distributions of S‐protein in bound state and in unbound state are derived separately, as shown in Figures S2a and S3a. In this work, all structures were treated as a whole to expand coverage and reduce ambiguity when residues are missing. Statistical breakdown of the dataset (experimental method used, resolution) is available in Figure S4.

5. RESULTS AND DISCUSSION

First, bound structures are used to calculate BSA and identify IRs. The BSA calculated over all the bound structures and over full sequences of ACE2 and the viral Spike protein (S‐protein) are shown as heatmaps in Figure 2a and Figure 2b, respectively. Residues missing in a sequence are marked by gray shade. The IRs with higher BSA values are distinctly highlighted with darker shades of red, whereas the rest of the residues appear in fainter shades of red. By applying a threshold, BSA >1.5 Ų, 32 residues of ACE2 and 38 residues of S‐protein are identified as the most probable IRs in ACE2–S‐protein complex, as shown in Table 1. Noticeably, the list of IRs derived in this study is more extensive as compared to previous reports, for example, based on molecular dynamics simulations or structural analysis of a single‐bound structure (Ali & Vijayan, 2020; Lan et al., ²⁰²⁰). In Table 1, the IRs common in result of IRAA and previous reports are shown by entries in bold black color, while extended members identified by IRAA are shown in italic. Figure 2c,d shows the BSA heatmaps of only the IRs of ACE2 and S‐protein. Results confirm that the known IRs, such as K353, K31, H34, T27, and Q24 for ACE2 and F486, T500, Y489, and Y505 for S‐protein (Lan et al., 2020), are the most deeply buried residues (Figure 2c,d). Interestingly, their distributions of BSA significantly vary across bound structures, indicating localized flexibility. Figure 3 shows the heatmap of SASA for the IRs listed in Table 1 for S‐protein from unbound structures.

FIGURE 2.

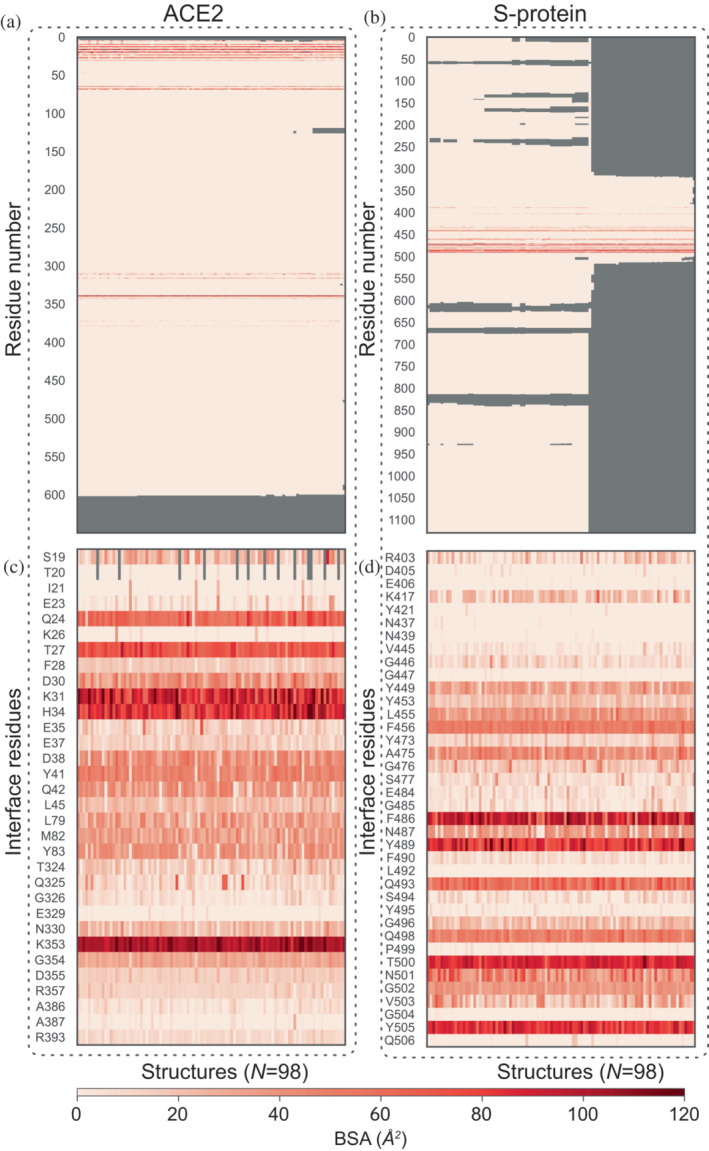
Heatmap of BSA. Panels (a) and (b) show the BSA per residue across all bound structures (N = 98) and over the full sequence of ACE2 and S‐protein, respectively. Among these, the most probable IRs of ACE2 and S‐protein are easily identified as those with BSA greater than a threshold set at 1.5 Ų, and are plotted in panels (c) and (d), respectively. BSA, buried surface area; IR, interface residue.

TABLE 1.

Identified interface residues

	Identified interface residues
ACE2 protein	S19, T20, I21, E23, Q24, K26, T27, F28, D30, K31, H34, E35, E37, D38, Y41, Q42, L45, L79, M82, Y83, T324, Q325, G326, E329, N330, K353, G354, D355, R357, A386, A387, R393
SARS‐CoV‐2 S‐protein	R403, D405, E406, K417, Y421, N437, N439, V445, G446, G447, Y449, Y453, L455, F456, Y473, A475, G476, S477, E484, G485, F486, N487, Y489, F490, L492, Q493, S494, Y495, G496, Q498, P499, T500, N501, G502, V503, G504, Y505, Q506

Note: Interface residues (IRs) are identified as residues with BSA values higher than a threshold set at 1.5 Å². The set of IRs identified by IRAA consists of 32 residues of ACE2 and 38 residues of S‐protein. IRs in black bold are common in both, output of IRAA and that are previously reported in the literature (Ali & Vijayan, 2020; Lan et al., ²⁰²⁰), while the rest of the IRs printed in italics are identified by IRAA as the extended members of the interface through a collective analysis of all structures.

FIGURE 3.

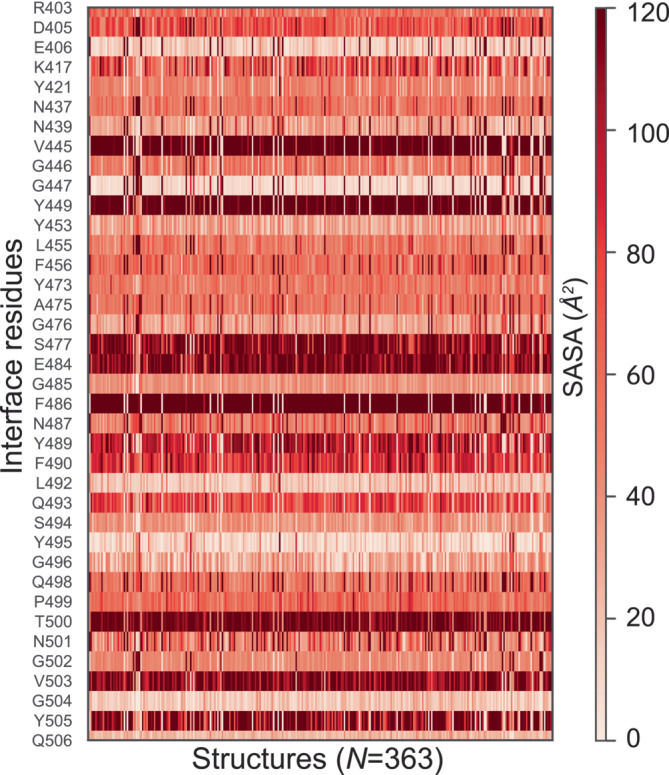
Heatmap of SASA values per IRs of S‐protein across all unbound structures (N = 340). IR, interface residue; SASA, solvent accessible surface area.

To better analyze the behavior of the IRs between their unbound to bound states, a side‐by‐side comparison of their corresponding SASA distributions is shown as split‐violin plots in Figure 4. To quantitatively assess their differences (or similarity), a full Bayesian parameter estimation is performed on every pair of distributions using a Markov chain Monte Carlo (MCMC) based python package PyMC3 (see Section 4.7). The Bayesian effect sizes are calculated, and are represented by a color bar on the right edge of Figure 4. The higher the value, the greater is the difference between the two distributions. The IRs, specifically, K417, Y449, Y453, L455, F456, A475, G476, F486, N487, Y489, Q493, Q498, and Y505 of S‐protein are highly heterogeneous across the data, depicted by distinct differences in their split‐violins, and also their Bayesian effect size values. However, IRs, specifically, D405, E406, N437, N439, G485, and S494 of S‐protein are systematically showing minor variations, depicted by lower differences in split‐violins and their corresponding Bayesian effect size values. Despite the nature of the Glycine (G) residue, which contains only a hydrogen as side‐chain, it is critical to note that the list of residues exhibiting minor conformational variations also includes Phenylalanine (F) and Glutamine (Q), residues with large side‐chains. The analysis described above highlights an extensive variation on a per‐residue basis for both the SASA and the BSA. The reported variability is observed for various residues, including those with smaller and larger side chains. These observed distinct differences in the SASA could be attributed to the conformational variations present among different structures. However, variation or non‐uniformity in the resolution, type of structural determination method, as well as other experimental parameters may also contribute to the variation depicted in the SASA values. Only by collectively analyzing several static snapshots of structures, which can also come from MD or Monte‐Carlo simulations, one can observe such variations and create a dynamic representation of the system. IRAA, for example, can be applied on MD simulations (Figure S5), showing recovery of IRs and BSAs comparable to those retrieved form the ACE2‐S‐protein structures, as described in Section 4.8. Moreover, comparing the IRs identified by IRAA from the experimental data set as well as from the frames of MD simulation have a high overlap with a few differences summed up in Figure S6 and Table S3 for IRs of S‐protein and Table S4 in case of ACE2.

FIGURE 4.

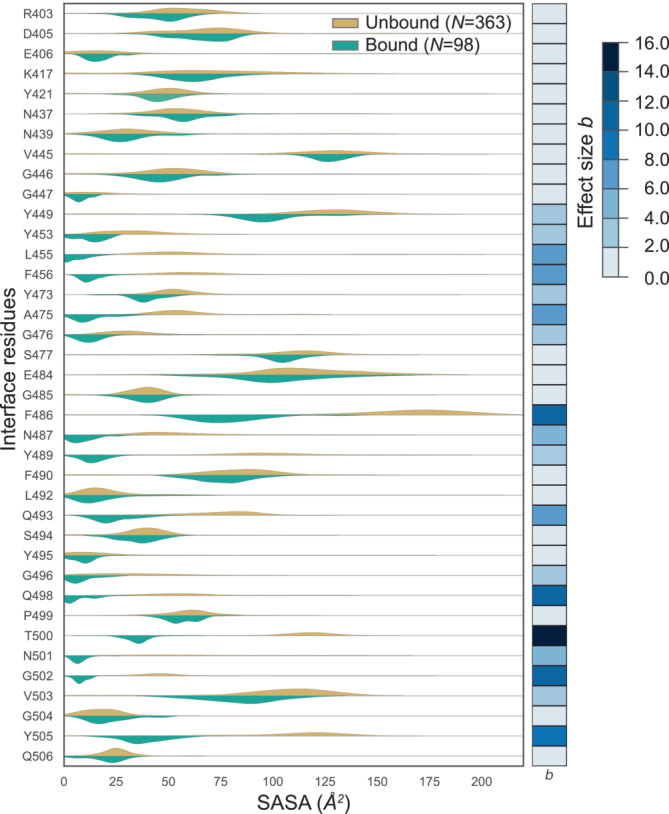
Comparison of SASA of S‐protein in unbound versus bound states. For each IR of S‐protein the distribution of SASA values from all isolated S‐protein from bound complexes (green shaded curves) are compared with the distribution of its SASA values from all unbound states (orange curves). To quantitatively assess the differences in the behavior of any residue between the two states, we calculated Bayesian effect size (b), following the Bayesian parameter estimation performed on every pair of distributions. The effect sizes (b) are plotted as a color bar on the right edge; higher values signify higher difference between the two distributions. c.

We observe that higher difference in SASA in general is not correlated to size of the residue. This is evident when the Bayesian effect sizes (from Figure 4) calculated for SASA distribution for each IR in unbound and bound states of S‐protein are plotted (on y‐axis) against the maximum SASA of an individual amino acid (on x‐axis) in increasing order, see Figure 5a. This plot also visualizes very well that the IRs with highest values of Bayesian effect, belong to most of IRs previously reported in the literature with addition of three residues identified in this work (G476, V503, and Y473). The residues from each group were visualized (PDB ID: 7A94) and color‐coded accordingly (Figure 5b). The visualization demonstrates that the residues (red shade) with effect size (b‐value) above 9.0 are within the ACE2 interface (gray). The residues from the second and third groups (b‐values between 4.0 and 9.0 as well as between 2.0 and 4.0, respectively, orange and yellow shade in Figure 5b) are surrounding the abovementioned core residues. Finally, the residues from the group below 2.0 are located in the rim regions of the interface (shades of blue). This correlation between b‐value and residue localization at the ACE2‐S‐protein interface is intriguing and connected to residue‐specific conformational changes that possibly relate to the underlying recognition mechanism (Ali & Vijayan, 2020; Yan et al., ²⁰²⁰).

FIGURE 5.

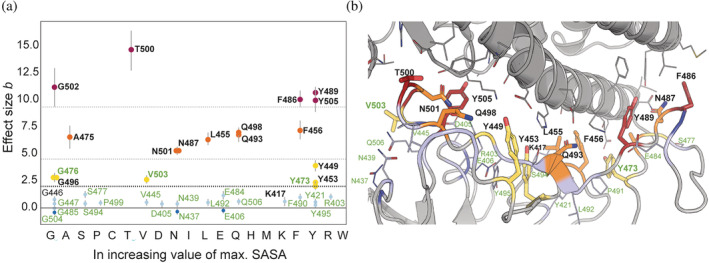
Bayesian effective size (b) versus SASA of amino acids in increasing order. (a) Values of Bayesian effective size calculated for pairs of SASA distributions for isolated S‐protein from ACE2‐S‐protein complex and for unbound S‐protein for each of the IRs (Figure 4) plotted versus maximal SASA value for each of the proteinogenic amino acids. The names of each of the IRs correspond to WT residue at the position. In bold are represented residues with the effect size above 2.0 (lower dotted line). Those are the majority of the IRs identified in previous publications (black) as well as three IRs identified in present study (green): G476, V503, and Y473. Additionally, we noticed that we can separate the IRs into groups whose effective size lies below 2.0 (light blue), between 2.0 and 4.0 (yellow), between 4.0 and 9.0 (orange), and above 9.0 (red). The mentioned thresholds are marked with dotted lines. The residues from each group were visualized (PDB ID: 7A94) and color‐coded accordingly (b). The visualization demonstrates that the residue (red shade) above the threshold of 9.0 is closest to the ACE2 interface (gray). The residues from the second and third groups (between 4.0 and 9.0 as well as 2.0 and 4.0, respectively) are more distant (orange and yellow shades), and the residues from the group below 2.0 are placed in the rim regions of the interface (shades of blue). IR, interface residue; SASA, solvent accessible surface area.

Furthermore, we perform a side‐by‐side comparison of the BSA values of IRs from S‐protein—values stemming from only the bound structures against those calculated by the Monte Carlo method. This comparison is shown by split‐violins in Figure 6. The corresponding Bayesian effect size values are calculated and are represented by a color bar on the right edge of Figure 6. Residues that show distinct differences (as depicted by the Bayesian effect size values) are K417, Y449, L455, F456, F486, N487, Q493, Q498, and Y505, already identified as participating IRs.

FIGURE 6.

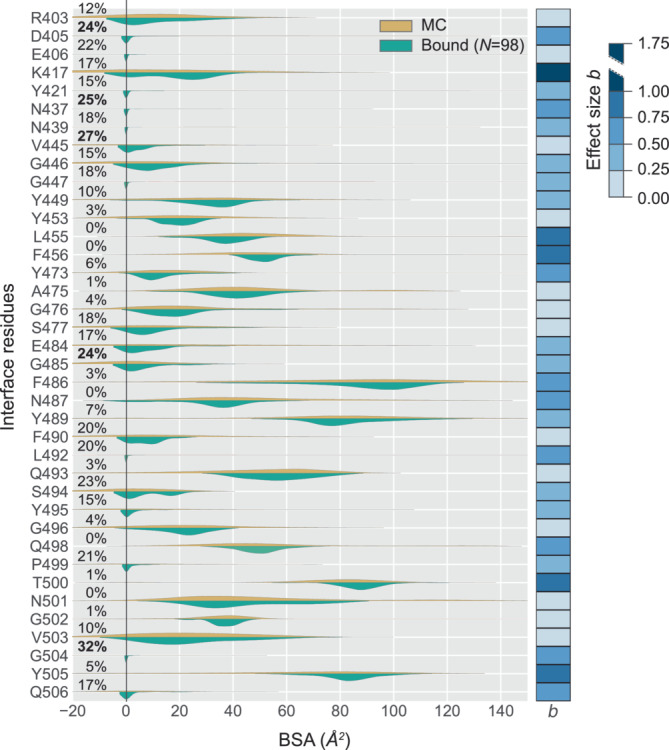
Compare BSA of S‐protein from bound versus Monte Carlo (MC) analysis. For each IR of S‐protein, the distribution of BSA values from S‐protein derived from analysis of bound complexes (green shaded curves) are compared with the distribution of its BSA values derived from the MC method (orange curves). Interestingly, some of the IRs show a fraction (shown in percentages on the left edge) of negative BSA values resulted from the MC method. This is expected when a specific residue is relatively more buried in the unbound state compared to the bound state. To quantitatively assess the differences in the behavior of any residue between the two states, we calculated Bayesian effect size (b), following the Bayesian parameter estimation performed on every pair of distributions. The effect sizes (b) are plotted as a color bar on the right edge; higher values signify higher difference between the two distributions. BSA, buried surface area; IR, interface residue.

Noticeably, for some of the IRs the distribution of BSA from Monte Carlo method results in a tail extending toward negative values. The fraction of negative BSA values (shown in percentages on the left edge of Figure 6) resulted from the Monte Carlo method. This is expected when a specific residue is relatively more buried in the unbound state compared to the bound state. Top 5 such residues (fraction values highlighted in dark black) are G504, V445, N437, G485, and D405. Identification of such residues is extremely interesting for drug target or for stability studies. Our method allows an easy identification of such residues due to the algorithm that combines the information from both bound and unbound structures.

Finally, we compare the sum of BSA over all IRs, obtained over all bound‐only structures against that calculated by Monte Carlo method, see Figure 7a. We notice that IRAA reports comparably lower BSA values with a significantly broader distribution. Recognition of ACE2 and S‐protein may involve the formation of weak interfaces during association. Because IRAA utilizes a random sampling of all known component conformations, it effectively simulates interface areas of all possible interaction strengths between the component proteins. Consequently, the retrieved combined distribution of BSA of the interface may reflect intrinsic properties underlying the biomolecular recognition.

FIGURE 7.

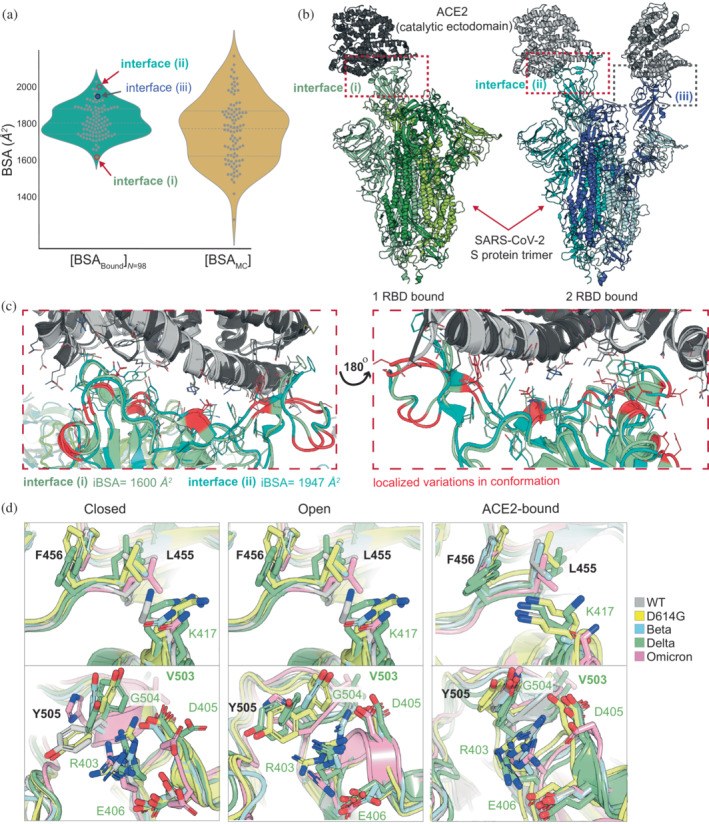
Total BSA [A+B] bound versus Monte Carlo (MC) and structural insights. (a) Comparison of BSA value distributions for ACE2‐S‐protein interfaces calculated from 98 complexes (bound structures) and using the MC method with inclusion of SASA values for IRs from available 340 unbound S‐protein structures. (b) View of the ACE2‐S‐protein interfaces for which one the lowest (PDB ID: 7a94, interface [i]) and the highest (PDB ID: 7a97, interface [ii] and interface [iii]) BSA values were calculated. (c) Identification of the most flexible regions at the ACE2‐S‐protein interface (marked red) by aligning the interfaces with one of the lowest (interface [i]) and one of the highest (interface [ii]) calculated BSA values. The interface is shown from two different viewpoints: The frontal as represented in subsection (b) and the view by turning the structure 180° around the Z‐axis. (d) Comparison of some IRs in closed, open, and ACE2‐bound states of RBD in different lineages (WT, D614G, Beta, Delta, and Omicron). D614F and Delta lineages are represented in each state by two different structural models due to their frequent appearance in PDB. The names of the residues correspond to WT residue at the position. K417 (upper panel) shows the highest effect size comparing two distributions from Figure 6 and is in different conformational states before and after binding to ACE2. Its neighboring residues, F456 and L455 do not show such distinct conformational rearrangements upon binding. Y505 (lower panel) shows very broad conformational dispersity in closed and open conformation and well‐defined conformation in ACE2‐bound state. The analysis shows that this flexibility of Y505 influences the surrounding residues such as G504, which has high proportion of negative BSA values (~30%) (Figure 6). Moreover, together with D405 and E406, it stabilizes R403 in ACE2‐bound state. BSA, buried surface area; IR, interface residue; SASA, solvent accessible surface area.

Surprisingly, even the experimentally‐characterized bound complexes exhibit relatively broad distributions of BSA, spanning from ~1600 to ~2100 Ų, see Figure 7a. By translating these values to binding affinities using the monotonic relation of interface size and experimental energy for transient protein interactions (Kastritis et al., 2011; Kastritis et al., ²⁰¹⁴), a twofold deviation in binding affinity can be expected. As an example, we compare the interface regions of two bound complexes that were resolved by the same group using cryo‐EM (Benton et al., 2020), see Figure 7a. One structure (PDB ID: 7A94) has one RBD of the trimeric S‐protein in complex with ACE2. The other structure (PDB ID: 7A97) has two RBDs of the trimeric S‐protein in complex with two ACE2. All three interfaces are marked in Figure 7b and are connected to their corresponding BSA values in Figure 7a. The subtle structural differences between interface (i) and (ii) (with BSA of 1600 and 1947 Å, respectively) are shown in Figure 7c.

We took a look into some of IRs those calculated BSA distributions differ significantly (represented by the Bayesian effect size), as well as IRs with a large proportion of negative BSA values. For that, we aligned RBD domains of S‐protein in its three main conformational states: closed, open, and ACE2‐bound (Figure 7d). Here, we considered structures of different lineages (Wild Type (WT), D614G, Beta, Delta, and Omicron), including D614G and Delta structures two times, since they are broadly represented in PDB (Table S5). The IRs with significantly different BSA distributions should be ones that are represented by different rotamers in unbound and bound states, which cannot be detected via BSA calculations when the complex is separated. Negative BSA value of a residue means that the residue is more solvent accessible after the complex is build. These effects may be caused by the conformational changes that the protein undergoes before binding and can be limited to a few residues, or may involve a movement and structural rearrangement of a domain or the whole protein. In addition, substitutions of the position which occur in considered structures may also be a cause of the described effects. Thus, for residue 417 (WT is Lysine), we measured the highest Bayesian effect size for BSA of ~1.5 (Figure 6). In most of the lineages, the position is occupied by Lysine but in Omicron the position is substituted by Asparagine and in Beta lineage by Asparagine or Threonine. In closed and open S‐protein states, residue 417 does not have preferable position, whereas upon binding to ACE2, two distinct rotamers are observed (Figure 7d, upper panel). The two rotamers of position 417 are also captured by the bimodal distribution calculated from the complexed structures. In contrary, the neighboring residues 455 and 456, which correspond to L455 and F456 in all considered lineages, do not differ in their conformational states that much in all three main conformational states of S‐protein. Therefore, the effect size comparing both distributions is relatively low, being around ~1. Another residue, 505, which correspond to Y505 in most of the lineages under exception of Omicron (H505), shows very broad rotamer conformational dispersity in closed and open states, but has a very well‐defined conformation in ACE2‐bound state (Figure 7d, lower panel). Although this conformational dispersity was not captured by the Bayesian effect size (probably due to its positioning at the S‐protein rim region and good water accessibility for most of the rotamers), we observe that the negative BSA values for the neighboring residue 504 (G504) (Figure 6) possibly reflect the conformational flexibility of the region in closed and open states comparing to the ACE2‐bound state. Another residue with a high proportion of negative BSA values is 405 (D405). The residue does not show an extensive rotamer variability in open and ACE2‐bound states but has two distinct states is closed conformation. This conformational duality as well as the conformational flexibility of the neighboring 505, may be a cause of such a high proportion of negative BSA values. An interesting observation can be done for the neighboring residue R403, which is stabilized via cation‐π interaction with Y505 and salt‐bridge with D405 and only in the Delta lineage is stabilized by Y453 and E406. These two conformational states of R403 are also captured by the binomial distribution with one prevalent state.

5.1. Limitations, importance, and future applicability

IRAA, in essence, relies on random sampling of the underlying set of distributions (of SASA per IR). Each underlying distribution approximates the ground truth distribution based on the Gaussian kernel, when there is a large number of multiple structures available. IRAA is based on the widely‐applicable Lee & Richards algorithm, reporting results with a standard probe radius of 1.4 Å; Depending on algorithm and probe radius used, BSAs can slightly vary (Figure S1). To find out how many unique proteins have multiple structures available, we performed a quick check on Uniprot database and PDB database. As of July 2022, approximately 31,500 unique Uniprot IDs were extracted; for each Uniprot ID, we identified number of PDB structures present. To our surprise, we found >50% of the Uniprot IDs which mapped to 3 or more PDB entries. For some Uniprot IDs, the number of structures is seen as high as 900. A histogram of number of PDB structures against the number of Uniprot IDs having those many structures is plotted, as shown in Figure S7. The top 10 most frequent Uniprot IDs are listed therein. Note that PDB does not represent all possible states from different type of proteins but for those that have multiple solved structures it represents a higher degree of heterogeneity. IRAA takes advantage of this heterogeneity to further elucidate the properties of IRs from ensembles.

Some of the examples include not only the human ACE2‐S‐protein, but also chaperones such as the HSP‐90, HSP‐70, and similar systems (Schopf et al., 2017). As it is evident from the current SARS‐CoV‐2 pandemic as well as previous SARS‐CoV and MERS epidemics, investigation of the underlying molecular system may demand extreme urgency. Our method can be a valuable tool for such investigations but also provide insights on residue level behavior. As PDB structures are bound to exponentially increase in the light of current structural biology advances, IRAA can be used in the future to discern effects stemming from experimental method used, resolution achieved, as well as biochemical conditions such as pH‐value, that may also improve the detectability of calculated IRs.

However, if there are less than three structures available, then it is recommended to either use the traditional way of selecting either one (or more) of the best bound structures available as defined by resolution criteria or/and method consistency, or to produce structural models of the binding partners in unbound and bound conformational states applying any computational method for protein structure prediction (AI‐based methods, but also homology modeling, fold recognition or ab initio, depending on available data) and to refine those via molecular dynamics simulations, molecular docking experiments or any other method.

Application of computational methods may bring a great value to such investigations since those enable production of structural models in slightly different conformational states that are biochemically and stereochemically plausible, covering at least a part of the conformational energy surface and representing the dynamical nature of the binding partners in unbound and bound states. Other problem is, so‐called, dark proteome, the protein regions which have never been observed by experimental structure determination and therefore are not well accessible to modeling since they do not have well‐defined 3D structure—also revealed recently by Alphafold. Thus, more than 50% of proteins in eucaryotic as well as viral genome has been predicted to contain long Intrinsically Disordered Protein Regions (IDPRs) or even being fully Intrinsically Disordered Proteins (IDPs) (Dunker et al., 2000; Perdigao et al., ²⁰¹⁵). Molecular recognition of IDPRs/IDPs often goes along with disorder‐to‐order transition (Zhou et al., 2020), so that structure of some protein regions or proteins is known only in the bound state. In that case, the SASA for unbound state can be calculated via separation and calculation of SASA for each of the binding partners as it has been done in the present work on the example of ACE2‐S‐protein complex. Interestingly, disorder‐to‐order transition was also reported for the binding IRs of SARS‐COV‐2 Spike protein upon binding to its receptor ACE2 (Yesudhas et al., 2021). Another interesting aspect of IRAA is its inference of conformational variability, complementing current methods identifying structural variations in flexible proteins (Hrabe et al., 2016), for example, methods accounting for a single protein complex to calculate the radius of gyration per residue or its surface area (Zhou et al., 2020). Implications of such calculations and future integration with IRAA would further shed light onto IDPRs/IDPs that have distinct interface properties (Gunasekaran et al., 2004).

Calculated IRAA properties concern amino acid residues and can be applicable to nucleotides and water molecules as well. However, user‐defined criteria have to be implemented for BSA calculations, for example, co‐factors (Mitternacht, 2016). At present IRAA excludes all HETATM entries. In the case of ACE2‐S protein interaction, glycans, indeed are extremely important; Both S‐protein and its receptor ACE2 are heavily glycosylated but most glycans are flexible and cannot be resolved, and, therefore, are predicted (Choi et al., 2021; Woo et al., ²⁰²⁰). In addition, glycosylation patterns may change according to experimental setups (Allen et al., 2021). Nevertheless, glycosylation has high impact on binding affinity, sometimes strengthening the complex formation (Mehdipour & Hummer, 2021). Glycans present in the interface will naturally increase the BSA. Such an increase is positively correlated with an increase in binding affinity because BSA and binding affinity are positively correlated (Kastritis et al., 2014).

IRAA can also be applied on protein structures consisting of mutations and, therefore, monitor conservation. This is particularly interesting for SARS‐CoV‐2 S variants if their unbound and bound structures are available in multiples. To date, S‐protein of only few variants of interest have been structurally characterized in both unbound and bound states. Limited structural data prohibit comparative analysis but the increase in structural characterization trend in the future will bring conservation analysis with IRAA within reach. Finally, IRAA can be used to more confidently define an epitope region since any kind of protein–protein interface can be calculated considering it has been characterized structurally in multiples.

In summary, IRAA, a method to collectively estimate SASA of biomolecules prior and after building a complex is of importance for various research areas such as development of new drugs where solvent accessibility plays a major role (Samanta et al., 2002; Trisciuzzi et al., ²⁰¹⁹) but also for better understanding of protein folding and binding processes (Lins et al., 2003). Moreover, it was reported that SASA is crucial for estimation of disease‐related single residue variations in a protein. With machine learning‐based methods, it was possible to show that for all residues the proportion of pathogenic single residue variations largely increases when the wild‐type residue is buried and decreases when it is exposed (Savojardo et al., 2020).

6. CONCLUSIONS

IRAA provides a more realistic distribution of BSA of the ACE2‐S‐protein complex than a single value obtained from either a single or multiple bound structures only. As in the latter case, it is inherently assumed that the components are rigid and a complex is then formed by a lock‐and‐key recognition mechanism (Tripathi & Bankaitis, 2017). However, it is well known that all complexes undergo some level of conformational changes during biomolecular recognition. To complicate the matter further, occurrence of a mutation in any components, as evident in the case of SARS‐CoV‐2 S‐protein, may induce conformational variations. Many protein–protein docking algorithms, for example, HADDOCK (Dominguez et al., 2003) and Rosetta (Gray et al., 2003), offer a platform to investigate such effects through molecular modeling. Our method provides a recipe for identifying the IRs from ensemble of single static structures and create a representative dynamic picture out of the system, subsequently derive a combined distribution of BSA, regardless of the experimental method used, including X‐ray crystallography (X‐ray diffraction, XRD) or cryo‐electron microscopy (cryoEM). It should be noted that variations in the interface are not necessarily purely indicative of dynamics within certain residues. IRAA, however, is a valid approach to assess confidence in the contribution of an IR to the BSA, but the source of the confidence is complex, multi‐factorial and not always possible to dissect into every possible contributing component. Quantitative parameters calculated with IRAA will serve as a valuable input to effectively restrain molecular modeling in docking algorithms and to better understand PPIs. Furthermore, this method can be applied to any system that has multiple structures available, including, in future, if any SARS‐like complex becomes prevailing and would need investigations of behavior of the IRs collectively over a large number of single multiple structures.

AUTHOR CONTRIBUTIONS

Jaydeep S. Belapure: Formal analysis (lead); investigation (lead); methodology (lead); software (lead); validation (lead); visualization (lead). Marija Sorokina: Data curation (equal); visualization (equal). Panagiotis L. Kastritis: Supervision (equal).

CONFLICT OF INTEREST

The authors declare no conflict of interest.

Supporting information

Data S1. Supporting Information

Belapure J, Sorokina M, Kastritis PL. IRAA: A statistical tool for investigating a protein–protein interaction interface from multiple structures. Protein Science. 2023;32(1):e4523. 10.1002/pro.4523

DATA AVAILABILITY STATEMENT

All the scripts and list of PDB structures that were used in the present analysis are uploaded on the Kastritis Lab Github page https://github.com/kastritislab/IRAA. The PDB structures used in this work are listed in Table S2. The corresponding PDB files can be accessed from www.rcsb.org.