Deterministic and Stochastic Components of Cortical Down States: Dynamics and Modulation

Abstract

Slow oscillations are an emergent activity of the cerebral cortex network consisting of alternating periods of activity (Up states) and silence (Down states). Up states are periods of persistent cortical activity that share properties with that of underlying wakefulness. However, the occurrence of Down states is almost invariably associated with unconsciousness, both in animal models and clinical studies. Down states have been attributed relevant functions, such as being a resetting mechanism or breaking causal interactions between cortical areas. But what do Down states consist of? Here, we explored in detail the network dynamics (e.g., synchronization and phase) during these silent periods in vivo (male mice), in vitro (ferrets, either sex), and in silico, investigating various experimental conditions that modulate them: anesthesia levels, excitability (electric fields), and excitation/inhibition balance. We identified metastability as two complementary phases composing such quiescence states: a highly synchronized “deterministic” period followed by a low-synchronization “stochastic” period. The balance between these two phases determines the dynamical properties of the resulting rhythm, as well as the responsiveness to incoming inputs or refractoriness. We propose detailed Up and Down state cycle dynamics that bridge cortical properties emerging at the mesoscale with their underlying mechanisms at the microscale, providing a key to understanding unconscious states.

SIGNIFICANCE STATEMENT The cerebral cortex expresses slow oscillations consisting of Up (active) and Down (silent) states. Such activity emerges not only in slow wave sleep, but also under anesthesia and in brain lesions. Down states functionally disconnect the network, and are associated with unconsciousness. Based on a large collection of data, novel data analysis approaches and computational modeling, we thoroughly investigate the nature of Down states. We identify two phases: a highly synchronized “deterministic” period, followed by a low-synchronization “stochastic” period. The balance between these two phases determines the dynamic properties of the resulting rhythm and responsiveness to incoming inputs. This finding reconciles different theories of slow rhythm generation and provides clues about how the brain switches from conscious to unconscious brain states.

Introduction

Slow oscillations are a multiscale phenomenon that dominate cerebral cortex dynamics not only in slow wave sleep but also in a variety of situations including deep anesthesia, disorders of consciousness and perilesional activity. They also emerge in isolated gyri or slabs in vivo and cortical slices in vitro, such that this activity has been proposed as the default activity pattern of the cortical network (for review, see Sanchez-Vives et al., 2017). This is a network emergent pattern that results from the integration of cellular and network properties, which shape this activity and its propagation as a slow wave (Massimini et al., 2004; Capone et al., 2019). For this reason, the resulting pattern of slow wave activity can vary within a relatively wide spectrum, tightly depending on the physiological, pharmacological, or pathologic state of the network.

Slow oscillations consist of the alternation of Up states, active periods with neuronal firing, and Down states or periods of silence, also known as “off-periods” (Vyazovskiy et al., 2011; Nir et al., 2011). Up states share properties with wakefulness: persistent activity generated by recurrent networks with comparable firing rates (McCormick et al., 2003; Constantinople and Bruno, 2011), eventual synchronization in β and γ frequencies (Hasenstaub et al., 2005; Compte et al., 2008; Ruiz-Mejias et al., 2011), or a balanced excitation and inhibition (Shu et al., 2003; Compte et al., 2009). Indeed, Up states have been referred to as “fragments of wakefulness” (Destexhe et al., 2007), since in a sleeping or anesthetized brain, this seemingly awake activity can be recorded at intervals.

So, what separates these “windows into wakefulness” from actual wakefulness and thus from conscious states? The answer is the silent periods in between, or Down states. Intracellular recordings from cortical neurons transitioning between wakefulness and slow wave sleep (Steriade et al., 2001) or between wakefulness and anesthesia (Constantinople and Bruno, 2011) provide evidence that the main difference associated with the collapse of wakefulness is the appearance of these quiescent Down states. Down states are not only a temporal interruption in the information processing and a reset of the system that has been associated with different metabolic and recalibration functions (Tononi and Cirelli, 2003), they also imply a spatial interruption of functional connectivity that breaks the causal interactions between areas (Tononi and Massimini, 2008; Pigorini et al., 2015). The role of Down states, or “off-periods,” on consciousness levels has been thoroughly studied, since evoking prominent “off-periods” using transcranial magnetic stimulation in humans has been consistently associated with the absence of consciousness in unresponsive patients (Rosanova et al., 2018).

Off-periods can also be evoked in the perilesional area of awake stroke patients (Sarasso et al., 2020), and they can also percolate to distant connected areas where they disrupt physiological activity. Loss of consciousness associated with focal limbic seizures has also been associated with slow waves (Yue et al., 2020). Even in awake healthy brains, the propagation of isolated sleep-like slow waves causes lapses of attention (Andrillon et al., 2021), evidencing their disruptive impact on processing.

All this evidence suggests that a detailed understanding of Down states is important since these silent periods are critical for cortical function and for the cancellation of conscious processing. In the current study, we have used novel analytical approaches for the analysis of Up and Down state transitions and found that Down states are not only silent periods but have a dynamical structure including “deterministic” and “stochastic” stages. With this, we define a cycle for slow oscillations that is compatible with different frequencies of oscillation and that provides a novel framework that connects network properties and cellular mechanisms.

Materials and Methods

Experimental methods

Extracellular local field potential (LFP) recordings from different preparations were used. The in vivo data were recorded with a 32-channel electrode array placed on the cortical surface of deeply anesthetized adult male C57BL/6J mice (N = 5, Fig. 1A; for details, see Dasilva et al., 2021). The in vitro recordings were obtained from a 16-channel electrode array placed on the top of slices of ferret visual cortex (N = 6 slices from two ferrets either sex; Fig. 1B; details in Capone et al., 2019). All procedures were approved by the Ethics Committee at the Hospital Clinic of Barcelona and were conducted to the standards laid down in Spanish regulatory laws (BOE 34/11370-421, 2013) and in the European Union directive 2010/63/EU. The in silico data were measured from numerical simulations of a spiking neural network model reproducing the activity of a cortical slice (Fig. 1C) as previously shown (Capone et al., 2019), further details about the model can be found below (see Computational methods: spiking neuron networks).

Figure 1.

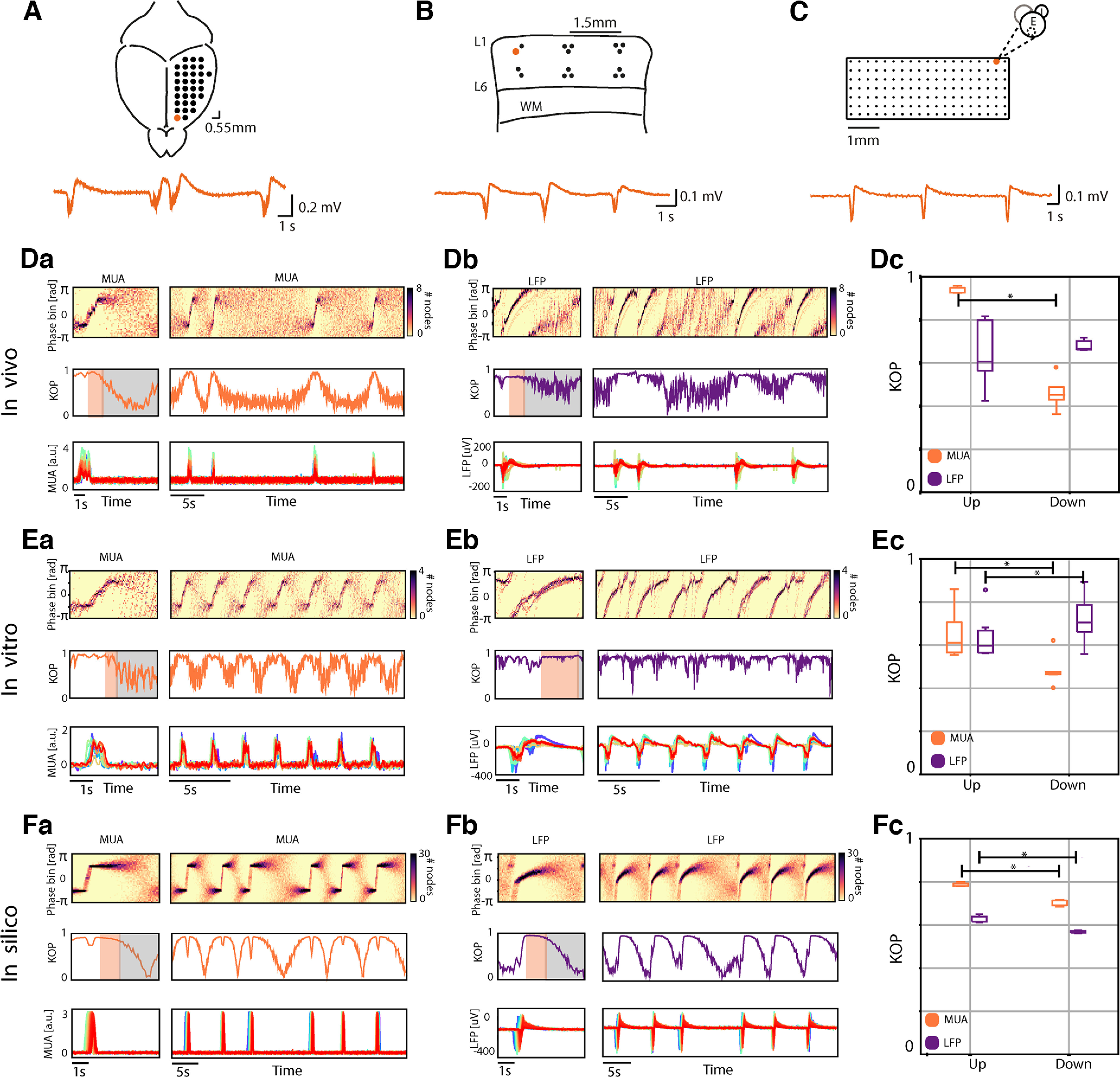
Dynamics phase histograms and state related synchronization in in vivo, in vitro, and in silico cortical networks. Schematic representation of the in vivo (A), in vitro (B), and in silico (C) cortical networks, the orange traces represent the extracellular local field potential (LFP) recorded by one electrode or one node of the network (orange circle). Representation of dynamic phase histograms, the corresponding Kuramoto order parameter (KOP) and cortical activity for multiunit activity (MUA) signals in vivo (Da), in vitro (Ea), and in silico (Fa), and LFP signals in vivo (Db), in vitro (Eb), and in silico (Fb). Orange and gray shades represent the “deterministic” and “stochastic” periods of the Down states, respectively. Boxplots of the average KOP during Up and Down states of the MUA in orange and the LFP in purple: in vivo (Dc, N = 5 mice, n = 75 Down states Wilcoxon signed-rank test in vivo: Up vs Down p = 0.04), in vitro (Ec, N = 6 slices, n = 478 Down states Wilcoxon signed-rank test in vitro: Up vs Down p = 0.02), and in silico (Fc, N = 5 simulations, n = 113 Down states Wilcoxon signed-rank test in silico: Up vs Down p = 0.04).

Computation of the phase signal

The activity of a system of oscillators can be sufficiently represented by its circular phase alone, according to previously published work (Kuramoto, 1984). For this reason, to understand the collective behavior of a network of oscillators, here we start by computing the instantaneous phase at each network node.

The instantaneous phase at each network node was estimated via the analytic signal framework (Le Van Quyen et al., 2001; Muller et al., 2014). This approach entails transforming a real-valued time series into a complex phasor, whose modulus (length) and argument (angle) in the complex plane represent the signal instantaneous amplitude and phase, respectively. Given the time series $x_i(t)$, with $i$ corresponding to the recording channel, its analytic representation is given by:

$$z_i\left(t\right)=x_i\left(t\right)+jH[x_i(t)],$$

where $H\left[x_i\left(t\right)\right]$denotes the Hilbert transform of the signal $x_i\left(t\right)$and the instantaneous phase of the time series can be obtained as follows (Fig. 1D,E):

$${\phi }_i\left(t\right)={\tan }^{-1}\left(\frac{\text{Im}\left[z_i\left(t\right)\right]}{\mathrm{Re}\left[z_i\left(t\right)\right]}\right).$$

Similar to Davis et al. (2020), to preserve the spectral content of the signals and obtain a representation that captures the dominant phase fluctuations of the signals over time, avoiding distortions and artifacts introduced by filtering, we applied the Hilbert transform to broadband signals [multiunit activity (MUA) and LFP]. We did not resort to any narrow-band filtering of MUA and LFP on purpose. In this way we aimed at having an unbiased approach in determining the time scales associated with the adaptation-driven recovery phase; that is, the one characterizing the determinist stage of the Down states. This comes with a caveat in considering as reliable the phase ${\phi }_i\left(t\right)$ of the unfiltered signals when they differ from smooth sinusoidal waveforms as in the case of the relatively fast MUA Up-Down transitions.

Network synchronization, Kuramoto order parameter (KOP)

The instantaneous phase computed as explained above was used to quantify the network-level phase synchrony as a function of time (Le Van Quyen et al., 2010; Yang et al., 2012). According to Strogatz (Strogatz, 2001) and Acebrón and colleagues (Acebrón et al., 2005), we can consider our networks as systems composed of weakly coupled, nearly identical, interacting limit-cycle oscillators, where all the oscillators exert a phase-dependent influence on the others. When the frequencies of the oscillators are too diverse, they are not able to synchronize and the system behaves incoherently, whereas when the coupling is strong enough, the oscillators behave in a synchronized way (Arenas et al., 2008). Kuramoto (Kuramoto, 1984) proposed a mathematical model to outline network synchronization, which is suited to the mean field approach, where the dynamics of the neuronal population is measured by the macroscopic complex order parameter whose modulus measures the phase coherence of the population over time. The use of the Kuramoto model to quantify the degree of phase synchrony of a network of oscillators provides an effective method in a simple algebraic form able to capture the essential features of a dynamical system. The KOP is a time-resolved measure of phase synchrony that is widely used in neuroscience since it allows us to compute synchronization in specific frequency bands; for example, bands associated with specific brain rhythms, and it is not affected by noisy fluctuations in the amplitude of the signals. With respect to other linear measures; for example, cross-correlation and coherence, it has the advantage of being only sensitive to the phase of the signals (i.e., amplitude independent), and of having a better time resolution (Quiroga et al., 2002), while also being easier to compute than nonlinear measures as mutual information, transfer entropy and Granger causality. The values $r=1$ and $r=0$ describe the limits in which all oscillators are either phase locked or move incoherently, respectively. We considered each of our recording electrodes in the experimental preparations as a node of the network, and estimated the instantaneous synchrony among the nodes computing the KOP given by:

$$r\left(t\right)=\frac{1}{n}\left|{\displaystyle \sum }_{j=1}^n{e}^{-i{\phi }_j(t)}\right|,$$

where $n$ is the number of recording channels and ${\phi }_j\left(t\right)$ is the instantaneous phase of each of them defined above. The same was done in the simulated data, considering each module of the model as a node of the network, and estimating the instantaneous synchrony among them. Periods of high phase synchrony (i.e., low phase difference) corresponded to values of $r$ close to 1, while periods of low network synchronization corresponded to values of $r$ close to 0. To obtain a visual representation of network synchronization over time, we imaged the instantaneous phases versus time using dynamic phase histograms as previously shown (Yang et al., 2012).

Dynamical parameters estimation

We estimated the duration of the Down states in each SO cycle from the MUA as previously shown (Ruiz-Mejias et al., 2011). Then, we estimated the time constant of the LFP synchronization dynamics in all the experimental conditions and in the simulated data. To do so, we extracted from the dynamic phase histograms Figure 1Db,Eb,Fb phase related to the maximum counts over time (Fig. 4D). Using this time series, we fitted an exponential curve,

$$f\left(t\right)=A\left(1-e^{-\frac{t}{\tau }}\right)+c,$$

in the time periods right after each Up-to-Down transition (Fig. 4D, orange area) and extracted the variable $\tau$ which is the characteristic time constant of the exponential (computed in Python using scipy.optimize.curve_fit). Note that in the simulated data the $\tau$ parameter is known, therefore we used the simulation to validate our fitting method, comparing the estimated and the actual $\tau$ (Fig. 4E, bottom right). According to this validation, and to avoid high fitting errors, we included here only the estimations in which one standard deviation errors on the parameters' estimation is lower than 1.

Figure 4.

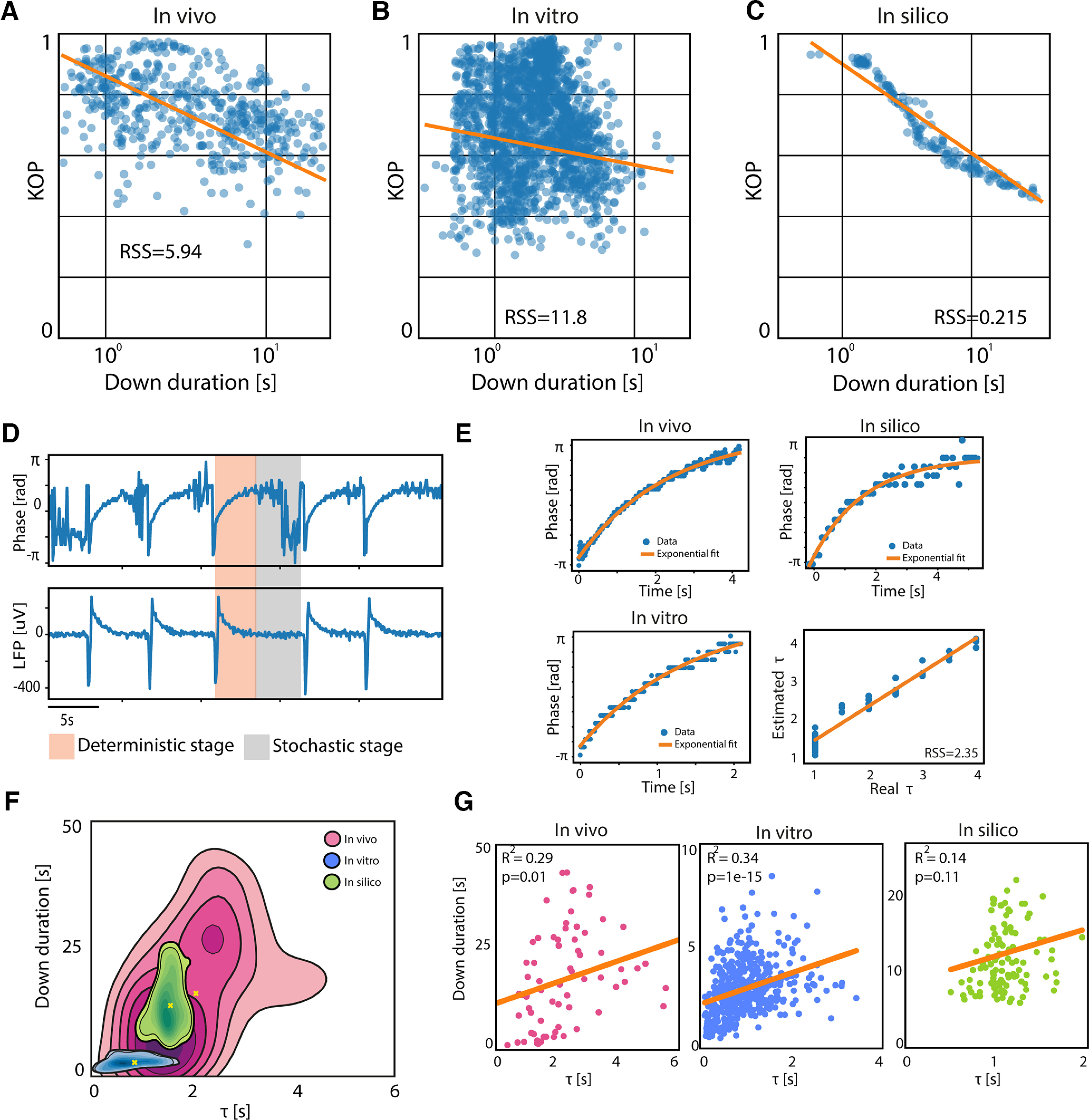
Metastability of the Down state and its characteristic time scale. Correlation between the mean Kuramoto order parameter (KOP) of the LFP during the Down states, and the Down state duration. Each point in the figures represents a single Down state, where the modulation of its duration was obtained through varying anesthesia in vivo (A; R² = −0.45, p = 1e-29), using DC fields of different polarities in vitro (B; R² = −0.1, p = 0.02) and changing model's parameters in silico (C; R² = −0.9, p = 1e-93). D, τ estimation method: bottom panel shows the local field potential (LFP) extracted from one module of a simulated network (in silico); upper panel shows the corresponding time evolution of the maximum of the LFP phase histogram; the gray area corresponds to the “deterministic” stage of the Down state where we estimated the τ, while the pink area corresponds to the “stochastic” stage. E, Example of exponential fitting for τ estimation in vivo (top left), in vitro (bottom left), and in silico (top right); regression plot of the real τ versus the estimated τ in silico with residual sum of squares (RSS) of 1.46. F, Kernel density estimation (KDE) of Down durations versus τ in vivo, in vitro, and in silico. G, Linear correlation between Down duration and τ in vivo (RSS = 9e+03), in vitro (RSS = 681), and in silico (RSS = 2e+03).

Computational methods: spiking neuron networks

We modeled a cortical slice using a spiking neural network; details about single neuron parameters and network connectivity can be found in Capone et al. (2019). Briefly, the network model is composed of a two-dimensional $7\times 20$ lattice of interacting cortical modules.

Each module is a subnetwork of two homogenous populations of 502 excitatory and 126 inhibitory leaky integrate-and-fire (LIF) neurons. The membrane potential $V_i\left(t\right)$ of the $i$th neuron evolves according to $\dot{V_i}=-V_i/\tau +I_i-a_i$, where $I_i(t)$ is the input synaptic current and $a(t)$ is an activity-dependent hyperpolarizing current present only in excitatory neurons, responsible for spike-frequency adaptation. The decay constant $\tau$ of the membrane potential is 20 and 10 ms for excitatory and inhibitory neurons, respectively. The synaptic current is a linear combination of the spikes emitted by the presynaptic neurons: $I_i\left(t\right)={\displaystyle \sum }_{k}J\_ik\delta \left(t-t_k-d_{ik}\right)+I_{ext}$, with additional contribution $I_{ext}$ given by the spikes emitted by external neurons, modeled as Poisson processes with spike rate $C_{ext}{\nu }_{ext}$ that is 1466 Hz for the “foreground,” 1511 Hz for the “background” and 2100 Hz for the inhibitory. Each spike emitted at time $t_k$ by the $k$th presynaptic neuron contributes with an instantaneous current $J_{ik}$ (synaptic efficacy). Spikes were delivered with a transmission delay $d_{ik}$. The current $a_i(t)$ follows the first-order dynamics ${\tau }_a\dot{a_i}=-a_i+g_a{\tau }_a{\displaystyle \sum }_i\delta (t-t_i)$. In the absence of emitted spike by the $i$th neuron, the adaptation current decays with a time constant ${\tau }_a=1$ s. The adaptation strength $g_a=0.06$mV/ms determines the sudden increase in $a_i$ when a spike is emitted. We also modulated the decay time ${\tau }_a$ of the adaptation current by setting sequentially the values $\{1,2,2.5,3,3.5,4\}$ s every 100 s. In doing so, we fixed the mean adaptation current by changing the adaptation strength while keeping constant the product ${\tau }_a{g}_a$. Neurons emit a spike when $V\left(t\right)$ crosses the threshold $\theta =20$mV, after which the potential reset to 15 mV during an absolute refractory period of 2 and 1 ms for excitatory and inhibitory neurons, respectively. The connectivity (i.e., the probability of having two neurons synaptically coupled) is determined by the position of the postsynaptic module in the lattice, and by the relative distance with the presynaptic population in the lattice (Capone et al., 2019). The connectivity is not homogeneous in space, aiming at modeling a strip of more excitable assemblies representing layer five neurons. Numerical simulations of the model network were performed in NEST (Kunkel et al., 2017).

In order to use the same analytical approach developed for in vitro and in vivo recordings, we transformed the simulated activity (i.e., the emitted spikes) in an in silico representation of MUA and LFP. The MUA is computed starting from the firing rate of the foreground excitatory neurons ${\nu }_{fg}\left(t\right)$and adding a proper white noise $\zeta (t)$ with $〈\zeta \left(t\right)〉=0.3$ and $〈{\zeta }^2\left(t\right)〉=3$ to reproduce the background fluctuations observed in the experiments. LFP is computed as a linear combination of the average (across neurons) incoming currents $a_{fg}=〈a_i\left(t\right)〉$ (adaptation-related) and $I_{fg}=〈I_i\left(t\right)〉$ to the foreground excitatory neurons in a cortical module, while adding a noise $\eta (t)$ with zero mean and variance $〈{\eta }^2\left(t\right)〉=〈0.25{(5a_{fg\left(t\right)}-I_{fg\left(t\right)})}^2〉$, resulting in the following equation: $LFP=5a_{fg}-I_{fg}+\eta$.

This network configuration is the one used to obtain in silico control simulations (N = 5). We operated several changes to investigate how different microscopic and mesoscopic features of the system affect the properties of the spontaneous slow-wave activity. To model the effects of a stimulation by a homogeneous direct current (DC) field applied to a cortical slice, the synaptic input current was modulated by adding an extra DC current $I_{DC}=\{-1,-0.5,-0.25,+2.5,+5,+10,+20\}pA$ to make the membrane potential more or less polarized (DC– and DC+ simulations; D'Andola et al., 2018).

Data availability

Data presented in the main figures and in extended data figures are available in the data source files in Zenodo (https://doi.org/10.5281/zenodo.5070570). Human Brain Project Neuroinformatics Platform, doi:10.25 493/WKA8-Q4T. Raw data are available on reasonable request, owing to their size. Source data are provided with this paper.

Code accessibility

Numerical simulations of the model network were performed in NEST (2.12.0, doi:10.5281/zenodo.259534) on the high-performance computing facility hosted by the Istituto Superiore di Sanità. Python code of the simulation is freely available in EBRAINS Knowledge Graph where all the parameters and information of the network design are fully accessible (https://kg.ebrains.eu/search/instances/Model/db8c315ee902bee98025d8c78d4a0e0432b92ec0).

Results

To investigate the cerebral cortex network dynamics and underlying mechanisms during Up and Down states, we studied in parallel three cortical networks: in vivo, in vitro, and in silico, while expressing slow oscillations. We focused on the dynamic properties of Down states and their relationship with the microscale and mesoscale networks, both in control conditions and under different experimental manipulations, which allowed us a broader investigation of the key elements governing this cortical dynamic space.

Network dynamics revealed by input versus output synchronization

First, to investigate the network dynamics occurring at different scales in vivo, in vitro, and in silico (Fig. 1A; Fig. 3), we computed the time evolution of the phase and the synchronization during the oscillatory cycles (i.e., during ongoing slow-wave activity). To determine the dominant phase fluctuations of the signals over time, we calculated the instantaneous phase at each network node via the analytic signal framework (Le Van Quyen et al., 2010; Muller et al., 2014) applying the Hilbert transform to broadband signals [multiunit activity (MUA) and local field potential (LFP); Davis et al., 2020]. The instantaneous phase was used to quantify the network-level phase synchrony as a function of time (Le Van Quyen et al., 2001; Yang et al., 2012). We considered each of our recording electrodes in the experimental preparations as a node of the network and estimated the instantaneous synchrony among the nodes computing the Kuramoto order parameter (KOP; Materials and Methods).

Figure 3.

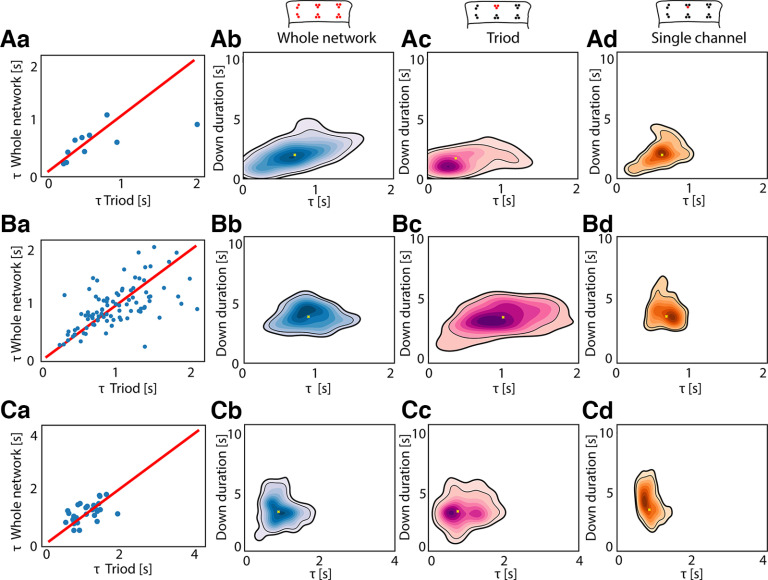
Whole network versus local network dynamics estimation. Scatterplots showing the linear correlation between the τ estimated at the whole network level and the one estimated in a single triode in vitro (i.e., three electrodes placed close to each either in the 16-channels MEA used for in vitro recording, see Materials and Methods), in three different slices (Aa: Pearson correlation = 0.64, p = 0.04; Ba: Pearson correlation = 0.59, p = 0.002; Ca: Pearson correlation = 0.56, p = 0.001). Kernel density estimation (KDE) of in vitro Down durations versus τ estimated at whole network level in the same three slices (Ab, Bb, Cb). KDE of in vitro Down durations versus τ estimated using data from one triode (see scheme above) in the same three slices (Ac, Bc, Cc). KDE of in vitro Down durations versus τ estimated using data from one recording channel (see scheme above) in the same three slices (Ad, Bd, Cd).

To capture the multiscale processes underlying network activity, we studied the synchronization dynamics at two different levels: between neuronal populations in the LFP signal and the MUA, considered as signals mainly made of synaptic input currents and of the output action potentials generated by the neurons, respectively (Buzsáki et al., 2012). We show the network phase time course with dynamic phase histograms (Fig. 1D). In it, the color scale indicates the number of electrodes with a given phase (vertical axis) at a given time (horizontal axis). Phase bundles marked by dark pixels over time indicate many sites with the same phase (in-phase locking; Yang et al., 2012).

The dynamic phase histograms reveal differences in the synchronization dynamics of the MUA and LFP, supporting the idea that the two components of the electrophysiological activity provide different information about network dynamics. The MUA signals exhibited patterns of synchronization characterized by in-phase locking during the Up states and thus high synchronization (high KOP; Fig. 1Da,Ea,Fa). This high synchronization was partially maintained during the early phases of the Down state, but progressively decayed, displaying asynchronous “stochastic” behavior in the later phases with a significant decrease of the KOP. This result was confirmed at a population level, where we computed the average network synchronization associated with the Up and Down states, respectively, as shown in Figure 1Dc,Ec,Fc. We found that, on average, the KOP of the MUA is high during the Up states, but significantly decreases on average during the Down states, all in vivo, in vitro, and in silico (Fig. 1Dc; Wilcoxon signed-rank test in vivo: Up vs Down p = 0.04; Fig. 1Ec, in vitro Up vs Down: p = 0.02; Fig. 1Fc, in silico Up vs Down: p = 0.04).

To study the dynamics arising in the extracellular voltage resulting from the combination of synaptic activity and neuronal transmembrane processes (i.e., ionic channels), we also studied the network synchronization of the LFP signal. Here, we found an intermediate level of synchronization associated with the Up states (KOP mean ± standard deviation (SD): in vivo 0.65 ± 0.14, in vitro 0.64 ± 0.10, in silico 0.62 ± 0.01). Interestingly, in the LFP, the absolute difference between the Up and Down synchronization was not as consistent as in the MUA: no significant difference was found between channels in vivo (Fig. 1Dc), while we found significantly higher synchronization in the Down states in vitro (Fig. 1Ec), and significantly lower synchronization during Down states in silico (Fig. 1Fc).

The explanation for this diversity can be found when exploring the dynamics of Down states: as suggested by the MUA analysis, the LFP clearly expressed a metastable dynamics, such that the network transiently persists in a quasi-stationary state, temporarily failing to express an ergodic wandering of its phase space until a sudden and stereotyped (Down-to-Up) transition drives it into another metastable condition (the Up state; Yang and Tang, 2000). The metastability of the Down states consists of the coexistence of two different states of equilibrium. As such, the metastable Down states were characterized by two phases: (1) a sustained period of high synchronization immediately after the Up-to-Down transition, where the collective phase behavior shows an exponential trend and the KOP is close to 1 (Fig. 1, orange); and (2) a second period characterized by a loss in network synchronization, in which the collective phase randomly fluctuates between plus and minus π (Fig. 1, gray). According to previously proposed models, a random fluctuation in the second period would be critical to trigger the subsequent Up state (Compte et al., 2003; Mattia and Sanchez-Vives, 2012; Sancristóbal et al., 2016; Jercog et al., 2017; Capone et al., 2019; Levenstein et al., 2019). Given the properties of these two periods, we decided to name these stages “deterministic” and “stochastic,” respectively.

To investigate in depth the metastability of Down states as well as the differences in the synchronization dynamics in the MUA and LFP, we zoomed into single slow oscillation (SO) cycles. The 3D representation of a signal amplitude, phase and synchrony over time provides significant insights into the dynamics of the network activity in this framework. In Figure 2, we show a comparison of the one-cycle dynamics of MUA and LFP. Independently of the network (in vivo, in vitro, in silico), high values of MUA (i.e., the Up states) correspond to periods of high synchronization (purple and turquoise points). After the end of the Up state, and once the firing rate is collapsed, the synchrony is progressively lost (in orange), KOP decreases and transitions into a “stochastic” phase regime characterizing the Down states in the MUA (Fig. 2Aa,Ba,Ca, gray points).

Figure 2.

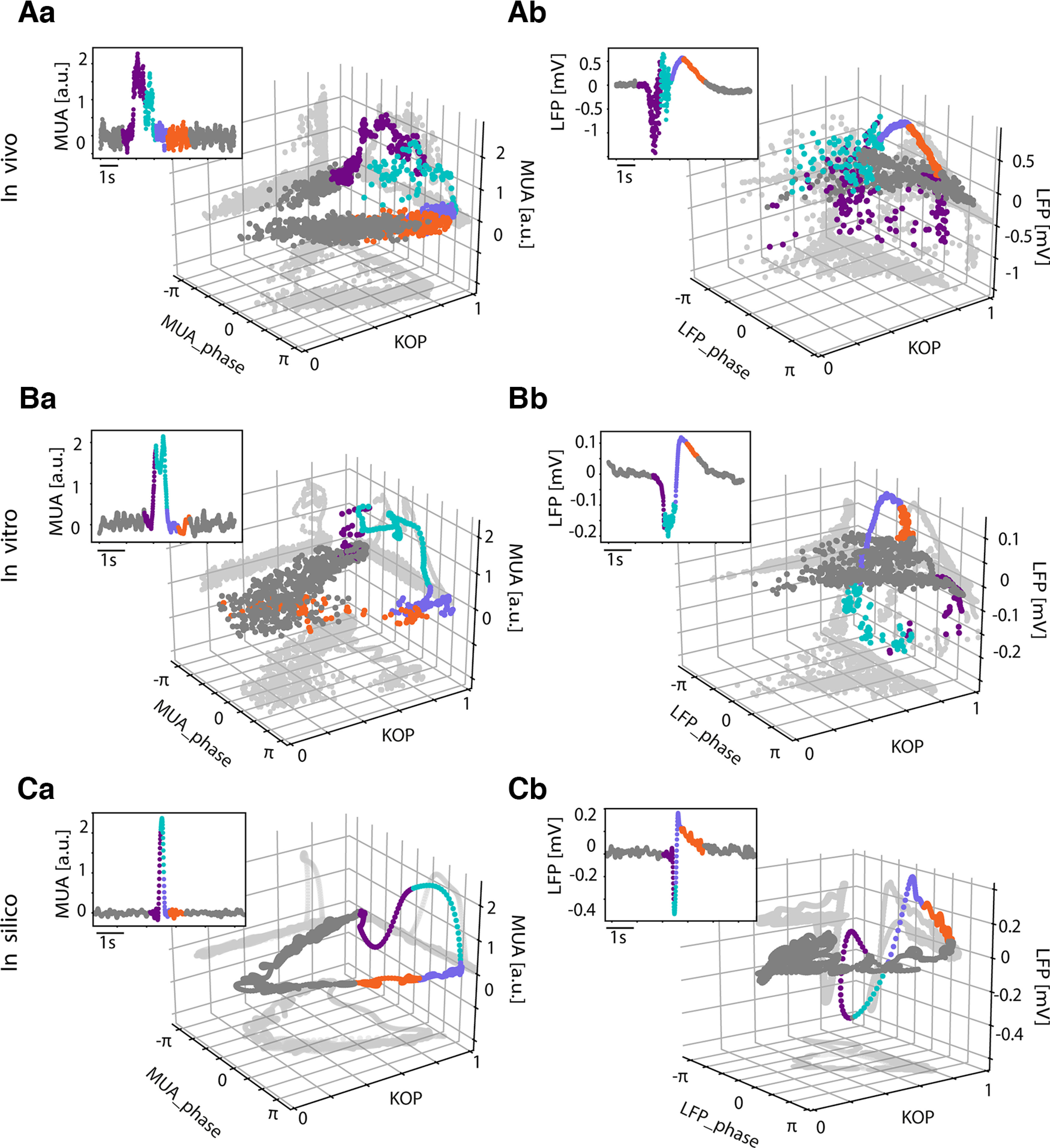
Multiunit activity (MUA) and local field potential (LFP) synchronization dynamics. A, In vivo 3D representation of the phase, amplitude, and Kuramoto order parameter (KOP) corresponding to the slow oscillation cycle depicted in the 2D insert in MUA (Aa) and LFP (Ab). B, In vitro 3D representation of the phase, amplitude, and KOP corresponding to the SO cycle depicted in the 2D insert in MUA (Ba) and LFP (Bb). C, In silico 3D representation of the phase, amplitude, and KOP corresponding to the slow oscillation cycle depicted in the 2D insert in MUA (Ca) and LFP (Cb). The points are colored according to time, the purple coincides with the Down-to-Up transition, turquoise corresponds to the Up state, violet is the Up-to-Down transition, orange is the beginning of the Down state and the rest of the Down state is in gray; gray shades represent the projections of the cloud on each plane.

Conversely, in the LFP, the period immediately after the Up-to-Down transition, thus the beginning of the Down state (in orange), is still characterized by a high synchronization with a KOP ≈ 1, highlighting again the presence of the “deterministic” stage at the beginning of the Down state at the local population level. This “deterministic” state then transitions toward a “stochastic” one (in gray), which will eventually lead to the next Up state. Thus, we demonstrate that it is not possible to distinguish the different stages of the metastable quiescent states by looking at the MUA synchronization dynamics alone, stressing the importance of the simultaneous recording and analysis of the LFP and MUA signals.

Characteristic time scales of the metastable Down states

The synchronization analysis at the level of neuronal populations in the LFP revealed the existence of a metastable dynamic during the Down states. A “deterministic” and a “stochastic” period were identified in this order and with a respective duration that could vary depending on the system or the experimental manipulations. The “deterministic” stage is the one arising immediately after the Up-to-Down transition. During this stage, we observed a correlation between the synchronization dynamics and the strength and time course of the afterhyperpolarization that follows the end of the Up states (Compte et al., 2003). Accordingly, we propose here that it could be possible to infer dynamical features at the microscale; that is, the evolution of the afterhyperpolarization following Up states (Sanchez-Vives and McCormick, 2000; Sanchez-Vives et al., 2010); through the study of macroscopic variables, such as the time constant of network synchronization. To quantitatively characterize these phenomena, we estimated the time constant of the exponential phase growth (τ; Fig. 4D, orange area; see Materials and Methods) during the “deterministic” stage of the Down states. This estimation was done for cortical networks in vivo, in vitro, and in silico.

For the in silico network, we modeled a cortical slice using a network of spiking neurons (single neuron parameters and network connectivity as previously shown (Capone et al., 2019). Briefly, the network model is composed of a two-dimensional 7 × 20 lattice of interacting cortical-like modules. Each module is composed of excitatory (80%) and inhibitory (20%) neurons. Excitatory neurons incorporated activity-dependent afterhyperpolarizing currents underlying spike-frequency adaptation. In order to use the same analytical approach developed for in vitro and in vivo recordings, we transduced the simulated activity (i.e., emitted spikes) in an in silico representation of MUA and LFP (for details, see Materials and Methods). We modulated the decay time τ_a of the adaptation current and in doing so, we fixed the mean adaptation current by changing the adaptation strength.

The estimation of τ used in vivo, in vitro, and in silico was validated by computing the Pearson correlation and the residual sum of squares (RSS) of the regression between the real τ_a set in the simulated neurons and the one estimated from the in silico LFP synchronization (Pearson correlation = 0.97, p < 0.001, RSS = 2.35; Fig. 4E, bottom right panel). The significant linear relationship between the single-neuron parameter τ_a and the synchronization decay constant τ of the whole network provided an unexpected opportunity to bridge the gap between experimental observations at the macroscale and the microscopic parameters of the system.

Through a multiscale exploration of the in vitro cortical preparations, we verified that the τ estimated at the whole network level is linearly correlated with the one estimated in a single triode of the recording array (Fig. 3: Pearson correlation = 0.64, p = 0.04; Fig. 3Ba: Pearson correlation = 0.59, p = 0.003; Fig. 3Ca: Pearson correlation = 0.56, p = 0.001), that is in turn correlated with the exponential decay time constant directly estimated from the LFP trace of a single channel (Fig. 3Ad,Bd,Cd). Our results are represented here as continuous probability density curves (Python seaborn.kdeplot) showing the distribution of Down state duration and τ obtained through a kernel density estimation (KDE). We thus show that neuronal properties as the characteristic time constant of the adaptation—and associated afterhyperpolarization currents (Compte et al., 2003)—may be estimated at network level, highlighting the scalability of such phenomena in both experimental and simulated environments.

When comparing the in vivo, in vitro, and in silico joint distributions of the Down state durations and τ, time constants of the network synchronization (Fig. 4F), we found a much larger range of Down state durations and τ in vivo under deep anesthesia (mean ± SD: Down duration 18.8 ± 7.8 s, τ duration 2.1 ± 1.5 s) with respect to the in vitro (mean ± SD: Down duration 2.9 ± 1.3 s, τ duration 0.95 ± 0.61 s) and in silico cases (Down duration 9.4 ± 3.9 s, τ duration 1.35 ± 0.13 s).

To be able to explain the Down state metastability in different systems at various scales, we performed a linear regression analysis between the Down duration and τ. Our results show that a significant correlation between the two parameters is present when the metastable quiescent dynamics are dominated by the “deterministic” period, which is more common in the control conditions in vitro, as seen in Figure 1Eb. For in vitro cortical networks, the relationship between τ and Down states (0.51–8.42 s) was of R² = 0.34 (RSS = 681, $P={10}^{-15}$; Fig. 4G).

The case of Down states in vivo included a much larger range of Down state durations (0.76–43.2 s) and the τ was significantly larger than in vitro, with an average value of 2.4 ± 1.5 s. Even when in vivo Down states were characterized by both “deterministic” and “stochastic” stages (Fig. 1Db), the “deterministic” stage still ruled the Down states to some extent, although with a slightly lower correlation with respect to the in vitro case (R² = 0.29, RSS = 9000, p = 0.01) (Fig. 4G). This positive relationship was almost nonexistent in the in silico cortical network model (R² = 0.14, RSS = 2 × 10³, p = 0.11) (Fig. 4G), suggesting that the correlation between Down state duration and τ may be used as a relevant variable in the study of the cellular and network mechanisms dominating cortical off-period dynamics.

The modulation of cortical activity reveals state-dependence of Down state metastability

We have shown that different cortical networks express different degrees of metastability in Down states, conveyed by the synchronization dynamics of neuronal pools in the LFP. By examining the characteristics of each network, we systematically observed that the linear regression between the mean values of KOP in each Down state and the Down state duration revealed a significant negative correlation (Fig. 4A,B,C) shorter Down states are more synchronized than longer ones. Thus, the KOP is high when the Down states have short durations and their dynamics is dominated by the afterhyperpolarizing periods (“deterministic” stage), while the KOP decreases when the Down states have longer durations and the network has the time to desynchronize and shows “stochastic” fluctuations (stochastic stage). Still, we will show below that there can be exceptions to this rule, with specific experimental manipulations that enhance afterhyperpolarization. In light of these results, we speculate that the metastability of the Down states is a state-dependent phenomenon that varies with the dynamical conditions independently of the network structure and observation scale, which is reflected in the overall degree of network synchronization.

Exogenous modulation of Down state metastability and tuning of system dynamics

To explore a wider spectrum of cortical dynamics and to assess metastability quantitatively, we introduced here some experimental manipulations that vary the duration of Down states and thus the cortical dynamics. We did this in the three networks: in vivo, in vitro, and in silico.

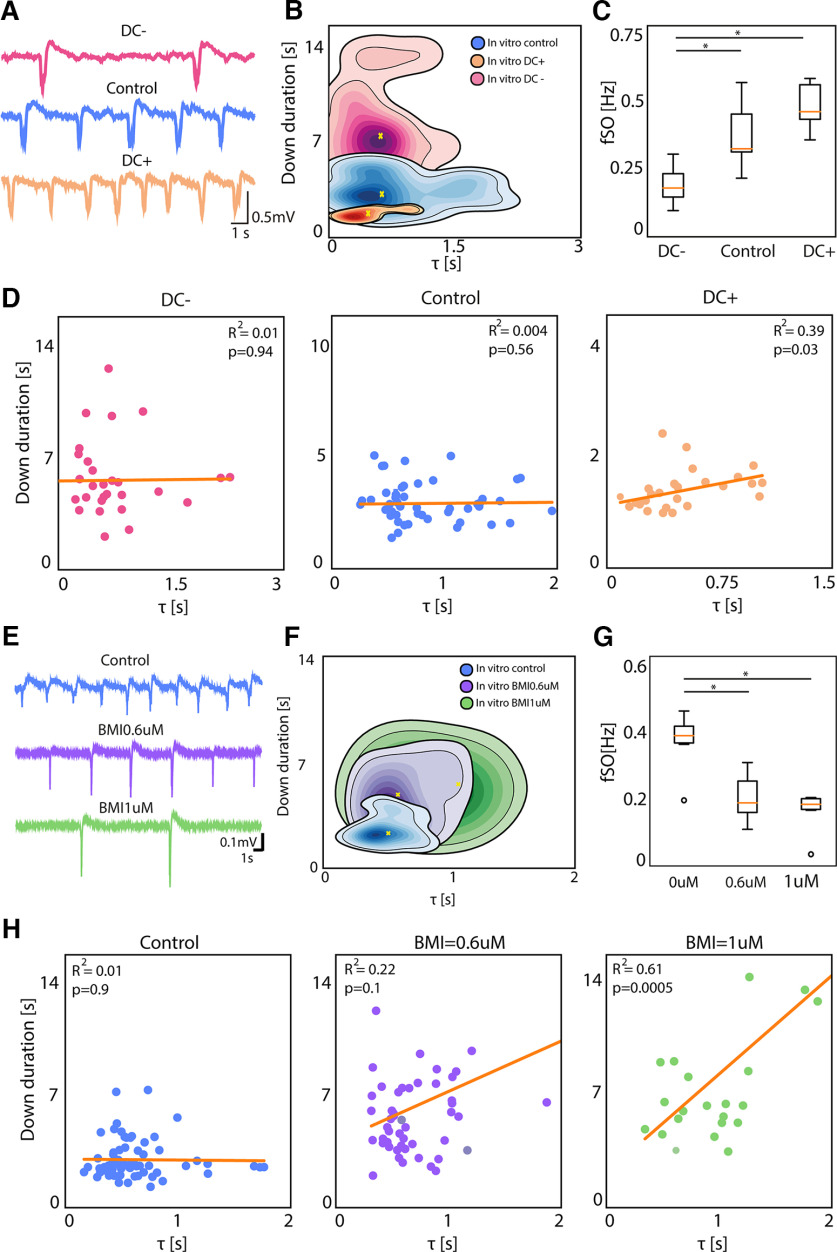
In vivo, we analyzed the emergent cortical dynamics under three different levels of anesthesia (Fig. 5), which provided us with a significant modulation of the SO frequency (Fig. 5C) and Down state duration, as we have described previously (De Bonis et al., 2020; Dasilva et al., 2021). The three levels of anesthesia expressed different Down state durations (Down duration (mean ± SD): Deep anesthesia: 18.82 ± 7.76 s; Mid anesthesia level: 5.35 ± 1.02 s; Light anesthesia level: 1.81 ± 1.01 s; Friedman test p = 0.006, Wilcoxon signed-rank test: p < 0.05). This experimental manipulation resulted in significantly different time constants of synchronization (Fig. 5B,D), such that deep anesthesia had the longest and light anesthesia the shortest τ and Down state durations (τ duration mean ± SD: Deep anesthesia: 2.36 ± 1.53 s; Mid anesthesia level: 1.42 ± 1.09 s; Light anesthesia level: 0.72 ± 0.94 s). The correlation between τ and Down state duration significantly increased when moving from deep anesthesia to lighter anesthesia states, the light levels of anesthesia expressing the highest correlation: shortest Down states of high regularity (Tort-Colet et al., 2021) correspond to a cycle sharply controlled by the “deterministic” stage of the Down state.

Figure 5.

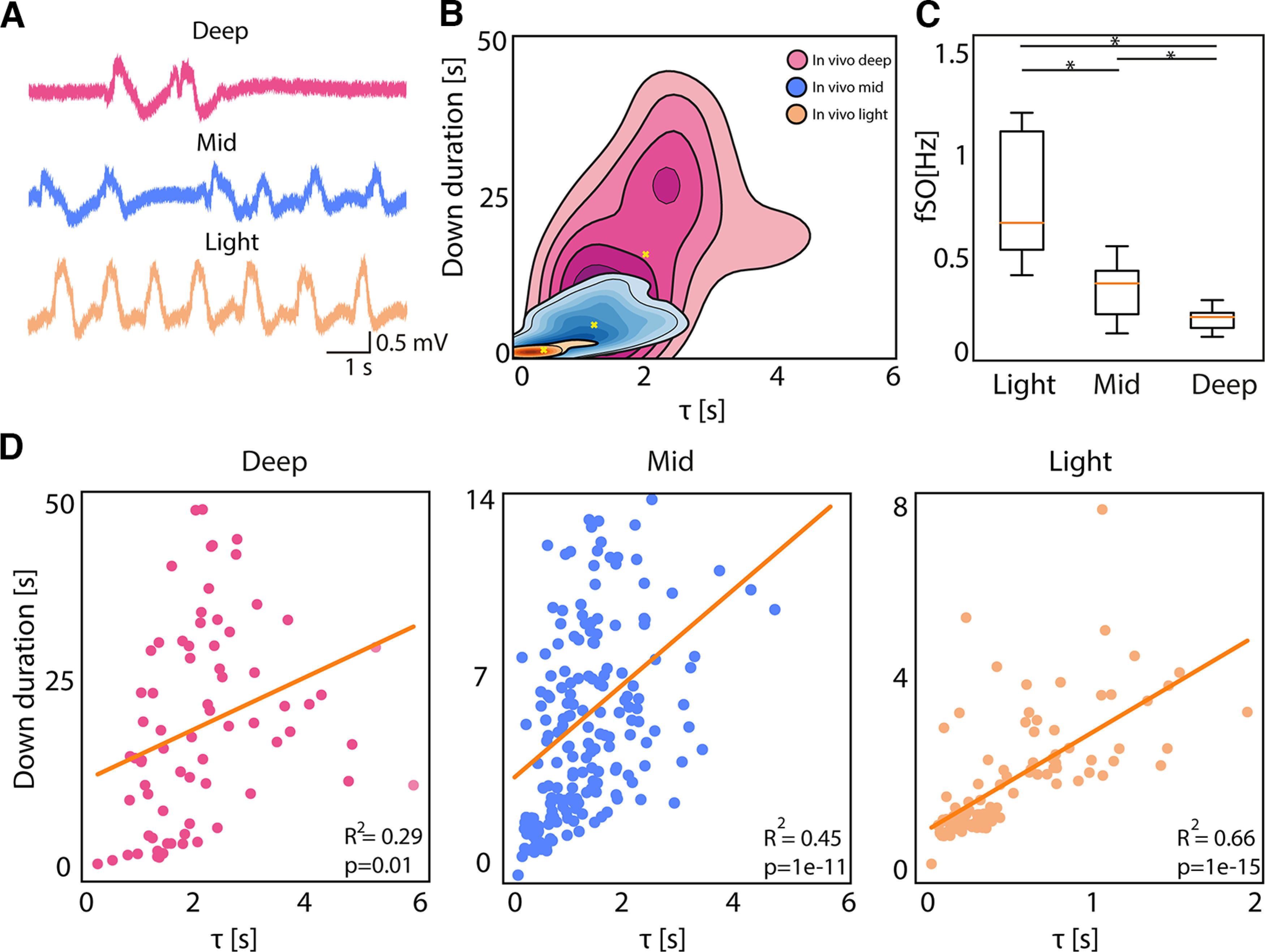
Activity modulation effect on network dynamics. A, Traces representing the local field potential (LFP) recording from one electrode in vivo at Deep, Mid, and Light anesthesia level (adapted from Dasilva et al., 2021). B, Kernel density estimation (KDE) of Down durations versus τ in vivo under Deep, Mid, and Light anesthesia levels. C, Boxplot of the average frequency of the slow oscillations for each subject (N = 5) under Light, Mid, and Deep anesthesia (Friedman test p = 0.002, Wilcoxon signed-rank test: *p < 0.05). D, Linear correlation between τ and Down duration in vivo under Deep (RSS = 9e+03), Mid (RSS = 1e+03), and Light anesthesia (RSS = 114).

In vitro we used two experimental manipulations to modulate the Down state duration. First, the modulation of slow oscillatory activity by using constant electric fields of different polarities (+3 and −3 V/m). Exogenous electric fields vary the neuronal membrane potential (0.5 mV per 2V/m; Fröhlich and McCormick, 2010) causing a net depolarization/hyperpolarization in pyramidal neurons. The variation of direct current (DC) causes an exponential modulation of the slow oscillatory frequency in cortical slices that we have described in detail previously (Barbero-Castillo et al., 2019 and D'Andola et al., 2018; Fig. 6A). With positive DC stimulation, we obtained a decrease in Down state duration and an increase in oscillatory frequency, while negative DC stimulation induced an increase in Down duration and a decrease in oscillatory frequency with respect to the control condition (Down duration mean ± SD: Control: 2.89 ± 1.28 s; Positive DC: 1.44 ± 0.46 s; Negative DC: 6.36 ± 3.11; Fig. 6B,C). The linear regression analysis reveals a lack of significance in the τ versus Down state duration for control and DC− (Fig. 6D). However, DC+, which corresponds to the highest frequency of slow oscillations, displayed an R² of 0.39 (p = 0.03), being a situation with short and mostly “deterministic” Down states that tightly control the triggering of the subsequent Up state and reminiscent of light anesthesia.

Figure 6.

In vitro activity modulation effect on network dynamics. A, Traces representing the local field potential (LFP) recording from one electrode in vitro under negative DC stimulation, control conditions and positive DC stimulation. B, Kernel density estimation (KDE) of Down durations versus τ in vitro with negative DC, control conditions and positive DC. C, Boxplot of the average frequency of slow oscillations for each slice (N = 6) under negative DC stimulation, control conditions and positive DC stimulation (Friedman test p = 0.014, *p < 0.05). D, Linear correlation between Down duration and τ in vitro under negative DC stimulation (RSS = 201), control conditions (RSS = 19.9) and positive DC stimulation (RSS = 3.6). E, Traces representing the LFP recording from one electrode in vitro under control conditions and with bath application of bicuculline (BMI) at two different concentrations: 0.6 and 1 μm. F, KDE of Down durations versus τ in vitro under control conditions and with BMI at 0.6 and 1 μm. G, Boxplot of the average frequency of slow oscillations for each slice (N = 6) under control conditions and with BMI at 0.6 and 1 μm (Friedman test p = 0.014, *p < 0.05). H, Linear correlation between Down duration and τ in vitro under control conditions (RSS = 88.6), with BMI 0.6 μm (RSS = 1e+03), and BMI 1 μm (RSS = 721).

However, is it that simple? Are shorter Down states invariably and tightly bound to a highly “deterministic” interval? Our second manipulation in vitro shows that this physiological relationship, which dominates in control states, can be altered in nonphysiological conditions. In this case, departing from the control slow oscillation at a frequency of 0.36 ± 0.09 Hz, we blocked GABA_A receptors using bicuculline methiodide (BMI). The blockade of fast inhibition led to highly synchronized Up states of lower frequency, which were followed by increasingly prominent afterhyperpolarizations (Fig. 6E), as we have previously described (Sanchez-Vives et al., 2010; Barbero-Castillo et al., 2021). The τ versus Down state regression analysis (Fig. 6H) revealed a highly significant relation for 1 μm BMI, despite corresponding to the longest Down states. This finding reveals that it is not simply the duration of the Down states, but the mechanism underlying this duration that is critical: when inhibition is blocked, the afterhypolarization increases in amplitude (Fig. 6E), corresponding to a larger intracellular afterhyperpolarization attributed to potassium currents (Sanchez-Vives et al., 2010). This is highly suggestive of the mechanism bridging cellular and network properties during Down states.

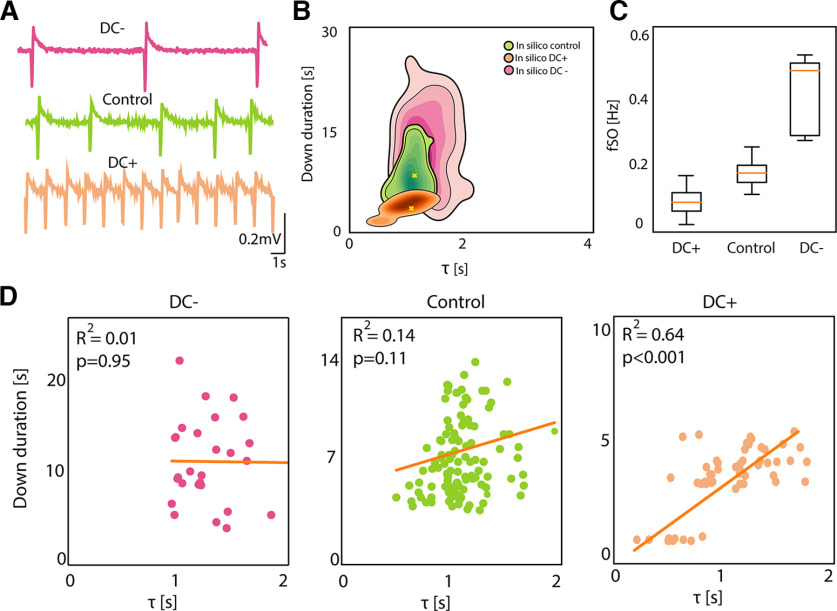
Finally, in silico we modulated the Down state duration simulating the excitability changes posed by positive and negative DC stimulation. We did this by modulating the synaptic input current (Down duration mean ± SD; Control: 9.4 ± 3.9 s; positive DC: 3.1 ± 1.5 s; negative DC: 13.7 ± 8.8 s; Fig. 7A,B). As shown for the experiments, the frequency of the oscillations increased with increased excitability or positive DC (and decreased with negative DC; Fig. 7C). The relation between τ and Down state duration was absent for decreased excitability (negative DC; Fig. 7D), with long Down states and thus longer “stochastic” periods. The strongest relationship was, as for the data, for positive DC (R² = 0.64; p < 0.001), thus for shorter Down states dominated by the “deterministic” period.

Figure 7.

In silico activity modulation effect on network dynamics. A, Traces representing the local field potential (LFP) reconstructed from one network module in silico under decreased excitability (negative DC stimulation), control conditions and increased excitability (positive DC stimulation). B, Kernel density estimation (KDE) of Down durations versus τ in silico under decreased excitability, control conditions and increased excitability. C, Boxplot of the average frequency of slow oscillations for each simulation (N = 5) under decreased excitability, control conditions and increased excitability (Friedman test p = ns). D, Linear correlation between Down duration and τ in silico under decreased excitability (RSS = 696), control conditions (RSS = 2e+03) and increased excitability (RSS = 50.6).

A global picture of slow oscillations and Down state metastability across states

In this final section, we integrate the concepts presented with these results. Through the analysis of the cortical network dynamics using phase and synchronization of MUA and LFP, we found that Down states are more than just silent periods in between Up states. They have a structure that determines the degree of their metastability and the features of the emergent oscillatory pattern. We have differentiated two dynamical phases in Down states (Fig. 8A): a “deterministic” phase, with high synchronization (KOP) and a time course determined by the exponential growth of the phase (τ); and a “stochastic” phase, with low synchronization (Figs. 1 and 2). In sum, Figure 8A represents the oscillatory cycle between Up and Down states that our data and analysis support: the end of the Up state is highly synchronous as commonly reported (Volgushev et al., 2006; Mochol et al., 2015), the network goes into a silent, synchronized and “deterministic” period, synchrony starts decreasing and enters a “stochastic” stage of low synchronization. The system does not always go through all these stages, and very short Down states are commonly dominated by the “deterministic” stage, thus the inverse relation between KOP and Down state duration (Fig. 4A–C), while longer Down states spend more time in “stochastic” mode.

Figure 8.

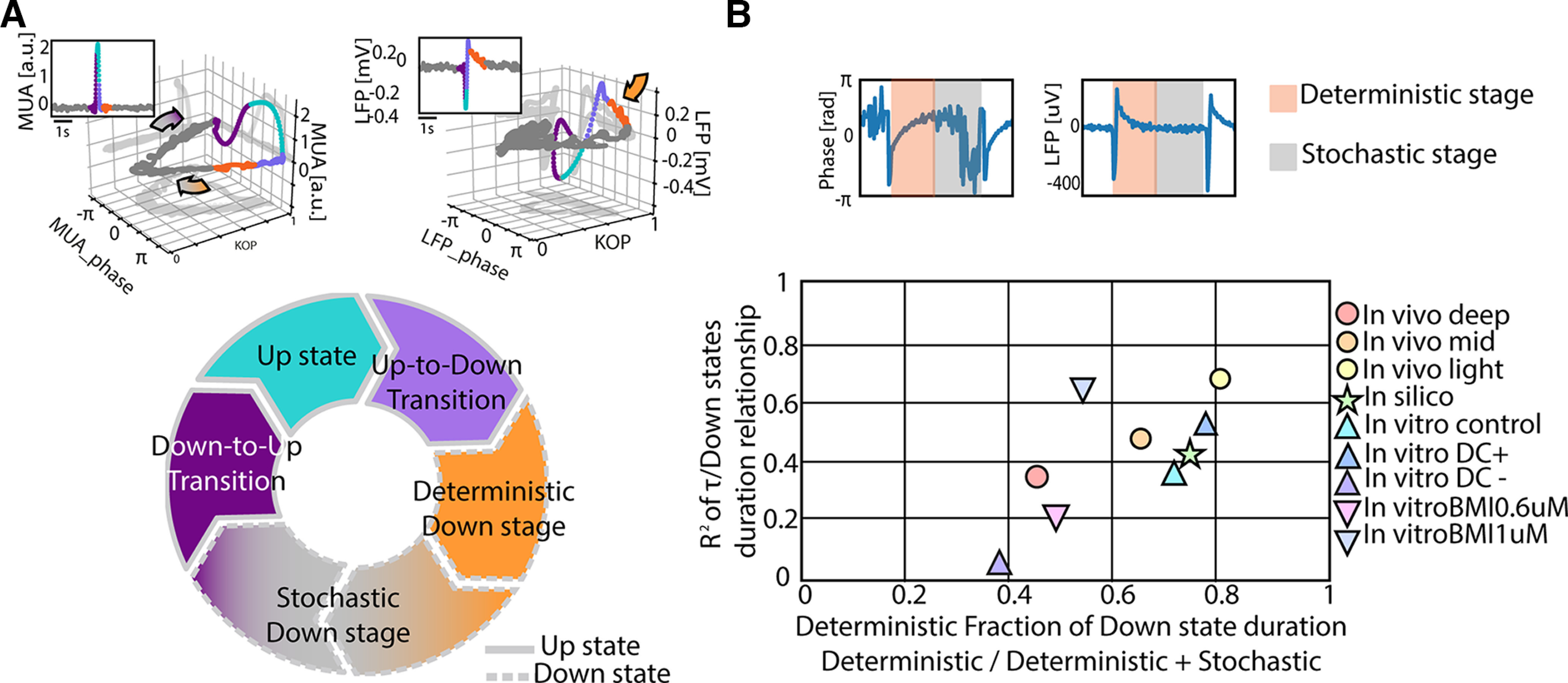
The slow oscillatory cycle mechanisms and its effect on the dynamics of different cortical networks. A, Schematic representation of the periods composing an oscillatory cycle in relation to network synchronization dynamics of multiunit activity (MUA) and local field potential (LFP) activity (upper panels). B, Representation of the state-dependent metastability in different cortical networks in the space defined by the deterministic fraction of the Down states and the correlation between the duration of the entire Down states and the time constant of the “deterministic” period (τ).

Throughout this study, we have used the linear regression of the τ versus Down state duration as a measure of how tightly the duration of the Down states was driven by the time constant of the phase and thus, by the synchronized or “deterministic” period. In order to cover a wide parameter space of slow oscillatory cycles, not only we have used three networks (in vivo, in vitro, and in silico) but also explored experimental manipulations of these cycles. In Figure 8B, we integrate all these results in the same axes, namely the “deterministic” fraction of Down states (“deterministic”/“deterministic + stochastic”) against the regression values displayed along the figures, providing a final picture that depicts the state-dependence of the metastability of Down states and that connects the mechanisms with the network emergent properties.

Discussion

The mechanisms underlying slow oscillations, or the alternation between Up and Down states, have been a matter of debate since the seminal work of Steriade et al. (1993) which characterized this activity pattern. That a relatively simple spontaneous rhythm is so difficult to fully understand is mainly because of self-feedback in recurrent networks and close-loop processes, which led to a causality dilemma. In the case of Up and Down states, the properties of the Up state (e.g., activity pattern, synchrony) determine the subsequent Down state, and vice versa (Sanchez-Vives et al., 2010). This being an emergent pattern from a complex network, where all sort of elements from ionic currents to excitation/inhibition or to synaptic properties have an impact on the resulting rhythm, there has been space for various experimental, computational, and clinical studies investigating this intriguing and prevalent oscillation (for reviews, see Neske, 2016; Sanchez-Vives et al., 2017; Sanchez-Vives, 2020). In order to clarify this picture, here we have focused on the less-studied silent period, the Down state, and found that it has more structure than a simple “absence of activity.”

State-dependent changes of Down states

The synchronization analysis at the level of neuronal pools in the LFP revealed the metastability of the cortical Down states emphasized by the existence of two complementary periods: (1) a highly synchronized period following the Up-to-Down transition that we have called the “deterministic” and ubiquitous state, with a time course that is defined by the exponential decay of the phase, and (2) a desynchronized, not always present, period that we have referred to as “stochastic.”

The identification of these periods and the possibility of inferring local and global features of network dynamics through the analytical approach used here, illustrates the value of the combined recording and analysis of LFPs and spiking activity, which offer insights that cannot be obtained at present by examining spikes alone (Mazzoni et al., 2013).

Interestingly, we reported that different levels of anesthesia resulted in significantly different time constants of synchronization (Fig. 5B), which indeed were nonsignificant in the different experimental conditions in vitro (Fig. 6B,F) and in silico (Fig. 7B). In fact, in models, it is unusual to modify the time constant assuming an invariant relaxation dynamics, and rather regulating the amplitude. However, our findings in vivo suggest that this concept should be revised, and that different mechanisms may be recruited at different levels of anesthesia. In Dasilva et al. (2021), a decreased cortical complexity was reported for deep anesthesia (De Bonis et al., 2020). This decrease is associated with the elongated permanence in the deterministic state, which imposes a break in cortical interactions that has also been described in humans for similarly evoked “off-periods” (Rosanova et al., 2018), even if in that case healthy subjects under anesthesia were not investigated.

A new proposal for an oscillatory cycle

These newly identified periods within Down states give rise to a detailed Up and Down state cycle (Fig. 8A), closely connected to the underlying cellular and network mechanisms, revealing the possibility of inferring microscopic features (i.e., time scales of potassium currents causing adaptation) in network dynamics by studying macroscopic variables such as collective synchronization. Our computational model (Capone et al., 2019) has further proven this extreme, where the adaptation time constant has been used to validate the τ of the population phase during the “deterministic” period (Fig. 4E). Further, the newly proposed stages of the oscillatory cycle can be used to predict the responsiveness of the network in different time windows of the Down states, the period of refractoriness to the generation of a new Up state (Sanchez-Vives and McCormick, 2000; Kroeger and Amzica, 2007), or the probability of inducing a new Up state as a response to an input.

Moreover, this more detailed cycle conciliates existing models of the mechanisms underlying Up and Down states. We propose that there is an inescapable Down state that is the “deterministic” period, which is dependent on the activity on the precedent Up state (Compte et al., 2003; Hill and Tononi, 2005; Mattia and Sanchez-Vives, 2012), probably because of the same mechanism that terminated the Up state: slow hyperpolarizing potassium currents of a different kind (calcium- and sodium-dependent (Compte et al., 2003; Sanchez-Vives et al., 2010), ATP-dependent K⁺ current (Cunningham et al., 2006), or GABA_B receptor-mediated (Mann et al., 2009) are compatible in time course and properties). For example, intracellular recordings have demonstrated that the enhancement of this afterhyperpolarization elongates Down states, while the larger membrane conductance because of channel opening contributes to the refractoriness (Sanchez-Vives et al., 2010). Interestingly, with extracellular recordings, here we have demonstrated that for larger afterhyperpolarizations, the “deterministic” period can also be elongated (Fig. 6E,F,H).

Once this “deterministic” refractory period is terminated, the network can trigger a new Up state if there is enough excitability or inputs to the system. We have shown that this is the case under experimental manipulations such as light anesthesia (Fig. 5A) or positive DC injection in vitro (Fig. 6A) or in silico (Fig. 7A). Under those conditions, the Down state is mostly formed by the “deterministic” period, in association with the higher slow oscillatory frequency. However, under control conditions, or those with artificially decreased excitability (deep anesthesia, or negative DC) the Down state is longer than the “deterministic” period, and the system enters the “stochastic” period. Theoretical models of Up and Down states have proposed the initiation of Up states by the stochastic summation of miniature synaptic potentials (Bazhenov et al., 2002) or by spontaneous firing of layer 5 neurons (Compte et al., 2003), which build up the activity through recurrent connections eventually triggering a new Up state. The new cycle that we propose here (Fig. 8A) can explain the variety of slow oscillatory frequencies (and thus, of Down state durations) that can be expressed by the system, either spontaneously or under experimental manipulations (Sancristóbal et al., 2016; Barbero-Castillo et al., 2019, 2021; Dasilva et al., 2021; Tort-Colet et al., 2021), some of which have been represented with respect to the Down state periods in Figure 8B. Finally, we remark that similar modulations in the statistical properties of the slow oscillations, namely the mean and the coefficient of variation of the Down-Up cycles, display similar modulations in natural sleeping rodents (Levenstein et al., 2019), thus strongly suggesting that the same mechanistic underpinnings are at work in nonrapid eye movement (NREM) sleep as those we have highlighted here in anesthetized animals.

Down states versus “off-periods”

Down states are the periods of silence that, interspersed with Up states or active periods, configure slow oscillations. The terms Up and Down states can refer to the membrane potential, which is Up, or depolarized, versus Down, or hyperpolarized (Sanchez-Vives and McCormick, 2000; Beltramo et al., 2013; Sheroziya and Timofeev, 2014), and are therefore terms related to intracellular recordings. However, since slow oscillations are an emergent network activity, Up and Down states can also refer to the network being Up (for active) or Down (for silent), as detected in LFP, MUA or even by electroencephalographic (EEG) recordings (Buzsáki et al., 2012). Indeed, the terms “active” versus “silent states” have also been used as equivalent to Up and Down states (Chauvette et al., 2012). The terminology used for the periods of slow oscillations has differed across schools, brain recording techniques or fields of interest, and it is relevant to unify this terminology or at least, clarify the different terms and concepts being used. In the field of sleep (often using EEG recordings), the term “off-periods” has been frequently used for the spontaneous periods of silence during slow oscillations (Nir et al., 2011; Vyazovskiy et al., 2011). Therefore, spontaneous “off-periods” are equivalent to Down or silent states. Furthermore, the term “off-period” has also been used for the silent period that follows a response to cortical stimulation or perturbation. “Off-periods” are not always evoked following cortical stimulation, since they are contingent on the state of the network: if the network is in an awake, asynchronous state, it is not going to express “off-periods,” either spontaneous or following stimulation. Thus, “off-periods” following stimulation are evoked not only in slow wave sleep (Pigorini et al., 2015), but also in pathologic conditions such as unresponsive wakefulness syndrome (Rosanova et al., 2018) and even in perilesional regions (Russo et al., 2021). When “off-periods” are evoked following an excitatory stimulation, they break the causal interactions across areas and decrease the complexity of the cortical network, a clinical validated measure of consciousness levels (Casarotto et al., 2016; Comolatti et al., 2019). What “off-periods” are reflecting is a high synchrony of the network, where neurons fire and go into silence synchronously, a state therefore poor for information processing. We speculate that the metastability of the cortical Down states that we have described in the current study, is closely related to the phases observed in evoked “off-periods,” with a “deterministic” stage associated with the peak of hyperpolarization breaking causality (Rosanova et al., 2018) and the “stochastic” one associated with the period of recovery of network interactions and local excitability, highlighting the multiscale implications of Down state metastability (Capone et al., 2019; Dasilva et al., 2021).